Pool Boiling of Ethanol on Copper Surfaces with Rectangular Microchannels
Abstract
:1. Introduction
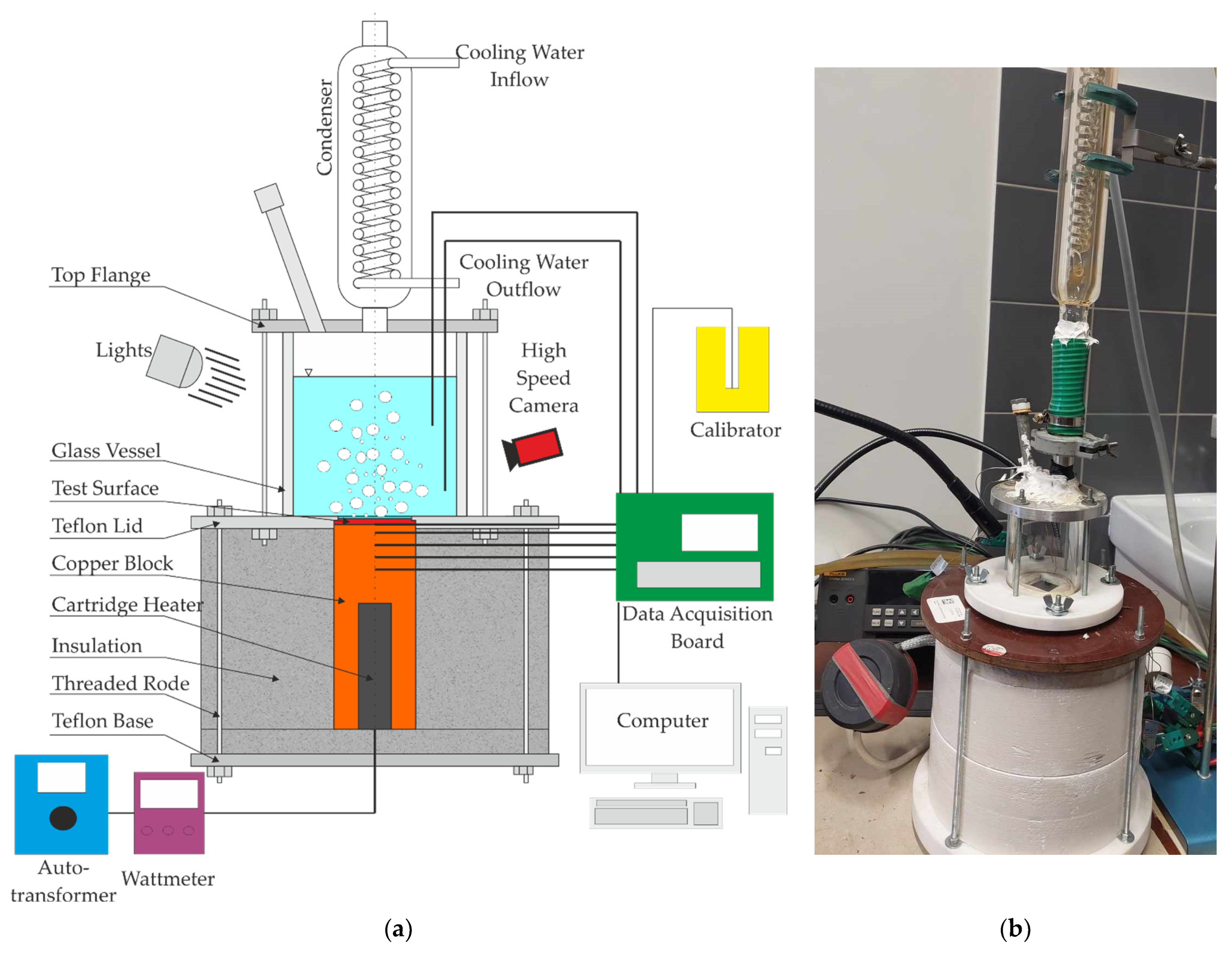
2. Materials and Methods
- starting the cooling section to obtain condensate from the boiling ethanol vapor;
- heating the liquid to saturation temperature (ethanol degassing);
- setting the appropriate electric voltage on the autotransformer (simulating the set value of the heat flux);
- waiting about 15 min until the system reaches thermal equilibrium (temperature indications will not change for the next 5 min);
- recording measurement data (temperature in the heating cylinder, fluid temperature, taking photos of the boiling fluid).
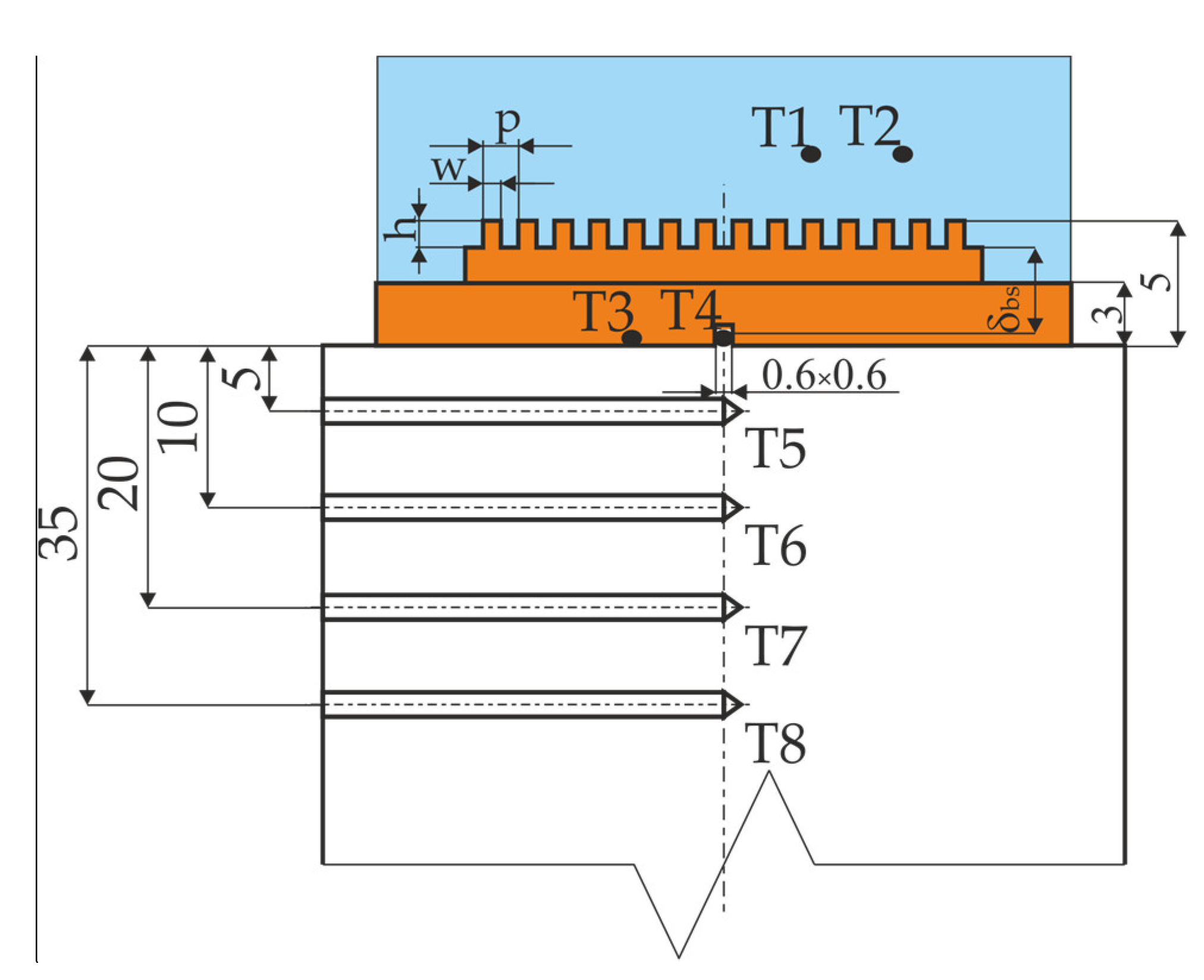
- TT1 to TT4—temperatures measured in the set-up,
- δbs—distance between the center of the thermocouple T4 and the bottom of the microchannel,
- λCu—copper thermal conductivity.
- δT8–T5—distance between thermocouples,
- dcyl—external diameter of the copper cylinder.
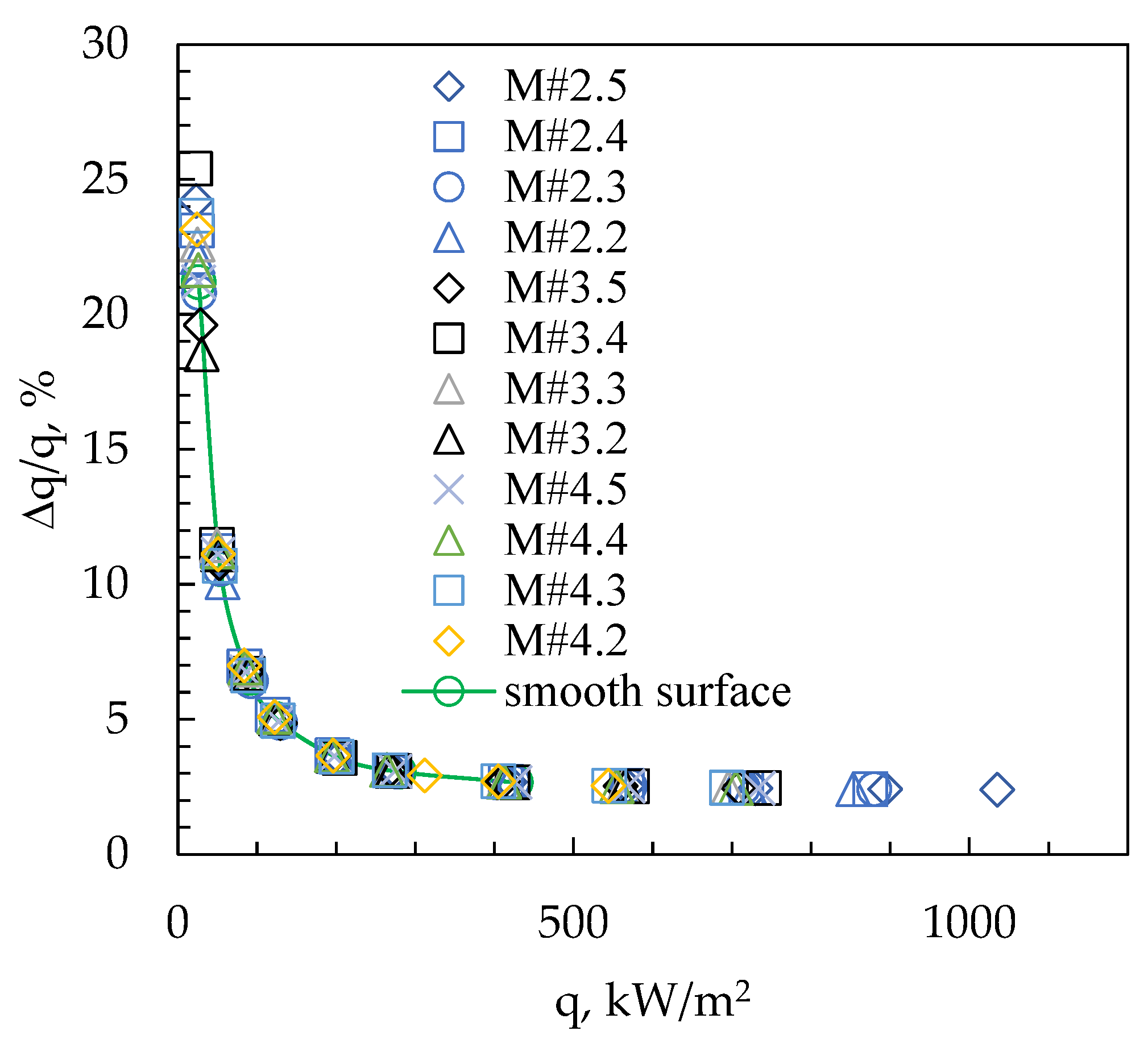
3. Results
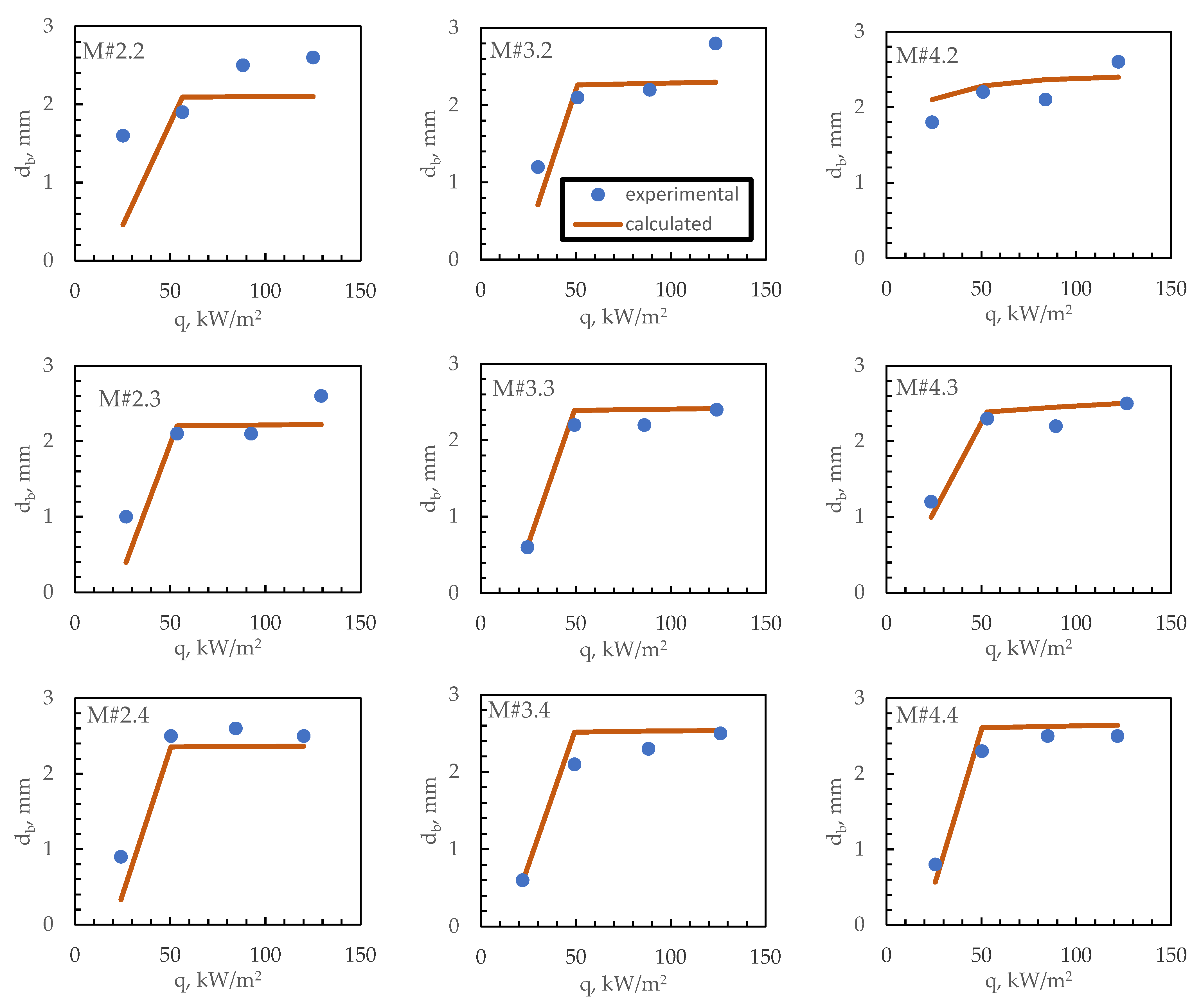
4. Bubble Departure Diameter
4.1. Pressure Difference Force
4.2. Buoyancy Force
4.3. Drag Force
4.4. Surface Tension Force
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | area, m2 |
| a | width of specimen, m |
| Bo | Bond number |
| C | constant |
| cp | specific heat, J/(kgK) |
| CHF | critical heat flux, W/m2 |
| d | diameter, m |
| F | force, N |
| f | frequency, Hz |
| g | gravitational acceleration, m/s2 |
| HTC | heat transfer coefficient, W/(m2K) |
| h | microchannel depth, m |
| i | enthaly, kJ/kg |
| L | length, m |
| q | heat flux, W/m2 |
| p | pitch, m |
| R | radius, m |
| Ra | roughness, μm |
| T | temperature, K |
| t | time, s |
| w | width, m |
| x, y | distance, m |
| Greek letters | |
| α | heat transfer coefficient, W/(m2K) |
| Δ | error, uncertainty |
| ΔT | superheat referred to the microfin base, K |
| δ | thickness, m |
| Θ | contact angle, rad |
| φ | surface extension factor |
| λ | thermal conductivity, W/(mK) |
| ρ | density, kg/m3 |
| μ | dynamic viscosity, Pas |
| σ | surface tension, N/m |
| Subscripts | |
| b | departing bubble |
| bs | base |
| bt | bottom |
| bu | buoyancy |
| Cu | copper |
| c | contact line |
| cap | capillary |
| cyl | cylinder |
| d | drag |
| ext | extended |
| h | hydraulic |
| g | growing |
| l | liquid |
| MC | microchannel |
| p | pressure difference |
| Sn | tin |
| sat | saturated |
| st | surface tension |
| t | top |
| T1,…,T8 | thermocouple number |
| v | vapor |
| w | wall |
References
- Liang, G.; Mudawar, I. Pool Boiling Critical Heat Flux (CHF)—Part 1: Review of Mechanisms, Models, and Correlations. Int. J. Heat Mass Transf. 2018, 117, 1352–1367. [Google Scholar] [CrossRef]
- Liang, G.; Mudawar, I. Review of Nanoscale Boiling Enhancement Techniques and Proposed Systematic Testing Strategy to Ensure Cooling Reliability and Repeatability. Appl. Therm. Eng. 2021, 184, 115982. [Google Scholar] [CrossRef]
- Kim, J.; Jun, S.; Laksnarain, R.; You, S.M. Effect of Surface Roughness on Pool Boiling Heat Transfer at a Heated Surface Having Moderate Wettability. Int. J. Heat Mass Transf. 2016, 101, 992–1002. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, C.; Wang, J.; Zhang, L. Critical Heat Flux Enhancement Using Composite Porous Structure Produced by Selective Laser Melting. Appl. Therm. Eng. 2021, 197, 117396. [Google Scholar] [CrossRef]
- Chatys, R.; Orman, Ł.J. Technology and Properties of Layered Composites as Coatings for Heat Transfer Enhancement. Mech. Compos. Mater. 2017, 53, 351–360. [Google Scholar] [CrossRef]
- Chatys, R. Aspects of Complexity of Metal-Fibrous Microstructure for the Construction of High-Performance Heat Exchangers: Estimation of Adhesive Strength. Aviation 2020, 24, 117–122. [Google Scholar] [CrossRef]
- Zupančič, M.; Fontanarosa, D.; Može, M.; Bucci, M.; Vodopivec, M.; Nagarajan, B.; Rosaria Vetrano, M.; Castagne, S.; Golobič, I. Enhanced Nucleate Boiling of Novec 649 on Thin Metal Foils via Laser-Induced Periodic Surface Structures. Appl. Therm. Eng. 2023, 236, 121803. [Google Scholar] [CrossRef]
- Manetti, L.L.; Moita, A.S.O.H.; Cardoso, E.M. A New Pool Boiling Heat Transfer Correlation for Wetting Dielectric Fluids on Metal Foams. Int. J. Heat Mass Transf. 2021, 171, 121070. [Google Scholar] [CrossRef]
- Shi, J.; Jia, X.; Feng, D.; Chen, Z.; Dang, C. Wettability Effect on Pool Boiling Heat Transfer Using a Multiscale Copper Foam Surface. Int. J. Heat Mass Transf. 2020, 146, 118726. [Google Scholar] [CrossRef]
- Tang, H.; Xia, L.; Tang, Y.; Weng, C.; Hu, Z.; Wu, X.; Sun, Y. Fabrication and Pool Boiling Performance Assessment of Microgroove Array Surfaces with Secondary Micro-Structures for High Power Applications. Renew. Energy 2022, 187, 790–800. [Google Scholar] [CrossRef]
- Pastuszko, R. Pool Boiling Heat Transfer on Micro-Fins with Wire Mesh—Experiments and Heat Flux Prediction. Int. J. Therm. Sci. 2018, 125, 197–209. [Google Scholar] [CrossRef]
- Chen, G.; Jia, M.; Zhang, S.; Tang, Y.; Wan, Z. Pool Boiling Enhancement of Novel Interconnected Microchannels with Reentrant Cavities for High-Power Electronics Cooling. Int. J. Heat Mass Transf. 2020, 156, 119836. [Google Scholar] [CrossRef]
- Kaniowski, R.; Pastuszko, R. Pool Boiling Experiment with Novec-649 in Microchannels for Heat Flux Prediction. Exp. Therm. Fluid Sci. 2023, 141, 110802. [Google Scholar] [CrossRef]
- Shen, B.; Hamazaki, T.; Ma, W.; Iwata, N.; Hidaka, S.; Takahara, A.; Takahashi, K.; Takata, Y. Enhanced Pool Boiling of Ethanol on Wettability-Patterned Surfaces. Appl. Therm. Eng. 2019, 149, 325–331. [Google Scholar] [CrossRef]
- Kalani, A.; Kandlikar, S.G. Enhanced Pool Boiling with Ethanol at Subatmospheric Pressures for Electronics Cooling. J. Heat Transf. 2013, 135, 111002. [Google Scholar] [CrossRef]
- Deng, D.; Feng, J.; Huang, Q.; Tang, Y.; Lian, Y. Pool Boiling Heat Transfer of Porous Structures with Reentrant Cavities. Int. J. Heat Mass Transf. 2016, 99, 556–568. [Google Scholar] [CrossRef]
- Deng, D.; Wan, W.; Feng, J.; Huang, Q.; Qin, Y.; Xie, Y. Comparative Experimental Study on Pool Boiling Performance of Porous Coating and Solid Structures with Reentrant Channels. Appl. Therm. Eng. 2016, 107, 420–430. [Google Scholar] [CrossRef]
- Hao, W.; Wang, T.; Jiang, Y.; Guo, C.; Guo, C. Pool Boiling Heat Transfer on Deformable Structures Made of Shape-Memory-Alloys. Int. J. Heat Mass Transf. 2017, 112, 236–247. [Google Scholar] [CrossRef]
- Vasauskas, V.; Baskutis, S. Failures and Fouling Analysis in Heat Exchangers. Mechanics 2006, 61, 24–31. [Google Scholar]
- Baskutis, S.; Vasauskas, V. Mechanics and Material Aspects in Serviceability Prediction of the Heat Exchangers. Mechanics 2011, 17, 239–245. [Google Scholar] [CrossRef]
- Kurp, P. Ideas and Assumptions of a New Kind Helical Metal Expansion Joints. In Proceedings of the Terotechnology XII, 12th International Conference on Terotechnology, Kielce, Poland, 20–21 October 2021; pp. 233–239. [Google Scholar]
- Kurp, P.; Danielewski, H.; Szwed, B.; Borkowski, K.; Zrak, A.; Gaponova, O.P. Discussion about Metal Expansion Joints Manufacturing Technology of Preventing Thermal Deformation Pipelines Intended for the Fluids Transport. Komunikácie 2023, 25, B110–B117. [Google Scholar] [CrossRef]
- Piasecka, M.; Strąk, K.; Maciejewska, B. Heat Transfer Characteristics during Flow along Horizontal and Vertical Minichannels. Int. J. Multiph. Flow 2021, 137, 103559. [Google Scholar] [CrossRef]
- Piasecka, M.; Strąk, K. Boiling Heat Transfer during Flow in Vertical Mini-Channels with a Modified Heated Surface. Energies 2022, 15, 7050. [Google Scholar] [CrossRef]
- Kowalczyk, J.; Madej, M.; Dzięgielewski, W.; Kulczycki, A.; Żółty, M.; Ozimina, D. Tribochemical Interactions between Graphene and ZDDP in Friction Tests for Uncoated and W-DLC-Coated HS6-5-2C Steel. Materials 2021, 14, 3529. [Google Scholar] [CrossRef] [PubMed]
- Skrzyniarz, M.; Nowakowski, L.; Miko, E.; Borkowski, K. Influence of Relative Displacement on Surface Roughness in Longitudinal Turning of X37CrMoV5-1 Steel. Materials 2021, 14, 1317. [Google Scholar] [CrossRef]
- Kim, J.; Oh, B.D.; Kim, M.H. Experimental Study of Pool Temperature Effects on Nucleate Pool Boiling. Int. J. Multiph. Flow 2006, 32, 208–231. [Google Scholar] [CrossRef]
- Hożejowska, S.; Kaniowski, R.; Pastuszko, R. Application of the Trefftz Method for Pool Boiling Heat Transfer on Open Microchannel Surfaces. Heat Transf. Eng. 2021, 43, 362–370. [Google Scholar] [CrossRef]
- Jaikumar, A.; Kandlikar, S.G. Enhanced Pool Boiling Heat Transfer Mechanisms for Selectively Sintered Open Microchannels. Int. J. Heat Mass Transf. 2015, 88, 652–661. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, J.; Zhou, W.; Qi, B.; Wei, J. CHF Correlation of Boiling in FC-72 with Micro-Pin-Fins for Electronics Cooling. Appl. Therm. Eng. 2018, 138, 494–500. [Google Scholar] [CrossRef]
- Jaikumar, A.; Kandlikar, S.G. Ultra-High Pool Boiling Performance and Effect of Channel Width with Selectively Coated Open Microchannels. Int. J. Heat Mass Transf. 2016, 95, 795–805. [Google Scholar] [CrossRef]
- Kim, S.H.; Lee, G.C.; Kang, J.Y.; Moriyama, K.; Kim, M.H.; Park, H.S. Boiling Heat Transfer and Critical Heat Flux Evaluation of the Pool Boiling on Micro Structured Surface. Int. J. Heat Mass Transf. 2015, 91, 1140–1147. [Google Scholar] [CrossRef]
- Gheitaghy, A.M.; Samimi, A.; Saffari, H. Surface Structuring with Inclined Minichannels for Pool Boiling Improvement. Appl. Therm. Eng. 2017, 126, 892–902. [Google Scholar] [CrossRef]
- Surtaev, A.; Serdyukov, V.; Zhou, J.; Pavlenko, A.; Tumanov, V. An Experimental Study of Vapor Bubbles Dynamics at Water and Ethanol Pool Boiling at Low and High Heat Fluxes. Int. J. Heat Mass Transf. 2018, 126, 297–311. [Google Scholar] [CrossRef]
- Nikulin, A.; Grosu, Y.; Dauvergne, J.-L.; Ortuondo, A.; del Barrio, E.P. Physical Dealloying for Two-Phase Heat Transfer Applications: Pool Boiling Case. Int. Commun. Heat Mass Transf. 2023, 146, 106913. [Google Scholar] [CrossRef]
- Beer, H. Das dynamische Blasenwachstum beim Sieden von Flüssigkeiten an Heizflächen. Forschung. Im Ingenieurwesen 1971, 37, 85–90. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Z.; Wei, J.; Sundén, B. Correlations for Prediction of the Bubble Departure Radius on Smooth Flat Surface during Nucleate Pool Boiling. Int. J. Heat Mass Transf. 2019, 132, 699–714. [Google Scholar] [CrossRef]
- Kumar, N.; Ghosh, P.; Shukla, P. Development of an Approximate Model for the Prediction of Bubble Departure Diameter in Pool Boiling of Water. Int. Commun. Heat Mass Transf. 2021, 127, 105531. [Google Scholar] [CrossRef]
- Zeng, L.Z.; Klausner, J.F.; Mei, R. A Unified Model for the Prediction of Bubble Detachment Diameters in Boiling Systems—I. Pool Boiling. Int. J. Heat Mass Transf. 1993, 36, 2261–2270. [Google Scholar] [CrossRef]
- Bucci, M.; Buongiorno, J.; Bucci, M. The Not-so-Subtle Flaws of the Force Balance Approach to Predict the Departure of Bubbles in Boiling Heat Transfer. Phys. Fluids 2021, 33, 017110. [Google Scholar] [CrossRef]
- Iyer, S.; Kumar, A.; Coventry, J.; Lipiński, W. Modelling of Bubble Growth and Detachment in Nucleate Pool Boiling. Int. J. Therm. Sci. 2023, 185, 108041. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, Y.; Wei, J. A Modified Bubble Dynamics Model for Predicting Bubble Departure Diameter on Micro-Pin-Finned Surfaces under Microgravity. Appl. Therm. Eng. 2018, 132, 450–462. [Google Scholar] [CrossRef]
- Kong, X.; Zhang, Y.; Wei, J. Experimental Study of Pool Boiling Heat Transfer on Novel Bistructured Surfaces Based on Micro-Pin-Finned Structure. Exp. Therm. Fluid Sci. 2018, 91, 9–19. [Google Scholar] [CrossRef]
- Zhao, Z.; Ma, X.; Li, S.; Yang, S.; Huang, L. Visualization-Based Nucleate Pool Boiling Heat Transfer Enhancement on Different Sizes of Square Micropillar Array Surfaces. Exp. Therm. Fluid Sci. 2020, 119, 110212. [Google Scholar] [CrossRef]
- Ramaswamy, C.; Joshi, Y.; Nakayama, W.; Johnson, W.B. Semi-Analytical Model for Boiling from Enhanced Structures. Int. J. Heat Mass Transf. 2003, 46, 4257–4269. [Google Scholar] [CrossRef]
- Murthy, S.; Joshi, Y.; Gurrum, S.; Nakayama, W. Enhanced Boiling Heat Transfer Simulation from Structured Surfaces: Semi-Analytical Model. Int. J. Heat Mass Transf. 2006, 49, 1885–1895. [Google Scholar] [CrossRef]
- Chien, L.-H.; Webb, R.L. A Nucleate Boiling Model for Structured Enhanced Surfaces. Int. J. Heat Mass Transf. 1998, 41, 2183–2195. [Google Scholar] [CrossRef]
- Walunj, A.; Sathyabhama, A. Comparative Study of Pool Boiling Heat Transfer from Various Microchannel Geometries. Appl. Therm. Eng. 2018, 128, 672–683. [Google Scholar] [CrossRef]
- Pastuszko, R.; Kaniowski, R.; Dadas, N.; Bedla-Pawlusek, M. Pool Boiling Enhancement and a Method of Bubble Diameter Determination on Surfaces with Deep Minichannels. Int. J. Heat Mass Transf. 2021, 179, 121713. [Google Scholar] [CrossRef]
- Mikic, B.B.; Rohsenow, W.M.; Griffith, P. On Bubble Growth Rates. Int. J. Heat Mass Transf. 1970, 13, 657–666. [Google Scholar] [CrossRef]
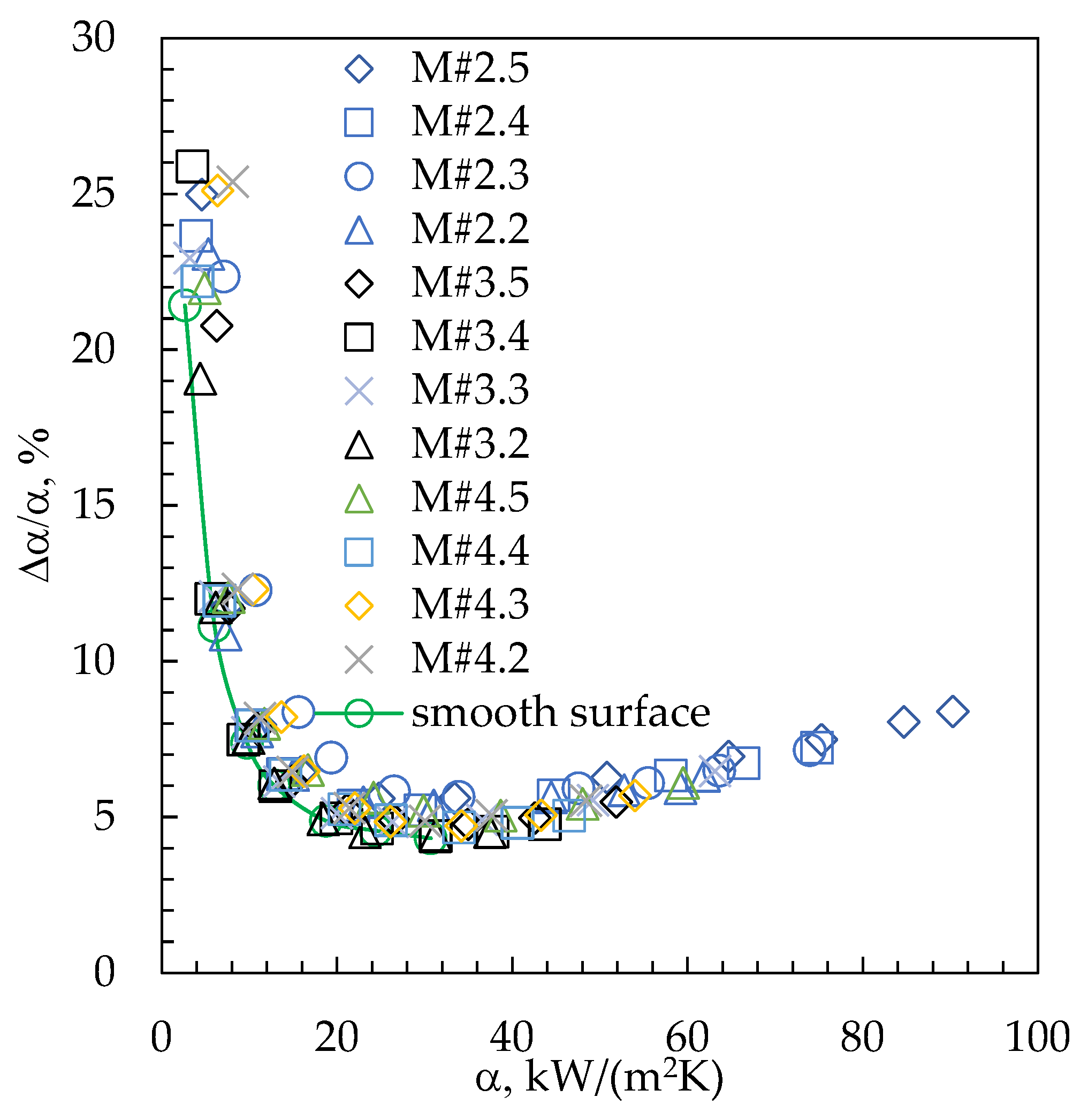
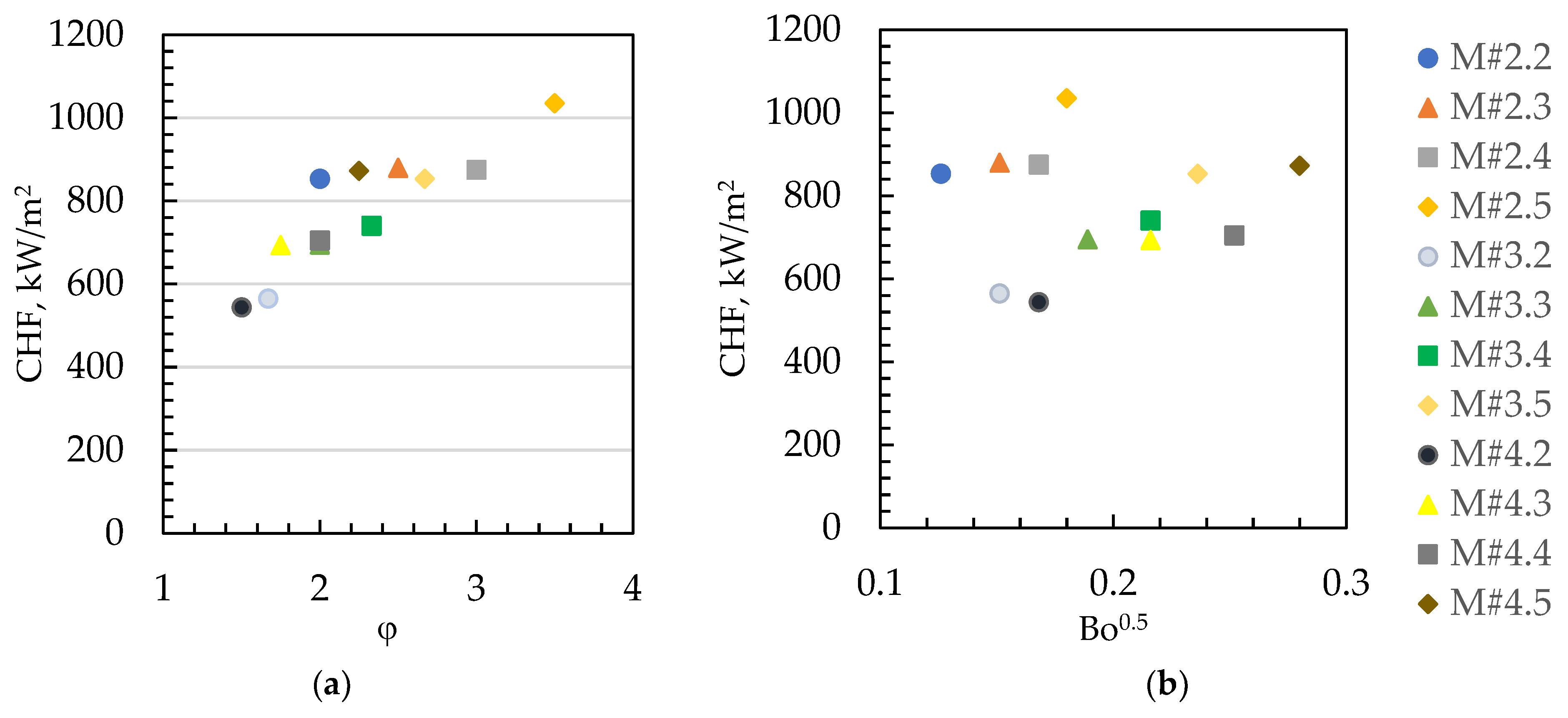
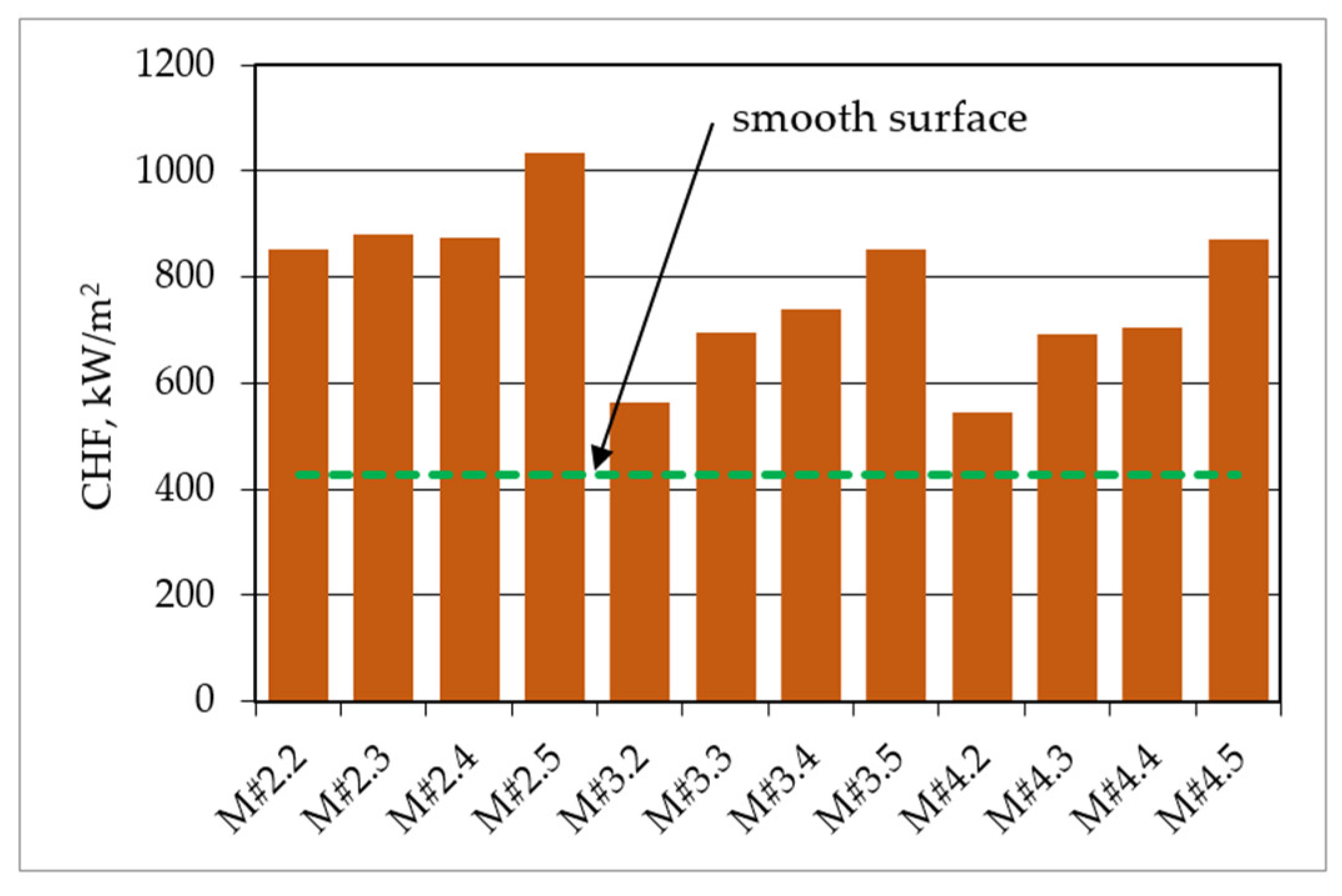
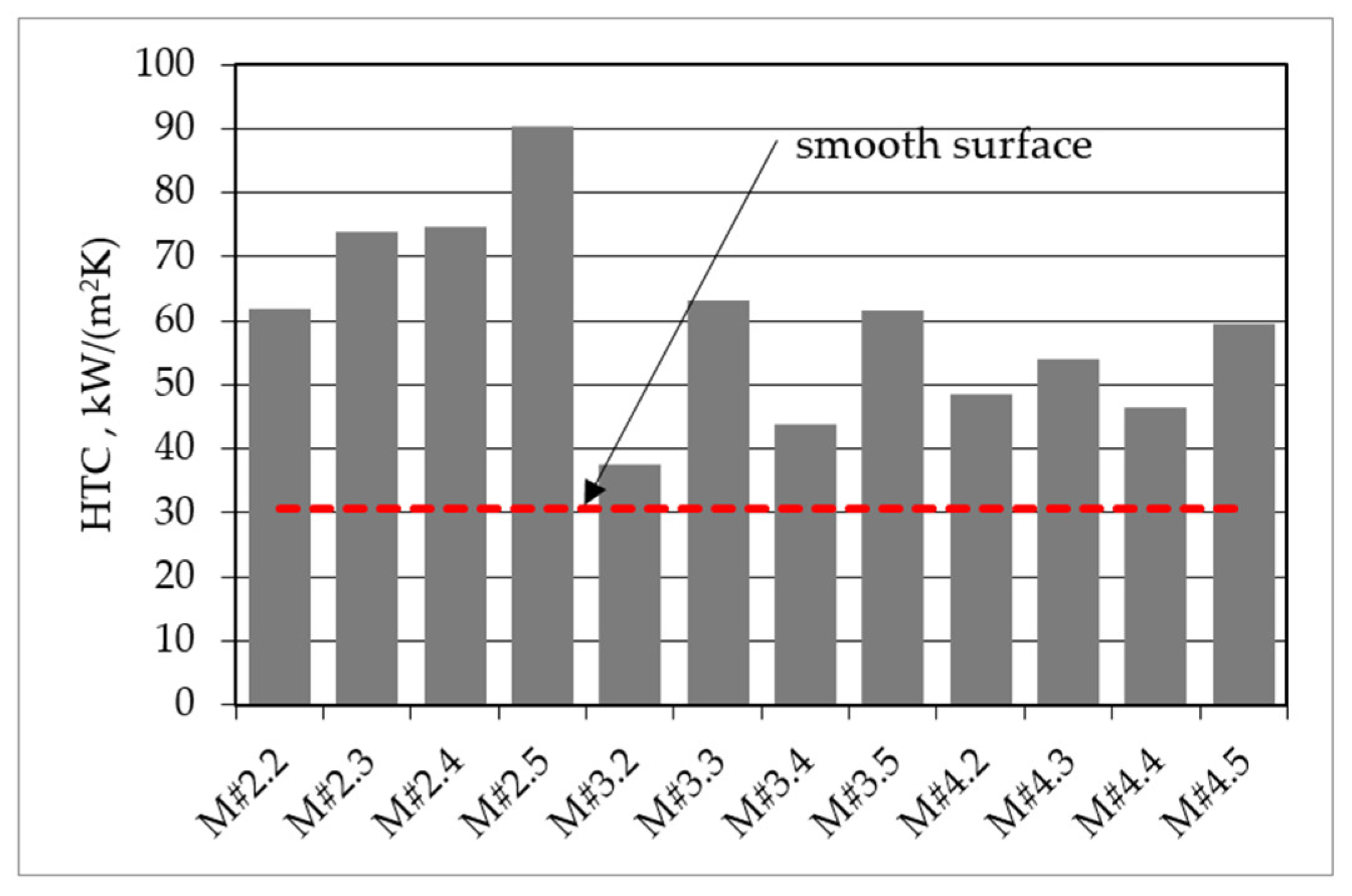

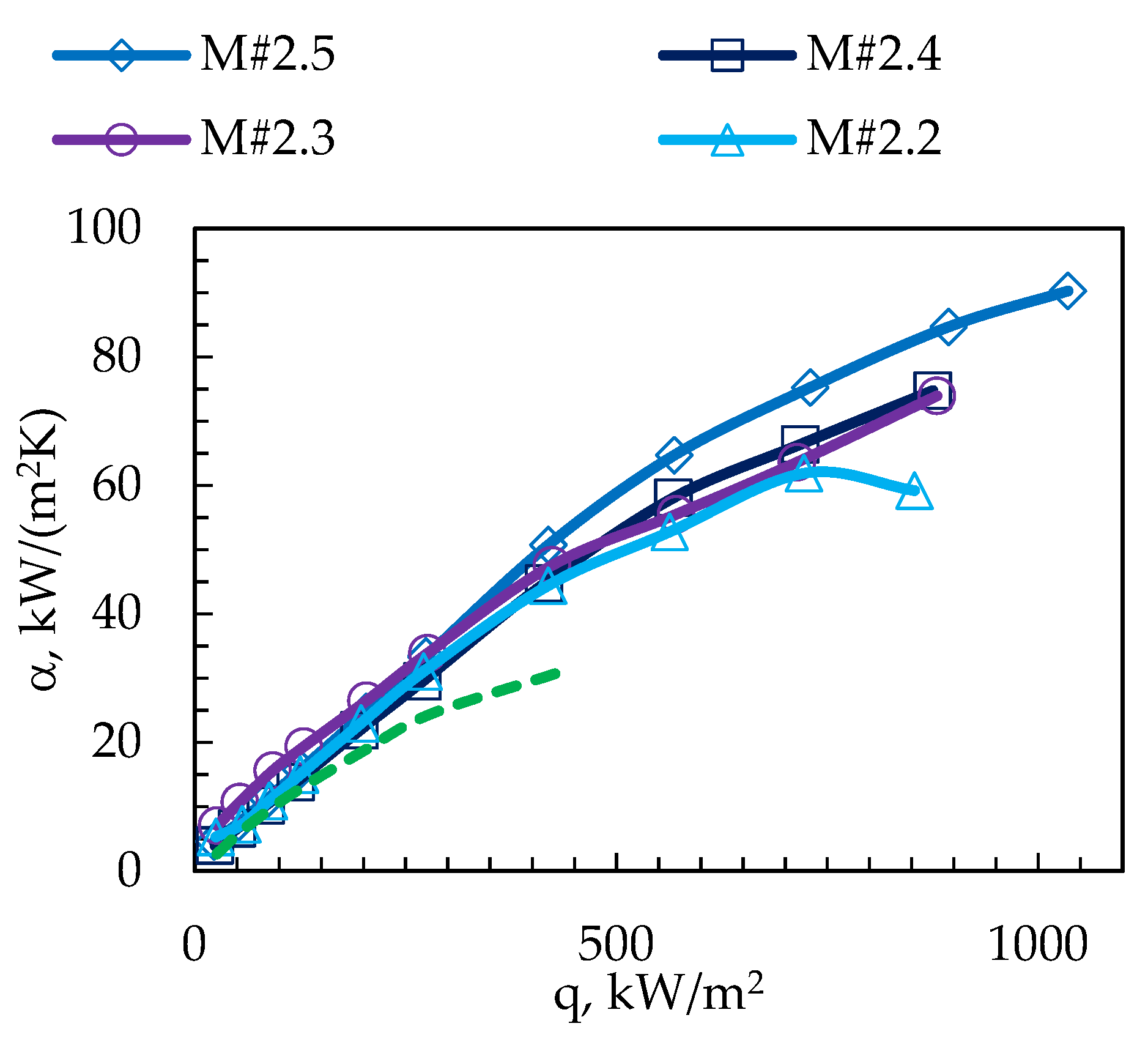

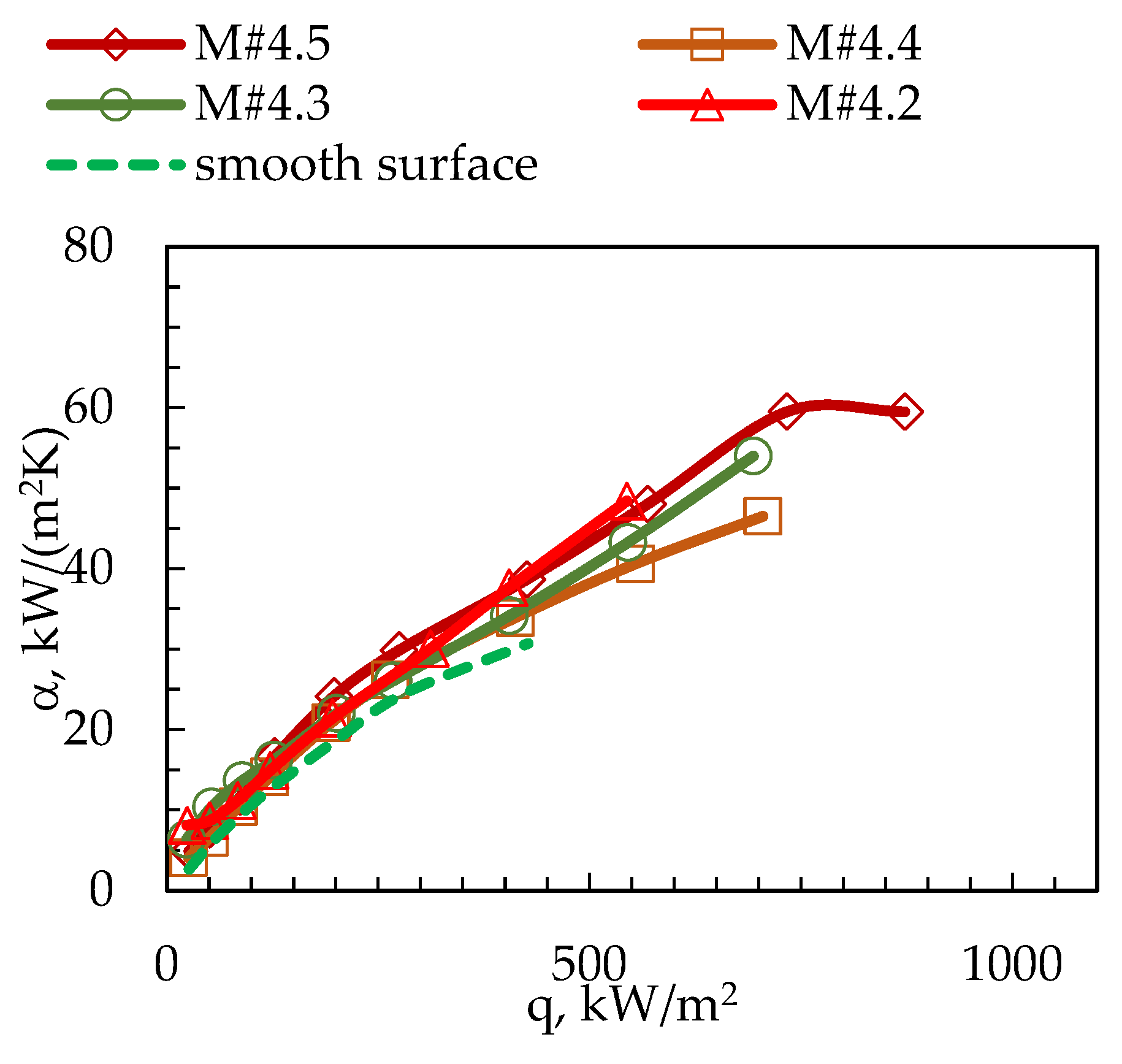
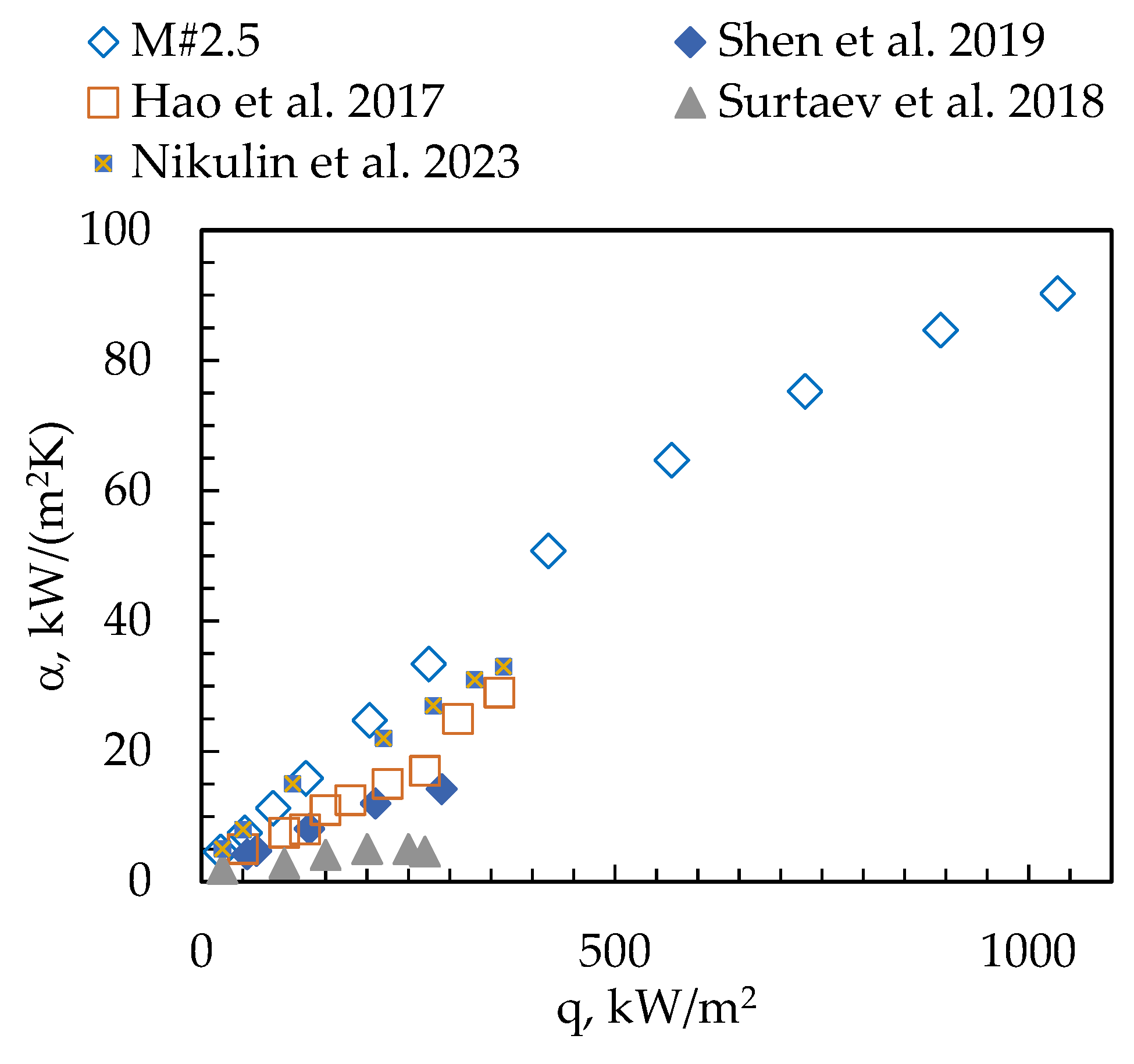
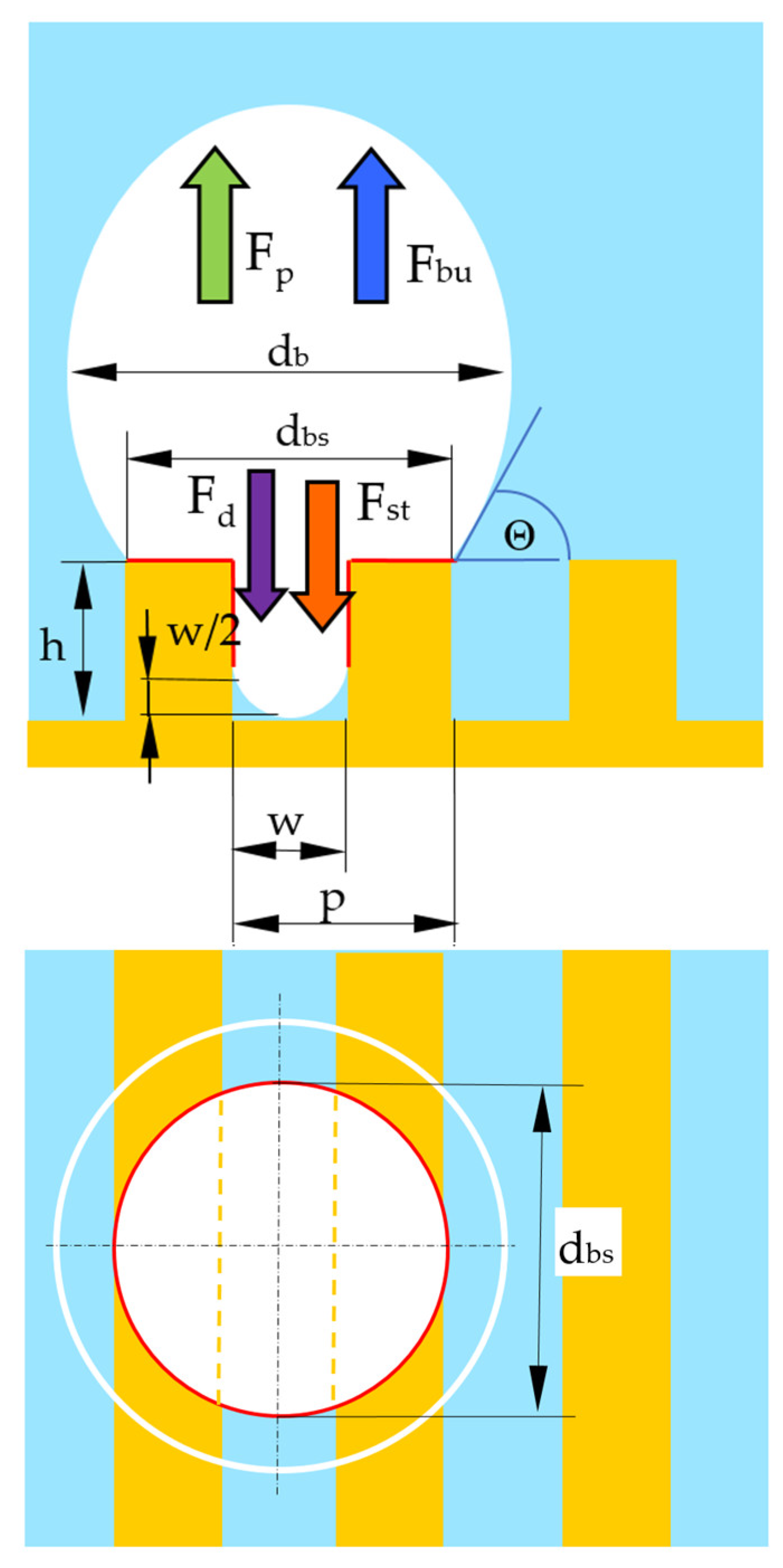

| Parameters at 1013.25 hPa | Ethanol |
|---|---|
| Tsat, °C | 78.3 |
| ρl, kg/m3 | 717 |
| ρv, kg/m3 | 1.43 |
| λl, W/(mK) | 0.17 |
| ilv, kJ/kg | 963 |
| σl, N/m | 0.0177 |
| μl, Pas | 0.00044 |
| cpl, J/(kgK) | 723 |
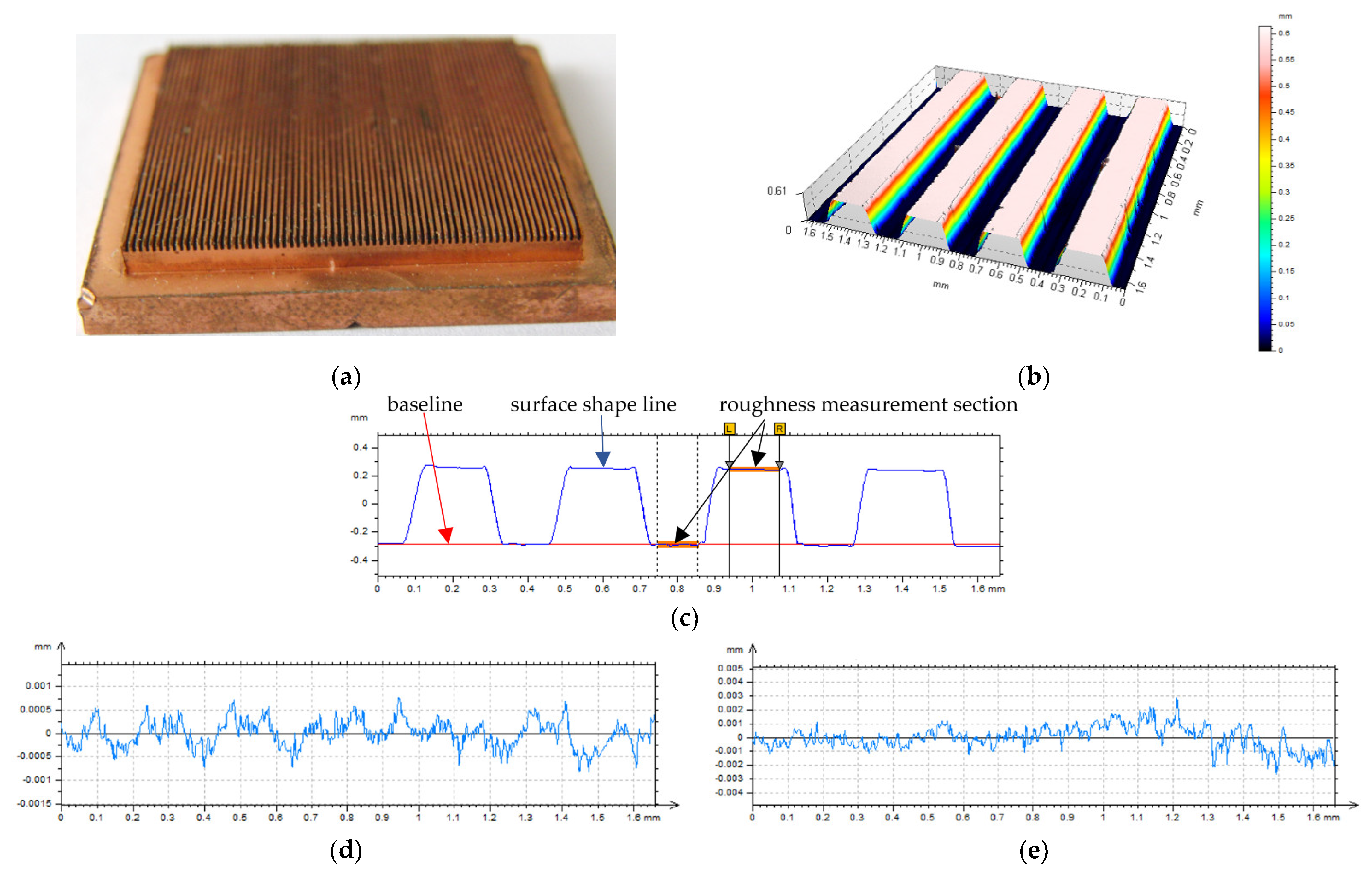
| Surface Code | p, mm | w, mm | h, mm | φ | dh, mm | Bo | Bo0.5 | Rat, µm | Rabt, µm |
|---|---|---|---|---|---|---|---|---|---|
| M#2.2 | 0.4 | 0.2 | 0.2 | 2.00 | 0.200 | 0.016 | 0.126 | 0.30 | 0.30 |
| M#2.3 | 0.4 | 0.2 | 0.3 | 2.50 | 0.240 | 0.023 | 0.151 | 0.30 | 0.40 |
| M#2.4 | 0.4 | 0.2 | 0.4 | 3.00 | 0.267 | 0.028 | 0.168 | 0.14 | 0.25 |
| M#2.5 | 0.4 | 0.2 | 0.5 | 3.50 | 0.286 | 0.032 | 0.180 | 0.24 | 0.30 |
| M#3.2 | 0.6 | 0.3 | 0.2 | 1.67 | 0.240 | 0.023 | 0.151 | 0.18 | 0.12 |
| M#3.3 | 0.6 | 0.3 | 0.3 | 2.00 | 0.300 | 0.036 | 0.189 | 0.20 | 0.12 |
| M#3.4 | 0.6 | 0.3 | 0.4 | 2.33 | 0.343 | 0.047 | 0.216 | 0.18 | 0.18 |
| M#3.5 | 0.6 | 0.3 | 0.5 | 2.67 | 0.375 | 0.056 | 0.236 | 0.14 | 0.25 |
| M#4.2 | 0.8 | 0.4 | 0.2 | 1.50 | 0.267 | 0.028 | 0.168 | 0.22 | 0.12 |
| M#4.3 | 0.8 | 0.4 | 0.3 | 1.75 | 0.343 | 0.047 | 0.216 | 0.25 | 0.15 |
| M#4.4 | 0.8 | 0.4 | 0.4 | 2.00 | 0.400 | 0.063 | 0.252 | 0.31 | 0.14 |
| M#4.5 | 0.8 | 0.4 | 0.5 | 2.25 | 0.444 | 0.078 | 0.280 | 0.25 | 0.12 |
| Parameter | Tools | Uncertainty |
|---|---|---|
| Temperature, K | K-type thermocouple calibrated | ±0.1 |
| The temperature difference in the Heating cylinder, K | K-type thermocouple calibrated | ±0.2 |
| Wall superheat, K | K-type thermocouple calibrated | ±0.2 |
| Geometric quantities, m | Calipers for precision | 0.00025 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaniowski, R.; Pastuszko, R.; Dragašius, E.; Baskutis, S. Pool Boiling of Ethanol on Copper Surfaces with Rectangular Microchannels. Energies 2023, 16, 7883. https://doi.org/10.3390/en16237883
Kaniowski R, Pastuszko R, Dragašius E, Baskutis S. Pool Boiling of Ethanol on Copper Surfaces with Rectangular Microchannels. Energies. 2023; 16(23):7883. https://doi.org/10.3390/en16237883
Chicago/Turabian StyleKaniowski, Robert, Robert Pastuszko, Egidijus Dragašius, and Saulius Baskutis. 2023. "Pool Boiling of Ethanol on Copper Surfaces with Rectangular Microchannels" Energies 16, no. 23: 7883. https://doi.org/10.3390/en16237883
APA StyleKaniowski, R., Pastuszko, R., Dragašius, E., & Baskutis, S. (2023). Pool Boiling of Ethanol on Copper Surfaces with Rectangular Microchannels. Energies, 16(23), 7883. https://doi.org/10.3390/en16237883








