A Fast Reconfiguration Technique for Boost-Based DMPPT PV Systems Based on Deterministic Clustering Analysis
Abstract
:1. Introduction
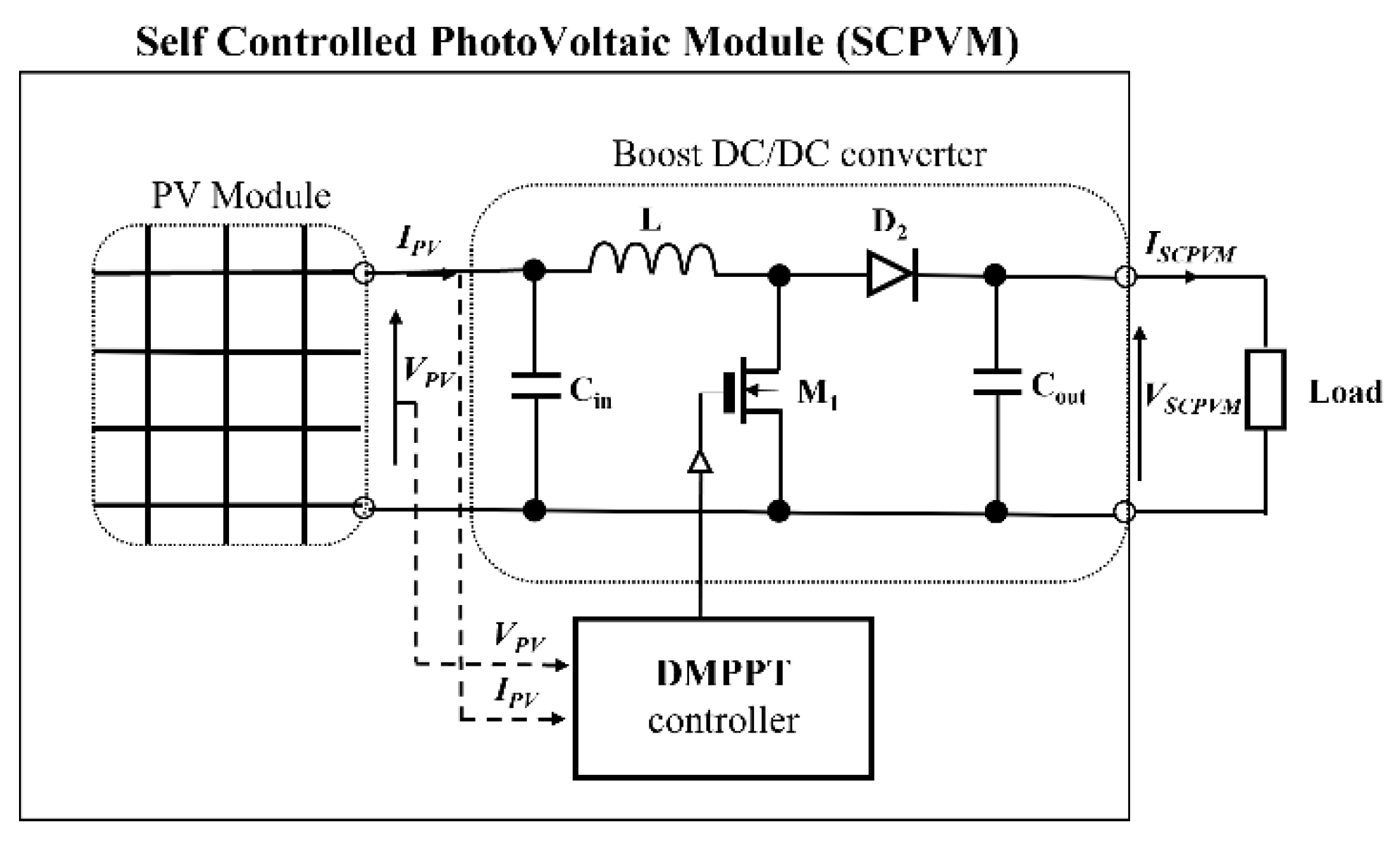
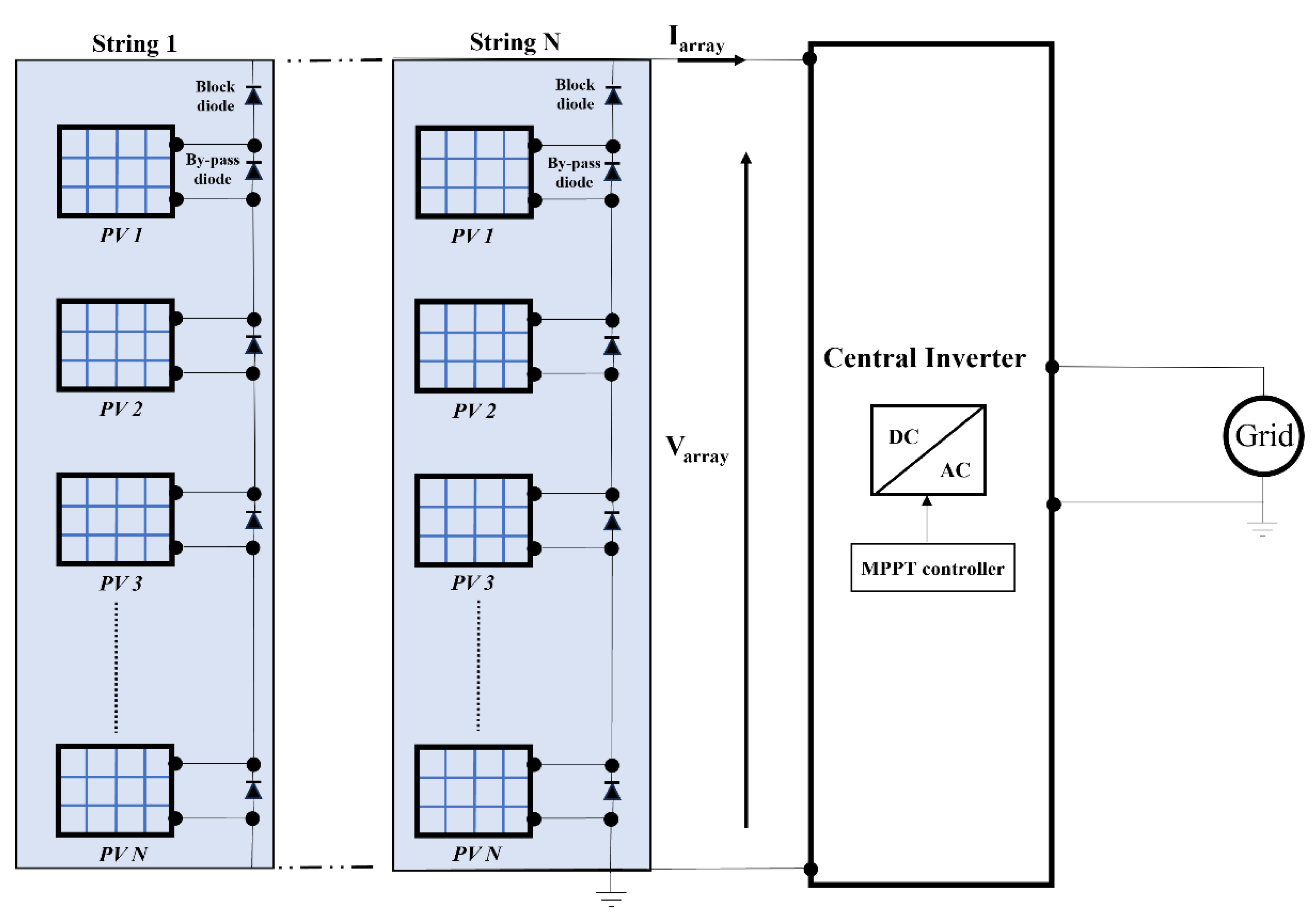
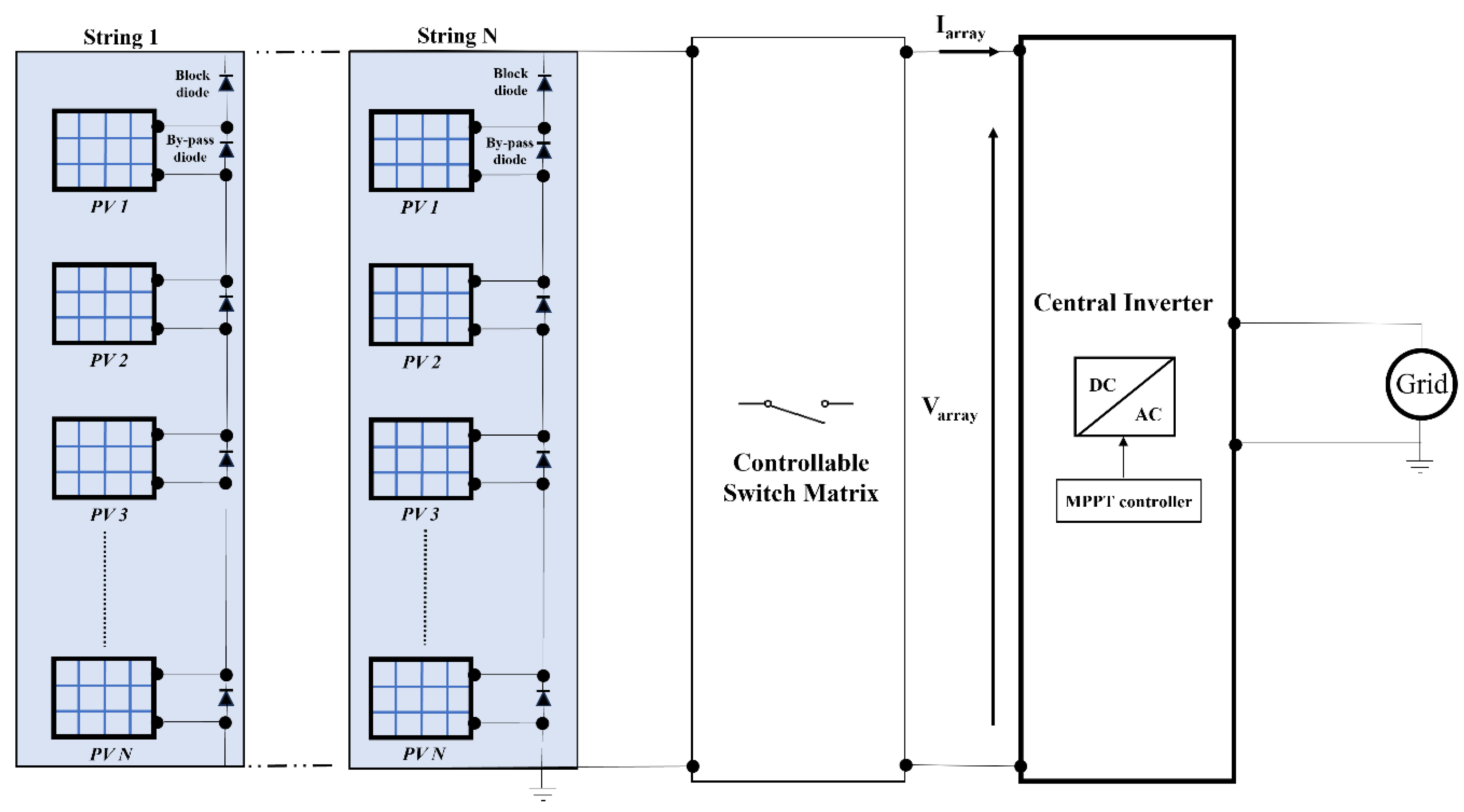
2. The Necessity of the Joint Adoption of Boost-Based DMPPT and Reconfiguration Approaches
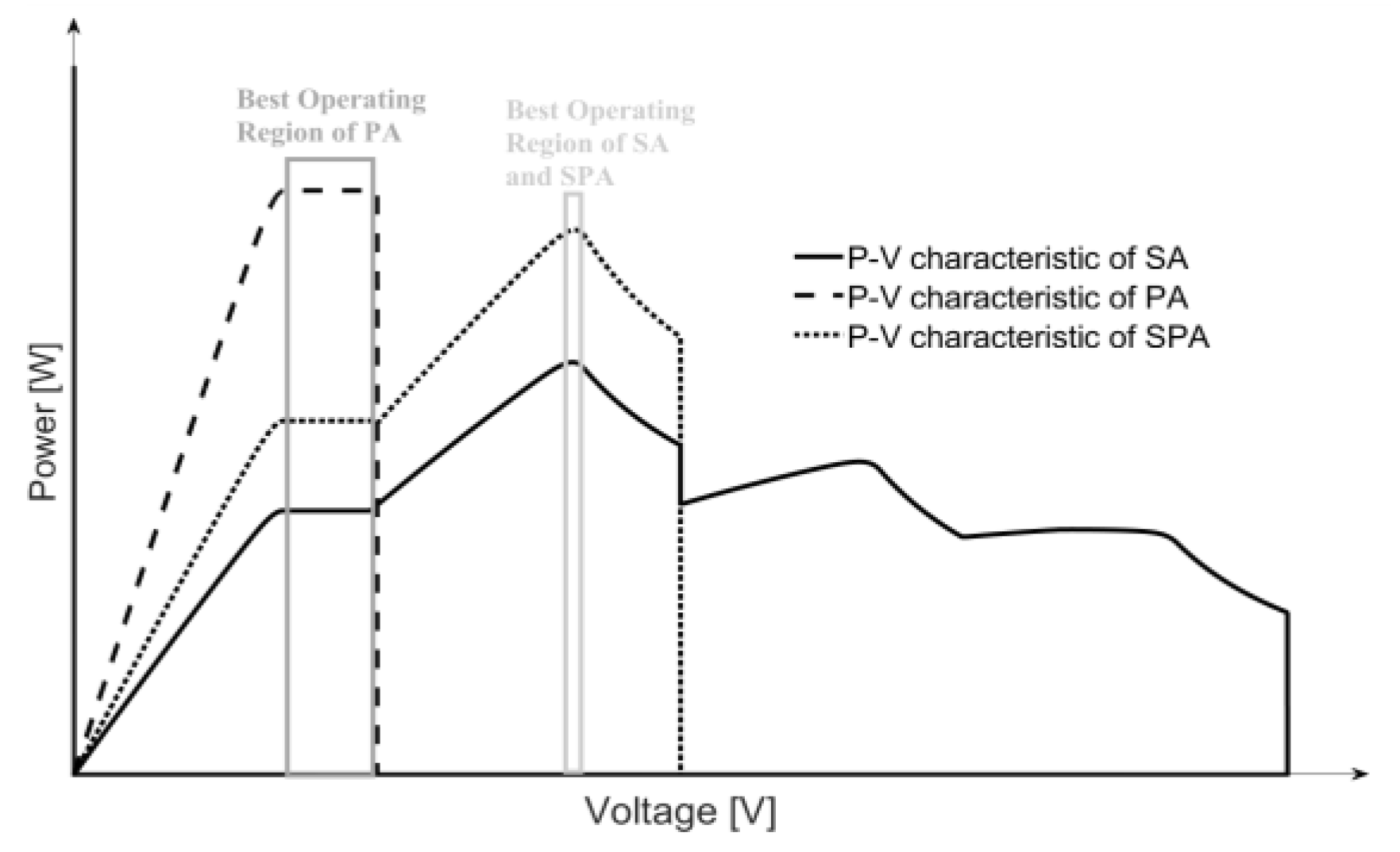
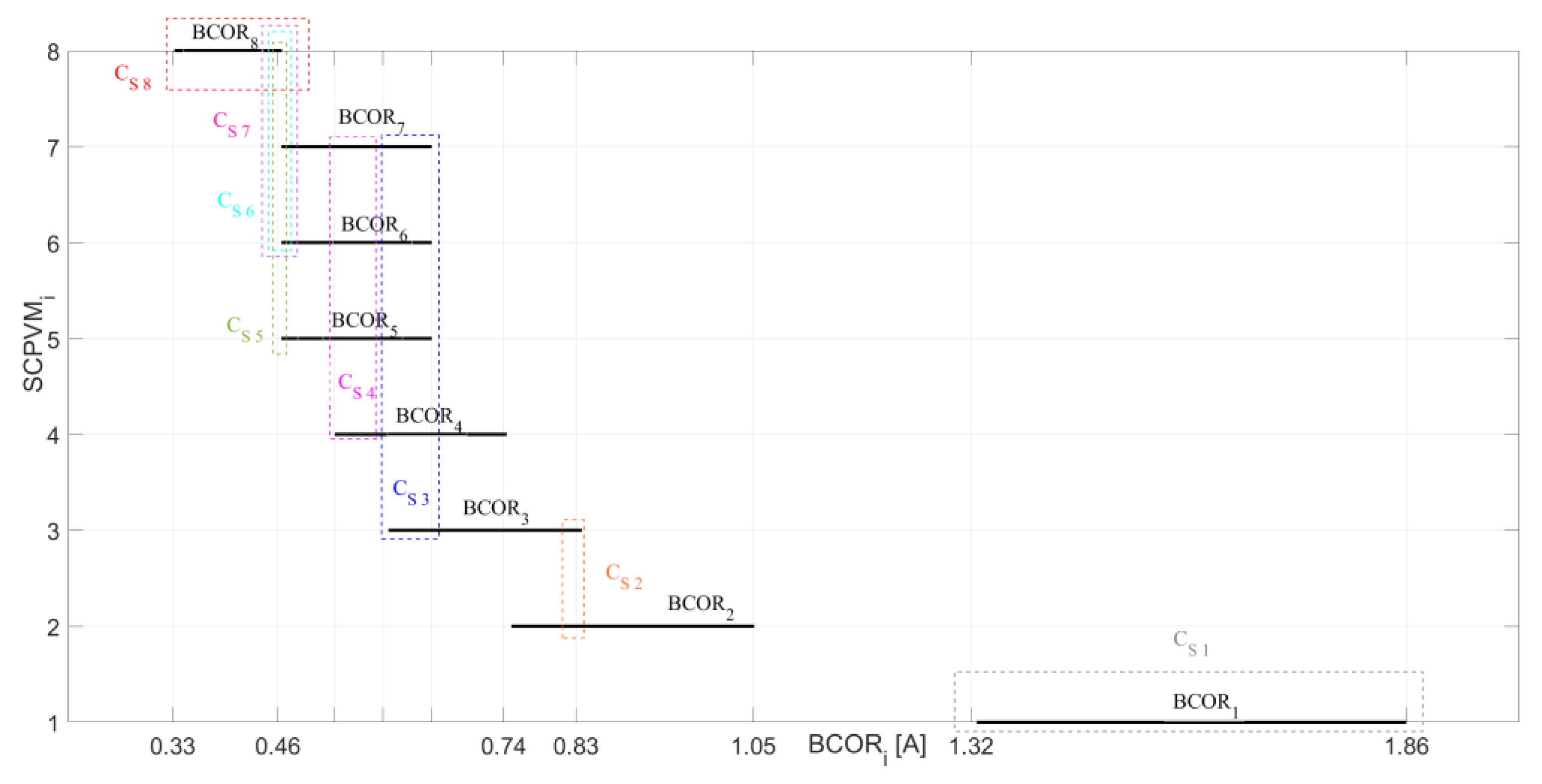
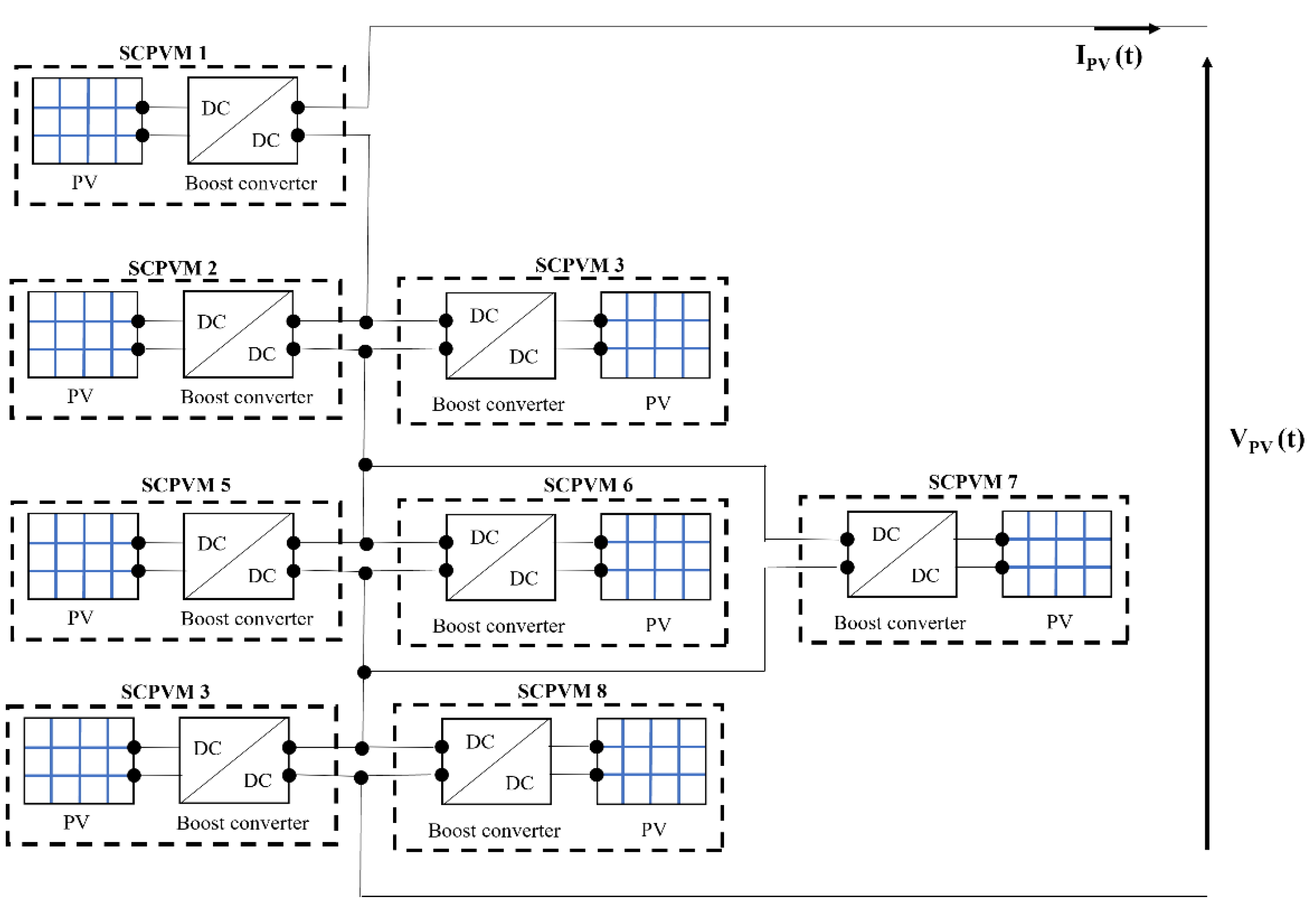
3. Fast Series-Parallel-Series Reconfiguration Algorithm
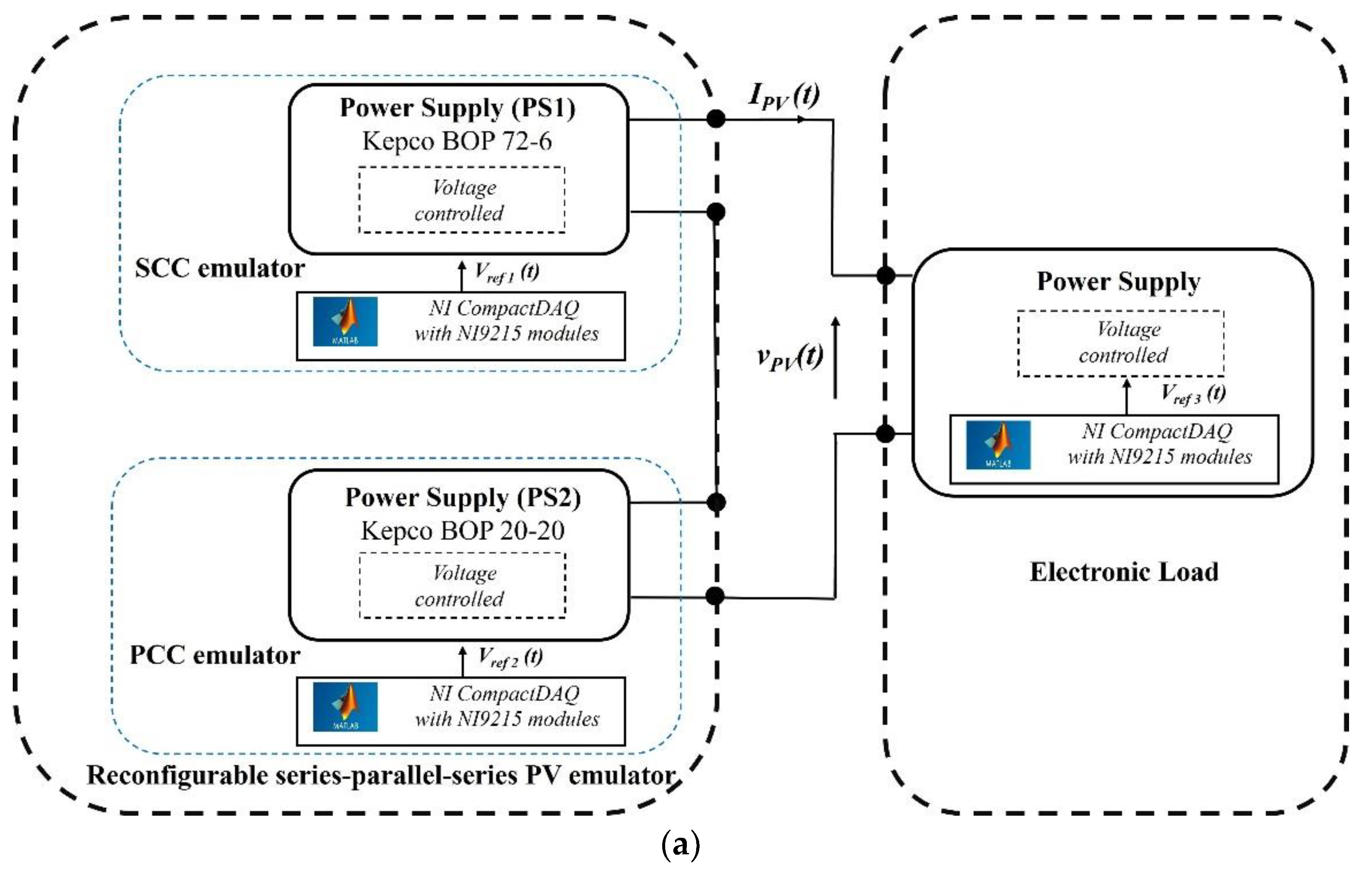
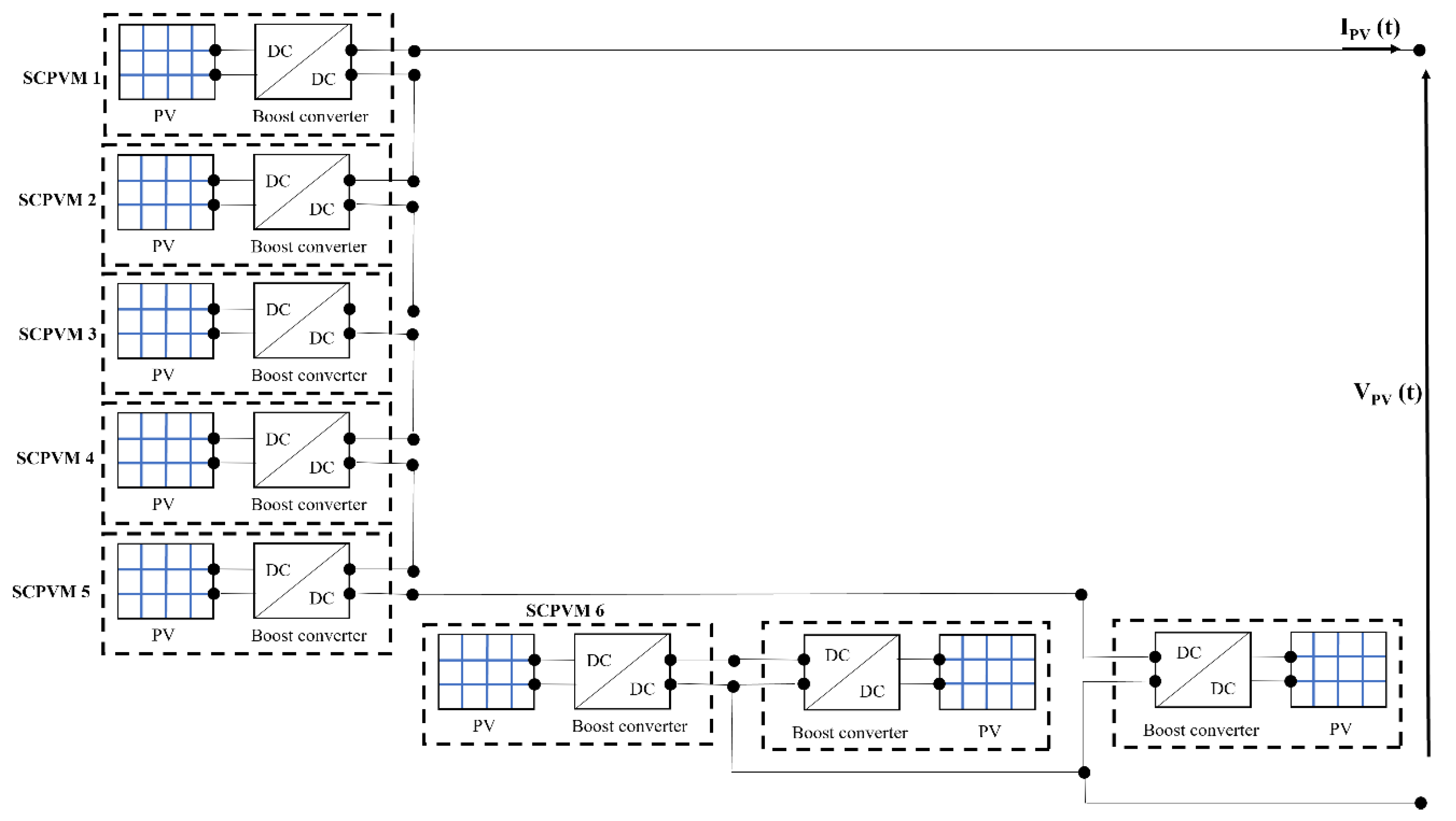
4. Reconfigurable Series-Parallel-Series Emulator
5. Experimental Results
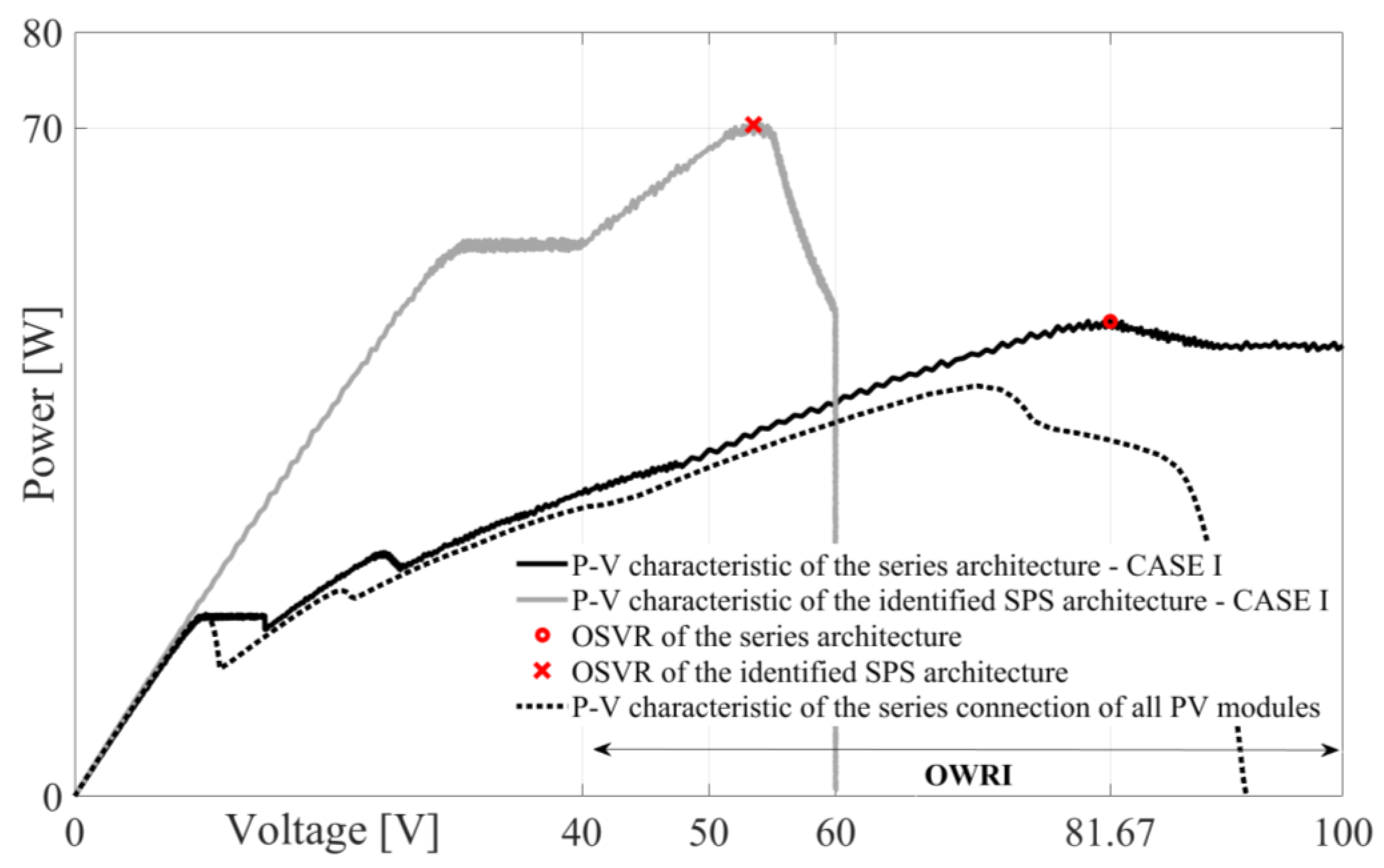
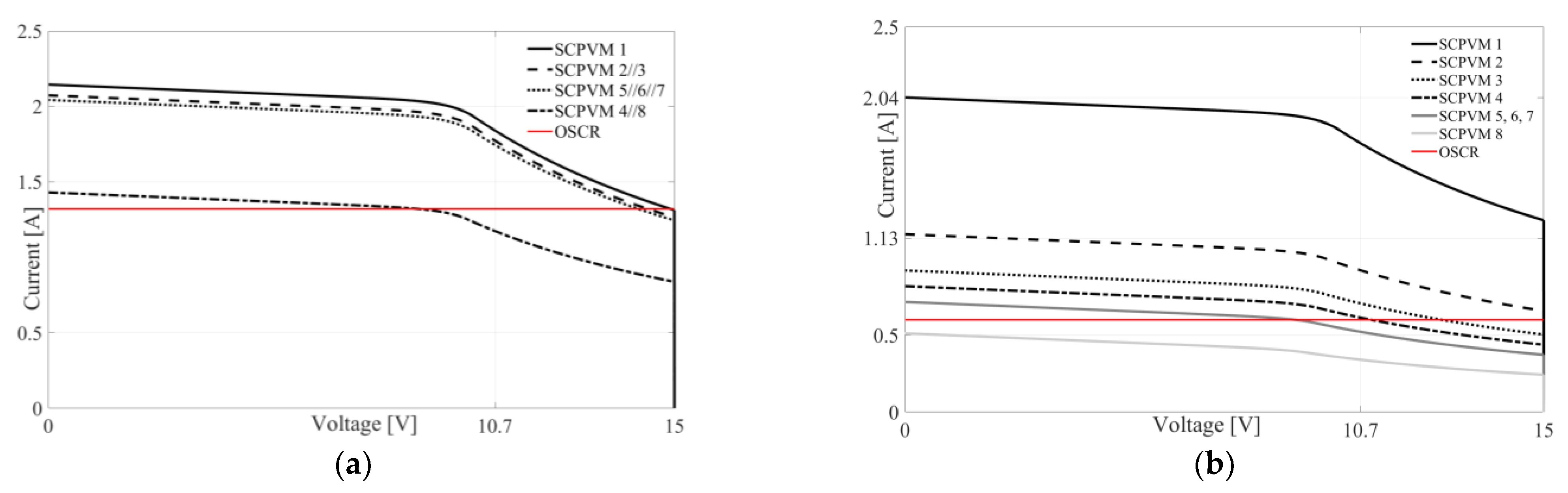
5.1. CASE I
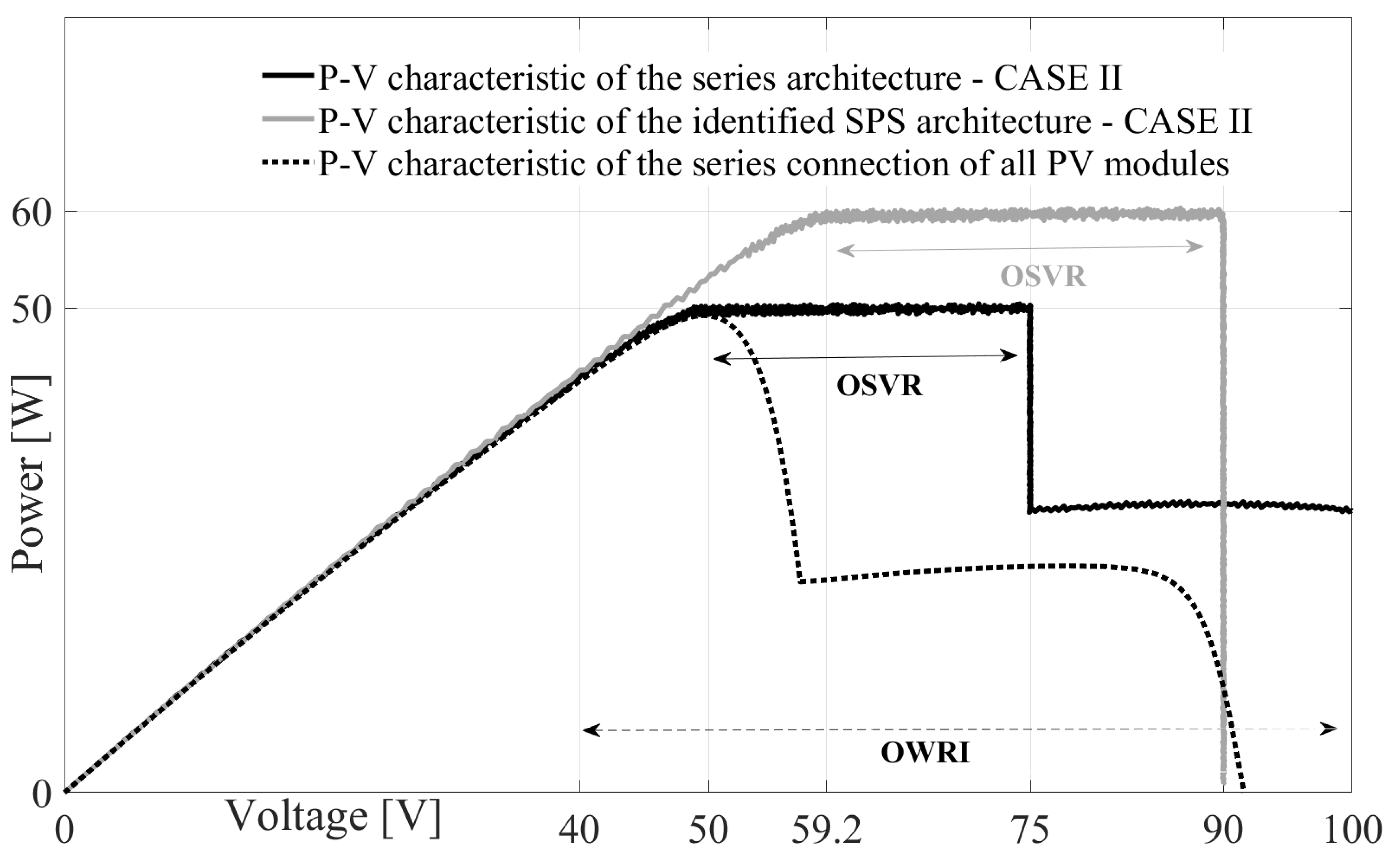
5.2. CASE II
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
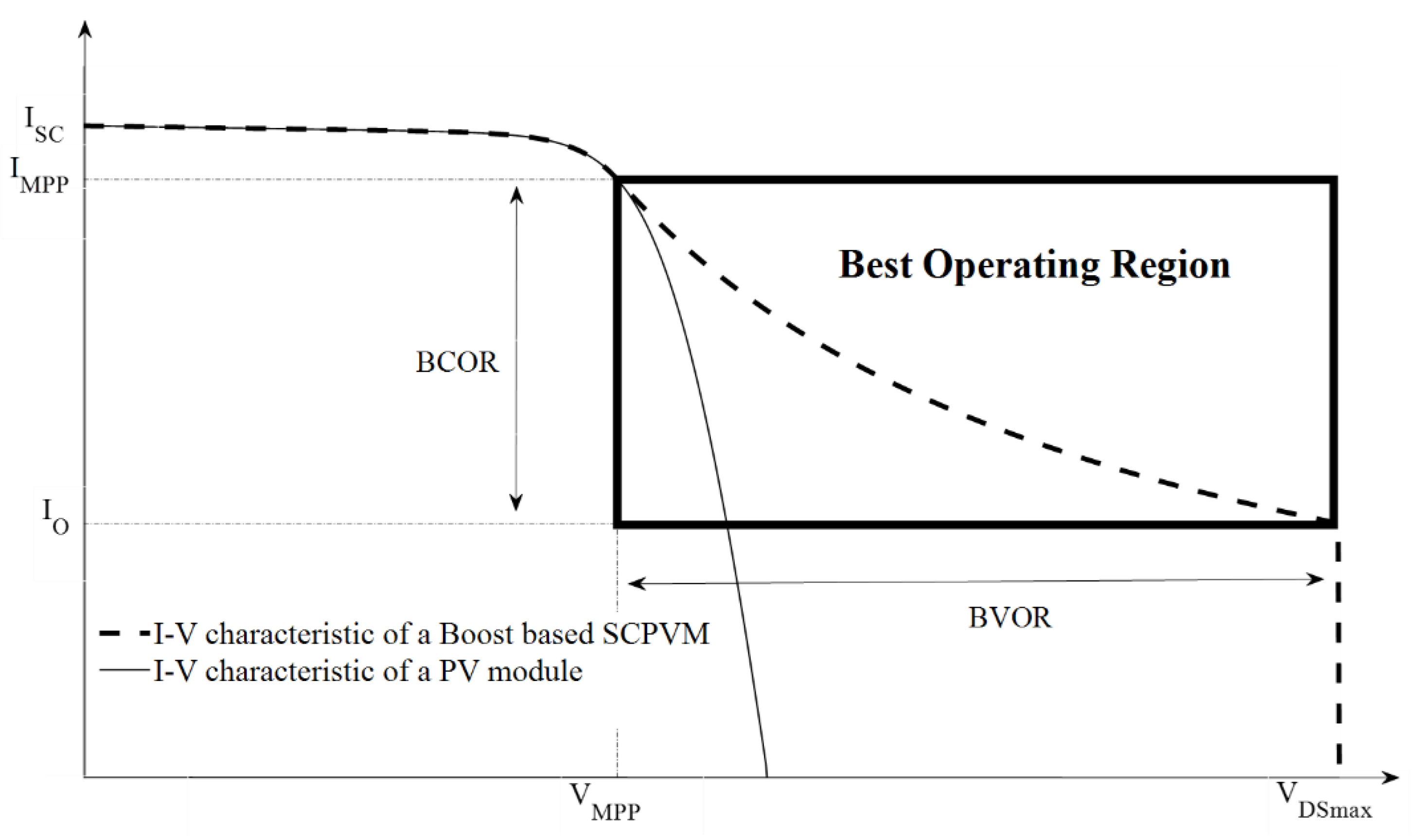
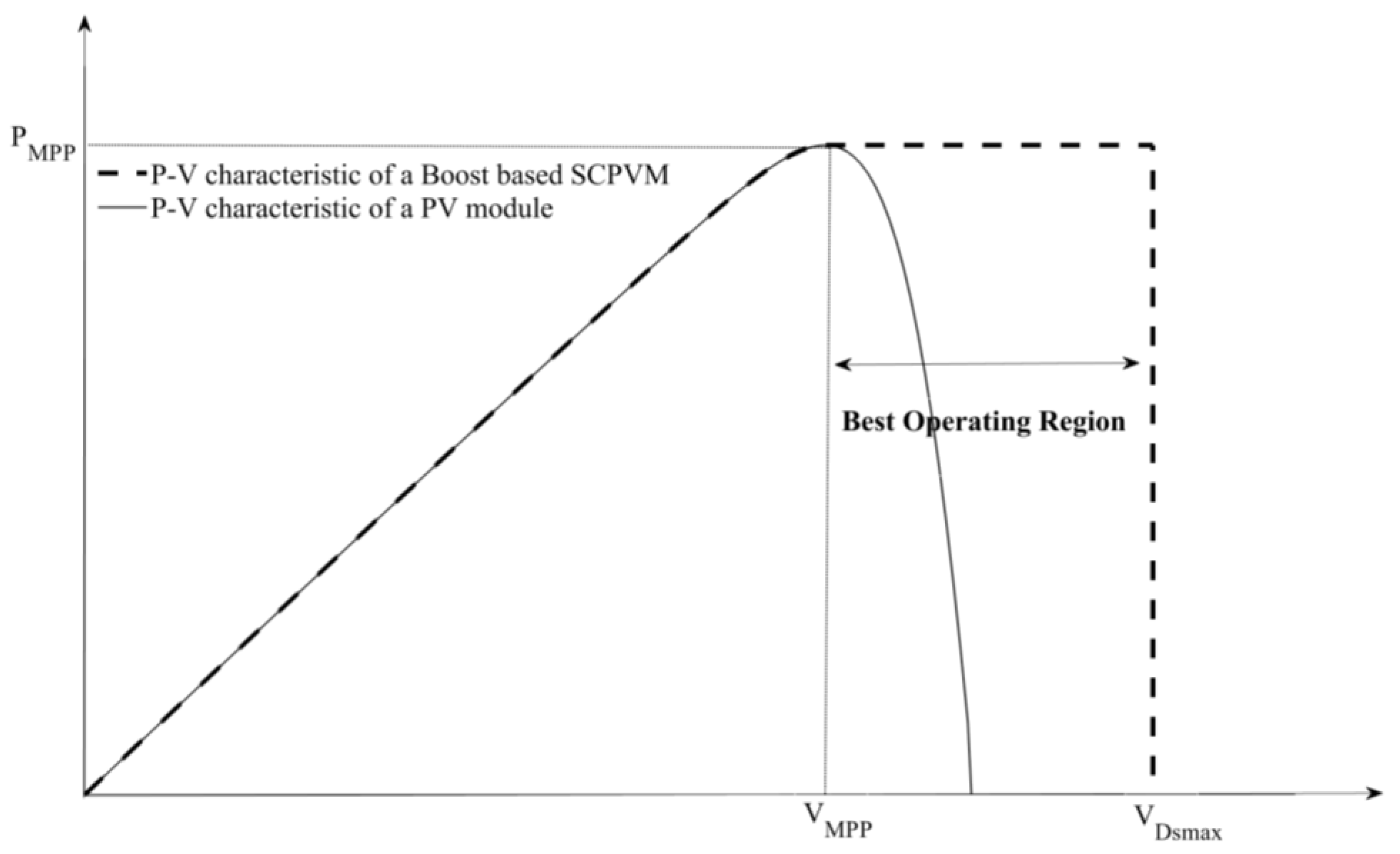
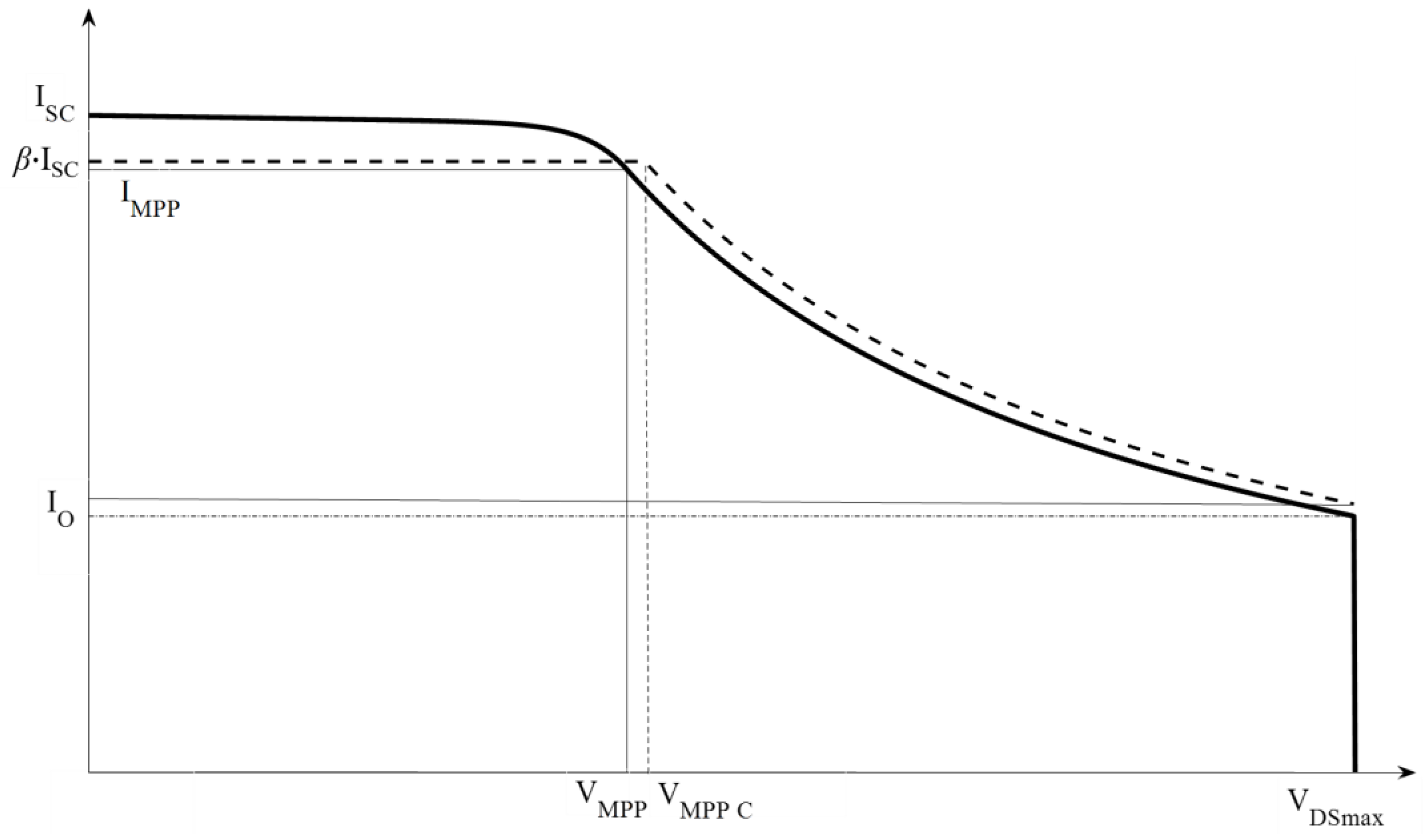
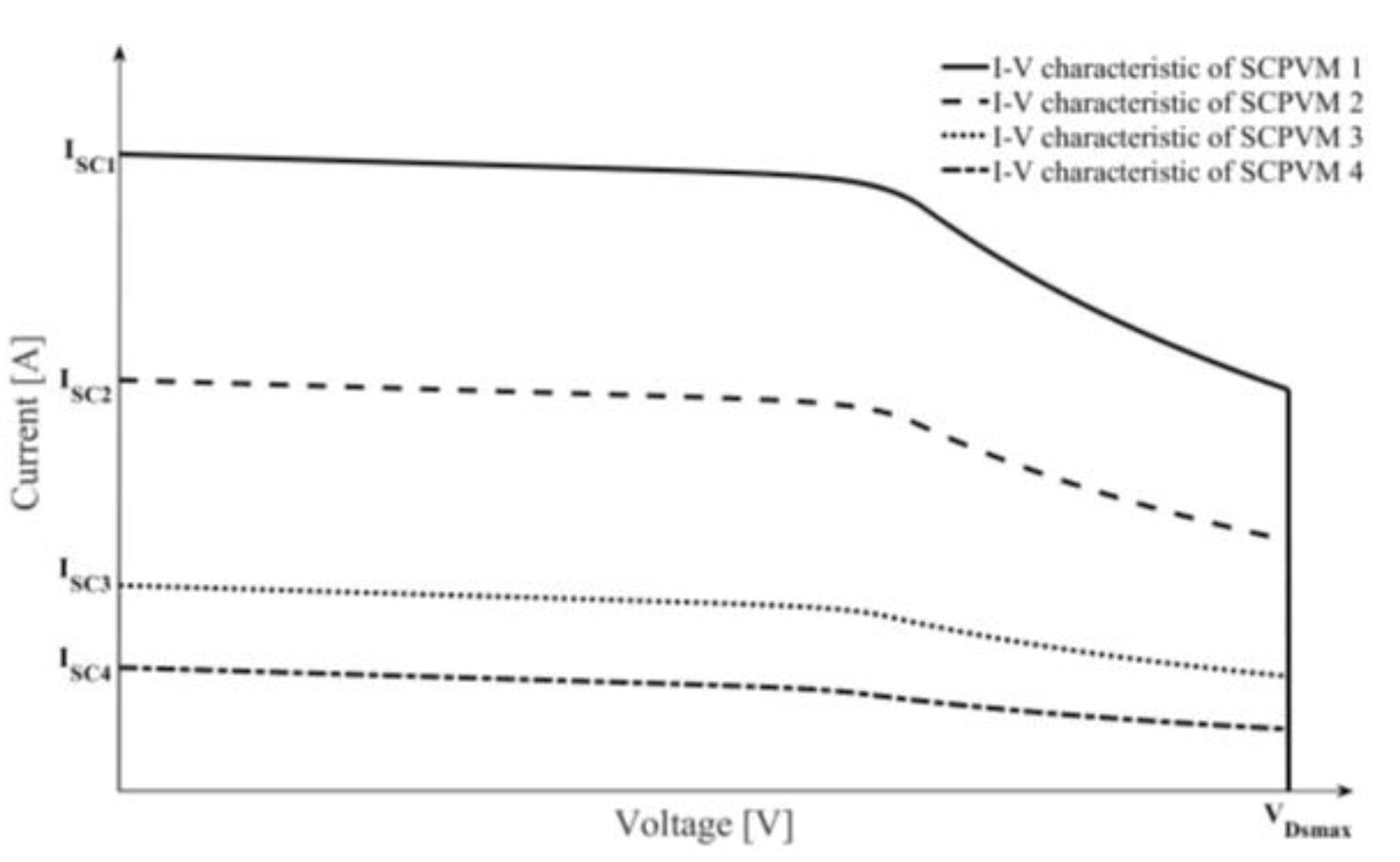
Appendix A. The Exact and Approximate I–V and P–V Characteristics of a Single Boost-Based SCPVM
References
- Renewables. Analysis and Forecast to 2022; Technical Report; International Energy Agency: Paris, France, 2023.
- Femia, N.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Power Electronics and Control Techniques for Maximum Energy Harvesting in Photovoltaic Systems; CRC Press, Taylor and Francis Group: Boca Raton, FL, USA, 2012. [Google Scholar]
- Eltamaly, A.M.; Abdelaziz, A.Y. Modern Maximum Power Point Tracking Techniques for Photovoltaic Energy Systems; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Liu, H.; Khan, M.Y.A.; Yuan, X. Hybrid Maximum Power Extraction Methods for Photovoltaic Systems: A Comprehensive Review. Energies 2023, 16, 5665. [Google Scholar] [CrossRef]
- Pikovsky, A.; Rosenblum, M.; Kurths, J. Synchronization. In A Universal Concept in Nonlinear Sciences; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Burbano-L, D.A.; Yaghouti, S.; Petrarca, C.; de Magistris, M.; di Bernardo, M. Synchronization in Multiplex Networks of Chua’s Circuits: Theory and Experiments. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 927–938. [Google Scholar] [CrossRef]
- Sarvi, M.; Azadian, A. A comprehensive review and classified comparison of MPPT algorithms in PV systems. Energy Syst. 2022, 13, 281–320. [Google Scholar] [CrossRef]
- Derbeli, M.; Napole, C.; Barambones, O.; Sanchez, J.; Calvo, I.; Fernández-Bustamante, P. Maximum Power Point Tracking Techniques for Photovoltaic Panel: A Review and Experimental Applications. Energies 2021, 14, 7806. [Google Scholar] [CrossRef]
- Yap, K.Y.; Sarimuthu, C.R.; Lim, J.M.Y. Artificial Intelligence Based MPPT Techniques for Solar Power System: A review. J. Mod. Power Syst. Clean Energy 2020, 8, 1043–1059. [Google Scholar] [CrossRef]
- Motahhir, S.; El Hammoumi, A.; Ghzizal, A. The most used MPPT algorithms: Review and the suitable low-cost embedded board for each algorithm. J. Clean. Prod. 2020, 246, 118983. [Google Scholar] [CrossRef]
- Kabalci, E. Maximum Power Point Tracking (MPPT) Algorithms for Photovoltaic Systems. In Energy Harvesting and Energy Efficiency; Lecture Notes in Energy; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Kottas, T.; Boutalis, Y.; Karlis, A. New maximum power point tracker for PV arrays using fuzzy controller in close cooperation with fuzzy cognitive networks. IEEE Trans. Energy Convers. 2006, 21, 793–803. [Google Scholar] [CrossRef]
- Daraban, S.; Petreus, D.; Morel, C. A novel MPPT (maximum power point tracking) algorithm based on a modified genetic algorithm specialized on tracking the global maximum power point in photovoltaic systems affected by partial shading. Energy 2014, 74, 374–388. [Google Scholar] [CrossRef]
- Bahgat, A.; Helwa, N.; Ahmad, G.; El Shenawy, E. Maximum power point traking controller for PV systems using neural networks. Renew. Energy 2005, 30, 1257–1268. [Google Scholar] [CrossRef]
- Al-hasan, A.; Ghoneim, A. A new correlation between photovoltaic panel’s efficiency and amount of sand dust accumulated on their surface. Int. J. Sustain. Energy 2005, 24, 187–197. [Google Scholar] [CrossRef]
- Silvestre, S.; Chouder, A. Effects of shadowing on photovoltaic module performance. Prog. Photovolt. 2008, 16, 141–149. [Google Scholar] [CrossRef]
- Adinoyi, M.J.; Said, S. Effect of dust accumulation on the power outputs of solar photovoltaic modules. Renew. Energy 2013, 60, 633–636. [Google Scholar] [CrossRef]
- Hussein, H.; Ahmad, G.; El-Ghetany, H. Performance evaluation of photovoltaic modules at different tilt angles and orientations. Energy Convers. Manag. 2004, 45, 2441–2452. [Google Scholar] [CrossRef]
- Romero-Cadaval, E.; Spagnuolo, G.; Franquelo, L.G.; Ramos-Paja, C.A.; Suntio, T.; Xiao, W.M. Grid-connected photovoltaic generation plants: Components and operation. IEEE Ind. Electron. Mag. 2013, 7, 6–20. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Lauss, G. The performance of perturb and observe and incremental conductance maximum power point tracking method under dynamic weather conditions. Appl. Energy 2014, 119, 228–236. [Google Scholar] [CrossRef]
- Sai Krishna, G.; Moger, T. Reconfiguration strategies for reducing partial shading effects in photovoltaic arrays: State of the art. Sol. Energy 2019, 182, 429–452. [Google Scholar] [CrossRef]
- Ram, J.P.; Pillai, D.S.; Jang, Y.-E.; Kim, Y.-J. Reconfigured Photovoltaic Model to Facilitate Maximum Power Point Tracking for Micro and Nano-Grid Systems. Energies 2022, 15, 8860. [Google Scholar] [CrossRef]
- Bonthagorla, P.; Mikkili, S. Performance analysis of PV array configurations (SP, BL, HC and TT) to enhance maximum power under non-uniform shading conditions. Eng. Rep. 2020, 2, e12214. [Google Scholar] [CrossRef]
- de Magistris, M.; di Bernardo, M.; Manfredi, S.; Petrarca, C.; Yaghouti, S. Modular experimental setup for real-time analysis of emergent behavior in networks of Chua’s circuits. Int. J. Circuit Theory Appl. 2016, 44, 1551–1571. [Google Scholar] [CrossRef]
- Prince Winston, D.; Kumaravel, S.; Praveen Kumar, B.; Devakirubakaran, S. Performance improvement of solar PV array topologies during various partial shading conditions. Sol. Energy 2020, 196, 228–242. [Google Scholar] [CrossRef]
- Graditi, G.; Adinolfi, G. Energy performances and reliability evaluation of an optimized DMPPT boost converter. In Proceedings of the 2011 International Conference on Clean Electrical Power (ICCEP), Ischia, Italy, 14–17 June 2011; pp. 69–72. [Google Scholar] [CrossRef]
- Balato, M.; Costanzo, L.; Vitelli, M. Multi-objective optimization of PV arrays performances by means of the dynamical reconfigu ration of PV modules connections. In Proceedings of the 2015 International Conference on Renewable Energy Research and Applications (ICRERA), Palermo, Italy, 22–25 November 2015; pp. 1646–1650. [Google Scholar] [CrossRef]
- Shimizu, T.; Hirakata, M.; Kamezawa, T.; Watanabe, H. Generation control circuit for photovoltaic modules. IEEE Trans. Power Electron. 2001, 16, 293–300. [Google Scholar] [CrossRef]
- Bergveld, H.; Büthker, D.; Castello, C.; Doorn, T.; de Jong, A.; van Otten, R.; de Waal, K. Module-Level DC/DC Conversion for Photovoltaic Systems: The Delta-Conversion Concept. IEEE Trans. Power Electron. 2013, 28, 2005–2013. [Google Scholar] [CrossRef]
- Shmilovitz, D.; Levron, Y. Distributed Maximum Power Point Tracking in Photovoltaic Systems—Emerging Architectures and Control Methods. Automatika 2012, 53, 142–155. [Google Scholar] [CrossRef]
- Femia, N.; Lisi, G.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Distributed maximum power point tracking of photovoltaic arrays: Novel approach and system analysis. IEEE Trans. Ind. Electron. 2008, 55, 2610–2621. [Google Scholar] [CrossRef]
- Román, E.; Martinez, V.; Jimeno, J.; Alonso, R.; Ibañez, P.; Elorduizapatarietxe, S. Experimental results of controlled PV module for building integrated PV systems. Sol. Energy 2008, 82, 471–480. [Google Scholar] [CrossRef]
- Balato, M.; Vitelli, M. A hybrid MPPT technique based on the fast estimate of the Maximum Power voltages in PV applications. In Proceedings of the 2013 8th International Conference and Exhibition on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 15 May 2013. [Google Scholar] [CrossRef]
- Balato, M.; Petrarca, C. The Impact of Reconfiguration on the Energy Performance of the Distributed Maximum Power Point Tracking Approach in PV Plants. Energies 2020, 13, 1511. [Google Scholar] [CrossRef]
- Balato, M.; Liccardo, A.; Petrarca, C. Dynamic Boost Based DMPPT Emulator. Energies 2020, 13, 2921. [Google Scholar] [CrossRef]




| Manufacturer | Vmin | Vmax |
|---|---|---|
| Growatt (Shenzhen, China) | 150 V | 550 V |
| Huawei (Shenzhen, China) | 90 V | 560 V |
| SMA (Niestetal, Germany) | 80 V | 600 V |
| SolarEdge (Herzliya, Israel) | 380 V | 480 V |
| ABB (Zurich, Switzerland) | 140 V | 580 V |
| Sungrow (Hefei, China) | 40 V | 560 V |
| Maximum allowed current | IPV MAX = 4 A |
| Maximum allowed voltage | VPV MAX = 100 V |
| Open circuit voltage (standard test conditions) | VOC_STC = 13.9 V |
| Short circuit current (standard test conditions) | ISC_STC = 3.1 A |
| Maximum power point voltage (standard test conditions) | VMPP_STC = 10.7 V |
| Maximum power point current (standard test conditions) | IMPP_STC = 2.8 A |
| Maximum allowed voltage (standard test conditions) | VDS MAX = 15 V |
| Minimum inverter voltage | 40 V |
| Maximum inverter voltage | 100 V |
| BCOR | Reference | ||
|---|---|---|---|
| Min [A] | Max [A] | ||
| SCPVM1 | 1.3268 | 1.8600 | Equation (2) |
| SCPVM2 | 0.7496 | 1.0509 | |
| SCPVM3 | 0.5971 | 0.8370 | |
| SCPVM4 | 0.5307 | 0.7440 | |
| SCPVM5 | 0.4644 | 0.6510 | |
| SCPVM6 | 0.4644 | 0.6510 | |
| SCPVM7 | 0.4644 | 0.6510 | |
| SCPVM8 | 0.3317 | 0.4650 | |
| Series Configuration Vector | MSCEPi [W] | OSCVRi [V] | Nin,i | Nex,i | NCP,i | |
|---|---|---|---|---|---|---|
| Min | Max | |||||
| C1 | 19.9020 | 10.700 | 15.000 | 1 | 7 | 120 |
| C2 | 20.2025 | 24.134 | 26.946 | 2 | 6 | 57 |
| C3 | 37.8138 | 58.085 | 63.333 | 5 | 3 | 4 |
| C4 | 28.8579 | 44.328 | 54.375 | 4 | 4 | 11 |
| C5 | 25.8726 | 55.640 | 55.714 | 4 | 4 | 11 |
| C6 | 18.9069 | 40.660 | 40.714 | 3 | 5 | 26 |
| C7 | 11.9412 | 25.680 | 25.714 | 2 | 6 | 57 |
| C8 | 4.9755 | 10.700 | 15.000 | 1 | 7 | 120 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balato, M.; Petrarca, C.; Liccardo, A.; Botti, M.; Verolino, L. A Fast Reconfiguration Technique for Boost-Based DMPPT PV Systems Based on Deterministic Clustering Analysis. Energies 2023, 16, 7882. https://doi.org/10.3390/en16237882
Balato M, Petrarca C, Liccardo A, Botti M, Verolino L. A Fast Reconfiguration Technique for Boost-Based DMPPT PV Systems Based on Deterministic Clustering Analysis. Energies. 2023; 16(23):7882. https://doi.org/10.3390/en16237882
Chicago/Turabian StyleBalato, Marco, Carlo Petrarca, Annalisa Liccardo, Martina Botti, and Luigi Verolino. 2023. "A Fast Reconfiguration Technique for Boost-Based DMPPT PV Systems Based on Deterministic Clustering Analysis" Energies 16, no. 23: 7882. https://doi.org/10.3390/en16237882
APA StyleBalato, M., Petrarca, C., Liccardo, A., Botti, M., & Verolino, L. (2023). A Fast Reconfiguration Technique for Boost-Based DMPPT PV Systems Based on Deterministic Clustering Analysis. Energies, 16(23), 7882. https://doi.org/10.3390/en16237882








