Synthesis of Solar Production and Energy Demand Profiles Using Markov Chains for Microgrid Design

Abstract

Uncertainties related to the energy produced and consumed in smart grids, especially in microgrids, are among the major issues for both their design and optimal management. In that context, it is essential to have representative probabilistic scenarios of these environmental uncertainties. The intensive development and massive installation of smart meters will help to better characterize local energy consumption and production in the following years. However, models representing these variables over large timescales are essential for microgrid design. In this paper, we explore a simple method based on Markov chains capable of generating a large number of probabilistic production or consumption profiles from available historical measurements. We show that the developed approach can capture the main characteristics and statistical variability of real data on both short-term and long-term scales. Moreover, the correlation between both production and demand is conserved in generated profiles with respect to historical measurements.

1. Introduction

The design and operation of microgrids are challenging and have to be robust, especially because many parameters (e.g., future energy demands, renewable production and electricity tariffs) are inherently uncertain. So, their future values cannot be predicted with perfect accuracy when making decisions during the system design phase or for setting the optimal operation strategy. On one hand, the design of microgrids under uncertainty might be based on stochastic programming optimization techniques [1] where a large number of scenarios are required. On the other hand, once the size of the assets has been fixed, short-term probabilistic forecasts might be needed for real-time operation strategies to optimize the power flows between the equipment under uncertainty. For instance, look-ahead control strategies [2] solve, at each time step, a multi-stage optimization problem, based on several probabilistic forecasts, each of them associated with a given probability. In both cases, a large amount of data over multi-time scales is essential to accurately solve the problems.

Having said that, decision-makers and modelers often lack appropriate data to run the models, especially in a stochastic context. In many real case studies, no historical data are available, or the dataset is of poor quality only covering short periods. Therefore, decision-makers might come up with inappropriate design decisions while modelers do not have enough data to assess the design and control approaches they are implementing. To overcome these difficulties, scenario generation methods have been widely implemented in the literature [3,4]. This work mainly focuses on the generation of solar production and energy demand (i.e., electricity and heat) profiles at an hourly time step. However, the generation procedure may be extended to a wide spectrum of environmental variables for any engineering system.

While short-term forecasting is a relatively new topic driven by efficient real-time operational needs, long-term forecasting for energy systems has been studied for a long time [3]. Indeed, the latter has been used for decades to anticipate energy demand growth in order to plan future energy production and transmission infrastructures. However, the recent and strong development of variable renewable energy (VRE) has led to new long-term forecast requirements where short temporal granularity (i.e., at an hourly time step) is needed to cope with the short-timescale variability of the production [5,6]. Also, as noticed by Hong et al. in [3] “another important step in the recent history is the transition from a deterministic to a probabilistic point of view”: taking into account the variability of production and consumption in future microgrids, exploiting a growing part of VRE requires a shift from optimal design with regard to a deterministic scenario to robust design under multiple scenarios. When generating multiple scenarios, integrating the correlations of those stochastic variables is then critical in order to assess the efficiency of the microgrid design [7].

Recently, Mavromatidis et al. [4] drew a great review of uncertainty characterization for the design of distributed energy systems, which is of primary interest for this work. A large number of methods are documented for both the generation of solar production and energy demand profiles [8]. The readers could refer to this article for an in-depth discussion about the different approaches. The objective of this part is to summarize the main conclusions and provide a clear insight into the direction of this paper. Therefore, the first observation from their review is that the generation method depends on whether or not historical data are available. These approaches can be classified into top-down (i.e., historical data are available) and bottom-up categories, respectively. While obtaining solar production data today is relatively straightforward [9], the availability of energy demand measurements is generally rarer. Furthermore, the synchronicity between all environmental variables must be kept via the data generation method: “in the particular case of a solar generator based microgrid system design, it is not the same to have a huge solar production during low energy demand or on the contrary during huge consumption phase”.

In the top-down case, the most frequent and easiest generation method is the use of probability distribution functions (PDFs), derived from historical profiles for each hour. Then, a scenario is built through sampling from the PDFs. The drawback of such a method is that the uncertain parameters are treated as independent random variables between consecutive time steps, which might lead to unrealistic behavior where the autocorrelation and periodicity of the initial dataset are lost. To overcome this issue, more sophisticated and hybrid methods have been developed, such as autoregressive models [10], Markov approaches [11] and machine learning-based methods [12], to name just a few. The latter is probably the most popular approach for both the production and energy demands when large datasets are available [13]. Other recent methods are presented in [14,15].

On the other hand, when the case study lacks adequate energy demand measurements (e.g., newly built buildings), physical model-based methods are usually implemented to generate profiles. In smart building applications, the most common approaches are probably the use of ready-made Building Performance Simulation (BPS) tools (e.g., energyPlus [16]), but other model-based techniques are also implemented (e.g., resistance–capacitance (RC) models [17], a stochastic model where the input parameters are characterized based on interview information [18]). More elaborate methods are derived for large-scale districts where the previous approaches might not be appropriate (creating a model for each building of a district is quite laborious) [19]. In the bottom-up case, uncertainty is added to the input parameters of the simulation. The drawback of these methods is that a non-negligible amount of development time is usually required to get familiar with BPS tools and collect all the numerous input parameters. Thus, energy modelers who are only seeking a fast generation method to test their design and operation algorithms might be discouraged by these approaches.

The main objective and contribution of this work is to provide an efficient and straightforward method to generate a large number of probabilistic energy production and demand profiles when historical measurements are available. It is essential to mention that this generation method keeps the correlation between production and demand time signals, which is really relevant where design and operation optimization issues are concerned. The energy modeler’s perspective is deliberately adopted in this work: the focus is on creating large datasets at an hourly time step to build different microgrid design and operation algorithms. Nevertheless, the last section will show that the proposed method can capture the main statistical features and variations of real data despite the method’s simplicity. Also, another important aspect is that the generation approach can be used simultaneously to generate long-term scenarios for design and short-term forecasts for optimal operation purposes. Hence, the method is intended for modelers seeking a simple generation approach without spending too much time on this phase.

Therefore, the method implemented in this work is based on Markov chains over representative periods. The approach only requires historical measurements of the time series of the uncertain parameters in order to provide a wide range of contingencies. Differently from other existing works, here the states of the Markov chain are represented by multiple environmental variables, so keeping the time relationships between them.

The rest of the paper is organized as follows: The methodology for generating synthetic profiles is developed in Section 2. Next, the performance of the approach is demonstrated on a microgrid in a residential case study from the Ausgrid (Australian distributor of electricity) dataset in Section 3. Finally, conclusions are drawn in Section 4

2. Methodology for Generating Synthetic Profiles from Historical Data

The uncertain parameters (here, the electricity consumption, heat demands and solar production) of multi-energy systems are modeled as discrete random variables. The following work aims at providing a method to build a discrete sample space where a scenario is a sequence of all the random variable realizations over a given time horizon H, associated with a given probability.

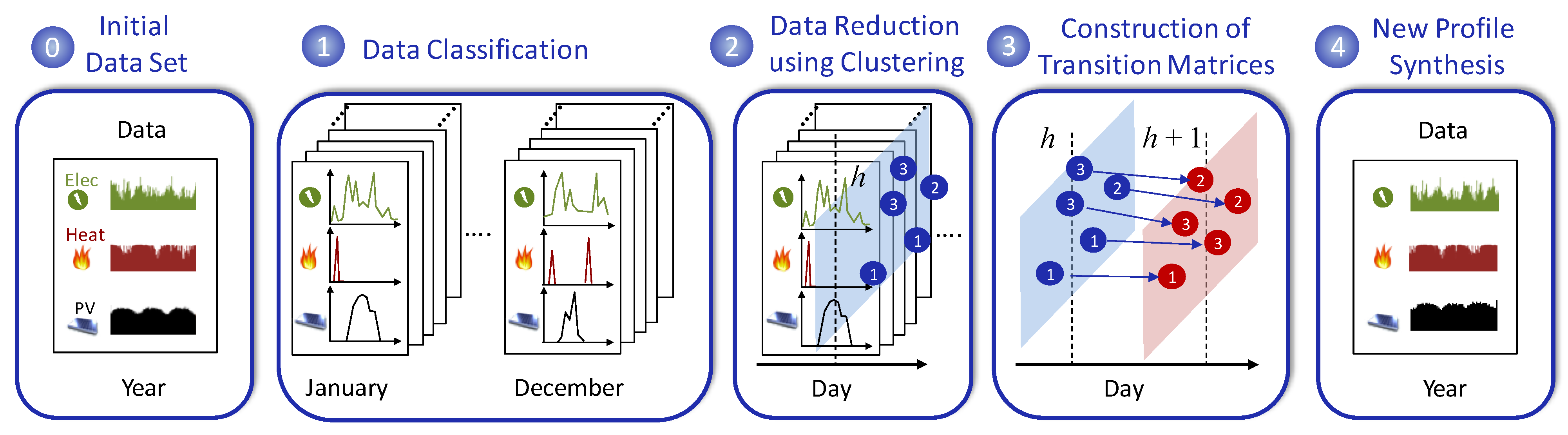
Starting from an initial set of historical data, the method for generating synthetic and representative profiles of the random variables is illustrated via the process in Figure 1, which can be divided into four different steps. The initial dataset contains the short- and long-term evolution of the random variables considered. Each element in this set can be defined as a sample state X(h) composed of observable realizations of the underlying random variables at hour h. The finite set of observed states is called the state space. In our case, as previously mentioned, states contain three components: the electricity and heat demands and the PV production measurements.

2.1. Analysis and Classification of the Initial Dataset

This first step of the methodology (step 1 in Figure 1) is to identify representative periods from the historical annual dataset to account for the different time scales’ variability. The Markov chains will be later computed over these periods. Therefore, in our case, each month of the year is considered separately to avoid losing seasonality features. Furthermore, week and weekend days of each month are considered separately, as the energy demand pattern usually depends on the working activity. One Markov chain is built for each of these representative days. Finally, each day is segmented into 23 hourly transitions to account for intraday variability (i.e., daily cycles for PV production and load demands). Thus, 552 (12 (months) × 2 (weeks or weekends) × 23 (hourly transitions)) Markov chains will be computed from the historical dataset. The classification of the representative periods is depicted in Figure 2.

It should be noted that this a priori classification is based on both statistical exploration of the historical dataset and the intuition of the authors for taking account of deterministic features in the random variables (i.e., daily and seasonal cycles). Other more refined segmentations could probably be used through analyzing the historical dataset in depth with classification methods such as [20,21], which are out of the scope of this paper.

2.2. Data Reduction Using Clustering

State variable data X(h) associated with the same hour h of a day (weekdays or weekend days) of the same month, for all available years, are gathered and reduced to ${\mathrm{C}}_i\left(h\right)$ clusters with a clustering algorithm [22]. In practice, this can be simply carried out with the k-means [23] or k-medoids [24] methods. It should be mentioned that the components of the state variables have to be normalized in order to take account of the different scaling between load demands and PV production data. This clustering step (step 2 in Figure 1) allows the determination of transitions matrices related to the state evolution between two consecutive hours (hourly transitions) as explained in the next section.

2.3. Data Reduction Using Clustering

Our generation process based on Markov chains [11,25] requires the exploitation of transition matrices related to the random states considered (step 3 in Figure 1). As indicated in Section 2.1, 23 transition matrices are built for each month and day type (weekday, weekend day) for characterizing the evolution of the random state variables during each day. The calculation of those matrices is illustrated in Figure 3 for a simple case of three clusters identified at hours h and h + 1 from eight historical data scenarios. In the general case, the expression of a transition matrix $T_{h+1}(i,j)$ is given by (1):

$$T_{h+1}(i,j)=\left(\frac{N({\mathrm{C}}_i\left(h\right)\to {\mathrm{C}}_j\left(h+1\right))}{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}\left({\mathrm{C}}_i\left(h\right)\right)}\right),$$

(1)

where $N({\mathrm{C}}_i\left(h\right)\to {\mathrm{C}}_j\left(h+1\right))$ denotes the number of elements in the cluster ${\mathrm{C}}_i\left(h\right)$ going to the cluster ${\mathrm{C}}_j\left(h+1\right)$, $\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}\left({\mathrm{C}}_i\left(h\right)\right)$ being the size of the cluster ${\mathrm{C}}_i\left(h\right)$. This matrix is of size n_c(h) × n_c (h + 1), where n_c(h) and n_c(h + 1), respectively, represent the number of clusters at hour h and at hour h + 1. This matrix contains the probabilities that an element of a cluster identified at hour h joins an element of a given cluster at time h + 1.

2.4. Scenario Generation

In this section, we describe in detail the profile synthesis process based on Markov chains (step 4 in Figure 1). Starting from an initial cluster C(0) at random, associated with the first month that has to be generated, the Markov process provides a sequence of 23 clusters over the first day using the transition matrices described in the previous section, according to (2):

$$\mathrm{C}\left(0\right)\stackrel{T_1}{\to }\mathrm{C}\left(1\right)\stackrel{T_2}{\to }\mathrm{C}\left(2\right)\cdots \stackrel{T_h}{\to }\mathrm{C}\left(h\right)\cdots \stackrel{T_{23}}{\to }\mathrm{C}\left(23\right)$$

(2)

For each cluster C(h) of the random sequence, a state X(h) ∈ C(h) can be, for instance, chosen with respect to three different strategies:

• X(h) is randomly selected among all elements of the cluster C(h) with uniform probability.
• X(h) is selected among all elements of the cluster C(h) considering the closest distance to the previous state X(h−1).
• X(h) is the medoid of the cluster: this strategy results in systematically replacing the cluster C(h) with its corresponding medoid.

While the first strategy should certainly improve the randomness and diversity of state sequences, the second, on the contrary, increases the deterministic characteristics of state transitions as in persistence models [26,27]. The third strategy, consisting of only generating medoids, can be considered as an intermediate between the previous ones.

If the previous process allows the complete generation of the states over the day, the transitions between days of a same month have also to be explained. Again, three strategies can be employed similar to what was described earlier. For each day to be generated:

• Start from an initial cluster C(0) at random (i.e., a random row of the first transition matrix T₁ of the month considered).
• Start from the first cluster C(0) that is the closest to the last of the previous day C(23).
• Build an additional transition matrix T₂₄ that characterizes the transition between consecutive days of the month in the initial dataset T₂₄ = T(X(23)→X(0)).

Here again, it should be mentioned that the first strategy implies that successive days are supposed to be uncorrelated while the second induces a persistence effect. The third strategy is probably a good compromise between the previous ones, but it requires the computation of a 24th transition matrix each month. Similar strategies can also be implemented for characterizing the transitions between consecutive months or years.

In order to define C(h + 1) knowing C(h), we apply a classical technique based on the drawing of a uniform density random number (between 0 and 1) which is compared to the sum of the probabilities of the line C(h). If we take the example of the matrix in Figure 3, let us suppose that we have C(h) = C₂, we draw a random number r between 0 and 1 (r = U(0, 1) with a uniform random probability distribution:

-

example 1: if r = 0.1 then the cluster C(h + 1) = C₂ is chosen as successor because r greater than p(C₁) = 0 but r lower than p(C₁) + p(C₂) = 2/3;

-

example 2: if r = 0.8, while r is between p(C₁) + p(C₂) and p(C₁) + p(C₂) + p(C₃)), the cluster C(h + 1) = C₃ is chosen as successor.

As a consequence, N random draws are thus necessary to define the N sequences of transitions related to the N transition matrices.

As a conclusion of this section, it is important to note that this Markov process only generates existing states of the historical data and, therefore, keeps the synchronicity and possible correlations between the state components (i.e., intercorrelations between PV production, and heat and electricity consumption). This issue is even more important as it concerns the sizing of devices: for example, storage device sizing is driven by the difference between production and demand over the time. On the other hand, Markov-based approaches are not able to predict and extrapolate extreme unforeseen behaviors (e.g., extreme weather conditions or consumption evolutions due to sudden policy changes) which are not present in the initial data set and will occur with small probabilities.

3. Evaluation on a Case Study

The generation method is evaluated using the Ausgrid (Australian distributor of electricity) dataset [28] where three years of measured energy demands and production time series (at a 30 min time step) are openly available for 300 residential customers: finally, historical data are upscaled to 1 h resolution. In order to illustrate the generation process, the 39th customer is arbitrarily chosen. Among all the strategies presented in Section 2.4, we only consider the following scheme for the scenario generation:

-

clustering is carried with the k-medoid algorithm considering a fixed value of k = 10;

-

states of each cluster are only represented by the medoids associated with random sequences of the cluster generated via the Markov process;

-

transition between days in a month are performed using a 24th transition matrix.

The investigation and the comparison of other generation strategies among the ones illustrated in Section 2.4 are not in the scope of the paper but naturally come into perspective in this work. While well-established metrics (e.g., root-mean-square error (RMSE), mean absolute error (MAE), etc.) are usually derived to assess the performance of short-term forecasting methods, the evaluation of long-term scenarios is less obvious at first glance. Therefore, following [11,12,18], the evaluation for long-term scenarios will be based on a combination of both statistical and visual examination in comparison with the measured data.

3.1. Statistical Assessment over Large Representative Periods

To run the evaluation, Markov chains are built from the 3-year historical dataset of measured data. Then, 1000 scenarios of one year at an hourly time step are generated for the study. Figure 4 shows the 3-year time series at an hourly time step for the electrical and thermal demands, in addition to the normalized solar production (in gray) followed by a 1-year scenario generated with the Markov model (in color). Note that the first hour corresponds to the 1st of July as the season cycle is opposite to Europe. A first general visual observation is that the shape of the profiles seems consistent with the measured data depicted in gray in the figure.

3.2. Short-Timescale Variability

Beyond those statistical similarities, the Markov model still introduces short-timescale variability from one scenario to another as shown in Figure 7, where the energy demands and production are depicted over one week for 10 scenarios randomly chosen in July. Indeed, power values are not simultaneously the same between scenarios, which leads to a wide range of contingencies. This latter aspect is of primary importance when dealing with the robust design and operation under uncertainties of microgrids. Also, remember that each scenario is associated with a given probability which is computed thanks to the transition matrices (see Section 2). Thus, the generation procedure is also suitable for short-term probabilistic forecasts, which can be later used by look-ahead control strategies [2] to operate microgrids.

3.3. Quantitative Comparisons

In addition to the previous qualitative comparisons, we provide in this section two quantitative criteria for characterizing our Markov synthesis process. Autocorrelation and load duration curves are computed over the 1000 scenarios generated and compared with those of the initial set of data (i.e., the 39th Ausgrid customer) for the three stochastic variables (PV generation, and heat and electricity demands). It should be noted that both criteria are commonly employed for assessing the quantitative correspondence of synthetized profiles with initial sets of data (e.g., [11,12] for the use of autocorrelation and [8,18] for the use of load duration curves). Note that other classic statistical criteria such as Probability Density Functions (PDF) and Cumulative Density Functions (CDF) could also have been used, but load duration curves are more meaningful and popular in the field of microgrid design.

Autocorrelation refers to the correlation of a time series with a lagged copy of itself. The goal is to determine if the signal shows similarities between observations at different time lags. The result is given as a function of the delay (also called lags in Figure 8). Despite the Markovian property attached to the generation method (i.e., the future state of the stochastic process only depends on the current state, without any memory of the past), the autocorrelation of the three variables is also recovered via the model, as shown in Figure 8. This might be explained as Markov chains are computed for each hour of representative days, leading to realistic power level sequences. Figure 8 also shows the duration curves of the three variables. The duration curve [29] defines in abscissa the number of hours during one year for which the production or demand power is greater or equal to the value defined in ordinate. For example, one can see that the PV production has a positive value during less than 4380 h (less than 2000 h for the heat demand) while the electric demand is nearly always positive along the year. The area under the duration curve corresponds to the total energy consumed (or produced) over the horizon. As shown in Figure 8, the Markovian approach tends to generate scenarios (blue curves) with annual energy demands close to the average of the 3-year historical dataset (in red): “the synthesis approach is then consistent in the sense of average values”. Furthermore, with this representation, the values are sorted in descending order, which makes the comparison easier between the real data and the synthetic scenarios at a yearly time scale. In this sense, this indicator can be assimilated by the CDF statistical indicator. While the whole shape of the duration curves is very close, comparing historical data and Markov’s model, one can also say that the statistical content of both signals is consistent on a large (yearly) timescale. Finally, the first values (h = 1) on the left of the duration curves provide clear information on the peak values, which are also in accordance between historical data and Markov’s model.

4. Conclusions and Perspectives

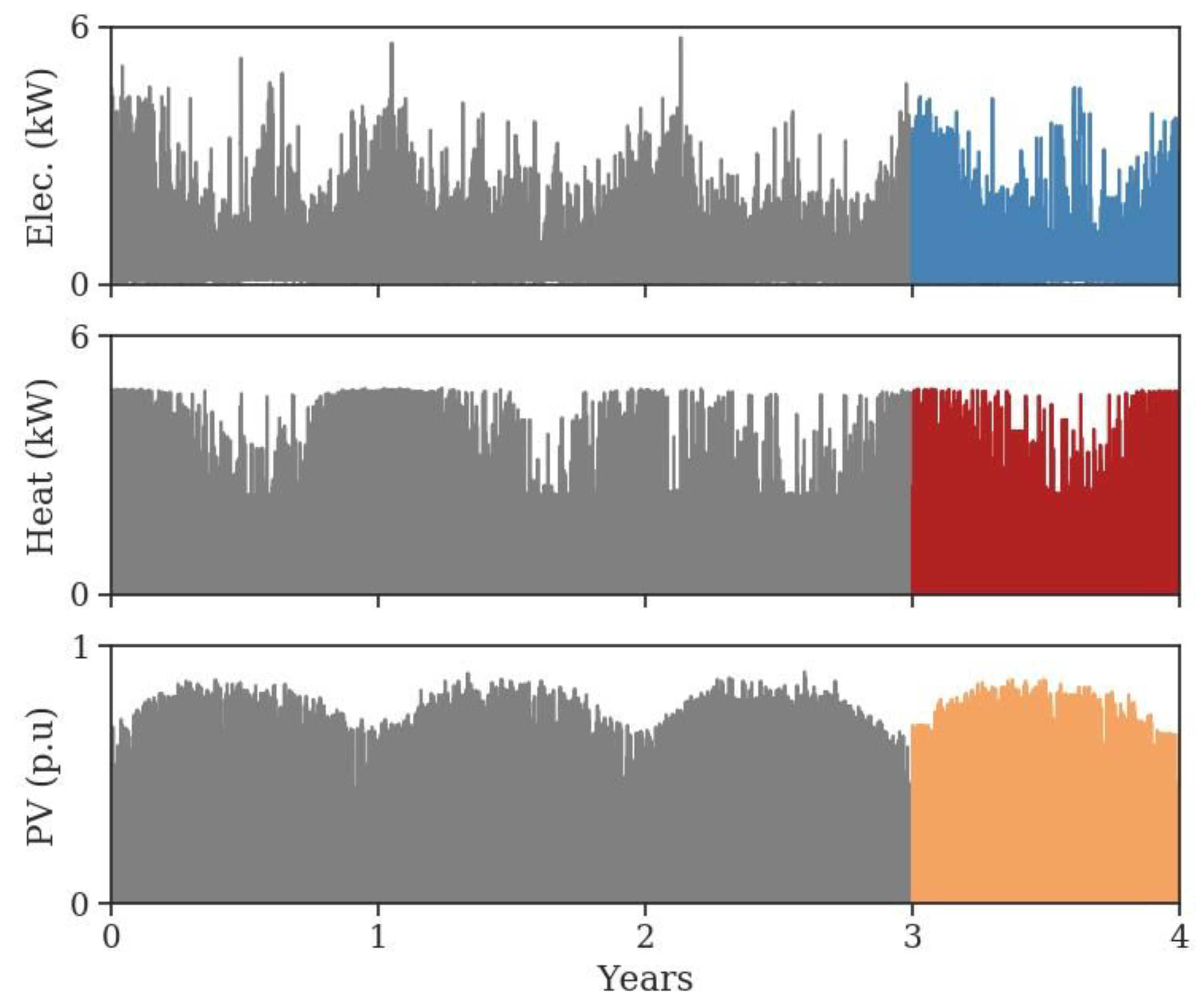
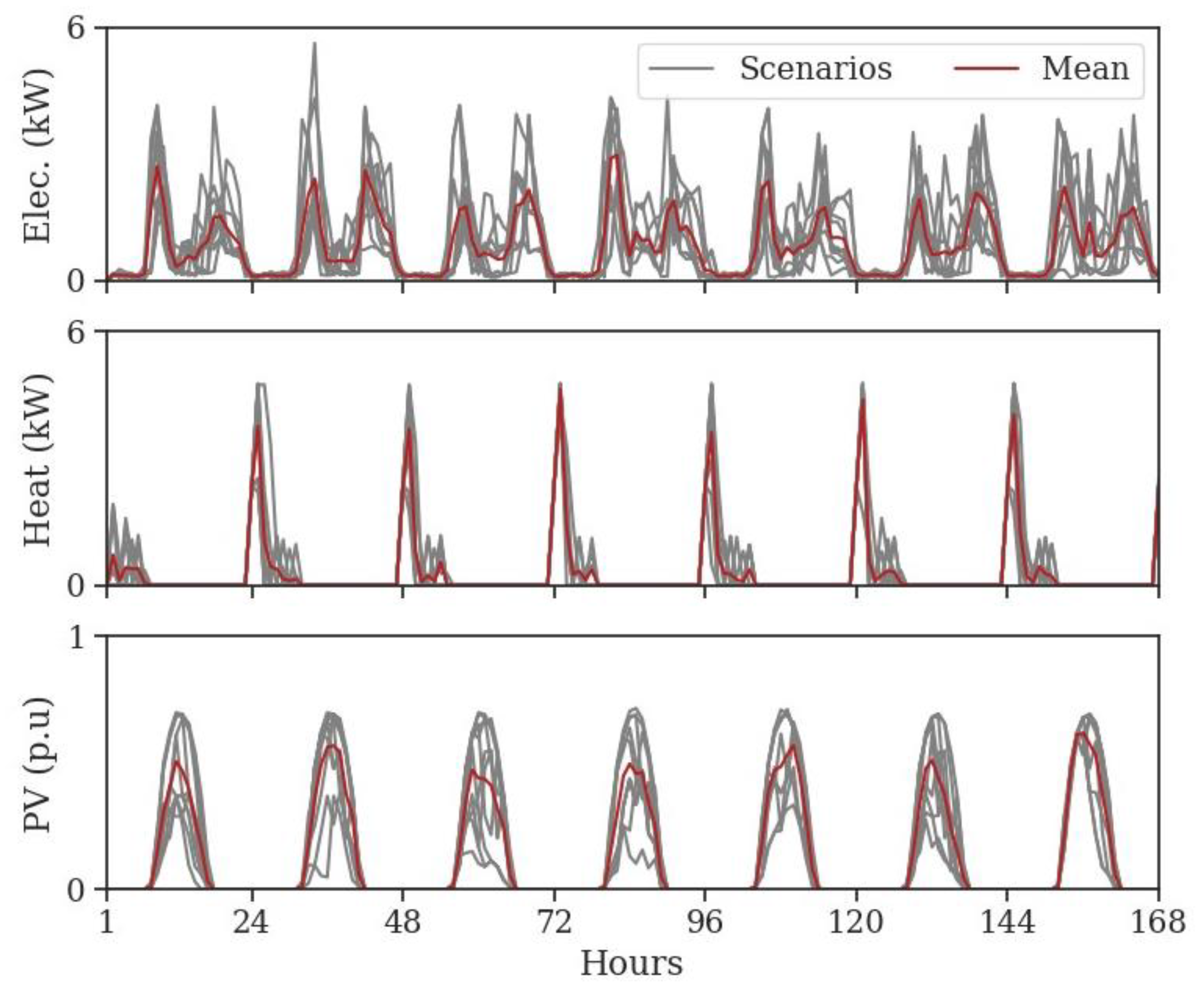
In order to generate scenarios for both long- and short-term applications, a simple but relevant stochastic model based on Markov chains was presented in this paper. First, the methodology was introduced where the Markov chains are computed over representative periods to account for the different timescale variability. Then, the method was applied to a residential case study where the objective was to build several (electric and heat) energy demands and solar production scenarios. The results have shown that the main cycle and statistical features of the initial dataset have been recovered with this straightforward Markov model while introducing realistic temporal variability to the annual time series. Finally, the last section has demonstrated that the Markovian approach is also suitable to generate short-term profiles, later used to control microgrids.

A primary perspective beyond this work may come from the classification procedure manually operated to identify the representative periods. Indeed, the performance of the Markov method is directly related to the expert knowledge concerning the structure and patterns of the initial dataset. Other approaches (mostly based on machine learning as in [12], for instance) do not require this first step and might be more relevant if little information is available about the stochastic processes. Concerning the generation process, several strategies were discussed in Section 2.4 but only one has been implemented. A good perspective should be to compare and evaluate them with regard to their complexity, CPU time and other performance criteria associated, for example, with the diversity of the synthesized profiles. Furthermore, fixed-size clustering has been used while the number of clusters per hour could be optimized through using metrics such as the silhouette [30] or other well-known statistical criteria [31]. It seems quite obvious that the number of clusters strongly differs during the day, especially between day and night (with null PV production) periods.

Since the Markov generation model is based on “historical data”, the relevance of the generated profiles clearly depends on the accuracy of these historical data. A complementary adaptation of the process is necessary to address prospective scenarios of data. For instance, what happens if the future PV production and the energy demands increase, or if the shape of the daily consumption changes due to policy changes or extreme weather conditions?

Finally, Markov-based approaches have to be compared with other profile synthesis methods (e.g., machine learning techniques or classical stochastic processes using regressive or autoregressive models) with respect to several criteria: accuracy, complexity, CPU time and sensitivity to possible errors in the initial datasets used as reference. These latter points are beyond the scope of this paper but should be addressed in future works.