Including Shield Wires in the Analysis of Transient Processes Occurring in HVAC Transmission Lines

Abstract

The article presents an analysis of electromagnetic transient processes in long ultra-high voltage transmission lines, taking into account shield wires. It was shown that EMTP and Matlab/Simulink software are currently widely used in the study of transient processes in power lines. The EMTP software package uses the finite element method when integrating the equation that mathematically models the distributed parameter transmission line. The Matlab/Simulink software uses the d’Alembert method. In both cases, it is not known how the boundary conditions for the partial differential equation that mathematically models the transmission line are determined. The power line is analyzed as a distributed parameter system, described by a second-order partial differential equation. The advantage of the proposed method of calculating the boundary conditions for the abovementioned equation is the use of boundary conditions of the second and third types of Neumann and Poincaré, which allowed us to take into account the mutual influence of shield wires and phase conductors of the line in one power system. On this basis, the methodology for obtaining time domain graphs, spatial distributions, and traveling wave distributions of voltages and currents for phase conductors and line shielding wires is presented. The results of a computer simulation of transient processes when switching on the power line, taking into account controlled phase commutation and under single-phase earth fault conditions, are presented. All calculation results of transient processes presented in the article were obtained exclusively using numerical methods.

1. Introduction

The power transmission line is an important element of the power infrastructure of each country. These lines not only transmit electricity from generation sites to consumers but also create connections between the local power systems of different countries. The reliability of their work directly affects the normal operation of the national economy. However, there are many factors that determine the normal operation of these lines, in particular, transient processes occurring during the change in operating modes, switching on and off of large loads, the occurrence of emergency modes, and also due to dangerous lightning strikes in power lines may have a negative impact on their operation. In such cases, high-voltage pulses are generated, which propagate in power lines and lead to overvoltages in the electricity transmission system. These overvoltages can damage electrical loads, reduce system performance, and even lead to power outages.

In order to prevent these overvoltages, shield wires are used in power lines, which are installed over the current carrying phase conductors and they act as protection against a direct lightning strike to the line’s phase conductors. However, the presence of shield wires in power transmission lines creates a problem of taking into account their impact on the electrical parameters of the line. For example, the presence of shield wires increases the capacitance between phase conductors and between phase conductors and the earth, which can reduce the effectiveness of overvoltage protective devices. Shield wires can also affect the electrical parameters of power lines, such as inductance, which undoubtedly affects the course of transient processes.

Currently, one of the most common methods of analyzing transient processes in power lines is the use of mathematical modeling [1,2,3,4,5,6,7]. Such popularity of mathematical modeling is associated with the high costs of conducting full-scale experiments and in some cases with the impossibility of carrying them out in their entirety.

In this paper, a mathematical model of the ultra-high voltage power line was developed, which takes into account shield wires. The model is based on the laws of the applied electrodynamics for distributed parameter systems. Based on this model, transient processes in the system under operating and fault conditions are analyzed. The proposed model is designed for high-voltage power lines, which makes it possible to analyze this model in a specific task. The vast majority of developed scientific and research models are formulated based on the universality of engineering approaches. However, computer programs used for the specific analyzed model more precisely take into account the influence of hidden movements and stresses determined in the dynamic system in accordance with Helmholtz’s theory using additional differential equations and non-stationary constraint equations. For this purpose, we actually used our original program to algorithmically implement the given task. In such power lines, transient processes are complex phenomena, because wave processes occur in them over long lengths, which are related to the movement of electromagnetic waves along the line [8,9].

It is obvious that work in this field has been going on for many years and many scientists from around the world contribute to the improvement of methods of mathematical modeling of power lines. Let us now present an overview of scientific works that are thematically closest to our article. The most important references include [10,11], where a method based on a frequency domain technique known as the numerical Laplace transform was used. This method can be used as a main analytical tool or as a support for time domain tools such as EMTP [10].

In paper [1], a mathematical model of a three-phase transmission line was presented directly in the time domain, without explicit use of inverse transformations. In addition, the article proposes the use of the procedure of analytical integration of the electromagnetic state equations, which enables the study of power line transients. The results were verified using the EMTP-RV software package. The article [2] presents a mathematical model of the power supply system, the key element of which is a long line supplied by a power transformer. Two first-order equations were used to model transient electromagnetic processes, with Dirichlet boundary conditions of the first type assumed to be known. The simulation model of the three-phase electricity transmission system was developed in [5] using the MATLAB software package, including the Simulink library.

The mathematical model of a high-voltage power line was developed in [6] with an emphasis on modeling transmission line supports. Transient states in the supply line were analyzed using two first-order linear equations without considering the distributed conductance: phase-to-ground and phase-to-phase. The results of computer simulations were presented, also in the case of atmospheric discharge to the supports. In the article [7], based on the interdisciplinary method of mathematical modeling, a distributed parameter mathematical model of an electrical network was developed. This approach allows the use of ordinary and partial differential equations. Electromagnetic transient processes for short-circuit state were analyzed.

Articles [12,13] present mathematical models of a power line involving cascades of equivalent linear circuits connected in series and taking into account complex line parameters. The electromagnetic state of each cascade is described by first-order ordinary differential equations. These models were validated using the inverse Laplace transform.

In the article [14], using an EMTP software development environment, a mathematical model of a 400 kV power transmission line with shield wires was presented. In this case, the line is treated as a system with lumped parameters, and the influence of shield wires is taken into account when calculating the parameters of the power transmission line. Based on this model, various methods of grounding power line supports are being investigated. The article [15] is based on research on the impact of direct lightning strikes on the characteristics of lightning arresters of 150 kV overhead power lines with a lightning cable. The authors of the article carried out computer modeling in the EMTP software development environment, taking into account distributed parameter lines. Article [16] is the result of research into various grounding schemes for shield wires. Within its scope, on the basis of computer modeling with the use of the EMTP software development environment, tests of overvoltages in the power transmission line during lightning discharges for various grounding schemes of shield wires were carried out. During the research, a model of a distributed parameter power transmission line including shield wires was considered. Test results have shown that the grounding of shield wires reduces the level of overvoltages compared to lines without the grounding of shield wires. The author of the article [17], using the EMTP software development environment, conducted research on the impact of lightning current on power lines. A mathematical model of a distributed parameter power transmission line including shield wires, built into the EMTP software development environment, was used for the research.

The main part of transmission line stresses, determining the requirements for the insulation of the electrical network and determining its reliable operation, are overvoltages. These are, in particular, overvoltages arising during lightning discharges, whose maximum values may be many times higher than the network voltage [18]. Computer simulations are usually used to determine high-frequency lightning overvoltages. Simulation programs should use appropriate models of electrical devices and transient states in electrical networks [19].

In article [20], the authors, using ANSYS and FLUENT software, developed a mathematical model of a power line for modeling electromagnetic processes. A distributed parameter line in a single-line version is considered here, and the distributed parameters were recalculated when calculating the operating parameters of the line. It is also worth noting that the electrical conductance of the power line was omitted in the mathematical model.

Article [21] presents a comprehensive review of the design of a multiphase power line. To analyze the operation modes of such a line, the authors used a mathematical model of a power line built into the MATLAB/Simulink software development environment and presented the results of a computer simulation. The advantages of a multiphase power line compared to traditional three-phase lines are also given.

In the papers [22,23], the authors use the equations of a transmission line containing shield wires to analyze transient processes. The equations are presented in matrix–vector form. The authors take into account the line’s losses in the boundary conditions. To integrate the equations, the authors use the finite difference method in the FDTD algorithm. The proposed concept makes it possible to take into account the influence of shield wires on transient processes in the phase conductors of the line.

In the article [24], using the ATP software development environment, computer simulations were carried out for various models of power lines in order to examine the impact of the configuration of their phase conductors and shield wires on overvoltages during a lightning strike. The authors show that a properly selected power line configuration has a significant impact on the results of overvoltage simulations. It has also been clearly shown that erroneous consideration of line resistance and capacitance can lead to underestimation of overvoltages.

In the article [25], the authors examine various aspects of transient processes in electrical networks: overvoltages, current increases, frequency responses, etc. The research is carried out using the EMTP software development environment. In particular, the transient processes in the 132 kV power transmission line, which was connected to the wind farm, were examined. During the study of transient processes, the line was analyzed as a distributed parameter system with one shield wires. In the article [26], the author, based on various mathematical models of power lines implemented in the EMTP software development environment, searches for a method and means of reducing the impact of atmospheric overvoltages on power lines. The author puts emphasis on the modeling of insulators, but the developed line models also take into account the presence of shield wires.

In the article [3], the authors emphasize the importance of taking into account all power line elements when modeling power processes, in particular: the parameters of supports, the method of their earthing, and the presence of lightning discharges. The authors compare the results of computer simulations obtained using the Matlab/Simulink software development environment, simulating different states of a power line during lightning strikes. The authors note that for a full representation of electromagnetic processes in the line, the presence of shield wires must be taken into account.

Summing up the review of the available literature, it can be noted that currently there are no only right, universal, and accepted approaches to modeling power lines, including shield wires. Each researcher builds their own models or uses available software packages, depending on the complexity of the task, to include a certain number of power line elements or to study a specific phenomenon. Currently, models of power lines with lumped parameters are used [14], which are impractical when examining the processes taking place in long power lines, because in the latter complex wave processes occur. Power line models are also used in the version of single line equivalents [20], which are not universal enough because they do not allow for the analysis of asymmetric operating states of the line as an element of the power system. The leaders in the analysis of transient processes based on computer modeling are programming tools: EMTP [14,15,16,17,25,26], its predecessor ATP [24], and the world-renowned Matlab/Simulink [3,21] package. The EMTP and ATP development tools use the finite element method to solve long-line equations. In [27], cable lines are modeled using the wideband cable model included in the EMTP-RV library, and impedance matrices are fitted to the cable at each frequency using a vector fitting technique. The article [28] presents a universal transmission line model for simulating electromagnetic transients (EMT) in power systems. This model can be applied to both overhead lines and cables, even in the presence of a strongly frequency-dependent transformation matrix and very different modal time delays. In the case of the Matlab/Simulink software package, the d’Alembert method (traveling wave method) [29] is used to solve the equations of a transmission line, but its use requires the analysis of an ideal line without taking into account the resistance and conductance of the line.

Thus, the study of transient processes in long power lines with shield wires is an important and urgent task in the field of power engineering. Properly considering the effects of shield wires when modeling power lines can help keep power systems safe and efficient. Therefore, the aim of this work is to improve and develop methods and approaches to mathematical modeling of transient processes in power lines with shield wires in order to ensure the most adequate simulation results and their effective use.

2. Mathematical Model of an Electric Power Network

Figure 1 shows the equivalent circuit of a fragment of the tested electricity transmission system, which is the basis for the calculations.

This fragment consists of a power transmission line supplying an equivalent power system 2. The power line is represented as a line with distributed parameters, including two shield wires. The phase conductors are represented as individual ones with corresponding equivalent radii. Such a line can therefore be considered a five-wire line including shield wires T1, T2, and phase conductors A, B, C. The equivalent power system is represented by the phase electromotive forces e_S2 (together with their corresponding modules and arguments, i.e., phase shift angles) and its internal resistances r_S2 and inductances L_S2. At the beginning of the power line, the supply voltage is applied to it. The shield wires T1 and T2 are short-circuited at the end of the line, and open at the beginning, i.e., they form an open circuit with earthing of the T2 conductor at the beginning of the line.

Based on the well-known laws of applied electrical engineering, let us write down the equations of the electrical power state of the tested object (Figure 1):

$$\frac{d{i}_{S2}}{dt}=L_{S2}^{-1}\left(u_{EL}^{S2}-r_{S2}{i}_{S2}-e_{S2}\right);$$

(1)

$$\frac{{\partial }^{2}u}{\partial t^2}={\left(LC\right)}^{-1}\left(\frac{{\partial }^{2}u}{\partial x^2}-\left(Lg+rC\right)\frac{\partial u}{\partial t}-rgu\right)\hspace{0.17em}.$$

(2)

In Equation (1) there are single-column matrices, i.e., column vectors, and diagonal matrices:

$$e_{S2}=\mathrm{col}\left(e_{S2}^{(A)},\hspace{0.17em}{e}_{S2}^{(B)},\hspace{0.17em}{e}_{S2}^{(C)}\right), i_{S2}=\mathrm{col}\left(i_{S2}^{(A)},\hspace{0.17em}{i}_{S2}^{(B)},\hspace{0.17em}{i}_{S2}^{(C)}\right), u_{EL}^{S2}=\mathrm{col}\left(u_{EL}^{(A)},\hspace{0.17em}{u}_{EL}^{(B)},\hspace{0.17em}{u}_{EL}^{(C)}\right);$$

(3)

$$r_{S2}=\mathrm{diag}\left(r_{S2}^{\left(A\right)},\hspace{0.17em}{r}_{S2}^{\left(B\right)},\hspace{0.17em}{r}_{S2}^{\left(C\right)}\right), L_{S2}=\mathrm{diag}\left(L_{S2}^{\left(A\right)},\hspace{0.17em}{L}_{S2}^{\left(B\right)},\hspace{0.17em}{L}_{S2}^{\left(C\right)}\right),$$

(4)

where e_S2^(A), e_S2^(B), e_S2^(C) are EMFs of the equivalent power system 2; i_S2^(A), i_S2^(B), i_S2^(C) are phase currents in branches of the equivalent power system 2; r_s, L_s are internal resistances and inductances of the phase branches, respectively.

In the Formula (2) there are column vectors of the phase-to-ground voltages, as well as currents of the shield wires and phase conductors as functions of x and t coordinates:

$$u=\mathrm{col}\left(u^{(T1)},u^{(T2)},u^{(A)},u^{(B)},u^{(C)}\right), i=\mathrm{col}\left(i^{(T1)},i^{(T2)},i^{(A)},i^{(B)},i^{(C)}\right),$$

(5)

The matrices in (2) are as follows:

$$\begin{array}{ll}L=\begin{array}{|ccccc|}\hline L_{T1}& M_{TT}& M_{TF}& M_{TF}& M_{TF}\\ M_{TT}& L_{T2}& M_{TF}& M_{TF}& M_{TF}\\ M_{FT}& M_{FT}& L_A& M_{FF}& M_{FF}\\ M_{FT}& M_{FT}& M_{FF}& L_B& M_{FF}\\ M_{FT}& M_{FT}& M_{FF}& M_{FF}& L_C\\ \hline\end{array},& C=\begin{array}{|ccccc|}\hline C1& -C_{TT}& -C_{TF}& -C_{TF}& -C_{TF}\\ -C_{TT}& C1& -C_{TF}& -C_{TF}& -C_{TF}\\ -C_{FT}& -C_{FT}& C2& -C_{FF}& -C_{FF}\\ -C_{FT}& -C_{FT}& -C_{FF}& C2& -C_{FF}\\ -C_{FT}& -C_{FT}& -C_{FF}& -C_{FF}& C2\\ \hline\end{array},\\ r=\begin{array}{|ccccc|}\hline r_{T1}+r_Z& r_Z& r_Z& r_Z& r_Z\\ r_Z& r_{T2}+r_Z& r_Z& r_Z& r_Z\\ r_Z& r_Z& r_A+r_Z& r_Z& r_Z\\ r_Z& r_Z& r_Z& r_B+r_Z& r_Z\\ r_Z& r_Z& r_Z& r_Z& r_C+r_Z\\ \hline\end{array};& g=\begin{array}{|ccccc|}\hline G1& -g_{TT}& -g_{TF}& -g_{TF}& -g_{TF}\\ -g_{TT}& G1& -g_{TF}& -g_{TF}& -g_{TF}\\ -g_{FT}& -g_{FT}& G2& -g_{FF}& -g_{FF}\\ -g_{FT}& -g_{FT}& -g_{FF}& G2& -g_{FF}\\ -g_{FT}& -g_{FT}& -g_{FF}& -g_{FF}& G2\\ \hline\end{array};\end{array}$$

(6)

$$C1=C_{T1T2}+3C_{TF}+C_{TZ}, C2=2C_{FT}+2C_{FF}+C_{FZ};$$

(7)

$$G1=g_{T1T2}+3g_{TF}+g_{TZ}, G2=2g_{FT}+2g_{FF}+g_{FZ}.$$

(8)

where u^(T1), u^(T2), u^(A), u^(B), u^(C) are phase-to-ground voltages of shield wires T1, T2 and phase conductors A, B, C, respectively; i^(T1), i^(T2), i^(A), i^(B), i^(C) are currents in the conductors T1, T2, and A, B, C, respectively; L_T1, L_T2, L_A, L_B, L_C—distributed (per unit length) inductances of conductors T1, T2 and A, B, C, respectively; M_TT, M_FT, M_FF are distributed mutual inductances: «shield wires—shield wires», «shield wires—phase conductor», «phase conductor—phase conductor», respectively; R_T1, R_T2, R_A, R_B, R_C, R_Z are distributed resistances of the conductors T1, T2, A, B, C, and earth, respectively; C_TT, C_TF, C_FF, g_TT, g_TF, g_TF are distributed capacitances and conductances between all conductors.

Equations (1) and (2) describe the electromagnetic state of the tested object. The first equation is an ordinary differential equation. Solving it is not a problem. Many specialized computer programs are used for this purpose, which easily gives solutions to the above-mentioned equation. As for Equation (2), the situation is completely different. Equation (2) describes wave electromagnetic transient processes in a power transmission line with distributed parameters. This is a second-order partial differential equation. Boundary conditions are needed to solve it. In general, they can be functions of voltages, currents, and charges at the beginning and end of the line. Since Equation (2) contains voltage functions, to solve it, voltages at the beginning and end of the power line are needed. In our case, the voltages of the phase conductors at the beginning of the power line are given as first-type conditions (Dirichlet boundary conditions). As for the voltages of the shield wires at the beginning and end of the line as well as the voltages of the phase conductors at the end of the line, the latter are not known, which is caused by the configuration of the connection of the shield wires and phase conductors of the line with other elements of the electricity transmission system. To find these voltages, it is suggested to use the second and third types of boundary conditions.

3. Determinations of Boundary Conditions

The boundary conditions for Equation (2) may be expressed by the following equation:

$$-\frac{\partial u}{\partial x}=L\frac{\partial i}{\partial t}+ri.$$

(9)

Equation (9) can be easily obtained from Kirchhoff’s second law for electrical circuits with distributed parameters. By definition, it can be used as the boundary condition of Equation (2).

By discretizing Equations (2) and (9) using the straight lines method and the concept of discretization of the central derivative [30], it can obtain:

$$\frac{d{v}_j}{dt}={\left(LC\right)}^{-1}(\frac{1}{{\left(\Delta x\right)}^2}\left(u_{j-1}-2u_j+u_{j+1}\right)-(Lg+rC)v_j\underset{}{\overset{}{-}}rg{u}_j), \frac{d{u}_j}{dt}=v_j, j=1,\dots ,N;$$

(10)

$$\frac{d{i}_j}{dt}=L^{-1}\left(\frac{1}{2\Delta x}\left(u_{j-1}-u_{j+1}\right)-r{i}_j\right), j=1,\dots ,N,$$

(11)

where Δx is discretization interval (delta), N is the number of discrete points (nodes).

Let us write Equations (10) and (11) for the first node j = 1 using the straight lines method:

$$\frac{d{v}_1}{dt}={\left(LC\right)}^{-1}(\frac{1}{{\left(\Delta x\right)}^2}\left(u_0-2u_1+u_2\right)-(Lg+rC)v_1\underset{}{\overset{}{-}}rg{u}_1), \frac{d{u}_1}{dt}=v_1;$$

(12)

$$\hspace{0.17em}\frac{d{i}_1}{dt}=L^{-1}\left(\frac{1}{2\Delta x}\left(u_0-u_2\right)-r{i}_1\right).$$

(13)

Analyzing Equations (12) and (13), it can be seen that in order to find the voltages for the first node of the line and the currents in the first discrete branch of the line, the virtual node voltage u₀ at the beginning of the line must be known. However, it has already been mentioned that the voltages of the phase conductors at the beginning of the line are known and the line supply voltages u₁^(A), u₁^(B), u₁^(C) are given. The voltage of the shield wires T2 at the beginning of the line is also known. 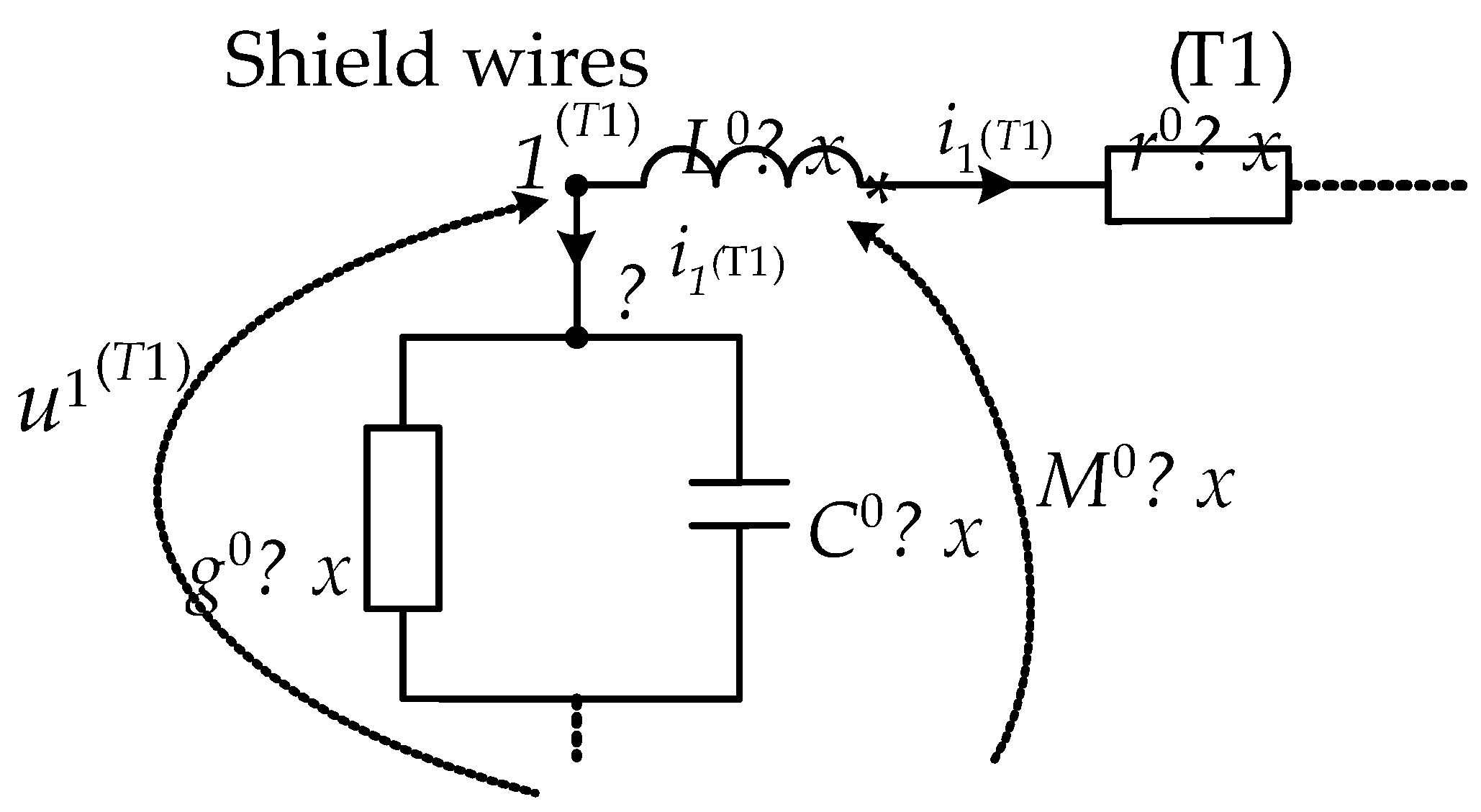It is equal to zero, i.e., u₁^(T2) = 0, because the shield wires T2 at the beginning of the power line is earthed, whereas the voltage of the shield wires T1 at the beginning of the line is unknown. This shield wires is in the open (non-operational) state at the beginning of the line. To find the voltage u₁^(T1) of the shield wires T1 at the beginning of the line using Equations (12), find the virtual voltage u₀^(T1) for the shield wires T1 at the beginning of the line. For this purpose, it is proposed to consider the first (at the beginning of the line) discrete section of the line in the Г version (the boundary conditions for the equations of the state of the T1 conductor at the beginning of the line are determined by the Г-type representation), which is shown in Figure 2.

Let us write the equation for the first node of the discretized conductor T1 (Figure 2) according to the first Kirchhoff law:

$$-i_1^{(T1)}-\Delta i_1^{(T1)}=0,$$

(14)

where Δi₁^(T1) is total leakage current from T1 conductor to: T2, A, B, C conductors and ground Z, respectively, for the first discrete section.

Let us calculate the total leakage current Δi₁^(T1) in Equation (14) as follows:

$$\Delta i_1^{(T1)}={\displaystyle \sum _{m=T2}^Z\left(\Delta x{g}_{T1,m}{u}_1^{(T1,m)}+\Delta x{C}_{T1,m}\frac{d{u}_1^{(T1,m)}}{dt}\right), m=T2,A,B,C,Z,}$$

(15)

where g_T1,m, C_T1,m are distributed mutual and self conductances and capacitances between the T1, T2, and A, B, C conductors; conductance and capacitance of earth Z; u^(T1,m) are voltages between the T1, T2, and A, B, C conductors; voltage of earth Z, for the first node.

For the same first node, let us extract from the matrix Equation (13) the elementary state equation of the conductor T1, which, taking into account the linear structure of vectors assumed in (5), will be written in the following form:

$$\frac{d{i}_1^{(T1)}}{dt}=\frac{1}{2\Delta x}\left({\displaystyle \sum _{k=1}^5\left({\mathrm{\Lambda }}_{1,k}{u}_0^{(k)}\right)}-{\displaystyle \sum _{k=1}^5\left({\mathrm{\Lambda }}_{1,k}{u}_2^{(k)}\right)}\right)-{\displaystyle \sum _{k=1}^5\left(K_{1,k}^{}{i}_1^{(k)}\right)},$$

(16)

where Λ = L^–1; K = Λ r; k is matrix column number and vector element number.

Now let us differentiate Equations (14) and (15) over time, taking into account the initial conditions [30]:

$$-\frac{d{i}_1^{(T1)}}{dt}-\frac{d\Delta i_1^{(T1)}}{dt}=0;$$

(17)

$$\frac{d\Delta i_1^{(T1)}}{dt}={\displaystyle \sum _{m=T2}^Z\left(\Delta x{g}_{T1,m}{v}_1^{(T1,m)}+\Delta x{C}_{T1,m}\frac{d{v}_1^{(T1,m)}}{dt}\right)}, m=T2,A,B,C,Z,$$

(18)

Since:

$$u^{(T1,m)}=u^{(T1)}-u^{(m)}, \frac{d{u}_{}^{(T1,m)}}{dt}=\frac{d{u}_{}^{(T1)}}{dt}-\frac{d{u}_{}^{(m)}}{dt}, \frac{d{v}_{}^{(T1,m)}}{dt}=\frac{d{v}_{}^{(T1)}}{dt}-\frac{d{v}_{}^{(m)}}{dt}, m=T2,A,B,C,Z,$$

(19)

Equation (18) takes the form:

$$\frac{d\Delta i_1^{(T1)}}{dt}=\Delta x{\displaystyle \sum _{m=T2}^Z\left(g_{T1,m}\left(v_1^{(T1)}-v_1^{(m)}\right)+C_{T1,m}\left(\frac{d{v}_1^{(T1)}}{dt}-\frac{d{v}_1^{(m)}}{dt}\right)\right)}, m=T2,A,B,C,Z,$$

(20)

Let us substitute dependencies (16) and (20) into Equation (17):

$$\begin{array}{c}-\frac{1}{2\Delta x}\left({\displaystyle \sum _{k=1}^5\left({\mathrm{\Lambda }}_{1,k}{u}_0^{(k)}\right)}-{\displaystyle \sum _{k=1}^5\left({\mathrm{\Lambda }}_{1,k}{u}_2^{(k)}\right)}\right)+{\displaystyle \sum _{k=1}^5\left(K_{1,k}^{}{i}_1^{(k)}\right)}\\ -\Delta x{\displaystyle \sum _{m=T2}^Z\left(g_{T1,m}\left(v_1^{(T1)}-v_1^{(m)}\right)+C_{T1,m}\left(\frac{d{v}_1^{(T1)}}{dt}-\frac{d{v}_1^{(m)}}{dt}\right)\right)}=0, m=T2,A,B,C,Z,\end{array}$$

(21)

Substituting (12) to (21) (only for the T1 conductor) we obtain the virtual node voltage (u₀^(T1)) at the beginning of the T1 conductor:

$$\begin{array}{c}{u}_0^{T1}=\frac{2\Delta x}{2C_{11}{P}_{11}+{\Lambda }_{11}}\{\frac{1}{2\Delta x}\left({\displaystyle \sum _{k=1}^5\left({\Lambda }_{1,k}{u}_2^{(k)}\right)}-{\displaystyle \sum _{k=2}^5\left({\Lambda }_{1,k}{u}_0^{(k)}\right)}\right)\\ +{\displaystyle \sum _{k=1}^5\left(K_{1,k}{i}_1^{(k)}\right)}-\Delta x\left(G_{11}{v}_1^{(T1)}-{\displaystyle \sum _{m=T2}^C\left(g_{T1,m}{v}_1^{(m)}+C_{T1,m}\frac{d{v}_1^{(m)}}{dt}\right)}\right)\\ -\Delta x{C}_{11}(\frac{1}{{\left(\Delta x\right)}^2}\left({\displaystyle \sum _{k=1}^5\left(P_{1,k}{i}_1^{(k)}+P_{1,k}{u}_2^{(k)}\right)}\right)\\ -\frac{2}{{\left(\Delta x\right)}^2}{\displaystyle \sum _{k=1}^5\left(P_{1,k}^{}{u}_1^{(k)}\right)}-{\displaystyle \sum _{k=1}^5\left(F_{1,k}^{}{v}_1^{(k)}+D_{1,k}^{}{u}_1^{(k)}\right)})\}, m=T2,A,B,C,Z,\end{array}$$

(22)

where P = (LC)^–1, D = Prg, F = P(Lg + rC), C₁₁, G₁₁ are elements of the C and G matrix, respectively.

Let us find the voltages at the beginning of the line for conductors T2 and A, B, C:

$$u_1^{(T2)}=0, u_1^{(m)}=U_{\mathrm{m}}^{(m)}\sin \left(\mathsf{\omega }t+{\mathsf{\phi }}^{(m)}\right), m=A,B,C,$$

(23)

and their derivatives in Formula (22) are as follows:

$$v_1^{(m)}=\mathsf{\omega }{U}_{\mathrm{m}}^{(m)}\cos \left(\mathsf{\omega }t+{\mathsf{\phi }}^{(m)}\right), \frac{d{v}_1^{(m)}}{dt}=-{\mathsf{\omega }}^2{U}_{\mathrm{m}}^{(m)}\sin \left(\mathsf{\omega }t+{\mathsf{\phi }}^{(m)}\right), m=A,B,C,$$

(24)

In this way, all the necessary voltage and current functions were obtained to find the voltages at the first node of the discretized line and the currents in the first discrete branches of the shield wires and phase conductors of the line.

Now let us write Equations (10) and (11) for the last node of the discretized power line j = N:

$$\frac{d{v}_N}{dt}={\left(LC\right)}^{-1}(\frac{1}{{\left(\Delta x\right)}^2}\left(u_{N-1}-2u_N+u_{N+1}\right)-(Lg+rC)v_N\underset{}{\overset{}{-}}rg{u}_N), \frac{d{u}_N}{dt}=v_N;$$

(25)

$$\frac{d{i}_N}{dt}=L^{-1}\left(\frac{1}{2\Delta x}\left(u_{N-1}-u_{N+1}\right)-r{i}_N\right).$$

(26)

After analyzing Equations (25) and (26), it can be concluded that in order to find the voltages at the last nodes and the currents in the last discrete branches of the shield wires and phase conductors of the line, the virtual node voltages u_N+1 at the end of the line must be determined.

In paper [8], based on the second-type boundary conditions, a universal expression was obtained for finding the virtual node voltage u_N+1 at the end of a three-phase line. Since the concept of finding this voltage has not changed, in order not to overload this article with mathematical calculations, the mentioned voltages will not be found again, but the final formula will be presented:

$$u_{N+1}=u_{N-1}+2\left(u_{EL}-u_N\right), u_{EL}=\mathrm{col}\left(u_{EL}^{(T1)},u_{EL}^{(T2)},u_{EL}^{(A)},u_{EL}^{(B)},u_{EL}^{(C)}\right).$$

(27)

This expression enables the autonomous use of the mathematical model of the power line for any configuration of connections between the network elements and the transmission line. However, expression (27) includes parameters such as voltages at the end of the power transmission line (u_EL^(T1), u_EL^(T2), u_EL^(A), u_EL^(B), u_EL^(C)). In fact, in this case, the task boils down to finding these voltages, i.e., the voltages of the conductors connected to the equivalent power grid 2. Since the shield wires and the phase conductors of the line have different connection configurations, finding the mentioned voltages should be carried out separately for each of the conductors.

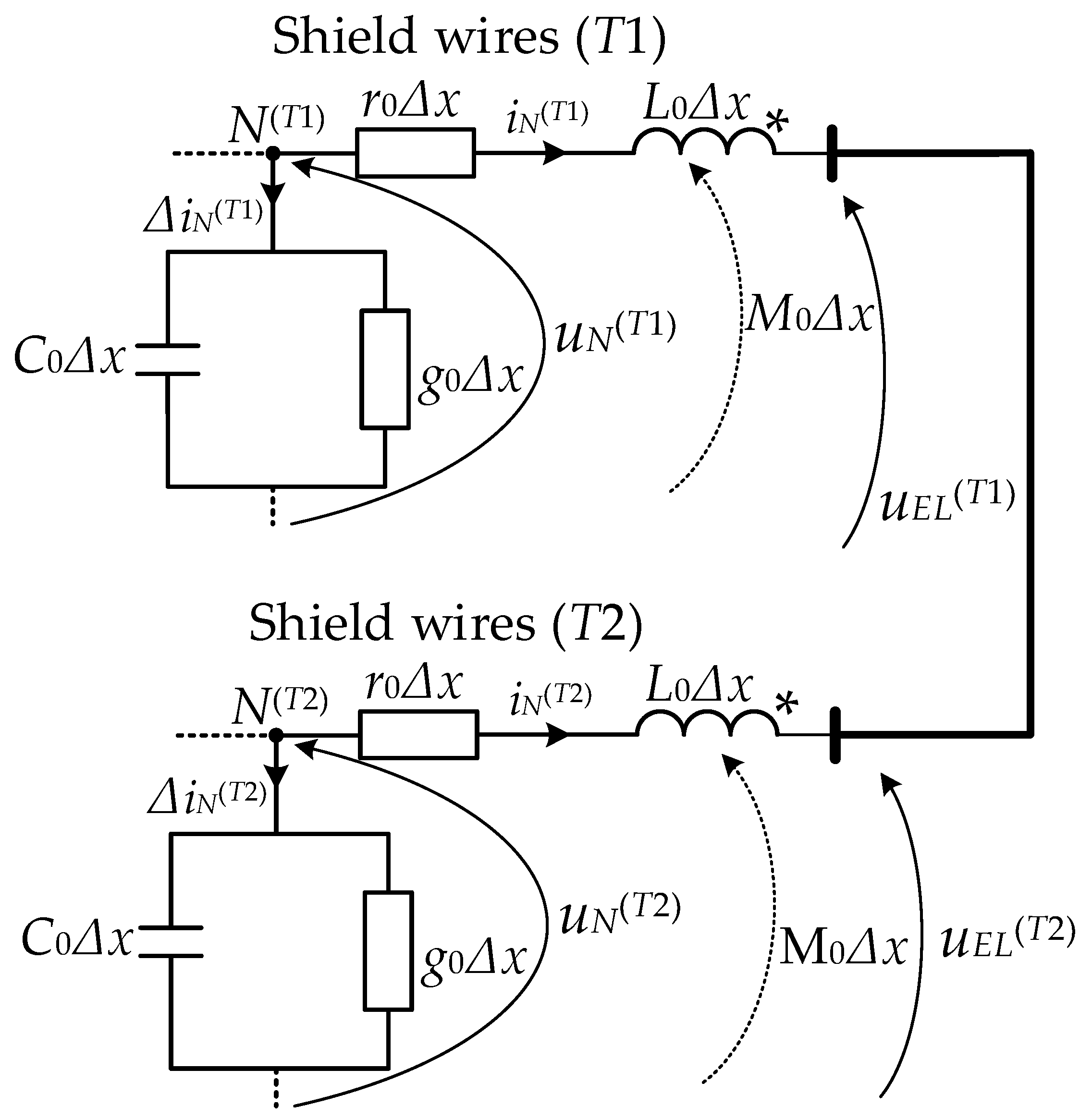
Let us find the voltages at the end of the line for the shield wires. Since the shield wires at the end of the line are short-circuited (see Figure 1), their voltages at the end of the line will be the same, i.e., u_EL^(T1) = u_EL^(T2) = u_EL^(T). In order to find this voltage, it is proposed to consider an equivalent circuit for the last sections of line discrete conductors (Figure 3). As in the previous case, the Г-type equivalent scheme was used.

Based on Kirchhoff’s first law, the following equation can be written for the circuit shown in Figure 3:

$$i_N^{(T1)}=-i_N^{(T2)}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{d{i}_N^{(T1)}}{dt}=-\frac{d{i}_N^{(T2)}}{dt}.$$

(28)

On the basis of Kirchhoff’s second law, further equations can also be written for the circuit shown in Figure 3:

$$\frac{d{i}_N^{(T1)}}{dt}=\frac{1}{\Delta x{L}_{T1}}(u_N^{(T1)}-\Delta x({\displaystyle \sum _{m=T2}^C\left(M_{T1,m}\frac{d{i}_N^{(m)}}{dt}\right)}+r_{T1}{i}_N^{(T1)}+r_Z{\displaystyle \sum _{m=A}^C\left(i_N^{(m)}\right)})-u_{EL}^{(T)}), m=T2,A,B,C;$$

(29)

$$\frac{d{i}_N^{(T2)}}{dt}=\frac{1}{\Delta x{L}_{T2}}(u_N^{(T2)}-\Delta x({\displaystyle \sum _{n=T1}^C\left(M_{T2,n}\frac{d{i}_N^{(n)}}{dt}\right)}+r_{T2}{i}_N^{(T2)}+r_Z{\displaystyle \sum _{n=A}^C\left(i_N^{(n)}\right)})-u_{EL}^{(T)}), n=T1,A,B,C,$$

(30)

where m, n are conductors; i_N^(Z) is the earth current in the last section of the discrete branch (i_N^(Z) = i_N^(A) + i_N^(B) + i_N^(C)).

The asterisks “*” indicate the ends of the shield wires, for which, with the same currents’ direction relative to these ends, the magnetic fluxes generated around the shield wires have the same directions. Now, substituting Equations (29) and (30) into the second expression in (28) and then deriving the voltage of the shield wires at the end of the line (u_EL^(T)), the following relationship is obtained:

$$\begin{array}{c}{u}_{EL}^{(T)}=\frac{1}{2}\{u_N^{(T2)}+u_N^{(T1)}-\Delta x({\displaystyle \sum _{m=T2,n=T1}^{C,C}(M_{T1,m}\frac{d{i}_N^{(m)}}{dt}+}{M}_{T2,n}\frac{d{i}_N^{(n)}}{dt})+2r_Z\left(i_N^{(A)}+i_N^{(B)}+i_N^{(C)}\right)\underset{}{\overset{}{}})\underset{}{\overset{}{}}\},\\ m=T2,A,B,C, n=T1,A,B,C.\end{array}$$

(31)

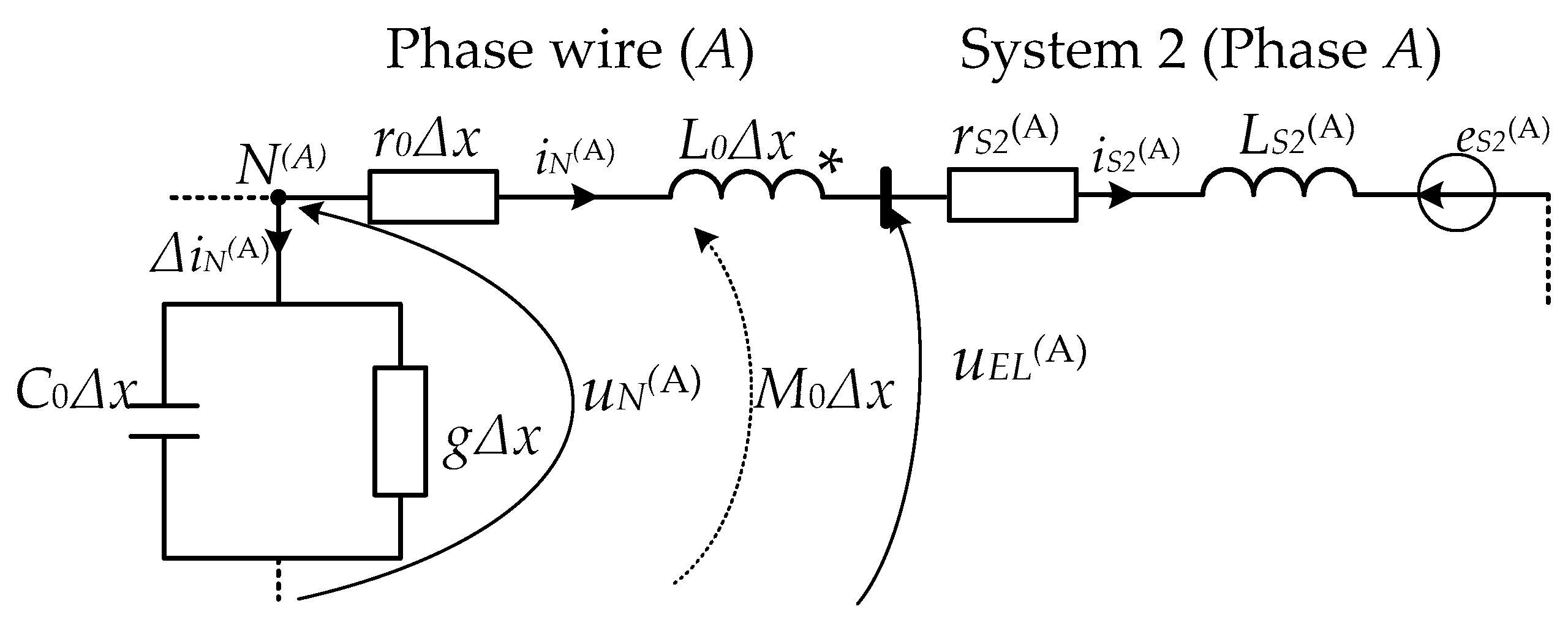
Now let us find the voltage of the phase conductors at the end of the line. Traditionally, let us present the equivalent circuit of the phase conductors for the last discrete section (Figure 4). For better perception, Figure 4 shows only the equivalent circuit for phase A of the line.

Let us write the following equation based on Kirchhoff’s first law (see Figure 4):

$$i_N^{(A)}=i_{S2}^{(A)}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Rightarrow \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{d{i}_N^{(A)}}{dt}=\frac{d{i}_{S2}^{(A)}}{dt}.$$

(32)

and the equation based on Kirchhoff’s second law (see Figure 4) [31]:

$$\frac{d{i}_N^{(A)}}{dt}=\frac{1}{\Delta x{L}_A}(u_N^{(A)}-\Delta x({\displaystyle \sum _{q=T1}^C\left(M_{A,q}\frac{d{i}_N^{(q)}}{dt}\right)}+\left(r_A+r_Z\right)i_N^{(A)}+r_Z{\displaystyle \sum _{q=B}^C\left(i_N^{(q)}\right)})-u_{EL}^{(A)}), q=T1,T2,B,C.$$

(33)

Now let us extract from the matrix Equation (1) the electromagnetic state equation for the phase A branch of the equivalent power system 2, taking into account Formulas (3) and (4):

$$\frac{d{i}_{S2}^{(A)}}{dt}=\frac{1}{L_{S2}^{(A)}}\left(u_{EL}^{(A)}-r_{S2}^{(A)}{i}_{S2}^{(A)}-e_{S2}^{(A)}\right).$$

(34)

Substituting Equations (33) and (34) into the second expression in (32), the following equation is obtained:

$$\begin{array}{c}\frac{1}{\Delta x{L}_A}(u_N^{(A)}-\Delta x({\displaystyle \sum _{q=T1}^C\left(M_{A,q}\frac{d{i}_N^{(q)}}{dt}\right)}+\left(r_A+r_Z\right)i_N^{(A)}+r_Z{\displaystyle \sum _{q=B}^C\left(i_N^{(q)}\right)})-u_{EL}^{(A)})\\ =\frac{1}{L_{S2}^{(A)}}\left(u_{EL}^{(A)}-r_{S2}^{(A)}{i}_{S2}^{(A)}-e_{S2}^{(A)}\right), q=T1,T2,B,C.\end{array}$$

(35)

Let us derive from (35) the voltage of the phase A conductor (u_EL^(A)) at the end of the line:

$$\begin{array}{c}{u}_{EL}^{(A)}=-\frac{\Delta x{L}_A{L}_{S2}^{(A)}}{\Delta x{L}_A-L_{S2}^{(A)}}\{-\frac{1}{\Delta x{L}_A}[u_N^{(A)}+\Delta x({\displaystyle \sum _{q=T1}^C\left(M_{A,q}\frac{d{i}_N^{(q)}}{dt}\right)}\\ +\left(r_A+r_Z\right)i_N^{(A)}+r_Z{\displaystyle \sum _{q=B}^C\left(i_N^{(q)}\right)})]-\frac{1}{L_{S2}^{(A)}}\left[r_{S2}^{(A)}{i}_{S2}^{(A)}+e_{S2}^{(A)}\right]\}, q=T1,T2,B,C.\end{array}$$

(36)

For phases B and C, the procedure is analogous:

$$\begin{array}{c}{u}_{EL}^{(B)}=-\frac{\Delta x{L}_B{L}_{S2}^{(B)}}{\Delta x{L}_B-L_{S2}^{(B)}}\{-\frac{1}{\Delta x{L}_B}[u_N^{(B)}+\Delta x({\displaystyle \sum _{d=T1}^C\left(M_{T1,d}\frac{d{i}_N^{(d)}}{dt}\right)}\\ +\left(r_B+r_Z\right)i_N^{(B)}+r_Z{\displaystyle \sum _{d=T2}^C\left(i_N^{(d)}\right)})]-\frac{1}{L_{S2}^{(B)}}\left[r_{S2}^{(B)}{i}_{S2}^{(B)}+e_{S2}^{(B)}\right]\}, d=T1,T2,A,C;\end{array}$$

(37)

$$\begin{array}{c}{u}_{EL}^{(C)}=-\frac{\Delta x{L}_C{L}_{S2}^{(C)}}{\Delta x{L}_C-L_{S2}^{(C)}}\{-\frac{1}{\Delta x{L}_C}[u_N^{(C)}+\Delta x({\displaystyle \sum _{p=T1}^B\left(M_{T1,p}\frac{d{i}_N^{(p)}}{dt}\right)}\\ +\left(r_C+r_Z\right)i_N^{(C)}+r_Z{\displaystyle \sum _{p=T2}^C\left(i_N^{(q)}\right)})]-\frac{1}{L_{S2}^{(C)}}\left[r_{S2}^{(C)}{i}_{S2}^{(C)}+e_{S2}^{(C)}\right]\}, p=T1,T2,A,B.\end{array}$$

(38)

Equations (1), (10) and (11) are subject to joint integration with the following formulas: (3), (4), (6)–(8), (22)–(24), (27), (31) and (36)–(38).

4. Computer Simulation Results

The simulation of electromagnetic transient processes was carried out for the case of switching the power line to the normal operating mode, followed by a single-phase short-circuit to earth (point K, Figure 1) (hereinafter short-circuit). The computer simulation was run in the following order from the time t = 0 s. The simulation was started with a single-phase connection of the power line wires so that the phase voltage functions would start from zero. This means that a simulation of power line switching on by gas circuit breakers was carried out phase-by-phase, taking into account the controlled switching. Modeling of the circuit breakers in the present operation did not take place, and the line was switched on by snap commutation.

Switching at the beginning of the line took place in the following instants: t₁^(A) = 0.0090277 s, t₁^(B) = 0.0056944 s, t₁^(C) = 0.0023611 s, and at the end of the line: t_EL^(A) = 0.0095833 s, t_EL^(B) = 0.0062499 s, t_EL^(C) = 0.0029305 s. After the end of the transient process and the start of the steady state, at the time t₂ = 0.18 s, a single-phase short-circuit of phase A of the line to earth occurred (point K, Figure 1).

The simulation was carried out for a real line between the “Zakhidnoukrainska” substation and the “Albertirsha” substation, with a rated voltage of 750 kV, 476 km long and with the following distributed parameters: r_0F = 1.9 × 10⁻⁵ Om/m, r_0T = 4.28 × 10⁻⁴ Om/m, r_0Z = 5 × 10⁻⁵ Om/m, L_0F = 1.647 × 10⁻⁶ H/m, L_0T = 2.4049 × 10⁻⁶ H/m, M_0FF = 7.41 × 10⁻⁷ H/m, M_0FT = 7.4 × 10⁻⁷ H/m, M_0TT = 7.05 × 10⁻⁷ H/m, g_0F = 3.253 × 10⁻¹¹ Sm/m, g_0FF = g_0FT = 3.253 × 10⁻¹³ Sm/m, g_0T ≈ 0, g_0TT ≈ 0, C_0F = 0.8647 × 10⁻¹¹ F/m, C_0FF = 0.103 × 10⁻¹¹ F/m, C_0FT = 0.0723 × 10⁻¹¹ F/m, C_0T = 0.3501 × 10⁻¹¹ F/m, C_0TT = 0.04162 × 10⁻¹¹ F/m. The equivalent power system had the following parameters for each phase of system 2: r_S2 = 2.41 Om, L_S2 = 0.141 H.

Computer simulation was performed with the following mode parameters: u₁^(A) = 617 sin(ωt + 18°) kV, u₁^(B) = 617 sin(ωt − 102°) kV, u₁^(C) = 617 sin(ωt + 138°) kV, e_S2^(A) = 600 sin(ωt + 8°) kV, e_S2^(B) = 600 sin(ωt − 112°) kV, e_S2^(C) = 600 sin(ωt + 128°) kV. The delta of spatial discretization of partial differential equations using the straight-line method is equal to Δx = l/20 = 476/20 = 23.8 km. Ordinary differential equations were integrated by the Gear method with a time-step of Δt = 27 μs.

The obtained results of the computer simulation are presented as waveforms in the figures. In these figures, the yellow lines represent phase A processes, the green lines represent phase B processes, and the red lines represent phase C processes. The black lines represent processes related to T1 and T2 shield wires.

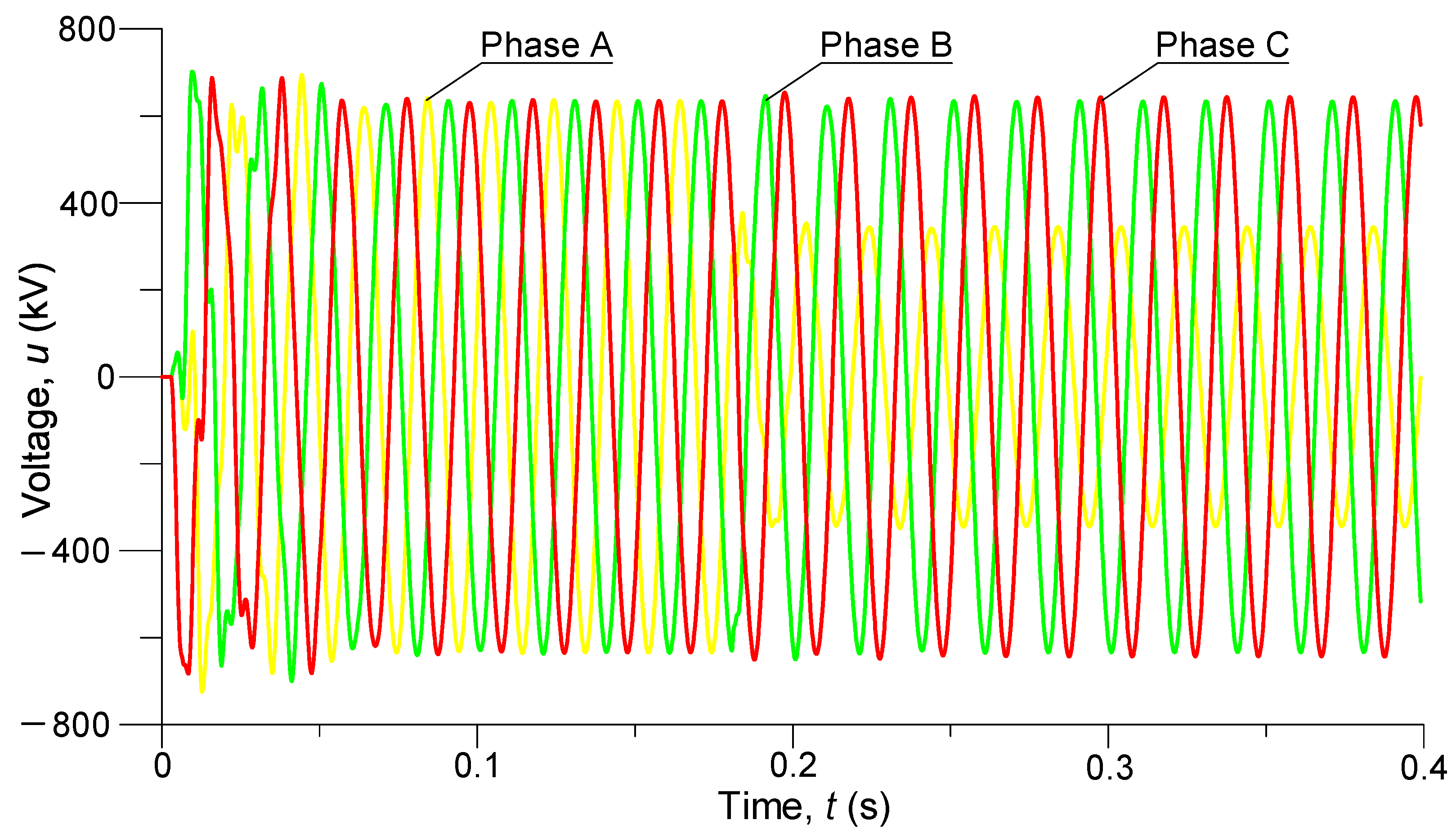
Figure 5 shows the transient waveforms of the phase voltages in the middle of the power line.

It can be seen that even when using controlled commutation phase-by-phase, there are overvoltages when connecting the power line, in particular, the maximum instantaneous voltage of phase A is 720 kV, for phase B—701 kV, and for phase C—687 kV, which is, respectively, 1.12, 1.09, 1.07 of the maximum working voltage per phase. In the steady state, the amplitudes of the phase voltages in the middle of the line were 633 kV. After the A-phase short-circuit to earth occurred, the value of the A-phase voltage amplitude in the middle of the line decreased to 341 kV, and the B- and C-phase voltage amplitudes did not change.

Figure 6 shows the transient waveforms of the last-node voltages of the discretized line (24 km from the end of the line). It can be observed that for this distance, at the moment of switching on the line, the overvoltage occurred only in phase C.

Its maximum was 686 kV, which was 1.06 of the operating voltage. In the steady state, the voltage amplitudes were 615 kV. After the short-circuit occurred, the A phase voltage amplitude decreased to 26 kV, the B phase voltage amplitude did not change, while the C phase voltage amplitude, on the contrary, increased to 645 kV.

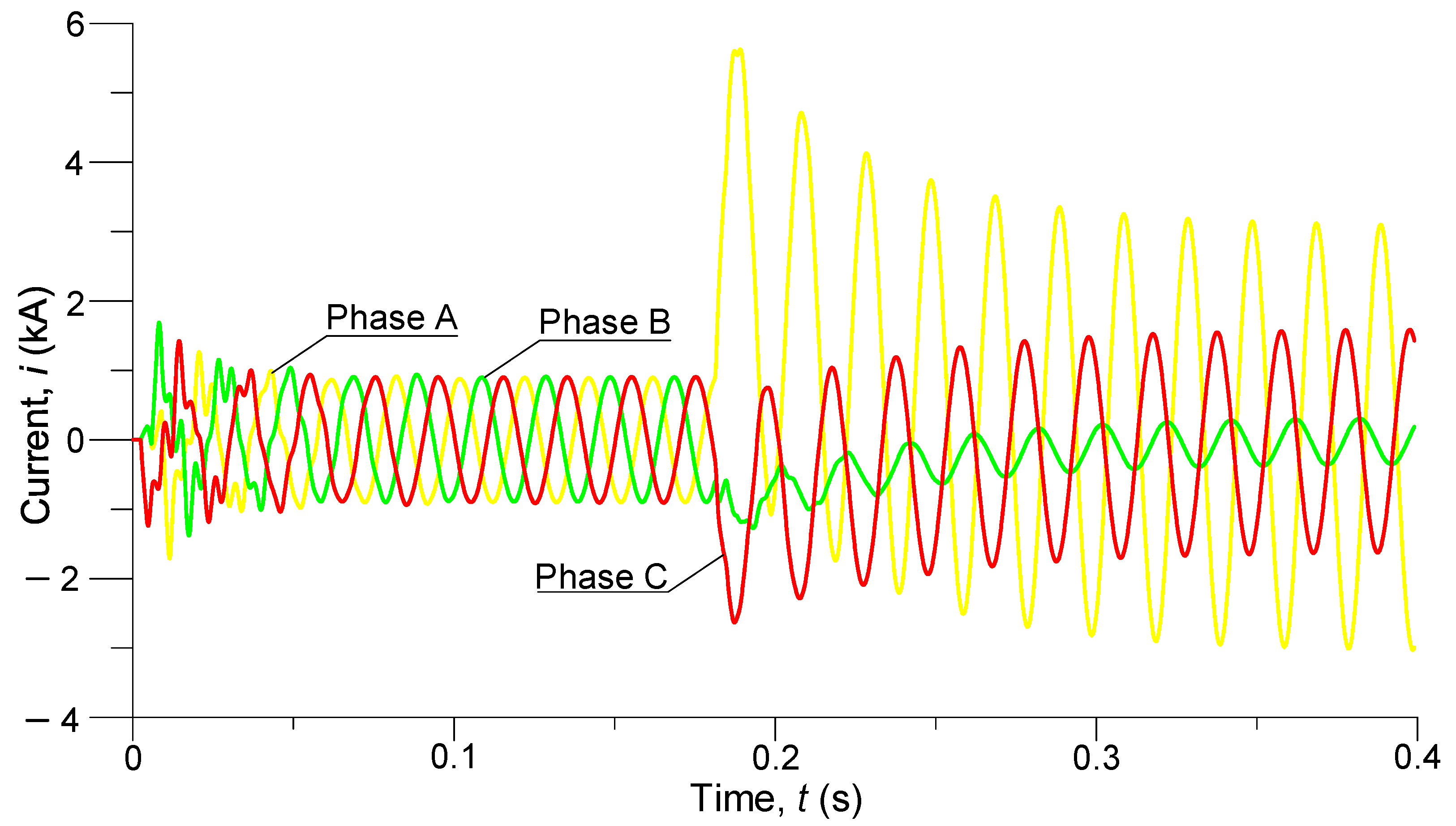
Figure 7 shows transient waveforms of phase currents at the beginning of the power line.

It can be seen that after switching on the transmission line, at its beginning there were small surge currents with maximum values of 1.7 kA in phases A and B and 1.44 kA in phase C. In a steady state, the phase currents of the line had an amplitude of 0.85 kA. After a short-circuit occurred at the end of the line, the phase A surge current at the beginning of the line reached a maximum value of 5.63 kA, then in steady state it had an amplitude of 3.1 kA. After the short-circuit occurred, a slight overcurrent with a maximum value of 1.24 kA was observed in phase B, and the amplitude decreased to 0.35 kA in the steady state. After the short-circuit occurred, the surge current in phase C reached a maximum value of 2.62 kA, and in steady state, it had an amplitude of 1.57 kA.

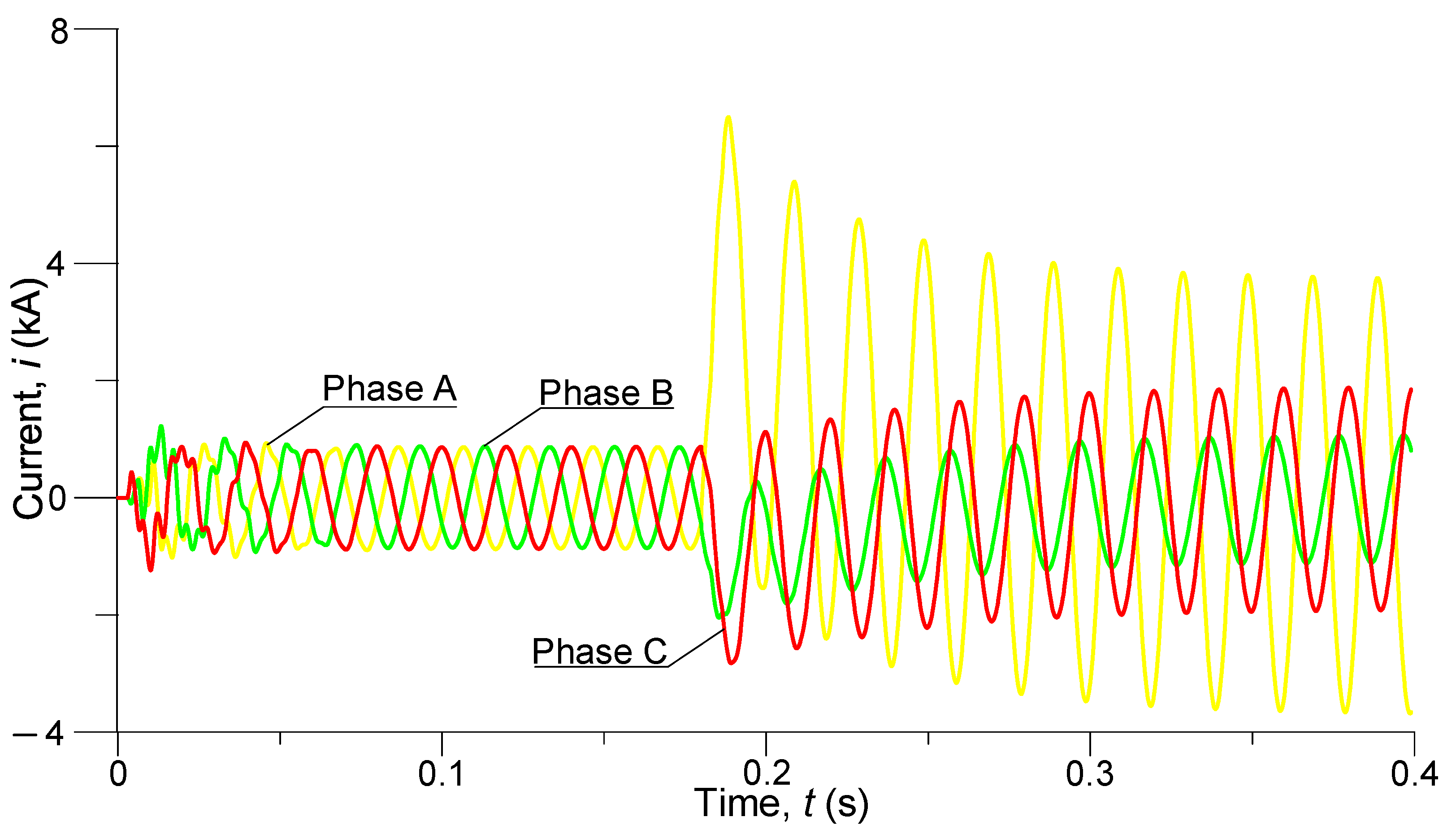
Figure 8 shows transient waveforms of phase currents at the end of a power line.

The figure shows that there were practically no overcurrents when switching on the line, although there was a transient process caused by successive switching on of the line phases. In the steady state, as well as at the beginning of the line, the amplitudes of the phase currents were 0.85 kA. However, in the case of a short-circuit fault, the maximum value of the phase A surge current is greater than at the beginning of the line and amounts to 6.5 kA, and for the steady-state fault, the current amplitude of this phase is 3.76 kA. As for the currents of phases B and C, they did not change that much. In the event of a short-circuit fault, the maximum values of the B and C phase surge currents were 2 kA and 2.8 kA, respectively. The amplitudes of these currents for the steady-state short-circuit fault were 1.09 kA and 1.88 kA, respectively. Greater values of maximum surge currents and current amplitudes for the steady-state fault depend on the distance of the fault location.

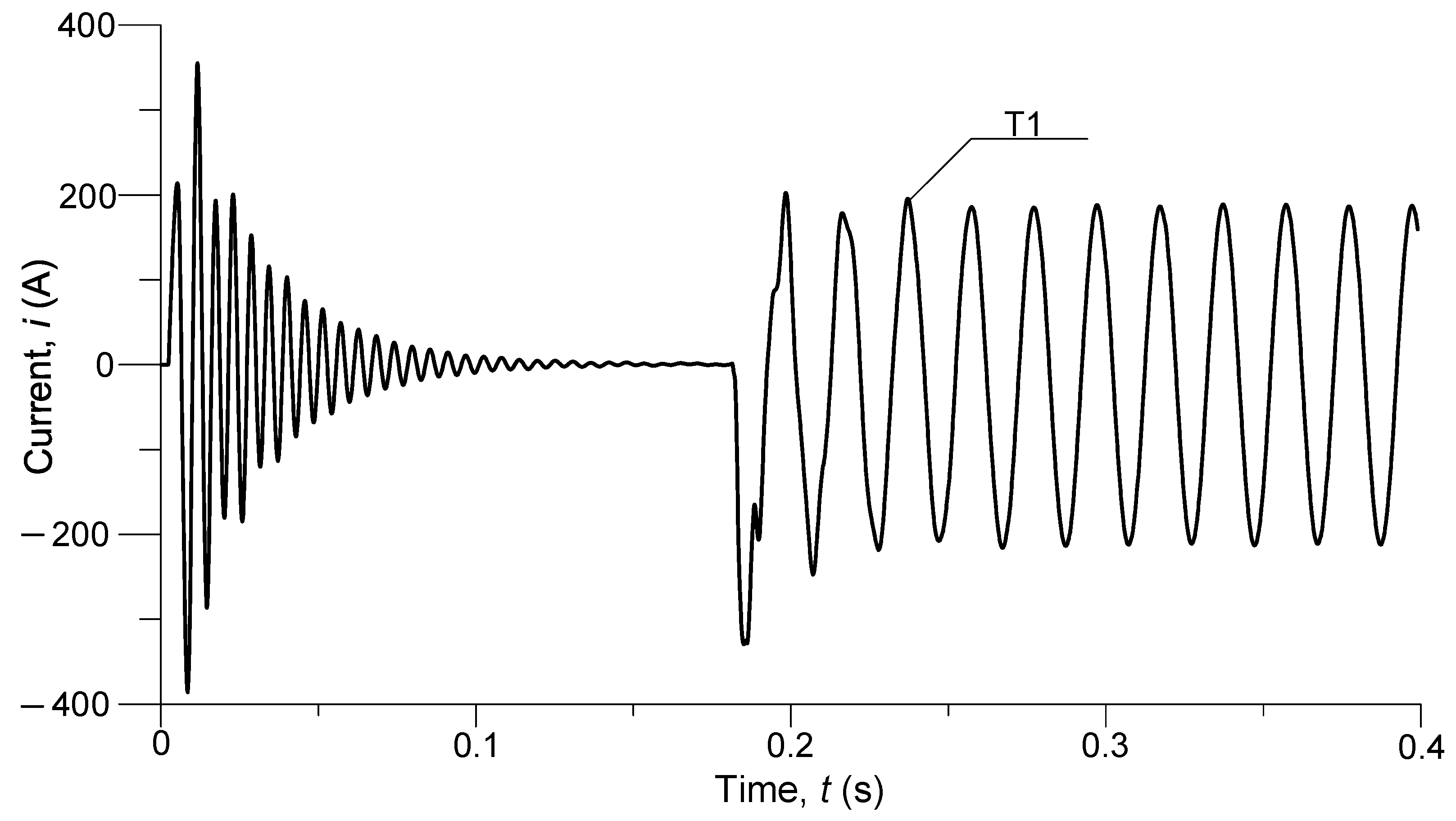
Let us now present an analysis of the transient processes taking place in the shield wires of a power line. Figure 9 shows the transient current in the shield wires T1 at the beginning of the line.

It can be seen that after switching on the line, in the shield wires T1 there are significant surge currents that reach maximum values of up to 400 A. Then the current is oscillating with a decaying amplitude and in the steady state this current decreases to zero. Such a course of the transient process, when the line is switched on and then goes to the steady state, fully confirms the theoretical expectations, and with the symmetrical operation of the line in the steady state, the currents in the shield wires should be zero. After a short-circuit occurs, a surge current is induced in the shield wires T1, which has a maximum value of 327 A, and in steady-state fault, the amplitude of this current is 212 A.

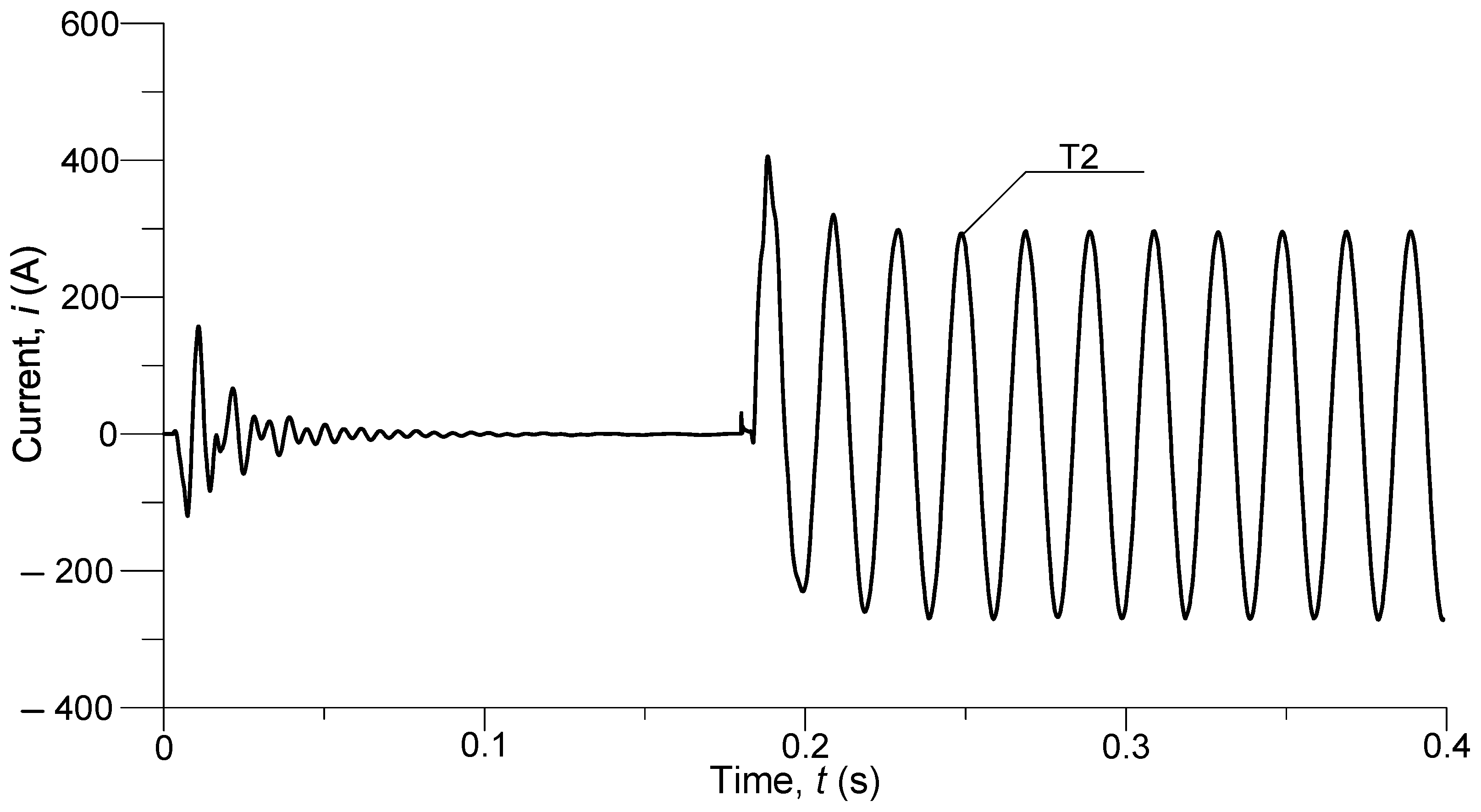
Figure 10 shows the transient current in the shield wires T2 at the end of the line.

It can be seen that this current is accompanied by smaller fluctuations, however, when the line is switched on, there is a surge current with a maximum instantaneous value of 157 A. After disappearing the vibrations, the current in the shield wires returns to the expected zero value. When a short-circuit occurs, the surge current in the T2 conductor reaches a maximum instantaneous value of 406 A, followed by the steady state with a current amplitude of approx. 295 A.

Figure 11 shows the transient voltage of the shield wires T1 at the end of the line.

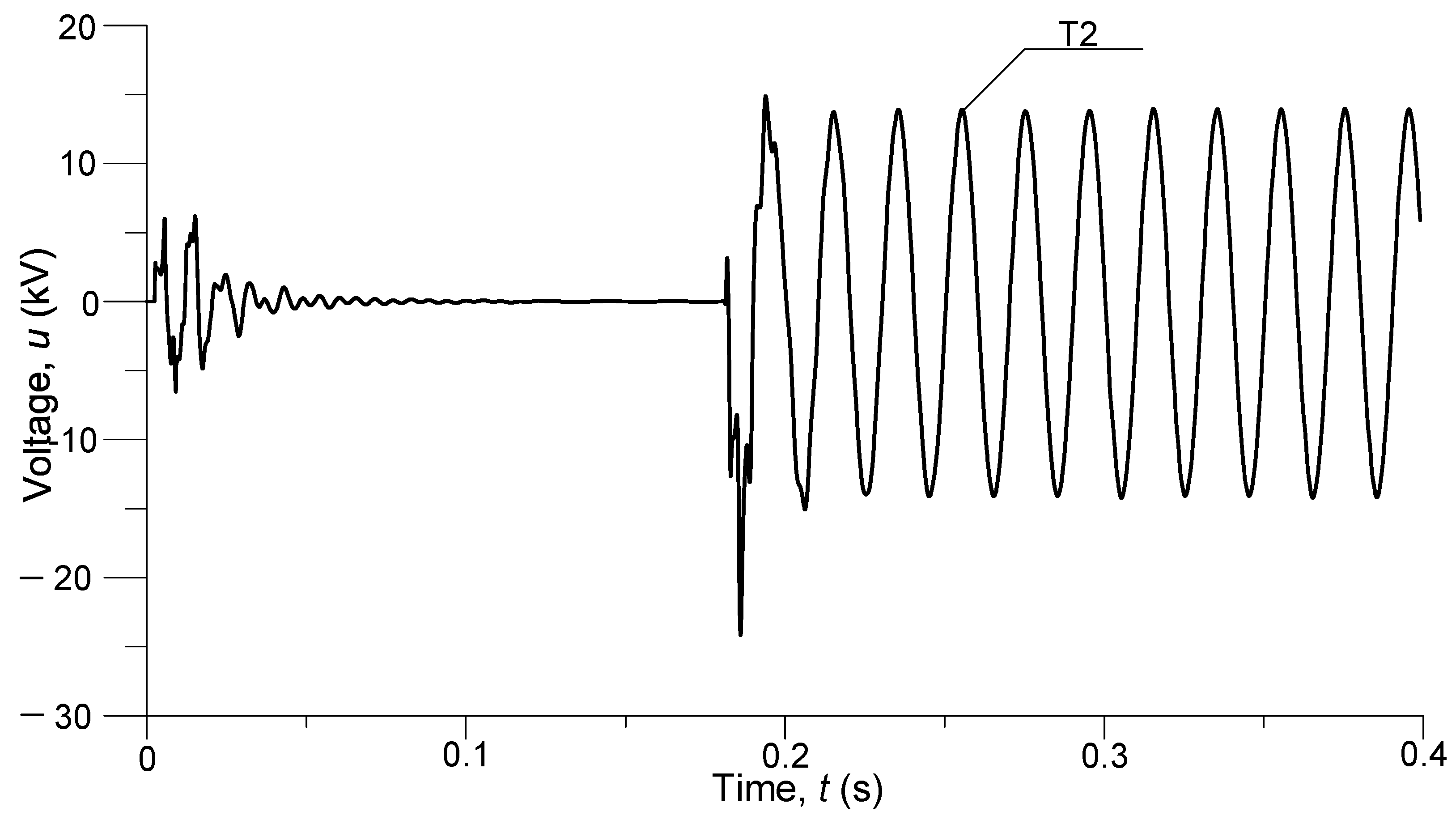
The figure shows that after switching on the line, there is an overvoltage in the shield wires T1 at the end of the line, which reaches a maximum instantaneous value of approx. 230 kV, followed by a damped oscillatory process and the voltage drops to zero. When a short-circuit in the shield wires T1 at the end of the line occurs, there is an overvoltage again, reaching a maximum instantaneous value of 320 kV, and after entering the steady state, the voltage has an amplitude of 250 kV.

Figure 12 shows the transient voltage of the shield wires T2 at a distance of 24 km from the beginning of the line.

Analyzing this transient voltage, it can be seen that here, unlike the shield wires T1, its values are not so significant. This is due to the proximity of the earthing point of the T2 conductor at the beginning of the line. In particular, the maximum instantaneous voltages that occur when the line is on are around 5 kV, after which the weak oscillatory process quickly decays, and the voltage tends to zero. In the event of a short-circuit, overvoltages reach a maximum instantaneous value of 25 kV, and in a steady short-circuit state, they have an amplitude of 15 kV.

The developed mathematical model and the computer program written on its basis make it possible to reproduce not only the voltage and current as a function of time but also their spatial distributions. Let us present a brief analysis of them.

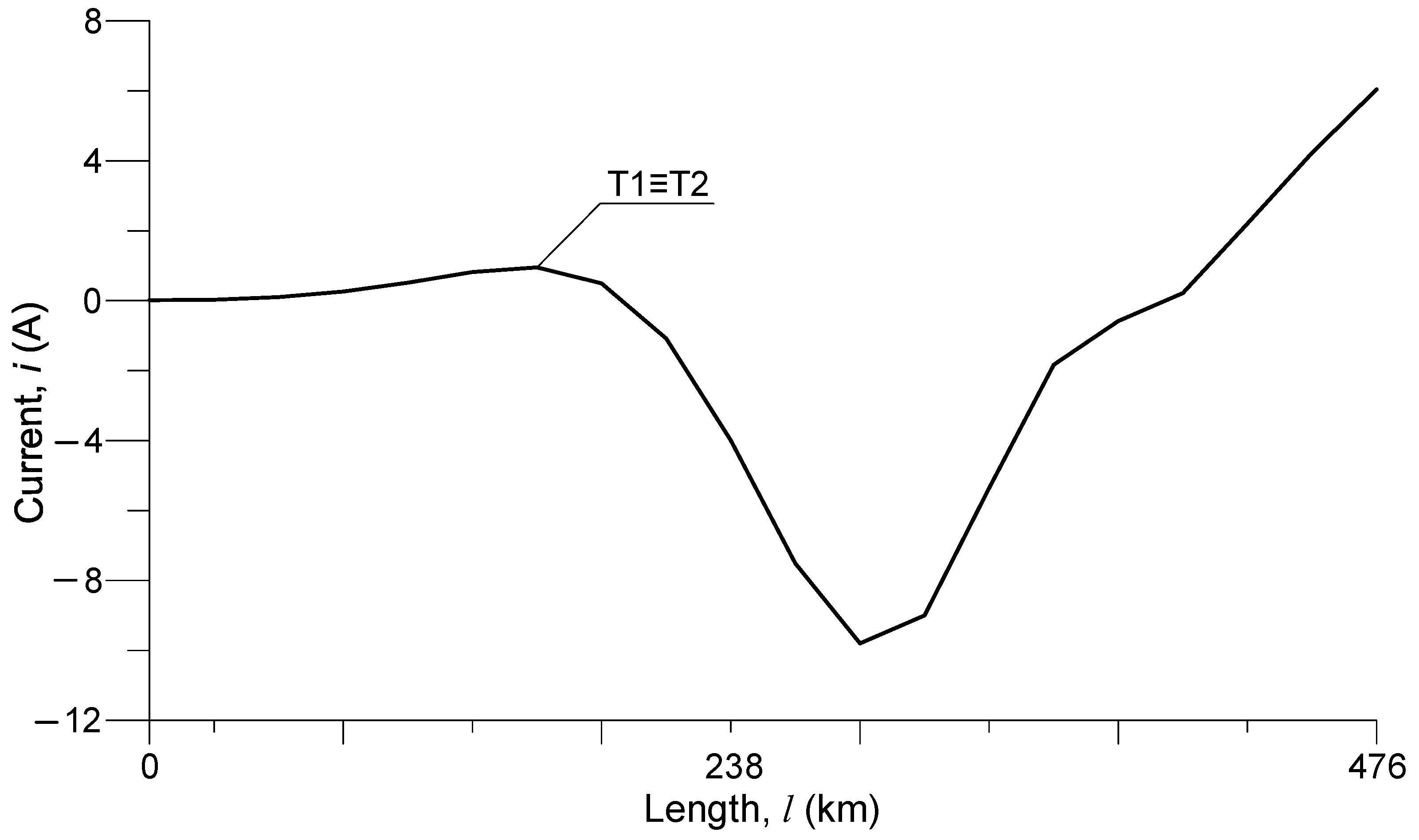
Figure 13 shows the spatial distribution of the current in the shield wires T1 and T2 at the time t = 0.181 s, after 0.001 s from the occurrence of the short-circuit, which was preceded by a steady state with zero current in the shield wires.

It can be seen that after 0.001 s from the occurrence of the short-circuit, the spatial distribution of the current in the shield wires had already started to change. Thus, at the beginning of the line, the current in the wires was still zero, increasing to −10 A in the middle of the line, and dropping again to 6 A at the end of the line. This is related to the fact that the electromagnetic wave that traveled from the end of the line did not have time to reach the beginning and be reflected.

Figure 14 shows the spatial distribution of voltage in the shield wires T1 and T2 at the time t = 0.183 s.

Analyzing this figure, it can be seen that at the time t = 0.183 s, the electromagnetic state of the line has already changed significantly. The electromagnetic wave has already reached the beginning of the line and has been reflected and superimposed on other waves. As a result, the spatial distributions of the voltages of the shield wires T1 and T2 are different. In particular, the voltage of the T1 shield wires at the beginning of the line is −50 kV, gradually increasing along the line to −60 kV in the middle of the line and to −105 kV at its end. As for the T2 shield wires, here the voltage is zero at the beginning of the line (this conductor is earthed at the beginning of the line), gradually increasing to −70 kV in the middle of the line and −105 kV at the end of the line. It can also be seen that the voltages of the T1 and T2 conductors at the end of the line are the same because these conductors are connected together (short-circuited) there.

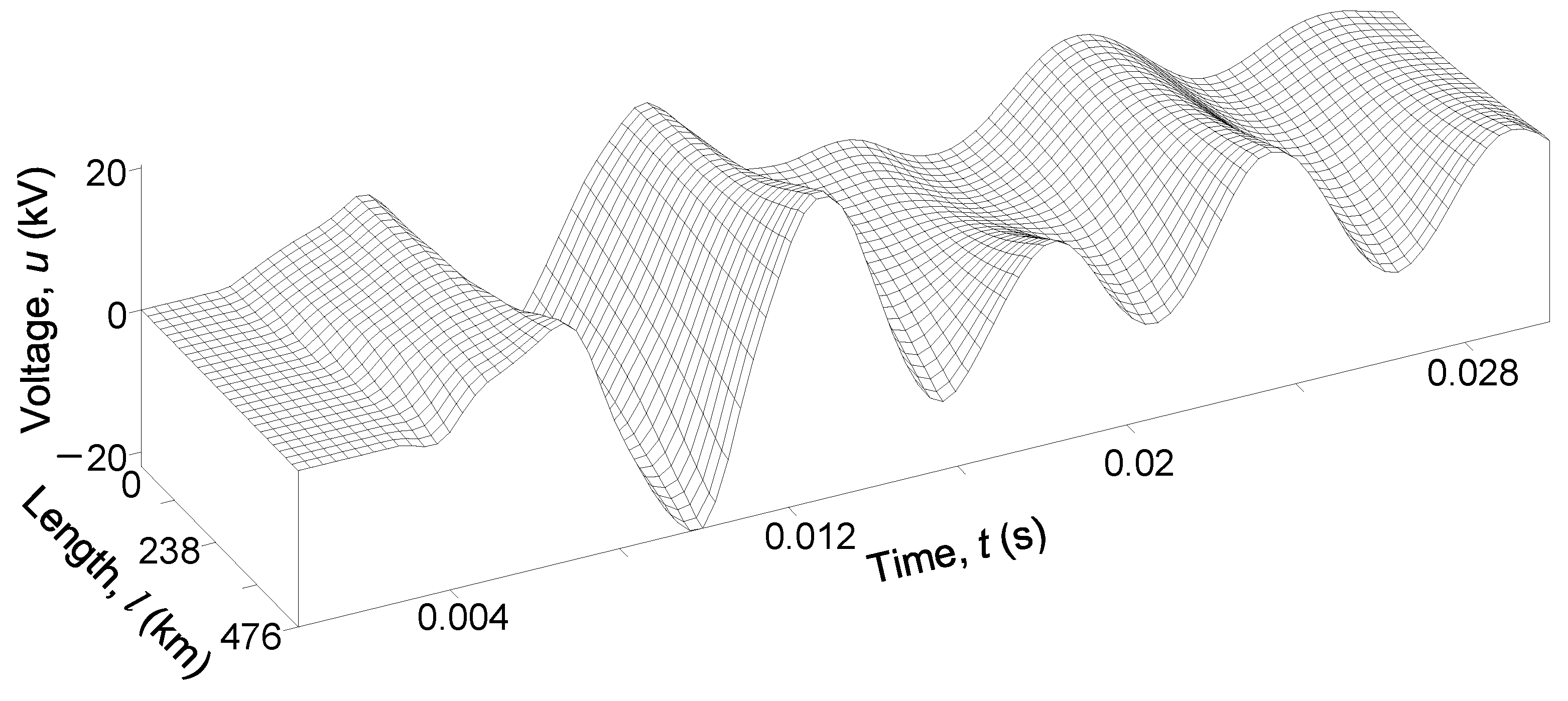
Another advantage of the developed computer model is the ability to obtain not only time dependencies or spatial distributions of currents and voltages but also their combinations, i.e., traveling wave distributions. For example, Figure 15 and Figure 16 show the voltage traveling wave distribution of the T1 conductor and the current traveling wave distribution of the T2 conductor within the time interval t ∈ (0; 0.03) s.

Figure 15 and Figure 16 are shown in 3D format. They enable a visual analysis of the physics of electromagnetic transient processes in long ultra-high voltage power lines with shield wires. It can be seen that the voltage function of the shield wires T1 (Figure 15) changes almost identically along the entire length of the line, but with a time delay, which is related to the considerable length of the power line. On the other hand, the current function of the shield wires T2 (Figure 16) at the beginning of the line shows greater fluctuations than at the end. This is due to the grounding of the T2 shield wires at the beginning of the line. Figure 15 and Figure 16 should be analyzed together with Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14.

5. Conclusions

The use of boundary conditions of the second and third type (Neumann and Poincaré conditions) to solve the differential equation of a long ultra-high voltage power line with shield wires makes it possible to find not only the voltage and current waveforms for the live conductors of the line but also for the shield wires. This allows the line model to fully take into account the presence of shield wires and study the transient processes at any point of the line, and, if necessary, to reconstruct the time dependencies and spatial distributions as well as the traveling wave distributions for voltages and currents in all line conductors.

The results of the computer simulation confirm the theoretical expectations, in particular: the lack of voltages and currents in the shield wires during the symmetrical operation of the power line and their occurrence in switching, asymmetric, and fault states, which gives grounds for stating the adequacy of the developed mathematical model of the power line with shield wires.

The computer model developed in this work allows for reconstructing not only the time dependencies and spatial distributions of voltages and currents, but also the distributions of the traveling wave (in 3D format). This gives us a better opportunity to analyze complex wave phenomena occurring in power lines, which is very important at the design and operation stages of power lines in order to prevent potential failures in electricity transmission systems.

The developed mathematical model of a power line with shield wires and other results obtained in this article are planned to be used in the future study of electromagnetic processes in ultra-high voltage power lines during complex repair works.