Abstract
In this study the flow field of a centrifugal electronic cooling fan operating at an off-design point of 0 Pa static fan pressure is investigated by means of Computational Fluid Dynamics. The results obtained by four different turbulence models, the realizable k- model, the SST k- model, a Reynolds Stress Model, and Scale-Adaptive Simulation are analyzed and compared. The focus lies on describing how the flow through impeller and volute influences the fan outlet flow field, and velocity profiles and velocity fluctuations at the outlet are compared to previously published measurements. All models tend to underpredict the measured outlet flow rate, but are capable of producing the characteristic C-shaped profile of high velocities, previously determined in Constant Temperature Anemometry measurements. However, the realizable k- model is significantly too diffusive, leading to blurred velocity contours. The other models exhibit reasonable agreement with the measured flow field, but show differences in a number of aspects. The SST k- model, for instance, even produces local inflow in a confined area. The SAS approach overpredicts the length of the lower lobe of the C-shape. The research is relevant to improve simulation results of impingement cooling and heat sink optimization using centrifugal fans.
1. Introduction
As continuous miniaturization and integration of electronic devices leads to increasing thermal loads, the demand for more efficient cooling methods as well as for the optimization of existing cooling concepts continues to increase. Highly integrated microchips or high-powered light emitting diodes (LEDs) produce high, and often very localized, heat flux densities, which require active cooling for safe operation. Even though highly efficient electronic cooling techniques, like liquid jet impingement cooling, spray cooling, electrowetting, heat-pipes, thermoelectric cooling, etc., have been developed [1], conventional convective air cooling using electronic cooling fans remains the preferred cooling method for various applications. As for automotive LED headlamps forced convection cooling is still the predominant method, even though concepts involving heat pipes [2,3], cold plates [2] or vapor chambers [4] have been investigated and developed. The reasons for the preference of cooling fans involve high cost pressures in the automotive industry, and the fact that the operating temperature range of headlamps typically lies between −40 °C and 105 °C. One further practical reason is that the heated airflow can be directed towards the transparent cover lens in order to meet decondensation requirements.
Air jet impingement cooling, especially when combined with an optimized heat sink design, can be an effective cooling method for the very localized heat loads of LEDs, since high Nusselt numbers [5] can be obtained. Hence, this convective cooling method is frequently considered in the thermal management design of headlamps. Sui et al. [6,7,8] as well as Stafford et al. [9,10] have studied impingement heat transfer of jets produced by axial electronic cooling fans on a flat plate. Sui et al. recorded circumferentially averaged Nusselt numbers and found considerably lower values in the secondary stagnation point region behind the fan hub when compared to the circular primary stagnation point region downstream of the fan outlet. This reduction of the central Nusselt number was more pronounced when the fan was positioned close to the plate, but could still be detected when the fan was located at a distance of two fan diameters away from the wall. Stafford et al. were able to obtain detailed heat transfer distributions by using a heated thin-foil and infrared thermography technique and could therefore also study the influence of motor support struts on the flow field and consequently on the local heat transfer. The circumferentially averaged radial Nusselt number distributions of these measurements show a strong reduction of heat transfer in the center. In some cases less than 30% of the maximum values obtained in the primary stagnation point region were measured. They also observed strong inhomogeneities with local minima and maxima in the heat transfer distribution due to the impact of the support struts. They concluded that increases in heat transfer can be achieved by careful positioning of heat sources, which also implies that the potential for significantly reduced heat transfer exists for non-optimized arrangements.
As an alternative to axial fan jets, the jet produced by small centrifugal fans can be used for impingement cooling, with the possible advantage that a concentrated jet can be aimed directly at the heat source. However, there are still design challenges to overcome in that case. On the one hand, the jet direction is not necessarily normal to the fan’s outlet nozzle plane. This is not only the case for flat centrifugal fans predominantly used in notebook computers [11], but has been observed for fans with nearly quadratic outlet nozzles, as well [12]. On the other hand, the outlet flow field of a centrifugal fan is usually not homogeneous and typically contains significant crossflow and swirl, which is mostly generated by the inevitable secondary flow motion in the volute and by impeller volute interactions [13,14]. Several flow measurement studies have demonstrated that strong vortices can exist at or close to the outlet of centrifugal fans [12,15,16], which can also result in a rotation of the emanating jet. Hence, the design of impingement cooling arrangements involving centrifugal fans is not a straightforward process, if heat transfer shall be optimized and, potentially also, if the hot airflow shall subsequently be redirected in an ideal manner. Usually, Computational Fluid Dynamic (CFD) is applied in such a design process. In that case, it is essential that the simulations produce a realistic outlet flow field of the fan, since this is a prerequisite to realistically predict the exact location of jet impingement as well as the flow’s interaction with the heat sink and flow guiding geometry. Several flow characteristics of centrifugal fans, like flow rotation, secondary flows or boundary layer separation, complex anisotropic turbulence and backscatter in the interaction of the volute flow with the jet-wake flow emanating from the rotor [17,18,19], make turbulence modeling an important aspect of the prediction accuracy of CFD simulations.
Numerous studies have employed steady simulations using two-equation Reynolds-Averaged Navier-Stokes (RANS) turbulence models to investigate centrifugal fan flows or to improve or optimize fan design and performance [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]. These publications cover centrifugal fans of different sizes, ranging from flat miniature fans [20,23] to large industrial fans with impeller diameters exceeding one meter [24,28]. They also cover a wide variety of impeller types, ranging from classical fan wheels with backward-swept or backward-curved blades [22,24,25] to Sirocco runners with forward-curved blades [21,26,31,32,33,34]. All of these studies used the frozen rotor approach to account for the impeller rotation, except for [21], where an impeller body force model was employed. In the majority of these works, the standard k- model was used for turbulence modeling, but more recent studies, tended to apply different models, like the RNG k- model [26,31] or, notably, the SST k- model [27,30,32,33,34]. Nearly all of these studies provide comparisons of overall performance parameters like fan pressure or efficiency over the volumetric flow rate between experiments and simulations. Generally, reasonable agreement was observed, with typical deviations ranging from 3% to 6%, sometimes higher deviations were predicted for flow rates further away from the design point [28]. Burgmann et al. [30] also performed Particle Image Velocimetry (PIV) measurements in the diffuser section between impeller and volute. They compared measurement and simulation results of the circumferentially averaged radial velocity and observed reasonable agreement for medium and high flow rate cases. For low flow rates, however, the simulations markedly underpredicted the size of the observed recirculation region. Unsteady Reynolds-Averaged Navier-Stokes
(URANS) simulations have been performed by Ding et al. [35] and Rui et al. [36]. In the first study the dependence of transient pressure fluctuations in the volute and outlet area on the blade outlet angle of an industrial fan with backward-swept blades was investigated. In the latter study, the results of RANS and URANS simulations of a Sirocco fan, obtained with the realizable k- model and the frozen rotor approach, were compared. Even though the general flow patterns predicted by both approaches were similar, the investigation revealed significant differences of RANS and URANS results, when a detailed quantitative comparison of averaged velocities in the blade channels or of averaged pressure results at specific control points was carried out.
Two aspects that none of the studies cited thus far cover are:
- (a)
- a comparative study on the results obtained for different turbulence models,
- (b)
- detailed results of the outlet flow field.
An extensive study for a Sirocco fan, in which five different operating points were simulated using the Spalart-Allmaras, the realizable k- and the SST k- turbulence models was performed by Darvish and Frank [37]. Steady simulations were conducted for four different types of meshes of comparable resolution and comparisons with measurement data of static fan pressure and torque showed that the best agreement was obtained with the SST k- model on a polyhedral mesh. Further improvement of the results could be obtained by URANS simulations using a sliding mesh approach. A comparison with PIV measurements for the best efficiency point revealed that the unsteady simulations could decrease the prediction error particularly in the region downstream of the volute nose.
Several studies investigated centrifugal fans using Scale-Resolving Simulations (SRSs), often in combination with or even focusing on aerodynamic noise predictions. Liu et al. [38], Lu et al. [39] and Cai et al. [40] investigated the same fan model with 12 forward-curved blades. In [38] Large Eddy Simulations (LESs) were performed on a relatively coarse mesh of 2.2 million cells for the fan’s design point. Overall performance results and aerodynamic noise were compared to measurements. The simulations overpredicted the efficiency by 1.37%, the total pressure coefficient by 3.68% and the power coefficient by even 8.06%. The frequency distribution of the calculated sound pressure followed the trend of the measurements but showed deviations in the pressure levels. The study also included a rudimentary comparison of two URANS simulations, but without providing a substantial discussion. In [39] the pressure fluctuation amplitudes at the volute casing obtained by simulations using URANS (standard k- model, 1.8 mio. cells) and LES (4.2 mio. cells) were compared. LES consistently predicted higher pressure variations. Based on these results, the authors optimized the thickness of the volute walls to reduce vibrations and validated the results using vibroacoustic simulations. In [40] a Detached Eddy Simulation
(DES) study for this fan model including a downstream pipe was performed. The authors compared the mean flow field as well as the pressure and velocity fluctuations for three different operating points. They found highly elevated pressure fluctuations at the impeller and the volute nose for an off-design point with 1.49 times the volume flow rate at the design point. Younsi et al. [41] carried out Scale-Adaptive Simulations (SASs) on a mesh of 2.2 million nodes for a squirrel cage fan at the best efficiency point and could achieve close agreement with experimental data, both regarding overall performance parameters (static fan pressure and efficiency) and pressure fluctuation spectra at two sensor positions. The simulations overpredicted pressure fluctuations at low frequencies, which was attributed to insufficient sampling time. Sorguven et al. [42] used LES to investigate noise generation of two Sirocco-type fans with similar impeller diameters operating at the same rotational speed. Both fan models included an outlet pipe, but differed in the number of impeller blades, in the fan depth and, particularly, in the volute geometry. While fan one featured a tight volute, but a volute nose with a large radius, fan two was characterized by a very wide volute, a large volute nose to impeller distance, but a rather acute nose geometry. The study highlighted the relation between vorticity production, vorticity transport and noise generation. For fan two, areas of high vorticity were only detected in the impeller region, which was therefore the only relevant source of noise generation. In fan one, high magnitudes of vorticity also occurred in the volute, around the volute nose and in the outlet pipe, which all significantly contributed to noise generation and what resulted in higher average sound pressure levels. Overall, acoustic simulation and measurement results agreed well with respect to direction and the narrow band sound pressure levels. Discrepancies were attributed to insufficient grid resolution and acoustic simulation time. Lin and Tsai [25] investigated a flat centrifugal fan with a large rectangular outlet port and backwards-curved impeller blades both experimentally and numerically. Flow and pressure field comparisons of URANS simulations using the standard k- model and LES at maximum flow rate revealed that the latter showed significantly higher local velocities in the proximity of the blade surfaces with peak-to-peak differences of over 30% in the blade channels close to the volute tongue, which also lead to higher pressure fluctuations on the impeller surface. The LES could realistically reproduce the measured sound pressure level spectrum in the entire measured frequency range up to 2 , with slight deviations being attributed to motor noise and structural vibrations, while the URANS simulation severely underpredicted the noise levels in the entire frequency range, including the blade passing frequency. Darvish [43] performed an extensive numerical analysis of an industrial Sirocco-type fan with rectangular pipe attached at the outlet and compared the results with overall performance and sound measurement data. Three different meshes with cell numbers ranging from 12.5 to 102 million and RANS, URANS, Improved Delayed Detached Eddy Simulation (IDDES) and LES turbulence modeling approaches were compared. One result was that the RANS simulation, which was only conducted for the coarsest grid, showed the lowest deviations from the measured values close to the point of best efficiency regarding overall fan pressure rise and static efficiency. Concerning the acoustic simulations, URANS was able to predict tonal noise levels at the blade passing frequency, but severely underpredicted broadband noise. LES, even on the medium grid, was able to resolve turbulent vortex structures better than IDDES on the fine grid, which resulted in LES outperforming IDDES in the broadband noise predictions. Iwase et al. [44] investigated a voluteless centrifugal fan applied in Heating, Ventilation and Air Conditioning (HVAC) units. LES results for one operating point were obtained using three block-structured meshes with 10, 60 and 500 million cells and compared to measurements of static fan pressure, velocity profiles and sound pressure levels. While the results of the coarse grid showed strong deviations from the measured values in all comparisons, the agreement improved significantly for the medium mesh and again slightly when the fine mesh was used. Ottersten et al. [45] investigated a similar HVAC fan in an off-design point using IDDES. They reported very close agreement with measured torque and fan pressure using a mesh of 52 million cells and small time steps. The main point of the study was that they could demonstrate that the interaction of turbulence generated in the gap between the bell mouth entrance and the impeller with the rotor blades was a significant source of tonal noise. Jiang et al. [46] carried out an LES study for a slice model of the squirrel cage fan investigated by Liu et al. [33]. They could perform detailed investigations of vortex formation and progression in the blade channel and due to interaction of the impeller and the volute nose for different fan operating points. In summary, SRS did not consistently lead to higher prediction accuracy concerning overall fan parameters, but was capable of resolving flow details regarding vorticity production and transport, pressure fluctuations and their interaction with the fan geometry.
The main motivation behind the current study is to improve the flow and heat transfer prediction accuracy involving jets produced by centrifugal electronic cooling fans in complex industrial environments. While proper LES studies, where turbulent fluctuations are predominantly resolved, will be prohibitively costly for such purposes in the foreseeable future, this might not be the case for hybrid or bridging turbulence modeling methods [47,48]. Scale-Adaptive Simulations have the ability to transition from a RANS mode to a scale resolving mode due to a source term in the -equation, which is dependent on local turbulent length scales and the grid resolution [49,50], thus locally adjusting the turbulent viscosity to the capability of the mesh to resolve turbulent scales. In this study Scale-Adaptive Simulations are performed for a centrifugal fan, and the results are compared to those obtained with three different RANS models. The outlet flow field of this fan was investigated using Constant Temperature Anemometry (CTA) and PIV measurements. The goal is to analyze how differences in the flow through impeller and volute predicted by the four turbulence models impact the results of the velocity distribution at the fan outlet. The article is organized as follows: first the fan geometry and the fan data are introduced, then the numerical setup and the computational domain are presented, followed by a grid resolution study and numerical tests. Subsequently, the results are presented, including overall fan performance data, impeller and blade channel flow data, turbulence quantities and the velocity distribution at the fan outlet, which is compared with the existing measurement data.
2. Fan Data and Nomenclature
2.1. Fan Geometry
The fan is made by Mechatronic Systems GmbH (MSG) in Austria. During operation air is sucked in over a 31 mm diameter circular intake at the top of the fan and blown out through a 20 mm × 20 mm nearly quadratic outlet. The fan’s impeller consists of 64 blades in total, whereby half of them are splitter blades. The rotor does not cover the whole height of the fan, but has an effective height of 9.7 mm and resides on a 9 mm high motor housing unit.
Original CAD data of the fan were provided by the supplier. To investigate whether these original schematics match with the geometry dimensions of the real product Computer Tomography (CT) scans of two different fan samples were conducted. In Figure 1 the CT scans of the fan wheel and casing are compared to the existing CAD data. The deviations between the two geometries have been calculated using the software ZEISS Reverse Engineering and are shown in millimeters. As can be derived from the figures the CAD data is of high quality and matches well with the scan. Only some surfaces show deviations in the order of 0.1 mm. The geometry has subsequently been simplified using the software ANSYS SpaceClaim. In this step some straightening of the outer housing geometry (reducing imprints, injection molding related imperfections, etc.) and the upper impeller geometry were performed. In addition the entire electronics and drive components have been removed from the geometry. This should have negligible impact on the simulation results since it only affects a very restricted area below the fan wheel. Figure 2 shows the simplified fan geometry in different cut planes and views. Rotating components are shown in red. In addition, coordinate systems, blade angles, evaluation surfaces and the boundary of the rotating reference frame are indicated and will be referred to later.
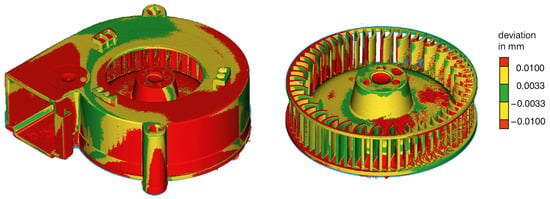
Figure 1.
CT scan of the investigated centrifugal fan, which shows good agreement with the CAD model.
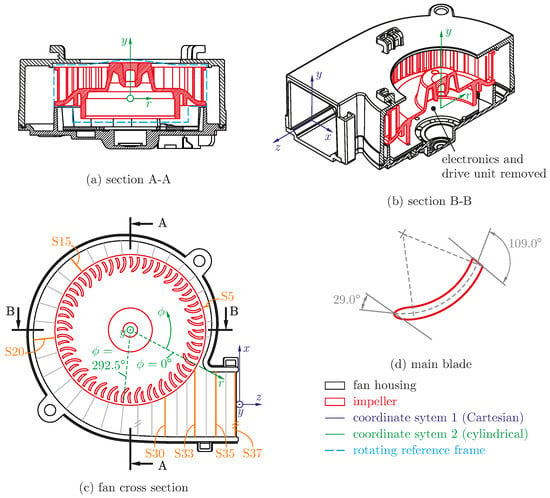
Figure 2.
Sections through the fan and rotor, showing the definition of the coordinate systems and evaluation surfaces.
2.2. Coordinate Systems, Evaluation Lines, Surfaces and Sections
As indicated in Figure 2, two coordinate systems are used to present the fan data. The origin of the first system is located at the center of the fan outlet. Here, Cartesian coordinates x, y and z are used, where the z-component is normal to the fan outlet plane and points outward, and the y-component is parallel to the fan wheel axis. The velocity components are called , , for this system. The second coordinate system is located at the center of the fan wheel. Cylindrical coordinates r, and y are used to described the radial, tangential and axial directions, respectively. The corresponding velocity components are denoted as , and . The angular coordinate is set to zero at the edge of main blade closest to the volute nose, as indicated in Figure 2. The second coordinate system’s origin location is chosen so that both systems are aligned with respect to the y-coordinate. Regarding the nomenclature of the velocities, capital letters are used for time-averaged velocities, e.g., , , for the second coordinate system. Velocities averaged over the impeller height are denoted as , and . Area-averaged velocities are denoted by an overbar, e.g., refers to a mean z-velocity at a given point in time and denotes the corresponding area- and time-averaged z-velocity. The areas of the impeller outlet and the fan outlet are called and , respectively. Time- and area-weighted velocities and refer to the mean radial velocity at the impeller outlet and the mean normal fan outlet velocity, respectively. Velocity magnitudes are denoted as or . To distinguish resolved from modeled turbulence quantities in the case of the SAS model, the subscript ‘res’ is used. Time-averaged pressures and turbulence quantities are denoted by the subscript ‘tavg’.
To evaluate impeller outlet quantities, 19 evaluation lines equally distributed over the impeller outlet height were defined (shown in Figure 3). A total number of 37 evaluation surfaces (S1–S37) are introduced to analyze the flow inside the fan. Surface S1 corresponds to the angle . The surfaces S1 to S27 () are aligned with the cylindrical coordinate system and are separated by , whereas the surfaces S28 to S37 are aligned with the outlet port area and are therefore perpendicular to the z-coordinate. The surfaces are indicated in grey in Figure 2c, individual colored lines indicate those surfaces chosen for the presentation of the results.

Figure 3.
Visualization of the nineteen evaluation lines located at the outer surface of the impeller.
2.3. Fan Performance Data
The fan has a nominal supply voltage of 13.5 V, leading to a speed-controlled rotor rotation rate of 5000 . For its nominal point of operation the manufacturer lists a Volume
Flow Rate (VFR) of at a total pressure difference of and a 135 mA DC supply current. The nominal overall fan efficiency is 12% according to the datasheet. An independently measured fan characteristics curve of the static fan pressure over its VFR can be found in [12]. The maximum measured VFR at a static fan pressure of 0 was found to be . Table 1 provides an overview of fan dimensions and performance data.

Table 1.
Specifications of fan MSG L775.
PIV and CTA measurements of the outflow field of this fan were published in [12,51]. These measurements were conducted at a static fan pressure of 0 and will serve as reference data for the simulations. Note that this point of operation deviates from the nominal configuration described above. In the reference measurements, the fan drew 187 mA which is considerably higher than the nominal value.
3. Simulation Setup and Meshing
3.1. Computational Domain
The computational domain consists of four subdomains namely the outer-, jet-, fan- and impeller domain. Figure 4 shows all domains and the respective dimensions. These four domains have been specified to better influence the mesh density. The impeller domain is used the rotation modeling and encloses the airspace around the impeller as closely as the meshing process allows to yield acceptable mesh qualities. The exact boundaries of the impeller domain are shown in both Figure 2a and Figure 4. Table 2 provides the dimensions of the domains. The size of the jet domain has been chosen according to the measurement domain in [12].
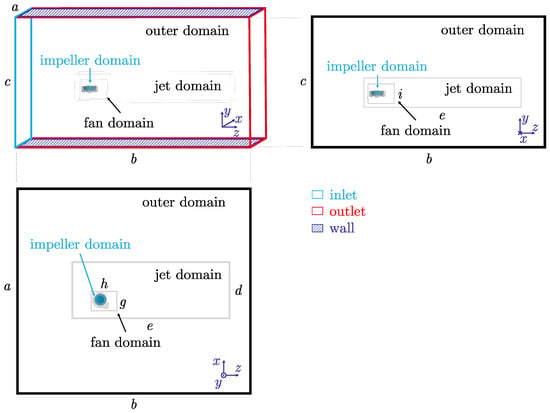
Figure 4.
Visualisation of the computational domains and its dimensions.

Table 2.
Mesh domain dimensions.
3.2. Boundary Conditions and Rotation Modeling
The boundary conditions are set at the borders of the outer domain as indicated in Figure 4. The area colored in blue represents a velocity inlet and the area colored in red a pressure outlet. The remaining domain boundaries are set as walls. A very low inlet velocity of has been defined at the velocity inlet and 0 were set at the pressure outlet. This setup improved numerical stability when compared to a configuration where only outer pressure boundaries were used. With regard to turbulence settings at the boundary surfaces, a turbulent intensity of 5% and a turbulent viscosity ratio of 10 were prescribed. Air was modeled as an incompressible fluid with constant viscosity. The values are given in Table 3.

Table 3.
Material properties of the fluid air.
With respect to the rotation modeling of the impeller, a frozen rotor approach was used for both steady and transient simulations. This approach is also called the Multiple
Reference Frame Model (MRF) approach, where the mesh remains stationary throughout the simulation and the effects of the impeller rotation are considered by including the centrifugal and Coriolis acceleration terms in the momentum equations. In all simulations a rotational velocity n of 5000 or was applied to the impeller domain.It must be noted that the sliding mesh approach was intentionally not applied in the transient simulations, even though it usually leads to more accurate simulation results. This approach maintains comparability between the different simulation cases, i.e., differences in the results are only due to turbulence modeling and temporal treatment. This way, an exact comparison of the flow rate distribution over the impeller outlet could be performed for each blade channel.
3.3. Grid Generation
The meshing was performed with the commercial software SPIDER v2.2.09 [52], which offers the possibility to quickly mesh even complex geometries at a fair overall grid quality and is therefore suited for industrial applications. The software produces a hex-dominant hybrid mesh, where pyramids and prisms are used to better adapt to the geometry and to achieve transitions between areas of different cell sizes. The meshing software works on the basis of a global cell size in combination with refinement levels for size adjustments in specified regions and boundary sections. The maximum cell size S is calculated according to: . In addition to the four domains described in Section 3.1, additional refinement was applied to different fan surfaces and the highest refinement level was set at the impeller blades. The meshing algorithm does not take into account the border between rotating and stationary reference frames during mesh generation. The rotating fluid domain is defined after mesh generation, which leads to a non-smooth border following the hexahedral cells.
With respect to cell sizes used in this study, the industrial standards currently applied to simulate automotive headlamps were the initial reference point. According to these standards, fans of that size are normally meshed with a 1 mm resolution for the impeller domain and 0.2 mm at the blade tips. Four different meshes have been created in order to perform a RANS grid resolution study and to assess turbulent length scales. The different meshes have total cell numbers of 5, 9, 21 and 34 millions, respectively, and are termed very rough, rough, fine and very fine. The two coarser grids approximately reflect the current industrial standard. Table 4 lists information about the grid resolutions and the results for the average values of the RANS simulations are also provided. The results of the grid resolution study will be discussed in Section 4. The majority of the cells has a perfect aspect ratio of 1, however, individual cells in the vicinity of the fan wall show values below 0.1. In general, the grid quality improves with increasing grid resolution. Figure 5 presents three images of the fine mesh. Figure 5a shows the wall mesh looking from the outlet port towards the impeller. Figure 5b shows the mesh in a cut-plane at , containing the outlet region, the volute nose and some impeller blades. Figure 5c shows the mesh in a blade channel and around the blades in detail. The latter two plots show the moving reference frame colored in cyan and they demonstrate that the meshing software under the chosen settings produces relatively sharp transitions with large cell size changes between regions of different grid resolution.

Table 4.
Mesh sizes, maximum cell sizes and average values of the created meshes.

Figure 5.
Details of the generated fine mesh; the region colored in cyan in the lower two images indicates the rotating reference frame. (a) Fan wall mesh; looking into the fan via the outlet port. (b) Mesh detail for a cut-plane at , including outlet and volute nose. (c) Mesh detail for blade channel 27 for a cut-plane at .
3.4. Numerical Settings and Turbulence Models
All of the CFD simulations were carried out using the software ANSYS FLUENT 2020 R2. Four different turbulence models were used, namely
- k- realizeable (abbreviated as rke),
- Shear Stress Transport k- (abbreviated as SST),
- Reynolds Stress Omega (abbreviated as RSM) and
- Scale-Adaptive Simulation (abbreviated as SAS),
To compare the results, the solver settings had to be adjusted with respect to the turbulence model and the temporal treatment. In the following, the main settings are listed for each model. In cases where more than one temporal treatment was used, multiple specifications are provided.
3.4.1. k-ϵ Realizeable Turbulence Model
- convective term discretization: second order upwind
- pressure discretization: second order
- near-wall treatment: Enhanced Wall Treatment [53]
- temporal treatment:
- (a)
- steady, pressure-velocity coupling: SIMPLE
- (b)
- pseudo-transient, automatic time step, pseudo time scale factor 0.5, pressure-velocity coupling: Coupled
- (c)
- transient, time step: 1 × 10−5 s, pressure-velocity coupling: Coupled
3.4.2. SST k-ω Turbulence Model
- convective term discretization: second order upwind
- pressure discretization: second order
- temporal treatment: pseudo-transient, automatic time step, pseudo time scale factor: 0.05
- pressure-velocity coupling: Coupled
- transition modeling: one-equation model by Menter and Smirnov [54]
3.4.3. RSM Turbulence Model
- Reynolds Stress Model: Stress-Omega
- convective term discretization: bounded central differencing
- pressure discretization: second order
- temporal treatment: transient, time step: 1 × 10−4 s
- pressure-velocity coupling: Coupled
3.4.4. SAS Turbulence Model
- convective term discretization: bounded central differencing
- pressure discretization: second order
- temporal treatment: transient, time step: 5 × 10−6 s
- pressure-velocity coupling: Coupled
- transition modeling: one-equation model by Menter and Smirnov [54]
The bounded central differencing scheme for the Reynolds Stress Model (RSM) calculation was used to achieve better comparability with the SAS simulation.
4. Numerical Tests
4.1. URANS Grid Independence Study
A URANS grid independence study was carried out using the realizeable k- turbulence model. Since steady convergence was unsatisfactory for the very rough grid, transient simulations with a very small time step of 1 × 10−5 s were conducted for all meshes and the simulations were run until the monitors demonstrated that a steady state had been reached. Uncertainty estimations were performed according to the method described in [55]. Figure 6 shows the convergence behavior of the four different meshes for two selected integral flow quantities. The massflow-weighted total pressure difference between fan inlet and outlet as well as the impeller outlet volumetric flow rate were chosen for this purpose. These quantities are plotted over the mean cell size ratio . The mean cell sizes h were calculated by evaluating the average cell volume and the values correspond well with the average sizes in the jet domain given in Table 4. The solid blue line in each graphic represents the flow quantity result for the individual meshes. The black dashed line represents the power series expansion calculated from these results and the blue vertical dashed lines represent an estimate for the uncertainty which contains the exact solution with a probability of 95%. The results show mostly monotonic grid convergence with a continuously decreasing uncertainty. The maximum deviation in the total pressure difference and the volumetric flow rate amount to 4.5% and 2.2%, respectively.
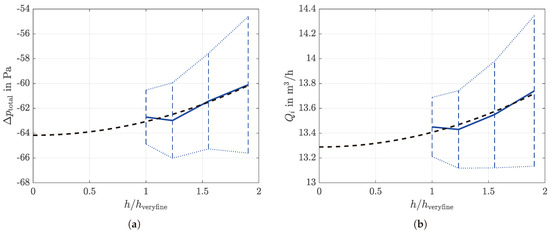
Figure 6.
Convergence trend of the massflow weighted total pressure difference between fan inlet and the trend of the VFR at the impeller outlet; solid blue lines represent the simulation results, dashed black lines the power series expansion, and vertical dashed lines the 95% uncertainty estimates. (a) Total pressure difference between fan in- and outlet. (b) VFR at the impeller outlet.
In addition, the changes of the normalized fan outlet velocity profiles with grid resolution were investigated. The velocities have been made dimensionless using the different volume flow rates of the fan and the fan outlet area . Figure 7 presents normalized velocity magnitude results on a horizontal evaluation line over the fan outlet at . The normalized velocity magnitude contours for the fine mesh, overlaid with streamlines calculated using the line integral convolution (LIC) method [56], are also shown to allow for a better interpretation. The results reveal some qualitative differences in the outlet velocity field, which in general exhibits a C-shape. Three aspects are notable when comparing the normalized velocity magnitude profiles.
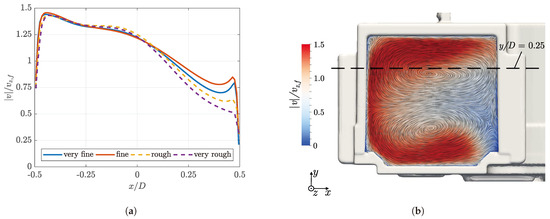
Figure 7.
Mesh convergence study: Comparison of the normalized velocity magnitude results on a horizontal evaluation line over the fan outlet at (black dashed line) and visualization of the velocity contours of the fine mesh. (a) Evaluation line results. (b) Normalized velocity magnitude contours for the fine mesh.
- For all the velocity magnitude profiles show little deviation except for the near-wall region where the improved near-wall resolution of the two finer meshes leads to a steeper gradient.
- For the two coarser meshes overestimate the velocity since the upper lobe of the C-shape experiences slightly stronger diffusion. It is also notable that the curves of the two finer meshes are almost identical in that region.
- For the results exhibit the strongest differences, which mainly result from the crossflow in the outlet plane. The two coarser meshes significantly underestimate the x-velocity in the upper lobe of the C-shape and consequently the velocity profiles in the vicinity of the wall do not exhibit a discernible local velocity maximum. It is also notable that this maximum is more pronounced for the fine grid in comparison to the very fine grid, which might be influenced by slight differences in the flow through the final two impeller blade channels ().
In general, the two coarser grids show noticeable deviations in the entire outlet flow field compared to the finer grids. The analysis of the results from the finer grids shows only deviations in specific regions.
4.2. Steady vs. Transient Solvers
Numerical tests where also performed with regard to the temporal formulation. Steady RANS as well as URANS simulations for the fine mesh were carried out. The latter has already been specified in Section 4.1. In addition, pseudo-transient simulations were also performed. ANSYS FLUENT offers pseudo-time-stepping as a dynamic under-relaxation method [53]. The unsteady transport equations are solved using the pseudo-time-step, which is automatically determined by the time scales of the individual terms of the momentum equation. The determined global pseudo-time-step was scaled by a factor of 0.5 to improve convergence. In the following, three fan simulations are compared:
- realizable k-, steady (abbreviated as rke-s);
- realizable k-, pseudo-transient, global pseudo time step and time scale factor 0.5 (abbreviated as rke-pt);
- realizable k-, unsteady, time step size 1 × 10−5 s (abbreviated as rke-t).
Figure 8a compares the dimensionless velocity magnitudes at the impeller outlet area. The velocity values have been averaged over the evaluation lines visualized in Figure 3. In addition, a moving average over 11.25° (i.e., one blade channel width) was calculated to eliminate the fluctuations due to the individual blade channels that would result from the MRF modeling. The values were also normalized by the area-weighted radial velocities of the respective simulation. Since the differences of the three curves seem negligible in this depiction, the deviations with respect to the unsteady results are highlighted in Figure 8b. This figure reveals that the steady and the pseudo-transient results agree very well over the entire impeller outlet. Differences to the unsteady results are within ±1% over most of the impeller circumference, except for the range between 300° and 340°, where a strong decline of the outlet flow rate occurs. This is accompanied by the development of local flow separations and consequently strong unsteady fluctuations. The URANS simulation can resolve these transient phenomena which results in differences of 1.1% and 1.7% in time-averaged volumetric flow rates at the impeller and fan outlet, respectively. The resulting fan outlet flow field and vortex structure are, however, hardly affected by these differences.
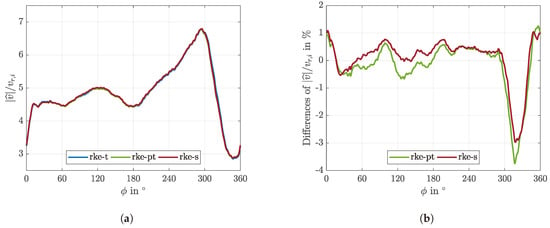
Figure 8.
Height-averaged normalized velocity magnitude results at the rotor outlet of the steady, pseudo-transient and transient realizable k- simulations and the deviations with respect to the transient results. (a) Normalized velocity magnitude result. (b) Differences of the normalized velocity magnitude.
4.3. Estimation of Turbulent Scales
The realizable k- results for the turbulent kinetic energy k and the turbulent dissipation rate can be used to estimate the integral length scale L and the Kolmogorov scale of the turbulent eddies. For isotropic turbulence this scales can be estimated by [57]
with as kinematic viscosity. The scales are compared to the cell length which is estimated from
with being the cell volume.
The ratios and are shown in Figure 9 for the fine and very fine mesh in a cut-plane at . The results for the integral length scale demonstrate that within the fan the ratios are below one, except for the boundary layers. Due to the coarser mesh in the jet domain, the value of one is partially exceeded in the jet shear layer at a short distance behind the fan outlet. The grid resolution of the very fine mesh is not fine enough to remarkably improve the scale estimates. The results for the Kolmogorov length scale are below 30 in the entire fan domain, but exceed this value in the jet domain. Figure 9c,d show the same results for a detailed view of the blade channels. The integral length scale ratio is only higher than one in the first cell layer at the blade boundary. The Kolmogorov length scale stays below fifteen in these regions.
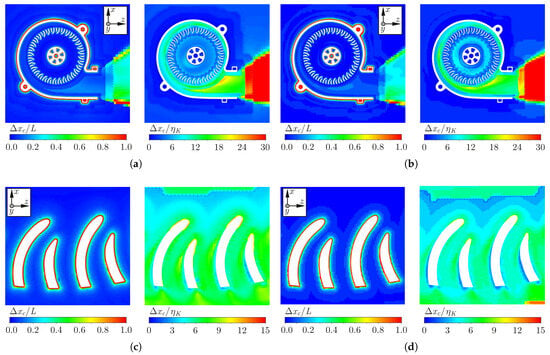
Figure 9.
Fraction of cell width to integral length scale L and the Kolmogorov length scale , respectively, obtained from URANS simulations. A cut-plane at is used to evaluate the results for the fine and very fine mesh, including the detailed situation between selected blade channels. Turbulent length scale estimation for the (a) fine mesh: fan cross section, (b) very fine mesh: fan cross-section, (c) fine mesh: blade channel detail, (d) very fine mesh: blade channel detail.
Judging from these results, the grid resolution can resolve the inertial subrange of the turbulence spectrum in the fan domain, but not in the jet domain. A problem resulting from the mesh transition produced by the software SPIDER and the chosen settings is that sharp transitions (within two cell layers) occur between regions of different grid resolution, which will lead to problems of transferring resolved turbulent scales over these transition zones in scale resolving simulations. An advantage of SAS is that the calculated turbulent viscosity is grid-dependent, which allows for a progression from an LES-like mode to a URANS-mode, e.g., in the jet domain. In addition, a full resolution of the boundary layer zones is not required and an improved behavior in non-LES compatible meshes can be expected. Due to these considerations, scale-resolving simulations for this fan are performed using SAS. As the very fine mesh does not provide significant advantages in the turbulent length scale resolution and would require approximately twice the computing time, the fine mesh was chosen for the analyses presented in the subsequent sections.
5. Numerical Simulations and Results
All results presented in this section were calculated using the fine mesh. Solver settings, time discretization method and the time step sizes used for the different turbulence models were adapted with regard to the convergence behavior and, in the case of SAS, also with regard to the Courant-Friedrichs-Lewy (CFL) condition. In the following, the main settings are listed for each model. In cases were more than one temporal treatment was used, multiple specifications are provided.
- k- realizeableThe results were evaluated from the transient simulation mentioned in Section 4.2. The scaled residuals for the continuity equation dropped by eight orders of magnitude.
- SST k-Steady convergence was unsatisfactory. The results presented were obtained by a pseudo-transient simulation with a time scale factor of 0.05. The scaled residuals for the continuity equation dropped by five orders of magnitude.
- Reynolds-Stress OmegaSteady convergence was impossible to attain. Transient simulation with a time step size of 1 × 10−4 s yielded stable convergence, where the scaled residuals for the continuity equation dropped by three orders of magnitude.
- SASA time step size of 5 × 10−6 s was necessary to ensure in the blade channels. Scaled residuals for the continuity equation dropped by five orders of magnitude.
5.1. Overall Performance Results
Performance results presented in this section are calculated from time-averaged pressure and velocity fields. In the case of the pseudo-transient SST simulation the values have been averaged over 20,000 iterations to account for small fluctuations.
5.1.1. Fan Performance Results
Table 5 shows the results for the VFR of the fan , the total pressure difference between fan outlet and inlet and the Reynolds number at the fan outlet . The latter is defined as

Table 5.
Comparison of fan performance results obtained with the four different turbulence models.
It becomes apparent from these data that the simulated volume flow rates significantly underestimate the measured value of . The results for vary from 85.7% to 91.6%. Even for an off-design point, these deviations are relatively high. This aspect will be revisited in the context of the CTA measurements in Section 5.7.1. The predicted fan flow rates deviate by 6.6% when using the SAS data as a reference. There is no obvious distinction between the results of the two equation models and RSM or SAS, respectively. However, the results for the total pressure difference seem to indicate that the two equation models overpredict .
From these quantities the dimensionless performance parameters flow coefficient
head coefficient
specific speed and specific diameter
can be calculated. The resulting values are compared in Table 6.

Table 6.
Comparison of dimensionless fan performance parameters obtained with the four different turbulence models.
Using the SAS data as a reference, the results for and vary by 6.1% and 13.0%, respectively. The related deviations for and amount to 10.2% and 4.1%. The two equation models tend to underpredict the specific speed and the SST k- model significantly overpredicts the specific diameter. With regard to the Cordier diagram [13], the specific diameter deviates from the typical optimum for centrifugal fans by approximately 30%. A discrepancy can be expected, since these data were obtained for an off-design point. However, the corresponding calculation using the nominal data from the manufacturer given in Table 1 results in a similar deviation. These data indicate that compromises regarding efficiency were made in the design of the fan to obtain a higher total pressure build-up in combination with a reduced fan size.
5.1.2. Impeller Performance Results
Common nomenclature for velocity triangles refers to the absolute velocity vector as , the relative velocity vector as and the impeller tangential velocity as U. Indices 1 and 2 refer to the rotor inlet and outlet, respectively. These velocities are related to the previously introduced velocities by
The magnitudes of and will simply be referred to as C and W, respectively. The Euler equation for turbomachinery reads [13]
The pressure components , and refer to the centrifugal component, the dynamic pressure increase and the relative velocity component, respectively. These are related to the velocities by
These individual pressure components were evaluated using area- and time-weighted velocities. They are listed in Table 7 and compared to the mass-weighted total pressure difference evaluated from the simulations. In addition, the volumetric flow rate and the corresponding mean radial velocity evaluated at the impeller outlet are also included in the table.

Table 7.
Comparison of impeller performance results obtained with the four different turbulence models.
Regarding the total pressure results, varies by 10.1% and by 12.4%, again using the SAS results as a reference. The observed differences between and are an indication for deviations between the mean velocities and the actual velocity distribution at the impeller outlet. The realizable k- model seems to strongly overpredict the dynamic pressure increase. This deviation can not be explained by the higher impeller flow rate, but must also be a result of increased tangential velocities. The other three models predict a reaction ratio [13] of slightly below 0.5, which indicates that the fan was designed for a high static pressure increase. The predicted impeller flow rates deviate by 4.5%, which is more than 1% lower than the observed deviation at the fan outlet.
5.1.3. Efficiencies
The overall fan efficiency and its subdivisions regarding different types of losses are calculated from the time-averaged data of the different simulations. The electrical power consumption during the measurements [12] is calculated from the voltage and current listed in Table 1. The time-averaged impeller torque was evaluated during the simulations and the corresponding impeller power was calculated from . All other values used in the following calculations are listed in the Table 5 and Table 7. The different efficiencies are calculated by
The results calculated according to these definitions are listed in Table 8.

Table 8.
Comparison of fan efficiency results obtained with the four different turbulence models.
The overall efficiency varies by 13.2% and is overpredicted by the realizable k- model. There is a remarkable difference between the two equation models. While the realizable k- model predicts a high torque and a high volumetric efficiency, the SST k- model predicts a high impeller efficiency and a relatively low torque. The lowest overall efficiency is obtained by the Reynolds Stress Model, mainly due to the low impeller efficiency caused by high friction losses between the impeller and the surrounding air. Regarding the consistency of the models with respect to the efficiency components, the lowest deviations are obtained for the volumetric efficiency with 1.2% and the highest for the impeller efficiency with 11.8%. Regarding the volumetric efficiency, the main loss occurs at the upper gap (higher y-coordinate) between the impeller and housing, where air can flow back from the impeller outlet towards the blade channels. This path is responsible for approximately 90% of the backflow.
5.2. Results at the Impeller In- and Outlet
5.2.1. Velocity Triangles
Velocity triangles were calculated from the mean time-averaged velocities at the impeller in- and outlet. Using the nomenclature introduced in the Section 5.1.2, the resulting velocities and angles are listed in Table 9 and Table 10. Indices 1 and 2 refer to the impeller inlet and outlet, respectively. The angles and denote the absolute and relative flow angles. The velocity triangles for the SAS results are shown in Figure 10 for illustration purposes.

Table 9.
Comparison of the velocities and angles of the velocity triangles at the impeller inlet for the different turbulence models.

Table 10.
Comparison of the velocities and angles of the velocity triangles at the impeller outlet for the different turbulence models.
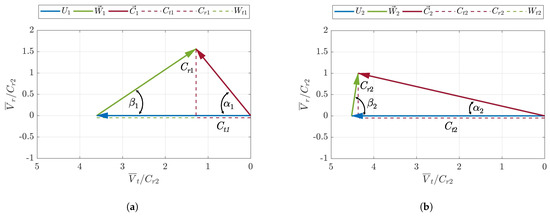
Figure 10.
Velocity triangles at the impeller inlet and outlet calculated from time- and spatially-averaged SAS results. Common nomenclature for velocity triangles is used here, absolute velocity, relative velocity, impeller tangential velocity. Indices 1 and 2 refer to the rotor inlet and outlet, respectively. (a) Velocity triangle at the impeller inlet. (b) Velocity triangle at the impeller outlet.
The results for the inlet triangles reveal small discrepancies in the absolute flow angle and the absolute and relative velocity magnitudes. The relative flow angle does not markedly deviate from the inlet blade angle of 29°, which indicates only minor disturbances at the inlet despite the deviation from the nominal point of operation. At the outlet, however, strong differences in the relative flow angle were found. The flow angles significantly deviate from the outlet blade angle of 109°. Despite the presence of splitter blades the results hint at the existence of recirculation areas in the blade channels, which apparently depend on the turbulence model used.
5.2.2. Velocity Distributions at the Impeller Outlet
The 19 evaluation lines defined in Section 2.2 are used to evaluate the velocity distributions over the circumference of the impeller outlet. Figure 11 shows the normalized time-averaged velocity field for the realizable k- model at the impeller outlet. The location of the bottom, mid and top evaluation lines are included in the plot for interpretation purposes. The velocity fluctuations due to the blade channels resulting from the MRF method can clearly be identified in this plot. For all subsequent plots of the evaluation line plots, a moving average filter was applied to smooth out the velocity distributions.
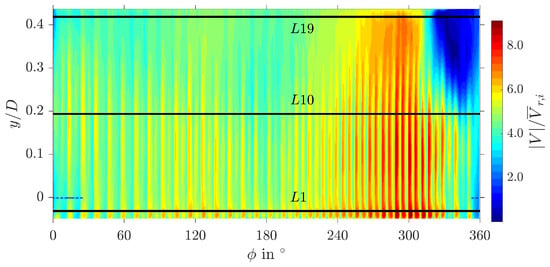
Figure 11.
Normalized time-averaged velocity magnitude results of the realizable k- simulation at the impeller outlet surface. The aspect ratio of the plot (impeller outlet height vs. outlet circumference) is increased by a factor of 8. Note: No moving average filter was applied.
Figure 12 presents time-averaged velocity magnitude distributions for each turbulence model. The lower (L1), mid (L10) and upper (L19) evaluation line results are highlighted in different colors, whereas the results of all the other lines are shown in light grey to demonstrate the velocity variation over the impeller height. It is evident that the velocity distribution varies significantly over the circumference. These distributions can roughly be subdivided in three areas.
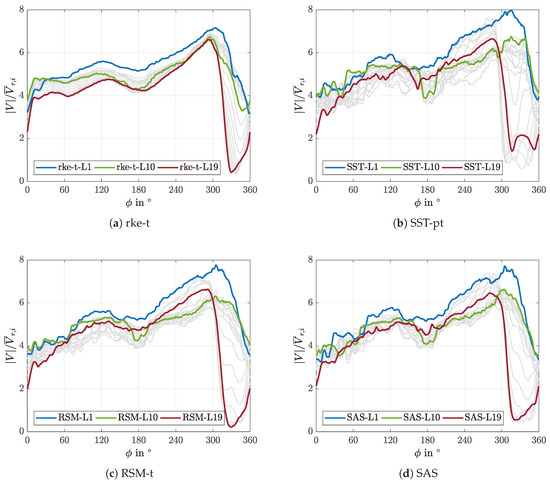
Figure 12.
Normalized time-averaged velocity magnitude results for the evaluation lines at the impeller outlet surface for the different turbulence models; bottom (blue, L1), mid (green, L10), top (red, L19), others (grey).
- : Velocity magnitudes tend to increase continuously up to and subsequently decrease slightly. Differences over the impeller height remain below 5 .
- : Velocity magnitudes rise steadily until they reach the maximum at approximately . With the exception of the realizable k- model results, the differences over the impeller height increase as well.
- : Velocity magnitudes decrease strongly and reach their minima in the vicinity of the nose. The deviations over the evaluation lines become very high, since the drop in velocity is more pronounced for the upper evaluation lines. The minimum values are followed by a steep increase until reaches 30°.
Regarding the turbulence models, it is noticeable that the curves for the realizable k- model are significantly smoother and show lower variations between the evaluation lines in comparison to all other models. In addition, the velocity values remain mostly bounded between those of the lower and upper evaluation line for the realizable k- model, a behavior that is not replicated by the other models. In general, the pseudo-transient SST k- results are similar to both the transient RSM- and SAS results. The strongest deviations between the models occur in the vicinity of the volute nose. It can already be concluded from these results that the flow will become complex in the area towards the nose. It is noticeable that the main flow tends to follow the curved impeller base plate, which is shown in Figure 2, since the velocity magnitudes are highest at the lower evaluation line (L1) over the entire circumference. In the upper impeller region, however, a significant velocity deficit develops between and .
Further evaluation of the impeller outlet flow field is shown in Figure 13 on the basis of height- and time-averaged velocity components. The tangential velocity curves largely follow the previously described behavior regarding the velocity magnitude, since it is the main velocity component. For the realizable k- model a notable difference to results of the other models is evident between and . In addition, large discrepancies between the different turbulence model results are found in the region from to . It is also noticeable that the maximum tangential velocity supersedes the impellers rotational velocity. The reason for this result is, that the fluid exits the blade channels with high radial velocity in this area. This leads to an additional deflection of the exiting fluid immediately outside the blade channels by the main flow in the volute. The minimum tangential velocity occurs upstream of the nose, since the fluid exiting the blade channels flows towards the exit of the fan and does not follow the impeller towards the tight nose gap. The axial velocity follows roughly the same trend as the tangential velocity, however, the velocity values are mostly negative. This agrees with the previous observation, that the main flow tends to follow the base plate contour of the impeller. There is only one small angular range downstream of the nose, where the axial velocity is slightly positive. This is mainly due to tight gaps in the volute cross-section, which will be briefly addressed in Section 5.3. With exception of the realizable k- model, the results are very similar for all turbulence models in the region between and . The radial velocity distribution is characterized by strong non-uniformity. All turbulence models predict a pronounced maximum at . The largest differences are observed for the two-equation models around the peak and at the nose, i.e., at . Figure 13d shows the contribution of each blade channel to the total impeller volume flow rate in percent. The distribution is, of course, essentially the same as that for the radial velocity, but allows for an easier aggregate analysis. More than 50% of the total volumetric flow rate is generated by the ten blade channels from 21 to 31, i.e., between and .
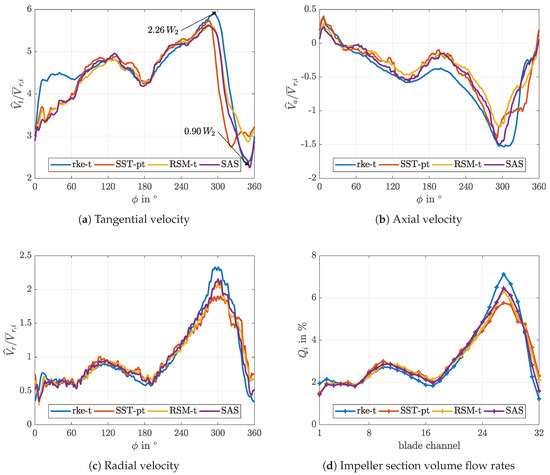
Figure 13.
Time-averaged normalized tangential, axial and radial velocity averaged over all 19 evaluation lines at the impeller outlet as well as the blade channel volume flow rates for the different turbulence models.
5.3. Volute Flow Results
The flow development in the volute is illustrated by velocity contour plots for selected evaluation surfaces. The locations of the surfaces presented in Figure 14 and Figure 15 are indicated in Figure 2, and were chosen to show the main phases of flow evolution.
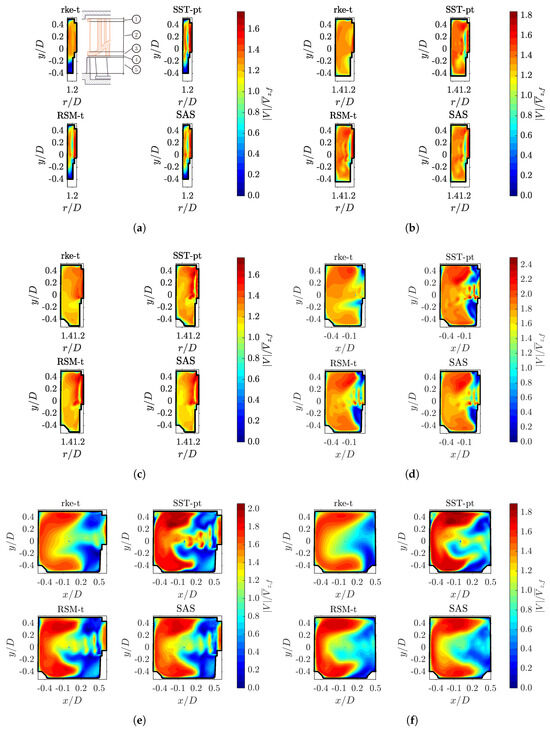
Figure 14.
Time-averaged normalized velocity magnitude results for six different evaluation surfaces of the fan volute and the different turbulence models. (a) includes a sketch of the cross-section of the fan for orientation purposes: ➀ …upper impeller ring, ➁ …blade channel, ➂ …impeller base plate, ➃ …lower impeller gap, ➄ …lower volute extension. Velocity magnitude for evaluation surface (a) S5, (b) S15, (c) S20, (d) S30, (e) S33, (f) S35.
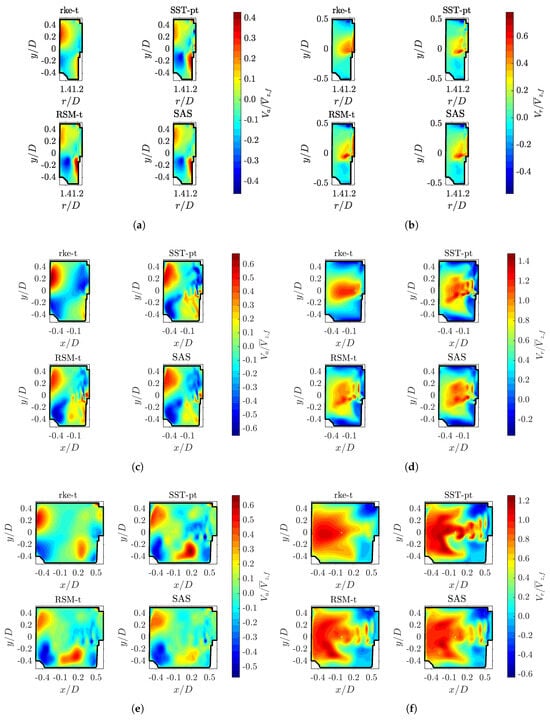
Figure 15.
Time-averaged normalized axial and radial velocity results for three different evaluation surfaces of the fan volute and the different turbulence models. (a) Axial velocity for evaluation surface S20. (b) Radial velocity for evaluation surface S20. (c) Axial velocity for evaluation surface S30. (d) Radial velocity for evaluation surface S30. (e) Axial velocity for evaluation surface S33. (f) Radial velocity for evaluation surface S33.
Figure 14 compares contours of the normalized mean velocity magnitude for the four turbulence models. Evaluation surface S5 demonstrates that in the first quarter of the volute the results for the realizable k- model already differ substantially from those of all other models. The SST, RSM and SAS contours show distinct regions of high and low velocity. The high velocity region close to the volute wall stems from the flow attached to the pressure sides of the main blades, which exits the blade channels with high radial velocity and gets redirected in tangential direction at the volute wall. The high velocity region at the opposite side represents this attached flow for the fifth main blade, which is about to exit into the volute. The low velocity region in-between develops from the large recirculation areas at the suction side of the main and splitter blades. The realizable k- model strongly diffuses these structures so that they can hardly be distinguished. The flow already exits from the blade channels at a lower velocity and radial momentum, which contributes to blurring of the flow structures. The realizable k- model does not even predict the outflow between the impeller base plate and the fan housing (denominated as gap in Figure 14a). At evaluation surface S5, the lower extension of the volute is so narrow that it hardly permits any flow, but despite that the results for the realizable k- model differ from that of the other models.
For evaluation surface S15, it is again evident that the realizable k- model cannot adequately resolve the flow structures. This circumstance remains the case for all the subsequently discussed evaluation surfaces and will therefore no longer be specifically mentioned. The contours for this surface also reveal differences between the SST k- model and RSM or SAS. The main flow structure is still correctly predicted by the SST model, however, small details of the flow are slightly less distinct. The lower extension of the volute has sufficiently widened, so that the fluid enters on the outer side of the volute and subsequently leads to the formation of a vortex. While the RSM and SAS results coincide in both the velocity magnitude and center location of this vortex, the SST results are markedly different.
Concerning evaluation surface S20, it is difficult to describe the flow development on the basis of the velocity magnitudes. Further analysis will be provided in a later paragraph on the basis of the velocity component contours. It is noticeable, that the RSM and SAS results show slight differences especially regarding the vortex development within the lower extension of the volute.
In evaluation surface S30, a double vortex structure has clearly been established, which will develop into a characteristic C-shape further downstream. It can be assumed that two main factors contribute to this outcome. First, the typical development of secondary flows due to an imbalance of the centrifugal and the pressure force at the upper and lower volute boundaries will drive the fluid inwards at these boundaries, and will subsequently produce a double vortex structure. Second, since the fan operates at a static fan pressure of 0 , the pressure in the volute will decrease and homogenize as the outlet is approached. This will disturb the equilibrium between pressure gradient and centrifugal forces which will drive the flow towards the outer wall in the volute center. The second effect is enhanced since the flow exits the impeller in the form of small jets with high radial velocity and high radial momentum in this section of the volute. As demonstrated in Figure 13c, at the impeller outlet of evaluation surface S30 at , the radial velocity is close to its maximum. It must be noted that the strong non-uniformity of the radial flow distribution is a consequence of the pressure decrease towards the fan outlet. The pressure distribution will be discussed in more detail in Section 5.4. Further elaboration should be added to the first point of the above analysis. The development of a secondary flow due to the first mechanism vanishes when the radial pressure field in the volute becomes more homogeneous. However, a secondary flow which has established further upstream will persist due to inertia. It is worth noting that all turbulence models are able to predict the main flow development. Again, the realizable k- model results differ substantially, while only small variations in the velocity contours are present in all the other models.
Evaluation surface S33 is the last surface upstream of the nose (Figure 2). Here, the main flow has been driven towards the outer volute wall mainly due to the influence of the centrifugal force, which leads to the C-shape becoming more pronounced. Distinct high velocity regions stemming from the previous three blade channels are clearly discernible, which are, of course, an artifact due to the MRF modeling of the impeller rotation. It is interesting to note that these structures seem to have experienced lower diffusion for the SST model. Even the maximum velocity of the main flow is highest for this model.
At evaluation surface S35, the C-shape has been fully established for all turbulence models. In the realizable k- case, the shape is very diffuse and the details of the jets, which emanated from the last blade channels have largely diffused, as well. The contours of the SST model and RSM show similarities regarding the width and the evolution of the upper and lower lobe of the C-shape. The main difference is that the structures in-between the lobes are still more pronounced in the SST case. Two features are different in the SAS results. One is that the vertical part of the C-shape contour is significantly thinner. The other concerns the lower lobe, which does not bend towards the center, but follows the lower outlet contour.
Axial and radial velocity contours are provided in Figure 15 for three evaluation surfaces to better analyze the secondary flow inside the volute. In S20 the axial velocity contours reveal, that the double vortex structure, mentioned before in the discussion about the velocity magnitude of S30, already exists further upstream. Again, the realizable k- results substantially deviate from those of the other models, as it shows higher velocities in the upper vortex compared to the lower one. The situation is reversed for the other three models. The reason for this deviation is related to the height distribution of the radial velocity at the blade outlets. The flow exiting the blade channels is concentrated in the vicinity of the impeller base plate and shows a slight inclination downwards in all four models. However, in the realizable k- case the height distribution is not as concentrated towards the base plate (Figure 15b), which leads to a difference in the amount of fluid circulating in the upper and lower vortices.
The contours for the evaluation surface S30 reveal that the vortices inside the volute have grown in size and strength. The upper vortex certainly influences the height distribution of the blade channel outflow, since the radial backflow inhibits fluid exiting from the upper parts of the blade channels. The axial velocity differences of the double vortex structure between the models persist. They are, however, less pronounced. The SST model and RSM reveals striking similarities in the contour structures especially regarding the axial velocity. The SAS model shows slight differences particularly in the contours of the lower vortex.
The evaluation surface S33 demonstrates differences in the development of the lower vortex between SAS and the RSM/SST cases. The axial velocity contours of the latter show three distinct areas of downward and upward movement. To be specific, in the lower right corner downward movement can be detected, which mainly results from the flow emanating from blade channel one, which is deflected downwards at the volute nose and produces a local subvortex. This structure can even be detected for the k- model, albeit in a less pronounced manner. The SAS model shows large fluctuations in the lower right corner, but the development of a distinct area of downward movement is less pronounced, since the flow direction emanating from blade channel one varies over time. The average flow field therefore tends to follow the lower volute wall contour and does not produce a strong axial upward component. It must be noted, that these local flow structures are partly an artifact of the MRF model, since a moving impeller would lead to different flow interactions with the volute nose.
5.4. Fan Flow Field Overview and Blade Channel Details
To present an overview of the pressure and velocity field in the fan and to illustrate the flow field through the blade channels, contour plots on an evaluation surface at , approximately in the middle of the impeller outlet height, are presented in Figure 16 and Figure 17. All contour plots are overlaid with LIC lines to visualize flow separations, vortical structures and the complexity of the flow. In general, the relative velocity components were used as input for the LIC line calculation, with exception of the lines in Figure 16b, where the absolute velocity components were selected. This allows for a direct comparison of the relative and absolute velocity fields, whereby the relative LIC lines are convenient for analyzing the flow through the blade channels, whereas the absolute LIC lines better illustrate the flow in the entire inflow area, the volute and the outlet area. The relative velocity vector is defined as:
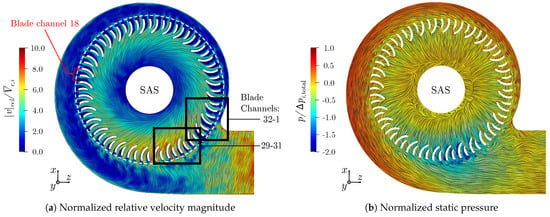
Figure 16.
Normalized relative velocity magnitude and normalized static pressure results for a selected time step at an evaluation surface at , slightly above the middle height of the impeller outlet. Note: The white dashed line indicates the MRF border. Overlaid LIC lines: (a) shows LIC lines calculated from the relative velocity field, (b) from the absolute velocity field.
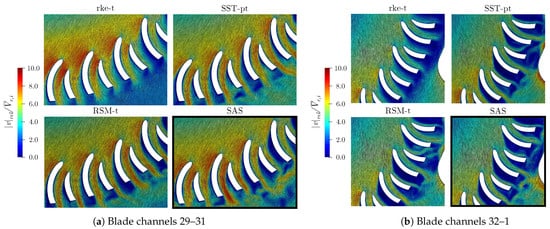
Figure 17.
Normalized relative velocity magnitude results for selected blade channels at an evaluation surface inside the fan at , slightly above the middle height of the impeller outlet.
Figure 16a shows the instantaneous relative velocity field for a selected time step of the SAS case. The non-uniformity of the impeller flow, discussed in Section 5.2, leads to differences in the incoming flow angle relative to the impeller blades. For the blade channels 1–18, the stagnation point is located very close to the blades’ leading edge. For the other blade channels, where the volume flow rates are higher, the stagnation points move away from the leading edge tips towards the pressure side. The flow remains completely attached on the pressure sides, but detaches from the suction sides of both the main and splitter blades. For most of the impeller circumference the sizes of the separation regions are actually larger than the attached flow regions. In the part where the local flow rate is increased, particularly for the blade channels 27–30, the sizes of the separation regions are significantly reduced. All these separation regions lead to complex vortex structures downstream of the blunt trailing edges of the blades. The white dashed line marks the border of the rotating reference frame. The radial extension of the recirculation areas seems to be influenced by this MRF-boundary, i.e., the transition from rotating to stationary reference frame might lead to some disturbances in the calculated velocity field.
Figure 16b shows the instantaneous normalized static pressure contours for the same time step. This figure is crucial for explaining the non-uniformity of the volumetric flow rate distribution over the impeller. Between blade channels 2 and 20, the static pressure increase between impeller inlet and volute amounts to approximately 40 , which is equal to about 70% of the average total pressure increase of the fan. This leads to a significantly higher static pressure inside the volute compared to the fan outlet, which is at 0 and the flow must therefore accelerate towards the fan outlet. The resulting reduction in the static pressure is the main reason why the volume flow rate in the final third of the impeller circumference, particularly blade channels 20–31, is considerably increased. A large amount of the total pressure build-up over these blade channels takes place in form of a dynamic pressure rise. It should be highlighted that this behavior is essentially related to the fact that the fan is not operating at its design point, but at a static fan pressure of 0 . This leads to increased local velocities, an overall reaction ratio below 0.5, and consequently to high losses due to friction and turbulence. This is also the main reason why the blade efficiency is below 50%, as shown in Table 8.
In Figure 17a, the relative velocity magnitude contours of all turbulence models are shown for a detailed area encompassing the blade channels 29, 30 and 31 (refer to the left box in Figure 16a). In this area, the local volume flow rate is relatively high and the size of recirculation regions is not very pronounced. The deviation of the incoming flow angle from the blade angle does not produce local flow separation at the leading edge due to the rounded blade tip. Separation occurs on the pressure side of the main and splitter blades at approximately 20% to 30% of the blade length, slightly varying from blade to blade. It is evident that the size of the resulting recirculation regions predicted by the realizable k- model is significantly smaller than that predicted by the other models. As a consequence, the recirculation regions downstream of the blunt trailing edges of the blades are considerably smaller for the realizable k- model, leading to lower transient fluctuations in the outflow of the blade channels. As expected, the SAS results show the highest degree of irregularity and the largest amount of small vortex structures in these recirculation regions.
Figure 17b shows the corresponding situation around the blade channels 32 and 1 (refer to the right box in Figure 16a). This is the region where the local flow rate reaches its minimum. Large separation regions are visible due to leading edge separation on the main blades. The flow between the suction side of the main blade and the pressure side of the splitter-blade is largely inhibited by complex vortex structures. Again, the size of the recirculation regions is significantly less pronounced for the realizable k- model. The area downstream of the blade channel outlets is characterized by a high degree flow irregularities including vortex structures and turbulent fluctuations.
The fact that the realizable k- model does lead to relatively steady flow behavior at the impeller outlet is likely to be the one of the main reasons why a converged solution could be obtained using the steady solver. The pseudo-transient solver used for the SST simulation allows for variations of the flow results between the pseudo time steps. A comparison of the results obtained over the course of a simulation run reveals significant variation in this area. Using the pseudo-transient solver requires averaging to calculate the mean flow field.
5.5. Outlet Flow Field
Figure 18 compares the contours of the velocity magnitude, the x-, y- and z-velocity components at the fan outlet (evaluation surface S37) of all simulations. The general tendencies of the flow field are predicted by all turbulence models:
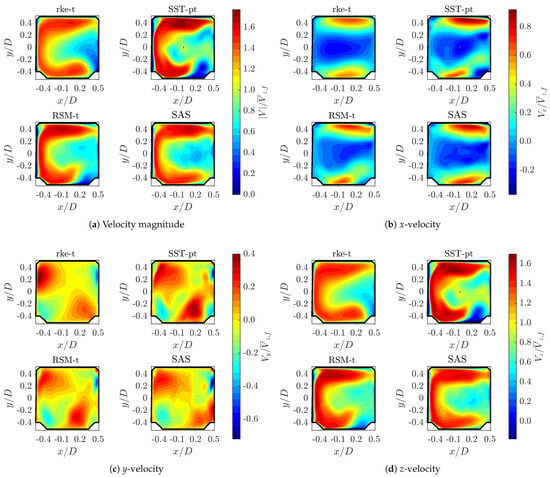
Figure 18.
Time-averaged normalized velocity magnitude, x-, y- and z- velocity results at the fan outlet (S37) for the different turbulence models.
- The z-velocity and the velocity magnitude contours exhibit a C-shape.
- The x-velocity field shows negative values in the center, i.e., a flow from right to left, and positive values in the upper and lower lobe of the C-shape.
- The y-velocity of the vertical part of the C-shape is zero at and exhibits positive values as the upper left corner of the fan outlet is approached and likewise, negative values as the lower left corner is approached.
- At the end of the lower lobe (lower right corner of the fan outlet) the x-velocity is noticeably positive. Conversely, the end of the upper lobe does not show a significant downward movement.
Despite this agreement in general trends, the results for the different turbulence models exhibit significant differences. The main observations are:
- The C-shape is the widest for the realizable k- model. Consequently, the velocity magnitude or z-velocity values are the lowest.
- The x-velocities in the upper and lower lobes are also lowest for the realizable k- model.
- The y-velocities values in the upper left corner are highest for the realizable k- model. The contours are significantly smoother than those of the other models in the entire outlet plane.
- The SST model shows the highest local velocities for the x- and z-components as well as for the magnitude.
- The SST model is the only one which produces local backflow. Negative z-velocities occur in the vicinity of the lower right corner.
- The flow structures in-between the lobes have experienced the lowest diffusion for the SST model.
- The lower lobe is significantly shorter in the SST and RSM results, and it exhibits a notable upwards movement at its end. This is a direct consequence of the flow development in the vicinity of the nose, as previously discussed in the context of Figure 15e. In the SAS results, the lower lobe extends towards the lower right corner, since, the subvertex identified in evaluation surface S33 was considerably weaker. As previously mentioned, these differences might be influenced by the MRF modeling of the impeller rotation.
- The SAS model shows the thinnest vertical part of the C-shape. The upper and lower lobe extend over the entire width of the fan outlet. As a consequence, in a thin layer at the right border of the outlet, the y-velocities show pronounced values in up- and downward direction, respectively.
- The z-velocities in-between the upper and lower lobe are the lowest for the SAS model.
5.6. Comparison of Turbulence Quantities
To interpret the reasons for the differences and similarities in the velocity fields, which have been the focus of the analysis thus far, turbulence quantities are discussed in this section. The analysis encompasses comparisons of turbulent kinetic energy fields of all four simulation cases and the Reynolds stresses of the SST k- and the RSM simulations. In addition, an investigation of the grid dependency of the resolved turbulence of the SAS case is performed. Finally, fluctuations at the fan outlet are compared to CTA measurements.
5.6.1. Turbulent Kinetic Energy
The kinetic energy of turbulent fluctuations per unit mass, also referred to as turbulent kinetic energy, is defined as
where stands for the deviation of the instantaneous velocity component in i-direction from the Reynolds-averaged velocity in the same direction, and the overline represents Reynolds-averaging. Figure 19 shows the turbulent kinetic energy normalized by the mean impeller outlet velocity evaluated at selected time steps at an evaluation surface at . Note that only the modeled, and not the resolved turbulent kinetic energy is shown for the SAS case. For the analysis of the differences, four main areas are considered.
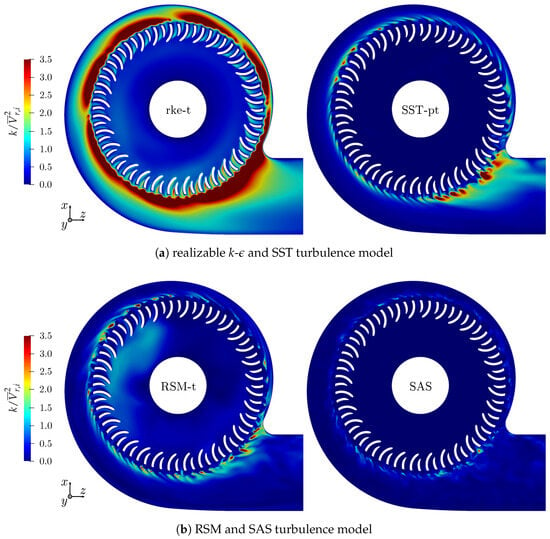
Figure 19.
Normalized turbulent kinetic energy of all turbulence models for selected time steps at an evaluation surface at , slightly above the middle height of the impeller outlet.
- Inlet area upstream of the impeller blades:The turbulent kinetic energy is essentially zero for both the SST and SAS model. For the realizable k- model, k is already produced when the air accelerates while moving through the fan inlet port. In the RSM case, the inlet turbulence field exhibits transient behavior leading to patches of increased turbulent kinetic energy which change over time, while in other areas k is almost zero.
- Blade channels:For the realizable k- model the flow around the blades is modeled as fully turbulent due to the turbulent inflow and the enhanced wall treatment model applied at the blade boundary layers. This leads to production of k especially between the suction side of the main blade and the pressure side of the splitter blade, as well as at the suction side of the splitter blade. Essentially, in those areas where the other turbulence models show significant flow separation the realizable k- model responds with a high production of k, which prevents massive flow separation. All -based models show high values of in the wall-adjacent cells, which leads to turbulent viscosity ratios below one in the RSM case. The intermittency transmission model applied in the SST and SAS cases predicts intermittency values below 0.3 over the entire blade boundary layers, which leads to even lower turbulent viscosity ratios in these areas. This consequently facilitates the development of flow separations.
- Outlets of the blade channels 1–27:In the case of the realizable k- model, high production of k takes place in the shear-layers where the small jets emanating from the blade channels merge with the volute flow. This leads to elevated turbulent kinetic energy over the entire circumference of the impeller outlet. In addition to the low flow separation in the blade channels, these high levels of turbulence generated at the impeller outlet lead to highly blurred velocity contours and a lack of resolution of flow details, as was discussed in Section 5.3. The high degree of flow separation predicted in the SST and RSM cases leads to thin jets entering the volute, where they get deflected in circumferential direction. Distinct areas of high turbulent kinetic energy develop in the shear layers. In general, the production of k in the SST model and the RSM case are relatively similar, which explains the observation that the resulting mean velocity fields in the volute only exhibit small differences, as presented in the context of Figure 14 and Figure 15. The levels of modeled k in the SAS case reach values above 1.5 in distinct spots downstream of the impeller outlet. Further discussion regarding the ratio of modeled and resolved k will follow later in this section.
- Outlets of the blade channels 28–32 towards the fan outlet:The impeller outlet area downstream of the final blade channels is characterized by a high degree of unsteady fluctuations and turbulence production, since the main volute flow follows the outer wall towards the fan outlet. A high degree of turbulence production is predicted by all models. However, the differences are quite apparent. The realizable k- model shows a confined area with high levels of k, which strongly decreases towards the outlet. The SST model only produces similar levels of turbulent kinetic energy in distinct regions, where jets exit the blade channels. Particularly in this area, the pseudo-transient approach leads to a certain degree of fluctuations in the turbulence field, so that both size and location of the regions of higher turbulent kinetic energy change over the course of the simulation. In the RSM case, the turbulence field is highly unsteady. Only small regions of elevated levels of k related to jets emanating from the blade channels appear. Unsteady patches of higher k can occur towards the outlet, but generally, turbulence levels decrease strongly. In the SAS case confined regions of high levels of k can be detected at the impeller outlet, depending on the unsteady local flow situation. In these cases large turbulent eddies are locally not fully resolved.
Figure 20 shows the turbulent kinetic energy contours for the evaluation surfaces S33 and S37, now normalized by the squared mean fan outlet velocity. These contour plots allow for better interpretation of the turbulence field development towards the outlet. The realizable k- model results of evaluation surface S33 not only feature high levels of k directly downstream of the blade channel outlets, but an additional peak is visible at approximately , , which stems from the local subvortex structure discussed in context of Figure 15e. In the other models such a local peak can also be detected, but is less pronounced and overlaid with local flow structures, which lead to production of k. A comparison of the turbulent kinetic energy contours and the time-averaged radial and axial velocity contours reveals that the k contours of the SST model reflect the areas of high shear rates, while the k-contours in the RSM case are more distorted due to higher unsteady fluctuations of the velocity field. The modeled k-field of the SAS case, again, shows only small distinct peaks.
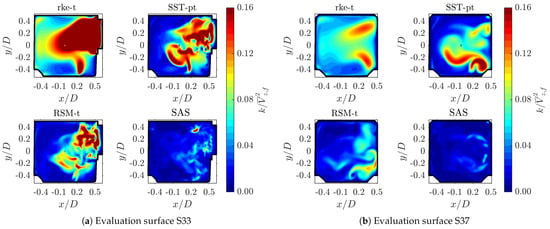
Figure 20.
Normalized turbulent kinetic energy at the evaluation surfaces S33 and S37 (fan outlet) for the different turbulence models.
In the fan outlet area S37 the k-contours of the realizable k- case show two distinct peaks which are perfectly aligned with the highest gradients in the z-velocity field (see Figure 18). The k-contours of the SST model are slightly more complex, but generally agree well with areas of high shear rates. The highest levels of turbulent kinetic energy are produced in the backflow area at the lower right corner of the outlet. In the RSM case, the maximum k-levels are lower than the in SST case and tend to coincide with local unsteady vortex structures, and not with the mean velocity field. The same is true for the SAS model results, albeit the modeled turbulent kinetic energy is, of course, significantly lower.
Figure 21 compares the time-averaged resolved turbulent kinetic energy for the SAS model, calculated from the Root Mean Square Error (RMSE) values of the velocity components. A comparison of the modeled k values of the SST and RSM cases demonstrates better alignment of the resolved SAS results with the levels of the SST model. This becomes particularly evident in the contours of the fan outlet. Within the impeller domain and the volute, the ratio between resolved k and total k is larger than 0.75, except for distinct spots. The SAS model works in a LES mode within the fan and starts transitioning into a RANS mode outside of the fan, as was expected in the analysis conducted in Section 4.3.
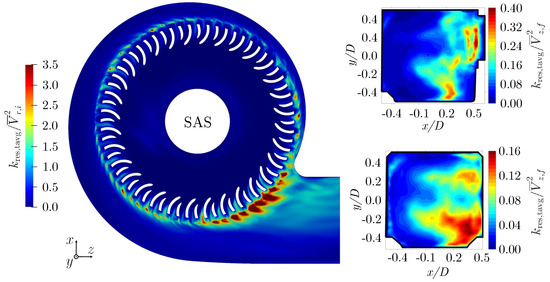
Figure 21.
Normalized time-averaged resolved turbulent kinetic energy results of the SAS model at an evaluation surface at and at the evaluation surfaces S33 and S37 (fan outlet).
5.6.2. Reynolds Stresses
The analysis of the turbulent kinetic energy revealed that the SST k- model is capable of predicting realistic levels of k. The following evaluation will focus on components of the Reynolds stress tensor. In the SST case, Reynolds stresses are calculated using the Boussinesq hypothesis
Here, overlines stand for Reynolds averaging, represents the kinematic turbulent viscosity and represents the Kronecker symbol. Figure 22 compares the normal stresses and Figure 23 the shear stress of the SST and RSM simulations. The contours show instantaneous values at selected time steps normalized by the mean impeller outlet velocity in an evaluation surface at . The most obvious differences regarding the normal stresses appear in the region downstream of the blade channels 28–32. In the RSM case the stresses, which represent fluctuations normal to the evaluation surface, and the stresses are significantly weaker than the stresses. The SST model is capable of correctly capturing this tendency, however, the differences are less pronounced. In addition, the orientations of the regions of high normal Reynolds stresses significantly depend on the particular stress in the RSM case. This becomes especially obvious when the and stresses are compared in the vicinity of the nose. The SST model is not capable of predicting such intricate details. Apart from the slightly elevated levels of k, the areas of increased normal stresses are reproduced fairly accurately by the SST model. The differences are, however, more pronounced when the Reynolds shear stresses are compared. In the SST case the stresses downstream of the impeller outlet are characterized by a succession of alternating positive and negative stresses of comparable intensities over most of the circumference. The shear stress levels are directly related to the alternating velocity gradients. In the RSM case, the situation is remarkably different, particularly between the blade channels 20 and 27. Here, negative stress levels exceed positive stresses. This behavior is associated with the convective transport of the shear stresses due to the volute main flow. It must be noted that, the SST modeling can account for reduced turbulent kinetic energy production in separated shear layers. Yet, it cannot reproduce the transport of shear stresses. As a consequences, the jets emanating from the impeller tend to diffuse slightly faster in the SST case, but the differences are relatively minor.
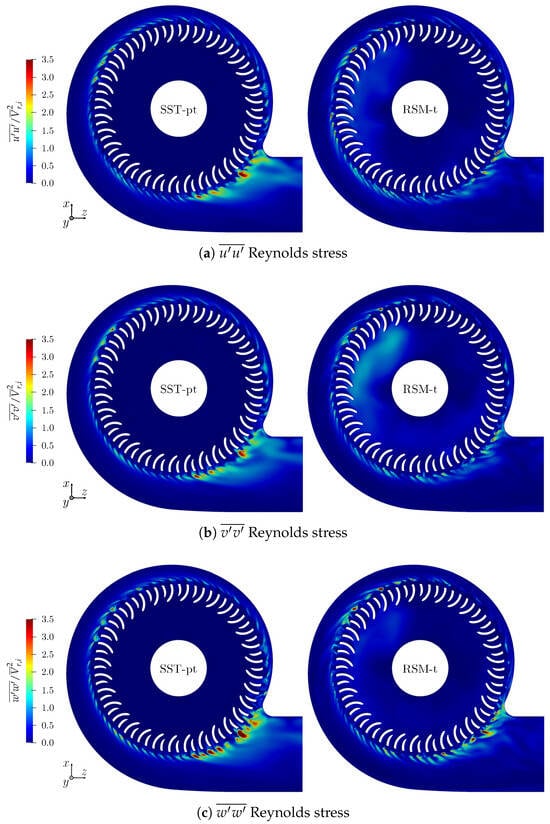
Figure 22.
Comparison of normalized Reynolds stress results of the SST k- and RSM simulation for a selected time step at an evaluation surface at .
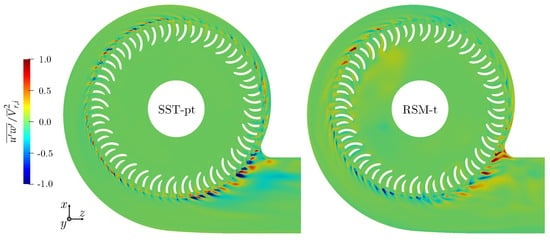
Figure 23.
Comparison of normalized Reynolds stress results of the SST k- and RSM simulation for a selected time step at an evaluation surface at .
5.6.3. Grid Resolution Dependency of SAS Results
Since the ratio between resolved and modeled turbulence of the SAS model is grid resolution dependent, a more detailed investigation will be performed in the following. The grid resolution transitions from a cell size of 0.125 mm in the blade channels to a size of 0.25 mm in the volute within two rows of cells. Since this is a non-ideal situation for the SAS model, turbulence quantities, particularly the turbulent viscosity, and eventually the velocity and pressure field might be impacted.
If the local cell resolution is capable of resolving turbulent scales, an extra source term will cause an increase of the specific dissipation rate and due to the relation , this will, in turn, lead to a reduction in the turbulent viscosity . A coarsening of the grid resolution can consequently lead to a reduction in , an increase in and finally result in an increase of the ratio of modeled to resolved k.
Figure 24 and Figure 25 show cell-value contours of different flow and turbulence quantities evaluated at . These detailed plots show how the quantities change over the boundary of the rotating reference frame (white line) and the transition lines of the grid resolution (black lines). It is evident that the reference frame boundary does influence the results, creating local disturbances in the velocity and pressure fields. This rather abrupt change in grid resolution, which is directly associated with a change in the size of the resolvable turbulent scales, does not lead to a sudden decrease of the resolved portion of k or the Reynolds shear-stresses, nor does it cause an immediate rise of the turbulent viscosity. The SAS approach seems to be rather robust in this regard and is able to deal with non-ideal meshes which are typical in an industrial context.
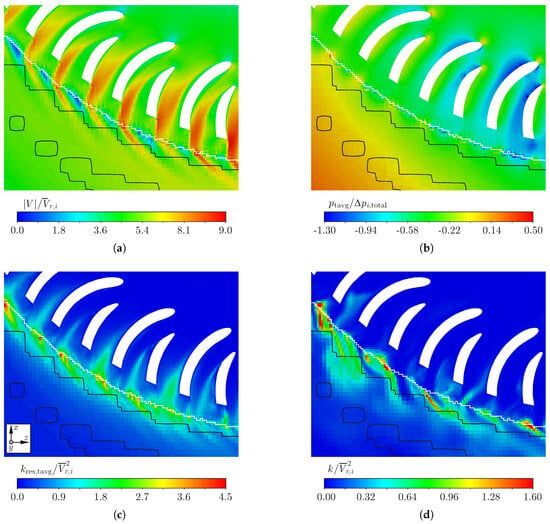
Figure 24.
Cell-value contours of SAS simulation results for velocity, pressure and turbulent kinetic energy; details in the vicinity of blade channels 24 and 25; black lines indicate borders of regions with uniform mesh resolution, the white line indicates the boundary of the rotating reference frame. (a) normalized time-averaged velocity magnitude. (b) normalized time-averaged static pressure. (c) normalized time-averaged resolved turbulent kinetic energy. (d) normalized modeled turbulent kinetic energy.
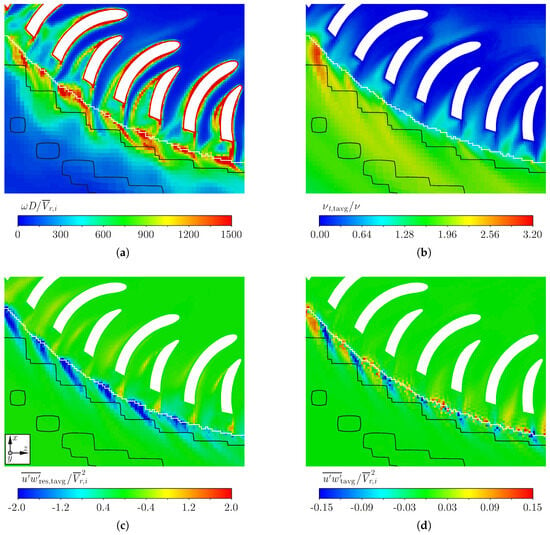
Figure 25.
Cell-value contours of SAS simulation results for different turbulence quantities; details in the vicinity of blade channels 24 and 25; black lines indicate borders of regions with uniform mesh resolution, the white line indicates the boundary of the rotating reference frame. (a) normalized modeled specific dissipation rate. (b) normalized time-averaged turbulent viscosity ratio. (c) normalized time-averaged resolved -stress. (d) normalized time-averaged modeled -stress.
A comparison of the resolved and modeled Reynolds stresses with the results shown in Figure 23 demonstrates a reasonable alignment with the contours of the RSM case. The stresses are predominantly negative downstream of the blade channel exits in this region. However, the values obtained with the SAS model are markedly higher than in the RSM case, as was already noted before when comparing the turbulent kinetic energy levels. The structures of the modeled Reynolds stresses qualitatively correspond to those predicted by the SST model, i.e., a sequence of positive and negative stresses occurs. This is not very surprising since the SST model, with a reduced turbulent viscosity, functions basically as the subgrid model in Scale-Adaptive Simulations, which are in LES mode.
5.7. Comparison with CTA and PIV Measurements
In this section the simulation results are compared to CTA and PIV measurement results previously published in [12,51]. Since the focus of the evaluation lies on the outlet flow field and the near field jet development, some additional evaluations were performed on the measurement data in this area. Far field jet development data are not included since they are not the main aspect of the current study.
5.7.1. Simulated vs. Experimental Time-Averaged Outlet Flow Field Data
The CTA measurement results in [12] are obtained by scanning a surface immediately downstream of the fan outlet at by using a straight miniature single-wire probe. Two different scans were performed with the wire-axis aligned in x- and y-direction, respectively, and the results were averaged over one second of measurement time per evaluation point. Since the probe wire records the velocity magnitudes perpendicular to the wire, the resulting velocity data are and , respectively. The simulation data were exported to Mathworks MATLAB, and the same routines developed for the evaluation of the measurement data were used for the simulation data. The CTA measurement had a resolution of 1 mm × 1 mm, and consequently the time-averaged simulation results were interpolated onto the same grid.
Figure 26 compares the normalized velocity data. The contours in Figure 26a represent the normal velocity and the crossflow velocity component in x-direction, whereas Figure 26b shows the contours of the normal velocity and the crossflow velocity component in y-direction. The wire orientation manifests, for instance, in small differences in the velocities of the upper and lower lobe of the C-shape. There, the contours of the CTA measurements are slightly higher than the respective contours. This is also the case for all simulations, however, the velocities of all simulations are markedly higher in the entire C-shape. The measurement and simulation results agree or deviate in the following points:
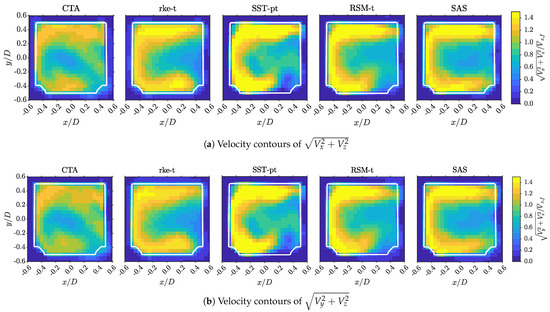
Figure 26.
Time-averaged normalized and velocity contours at the fan outlet slightly downstream of evaluation surface S37 at for the CTA measurements and the different turbulence models. Note: The white lines indicate the fan outlet edges.
- The measurement and all simulated contours agree concerning the width of the upper lobe, but only the SAS results agree with the measurements in indicating a stagnation point in the upper right corner.
- All simulation models overpredict the width of the vertical part of the C-shape on the left side of the contours. In this regard, the SAS model demonstrates the highest level of agreement.
- In the measurement the lower lobe of the jet ends at approximately . Here, the best fit is obtained by the RSM model. Moreover, the SST model exhibits a nearly similar behavior.
- The measurements exhibit a region of increased velocity outside of the C-shape, starting above the right corner of the outlet at and and ending at and . This detail is not predicted by any of the simulation models. The SST model is the only model which shows elevated velocities in the proximity of this area, however, the shape of the velocity contours do not match the experiments. A plausible reason for these differences might be related to the MRF modeling, which does not accurately represent certain dynamic effects, especially regarding the outflow of the final three blade channels and the flow around the nose.
- Although the SAS model overestimates the width of the lower lobe of the C-shape, in Figure 26a the location of the velocity maximum aligns relatively well with the measurements.
In [12], the CTA measurement data at were also used to calculate fan volume flow rates corresponding to the measured flow quantities and . The same evaluation on a 1 mm × 1 mm grid was carried out for the simulation data. In Table 11 these flow rates are compared. The table also includes the results for calculated without the crossflow components to assess the accuracy of the evaluation method. The deviations between and (from Table 5) demonstrate that using the coarser evaluation grid consistently overpredicts the volume flow rates. The deviations range between 0.3 and , or between 2.5% and 4%.

Table 11.
Comparison of the volume flow rates derived from CTA measurements and the conducted simulations.
In this direct comparison between measured and simulated data, it is evident that a significantly lower deviation is determined compared to the values presented in Section 5.1.1, where the volume flow rate measured by an independent fan testing rig was used as a reference. It should be noted, that the measurement conditions during the CTA measurements are in better agreement with the simulation model, since the inlet and outlet ports of the fan are not separated, like in the fan testing rig. In our estimation, the measurement setup itself is the most plausible explanation for the differences, especially since the fan is rpm-controlled and the CT scans of two fan samples showed hardly any geometric deviations. The comparison between the results reveals that the lowest deviations are obtained by the realizable k- model, followed by the SAS, RSM and SST cases. The deviations for are higher ranging from 3.9% to 8.2%, while for the range is 0.7% to 7.2%. It is also noteworthy that the simulation results show lower differences between and than the measurements.
5.7.2. Simulated vs. Experimental RSME Data at the Outlet
Unsteady and turbulent velocity fluctuations at the outlet port are quantified by the RMSE of and . Figure 27 compares the results of the CTA measurements with the pseudo-transient SST and SAS results. The SST results are included in this comparison to demonstrate that a pseudo-transient solver can produce significant fluctuations, however, without providing a time-scale. The SAS results show similarities to the measured fluctuations in the vertical part of the C-shape and in the vicinity of its lower lobe. In this area, there is good agreement in terms of the spatial distribution, the calculated fluctuation values, and the crossflow velocity differences. The highest discrepancies are actually found at the borders of the upper lobe, where the SAS predicts significant fluctuations, which are not present in the measurements.
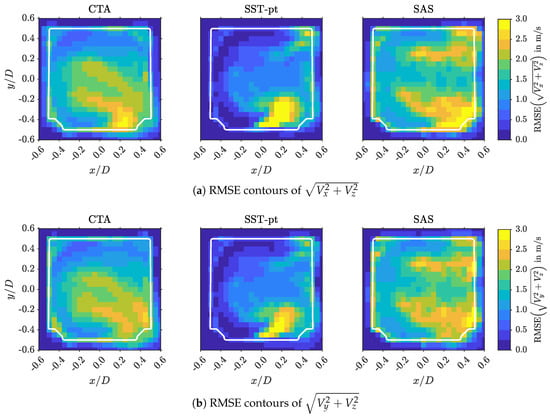
Figure 27.
RMSE values of and at the fan outlet slightly downstream of evaluation surface S37 at for the CTA measurements and selected turbulence models. Note: The white lines indicate the fan outlet edges.
5.7.3. Comparison of the Near-Field Jet Development
Figure 28 compares the jet development of the PIV measurement data and the different simulations up to downstream of the outlet port. The PIV results were obtained using a 2.5D technique, by recording 2D-images for 83 -planes and 100 -planes and calculating the 3D flow field from these data. A detailed description of the measurement setup, the PIV settings and data processing is provided in [51]. The comparison is limited to the near-field of the fan jet, since the mesh resolution is not high enough to adequately resolve the jet development further downstream.
Figure 28.
Time-averaged normalized velocity contours of various -planes showing the development of the jet’s cross section with increasing outlet distance. Note: Red lines indicate FWHM.
According to the PIV measurements the fan jet development can be described by three main characteristics. The upper lobe of the C-shape slightly rotates in clockwise direction and its width increases from to . The lower lobe performs a counterclockwise rotation and moves towards the jet center. The entire outlet flow field performs a movement towards the right (positive x-direction) and slightly downwards (negative y-direction).
In the realizable k- case the outlet profile is simply stretched towards the right due to the positive x-velocity in the upper and lower lobes, and both lobes perform only slight rotations. The velocity profile of the SST k- model exhibits the highest velocity maxima at the outlet and these high velocities only experience a slight gradual reduction, so that at local velocity peaks of persist. The upper lobe performs a clockwise rotation, but contrary to the measurements, experiences significant lateral stretching. In addition, the upper lobe does not remain a straight line, but a distinct hump in the profile contour emerges directly at the velocity peak. The lower lobe does not perform a significant rotation, but shows a slight downward movement. In summary, at a significantly distorted full width at half maximum (FWHM) contour has developed, which has little resemblance with the measured contour. While the RSM results show comparable velocity maxima at the outlet port similar to the SST model, the subsequent velocity reduction is much more pronounced, leading to closer alignment with the measurement results. The upper lobe performs a similar rotation compared to the measurements, and until the velocity distribution is also similar. At the right end, however, it experiences higher diffusion and higher stretching. The position of the lower lobe’s velocity maximum does not change significantly, but the right end of the lobe does move towards the center in a manner similar to the measurement results. The SAS case shows the best agreement with the measurements with respect to the development of the upper lobe. The velocity levels show very good agreement up to . The lower lobe does, indeed, perform a counterclockwise rotation, however, since its width was overpredicted at the outlet, the rotation causes higher velocities to occur further to the right than in the measurements. Consequently, the velocity contours, particularly in the central and lower areas, noticeably deviate from the measured contours.
In summary, RSM and the SAS results are able to correctly predict some aspects of the jet development. The right side of the FWHM contour extends too far to the right at , primarily due to significant diffusion in the x-direction. The latter is likely a consequence of insufficient mesh resolution to properly resolve the jet development.
6. Conclusions
Numerical simulations for a centrifugal electronic cooling fan operating at static fan pressure of 0 were performed for four different turbulence models, the realizable k- model, the SST k- model, an RSM- model and SAS.
The overall fan performance results showed significant deviations between the four turbulence models. The SST model predicted the largest deviations compared to those of the other models for a number of integral performance data.
The strong non-uniformity of the outlet flow field involving a C-shaped high velocity area, which was observed in the measurements, could basically be reproduced by all turbulence models. The primary reasons for this result could be interpreted on the basis of the simulation results. Over the first two thirds of the impeller circumference a static pressure rise of approximately 40 is achieved between the impeller inlet and the volute. Since the outlet pressure at this operating point is, however, 0 , the flow in the volute accelerates towards the outlet, leading to a reduced pressure in the last third of the impeller circumference. On the one hand this is responsible for a highly unequal flow rate distribution over the impeller, on the other hand the pressure gradient field is no longer able to counteract the centrifugal forces in the volute. This is the primary reason why the main flow is pushed towards the outer wall of the volute and why the outflow is subsequently concentrated at the outer, upper and lower walls of the fan outlet. In addition, an area of unsteady flow and low velocities establishes downstream of the blade channels 29–32, where the jets emanating from the blade channels lead to high turbulence production. In this region, strong deviations of the turbulence models’ results can be observed, which influence important details in the calculated outlet flow fields, such as the extensions of the upper and lower lobes of the C-shape.
The following main observations can be made regarding the different turbulence models:
- The realizable k- model shows steady convergence. Pseudo-transient and transient simulations do not lead to significant differences in the results. The main reason is very high turbulent kinetic energy production at the outlet of the blade channels, which, due to high turbulent diffusion, does not allow for the development of distinct and unsteady vortex structures.
- For the SST k- model steady convergence could not be obtained since the turbulent kinetic energy production at the blade outlet channel was similar to that of the more sophisticated models, which allowed for the resolution of a high degree of flow details and vortex structures. Only the SST model produced inflow in a small area close to the lower right corner of the outlet port. Reasonable convergence could be obtained using the pseudo-transient solver. However, the results showed significant fluctuations, particularly in the highly unsteady flow region towards the outlet. One main advantage of using a pseudo-transient solver in this situation is the reduced solving time and the greatest disadvantage is the lack of information regarding the temporal evolution of the results.
- In general, the results produced by the RSM- model are satisfactory. Several aspects of the outlet flow field could be predicted with reasonably accuracy, particularly the length of the lower lobe of the C-shape. The complexity of the RSM case required an unsteady simulation, however, a relatively high time-step was permissible, which lead to overall lower computational costs compared to the SAS model.
- The SAS model was able to predict the development of the left part and the upper lobe of the C-shape very accurately. However, discrepancies from the measurements were observed for the lower lobe. The model could adapt well to the relatively abrupt jumps in the mesh discretization without producing discernible errors in the pressure or velocity field. The requirement to satisfy the CFL condition lead to a very small time step and long simulation times to produce robust mean values.
Finally, it must be noted that using the frozen rotor approach, even in the case of unsteady simulations, was a deliberate choice to ensure that all the differences in the results between RANS, URANS and SAS were only due to the applied turbulence models. The investigation of the results indicated that some observed differences in comparison to the measurement results on the right side of the outlet port were caused by the MRF modeling. Future investigations will focus on investigations using a sliding mesh approach and will also incorporate a finer mesh downstream of the outlet port to perform further comparisons with the measured jet development.
Author Contributions
Conceptualization, M.K. (Martin Kirchhofer) and M.K. (Michael Krieger); methodology, M.K. (Martin Kirchhofer), M.K. (Michael Krieger) and D.H.; preprocessing, M.K. (Martin Kirchhofer); simulation modeling, M.K. (Martin Kirchhofer) and M.K. (Michael Krieger); experimental data, D.H.; writing—original draft preparation, M.K. (Martin Kirchhofer) and M.K. (Michael Krieger); writing—review and editing, M.K. (Martin Kirchhofer), M.K. (Michael Krieger) and D.H.; project administration, M.K. (Martin Kirchhofer) and M.K. (Michael Krieger); funding acquisition, M.K. (Martin Kirchhofer) and M.K. (Michael Krieger). All authors have read and agreed to the published version of the manuscript.
Funding
This work has been supported by the COMET-K2 Center of the Linz Center of Mechatronics (LCM) funded by Johannes Kepler Open Access Publishing Fund and the federal state of Upper Austria.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
The authors want to thank Markus Schörgenhumer of LCM and Thomas Paier for administrative work regarding funding. The authors also want to thank Mechatronic Systems GmbH for providing fan CAD data. Open Access Funding by the University of Linz.
Conflicts of Interest
Author Martin Kirchhofer was employed by the company ZKW Lichtsysteme GmbH. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Correction Statement
This article has been republished with a minor correction to the Funding statement. This change does not affect the scientific content of the article.
References
- Zhang, Z.; Wang, X.; Yan, Y. A review of the state-of-the-art in electronic cooling. e-Prime—Adv. Electr. Eng. Electron. Energy 2021, 1, 100009. [Google Scholar] [CrossRef]
- Schlüter, M.A. Innovative Kühlkonzepte für LED-Scheinwerfer. Ph.D. Thesis, Ruhr-Universität Bochum, Bochum, Germany, 2011. [Google Scholar]
- Wang, J.; Cai, Y.X.; Zhao, X.J.; Zhang, C. Thermal design and simulation of automotive headlamps using white LEDs. Microelectron. J. 2014, 45, 249–255. [Google Scholar] [CrossRef]
- Lu, Z.; Bai, P.; Huang, B.; Henzen, A.; Coehoorn, R.; Liao, H.; Zhou, G. Experimental investigation on the thermal performance of three-dimensional vapor chamber for LED automotive headlamps. Appl. Therm. Eng. 2019, 157, 113478. [Google Scholar] [CrossRef]
- Sagot, B.; Antonini, G.; Christgen, A.; Buron, F. Jet impingement heat transfer on a flat plate at a constant wall temperature. Int. J. Therm. Sci. 2008, 47, 1610–1619. [Google Scholar] [CrossRef]
- Sui, D.; Kim, T.; Xu, M.L.; Lu, T.J. Flow and heat transfer characteristics of impinging axial fan flows on a uniformly heated flat plate. Int. J. Transp. Phenom. 2008, 10, 353–363. [Google Scholar]
- Sui, D.; Wang, S.S.; Mao, J.R.; Kim, T.; Lu, T.J. Exit flow behavior of axial fan flows with/without impingement. J. Fluid Eng. 2009, 131, 061103–061109. [Google Scholar] [CrossRef]
- Sui, D.; Kim, T.; Xu, M.L.; Lu, T.J. Novel hub fins for axial flow fans for the enhancement of impingement heat transfer on a flat plate. J. Heat Trans. 2009, 131, 074502–074504. [Google Scholar] [CrossRef]
- Stafford, J.; Walsh, E.J.; Egan, V.; Grimes, R. Flat plate heat transfer with impinging axial fan flows. Int. J. Heat Mass Transf. 2010, 53, 5629–5638. [Google Scholar] [CrossRef]
- Stafford, J.; Walsh, E.J.; Egan, V. Local heat transfer performance and exit flow characteristics of a miniature axial fan. Int. J. Heat Fluid Flow 2010, 31, 952–960, In Proceedings of the 6th International Symposium on Turbulence, Heat and Mass Transfer, Rome, Italy, 14–18 September 2009. [Google Scholar] [CrossRef]
- Yen, S.C.; Liu, J.H. PIV measurements of exit flow field of centrifugal fans with conditional sampling. J. Mar. Sci. Technol. 2007, 15, 232–240. [Google Scholar] [CrossRef]
- Hofer, D.; Krieger, M.; Kirchhofer, M. Particle image velocimetry and constant temperature anemometer measurements of the jet produced by a centrifugal fan. Phys. Fluids 2021, 33, 065126. [Google Scholar] [CrossRef]
- Eck, B. Fans: Design and Operation of Centrifugal, Axial-Flow and Cross-Flow Fans, 1st ed.; Pergamon Press: Oxford, UK, 1973. [Google Scholar]
- González, J.; Fernández, J.; Blanco, E.; Santolaria, C. Numerical Simulation of the Dynamic Effects Due to Impeller-Volute Interaction in a Centrifugal Pump. J. Fluids Eng. 2002, 124, 348–355. [Google Scholar] [CrossRef]
- Kwon, E.Y.; Baek, K.W.; Cho, N.H.; Kim, H.K.; Jung, I.J. Some Aerodynamic Aspects of Centrifugal Fan Characteristics of an Automotive HVAC Blower. In SAE 2001 World Congress; SAE Technical Paper Series; SAE: Warrendale, PA, USA, 2001; p. 2001-01-0291. [Google Scholar] [CrossRef]
- Sardar, A.M. Centrifugal Fans: Similarity, Scaling Laws, and Fan Performance. Ph.D. Thesis, State University of New York at Buffalo, Amherst, NY, USA, 2001. [Google Scholar]
- Akbari, G.; Montazerin, N.; Akbarizadeh, M. Stereoscopic particle image velocimetry of the flow field in the rotor exit region of a forward-blade centrifugal turbomachine. Proc. Inst. Mech. Eng. Part A J. Power Energy 2012, 226, 163–181. [Google Scholar] [CrossRef]
- Akbari, G.; Montazerin, N. A-priori study of subgrid-scale models for the flow field in the rotor exit region of a centrifugal turbomachine. Int. J. Heat Mass Transf. 2013, 66, 423–439. [Google Scholar] [CrossRef]
- Montazerin, N.; Akbari, G.; Mahmoodi, M. Contribution of jet–wake–volute interactions to flow characteristics and turbulence models. In Developments in Turbomachinery Flow; Montazerin, N., Akbari, G., Mahmoodi, M., Eds.; Woodhead Publishing: Sawston, UK, 2015; pp. 113–131. [Google Scholar] [CrossRef]
- Lin, S.C.; Huang, C.L. An integrated experimental and numerical study of forward–curved centrifugal fan. Exp. Therm. Fluid Sci. 2002, 26, 421–434. [Google Scholar] [CrossRef]
- Seo, S.J.; Kim, K.Y. Design Optimization of Forward-Curved Blades Centrifugal Fan with Response Surface Method. In Proceedings of the Heat Transfer Summer Conference, Charlotte, NC, USA, 11–15 July 2004; Volume 2, pp. 551–556. [Google Scholar] [CrossRef]
- Yu, Z.; Li, S.; He, W.; Wang, W.; Huang, D.; Zhu, Z. Numerical Simulation of Flow Field for a Whole Centrifugal Fan and Analysis of the Effects of Blade Inlet Angle and Impeller Gap. HVAC&R Res. 2005, 11, 263–283. [Google Scholar] [CrossRef]
- Tsai, B.J.; Wu, C.L. Investigation of a miniature centrifugal fan. Appl. Therm. Eng. 2007, 27, 229–239. [Google Scholar] [CrossRef]
- Lee, Y.T. Impact of Fan Gap Flow to the Centrifugal Impeller Aerodynamics. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010; Volume 7, pp. 1793–1803. [Google Scholar] [CrossRef]
- Lin, S.C.; Tsai, M.L. An integrated performance analysis for a backward-inclined centrifugal fan. Comput. Fluids 2012, 56, 24–38. [Google Scholar] [CrossRef]
- Huang, C.; Li, D. The performance analysis and optimal design of multi-blade centrifugal fan with Fluent. In Proceedings of the 2014 International Conference on Information Science, Electronics and Electrical Engineering, Sapporo, Japan, 26–28 April 2014; Volume 2, pp. 1257–1261. [Google Scholar] [CrossRef]
- Heo, M.W.; Kim, J.H.; Kim, K.Y. Design Optimization of a Centrifugal Fan with Splitter Blades. Int. J. Turbo-Jet-Engines 2015, 32, 143–154. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, Q.; Zhang, Y. Meridional shape design and the internal flow investigation of centrifugal impeller. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 4319–4330. [Google Scholar] [CrossRef]
- Patil, S.R.; Chavan, S.T.; Jadhav, N.S.; Vadgeri, S.S. Effect of Volute Tongue Clearance Variation on Performance of Centrifugal Blower by Numerical and Experimental Analysis. Mater. Today Proc. 2018, 5, 3883–3894. [Google Scholar] [CrossRef]
- Burgmann, S.; Fischer, T.; Rudersdorf, M.; Roos, A.; Heinzel, A.; Seume, J. Development of a centrifugal fan with increased part-load efficiency for fuel cell applications. Renew. Energy 2018, 116, 815–826. [Google Scholar] [CrossRef]
- Ni, S.; Cao, W.; Xu, J.; Wang, Y.; Zhang, W. Effects of an Inclined Blade on the Performance of a Sirocco Fan. Appl. Sci. 2019, 9, 3154. [Google Scholar] [CrossRef]
- Benchikh Le Hocine, A.E.; Poncet, S.; Fellouah, H. CFD modeling and optimization by metamodels of a squirrel cage fan using OpenFoam and Dakota: Ventilation applications. Build. Environ. 2021, 205, 108145. [Google Scholar] [CrossRef]
- Liu, H.; Jiang, B.; Yang, X.; Xiao, Q. Numerical and experimental investigations on non-axisymmetric D-type inlet nozzle for a squirrelcage fan. Eng. Appl. Comput. Fluid Mech. 2021, 15, 363–376. [Google Scholar] [CrossRef]
- Zhou, S.; Zhou, H.; Yang, K.; Dong, H.; Gao, Z. Research on blade design method of multi-blade centrifugal fan for building efficient ventilation based on Hicks-Henne function. Sustain. Energy Technol. Assess. 2021, 43, 100971. [Google Scholar] [CrossRef]
- Ding, H.; Chang, T.; Lin, F. The Influence of the Blade Outlet Angle on the Flow Field and Pressure Pulsation in a Centrifugal Fan. Processes 2020, 8, 1422. [Google Scholar] [CrossRef]
- Rui, X.; Lin, L.; Wang, J.; Ye, X.; He, H.; Zhang, W.; Zhu, Z. Experimental and Comparative RANS/URANS Investigations on the Effect of Radius of Volute Tongue on the Aerodynamics and Aeroacoustics of a Sirocco Fan. Processes 2020, 8, 1442. [Google Scholar] [CrossRef]
- Darvish, M.; Frank, S. Toward the CFD Simulation of Sirocco Fans: From Selecting a Turbulence Model to the Role of Cell Shapes. In Proceedings of the International Conference on Fan Noise, Fan Technology and Numerical Methods—FAN 2012, CETIAT, Senlis, France, 18–20 April 2012. [Google Scholar]
- Liu, Q.; Qi, D.; Tang, H. Computation of aerodynamic noise of centrifugal fan using large eddy simulation approach, acoustic analogy, and vortex sound theory. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2007, 221, 1321–1332. [Google Scholar] [CrossRef]
- Lu, F.; Qi, D.; Wang, X.; Zhou, Z.; Zhou, H. A numerical optimization on the vibroacoustics of a centrifugal fan volute. J. Sound Vib. 2012, 331, 2365–2385. [Google Scholar] [CrossRef]
- Cai, J.C.; Chen, H.J.; Brazhenko, V.; Gu, Y.H. Study of the Hydrodynamic Unsteady Flow Inside a Centrifugal Fan and Its Downstream Pipe Using Detached Eddy Simulation. Sustainability 2021, 13, 5113. [Google Scholar] [CrossRef]
- Younsi, M.; Djerrada, A.; Belamri, T.; Menter, F. Application of the SAS turbulence model to predict the unsteady flow field behaviour in a forward centrifugal fan. Int. J. Comput. Fluid Dyn. 2008, 22, 639–648. [Google Scholar] [CrossRef]
- Sorguven, E.; Dogan, Y.; Bayraktar, F.; Sanliturk, K.Y. Noise prediction via large eddy simulation: Application to radial fans. Noise Control Eng. J. 2009, 57, 169–178. [Google Scholar] [CrossRef]
- Darvish, M. Numerical and Experimental Investigations of the Noise and Performance Characteristics of a Radial Fan with Forward-Curved Blades. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2015. [Google Scholar]
- Iwase, T.; Obara, H.; Yamade, Y.; Kato, C. Influence of Grid Resolution on Flow Field and Aerodynamic Noise Prediction of Centrifugal Fan for Packaged Air Conditioner. Int. J. Fluid Mach. Syst. 2020, 13, 190–202. [Google Scholar] [CrossRef]
- Ottersten, M.; Yao, H.D.; Davidson, L. Tonal noise of voluteless centrifugal fan generated by turbulence stemming from upstream inlet gap. Phys. Fluids 2021, 33, 075110. [Google Scholar] [CrossRef]
- Jiang, B.; Huang, Y.; Yang, X.; Xiao, Q.; Yang, W.; Wang, J. Large eddy simulation on the vortex evolution in a squirrel-cage fan based on a slice computational model. Eng. Appl. Comput. Fluid Mech. 2022, 16, 1324–1343. [Google Scholar] [CrossRef]
- Fröhlich, J.; von Terzi, D. Hybrid LES/RANS methods for the simulation of turbulent flows. Prog. Aerosp. Sci. 2008, 44, 349–377. [Google Scholar] [CrossRef]
- Pereira, F.S.; Eça, L.; Vaz, G.; Girimaji, S.S. Toward Predictive RANS and SRS Computations of Turbulent External Flows of Practical Interest. Arch. Comput. Methods Eng. 2021, 28, 3953–4029. [Google Scholar] [CrossRef]
- Menter, F.R.; Egorov, Y. The Scale-Adaptive Simulation Method for Unsteady Turbulent Flow Predictions. Part 1: Theory and Model Description. Flow Turbul. Combust. 2010, 85, 113–138. [Google Scholar] [CrossRef]
- Egorov, Y.; Menter, F.R.; Lechner, R.; Cokljat, D. The Scale-Adaptive Simulation Method for Unsteady Turbulent Flow Predictions. Part 2: Application to Complex Flows. Flow Turbul. Combust. 2010, 85, 139–165. [Google Scholar] [CrossRef]
- Hofer, D.; Krieger, M.; Kirchhofer, M. High-Resolution 2.5D Particle Image Velocimetry Measurements of the Flow Fields Generated by Small Fans. J. Fluids Eng. 2021, 143, 121101. [Google Scholar] [CrossRef]
- CAE Software Solutions. SPIDER Manual, Version 2.0.13; CAE: Eggenburg, Austria, 2013. [Google Scholar]
- ANSYS, Inc. ANSYS Fluent Theory Guide, Release 2020 R2; ANSYS: Canonsburg, PA, USA, 2020. [Google Scholar]
- Menter, F.; Smirnov, P.; Liu, T.; Avancha, R. A One-Equation Local Correlation-Based Transition Model. Flow Turbul. Combust. 2015, 95, 583–619. [Google Scholar] [CrossRef]
- Eça, L.; Hoekstra, M. A procedure for the estimation of the numerical uncertainty of CFD calculations based on grid refinement studies. J. Comput. Phys. 2014, 262, 104–130. [Google Scholar] [CrossRef]
- Cabral, B.; Leedom, L.C. Imaging Vector Fields Using Line Integral Convolution. In Proceedings of the P20th Annual Conference on Computer Graphics and Interactive Techniques—SIGGRAPH’93, Anaheim, CA, USA, 2–6 August 1993; ACM Press: New York, NY, USA, 1993; pp. 263–270. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).