Hydrothermal Conversion of Microalgae Slurry in a Continuous Solar Collector with Static Mixer for Heat Transfer Enhancement
Abstract
:1. Introduction
2. Numerical Model and Simulations
2.1. Physical Condition and Model Assumptions
2.2. Governing Equations
2.3. Numerical Method
3. Results and Discussion
3.1. Grid Independence and Model Validation
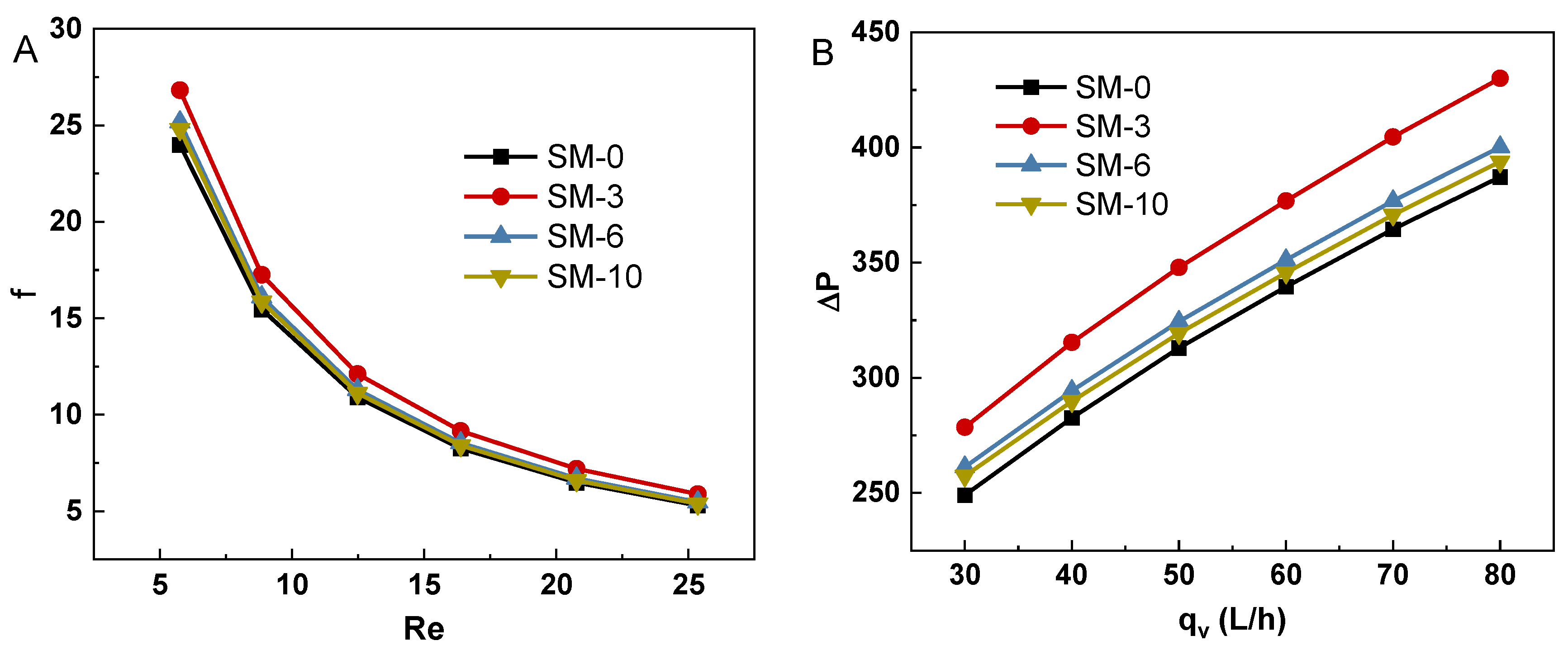
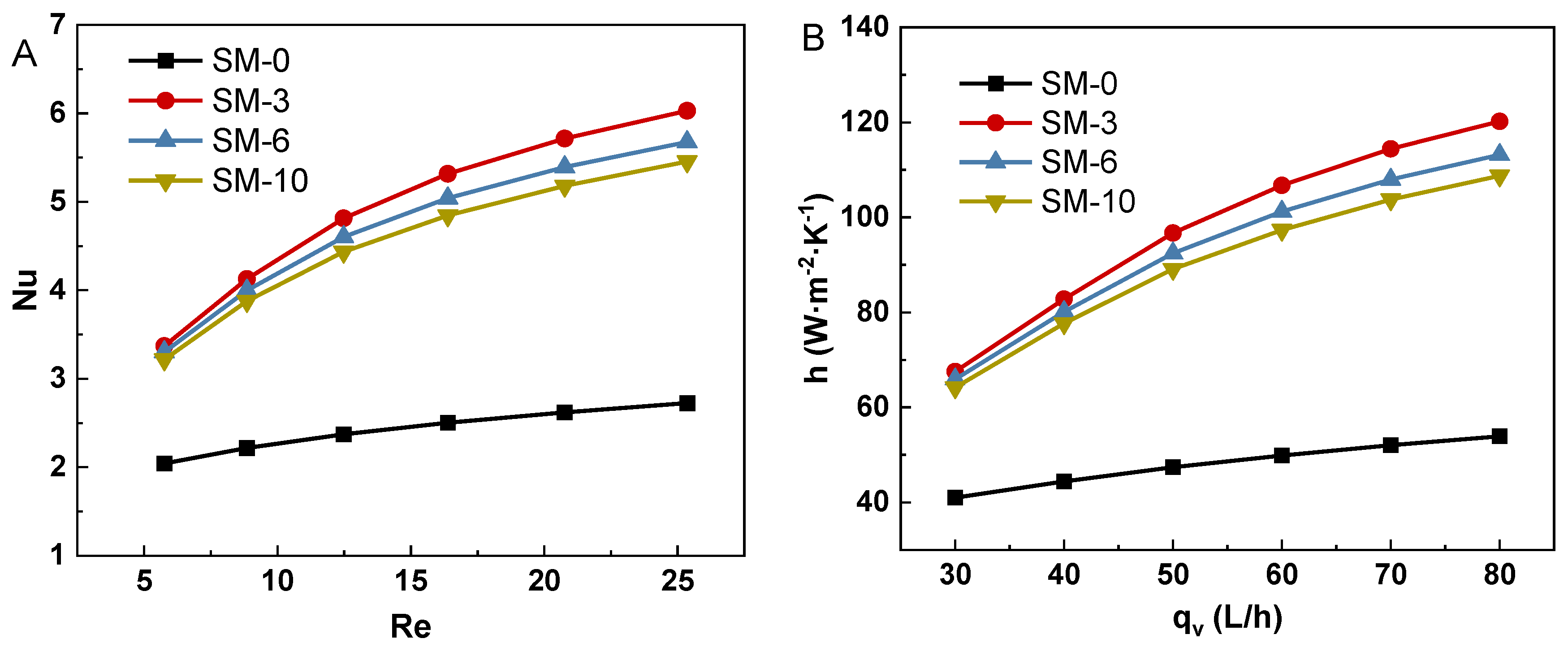
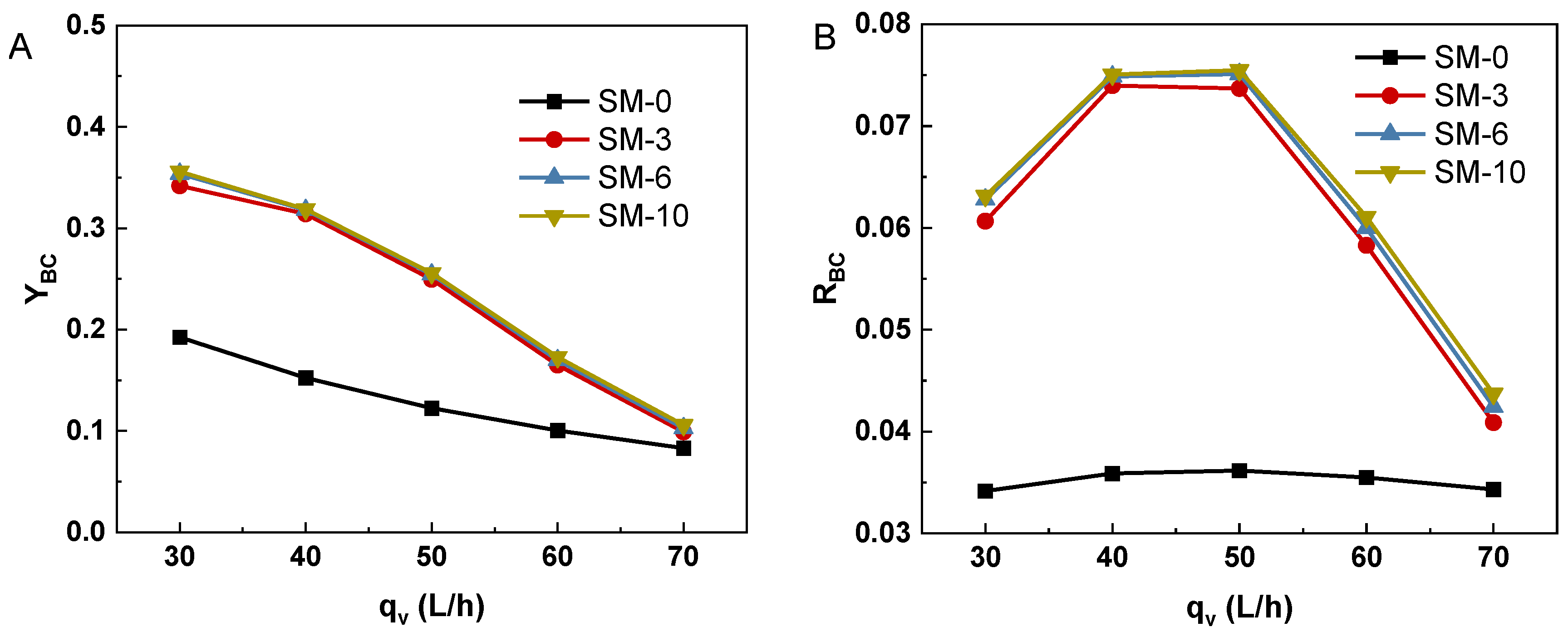
3.2. Flow Resistance of Algal Slurry in the Reactor with Static Mixer
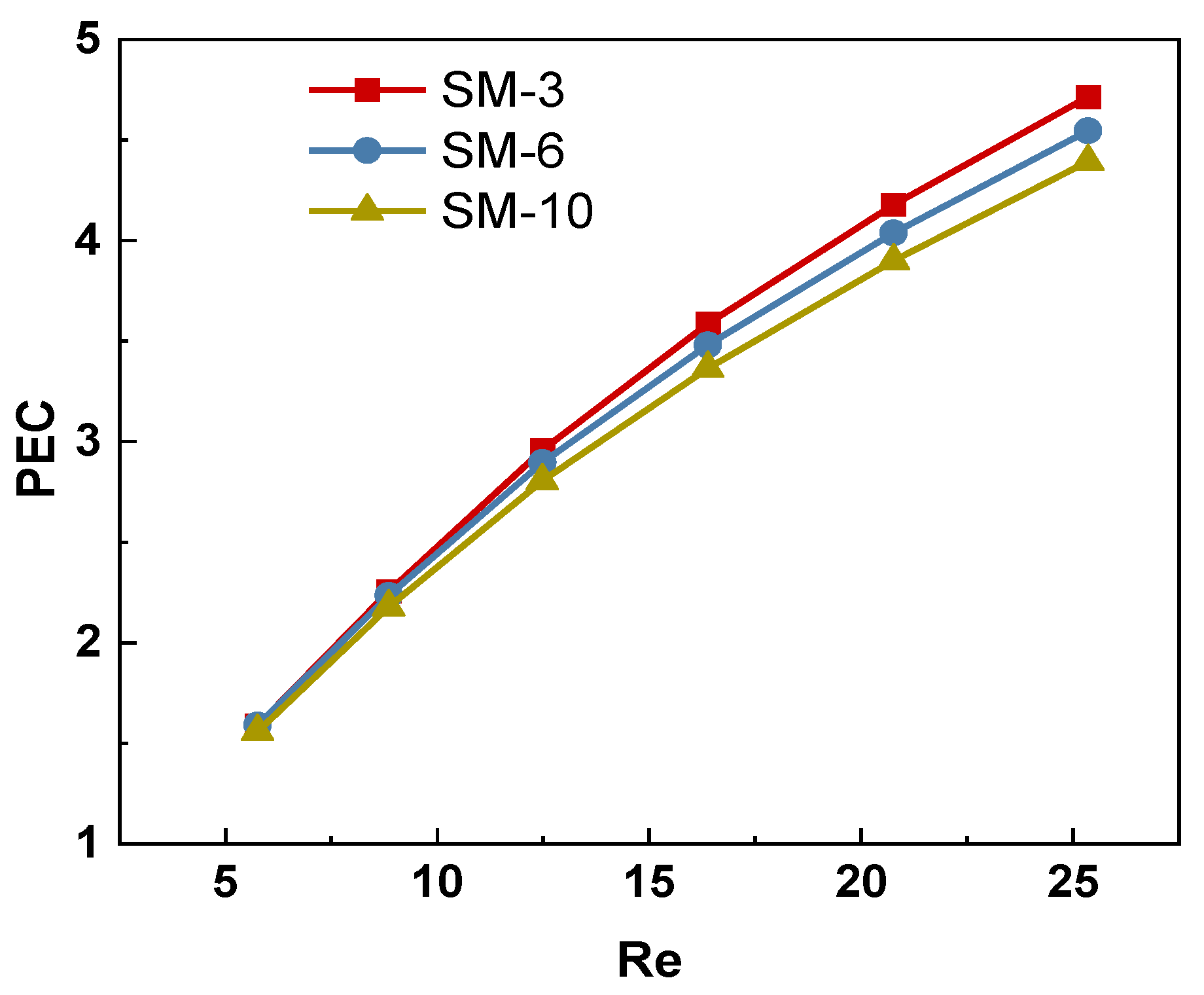
3.3. Heat Transfer Enhancement of Algal Slurry by Static Mixer
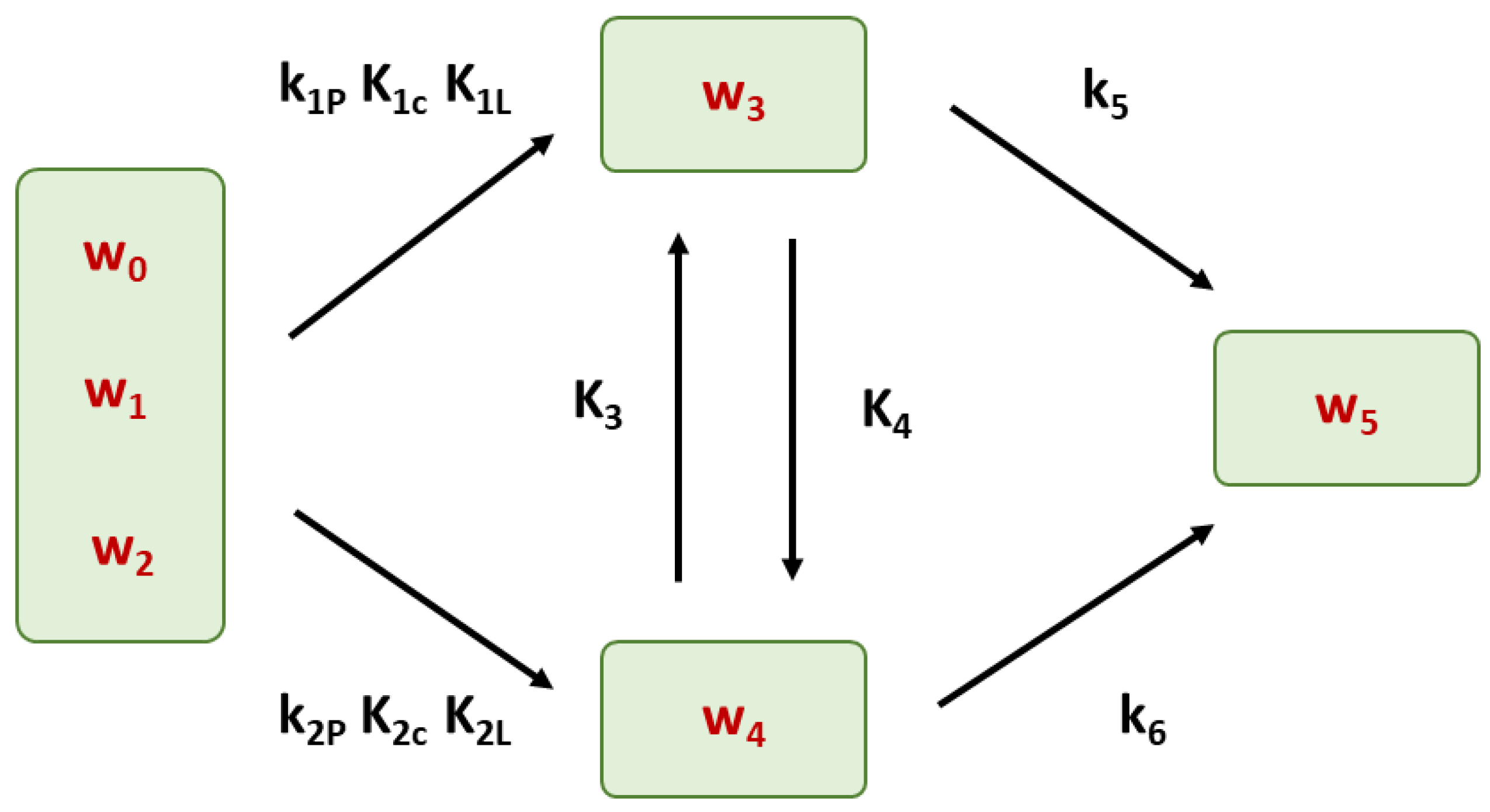
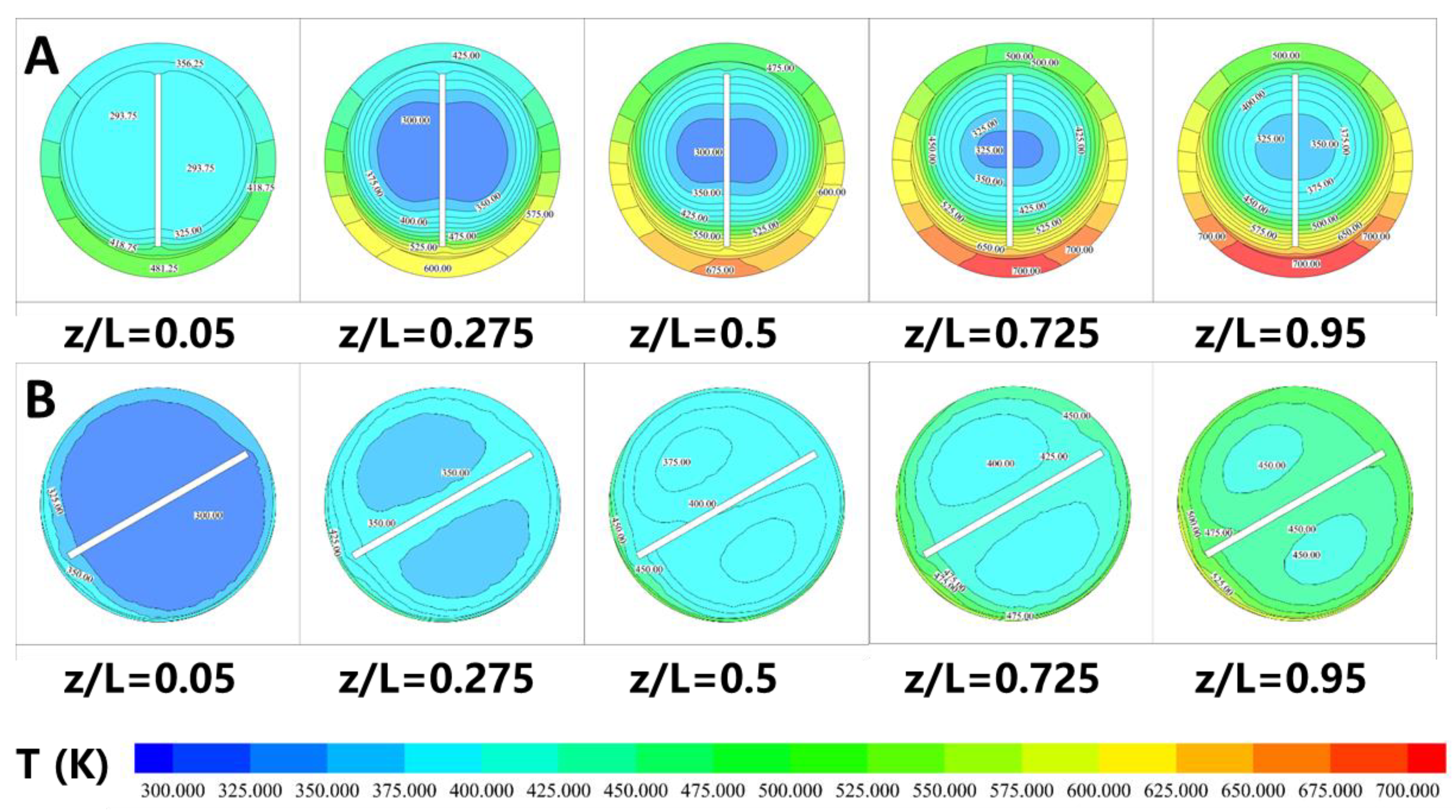
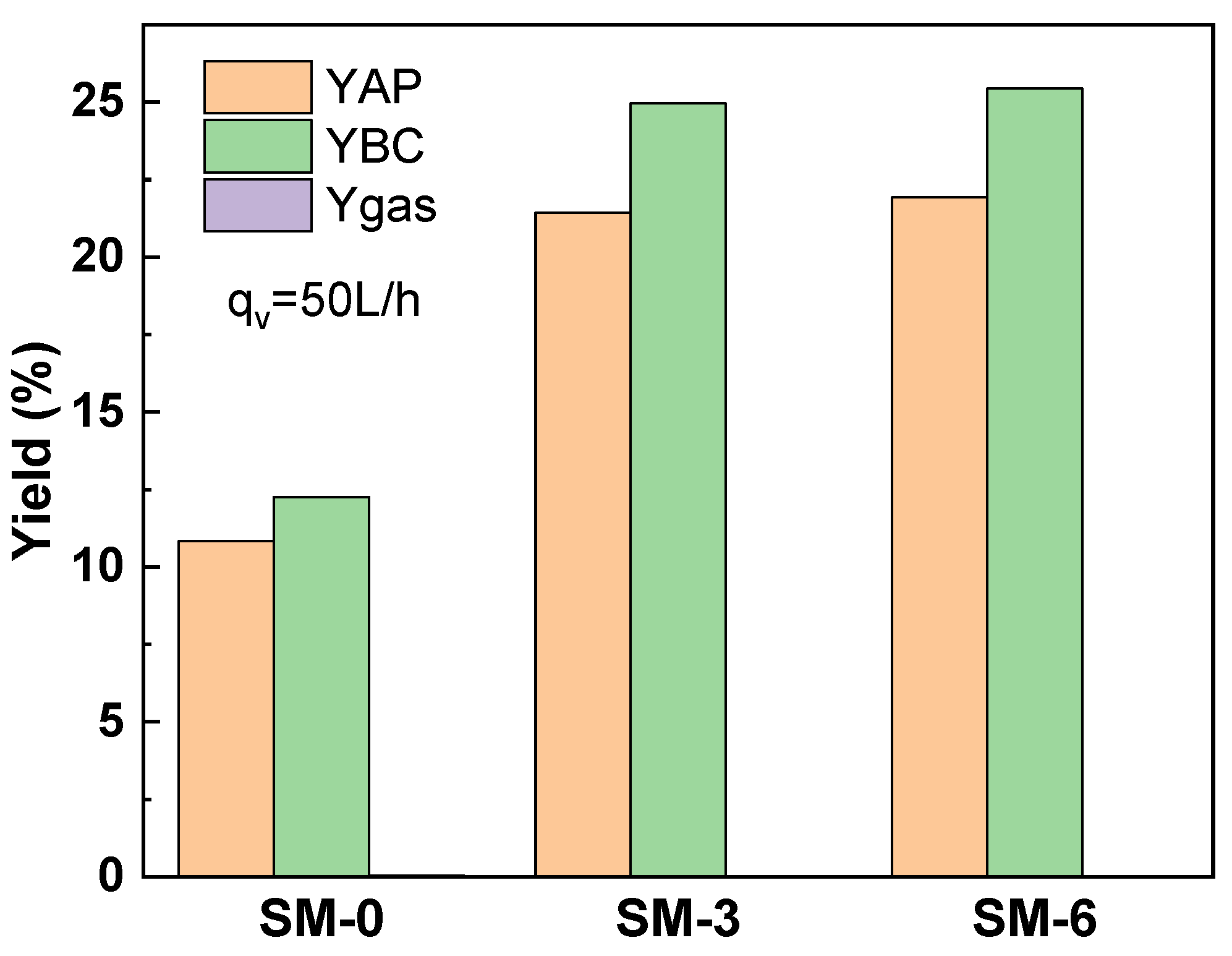
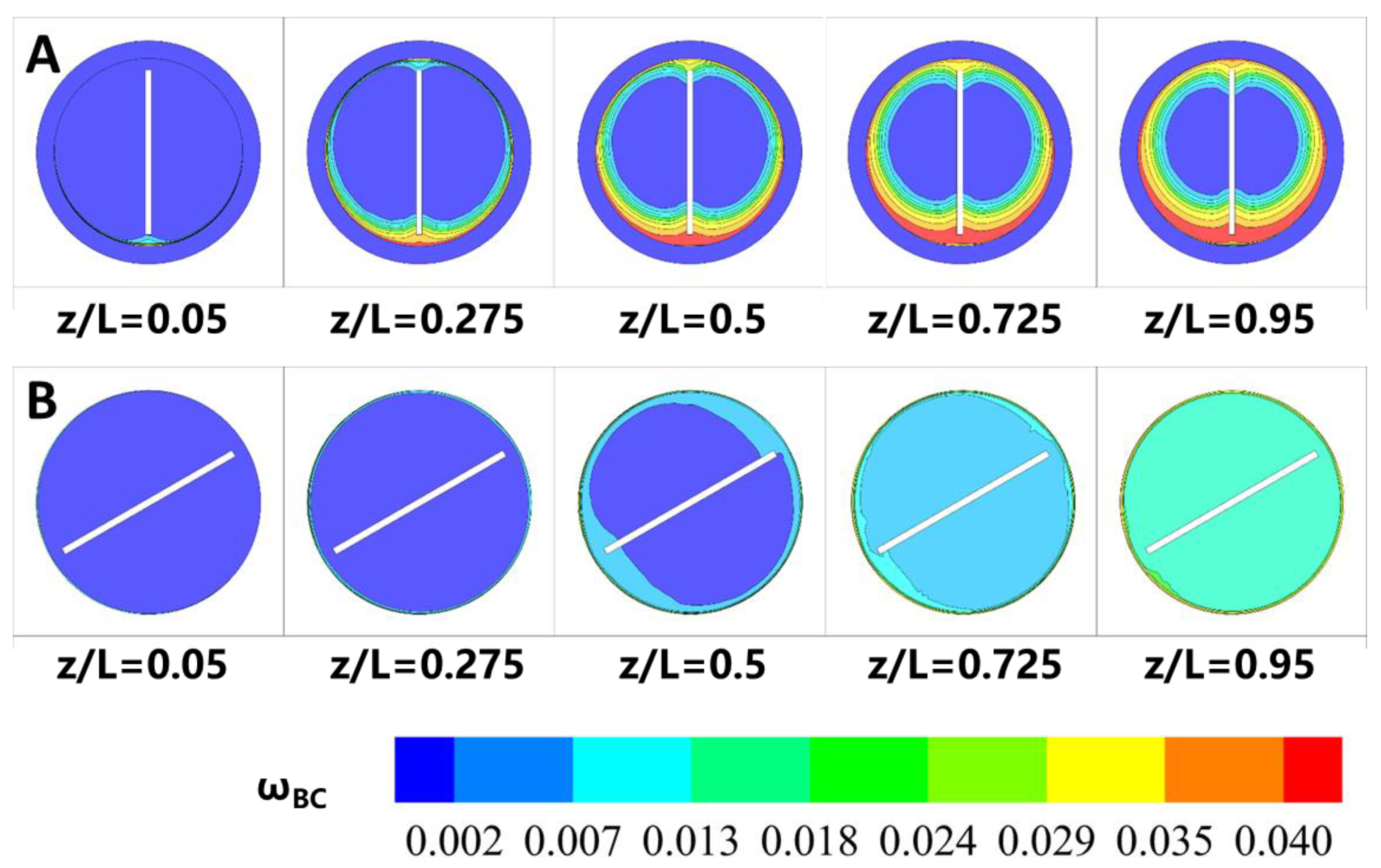
3.4. Effect of Swirl Flow Induced by Static Mixer on HTL of Microalgae Biomass
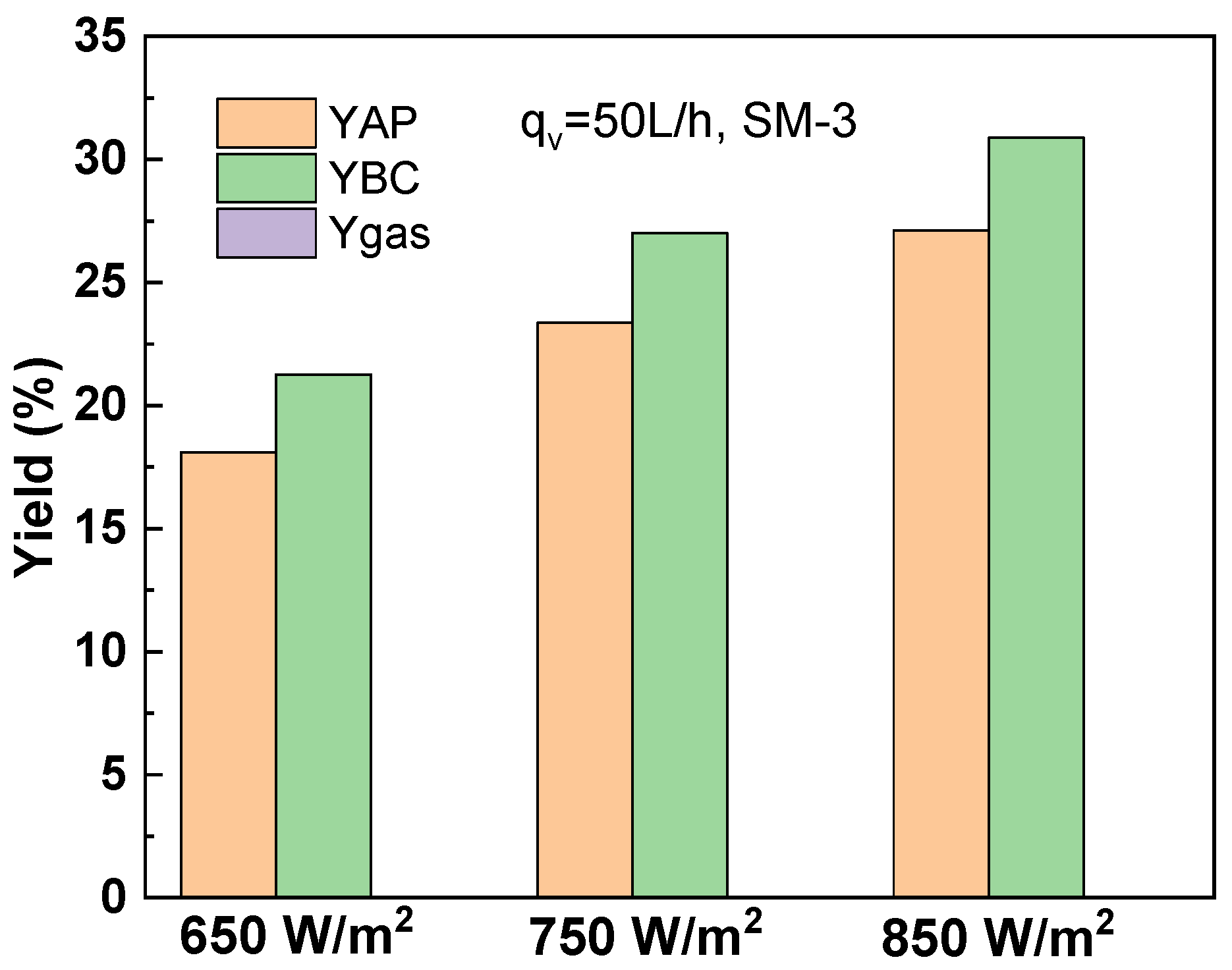
3.5. Effect of Solar Radiation on the HTL in Solar-Driven Reactor
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| A | Heat transfer area (m2) |
| Ai | Arrhenius constant (s−1) |
| cp | Specific heat capacity (kJ·kg−1·K−1) |
| D | Diffusivities of all species (m2·s−1) |
| d | Diameter of tube (m) |
| Ea | Activation energy (kJ·mol−1) |
| f | Flow resistance |
| h | Convective heat transfer coefficient (W·m−2·K−1) |
| k | Reaction rate constant (s−1) |
| L | Length of the tube (m) |
| Nu | Nusselt number |
| P | Pressure (Pa) |
| Pe | Peclet number |
| PEC | Heat transfer enhancement factor |
| q | Heat flux (W/m2) |
| R | Gas constant (J·mol−1·K−1) |
| Ri | Conversion rate of organics (g·L−1·s−1) |
| Re | Reynolds number |
| r | Reaction rates of organics (g·L−1·s−1) |
| T | Temperature (K) |
| ΔTm | Mean temperature difference (K) |
| t | Residence time (s) |
| u | Velocity (m·s−1) |
| um | Average velocity (m·s−1) |
| w | Mass fraction of organics |
| Y | The yield of organics |
| x | X-direction distance of the tube (m) |
| y | Y-direction distance of the tube (m) |
| z | Axial position of the tube (m) |
| Greek symbols | |
| ρ | Density (kg·m−3) |
| λ | Thermal conductivity (W·m−1·K−1) |
| μ | Viscosity (Pa·s) |
| ω | Mass fraction of microalgae biomass |
| γ | Shear rate (s−1) |
| Subscripts | |
| BC | Biocrude |
| f | Liquid phase |
| i | Number of organics in HTL pathways |
| in | Inlet |
| out | Outlet |
| s | Solid phase |
| w | Tube wall |
References
- Elliott, D.C.; Biller, P.; Ross, A.B.; Schmidt, A.J.; Jones, S.B. Hydrothermal liquefaction of biomass: Developments from batch to continuous process. Bioresour. Technol. 2015, 178, 147–156. [Google Scholar] [CrossRef] [PubMed]
- Hoang, A.T.; Ong, H.C.; Fattah, I.M.R.; Chong, C.T.; Cheng, C.K.; Sakthivel, R.; Ok, Y.S. Progress on the lignocellulosic biomass pyrolysis for biofuel production toward environmental sustainability. Fuel Process. Technol. 2021, 223, 106997. [Google Scholar] [CrossRef]
- Li, S.; Li, X.; Ho, S.H. Microalgae as a solution of third world energy crisis for biofuels production from wastewater toward carbon neutrality: An updated review. Chemosphere 2022, 291 Pt 1, 132863. [Google Scholar] [CrossRef] [PubMed]
- Cronin, D.; Schmidt, A.J.; Billing, J.; Hart, T.R.; Fox, S.P.; Fonoll, X.; Norton, J.; Thorson, M.R. Comparative Study on the Continuous Flow Hydrothermal Liquefaction of Various Wet-Waste Feedstock Types. ACS Sustain. Chem. Eng. 2021, 10, 1256–1266. [Google Scholar] [CrossRef]
- Chen, H.; Xia, A.; Zhu, X.; Huang, Y.; Zhu, X.; Liao, Q. Hydrothermal hydrolysis of algal biomass for biofuels production: A review. Bioresour. Technol. 2022, 344 Pt B, 126213. [Google Scholar] [CrossRef]
- Chen, W.-H.; Lin, B.-J.; Huang, M.-Y.; Chang, J.-S. Thermochemical conversion of microalgal biomass into biofuels: A review. Bioresour. Technol. 2015, 184, 314–327. [Google Scholar] [CrossRef] [PubMed]
- Osman, A.I.; Mehta, N.; Elgarahy, A.M.; Al-Hinai, A.; Al-Muhtaseb, A.A.H.; Rooney, D.W. Conversion of biomass to biofuels and life cycle assessment: A review. Environ. Chem. Lett. 2021, 19, 4075–4118. [Google Scholar] [CrossRef]
- Gollakota, A.; Savage, P.E. Fast and Isothermal Hydrothermal Liquefaction of Polysaccharide Feedstocks. ACS Sustain. Chem. Eng. 2020, 8, 3762–3772. [Google Scholar] [CrossRef]
- Ghavami, N.; Özdenkçi, K.; Chianese, S.; Musmarra, D.; De Blasio, C. Process simulation of hydrothermal carbonization of digestate from energetic perspectives in Aspen Plus. Energy Convers. Manag. 2022, 270, 116215. [Google Scholar] [CrossRef]
- Liu, H.; Basar, I.A.; Eskicioglu, C. Hydrothermal liquefaction for sludge-to-energy conversion: An evaluation of biocrude production and management of waste streams. Energy 2023, 281, 128268. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, Y.; Yang, W.; Li, Y.; Yang, H.; Chen, Y.; Wang, X.; Chen, H. Valorization of the microalgae fixing CO2 from flue gas by co-hydrothermal liquefaction with high-protein microalgae: Denitrogenation of bio-oil by ash and high energy recovery. Fuel 2023, 340, 127566. [Google Scholar] [CrossRef]
- Ağbulut, Ü.; Sirohi, R.; Lichtfouse, E.; Chen, W.-H.; Len, C.; Show, P.L.; Le, A.T.; Nguyen, X.P.; Hoang, A.T. Microalgae bio-oil production by pyrolysis and hydrothermal liquefaction: Mechanism and characteristics. Bioresour. Technol. 2023, 376, 128860. [Google Scholar] [CrossRef]
- Cheng, F.; Cui, Z.; Mallick, K.; Nirmalakhandan, N.; Brewer, C.E. Hydrothermal liquefaction of high- and low-lipid algae: Mass and energy balances. Bioresour. Technol. 2018, 258, 158–167. [Google Scholar] [CrossRef]
- Ayala-Cortés, A.; Arcelus-Arrillaga, P.; Millan, M.; Arancibia-Bulnes, C.A.; Valadés-Pelayo, P.J.; Villafán-Vidales, H.I. Solar integrated hydrothermal processes: A review. Renew. Sustain. Energy Rev. 2021, 139, 110575. [Google Scholar] [CrossRef]
- Ayala-Cortés, A.; Arcelus-Arrillaga, P.; Millan, M.; Okoye, P.U.; Arancibia-Bulnes, C.A.; Pacheco-Catalán, D.E.; Villafán-Vidales, H.I. Solar hydrothermal processing of agave bagasse: Insights on the effect of operational parameters. Renew. Energy 2022, 192, 14–23. [Google Scholar] [CrossRef]
- Sheehan, J.D.; Savage, P.E. Modeling the effects of microalga biochemical content on the kinetics and biocrude yields from hydrothermal liquefaction. Bioresour. Technol. 2017, 239, 144–150. [Google Scholar] [CrossRef]
- Xiao, C.; Liao, Q.; Fu, Q.; Huang, Y.; Chen, H.; Zhang, H.; Xia, A.; Zhu, X.; Reungsang, A.; Liu, Z. A solar-driven continuous hydrothermal pretreatment system for biomethane production from microalgae biomass. Appl. Energy 2019, 236, 1011–1018. [Google Scholar] [CrossRef]
- Ischia, G.; Orlandi, M.; Fendrich, M.A.; Bettonte, M.; Merzari, F.; Miotello, A.; Fiori, L. Realization of a solar hydrothermal carbonization reactor: A zero-energy technology for waste biomass valorization. J. Environ. Manag. 2020, 259, 110067. [Google Scholar] [CrossRef]
- Giaconia, A.; Turchetti, L.; Ienna, A.; Mazzei, D.; Schiavo, B.; Scialdone, O.; Caputo, G.; Galia, A. Conceptual study of the coupling of a biorefinery process for hydrothermal liquefaction of microalgae with a concentrating solar power plant. In AIP Conference Proceedings; AIP Publishing: New York, NY, USA, 2017. [Google Scholar]
- Narvaez Saucedo, M.E.; Arancibia-Bulnes, C.A.; Macias, J.D.; Ramirez-Cabrera, M.A.; Valades-Pelayo, P.J. Heat transfer and chemical kinetics analysis of a novel solar reactor for hydrothermal processing. Solar Energy 2022, 241, 372–385. [Google Scholar] [CrossRef]
- Briongos, J.V.; Taramona, S.; Gómez-Hernández, J.; Mulone, V.; Santana, D. Solar and biomass hybridization through hydrothermal carbonization. Renew. Energy 2021, 177, 268–279. [Google Scholar] [CrossRef]
- Ranganathan, P.; Savithri, S. Computational Fluid Dynamics simulation of hydrothermal liquefaction of microalgae in a continuous plug-flow reactor. Bioresour. Technol. 2018, 258, 151–157. [Google Scholar] [CrossRef]
- Xiao, C.; Liao, Q.; Fu, Q.; Huang, Y.; Xia, A.; Chen, H.; Zhu, X. Numerical investigation of laminar mixed convection of microalgae slurry flowing in a solar collector. Appl. Therm. Eng. 2020, 175, 115366. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, X.; Fan, X.; Li, Z.; Qian, L.; Zhang, B.; Wang, S. Convective enhancement of microalgae slurry in continuous tubular reactors for biocrude production during hydrothermal liquefaction. Appl. Therm. Eng. 2023, 220, 119725. [Google Scholar] [CrossRef]
- Chen, H.; Liao, Q.; Fu, Q.; Huang, Y.; Xia, A.; Xiao, C.; Zhu, X. Convective heat transfer characteristics of microalgae slurries in a circular tube flow. Int. J. Heat Mass Transfer 2019, 137, 823–834. [Google Scholar] [CrossRef]
- Chu, W.-X.; Tsai, C.-A.; Lee, B.-H.; Cheng, K.-Y.; Wang, C.-C. Experimental investigation on heat transfer enhancement with twisted tape having various V-cut configurations. Appl. Therm. Eng. 2020, 172, 115148. [Google Scholar] [CrossRef]
- Taheran, E.; Javaherdeh, K. Experimental investigation on the effect of inlet swirl generator on heat transfer and pressure drop of non-Newtonian nanofluid. Appl. Therm. Eng. 2019, 147, 551–561. [Google Scholar] [CrossRef]
- Klemeš, J.J.; Wang, Q.-W.; Varbanov, P.S.; Zeng, M.; Chin, H.H.; Lal, N.S.; Li, N.-Q.; Wang, B.; Wang, X.-C.; Walmsley, T.G. Heat transfer enhancement, intensification and optimisation in heat exchanger network retrofit and operation. Renew. Sust. Energy Rev. 2020, 120, 109644. [Google Scholar] [CrossRef]
- Feng, Z.; Ai, X.; Wu, P.; Lin, Q.; Huang, Z. Experimental investigation of laminar flow and heat transfer characteristics in square minichannels with twisted tapes. Int. J. Heat Mass Transf. 2020, 158, 119947. [Google Scholar] [CrossRef]
- Chen, H.; Fu, Q.; Liao, Q.; Zhang, H.; Huang, Y.; Xia, A.; Zhu, X. Rheological properties of microalgae slurry for application in hydrothermal pretreatment systems. Bioresour. Technol. 2018, 249, 599–604. [Google Scholar] [CrossRef]
- Singh, S.K.; Kacker, R.; Chaurasiya, P.K.; Gautam, S.S. Correlations on heat transfer rate and friction factor of a rectangular toothed v-cut twisted tape exhibiting the combined effects of primary and secondary vortex flows. Int. Commun. Heat Mass Transf. 2022, 139, 106503. [Google Scholar] [CrossRef]
- Varun; Garg, M.O.; Nautiyal, H.; Khurana, S.; Shukla, M.K. Heat transfer augmentation using twisted tape inserts: A review. Renew. Sustain. Energy Rev. 2016, 63, 193–225. [Google Scholar] [CrossRef]
- Maluta, F.; Paglianti, A.; Montante, G. A PBM-Based Procedure for the CFD Simulation of Gas–Liquid Mixing with Compact Inline Static Mixers in Pipelines. Processes 2023, 11, 198. [Google Scholar] [CrossRef]
- Cao, Q.; Zhou, J.; Qian, Y.; Yang, S. Three-Dimensional Model on Liquid–Liquid Mass Transfer of the Kenics Static Mixer: Considering Dynamic Droplet Size Distribution. Ind. Eng. Chem. Res. 2023, 62, 10507–10522. [Google Scholar] [CrossRef]
- Mahian, O.; Kolsi, L.; Amani, M.; Estellé, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Siavashi, M.; Taylor, R.A.; Niazmand, H.; et al. Recent advances in modeling and simulation of nanofluid—Part I: Fundamentals and theory. Phys. Rep. 2019, 790, 1–48. [Google Scholar] [CrossRef]
- Mahian, O.; Kolsi, L.; Amani, M.; Estellé, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Taylor, R.A.; Abu-Nada, E.; Rashidi, S.; et al. Recent advances in modeling and simulation of nanofluid flows—Part II: Applications. Phys. Rep. 2019, 791, 1–59. [Google Scholar] [CrossRef]
- Wagner, W.; Kretzschmar, H. International Steam Tables-Properties of Water and Steam Based on the Industrial Formulation IAPWS-IF97: Tables, Algorithms, Diagrams, and CD-ROM Electronic Steam Tables-All of the Equations of IAPWS-IF97 Including a Complete Set of Supplementary Backward Equations for Fast Calculations of Heat Cycles, Boilers, and Steam Turbines; Springer Science & Business Media: Berlin, Germany, 2007. [Google Scholar]
- Valdez, P.J.; Tocco, V.J.; Savage, P.E. A general kinetic model for the hydrothermal liquefaction of microalgae. Bioresour. Technol. 2014, 163, 123–127. [Google Scholar] [CrossRef]
- Brown, T.M.; Duan, P.; Savage, P.E. Hydrothermal Liquefaction and Gasification of Nannochloropsis sp. Energy Fuels 2010, 24, 3639–3646. [Google Scholar] [CrossRef]
- Chhabra, R.P.; Richardson, J.F. Non-Newtonian Flow in the Process Industries; Butterworth-Heinemann: Oxford, UK, 1999; pp. 147–158. [Google Scholar]
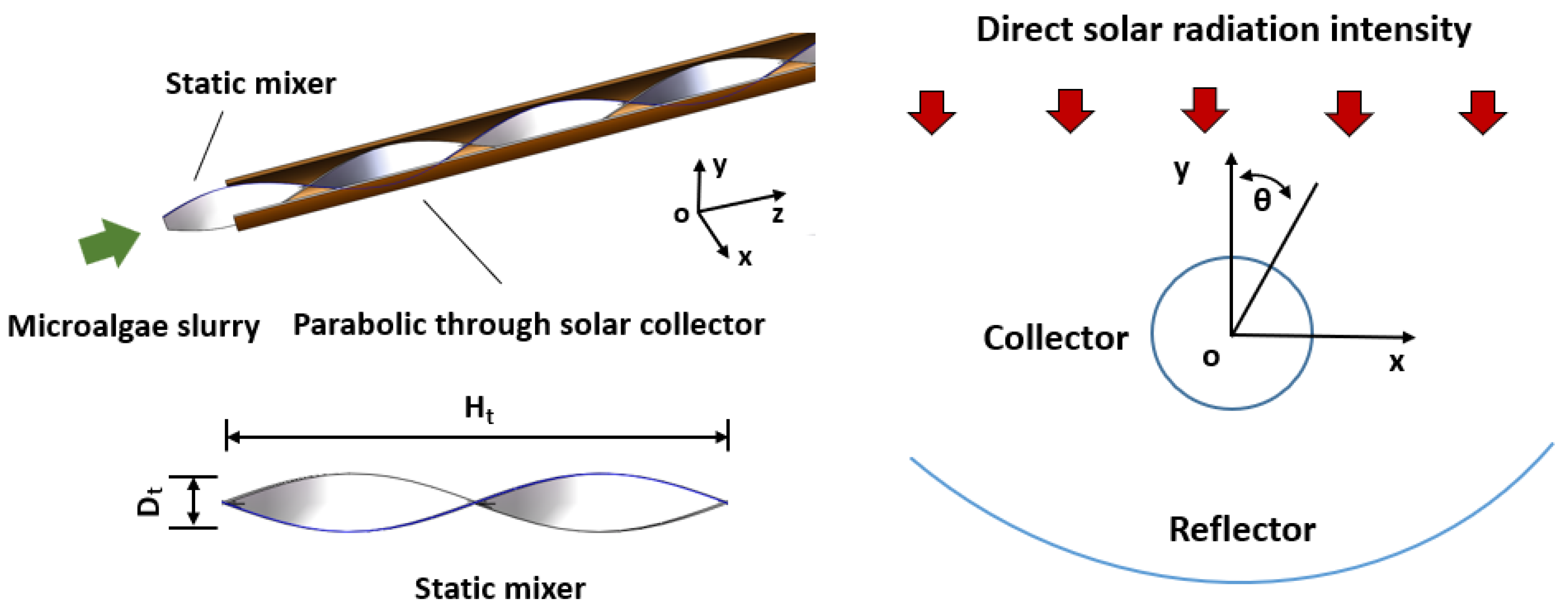
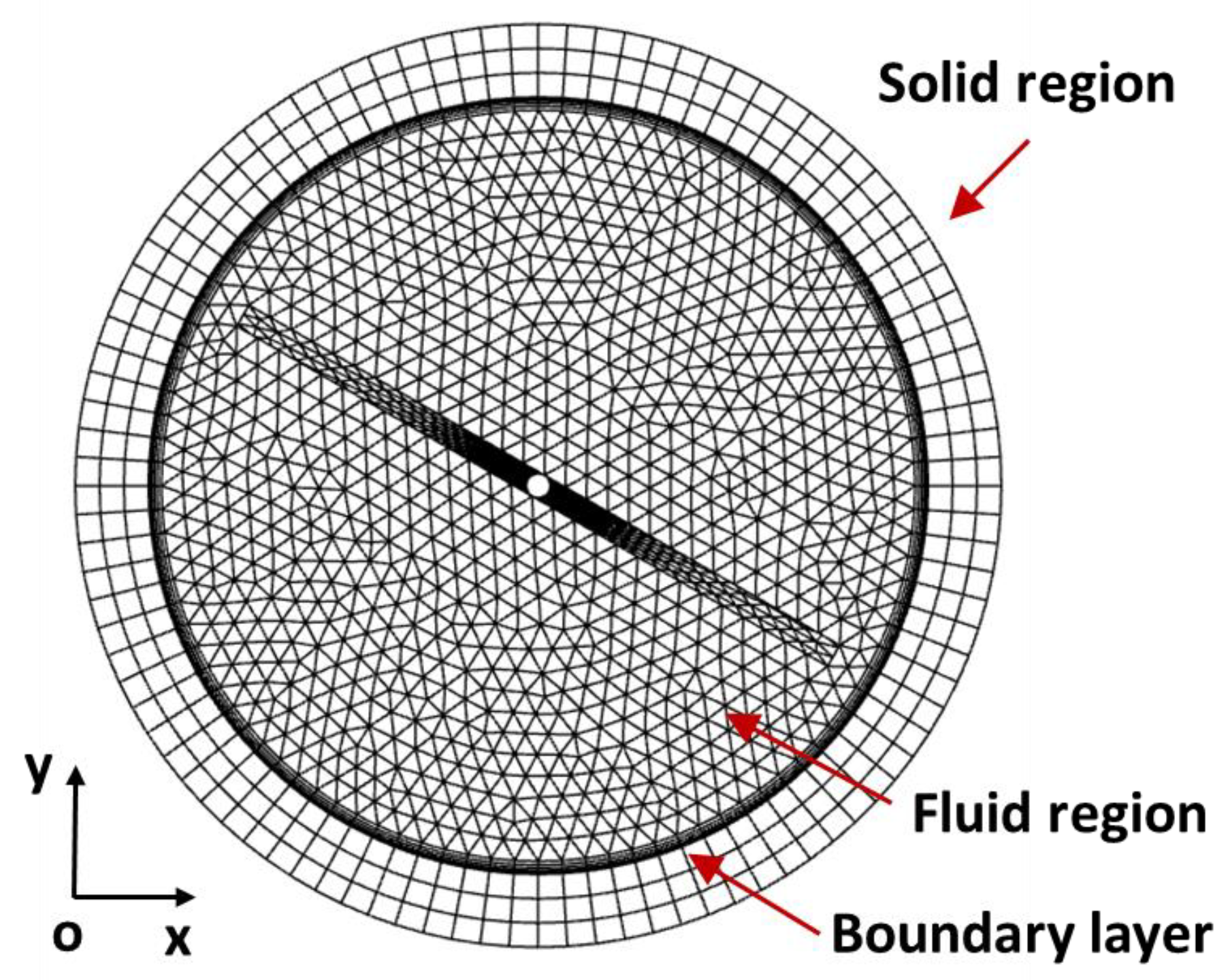



| Boundary Condition | Value |
|---|---|
| Flow rate at the inlet | 30, 40, 50, 60, 70, 80 L/h |
| Mean temperature at the inlet | 300 K |
| Pressure at the outlet | 20 MPa |
| Direct solar radiation intensity | 650, 750 and 850 W/m2 |
| Heat flux at the wall | Equation (1), Equation (2), Equation (3) |
| Studied parameters | f, Nu, PEC, Re, yield of water-soluble organics, biocrude, biogas, formation rate of biocrude |
| Grid Number | ΔP (Pa) | ΔP Error (%) | h (W·m−2·k−1) | h Error (%) | YBC | YBC Error (%) |
|---|---|---|---|---|---|---|
| 7642715 | 358.2 | −1.06% | 150.8 | 41.88% | 14.7% | −15.84% |
| 10239632 | 361.0 | −0.28% | 122.3 | 15.05% | 16.2% | −7.23% |
| 14066514 | 362.0 | Baseline | 106.3 | Baseline | 17.4% | Baseline |
| 26082444 | 363.5 | 0.42% | 112.3 | 5.65% | 18.5% | 6.29% |
| Mesh | l | C | δ | Dt |
|---|---|---|---|---|
| No.1 (7,642,715) | 2000 | 40 | 1 | 20 |
| No.2 (10,239,632) | 2400 | 50 | 1 | 28 |
| No.3 (14,066,514) | 3000 | 50 | 1 | 28 |
| No.4 (26,082,444) | 4000 | 60 | 1 | 28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Lou, F.; Zhang, X.; Shen, C.; Pan, W.; Wang, S. Hydrothermal Conversion of Microalgae Slurry in a Continuous Solar Collector with Static Mixer for Heat Transfer Enhancement. Energies 2023, 16, 7986. https://doi.org/10.3390/en16247986
Chen H, Lou F, Zhang X, Shen C, Pan W, Wang S. Hydrothermal Conversion of Microalgae Slurry in a Continuous Solar Collector with Static Mixer for Heat Transfer Enhancement. Energies. 2023; 16(24):7986. https://doi.org/10.3390/en16247986
Chicago/Turabian StyleChen, Hao, Fangfang Lou, Xueyi Zhang, Chengjun Shen, Weicheng Pan, and Shuang Wang. 2023. "Hydrothermal Conversion of Microalgae Slurry in a Continuous Solar Collector with Static Mixer for Heat Transfer Enhancement" Energies 16, no. 24: 7986. https://doi.org/10.3390/en16247986
APA StyleChen, H., Lou, F., Zhang, X., Shen, C., Pan, W., & Wang, S. (2023). Hydrothermal Conversion of Microalgae Slurry in a Continuous Solar Collector with Static Mixer for Heat Transfer Enhancement. Energies, 16(24), 7986. https://doi.org/10.3390/en16247986







