Abstract
This paper presents an experimental measurement of the heat transfer coefficient (HTC) in a direct, oil-cooled lithium-ion battery at low Reynolds numbers. As demands on the electric vehicle battery pack increase, the role of thermal management to safeguard the pack becomes more important. Therefore, it is expected that various means for enhancing the HTC are sought. One way to increase the HTC is by shifting from air cooling to liquid cooling. The application of direct oil cooling in batteries has not yet been implemented. This paper explores this by developing the concept and an experimental steady-state technique to measure the HTC for direct oil cooling on a cylindrical 18650-cell battery at low Reynolds numbers. The experimental measurements are validated against known empirical correlations in the literature, showing that, despite the complex arrangement of cylindrical battery cells in packs, the classical correlations can be a useful tool to develop an oil-cooled battery thermal management system. A simplified correlation was also developed.
1. Introduction
Progress in battery technology has been a major enabler for the shift towards road transport electrification. Lithium-ion batteries are the most commercially mature energy storage technology and have become the power source of choice. The global production of lithium-ion batteries grew from ca. 46 GWh in 2011 to 948 GWh in 2022 [1]. Over a quarter of the 2022 battery production capacity was used to cater for the demand from the automotive industry. This growth in demand is expected to continue in the near future. Due to the continuous effort to reduce costs and improve safety and energy density [2,3], Li-ion batteries have found mass adoption in electric vehicles (EVs). However, they are not without drawbacks. Their battery performance is affected by temperature [4,5]. The lithium-ion cell has a very narrow comfort temperature of 15–35 °C [6]. At temperatures below 25 °C, the cell experiences a loss in energy storage capacity. Conversely, at temperatures higher than 35 °C, the cell risks damage to its life. The application of Li-ion cells in EVs stretches their operating envelope. As a result, battery cells may suffer from degradation or safety issues, which, in turn, are intrinsically linked with battery temperature.
Offer et al. [7] highlight how, so far, the industry has paid too little attention to battery thermal management systems (BTMSs). While in the past decade, the effort was placed on reducing costs and increasing energy density, the focus is now shifting towards maximizing lifetime, enhancing power capability, and reducing safety risks associated with thermal runaway.
Thermal management is becoming an essential auxiliary system, with OEMs developing proprietary thermal management strategies [8,9,10]. The increased attention paid to BTMSs is also reflected in the vehicles entering the market. Early vehicles, such as the Renault ZOE and the Nissan LEAF, implemented natural air cooling, with later models using forced air-cooling strategies. While this might have been sufficient in low-duty cycles, customer demands for long range pushed for increased volumetric energy density and faster charging rates, and the low thermal capacity became insufficient [11,12,13]. Later models, such as Tesla and BMW i3, sought an indirect liquid cooling strategy. In this case, liquid is passed through channels in an aluminum plate, which is in thermal contact with battery cells [14]. This technique is an adaptation of liquid-cooled cold plates for industrial high-power electronic devices [15]. Despite the higher thermal capacity, indirect liquid cooling is still unable to absorb sustained high heat flux, such as that generated through fast charging. Moreover, the part of the battery that is in contact with the cooling channel is naturally cooler than the parts that are not, leading to a temperature gradient within the cell [16]. This affects the resistance to current flow in its various layers, which, in turn, has an effect on degradation rates. Furthermore, as the coolant passes through the channels along the pack, it absorbs heat and warms up. Thus, its effectiveness in cooling subsequent cells reduces, causing a temperature gradient along the battery pack. This, in turn, causes adverse voltage distribution and uneven cell aging [17,18], which is reflected in the performance of the pack. While several designs with an increasing number of channels and serpentine flow patterns have been studied [19], the limitations of this technology persist.
One emerging alternative for enhancing heat transfer in battery thermal management systems is direct oil cooling. In this type of cooling, the battery is sealed in a compartment, and a dielectric liquid is injected in direct contact with the battery cells. This decreases the thermal path between the coolant and the cells, thus enabling a higher ability to extract heat. The choice of coolant is important, as it is required to have dielectric properties to avoid dielectric breakdown between cell connections, have non-corrosive and non-toxic properties, have good chemical stability, and act as a fire retardant. The liquid is also required to have desirable thermodynamic properties, such as a high specific heat capacity, high thermal conductivity, and low viscosity, to enable higher flow. A review of battery immersion cooling and the choice between silicone-based and mineral oils was provided in [20]. While immersion liquid cooling has not yet been applied to battery thermal management systems of the EVs that are already on the market, there is great interest in moving in that direction. A comparison between the temperature profiles of immersion cooling and cold-plate-based cooling for automotive Li-ion battery modules was made in [21]. It was shown that, in direct immersion cooling, the axial temperature gradient across a cell is reduced from 32 °C to 2.7 °C. Conversely, the radial temperature gradient tends to increase from 0.6 °C to 5 °C. Overall, direct immersion cooling offers significantly lower maximum and average battery cell temperatures when compared with cold-plate cooling strategies. However, depending on the flow pattern, the temperature homogeneity across the pack may deteriorate (despite the fact that the cells would operate at lower temperatures). Ref. [22] also compares direct cooling strategies to indirect liquid cooling systems with the aim of identifying shortcomings and offering mitigation strategies. The authors highlight that direct liquid cooling has some disadvantages, such as the pumping losses associated with high-viscosity fluids, the high cost of the liquid itself, the compatibility of the material, and an increase in the battery system due to the added coolant weight. However, the overall cooling performance is improved, and the technique can add an added layer of safety to the threat of thermal runaway.
The trend to shift from indirect cooling to direct oil cooling was also seen in other areas of electric vehicle components, for example, in electrical motor cooling [23,24,25], which has also proved to be effective in improving current densities. As we shift in this direction, battery pack design becomes very multidisciplinary, involving electrical, structural, and thermos-fluid specialists who can develop accurate modeling [26].
There is currently a gap in knowledge in identifying the heat transfer coefficient when direct oil cooling is applied to battery technology. This is a key parameter, as it is critical for the accuracy of thermal models and battery thermal management systems. This is the subject of this paper, which aims to experimentally measure the heat transfer coefficient on a direct, oil-cooled cell and compare the results to classical empirical correlations found in the literature. This paper is therefore organized in the following manner: Section 2 introduces the concept of direct liquid cooling in battery packs. This is followed by a description of the experimental work undertaken in this research in Section 3. The results are presented in Section 4, where the experimental measurements are compared to empirical correlations. Finally, Section 5 draws a conclusion for this study.
2. A Direct, Oil-Cooled Battery Pack
2.1. Conceptual Development
This research investigated the geometry of a battery pack composed of 18650 cylindrical cells. This cell type remains one of the most popular cells. Its manufacturing process has been optimized for the mass market and has been an important factor in keeping costs down. However, the packaging of cylindrical cells often results in lower volumetric efficiency due to the unused volume between the cells. In this paper, we propose that the flow is injected along the length of the battery cell, thus using the volume between cells, as shown in Figure 1.

Figure 1.
Schematic of the battery pack with 18650 cells. The flow geometry along the battery cell length is highlighted and flow direction are highlighted in the document.
2.2. Empirical Correlations
The 18650 cell battery has geometrical proportions of 18 mm in diameter and 65 mm in length. The viscous nature of the oil being used as the coolant at low-to-moderate flow rates will result in a large portion of the battery being under developing flow conditions. This study focuses on this aspect and highlights the importance of having appropriate empirical correlations that will be used as reference points for this flow condition. The Seider–Tate equation [27] provides a prediction of the Nusselt number Nu for laminar flow in pipes (Reynolds number Re < 2300) and fluids with a Prandtl number between Pr > 0.6 and Pr < 5 with developing thermal and fluid boundary layers:
where is the fluid dynamic viscosity at the bulk fluid temperature and is the fluid viscosity at the wall temperature. The ratio of dynamic viscosities is a corrective factor that accounts for the change in viscosity at the hot wall surface [27]. Re is the Reynolds number, defined as follows:
where is the fluid density, v is the fluid velocity, and Dh is the hydraulic diameter of the flow channel (the void between battery cells), defined as
where A and p are the flow area and the perimeter, respectively. Likewise, Mills [28] defines the Nusselt number for laminar flow Re < 2300 and fluids with Prandtl number Pr > 5 with a developing hydrothermal boundary layer as follows:
where L is the length along the battery.
Where Section 2 discussed the concept and empirical correlations, the focus of the following section is turned to experimental work.
3. Experimental Work
3.1. Heat Flux Measurement: Application in Oil Cooling
The convective heat transfer coefficient (HTC), whose symbol is h, is found as follows:
where is the heat flux, Ts is the surface temperature, and Tref is the fluid reference temperature. Tref should theoretically be the local fluid temperature immediately above the test surface. However, it is difficult to measure and is often replaced by an alternative fluid reference temperature, for example, the fluid inlet temperature.
Several techniques for measuring the heat flux and the surface temperature Ts have been developed and described in the literature [29,30]. Thin-film heat-flux gauges (TFHFGs) are one such technique. They measure the change in the electrical resistance of a thin platinum film that is sputtered onto an insulating substrate. The gauges’ electrical resistance R varies with temperature and can be described using the following linear relationship:
where is a reference resistance of the platinum film, typically at a reference temperature . This is typically chosen to be 0 °C. The temperature coefficient of electrical resistance is the gradient of the change in the film’s electrical resistance with temperature T. When measuring the heat flux from a body, the surface temperature of the body is inferred by the change in electrical resistance and the gauge parameters. The parameters of the TFHFGs are achieved by an initial calibration process, which typically involves a water bath. The TFHFG fabrication process was described in [31]. These gauges were found to have a very fast response (100 kHz), which makes them fit for transient measurement. Their data reduction is, however, complex. The basic principles for the data reduction process in a transient measurement were described in [32].
The application of TFHFGs has become the preferred method for measuring heat flux in gas turbine blades [33]. Their use in transient tests has been well documented, for example, by Oldfield [34].
In oil-cooled components, the large thermal capacity of the oil-cooling system makes transient experiments inadequate. However, Camilleri et al. [35] modified the technique so that a steady-state measurement of the HTC in direct oil-cooled electrical machine windings could be made. The authors showed that the gauges are compatible with dielectric oil coolants, as the gauges were found to experience no degradation over time. In their modified steady-state technique, the metal pole piece that simulated the electrical machine winding was heated to a temperature in which a steady-state condition was reached. The metal temperature was measured using two k-type thermocouples, while the temperature across an insulating substrate was used to establish the heat flux, as shown in Figure 2.

Figure 2.
Schematic of a double-sided thin-film heat flux gauge [27].
The steady-state heat flux was determined using the one-dimensional Fourier conduction equation across the insulating substrate as follows:
where k is the thermal conductivity, x is the thickness between the resistive films, is the temperature measured on the inner layer, and is the temperature measured on the outer layer.
3.2. The Instrumented Cell
The experimental technique presented here also makes use of steady-state heat transfer and makes use of the one-dimensional Fourier conduction equation in cylindrical geometry. Instead of a double-sided thin-film heat-flux gauge, whose sensors are separated by a thin polyimide insulating layer, a cylindrical geometry representative of the 18650-cell battery was manufactured out of acrylic—a thermally non-conductive material. A heating element is used to replicate the battery’s heat loss. Thus, a 10 mm hole was machined at its center, such that, when fitted with a 5 W stainless-steel heater rod to replicate the heat generation from within the cell, a temperature gradient across the acrylic dummy cell was established. The cell was instrumented with T-type thermocouples next to the heating element and on the surface of the cell, thus allowing us to measure the temperature difference across it. A schematic of the dummy cell is shown in Figure 3.

Figure 3.
Schematic of the instrumented dummy cell with red dots indicating temperature sensors.
While the overall heat capacity of the dummy cell is lower than that of a real cell, careful considerations were made to ensure that the experiment was run under steady-state conditions, thus eliminating this issue. The low thermal conductivity of acrylic allows for a temperature gradient across the radial cross-section, and by measuring the power input to the heating element, the dummy cell acts as a heat gauge. The choice of material for the heat gauge is important as the accuracy of the experiment hinges on this temperature difference. The thermal resistance across the radial direction was computed to be over 100-times smaller than the thermal resistance along the axial direction. This allowed us to reduce the problem to one-dimensional heat transfer, as shown in Figure 4.

Figure 4.
Schematic of a simple heat-flux gauge used in the experiments.
3.3. The Flow Test Rig
The dummy cell was assembled in the middle of a set of non-energized battery geometries, thus recreating the flow channels between the cells, as shown in Figure 5. The battery stack was mounted inside a flow chamber through which the coolant would flow. In this investigation, a synthetic coolant, Opticool Fluid [36], was adopted. Such fluids are highly sensitive to temperature. The fluid properties vary with temperature, as shown in [35] and recreated in Table 1. These were used to calculate the properties of the flow and later compare the experimental results with empirical correlations. The coolant was circulated from a reservoir into the test box and then pumped through a heat exchanger to reject heat to ambient before being returned to the reservoir. The flow rate was regulated using a globe valve and measured using a variable area flow meter. The liquid circuit is shown in Figure 6.

Figure 5.
Test rig with insert of the battery back and instrumented cell.

Table 1.
Variation in coolant properties with temperature [28].

Figure 6.
Schematic of the test setup with (1) oil reservoir, (2) temperature sensors, (3) test box, (4) pump, (5) heat exchanger, (6) variable area flow meter, (7) globe valve, and (8) dc power supply. © 2018 IEEE. Reprinted, with permission, from [36].
During these tests, the oil flow was set and run at a fixed flow rate. The current and voltage across the heating element were measured and recorded. The heat input P into the active dummy cell was calculated as the product of the current I and voltage V as follows:
The heat input to the cell was set, and the increase in the temperature of the dummy cell was monitored and recorded. The experiment was repeated for varied flow rates, as shown in Table 2.

Table 2.
Test conditions.
3.4. Flow Calibration
Variable area flow meters were used to measure the flow rate of the oil coolant through the test piece. Such flow meters are calibrated by the manufacturer for water flow rate at a temperature of 20 °C. To account for the oil flow through the meter and the variation in the properties of Opticool Fluid with the temperature, a recalibration process of the flow meter was performed. The calibration of variable flow meters is classified by weight or by volume in Standards APTI435 and ISA-RP16.6-1961. In this work, the two procedures were followed and cross-compared. The calibration setup is shown in Figure 7.

Figure 7.
Schematic showing flow meter calibration by mass using (1) gate valve, (2) pump, (3) heat exchanger, (4) thermometer, (5) flow meter, (6) three-way valve, (7) reservoir, (8) collecting beaker, (9) scales, and (10) video camera [23]. © 2015 IEEE. Reprinted, with permission, from [24].
The flow pump was started with the three-way valve (6), positioned to allow the oil to recirculate. The valve was shifted to the measuring cylinder. The position of the flow meter was noted, and the mass and volume of the fluid collected were measured and timed. A chart of the calibrated scales is shown in Figure 8.

Figure 8.
Calibration chart for flow meter (originally calibrated for a water flow rate range between 0.2 and 2 lpm at 20 °C).
3.5. Uncertainty Analysis
The standard deviation of the steady-state temperature measurements logged over an hour at a rate of 1 Hz was 0.18 K, and the random uncertainty of steady-state temperature measurements, as defined in [37], was estimated at 0.006 K. The systematic uncertainty of temperature measurement is defined in terms of the uncertainty in the offset u(TTC) of the thermocouple, the reference temperature accuracy u(TRT)—to which the thermocouples are calibrated—and the oven temperature hysteresis u(TOH) during calibration. The temperature systematic uncertainty u(T)SYS was calculated as follows:
The temperature systematic uncertainty was calculated as 0.35 K. The overall uncertainty in temperature measurement is, hence, expressed as a function of the systematic and random uncertainty :
The overall uncertainty of temperature measurements was calculated at 0.35 K.
As the flow rate curves vary with temperature, the maximum uncertainty in measurement was reported. The uncertainty in measurement of the flow meter u(Q) was calculated using the following equation:
where u(V) is the uncertainty of the readings from the volume beaker. The reading error was estimated to be ±5 mL. V is the measured volume, set to 900 mL. u(t) is the uncertainty in the time measurement t. This was calculated using a stopwatch with a reading error of ±1 s (note that the uncertainty time must be measured in minutes to keep units consistent with the flow rate, measured in L/min). t is the time taken to calibrate each point, and it was kept to 1 min. The uncertainty in the flow meter u(Qfm) was found to be ±0.1 L/min. The systematic uncertainty of the measured flow rate was computed to ±0.1 L/min.
The heating power injected into each pole piece was calculated using the multiplication of the measured current I and voltage V. The systematic uncertainty for the power injected in the pole pieces u(P) is defined as follows:
where u(V) is the uncertainty in the voltage meter, and it was measured at ±0.2 V. The uncertainty in the current meter u(A) was found to be ±0.01 mA. The uncertainty of the heat input was found to be 4 mW. The uncertainty of the heat transfer coefficient was found to be between 8 and 15%.
4. Test Results and Discussion
4.1. Analysis
The steady-state temperatures for the battery surface and a reference input temperature were measured. The heat conducted across the cylinder Q is defined as follows:
where L is the length of the acrylic cell, k is the conductivity of the acrylic, rin and rout are the inner and outer radii of the gauge, and Tin and Tout are the respective temperatures at the inner and outer radii.
Likewise, the heat transfer Q from the acrylic cell to the fluid is defined as follows:
where h is the HTC. As with Equation (5), the reference temperature Tref is the fluid temperature immediately above the surface. However, it was replaced by an alternative reference fluid temperature to mitigate the difficulty in measuring the temperature directly above the surface. Often, the inlet temperature at the test section is used. This convention was also adopted here. By equating Equations (18) and (19), the acrylic cylinder, whose thermal properties are known, can be used as a gauge of heat flux, from which the HTC could be calculated as follows:
The non-dimensional Nusselt number Nu was defined, thus allowing us to compare the experimental measurements with existing correlations defined earlier:
where all the symbols maintain the same definitions described earlier.
4.2. Comparison of Empirical and Experimental Results
A plot superimposing the experimental results for 3 < Re < 45 onto the empirical results of Nu vs. Re is shown in Figure 9.
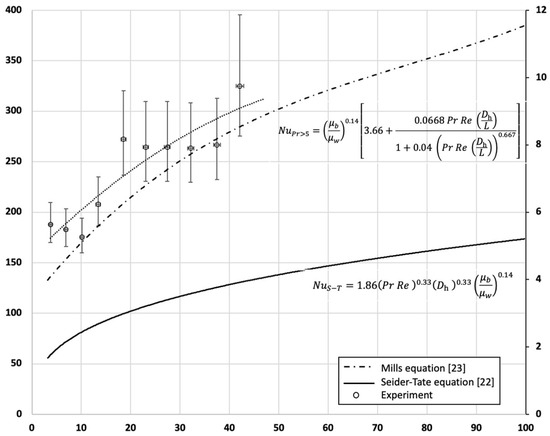
Figure 9.
Variation in the HTC and Nu with Re. A comparison between empirical correlations, CFD simulations, and experimental measurements.
It can be seen that the measured HTC varies between 150 and 350 W/m2 K, depending on the Reynolds number. The measured values are within 15% of the HTC values produced by the equation from Mills for a fluid with Pr > 5 and when corrected to the developing flow. The actual correlation of the experimental measurements was found to be the following:
A simpler quadratic correlation relating the Nusselt number to the Reynolds number can also be drawn as follows:
Conversely, the Seider–Tate equation, which is designed for fluids with 0.6 < Pr < 5, produced a significant underestimation of the HTC. The authors attribute this discrepancy to the Prandtl number of the fluid, shown in Figure 10. The large value makes the Seider–Tate equation inadequate. The result shown here, therefore, also highlights the importance of adequately assessing the properties of the fluid and the flow and ensures that any empirical correlations used fit within the regime for which they were designed.

Figure 10.
Variation in the Prandtl number Pr with temperature T for the coolant.
5. Conclusions
This paper focused on the heat transfer coefficient (HTC) from an 18650-cell battery in direct oil cooling. As the demands on the battery pack continue to increase, thermal management becomes a critical aspect for ensuring optimal battery operation, long life, and safety. Techniques for enhancing heat transfer from the battery pack are, therefore, necessary. It is expected that the industry will shift away from current air-cooling techniques and into liquid cooling. Direct liquid cooling offers a significant reduction in the thermal resistance path and is, therefore, very effective. This paper first presented a conceptual design in which direct oil cooling can be effectively integrated into the design of a battery pack made with 18650 cells. The paper also provided a method for measuring the HTC in a direct, oil-cooled battery pack and experimental measurements for Re < 100. The experimental results were compared to classical empirical correlations. The HTC values measured here confirm that classical empirical equations are reliable, but careful considerations need to be taken when choosing the correct correlations and ensuring that they fit within the regime for which they were designed.
Author Contributions
Conceptualization, R.C.; methodology, R.C.; experimental work, N.M.-V.; validation, R.C.; formal analysis, R.C.; investigation, R.C.; resources, R.C.; data curation, R.C.; writing—original draft preparation, R.C.; writing—review and editing, R.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xia, G.; Cao, L.; Bi, G. A review on battery thermal management in electrical vehicle application. J. Power Sources 2017, 367, 90–105. [Google Scholar] [CrossRef]
- Growth of Li-Ion Battery Manufacturing Capacity in Key EV Markets. S&P Global. Available online: https://www.spglobal.com/mobility/en/research-analysis/growth-of-liion-battery-manufacturing-capacity.html (accessed on 2 February 2023).
- Armand, M.; Tarascon, J.M. Building better batteries. Nature 2008, 451, 652–657. [Google Scholar] [CrossRef] [PubMed]
- He, F.; Ma, L. Thermal Management on Hybrid Power Systems Using Cylindrical and Prismatic Battery Cells. Heat Transf. Eng. 2015, 37, 581–590. [Google Scholar] [CrossRef]
- Bandhauer, T.M.; Garimella, S.; Fuller, T.F. A critical review of thermal issues in lithium-ion batteries. J. Electrochem. Soc. 2015, 138, R1–R25. [Google Scholar] [CrossRef]
- Pesaran, A.; Keyser, M.; Kim, G.; Santhanagopalan, S.; Smith, K. Tools for designing thermal management of batteries in electric drive vehicles. In Proceedings of the Advanced Automotive Battery Conference, Pasadena, CA, USA, 4–8 February 2013; Available online: https://www.nrel.gov/docs/fy13osti/57747.pdf (accessed on 10 January 2023).
- Offer, G.; Patel, Y.; Hales, A.; Diaz, L.B.; Marzook, M. Cool metric for lithium-ion batteries could spur progress. Nature 2020, 582, 485–487. [Google Scholar] [CrossRef]
- Tennessen, A.P.T.; Weingtraub, J.; Herman, W.A. Battery Coolant Jacket. U.S. Patent 20130004820A1, 11 February 2014. Available online: https://patents.google.com/patent/US20130004820A1/en (accessed on 20 December 2022).
- Chan, B.J.; Rao, V. Vehicle Battery Module with Cooling and Safety Features. U.S. Patent 9,620,830, 11 April 2017. Available online: https://patents.google.com/patent/US9620830B2/en (accessed on 20 December 2022).
- Ahn, J.; Woo, H.; Jung, D.Y.; Namgoong, J.E. Cooling System for Battery Packs. U.S. Patent 7,560,190, 14 July 2009. Available online: https://patents.google.com/patent/US7560190B2/en (accessed on 20 December 2022).
- Fan, L.; Khodadadi, J.M.; Pesaran, A.A. A parametric study on thermal management of an air-cooled lithium-ion battery module for plug-in hybrid electric vehicles. J. Power Sources 2013, 238, 301–312. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, X.; Li, G.; Hua, D. Assessment of the forced air-cooling performance for cylindrical lithium-ion battery packs: A comparative analysis between aligned and staggered cell arrangements. Appl. Therm. Eng. 2015, 80, 55–65. [Google Scholar] [CrossRef]
- Wang, T.; Tseng, K.J.; Zhao, J. Development of efficient air-cooling strategies for lithium-ion battery module based on empirical heat source model. Appl. Therm. Eng. 2015, 90, 521–529. [Google Scholar] [CrossRef]
- Hermann, W.A. Liquid Cooling Manifold with Multi-Function Thermal Interface. U.S. Patent 20100104938A1, 11 September 2012. Available online: https://patents.google.com/patent/US8263250B2/en (accessed on 20 December 2022).
- Kandlikar, S.G.; Hayner, C.N. Liquid cooled cold plates for industrial high power electronic devices—Thermal design and Manufacturing Considerations. Heat Transf. Eng. 2010, 30, 918–930. [Google Scholar] [CrossRef]
- Sawani, M.; Camilleri, R. Investigating the temperature profile of Li-ion battery cells under various cooling technologies. In Proceedings of the 16th UK Heat Transfer Conference (UKHTC2019), Nottingham, UK, 8–10 September 2019. [Google Scholar]
- Spitthoff, L.; Shearing, P.R.; Burheim, O.S. Temperature, Ageing and Thermal Management of Lithium-Ion Batteries. Energies 2021, 14, 1248–1278. [Google Scholar] [CrossRef]
- Leng, F.; Tan, C.M.; Pecht, M. Effect of Temperature on the Aging rate of Li ion Battery Operating above Room Temperature. Nat. Sci. Rep. 2015, 5, 12967. [Google Scholar] [CrossRef]
- Roe, C.; Feng, X.; White, G.; Li, R.; Wang, H.; Rui, X.; Wu, B. Immersion cooling for lithium-ion batteries—A review. J. Power Sources 2022, 525, 231094. [Google Scholar] [CrossRef]
- Jayarajan, S.A.; Azimov, U. CFD Modelling and thermal Analysis of a Cold Plate Design with a Zig-Zag Serpentine Flow Pattern for Li-Ion Batteries. Energies 2023, 16, 5243. [Google Scholar] [CrossRef]
- Dubey, P.; Pulugundla, G.; Srouji, A.K. Direct Comparison of Immersion and Cold-Plate Based Cooling for Automotive Battery Modules. Energies 2021, 14, 1259. [Google Scholar] [CrossRef]
- Anisha; Kumar, A. Identification and Mitigation of Shortcomings in Direct and Indirect Liquid Cooling-Based Battery Thermal Management System. Energies 2023, 16, 3857. [Google Scholar] [CrossRef]
- Camilleri, R.; Howey, D.A.; McCulloch, M.D. Predicting the temperature and flow distribution in a direct oil-cooled electrical machine with segmented stator. IEEE Trans. Ind. Electron. 2015, 63, 82–91. [Google Scholar] [CrossRef]
- Camilleri, R.; McCulloch, M.D. Assessing the Temperature and Current Density of Flat Winding Coils for Concentrated Windings Within a Segmented Stator Machine. IEEE Trans. Ind. Appl. 2021, 57, 2440–2448. [Google Scholar] [CrossRef]
- Camilleri, R.; McCulloch, M.D. Integrating a Heat Sink into Concentrated Wound Coils to Improve the Current Density of an Axial Flux, Direct Liquid Cooled Electrical Machine with Segmented Stator. Energies 2021, 14, 3619. [Google Scholar] [CrossRef]
- Özdemir, T.; Amini, A.; Ekici, Ö.; Köksal, M. Experimental Assessment of the Lumped Lithium-Ion Battery Model at Different Operating Conditions. Heat Transf. Eng. 2021, 43, 314–325. [Google Scholar] [CrossRef]
- Incropera, F.; Dewitt, D.P.; Bergman, T.L.; Lavine, A.S. Internal Flow: Laminar flow in circular tubes. In Introduction to Heat Transfer, 5th ed.; Wiley & Sons Inc.: New York, NY, USA, 2007; pp. 482–483+514. [Google Scholar]
- Mills, A.F.; Transfer, H.; Hall, P.; Jersey, N.; Mills, A.F. Heat Transfer, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 1999. [Google Scholar]
- Schultz, D.L.; Jones, T.V. Heat Transfer Measurements in Short-Duration Hypersonic Facilities; AGARD-AG-165; Advisory Group for Aerospace Research & Development (AGARD): Paris, France, 1973. [Google Scholar]
- Astarita, T.; Cardone, G.; Calomagno, G.M. Infrared thermography: An optical method in heat transfer and fluid flow visualization. Opt. Lasers Eng. 2006, 44, 261–281. [Google Scholar] [CrossRef]
- Collins, M.; Chana, K.; Povey, T. New Technique for the fabrication of miniature thin film heat flux gauges. Meas. Sci. Technol. 2015, 26, 025303. [Google Scholar] [CrossRef]
- Doorly, J.E.; Oldfield, M.L.G. The theory of advanced multi-layer thin film heat transfer gauges. Int. J. Heat Mass Transf. 1987, 30, 1159–1168. [Google Scholar] [CrossRef]
- Jones, T.V. The thin film heat transfer gauges—A history and new developments. In Proceedings of the 4th national UK Heat Transfer Conference, IMechE Conference Transaction, Manchester, UK, 26–27 September 1995. [Google Scholar]
- Oldfield, M.L.G. Impulse response processing of transient heat transfer gauge signals. ASME J. Turbomach. 2008, 130, 21–23. [Google Scholar] [CrossRef]
- Camilleri, R.; Beard, P.; Howey, D.A.; McCulloch, M.D. Prediction and measurement of the heat transfer coefficient in a direct oil-cooled electrical machine with segmented stator. IEEE Trans. Ind. Electron. 2018, 65, 94–102. [Google Scholar] [CrossRef]
- DSI. Opticool Fluid. Available online: http://dsiventures.com/electronics-cooling/opticool-fluid/ (accessed on 6 March 2015).
- Bell, S. A Beginner’s Guide to Uncertainty of Measurement; Measurement Good Practice Guide No. 11. Iss. 2; National Physical Laboratory: London, UK, 2001. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).