Research on the Improvement of Lithium-Ion Battery Performance at Low Temperatures Based on Electromagnetic Induction Heating Technology
Abstract
:1. Introduction
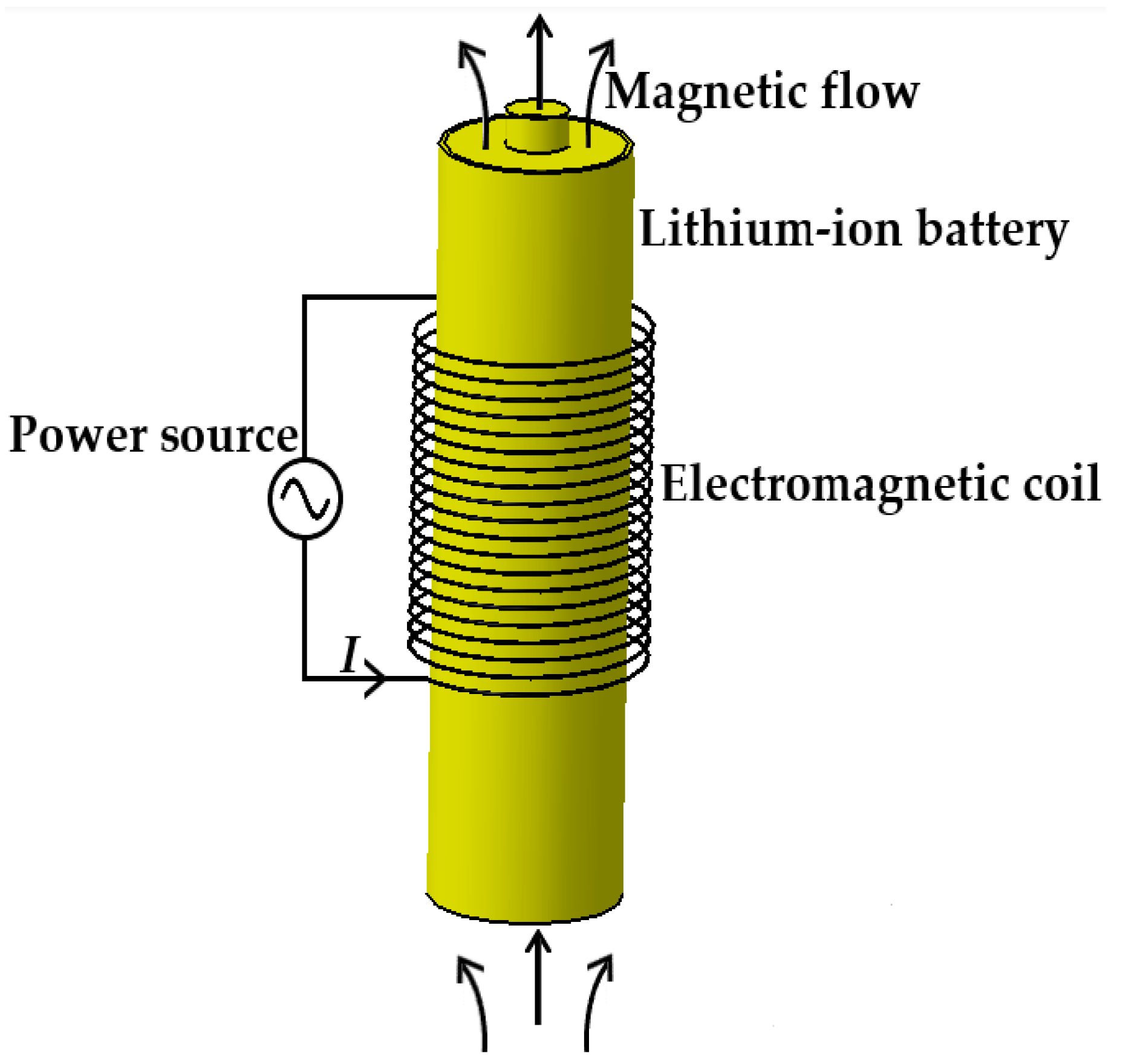
2. The Principle of Electromagnetic Induction Heating
2.1. System Structure
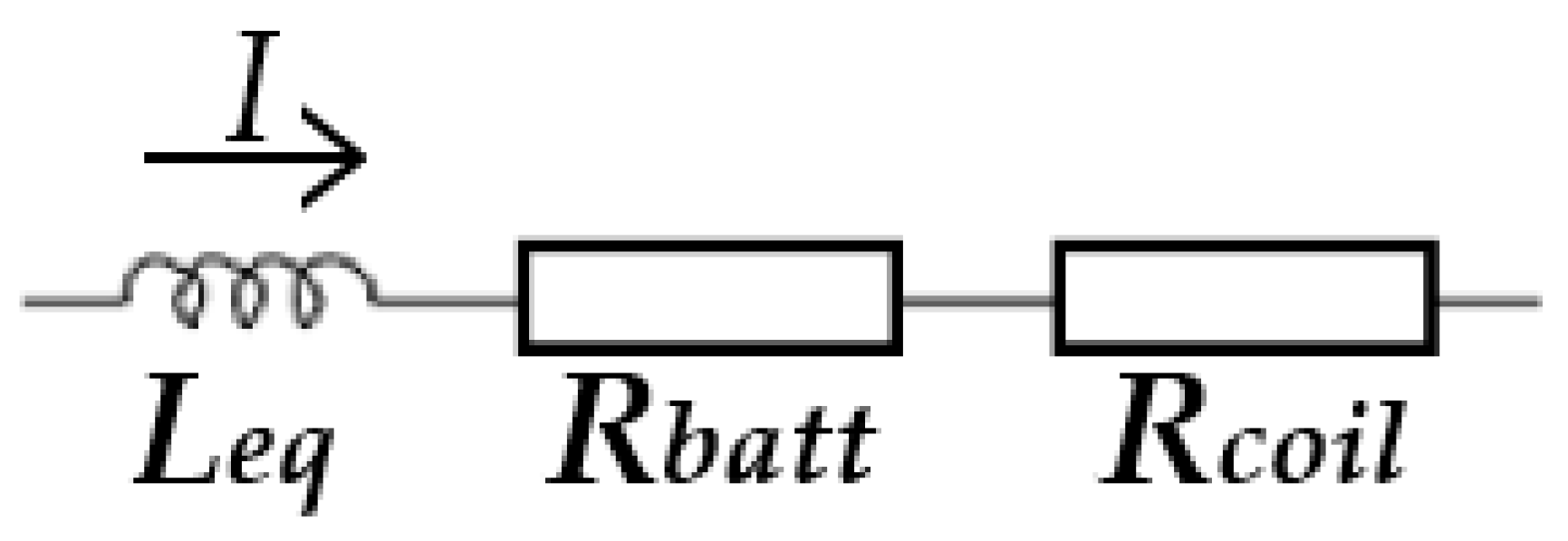
2.2. Theoretical Analysis
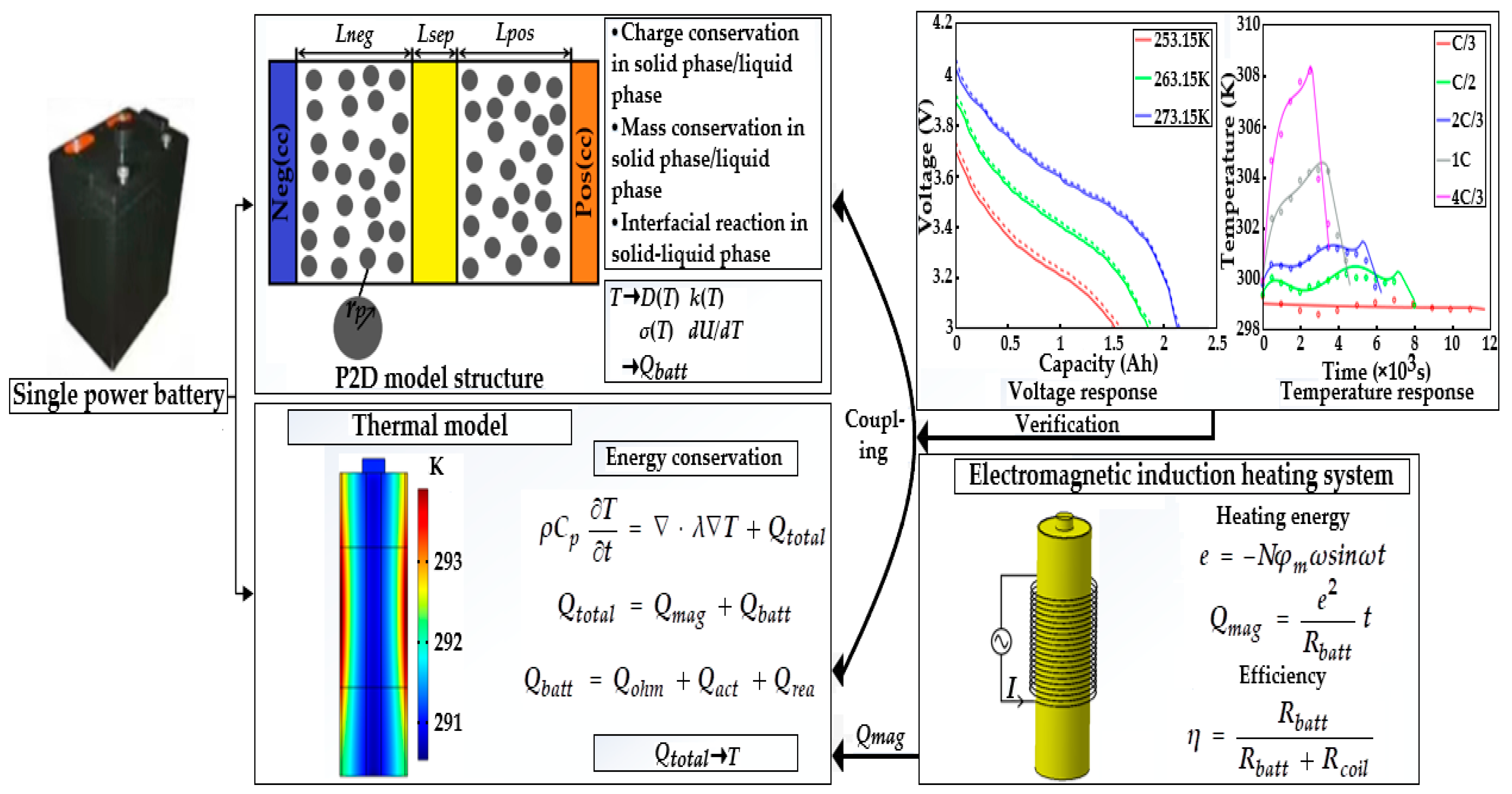
3. Model Development
3.1. Model Overview
3.2. Electrochemical Model
- (1)
- Mass conservation equations: Supposing that the reaction particle at each point on the spherical surface with a certain radius has the same concentration, then the mass balance in the process of Li+ extraction–insertion inside the spherical particles of solid-phase active materials is in line with Fick’s second law under the form of a polar coordinate system.
- (2)
- Charge conservation equations: The Li+ potentials in both the electrode and the electrolyte follow Ohm’s law, in which the potential distribution in the solid phase is written as:
- (3)
- Electrochemical reaction kinetics: The net velocity of the charge transfer reaction that occurs in the solid–liquid-phase interface can be described by the Butler–Volmer equation.
3.3. Thermal Model
3.4. Electrochemical–Thermal Coupling Characteristics
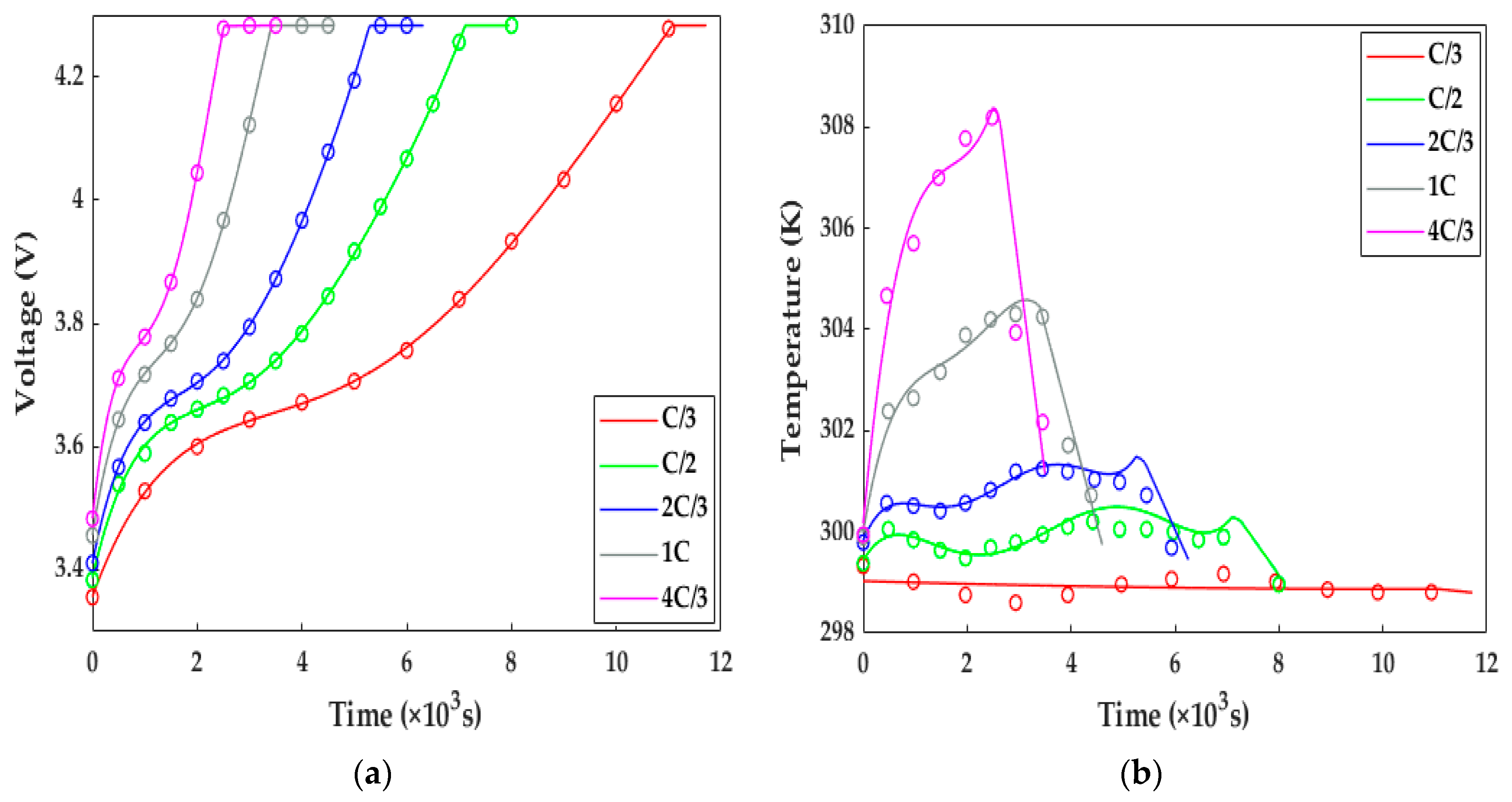
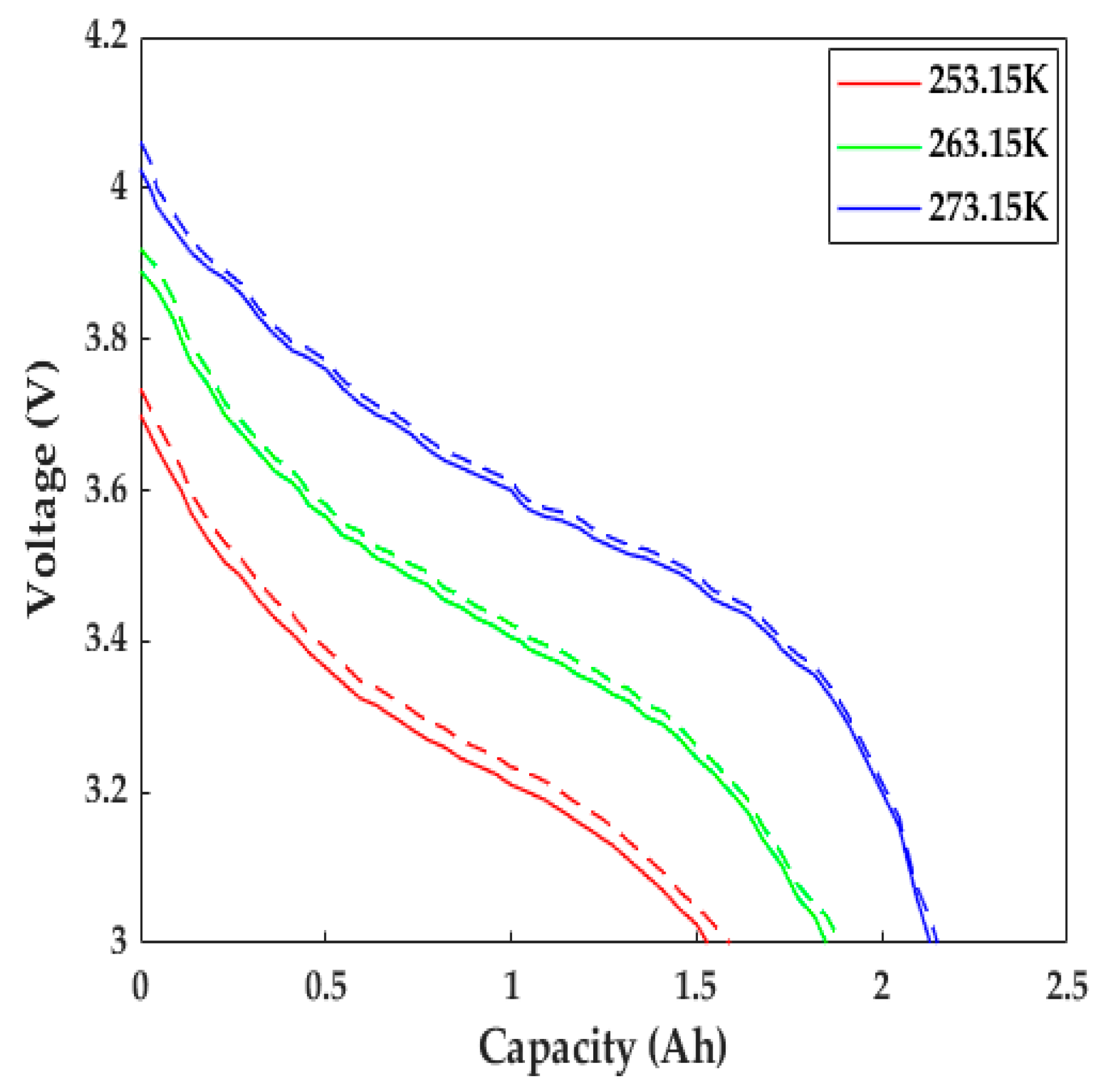
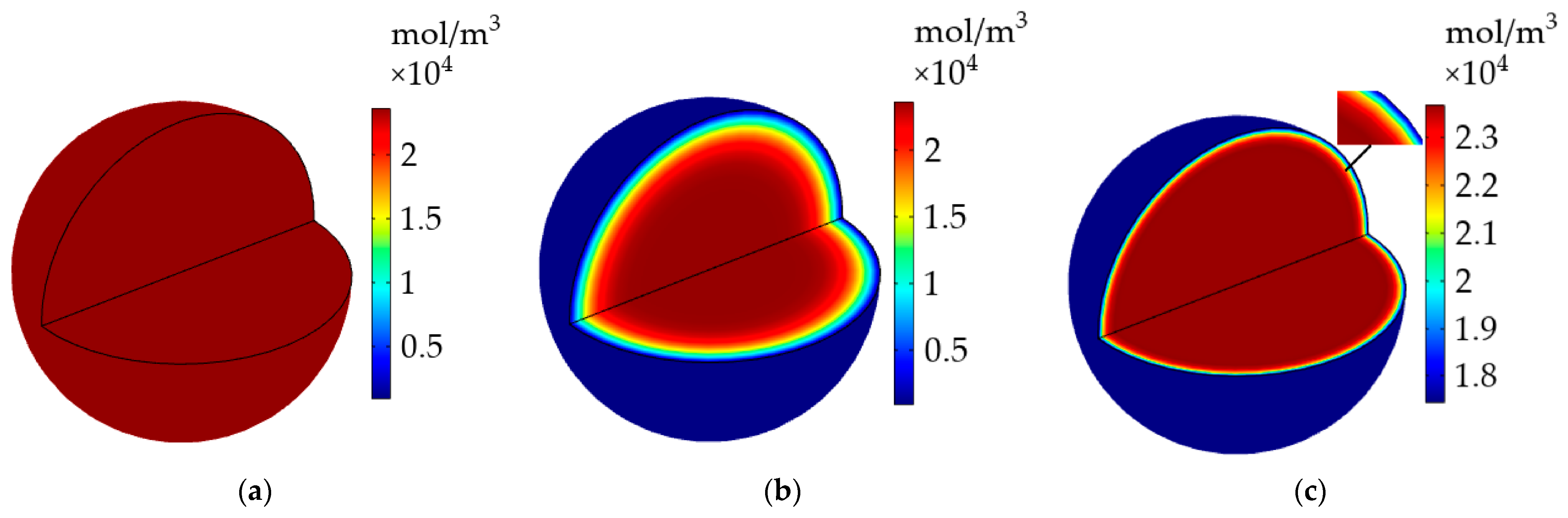
3.5. Model Validation
4. Simulation
4.1. Research Object
4.2. Heating Simulation
4.3. Electrochemical and Thermal Properties Simulation
5. Results and Discussion
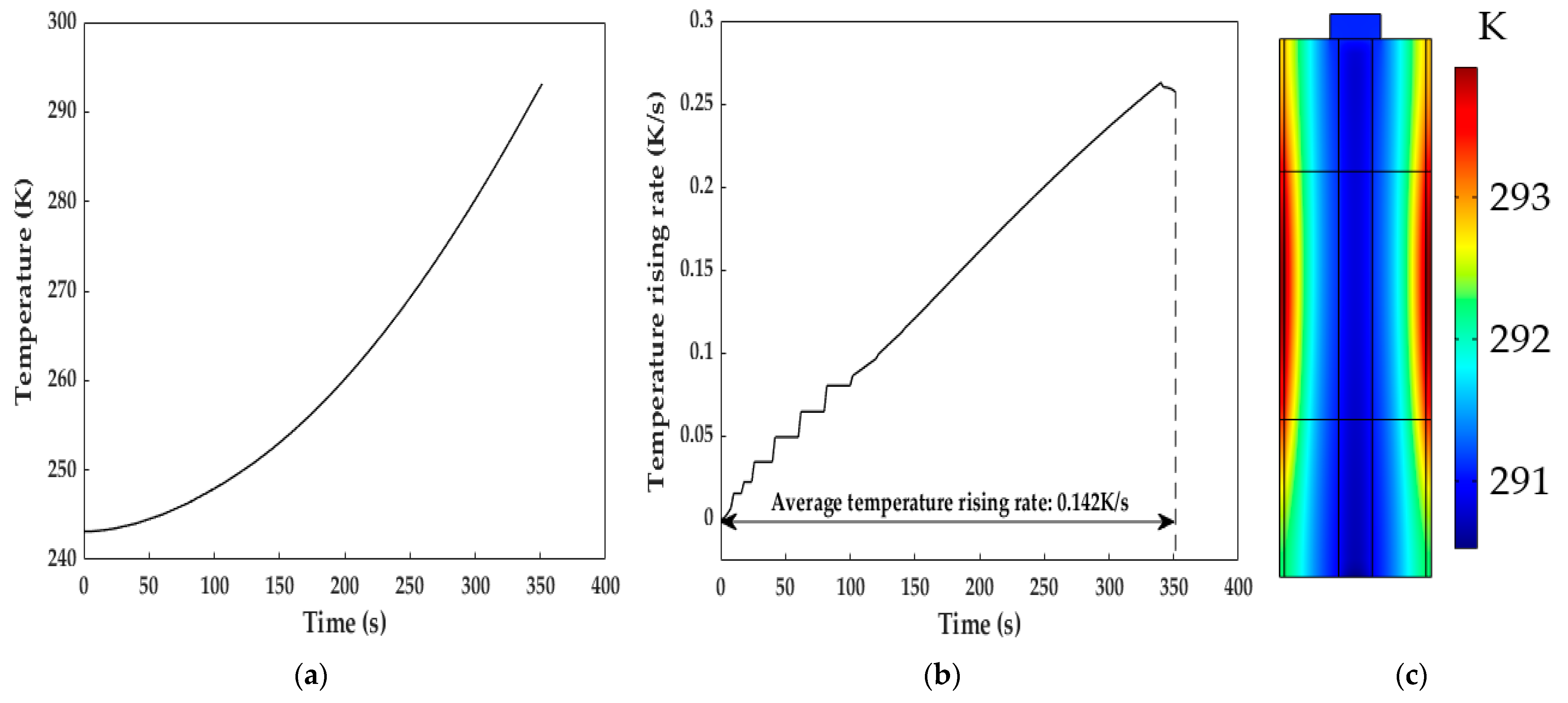
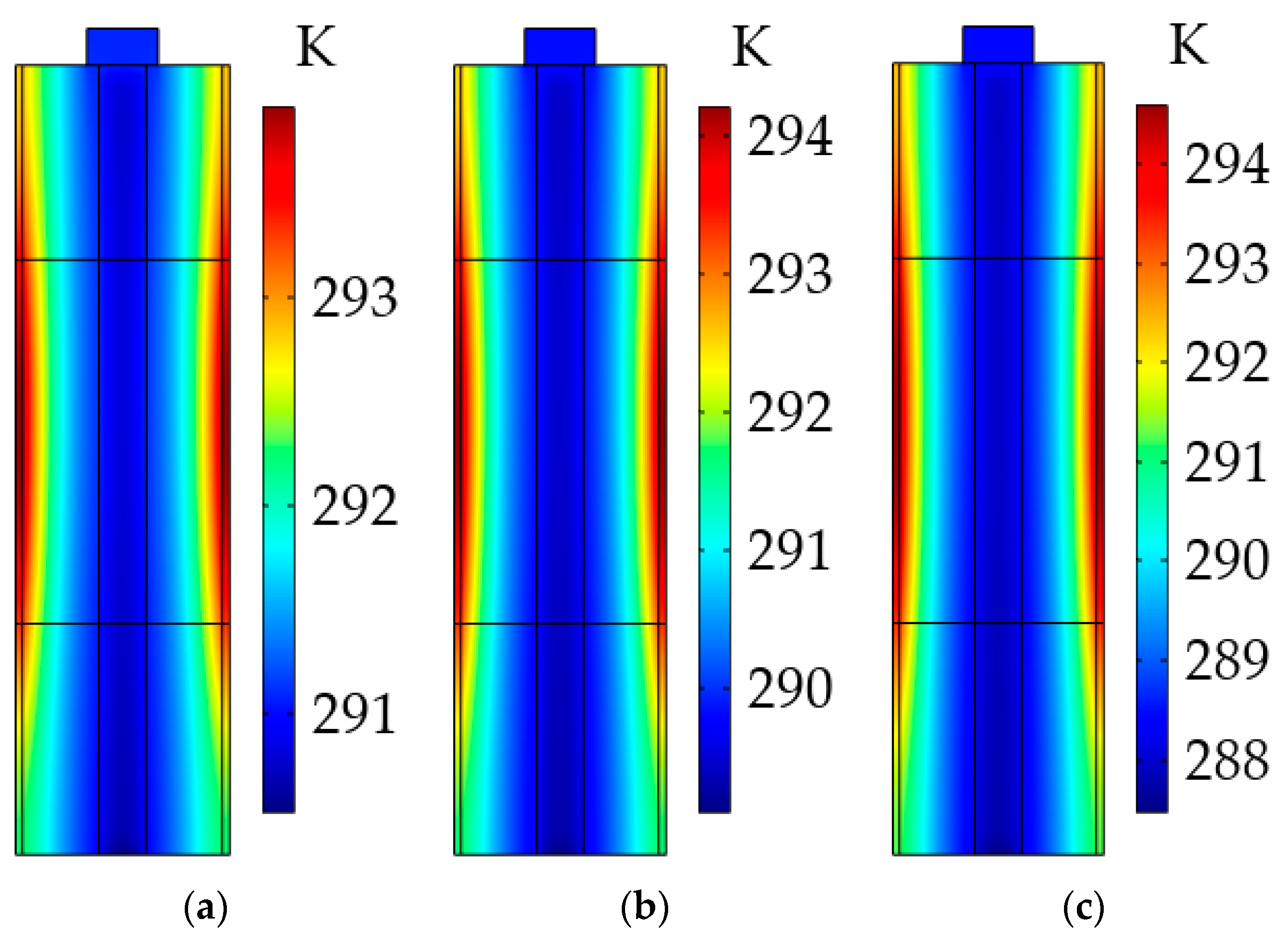
5.1. Research on Heating Effect
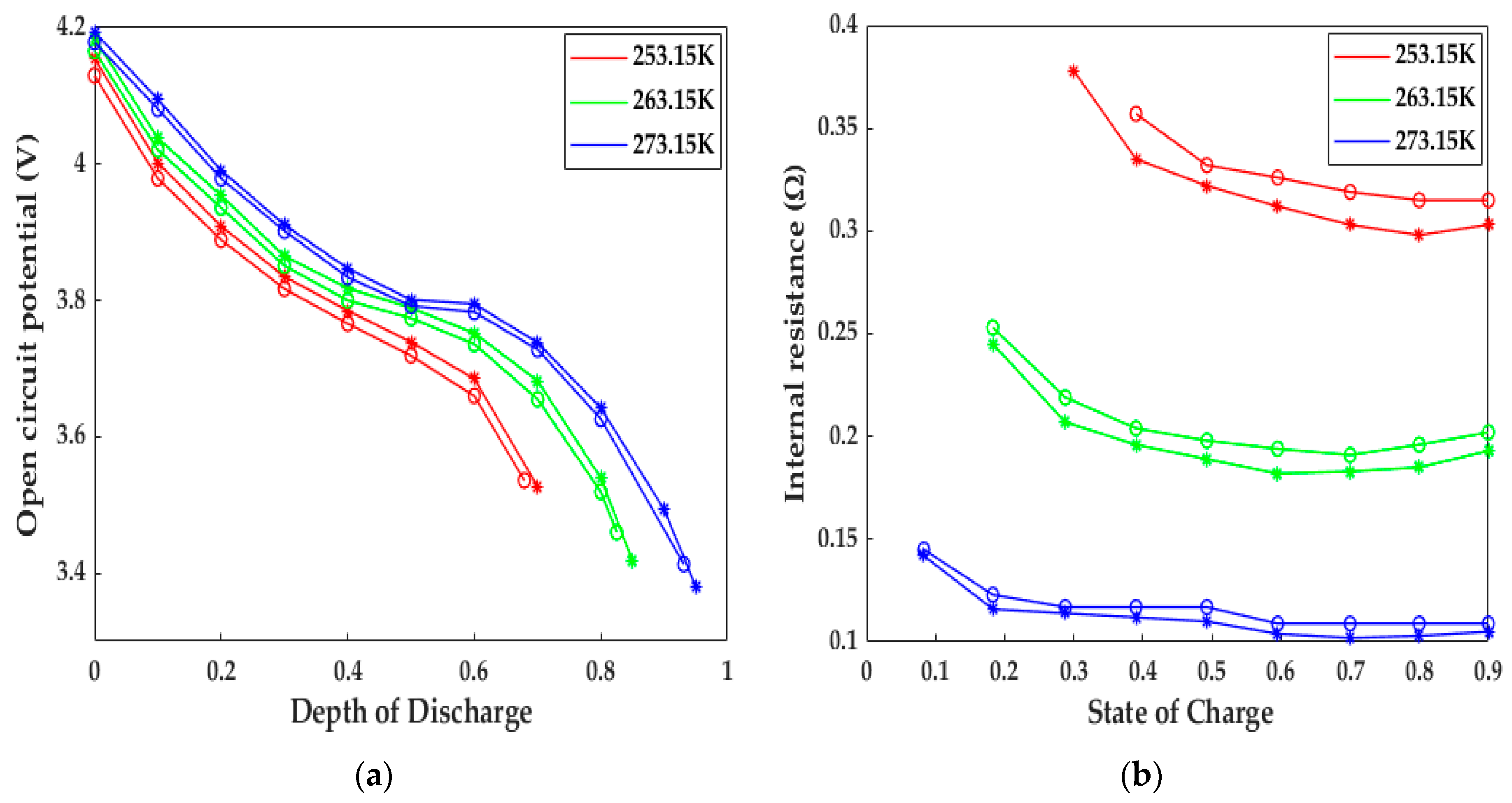
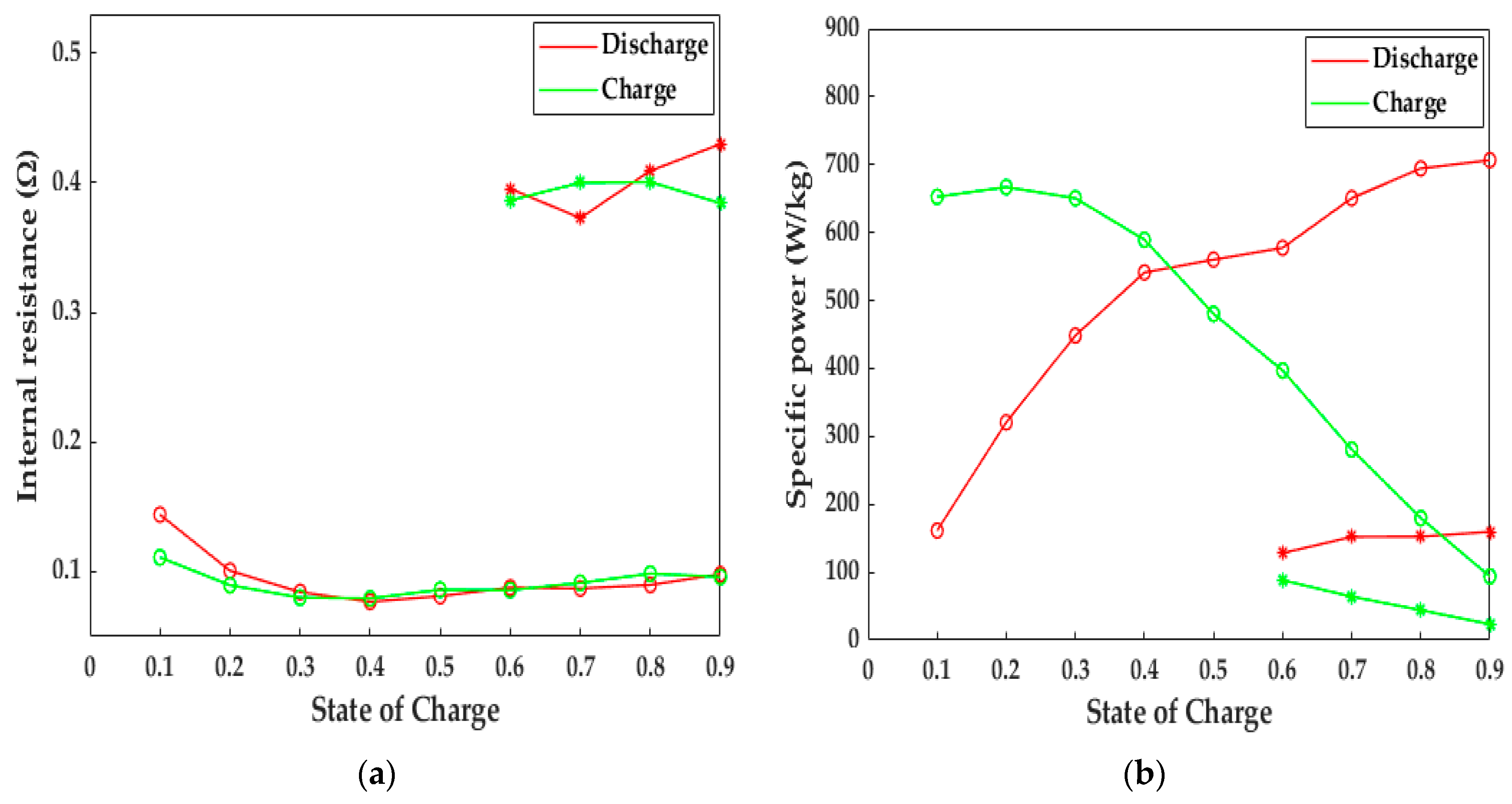
5.2. Analysis of HPPC Simulated Results
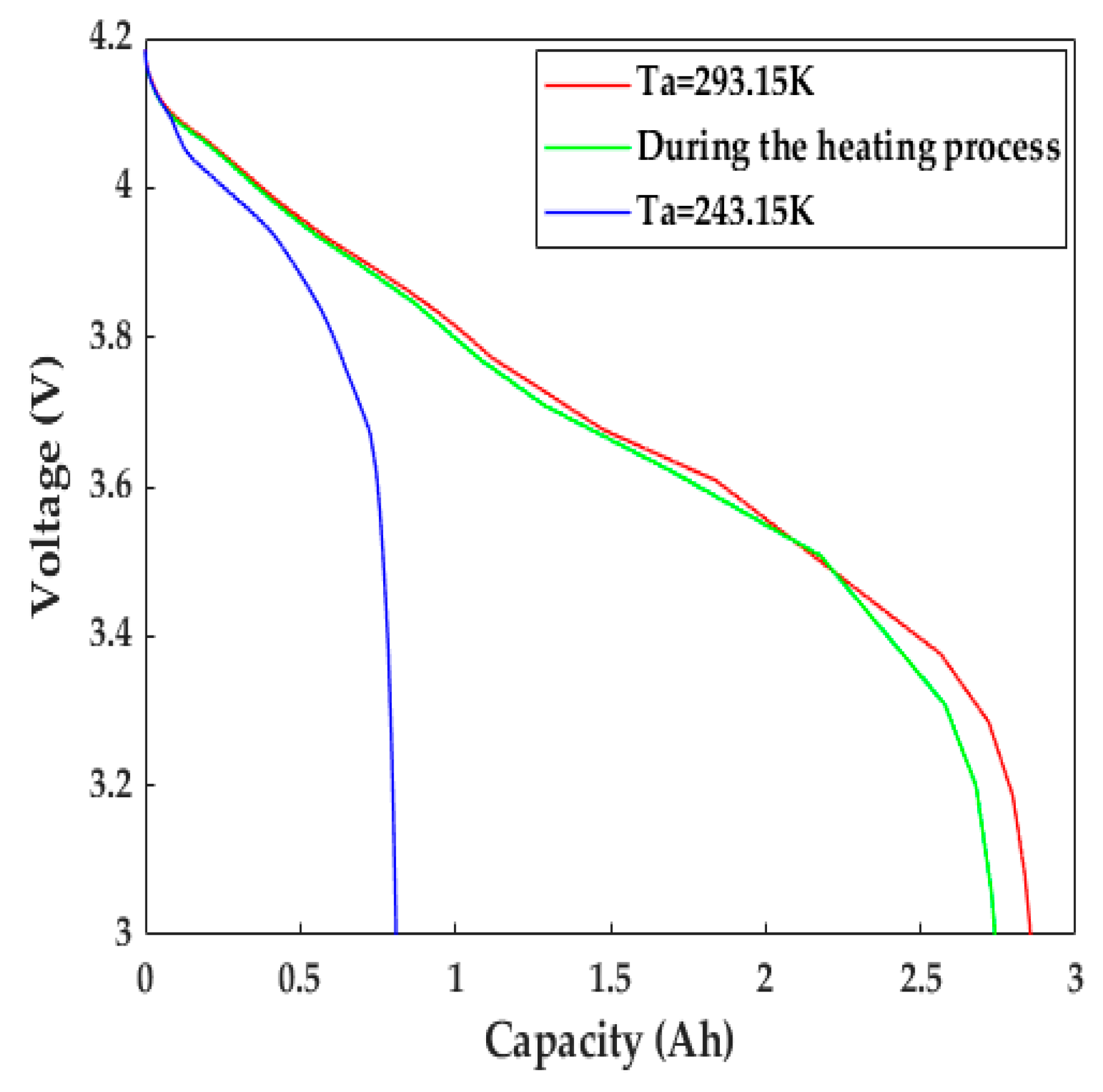
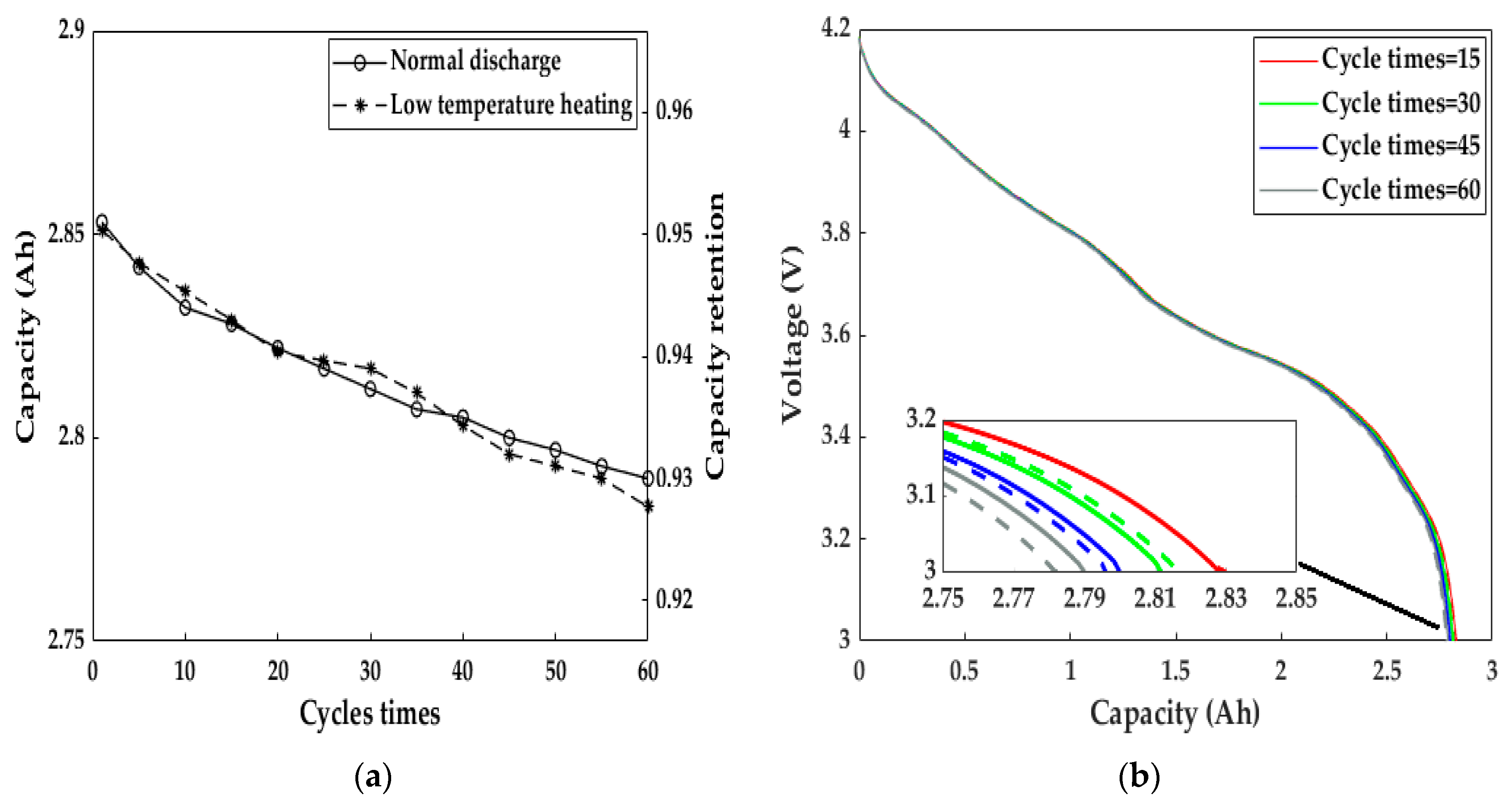
5.3. The Impact of the Heating Method on Battery Aging
5.4. Analysis of Influencing Factors
5.4.1. External Environmental Factors
5.4.2. Material Properties
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Nomenclature | |||
| as | specific superficial area (m−1) | RSEI | SEI film resistance (Ω) |
| Brugg | Bruggman coefficient | Rs | radius of the particles (m) |
| C | Li+ concentration (mol·m−3) | r | distance from the spherical center (m) |
| Cp | heat capacity at constant pressure (J·kg−1·K−1) | S | cross-sectional area of the copper coil (m2) |
| D | diffusivity (m2·s−1) | T | temperature (K) |
| dU/dT | entropy heat coefficient (V·K−1) | Ta | ambient temperature (K) |
| E | effective value of induced electromotive force (V) | t | time (s) |
| Ea | reaction activation energy (j·mol−1) | t+0 | transference number |
| e | induced electromotive force (V) | U | equilibrium potential of the electrode material (V) |
| F | Faraday’s constant (C·mol−1) | V | battery terminal voltage (V) |
| f | changing frequency of the magnetic flow (Hz) | Z | total equivalent impedance of the heating system (Ω) |
| h | surface heat transfer coefficient (W·m−2·K−1) | z+ | charge number |
| I | the SAC acting on the copper coil (A) | Greek | |
| i | current density (A·m−2) | αa, αc | charge transfer coefficient |
| iapp | applied current density (A·m−2) | ε | volume fraction |
| i0 | exchange current density (A·m−2) | η | efficiency of the heating system |
| j | local reaction current density (A·m−2) | ηs | reaction overpotential (V) |
| k | reaction rate constant (m·s−1) | λ | thermal conductivity (W·m−1·K−1) |
| L | total length of battery (m) | ν+ | stoichiometric number |
| Leq | equivalent inductor (H) | ρ | density (mol·m−3) |
| Lneg | length of negative electrode (m) | ρcoil | copper coil resistivity (Ω·m) |
| Lpos | length of positive electrode (m) | σ | electrical conductivity (S·m−1) |
| Lsep | length of separator (m) | Φ | potential (V) |
| l | length of the copper coil (m) | φ | magnetic flow (Wb) |
| N | turns of the copper coil | ψ | temperature-sensitive coefficient |
| Pbatt | the active power transmitted to the battery (W) | ω | angular velocity (rad·s−1) |
| Ptotal | the total active power transmitted to the copper coil (W) | Subscript/superscript | |
| Qact | polarization heat (J) | e | liquid phase |
| Qbatt | the heat produced by electrochemical reactions (J) | eff | effective value |
| Qmag | electromagnetic induction heat (J) | m | amplitude |
| Qohm | ohmic heat (J) | max | maximum value |
| Qrea | reaction heat (J) | ref | reference value |
| Qtotal | total heat (J) | s | solid phase |
| R | gas constant (j·mol−1·K−1) | surf | surface |
| Rbatt | battery resistance (Ω) | 1 | electrode |
| Rcoil | copper coil resistance (Ω) | 2 | electrolyte |
References
- Wu, S.; Xiong, R.; Li, H.; Nian, V.; Ma, S. The state of the art on preheating lithium-ion batteries in cold weather. J. Energy Storage 2020, 27, 101059.1–101059.13. [Google Scholar] [CrossRef]
- Chen, Q.; Zheng, B. Development concept of new energy vehicle based on innovative thinking. Strateg. Study CAE 2019, 21, 70–75. [Google Scholar] [CrossRef]
- Xiong, R.; Cao, J.; Yu, Q.; He, H.; Sun, F. Critical review on the battery state of charge estimation methods for electric vehicles. IEEE Access 2018, 6, 1832–1843. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, K.; Jow, T. Electrochemical impedance study on the low temperature of Li-ion batteries. Electrochim. Acta 2003, 49, 1057–1061. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, K.; Jow, T. The low temperature performance of Li-ion batteries. J. Power Sources 2003, 115, 137–140. [Google Scholar] [CrossRef]
- Senyshyn, A.; Mühlbauer, M.; Dolotko, O.; Ehrenberg, H. Low-temperature performance of Li-ion batteries: The behavior of lithiated graphite. J. Power Sources 2015, 282, 235–240. [Google Scholar] [CrossRef]
- Ren, D.; Kandler, S.; Guo, D.; Han, X.; Feng, X.; Lu, L.; Ouyang, M.; Li, J. Investigation of lithium plating-stripping process in Li-Ion batteries at low temperature using an electrochemical model. J. Electrochem. Soc. 2018, 165, A2167–A2178. [Google Scholar] [CrossRef]
- Chen, Y.; Dou, X.; Wang, K.; Han, Y. Lithium dendrites inhibition via diffusion enhancement. Adv. Energy Mater. 2019, 9, 1900019.1–1900019.7. [Google Scholar] [CrossRef]
- Zhang, J.; Ge, H.; Li, Z.; Ding, Z. Internal heating of lithium-ion batteries using alternating current based on the heat generation model in frequency domain. J. Power Sources 2015, 273, 1030–1037. [Google Scholar] [CrossRef]
- Saw, L.; Ye, Y.; Tay, A. Electro-thermal analysis and integration issues of lithium ion battery for electric vehicles. Appl. Energy 2014, 131, 97–107. [Google Scholar] [CrossRef]
- Ruan, H.; Jiang, J.; Sun, B.; Zhang, W.; Gao, W.; Wang, L.; Ma, Z. A rapid low-temperature internal heating strategy with optimal frequency based on constant polarization voltage for lithium-ion batteries. Appl. Energy 2016, 177, 771–782. [Google Scholar] [CrossRef]
- Jiang, J.; Ruan, H.; Sun, B.; Zhang, W.; Gao, W.; Wang, L.; Zhang, L. A reduced low-temperature electro-thermal coupled model for lithium-ion batteries. Appl. Energy 2016, 177, 804–816. [Google Scholar] [CrossRef]
- Kuang, K.; Sun, Y.; Ren, D.; Han, X.; Zheng, Y.; Geng, Z. Efficient approach for electrochemical-thermal coupled modeling of large-format lithium-ion power battery. J. Mech. Eng. 2021, 57, 10–22. [Google Scholar]
- Xu, L.; Deng, Z.; Xie, Y.; Hu, X. Comparative study of electrochemical-thermal models for Li-ion batteries. J. Mech. Eng. 2022, 58, 304–320. [Google Scholar]
- Doyle, M.; Fuller, T.; Newman, J. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Newman, J.; Thomas-Alyea, K. Electrochemical Systems, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004; pp. 517–558. [Google Scholar]
- Xiong, R.; Ma, S.; Chen, Z.; Sun, F. Electrochemical thermal coupling characteristics and modeling for lithium-ion battery operating with extremely self-fast heating. J. Mech. Eng. 2021, 57, 179–189. [Google Scholar]
- Yang, X.; Zhang, G.; Wang, C. Computational design and refinement of self-heating lithium ion batteries. J. Power Sources 2016, 328, 203–211. [Google Scholar] [CrossRef]
- Yaakov, D.; Gofer, Y.; Aurbach, D.; Halalay, I. On the study of electrolyte solutions for Li-Ion batteries that can work over a wide temperature range. J. Electrochem. Soc. 2010, 157, A1383–A1391. [Google Scholar] [CrossRef]
- Zhang, M.; Lei, X.; Lv, Y.; Liu, X.; Ding, Y. Reversible low temperature Li-Storage in liquid metal based anodes via a co-solvent strategy. Chin. J. Chem. 2021, 39, 2801–2807. [Google Scholar] [CrossRef]
- Lei, Z.; Zhang, C.; Lei, X.; Li, J. Study on heating method of lithium-ion battery used in electric vehicle. J. Power Supply 2016, 14, 102–108. [Google Scholar]
- Stuart, T.; Hande, A. HEV battery heating using AC currents. J. Power Sources 2004, 129, 368–378. [Google Scholar] [CrossRef]
- Chen, Z.; Xiong, R.; Li, S.; Zhang, B. Extremely fast heating method of the lithium-ion battery at cold climate for electric vehicle. J. Mech. Eng. 2021, 57, 113–120. [Google Scholar]
- Wang, F.; Zhang, J.; Wang, L. Design of electric air-heated box for batteries in electric vehicles. Chin. J. Power Sources 2013, 37, 1184–1187. [Google Scholar]
- Li, G.; Huang, X.; Fu, X.; Yang, Y. Design research on battery heating and preservation system based on liquid cooling mode. J. Hunan Univ. (Nat. Sci.) 2017, 44, 26–33. [Google Scholar]
- Teng, H.; Ma, Y.; Yeow, K.; Thelliez, M. An analysis of a lithium-ion battery system with indirect air cooling and warm-up. SAE Int. J. Passeng. Cars Mech. Syst. 2011, 4, 1343–1357. [Google Scholar] [CrossRef]
- Laurenzi, S.; Casini, A.; Pocci, D. Design and fabrication of a helicopter unitized structure using resin transfer moulding. Compos. Part A Appl. Sci. Manuf. 2014, 67, 221–232. [Google Scholar] [CrossRef]
- Lin, C.; Xu, S.; Chang, G.; Liu, J. Experiment and simulation of a LiFePO4 battery pack with a passive thermal management system using composite phase change material and graphite sheets. J. Power Sources 2015, 275, 742–749. [Google Scholar] [CrossRef]
- Salameh, Z.; Alaoui, C. Modeling and simulation of a thermal management system for electric vehicles. In Proceedings of the 29th Annual Conference of the IEEE Industrial Electronics Society, Roanoke, VA, USA, 2–6 November 2003. [Google Scholar]
- Alaoui, C.; Salameh, Z. A novel thermal management for electric and hybrid vehicles. IEEE Trans. Veh. Technol. 2005, 54, 468–476. [Google Scholar] [CrossRef]
- Lei, Z.; Zhang, C.; Dong, Y.; Lin, Z. Low-temperature performance and heating method of lithium battery in electric vehicles. J. Beijing Univ. Technol. 2013, 39, 1399–1404. [Google Scholar]
- Zhang, C.; Lei, Z.; Dong, Y. Method of heating low-temperature lithium battery in electric vehicle. Trans. Beijing Inst. Technol. 2012, 32, 921–925. [Google Scholar]
- Guo, S.; Xiong, R.; Wang, K.; Sun, F. A novel echelon internal heating strategy of cold batteries for all-climate electric vehicles application. Appl. Energy 2018, 219, 256–263. [Google Scholar] [CrossRef]
- Waag, W.; Kbitz, S.; Sauer, D. Experimental investigation of the lithium-ion battery impedance characteristic at various conditions and aging states and its influence on the application. Appl. Energy 2013, 102, 885–897. [Google Scholar] [CrossRef]
- Wang, T.; Tseng, K.; Zhao, J.; Wei, Z. Thermal investigation of lithium-ion battery module with different cell arrangement structures and forced air-cooling strategies. Appl. Energy 2014, 134, 229–238. [Google Scholar] [CrossRef]
- Pesaran, A.; Vlahinos, A.; Stuart, T. Cooling and preheating of batteries in hybrid electric vehicles. In Proceedings of the 6th ASME-JSME Thermal Engineering Joint Conference, Kohala Coast, HI, USA, 16–20 March 2003. [Google Scholar]
- Wang, C.; Zhang, G.; Ge, S.; Xu, T.; Ji, Y.; Yang, X.; Leng, Y. Lithium-ion battery structure that self-heats at low temperatures. Nature 2016, 529, 515–518. [Google Scholar] [CrossRef] [PubMed]
- Xiong, R.; Wang, K.; Guo, S. Hybrid preheating method for lithium-ion battery used in cold environment. J. Mech. Eng. 2019, 55, 53–59. [Google Scholar]
- Fang, Z.; Gong, Z.; Li, Y.; Yao, Y. Simulation and experiment of electromagnetic induction heating system based on ANSYS. Exp. Technol. Manag. 2021, 38, 129–133. [Google Scholar]




| LiB Material/Specification | Value |
|---|---|
| Positive electrode material | NCA (LiNi0.8Co0.15Al0.05O2) |
| Negative electrode material | Graphite |
| Electrolyte material | LiPF6 in 3:7 EC:EMC |
| Shell material | Steel AISI 4340 |
| Connector material | Steel AISI 4340 |
| Mandrel material | Nylon |
| Nominal capacity | 3.0 Ah |
| Nominal voltage | 3.7 V |
| Charging cutoff voltage | 4.2 V |
| Discharging cutoff voltage | 3.0 V |
| Height/diameter | 65/18 mm |
| Mass | 48.0 g |
| Specific heat capacity | 1.72 J·g−1·K−1 |
| Symbol | Unit | Description | Value | |||
|---|---|---|---|---|---|---|
| Constant | ||||||
| F | C·mol−1 | Faraday’s constant | 96,485.33 | |||
| R | J·mol−1·K−1 | Gas constant | 8.3145 | |||
| Induction coil parameters | ||||||
| IA | A | Excitation current amplitude | 8 | |||
| f | Hz | Excitation current frequency | 50 | |||
| N | 1 | Turns | 201 | |||
| Scoil | m2 | Cross-sectional area | 1 × 10−6 | |||
| εr | 1 | Relative dielectric constant | 1 | |||
| μr | 1 | Relative magnetic conductivity | 1 | |||
| σcoil | S·m−1 | Electrical conductivity | 5.998 × 107 | |||
| Electrochemical parameters | Negative electrode | Separator | Positive electrode | |||
| as | m−1 | Specific superficial area | 3 εs/Rs | 3 εs/Rs | ||
| Cs,max | mol·m−3 | Maximum Li+ concentration | 31,507 | 48,000 | ||
| De | m2·s−1 | Liquid-phase diffusivity | ||||
| Deeff | m2·s−1 | Liquid-phase effective diffusivity | εe1.5De | εe1.5De | εe1.5De | |
| Ds | m2·s−1 | Solid-phase diffusivity | 1.5 × 10−15 | |||
| dU/dT | V·K−1 | Entropy heat coefficient | Built-in COMSOL | Built-in COMSOL | ||
| k | m·s−1 | Reaction rate constant | ||||
| L | m | Length | 55 × 10−6 | 30 × 10−6 | 55 × 10−6 | |
| RSEI | Ω | SEI film resistance | 0.001 | |||
| Rs | m | Radius of the particles | 2 × 10−6 | 2 × 10−6 | ||
| t+0 | 1 | Li+ transference number | 1 | |||
| αa, αc | 1 | Charge transfer coefficient | 0.5 | 0.5 | ||
| εe | 1 | Liquid-phase volume fraction | 0.444 | 0.37 | 0.41 | |
| εs | 1 | Solid-phase volume fraction | 0.384 | 0.43 | ||
| ν+ | 1 | Li+ stoichiometric number | 1 | 1 | ||
| σe | S·m−1 | Liquid-phase electrical conductivity | ||||
| σeeff | S·m−1 | Liquid-phase effective electrical conductivity | εe1.5σe | εe1.5σe | εe1.5σe | |
| σs | S·m−1 | Solid-phase electrical conductivity | 100 | 91 | ||
| σseff | S·m−1 | Solid-phase effective electrical conductivity | εs1.5σs | εs1.5σs | ||
| Thermal parameters | Shell | Active material | Mandrel | Connector | ||
| Cp | J·Kg−1·K−1 | Heat capacity at constant pressure | 475 | 1399.1 | 1700 | 475 |
| h | W·m−2·K−1 | Surface heat transfer coefficient | 20 | |||
| λ | W·m−1·K−1 | Thermal conductivity | 44.5 | 0.9 (for radial direction) 42 (for axial direction) | 0.26 | 44.5 |
| ρ | Kg·m−3 | Density | 7850 | 2055.2 | 1150 | 7850 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Yan, M. Research on the Improvement of Lithium-Ion Battery Performance at Low Temperatures Based on Electromagnetic Induction Heating Technology. Energies 2023, 16, 7780. https://doi.org/10.3390/en16237780
Wang B, Yan M. Research on the Improvement of Lithium-Ion Battery Performance at Low Temperatures Based on Electromagnetic Induction Heating Technology. Energies. 2023; 16(23):7780. https://doi.org/10.3390/en16237780
Chicago/Turabian StyleWang, Borui, and Mingyin Yan. 2023. "Research on the Improvement of Lithium-Ion Battery Performance at Low Temperatures Based on Electromagnetic Induction Heating Technology" Energies 16, no. 23: 7780. https://doi.org/10.3390/en16237780
APA StyleWang, B., & Yan, M. (2023). Research on the Improvement of Lithium-Ion Battery Performance at Low Temperatures Based on Electromagnetic Induction Heating Technology. Energies, 16(23), 7780. https://doi.org/10.3390/en16237780





