Abstract
In the current framework of energy transition, renewable energy production has gained a renewed relevance. A set of 75 papers was selected from the existing literature and critically analyzed to understand the main inputs and tools used to calculate solar energy and derive theoretical photovoltaic production based on geographic information systems (GISs). A heterogeneous scenario for solar energy estimation emerged from the analysis, with a prevalence of 2.5D tools—mainly ArcGIS and QGIS—whose calculation is refined chiefly by inputting weather data from databases. On the other hand, despite some minor changes, the formula for calculating the photovoltaic potential is widely acknowledged and includes solar energy, exploitable surface, performance ratio, and panel efficiency. While sectorial studies—targeting a specific component of the calculation—are sound, the comprehensive ones are generally problematic due to excessive simplification of some parts. Moreover, validation is often lacking or, when present, only partial. The research on the topic is in constant evolution, increasingly moving towards purely 3D models and refining the estimation to include the time component—both in terms of life cycle and variations between days and seasons.
1. Introduction
In the current framework of energy transition, two concepts drafted at the European level have acquired relevance, i.e., Renewable Energy Communities and the Nearly Zero Energy Building. A common element of the two is the renewed attention given to renewable energy sources to meet—at least partially—energy needs.
The fit for 55 package [1]—aiming to bring the European Union in line with its decarbonization objectives by 2050—implied the revision of two key directives on energy matters, which are the Energy Performance of Buildings Directive and the Renewable Energy Directive. The proposal for the revision of the former [2] requires minimum performance requirements to be met in a twofold way. On the one hand, the building stock must be renovated according to the energy class, currently reported by the Energy Performance Certificates—carried out for a single building or building unit—but potentially estimated through alternative methodologies, as proposed in Deng et al. [3] or Anselmo et al. [4]. On the other hand, the share of energy produced from Renewable Energy Sources, which are the focus of the revised version of the Renewable Energy Directive [5], must be increased. Indeed, as claimed by Corgnati and Cattaneo [6], it is crucial that actions for the reduction of the energy demand are coupled with a coverage of the energy needs through renewable sources to meet the decarbonization goals set at the international level by both the European Union and the United Nations.
The Renewable Energy Directive also promoted the creation of Renewable Energy Communities, defined by Roberts as “collective cooperation[s] of an energy related activity around specific ownership, governance and a non-commercial purpose” [7]. These entities are meant to self-produce part of their energy needs and therefore require a dedicated study to assess their feasibility. In this framework, photovoltaic potential has generated specific interest, since PV panels are widely recognized as one of the most suitable renewable sources for urbanized areas thanks to the possibility of integrating them within roofs, as testified by worldwide data showing a rapid increase of installed capacity [8].
A particular commitment by the European Union to solar energy—especially integrated within roofs—is represented by the EU solar energy strategy [9], part of the REPowerEU plan. It targets an installed capacity of 320 GW of PV production by 2023 and 600 GW by 2030. It is articulated in three principal initiatives:
- The European Solar Rooftops Initiative, promoting—and possibly setting requirements for—a growing installation of PV panels;
- A large-scale skills partnership, developing an expert workforce in the sector;
- An industry alliance, a forum of stakeholders that aims to maximize investment opportunities and diversify the supply chain.
Especially considering the first point, studies determining the most productive pitches are required. In this way, the path towards decarbonization would be sped up, ensuring that the potential is exploited as much as possible.
In this framework, Geographic Information Systems (GISs) are powerful tools for extensive modelling of solar potential, thanks to the possibility of integrating multiple geospatial data in complex analyses. GISs model entities—or objects—as made up of geometrical, alphanumerical, and relational components, allowing spatial analyses. These can be acquired for the scope of the research or gathered from public repositories and online geoportals or Volunteered Geographic Information–based websites such as OpenStreetMap. Archives are translated into GeoDataBases, storing data with the maximum accuracy possible, differently from traditional maps whose geographic information is subject to generalization and graphical errors [10]. The different data structures—further detailed in Section 4.1—can be processed to return multiple layers. The PV production layer, as specified in studies such as the ones cited in this review, can provide key information for Urban Energy Digital Twins, 3D platforms for the visualization and sharing of geodata. Digital Twins are virtual replicas of a physical object or system, allowing the simulation of the behavior of the object alone and in its environment for its whole lifecycle [11]. In this case, a Digital Twin makes it possible to identify the most productive pitches and simulate the productivity in different conditions.
2. Research Outline and Methodology
This study consists of a review of the use of three-dimensional GISs for the definition of the photovoltaic potential. The scientific literature to support the analysis was accessed through Scopus, an abstract and citation database curated by Elsevier, which lists papers from journals and conference proceedings from a wide set of disciplines. At first, the concepts “3D GIS” and “photovoltaic” were used as keywords. However, after having analyzed this first set of publications, it was chosen to also include the articles with “3D GIS” and “solar radiation” or “solar potential”, because of the relevance this aspect—the one with the highest variability according to different simulations—has in the definition of the photovoltaic potential. The query—limiting the language to English only—returned a total of 125 papers. After the selection process, which excluded non-accessible and non-relevant papers, 75 of them were kept—equal to 60%—as shown in Table 1. The analysis was based on a set of parameters concerning the whole estimation process, from the required inputs to the scale of the analysis. Specific aspects—tackled only by a subset of the sample—were also deepened.

Table 1.
List of papers considered in this study.
Figure 1 reports the publication timeline, dividing the articles according to the keywords. With 3D GIS as the enabling technology—being therefore a keyword of all the research—the recurrence of the other keywords—namely photovoltaic (PV), solar radiation (SR), both (PV+SR), or solar potential (SP)—provides insights into the interest in the topic within the scientific community. It can be observed that the first articles were published in the early 2010s, a period characterized by different trends in Europe and worldwide. As described by IRENA [8], the installed solar capacity in Europe had a sharp increase from 2009 to 2012, followed by a stabilization that continued until 2019. On the other hand, photovoltaic production in Asia boomed from 2012 onward. Oceania and the Americas never had a boom in production values but only slight increases from 2011 onward. In this framework, there were several reasons for increased interest in the assessment of photovoltaic potential for both policymakers and industries. In Asia, it was necessary to conduct feasibility studies and analyses of the localization of photovoltaic panels to maximize the production, while in Europe similar research was required to rationalize the new installations. Indeed, several policies at international and national scales—such as the five Conti Energia (energy bills) in Italy, introduced in the Italian legislation with a Legislative Decree [87] following the European Directive [88]—were pushing the introduction of photovoltaic technologies across Europe, leading to alterations in the market. The subsidies favoring panel installations led to systems that did not receive enough solar energy to minimize the payback time and thus ensure profitability. A sharp increase in the publications per year was followed by a two-year plateau—2016 and 2017—and another increase in recent years, especially in 2020 and 2022, with the trend likely to be confirmed in 2023 as well.
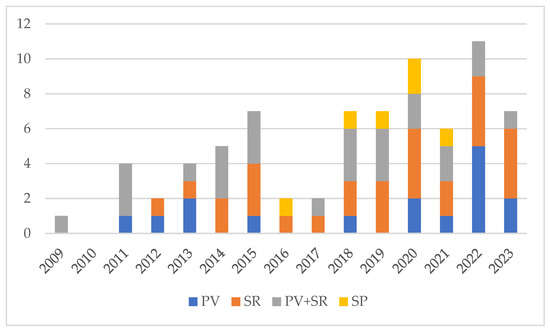
Figure 1.
Publications per year, divided by topic.
Such widespread interest in PV is demonstrated by the countries in which the 69 studies were carried out. Indeed, Figure 2—plotting the spatial distribution of the analyzed papers—shows that despite the presence of several papers originating from Europe, the test studies are widespread across the world. Most of the case studies—35—are in Europe, followed by Asia, with 24. The two areas make up 85% of the total. However, considering countries instead of continents, the USA is the country with the third highest number of papers, after Italy and China. With further disaggregation, three of these studies (43%), namely [28,44,78], were carried out in Pennsylvania.
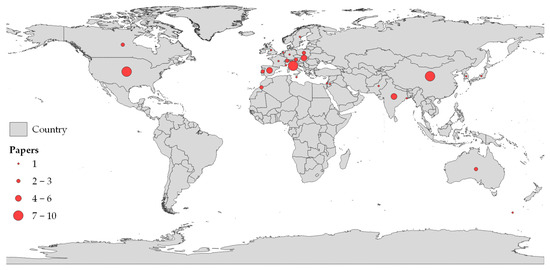
Figure 2.
Spatial distribution of analyzed papers.
As for the type of paper, there is a clear prevalence of journal articles—52—over the conference proceedings, as shown in Figure 3. The conferences where most studies on the topic were presented belong to the International Society of Photogrammetry and Remote Sensing, oriented toward the advancements in Geomatics. On the contrary, there is a clear prevalence of energy-oriented journals compared to ones concerning remote sensing. In particular, seven papers [19,28,30,35,41,48,57] were published on Solar Energy and four [37,49,50,71] on Energies.
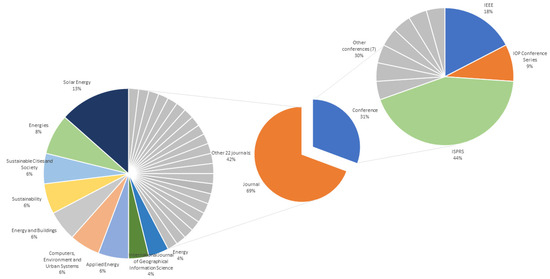
Figure 3.
Conferences and journals of the selected papers.
A total of 257 authors contributed to the works included in this research, with 49 of them recurring at least twice. The most frequent author is Shuhua Zhang, currently at Xi’an University of Science and Technology (China). His name appears in seven studies, with one study citing him as the first author. Shuyi Li (Nanjing University) and Yongjun Sun (City University of Hong Kong) appear six and five times. They are most commonly last authors—generally recognized as project supervisors—three times each. Jianming Liang, from the Institute of Remote Sensing and Digital Earth of Beijing (China), is the first author—the one with the highest contribution to the research—in all of the four publications to which he contributed.
3. Results: Framework of the Studies
3.1. Scope
The first relevant aspect to be tackled is the scope of the work. The photovoltaic potential and the solar radiation are not only interesting per se but also considering other applications they could have when integrated with other datasets. Nevertheless, based on the specificity of the query, it is not surprising that most papers are focused on photovoltaic potential—22—and solar radiation—31. The other three thematic groups of the papers—according to which this section is structured—are shown in Figure 4.
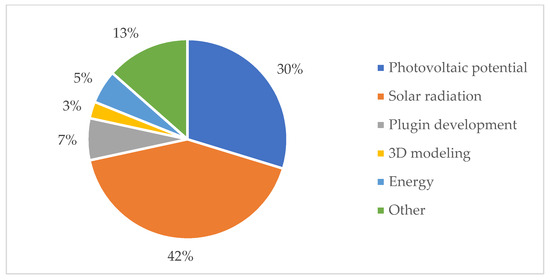
Figure 4.
Classification of papers based on the scope.
The photovoltaic potential is mostly analyzed in terms of produced energy, with one case in which Mutani et al. [73] related the PV production to its costs, thus assessing the economic feasibility of a wide-scale installation of panels on bus stops and optimizing the system accordingly. Similar research was described in [39], which gives specific attention to public incentives to quantify the financial requirements for economically sustainable PV production.
However, an element to be highlighted emerged in the contrast between the two queries. Some articles, such as [21,35], claim in the title and abstract to have photovoltaic energy as the research objective but stop at the calculation of solar radiation. In this case, PV is the framework to contextualize the research, making the relevance of the topic explicit, but it may lead to misunderstandings. The same applies to other studies in the opposite situation, e.g., [17,26,74,81]. These papers limit their application to solar energy—in two cases adding the term “potential”—in the title and abstract, despite the fact that they also include the calculation of the photovoltaic potential. For the proper dissemination of the research, this emerges as an extremely critical element, requiring scholars to widen the research in order to collect all the pertinent information.
Given the interest generated about the topic, some authors proposed the development of tools to calculate solar radiation or coded new plugins for GISs. Liang et al. [56] extended r.sun—a processing tool of GRASS GIS integrated into QGIS (for a better understanding, see Section 4.3)—to three-dimensional models, implementing a tool to be used to evaluate the solar energy received not only by the roofs, as with traditional methods, but also the facades. SURFSUN3D, whose implementation is reported in [54], was realized by the same authors 5 years later, perfecting the previous study. Also, SOLIS, developed by Kazak and Świąder [50], is an integration of existing tools—in this case, the ones included in ArcGIS—that returns the radiation divided by roof. Another study [64] implemented a deep learning algorithm to estimate solar radiation starting from imagery and an Energy Plus Weather dataset. Finally, Pružinec and Ďuračiová [71] describe the realization of a point cloud solar radiation tool, which uses the ESRA model to calculate solar radiation by aggregating points into a voxel. From these tools, it is evident that there is a multiplicity of inputs that can be used to calculate solar energy, an aspect that is further addressed in the following paragraphs.
The previous paragraphs highlight the introduction of the vertical component in the estimation of solar radiation with GIS. For this, it is crucial to have a reliable 3D model. Hippenstiel et al. [44] studied the accuracy of a 3D model realized from LiDAR data, while [27] concerns 3D modeling starting from a DSM and structure using motion. In both cases, solar radiation estimation is used to evaluate the model, given the complexity it entails. In particular, the second study compares the outcomes of the solar radiation when using a validation DSM and the 3D model created during the research: the maximum discrepancy is 0.32%, with most cases not above 0.1%. Similarly, Beltran-Velamazan et al. [18] studied how to produce an accurate 3D model—to be reconverted in a DSM for solar processing—and the discrepancies between alternative techniques and datasets.
A group of papers is more related to energetic aspects, specifying some of the aspects that contribute to a comprehensive study of photovoltaic potential. Fijałkowska et al. [37] consider the impacts of shadows on the panel producibility, focusing on energy losses, while de Vries et al. [30] assess the energy yield by comparing alternative algorithms and defining a coefficient to increase the accuracy of high-precision evaluations. Energy aspects are also tackled when comparing the producible energy to the consumption, as in [69]. Thermal demand and retrofitting benefits are assessed together with the PV potential in [4], thus targeting the definition of a comprehensive energy model able to orient future energy policies. An energy model was produced also in [46,76], which have a specific focus on the capability of the CityGML data structure to integrate energy aspects. The former simply returns the energy balance between production and consumption, while the latter aims to define a comprehensive repository of energy-related data, grouped in geometric and non-geometric parameters.
In contrast, there is an extremely specific paper [51] tackling a single aspect of the calculation of PV producibility. By addressing the disturbances, it quantifies the exploitable surface to be used in the equations. It considers the shadowing factor, the tilt, and the type of covering to define correction factors to move from the whole roof surface to the actual area that can be considered for the installation of photovoltaic panels.
Finally, some works include the calculation of the solar energy or the PV potential as instrumental for research not related to energy production. The following are examples of this:
- Helbich et al. [43], looking for a correlation between the potential energy production and the housing market through the hedonic prices method;
- Hofierka [45], using solar energy predictions to correct land surface temperature estimations;
- Sun et al. [79], adopting solar radiation as one of the factors influencing the choice of adequate points to install a wireless sensor network;
- Palliwal et al. [66], requiring the quantification of solar energy to define the feasibility of urban farming in Singapore;
- Peng et al. [68], analyzing Urban Heat Islands and thus requiring solar energy as one of the parameters to predict the incidence of this phenomenon.
3.2. Scale of Analysis
The assessment of the photovoltaic potential can be conducted on different scales, according to the final purpose of the study. Figure 5 plots a classification of the selected papers based on the analyzed scale. A GIS is generally used for larger-scale analyses, making it different from Building Information Modeling, which is specifically designed for building scale. Moreover, raster datasets enable better visualization of extremely variable phenomena, thanks to the continuity of the data and the homogeneous level of detail, with the Ground Sampling Distance reaching values of a few centimeters.
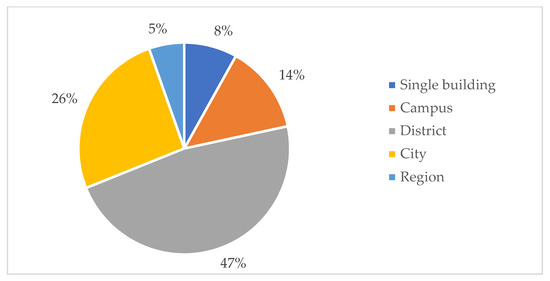
Figure 5.
Classification of papers based on the analyzed scale.
Three of the analyzed studies [16,52,76] focused on single buildings, with two others [37,73] assessing public transport stops. While the attention was focused on single elements, the surrounding context was crucial. Indeed, when considering bus stops—at comparatively low height levels in an urban setting—particular attention was paid to the shadowing effect of buildings nearby, resulting in relevant constraints for PV production.
As mentioned previously, one of the possible uses of these studies is to identify the most suitable pitches and slopes for the installation of photovoltaic panels. This is especially relevant when looking at groups of buildings; the impact that each building has on the others is taken into account—at this scale, other elements of disturbance, such as trees, can be included in the model—together with slope and orientation in order to define, among a restricted set of alternatives, the most profitable. In this group, all the papers considering this scale [25,27,28,32,49,59,72,74,77,82] focused on a university campus. However, the number of buildings in this category of papers ranges from two and three in [49,72], respectively, to tens in [32]. This results in heterogeneous processing methods, with some studies being more similar to single-building studies and others closer to district-scale analyses. In all cases, the possibility to work on a campus makes it possible to have a controlled environment—without requiring the support of external bodies such as public institutions—and potentially to validate the results with devices whose installation does not require additional authorizations.
The most prominent group of papers—47%—belongs to studies conducted on a district scale. In this study, districts are defined as aggregations of buildings covering more than two blocks but not identifiable as a whole city nor controlled by the same body (such as university campuses). Still, it is to be recognized that a district can be very small or can be comparable to a small city. The former is the case of [17], whose square study areas have borders of 500 m only; in contrast, [53] takes into account a large part of Boston consisting of more than 22,000 buildings.
Another set of articles concerned studies conducted on a city scale. This is the most relevant for policymakers, who use this kind of research to identify the most suitable areas for the installation of photovoltaic panels on public land and buildings. Moreover, based on the current attention towards Positive Energy Districts and Renewable Energy Communities—whose creation is supported at the European level—it is crucial to define the most productive areas in order to identify where self-production would be sufficient to meet the entire energy demand. Despite the definition of city being agreed upon, in this context, some differences may emerge too, with Shanghai—whose population is more than 26 million—and Turin—with less than 1 million inhabitants—as case studies of [62,83], respectively.
A multi-scale approach is used by Aleksandrowicz et al. [15], starting their analyses from a pilot study area and extending it to the whole city of Tel Aviv. This explores the possibility to assess the methodology on a relatively small sample—to validate it more easily—and scale it up immediately to display its applicability.
Finally, a limited number of studies focused on larger scales. This is the case of [79], in which solar radiation is used to determine the most prominent nodes for installing wireless sensors in a whole forest. In three papers, namely [31,68,85], a whole region is taken into account. In this case, the heterogeneity is given not only by the different surfaces but also by the land use. Indeed, while districts and cities have an intrinsic urban character, despite minor differences in terms of form and morphology, regions can differ based on urban or rural characteristics. In particular, the three papers considered the Canton of Geneva (Switzerland), consisting of 300 km2 with a central urban area—Geneva city—and rural surroundings; Kowloon Peninsula (Hong Kong), a 160 km2 fully urbanized area with one of the highest population densities in the world; and the Tizinafu watershed (China), an arid mountain region with a negligible population.
3.3. Relationships between Scope and Scale
By comparing the different findings of this chapter—as shown in Table 2—it is possible to highlight some major elements. First, there is not a category for which all scales were covered, nor a scale on which the studies of all categories were conducted.

Table 2.
Papers divided according to scale and scope.
On average, there are 2.43 papers per cell, or 4.06 when excluding the zero values. As described in previous chapters, most papers—55% of the total—are conducted on a district or city scale and concern solar radiation or photovoltaic potential. In particular, solar radiation studies on a district scale are the most numerous—16.
It is then possible to read Table 2 by rows and columns, which are categories and scales, respectively. Looking at how studies of the same category are distributed on different scales, it emerges that 80% of the studies on plugin developments are carried out at a district scale. From this emerges the need to test the proposed methodology on a sufficiently wide and heterogeneous scale while at the same time keeping the process as compact as possible for efficiency. Once the developed tool passes the research phase, it would be possible to scale up the prototype. For both photovoltaic potential and solar radiation, around 20% of studies are conducted on single buildings or campuses, while district-scale analyses are the most recurrent (41% and 52%, respectively). From this, it emerges that, despite the use of validated methodologies, the need for high-consuming technologies—in terms of both computing power and required time—results in the scholars orienting their research toward medium scales.
Observing instead the incidence of the different scopes inside the same scale of analysis, it emerges that for all scales except for single buildings, photovoltaic potential and solar radiation are the most recurring topics, totaling, on average, 75% of studies. As mentioned, an exception is represented by the building scale, for which energy-related papers account for 33% of the total. Energy studies are especially relevant on this scale—with half of the research concerning single buildings—because of the need to deepen technical parameters, reducing the use of archetypes for estimating the aspects under investigation.
4. Results: Solar Energy Calculation
As mentioned, one of the most prominent aspects to be considered when calculating the photovoltaic potential is solar radiation. GIS-based calculations for the estimation of the incident solar energy are multiple and can be classified according to two main parameters, i.e., the required geographic dataset to be used as input—according to which they can be divided into purely three-dimensional or 2.5D methods—and the tool used for the estimation of solar radiation. Moreover, the latter requires in most cases the setting of specific parameters involving the average weather conditions, thus representing a further aspect to be explored.
4.1. Geographical Input
A GIS-based solar radiation estimation tool requires the input of a geographical dataset to establish a direct connection between the geographical location and the calculated solar energy received. In GIS software, two data structures can be used, i.e., vector and raster. The former is object-based, using the geometrical primitives to describe the spatial component and a table to report the known characteristics of each entity; the latter is field-based and represents surfaces as divided into regular tiles. A specific kind of raster is the Digital Surface Model (DSM), which describes the morphology of the observed area by reporting the height of the surfaces of both terrain and emerging objects (buildings, trees, etc.). DSMs are referred to as 2.5D because they include the vertical component—thus allowing the three-dimensional reconstruction—in a bidimensional representation. 3D models—known as city models—are vector representations in which polygons are not only planar but variously oriented in the space, potentially representing a solid when topological relationships between them allow the identification of a closed boundary.
Fifty-seven of the analyzed papers are based either on 3D models or DSMs. In particular, 27 used 3D models as input, and 30 used DSM. From this division—plotted in Figure 6—an aspect of the original query emerges. In the field, 2.5D analyses are widely recognized as included in the three-dimensional category, not considering only vectorial representations.
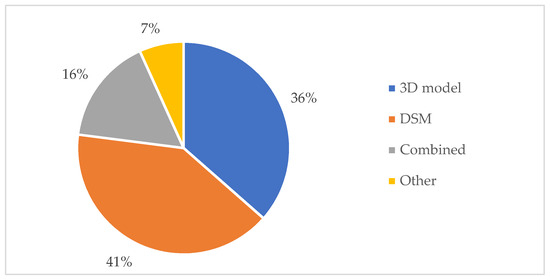
Figure 6.
Classification of papers based on the geographical input.
In most cases, it is not mentioned how the city model was realized. Nevertheless, in three cases it is made explicit. Yan et al. [83] modelled the urban environment with a deep learning network that correlates high-resolution pictures for the segmentation and three-dimensional reconstruction of roofs where PV panels could be installed. The picture correlation process, used to create the city model, collimates homologous points—observable in two or more pictures—to create a point cloud, with which the actual model is created. LiDAR point clouds remove a step of the process—the collimation—thus simplifying the model production. Point clouds of this kind were used in [23,63], which keep the process hidden and do not make the workflow for the model production explicit. Nevertheless, two main methods can be used, i.e., feature extraction and machine learning. The former is based on radiometric information, and the latter takes advantage of recent evolutions in IT.
In twelve cases, LiDAR point clouds were also used for the creation of the DSM. However, it is particularly interesting to note that in [57] there is a combined use of LiDAR-derived DSM and fully 3D objects; the DSM is first used to calculate the shadows, with the output further enriched by the processing of the three-dimensional objects. In contrast, Bremer et al. [23] divided the shadowing objects into buildings and trees, using the DSM for the former and a 3D model for the latter. Other combinations of LiDAR-based DSMs and 3D models are reported in [37,72]. The former—like the previously mentioned study—cast the shadows through the city model, while the latter used the 3D model values to calibrate the algorithm to be later implemented.
Another combined application of 2.5D and 3D, with the source of the first not being explicated, is reported in [56], where the DSM is used to produce the solar radiation map, later draped on the 3D model through correction algorithms. In [41], the 3D model is used to derive a DSM for the solar energy analysis. Liang et al. [54] presented a merger between the two methodologies: the plugin developed in this study converts the 3D model into a DSM to be used for calculating solar radiation, then moves back to the three-dimensional representation by draping the results on the original model.
Just as in city models, DSMs can be produced from imagery through collimation. This is the case in [40], whose DSM was realized by LMKR (a Pakistan company) from stereo paired satellite imagery, and [42], whose pictures were acquired with a UAV. Both Teofilo et al. [81] and Achbab et al. [12] mention their use of stereo imagery for the realization of the products for the calculations, but they do not describe whether the dataset was acquired using a plane or from a satellite. The former explains that images were taken from world imagery in ArcGIS Pro, whose support describes the dataset as composed of mixed acquisitions. Other DSMs were produced by extruding bidimensional vectors, as in Eldesoky et al. [34].
Some papers considered alternative inputs for their calculation, especially when developing procedures alternative to the standard GIS tools—mostly depending on DSMs. This is the case of DeepRadiation [64], which processes 360° panoramic pictures for the punctual estimation of solar radiation. This implies the possibility of working with both acquired pictures and Google Street View imagery. The study in [59] is specifically focused on mobile-acquired pictures. A RedMi 3S prime camera was calibrated through MATLAB, and its pictures are processed by segmenting the content into sky and non-sky zones, thus creating masks to compute the shadowing.
Inputs can be evaluated in terms of spatial resolution. About half of the studies—32—made the resolution explicit, with approximately one-third having a value of 0.5 m, as in [29,80]. While in five cases the resolution is higher than 0.5 m, nine other studies used models with a 1 m resolution. It is interesting to note that five studies use multi-resolution inputs, thus enabling an assessment of the proper value to use and the variations with different datasets. Finally, it is not surprising that two of the three studies mentioned in Section 3.2 as having small scales are the ones with lower spatial resolution: 30 m for [68] and 1 km for [85]. The difference between the two derives from the fact that—even on small scales—urban areas need to be more detailed compared to a natural region in which the principal disturbing element is the terrain.
As for city models, the Open Geospatial Consortium codified the CityGML data structure, which uses five Levels of Detail (LoDs). The concept of LoD involves spatial resolution, requiring increasing precision when moving up in the scale. Twelve papers describe the LoD of the used dataset: [53,66] are limited to LoD1, [45,46,82] to LoD2, and [47,76,84] to LoD3. Moreover, it is interesting to note that in three cases, multiple Levels of Detail are considered in the same study, making the study multi-resolution. In particular, [55] ranges from LoD1 to LoD4, showing the improvements of their ray-casting method while increasing the Level of Detail.
4.2. Weather Parameter Sources
Thirty-four papers specify the source of the additional information used to calibrate the solar radiation calculation. Indeed, in this elaboration, along with the latitude—which determines the angle of incidence of the sun rays—it is relevant to input additional parameters describing the average weather conditions. The cloudiness and the potential presence of other shading elements—such as high humidity or smog—determine the share of solar radiation actually striking the Earth’s surface. According to this source, it is possible to classify the papers into six main groups based on database, observed data, online tools, algorithms, and combined sources. These are described in Figure 7.
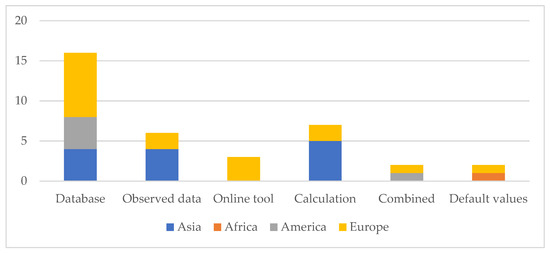
Figure 7.
Classification of papers based on the weather input.
First, 16 papers accessed various databases to retrieve the necessary data, half of them in Europe. In three cases [24,26,31], Meteonorm was accessed. This is a software that includes historical time series of irradiation, temperature, humidity, precipitation, and wind, thus allowing not only a precise definition of the parameters required for the calculation but also the validation of the elaborated data. It reports the information gathered by five satellites and 8320 weather stations worldwide [89]; their even distribution makes it possible to have reliable data for both Switzerland—where [24,31] calculated solar radiation—and China—where the case study of An et al. [17] is located. Meteonorm also includes TMY3 (Typical Meteorological Year 3), data collection based on 1020 USA locations’ data from a 1976–2005 time series. TMY3 was used in [28,41], whose test areas are in the USA and Taiwan, respectively. Therefore, it can be assumed that the accuracy of the latter is slightly lower. The NASA climatic dataset—accessed by default by ArcGIS—was used for [78], while the EPW (Energy Plus Weather) format—reporting climatic information calculated through Energy Plus, software specifically designed for energy calculations—is inputted in the tools used in [15,60,64]. Three other studies—namely [13,37,71]—calibrated their calculation based on SoDa (the Solar radiation Database), specifically devoted to solar energy. This database can be accessed on different time scales—from 1 minute to 1 month. It is based on Meteosat-11 images with a time series starting from February 2004 [90]. Mutani et al. [62] used the database of the regional agency for environmental protection (ARPA), taking advantage of the possibility of a site-specific time series, while the Japanese Meteorological Agency provided the cloud clover data (from 2015 to 2020) for [63]. National data were also provided for [26], on a 30-year time series. In another case [20], the historical irradiance data measured by a single station was downloaded from the International Weather for Energy dataset (published by the American Society of Heating, Refrigerating and Air-Conditioning Engineers), while cloud cover data from World Weather Online [91] were used in Zhu et al. [86], combined with an online tool.
Five studies used observed data gathered for the purpose of the research. In particular, Lindberg et al. [57] measured data concerning solar radiation and its components—direct and diffuse—while only the monthly average daily total radiation at the site was measured for [82]. Gergelova et al. [39] gathered data over 11 years (2009–2019) about the weather conditions (sunny, partly cloudy, cloudy, or rainy) of each month in a specific Slovakian municipality.
When it is not possible to access an existing database or directly measure the phenomenon, online tools that interpolate existing data can be used. The European Commission developed PVGIS (Photovoltaic Geographic Information System), which returns weather and irradiation data with different aggregations—monthly, daily, and hourly. Borfecchia et al. [21] used PVGIS values of monthly direct and diffuse irradiance, while Borfecchia et al. [22] used this information to compute the Linke turbidity factor. This online tool also allows the user to compute the Typical Meteorological Year data, aggregating values of the PVGIS-SARAH 2 database, ranging from 2005 to 2020. Hubinský et al. [47] calculated annual irradiance values in this way, thus reducing the possibility of having the results biased by extraordinary events. PVGIS is not the only energy-related online tool. Zhu et al. [86] used Sun Earth Tools to calculate the position of the sun. This website [92] includes several widgets to compute information related to solar energy and photovoltaic production, such as the payback time and the position of the sun, as well as basic geographic tools for calculating distances and visualizing GPS tracks. It can be observed that all three studies using online tools have European case studies; the reliability of institutional widgets for calculation—such as PVGIS—led multiple scholars to consider those values as usable, despite the spatial resolution not always being the best available.
Another option is to use algorithms to compute the necessary inputs. An example is provided by Helbich et al. [43], who used the SOLPOS code, developed by the National Renewable Energy Laboratory, to calculate the position of the sun. Similarly, PySolar is a Python library that can be used for calculations related to solar energy. It is able to compute the PV production, but it can also return intermediate values. In this case, it was used to calculate the sun’s location. Another example of code is MODTRAN, whose 4.0 version was used in [16] to estimate atmospheric transmissivity and radiances.
Some authors combined various sources to calibrate their models, thus solving problems of data availability. This is the case of [85], which used MODIS satellite data for the cloudiness factor and algorithms from the literature e.g., [93,94], for the atmospheric transmittance in clear and cloudy sky conditions. In another case [48], some assumptions—on the implication of geometrical simplifications—are used together with an institutional database that improves the calculation of reflected energy.
Nevertheless, two studies [12,36] adopted the default values proposed by the calculation tool to compute solar radiation.
4.3. Tools for Solar Radiation Estimation
As previously mentioned, GIS 3D models are quite new compared to 2.5D datasets. Therefore, it is not surprising that out of the 67 papers that report the software used to compute solar radiation, nearly half of them—23—are based on widespread tools requiring a DSM for the principal geographical input, namely ArcGIS Area Solar Radiation and QGIS r.sun. Despite these being the most common ones, they are part of a wider set of tools, which are included in a complete review by Freitas et al. [95]. The subdivision of papers according to the software they used to calculate the incoming solar energy is plotted in Figure 8.
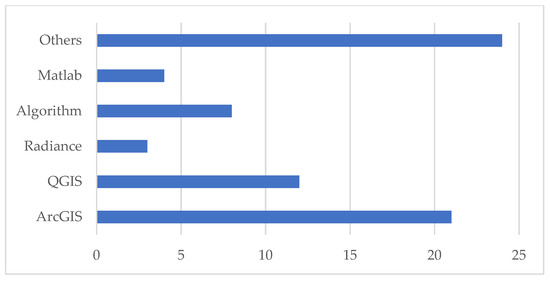
Figure 8.
Classification of papers based on the tool used to compute solar radiation.
Fourteen papers used the ArcGIS Area Solar Radiation tool, based on the viewshed algorithm. It is part of the Spatial Analyst, calculating solar energy based on a DSM. Its parameters are grouped into two principal clusters:
- Topographic parameters: the “z factor” corrects biases deriving from the use of different scales in planar and vertical units; the “slope and aspect input type” establishes whether the elaboration assumes a planar surface or requires the calculation of orientation and inclination of the receiving surfaces; “calculation directions” refers to the viewshed calculation.
- Radiation parameters: zenith and azimuth divisions are instrumental for the definition of the sky map; the correlation between diffuse radiation and zenith angle is defined according to the “diffuse model type”; “diffuse ratio” quantifies the share of diffuse radiation over the global radiation; “transmissivity” is the fraction of radiation passing through the atmosphere.
It is possible to run the simulation in different time configurations, from single hours to whole years. ESRI, the developer of ArcGIS, has already developed two tools for the estimation of solar radiation on three-dimensional elements. Points Solar Radiation works on point clouds using the same inputs as Area Solar Radiation. The difference lies in the possibility of having as output not only a raster dataset—on which 3D facades are hidden—with solar radiation values but a cloud of 3D points enriched with solar energy information. Calculate Solar Radiation is a configuration of ArcGIS Pro that can be used by local governments to calculate solar energy on 3D city models; however, there is no documentation available. Two studies mention they used ArcGIS without specifying the tool. However, from the inputs they use, it can be assumed that both Hippenstiel et al. [44] and Nakazato et al. [63] used the three-dimensional configuration. Therefore, in total, thirteen studies used Area Solar Radiation, four used Calculate Solar Radiation, and two used Points Solar Radiation. Moreover, three studies can be added to this group, because they used ArcGIS in combination with other tools. Fijałkowska et al. [37] targeted a 3D extension of Area Solar Radiation output by casting shadows through the Sun Shadow Volume tool. The authors created a script through the ArcPy library by which they automatized the process, merging different data sources in a single output. Machete et al. [61] compared Area Solar Radiation with ECOTECT—a three-dimensional algorithm integrated in the Revit product family—concluding by highlighting the easier calibration of the latter, which reads Energy Plus Weather files to apply local weather conditions to the elaboration. Finally, as already mentioned in Section 3.1, one study [28] aimed at developing a 3D extension—alternative to Calculate Solar Radiation—for ArcGIS, named PV Analyst.
Ten works were carried out using r.sun, a GRASS GIS model that is informed by ESRA (European Solar Radiation Atlas) model. Its reliability is confirmed by its institutional use, being the basis of the PVGIS database [96]. It has been integrated into QGIS, and—differently from ArcGIS—it is also able to compute the reflected solar energy. r.sun works in two modes, calculating solar incidence and solar irradiance for a specific time or summing daily values of solar radiation. However, in the analyzed studies, there is a prevalence of uses in the first mode. Its parameters are more disaggregated compared to ArcGIS Area Solar Radiation—with which it shares the DSM as principal input—thus requiring more complete knowledge about the territory under analysis. It does not compute every time slope and aspect, whose maps can be calculated ex ante and inputted directly into the model. As for the Linke turbidity factor, the user can choose between inserting a single value or a raster reporting the variations in turbidity inside the study area. The same applies to the albedo. Further parameters quantify the beam and diffuse radiation, the horizon values for the shadowing calculation, the days of the year for which the radiation is calculated, the time step for the computation of daily radiation sums (in the second mode), and the solar constant. The multiple options it gives in terms of producible outputs lead to different usages in the analyzed studies. For instance, Agugiaro et al. [13] chose to focus on the direct component only because of the interest the authors had in shadowing, while Liang et al. [54] considered global radiation as a whole and Nex et al. [67] disaggregated it into basic components. Similarly to [28], Ref. [55] also proposed an extension of the r.sun calculation to 3D, though an add-in for city models—named v.sun—had been previously developed. This was used in [45] for the city of Košice (Slovakia), where a LoD2 city model was available.
Another QGIS plugin is UMEP (Urban Multi-scale Environmental Predictor). It also uses the DSM as the principal input, together with a climatic file in the Energy Plus Weather format, outputting a global radiation map. It was used in two cases in Spain, namely for the city of Irun in [67] and the city of Vitoria-Gasteiz in [70]. An UMEP plugin called SEBE—Solar Energy on Building Envelopes—which can also calculate irradiance from a DSM on vertical elements, was used by Aleksandrowicz et al. [15]. Nevertheless, its main limitation is the high computation time, resulting in the need to adopt ArcGIS Area Solar Radiation to calculate solar energy for the whole city of Tel Aviv.
The ESRA model was used not only for the r.sun implementation but also in a newly developed tool reported in [71]. Indeed, it proved to be sound in the calculation of direct and diffuse components of solar radiation and therefore dependable for the development of new instruments.
Five other studies are based on Radiance, a validated ray-tracing tool. In two cases [58,60], it was integrated into an environmental analysis program, Honeybee, while [17,48] rely on derived software, Daysim. The principal characteristic of Radiance is the possibility to customize the optical surface properties, such as reflectance and absorptivity. In contrast to the tools analyzed previously, it supports 3D models without the need for extensions. Therefore, it was integrated into 3D modelling software such as Rhinoceros (with the Ladybug tool) and Grasshopper (which takes advantage of a Honeybee plugin). Also, Blender (open-source software for 3D modelling)—in particular its add-on package VI-Suite—incorporates Radiance in the modules to calculate the sun path, shadows, and lighting analysis. Palliwal et al. [66] calculated irradiance values through the Climate-Based Daylight Modeling, starting from the lighting values.
Similarly, the RayMan model, used by Ren et al. [74], can process three-dimensional data by considering the sunshine duration and shadowing. It requires the input of basic meteorological data, like temperature and humidity, as well as the characterization of solid surfaces, mainly in terms of emissivity.
A wide set of papers concerned the definition and application of algorithms. While in five cases [24,25,57,72,73] it is specified that MATLAB was used to implement the algorithm, and in another case [85] a raster calculator was chosen, eight other studies [19,26,30,31,41,59,69,77] based on algorithms specify the formulas but not how they were applied to the test study from a software perspective. The development of specific algorithms allowed scholars to include or exclude distinct factors, thus improving the quality of the results or simplifying the calculation by limiting the inputs. In particular, in [19] the authors claim they aim to develop a simplified version of the solar energy calculation.
Finally, there are multiple studies that used other tools for estimating the solar energy striking the analyzed case studies:
- The paper by Nakhaee and Paydar [64] was specifically devoted to the elaboration of a tool to compute solar radiation through artificial intelligence. The authors used data from QGIS and Ladybug for training but then ran elaborations on their own.
- Esclapés et al. [35] used the open-source software gvSIG, designing with Java a specific code to be run in its environment.
- PySolar, which was mentioned in the previous paragraph because of the intermediate outputs it can provide, was used by Lagahit and Blanco [52]. It is based on data from the USA, and it can compute direct clear-sly solar irradiation.
- Saran et al. [76] used the SunCast application in Virtual Environment Software to calculate the solar intensity on wall surfaces, using a CityGML LoD2 model as geometrical input.
From this brief overview of the main processing tools, it is evident that scholars have widely recognized the limits of the most widespread processing tools—mainly the over-simplification of ArcGIS Area Solar Radiation compared to the need for extensive data to be inputted in GRASS GIS r.sun—thus exploring a wide set of possibilities for the calculation of the solar energy.
5. Results: Photovoltaic Potential Calculation
After the gathering of the necessary parameters, the actual photovoltaic potential can be calculated. Before addressing the equations used for the calculation, the following section is devoted to the understanding of the conditions that make the roofs exploitable for the calculation of the photovoltaic potential according to the scientific community. It is to be mentioned that data reported in this section pertain to a subsample of the analyzed papers, including only the buildings that concern the photovoltaic potential calculation, approximately one-third of the whole sample.
5.1. Pre-Filtering
In thirteen studies, the calculation of the photovoltaic potential was preceded by a selection of suitable roofs for the installation of the panels. A total of seven parameters—shown in Figure 9—was considered, with most studies defining the suitability based on at least two parameters.
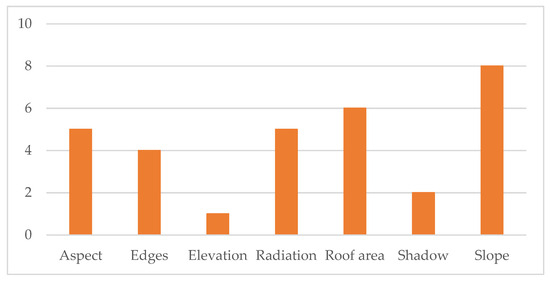
Figure 9.
Classification of papers based on the filtering parameter.
In one case only [40], the elevation is taken into account, setting a threshold at 3 m. Despite not being justified in the paper, it can be assumed that this is meant to remove the areas below the first floors, thus the most shadowed ones.
Shadowing is another parameter for the pre-filtering. In Hafeez et al. [40], only the shadows deriving from the vegetation are considered. They are calculated through Ecotect software, inputting a 3D model realized with Google Sketchup according to an unsupervised classification of aerial pictures, for 10:30 AM and 3:30 PM of the solstices. By contrast, the authors of [12] calculated the shadows with the Hillshade tool in ArcGIS for every hour of the year 2020, considering as non-suitable all the areas that were shadowed in at least one elaboration.
When installing a photovoltaic panel, it is relevant to consider the surface. From this, it derives the dimensioning of the system and therefore the producibility; however, some constraints must be taken into account. First, installation and maintenance require the definition of buffer areas located on the edges, which should be removed from the theoretically useful area. It is generally accepted that this buffer is equal to 1 m, a value considered in [12,75,78]. In one study [75], this constraint is combined with the requirement of a minimum surface for panel installation, equal to 5 m2. Indeed, this and five other papers assumed that it is necessary to have a minimum available surface to grant sufficient revenues for justifying the installation costs, therefore being able to grant a minimum production. Moreover, there is a minimum dimensioning of the panels. The value to be set as the threshold is not shared: another study [47] takes 5 m2 as the reference value, one [50] requires an even smaller surface—2 m2—and a third one [46] requires at least 40 m2. For this purpose, it is interesting to note that Gawley et al. [38] set not only a minimum requirement but also a maximum, according to the values included in the British Energy Saving Trust sizing guide [97]. These return a producible output from 1 kWp—generally used in European studies—to 4 kWp—representing an average UK configuration.
Another aspect directly affecting the producibility is the radiation striking the surface. In five cases, this was used as a limiting element, with different thresholds, ranging from 700 kWh/m2 [38] to 1355 kWh/m2 [40]. This depends on the case study, with some places receiving less solar energy compared to others, e.g., 700 kWh/m2 is set for Northern Ireland, while 1355 kWh/m2 for Pakistan. Moreover, considering the direct correlation between the radiation striking the panel and the photovoltaic potential, it is also possible to assume that, when focusing on the economical aspect, places where the electricity price is lower will require a bigger surface to ensure a good payback time.
Finally, two elements correlated to solar radiation were tackled when defining the parameters for filtering, i.e., aspect and slope. Out of the five times that aspect is considered, slope is also taken into account. In the case of [12], there is no clear indication of the orientations and inclinations to exclude because of the use of a formula to calculate the losses—with 20% loss set as threshold.
As for the aspect, this filter aims to orient the panels towards the portion of the sky where the sun remains for longer, thus maximizing the production. South-facing panels are the most productive, but a degree of tolerance is generally accepted. This depends on the author and—as for solar radiation—on the geographical position of the case study. Two studies exclude only 45° from their calculations, namely [38,39]. The former aims to avoid the panels oriented from 315° to 0°, while the latter tends to exclude north-facing panels—oriented from 337.5° to 22.5°. These two studies pertain to Switzerland and Northern Ireland, respectively, thus needing a broader usable surface to receive the necessary amount of solar radiation. On the other hand, [40,75], studying areas in Morocco and Pakistan, can be more selective, excluding 270°. The Pakistani research is shifted westwards compared to the Moroccan research, with the two selecting portions from 135° to 225° and from 115° to 205°, respectively.
A similar distribution can be observed for the thresholds defined for the slope. All authors except for Gawley and McKenzie [38] define only an upper threshold. Gawley and McKenzie [38] include a range of permissible slopes from 30° to 60°, defining as optimal inclination the one between 39° and 40°. Three other studies [39,48,78] set as the maximal slope 60°, excluding vertical elements, while [47]—dividing roof planes in two inclination categories—does not exclude vertical walls, setting the threshold at 90°. Nevertheless, there are more restrictive studies, which limited the maximum slope at 5° [56] and 35° [40]. The former justifies this extreme selection based on the claim of loss of geometrical information caused by the rasterization of three-dimensional surfaces, thus using the DSM only for quantifying heights and not inclination.
5.2. Equation Used
Once having selected the buildings suitable for assessing the photovoltaic potential and gathered the necessary inputs, the actual calculation can be conducted. Several methods have been explored in the analyzed sample, thus requiring an overview of the different equations that can be used.
The most used equation is as follows:
where E is the electricity output, I is the annual solar radiation expressed in kWh/m2, η is the conversion efficiency of the panel—the ratio of solar energy converted into produced electricity, PR is the performance ratio—returning the efficiency of the supporting system, and A is the area for the installation of PV panels.
E = I × η × PR ×A,
It emerges that the impact of the performance ratio and the cell efficiency is relevant. However, the values adopted for both are generally similar. PR is generally about 80%, a percentage considered in three studies [12,38,83]. Similar values, in the range of ±5%, are adopted in [46,58,67]. Pedrero et al. [67] calculated the PV potential based on two different PR values, 79% and 83%, much closer to each other compared to the values used by El-Bouzaidi et al. [33], 66% and 85%. This 19% difference would lead to considerable discrepancies between production values in comparable contexts, thus highlighting the need for a reliable supporting system. Low values, with a reduced producibility—resulting in higher payback times—were adopted also by Nakazato et al. [63].
As for the conversion efficiency, this strongly depends on the technology considered. For example, [12] is the only study that took into account the possibility of installing thin film modules, with an efficiency equal to 8%. By contrast, [47] considered technologies that reach an efficiency of 39%. In general, values range from 15% to 22%, standard values for polycrystalline and monocrystalline silicon cells, respectively. This is the case of [26,46,58,62,78,83]. However, solar cell efficiency tables, such as specified in [98], can be used for a better quantification of this parameter.
Despite Equation (1) being widely recognized as a simple yet reliable method to calculate the PV potential according to four macro-parameters, in some cases it is modified. Sometimes, the performance ratio is not taken into account, thus limiting the analysis at the level of the panel, not considering the actual electricity that can be injected into the grid. Soares et al. [78] calculate the photovoltaic potential together with its potential revenues, but the energy part can be isolated by removing the economic indicators. A formula emerges that considers a 15% conversion efficiency but no performance ratio, thus overestimating the theoretical benefits (≅+20%). Similarly, Cheng et al. [26] quantify the power production as the product of efficiency and solar irradiation—estimated in absolute values, not referred to as square meters, and corrected with sunshine duration. On the contrary, Liu et al. [58] elaborated on Equation (1) to include additional elements, thus providing a more stable assessment, using Equation (2).
where N is the life cycle of the panel, 25 years; and R is the yearly attenuation rate of the module, 0.7%.
Therefore, Equation (2)—differently from Equation (1)—takes into account not only the productivity at the moment of the installation but also the trends throughout the life cycle. This is particularly relevant, considering that in this study the decrease is equal to 0.7% and the life cycle is 25 years.
Another study [38] started from the assumption of panels with a known peak production. The concept of peak production involves the efficiency of the panel and its area, so it was sufficient to multiply this value by the solar energy and the performance ratio.
Nakazato et al. [63] focus on daily rather than on yearly production. They compute the productivity based on Equation (3).
where P quantifies the system capacity, 0.208 kW/m2; and D is the solar radiation intensity under standard conditions.
Therefore, Equation (3) can also be considered as an extension of Equation (1) because of the inclusion of the efficiency and the area in the calculation of the system capacity. However, the radiation intensity is added.
Another set of papers used correction factors on solar radiation to compute the photovoltaic potential. Nex et al. [65] take into account an alpine area, where the impact of temperature on the module’s efficiency is highly relevant. Therefore, the authors adopted correction factors based on temperature to estimate the losses derived from unfavorable conditions. By contrast, Ren et al. [74] consider a densely urbanized area, where shadows have a high impact. Therefore, they reduced the incoming solar radiation according to shading, considering the result as electricity that is potentially producible. Two other papers [35,48] correct the incoming solar energy according to geometric parameters, slope and orientation, whose relevance was cited in the previous paragraph, with the latter including shading too.
Hafeez et al. [40] took advantage of an automatized procedure embedded in PVsyst software, not explicating the equation used. Similarly, Choi et al. [28] integrated TRNSYS into ArcGIS, using the first to compute the photovoltaic potential by applying its own four- and five-parameter PV array performance models. Both include reference values at standard test conditions, the electron charge constant, the Boltzmann constant, voltage, and the module series resistance, with the latter adding the module shunt resistance. All these parameters, in contrast to basic technical information about the panel and the supporting systems, require an extensive analysis that is much more complex compared to the one required for Equation (1).
6. Discussion
6.1. Validation of Results
Twenty-six papers with different focuses were validated, with fourteen related to solar radiation and eight assessing the photovoltaic potential. They can be divided into two main groups: validation using observed data (11) and an elaboration on an alternative tool or software (12).
When observing the validation process of the observed data, the first element that emerges is that in many cases only a component of the final calculation is validated, for both PV potential and solar radiation analysis. While [48,65] used real PV production data—despite considering two validation sets vastly different in terms of dimension, with respectively 2 and 252 panels—other studies validated partial results only. For example, in [58] only the global radiation was measured. However, this could be considered sufficient when having reliable data on the technical parameters of the panel and the system. Further problems arise in [74], which validated the shadowing analysis only by comparing the simulation with acquired pictures. The same applies to [59,77], whose focus is on solar radiation.
In other studies, the results are validated by running the simulation on a platform or software and comparing the outcomes. In one case [13], the outcome was compared to PVGIS, with the problem of strong discrepancies in the resolution. Indeed, the study worked on a DSM with a resolution of up to 25 cm, while PVGIS calculates based on 1 km2 cells. This is also the case in [38], which compared its 40 cm accurate results with PVGIS and two other online tools—PVWatts by NREL and a tool by the Energy Saving Trust—whose accuracy depends on data availability (with some results being interpolated). NREL data were also accessed for validation by Harikesh et al. [42]. Different scholars confronted their results with solar radiation tools that were mentioned previously—r.sun, Area Solar Radiation, and Ladybug—while some others evaluated the reliability of their models on a subsample. Prades-Gil et al. [69] realized the model of six test buildings in Design Builder—a 3D modelling software that uses EnergyPlus as a calculation engine—while Liang et al. [54] coupled the single-building validation—conducted with Ecotect—to a comprehensive test using SURFSUN3D. Another example of validation carried out in a twofold way is [31], which used an approach developed by the University of Geneva for validating the solar energy striking horizontal surfaces and PVsyst software for the analysis of vertical walls.
The three papers not included in the previous two groups validated their outcomes in the following ways:
- Hafeez and Atif [40] used the Marksim model.
- Zhang et al. [85] compared the results to previous studies on the same case study.
- Biljecki et al. [20] calculated the RMSE with a model whose reliability was assessed.
6.2. Limitations and Future Perspectives
Before the advent of GIS, different calculation methods for solar energy had already been validated. This is the case of the algorithm proposed by Zhang et al. [99], whose reliability is attested to by the more than 800 citations. This method starts from the estimation of the daily irradiation and—by calculating the hourly diffuse and beam radiation—makes it possible to estimate the cumulative daily or monthly radiation as well as how radiation changes throughout the day. However, this approach has several limitations. First, its level of detail is quite poor, requiring a multitude of acquisitions for refining the results in wider areas; in the case in which a single acquisition is performed, all buildings will have the same irradiation value. Another constraint is given by the impossibility of considering aspect, inclination, and shadowing, including the hours of light but not the sun’s altitude or the sun’s path. This makes this approach unsuitable to quantify the solar potential, not being able to identify the surfaces struck by the most by sun rays—i.e., vertical elements at high latitudes and roofs at low latitudes.
GIS technologies make it possible to include the third dimension—height—in the estimation of solar potential. First, it is possible to interpolate data, in order to model local changes with a lower number of measurements compared to traditional approaches. As explained in Section 4.2, this enabled the use of databases with different spatial resolutions. Second, accurate DSMs allow modelling of urban contexts to create a 3D reconstruction from which it is possible to cast shadows. These are relevant especially in contemporary cities, with the emergence of tall buildings shadowing wide neighboring areas. Nevertheless, these models, despite their accuracy, are simplified versions of complex three-dimensional objects, e.g., trees are returned as cylinders, not differentiating between trunk and crown. It is possible to perfect the calculation by using 3D models, as was done in some of the studies presented herein. According to the Level of Detail—in particular from LoD2, it is possible to better observe the variations in the objects rather than returning simple blocks. However, it was mentioned that pure three-dimensional tools are intensive in terms of both time and computational capacity.
It was previously mentioned that some studies over-simplify the calculation by using default or inaccurate values as input for the estimation. Some of the analyzed studies use highly accurate geographical input while lacking accuracy in the weather parameters. This makes it difficult to ensure satisfactory results, especially in areas characterized by extreme variability. For example, big cities with relevant urban heat island phenomena can show different cloudiness factors from district to district due to air moves caused by this phenomenon. Another simplification that leads to discrepancies is that—despite the diffuse ratio and transmissivity being computed by all tools—traditional GIS approaches compute the solar radiation in clear sky conditions, not being able to predict the variations caused by additional shadows derived from compact clouds. At the same time, it is likely that—for areas with a high average diffuse ratio—the software returns lower irradiation values compared to the real ones in clear sky days.
7. Conclusions
This research highlighted that progress is being made in the field of three-dimensional calculation of photovoltaic potential and its components—such as the solar radiation or the evaluation of suitable areas. With growing interest in the field following the issue of the EU Solar Strategy, this topic is likely to be further explored, increasing the body of studies and refining the outcomes.
In summary, it emerged that 3D GIS is an evolving field, thus highlighting the importance of intermediate technological progress—such as 2.5D models—in the calculation of the incident solar energy. Nevertheless, a wide variety of inputs, from three-dimensional models to point clouds, have been used by the authors of the sampled papers, resulting in a heterogeneous bunch of tools used for highly detailed solar radiation estimation, either directly embedded into widespread GIS software or running on dedicated programs or energy-oriented modelling tools. Moreover, some authors developed their own algorithms, implemented through programming code or working on pixels in GIS. In some cases, the calculation of photovoltaic potential is preceded not only by data gathering but also by a filtering phase in which suitable roofs are selected considering a wide set of parameters—the most relevant are slope and available roof area. The actual evaluation of photovoltaic potential takes place with different formulas, whose principal parameters are the cell efficiency—which varies according to the used technology—the solar radiation, and the available surface. Some authors added other elements, first the performance ratio of the supporting system, while others kept the necessary values only. Finally, validation is often conducted partially, not being able to prove the reliability of the model in all its components.
Therefore, from this review, a complex framework emerges. On the one hand, extensive studies have been conducted on the topic, but on the other, some critical elements often recur. For example, often the input parameters for the calculation of solar radiation are standard, kept by default or partially improved with information from low-precision databases. This is the case of the Linke turbidity factor, with values aggregated in big areas or estimated based on the urban or rural setting of the case study. Once having computed the solar radiation, there are not widely accepted criteria for defining suitable roofs, and the photovoltaic potential is then calculated based on assumed parameters, with few studies providing technical evidence on the reasons to adopt a specific conversion efficiency value; this does not take into account the degradation of the panel throughout its life cycle. Finally, the differences in productivity during the day are rarely considered, limiting the studies on the possible necessity of storage systems.
As for the geomatic aspects, data availability is often a discriminating factor, with spatial resolutions ranging from a few centimeters to one kilometer. Similarly, three-dimensional modelling must be improved, using at least LoD 2, to establish the slope and orientation of the pitches. Moreover, considering that not all energy experts are knowledgeable in the programming and GIS fields, it will be necessary to publish validated tools for solar energy calculations on 3D models.
A final aspect that was little considered is the difference in the output of alternative tools on a heterogeneous set of buildings. It is likely that different GIS tools will return similar values in some contexts and very different outcomes in others. Therefore, it is necessary to perform comparative analyses on the basis of a validated set of inputs, as discussed in Section 6.2.
In conclusion, future works should focus on the assessment of the differences between alternative tools in the same case study. A complete assessment of the reliability of the inputs should precede the work, making the outputs of tools and formulas comparable. Moreover, it is necessary to consider real values—of both solar radiation and photovoltaic production—for the validation of the results. Finally, the time component should be appropriately tackled, thus defining the sizing of the system and the requirements in terms of storage capacity and efficiency.
Author Contributions
Conceptualization, M.F.; Methodology, M.F. and S.A., investigation, S.A.; writing—original draft preparation, S.A.; writing—review and editing, M.F.; visualization, S.A.; supervision, M.F. All authors have read and agreed to the published version of the manuscript.
Funding
This paper reports part of the work developed within the project NODES, which has received funding from the MUR - M4C2 1.5 of PNRR with grant agreement no. ECS00000036. Maria Ferrara’s activity was funded by Italian MUR within the PON “Ricerca e Innovazione” 2014–2020, Asse IV “Istruzione e ricerca per il recupero”—Azione IV.4—“Dottorati e contratti di ricerca su tematiche dell’innovazione” e Azione IV.6—“Contratti di ricerca su tematiche Green. Further, this work was developed in accordance with the framework agreement between the City of Turin and the Polytechnic of Turin, signed on 9th February 2023, for the realisation of pilot projects towards the implementation of a Digital Twin.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Council of the European Union Fit for 55. Available online: https://www.Consilium.Europa.Eu/En/Policies/Green-Deal/Fit-for-55-the-Eu-Plan-for-a-Green-Transition/ (accessed on 10 October 2023).
- European Commission. Proposal for a Directive of the European Parliament and of the Council on the Energy Performance of Buildings. Recast. 2021. [Google Scholar]
- Deng, Y.; Dewil, R.; Baeyens, J.; Ansart, R.; Zhang, H. The “Screening Index” to Select Building-Scale Heating Systems. IOP Conf. Ser. Earth Environ. Sci. 2020, 586, 012004. [Google Scholar] [CrossRef]
- Anselmo, S.; Ferrara, M.; Corgnati, S.; Boccardo, P. Aerial Urban Observation to Enhance Energy Assessment and Planning towards Climate-Neutrality: A Pilot Application to the City of Turin. Sustain. Cities Soc. 2023, 99, 104938. [Google Scholar] [CrossRef]
- Directive (EU) 2018/2001 of the European Parliament and of the Council of 11 December 2018 on the Promotion of the Use of Energy from Renewable Sources. Recast. 2018.
- Corgnati, S.P.; Cattaneo, S. Efficientamento Energetico Degli Edifici e Soluzioni Innovative Di Decarbonizzazione. In Le città a Impatto Climatico Zero: Strategie e Politiche; Ministero delle Infrastrutture e della Mobilità Sostenibili: Rome, Italy, 2022; pp. 37–56. [Google Scholar]
- Roberts, J.; Frieden, D.; d’Herbemont, S. Energy Community Definitions. 2019. Available online: https://main.compile-project.eu/wp-content/uploads/Explanatory-note-on-energy-community-definitions.pdf (accessed on 10 October 2023).
- IRENA. IRENASTAT Online Data Query Tool. Available online: https://www.irena.org/Data/Downloads/IRENASTAT (accessed on 28 September 2023).
- European Commission. Communication from the Commission to the European Parliament, the Council, the European Economic and Social Committee and the Committee of the Regions—EU Solar Energy Strategy 2022. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=COM%3A2022%3A221%3AFIN (accessed on 10 October 2023).
- Amadio, G. Introduzione Alla Geomatica; Dario Flaccovio Editore: Palermo, Italy, 2012. [Google Scholar]
- Minerva, R.; Lee, G.M.; Crespi, N. Digital Twin in the IoT Context: A Survey on Technical Features, Scenarios, and Architectural Models. Proc. IEEE 2020, 108, 1785–1824. [Google Scholar] [CrossRef]
- Achbab, E.; Lambarki, R.; Rhinane, H.; Saifaoui, D. Estimation of Photovoltaic Potential at the Urban Level from 3d City Model (Solar Cadaster): Case of Casablanca City, Morocco. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, 46, 9–16. [Google Scholar] [CrossRef]
- Agugiaro, G.; Remondino, F.; Stevanato, G.; De Filippi, R.; Furlanello, C. Estimation of Solar Radiation on Building Roofs in Mountainous Areas. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 38, 155–160. [Google Scholar] [CrossRef]
- Alam, N.; Coors, V.; Zlatanova, S.; Oosterom, P.J.M. Shadow Effect on Photovoltaic Potentiality Analysis Using 3D City Models. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 209–214. [Google Scholar] [CrossRef]
- Aleksandrowicz, O.; Zur, S.; Lebendiger, Y.; Lerman, Y. Shade Maps for Prioritizing Municipal Microclimatic Action in Hot Climates: Learning from Tel Aviv-Yafo. Sustain. Cities Soc. 2020, 53, 101931. [Google Scholar] [CrossRef]
- Alomari, K.; AlTal, B.; Ayadi, O. The Efficiency of Using of Solar Cells on the Multistory Residential Buildings in Jordan (Housing Building as a Case Study). Int. J. Sustain. Dev. Plan. 2023, 18, 1833–1839. [Google Scholar] [CrossRef]
- An, Y.; Chen, T.; Shi, L.; Heng, C.K.; Fan, J. Solar Energy Potential Using GIS-Based Urban Residential Environmental Data: A Case Study of Shenzhen, China. Sustain. Cities Soc. 2023, 93, 104547. [Google Scholar] [CrossRef]
- Beltran-Velamazan, C.; Monzón-Chavarrías, M.; López-Mesa, B. A Method for the Automated Construction of 3d Models of Cities and Neighborhoods from Official Cadaster Data for Solar Analysis. Sustainability 2021, 13, 6028. [Google Scholar] [CrossRef]
- Bernabé, A.; Musy, M.; Andrieu, H.; Calmet, I. Radiative Properties of the Urban Fabric Derived from Surface Form Analysis: A Simplified Solar Balance Model. Sol. Energy 2015, 122, 156–168. [Google Scholar] [CrossRef]
- Biljecki, F.; Heuvelink, G.B.M.; Ledoux, H.; Stoter, J. Propagation of Positional Error in 3D GIS: Estimation of the Solar Irradiation of Building Roofs. Int. J. Geogr. Inf. Sci. 2015, 29, 2269–2294. [Google Scholar] [CrossRef]
- Borfecchia, F.; Pollino, M.; De Cecco, L.; Martini, S.; La Porta, L.; Marucci, A.; Caiaffa, E. Integrated GIS and Remote Sensing Techniques to Support. PV Potential. Assessment of Roofs in Urban. Areas; Springer: Berlin, Germany, 2013; Volume 7973, LNCS; ISBN 9783642396458. [Google Scholar]
- Borfecchia, F.; Caiaffa, E.; Pollino, M.; De Cecco, L.; Martini, S.; La Porta, L.; Marucci, A. Remote Sensing and GIS in Planning Photovoltaic Potential of Urban Areas. Eur. J. Remote Sens. 2014, 47, 195–216. [Google Scholar] [CrossRef]
- Bremer, M.; Mayr, A.; Wichmann, V.; Schmidtner, K.; Rutzinger, M. A New Multi-Scale 3D-GIS-Approach for the Assessment and Dissemination of Solar Income of Digital City Models. Comput. Environ. Urban. Syst. 2016, 57, 144–154. [Google Scholar] [CrossRef]
- Carneiro, C.; Morello, E.; Desthieux, G. Assessment of Solar Irradiance on the Urban Fabric for the Production of Renewable Energy Using Lidar Data and Image Processing Techniques; Springer: Berlin, Germany, 2009; ISBN 9783642003172. [Google Scholar]
- Catita, C.; Redweik, P.; Pereira, J.; Brito, M.C. Extending Solar Potential Analysis in Buildings to Vertical Facades. Comput. Geosci. 2014, 66, 1–12. [Google Scholar] [CrossRef]
- Cheng, L.; Zhang, F.; Li, S.; Mao, J.; Xu, H.; Ju, W.; Liu, X.; Wu, J.; Min, K.; Zhang, X.; et al. Solar Energy Potential of Urban Buildings in 10 Cities of China. Energy 2020, 196, 117038. [Google Scholar] [CrossRef]
- Chiabrando, F.; Danna, C.; Lingua, A.; Noardo, F.; Osello, A. 3D Roof Model Generation and Analysis Supporting Solar System Positioning. Geomatica 2017, 71, 137–153. [Google Scholar] [CrossRef]
- Choi, Y.; Rayl, J.; Tammineedi, C.; Brownson, J.R.S. PV Analyst: Coupling ArcGIS with TRNSYS to Assess Distributed Photovoltaic Potential in Urban Areas. Sol. Energy 2011, 85, 2924–2939. [Google Scholar] [CrossRef]
- Chow, A.; Fung, A.S.; Li, S. GIS Modeling of Solar Neighborhood Potential at a Fine Spatiotemporal Resolution. Buildings 2014, 4, 195–206. [Google Scholar] [CrossRef]
- de Vries, T.N.C.; Bronkhorst, J.; Vermeer, M.; Donker, J.C.B.; Briels, S.A.; Ziar, H.; Zeman, M.; Isabella, O. A Quick-Scan Method to Assess Photovoltaic Rooftop Potential Based on Aerial Imagery and LiDAR. Sol. Energy 2020, 209, 96–107. [Google Scholar] [CrossRef]
- Desthieux, G.; Carneiro, C.; Camponovo, R.; Ineichen, P.; Morello, E.; Boulmier, A.; Abdennadher, N.; Dervey, S.; Ellert, C. Solar Energy Potential Assessment on Rooftops and Facades in Large Built Environments Based on LiDAR Data, Image Processing, and Cloud Computing. Methodological Background, Application, and Validation in Geneva (Solar Cadaster). Front. Built Environ. 2018, 4, 14. [Google Scholar] [CrossRef]
- Dewanto, B.G.; Novitasari, D.; Tan, Y.C.; Puruhito, D.D.; Fikriyadi, Z.A.; Aliyah, F. Application of Web 3D GIS to Display Urban Model and Solar Energy Analysis Using the Unmanned Aerial Vehicle (UAV) Data (Case Study: National Cheng Kung University Buildings). In Proceedings of the IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2020; Volume 520. [Google Scholar]
- El-Bouzaidi, R.D.; Rhinane, H.; Hilali, A.; El Hassan, E.A.; Maanan, M.; Saddiqi, O. Technical and Economical Photovoltaic Potential Assessment on Flat Roofs in Urban Area Case Study: Casablanca, Morocco. In Proceedings of the 2018 4th International Conference on Renewable Energies for Developing Countries (REDEC), Beirut, Lebanon, 1–2 November 2018. [Google Scholar]
- Eldesoky, A.H.; Colaninno, N.; Morello, E. An Integrated, Agile Approach for Estimating Solar Radiation on Building Facades in Complex Urban Environments. J. Phys. Conf. Ser. 2019, 1343, 012015. [Google Scholar] [CrossRef]
- Esclapés, J.; Ferreiro, I.; Piera, J.; Teller, J. A Method to Evaluate the Adaptability of Photovoltaic Energy on Urban Façades. Sol. Energy 2014, 105, 414–427. [Google Scholar] [CrossRef]
- Fichera, A.; Gagliano, A.; Nocera, F.; Pagano, A.; Volpe, R.; Bisegna, F. Application of a Geographical Information System to Plan Energy Policy at a Neighborhood Scale. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I and CPS Europe), Palermo, Italy, 12–15 June 2018. [Google Scholar]
- Fijałkowska, A.; Waksmundzka, K.; Chmiel, J. Assessment of the Effectiveness of Photovoltaic Panels at Public Transport Stops: 3D Spatial Analysis as a Tool to Strengthen Decision Making. Energies 2022, 15, 1230. [Google Scholar] [CrossRef]
- Gawley, D.; McKenzie, P. Investigating the Suitability of GIS and Remotely-Sensed Datasets for Photovoltaic Modelling on Building Rooftops. Energy Build. 2022, 265, 112083. [Google Scholar] [CrossRef]
- Gergelova, M.B.; Kuzevicova, Z.; Labant, S.; Kuzevic, S.; Bobikova, D.; Mizak, J. Roof’s Potential and Suitability for PV Systems Based on LiDAR: A Case Study of Komárno, Slovakia. Sustainability 2020, 12, 10018. [Google Scholar] [CrossRef]
- Hafeez, S.; Atif, S. 3D Rooftop Photovoltaic Potential Calculation Using GIS Techniques: A Case Study of F-11 Sector Islamabad. In Proceedings of the 12th International Conference on Frontiers of Information Technology, Islamabad, Pakistan, 17–19 December 2014; pp. 187–192. [Google Scholar]
- Han, J.-Y.; Chen, Y.-C.; Li, S.-Y. Utilising High-Fidelity 3D Building Model for Analysing the Rooftop Solar Photovoltaic Potential in Urban Areas. Sol. Energy 2022, 235, 187–199. [Google Scholar] [CrossRef]
- Harikesh; Singh, S.; Shrivastava, V.; Sharma, V. CityGML Based 3D Modeling of Urban Area Using Uav Dataset for Estimation of Solar Potential; Springer: Berlin, Germany, 2020; Volume 51. [Google Scholar]
- Helbich, M.; Jochem, A.; Mücke, W.; Höfle, B. Boosting the Predictive Accuracy of Urban Hedonic House Price Models through Airborne Laser Scanning. Comput. Environ. Urban. Syst. 2013, 39, 81–92. [Google Scholar] [CrossRef]
- Hippenstiel, R.; Brownson, J.R.S. Computing Solar Energy Potential of Urban Areas Using Airborne Lidar and Orthoimagery. In Proceedings of the World Renewable Energy Forum, WREF 2012, Including World Renewable Energy Congress XII and Colorado Renewable Energy Society (CRES) Annual Conference, Denver, Colorado, 13–17 May 2012; Volume 3, pp. 2004–2008. [Google Scholar]
- Hofierka, J. Assessing Land Surface Temperature in Urban Areas Using Open-Source Geospatial Tools. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, 48, 195–200. [Google Scholar] [CrossRef]
- HosseiniHaghighi, S.; de Uribarri, P.M.Á.; Padsala, R.; Eicker, U. Characterizing and Structuring Urban GIS Data for Housing Stock Energy Modelling and Retrofitting. Energy Build. 2022, 256, 111706. [Google Scholar] [CrossRef]
- Hubinský, T.; Hajtmanek, R.; Šeligová, A.; Legény, J.; Špaček, R. Potentials and Limits of Photovoltaic Systems Integration in Historic Urban Structures: The Case Study of Monument Reserve in Bratislava, Slovakia. Sustainability 2023, 15, 2299. [Google Scholar] [CrossRef]
- Jakubiec, J.A.; Reinhart, C.F. A Method for Predicting City-Wide Electricity Gains from Photovoltaic Panels Based on LiDAR and GIS Data Combined with Hourly Daysim Simulations. Sol. Energy 2013, 93, 127–143. [Google Scholar] [CrossRef]
- Jately, V.; Balaji, V.V.; Azzopardi, S.; Azzopardi, B. Design and Performance Investigation of a Pilot Micro-Grid in the Mediterranean: Mcast Case Study. Energies 2021, 14, 6846. [Google Scholar] [CrossRef]
- Kazak, J.K.; Świa̧der, M. SOLIS—A Novel Decision Support Tool for the Assessment of Solar Radiation in ArcGIS. Energies 2018, 11, 2105. [Google Scholar] [CrossRef]
- La Gennusa, M.; Lascari, G.; Rizzo, G.; Scaccianoce, G.; Sorrentino, G. A Model for Predicting the Potential Diffusion of Solar Energy Systems in Complex Urban Environments. Energy Policy 2011, 39, 5335–5343. [Google Scholar] [CrossRef]
- Lagahit, M.L.R.; Blanco, A.C. Using Openly Sourced 3D Geographic Information Systems (GIS) in Determining the Photovoltaic Potential of Quezon City Hall in Terms of Received Direct Solar Radiation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 263–270. [Google Scholar] [CrossRef]
- Liang, J.; Gong, J.; Li, W.; Ibrahim, A.N. A Visualization-Oriented 3D Method for Efficient Computation of Urban Solar Radiation Based on 3D-2D Surface Mapping. Int. J. Geogr. Inf. Sci. 2014, 28, 780–798. [Google Scholar] [CrossRef]
- Liang, J.; Gong, J.; Zhou, J.; Ibrahim, A.N.; Li, M. An Open-Source 3D Solar Radiation Model Integrated with a 3D Geographic Information System. Environ. Model. Softw. 2015, 64, 94–101. [Google Scholar] [CrossRef]
- Liang, J.; Gong, J. A Sparse Voxel Octree-Based Framework for Computing Solar Radiation Using 3d City Models. ISPRS Int. J. Geo-Inf. 2017, 6, 106. [Google Scholar] [CrossRef]
- Liang, J.; Gong, J.; Xie, X.; Sun, J. Solar3D: An Open-Source Tool for Estimating Solar Radiation in Urban Environments. ISPRS Int. J. Geo-Inf. 2020, 9, 524. [Google Scholar] [CrossRef]
- Lindberg, F.; Jonsson, P.; Honjo, T.; Wästberg, D. Solar Energy on Building Envelopes—3D Modelling in a 2D Environment. Sol. Energy 2015, 115, 369–378. [Google Scholar] [CrossRef]
- Liu, J.; Wu, Q.; Lin, Z.; Shi, H.; Wen, S.; Wu, Q.; Zhang, J.; Peng, C. A Novel Approach for Assessing Rooftop-and-Facade Solar Photovoltaic Potential in Rural Areas Using Three-Dimensional (3D) Building Models Constructed with GIS. Energy 2023, 282, 128920. [Google Scholar] [CrossRef]
- Lohani, B.; Kumar Singh, S.; Choudhary, D.; Nagarajan, B. A New Approach to Determine Solar Potential Using Terrestrial Images. Remote Sens. Lett. 2018, 9, 636–645. [Google Scholar] [CrossRef]
- Lu, Y.; McCarty, J.; Sezto, J.; Cheng, Z.; Martino, N.; Girling, C.; Rysanek, A.; Barron, S.; Matasci, G. Modeling the Shading Effect of Vancouver’s Urban Tree Canopy in Relation to Neighborhood Variations. Arboric. Urban For. 2022, 48, 95–112. [Google Scholar] [CrossRef]
- Machete, R.; Falcão, A.P.; Gomes, M.G.; Moret Rodrigues, A. The Use of 3D GIS to Analyse the Influence of Urban Context on Buildings’ Solar Energy Potential. Energy Build. 2018, 177, 290–302. [Google Scholar] [CrossRef]
- Mutani, G.; Casalengo, M.; Ramassotto, M.A. The Effect of Roof-Integrated Solar Technologies on the Energy Performance of Public Buildings: Tthe Case Study of the City of Turin (IT). In Proceedings of the INTELEC, International Telecommunications Energy Conference (Proceedings), Turino, Italy, 7–11 October 2018; Volume 2018. [Google Scholar]
- Nakazato, R.; Yokogawa, S.; Ichikawa, H.; Ushirokawa, T.; Takeda, T. Compact Model for Estimating Area-Level Photovoltaic Power Generation on Facade Surface Using 3D City Model and Solar Radiation Simulation. In Proceedings of the 2021 IEEE PES Innovative Smart Grid Technologies—Asia (ISGT Asia), Brisbane, Australia, 5–8 December 2021. [Google Scholar]
- Nakhaee, A.; Paydar, A. DeepRadiation: An Intelligent Augmented Reality Platform for Predicting Urban Energy Performance Just through 360 Panoramic Streetscape Images Utilizing Various Deep Learning Models. Build. Simul. 2023, 16, 499–510. [Google Scholar] [CrossRef]
- Nex, F.; Remondino, F.; Agugiaro, G.; De Filippi, R.; Poletti, M.; Furlanello, C.; Menegon, S.; Dallago, G.; Fontanari, S. 3D SolarWeb: A Solar Cadaster in the Italian Alpine Landscape. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 40, 173–178. [Google Scholar] [CrossRef]
- Palliwal, A.; Song, S.; Tan, H.T.W.; Biljecki, F. 3D City Models for Urban Farming Site Identification in Buildings. Comput. Environ. Urban. Syst. 2021, 86, 101584. [Google Scholar] [CrossRef]
- Pedrero, J.; Hermoso, N.; Hernández, P.; Munoz, I.; Arrizabalaga, E.; Mabe, L.; Prieto, I.; Izkara, J.L. Assessment of Urban-Scale Potential for Solar PV Generation and Consumption. In Proceedings of the IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2019; Volume 323. [Google Scholar]
- Peng, F.; Wong, M.S.; Nichol, J.E.; Chan, P.W. Historical GIS Data and Changes in Urban Morphological Parameters for the Analysis of Urban Heat Islands in Hong Kong. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 55–62. [Google Scholar] [CrossRef]
- Prades-Gil, C.; Viana-Fons, J.D.; Masip, X.; Cazorla-Marín, A.; Gómez-Navarro, T. An Agile Heating and Cooling Energy Demand Model for Residential Buildings. Case Study in a Mediterranean City Residential Sector. Renew. Sustain. Energy Rev. 2023, 175, 113166. [Google Scholar] [CrossRef]
- Prieto, I.; Izkara, J.L.; Usobiaga, E. The Application of Lidar Data for the Solar Potential Analysis Based on Urban 3D Model. Remote Sens. 2019, 11, 2348. [Google Scholar] [CrossRef]
- Pružinec, F.; Ďuračiová, R. A Point-Cloud Solar Radiation Tool. Energies 2022, 15, 7018. [Google Scholar] [CrossRef]
- Redweik, P.M.; Catita, C.; Brito, M.C. 3D Local Scale Solar Radiation Model Based on Urban LiDAR Data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 38, 265–269. [Google Scholar] [CrossRef]
- Ren, H.; Ma, Z.; Ming Lun Fong, A.; Sun, Y. Optimal Deployment of Distributed Rooftop Photovoltaic Systems and Batteries for Achieving Net-Zero Energy of Electric Bus Transportation in High-Density Cities. Appl. Energy 2022, 319, 119274. [Google Scholar] [CrossRef]
- Ren, H.; Xu, C.; Ma, Z.; Sun, Y. A Novel 3D-Geographic Information System and Deep Learning Integrated Approach for High-Accuracy Building Rooftop Solar Energy Potential Characterization of High-Density Cities. Appl. Energy 2022, 306, 117985. [Google Scholar] [CrossRef]
- Saadaoui, H.; Ghennioui, A.; Ikken, B.; Rhinane, H.; Maanan, M. Using GIS and Photogrammetry for Assessing Solar Photovoltaic Potential on Flat Roofs in Urban Area Case of the City of Ben Guerir/Morocco. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 155–166. [Google Scholar] [CrossRef]
- Saran, S.; Wate, P.; Srivastav, S.K.; Krishna Murthy, Y.V.N. CityGML at Semantic Level for Urban Energy Conservation Strategies. Ann. GIS 2015, 21, 27–41. [Google Scholar] [CrossRef]
- Singh, S.K.; Lohani, B.; Arora, L.; Choudhary, D.; Nagarajan, B. A Visual-Inertial System to Determine Accurate Solar Insolation and Optimal PV Panel Orientation at a Point and over an Area. Renew. Energy 2020, 154, 223–238. [Google Scholar] [CrossRef]
- Soares, P.; Bayrakci-Boz, M.; Brownson, J.R.S. GIS Information for Solar PV Energy Siting: A Case Study in the Borough of State College, PA, USA. In Proceedings of the Conference Record of the IEEE Photovoltaic Specialists Conference, Calgary, AB, Canada, 15 June–21 August 2020; Volume 2020, pp. 1749–1753. [Google Scholar]
- Sun, D.; Tan, Y.; Zhang, S. Research and Application of GIS in Wisdom Forestry Wireless Sensor Networks Node Location Selection. In Proceedings of the 2019 IEEE 4th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chengdu, China, 20–22 December 2019; pp. 232–235. [Google Scholar]
- Tara, A.; Patuano, A.; Lawson, G. Between 2d and 3d: Studying Structural Complexity of Urban Fabric Using Voxels and Lidar-Derived Dsms. Fractal Fract. 2021, 5, 227. [Google Scholar] [CrossRef]
- Teofilo, A.; Sun, Q.C.; Radosevic, N.; Tao, Y.; Iringan, J.; Liu, C. Investigating Potential Rooftop Solar Energy Generated by Leased Federal Airports in Australia: Framework and Implications. J. Build. Eng. 2021, 41, 102390. [Google Scholar] [CrossRef]
- Wate, P.; Saran, S. Implementation of CityGML Energy Application Domain Extension (ADE) for Integration of Urban Solar Potential Indicators Using Object-Oriented Modelling Approach. Geocarto Int. 2015, 30, 1144–1162. [Google Scholar] [CrossRef]
- Yan, L.; Zhu, R.; Kwan, M.-P.; Luo, W.; Wang, D.; Zhang, S.; Wong, M.S.; You, L.; Yang, B.; Chen, B.; et al. Estimation of Urban-Scale Photovoltaic Potential: A Deep Learning-Based Approach for Constructing Three-Dimensional Building Models from Optical Remote Sensing Imagery Imagery. Sustain. Cities Soc. 2023, 93, 104515. [Google Scholar] [CrossRef]
- Yoon, D.H.; Song, J.H.; Koh, J.H. Estimation of Solar Radiation Potential in the Urban Buildings Using CIE Sky Model and Ray-Tracing. J. Korean Soc. Surv. Geod. Photogramm. Cartogr. 2020, 38, 141–151. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; She, J.; Peng, X. Assimilating Remote Sensing Data into GIS-Based All Sky Solar Radiation Modeling for Mountain Terrain. Remote Sens. Environ. 2019, 231, 111239. [Google Scholar] [CrossRef]
- Zhu, R.; Cheng, C.; Santi, P.; Chen, M.; Zhang, X.; Mazzarello, M.; Wong, M.S.; Ratti, C. Optimization of Photovoltaic Provision in a Three-Dimensional City Using Real-Time Electricity Demand. Appl. Energy 2022, 316, 119042. [Google Scholar] [CrossRef]
- Decreto Legislativo 387/2003 2003. Available online: https://www.parlamento.it/parlam/leggi/deleghe/03387dl.htm (accessed on 10 October 2023).
- Directive 2001/77/CE of the European Parliament and of the Council of 27 September 2001 on the Promotion of Electricity Produced from Renewable Energy Sources in the Internal Electricity Market 2001.
- Meteonorm Intro. Available online: https://Meteonorm.Com/En/ (accessed on 11 October 2023).
- SoDa. Available online: https://Www.Soda-pro.Com/ (accessed on 11 October 2023).
- World Weather Online. Available online: https://Www.Worldweatheronline.Com/ (accessed on 11 October 2023).
- Sun Earth Tools. Available online: https://Www.Sunearthtools.Com/ (accessed on 11 October 2023).
- Iqbal, M. An Introduction to Solar Radiation; Elsevier: Amsterdam, The Netherlands, 1983; ISBN 9780123737502. [Google Scholar]
- Xie, Y.; Sengupta, M.; Dudhia, J. A Fast All-Sky Radiation Model for Solar Applications (FARMS): Algorithm and Performance Evaluation. Sol. Energy 2016, 135, 435–445. [Google Scholar] [CrossRef]
- Freitas, S.; Catita, C.; Redweik, P.; Brito, M.C. Modelling Solar Potential in the Urban Environment: State-of-the-Art Review. Renew. Sustain. Energy Rev. 2015, 41, 915–931. [Google Scholar] [CrossRef]
- Šúri, M.; Huld, T.A.; Dunlop, E.D. PV-GIS: A Web-Based Solar Radiation Database for the Calculation of PV Potential in Europe. Int. J. Sustain. Energy 2005, 24, 55–67. [Google Scholar] [CrossRef]
- Energy Saving Trust Solar Energy Calculator Sizing Guide. Available online: https://www.pvfitcalculator.energysavingtrust.org.uk/Documents/150224_SolarEnergy_Calculator_Sizing_Guide_v1.pdf (accessed on 10 October 2023).
- Green, M.A.; Dunlop, E.D.; Yoshita, M.; Kopidakis, N.; Bothe, K.; Siefer, G.; Hao, X. Solar Cell Efficiency Tables (Version 62). Prog. Photovolt. Res. Appl. 2023, 31, 651–663. [Google Scholar] [CrossRef]
- Zhang, H.L.; Baeyens, J.; Degrève, J.; Cacères, G. Concentrated Solar Power Plants: Review and Design Methodology. Renew. Sustain. Energy Rev. 2013, 22, 466–481. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).