Analysis of Offline Transient Power Oscillation and Its Suppression Method in the Microgrid with Multiple Virtual Synchronous Generators
Abstract
:1. Introduction
- Establishes an equivalent RLC circuit model for VSGs, which is more intuitive and scalable than existing multi-VSG analysis based on state space equations and other modeling methods. The VSG offline transient expressions of multi-VSG systems are then easily derived.
- Discovers that the third-order oscillatory term in the output power expression is the root cause of the power oscillations during the VSG offline transient process.
- Proposes a configuration scheme for the equivalent circuit parameters to eliminate the resonance in the paralleled equivalent RLC circuits. Equivalently, the virtual inertia, damping coefficient and virtual impedance of VSGs are configured to eliminate the power oscillation in multi-VSG systems.
- An experimental platform with a three-VSG-based microgrid is constructed, and a significant improvement of the power oscillation during the VSG offline transient process is obtained with the proposed parameter configuration scheme.
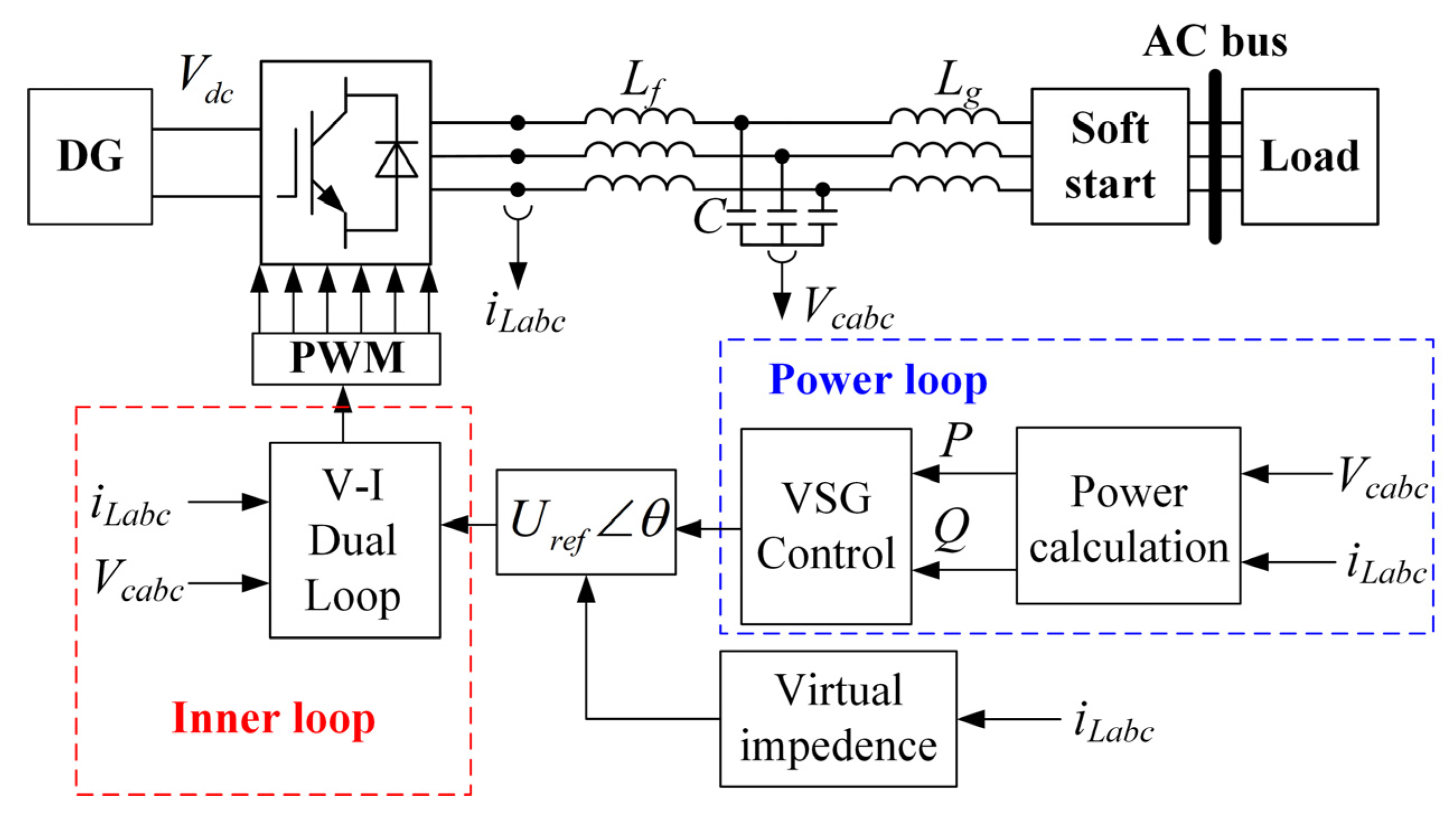
2. Multi-VSG System Modeling
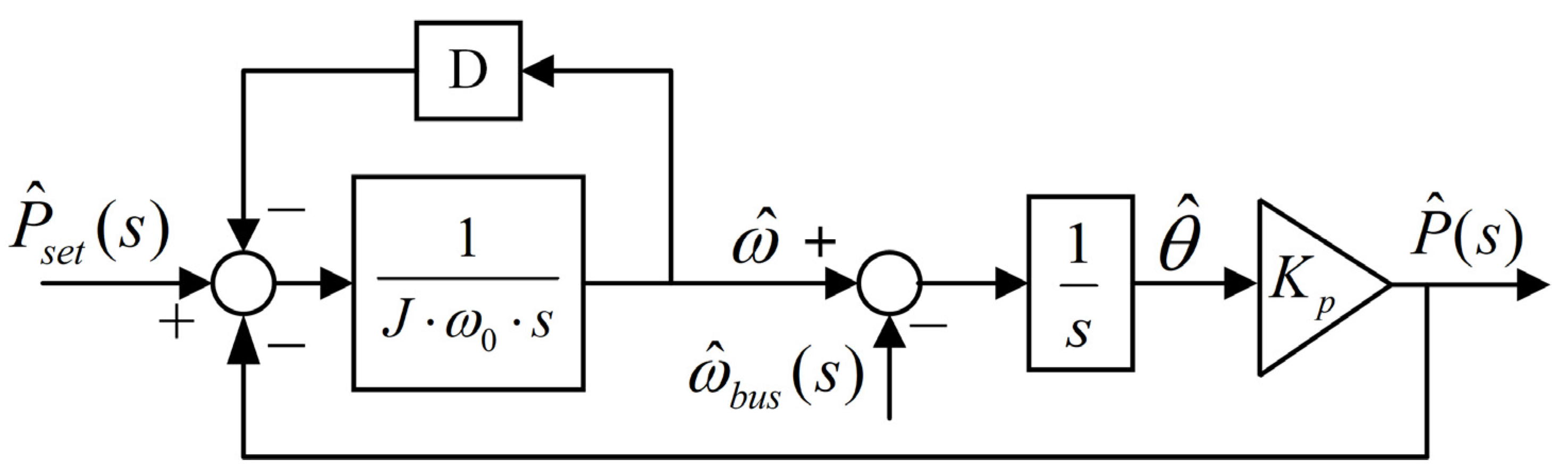
2.1. VSG Fundamentals
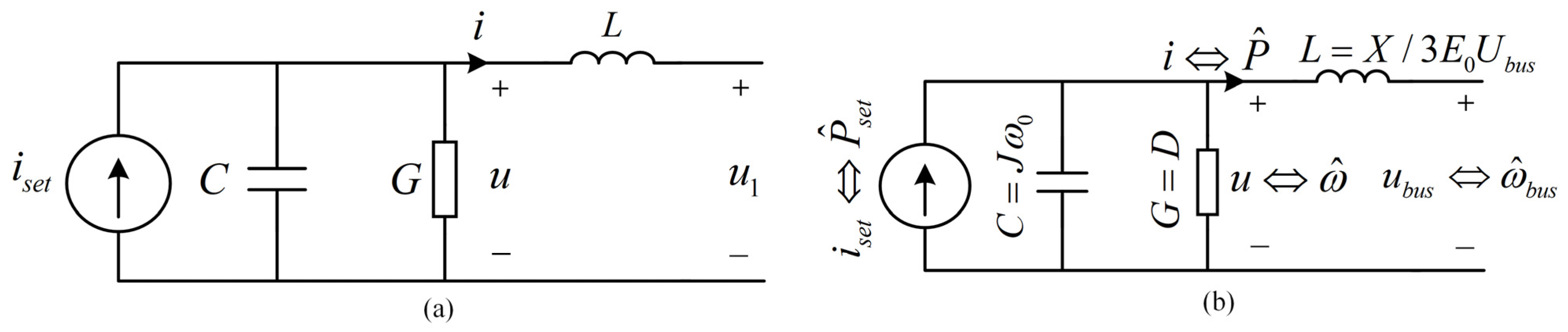
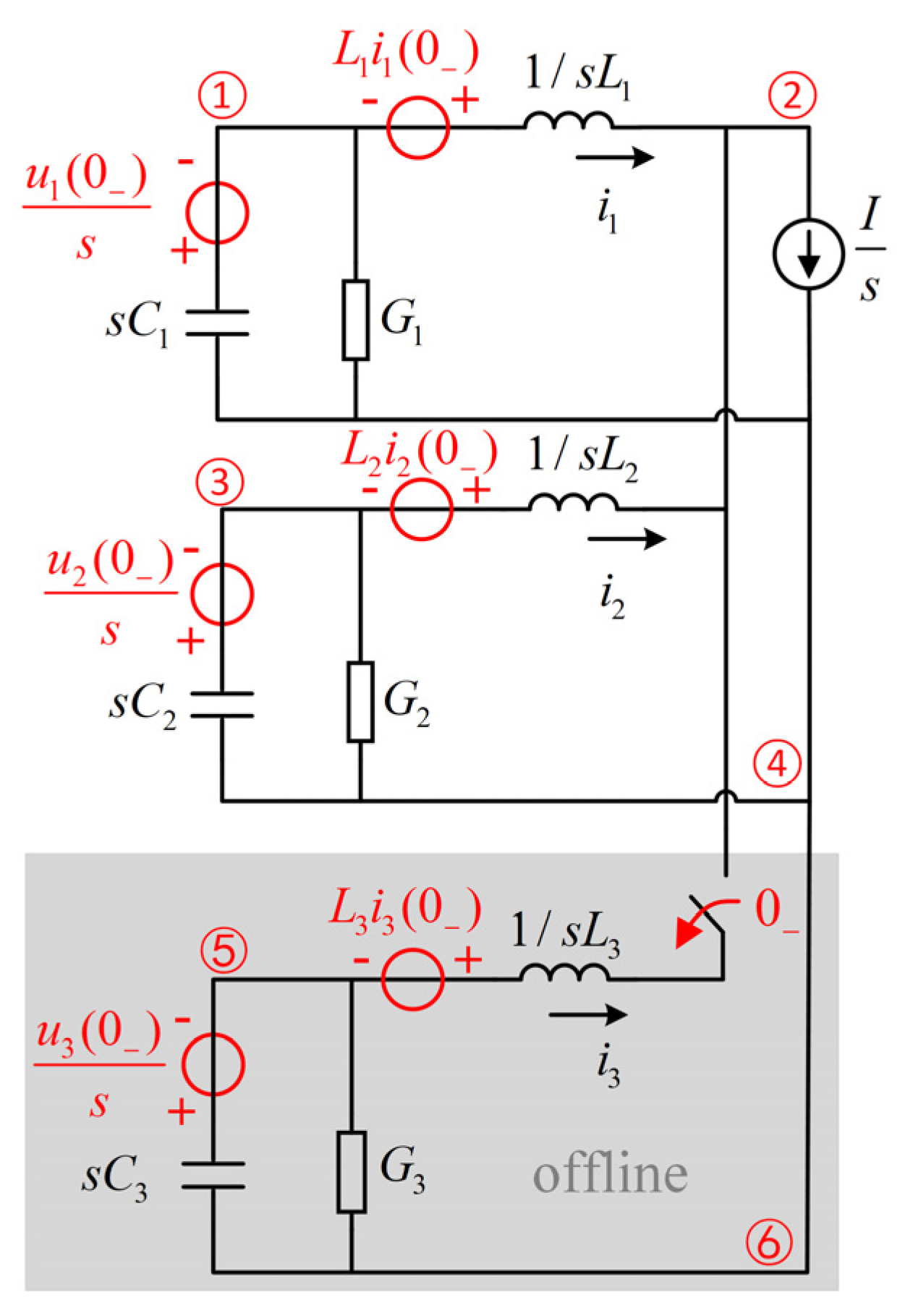
2.2. Equivalent Circuit Model of VSG Active Loop
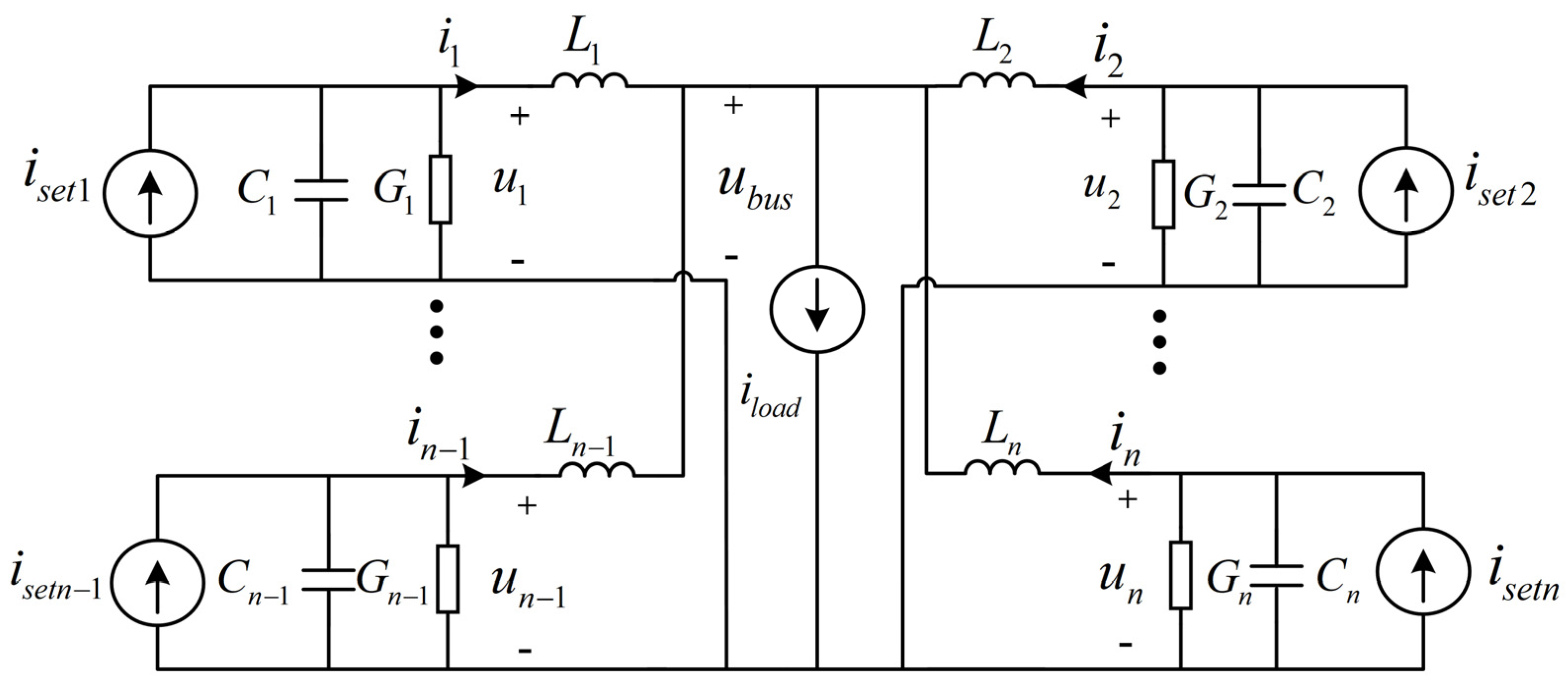
3. Analysis and Suppression of VSG Offline Transients
3.1. Analysis of VSG Offline Transient Process
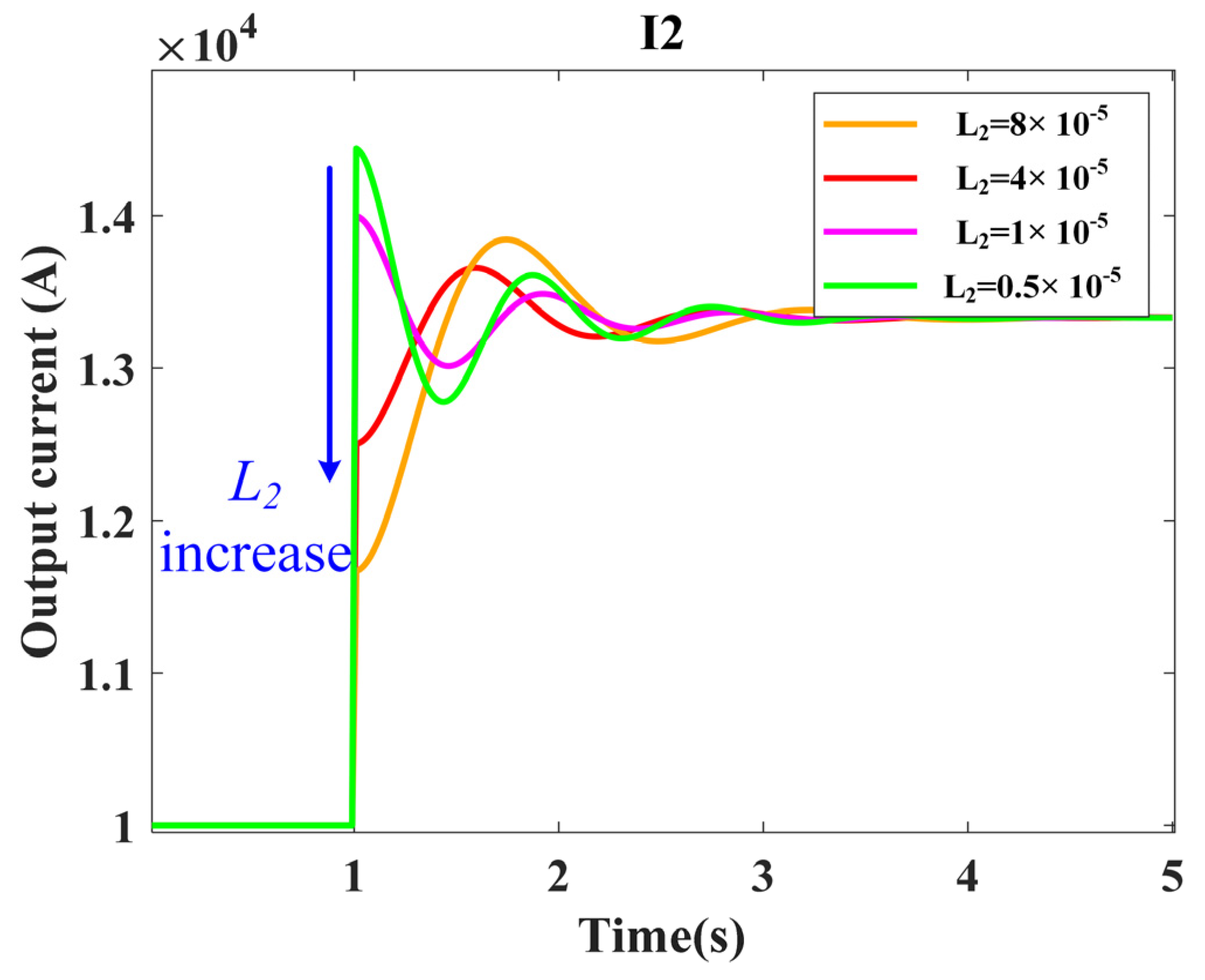
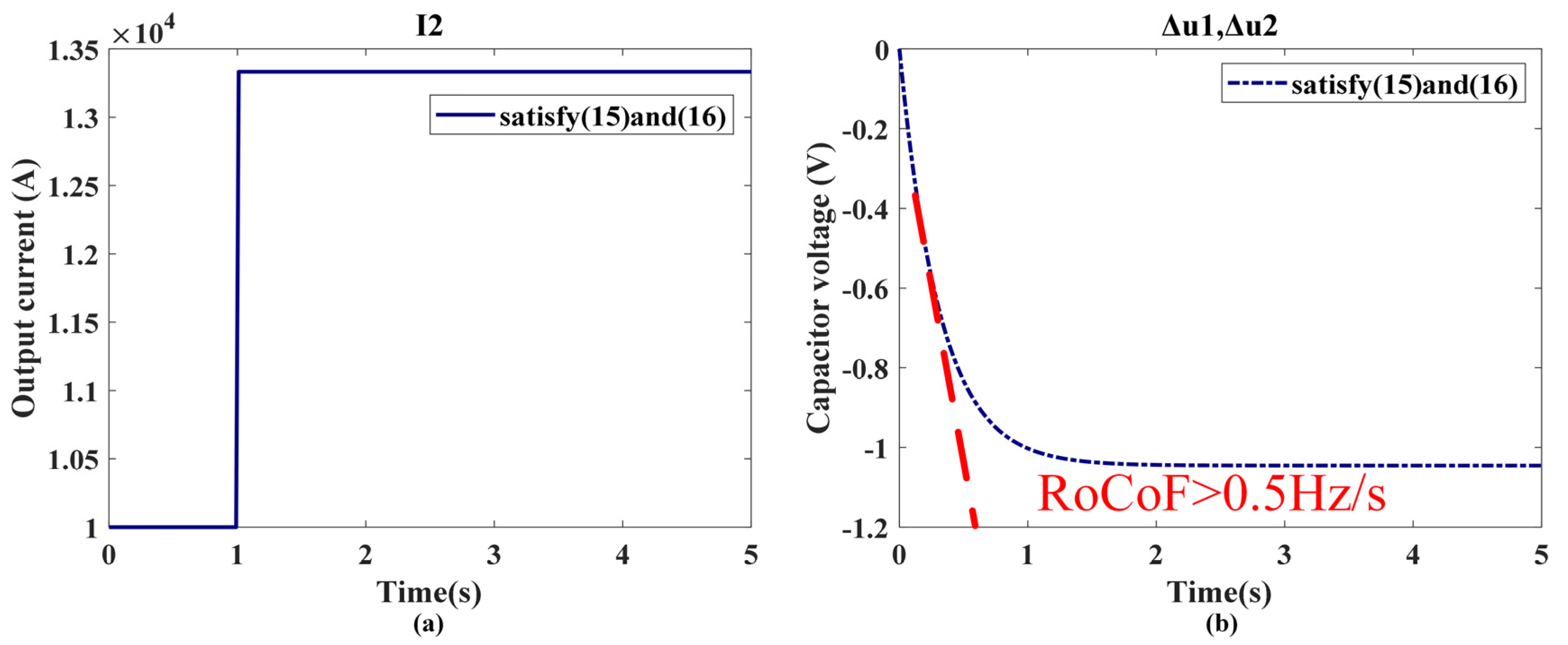
3.2. Configuration of VSG Equivalent Circuit Parameters to Eliminate Offline Transient
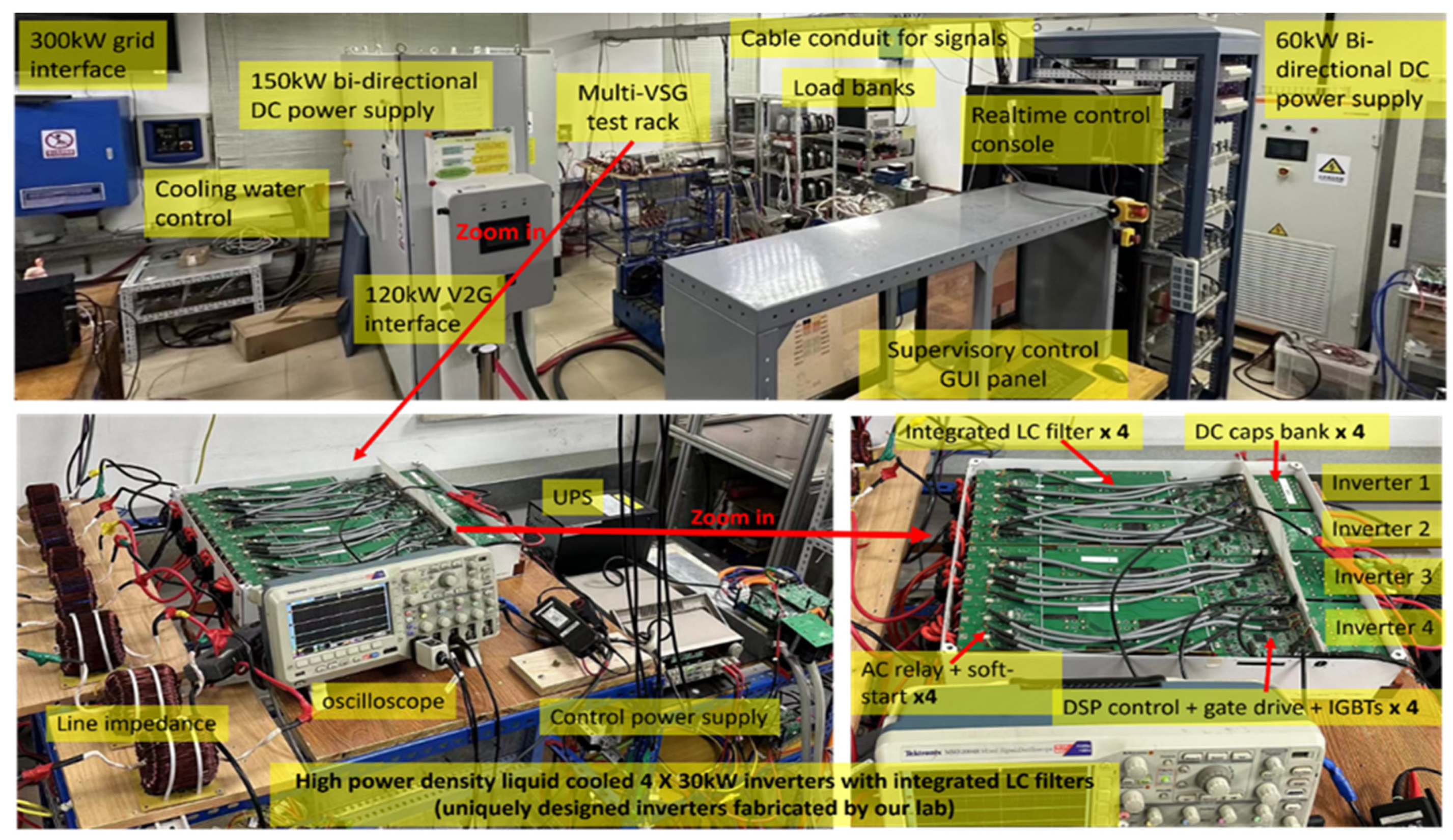
4. Experimental Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shuai, Z.; Sun, Y.; Shen, Z.J.; Tian, W.; Tu, C.; Li, Y.; Yin, X. Microgrid stability: Classification and a review. Renew. Sustain. Energy Rev. 2016, 58, 167–179. [Google Scholar] [CrossRef]
- Markovic, U.; Stanojev, O.; Aristidou, P.; Vrettos, E.; Callaway, D.S.; Hug, G. Understanding Small-Signal Stability of Low-Inertia Systems. IEEE Trans. Power Syst. 2021, 36, 3997–4017. [Google Scholar] [CrossRef]
- Zhang, W.; Cantarellas, A.M.; Rocabert, J.; Luna, A.; Rodriguez, P. Synchronous Power Controller With Flexible Droop Characteristics for Renewable Power Generation Systems. IEEE Trans. Sustain. Energy 2016, 7, 1572–1582. [Google Scholar] [CrossRef]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. On the Inertia of Future More-Electronics Power Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 7, 2130–2146. [Google Scholar] [CrossRef]
- Sun, P.; Xu, H.; Yao, J.; Chi, Y.; Huang, S.; Cao, J. Dynamic Interaction Analysis and Damping Control Strategy of Hybrid System with Grid-forming and Grid-following Control Modes. IEEE Trans. Energy Convers. 2023, 38, 1639–1649. [Google Scholar] [CrossRef]
- Zhong, Q.-C.; Weiss, G. Synchronverters: Inverters that Mimic Synchronous Generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Pan, D.; Wang, X.; Liu, F.; Shi, R. Transient Stability of Voltage-Source Converters With Grid-Forming Control: A Design-Oriented Study. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1019–1033. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.; Cao, Y.; Wang, L.; Blaabjerg, F.; Dragicevic, T. Frequency and Voltage Stability Analysis of Grid-Forming Virtual Synchronous Generator Attached to Weak Grid. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 10, 2662–2671. [Google Scholar] [CrossRef]
- Abuagreb, M.; Ajao, B.; Herbert, H.; Johnson, B.K. Evaluation of Virtual Synchronous Generator Compared to Synchronous Generator. In Proceedings of the 2020 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 17–20 February 2020; pp. 1–5. [Google Scholar]
- Li, M.; Wang, Y.; Hu, W.; Shu, S.; Yu, P.; Zhang, Z.; Blaabjerg, F. Unified Modeling and Analysis of Dynamic Power Coupling for Grid-Forming Converters. IEEE Trans. Power Electron. 2021, 37, 2321–2337. [Google Scholar] [CrossRef]
- Duan, Q.; Zhao, C. Improved VSG Controlled SST in a Low-Voltage AC Distribution Network. In Proceedings of the 2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, 23–25 December 2021; pp. 428–435. [Google Scholar]
- Lei, J.; Xiang, X.; Liu, B.; Li, W.; He, X. Quantitative and Intuitive VSG Transient Analysis With the Concept of Damping Area Approximation. IEEE Trans. Smart Grid 2023, 14, 2477–2480. [Google Scholar] [CrossRef]
- Wu, H.; Ruan, X.; Yang, D.; Chen, X.; Zhao, W.; Lv, Z.; Zhong, Q.-C. Small-Signal Modeling and Parameters Design for Virtual Synchronous Generators. IEEE Trans. Ind. Electron. 2016, 63, 4292–4303. [Google Scholar] [CrossRef]
- Wu, W.; Zhou, L.; Chen, Y.; Luo, A.; Dong, Y.; Zhou, X.; Xu, Q.; Yang, L.; Guerrero, J.M. Sequence-Impedance-Based Stability Comparison Between VSGs and Traditional Grid-Connected Inverters. IEEE Trans. Power Electron. 2018, 34, 46–52. [Google Scholar] [CrossRef]
- Harnefors, L.; Hinkkanen, M.; Riaz, U.; Rahman, F.M.M.; Zhang, L. Robust Analytic Design of Power-Synchronization Control. IEEE Trans. Ind. Electron. 2018, 66, 5810–5819. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Ise, T. Comparison of Dynamic Characteristics Between Virtual Synchronous Generator and Droop Control in Inverter-Based Distributed Generators. IEEE Trans. Power Electron. 2016, 31, 3600–3611. [Google Scholar] [CrossRef]
- Alipoor, J.; Miura, Y.; Ise, T. Stability Assessment and Optimization Methods for Microgrid With Multiple VSG Units. IEEE Trans. Smart Grid 2016, 9, 1462–1471. [Google Scholar] [CrossRef]
- Alipoor, J.; Miura, Y.; Ise, T. Power System Stabilization Using Virtual Synchronous Generator With Alternating Moment of Inertia. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 3, 451–458. [Google Scholar] [CrossRef]
- Li, D.; Zhu, Q.; Lin, S.; Bian, X.Y. A Self-Adaptive Inertia and Damping Combination Control of VSG to Support Frequency Stability. IEEE Trans. Energy Convers. 2016, 32, 397–398. [Google Scholar] [CrossRef]
- Hu, W.; Shen, Y.; Lun, J.; Yang, F.; Zhao, S. Study on Secondary Non-Differential Frequency Modulation Control Strategy of VSG in Islanding Mode. IEEE Access 2023, 11, 116979–116989. [Google Scholar] [CrossRef]
- Zhang, X.; Mao, F.; Xu, H.; Liu, F.; Li, M. An optimal coordination control strategy of micro-grid inverter and energy storage based on variable virtual inertia and damping of vsg. Chin. J. Electr. Eng. 2017, 3, 25–33. [Google Scholar]
- Meng, X.; Liu, J.; Liu, Z. A Generalized Droop Control for Grid-Supporting Inverter Based on Comparison Between Tradi-tional Droop Control and Virtual Synchronous Generator Control. IEEE Trans. Power Electron. 2019, 34, 5416–5438. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Bevrani, H.; Ise, T. Enhanced Virtual Synchronous Generator Control for Parallel Inverters in Microgrids. IEEE Trans. Smart Grid 2016, 8, 2268–2277. [Google Scholar] [CrossRef]
- Paquette, A.D.; Reno, M.J.; Harley, R.G.; Divan, D.M. Sharing Transient Loads: Causes of Unequal Transient Load Sharing in Islanded Microgrid Operation. IEEE Ind. Appl. Mag. 2013, 20, 23–34. [Google Scholar] [CrossRef]
- Chen, M.; Zhou, D.; Wu, C.; Blaabjerg, F. Characteristics of Parallel Inverters Applying Virtual Synchronous Generator Control. IEEE Trans. Smart Grid 2021, 12, 4690–4701. [Google Scholar] [CrossRef]
- Shuai, Z.; Huang, W.; Shen, Z.J.; Luo, A.; Tian, Z. Active Power Oscillation and Suppression Techniques Between Two Parallel Synchronverters During Load Fluctuations. IEEE Trans. Power Electron. 2019, 35, 4127–4142. [Google Scholar] [CrossRef]
- Li, M.; Yu, P.; Hu, W.; Wang, Y.; Shu, S.; Zhang, Z.; Blaabjerg, F. Phase Feedforward Damping Control Method for Virtual Synchronous Generators. IEEE Trans. Power Electron. 2022, 37, 9790–9806. [Google Scholar] [CrossRef]
- Rathnayake, D.B.; Razzaghi, R.; Bahrani, B. Generalized Virtual Synchronous Generator Control Design for Renewable Power Systems. IEEE Trans. Sustain. Energy 2022, 13, 1021–1036. [Google Scholar] [CrossRef]
- Yang, D.; Ruan, X.; Wu, H. Using virtual impedance network to improve the control performances of LCL-type grid-connected inverter under the weak grid condition. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition—APEC 2014, Fort Worth, TX, USA, 16–20 March 2014; pp. 3048–3054. [Google Scholar]
- Li, C.; Yang, Y.; Cao, Y.; Aleshina, A.; Xu, J.; Blaabjerg, F. Grid Inertia and Damping Support Enabled by Proposed Virtual Inductance Control for Grid-Forming Virtual Synchronous Generator. IEEE Trans. Power Electron. 2022, 38, 294–303. [Google Scholar] [CrossRef]
- Qin, B.; Xu, Y.; Yuan, C.; Jia, J. A Unified Method of Frequency Oscillation Characteristic Analysis for Multi-VSG Grid-Connected System. IEEE Trans. Power Deliv. 2021, 37, 279–289. [Google Scholar] [CrossRef]


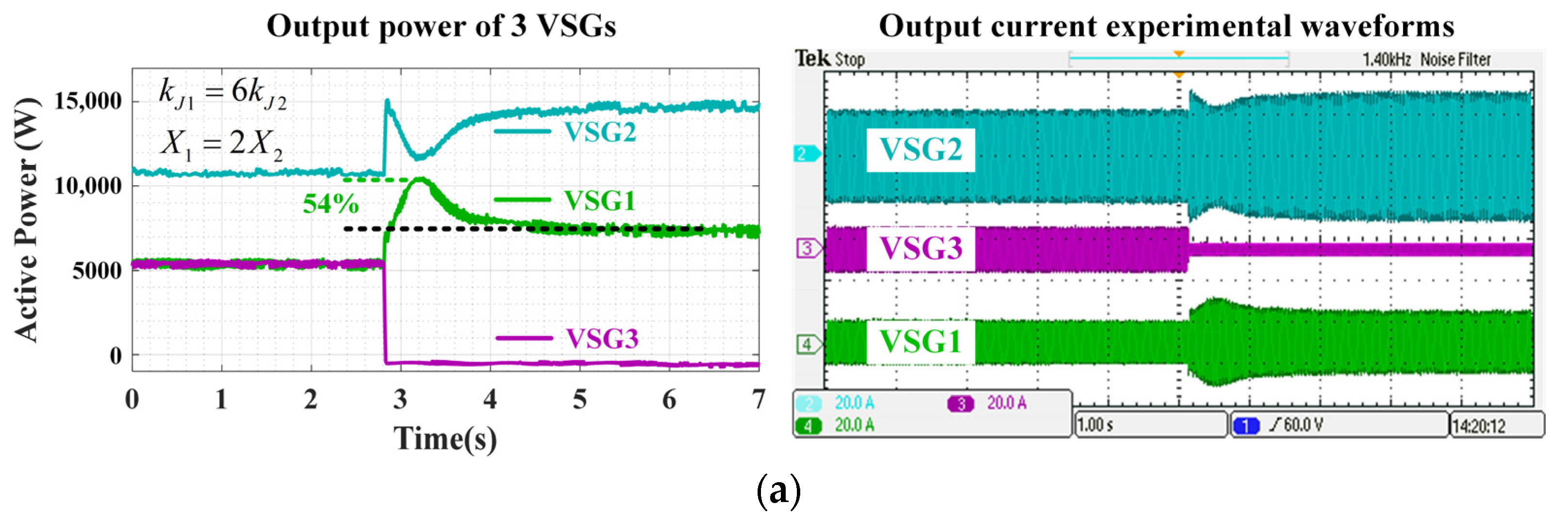
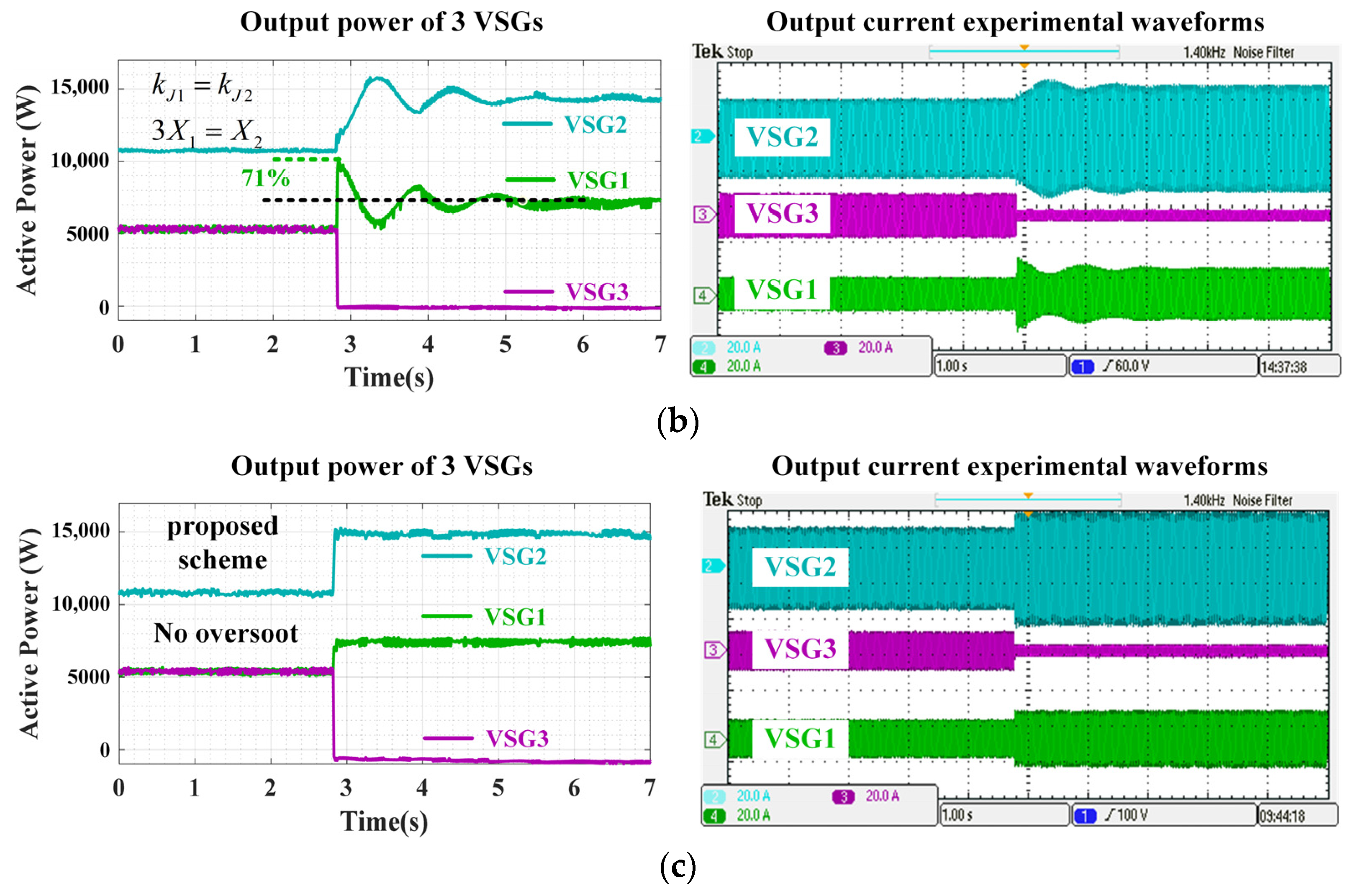
| Parameters | Ci (F) | Gi (S) | Li (H) | |
|---|---|---|---|---|
| Serial Number | ||||
| VSG1 | 2000 | 4000 | 2 × 10−5 | |
| VSG2 | 4000 | 8000 | 1 × 10−5 | |
| VSG3 | 2000 | 4000 | 2 × 10−5 | |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| E0 | 220 V | S1, S3 | 10 kVA |
| ω0 | 100 π rad/s | S2 | 20 kVA |
| RoCoF | 1 Hz/s | Lg1, Lg3 | 700 μH |
| ∆fmax | ±0.5 Hz | Lg2 | 1200 μH |
| fs | 20 kHz | Lf(1,2,3) | 300 μH |
| Pload | 20 kW | C(1,2,3) | 30 μF |
| Parameters | J (kg·m2) | D (N·s/m) | X (Ω) | |
|---|---|---|---|---|
| Serial Number | ||||
| VSG1 | 1885 | 4000 | 1.9 | |
| VSG2 | 3770 | 8000 | 0.95 | |
| VSG3 | 1885 | 4000 | 1.9 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, L.; Yang, B.; Lu, S. Analysis of Offline Transient Power Oscillation and Its Suppression Method in the Microgrid with Multiple Virtual Synchronous Generators. Energies 2023, 16, 7711. https://doi.org/10.3390/en16237711
Shan L, Yang B, Lu S. Analysis of Offline Transient Power Oscillation and Its Suppression Method in the Microgrid with Multiple Virtual Synchronous Generators. Energies. 2023; 16(23):7711. https://doi.org/10.3390/en16237711
Chicago/Turabian StyleShan, Liang, Bo Yang, and Shuai Lu. 2023. "Analysis of Offline Transient Power Oscillation and Its Suppression Method in the Microgrid with Multiple Virtual Synchronous Generators" Energies 16, no. 23: 7711. https://doi.org/10.3390/en16237711
APA StyleShan, L., Yang, B., & Lu, S. (2023). Analysis of Offline Transient Power Oscillation and Its Suppression Method in the Microgrid with Multiple Virtual Synchronous Generators. Energies, 16(23), 7711. https://doi.org/10.3390/en16237711





