Next Article in Journal
The Role of Green Finance in Fostering the Sustainability of the Economy and Renewable Energy Supply: Recent Issues and Challenges
Previous Article in Journal
Analysis of Offline Transient Power Oscillation and Its Suppression Method in the Microgrid with Multiple Virtual Synchronous Generators
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 16
Issue 23
10.3390/en16237709
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Estimating Compressional Velocity and Bulk Density Logs in Marine Gas Hydrates Using Machine Learning

by
Fawz Naim
*,
Ann E. Cook
and
Joachim Moortgat
School of Earth Sciences, The Ohio State University, Columbus, OH 43210, USA
*
Author to whom correspondence should be addressed.
Energies 2023, 16(23), 7709; https://doi.org/10.3390/en16237709
Submission received: 17 October 2023 / Revised: 13 November 2023 / Accepted: 17 November 2023 / Published: 22 November 2023
(This article belongs to the Section H: Geo-Energy)
Browse Figures
Versions Notes

Abstract

:
Compressional velocity (Vp) and bulk density (ρb) logs are essential for characterizing gas hydrates and near-seafloor sediments; however, it is sometimes difficult to acquire these logs due to poor borehole conditions, safety concerns, or cost-related issues. We present a machine learning approach to predict either compressional Vp or ρb logs with high accuracy and low error in near-seafloor sediments within water-saturated intervals, in intervals where hydrate fills fractures, and intervals where hydrate occupies the primary pore space. We use scientific-quality logging-while-drilling well logs, gamma ray, ρb, Vp, and resistivity to train the machine learning model to predict Vp or ρb logs. Of the six machine learning algorithms tested (multilinear regression, polynomial regression, polynomial regression with ridge regularization, K nearest neighbors, random forest, and multilayer perceptron), we find that the random forest and K nearest neighbors algorithms are best suited to predicting Vp and ρb logs based on coefficients of determination (R2) greater than 70% and mean absolute percentage errors less than 4%. Given the high accuracy and low error results for Vp and ρb prediction in both hydrate and water-saturated sediments, we argue that our model can be applied in most LWD wells to predict Vp or ρb logs in near-seafloor siliciclastic sediments on continental slopes irrespective of the presence or absence of gas hydrate.

1. Introduction

Natural gas hydrate occurs in near-seafloor sediments worldwide; detecting and quantifying gas hydrate is a challenge but important for understanding the amount and contribution of gas hydrate in the global carbon cycle and for assessing gas hydrate as a prospective energy resource [1,2]. Out of the different methods for interpreting hydrate, downhole logging measurements are the most accurate way to identify the amount of gas hydrate in the subsurface.
The most common downhole logs used for interpreting gas hydrate are compressional velocity (Vp), resistivity, and bulk density (ρb) [3]. The measurement response for Vp in hydrate-bearing sediments depends on whether hydrate occurs in the primary pore space or as fill-in veins or fractures. In coarse-grained sand or silt, hydrate nucleates in the primary pore space [4,5]. When hydrate saturation exceeds ~40%, hydrate begins to form a rigid framework; at that saturation, there is a distinct increase in formation moduli that increases Vp relative to water-saturated sediments [6]. Hydrate in marine muds and clays is usually observed in fractures, and those fractures likely grow in place due to the formation of hydrate and methane supplied via microbial methanogenesis [7]. Vp, however, does not usually increase significantly in hydrate-filled fractures, as these accumulations usually have lower hydrate saturation than sand or silt layers [8].
Gas hydrate increases electrical resistivity, as it is an electrical insulator [3]. When hydrate is in the primary pore space, resistivity increases with increasing hydrate saturation [9,10]. However, when hydrate is in near-vertical fractures, the increase in resistivity is not only related to the amount of hydrate but also depends on fracture orientation [11].
Bulk density in near-seafloor sediments provides the most accurate measurement of porosity (e.g., [3]). Porosity is essential for calculating hydrate saturation using both resistivity and Vp [12,13]. Therefore, bulk density is linked to the interpretation of hydrate. However, the small difference in the bulk density of hydrate (0.92 g/cm3 [12]) and porewater (1.02 g/cm3) makes hydrate effectively undetectable from the bulk density log.
Hydrate interpretation relies on good quality Vp and ρb logs; however, these logs are sometimes poor quality or are not acquired in near-seafloor sediments. For example, there are ~70 LWD scientific ocean drilling holes with missing Vp or ρb logs in the Lamont–Doherty Earth Observatory database.
Machine learning is an effective tool that can be used for building both linear and non-linear correlations to predict or fill in missing data [14,15]. Supervised learning is a type of machine learning that trains a model using input and output features from a labeled input dataset and predicts based on a new or novice dataset to test the accuracy of the model [16]. For supervised learning, available data are often split into training and validation datasets [16]. The training dataset is used so that the computer model can learn; in addition, a small proportion of the training dataset is used to validate the model [16].
Supervised machine learning models have been applied to marine geology [17,18,19,20,21,22] and geophysics [23,24], geochemistry [25,26], and gas hydrate [26,27,28,29] datasets to predict different physical properties. For example, Graw et al. [30] used the random forest algorithm to predict global seafloor sediment bulk density using core measurements acquired with scientific ocean drilling programs. Sain and Kumar [31] used artificial neural networks to interpret subsurface geological features with a combination of seismic attributes. Similarly, Farfour, and Mesbah; Ismail et al.; and Ramya et al. [17,18,19] used artificial neural networks to interpret subsurface features such as gas chimneys, channels, and hydrocarbon-saturated rocks using marine seismic data. Dumke and Berndt [32] used Vp logs, local geological information (such as water depth and distance to the basement), and the random forest algorithm to predict subseafloor Vp trends worldwide. In a more related study conducted in an Arctic permafrost region, Singh et al. [27] used a variety of different machine learning algorithms and well log combinations to predict gas hydrate saturation.
In this work, we use a machine learning model to predict Vp and ρb logs in near-seafloor sediments, which includes both water-saturated and hydrate-bearing sediments. This includes predicting Vp and ρb logs and their variations with different depths and different hydrate morphologies, including hydrate in pores and hydrate in fractures. Our model results have broad relevance and are not only applicable to marine hydrate systems but may also be useful for researchers working to identify shallow natural hazards such as overpressure intervals or landslides in near-seafloor marine sediments [33,34]. In these cases, Vp and ρb are essential inputs for computing overburden stress and pore pressure [33,35]. In addition, our model results will be useful for well-to-seismic ties since Vp and ρb logs are essential inputs for linking seismic data (measured in time) to well logs (measured in depth) (e.g., [36]).

2. Data

For our machine learning model, we use data only acquired by logging-while-drilling (LWD) tools as they collect the highest-quality well-logging datasets in a borehole. This is because LWD tools are placed directly behind the drill bit and acquire data before sediments have time to erode [3]. This ensures that the machine learning model is trained on quality data and can make predictions with high accuracy.
We downloaded all the available LWD data from 22 holes from three primary locations on continental slopes from the Lamont–Doherty Earth Observatory database to train, validate, and test each machine learning model (Figure 1): 7 holes from the Gulf of Mexico collected by the Gas Hydrate Joint Industry Project (JIP) Leg II [37], 3 holes from Cascadia Margin collected during the Integrated Ocean Drilling Program (IODP) Expedition 311 [38], and 12 holes from the Bay of Bengal collected during Indian National Gas Hydrate Program (NGHP) Expedition 01 [39]. All these holes host a range of siliciclastic sediment types, and some of these holes contain natural gas hydrates.

2.1. Training Holes

We use LWD datasets from 20 holes from the Gulf of Mexico, the Cascadia Margin, and the Bay of Bengal to train the machine learning model (Figure 1).
The training holes from the northern Gulf of Mexico were drilled by JIP Leg II and are in Green Canyon (Figure 1) and Alaminos Canyon (Figure 1) [37]. The three holes in Green Canyon in Block 955 (GC955) are in ~2 km of water and with sediments sourced from turbidite channel–levee complexes and hemipelagic marine muds [40,41]. Hole GC955-H has high-quality LWD data drilled to 590 mbsf that include 412 m of water-saturated sediments, 144 m of near-vertical gas-hydrate-filled fractures in clay sediments with low hydrate saturations, and 34 m of hydrate in the primary pore space of a coarse silt reservoir with saturation ranging from 30 to 80% [42]. Holes GC955-Q and GC955-I also have high-quality LWD data to 461 and 671 mbsf in mostly water-saturated sediments [37]. Alaminos Canyon Block 21 (AC21) lies in the northwestern Gulf of Mexico at a water depth of ~1.5 km. Holes AC21-A and AC21-B are drilled to depths of 536 and 340 mbsf. Sediments in both holes are primarily water-saturated marine muds, with one ~60 m water-saturated sand interval that is part of a large submarine fan system [43,44].
IODP Expedition 311 drilled and logged turbidite sequences on the Cascadia subduction zone (Figure 1). Training Holes U1325A, U1327A, and U1328A from the Cascadia Margin (the yellow dots in Figure 1) are mostly water-saturated but also have gas hydrate accumulations. The average gas hydrate saturation ranges from 4 to 10%, with local maximums of up to 80% [10]. In Hole U1325A, drilled to a depth of 350 mbsf, most of the hydrate is present in thin sands (<23 cm) [10]. Hole U1327A, drilled to a depth of 300 mbsf, is water-saturated except for an 18 m thick high-resistivity interval composed of hydrate-saturated turbidite lenses [45]. Hole U1328A is drilled to a depth of 300 mbsf; in this hole, gas-hydrate-filled fractures were identified from resistivity image logs from the seafloor to 46 mbsf, while the remaining 254 m are water-saturated marine muds [45].
The training holes drilled and logged offshore of India as a part of NGHP-01 have high-quality LWD data. Holes 2A, 2B, 3A, 4A, 5A, 5B, 6A, 7A, 10A, and 11A lie in the Krishna–Godavari Basin, and the Holes 8A and 9A are located in the more northern Mahanadi Basin (Figure 1; Table 1). Both locations have clay-rich sediments that are primarily water-saturated; almost all gas hydrate encountered during the NGHP-01 Expedition occurred in marine muds in near-vertical fractures [39].
We use all the available LWD logging data from NGHP-01 holes except some data from Hole 10A. Hole 10A is located at a paleo-vent site in the Krishna–Godavari Basin and consists of a webby network of veins and fractures [46]. The propagation resistivity logs in Hole 10A exceed the accuracy range in an interval of 43–90 mbsf and are not valid measurements [11]. Therefore, we do not use the data in the 43–90 mbsf interval from Hole 10A to train the model and use the data below 90 mbsf.

2.2. Test Holes

We use two Walker Ridge LWD holes, Holes WR313-G and WR313-H, for testing, thus assessing the predictability of the model (the white dot in the Gulf of Mexico, Figure 1). We selected these two holes for testing as they host the three key intervals that we are focusing on for our machine learning model: water-saturated sediments, hydrate in the primary pore space, and hydrate in near-vertical fractures.
These holes were drilled in the Terrebonne mini-basin in the Gulf of Mexico with a water depth of about 2 km [47]. A total of ~1220 m in Holes WR313-G and WR313-H is water-saturated with a low background resistivity that ranges from 1 to 2 Ωm. Hydrate with a hydrate saturation of 50–90% occurs in the primary pore space of the sand and silt layers a total of 50 m between both holes [47].
Hydrate also occurs in near-vertical fractures in marine mud over a total thickness of ~520 m between both holes [48]. Free gas is also present in an interval of ~2 m in Hole WR313-G just below the gas hydrate stability zone [48]. However, we did not include free gas in our machine learning model, as this was the only hole with any free gas intervals. The lack of data in free gas intervals is not surprising; in general, free gas intervals are carefully avoided during scientific ocean drilling because they present a potential drilling hazard.

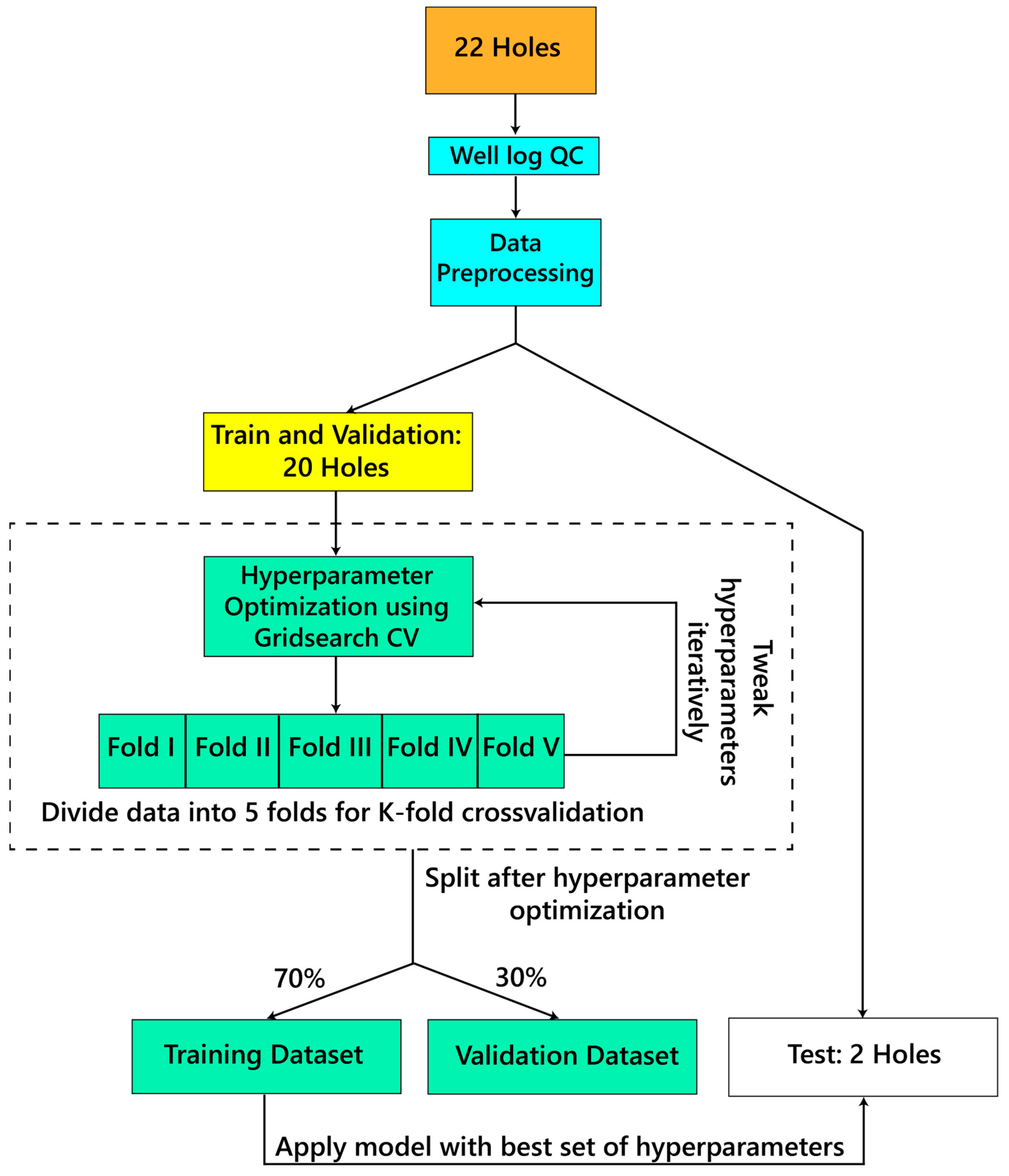
3. Methods

3.1. Machine Learning Algorithms

We predict Vp logs using gamma ray, ρb, and resistivity as inputs and ρb logs using gamma ray, Vp, and resistivity as inputs using the 20 training holes (Table 2) and test the model with the two Walker Ridge holes (Holes WR313-G and WR313-H). We use all these logs as inputs because they are important for interpreting sediment types, the morphology of hydrate, and hydrate saturation. For example, gamma ray differentiates between sand- and clay-rich sediments. Bulk density measures the electron density of matrix and pore fluids. Resistivity is used to identify gas hydrate at low and high saturations, and Vp is used to identify gas hydrate at high saturation [49]. We focus on predicting Vp and ρb logs because they are often poor quality in near-seafloor sediments. We do not predict resistivity logs because there are often many resistivity channels collected, and in general, deeper penetrating resistivity logs are often the highest-quality measurements in near-seafloor sediments.
We use six supervised machine learning algorithms and compare the accuracy and error for each algorithm using R2 and the mean absolute percentage error (MAPE). We selected these algorithms as they have been used previously in geoscience applications [27,30,31,32]. Some machine learning algorithms have hyperparameters that can be tuned to predict outputs with the highest accuracy and least error. We use the gridsearchcv technique to select the best set of hyperparameters for predicting Vp and ρb. Gridsearchcv is a cross-validation method that splits the training data into different parts and validates the model on each part iteratively while training the model on the remaining set of data points, searching for the optimum set of hyperparameters using all the possible user-defined hyperparameter combinations [50]. We split our training data into five folds and perform hyperparameter tuning with gridsearchcv using the process as described by [51,52] (Figure 2). The spreadsheets generated after gridsearchcv, with all the possible combinations of hyperparameters for each algorithm, are provided in the Supplementary Materials. We perform k-fold cross-validation for all the algorithms using the 20 holes to predict Vp and ρb logs based on different parts of the dataset (statistics appear in the Supplementary Materials). We use a k-fold of five that divides the training data into five parts and validates the machine learning model on each part (Figure 2). This helps identify which algorithms are more consistent in predicting Vp and ρb that are not biased for a specific set of data points.
A brief description of each algorithm is provided below:
a.
Multilinear Regression: Multilinear regression develops a correlation between the provided inputs and outputs on a labeled training dataset using a linear relationship, and the resulting linear model is used to predict values for a new dataset [53]. This algorithm does not require hyperparameter tuning.
b.
Polynomial Regression: This algorithm defines a relationship between the input and output parameters based on an nth-degree polynomial. The user defines the degree of the polynomial, and then, the algorithm transforms the input data into a polynomial equation [54]. For a supervised learning model, the same equation is then used to predict outputs based on a novice dataset. Herein, we tested polynomial equations from orders two to six and chose a 4th order polynomial equation after hyperparameter tuning.
c.
Polynomial Regression with Ridge Regularization (L2): L2 regularization reduces overfitting by adding a penalty term that can be used to reduce the magnitude of large coefficients in the equation [55]. Here, we combine a 4th-order polynomial equation with a ridge regression fit on the training data. We use regularization values of 0.001 and 0.01 to predict Vp and ρb, respectively.
d.
K Nearest Neighbors: This algorithm uses feature similarity between input and output points in a space to make predictions [16]. Whenever a new dataset is input into the model, the Euclidean distance from the training data points is calculated for all the new data points, and then, the nearest neighboring values are selected based on the k value, which defines the search criteria and selects k nearest neighbors from the input (e.g., [16]). Another parameter, the weight attribute, weighs different points in the neighborhood corresponding to their respective Euclidean distances. The closeness that is calculated as the Euclidean distance from training points is then used to predict an output based on the class of the nearest neighbors [56]. We select k = 7 and ‘distance’ as the weight attribute as they fit the model best for predicting Vp and ρb.
e.
Random Forest: As described in [57] and other research works in geosciences such as Bressan et al., Hou et al., and Shalaby et al. [20,22,25], random forest uses a bootstrap aggregating method that uses a combination of decision trees and takes the mean out of all the decision trees to generate the final output. Decision trees mimic the structure of a tree and consist of several nodes that terminate on a leaf node [58]. Leaf nodes are representative of class labels, and all other nodes signify feature attributes. Each branch of the tree used in random forest is subdivided into nodes based on the conditions that the algorithm tries to construct with reference to the input data provided [58]. This structure of random forest reduces variance and avoids overfitting. Herein, we use random forest by constructing a forest with ‘400’ trees, ‘sqrt’ as the max_features, which defines the size of the features to be considered while splitting a node; ‘1’ as the min_samples_leaf, which refers to the minimum number of samples at the leaf node; ‘15’ as max_depth, which refers to the maximum depth of the tree from the root node to the leaf node; and ‘2’ as the min_samples_split, which refers to the minimum number of samples required to split a node.
f.
Multilayer Perceptron: A multilayer perceptron is an artificial neural network that uses artificial neurons with an input layer, a hidden layer, and an output layer to make non-linear predictions based on the inputs provided to it [59]. It is inspired by the structure of biological neurons that receive signals from other neurons via interconnections [60,61]. It has been frequently applied in the geosciences [17,18,19,20,21,22,23,25,27,29,31]. An important part of a multilayer perceptron is the choice of activation function, which defines the output from a neuron. We use the ‘relu’ activation function, which is a piecewise linear function [62], along with four and five hidden layers to predict Vp and ρb, respectively, as it provides the best fit.
In order to implement the machine learning algorithms, we use only well log data sampled at 0.5 ft (0.1524 m) depth intervals. We also normalize the inputs to a range from 0 to 1 [63]. This ensures that each variable is contributing equally to the model. Normalization is particularly important for algorithms that use distance-based attributes to improve accuracy and reduce error [64]. We normalize the inputs when using all the above algorithms except for random forest because it does not depend on distance-based attributes.

3.2. Prediction of ρb and Vp

We predict ρb and Vp for Holes WR313-G and WR313-H using the six machine learning algorithms by creating a training dataset from the 20 holes with the available LWD logs from the Gulf of Mexico, the Cascadia Margin, and the Bay of Bengal (Table 2). As a part of the well log quality control for the training dataset, we eliminate washout zones >5 m thick where borehole diameters are ≥5 cm more than the bit size to remove intervals with poor data. We keep thinner washout intervals because the machine learning model needs to be trained on some poor-quality data along with good-quality data to avoid overfitting.
For all algorithms, the training dataset consists of 34,341 sets of data at discrete depths with 30,478 data points corresponding to water-saturated intervals, 2938 data points corresponding to intervals with gas hydrate in near-vertical fractures, and 925 data points corresponding to intervals with gas hydrate in the primary pore space. Each well log in the training dataset has 34,341 sets of data at discrete depths or 34,341 values of gamma ray, ρb, ring resistivity, propagation resistivity, and Vp. We split the training dataset and use 70% for training the model and 30% for validation (Figure 2). The validation dataset is kept separate from the training dataset to observe if the model is consistent enough in making predictions. We also perform feature selection analysis to select the best combination of input well logs to predict Vp and ρb using both workflows (the statistics are shown in Section 5 of the Supplementary Materials).
We predict Vp and ρb using different sets of well logs as inputs and describe each of these sets as a Case. We use two different workflows to predict Vp: Case 1 and 2, where we use bulk density and gamma-ray logs, but different resistivity logs. For Case 1, ring resistivity is the only resistivity dataset used as an input. For Case 2, we use propagation resistivities (A16L, A40L, P16H, P28H, P40H) instead of ring resistivity along with gamma ray and bulk density. To predict ρb Case 1, we use gamma ray, ring resistivity, and Vp as input well logs, and for ρb Case 2, we use gamma ray, propagation resistivities, and Vp as input well logs.

3.3. Downsampling the Predicted Results

Vp and ρb logs have a lower vertical resolution than the other logs. For example, Vp has a vertical resolution of ~61 cm [65], and ρb has a vertical resolution of ~30 cm [66], while ring resistivity has a resolution of ~5–7 cm [67], and gamma ray have a vertical resolution of ~31 cm [66]. The vertical resolution of the propagation resistivity logs ranges from ~21 cm to ~121 cm [66]. Therefore, we downsample the predicted outputs using a moving average filter while estimating Vp for Cases 1 and 2 and ρb for Case 1 only.

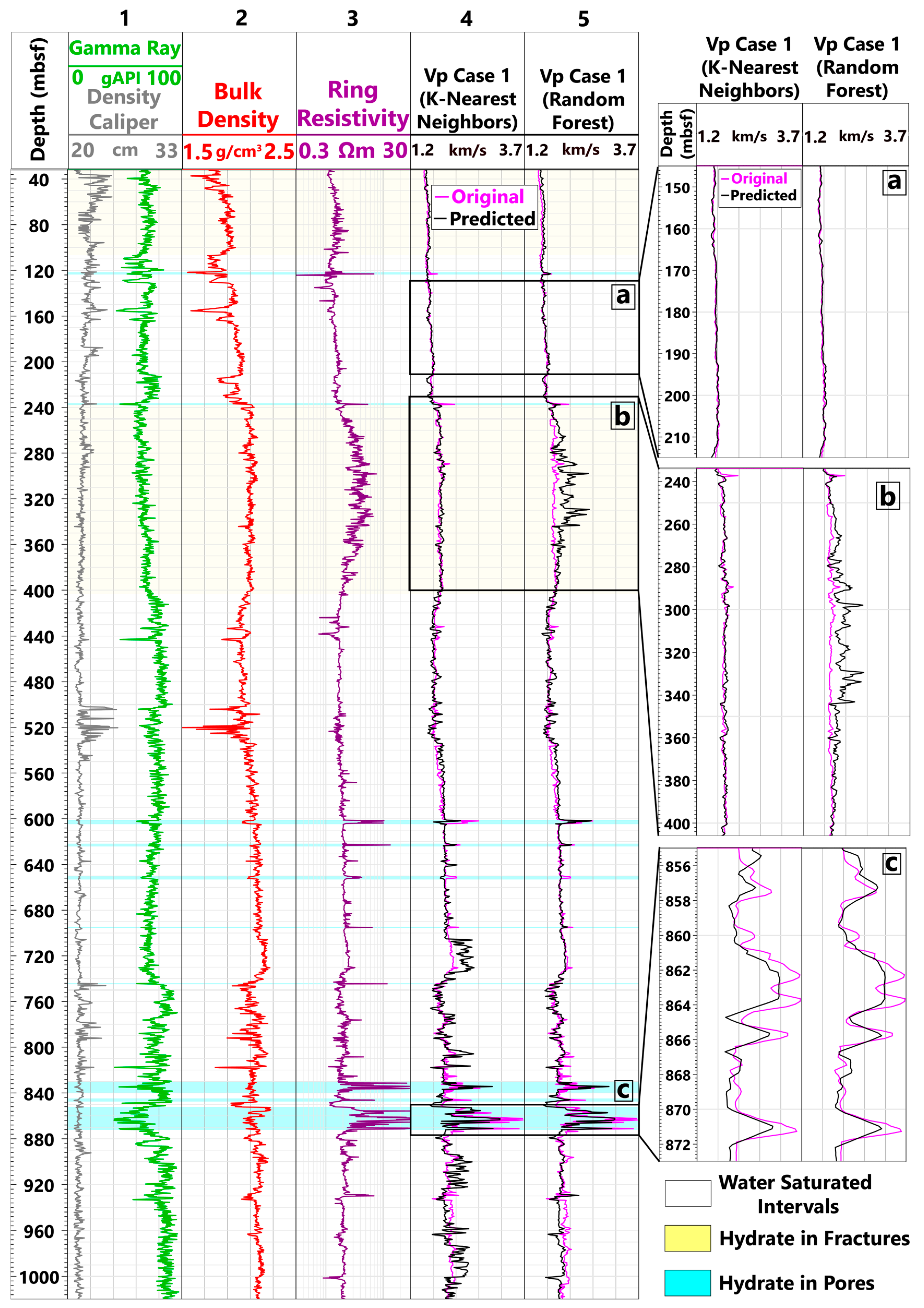
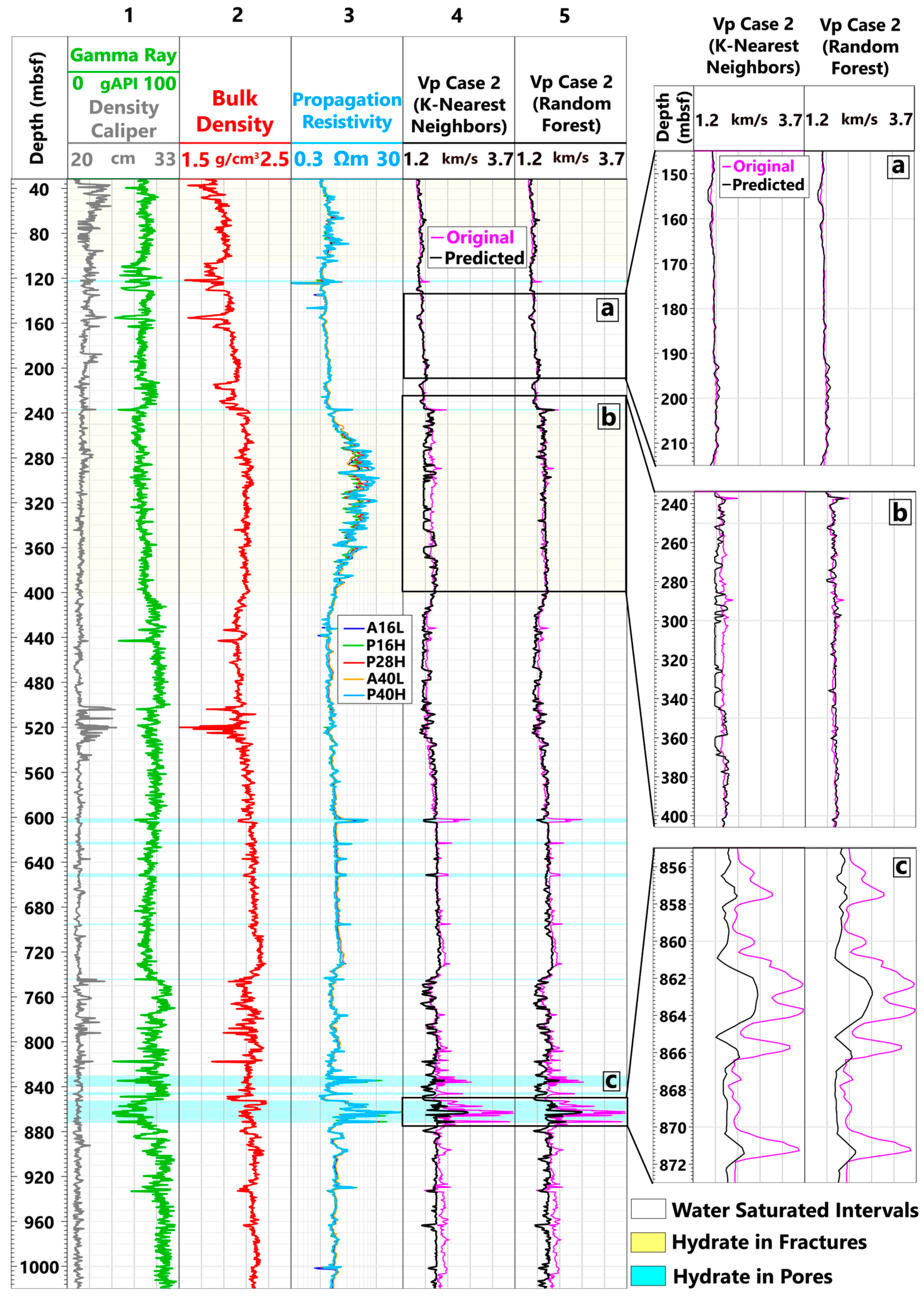
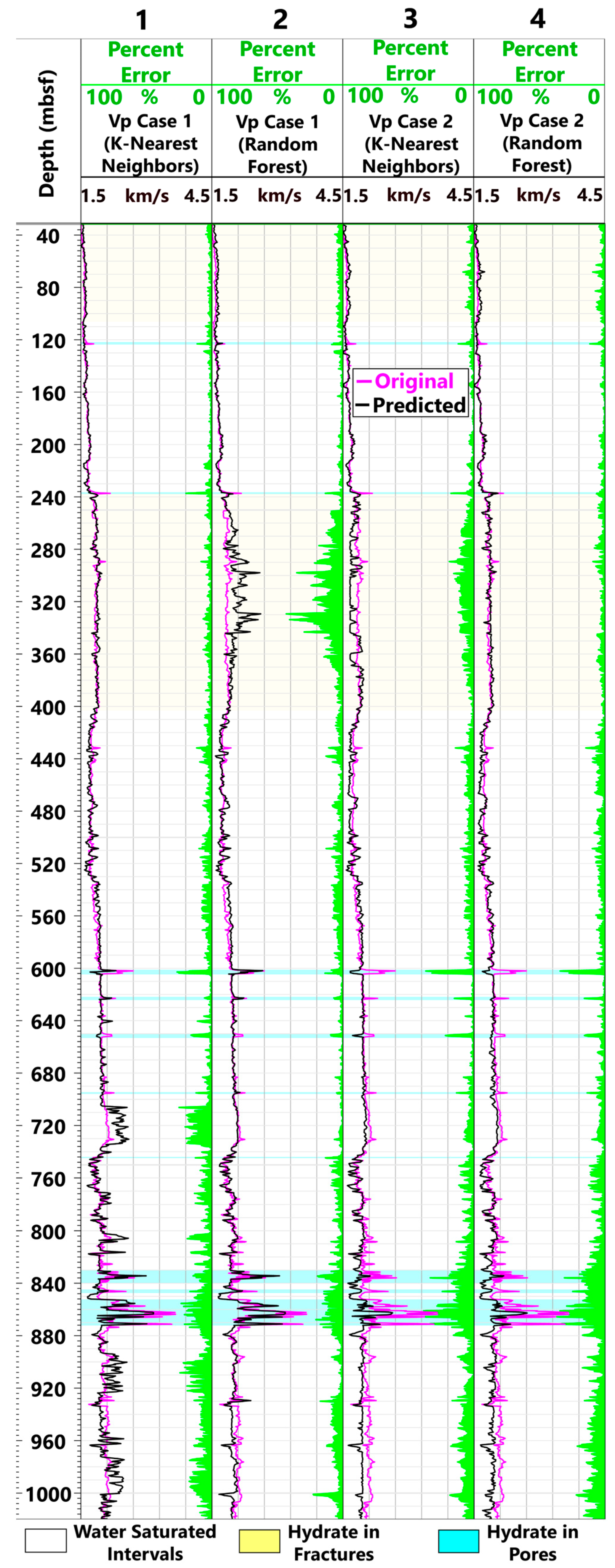
4. Results and Discussion

Our study is the first to use centimeter-scale resolution LWD data to predict Vp and ρb logs in near-seafloor sediments. Out of the six algorithms, we find that random forest and K nearest neighbors are more robust and can predict Vp and ρb logs with high accuracy (R2), greater than 70%, and low error (MAPE), less than 4%, on training, validation, and test data (Figure 3 and Table 3). In addition, random forest and K nearest neighbors have consistently high accuracy for k-fold cross-validation across different folds (Supplementary Materials). Random forest has been used across the geosciences to tackle a variety of different problems [30,68,69]; however, our study shows that K nearest neighbors is a strong machine learning method and may be viable for other geoscience applications.
Multilinear regression and multilayer perceptron have also been used in geoscience studies [27,31,70] but have not performed as well herein as random forest or K nearest neighbors in predicting Vp and ρb logs. Multilinear regression has an accuracy of only ~30–60% and a higher error of 4–6% for training, validation, and test data (Figure 3 and Table 3). This low accuracy shows that the relationship between different well logs is not linear; this is an important point because missing log data are commonly approximated using linear equations. Similarly, multilayer perceptron has overall low accuracy, varying from 55 to 59% on training, validation, and test data.
Polynomial regression and polynomial regression with ridge regularization have extremely poor accuracy in the main hydrate-bearing sands in WR313-G and WR313-H (Figure 3 and Table 3). Moreover, polynomial regression and polynomial regression with ridge regularization perform poorly on different folds while performing k-fold cross-validation (Supplementary Materials).

4.1. Formation Vp Prediction

Random Forest and K Nearest Neighbors have high R2 and low MAPE and are more consistent than the other algorithms; therefore, we compare these two algorithms and focus on how these results vary in water-saturated intervals, hydrate in the primary pore space, and hydrate in fractures (Table 4). A unique aspect of our study is that we consider hydrate in different morphologies and the effect on machine learning results.
a.
Water-Saturated Intervals
In Figure 4 and Figure 5, water-saturated intervals are primarily identified by their low resistivity and are represented by a white background. In these water-saturated intervals, the predicted Vp closely matches the measured Vp with a low percentage error (Figure 6) for both algorithms using Vp Case 1 (R2 ~75%). However, the R2 for the predicted Vp for Vp Case 2 is 66% (MAPE 4.7%) for random forest and 70% (MAPE 4.0%) for K nearest neighbors. This indicates that either random forest or K nearest neighbors can be used for estimating Vp in water-saturated intervals with ring resistivity as one of the inputs in the training model. However, the propagation resistivity can also be used to predict Vp in water-saturated sediments if ring resistivity is not available (Case 2). The high accuracy and low percentage error for these results may suggest that these models could be applied to datasets in near-seafloor water-saturated sediments to accurately predict Vp where high-quality input logs are available.
b.
Hydrate in Fractures
We compare the predicted Vp results with the measured Vp for WR313-G and WR313-H in the intervals where hydrate is identified in near-vertical fractures. Intervals where hydrate occurs in near-vertical fractures are highlighted in yellow in Figure 3 and Figure 4. Propagation resistivity measurements are the most sensitive to resistivity anisotropy caused by near-vertical hydrate-filled fractures; near-vertical resistivity fractures cause a characteristic curve separation in propagation resistivity curves that depends on the fracture angle, hydrate resistivity, the measurement type, and the spacing of the measurement sondes [11]. In general, no significant increase in Vp is observed in near-vertical fracture intervals, which is likely due to the low concentration of hydrate in the bulk sediment [8]. The random forest Vp prediction results have low accuracy and high percentage error (Figure 6) using Case 1 (using ring resistivity) but high accuracy and low percentage error (Figure 6) with Case 2 (using propagation resistivity: A16L, A40L, P16H, P28H, P40H) (Table 4); this is consistent with the observation that a set of propagation resistivity logs is sensitive to near-vertical fractures while a single resistivity measurement (in this case, ring resistivity) cannot be used to identify near-vertical gas-hydrate-filled fractures. However, the accuracy of the K nearest neighbors algorithm is lower for Case 2 (R2 = 48% and MAPE = 4.2%) as compared with Case 1 (R2 = 73% and MAPE = 2.4%). These contradictory results may be due to the fact that gas-hydrate-filled fractures form complex 3D networks [46] with a variety of fracture angles [8], and the anisotropy caused by these networks may result in data that are difficult to fit with a machine learning model.
This suggests that some caution is required while predicting Vp when hydrates occur in near-vertical fractures. Thus, in order to predict Vp for hydrates in near-vertical fractures, the random forest algorithm with propagation resistivities (Case 2) and the K nearest neighbors algorithm with ring resistivity (Case 1) are the best algorithms and datasets.
c.
Hydrate in Pores
Hydrate-bearing sands are highlighted in blue in Figure 4 and Figure 5. These intervals have a significant increase in the measured Vp log and a corresponding increase in the resistivity logs. In hydrate-bearing sands (Figure 4 and Figure 5), the random forest algorithm closely replicates the measured Vp log using Case 1 (R2 = 81% and MAPE = 6.5%), and we recommend this algorithm over K nearest neighbors (R2 = 71% and MAPE = 10%) in locations with high-saturation gas hydrate. This is because random forest predictions better match the measured Vp log both in thick sand accumulations and thin sands (<5 m in thickness) as compared with K nearest neighbors. In addition, a higher accuracy is observed when the ring resistivity log (Case 1) is used over a suite of propagation resistivity logs (Case 2). This is likely due to the better vertical resolution of ring resistivity (5–7 cm) from the geoVISION* tool [67] as compared with the propagation resistivities (~21–121 cm resolution) from the EcoScope* tool [66]. Therefore, the ring resistivity measurement is able to resolve thinner beds and improves the accuracy of Vp prediction using Case 1.
Of course, high-saturation gas hydrate is not a common occurrence. Even so, data in these intervals may still benefit from prediction algorithms. For example, ref. [71] observed that the presence of high-saturation hydrate in pores can cause a loss of signal while acquiring Vp logs in boreholes. This may make it difficult to interpret formation Vp logs due to poor data quality. Our prediction results for hydrate in pores may improve the interpretation of Vp logs in such cases where Vp data are compromised due to loss of signal.

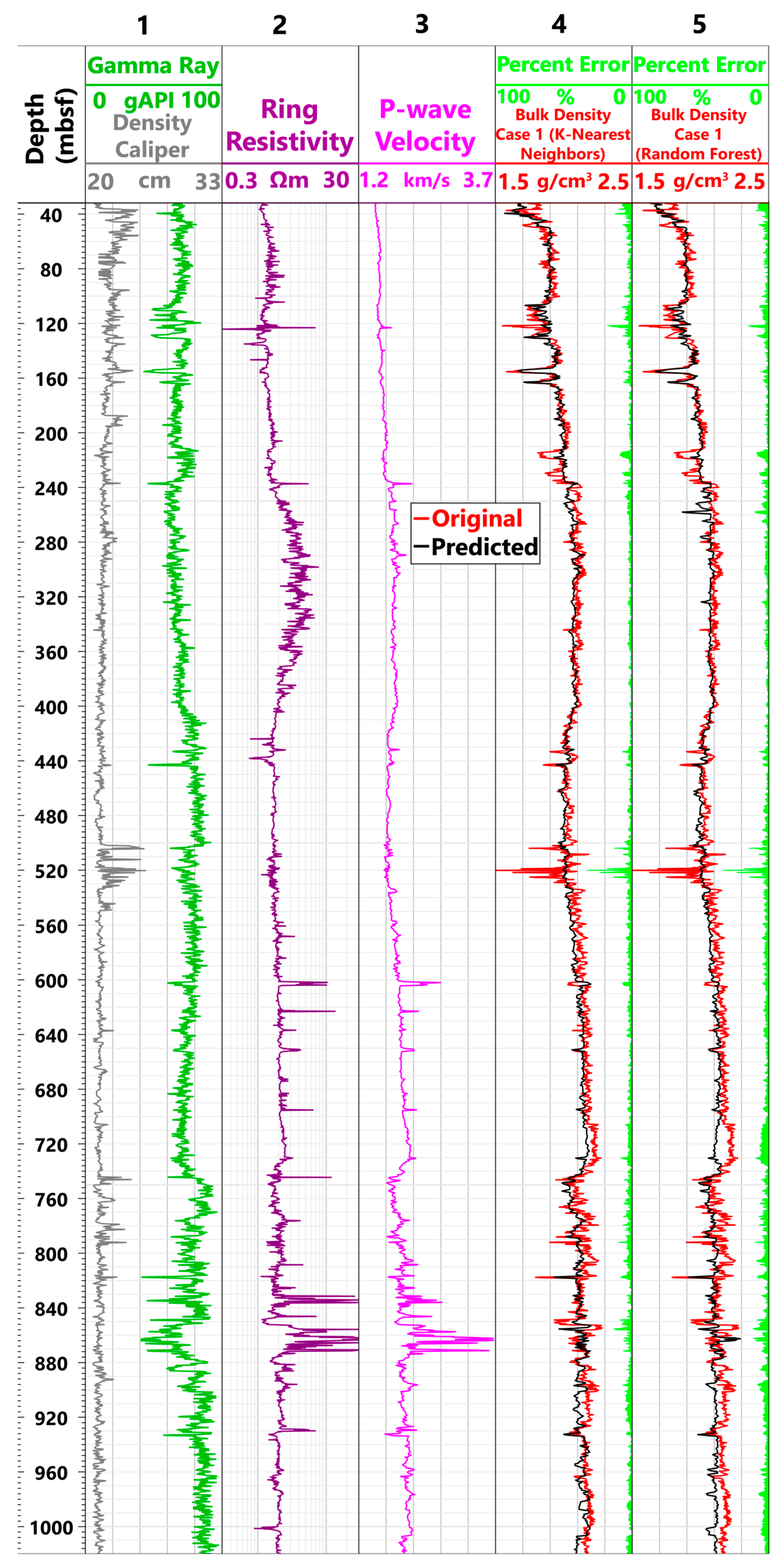
4.2. Bulk Density Prediction

We predict ρb log with high accuracy and low error using the random forest and K nearest neighbors algorithms. We choose Case 1 (with gamma ray, ring resistivity, and Vp as inputs) for ρb prediction over Case 2 (with gamma ray, propagation resistivities, and Vp as inputs) since ρb Case 2 overfits the model. This is because ρb Case 2 predicts ρb with high accuracy and low error on training and validation datasets, but the prediction becomes poor for the test holes (Table 3). Unlike Vp prediction, we do not assess the different hydrate morphologies for ρb prediction, as Case 1 fits all the intervals (Figure 7).
The bulk density measurement is important for hydrate interpretation as it provides the most accurate measurement of porosity in near-seafloor sediments. Porosity is used to compute hydrate saturation along with resistivity and Vp. Our bulk density model (Case 1), therefore, will be valuable to estimate the bulk density measurement in the near-seafloor sediments in locations where bulk density is not collected, such as the Nankai Trough [72] and the Hikurangi Margin [34,73].

4.3. Prediction at Deeper Depths

We observe that accuracy decreases and error increases for Vp and ρb prediction at deeper depths (>600 mbsf) in the test dataset (Figure 6 and Figure 7). This is likely because the total drilled depth for the training holes ranges from ~200 to 600 mbsf; however, the total drilled depth for the validation holes is ~1000 mbsf. Both Vp and ρb are a function of depth; i.e., both increase with increasing depth. Therefore, the model can predict Vp and ρb with a high accuracy and low error for depths where training data are available (<600 mbsf).

4.4. Further Data Limitations

One work is limited by the availability of scientific ocean drilling LWD data. We use all the publicly available data (22 holes) from the Lamont–Doherty Earth Observatory database to train, validate, and test the model. If more data become publicly available in the future, further data can be incorporated to improve the model.
If a user wants to apply our models to new data, the Vp model requires gamma ray, resistivity, and ρb logs, and the ρb model requires gamma ray, resistivity, and Vp logs; otherwise, the model cannot be accurately applied. Moreover, our model is only applicable to siliciclastic near-seafloor sediments in marine settings. It cannot be used for permafrost environments or in lithified rock.
The well log data that we use for this project are a few tens to a few hundreds of megabytes in size, and the machine learning algorithms take 30 s to 2 min for execution. However, the computation time increases to 3–4 h while performing hyperparameter optimization, which compares several hundreds of combinations of different hyperparameters for different algorithms. For random forest, the computation time for hyperparameter optimization is higher and takes about 10 h.

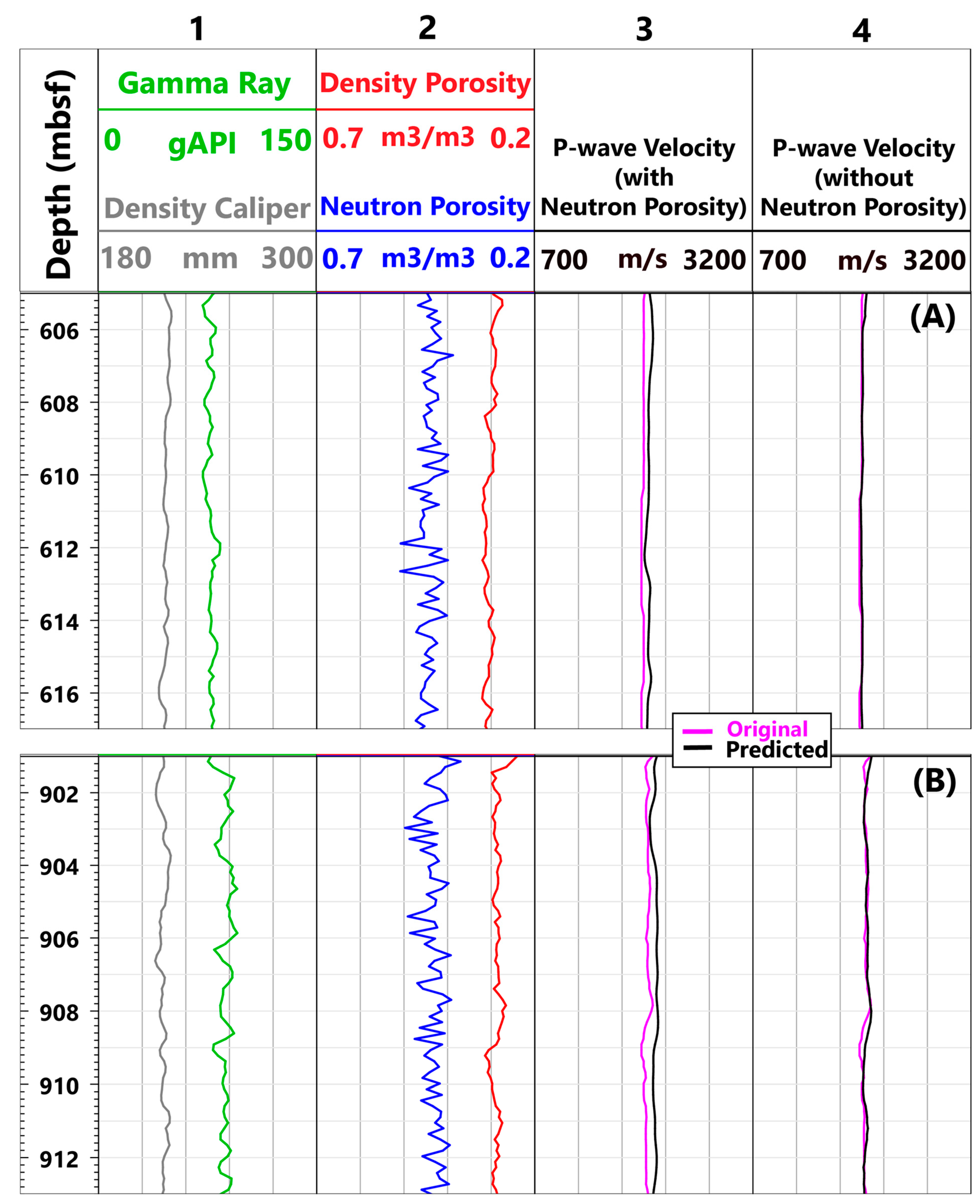
4.5. Neutron Porosity

The neutron porosity log measures the hydrogen concentration in the formation, which is related to the porosity of the formation [49]. In clay-rich environments, however, the apparent neutron porosity can be larger and noisier due to the presence of hydroxyl ions (OH-) associated with clay minerals [49]. Therefore, bulk density is the preferred log in near-seafloor sediments for interpreting porosity because it most closely replicates in situ porosity [3]. For this reason, we use bulk density as an input log in Case 1 and 2.
We test the neutron porosity log as an input for our machine learning model to predict Vp (Figure 8). When applying neutron porosity to the two Walker Ridge holes (WR313-G and WR313-H), we find that the predicted Vp in clayey zones does not correlate as well as when bulk density is used (Case 1). In contrast, [27] shows that both neutron porosity and porosity derived from bulk density can be used interchangeably as input in a machine learning model used to compute hydrate saturation in a permafrost location in Canada (Figure 8). The neutron porosity works in the model of [27] because the lithology is primarily sand, whereas we apply our machine learning model to both sand- and clay-rich intervals. Caution should always be exercised if using neutron porosity in mud- or clay-rich environments.

4.6. Model Application in Non-Hydrate Sites

Even though we train our machine learning model using borehole data from hydrate drilling expeditions in the Gulf of Mexico, Cascadia Margin, and offshore India, we argue that our model can still be applied in boreholes missing data not only in hydrate systems but also in siliciclastic near-seafloor sediments on continental slopes. While this paper is focused on hydrate systems; most of the data used in the model (89%) is from water-saturated marine sediments; in these systems, our model can predict Vp and ρb with high accuracy and low percentage error (Figure 6 and Figure 7).
One factor that might affect the machine learning model is porewater salinity. This is because resistivity is a function of porewater salinity in high-porosity sediments. In general, an increase in porewater salinity will reduce resistivity. This can reduce predicted Vp and ρb. Conversely, a decrease in porewater salinity can increase resistivity and the predicted Vp and ρb. For example, porewater salinity variations can be due to the formation or dissociation of hydrate [10,74]. Porewater salinity can also vary in places with shallow salt diapers [75]. While situations where porewater salinity varies are not very common and porewater salinity is normally standard for seawater, caution should be taken in any location where there may be a significant change in porewater salinity. There are many holes where this model can be applied in marine sediments on continental margins. For example, our model could be used to predict Vp and ρb logs for the ~70 LWD scientific ocean drilling holes in the Lamont–Doherty Earth Observatory database with missing Vp or ρb logs. Even more holes have missing or damaged Vp or ρb logs where our model could be applied.

5. Conclusions

In this work, we present a novel machine learning approach to predict Vp and ρb logs in marine gas hydrates and their variations with different depth intervals and different hydrate morphologies. We predict Vp logs using gamma ray, bulk density, and resistivity as inputs and ρb logs using gamma ray, Vp, and resistivity logs as inputs. To identify the best algorithms, we use six machine learning algorithms and compare the results. We find that the random forest and K nearest neighbors algorithms can be used to predict Vp and ρb logs with a high degree of accuracy and low error in near-seafloor sediments with water-saturated intervals, intervals where hydrate fills fractures, and intervals where hydrate is in the primary pore space. Due toa good match between the measured and predicted logs in both hydrate-bearing and water-saturated intervals, our model can be applied to siliciclastic near-seafloor sediments where either Vp or ρb logs are missing. Our model for Vp or ρb prediction is applicable not only to hydrate systems but also useful for researchers working to identify shallow natural hazards such as submarine landslides and conducting studies by integrating well and seismic data.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/en16237709/s1: Figure S1: Vp prediction using Case 1 for WR313-H; Figure S2: Vp prediction using Case 2 for WR313-H; Figure S3: Vp prediction percentage error for WR313-H; Figure S4: ρb prediction using Case 1 for WR313-H; Figure S5: Vp prediction for WR313-H with and without neutron porosity input; Figure S6: Hyperparameter tuning for k nearest neighbors; Figure S7: L-curve for k nearest neighbors; Table S1: k-fold cross validation statistics; Table S2: Training data distribution; Table S3: WR313-G data distribution; Table S4: WR313-H data distribution; Table S5: Feature selection statistics for Vp prediction; Table S6: Feature selection statistics for ρb prediction.

Author Contributions

F.N. conceived the main idea for the manuscript and designed the figures. F.N. and A.E.C. wrote the manuscript. A.E.C. secured the funding. J.M. reviewed and improved the codes. All authors have read and agreed to the published version of the manuscript.

Funding

This research and APC was funded by US Department of Energy [DE-FE0023919] and National Science Foundation [1752882].

Data Availability Statement

Detailed information related to the WR313-H log figures, k-fold cross-validation, hyperparameter tuning for all the algorithms using gridsearchcv (available as spreadsheets), and the distribution of observed data points is available in the Supplementary Materials.

Acknowledgments

The authors would like to thank Debashis Konwar for helping with interpreting borehole sonic data and Schlumberger for providing the Techlog software v2022 at Ohio State University. The LWD log data in this paper was Idownloaded from the Lamont–Doherty Earth Observatory (https://mlp.ldeo.columbia.edu/logdb/, accessed on 15 September 2023). All machine learning codes are provided at the following link: https://colab.research.google.com/drive/10oUw7hIh5aBD3q56Ix8iu0a3mUJTyRWF#scrollTo=mZ_q2FHcxv4K, accessed on 15 September 2023. All the machine learning codes, along with the training and testing data files (csv format), are attached to the Supplementary Materials. We also thank the anonymous reviewers.

Conflicts of Interest

The authors declare no conflict of interest.

Disclaimer

This report was prepared as an account of work sponsored by an agency of the United States government. Neither the United States government nor any agency thereof nor any of their employees make any warranty, express or implied, or assume any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represent that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States government or any agency thereof. The views and opinions of the authors expressed herein do not necessarily state or reflect those of the United States government or an agency thereof.

References

  1. Collett, T.S.; Johnson, A.H.; Knapp, C.C.; Boswell, R. Natural gas hydrates: A review. In AAPG Memoir; American Association of Petroleum Geologists: Tulsa, OK, USA, 2009. [Google Scholar]
  2. Kvenvolden, K.A.; Lorenson, T.D. The global occurrence of natural gas hydrate. In Geophysical Monograph Series; AGU: Washington, DC, USA, 2001; Volume 124. [Google Scholar] [CrossRef]
  3. Goldberg, D.; Kleinberg, R.L.; Weinberger, J.L.; Malinverno, A.; McLellan, P.J.; Collett, T.S. Evaluation of Natural Gas-Hydrate Systems Using Borehole Logs. In Geophysical Characterization of Gas Hydrates; Society of Exploration Geophysicists: Houston, TX, USA, 2010; Chapter 16. [Google Scholar] [CrossRef]
  4. Kerkar, P.B.; Horvat, K.; Mahajan, D.; Jones, K.W. Formation and dissociation of methane hydrates from seawater in consolidated sand: Mimicking methane hydrate dynamics beneath the seafloor. Energies 2013, 6, 6225–6241. [Google Scholar] [CrossRef]
  5. Li, Z.D.; Tian, X.; Li, Z.; Xu, J.Z.; Zhang, H.X.; Wang, D.J. Experimental study on growth characteristics of pore-scale methane hydrate. Energy Rep. 2020, 6, 933–943. [Google Scholar] [CrossRef]
  6. Yun, T.S.; Francisca, F.M.; Santamarina, J.C.; Ruppel, C. Compressional and shear wave velocities in uncemented sediment containing gas hydrate. Geophys. Res. Lett. 2005, 32, L10609. [Google Scholar] [CrossRef]
  7. Oti, E.A.; Cook, A.E.; Phillips, S.C.; Holland, M.E. Using X-ray computed tomography to estimate hydrate saturation in sediment cores from Green Canyon 955, northern Gulf of Mexico. AAPG Bull. 2022, 106, 1127–1142. [Google Scholar] [CrossRef]
  8. Cook, A.E.; Goldberg, D.S.; Malinverno, A. Natural gas hydrates occupying fractures: A focus on non-vent sites on the Indian continental margin and the northern Gulf of Mexico. Mar. Pet. Geol. 2014, 58, 278–291. [Google Scholar] [CrossRef]
  9. Collett, T.S.; Ladd, J. Detection of gas hydrate with downhole logs and assessment of gas hydrate concentrations (saturations) and gas volumes on the Blake Ridge with electrical resistivity log data. In Proceedings of the Ocean Drilling Program: Scientific Results; Texas A&M University: College Station, TX, USA, 2000. [Google Scholar] [CrossRef]
  10. Malinverno, A.; Kastner, M.; Torres, M.E.; Wortmann, U.G. Gas hydrate occurrence from pore water chlorinity and downhole logs in a transect across the northern Cascadia margin (Integrated Ocean Drilling Program Expedition 311). J. Geophys. Res. Solid Earth 2008, 113, B08103. [Google Scholar] [CrossRef]
  11. Cook, A.E.; Anderson, B.I.; Malinverno, A.; Mrozewski, S.; Goldberg, D.S. Electrical anisotropy due to gas hydrate-filled fractures. Geophysics 2010, 75, F173–F185. [Google Scholar] [CrossRef]
  12. Helgerud, M.B.; Dvorkin, J.; Nur, A.; Sakai, A.; Collett, T. Elastic-wave velocity in marine sediments with gas hydrates: Effective medium modeling. Geophys. Res. Lett. 1999, 26, 2021–2024. [Google Scholar] [CrossRef]
  13. Lee, M.W.; Collett, T.S. In-situ gas hydrate hydrate saturation estimated from various well logs at the Mount Elbert Gas Hydrate Stratigraphic Test Well, Alaska North Slope. Mar. Pet. Geol. 2011, 28, 439–449. [Google Scholar] [CrossRef]
  14. Nelwamondo, F.V.; Golding, D.; Marwala, T. A dynamic programming approach to missing data estimation using neural networks. Inf. Sci. 2013, 237, 49–58. [Google Scholar] [CrossRef]
  15. Pelckmans, K.; De Brabanter, J.; Suykens, J.A.K.; De Moor, B. Handling missing values in support vector machine classifiers. Neural Netw. 2005, 18, 684–692. [Google Scholar] [CrossRef] [PubMed]
  16. Han, J.; Kamber, M.; Pei, J. Data Mining: Concepts and Techniques. In Data Mining: Concepts and Techniques; University of Illinois at Urbana-Champaign Micheline Kamber Jian Pei Simon Fraser University: Champaign, IL, USA, 2012. [Google Scholar] [CrossRef]
  17. Farfour, M.; Mesbah, M. Machine intelligence vs. human intelligence in geological interpretation of seismic data. In Proceedings of the 2020 International Conference on Decision Aid Sciences and Application, DASA 2020, Sakheer, Bahrain, 8–9 November 2020. [Google Scholar] [CrossRef]
  18. Ismail, A.; Ewida, H.F.; Nazeri, S.; Al-Ibiary, M.G.; Zollo, A. Gas channels and chimneys prediction using artificial neural networks and multi-seismic attributes, offshore West Nile Delta, Egypt. J. Pet. Sci. Eng. 2022, 208, 109349. [Google Scholar] [CrossRef]
  19. Ramya, J.; Somasundareswari, D.; Vijayalakshmi, P. Gas chimney and hydrocarbon detection using combined BBO and artificial neural network with hybrid seismic attributes. Soft Comput. 2020, 24, 2341–2354. [Google Scholar] [CrossRef]
  20. Bressan, T.S.; Kehl de Souza, M.; Girelli, T.J.; Junior, F.C. Evaluation of machine learning methods for lithology classification using geophysical data. Comput. Geosci. 2020, 139, 104475. [Google Scholar] [CrossRef]
  21. Ismail, A.; Radwan, A.A.; Leila, M.; Abdelmaksoud, A.; Ali, M. Unsupervised machine learning and multi-seismic attributes for fault and fracture network interpretation in the Kerry Field, Taranaki Basin, New Zealand. Geomech. Geophys. Geo-Energy Geo-Resour. 2023, 9, 122. [Google Scholar] [CrossRef]
  22. Hou, M.; Xiao, Y.; Lei, Z.; Yang, Z.; Lou, Y.; Liu, Y. Machine Learning Algorithms for Lithofacies Classification of the Gulong Shale from the Songliao Basin, China. Energies 2023, 16, 2581. [Google Scholar] [CrossRef]
  23. Lou, Y.; Li, S.; Liu, N.; Liu, R. Seismic volumetric dip estimation via a supervised deep learning model by integrating realistic synthetic data sets. J. Pet. Sci. Eng. 2022, 218, 111021. [Google Scholar] [CrossRef]
  24. Yang, L.; Sun, S.Z. Seismic horizon tracking using a deep convolutional neural network. J. Pet. Sci. Eng. 2020, 187, 106709. [Google Scholar] [CrossRef]
  25. Shalaby, M.R.; Jumat, N.; Lai, D.; Malik, O. Integrated TOC prediction and source rock characterization using machine learning, well logs and geochemical analysis: Case study from the Jurassic source rocks in Shams Field, NW Desert, Egypt. J. Pet. Sci. Eng. 2019, 176, 369–380. [Google Scholar] [CrossRef]
  26. Gjelsvik, E.L.; Fossen, M.; Tøndel, K. Current overview and way forward for the use of machine learning in the field of petroleum gas hydrates. Fuel 2023, 334 Pt 2, 126696. [Google Scholar] [CrossRef]
  27. Singh, H.; Seol, Y.; Myshakin, E.M. Prediction of gas hydrate saturation using machine learning and optimal set of well-logs. Comput. Geosci. 2021, 25, 267–283. [Google Scholar] [CrossRef]
  28. Yu, Z.; Tian, H. Application of Machine Learning in Predicting Formation Condition of Multi-Gas Hydrate. Energies 2022, 15, 4719. [Google Scholar] [CrossRef]
  29. Rebai, N.; Hadjadj, A.; Benmounah, A.; Berrouk, A.S.; Boualleg, S.M. Prediction of natural gas hydrates formation using a combination of thermodynamic and neural network modeling. J. Pet. Sci. Eng. 2019, 182, 106270. [Google Scholar] [CrossRef]
  30. Graw, J.H.; Wood, W.T.; Phrampus, B.J. Predicting Global Marine Sediment Density Using the Random Forest Regressor Machine Learning Algorithm. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020135. [Google Scholar] [CrossRef]
  31. Sain, K.; Kumar, P.C. Meta-Attributes and Artificial Networking: A New Tool for Seismic Interpretation; AGU-John Wiley & Sons: Hoboken, NJ, USA, 2022. [Google Scholar] [CrossRef]
  32. Dumke, I.; Berndt, C. Prediction of seismic p-wave velocity using machine learning. Solid Earth 2019, 10, 1989–2000. [Google Scholar] [CrossRef]
  33. Flemings, P.B.; Behrmann, J.H.; John, C.M.; the Expedition 308 Scientists. Expedition 308 summary. In Proceedings of the Integrated Ocean Drilling Program; IODP: College Station, TX, USA, 2006; Volume 308. [Google Scholar] [CrossRef]
  34. Pecher, I.A.; Barnes, P.M.; LeVay, L.J.; the Expedition 372 Scientists. Creeping Gas Hydrate Slides. In Proceedings of the International Ocean Discovery Program, College Station, TX, USA, 26 November 2017–4 January 2018; Volume 372. [Google Scholar] [CrossRef]
  35. Zoback, M.D. Pore pressure at depth in sedimentary basins. In Reservoir Geomechanics; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar] [CrossRef]
  36. Liner, C.L. (Ed.) Synthetic Seismogram, Tuning, and Resolution. In Elements of 3D Seismology; Society of Exploration Geophysicists: Houston, TX, USA, 2016; Chapter 19; pp. 213–228. [Google Scholar] [CrossRef]
  37. Collett, T.S.; Lee, M.W.; Zyrianova, M.V.; Mrozewski, S.A.; Guerin, G.; Cook, A.E.; Goldberg, D.S. Gulf of Mexico Gas Hydrate Joint Industry Project Leg II logging-while-drilling data acquisition and analysis. Mar. Pet. Geol. 2012, 34, 41–61. [Google Scholar] [CrossRef]
  38. Riedel, M.; Collett, T.S.; Malone, M.J.; Mitchell, M.; Guèrin, G.; Akiba, F.; Blanc-Valleron, M.M.; Ellis, M.; Hashimoto, Y.; Heuer, V.; et al. Gas hydrate drilling transect across northern Cascadia margin–IODP Expedition 311. Geol. Soc. Spec. Publ. 2009, 319, 11–19. [Google Scholar] [CrossRef]
  39. Collett, T.S.; Boswell, R.; Cochran, J.R.; Kumar, P.; Lall, M.; Mazumdar, A.; Ramana, M.V.; Ramprasad, T.; Riedel, M.; Sain, K.; et al. Geologic implications of gas hydrates in the offshore of India: Results of the National Gas Hydrate Program Expedition 01. Mar. Pet. Geol. 2014, 58, 3–28. [Google Scholar] [CrossRef]
  40. Kevin Meazell, P.; Flemings, P.B.; Santra, M.; Johnson, J.E. Sedimentology and stratigraphy of a deep-water gas hydrate reservoir in the northern Gulf of Mexico. AAPG Bull. 2020, 104, 1945–1969. [Google Scholar] [CrossRef]
  41. Santra, M.; Flemings, P.B.; Scott, E.; Kevin Meazell, P. Evolution of gas hydrate-bearing deep-water channel-levee system in abyssal Gulf of Mexico: Levee growth and deformation. AAPG Bull. 2020, 104, 1921–1944. [Google Scholar] [CrossRef]
  42. Flemings, P.B.; Phillips, S.C.; Boswell, R.; Collett, T.S.; Cook, A.E.; Dong, T.; Frye, M.; Goldberg, D.S.; Guerin, G.; Holland, M.E.; et al. Pressure coring a Gulf of Mexico deep-water turbidite gas hydrate reservoir: Initial results from the University of Texas-Gulf of Mexico 2-1 (UT-GOM2-1) Hydrate Pressure Coring Expedition. AAPG Bull. 2020, 104, 1847–1876. [Google Scholar] [CrossRef]
  43. Cook, A.E.; Tost, B.C. Geophysical signatures for low porosity can mimic natural gas hydrate: An example from Alaminos Canyon, Gulf of Mexico. J. Geophys. Res. Solid Earth 2014, 119, 7458–7472. [Google Scholar] [CrossRef]
  44. Frye, M.; Shedd, W.W.; Godfriaux, P.D.; Dufrene, R.S.; Collett, T.S.; Lee, M.W.; Boswell, R.; Jones, E.; McConnell, D.R.; Mrozewski, S.; et al. Gulf of Mexico gas hydrate joint industry project leg II: Results from the Alaminos Canyon 21 Site. In Proceedings of the Annual Offshore Technology Conference, Houston, TX, USA, 3–6 May 2010; Volume 2. [Google Scholar]
  45. Expedition 311 summary. In Proceedings of the IODP; IODP: College Station, TX, USA, 2006; Volume 311. [CrossRef]
  46. Rees, E.V.L.; Priest, J.A.; Clayton, C.R.I. The structure of methane gas hydrate bearing sediments from the Krishna-Godavari Basin as seen from Micro-CT scanning. Mar. Pet. Geol. 2011, 28, 1283–1293. [Google Scholar] [CrossRef]
  47. Frye, M.; Shedd, W.; Boswell, R. Gas hydrate resource potential in the Terrebonne Basin, Northern Gulf of Mexico. Mar. Pet. Geol. 2012, 34, 150–168. [Google Scholar] [CrossRef]
  48. Hillman, J.I.T.; Cook, A.E.; Daigle, H.; Nole, M.; Malinverno, A.; Meazell, K.; Flemings, P.B. Gas hydrate reservoirs and gas migration mechanisms in the Terrebonne Basin, Gulf of Mexico. Mar. Pet. Geol. 2017, 86, 1357–1373. [Google Scholar] [CrossRef]
  49. Ellis, D.V.; Singer, J.M. Well Logging for Earth Scientists; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar] [CrossRef]
  50. Wu, J.; Chen, X.Y.; Zhang, H.; Xiong, L.D.; Lei, H.; Deng, S.H. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar] [CrossRef]
  51. Kutty, A.A.; Wakjira, T.G.; Kucukvar, M.; Abdella, G.M.; Onat, N.C. Urban resilience and livability performance of European smart cities: A novel machine learning approach. J. Clean. Prod. 2022, 378, 134203. [Google Scholar] [CrossRef]
  52. Wakjira, T.G.; Ibrahim, M.; Ebead, U.; Alam, M.S. Explainable machine learning model and reliability analysis for flexural capacity prediction of RC beams strengthened in flexure with FRCM. Eng. Struct. 2022, 255, 113903. [Google Scholar] [CrossRef]
  53. Su, Y.; Gao, X.; Li, X.; Tao, D. Multivariate multilinear regression. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2012, 42, 1560–1573. [Google Scholar] [CrossRef]
  54. Ostertagová, E. Modelling using polynomial regression. Procedia Eng. 2012, 48, 500–506. [Google Scholar] [CrossRef]
  55. Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning：Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2017; Volume 27, pp. 83–85. [Google Scholar] [CrossRef]
  56. Wu, X.; Kumar, V.; Ross, Q.J.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.J.; Ng, A.; Liu, B.; Yu, P.S.; et al. Top 10 algorithms in data mining. Knowl. Inf. Syst. 2008, 14, 1–37. [Google Scholar] [CrossRef]
  57. Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
  58. Biau, G. Analysis of a random forests model. J. Mach. Learn. Res. 2012, 13, 1063–1095. [Google Scholar] [CrossRef]
  59. Liu, Z.; Liu, J. Seismic-controlled nonlinear extrapolation of well parameters using neural networks. Geophysics 1998, 63, 2035–2041. [Google Scholar] [CrossRef]
  60. McCormack, M.D. Neural computing in geophysics. Lead. Edge 1991, 10, 11–15. [Google Scholar] [CrossRef]
  61. McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
  62. Nielsen, M.A. Neural Networks and Deep Learning; Determination Press: San Francisco, CA, USA, 2014. [Google Scholar]
  63. García, S.; Luengo, J.; Herrera, F. Data Preprocessing in Data Mining; Intelligent Systems Reference Library; Springer International Publishing: Cham, Switzerland, 2015; Volume 72. [Google Scholar] [CrossRef]
  64. Aksoy, S.; Haralick, R.M. Feature normalization and likelihood-based similarity measures for image retrieval. Pattern Recognit. Lett. 2001, 22, 563–582. [Google Scholar] [CrossRef]
  65. Schlumberger. SonicVISION: Real-Time LWD Sonic for Advanced Drilling Optimization and Formation Evaluation; Schlumberger: Shenzhen, China, 2010. [Google Scholar]
  66. Schlumberger. EcoScope Log Quality Control Reference Manual; Schlumberger: Shenzhen, China, 2015. [Google Scholar]
  67. Schlumberger. GeoVISION Brochure: Resistivity Imaging for Productive Drilling; Schlumberger: Shenzhen, China, 2007. [Google Scholar]
  68. Nguyen, H.; Savary-Sismondin, B.; Patacz, V.; Jenssen, A.; Kifle, R.; Bertrand, A. Application of random forest algorithm to predict lithofacies from well and seismic data in Balder field, Norwegian North Sea. AAPG Bull. 2022, 106, 2239–2257. [Google Scholar] [CrossRef]
  69. Zou, C.; Zhao, L.; Xu, M.; Chen, Y.; Geng, J. Porosity Prediction With Uncertainty Quantification From Multiple Seismic Attributes Using Random Forest. J. Geophys. Res. Solid Earth 2021, 126, e2021JB021826. [Google Scholar] [CrossRef]
  70. Lorenzen, R. Multivariate linear regression of sonic logs on petrophysical logs for detailed reservoir characterization in producing fields. Interpretation 2018, 6, T543–T553. [Google Scholar] [CrossRef]
  71. Guerin, G.; Goldberg, D. Sonic waveform attenuation in gas hydrate-bearing sediments from the Mallik 2L-38 research well, Mackenzie Delta, Canada. J. Geophys. Res. 2002, 107, EPM-1. [Google Scholar] [CrossRef]
  72. Tobin, H.; Hirose, T.; Ikari, M.; Kanagawa, K.; Kimura, G.; Kinoshita, M.; Kitajima, H.; Saffer, D.; Yamaguchi, A.; Eguchi, N.; et al. Expedition 358 summary. In Proceedings of the Integrated Ocean Drilling Program; IODP: College Station, TX, USA, 2020. [Google Scholar] [CrossRef]
  73. Saffer, D.M.; Wallace, L.M.; Barnes, P.M.; Pecher, I.A.; Petronotis, K.E.; LeVay, L.J.; Bell, R.E.; Crundwell, M.P.; Engelmann de Oliveira, C.H.; Fagereng, A.; et al. Expedition 372B/375 summary. In Proceedings of the Integrated Ocean Drilling Program; IODP: College Station, TX, USA, 2019. [Google Scholar] [CrossRef]
  74. Almenningen, S.; Iden, E.; Fernø, M.A.; Ersland, G. Salinity Effects on Pore-Scale Methane Gas Hydrate Dissociation. J. Geophys. Res. Solid Earth 2018, 123, 5599–5608. [Google Scholar] [CrossRef]
  75. Hanor, J.S.; Mercer, J.A. Spatial variations in the salinity of pore waters in northern deep water Gulf of Mexico sediments: Implications for pathways and mechanisms of solute transport. Geofluids 2010, 10, 83–93. [Google Scholar] [CrossRef]
Energies 16 07709 g001
Figure 1. Maps showing the training holes (yellow dots) and testing holes (white dots). (A) Holes located at Cascadia Margin. (B) Holes located offshore of India. (C) Holes located in the Gulf of Mexico.
Figure 1. Maps showing the training holes (yellow dots) and testing holes (white dots). (A) Holes located at Cascadia Margin. (B) Holes located offshore of India. (C) Holes located in the Gulf of Mexico.
Energies 16 07709 g001
Energies 16 07709 g002
Figure 2. The workflow used for the data and the machine learning models in this study.
Figure 2. The workflow used for the data and the machine learning models in this study.
Energies 16 07709 g002
Energies 16 07709 g003
Figure 3. R2 accuracy and mean absolute percentage error (MAPE) for Vp and ρb prediction. Averaged over the two Walker Ridge holes, WR313-G and WR313-H.
Figure 3. R2 accuracy and mean absolute percentage error (MAPE) for Vp and ρb prediction. Averaged over the two Walker Ridge holes, WR313-G and WR313-H.
Energies 16 07709 g003
Energies 16 07709 g004
Figure 4. LWD data from 31–1043 mbsf (m below sea floor) in Hole WR313-G showing the original and predicted results from K nearest neighbors (Track 4) and random forest (Track 5) for Vp Case 1. Insets show (a) water-saturated intervals (b) intervals with hydrates in fractures and (c) intervals with hydrate in pore space.
Figure 4. LWD data from 31–1043 mbsf (m below sea floor) in Hole WR313-G showing the original and predicted results from K nearest neighbors (Track 4) and random forest (Track 5) for Vp Case 1. Insets show (a) water-saturated intervals (b) intervals with hydrates in fractures and (c) intervals with hydrate in pore space.
Energies 16 07709 g004
Energies 16 07709 g005
Figure 5. LWD data from 31–1043 mbsf (m below sea floor) in Hole WR313-G showing the original and predicted results from K nearest neighbors (Track 4) and random forest (Track 5) for Vp Case 2. Insets show (a) water-saturated intervals (b) intervals with hydrates in fractures and (c) intervals with hydrate in pore space.
Figure 5. LWD data from 31–1043 mbsf (m below sea floor) in Hole WR313-G showing the original and predicted results from K nearest neighbors (Track 4) and random forest (Track 5) for Vp Case 2. Insets show (a) water-saturated intervals (b) intervals with hydrates in fractures and (c) intervals with hydrate in pore space.
Energies 16 07709 g005
Energies 16 07709 g006
Figure 6. LWD data from 31–1043 mbsf (m below sea floor) in Hole WR313-G showing the original and predicted results for Vp Case 1 and 2 using K nearest neighbors and random forest along with the percentage error for different depth intervals.
Figure 6. LWD data from 31–1043 mbsf (m below sea floor) in Hole WR313-G showing the original and predicted results for Vp Case 1 and 2 using K nearest neighbors and random forest along with the percentage error for different depth intervals.
Energies 16 07709 g006
Energies 16 07709 g007
Figure 7. LWD logs showing bulk density Case 1 for Hole WR313-G comparing the results and percentage error associated with different depth intervals for K nearest neighbors and random forest algorithms.
Figure 7. LWD logs showing bulk density Case 1 for Hole WR313-G comparing the results and percentage error associated with different depth intervals for K nearest neighbors and random forest algorithms.
Energies 16 07709 g007
Energies 16 07709 g008
Figure 8. LWD logs for WR313-G showing two different clay-rich intervals, (A,B), with Vp prediction results using the random forest algorithm before and after eliminating neutron porosity (Case 1) from the training model.
Figure 8. LWD logs for WR313-G showing two different clay-rich intervals, (A,B), with Vp prediction results using the random forest algorithm before and after eliminating neutron porosity (Case 1) from the training model.
Energies 16 07709 g008
Table 1. Training, validation, and test datasets for the machine learning model. Holes WR313-G and WR313-H are used to test, and all the other holes are used to train and validate the model by splitting them into a 70% (train) and 30% (validation) ratio.
Table 1. Training, validation, and test datasets for the machine learning model. Holes WR313-G and WR313-H are used to test, and all the other holes are used to train and validate the model by splitting them into a 70% (train) and 30% (validation) ratio.
HoleLocationDrilling ProjectWater Depth (m)Total Depth Drilled (mbsf)Water
Saturated Intervals (m)		Hydrate in
Fractures (m)		Hydrate in Pores (m)
GC955-HGulf of MexicoJIP Leg II203359041214434
GC955-I20646716660~5
GC955-Q19854614370~24
AC21-A14905364367921
AC21-B1488340301039
WR313-G20001043<753>24644
WR313-H1966100062632549
U1325ACascadia
Margin		IODP
Expedition 311		2192350>3490<0.23
U1327A1305300282018
U1328A1267300254460
NGHP-01-02ABay of BengalNGHP
Expedition 01		1058505000
NGHP-01-02B105825025000
NGHP-01-03A1076300912090
NGHP-01-04A1081300280200
NGHP-01-05A945200161390
NGHP-01-05B945200163370
NGHP-01-06A1160350339110
NGHP-01-07A1285260220400
NGHP-01-10A1038205821230
NGHP-01-11A1007200180200
NGHP-01-08A1689350313370
NGHP-01-09A19353302301000
Table 2. Holes used for training the machine learning model. Vp is computed from the compressional slowness log, DTCO.
Table 2. Holes used for training the machine learning model. Vp is computed from the compressional slowness log, DTCO.
HolesLocationGas Hydrate OccurrenceLWD ToolsLogs Used
GC955-H
GC955-I
GC955-Q
AC21-A
AC21-B		Gulf of MexicoGas hydrate occurs in all the holes.EcoScope
geoVISION
sonicVISION		Density Caliper (DCAV), Bulk Density (RHOB), Calibrated and Filtered Gamma Ray (GRMA_FILT), RING Resistivity, Propagation Resistivity (A16L, A40L, P16H, P28H, P40H), Vp
U1327A
U1328A
U1325A		Cascadia
Margin		Gas hydrate occurs in holes U1327A and U1328A.adnVISION
EcoScope
geoVISION
sonicVISION		Density Caliper (DCAV), Bulk Density (RHOB), Calibrated and Filtered Gamma Ray (GRMA_FILT), RING Resistivity, Propagation Resistivity (A16L, A40L, P16H, P28H, P40H), Vp
NGHP-01-02A
NGHP-01-02B
NGHP-01-03A
NGHP-01-04A
NGHP-01-05A
NGHP-01-05B
NGHP-01-06A
NGHP-01-07A
NGHP-01-08A
NGHP-01-09A
NGHP-01-10A
NGHP-01-11A		Bay of BengalGas hydrate occurs in all the holes
except 02A and 02B		EcoScope
geoVISION
sonicVISION		Density Caliper (DCAV), Bulk Density (RHOB), Calibrated and Filtered Gamma Ray (GRMA_FILT), RING Resistivity, Propagation Resistivity (A16L, A40L, P16H, P28H, P40H), Vp
Table 3. Training/validation accuracy and error metrics computed over the 20 training holes with a 70:30 split over training data. Test metrics are computed for the two Walker Ridge holes, WR313-G and WR313-H (taking average R2 and MAPE for the two holes).
Table 3. Training/validation accuracy and error metrics computed over the 20 training holes with a 70:30 split over training data. Test metrics are computed for the two Walker Ridge holes, WR313-G and WR313-H (taking average R2 and MAPE for the two holes).
Multilinear Regression
Training R2 (%)Training MAPE (%)Validation R2(%)Validation MAPE (%)Test R2 (%)Test MAPE (%)
Vp Case 1564.18554.18595.69
Vp Case 2623.60643.46536.45
ρb Case 1315.18315.12495.17
ρb Case 2464.13484.13413.14
Polynomial Regression (4th Order)
Training R2 (%)Training MAPE (%)Validation R2(%)Validation MAPE (%)Test R2 (%)Test MAPE (%)
Vp Case 1912.46902.48503.79
Vp Case 2882.020.0154.837.071.4
ρb Case 1623.54603.4933160
ρb Case 2822.330110155
Polynomial Regression (4th Order) with Ridge Regularization
Training R2 (%)Training MAPE (%)Validation R2(%)Validation MAPE (%)Test R2 (%)Test MAPE (%)
Vp Case 1852.69832.7742.99
Vp Case 2822.42812.34554.99
ρb Case 1573.86573.8425.16
ρb Case 2752.78752.81252.70
K Nearest Neighbors
Training R2 (%)Training MAPE (%)Validation R2(%)Validation MAPE (%)Test R2 (%)Test MAPE (%)
Vp Case 11000941.98733.45
Vp Case 21000861.79644.4
ρb Case 11000762.55752.00
ρb Case 21000851.86662.65
Random Forest
Training R2 (%)Training MAPE (%)Validation R2(%)Validation MAPE (%)Test R2 (%)Test MAPE (%)
Vp Case 1991.07961.60703.96
Vp Case 2971.05911.60634.40
ρb Case 1931.51812.30722.19
ρb Case 2951.16891.71493.18
Multilayer Perceptron
Training R2 (%)Training MAPE (%)Validation R2(%)Validation MAPE (%)Test R2 (%)Test MAPE (%)
Vp Case 1564.20554.19595.66
Vp Case 2623.59633.45526.53
ρb Case 1464.47454.40572.70
ρb Case 206.3706.380.111
Table 4. Statistical analysis for Vp and ρb predictions averaged over Holes WR313-G and WR313-H for water-saturated sediments, gas hydrate in near vertical fractures, and gas hydrates in the primary pore space (MAPE = mean absolute percentage error).
Table 4. Statistical analysis for Vp and ρb predictions averaged over Holes WR313-G and WR313-H for water-saturated sediments, gas hydrate in near vertical fractures, and gas hydrates in the primary pore space (MAPE = mean absolute percentage error).
Random ForestK Nearest Neighbors
R2MAPER2MAPE
Vp Case 1
(Input Logs: Gamma Ray, Bulk Density, Ring Resistivity)		Complete Log Interval70%3.9%73%3.4%
Water-Saturated74%3.0%75%3.6%
Hydrate in Fractures54%5.9%73%2.4%
Hydrate in Pores81%6.5%71%10%
Vp Case 2
(Input Logs: Gamma Ray, Bulk Density, Propagation Resistivity)		Complete Log Interval63%4.4%64%4.4%
Water-Saturated66%4.7%70%4.0%
Hydrate in Fractures68%2.8%48%4.2%
Hydrate in Pores69%14%63%15%
ρb Case 1Complete Log Interval72%2.2%75%2.0%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Naim, F.; Cook, A.E.; Moortgat, J. Estimating Compressional Velocity and Bulk Density Logs in Marine Gas Hydrates Using Machine Learning. Energies 2023, 16, 7709. https://doi.org/10.3390/en16237709

AMA Style

Naim F, Cook AE, Moortgat J. Estimating Compressional Velocity and Bulk Density Logs in Marine Gas Hydrates Using Machine Learning. Energies. 2023; 16(23):7709. https://doi.org/10.3390/en16237709

Chicago/Turabian Style

Naim, Fawz, Ann E. Cook, and Joachim Moortgat. 2023. "Estimating Compressional Velocity and Bulk Density Logs in Marine Gas Hydrates Using Machine Learning" Energies 16, no. 23: 7709. https://doi.org/10.3390/en16237709

APA Style

Naim, F., Cook, A. E., & Moortgat, J. (2023). Estimating Compressional Velocity and Bulk Density Logs in Marine Gas Hydrates Using Machine Learning. Energies, 16(23), 7709. https://doi.org/10.3390/en16237709

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop