Abstract
The 21st century brings new challenges related to the rapid development of renewable energy sources. Increasingly ambitious climate targets adopted at the European and global level are stimulating an increase in the share of photovoltaic sources in electricity generation. Unfortunately, the intermittent supply of electricity with solar panels makes this energy much more difficult to use. The production of electricity only during the sunny period forces the need to collect it during the day and then use it at night or during unfavorable weather conditions. Therefore, energy storage facilities are important when producing energy from renewable sources. Their installation increases the flexibility of transmission systems and creates opportunities for stable operation with a large share of renewable energy sources. This article offers an economic evaluation of the use of energy storage for a photovoltaic farm under the conditions of using the prices of the Polish Power Exchange. The period from June 2020 to May 2023 was analyzed. The results in terms of productivity of PV installations from the village of Łęki and prices from the Commodity Energy Exchange in the same period were used. Analyzing the results, it can be seen that energy storage brings additional revenue, especially during periods with large spreads in the value of electricity prices. The use of energy storage also allows for more efficient use of energy from photovoltaic panels. The value of additional revenue from energy storage was particularly evident in 2022, when energy prices peaked.
Keywords:
energy storage; photovoltaic; hybrid; economic; Day-Ahead Market; duck curve; PV farm; Poland 1. Introduction
The 21st century brings new challenges related to the rapid development of renewable energy sources. Increasingly ambitious climate targets adopted at the European and global levels are stimulating an increase in the share of photovoltaic sources in electricity generation [1]. Unfortunately, the intermittent supply of electricity by solar panels makes this energy much more difficult to use. Producing electricity only during the sunny season necessitates the need to store it during the day and then use it at night or during adverse weather conditions [2,3,4].
Therefore, energy storage facilities are important when producing energy from renewable sources [3,5,6,7,8]. They are also a promising chance for some countries for energy transformation [9,10]. Their installation increases the flexibility of transmission systems and creates opportunities for stable operation with a large share of renewable energy sources [1,11]. In addition to being able to increase the efficiency of conventional power plants by preventing frequent changes in their operating parameters, energy storage also has a positive impact on the environment [12,13,14,15,16,17]. It will also reduce short-term fluctuations in power from RES sources and allow power plants to run without power coming from the National Grid (KSE) [18,19,20].
In Poland, energy is mainly stored using hydro-pumped storage power plants [12,21,22]. The installed capacity of storage systems in these power plants represents only 3.2% of the installed capacity of power plants in Poland [23]. Energy storage legislation is not yet fully developed and does not offer attractive business models for investors [1,24,25]. Prosumers pose a growing technical, investment and organizational challenge to the Polish energy system [26,27,28,29]. It is necessary to create system solutions that will ensure the possibility of connecting new prosumer installations to the grid in a situation in which the development of prosumerism means, for the distribution network, operators increasing costs of expansion, as well as modernization and maintenance of the grid, with decreasing demand of this group of consumers for energy from the grid [18,30,31,32].
The purpose of this article is to evaluate the economic application of electricity storage for a photovoltaic farm under the conditions of using the prices of the Polish Power Exchange (TGE). The period from June 2020 to May 2023 was analyzed. The results in the productivity of PV installations from the village of Łęki [33,34] and prices from the Day-Ahead Market (DAM) of the Polish Power Exchange during the same period were used (Figure 1). In Poland, on a daily basis, with relatively high energy production from PV, energy prices are relatively low. Therefore, the economic impact of energy storage was considered in order to avoid selling energy at the lowest prices and to sell the stored energy during the period with the highest electricity prices, usually between 7 pm and 9 pm.
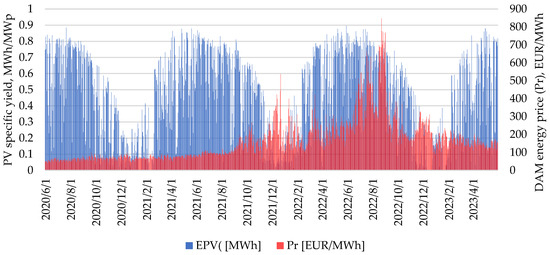
Figure 1.
Profile of electricity production and prices from June 2020 to May 2023 [35].
Analyzing Figure 1, the shape of the energy production graph is similar for each year, whereas energy prices vary significantly. A clear increase in these prices can be seen in the fourth quarter of 2021 and in 2022. This is also the period during which significant amplitudes of the prices during the day were recorded, so energy storage was the most profitable then. The maximum value of the price of electricity was 847.21 EUR/MWh, and this took place on 23 August 2022 [35].
2. Materials and Methods
The object of the study is a photovoltaic farm with a rated capacity of 1 MWp (typical size of PV farm in Poland [36,37,38], and productivity results are scalable). For the purpose of this analysis, energy production data from a photovoltaic installation with a rated capacity of 5.04 kWp located in the southern Polish town of Łęki were used. The installation consists of fourteen monocrystalline photovoltaic panels of 0.36 kWp each [33]. The obtained values of electricity production from the aforementioned installation were multiplied to reflect a photovoltaic farm with a rated capacity of 1 MWp. It was assumed that the energy productions in both cases would be proportional to each other [39,40,41,42]. The photovoltaic farm was simulatively integrated with an energy storage facility with a useful capacity of ES0 0.5 MWh. The efficiency of the storage was set at 87% [43], and the minimum electricity production at which energy storage was considered (EPV1) was set at 0.1 MWh. A scenario was created in which electricity was stored when its price on the Polish Power Exchange was the lowest and sold when the price was the highest. If the amount of energy produced in the hour was less than the useful energy storage capacity (ES0), energy was also stored when its price was the second lowest price of the day (taking into account the EPV1 condition). The analysis considered the billing period from June 2020 to May 2023.
Calculation methodology
The estimation of hourly energy production values from a 1 MWp PV installation based on values recorded at a 5.04 kWp installation is as follows:
where
is electricity production by an installation with a rated capacity of 1 MWp (MWh);
is the rated power of the photovoltaic installation (PPV = 1 MWp) (MWp);
is the hourly baseline energy production by an installation with a rated capacity of 5.04 kWp (MWh);
is the rated power of the primary photovoltaic installation (PPV0 = 5.04 kWp = 0.00504 MWp) (MWp) [34];
τ is the number of the hour for which the energy production measurement was made (τ ∈ 〈1, 26280〉) for three years (3 times 8760).
Electricity prices
The next step involved finding the minima and maxima of electricity prices for each day of the year.
The lowest value of the electricity price in the case of the existence of energy production by the PV installation at the minimum level defined as EPV1 was determined.
The values of electricity production for which the sought values will meet the assumed condition of energy storage (for all three years) were selected.
The second electricity price value based on the price vector vPr1 was determined.
where
is the vector of electricity prices. The values occur only for the case of the presence of parallel PV power generation at min EPV1);
is the electricity price (EUR/MWh);
is the electricity production by an installation with a rated capacity of 1 MWp (MWh);
is the value for the condition stating that the energy storage can accept energy only when the energy production of the PV installation is greater than the assumed 0.1 MWh;
is the minimum value of the price of electricity on a daily basis (EUR/MWh);
is the minimum value from the vector of electricity prices on a daily scale (EUR/MWh).
The second lowest value of the price of electricity was determined based on the restriction of the price vector vPr1 by the occurrence of the lowest energy price on the day:
where
is the second lowest value of the electricity price on a given day under the condition of EPV1 (EUR/MWh);
is the minimum value from the electricity price vector excluding the minimum value of the electricity price (EUR/MWh).
Then, the highest value of the electricity price was determined.
The hours were selected for which the maximum value of the electricity price for each day will be sought:
where
is the vector of electricity prices;
is the electricity price (EUR/MWh);
is the hour of the day ( ∈ ⟨1, 24⟩);
are the hours of occurrence of the lowest and second lowest electricity prices.
The highest value of the price of electricity was determined:
where
is the highest value of the electricity price on a given day under the condition of EPV1 (EUR/MWh);
is the maximum value from the electricity price vector (EUR/MWh).
The determination of the amount of energy sent to the grid in each hour (ES) is shown in Figure 2.
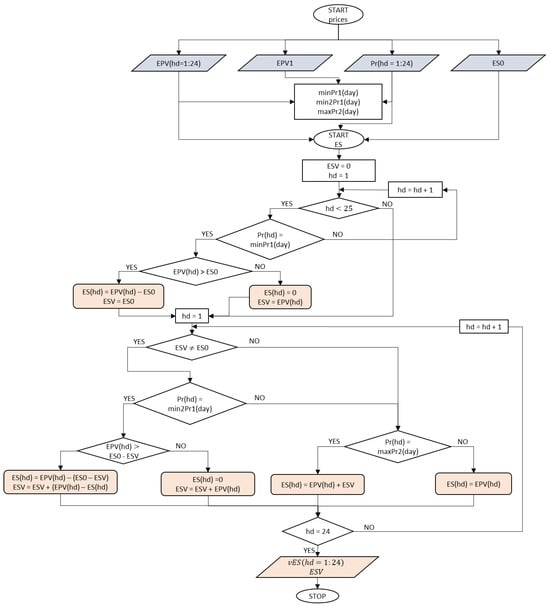
Figure 2.
Block diagram used to determine the value of electricity returned to the grid.
- At the first start (START price), the following values were taken: the production of electricity by the installation for each hour of the day (EPV(hd = 1:24)), the value for the condition that the energy storage can accept energy only when the production of energy by the photovoltaic installation is greater than the assumed 0.1 MW (EPV1), the price of electricity for each hour (Pr(hd = 1:24)) and the capacity of the energy storage (ES0 = 0.5 MWh).
- The lowest value of the electricity price minPr1(day) (3), the second lowest value of the electricity price min2Pr1(day) (4) and the highest value of the electricity price maxPr2(day) (6) were determined.
- At the second start (START ES), the corresponding values were assigned to the amount of energy sent to storage (ESV) and to the hour of the day (hd).
- It was checked whether the value of hd < 25. If so, the following steps were followed, and if not, it was necessary to go to step 10.
- It was checked whether (Pr(hd)) is equal to minPr1(day). If yes, proceed according to the next points, and if no, go to point 9.
- It was checked whether (EPV(hd)) is greater than ES0. If so, the following points were followed, and if not, proceed to point 8.
- The values of the variable determining the amount of electricity returned to the grid (ES(hd) = EPV(hd) − ES0) and the variable ESV (ESV = ES0) were assigned, and it was necessary to proceed to point 10.
- The values of the variable ES(hd) (ES(hd) = 0) and the variable ESV (ESV = EPV(hd)) were assigned, and it was necessary to go to point 10.
- The variable hd was assigned the value “hd + 1”.
- The variable hd was assigned the value “1”.
- It was checked whether the value of ESV is different from ES0. If it is, the following steps were followed; if not, proceed to step 16.
- It was checked whether (Pr(hd)) is equal to min2Pr1(day). If yes, proceed according to the next points, and if no, go to point 16.
- It was checked whether (EPV(hd)) is greater than ES0-ESV. If so, the following points were followed, and if not, proceed to point 15.
- Values were assigned to the variable ES(hd) (ES(hd) = EPV(hd)-(ES0-ESV)) and the variable ESV (ESV = ESV + (EPV(hd)-ES(hd)), and it was necessary to proceed to point 19.
- Values were assigned to the ES(hd) variable (ES(hd) = 0) and the ESV variable (ESV = ESV + (EPV(hd)); then, go to step 19.
- It was checked whether (Pr(hd)) is equal to maxPr2(day). If yes, then follow the next steps, and if no, then proceed to step 18.
- The value of the variable ES(hd) was assigned (ES(hd) = EPV(hd) + ESV), and it was necessary to proceed to point 19.
- The value of the variable ES(hd) was assigned (ES(hd) = EPV(hd)). Then, proceed to the next points.
- It was checked whether the value of the variable hd is equal to “24”. If so, proceed to point 21, and if not, proceed according to the following points.
- The variable hd was assigned the value “hd + 1”, the next hour of the day.
- The values of the vector vES(hd:1:24) and the variable ESV were recorded.
- The calculation was completed (for one day of calculation).
The amount of energy charged to the energy storage in each hour was calculated:
where
is the amount of energy transmitted to the storage in a given hour (MWh);
is the value of energy production by the photovoltaic installation in a given hour (MWh);
is the energy sent to the grid: the value of energy production by the photovoltaic installation minus the value of stored energy in a given hour, or the value of energy sent from the process of discharging the energy storage (MWh).
The monetary value of the produced electricity in the PV system was determined. This is in order to produce electricity by a photovoltaic system without energy storage for each hour:
where
is the hourly monetary value of electricity produced (without energy storage) (EUR);
is the hourly value of energy production by the photovoltaic installation (MWh);
is the Day-Ahead Market electricity price (EUR/MWh).
For electricity production by the photovoltaic installation with energy storage, the following formula was used:
where
is the hourly monetary value of electricity produced (with energy storage) (EUR);
is the hourly value of energy sent to the grid: the value of energy production by the photovoltaic installation minus the value of stored energy in a given hour (MWh);
is the Day-Ahead Market electricity price (EUR/MWh);
is the amount of energy stored on a given day (MWh);
is the efficiency of electricity storage (ESE = 0.87) (source: NREL [43]);
is the hour of the day ( ∈ 〈1, 24〉);
is the highest value of the electricity price on a given day (EUR/MWh).
The difference in revenue when using energy storage versus the option without energy storage was determined:
where
is the hourly difference due to energy storage (EUR);
is the monetary value of electricity sent to the grid (with energy storage) (EUR);
is the monetary value of electricity produced (without energy storage) (EUR).
The corrected amount of effectively stored energy was determined (unprofitable stored operation was avoided):
where
is the amount of effectively stored energy on an hourly basis (MWh);
is the amount of stored energy on an hourly basis (MWh);
is the daily difference due to energy storage (EUR).
The adjusted economic effect was determined:
where
is the hourly adjusted economic effect in the form of revenue difference (EUR);
is the hourly additional revenue due to energy storage (EUR).
The additional revenue from the electricity produced by the photovoltaic system with energy storage in the years studied was determined:
where
is the annual additional revenue due to energy storage (EUR);
is the number of the hour determining the beginning of the year;
is the hour number defining the end of the year;
is the hourly adjusted revenue due to energy storage (EUR).
The adjusted economic effect from the electricity produced by the photovoltaic installation with energy storage in the years studied was determined:
where
is the annual adjusted economic effect (EUR);
is the number of the hour determining the beginning of the calculation year;
is the hour number defining the end of the calculation year;
is the hourly adjusted economic effect (EUR).
The number of cycles of charging the energy storage with energy from the photovoltaic installation was determined:
where
is the number of cycles;
is the amount of effectively stored energy (MWh);
is the hour number specifying the beginning of the period for which the number of cycles is counted;
is the hour number specifying the end of the period for which the number of cycles is counted;
is the energy storage capacity (ES0 = 0.5 MWh).
3. Results
The results in the form of energy flows in the proposed installation for a day with a relatively large difference in revenue are presented in Figure 3. The opposite situation in terms of the difference in revenue is presented in Figure 4.
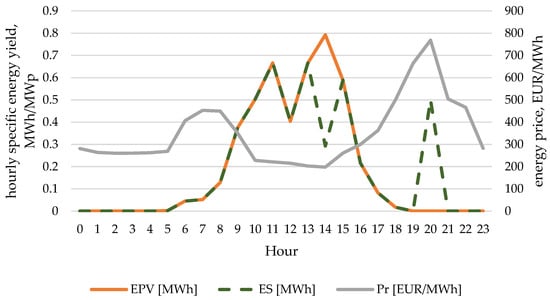
Figure 3.
Values of energy production, energy returned to the grid and energy price for individual hours on 1 September 2022.
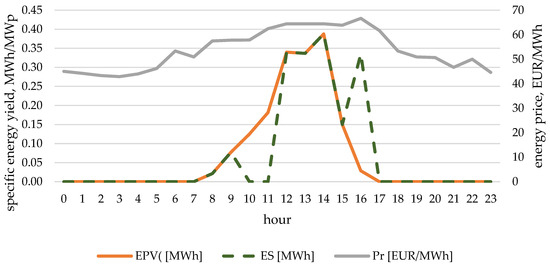
Figure 4.
Values of energy production, energy returned to the grid and energy price for individual hours on 18 November 2020.
On 1 September 2022, the largest additional revenue due to energy storage was recorded. It was caused by significant differences in electricity prices on that day and a very high maximum price, which amounted to 768.46 EUR/MWh. Energy was stored at 2 pm and returned to the grid at 8 pm.
One of the smaller additional spikes in revenue from charging the energy storage with PV electricity was recorded on 18 November 20. On that day, it was profitable to store energy only at 10 o’clock; storing it at 11 o’clock already brought additional revenue to a negative level. Energy prices on 18 November 2020 were significantly lower those on 1 September 2022. Also, they did not vary significantly throughout the day, which made the value of the adjusted economic effect small.
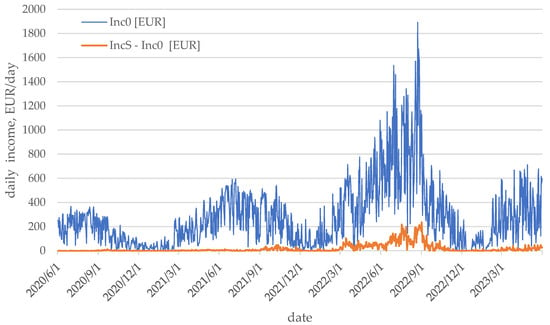
Figure 5.
Inc0 and IncS income over 3 years.
As can be observed in the chart above, for most days, the monetary value of electricity produced with energy storage is greater than the monetary value of electricity produced without energy storage. This means that such a combination of two systems generates additional revenue at a lower value of energy returned to the grid. A yearly sum of the abovementioned values is presented in Table 1 and Table 2.

Table 1.
Income from electricity production by photovoltaic installation without and with energy storage for 3 years.

Table 2.
Profit and adjusted economic impact from electricity storage for 3 years.
The monetary value of electricity produced both with and without energy storage is highest for the third year. It is almost three times higher than for the first year, in which Inc0 as well as IncS values were at similar levels. This is related to the profile of energy prices during this period.
The table above shows the difference in the use of energy storage derived from the sale of stored electricity. It is shown for three years. The highest value of both revenue and adjusted additional revenue was recorded in the year 2022–2023. As read from the first figure, electricity prices were much higher in that year, which largely affected the recorded additional revenue. A very small additional revenue of about EUR 200 was recorded in the first year. The adjusted economic effect this year was more than EUR 400, which was influenced by the possibility of not storing energy during hours when it was not profitable to do so.
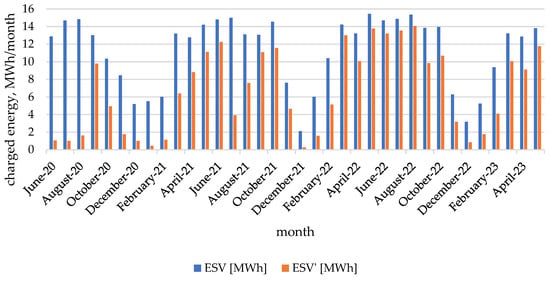
Figure 6.
Unadjusted and adjusted amount of stored electricity for each month.
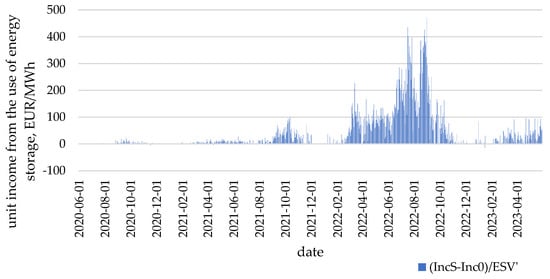
Figure 7.
Unit (per 1 MWh energy stored) additional income from the use of electricity storage (per 1 MWh storage capacity) for 3 years.
The values of the amount of effectively stored energy are very different from each other. In 2022, there is a significant increase in these values, and the difference between ESV and ESV’ is not as high as in the studied period of 2020. Analyzing the above graph, it can also be observed that in the winter months, both the ESV and ESV’ values are significantly lower compared to the other months. This is due to the fact that energy production is incomparably lower in these months.
Differences in income in the year 2020 are shown on a daily scale in Figure 8, and monthly charged energy is shown in Figure 9.
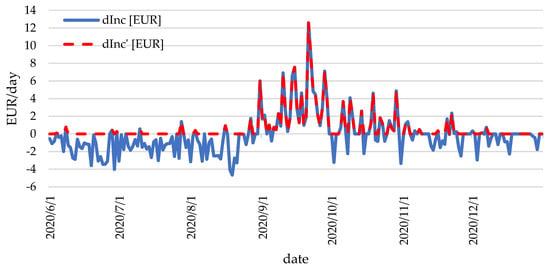
Figure 8.
The course of profit and adjusted economic effect from electricity storage in 2020.
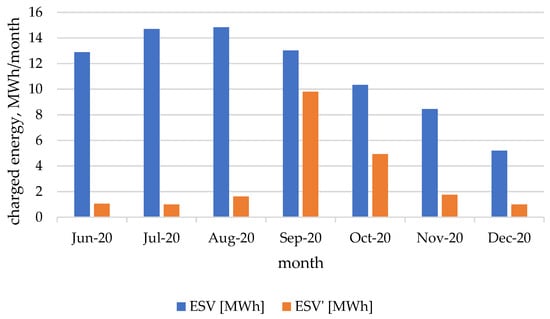
Figure 9.
Amount of stored electricity (ESV and ESV’) for months from May to December 2020.
The chart above shows the course of additional revenue and adjusted economic effects for 2020. It can be clearly seen that in the period from June to the end of August, the additional revenue was negative for most days. In September and October, there was an increase in the value of the adjusted economic effect, and for most of November and December, it would be at zero.
In the chart above, it can be read that the energy storage was charged with the highest amount of energy from the photovoltaic installation in September. In the first three months (June, July and August) and in the last two (November and December), it was not profitable, which is why the ESV’ bars are much lower than the ESV bars.
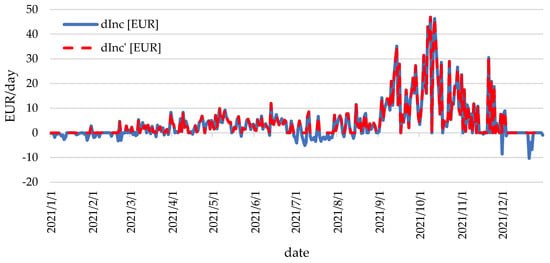
Figure 10.
The course of profit and adjusted economic effect from electricity storage in 2021.
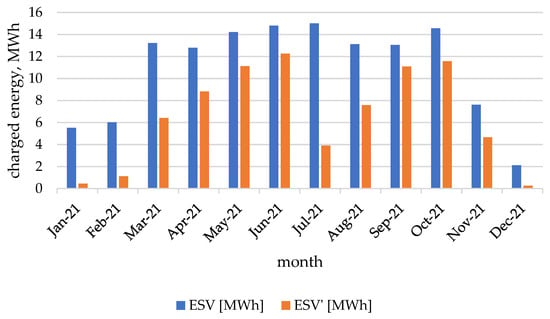
Figure 11.
Amount of stored electricity (ESV and ESV’) for each month of 2021.
In 2021, there was significant additional revenue from electricity storage in September and October. Also, in the months of March to June, as well as August and November, the additional revenue was positive for most days. In the remaining months, the adjusted economic effect was sporadic.
In the months of May, June, September and October, effective energy storage took place for most of the month. In January, February and December, for most of the days, even if storage was possible, the electricity from the PV system would not charge all the storage (with the EPV1 condition).
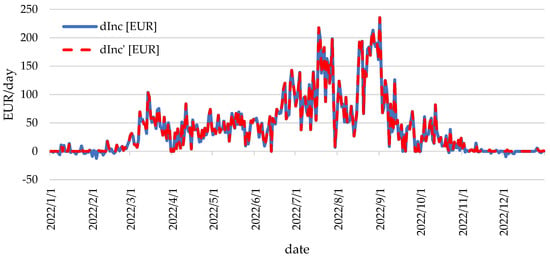
Figure 12.
The course of profit and adjusted economic effect from electricity storage in 2022.
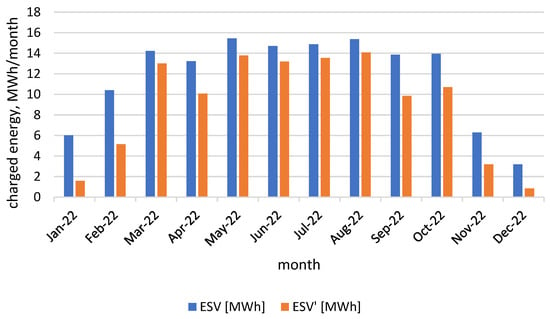
Figure 13.
Amount of stored electricity (ESV and ESV’) for each month of 2022.
The year 2022 saw the highest additional revenue coming from the storage of photovoltaic electricity. In the chart above, it can be seen that for much of the year, the values of additional revenue from energy storage coincided with the values of the adjusted economic effect. This means that the differences between the prices during the day were significant. In 2022, as in previous years, the largest additional revenue was in the period from July to September.
In the period from March to the end of October 2022, energy storage was effective, as can be seen from the height of the bars in orange in the chart above. In the other months, energy was stored on very few days, and in addition, the storage capacity was not covered.
The difference in income and charged energy for part of the year 2023 is shown in Figure 14 and Figure 15.
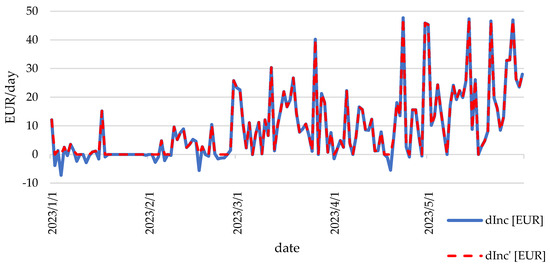
Figure 14.
The profile of profit and adjusted economic effect from electricity storage in 2023.
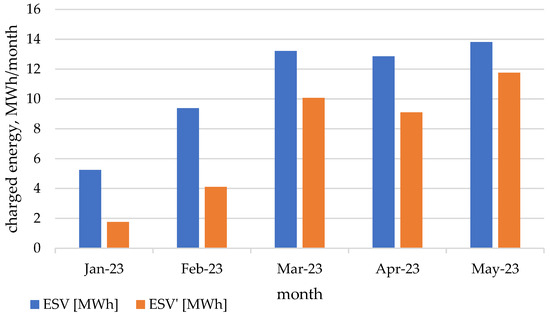
Figure 15.
Unadjusted and adjusted amount of stored electricity in the months from January to May 2023.
In 2023, for three months starting in March, the values of the adjusted economic effect coincided with the additional revenue. This means that for a large part of the days in these months, it was profitable to store electricity from the photovoltaic installation. For the first two months of the year, the additional revenue was close to zero.
In the period from March to the end of May 2023, effective energy storage was recorded for many days. In January, the value of ESV’ did not even reach 2 MWh, and in February, it took the value of 4 MWh, which is equivalent to eight full cycles of charging the energy storage with PV energy.
In the next step, the number of calculated cycles of energy storage was obtained (as energy stored divided by ES0), as shown in Table 3.

Table 3.
Number of energy storage charging cycles with energy from photovoltaic installation for 3 years.
The most charging cycles of the energy storage were recorded in the third year. In the period from 1 June 2020 to 31 May 2023, which corresponds to 1095 days, the energy storage was charged with electricity from the photovoltaic installation around 491 times. To convert this value to a percentage of days, this means that the energy storage was charged for about 45% of the days.
The main limitations in the study are the adopted proportion between the power of the PV installation and the energy storage capacity. Additionally, the energy storage system’s operation has been restricted to only be powered by sufficiently high levels of PV energy production and not, for example, by using energy from the grid as well.
4. Conclusions
Energy storage is a very important aspect with photovoltaic energy production growing so rapidly in Poland. It provides additional revenue for prosumers, and it helps to relieve the grid of excess energy. This paper analyzes the economic role of energy storage in the context of photovoltaic farms in Poland. The economic aspects of using energy storage in the production of electricity from photovoltaic panels were studied, based on data from a 1 MWp farm and energy prices on the Polish Power Exchange from June 2020 to May 2023.
The results of the analysis indicate that for 3 years, a photovoltaic installation would generate 303,605 EUR/MWp in revenue, and a photovoltaic installation combined with 0.5 MWh capacity energy storage would generate 321,789 EUR/MWp, or 6% more than that without additional energy storage. The revenue from energy storage is a small percentage of the revenue from the photovoltaic installation. In the third year of the installation’s operation, when the revenue was the highest among the analyzed period, thanks to the energy storage, the revenue would have been 9% higher.
The energy storage was charged and discharged. For a quite small amount of energy storage, a smaller capacity means a lower number of days using storage—for example, the storage was in use on only 45% of the days. For the remaining 55% of days, energy storage was either unprofitable or impossible due to the photovoltaic plant’s energy production being too low.
The above work shows that energy storage facilities do not generate much additional revenue. However, one can see the potential for further research and development of the work. It is proposed to analyze the combination of a photovoltaic installation with energy storage with other capacity sizes. This will allow one to see for what size of energy storage capacity the most revenue can be generated. The second aspect that can be explored is the expansion of the range of conditions, such as EPV1 (meaning the value for the condition stating that the energy storage can only accept energy when the photovoltaic plant’s energy production is greater than assumed), whose value can be both increased and decreased, and the number of hours for which the price of electricity is low. This will allow for increasing the amount of stored energy.
The economic results were obtained for an energy storage intensification scenario (low energy storage capacity relative to daily PV energy production values), resulting in a relatively high unit additional revenue from energy storage utilization. Nevertheless, the obtained values of the additional revenue are low in comparison to the potential investment expenditures for energy storage. This information can be useful for potential investors, policymakers and grid operators. Several directions for further study include economic analyses of the investment costs of energy storage and the impacts of panel depreciation on reducing costs.
Author Contributions
Conceptualization, K.R. and P.O.; methodology, K.R., P.O. and D.M.; validation, P.O.; formal analysis, K.R. and D.M.; data curation, K.R. and P.O.; writing—original draft preparation, K.R.; writing—review and editing, P.O. and D.M.; visualization, K.R. and P.O.; supervision, P.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| DAM | Day-Ahead Market |
| dInc | Hourly difference due to energy storage, EUR |
| dInc’ | Hourly adjusted economic effect in the form of revenue difference, EUR |
| EPV | Electricity production by an installation with a rated capacity of 1 MWp, MWh |
| EPV0 | Hourly baseline energy production by an installation with a rated capacity of 5.04 kWp, MWh |
| EPV1 | The amount of minimum electricity production at which energy storage was considered |
| ES | Energy sent to the grid: the value of energy production by the photovoltaic installation minus the value of stored energy in a given hour, or the value of energy sent from the process of discharging the energy storage, MWh |
| ES0 | Useful capacity of energy storage, MWh |
| ESV | The amount of energy transmitted to the storage in a given hour, MWh |
| hd | Hour of the day (hd ∈ 〈1, 24〉) |
| hd(min(Pr1(day)), hd(min(2Pr1(day))) | Hour of occurrence of the lowest and second lowest electricity price |
| Inc0 | Hourly monetary value of electricity produced (without energy storage), EUR |
| IncS | Hourly monetary value of electricity produced (with energy storage), EUR |
| KSE | National grid |
| max(Pr2(day)) | The highest value of electricity price of a given day under the condition of EPV1, EUR/MWh |
| max(vPr2(day)) | The maximum value from the electricity price vector, EUR/MWh |
| minPr1(day) | The minimum value of the price of electricity on a daily basis, EUR/MWh |
| min(vPr1(day)) | The minimum value from the vector of electricity prices on a daily scale, EUR/MWh |
| min2Pr1(day) | The second lowest value of electricity price on a given day under the condition of EPV1, EUR/MWh |
| min(vPr1(day)∖min(Pr1(day)) | The minimum value from the electricity price vector excluding the minimum value of the electricity price, EUR/MWh |
| NoC | Number of cycles |
| PPV | Rated power of the photovoltaic installation (PPV = 1 MWp), MWp |
| PPV0 | Rated power of the primary photovoltaic installation, MWp |
| Pr | DAM energy price, EUR/MWh |
| RES | Renewable energy source |
| TGE | Polish Power Exchange |
| vPr1 | Vector of electricity prices (the values occur only for the case of the presence of parallel PV power generation at min EPV1) |
| vPr2 | Vector of electricity prices |
| Greek symbols: | |
| Hour | |
| Number of the hour determining the beginning of the year | |
| Hour number defining the end of the year | |
References
- Rafał, K.; Grabowski, P. Magazynowanie Energii. ACADEMIA Mag. Pol. Akad. Nauk. 2023, 34–40. [Google Scholar] [CrossRef]
- Harasimczuk, M. Hybrydowy system magazynowania energii fotowoltaicznej. Pozn. Univ. Technol. Acad. J. Electr. Eng. 2016, 87, 109–118. [Google Scholar]
- Ceran, B.; Jurasz, J.; Mielcarek, A.; Campana, P.E. PV Systems Integrated with Commercial Buildings for Local and National Peak Load Shaving in Poland. J. Clean. Prod. 2021, 322, 129076. [Google Scholar] [CrossRef]
- Ceran, B.; Mielcarek, A.; Hassan, Q.; Teneta, J.; Jaszczur, M. Aging Effects on Modelling and Operation of a Photovoltaic System with Hydrogen Storage. Appl. Energy 2021, 297, 117161. [Google Scholar] [CrossRef]
- Sobczyk, W.; Sobczyk, E.J. Varying the Energy Mix in the EU-28 and in Poland as a Step towards Sustainable Development. Energies 2021, 14, 1502. [Google Scholar] [CrossRef]
- Jurasz, J.; Ciapała, B. A Solar- and Wind-Powered Charging Station for Electric Buses Based on a Backup Batteries Concept. In ICT for Electric Vehicle Integration with the Smart Grid; 2019; pp. 317–335. Available online: https://digital-library.theiet.org/content/books/10.1049/pbtr016e_ch12 (accessed on 18 July 2023).
- Kuta, M. Mobilized Thermal Energy Storage (M-TES) System Design for Cooperation with Geothermal Energy Sources. Appl. Energy 2023, 332, 120567. [Google Scholar] [CrossRef]
- Kuta, M.; Matuszewska, D.; Wójcik, T.M. The Role of Phase Change Materials for the Sustainable Energy. E3S Web Conf. 2016, 10, 00068. [Google Scholar] [CrossRef]
- Dyczko, A.; Kamiński, P.; Stecuła, K.; Prostański, D.; Kopacz, M.; Kowol, D. Thermal and Mechanical Energy Storage as a Chance for Energy Transformation in Poland. Polityka Energetyczna Energy Policy J. 2021, 24, 43–60. [Google Scholar] [CrossRef]
- Kulpa, J.; Kamiński, P.; Stecuła, K.; Prostański, D.; Matusiak, P.; Kowol, D.; Kopacz, M.; Olczak, P. Technical and Economic Aspects of Electric Energy Storage in a Mine Shaft—Budryk Case Study. Energies 2021, 14, 7337. [Google Scholar] [CrossRef]
- Zdonek, I.; Tokarski, S.; Mularczyk, A.; Turek, M. Evaluation of the Program Subsidizing Prosumer Photovoltaic Sources in Poland. Energies 2022, 15, 846. [Google Scholar] [CrossRef]
- Olczak, P.; Matuszewska, D. Energy Storage Potential Needed at the National Grid Scale (Poland) in Order to Stabilize Daily Electricity Production from Fossil Fuels and Nuclear Power. Energies 2023, 16, 6054. [Google Scholar] [CrossRef]
- Lin, Y.; Johnson, J.X.; Mathieu, J.L. Emissions Impacts of Using Energy Storage for Power System Reserves. Appl. Energy 2016, 168, 444–456. [Google Scholar] [CrossRef]
- Chwieduk, D.; Bujalski, W.; Chwieduk, B. Possibilities of Transition from Centralized Energy Systems to Distributed Energy Sources in Large Polish Cities. Energies 2020, 13, 6007. [Google Scholar] [CrossRef]
- Koval, V.; Sribna, Y.; Gaska, K. Energy Cooperation Ukraine-Poland to Strengthen Energy Security. E3S Web Conf. 2019, 132, 1009. [Google Scholar] [CrossRef]
- Koval, V.; Sribna, Y.; Mykolenko, O.; Vdovenko, N. Environmentalconcept of energy security solutions of local communities based on energy logistics. In Proceedings of the 19th International Multidisciplinary Scientific GeoConference SGEM 2019, Sofia, Bulgaria, 28 June–7 July 2019; Volume 19, pp. 283–290. [Google Scholar]
- Mikhno, I.; Redkva, O.; Udovychenko, V.; Tsimoshynska, O.; Koval, V.; Kopacz, M. Sustainable Energy Supply Management in the Mechanical-Engineering Industry. Polityka Energetyczna Energy Policy J. 2022, 25, 39–54. [Google Scholar] [CrossRef]
- Adamska, B. Magazyny Energii Niezbędnym Elementem Transformacji Energetycznej. Energetyka Rozproszona 2022, 7, 55–61. [Google Scholar] [CrossRef]
- Piwowar, A.; Dzikuć, M.; Dzikuć, M. The Potential of Wind Energy Development in Poland in the Context of Legal and Economic Changes. Acta Polytech. Hung. 2023, 20, 145–156. [Google Scholar] [CrossRef]
- Dzikuć, M.; Dzikuć, M. The Development of Photovoltaics in the Visegrad Group Countries. Hradec Econ. Days 2022. [Google Scholar] [CrossRef]
- Paska, J.; Surma, T.; Terlikowski, P.; Zagrajek, K. Electricity Generation from Renewable Energy Sources in Poland as a Part of Commitment to the Polish and EU Energy Policy. Energies 2020, 13, 4261. [Google Scholar] [CrossRef]
- Kaszyński, P.; Komorowska, A.; Zamasz, K.; Kinelski, G.; Kamiński, J. Capacity Market and (the Lack of) New Investments: Evidence from Poland. Energies 2021, 14, 7843. [Google Scholar] [CrossRef]
- Lepszy, S. Analysis of the Storage Capacity and Charging and Discharging Power in Energy Storage Systems Based on Historical Data on the Day-Ahead Energy Market in Poland. Energy 2020, 213, 118815. [Google Scholar] [CrossRef]
- Rogus, Radomir; Soltysik, Maciej; Czapaj, Rafal Application of Similarity Analysis in PV Sources Generation Forecasting for Energy Clusters. E3S Web Conf. 2019, 84, 1009. [CrossRef]
- Pieczarko, R.; Sołtysik, M. Analysis of the Impact of Wind Sources Generation on the Level of Electricity Prices on the SPOT Market. Przegląd Elektrotechniczny 2017, 93. [Google Scholar] [CrossRef]
- Kaczmarzewski, S.; Olczak, P.; Sołtysik, M. The Impact of Electricity Consumption Profile in Underground Mines to Cooperate with RES. Energies 2021, 14, 5775. [Google Scholar] [CrossRef]
- Kaczmarzewski, S.; Matuszewska, D.; Sołtysik, M. Analysis of Selected Service Industries in Terms of the Use of Photovoltaics before and during the COVID-19 Pandemic. Energies 2022, 15, 188. [Google Scholar] [CrossRef]
- Mirowski, T.; Sornek, K. Potential of Prosumer Power Engineering in Poland by Example of Micro PV Installation in Private Construction. Energy Policy J. 2015, 18, 73–84. [Google Scholar]
- Olczak, P.; Żelazna, A.; Stecuła, K.; Matuszewska, D.; Lelek, Ł. Environmental and Economic Analyses of Different Size Photovoltaic Installation in Poland. Energy Sustain. Dev. 2022, 70, 160–169. [Google Scholar] [CrossRef]
- Dzikuć, M.; Gorączkowska, J.; Piwowar, A.; Dzikuć, M.; Smoleński, R.; Kułyk, P. The Analysis of the Innovative Potential of the Energy Sector and Low-Carbon Development: A Case Study for Poland. Energy Strategy Rev. 2021, 38, 100769. [Google Scholar] [CrossRef]
- Hansen, P. Optimising Shared Renewable Energy Systems: An Institutional Approach. Energy Res. Soc. Sci. 2021, 73, 101953. [Google Scholar] [CrossRef]
- Syed, M.M.; Hansen, P.; Morrison, G.M. Performance of a Shared Solar and Battery Storage System in an Australian Apartment Building. Energy Build. 2020, 225, 110321. [Google Scholar] [CrossRef]
- Olczak, P.; Komorowska, A. An Adjustable Mounting Rack or an Additional PV Panel? Cost and Environmental Analysis of a Photovoltaic Installation on a Household: A Case Study in Poland. Sustain. Energy Technol. Assess. 2021, 47, 101496. [Google Scholar] [CrossRef]
- Olczak, P. Comparison of Modeled and Measured Photovoltaic Microinstallation Energy Productivity. Renew. Energy Focus 2022, 43, 246–254. [Google Scholar] [CrossRef]
- TGE SA Polish. Day-Ahead Market. Available online: https://tge.pl/electricity-dam (accessed on 18 July 2023).
- Benalcazar, P.; Komorowska, A.; Kamiński, J. A GIS-Based Method for Assessing the Economics of Utility-Scale Photovoltaic Systems. Appl. Energy 2024, 353, 122044. [Google Scholar] [CrossRef]
- Boduch, A.; Mik, K.; Castro, R.; Zawadzki, P. Technical and Economic Assessment of a 1 MWp Floating Photovoltaic System in Polish Conditions. Renew. Energy 2022, 196, 983–994. [Google Scholar] [CrossRef]
- Igliński, B.; Piechota, G.; Kiełkowska, U.; Kujawski, W.; Pietrzak, M.B.; Skrzatek, M. The Assessment of Solar Photovoltaic in Poland: The Photovoltaics Potential, Perspectives and Development. Clean Technol. Environ. Policy 2023, 25, 281–298. [Google Scholar] [CrossRef]
- Trela, M.; Dubel, A. Comparing the Support Systems for Renewable Energy Sources in Poland Green Certificates vs Auction Systems. Polityka Energetyczna Energy Policy J. 2017, 20, 105–116. [Google Scholar]
- Zołądek, M.; Filipowicz, M.; Sornek, K.; Figaj, R.D. Energy Performance of the Photovoltaic System in Urban Area—Case Study. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2019; p. 012123. [Google Scholar]
- Filipowicz, M.; Musilek, P.; Gulkowski, S. Specific Yield Analysis of the Rooftop PV Systems Located in South-Eastern Poland. Energies 2022, 15, 3666. [Google Scholar] [CrossRef]
- Kreft, W.; Filipowicz, M.; Żołądek, M. Reduction of Electrical Power Loss in a Photovoltaic Chain in Conditions of Partial Shading. Optik 2020, 202, 163559. [Google Scholar] [CrossRef]
- NREL Commercial Battery Storage. Available online: https://atb.nrel.gov/electricity/2022/commercial_battery_storage#QASDZMI6 (accessed on 3 January 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).