Abstract
Growth in renewable energy systems, direct current (DC) microgrids, and the adoption of electric vehicles (EVs) will substantially increase the demand for bi-directional converters. Precise control mechanisms are essential to ensure optimal performance and better efficiency of these converters. This paper proposes a deep neural network (DNN)-based controller designed to precisely control bi-directional converters for vehicle-to-vehicle (V2V) and vehicle-to-grid (V2G) applications. This control technique allows the converter to quickly attain new reference values, enhancing performance and efficiency by significantly reducing the overshoot duration. To train the DNN controller, large synthetic data are used by performing simulations for various sets of conditions, and the results are validated with a hardware setup. The real-time performance of the DNN controller is compared with a conventional proportional–integral (PI)-based controller through simulated results using MATLAB Simulink (version 2023a) and with a real-time setup. The converter attains a new reference of about 975 s with the proposed control technique. In contrast, the PI controller takes about 220 ms, which shows that the proposed control technique is far better than the PI controller.
1. Introduction
In recent times, there has been a significant shift towards using electric vehicles (EVs) in comparison to traditional fuel-based vehicles. This transition can be attributed to the limitations of conventional vehicles, such as their harmful impact on the environment due to increased pollution and reliance on non-renewable energy sources [1,2]. On the other hand, EVs have garnered immense popularity due to their eco-friendliness and the ability to charge them with renewable energy sources, as they can run on a direct current (DC) supply [3]. According to the International Energy Agency (IEA), the number of electric cars on the road exceeded 15 million in 2022, up from just a few thousand a decade ago. China has become the largest EV market, accounting for about half of the world’s EV sales [4]. In India, the electric vehicle market has experienced substantial growth, thanks to the implementation of favorable government policies and programs. It is exciting to note that between 2024 and 2035, a remarkable compound annual growth rate (CAGR) of 49% is expected for the domestic EV market in India. Despite this growth, EV adoption in India is still limited, with only 13 lakh EVs currently on Indian roads as of August 2022.
1.1. Motivation
One of the biggest challenges to EV growth in India is the lack of sufficient charging stations, which leads to longer charging times and limited options for EV owners. Electric vehicle owners often experience range anxiety while on the road. When driving conventional fuel-based vehicles, the convenience of refilling at readily available fuel stations provides a safety net in case of running out of fuel. In contrast, for electric vehicles, the limited availability of charging stations creates severe concerns about their widespread adoption, as an unexpected stoppage due to a lack of charging infrastructure becomes a real worry. However, a potential solution to this problem is V2V charging [5]. V2V charging enables EV owners to transfer charge between two vehicles, reducing the need for charging stations and the burden on the grid. This technology is particularly useful in emergencies or when a vehicle is parked for an extended period. Transferring excess charge from one vehicle to another can provide a quick and convenient charging solution without requiring a traditional charging station.
Furthermore, V2V charging holds significant promise, offering many advantages, such as extending the operational range of electric vehicles during travel and reducing reliance on an expansive and costly charging infrastructure, often associated with high expenses and space consumption [6]. These applications necessitate the inclusion of bi-directional converters. Various types of bi-directional converters are available for the readily accessible transfer charge between two vehicles, forming the basis for creating a V2V charging system [7]. One prominent example is the non-isolated bi-directional converter (NIBC), known for its minimal energy losses, impressive efficiency, and lesser components, rendering it particularly well suited for low-voltage-level applications in comparison to other non-isolated and isolated converter topologies [8]. Beyond V2V charging, these converters also prove valuable in fuel cell hybrid power systems and V2G applications, enabling vehicles to draw power from the grid during off-peak periods and contribute electricity back into the grid during peak hours. This technology benefits the grid and provides electric vehicle owners with compensation based on the energy transferred, potentially incentivizing greater EV adoption. Various functions of the bi-directional converter are shown in Figure 1. Designing a control mechanism for these converters is challenging, as improper design may lead to an overshoot when acquiring new reference values. The extended overshoot of currents could result in reduced converter performance and efficiency by degrading the life of the components in the converter.
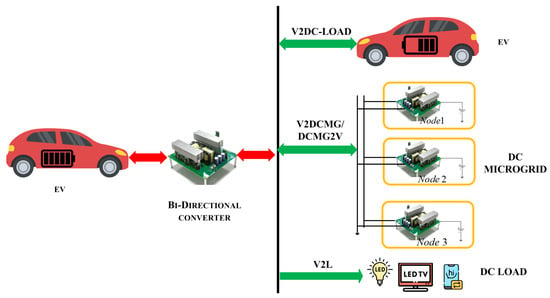
Figure 1.
Comprehensive functions of the bi-directional converter.
1.2. Literature Review
The performance of switched-mode DC-DC power converters depends on various factors, including a more comprehensive and stable operating range, high accuracy in maintaining a constant output voltage, and faster dynamic response. Achieving these parameters requires the development of effective control techniques, which can be challenging. Over the years, researchers have developed various control techniques [9], such as the voltage mode controller [10] and current mode controller [11]. These two are basic controllers, which give slower responses to converters. The most used control techniques are the sliding mode controller [12] and proportional–integral–derivative (PID)-based control technique. Even though sliding mode controllers have a faster transient response than PID controllers, due to the chattering effect [13] and small changes in the system, the parameters may affect the controller performance, which makes these controllers not often used. PID controllers are widely used in industries due to their robustness and simple implementation. However, tuning PID control gains can be difficult, and gains from PID control need to be changed by altering the system parameters. In [14], a PID-based converter is designed. Using this control technique, the converter attains a new reference value in 120 ms. Fuzzy logic control [15] is another type of control technique that has a more comprehensive operating range and is cheaper to implement. In [16], a new fuzzy logic-based controller is developed, and its performance compares with various sliding mode controllers. The controller takes about 7 ms to attain a new reference value. In [17], a new observer-based adaptive fuzzy logic control is used, which gives a response time of about 1 ms to attain a new reference value, which is faster, but implementing this control technique is quite complex, as it involves the design and tuning of fuzzy logic as well as the observer, which makes it difficult for complex systems. In [18], a unified digital control logic is used for controlling NIBC, which is based on a dual voltage system and has a slower transient response. In [19], a model-predictive control of a bi-directional converter for battery-charging applications is discussed, which gives a response time of about 70 ms to obtain new reference values. Model-predictive controllers have computational complexity, uncertainty problems, and involve complex tuning, which may degrade the controller performance. In recent years, researchers have shown interest in the ANN-based control technique [20,21], a data-driven control technique that does not depend on system parameters. This technique decreases inaccuracy and improves the system’s stability, with a faster response to dynamic changes. In [22], a detailed analysis of ANN control techniques is discussed. In [23], the ANN-based control algorithm is compared with PI and fuzzy control algorithms, and the settling time of this control technique is approximately 10 ms, which are better results than the other two control techniques. In [24], a bi-directional converter with a back propagation and adaptive neuro-fuzzy interference control technique is designed, and the settling time of the controller for attaining a new reference value is about 50 ms. In [25], an approximate dynamic programming and artificial neural network-based control technique is used to control the converter. When load change happens, it takes about 4 ms to settle.
While traditional control techniques such as PID control will continue to be used in industries, data-driven control techniques such as ANN are the future of power converter control. In this paper, we propose a control mechanism based on deep neural networks (DNNs), which gives a faster response to converters to obtain new reference values for V2V and V2G charging applications. This approach helps to reduce the overshoot of currents over longer durations and improves converter performance and efficiency.
1.3. Key Contributions
- 1.
- Design of a highly efficient, modular bi-directional converter for V2V charging.
- 2.
- Design of DNN-based closed-loop control for bi-directional V2V and V2G charger.
- 3.
- Comparison of proposed controller with PI controller.
1.4. Organization
This paper presents a novel control technique of a NIBC for V2V charging. It is structured as follows: In Section 2, the operation of the converter in both charging and discharging modes is explained. Section 3 outlines the proposed design for the converter’s controller. Section 4 presents the simulation results of the bidirectional converter with the PI controller, and also the real-time implementation of V2V charging using the proposed DNN control technique.
2. Operation of Non Isolated Bi-Directional Converter (NIBC)
The NIBC is a circuit that consists of several components, including two switches ( and ) with an on-state resistance , an inductor (L) with an internal resistance of , and capacitors on both sides of the source to filter out voltage variations ( and ). The two batteries, HV (high voltage ) and LV (low voltage ), are connected at either side of the converter. The HV battery, with an internal resistance of , and the LV battery, with an internal resistance of , form two voltage sources, and , respectively, as shown in Figure 2. The converter can operate in two modes: charging and discharging. In charging mode, the HV side battery charges the LV side battery. In contrast, in discharging mode, the LV side battery charges the HV side battery. Understanding these modes is crucial to developing a control strategy for the NIBC.
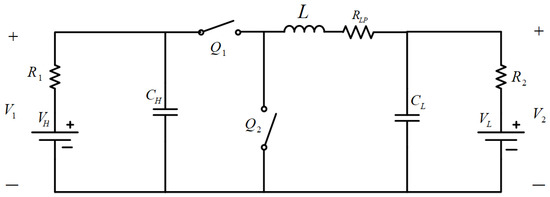
Figure 2.
Circuit diagram of non-isolated bi-directional converter.
The operation of two modes are explained below.
2.1. Mode I
During this mode, the HV side battery charges the LV side battery, operating in buck mode. When the switch is turned on, inductor L accumulates energy during the on period. remains on for the DTs period, and the current flows as --L-- as illustrated in Figure 3a. When is turned off, the energy stored in the inductor is transferred to the LV side by turning on the switch. remains off for the (1-D) Ts period, and the current flows as L---L as illustrated in Figure 3b.
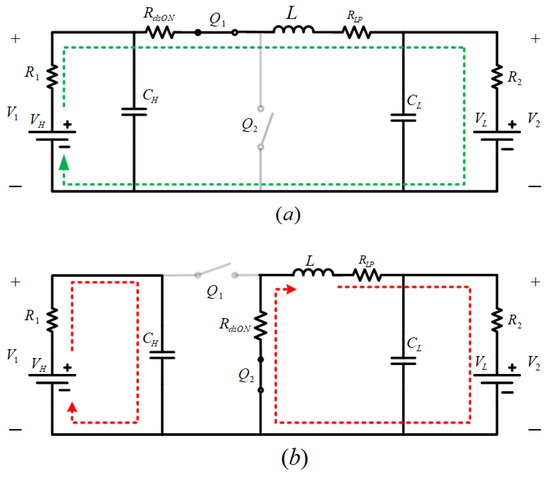
Figure 3.
Operation of converter in charging mode: (a) switch on, and (b) switch off.
2.2. Mode II
During this mode of operation, the LV side battery charges the HV side battery in a boost mode of operation. Inductor L accumulates energy from the LV side battery when is turned on. During this period, the capacitor charges the HV side battery. The switch remains on for the duration of DTs. The current path during this period is -L-- and -- as depicted in Figure 4a. When is turned off, the energy stored in the inductor and the LV side battery combine to charge the HV side battery by turning on the switch. The switch remains off for the duration of (1-D) Ts. The current path during this period is -L--- as shown in Figure 4b.
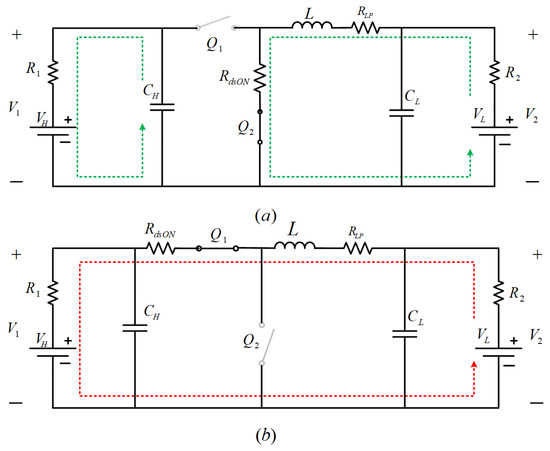
Figure 4.
Operation of converter in discharging mode: (a) switch on, and (b) switch off.
Designing a controller requires the small-signal modeling of the converter. The small-signal model for a DC-DC converter is a linearized representation of the converter around an operating point. It is used to design control systems that regulate the converter’s output and achieve the desired performance.
To create a small-signal model for a DC-DC converter, it typically begins with the nonlinear equations that describe the converter’s behavior, such as the current and voltage equations for the inductor and capacitor. We then linearize these equations around an operating point, usually the converter’s steady-state point.
From the above modes of operation, whether in charging or discharging mode, only two sub-intervals occur when and are on. The nonlinear equations for the two modes are similar. Therefore, the steady-state representation of the charging mode is:
Buck mode (on):
Buck mode (off):
By averaging the two,
The dynamic model consists of steady-state representation and a small-signal model. Now substituting:
Now, the differentiation of steady-state values is zero, and the product of the small-signal models are neglected, i.e.,
and
then the state–space representation becomes:
so, the above state–space is represented as:
The linearized equations resulting from the small-signal model provide a description of the converter’s behavior near the operating point, enabling the design of a controller to regulate the load current. Typically, the controller adjusts the converter’s duty cycle based on the difference between the desired and actual current to achieve the desired response.
The small-signal model is represented by a transfer function that relates the converter’s duty cycle to the desired output. This transfer function can be used to design a controller using control theory techniques, such as pole placement or optimal control.
3. Controller Design
The design of a control technique based on a deep neural network (DNN), as depicted in Figure 5, enables bidirectional flow in the converter. This controller produces a duty cycle based on the HV side battery voltage, LV side battery voltage, output current and current reference. The micro controller then feeds this duty cycle to the converter [26]. The converter generates two complementary pulses based on the received duty cycle using the driver, which drives the switches in the converter, enabling them to work as intended. This DNN-based control design offers several benefits, such as improved accuracy, faster response time, and enhanced stability, making it an excellent option for various applications. By integrating the latest developments in deep learning and control systems design, this control technique opens up opportunities for more efficient and dependable converter operation.
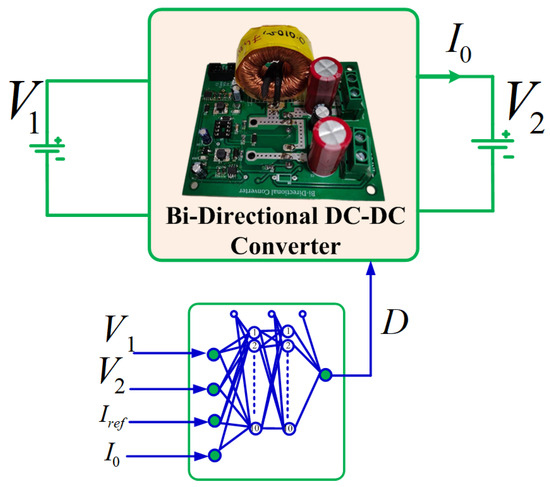
Figure 5.
Implementation of DNN based bi-directional converter.
The DNN network comprises three inputs and one output, with the output being dependent on these three inputs as shown in Equation (10):
The power flow through the converter heavily relies on the duty cycle and direction of the current. Therefore, the DNN-based control technique was used to determine the duty cycle required for efficient converter operation. The duty cycle is based on two instances, which are discussed below.
The first instance involves setting high and low limits for the two battery voltages. The DNN generates the duty cycle based on these limits, and the converter operates either in charging or discharging mode, depending on the battery voltages. The converter is in charging mode when the HV side battery voltage is higher than and the LV side battery voltage is lower than . Conversely, if the HV side battery voltage is lower than , and the LV side battery voltage is higher than , the converter operates in discharging mode. However, this instance is rare, as the converter’s operation mainly depends on the current reference.
In the second instance, the DNN generates the duty cycle based on the current reference, which determines the mode of operation. If the current reference is positive, the converter operates in a buck or charging mode, with the HV side battery charging the LV side battery. On the other hand, if the current reference is negative, the converter operates in boost or discharging mode, with the LV side battery charging the HV side battery. Therefore, the DNN-based control design ensures that the bi-directional converter operates smoothly and efficiently, with minimal loss of power during the transition between different modes of operation.
3.1. Training and Testing of Proposed DNN Controller
To design a controller capable of managing a broader operating range and delivering a quicker dynamic response to the system, it is essential to consider data sets that reflect uncertainties and disturbances present in real-world scenarios. Although data sets created with past historical data can be helpful, they may not accurately reflect the uncertainties in real-time setups. To overcome this limitation, simulation data of the converter, incorporating all uncertainties and disturbances present in the system using MATLAB software, are obtained. Integrating these data into DNN models creates resilient and efficient controllers, assuring exceptional performance in practical, real-world scenarios. The generated data sets include both normal and abnormal data, enabling the development of more comprehensive models that can handle a wide range of scenarios. Following data set preparation, inputs and outputs are allocated to the model. Next, a neural network model is constructed, consisting of an input layer with a defined number of input nodes, hidden layers, and an output layer with a defined number of output nodes. The model’s hyperparameters are configured, and the training process is initiated using these parameters. Afterward, the model’s performance is evaluated, particularly on the root mean square error (RMSE) metric. If the RMSE value is greater, the hyperparameters are changed, and the model is retrained until an RMSE value approximately equal to zero is achieved. Once the desired RMSE value is achieved, the training is concluded. The complete flow of the proposed algorithm is shown in Figure 6.
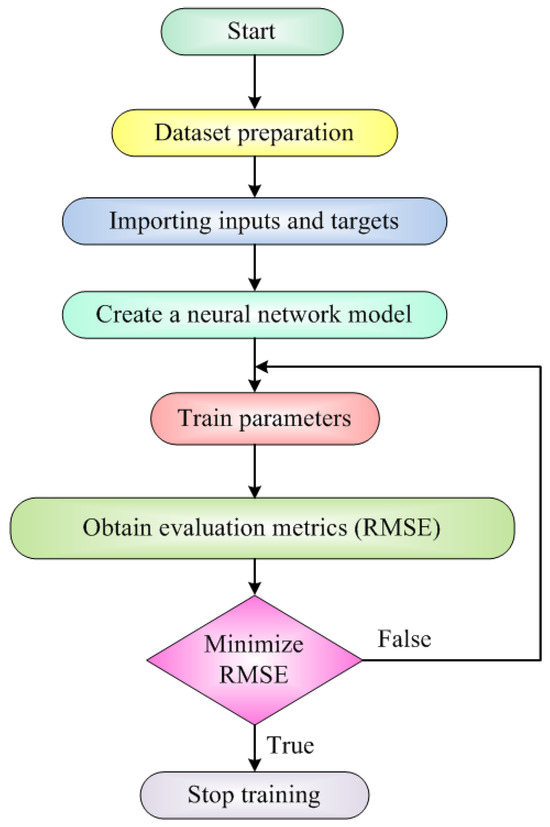
Figure 6.
Flowchart of proposed DNN technique.
3.1.1. Building Model Using MATLAB
We used the MATLAB software as our primary tool to build the model. Within MATLAB, the neural network (NN) tool, an essential component, offers a range of DNN methods for access. Amidst these options, we chose the regression-based DNN method to suit our objectives. With the method in place, the next step is the selection of input and output variables, which form the basis for building the model. Following this, we divided the data into training, testing, and validation sets. We changed various hyperparameter combinations during the training phase to optimize model performance, evaluating model performance with the root mean square error (RMSE). The iterative process of adjusting hyperparameters continues until the RMSE approaches nearly zero, signifying the achievement of an acceptable model. It is essential that selecting the correct hyperparameters is pivotal to training an effective DNN model. Once the desired RMSE is reached, the model is exported into Simulink for practical application. We used Intel(R) Core(TM) i7-10870H CPU processor with a clock speed of 2.21 GHz with 16 GB RAM, which takes about 5 min to train the model.
3.1.2. Hyperparameter Selection
Hyperparameter selection involves choosing the appropriate number of epochs, activation function, weight update rule, and network architecture parameters to train an effective neural network model that minimizes error. The activation function introduces nonlinearities in the system and improves the trained model’s efficiency for non-linear systems. Among the available activation functions, sigmoid (), tanh () and ReLU () are the most used.
The weight update policy minimizes the error between the obtained and reference output. Optimizers, such as stochastic gradient descent (SGD), adaptive moment estimation (ADAM), and root mean square propagation (RMSprop), are generally used for the weight updating policy.
Selecting the right hyperparameters is crucial for developing efficient deep learning models. Root mean square error (RMSE) is a commonly used metric for evaluating model performance, which measures the difference between the predicted and actual values. Choosing the optimal combination of optimization techniques and activation functions is essential for optimal performance. Table 1 provides a list of RMSE values for different combinations of these techniques and functions, with each epoch consisting of a single weight update. The RMSE values are reported for 50, 100, and 150 epochs, providing a comprehensive overview of each combination’s performance. By selecting the combination with the lowest RMSE value, we can determine the optimal hyper parameters for our deep learning model.

Table 1.
Hyperparameter selection.
According to Table 1, the ReLU activation function with SGD optimization function gives a lower RMSE compared to other combinations.
The collected data set contains a diverse range of values, and normalizing the data between −1 and +1 or 0 and 1 is necessary for accurate and reliable analysis. The normalization process is typically performed using standard scalar and min–max functions. In our case, we opted for the min–max function to normalize the data from 0 to 1 to enhance our data analysis and interpretation [27,28,29,30,31,32,33,34,35,36].
The scaled input is given in (11):
where represents the current input value of parameter x
represents the minimum value of x and
represents the maximum value of x
After scaling the data, we divided them into three sections for optimal utilization. The training process used 70% of the data, while 15% was used for validation and another 15% for testing. This approach helped us achieve an optimal balance between training the model, validating its performance, and testing its accuracy, ensuring that the model’s predictions were reliable [37,38,39,40,41,42,43,44,45,46].
3.2. Algorithm
The DNN model comprises four layers, with one input layer consisting of four input nodes denoted as “”, while two hidden layers with ten nodes each represent “” and “”, respectively. The output layer with one output node is indicated as “”. The weight parameters between “” and “”, “” and “”, and “” and “” are represented by , , and , respectively, as shown in Figure 7.
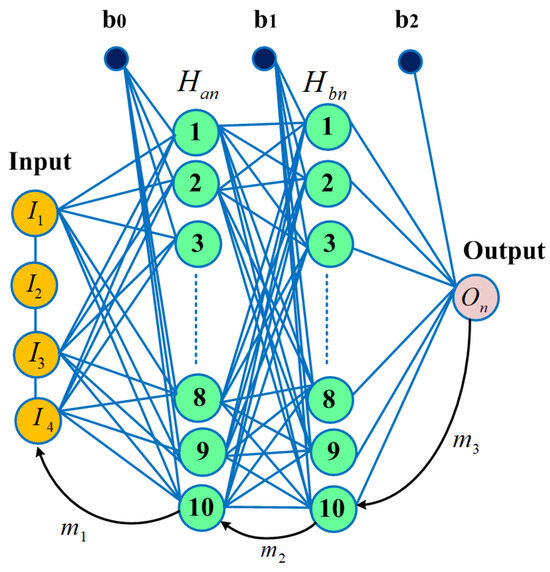
Figure 7.
DNN model: 1, input layer; 2, two hidden layers; and 3, output layer.
To predict the output , the proposed model begins by learning parameters of , , and , which are used as the initial conditions. Equations (12)–(14) show the output prediction.
The model is trained using the ReLU activation function and SGD optimization function, which yields better results compared to other combinations:
The cost function is used to minimize RMSE between the predicted and output value and is shown in (16)
Stochastic gradient descent (SGD) selects a small subset of training data from the entire training state–space randomly. As a result, the time taken for a single weight update iteration in SGD is significantly lower compared to gradient descent (GD) [47,48,49,50,51,52,53,54,55] In general, the weight update for the input and hidden layer is (17)
The weight update for bias is given in (18)
To ensure the accuracy and robustness of a DNN model, the model parameters are typically trained over multiple epochs. After the training is complete, the resulting model is tested and validated to assess its performance on new, unseen data. This iterative training, testing, and validation process allows fine-tuning of the model to achieve better results and improve its predictive power.
The complete diagram of the proposed technique with a comparison of the model predictive technique in [56] is shown in Figure 8.
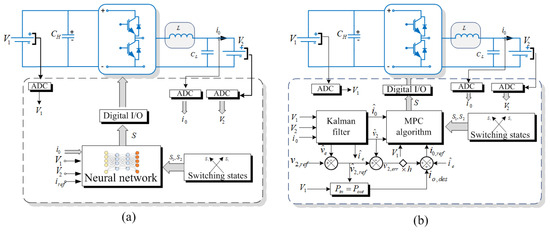
Figure 8.
Complete diagram of controller: (a) proposed control technique, and (b) control technique used in [56].
4. Results
In this section, we evaluate the performance of a bi-directional converter using two different controllers, namely PID and DNN. The performance of the bi-directional converter is evaluated using the PID controller in both simulations using MATLAB simulink and with the real-time hardware setup. Simultaneously, same real-time setup of the bi-directional converter was used to evaluate the performance with the DNN controller. We discuss the performance of these two different controllers in detail below.
4.1. Simulation of Bi-Directional Converter Using PID Controller
A MATLAB simulation was conducted on a bi-directional converter with a PID controller for both charging to discharging and discharging to charging operations. For the charging operation, we used a positive current reference, and for the discharging operation, we used a negative current reference. The simulation results are presented below.
4.1.1. Charging to Discharging Mode
In this case, by altering the current reference from −2 A to 2 A, we successfully transitioned the operation of the bi-directional converter from charging to discharging mode using the PID controller. The load current in the bi-directional converter reached the new reference value in a mere 138 ms as shown in Figure 9.
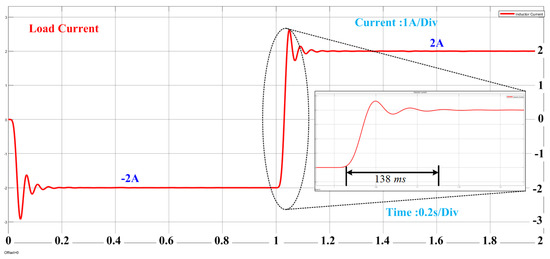
Figure 9.
Loadcurrent for mode transition from charging to discharging using PID controller.
4.1.2. Discharging to Charging Mode
Upon implementing the PID controller for the bi-directional converter, we adjusted the current reference from 2 A to −2 A, which caused the converter to switch from discharging to charging mode. The time taken by the load current to reach the reference current during this transition is illustrated in Figure 10, and it was measured to be 140 ms.
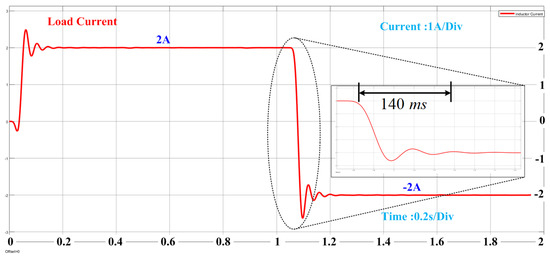
Figure 10.
Load current for mode transition from discharging to charging using PID controller.
4.2. Hardware Implementation of Bi-Directional Converter Using PID Controller
The hardware setup we designed and used in this paper for V2V and V2G charging applications has a capacity of 1.5 kW, and the converter will operate with wide input voltage ranges from 15 V to 80 V and has an output of 50 V and 30 A. Table 2 shows the complete information about the converter.

Table 2.
Parameters of the proposed controller.
The real-time implementation of a bi-directional converter featuring two batteries, which are replicas of those found in two vehicles, is presented. The setup showcases a higher voltage on one end and a lower voltage on the other end of the converter as depicted in Figure 11. The detailed converter parameters are shown in Table 3. The converter operation is controlled using the PID control technique. The results below show the effectiveness of the PID control technique of the load current for mode transitions between the charging to discharging and discharging to charging operations of a bi-directional converter.
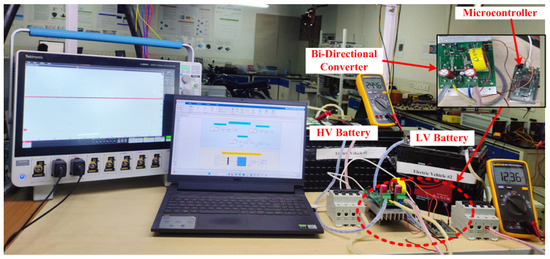
Figure 11.
Real-time setup of a bi-directional converter.

Table 3.
Converter specifications.
4.2.1. Charging to Discharging Mode
In this case, we performed a charging to discharging mode transition in a bi-directional converter by changing the current reference from 2 A to −2 A using a PID controller. Figure 12 shows the waveform of the load current during the transition from the charging to discharging mode. The load current reached the new reference value in approximately 220 ms. Figure 13 shows the response of the load current from the charging to discharging mode transition.
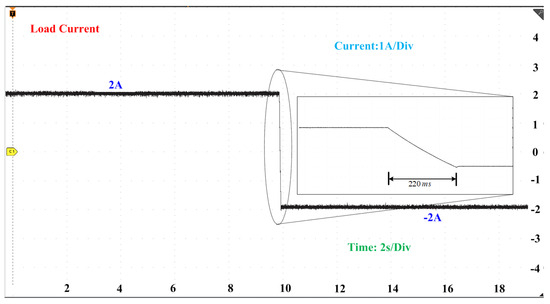
Figure 12.
Load current during mode transition from charging to discharging using PID.
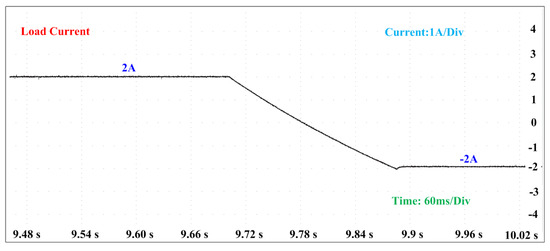
Figure 13.
Zoomed version of Load current during mode transition from charging to discharging using PID.
4.2.2. Discharging to Charging Mode
In this case, we conducted a mode transition from discharging to charging in a bi-directional converter. We achieved this by changing the current reference from −2 A to 2 A. Figure 14 illustrates the waveform of the load current during the transition. The load current reached the new reference value in roughly 200 ms using the PID controller.
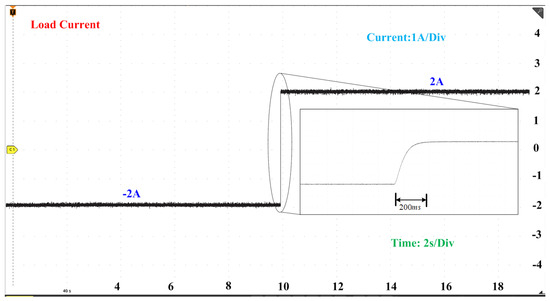
Figure 14.
Load current during mode transition from charging to discharging using PID.
4.3. Hardware Implementation of Bi-Directional Converter Using DNN Controller
Real-time implementation of a bi-directional converter with a DNN controller can facilitate smooth transitions from charging to discharging and vice versa. To demonstrate the effectiveness of this setup, we included the output current for both mode transitions, as well as the voltage across the two batteries.
Standalone implementation of the DNN controller algorithm is deployed in a micro controller. To begin, diverse data sets were meticulously prepared under various conditions using a practical DC-DC converter. These data sets were then saved in comma-separated values (CSV) format, conveniently stored in an Excel file. The obtained data were used to train the DNN model using the neural network model, available in MATLAB 2022a software. Once the training phase was completed, the DNN model was deployed onto an ATMEGA2560 micro controller using the supported package provided by MATLAB [57]. This deployment allowed the controller to function independently, operating in a standalone mode. Remarkably, the microcontroller’s memory usage for this implementation amounted to a mere 21 kb [58,59,60,61,62].
4.3.1. Charging to Discharging Mode
Load Current:
In this case, we performed a charging to discharging mode transition in a bi-directional converter by changing the current reference from 2 A to −2 A. Figure 15 shows the waveform of the load current during the transition from charging to discharging mode. Impressively, the load current reached the new reference value in approximately 975 s, significantly faster than what the PID controller achieved. This outcome highlights the superior performance of the DNN controller over the PID controller in achieving a new reference value for the output current.
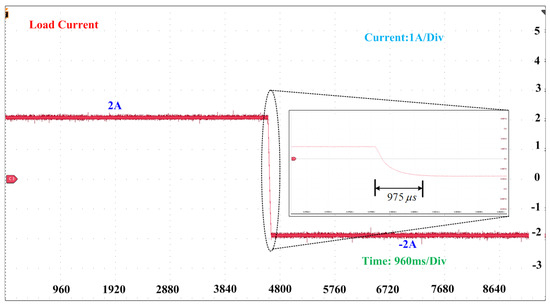
Figure 15.
Load current during mode transition from charging to discharging using DNN.
HV Battery ():
In this case, we discuss the voltage behavior of an HV side battery during the mode transition from charging to discharging operations. When the converter is in charging mode, the HV side battery will discharge and charge the LV side battery. The voltage across the HV side battery in this mode is around 24.48 V. However, when the converter switches from charging to discharging operation, the HV side battery is charged by the LV side battery, causing a slight increase in the HV side battery voltage to around 24.75 V. To accurately depict these slight changes in voltage, we used a voltage scale of 0.34 V/Div, as shown in Figure 16.
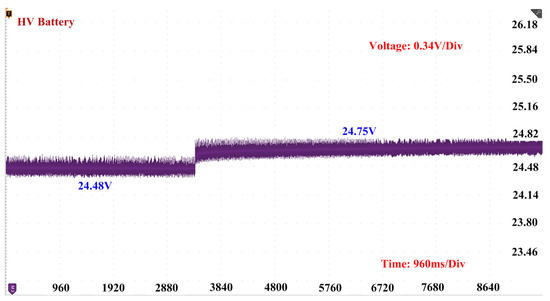
Figure 16.
Voltage of HV battery during mode transition from charging to discharging using DNN.
LV Battery ():
In this case, we will discuss the voltage behavior of an LV side battery during the mode transition from charging to discharging operations. When the converter operates in charging mode, the HV side battery charges the LV side battery. The voltage across the LV side battery in this mode is approximately 12.7 V. However, when the converter switches from the charging to discharging operation, the LV side battery discharges and charges the HV side battery, leading to a decrease in the LV side battery voltage to about 12.39 V. To precisely depict these slight changes in voltage, we used a voltage scale of 0.125 V/Div as demonstrated in Figure 17.
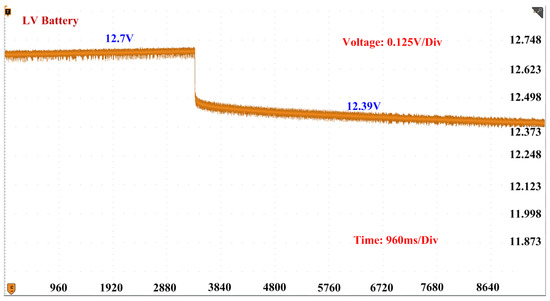
Figure 17.
Voltage of LV battery during mode transition from charging to discharging using DNN.
4.3.2. Discharging to Charging Mode
Load Current:
In this case, we conducted a mode transition from discharging to charging in a bi-directional converter. We achieved this by changing the current reference from −2 A to 2 A. Figure 18 illustrates the waveform of the load current during the transition. Impressively, the load current reached the new reference value in roughly 960 s, which is considerably quicker than what the PID controller accomplished. This outcome highlights the DNN controller’s superior performance over the PID controller in achieving a new reference value for the load current.
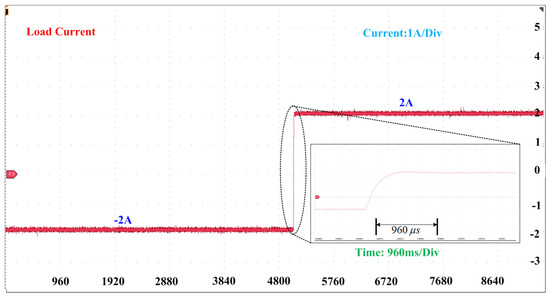
Figure 18.
Load current during mode transition from discharging to charging using DNN.
HV Battery ():
In this case, we will discuss the voltage behavior of an HV side battery during the mode transition from discharging to charging operations. When the converter is in discharging mode, the HV side battery charges by the LV side battery. The voltage across the HV side battery in this mode is around 24.9 V. However, when the converter switches from the discharging to charging operation, the HV side battery discharges and charges the LV side battery, causing a slight decrease in the voltage to around 24.2 V. To accurately depict these slight changes in voltage, we used a voltage scale of 1 V/Div as shown in Figure 19.
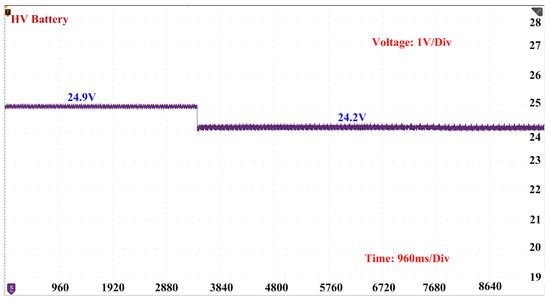
Figure 19.
Voltage of HV battery during mode transition from discharging to charging using DNN controller.
LV Battery ():
In this case, we will be discussing the voltage behavior of the LV side battery during the transition from discharging to charging operations in a bi-directional converter. While the converter is in discharging mode, the LV side battery discharges and charges the HV side battery. During this, the voltage across the LV side battery is around 12.36 V. However, when the converter switches from the discharging to charging operation, the LV side battery will be charged by the HV side battery, resulting in a slight increase in the voltage of the LV side battery to around 12.6 V. To accurately display these slight voltage changes, we used a voltage scale of 0.125 V/Div as shown in Figure 20.
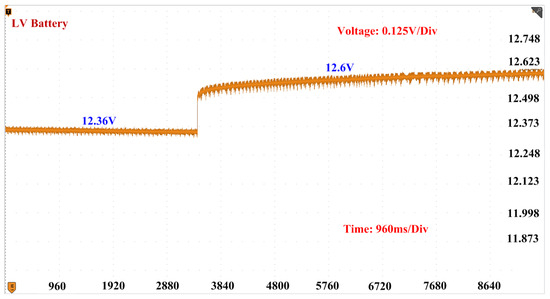
Figure 20.
Voltage of LV battery during mode transition from discharging to charging using DNN controller.
Limitations and future scope of proposed technique:
The application of deep learning has experienced a transformative evolution, emerging as a powerful tool for enhancing the efficiency and stability of power electronic converters. However, this technology raises some ethical concerns. Deep neural networks depend on extended data sets, and biased data can give rise to inequitable predictions, casting a shadow on the integrity of the results. Over reliance on deep neural networks without alternative safety nets can precipitate substantial reliability risks. Thus, while deep learning promises excellent strides in power electronics, collaborating with experts in power electronics and ethics may become essential for proper usage.
There will be sufficient growth in intelligent controls in power electronic converters in the future, and reinforcement learning may replace the DNN controllers. It is an online training model that trains the model automatically. Research is gradually transitioning from DNN controllers to physics-informed neural networks (PINNs), combining physical and deep learning models to enhance control reliability and performance. The comparison of proposed controller with different controllers are given in Table 4.

Table 4.
Comparison of proposed controller with different controllers.
5. Conclusions
This paper presents the significance of V2V and V2G charging and proposes a novel approach that employs a DNN-based non-isolated bi-directional converter. We conducted a hardware experiment of our proposed controller and compared the transition time of the load current with a traditional PID controller using MATLAB Simulink software. The results demonstrate that the DNN controller attains the reference value in 975 s, whereas PID controller attains a new reference value in 220 ms, which shows that the DNN controller has a faster response time than the PID controllers. Additionally, we analyzed the behavior of HV and LV side battery voltages during the transition from charging to discharging and vice versa. The results show that the DNN-based controller outperforms conventional PID controllers in terms of performance. These findings demonstrate the potential benefits of using DNN-based controllers for bi-directional converters.
Author Contributions
Conceptualization, M.K.B. and S.M.; methodology, M.K.B.; software, M.K.B.; validation, M.K.B., S.M. and S.K.N.B.; formal analysis, M.K.B.; investigation, M.K.B.; resources, S.M.; data curation, M.K.B.; writing—original draft preparation, M.K.B.; writing—review and editing, S.M.; visualization, M.K.B.; supervision, S.M.; project administration, S.M.; funding acquisition, S.M. All authors have read and agreed to the published version of the manuscript.
Funding
Department of Science and Technology: DST/TMD/CERI/RES/2020/27.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mai, T.; Hand, M.M.; Baldwin, S.F.; Wiser, R.H.; Brinkman, G.L.; Denholm, P.; Arent, D.J.; Porro, G.; Sandor, D.; Hostick, D.J.; et al. Renewable electricity futures for the United States. IEEE Trans. Sustain. Energy 2013, 5, 372–378. [Google Scholar] [CrossRef]
- Zhang, Y.; Gatsis, N.; Giannakis, G.B. Robust Energy Management for Microgrids with High-Penetration Renewables. IEEE Trans. Sustain. Energy 2013, 4, 944–953. [Google Scholar] [CrossRef]
- Haegel, N.M.; Kurtz, S.R. Global Progress Toward Renewable Electricity: Tracking the Role of Solar. IEEE J. Photovolt. 2021, 11, 1335–1342. [Google Scholar] [CrossRef]
- Li, W.; Yang, M.; Sandu, S. Electric vehicles in China: A review of current policies. Energy Environ. 2018, 29, 1512–1524. [Google Scholar] [CrossRef]
- Vempalli, S.K.; Deepa, K.; Prabhakar, G. A Novel V2V Charging Method Addressing the Last Mile Connectivity. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 18–21 December 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, K.; Huang, Y.; Qin, Y.; Hu, C.; Tang, X. Potential and challenges to improve vehicle energy efficiency via V2X: Literature review. Int. J. Veh. Perform. 2021, 7, 244–265. [Google Scholar] [CrossRef]
- Chaitanya, M.; Vinayak, A.; Pavan, B.G.; Lakshmi, N.; Sandeep, K. A Review of Bidirectional DC-DC, DC-AC Converters for V2G and G2V Applications. In Proceedings of the 2023 International Conference on Power, Instrumentation, Energy and Control (PIECON), Aligarh, India, 10–12 February 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Tytelmaier, K.; Husev, O.; Veligorskyi, O.; Yershov, R. A review of non-isolated bidirectional dc-dc converters for energy storage systems. In Proceedings of the 2016 II International Young Scientists Forum on Applied Physics and Engineering (YSF), Kharkiv, Ukraine, 10–14 October 2016; pp. 22–28. [Google Scholar]
- Viswanatha, V.; Ramachandra, A.C.; Reddy, V.S. Bidirectional DC-DC Converter Circuits and Smart Control Algorithms: A Review. J. Electr. Syst. Inf. Technol. 2022, 9, 6. [Google Scholar] [CrossRef]
- Mummadi, V.; Mohan, B.K. Robust digital voltage-mode controller for fifth-order boost converter. IEEE Trans. Ind. Electron. 2010, 58, 263–277. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Das, S. A Digital Current-Mode Control Technique for DC–DC Converters. IEEE Trans. Power Electron. 2006, 21, 1718–1726. [Google Scholar] [CrossRef]
- Sliding mode control of DC/DC converters. J. Frankl. Inst. 2013, 350, 2146–2165. [CrossRef]
- Utkin, V. Chattering Problem in Sliding Mode Control Systems. In Proceedings of the International Workshop on Variable Structure Systems 2006, VSS’06, Alghero, Sardinia, 26 June 2006; Volume 39, p. 1. [Google Scholar] [CrossRef]
- Ramya, K.; Jegathesan, V. Comparison of pi and pid controlled bidirectional dc-dc converter systems. Int. J. Power Electron. Drive Syst. 2016, 7, 56. [Google Scholar] [CrossRef]
- Mattavelli, P.; Rossetto, L.; Spiazzi, G.; Tenti, P. General-purpose fuzzy controller for DC-DC converters. IEEE Trans. Power Electron. 1997, 12, 79–86. [Google Scholar] [CrossRef]
- Babes, B.; Mekhilef, S.; Boutaghane, A.; Rahmani, L. Fuzzy approximation-based fractional-order nonsingular terminal sliding mode controller for DC–DC buck converters. IEEE Trans. Power Electron. 2021, 37, 2749–2760. [Google Scholar] [CrossRef]
- Yang, C.; Hua, T.; Dai, Y.; Liu, G.; Huang, X.; Zhang, D. Disturbance-Observer-Based Adaptive Fuzzy Control for Islanded Distributed Energy Resource Systems. Math. Probl. Eng. 2022, 2022, 1527705. [Google Scholar] [CrossRef]
- Modelling and control of a non-isolated half-bridge bidirectional DC-DC converter with an energy management topology applicable with EV/HEV. J. King Saud Univ.-Eng. Sci. 2023, 35, 116–122. [CrossRef]
- Pirooz, A.; Noroozian, R. Model predictive control of classic bidirectional DC-DC converter for battery applications. In Proceedings of the 2016 7th Power Electronics and Drive Systems Technologies Conference (PEDSTC), Tehran, Iran, 16–18 February 2016; pp. 517–522. [Google Scholar]
- Machina, V.S.P.; Koduru, S.S.; Madichetty, S.; Mishra, S. Design of ANN Based Controller for Cyberattack Detection in DC-DC Buck Converter. In Proceedings of the 2022 22nd National Power Systems Conference (NPSC), New Delhi, India, 17–19 December 2022; pp. 460–464. [Google Scholar] [CrossRef]
- Zhao, S.; Blaabjerg, F.; Wang, H. An overview of artificial intelligence applications for power electronics. IEEE Trans. Power Electron. 2020, 36, 4633–4658. [Google Scholar] [CrossRef]
- Meireles, M.; Almeida, P.; Simoes, M. A comprehensive review for industrial applicability of artificial neural networks. IEEE Trans. Ind. Electron. 2003, 50, 585–601. [Google Scholar] [CrossRef]
- Srikanth, R.; Venkatesan, M.; Subba Rao, M. Design and performance evaluation of PID, Fuzzy logic and ANN controllers based MPPTs for hybrid electric vehicle applications. Int. J. Ambient Energy 2022, 43, 3661–3675. [Google Scholar] [CrossRef]
- Sankarananth, S.; Sivaraman, P. Performance enhancement of multi-port bidirectional DC-DC converter using resilient backpropagation neural network method. Sustain. Comput. Inform. Syst. 2022, 36, 100783. [Google Scholar] [CrossRef]
- Dong, W.; Li, S.; Fu, X.; Li, Z.; Fairbank, M.; Gao, Y. Control of a buck DC/DC converter using approximate dynamic programming and artificial neural networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 1760–1768. [Google Scholar] [CrossRef]
- Banda, M.K.; Koduru, S.S.; Machina, V.S.P.; Madichetty, S. A Deep Learning Based Cyber Attack Detection and Mitigation Scheme in Synchronous Buck Converter. In Proceedings of the 2022 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 14–17 December 2022; pp. 1–6. [Google Scholar]
- Tian, H.; Liu, J.; Wang, Z.; Xie, F.; Cao, Z. Characteristic analysis and circuit implementation of a novel fractional-order memristor-based clamping voltage drift. Fractal Fract. 2022, 7, 2. [Google Scholar] [CrossRef]
- Fan, X.; Wei, G.; Lin, X.; Wang, X.; Si, Z.; Zhang, X.; Shao, Q.; Mangin, S.; Fullerton, E.; Jiang, L.; et al. Reversible switching of interlayer exchange coupling through atomically thin VO2 via electronic state modulation. Matter 2020, 2, 1582–1593. [Google Scholar] [CrossRef]
- Wu, Z.; Lin, B.; Fan, J.; Zhao, J.; Zhang, Q.; Li, L. Effect of dielectric relaxation of epoxy resin on dielectric loss of medium-frequency transformer. IEEE Trans. Dielectr. Electr. Insul. 2022, 29, 1651–1658. [Google Scholar] [CrossRef]
- Ge, L.; Du, T.; Li, C.; Li, Y.; Yan, J.; Rafiq, M.U. Virtual collection for distributed photovoltaic data: Challenges, methodologies, and applications. Energies 2022, 15, 8783. [Google Scholar] [CrossRef]
- He, Y.; Wang, F.; Du, G.; Pan, L.; Wang, K.; Gerhard, R.; Plath, R.; Rozga, P.; Trnka, P. Revisiting the thermal ageing on the metallised polypropylene film capacitor: From device to dielectric film. High Voltage 2023, 8, 305–314. [Google Scholar] [CrossRef]
- Lin, X.; Wen, Y.; Yu, R.; Yu, J.; Wen, H. Improved weak grids synchronization unit for passivity enhancement of grid-connected inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 7084–7097. [Google Scholar] [CrossRef]
- Lin, X.; Yu, R.; Yu, J.; Wen, H. Constant coupling effect-based PLL for synchronization stability enhancement of grid-connected converter under weak grids. IEEE Trans. Ind. Electron. 2022, 70, 11310–11323. [Google Scholar] [CrossRef]
- Chen, C.; Wu, X.; Yuan, X.; Zheng, X. A New Technique for the Subdomain Method in Predicting Electromagnetic Performance of Surface-Mounted Permanent Magnet Motors with Shaped Magnets and a Quasi-Regular Polygon Rotor Core. IEEE Trans. Energy Convers. 2022, 38, 1396–1409. [Google Scholar] [CrossRef]
- Chung, K.L.; Tian, H.; Wang, S.; Feng, B.; Lai, G. Miniaturization of microwave planar circuits using composite microstrip/coplanar-waveguide transmission lines. Alex. Eng. J. 2022, 61, 8933–8942. [Google Scholar] [CrossRef]
- Muhammad, I.; Ali, A.; Zhou, L.; Zhang, W.; Wong, P.K.J. Vacancy-engineered half-metallicity and magnetic anisotropy in CrSI semiconductor monolayer. J. Alloys Compd. 2022, 909, 164797. [Google Scholar] [CrossRef]
- Gao, Y.; Doppelbauer, M.; Ou, J.; Qu, R. Design of a double-side flux modulation permanent magnet machine for servo application. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 1671–1682. [Google Scholar] [CrossRef]
- Zhu, L.; Li, Z.; Hou, K. Effect of radical scavenger on electrical tree in cross-linked polyethylene with large harmonic superimposed DC voltage. High Volt. 2022, 8, 739–748. [Google Scholar] [CrossRef]
- Cao, B.; Dong, W.; Lv, Z.; Gu, Y.; Singh, S.; Kumar, D.P. Hybrid Microgrid Many-Objective Sizing Optimization With Fuzzy Decision. IEEE Trans. Fuzzy Syst. 2020, 28, 2702–2710. [Google Scholar] [CrossRef]
- Li, J.; Deng, Y.; Sun, W.; Li, W.; Li, R.; Li, Q.; Liu, Z. Resource orchestration of cloud-edge–based smart grid fault detection. ACM Trans. Sens. Netw. TOSN 2022, 18, 1–26. [Google Scholar] [CrossRef]
- Wang, H.; Wu, X.; Zheng, X.; Yuan, X. Model predictive current control of nine-phase open-end winding pmsms with an online virtual vector synthesis strategy. IEEE Trans. Ind. Electron. 2022, 70, 2199–2208. [Google Scholar] [CrossRef]
- Liu, S.; Song, Z.; Dong, Z.; Liu, Y.; Liu, C. Generic carrier-based PWM solution for series-end winding PMSM traction system with adaptative overmodulation scheme. IEEE Trans. Transp. Electrif. 2022, 9, 712–726. [Google Scholar] [CrossRef]
- Tang, H.; Di, J.; Wu, Z.; Li, W. Temperature analysis for the asymmetric six-phase permanent magnet synchronous motor in healthy and fault-tolerant modes. IEEE Trans. Ind. Electron. 2022, 70, 6482–6493. [Google Scholar] [CrossRef]
- Liu, S.; Song, Z.; Liu, Y.; Chen, Y.; Liu, C. Flux-weakening controller design of dual three-phase PMSM drive system with copper loss minimization. IEEE Trans. Power Electron. 2022, 38, 2351–2363. [Google Scholar] [CrossRef]
- Liu, S.; Liu, C. Virtual-vector-based robust predictive current control for dual three-phase PMSM. IEEE Trans. Ind. Electron. 2020, 68, 2048–2058. [Google Scholar] [CrossRef]
- Liu, S.; Liu, C. Direct harmonic current control scheme for dual three-phase PMSM drive system. IEEE Trans. Power Electron. 2021, 36, 11647–11657. [Google Scholar] [CrossRef]
- Liu, S.; Liu, C.; Zhao, H.; Liu, Y.; Dong, Z. Improved flux weakening control strategy for five-phase PMSM considering harmonic voltage vectors. IEEE Trans. Power Electron. 2022, 37, 10967–10980. [Google Scholar] [CrossRef]
- Duan, Y.; Zhao, Y.; Hu, J. An initialization-free distributed algorithm for dynamic economic dispatch problems in microgrid: Modeling, optimization and analysis. Sustain. Energy Grids Netw. 2023, 34, 101004. [Google Scholar] [CrossRef]
- Taghieh, A.; Mohammadzadeh, A.; Zhang, C.; Kausar, N.; Castillo, O. A type-3 fuzzy control for current sharing and voltage balancing in microgrids. Appl. Soft Comput. 2022, 129, 109636. [Google Scholar] [CrossRef]
- Huang, N.; Chen, Q.; Cai, G.; Xu, D.; Zhang, L.; Zhao, W. Fault diagnosis of bearing in wind turbine gearbox under actual operating conditions driven by limited data with noise labels. IEEE Trans. Instrum. Meas. 2020, 70, 1–10. [Google Scholar] [CrossRef]
- Lin, L.; Zhang, J.; Gao, X.; Shi, J.; Chen, C.; Huang, N. Power fingerprint identification based on the improved VI trajectory with color encoding and transferred CBAM-ResNet. PLoS ONE 2023, 18, e0281482. [Google Scholar]
- Xu, S.; Huang, W.; Huang, D.; Chen, H.; Chai, Y.; Ma, M.; Zheng, W.X. A Reduced-Order Observer-Based Method for Simultaneous Diagnosis of Open-Switch and Current Sensor Faults of a Grid-Tied NPC Inverter. IEEE Trans. Power Electron. 2023. [Google Scholar] [CrossRef]
- Zhang, Z.; Altalbawy, F.M.; Al-Bahrani, M.; Riadi, Y. Regret-based multi-objective optimization of carbon capture facility in CHP-based microgrid with carbon dioxide cycling. J. Clean. Prod. 2023, 384, 135632. [Google Scholar] [CrossRef]
- Xiao, S.; Wang, Z.; Wu, G.; Guo, Y.; Gao, G.; Zhang, X.; Cao, Y.; Zhang, Y.; Yu, J.; Liu, P.; et al. The impact analysis of operational overvoltage on traction transformers for high-speed trains based on the improved capacitor network methodology. IEEE Trans. Transp. Electrif. 2023. [Google Scholar] [CrossRef]
- Hu, W.; Wang, T.; Chu, F. A novel Ramanujan digital twin for motor periodic fault monitoring and detection. IEEE Trans. Ind. Inform. 2023, 19, 11564–11572. [Google Scholar] [CrossRef]
- Kim, S.K.; Park, C.R.; Kim, J.S.; Lee, Y.I. A stabilizing model predictive controller for voltage regulation of a DC/DC boost converter. IEEE Trans. Control. Syst. Technol. 2014, 22, 2016–2023. [Google Scholar] [CrossRef]
- Matlab. Manual of Neural Network Toolbox [Online]. 2005. Available online: http://matlab.izmiran.ru/help/toolbox/nnet/ (accessed on 1 October 2022).
- Xiang, J.; Deng, L.; Zhou, C.; Zhao, H.; Huang, J.; Tao, S. Heat transfer performance and structural optimization of a novel micro-channel heat sink. Chin. J. Mech. Eng. 2022, 35, 1–12. [Google Scholar] [CrossRef]
- Xiang, J.; Yang, W.; Liao, H.; Li, P.; Chen, Z.; Huang, J. Design and thermal performance of thermal diode based on the asymmetric flow resistance in vapor channel. Int. J. Therm. Sci. 2023, 191, 108345. [Google Scholar] [CrossRef]
- Dang, W.; Liao, S.; Yang, B.; Yin, Z.; Liu, M.; Yin, L.; Zheng, W. An encoder-decoder fusion battery life prediction method based on Gaussian process regression and improvement. J. Energy Storage 2023, 59, 106469. [Google Scholar] [CrossRef]
- Wang, J.; Tian, J.; Zhang, X.; Yang, B.; Liu, S.; Yin, L.; Zheng, W. Control of time delay force feedback teleoperation system with finite time convergence. Front. Neurorobotics 2022, 16, 877069. [Google Scholar] [CrossRef]
- Gu, Q.; Tian, J.; Yang, B.; Liu, M.; Gu, B.; Yin, Z.; Yin, L.; Zheng, W. A novel architecture of a six degrees of freedom parallel platform. Electronics 2023, 12, 1774. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).