Power Supply Reliability Analysis of Distribution Systems Considering Data Transmission Quality of Distribution Automation Terminals
Abstract
:1. Introduction
2. Reliability Assessment Preliminary Model and Fundamental Principles
2.1. M-Segment and N-Connection Structure of Distribution System
2.2. Principle of Failure Mode Effect Analysis (FMEA)
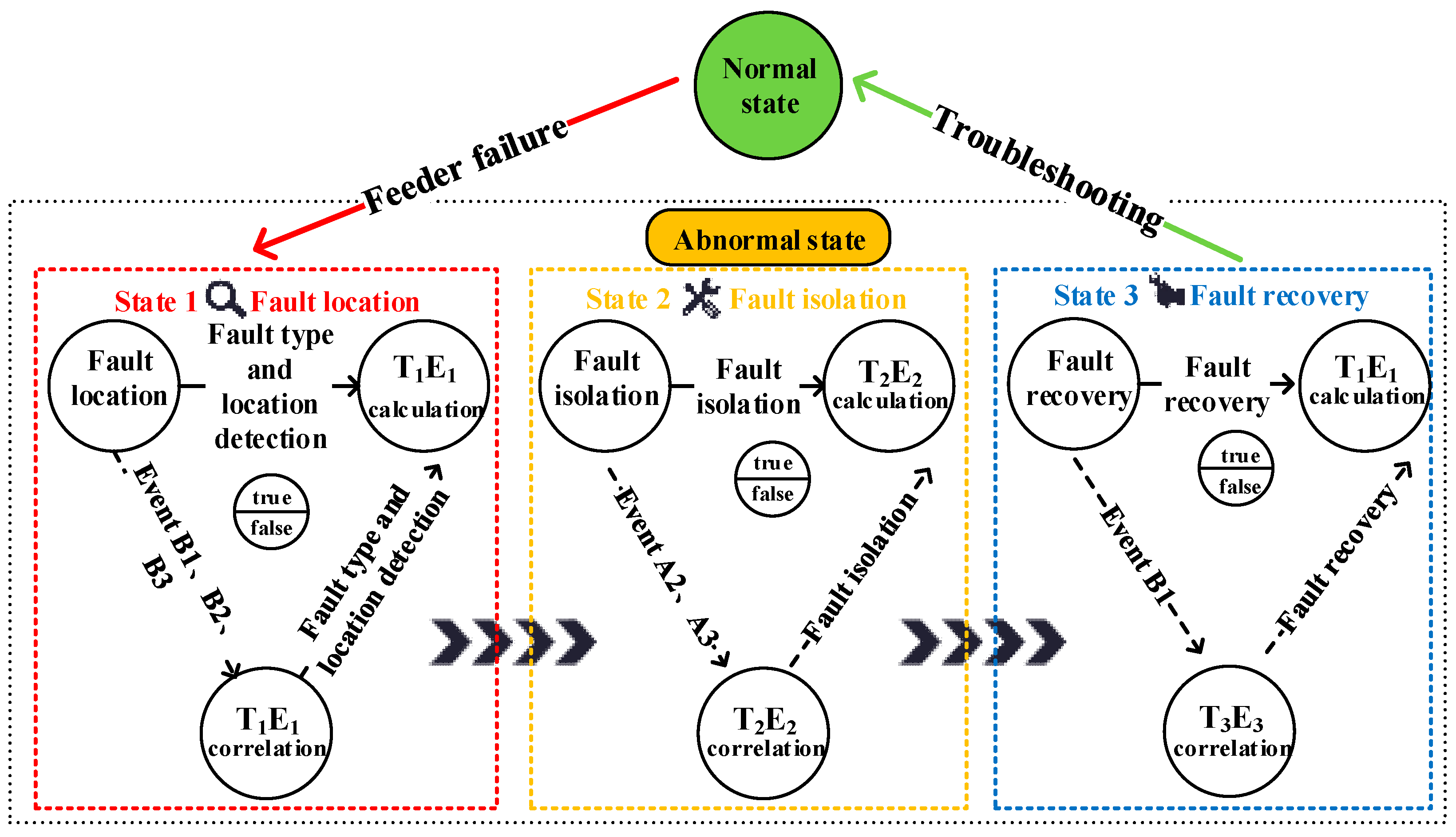
3. Failure Mode Effect Analysis (FMEA) Model Considering DAS
3.1. Distribution System Equipped with “3R” RTUs
3.1.1. Failure Location Time
3.1.2. Failure Isolation Time
3.1.3. Failure Recovery Time
3.2. Distribution System Equipped with “2R” RTUs
3.3. Distribution System Equipped with Both “3R” and “2R” RTUs
3.4. General Formula for the ENS and SID
4. Quantitative Assessment Model Considering Unreliable Information Transmission
4.1. The Revised Model Equipped with “3R” RTUs
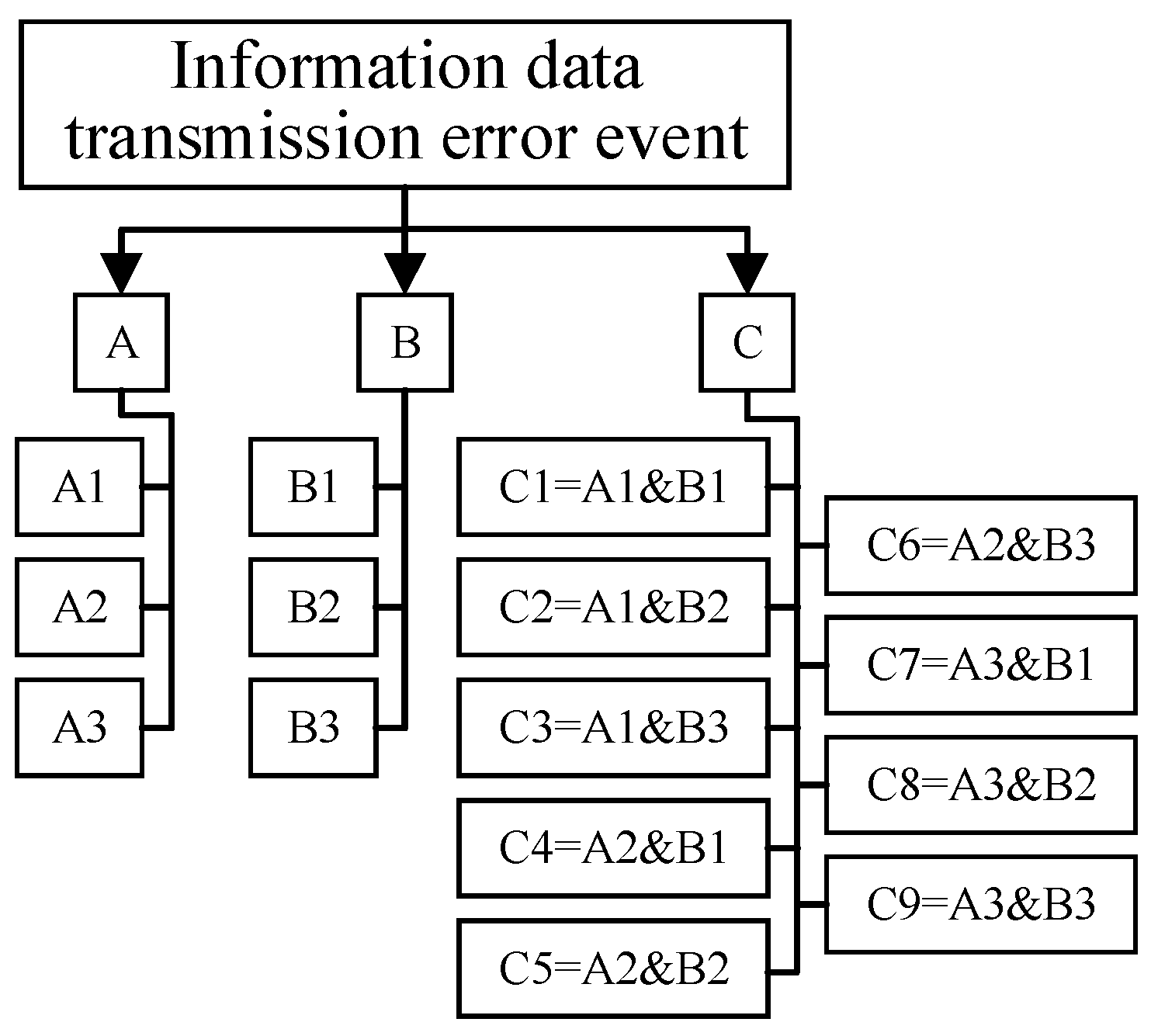
4.1.1. The Remote Communication and Remote Control Information Are Wrong, While the Remote Measurement Information Is Correct
- Event A1: The remote control information is correct, but the remote communication information is wrong. The probability of occurrence is set as p11. In this condition, after the failure occurs, because the remote control can act correctly, the failure can be successfully isolated. However, the information that is reflected by the remote communication is still the information before the failure isolation, that is, the remote information reflects that the failure is not effectively isolated. Since the substation detects that the feeder is not faulty through the failure indicator, the remote communication function needs to be checked and the information needs to be corrected. Then, the failure recovery time should be corrected as follows (17):where t3 represents the time for failure recovery when the remote communication information is accurate, and represents the time for checking the remote communication functionality and correcting information. In this scenario, failure detection and the failure isolation time are considered unaffected.
- Event A2: The remote control information is wrong, but the remote communication is correct. The probability of occurrence is set as p12. After the failure occurs, because the remote control information is incorrect, the failure is not effectively isolated. Therefore, the failure correctly reflected by the remote information is not isolated and the remote control function needs to be checked and the information needs to be corrected, and then the failure will be controlled. It is assumed that the RTU operates in a centralized monitoring mode, with maintenance personnel remotely monitoring the RTU from a control station and the RTU locking the manual isolation of the failure carried out by the local maintenance personnel. Since the failure is not effectively isolated, the ENS is expressed as follows:where t2″ = t212 is the time required to check and correct the remote control signal and to re-isolate the failure. In this scenario, the failure detection time and failure recovery time are considered not affected. In practical scenarios, it is also conceivable to manually switch the RTU from remote control mode to local control mode, and the time required for this switch is included in the parameter t2″.
- Event A3: The remote control and the remote communication information are both incorrect. The probability of occurrence is set as p13. In this scenario, after the failure occurs, the failure is not effectively isolated due to the wrong remote control information, while the failure is reflected as being effectively isolated due to the incorrect remote communication. However, because the sub-station can detect that the feeder is faulty through the failure indicator, the remote control function and the remote communication function need to be checked, the remote control and remote communication signals need to be corrected, and finally, the failure re-isolation is carried out. As the failure is not effectively isolated, the system ENS of the failure isolation stage can be calculated as in (18). At this time, t2″ in (18) needs to be replaced by t213, and t213 indicates the time required to check the function and to correct the information of remote control and remote communication. In this scenario, the failure detection time and failure recovery time are unaffected.
4.1.2. The Remote Communication and Control Information Are Correct but the Remote Measurement Information Is Wrong
- Event B1: The remote measurement information error affects the determination of the failure location. The probability of occurrence is set as p21. In this condition, after the failure occurs, the distribution RTU collects the information to determine the location of the failure according to the wrong information, affecting the effective isolation and recovery of the failure. At this point, it is necessary to check the remote measurement function and correct the information firstly, and then to find the correct failure location manually. Thus, the time of the failure location phase is corrected as follows (19):
- b.
- Event B2: The remote measurement information error affects the determination of the failure type. The probability of occurrence is set as p22. In this condition, after the failure occurs, the distribution RTU collects the information to determine the type of failure, but the wrong transmission information affects the effective failure isolation and recovery. At this point, it is needed to correct the remote measurement information and re-judge the type of failure in order to correctly isolate the failure.
- c.
- Event B3: The remote measurement information error affects both the detection of the failure location and the determination of the failure type. Setting the probability of occurrence as p23, the time of the failure location phase is as follows:
4.1.3. Remote Control, Remote Communication and Remote Measurement Information Are Wrong
- Time calibration of the failure location phase:
- b.
- Time calibration of the failure isolation phase:
- c.
- Time calibration of the failure recovery phase:
4.2. The Revised Model Equipped without “3R” RTUs
5. Case Analysis
5.1. Introduction of the Case
5.2. Verification of Accuracy
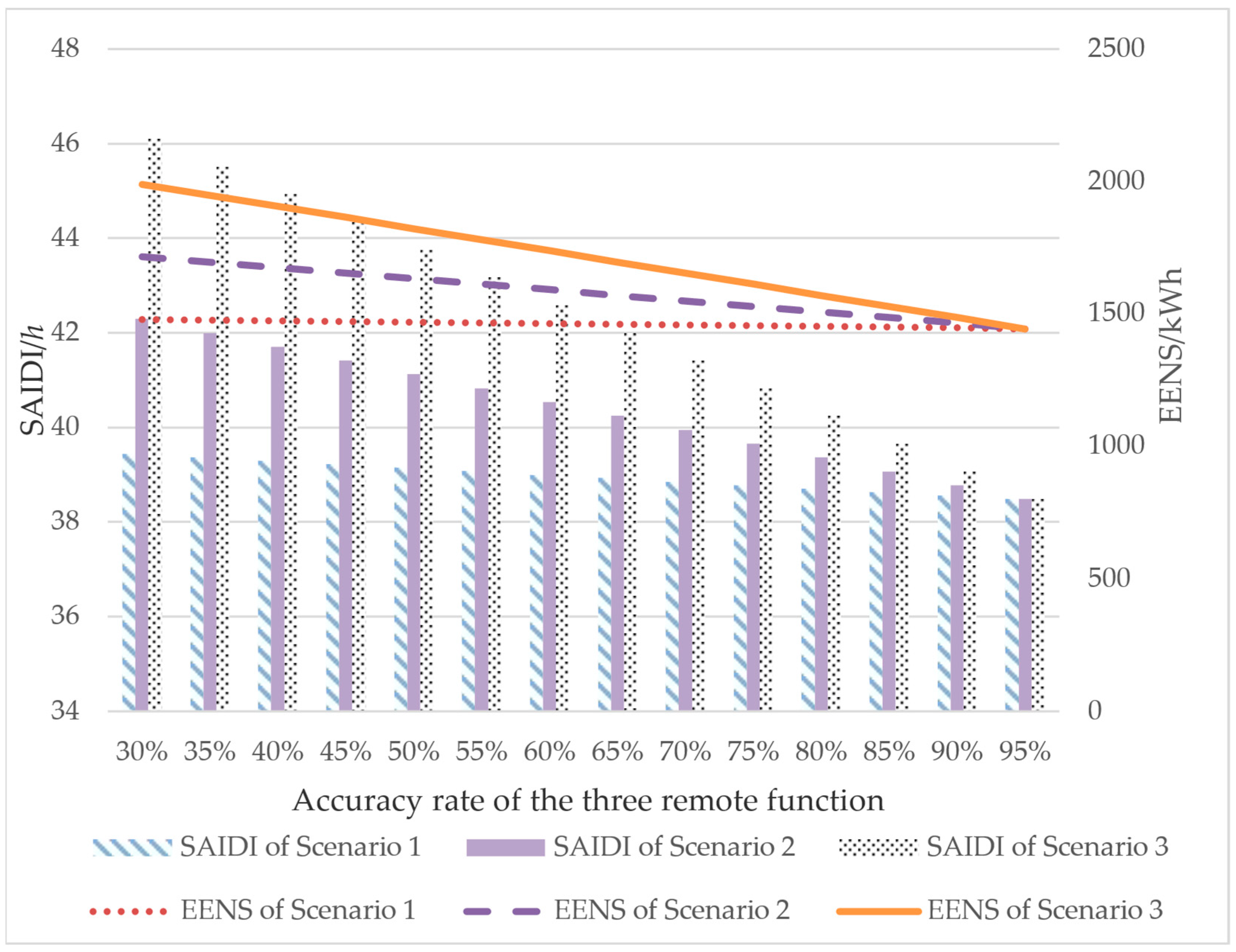
5.3. Analysis of the Impact of Unreliable Information Transmission on the Reliability of Distribution System
- With the decrease in the accuracy rate of the remote communication function, the increase rate of the SAIDI and EENS is basically the same.
- With the decrease in the accuracy rate of the remote measurement, the increase rate of the SAIDI and EENS is slightly reduced.
- With the decrease in the accuracy rate of remote control, the SAIDI and EENS of the system increase greatly, which shows that the system can achieve greater economy and reliability improvements when the remote control accuracy is high.
6. Conclusions
- (1)
- Considering the large quantity and wide range of distribution RTUs with limited investment, the RTUs of a DAS cannot cover all the distribution network buses; therefore, the impact of the DA information system on the power supply reliability cannot be ignored.
- (2)
- The rate of increase in the distribution network reliability caused by improving the accuracy rate of remote communication, remote measurement or remote control is not consistent. Therefore, in the case of limited investment, the procurement of RTU equipment is in accordance with the order of remote control, remote measurement, and remote communication.
- (3)
- When the accuracy of the “3R” functions has to be reduced due to bad weather or unexpected reasons, the utility company should give priority to inspecting and maintaining the remote control function. It should also ensure the accuracy rate of the remote control function followed by the check and repair of remote measurement and remote communication.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bassett, D.; Clinard, K.; Grainger, J.; Purucker, S.; Ward, D. Tutorial Course: Distribution Automation; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 1988. [Google Scholar]
- Wang, H.; Zhong, G. Research of the self-healing technologies in the optical communication network of distribution automation. In Proceedings of the IOP Conference Series Materials Science and Engineering, Shanghai, China, 1–4 November 2018. [Google Scholar]
- Huang, A.Q.; Baliga, J. FREEDM System: Role of power electronics and power semiconductors in developing an energy internet. In Proceedings of the 2009 21st International Symposium on Power Semiconductor Devices & IC’s, Barcelona, Spain, 14–18 June 2009. [Google Scholar]
- Liu, W.; Gong, Q.; Han, H.; Wang, Z.; Wang, L. Reliability modeling and evaluation of active cyber physical distribution system. IEEE Trans. Power Syst. 2018, 33, 7096–7108. [Google Scholar] [CrossRef]
- Yan, D. Analysis of Safe Operation Strategy of Electrical Automation Equipment in Natural Gas Station. Archit. Eng. Manag. 2021, 3, 98–100. [Google Scholar]
- Qinfei, W. The Design and Implementation of Intelligent Water Dispatching System. Master’s Thesis, Xi’an University of Science and Technology, Xi’an, China, 2019. [Google Scholar]
- Vellaithurai, C.; Srivastava, A.; Zonouz, S.; Berthier, R. CPIndex: Cyber-physical vulnerability assessment for power-grid infrastructures. IEEE Trans. Smart Grid 2015, 6, 566–575. [Google Scholar] [CrossRef]
- Mello, J.C.O.; Pereira, M.V.F.; Leite Da Silva, A.M. Evaluation of reliability worth in composite systems based on pseudo-sequential Monte Carlo simulation. IEEE Trans. Power Syst. 1994, 9, 1318–1326. [Google Scholar] [CrossRef]
- Billinton, R.; Wenyuan, L. Hybrid approach for reliability evaluation of composite generation and transmission systems using Monte-Carlo simulation and enumeration technique. IEE Proc. C Gener. Transm. Distrib. 1991, 138, 233–241. [Google Scholar] [CrossRef]
- Billinton, R.; Wang, P. Teaching distribution system reliability evaluation using Monte Carlo simulation. IEEE Trans. Power Syst. 1999, 14, 397–403. [Google Scholar] [CrossRef]
- Wang, P.; Billinton, R. Time sequential distribution system reliability worth analysis considering time varying load and cost models. IEEE Trans. Power Deliv. 1999, 14, 1046–1051. [Google Scholar] [CrossRef]
- Liu, H.; Huang, J. Reliability Evaluation for Complex Distribution System Based on the Simplified Zone Model and the Minimal Path; IEEE Computer Society: Washington, DC, USA, 2011. [Google Scholar]
- Xie, K.; Zhou, J.; Billinton, R. Reliability evaluation algorithm for complex medium voltage electrical distribution networks based on the shortest path. IEE Proc. Gener. Transm. Distrib. 2003, 150, 686–690. [Google Scholar] [CrossRef]
- Billinton, R.; Wang, P. Reliability-network-equivalent approach to distribution-system-reliability evaluation. IEE Proc. Gener. Transm. Distrib. 1998, 145, 149–153. [Google Scholar] [CrossRef]
- Li, W.; Wang, P.; Li, Z.; Liu, Y. Reliability evaluation of complex radial distribution systems considering restoration sequence and network constraints. IEEE Trans. Power Deliv. 2004, 19, 753–758. [Google Scholar] [CrossRef]
- Cao, W.; Li, Z.; Li, Y. Optimisation Configuration of Overhead-Line Segmentation Switch of a Distribution Network Based on Global Combination Criterion. Processes 2022, 10, 1976. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, L.; Xiang, Y.; Ten, C. Power System Reliability Evaluation with SCADA Cybersecurity Considerations. IEEE Trans. Smart Grid 2015, 6, 1707–1721. [Google Scholar] [CrossRef]
- Hajian-Hoseinabadi, H.; Hasanianfar, M.; Golshan, M.E.H. Quantitative reliability assessment of various automated industrial substations and their impacts on distribution reliability. IEEE Trans. Power Deliv. 2012, 27, 1223–1233. [Google Scholar] [CrossRef]
- Xin, S.; Guo, Q.; Sun, H.; Zhang, B.; Wang, J.; Chen, C. Cyber-physical modeling and cyber-contingency assessment of hierarchical control systems. IEEE Trans. Smart Grid 2015, 6, 2375–2385. [Google Scholar] [CrossRef]
- Jiamei, Y.; Jianbing, X.; Ming, N. Impact of Communication System Interruption on Power System Wide Region Protection and Control System. Autom. Electr. Power Syst. 2016, 40, 17–25. [Google Scholar]
- Lin, D.; Liu, Q.; Zeng, G.; Wang, Z.; Yu, T. Refined modeling and evaluation of reliability for cyber-physical system of distribution network. Dianli Xitong Zidonghua/Autom. Electr. Power Syst. 2021, 45, 92–101. [Google Scholar] [CrossRef]
- Duckhwa, H.; Younghun, L. A study on the compound communication network over the high voltage power line for dis-tribution automation system. In Proceedings of the 2008 International Conference on Information Security and Assurance (ISA 2008), Busan, Republic of Korea, 24–26 April 2008; IEEE Computer Society: Busan, Republic of Korea, 2008; pp. 410–414. [Google Scholar]
- Kim, J.; Tong, L. On topology attack of a smart grid: Undetectable attacks and countermeasures. IEEE J. Sel. Areas Commun. 2013, 31, 1294–1305. [Google Scholar] [CrossRef]
- Yongfeng, L.; Liang, C.; Guoqiang, Z. Research of Distribution Automation Terminal Information Security Risk Evaluation Methods. Autom. Instrum. 2015, 30, 11–14. [Google Scholar]
- Wang, P.; Ashok, A.; Govindarasu, M. Cyber-physical risk assessment for smart grid System Protection Scheme. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; IEEE Computer Society: Denver, CO, USA, 2015. [Google Scholar]
- Wang, Q.; Pipattanasomporn, M.; Kuzlu, M.; Tang, Y.; Li, Y.; Rahman, S. Framework for vulnerability assessment of communication systems for electric power grids. IET Gener. Transm. Distrib. 2016, 10, 477–486. [Google Scholar] [CrossRef]
- Meimei, Y.; Bingyao, L.; Lingzhong, H. Summary and prospect of ubiquitous power internet of things in intelligent power distribution system. Electr. Eng. 2020, 88–89. [Google Scholar]
- Yohanandhan, R.V.; Elavarasan, R.M.; Pugazhendhi, R.; Premkumar, M.; Mihet-Popa, L.; Zhao, J.; Terzija, V. A specialized review on outlook of future Cyber-Physical Power System (CPPS) testbeds for securing electric power grid. Int. J. Electr. Power Energy Syst. 2022, 136, 107720. [Google Scholar] [CrossRef]
- Qiang, Q.; Wenze, L.; Weihao, T.; Zexiang, C.; Bowei, C.; Pei, K. An optimal deployment method of distribution edge computing terminals for software defined network. Electr. Power Constr. 2023, 44, 82–90. [Google Scholar]
- Jianing, L.; Zhuo, S.; Ke, W.; Bowei, C.; Zexiang, C.; Zhigang, W. Elastic Configuration Method of Cloud-Edge Collaborative Resources for Distribution Internet of Things Automation Business. Electr. Power Constr. 2023, 44, 118–127. [Google Scholar]
- Wang, Y.; Li, W.; Lu, J.; Liu, H. Evaluating multiple reliability indices of regional networks in wide area measurement system. Electr. Power Syst. Res. 2009, 79, 1353–1359. [Google Scholar] [CrossRef]
- Falahati, B.; Fu, Y. Reliability assessment of smart grids considering indirect cyber-power interdependencies. IEEE Trans. Smart Grid 2014, 5, 1677–1685. [Google Scholar] [CrossRef]
- Falahati, B.; Fu, Y.; Wu, L. Reliability assessment of smart grid considering direct cyber-power interdependencies. IEEE Trans. Smart Grid 2012, 3, 1515–1524. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, T.; Luo, F.; Li, P.; Yao, L. Fault incidence matrix based reliability evaluation method for complex distribution system. IEEE Trans. Power Syst. 2018, 33, 6736–6745. [Google Scholar] [CrossRef]
- Billinton, R.; Allan, R.N. Reliability Evaluation of Power Systems; Plenum: New York, NY, USA, 1984. [Google Scholar]
- Zhang, T.; Wang, C.; Luo, F.; Li, P.; Yao, L. Optimal Design of the Sectional Switch and Tie Line for the Distribution Network Based on the Fault Incidence Matrix. IEEE Trans. Power Syst. 2019, 34, 4869–4879. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, T.; Luo, F.; Li, F.; Liu, Y. Impacts of Cyber System on Microgrid Operational Reliability. IEEE Trans. Smart Grid 2019, 10, 105–115. [Google Scholar] [CrossRef]

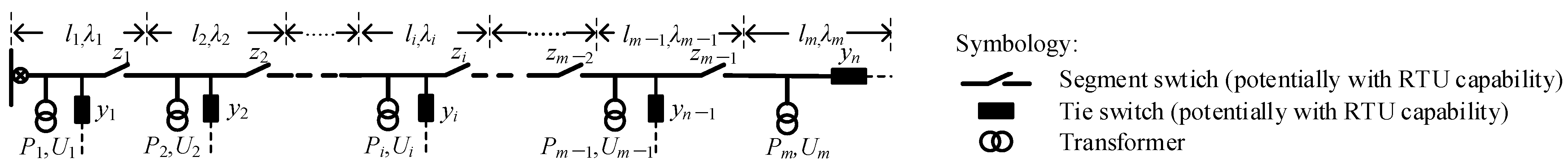

| Function | Type of Collected or Operated Data | Application |
|---|---|---|
| remote measurement | operating parameters of distribution systems (U, I, P, f) | determining the location and type of failures |
| remote communication | real-time status of distribution equipment | delivery of real-time information |
| remote control | on–off state of switch | failure isolation and recovery |
| Phase | Configured All with “3R” RTUs | Configured All with “2R” RTUs | Configured with Both “2R” and “3R” RTUs |
|---|---|---|---|
| Failure location T1 | 0 | 0 | 0 |
| Failure isolation T2 | 0 | ||
| Failure recovery T3 | |||
| Total | |||
| Phase | Configured All with “3R” RTUs | Configured All with “2R” RTUs | Configured with Both “2R” and “3R” RTUs |
|---|---|---|---|
| Failure location T1 | 0 | 0 | 0 |
| Failure isolation T2 | 0 | ||
| Failure recovery T3 | |||
| Total | |||
| Event | Remote Communication and Remote Control | Remote Measurement |
|---|---|---|
| A | wrong | correct |
| B | correct | wrong |
| C | wrong | wrong |
| Probability of the Transmission Error Events | Duration Calibration | ||
|---|---|---|---|
| p = 1 − pm·pc·ps | p1 = (1 − pc·ps)pm | p11 = pc·(1 − ps)·pm | tA1 = t3 + t311 |
| p12 = (1 − pc)·ps·pm | tA2 = t2 + t212 | ||
| p13 = (1 − pc) (1 − ps)·pm | tA3 = t2 + t213 | ||
| p2 = (1 − pm)·pc·ps | p21 = pc·ps·pm1 | tB1 = t1 + t121 | |
| p22 = pc·ps·pm2 | tB2 = t1 + t122 | ||
| p23 = pc·ps·pm3 | tB3 = t1 + t121 + t122 | ||
| p3 = (1 − pc·ps)·(1 − pm) | p31 = pc·(1 − ps)·pm1 | tC1 = tA1 + tB1 | |
| p32 = pc·(1 − ps)·pm2 | tC2 = tA1 + tB2 | ||
| p33 = pc·(1 − ps)·pm3 | tC3 = tA1 + tB3 | ||
| p34 = (1 − pc)·ps·pm1 | tC4 = tA2 + tB1 | ||
| p35 = (1 − pc)·ps·pm2 | tC5 = tA2 + tB2 | ||
| p36 = (1 − pc)·ps·pm3 | tC6 = tA2 + tB3 | ||
| p37 = (1 − pc) (1 − ps)·pm1 | tC7 = tA3 + tB1 | ||
| p38 = (1 − pc) (1 − ps)·pm2 | tC8 = tA3 + tB2 | ||
| p39 = (1 − pc) (1 − ps)·pm3 | tC9 = tA3 + tB3 | ||
| Probability of the Data Transmission Error Events | Duration Calibration | ||
|---|---|---|---|
| p = 1 − pm | pB = 1 − pm | p21 = pm1 | tB1 = t1 + t121 |
| p22 = pm2 | tB2 = t3 + t122 | ||
| p23 = pm3 | tB3 = tB1 + tB2 | ||
| Fault Incidence Matrix Method | Proposed Method | |
|---|---|---|
| EENS (kW·h) | 1443.99 | 1443.99 |
| SAIDI (h) | 38.4836 | 38.4836 |
| ASAI (%) | 99.56 | 99.56 |
| Accuracy Change Rate of Remote Communication (%) | Change in EENS (kW·h) | Change Rate of EENS (%) | Change in SAIDI (h) | Change Rate of SAIDI (%) |
|---|---|---|---|---|
| 100–95 | 1443.99–1446.61 | 0.1816 | 38.4836–38.5572 | 0.1913 |
| 95–90 | 1446.61–1449.23 | 0.1813 | 38.5572–38.6308 | 0.1909 |
| 90–85 | 1449.23–1451.85 | 0.1809 | 38.6308–38.7043 | 0.1903 |
| 85–80 | 1451.85–1454.47 | 0.1806 | 38.7043–38.7791 | 0.1933 |
| 80–75 | 1454.47–1457.1 | 0.1803 | 38.7791–38.8515 | 0.1867 |
| Accuracy Change Rate of Remote Measurement (%) | Change in EENS (kW·h) | Change Rate of EENS (%) | Change in SAIDI (h) | Change Rate of SAIDI (%) |
|---|---|---|---|---|
| 100–95 | 1443.99–1464.98 | 1.4542 | 38.4836–38.7766 | 0.7614 |
| 95–90 | 1464.98–1485.98 | 1.4332 | 38.7766–39.0695 | 0.7554 |
| 90–85 | 1485.98–1506.98 | 1.4129 | 39.0695–39.3625 | 0.7499 |
| 85–80 | 1506.98–1527.97 | 1.3933 | 39.3625–39.6555 | 0.7444 |
| 80–75 | 1527.97–1548.97 | 1.3742 | 39.6555–39.9485 | 0.7389 |
| Accuracy Change Rate of Remote Control (%) | Change in EENS (kW·h) | Change Rate of EENS (%) | Change in SAIDI (h) | Change Rate of SAIDI (%) |
|---|---|---|---|---|
| 100–95 | 1443.99–1485.98 | 2.9082 | 38.4836–39.0695 | 1.5225 |
| 95–90 | 1485.98–1527.97 | 2.8259 | 39.0695–39.6555 | 1.4999 |
| 90–85 | 1527.97–1569.97 | 2.7484 | 39.6555–40.2414 | 1.4775 |
| 85–80 | 1569.97–1611.96 | 2.6747 | 40.2414–40.8274 | 1.4562 |
| 80–75 | 1611.96–1653.95 | 2.6052 | 40.8274–41.4133 | 1.4351 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, F.; Ge, N.; Xu, J. Power Supply Reliability Analysis of Distribution Systems Considering Data Transmission Quality of Distribution Automation Terminals. Energies 2023, 16, 7826. https://doi.org/10.3390/en16237826
Luo F, Ge N, Xu J. Power Supply Reliability Analysis of Distribution Systems Considering Data Transmission Quality of Distribution Automation Terminals. Energies. 2023; 16(23):7826. https://doi.org/10.3390/en16237826
Chicago/Turabian StyleLuo, Fengzhang, Nan Ge, and Jing Xu. 2023. "Power Supply Reliability Analysis of Distribution Systems Considering Data Transmission Quality of Distribution Automation Terminals" Energies 16, no. 23: 7826. https://doi.org/10.3390/en16237826
APA StyleLuo, F., Ge, N., & Xu, J. (2023). Power Supply Reliability Analysis of Distribution Systems Considering Data Transmission Quality of Distribution Automation Terminals. Energies, 16(23), 7826. https://doi.org/10.3390/en16237826







