A Fast Screening Method of Key Parameters from Coal for Carbon Emission Enterprises
Abstract
:1. Introduction
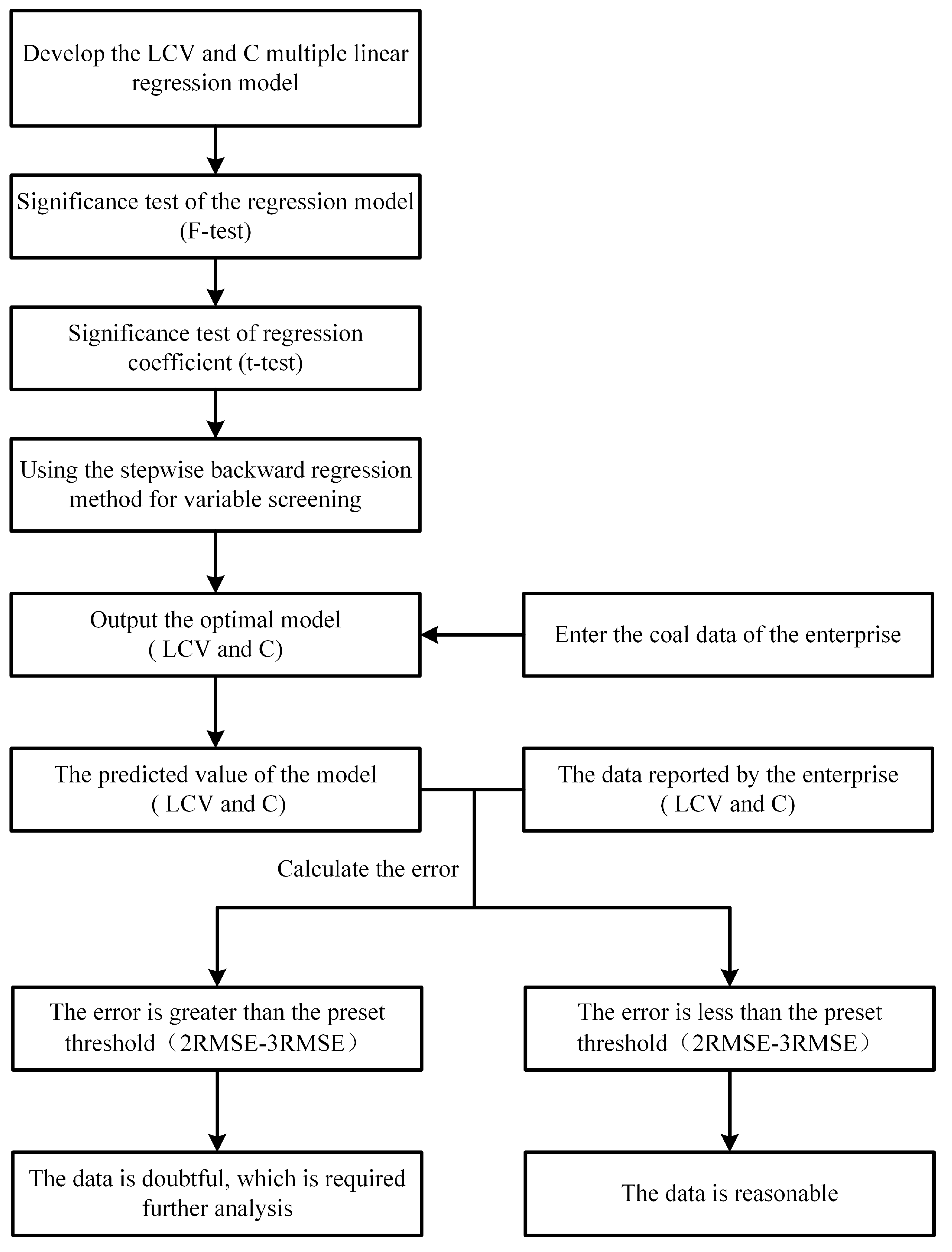
2. Materials and Methods
2.1. Sample Collection and Preparation
2.2. Methodology
2.2.1. Multiple Linear Regression
2.2.2. Stepwise Backward Regression Method
2.2.3. Model Evaluation Indicators
3. Results
3.1. Model Building
3.1.1. Low Calorific Value
3.1.2. Carbon Content
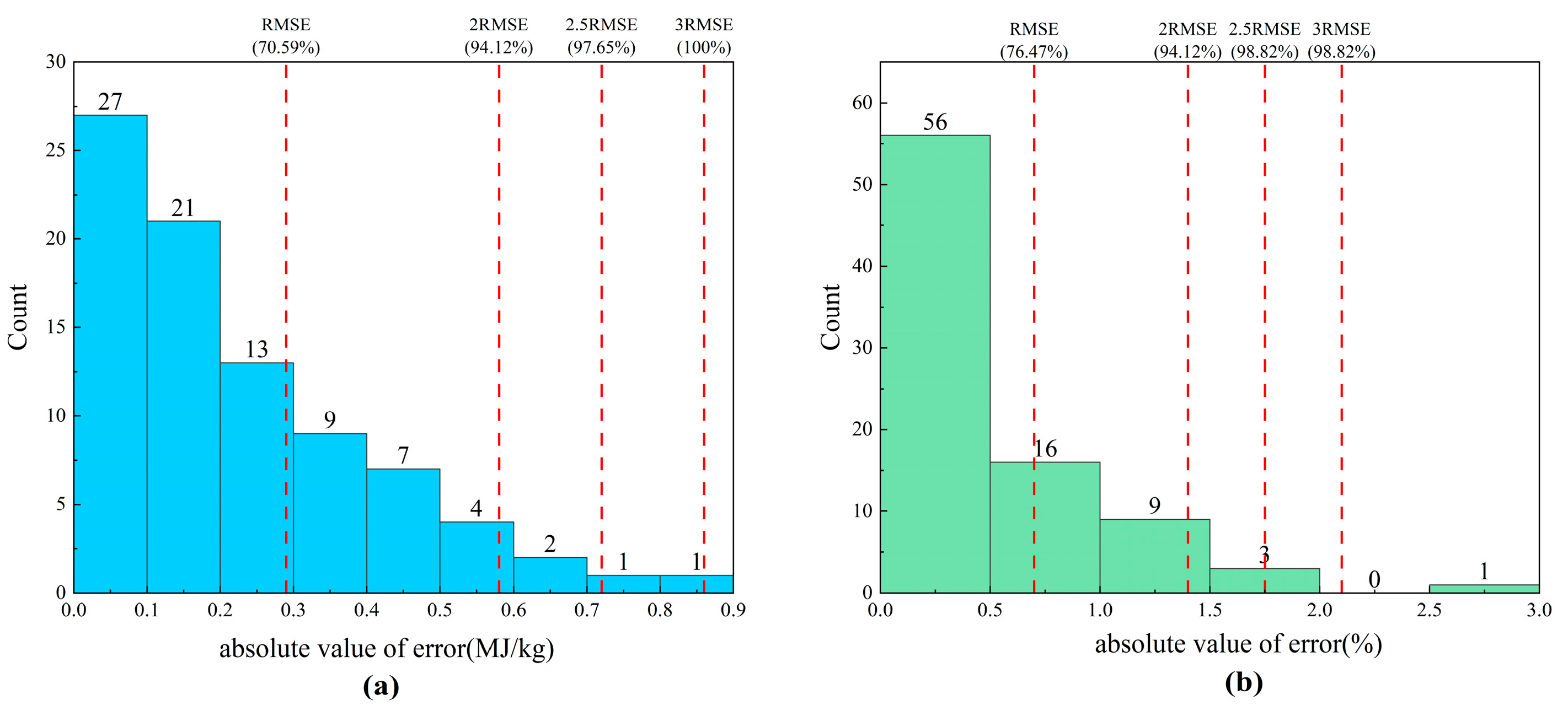
3.2. 33.2 Error Thresholds
3.2.1. LCV
3.2.2. C
3.3. Validation of Regression Model
4. Discussion
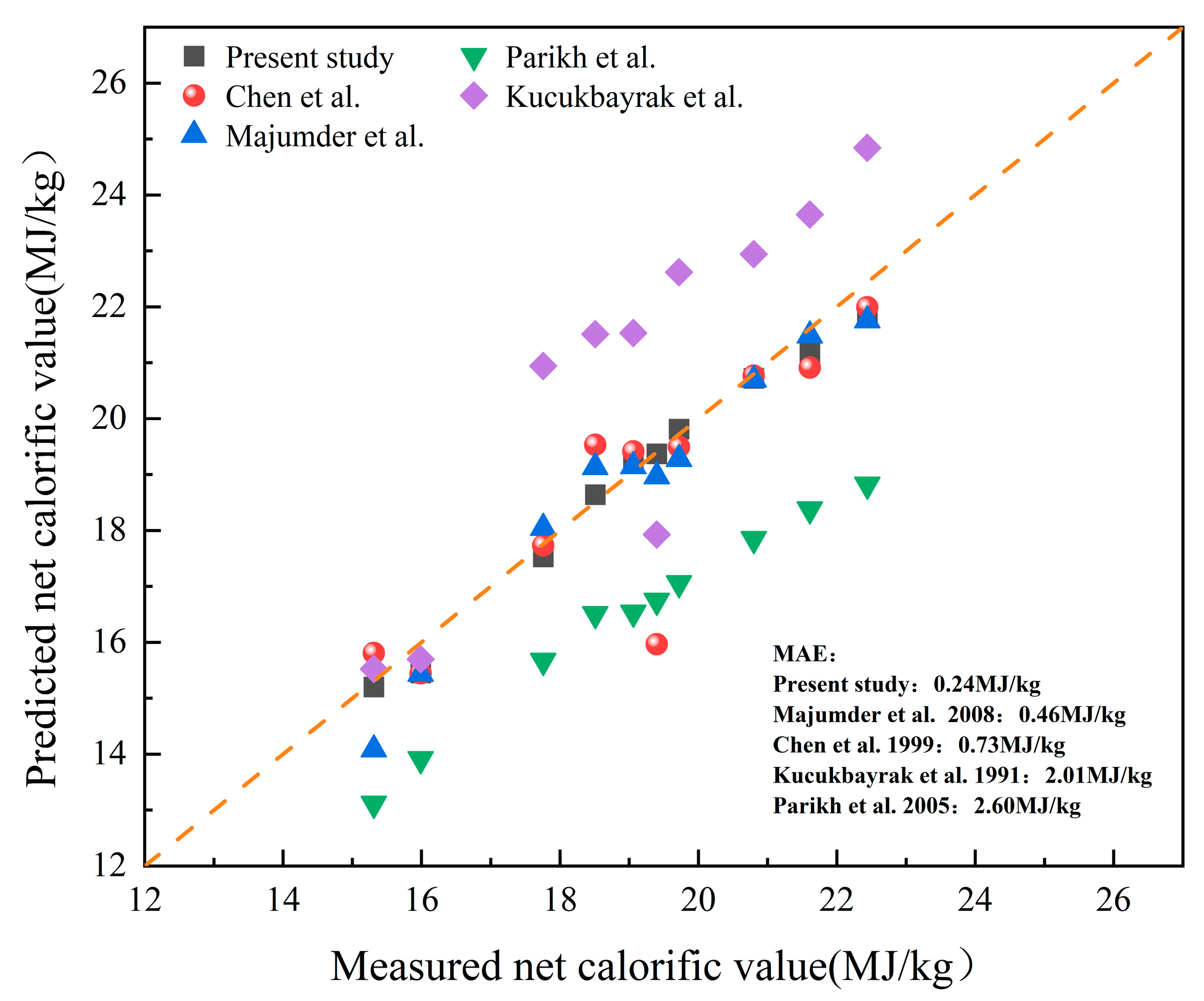
4.1. Comparison of the LCV Regression Models
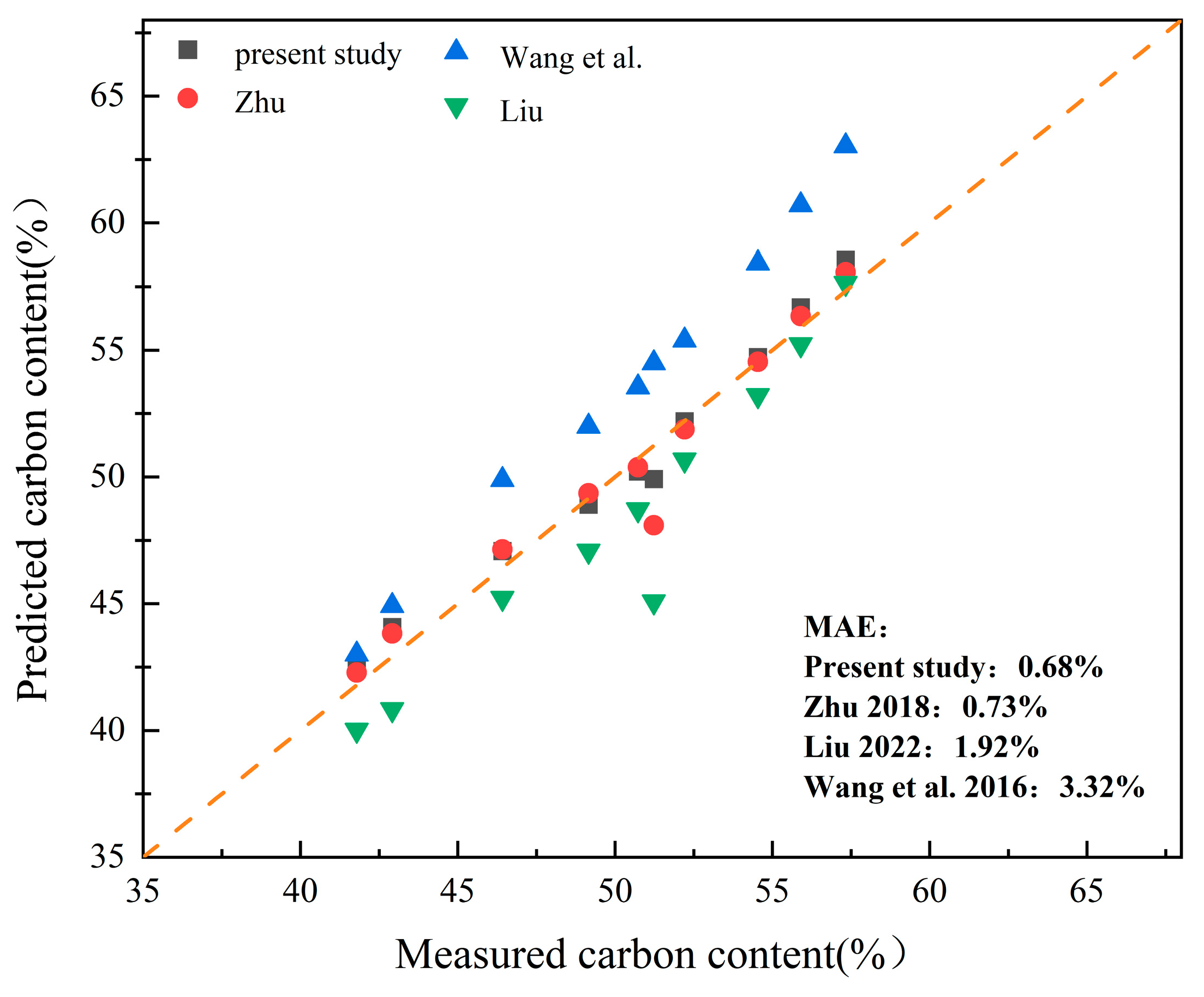
4.2. Comparison of Carbon Content Regression Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, R.; Bao, Y.; Lv, F.; Chen, F.; Hu, K.; Zhang, Y. Coal measure energy production and the reservoir space utilization in China under carbon neutral target. Front. Earth Sci. 2023, 11, 1122040. [Google Scholar]
- Liu, W.; Xu, X.; Han, J.; Wang, B.; Li, Z.; Yan, Y. Trend model and key technologies of coal mine methane emission reduction reduction arming for the carbon neutrality. J. China Coal Soc. 2022, 47, 470–479. (In Chinese) [Google Scholar]
- Wang, W.; Kuang, Y.; Huang, N. Study on the Decomposition of Factors Affecting Energy-Related Carbon Emissions in Guangdong Province, China. Energies 2011, 4, 2249–2272. [Google Scholar] [CrossRef]
- Lu, W.; Chen, X.; Lu, J.; Li, Y.; Yao, S. Analysis and suggestion on carbon accounting of thermal power enterprises under the background of carbon peak and carbon neutrality. Clean Coal Technol. 2023, 10, 194–203. (In Chinese) [Google Scholar]
- Liu, Y.; Wang, D.; Ren, X. Rapid Quantitation of Coal Proximate Analysis by Using Laser-Induced Breakdown Spectroscopy. Energies 2022, 15, 2728. [Google Scholar] [CrossRef]
- Ren, Z.; Fang, C.; Zhao, J. Calorific value estimation of fire coal based on historical test data of incoming coal. Coal Qual. Technol. 2016, 18–20. (In Chinese) [Google Scholar]
- Kucukbayrak, S.; Durus, B.; Mericboyu, A.E.; Kadioglu, E. Estimation of calorific values of Turkish lignites. Fuel 1991, 70, 979–981. [Google Scholar] [CrossRef]
- Parikh, J.; Channiwala, S.A.; Ghosal, G.K. A correlation for calculating HHV from proximate analysis of solid fuels. Fuel 2005, 84, 487–494. [Google Scholar] [CrossRef]
- Majumder, A.K.; Jain, R.; Banerjee, P.; Barnwal, J.P. Development of a new proximate analysis based correlation to predict calorific value of coal. Fuel 2008, 87, 3077–3081. [Google Scholar]
- Akkaya, A.V. Proximate analysis based multiple regression models for higher heating value estimation of low rank coals. Fuel. Process. Technol. 2009, 90, 165–170. [Google Scholar] [CrossRef]
- Mesroghli, S.; Jorjani, E.; Chelgani, S.C. Estimation of gross calorific value based on coal analysis using regression and artificial neural networks. Int. J. Coal Geol. 2009, 79, 49–54. [Google Scholar] [CrossRef]
- Kavsek, D.; Bednarova, A.; Biro, M.; Kranvogl, R.; Voncina, D.B.; Beinrohr, E. Characterization of Slovenian coal and estimation of coal heating value based on proximate analysis using regression and artificial neural networks. Cent. Eur. J. Chem. 2013, 11, 1481–1491. [Google Scholar]
- Chelgani, S.C.; Makaremi, S. Explaining the relationship between common coal analyses and Afghan coal parameters using statistical modeling methods. Fuel. Process. Technol. 2013, 110, 79–85. [Google Scholar] [CrossRef]
- Given, P.H.; Weldon, D.; Zoeller, J.H. Calculation of calorific values of coals from ultimate analyses: Theoretical basis and geochemical implications. Fuel 1986, 65, 849–854. [Google Scholar] [CrossRef]
- Channiwala, S.A.; Parikh, P.P. A unified correlation for estimating HHV of solid, liquid and gaseous fuels. Fuel 2002, 81, 1051–1063. [Google Scholar] [CrossRef]
- Feng, Q.; Zhang, J.; Zhang, X.; Wen, S. Proximate analysis based prediction of gross calorific value of coals: A comparison of support vector machine, alternating conditional expectation and artificial neural network. Fuel Process. Technol. 2015, 10, 120–129. [Google Scholar] [CrossRef]
- Erik, N.Y.; Yilmaz, I. On the Use of Conventional and Soft Computing Models for Prediction of Gross Calorific Value (GCV) of Coal. Int. J. Coal Prep. Util. 2011, 31, 32–59. [Google Scholar] [CrossRef]
- Wen, X.; Jian, S.; Wang, J. Prediction models of calorific value of coal based on wavelet neural networks. Fuel 2017, 199, 512–522. [Google Scholar] [CrossRef]
- Patel, S.U.; Kumar, B.J.; Badhe, Y.P.; Sharma, B.K.; Saha, S.; Biswas, S.; Chaudhury, A.; Tambe, S.S.; Kulkarni, B.D. Estimation of gross calorific value of coals using artificial neural networks. Fuel 2007, 86, 334–344. [Google Scholar] [CrossRef]
- Chelgani, S.C.; Hart, B.; Grady, W.C.; Hower, J.C. Study relationship between inorganic and organic coal analysis with gross calorific value by multiple regression and ANFIS. Int. J. Coal Prep. Util. 2011, 31, 9–19. [Google Scholar] [CrossRef]
- Qi, M.; Luo, H.; Wei, P.; Fu, Z. Estimation of low calorific value of blended coals based on support vector regression and sensitivity analysis in coal-fired power plants. Fuel 2019, 236, 1400–1407. [Google Scholar]
- Tan, P.; Zhang, C.; Xia, J.; Fang, Q.; Chen, G. Estimation of higher heating value of coal based on proximate analysis using support vector regression. Fuel Process. Technol. 2015, 138, 298–304. [Google Scholar] [CrossRef]
- Matin, S.S.; Chelgani, S.C. Estimation of coal gross calorific value based on various analyses by random forest method. Fuel 2016, 177, 274–278. [Google Scholar]
- Saptoro, A.; Vuthaluru, H.B.; Tade, M.O. A comparative study of prediction of elemental composition of coal using empirical modelling. IFAC Proc. Vol. 2006, 39, 747–752. [Google Scholar]
- Yi, L.; Feng, J.; Qin, Y.; Li, W. Prediction of elemental composition of coal using proximate analysis. Fuel 2017, 193, 315–321. [Google Scholar] [CrossRef]
- Liu, F. A comparison between multivariate linear model and maximum likelihood estimation for the prediction of elemental composition of coal using proximate analysis. Results Eng. 2022, 13, 100338. [Google Scholar]
- Zhu, D. Application of Carbon Ultimate Analysis into Greenhouse Gas Emissions Accounting for Coal-fired Power Plants. Power Gener. Technol. 2018, 39, 363–366. (In Chinese) [Google Scholar]
- Wang, Y.; Huang, J.; Wang, Y. Discussion on Deriving Formula of Carbon Content and CO2 Emissions from Coal Calorific. Northeast Electr. Power Technol. 2016, 37, 5–7. (In Chinese) [Google Scholar]
- Wen, X.; Li, G.; Sun, L.; Sun, Y.; Wang, G. Analysis of Carbon in Coal-fired Based on Partial Least Squares Regression Algorithm. J. Northeast Dianli Univ. 2012, 32, 31–36. (In Chinese) [Google Scholar]
- Wen, X.; Sun, L. Analysis on Coal-fired Carbon Based on Support Vector Machine. East China Electr. Power 2011, 39, 973–976. (In Chinese) [Google Scholar]
- Xu, Q.; Wang, Y.; Lin, W.; Liang, H.; Wan, J. Calculation of CO2 emissions in boilers based on ACO-LSSVM method for carbon element analysis of coal. J. Fuzhou Univ. Nat. Sci. Ed. 2015, 43, 548–553. (In Chinese) [Google Scholar]
- Bienvenido-Huertas, D.; Rubio-Bellido, C.; Perez-Ordoez, J.L.; Martínez-Abella, F. Estimating Adaptive Setpoint Temperatures Using Weather Stations. Energies 2019, 12, 1197. [Google Scholar]
- Ghani, I.M.M.; Ahmad, S. Stepwise Multiple Regression Method to Forecast Fish Landing. Procedia-Soc. Behav. Sci. 2010, 8, 549–554. [Google Scholar] [CrossRef]
- Lu, Z.; Chen, X.; Yao, S.; Qin, H.; Zhang, L.; Yao, X.; Yu, Z.; Lu, J. Feasibility study of gross calorific value, carbon content, volatile matter content and ash content of solid biomass fuel using laser-induced breakdown spectroscopy. Fuel 2019, 258, 116150. [Google Scholar]
- Chang, H.; Sun, W.; Gu, X. Forecasting Energy CO2 Emissions Using a Quantum Harmony Search Algorithm-Based DMSFE Combination Model. Energies 2013, 6, 1456–1477. [Google Scholar] [CrossRef]
- Szer, M.; Haykiri-Acma, H.; Yaman, S. Prediction of Calorific Value of Coal by Multi Linear Regression and Analysis of Variance. J. Energ. Resour-ASME 2021, 144, 1–28. [Google Scholar]
- GB/T 35985-2018; Calculation of Analyses to Different Bases for Coal. Standards Press of China: Beijing, China, 2018.
| Parameter | Reference | Model | Model Evaluation Indicators |
|---|---|---|---|
| Calorific value | Chen et al. (1999) [6] | LCV = 35,860 − 73.7V − 395.7A − 702M | n.g. |
| Kucukbayrak et al. (1991) [7] | GCV = 76.56 − 1.30(V + A) + 7.03 × 10−3(V + A)2 | R2 = 0.91 | |
| Parikh et al. (2005) [8] | GCV = 0.3536FC + 0.1559V − 0.0078A | MAE = 3.74% | |
| Majumder et al. (2008) [9] | GCV = −0.03A − 0.11M + 0.33V + 0.35FC | MAE = 1.49% | |
| Akkaya (2009) [10] | GCV = 0.836M−8.155A−3.559V0.35FC0.626 GCV = 0.561M−6.137V0.381FC0.666 GCV = 33.078 − 0.72M + 0.012M2 − 1.163M3 − 0.324A2 | R2 = 0.97 | |
| Mesroghli et al. (2009) [11] | GCV = 37.777 − 0.647M − 0.387A − 0.089V GCV = −26.29 + 0.275A + 0.605C + 1.352H + 0.840N + 0.321S | R2 = 0.97 | |
| Kavsek et al. (2013) [12] | GCV = −3.57 + 0.31V + 0.34FC | R2 = 0.971 | |
| Chelgani et al. (2013) [13] | GCV = 35.391 − 0.47M − 0.364A − 0.028V GCV = −0.408 + 1.243H + 0.348C−0.1N − 0.111O + 0.112S | R2 = 0.998 | |
| Given et al. (1986) [14] | GCV = 0.3278C +1.419H + 0.09257S − 0.1379O + 0.637 | n.g. | |
| Channiwala et al. (2002) [15] | GCV = 0.3491C + 1.1783H + 0.1005S − 0.1034O − 0.0151N − 0.0211A | MAE = 1.45% | |
| Carbon content | Saptoro et al. (2006) [24] | C = a0 + a1A + a2V + a3M + a4FC | n.g. |
| Yi et al. (2017) [25] | C = x1 + x2A + x3A2 + x4V + x5V2 + x6FC + x7FC2 (1) Anthracite: C = 306,540 − 3066.61A + 0.0229439A2 − 3066.31V + 0.0435868V2 − 3063.36FC − 0.0106054FC2 (2) High-rank bituminous: C = −143,398 + 1434.61A − 0.0138486A2 + 1435.78V − 0.0125349V2 + 1433.88FC + 0.0106647FC2 (3) Subbituminous: C = 40,521.2 − 403.482A − 0.085603A2 − 403.029V − 0.0193969V2 − 405.885FC + 0.0168029FC2 (4) Lignite: C = 5855.8 − 57.3735A − 0.0220361A2 − 58.4226V + 0.0131499V2 − 58.9345FC + 0.0195368FC2 | (1) Anthracite: R2 = 0.95, MAE = 0.53% (2) High-rank bituminous: R2 = 0.93, MAE = 0.51% (3) Subbituminous: R2 = 0.86, MAE = 0.93% (4) Lignite: R2 = 0.92, MAE = 1.87% | |
| Liu (2022) [26] | C = 50.7368 − 0.5799FC − 0.7066V + 2.8301GCV | MAE = 1.97% | |
| Zhu (2018) [27] | C = 35.411 − 0.341A − 0.199V − 0.412S + 1.632GCV | n.g. | |
| Wang et al. (2016) [28] | (1) C = LCV/356 (LCV: 5026–19,040 kJ/kg) (2) C = LCV/383 (LCV: 19,040–29,850 kJ/kg) | RE = −0.6~1.14% |
| Coal Property | Minimum | Maximum | Mean | Standard Deviation |
|---|---|---|---|---|
| Mad (%) | 2.48 | 19.92 | 7.24 | 4.04 |
| Aad (%) | 3.69 | 34.06 | 18.48 | 6.91 |
| Vad (%) | 25.52 | 42.41 | 31.14 | 4.57 |
| FCad (%) | 34.07 | 60.74 | 43.38 | 4.04 |
| St,ad (%) | 0.12 | 1.98 | 0.77 | 0.31 |
| Had (%) | 3.23 | 4.41 | 3.71 | 0.24 |
| Car (%) | 39.90 | 61.14 | 50.72 | 4.69 |
| LCVar (MJ/kg) | 14.85 | 22.78 | 19.05 | 2.02 |
| Model | Coefficient | Sig.(t) | Sig.(F) | R2 | |
|---|---|---|---|---|---|
| 1 | Intercept | −2.116 | 0.446 | 3.53 × 10−62 | 0.9775 |
| Mad | −0.025 | 0.384 | |||
| St,ad | 0.394 | 0.033 | |||
| Car | 0.393 | 4.91 × 10−41 | |||
| Had | 0.151 | 0.565 | |||
| FCad | 0.01 | 0.647 | |||
| Aad | 0.004 | 0.882 | |||
| Vad | 0.00032 | 0.993 | |||
| 2 | Intercept | −2.097 | 0.2 | 1.36 × 10−63 | 0.9778 |
| Mad | −0.025 | 0.325 | |||
| St,ad | 0.395 | 0.027 | |||
| Car | 0.393 | 2.21 × 10−47 | |||
| Had | 0.152 | 0.504 | |||
| FCad | 0.01 | 0.564 | |||
| Aad | 0.004 | 0.797 | |||
| 3 | Intercept | −1.726 | 0.024 | 4.85 × 10−65 | 0.9781 |
| Mad | −0.03 | 0.06 | |||
| St,ad | 0.408 | 0.017 | |||
| Car | 0.393 | 5.64 × 10−48 | |||
| Had | 0.107 | 0.454 | |||
| FCad | 0.008 | 0.601 | |||
| 4 | Intercept | −1.604 | 0.027 | 1.69 × 10−66 | 0.9783 |
| Mad | −0.034 | 0.016 | |||
| St,ad | 0.371 | 0.016 | |||
| Car | 0.397 | 9.91 × 10−59 | |||
| Had | 0.12 | 0.392 | |||
| 5 | Intercept | −1.202 | 0.027 | 6.32 × 10−68 | 0.9784 |
| Mad | −0.032 | 0.021 | |||
| St,ad | 0.359 | 0.019 | |||
| Car | 0.398 | 1.77 × 10−59 | |||
| Model | Coefficient | Sig.(t) | Sig.(F) | R2 | |
|---|---|---|---|---|---|
| 1 | Intercept | 13.819 | 0.037 | 8.32 × 10−61 | 0.9756 |
| Aad | −0.098 | 0.17 | |||
| Vad | −0.141 | 0.126 | |||
| Qnet,ar | 2.301 | 4.91 × 10−41 | |||
| St,ad | −0.533 | 0.238 | |||
| FCad | −0.018 | 0.737 | |||
| Mad | 0.013 | 0.853 | |||
| Had | 0.108 | 0.866 | |||
| 2 | Intercept | 13.881 | 0.035 | 3.39 × 10−62 | 0.9759 |
| Aad | −0.098 | 0.168 | |||
| Vad | −0.134 | 0.095 | |||
| Qnet,ar | 2.305 | 8.81 × 10−43 | |||
| St,ad | −0.529 | 0.238 | |||
| FCad | −0.017 | 0.744 | |||
| Mad | 0.011 | 0.873 | |||
| 3 | Intercept | 14.729 | 1.35 × 10−4 | 1.24 × 10−63 | 0.9762 |
| Aad | −0.107 | 0.016 | |||
| Vad | −0.142 | 0.023 | |||
| Qnet,ar | 2.301 | 6 × 10−45 | |||
| St,ad | −0.533 | 0.231 | |||
| FCad | −0.024 | 0.483 | |||
| 4 | Intercept | 13.553 | 8 × 10−5 | 5.04 × 10−65 | 0.9764 |
| Aad | −0.095 | 0.02 | |||
| Vad | −0.126 | 0.029 | |||
| Qnet,ar | 2.273 | 3.48 × 10−50 | |||
| St,ad | −0.549 | 0.215 | |||
| 5 | Intercept | 15.649 | 3.07 × 10−7 | 2.96 × 10−66 | 0.9762 |
| Aad | −0.129 | 3.40 × 10−5 | |||
| Vad | −0.159 | 0.002 | |||
| Qnet,ar | 2.228 | 7.99 × 10−56 | |||
| Absolute Errors | Proportion of Model Calculated Value (%) | |
|---|---|---|
| Low Calorific Value (RMSE = 0.29 MJ/kg) | Carbon Content (RMSE = 0.70%) | |
| ≤RMSE | 70.59 | 76.47 |
| ≤2RMSE | 94.12 | 94.12 |
| ≤2.5RMSE | 97.65 | 98.82 |
| ≤3RMSE | 100 | 98.82 |
| Sample | LCVar | Car | ||||||
|---|---|---|---|---|---|---|---|---|
| Measured Value (MJ/kg) | Predicted Value (MJ/kg) | Absolute Error (MJ/kg) | Relative Error (%) | Measured Value (%) | Predicted Value (%) | Absolute Error (%) | Relative Error (%) | |
| 1 | 22.44 | 21.82 | −0.62 | 2.77 | 57.33 | 58.55 | 1.22 | 2.12 |
| 2 | 21.61 | 21.18 | −0.43 | 2.00 | 55.90 | 56.69 | 0.79 | 1.41 |
| 3 | 19.72 | 19.81 | 0.09 | 0.44 | 52.21 | 52.20 | −0.01 | 0.01 |
| 4 | 19.40 | 19.37 | −0.03 | 0.13 | 51.23 | 49.92 | −1.31 | 2.56 |
| 5 | 19.06 | 19.23 | 0.17 | 0.90 | 50.73 | 50.22 | −0.51 | 1.00 |
| 6 | 17.76 | 17.53 | −0.23 | 1.31 | 46.42 | 47.08 | 0.66 | 1.42 |
| 7 | 18.51 | 18.64 | 0.13 | 0.71 | 49.16 | 48.91 | −0.25 | 0.50 |
| 8 | 20.80 | 20.72 | −0.08 | 0.39 | 54.54 | 54.73 | 0.19 | 0.35 |
| 9 | 15.31 | 15.20 | −0.11 | 0.69 | 41.79 | 42.50 | 0.71 | 1.70 |
| 10 | 15.99 | 15.45 | −0.54 | 3.40 | 42.92 | 44.08 | 1.15 | 2.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Chen, X.; Song, Z.; Li, Y.; Lu, J. A Fast Screening Method of Key Parameters from Coal for Carbon Emission Enterprises. Energies 2023, 16, 7592. https://doi.org/10.3390/en16227592
Lu W, Chen X, Song Z, Li Y, Lu J. A Fast Screening Method of Key Parameters from Coal for Carbon Emission Enterprises. Energies. 2023; 16(22):7592. https://doi.org/10.3390/en16227592
Chicago/Turabian StyleLu, Weiye, Xiaoxuan Chen, Zhuorui Song, Yuesheng Li, and Jidong Lu. 2023. "A Fast Screening Method of Key Parameters from Coal for Carbon Emission Enterprises" Energies 16, no. 22: 7592. https://doi.org/10.3390/en16227592
APA StyleLu, W., Chen, X., Song, Z., Li, Y., & Lu, J. (2023). A Fast Screening Method of Key Parameters from Coal for Carbon Emission Enterprises. Energies, 16(22), 7592. https://doi.org/10.3390/en16227592





