Leading-Edge Vortex Controller (LEVCON) Influence on the Aerodynamic Characteristics of a Modern Fighter Jet

Abstract

The purpose of this paper is to assess the influence of a novel type of vortex creation device called the leading-edge vortex controller (LEVCON) on the aerodynamic characteristics of a fighter jet. LEVCON has become a trending term in modern military aircraft in recent years and is a continuation of an existing and widely used aerodynamic solution called the leading-edge root extension (LERX). LEVCON is designed to operate on the same principles as LERX, but its aim is to generate lift-augmenting vortices, i.e., vortex lift, at higher angles of attack than LERX. To demonstrate the methodology, a custom delta wing fighter aircraft is introduced, and details about its aerodynamic configuration are provided. The LEVCON geometry is designed and then incorporated into an existing three-dimensional (3D) model of the aircraft in question. The research is conducted using OpenFOAM 8, a high-fidelity computational fluid dynamics (CFD) open-source software. The computational cases are designed to simulate the aircraft’s flight at stall velocities within a high range of angles of attack. The results are assessed and discussed in terms of aerodynamic characteristics. A conclusion is drawn from the analysis regarding the perceived improvements in fighter jet aerodynamics. The analysis reveals that both lift and critical angle of attack can be manipulated positively. With the addition of LEVCON, the average lift gain in the high angle of attack (α) range is between 8.5% and 10%, while the peak gain reaches 19.4%. The critical angle of attack has also increased by 2°, and a flatter stall characteristic has been achieved.

1. Introduction

Throughout the years, there have been many innovations and iterations of aerodynamic solutions or mechanisms integrated into aircraft wings [1]. The main purposes of these solutions are to control the boundary layer of air, modify the lift and drag forces generated by the wings, control the span-wise flow, or enhance the angle of attack capabilities of the aircraft [2,3,4,5,6,7]. Many of these mechanisms were either developed or improved thanks to advancements in organizations connected with military aviation, which is a key segment of aviation, due to the high focus on technological superiority and significant R&D financial outlays.

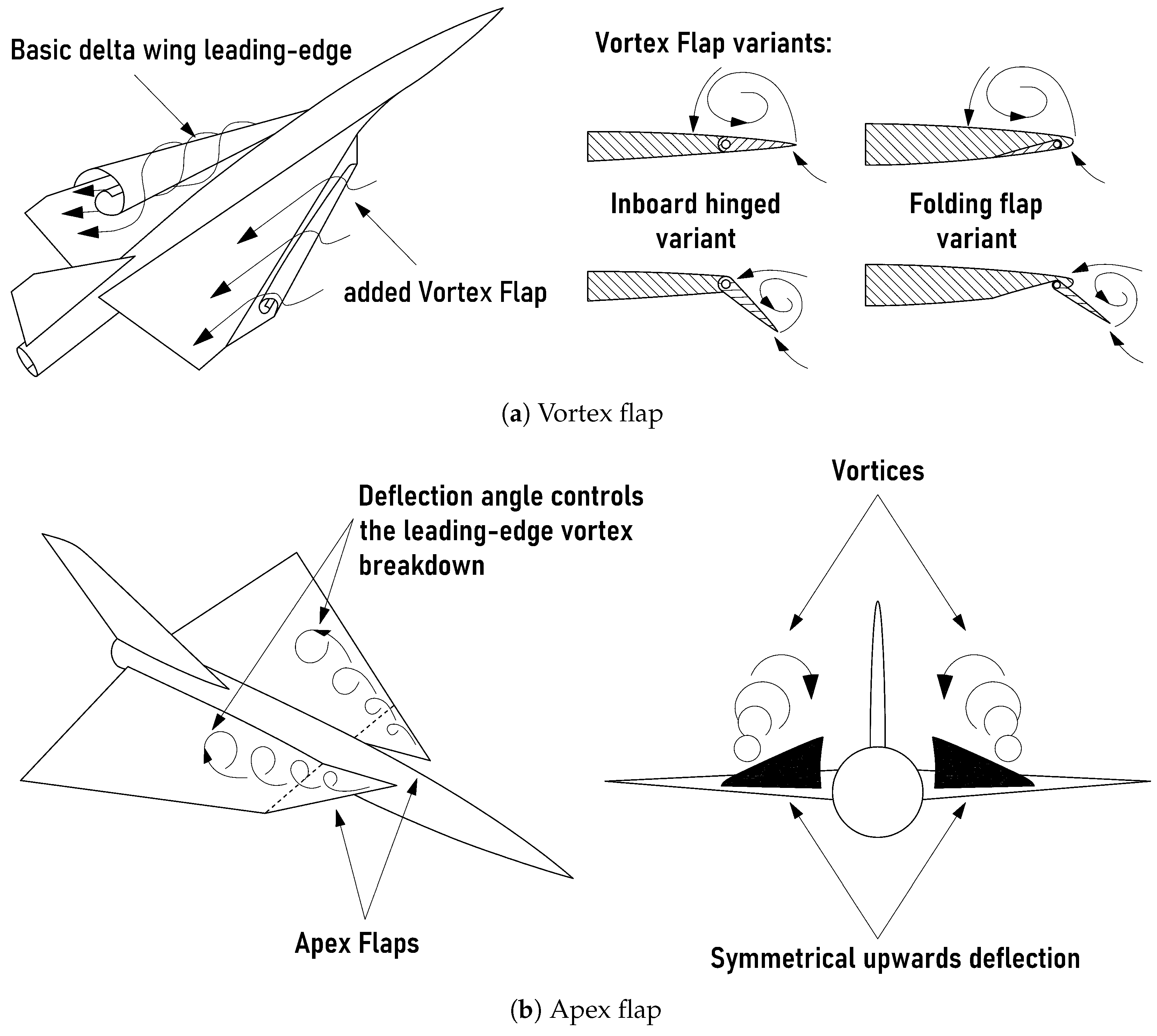
Amid actuated devices such as leading-edge flaps, trailing-edge flaps, or slats [8,9,10], a new type of device has been trending in recent years. This device is called the leading-edge vortex controller (LEVCON), and it is a continuation of an already existing and widely used aerodynamic solution called the leading-edge root extension (LERX). LEVCONs should not be confused with vortex flaps or apex flaps; their basic principles of operation are very similar, but the application and placement are different, as shown in Figure 1. The former are physically closer in resemblance to a conventional leading-edge flap, but instead of matching the upwash, they force separation on their upper surface to introduce a significant thrust component derived from vortex suction [11,12].

The latter devices typically compromise the apex portion of the delta wing, where they are hinged. Depending on the deflection direction (up or down), the apex flaps may produce positive or negative lift and pitching moment, and they are fully controllable regardless of the angle of attack [13].

In comparison, LEVCON is designed to operate similarly to LERX, with its aim being to generate lift-augmenting vortices, i.e., vortex lift, at high angles of attack. While LERX is a fixed aerodynamic component of the aircraft, LEVCONs are actuated devices, which improve their performance in areas beyond high-angle-of-attack scenarios [14]. A major difference between LEVCONs and vortex or apex flaps is that they can also be used for trimming and optimizing the lift-to-drag ratio in stable flight or for recovering the aircraft in post-stall scenarios. They can be deflected symmetrically and, similar to control surfaces such as ailerons or canards, asymmetrically for directional control [15]. Direct and concise conclusions about leading-edge vortex controllers have not yet been drawn in public research. In fact, this aerodynamic solution might have more significance in classified research, as it is currently implemented in only one operational aircraft type: the Russian Sukhoi Su-57. The second instance of usage is in the navy version of the Indian LCA Tejas, but this aircraft has not progressed beyond the prototype phase due to unsatisfactory carrier-based capabilities [16].

LEVCONs provide various improvements to delta wing aircraft due to the portion of lift, called vortex lift, that these wings produce. The origins of vortex lift can be traced back to low aspect ratio (AR) wings, which experience complex vortex flows that often lead to separation at the trailing edge. These types of wings exhibit a high angle of attack at maximum lift, a shallow lift curve slope, and reduced longitudinal stability as the angle of attack and sweep angles increase. Increased sweep concentrates the wing load further outboard, potentially causing tip stall. Another crucial aspect is the design of the leading edge, particularly for sweptback wings. Sharp leading edges induce premature flow separation, similar to what occurs with delta wings, even at low angle of attack [17,18].

In the 1930s, jet propulsion advantages were acknowledged [19], but high-speed wing design progress was somewhat behind. In 1935, Winter [20] conducted pioneering research on the topic of side-edge vortex, which introduced fundamental properties of what we now recognize as a separation-induced side-edge vortex [18]. During the 1940s, scientists conducted experiments on swept and unswept wings with AR = 1–5. The results revealed that maximum lift is relatively unaffected by AR > 2 and that the angle of attack, at which lift is achieved, remains almost constant. For smaller AR, the angle at which maximum lift occurs increases, reaching up to 30 degrees. In cases with AR < 1, studies indicate that the lift coefficients are significantly larger than those that can be predicted by linear wing theory. This increase in lift is attributed to strong interactions between tip vortices, causing the center of the wake to be pushed downward [17,21]. In that same time period, Lippisch designed a set of five tailless delta wing aircraft, which featured swept and tapered wings, along with thick airfoil sections [22]. The understanding of the advantages of wing sweep remained largely unknown until theoretical analysis was conducted by Jones [23] in 1945, whose work demonstrated the benefits of sweeping the wing behind the Mach cone for supersonic flight, shedding light on the advantages of sweep for subsonic speeds as well. Around the same time period, an unconventional full-scale delta wing configuration, known as DM-1, had been uncovered. During the experimental phase, a serious modification in the form of a sharp leading-edge strip was incorporated into the DM-1. Subsequent tests demonstrated substantial increases in lift, compared to the clean configuration, owing to the formation of leading-edge vortices over the wing. These lift increments have been attributed to the presence of the leading-edge vortices, which showed resemblances with the side-edge vortex flows documented earlier by Winter [20]. The obtained results clearly established the link between high angle of attack lift increments and leading-edge vortex flows [19,24]. The modified DM-1 marked the pioneering instance of an aircraft concept displaying leading-edge vortex flows, which became subjects of experimental study in the development of the new generation of slender-wing aircraft.

Experiments conducted on wings with high sweep angles have revealed that the root sections of the wing are not subject to significant peaks in pressure at the leading edge. Additionally, the pressure differences along the spanwise direction cause the boundary layer to move outward from these root sections. These two factors enhance the resistance of the root sections against flow separation, allowing them to generate lift coefficients that exceed the losses experienced when the wing’s tip sections stall. As a result, the wing’s root sections experience stalling at significantly higher angles, whereas the wingtip stalls at much lower angles. As the wing becomes thinner, the angle of attack at which vortex flow becomes observable decreases [17,25]. A major obstacle faced by delta wing aircraft was the significant reduction in the low-speed lift curve slope due to the effects of aspect ratio (AR), which necessitates significantly higher speeds and angles of attack for take-off and landing performance. The discovery of leading-edge vortex flows played a crucial role in resolving this issue [18,26,27]. This breakthrough led to the creation of the first jet-powered delta wing aircraft, the XF-92A. The leading-edge vortex flows discovered in this aircraft enhanced its low-speed, high angle-of-attack flight capabilities. Polhamus [28] summarized various advantages associated with leading-edge vortex flows. Initially, experimentation played a crucial role in the development of aerodynamic configurations, expanding to predict vortex flow aerodynamics. However, existing theories could not predict the intricate details of high angle-of-attack vortex flow aerodynamics. This challenge led to the evolution of theoretical methods, focusing on physics-based modeling of the leading-edge vortices near the lifting wing. These methods began with simplified models and gradually incorporated more intricate physics related to the vortex flows. Eventually, this approach shifted from modeling to capturing the vortices using computational fluid dynamics (CFD) [18].

In summary, vortex lift results from the action of leading-edge vortices and is generated by highly sweptback sharp leading edges or highly swept leading-edge root extensions added to wings with moderate sweep (Figure 2). Vortices generated by the swept wing leading edge are then captured under the airflow and remain trapped over the wing’s upper surface. This results in a negative pressure field over the wing’s top surface. The air flowing over the confined vortex is then pulled downwards, generating lift. Vortex lift generally increases with the angle of attack, but it also has its limits when the vortex bursts. One significant drawback is the increase in the drag component, resulting from the loss of suction behavior around the wing leading edge [29,30].

In addition to enhancing high-alpha capabilities, such as enabling flight at higher angles of attack and reducing stall speed, LEVCONs may also offer an improved lift-to-drag ratio across a broader range of attack angles [15], higher sustained turn rates [14], and enhanced directional controllability [31]. The potential applications of the leading-edge vortex controller are extensive, and it holds promise for providing various benefits to future fighter aircraft [32]. Researchers have already begun incorporating this device into the aircraft models they study [33,34,35]. CFD plays a pivotal role in such studies, given its advantages of lower research costs, time efficiency, and simplification of the prototype phase prior to wind tunnel testing [36,37].

The literature review presented above clearly indicates a lack of comprehensive studies related to vortex lift-augmenting devices that can be implemented in real-life aircraft. Neither vortex flaps nor apex flaps have progressed beyond the research and experimental phases. LEVCONs have already been introduced in two different types of airframes: tail and tailless delta wing combat aircraft. Apart from military aviation, this solution can also be applied to supersonic airliners, given the highly swept delta wings used in this type of aircraft, especially during take-off and landing scenarios.

The present study aims to fill this gap through state-of-the-art numerical modeling. This method allows us to quickly assess the benefits of this actuated device. Choosing CFD was evident since we were working with custom computer-aided design (CAD) three-dimensional (3D) models. The geometries could be directly prepared for numerical simulations with only minor changes made during the pre-processing phase. Such swift action is not possible with experimental studies, which require carefully prepared 3D-printed models and a wind tunnel capable of handling high Reynolds number flows.

In the current study, the following topics/issues have been investigated:

-

pre-processing of highly complex geometries for CFD study,

-

computational domain dimensions and boundary conditions for external flows around symmetrical aircraft,

-

mesh independence study,

-

aerodynamic characteristics without LEVCON,

-

aerodynamic characteristics with LEVCON deflected downwards at 10, 20, and 30 degrees in relation to the airframe, and at the optimal deflection angle in relation to the angle of attack,

-

vortex flow visualizations around aircraft with and without LEVCON.

The obtained results have provided new insights into the flow dynamics of vortex lift-augmenting actuated devices. These insights may enhance not only the maneuverability but also the take-off and landing capabilities of modern fighter aircraft and any high-velocity aircraft with highly swept delta wings. The CFD results not only demonstrate that further investigation of this topic is worthwhile but also highlight the substantial amount of time required to optimize such complex geometries in order to provide improved flight characteristics across a broad range of the flight envelope.

2. Materials and Methods

2.1. Mathematical Model

In this work, the flow was modeled by solving steady-state and incompressible Navier–Stokes equations:

$$\left(\mathbf{u}·\nabla \right)\mathbf{u}=-\nabla \left(p/\rho \right)+\nu {\nabla }^2\mathbf{u}$$

(1)

and the continuity equation given by:

$$\nabla ·\mathbf{u}=0$$

(2)

where $\mathbf{u}$ = $(u_x,u_y,u_z)$ is the fluid velocity vector, $\rho$ is the fluid density, p is pressure, and $\nu$ is the kinematic viscosity. The gravity term is not present in Equation (1) to avoid interference with the streaming flow. It is generally accepted that at Mach numbers much less than 1.0 (Ma < 0.3), the effect of air compressibility can be omitted, and the variations in gas density resulting from pressure waves may be safely ignored in the process of flow modeling [38]. Equations (1) and (2) were discretized using the finite volume method (FVM) approach and numerically solved using OpenFOAM, an open-source C++ toolbox primarily used for developing custom numerical solvers, as well as pre-processing and post-processing utilities that solve problems of continuum mechanics [39,40,41].

The simulations conducted in this study utilized the semi-implicit method for pressure linked equations (SIMPLE) solver algorithm [42,43,44] and the k-$\omega$ shear stress transport (SST) turbulence model, which is widely accepted as an industry standard. This turbulence model offers better predictions of flow separation compared to most Reynolds-averaged Navier–Stokes (RANS) models and demonstrates satisfactory behavior in adverse pressure gradient scenarios [45]. Moreover, it provides more accurate predictions of the creation, trajectory, and breakdown of edge-augmented vortices [46], making it the preferred choice for external aerodynamics simulations where separation is important [47,48]. The k-$\omega$ SST model is a hybrid model that combines the advantages of both the Wilcox k-$\omega$ model and the k-$ϵ$ model, using a blending function. One drawback of the k-$\omega$ model is its sensitivity to the freestream values of k, $\omega$, and $ϵ$. In contrast, the k-$ϵ$ model is more robust in this aspect. Hence, by using a blending function, it is possible to switch from the k-$ϵ$ model away from the wall to the k-$\omega$ model when close to the wall. The conservation form of the k-$\omega$ SST model is given by [49]:

$$\begin{array}{c}\frac{\partial \left(\rho k\right)}{\partial t}+\frac{\partial \left(\rho u_{j}k\right)}{\partial x_j}=P-{\beta }^{*}\rho \omega k+\frac{\partial }{\partial x_j}\left[(\mu +{\sigma }_k{\mu }_t)\frac{\partial k}{\partial x_j}\right]\end{array}$$

(3)

$$\begin{array}{c}\frac{\partial \left(\rho \omega \right)}{\partial t}+\frac{\partial \left(\rho u_j\omega \right)}{\partial x_j}=\frac{\gamma }{{\nu }_t}P-\beta \rho {\omega }^2+\frac{\partial }{\partial x_j}\left[(\mu +{\sigma }_{\omega }{\mu }_t)\frac{\partial \omega }{\partial x_j}\right]+2(1-F_1)\frac{\rho {\sigma }_{\omega 2}}{\omega }\frac{\partial k}{\partial x_j}\frac{\partial \omega }{\partial x_j}\end{array}$$

(4)

In the OpenFOAM user guide, the turbulence specific dissipation rate $\omega$ and the turbulence kinetic energy k are given by [50]:

$$\begin{array}{c}\frac{D}{Dt}\left(\rho \omega \right)=\nabla ·(\rho D_{\omega }\nabla \omega )+\frac{\rho \gamma G}{\nu }-\frac{2}{3}\rho \gamma \omega (\nabla ·u)-\rho \beta {\omega }^2-\rho (F_1-1)C{D}_{k\omega }+S_{\omega }\end{array}$$

(5)

$$\begin{array}{c}\frac{D}{Dt}\left(\rho k\right)=\nabla ·(\rho D_k\nabla k)+\rho G-\frac{2}{3}\rho k(\nabla ·u)-\rho {\beta }^{*}\omega k+S_k\end{array}$$

(6)

2.1.1. Aerodynamic Coefficients

Lift, drag, and momentum coefficients were defined as follows:

$$\begin{array}{c}{C}_L=\frac{F_L}{A_{ref}·p_d}\end{array}$$

(7)

$$\begin{array}{c}{C}_D=\frac{F_D}{A_{ref}·p_d}\end{array}$$

(8)

$$\begin{array}{c}{C}_M=\frac{M}{A_{ref}·l_{ref}·p_d}\end{array}$$

(9)

$$\begin{array}{c}{p}_d=\frac{{\rho }_{ref}·{U_{mag}}^2}{2}\end{array}$$

(10)

where $F_L$ and $F_D$ are forces perpendicular and parallel to the direction of the flow, M is the moment acting around the axis of rotation, $A_{ref}$ corresponds to total wing surface area and $l_{ref}$ in this case is the length of the airplane. Dynamic pressure $p_d$ is defined by the reference density ${\rho }_{ref}$ and the velocity magnitude $U_{mag}$. For incompressible cases, Equations (7)–(9) are solved using the kinematic pressure $p_k=p_d/\rho$ [51].

2.1.2. Mathematical Model Validation

In order to develop a reliable mathematical model, validation is necessary. For this purpose, a verification of the NACA 0012 airfoil was conducted. The NACA 0012 is a symmetrical airfoil with a maximum thickness of 12% of the chord length, located at 30% of the chord. The cross-section of this airfoil is illustrated in Figure 3, and the formulation describing this geometry is provided by Equation (11):

$$y=+-0.6\left[0.2969\sqrt{x}-0.1260x-0.3516x^2+0.2843x^3-0.1015x^4\right]$$

(11)

Specific information about the validation case can be found on the NASA website [52] and the OpenFOAM website [53]. The computational model, prepared according to the provided guidelines, should yield results very close to the experimental data. The only modification made to this validation was changing the turbulence model from Spalart–Allmaras to $k-\omega$ SST. To minimize mesh dependency in the results, a converted FAMILY II (2-D) 897 x 257 NASA mesh was used [54]. A graphical representation of the grid can be seen in Figure 4.

Validation cases simulated external flow around the two-dimensional (2D) airfoil geometry in steady state. The data on flow characteristics can be found in

Table 1. Flow characteristics of NACA 0012 validation case study.

Label	Quantity
Type	External 2D steady-state aerodynamics
Fluid	Newtonian, single-phase, incompressible
Material	Air at T = 20 °C
Reynolds number	Re = 6,000,000
Mach number	Ma = 0.15
Speed of sound	a = 343.21 $\frac{\mathrm{m}}{\mathrm{s}}$
Streamwise far-field flow speed	u = 51.4815 $\frac{\mathrm{m}}{\mathrm{s}}$
Characteristic length (airfoil chord)	c = 1 $\mathrm{m}$
Kinematic viscosity of fluid	$\nu$ = $8.58\times {10}^{-6}$ $\frac{{\mathrm{m}}^2}{\mathrm{s}}$

.

To implement the $k-\omega$ SST model, two approaches can be utilized. The low-Re turbulence model (no wall functions) is appropriate for meshes with a dimensionless wall distance of $y^{+}\approx 1$, while the high-Re model (wall functions) is mostly suitable for meshes with $y^{+}>30$. In OpenFOAM, certain wall functions are compatible with both $y^{+}$ regions. The NASA grid is reported to have $y^{+}<1$, indicating that boundary conditions (BC) for the low-Re model should be implemented. However, both approaches will still be compared. For the inlet and outlet, the freestream BC is recommended, which has two different possibilities. When the flow at the boundary is leaving the domain, a zero-gradient condition is applied. Otherwise, a fixed velocity is assigned, and the flow direction is based on the input values. The BC for the NACA 0012 validation can be found in

Table 2. Validation study boundary conditions for velocity and pressure.

BC/Field	u, $\frac{\mathbf{m}}{\mathbf{s}}$	p, $\frac{{\mathbf{m}}^2}{{\mathbf{s}}^2}$
Inlet/outlet	$\frac{\partial \mathbf{u}}{\partial n}=0$ and $\mathbf{u}=(u_x,u_y)$	$\frac{\partial p}{\partial n}=0$ and $p=0$
Left/right	empty	empty
Airfoil	$\mathbf{u}=0$	$\frac{\partial p}{\partial n}=0$

and

Table 3. Validation study boundary conditions for k, $\omega$, and ${\nu }_t$.

BC/Field	k, $\frac{{\mathbf{m}}^2}{{\mathbf{s}}^2}$	$\mathbf{\omega },$ $\frac{1}{\mathbf{s}}$	${\mathit{\nu }}_{\mathit{t}},$ $\frac{{\mathbf{m}}^2}{\mathbf{s}}$
Inlet/outlet	$\frac{\partial k}{\partial n}=0$ and $k=0.0011$	$\frac{\partial \omega }{\partial n}=0$ and $\omega =96.4$	solved by k-$\omega$ model
Left/right	empty	empty	empty
Airfoil	$k_{{}_{wall}}=0$	${\omega }_{{}_{wall}}=7·{10}^{11}$	${\nu }_{t_{wall}}=0$

.

The velocity components $u_x$, $u_y$ are calculated from the velocity magnitude u and angle of attack $\alpha$. Equations for k, $\omega$, and ${\omega }_{{}_{wall}}$ are taken from the OpenFOAM user guide [50] and are presented below:

$$\begin{array}{c}(u_x,u_y)=(\mathbf{u}cos\alpha ,\mathbf{u}sin\alpha )\end{array}$$

(12)

$$\begin{array}{c}k=\frac{3}{2}{\left(\mathbf{u}I\right)}^2\end{array}$$

(13)

$$\begin{array}{c}\omega =\frac{k^{0.5}}{C_{\mu }^{0.25}·L}\end{array}$$

(14)

$$\begin{array}{c}{\omega }_{{}_{wall}}=\frac{6\nu }{{\beta }_1{y}^2}\end{array}$$

(15)

where I is the turbulence intensity, u is the velocity magnitude inside the domain, $C_{\mu }$ is a constant of 0.09, L is the reference length scale, $\nu$ is the kinematic viscosity, ${\beta }_1$ is a constant of 0.075, and y is the wall normal distance. The convergence criterion utilized residual control for velocities $u_x|u_y\le 1\times {10}^{-8}$, kinematic pressure $p\le 1\times {10}^{-8}$, turbulent kinetic energy and specific dissipation rate $k|omega\le 1\times {10}^{-8}$, or total iterations of n = 100,000.

Drag coefficient values calculated with RANS models are usually higher than the values measured in wind tunnels because these models assume a turbulent boundary layer over the entire airfoil surface. However, in reality, the boundary layer starts as laminar in the front portion of the airfoil and then becomes turbulent. Since skin friction in a laminar boundary layer is lower than in a turbulent one, drag values measured in wind tunnels are typically lower than those from CFD simulations. To address this difference, a trip wire is attached to the leading edge of the airfoil, making the boundary layer turbulent from the leading edge. Experiments conducted in this manner provide better matching results with numerical simulations [55]. Therefore, numerical results were compared with Ladson’s experimental tripped data [56], and both sets of data are presented in

Table 4. Validation study results.

	k-$\mathit{\omega }$ SST High-Re WF		k-$\mathit{\omega }$ SST No WF		Ladson Tripped Data
$\mathit{\alpha }$, °	${\mathbf{C}}_{\mathbf{L}}$	${\mathbf{C}}_{\mathbf{D}}$	${\mathbf{C}}_{\mathbf{L}}$	${\mathbf{C}}_{\mathbf{D}}$	${\mathbf{C}}_{\mathbf{L}}$	${\mathbf{C}}_{\mathbf{D}}$
0.04	0.0044	0.00808	0.0044	0.00802	−0.0013	0.00811
4.06	0.4451	0.00861	0.4454	0.00854	0.4365	0.00814
10.18	1.0849	0.01239	1.0862	0.01225	1.0809	0.01165
15.24	1.5113	0.02206	1.5171	0.02157	1.5169	0.01870
16.33	1.5703	0.02633	1.5786	0.02562	1.5855	0.02186
17.13	1.5983	0.03074	1.6095	0.02975	1.6219	0.02513
18.21	1.6021	0.04007	1.6201	0.03831	1.0104	0.25899
19.27	1.5311	0.05813	1.5650	0.05430	1.0664	0.43446

.

Compared to Ladson’s data, OpenFOAM demonstrates high fidelity within $\alpha$ = 0–17°, albeit with a slight tendency to overpredict the stall by approximately $1$°. Minor deviations in the results might be attributed to the use of a medium-quality Family II grid in this validation case [54]. In the experimental data, the high values of drag coefficients in the upper $\alpha$ range can be attributed to the complexity of achieving 2D experiments. NASA acknowledges that near stall, experiments are significantly far from being 2D, leading to the presence of high drag values [52]. The comparison between CFD results and experimental data is shown in Figure 5.

2.2. Geometry for the CFD Case Study

The numerical simulations utilized a custom geometry of a fighter aircraft, which was developed through a comparative analysis of selected 4.5 and 5th generation fighter jets. As part of this analysis, the purposes of the aircraft, their dimensions, weights, and flight parameters were compared. The collected information contributed to the development of design assumptions for the custom aircraft. One of the final outcomes of this work was the creation of a three-dimensional (3D) model of an unmanned fighter aircraft named CFA Phantom. The most important requirements for the aircraft included high maneuverability and a small radar cross-section (RCS). All of this work was conducted within the BSc thesis of one of the authors [57]. The comparison involved aircraft such as the Dassault Rafale made by Dassault Aviation from Paris, France, Eurofighter Typhoon made by Eurofighter Jagdflugzeug GmbH, Hallbergmoos, Germany, which is a consortium based in Europe, Chengdu J-20 made by Chengdu Aircraft Industry Group from Chengdu, China, Sukhoi Su-57 made by Sukhoi Company from Moscow, Russia, and Lockheed Martin F-22 Raptor made by Lockheed Martin Aeronautics from Fort Worth, TX, USA. Detailed information on the aerodynamic configuration can be found in

Table 5. Aerodynamic configuration of the fighter jet 3D model [57].

Label	Quantity
Tailplane configuration	Conventional
Wing airfoil	NACA 64-206
Stabilizers airfoil	NACA 16-006
Wing planform	Cropped delta
Possible control surfaces	Ailerons, flaperons
Possible high-lift devices	LE flaps
Possible vortex devices	LERX, LEVCONs
Thrust vector control	Three-dimensional
Horizontal stabilizer	Stabilators
Vertical stabilizer	All-moving rudders
LERX LE sweep angle	64°
Delta LE sweep angle	42°
Delta wing sweep angle	30°
Delta TE crop angle	42°
Delta TE sweep angle	17°
Delta wing twist angle	−7°
Wing anhedral angle	−3°
Wing incidence angle	1°
Wingspan	13.8 m
Wing area	82.15 ${\mathrm{m}}^2$
Wing aspect ratio	2.32
Mean aerodynamic chord	7.69 m
Airplane length	20.28 m
Airplane height	2.92 m

.

Geometrical characteristics of utilized airfoils are listed in

Table 6. Basic geometrical characteristics of used airfoils.

Airfoil	Max Thickness	Max Camber	Modifications
NACA 64-206	6% at 40% chord	1.1% at 50% chord	LE & TE round-off
NACA 16-006	6% at 50% chord	symmetric	LE & TE round-off

. Original cross-sections are presented in Figure 6. Wing and stabilator edges were slightly modified by introducing fillets in order to ensure appropriate mesh generation without collapsing layers. Rendered images of a 3D model in clean configuration are presented in Figure 7.

The designed aircraft had a conventional tailplane configuration, because it provides a lower RCS than a canard layout. Given the high emphasis on stealth in 5th generation fighter aircraft, the preliminary design stage utilized two fundamental design principles for the entire structure: platform alignment for both the wing and the tail, and continuous curvature for the entire body. The fuselage was designed as a lifting blended body, equipped with stabilators and all-moving rudders.

The 3D model of the aircraft was also prepared to incorporate high-lift and vortex devices, enhancing its aerodynamic capabilities. Leading-edge root extensions (LERX) were already integrated into the airframe prior to this study. While significant improvements can be gained by incorporating leading-edge flaps and flaperons on the trailing edge, this study focuses solely on the differences in aerodynamic coefficients and characteristics between an aircraft with just leading-edge root extensions and the same aircraft equipped with leading-edge vortex controllers. For the CFD simulations, the 3D model was stripped of all external avionics, such as infrared search and track (IRST) and missile approach warning system (MAWS) sensors. The air intakes and afterburners were sealed off, as the influence of the turbofan engine is not considered in our external aerodynamics simulations. Additionally, sharp edges were treated with small fillets to ensure 100% layer coverage around the entire body. The final silhouette of the aircraft, obtained during the pre-processing phase before the CFD simulations, is shown in Figure 8.

2.2.1. Computational Domain Sizing

The sizing of the computational domain must be carefully conducted to ensure that the boundary conditions do not inadvertently affect the simulation results. In aerospace external aerodynamics, the downstream length is of great importance because to obtain valid results, the wake flow must be fully captured. For example, if a zero gradient boundary condition is applied at the outlet, it should be positioned far enough from the re-circulation zone. Computational domain dimensions are typically determined based on the dimensions of the studied object. For airfoils and wings, this is usually the mean aerodynamic chord (MAC), while for an entire aircraft, it is typically the maximum length of the entire model. The exact size of the computational domain needed to accurately capture the physics varies depending on the problem and can only be determined by an experienced aerodynamics engineer. Nevertheless, there are general guidelines for determining the dimensions. For 3D simulations of an aircraft, it is recommended that the domain length be at least 25 times the length of the aircraft. It is also advisable to place the outlet boundary condition significantly farther than just 10 reference lengths behind the object. When dealing with 3D simulations around the aircraft, some sources recommend extending the domain dimensions to around 25–50 times the maximum reference lengths. Apart from these requirements, feasibility and available computing power also need to be considered.

In this study, geometries were meshed using snappyHexMesh, a high-quality mesh utility provided with OpenFOAM. This tool generates 3D hex-dominant meshes from triangulated surface geometries in stereolithography (STL) format and inserts layers in the final phase of the meshing process. To validate the results, a mesh independence study was conducted involving a set of meshes. This study established the comparative baseline for the aerodynamic characteristics of the fighter jet without vortex controllers. Three grids were created: the coarse and medium grids shared the same domain components, while the fine grid had a larger cone-shaped slip-stream domain towards the outlet boundary condition (BC), as shown in Figure 9. Due to the symmetrical geometry, only half of the domain was meshed.

The airplane’s length is denoted as $\mathit{c}$ and is provided in Table 5. The overall size of the domain is as follows: 10c in the front, side, top, and bottom of the model, and 20c behind the model. This results in dimensions of 30c along the x-axis, $\mathit{20}\mathit{c}$ along the y-axis, and only 10c along the z-axis, as only half of the plane was meshed due to symmetry boundary condition. The center point of the mesh, $(x,y,z)=(0,0,0)$, represents the estimated aerodynamic center. The rotating cell-zone had a diameter of 1.5c to accommodate cell refinement zones around the aircraft and ensure proper layer inflation without distorted cells. The diameter of the slipstream domain was specified as 2.25c for the coarse and medium meshes, and for the fine mesh, it expands to 5c towards the outlet BC. Slipstream diameter values were chosen after investigating the outflow profile in the testing phase. The cone shape was designed for very high angles of attack scenarios of $\alpha >60°$, although it was not extensively utilized due to stall occurring much earlier. We satisfied the overall guideline of around 25–50 maximum reference lengths along the x-axis. However, smaller lengths were chosen for the y and z axes because the inflow direction does not change between the cases, i.e., the angle of attack is obtained by rotating the inner cell-zone housing the airplane model. This means that the overall flow predominantly follows the x-axis direction until it reaches the airplane model. The lengths in the y and z directions were chosen to account for flow deflection and turbulent behavior introduced by the aircraft. The elliptical shape of the domain and the cylindrical shape of the slipstream domain proved to be sufficient in capturing the downstream pattern, even at high $\alpha$.

Figure 10 illustrates the cell levels of all three grids. Each cell level step had a blending function of 3 cells in between the cell levels. In the arbitrary mesh interface (AMI) region, the coarse mesh had one refinement function of level 4 at a distance of 2 m from the fighter jet geometry. The medium and fine meshes had two refinement functions of levels 4 and 5 at distances of 2 m and 1 m, respectively. The model of the fighter jet was represented with a surface refinement cell level of 8, which corresponds to a cell edge length of 0.00625 m.

Due to substantial Reynolds number (Re = $9.25\times {10}^7$), all of the meshes incorporated the high-Re log-law approach with dynamic wall treatment and dimensionless wall distance ($y^{+}$) of around 50 at the wall. This approach was unavoidable due to surface refinement and the layers aspect ratio demand loop, i.e., to obtain flawless inflation of good quality layers, the surface refinement also has to be improved in order to avoid layer cells with critically high aspect ratios. In a steady-state solver, high aspect ratio cells can affect the coefficients in the pressure correction equation and make it more difficult to solve, because corrections to the pressure in adjacent cells will have less of an effect on each other, when the flow information is being transported across that smaller area and the larger distance between the cell centroids [58]. In addition, more refinement zones need to be added for a fluent step-up in cell levels.

While meshes in this study required 42–82 million cells, meshes with a $y^{+}$ of around 1 would require over 500 million cells with a minimal number of layers and refinement regions. In order to fully resolve the boundary layer, the memory requirements to create meshes are exponentially higher, which leads to the fact that this case study would demand robust high-performance computing (HPC) platforms with terabytes of RAM memory and even then, the computation times would be far greater than what was achieved here. This approach was out of reach, which is why the log-law approach was implemented.

In this study, multiple consumer platforms were utilized. The computation time for a single mesh ranged from 72 h on stronger platforms to up to 144 h on weaker platforms. With 90 meshes, the computations took more than a year of pure computation time. However, due to the workload being evenly distributed among the machines and the use of automated bash scripts, the computations were carried out in an overall time frame of 7 months. Data regarding the platforms used are presented in

Table 7. Specifications of utilized computing platforms.

CPU	Cores/Threads	Memory, GB
Ryzen 7 3700X	8/16	64
Ryzen 9 3900X	12/24	64
Ryzen 7 5950X	16/32	128
Ryzen 7 5950X	16/32	128
Xeon E5-2630 v4 ($\times 2$)	20/40	128
Ryzen Threadripper 2970WX	24/48	128

. Specific data on grid quality can be found in

Table 8. Specific data on mesh independence study grids quality.

Group	Parameter	Coarse	Medium	Fine
Layer specification	Number of layers	n = 5	n = 10	n = 15
	Expansion ratio	$\Delta$y = 1.3	$\Delta$y = 1.2	$\Delta$y = 1.1
	First layer thickness	y = $6.06\times {10}^{-4}$ m	y = $6.06\times {10}^{-4}$ m	y = $5.92\times {10}^{-4}$ m
	Overall thickness	$y_t$ = $5.48\times {10}^{-3}$ m	$y_t$ = $1.57\times {10}^{-2}$ m	$y_t$ = $1.88\times {10}^{-2}$ m
No. cells	Domain	11,317,113	11,317,113	19,835,301
	AMI	30,955,332	47,177,472	62,452,932
	Total	42,272,445	58,494,585	82,288,233

.

2.2.2. Leading-Edge Vortex Controller Sizing

Countless variations in the size and shape of LEVCON are possible, with two main measurable quantities being the leading-edge sweep angle and the surface area. Sharper sweep angles ($\Lambda >70°$) are expected to produce more energized vortices, and a larger surface area should contribute more to higher lift force generation. The maximum LEVCON deflection angle is unknown at this stage, as it would primarily be limited by design and constructional constraints. This means that each geometrical variation, including not only the shape but also different deflection angles, demands a separate mesh. If deflection angles of $\Lambda =(10,20,30)°$ are considered, this translates to 3 meshes for each angle of attack. In other words, when angles of attack of $\alpha =(0,10,20,30,40)°$ are considered, 15 separate meshes need to be calculated. This places significant demands on computational power, which is why this study focuses on only one LEVCON shape variation, which will be tested with multiple deflection angles. Developing an optimal geometry would require its own optimization study, which would be computationally intensive and time-consuming. Other methods, such as using a neural network approach, could be considered. The dimensions of the LEVCON geometry are presented in Figure 11. The device has a leading-edge (LE) sweep angle of exactly $\Lambda =70°$ and a surface area of $S=1.32$ ${\mathrm{m}}^2$.

2.3. Flow Characteristics, Configurations, and Boundary Conditions

Numerical cases simulated external flow around the aircraft geometry in steady state. The flow is subsonic with low Mach number and represents high Reynolds values. The material is air at international standard atmospheric conditions at 15 °C. The material is single-phase, non-reacting, and incompressible Newtonian fluid. The data on flow characteristics can be found in

Table 9. Flow characteristics.

Label	Quantity
Type	External steady-state aerodynamics
Fluid	Newtonian, single-phase, incompressible
Material	Air-ISA at 15 °C
Reynolds number	Re = 92,500,000
Mach number	Ma = 0.2
Speed of sound	a = 340.3 $\frac{\mathrm{m}}{\mathrm{s}}$
Streamwise far-field flow speed	U = 66.6 $\frac{\mathrm{m}}{\mathrm{s}}$
Characteristic length (airplane length)	c = 20.28 $\mathrm{m}$
Kinematic viscosity of fluid	$\nu$ = $1.461\times {10}^{-5}$ $\frac{{\mathrm{m}}^2}{\mathrm{s}}$

.

All of the considered $\alpha$ configurations are presented in

Table 10. Considered configurations at $\alpha$ = 0–40$°$.

$\mathit{\alpha },$$°$	Visual Representation	$\mathit{\alpha },$$°$	Visual Representation
0		4
5		6
10		15
20		25
30		31
32		33
34		35
40

. Each case was calculated separately for an airplane with LERX and LEVCON deflected at $\Lambda =(10,20,30)°$. There were exactly 60 configurations and 90 separate meshes calculated in this study. The mesh independence study consisted of 45 meshes, 15 meshes per each grid quality. LEVCON variations consisted of another 45 meshes, 15 meshes per deflection.

To implement the $k-\omega$ SST model in this case, the high-Re model approach has to be utilized, which is suitable for meshes with $y^{+}>30$. At the wall, the boundary conditions for this approach can be as follows:

• $k=$ kqRWallFunction or zeroGradient,
• $\omega =$ omegaWallFunction,
• ${\nu }_t=$ nutkWallFunction or nutUSpaldingWallFunction, etc.

For external flows in general, a low turbulence intensity value should be selected. Good quality wind tunnels can produce values as low as 0.05%. For this case, scenario $I=0.1\%$ was selected to initialize the simulation [59]. The eddy viscosity ratio for external flows should be in the range of 0.2–1.3, and the value of ${\mu }_t/\mu =1.3$ was selected.

Initialization values for k and $\omega$ were calculated by using Equations (13)–(15) [50]. The boundary conditions for all of the simulations can be found in

Table 11. Boundary conditions for velocity and pressure.

BC/Field	u, $\frac{\mathbf{m}}{\mathbf{s}}$	p, $\frac{{\mathbf{m}}^2}{{\mathbf{s}}^2}$
Inlet	$u_x=66.6$	$\frac{\partial p}{\partial n}=0$
Outlet	$\frac{\partial \mathbf{u}}{\partial n}=0$ and $u_x=66.6$	$p=0$
Left	symmetry	symmetry
AMI domain	cyclic	cyclic
AMI jet	cyclic	cyclic
Fighter jet	$\mathbf{u}=0$	$\frac{\partial p}{\partial n}=0$

and

Table 12. Boundary conditions for turbulent kinetic energy, dissipation ratio, and kinematic viscosity.

BC/Field	k, $\frac{{\mathbf{m}}^2}{{\mathbf{s}}^2}$	$\mathbf{\omega },$ $\frac{1}{\mathbf{s}}$	${\mathit{\nu }}_{\mathit{t}},$ $\frac{{\mathbf{m}}^2}{\mathbf{s}}$
Inlet	$k=0.067$	$\omega =351$	solved by k-$\omega$ model
Outlet	$\frac{\partial k}{\partial n}=0$ and $k=0.067$	$\frac{\partial \omega }{\partial n}=0$ and $\omega =351$	solved by k-$\omega$ model
Left	symmetry	symmetry	symmetry
AMI domain	cyclic	cyclic	cyclic
AMI jet	cyclic	cyclic	cyclic
Fighter jet	$k_{{}_{wall}}$ function	${\omega }_{{}_{wall}}$ function	${\nu }_{t_{wall}}$ function

.

The convergence criterion utilized residual control for velocities $u_x\left|u_y\right|u_z\le 1\times {10}^{-8}$, kinematic pressure $p\le 1\times {10}^{-6}$, and turbulent kinetic energy and specific dissipation rate $k|omega\le 1\times {10}^{-6}$. This means that simulations automatically stopped when all residuals reached the specified threshold. If these criteria were not satisfied, a backup convergence criterion was set at a total number of iterations $n=4000$. Convergence was typically reached within n = 1500–3300 iterations.

3. Results

Despite the significant differences in cell count between the grids, the results from the mesh independence study turned out to be very close to each other, proving that the simulations are not mesh-dependent. The results are presented in

Table 13. Results of mesh independence study for coarse grid.

$\mathit{\alpha },$$°$	$\mathbf{L},$ kgF	${\mathbf{C}}_{\mathbf{L}},$ −	${\mathbf{C}}_{\mathbf{D}},$ −	$\mathbf{L}/\mathbf{D},$ −	${\mathbf{C}}_{\mathbf{M}},$ −
0	297	0.010	0.008	1.179	−0.0011
4	4613	0.153	0.013	11.857	−0.0039
5	5704	0.189	0.015	12.220	−0.0045
6	6800	0.225	0.019	12.079	−0.0051
10	11,040	0.365	0.049	7.486	−0.0080
15	15,606	0.516	0.120	4.284	−0.0073
20	18,780	0.621	0.214	2.903	−0.0045
25	21,977	0.726	0.329	2.206	−0.0015
30	23,840	0.787	0.447	1.762	−0.0012
31	24,114	0.796	0.470	1.693	−0.0025
32	24,265	0.801	0.494	1.623	−0.0021
33	24,364	0.804	0.516	1.558	−0.0016
34	24,228	0.800	0.536	1.493	−0.0006
35	24,065	0.794	0.554	1.434	−0.0005
40	21,972	0.725	0.617	1.176	0.0016

,

Table 14. Results of mesh independence study for medium grid.

$\mathit{\alpha },$$°$	$\mathbf{L},$ kgF	${\mathbf{C}}_{\mathbf{L}},$ −	${\mathbf{C}}_{\mathbf{D}},$ −	$\mathbf{L}/\mathbf{D},$ −	${\mathbf{C}}_{\mathbf{M}},$ −
0	297	0.010	0.008	1.197	−0.0011
4	4588	0.152	0.013	11.944	−0.0040
5	5674	0.188	0.015	12.315	−0.0047
6	6770	0.224	0.018	12.172	−0.0053
10	11,061	0.366	0.048	7.545	−0.0081
15	15,726	0.520	0.120	4.322	−0.0077
20	18,796	0.621	0.213	2.917	−0.0049
25	22,140	0.731	0.330	2.217	−0.0021
30	24,218	0.800	0.451	1.773	−0.0038
31	24,375	0.805	0.474	1.697	−0.0029
32	24,389	0.805	0.496	1.624	−0.0021
33	24,405	0.806	0.517	1.558	−0.0016
34	24,285	0.802	0.537	1.493	−0.0007
35	23,975	0.792	0.553	1.431	0.0001
40	21,980	0.726	0.616	1.177	0.0009

and

Table 15. Results of mesh independence study for fine grid.

$\mathit{\alpha },$$°$	$\mathbf{L},$ kgF	${\mathbf{C}}_{\mathbf{L}},$ −	${\mathbf{C}}_{\mathbf{D}},$ −	$\mathbf{L}/\mathbf{D},$ −	${\mathbf{C}}_{\mathbf{M}},$ −
0	300	0.010	0.008	1.203	−0.0011
4	4591	0.152	0.013	11.912	−0.0040
5	5676	0.188	0.015	12.288	−0.0047
6	6772	0.224	0.018	12.150	−0.0052
10	11,184	0.370	0.048	7.759	−0.0080
15	15,749	0.520	0.120	4.328	−0.0078
20	18,799	0.621	0.213	2.919	−0.0049
25	22,198	0.733	0.330	2.219	−0.0021
30	24,207	0.799	0.451	1.774	−0.0038
31	24,381	0.805	0.474	1.698	−0.0032
32	24,439	0.807	0.497	1.625	−0.0020
33	24,436	0.807	0.518	1.557	−0.0013
34	24,285	0.802	0.537	1.493	−0.0005
35	23,998	0.792	0.554	1.431	0.0004
40	22,005	0.726	0.617	1.178	0.0009

.

The deviation between the average lift and drag coefficients was 0.4%, with a single maximum deviation reaching 1.7%. The momentum coefficient results showed a more significant average deviation of 22%, with a single maximum deviation of 80.9%, but it is to be expected with such small quantitative values. The critical angle of attack for an aircraft equipped with leading-edge root extensions (LERX) was approximately $\alpha =33°$. At the presumed stall speed of $u=66.6$ $\mathrm{m}·{\mathrm{s}}^{-1}$, a plain aircraft equipped only with LERX would generate around L = 24,400 kgF of lift force at best. The aircraft reached its peak lift-to-drag ratio of $L/D=12.3$ at $\alpha =5°$. The typical lift-to-drag ratio range for fighter jet aircraft at stall speeds is around $L/D$ = 8–10, with newer, highly sophisticated aircraft exceeding this range. However, this value will progressively decrease with the addition of high-lift and vortex devices, such as leading-edge vortex controllers and leading-edge and trailing-edge flaps. Figure 12 presents aerodynamic coefficients and lift-to-drag ratios for the grids from the mesh independence study.

Table 16. Results for LEVCON deflection of $\Lambda =10°$.

$\mathit{\alpha },$$°$	$\mathbf{L},$ kgF	${\mathbf{C}}_{\mathbf{L}},$ −	${\mathbf{C}}_{\mathbf{D}},$ −	$\mathbf{L}/\mathbf{D},$ −	${\mathbf{C}}_{\mathbf{M}},$ −
0	298	0.010	0.008	1.185	−0.0010
4	4597	0.152	0.013	11.499	−0.0049
5	5687	0.188	0.016	11.656	−0.0059
6	6786	0.224	0.020	11.292	−0.0069
10	11,179	0.369	0.054	6.878	−0.0123
15	16,378	0.541	0.127	4.262	−0.0176
20	22,451	0.742	0.241	3.075	−0.0229
25	25,279	0.835	0.364	2.296	−0.0265
30	25,900	0.855	0.478	1.789	−0.0242
31	25,805	0.852	0.500	1.702	−0.0213
32	25,989	0.858	0.526	1.630	−0.0206
33	26,143	0.863	0.551	1.568	−0.0215
34	26,241	0.866	0.574	1.508	−0.0220
35	26,229	0.866	0.597	1.451	−0.0225
40	24,783	0.818	0.683	1.198	−0.0201

,

Table 17. Results for LEVCON deflection of $\Lambda =20°$.

$\mathit{\alpha },$$°$	$\mathbf{L},$ kgF	${\mathbf{C}}_{\mathbf{L}},$ −	${\mathbf{C}}_{\mathbf{D}},$ −	$\mathbf{L}/\mathbf{D},$ −	${\mathbf{C}}_{\mathbf{M}},$ −
0	286	0.009	0.009	1.106	−0.0007
4	4589	0.152	0.013	11.720	−0.0046
5	5679	0.188	0.016	11.994	−0.0054
6	6778	0.224	0.019	11.724	−0.0063
10	11,153	0.368	0.052	7.076	−0.0112
15	16,473	0.544	0.126	4.334	−0.0151
20	22,135	0.731	0.234	3.120	−0.0210
25	24,536	0.810	0.350	2.317	−0.0211
30	26,325	0.869	0.478	1.820	−0.0231
31	26,408	0.872	0.501	1.742	−0.0232
32	26,398	0.871	0.523	1.665	−0.0225
33	26,402	0.871	0.548	1.591	−0.0207
34	26,416	0.872	0.571	1.526	−0.0204
35	26,388	0.871	0.595	1.464	−0.0205
40	24,814	0.819	0.679	1.205	−0.0185

and

Table 18. Results for LEVCON deflection of $\Lambda =30°$.

$\mathit{\alpha },$$°$	$\mathbf{L},$ kgF	${\mathbf{C}}_{\mathbf{L}},$ −	${\mathbf{C}}_{\mathbf{D}},$ −	$\mathbf{L}/\mathbf{D},$ −	${\mathbf{C}}_{\mathbf{M}},$ −
0	281	0.009	0.009	1.038	−0.0004
4	4584	0.152	0.013	11.741	−0.0043
5	5675	0.188	0.015	12.117	−0.0051
6	6775	0.224	0.019	11.292	−0.0059
10	11,066	0.366	0.051	7.210	−0.0102
15	16,519	0.546	0.123	4.430	−0.0143
20	21,267	0.702	0.225	3.127	−0.0170
25	23,375	0.772	0.336	2.298	−0.0147
30	25,772	0.851	0.467	1.824	−0.0173
31	26,151	0.863	0.494	1.749	−0.0178
32	26,390	0.871	0.521	1.673	−0.0172
33	26,508	0.875	0.547	1.600	−0.0163
34	26,470	0.874	0.571	1.531	−0.0150
35	26,322	0.869	0.593	1.466	−0.0141
40	24,522	0.810	0.674	1.202	−0.0127

present the results for LEVCON deflections of $\Lambda =(10,20,30)°$, and these will be further compared to medium grid results from the mesh independence study, as these cases use the same mesh creation settings.

LEVCON significantly increased lift in the higher range of angles of attack ($\alpha$) at a minor cost of producing more overall drag. However, it did not show much improvement in the range of $\alpha$ = (0–10)$°$ when compared to the aircraft with LERX. In the range of $\alpha$ = (10–40)$°$, the lift force generated by the aircraft with LEVCON increased significantly, with gains of up to $\Delta F=3650$ kgF observed. The aircraft with LEVCON produced more drag than lift in the lower range of $\alpha$, but it also generated more lift than drag in the upper range of $\alpha$. This characteristic is beneficial in highly maneuverable fighter aircraft, as they tend to operate in the upper range of $\alpha$ more frequently than traditional aircraft types. Figure 13 presents the lift, drag, momentum coefficients, and lift-to-drag ratios for the aircraft equipped with leading-edge vortex controllers deflected at $\Lambda =(10,20,30)°$.

To further highlight the differences in results between the aircraft in the clean configuration and with LEVCON, the gains and losses in terms of lift force and aerodynamic coefficients are shown in

Table 19. LEVCON gains compared between clean configuration and deflection of $\Lambda =10°$.

$\mathit{\alpha },$ $°$	$\mathbf{\Delta }\mathbf{L},$ kgF	$\mathbf{\Delta }{\mathbf{C}}_{\mathbf{L}},$ %	$\mathbf{\Delta }{\mathbf{C}}_{\mathbf{D}},$ %	$\mathbf{\Delta }\mathbf{L}/\mathbf{D},$ %
0	1	0.31	1.37	−1.05
4	9	0.16	4.03	−3.72
5	13	0.20	5.86	−5.35
6	16	0.20	8.01	−7.23
10	118	1.01	10.81	−8.84
15	653	4.10	5.55	−1.38
20	3654	19.40	13.29	5.40
25	3139	14.14	10.23	3.55
30	1681	6.93	5.99	0.89
31	1429	5.84	5.50	0.33
32	1600	6.54	6.19	0.34
33	1739	7.11	6.43	0.63
34	1956	8.04	6.95	1.02
35	2254	9.38	7.89	1.38
40	2803	12.76	10.80	1.75

,

Table 20. LEVCON gains compared between clean configuration and deflection of $\Lambda =20°$.

$\mathit{\alpha },$ $°$	$\mathbf{\Delta }\mathbf{L},$ kgF	$\mathbf{\Delta }{\mathbf{C}}_{\mathbf{L}},$ %	$\mathbf{\Delta }{\mathbf{C}}_{\mathbf{D}},$ %	$\mathbf{\Delta }\mathbf{L}/\mathbf{D},$ %
0	−11	−3.51	4.39	−7.57
4	1	0.00	1.92	−1.88
5	5	0.06	2.74	−2.60
6	8	0.09	3.91	−3.68
10	91	0.78	7.46	−6.22
15	748	4.70	4.40	0.29
20	3339	17.72	10.07	6.95
25	2397	10.79	6.03	4.48
30	2106	8.69	5.94	2.60
31	2032	8.32	5.53	2.65
32	2009	8.22	5.54	2.53
33	1997	8.16	5.93	2.11
34	2131	8.75	6.41	2.20
35	2413	10.04	7.51	2.35
40	2835	12.89	10.2	2.42

and

Table 21. LEVCON gains compared between clean configuration and deflection of $\Lambda =30°$.

$\mathit{\alpha },$ $°$	$\mathbf{\Delta }\mathbf{L},$ kgF	$\mathbf{\Delta }{\mathbf{C}}_{\mathbf{L}},$ %	$\mathbf{\Delta }{\mathbf{C}}_{\mathbf{D}},$ %	$\mathbf{\Delta }\mathbf{L}/\mathbf{D},$ %
0	−16	−5.43	9.08	−13.30
4	−4	−0.09	1.64	−1.70
5	1	0.00	1.64	−1.61
6	5	0.05	2.03	−1.94
10	4	0.00	4.64	−4.43
15	793	5.00	2.44	2.50
20	2471	13.08	5.52	7.17
25	1235	5.53	1.84	3.63
30	1554	6.41	3.47	2.84
31	1776	7.27	4.09	3.05
32	2000	8.19	5.06	2.98
33	2104	8.60	5.71	2.74
34	2186	8.99	6.30	2.53
35	2347	9.78	7.13	2.47
40	2542	11.58	9.29	2.09

.

Surprisingly, the highest deflection angle did not provide the best results in terms of adding lift, but it produced less drag when compared to lower deflection angles. Nevertheless, all configurations introduced more drag across the entire range of $\alpha$, which is expected with the addition of any wing devices. Due to the relatively low increase in lift in the lower range of $\alpha$ and the consistent increase in drag across the entire spectrum of $\alpha$, the lift-to-drag ratio experienced a downward trend at $\alpha$ = (0–15)$°$, but an increasing trend can be observed in the range $\alpha$ = (15–40)$°$.

What is also interesting is how the moment coefficients changed. The center of gravity was not moved between the configurations, and the aircraft with LEVCON exhibited stable static longitudinal stability and a pitch-down characteristic over a broader range of $\alpha$ = (0–20)$°$. Beyond $\alpha >25°$, the aircraft still had unstable static longitudinal stability, but the pitch-up characteristic was no longer present. This aspect would have to be further investigated by adjusting the center of gravity forward or aft to achieve the desirable longitudinal stability.

3.1. Flow Visualizations

In the following section, a closer look is taken at the flow patterns around the aircraft and how LEVCON improves lift force generation in high alpha scenarios. Up until $\alpha =10°$, the results for all deflections are very similar, and no significant improvement can be noted. From $\alpha =15°$ onwards, LEVCON starts providing more lift than the aircraft with LERX. However, the range of $\alpha$ = (20–35)$°$ is particularly interesting. For visualization purposes, three scenarios with $\alpha =(20,25,31)°$ were compared. Figure 14, Figure 15 and Figure 16 show flow visualizations and pressure distributions for $\alpha =(20,25,31)°$, respectively. The velocity magnitude is represented in $\mathrm{m}·{\mathrm{s}}^{-1}$, and the pressure distribution is represented by the kinematic pressure in ${\mathrm{m}}^2·{\mathrm{s}}^{-2}$, with 0 representing standard atmospheric pressure.

3.1.1. Leading-Edge Root Extension Results Interpretation

At $\alpha =20°$, the LERX forms a single vortex, which begins to establish at the root section of the wing and is completely formed about halfway along the extension’s leading edge, as shown in Figure 14b. This behavior is especially visible on the left side of the aircraft, where the pressure distribution is visualized. As expected, the LERX induces vortical flow over the top surface of the wing, but the vortex diverges too far from the wing and breaks too soon to provide enough pulling force to stimulate and accelerate the airflow underneath it. Consequently, separation occurs on the outer section of the main wing, while the majority of the lift comes from the blended fuselage, the LERX section, and the inner part of the wing, as demonstrated in Figure 14a,c.

At $\alpha =25°$, the root extension still generates a single strong vortex, but this time it forms closer to the fuselage section, as depicted in Figure 15b. The flow pattern in Figure 15a shows that a portion of the airflow is drawn in and under the vortex, but the velocity profile indicates that separation is also occurring on the outer part of the wing, though interestingly, on a much smaller scale than at $\alpha =20°$ (Figure 15c). Similar to the previous case, the pressure distribution corresponds with the high velocity profile, as a low-pressure area forms on the top surface of the root extension, where the main vortex is established. Another area worth noting is the connection between the LERX and the main wing. In this scenario, no significant vortical flow can be observed in that area, but the pressure is slightly lower when compared to the overall pressure distribution on the top surface of the aircraft. This is expected to change with the addition of LEVCON.

As shown in Figure 16b, at $\alpha =31°$, the vortex is created at the root of the extension and is partially influenced by vortices originating from the nose section of the aircraft. Figure 16a displays a significant change in the overall flow pattern, as a portion of the air from the nose section is drawn in and trapped under the vortex. This feeds the airflow over the main wing, delaying separation to some extent, as depicted in Figure 16c.

3.1.2. Leading-Edge Vortex Controller Results Interpretation

With the addition of vortex controllers, the vortical flow pattern becomes much more prominent compared to the configuration with LERX. In all deflection scenarios, typically two main vortices are formed. The primary vortex is always created by LEVCON’s leading edge and, when compared to the LERX vortex, it is much more concentrated and extends further away from the leading edge, as observed in the central column of Figure 14, Figure 15 and Figure 16. The secondary vortex is formed due to the highly swept edge connecting the LEVCON with the main wing. It is partially energized by the main vortex, but a significant portion of the airflow comes from underneath the device, feeding the vortical flow. In some scenarios, such as those shown in Figure 14f, Figure 15f and Figure 16f,i, the primary vortex is energized by the tertiary vortex, created by the gap between the device’s inner edge and the fuselage. It has been observed that this flow phenomenon is likely the main cause of why a particular deflection tends to produce the most lift at a certain angle of attack compared to other deflection angles. The way this operates is that the air flowing through the gap is dragged into the main vortex, further energizing its vortical flow, rather than following the flow pattern around the fuselage. This is evident in the case of deflections with $\Lambda =(20,30)°$ at $\alpha =(20,25)°$, as shown in Figure 14i,l, Figure 15i,l and Figure 16l. In a general sense, an important change has been introduced by the vortex controller device, and the flow pattern in the left column of Figure 14, Figure 15 and Figure 16 indicates that the majority of airflow is pulled in and under the vortices, significantly improving the velocity profile near the outer part of the wing. This improvement suggests that separation has been eliminated to a great extent. Furthermore, with the addition of the vortex controller, a flatter stall characteristic has been achieved, and the critical angle of attack has been shifted from $\alpha =33°$ to $\alpha =35°$, which is also a desirable outcome.

At $\alpha =(20,25)°$, the deflection angle of $\Lambda =10°$ provides the most lift force among the other considered deflection configurations. This can be specifically attributed to the flow phenomenon of the tertiary vortex being dragged into the primary vortex. The second-best deflection at $\alpha =(20,25)°$ is $\Lambda =20°$, which provides considerably lower lift force than the deflection of $\Lambda =10°$. The majority of the flow is quite similar, but the primary vortex appears to be more concentrated, especially visible in the pressure distribution in Figure 14h and Figure 15h. The secondary vortex bursts slightly sooner than in the $\Lambda =10°$ configuration. The tertiary vortex does not form in this scenario, and instead, the majority of the air flowing through the gap between LEVCON and the nose section follows the flow pattern towards the end of the fuselage. Although the primary vortex looks more concentrated, the velocity profile near the outer surface of the wing seems worse due to the secondary vortex diverging too far from the wing’s surface, resulting in a slightly inferior flow pattern in that region, as observed in Figure 14d,g and Figure 15d,g. However, more is not always better. This is also evident in the LEVCON deflection of $\Lambda =30°$, which yielded the worst results at $\alpha =(20,25)°$. Part of this result can once more be attributed to the tertiary vortex not forming and the airflow from within the gap following the flow pattern around the fuselage instead of strengthening the primary vortex. The vortical flow has a similar presence as in the two previous scenarios, but the higher deflection tends to push the vortex too far above the wing’s surface. This puts it at a disadvantage as it does not pull the air underneath itself with enough velocity to prevent separation near the wing’s tip. At this point, a significant conclusion can be drawn regarding the deflection angle. It must be high enough to produce an energized vortical flow but not too high to deflect the vortex too far from the wing’s surface.

At $\alpha =31°$, the performance of the LEVCON configurations varies. The $\Lambda =10°$ deflection yields the poorest results at this angle of attack. In Figure 16e, the primary vortex appears to burst prematurely, lacking significant energizing of the secondary vortex, which is less prominent than at lower angles of attack. This secondary vortex is primarily fed by the air from underneath the device and the downward flow from the aircraft’s nose section, trapped beneath the primary vortex created by the LEVCON. The vortex originating from the gap between the device and the fuselage is still present and partially fed by vortices from the nose section, as shown in Figure 16f. Separation starts occurring at the wing’s tip area, indicating the aircraft is approaching its critical angle of attack, as evident in Figure 16d. At $\alpha =31°$, the $\Lambda =20°$ deflection configuration provides the highest lift force among the compared configurations. This can be attributed to the more prominent primary vortex, likely due to the formation of the tertiary vortex within the gap, as illustrated in Figure 16i. The secondary vortex is also partially fed by vortices trailing from the nose section, enhancing the vortical flow and improving the overall flow pattern. As this angle of attack is nearly critical, separation occurs at the outer region of the wing, visible in Figure 16g. Although this deflection experiences separation, it handles it better than the $\Lambda =10°$ variant. Lastly, the $\Lambda =30°$ deflection provides slightly lower lift force than the $\Lambda =20°$ deflection. In Figure 16k, we observe the most energized vortical flow around LEVCON out of the three configurations. However, the results are suboptimal, likely due to the weak flow concentration in the crevice between the device and the fuselage, shown in Figure 16l. This is understandable given the larger gap resulting from the higher deflection. The higher deflection pushes the vortex away from the wing, reducing the potential of the airflow underneath the vortex, as evident in Figure 16j. On average, the $\Lambda =30°$ deflection performed worse at delaying separation at the wing’s tip region compared to the other vortex controller configurations. However, it still outperformed LERX, producing significantly more lift across the entire spectrum.

3.2. Stall Characteristics

The following section delves deeper into the topic of wing stall in the compared fighter jet configurations. Aircraft stalls are influenced by factors such as wing configuration, airfoil thickness, and aerodynamic features. The interplay between these design parameters and flight conditions significantly impacts the types of stalls that occur. Airspeed, angle of attack, and control surface effectiveness further contribute to the complexity of stall behavior. To understand the specific stall types occurring in the compared scenarios, it is essential to discuss the typical types of stall in correlation with airfoil maximum thickness. According to research conducted by McCullough and Gault [60,61], as elaborated upon by Polhamus [62], Whitford [30], and Luckring [63], stalls can be categorized into three basic groups: leading-edge, trailing-edge, and thin airfoil stall. Furthermore, these stall categories can be linked to airfoil thickness, as indicated by McCullough and Gault [60]. Airfoils with a small thickness-to-chord ratio (t/c < 9%) are susceptible to sudden thin airfoil stalls at steep angles of attack, resulting in turbulent airflow and separation over the upper surface. Thin airfoil stall occurs when the separation bubble forms near the leading edge of the wing and then reattaches further downstream in a turbulent manner. At higher angles of attack, the flow fully separates without reattachment on the airfoil. Intermediate airfoils (9% < t/c < 15%) exhibit prevalent leading-edge stalls, initiated at the airfoil’s leading edge due to steep angles of attack. Thicker airfoils (t/c > 15%) often experience trailing-edge stalls, with airflow separation starting at the wing’s rear section.

In the context of a fighter jet with a delta wing configuration featuring thin 6% t/c airfoils, the most prominent type of stall would be the thin airfoil stall. Delta wings with a moderate to high sweep angle are also susceptible to tip stall. The unique aerodynamics of delta wings, including the formation of strong tip vortices, can lead to tip stall conditions, especially during high angles of attack.

Similar to the methodology employed for vortex visualizations, this study examines three specific scenarios at $\alpha =(20,25,31)°$. Figure 17 provides a detailed analysis of Mach number distributions in nine selected cross-sections along the wingspan for both LERX and LEVCON configurations deflected at $\Lambda =(10,20,30)°$, with the goal of clearly distinguishing the stall patterns across the entire wing surface. When viewed from the left in each subfigure, cross-sections 1, 5, 6, 7, 8, and 9 maintain consistent position, however, cross-sections 2, 3, and 4 vary and are highlighted with red circles to emphasize the locations where full flow separation occurs. A portion of the color legend intentionally remains blank, as the transparent color is used to symbolize flow velocity similar to flight velocity.

As depicted in Figure 17a–c, our delta wing aircraft, with a leading-edge sweep angle of 42$°$ and no vortex devices or high-lift devices other than LERX, experiences a leading-edge stall as it approaches its critical angle of attack. Thanks to the higher leading-edge sweep of 64$°$, the root section of the wing maintains lift throughout the entire range of the angle of attack. The leading-edge stall occurs on the main wing, and the full separation, as shown in Figure 17a–c, happens at wing sections located approximately 2.3, 2.3, and 3.4 m along the wingspan, respectively. This stall occurs because the aircraft in this study has a hybrid wing design, where the delta wing has a moderate leading-edge sweep angle of 42° and lacks proper vortex and high-lift devices other than LERX, relying predominantly on lift resulting from attached-flow theory. In contrast, the leading-edge root extension (64° of sweep) and leading-edge vortex controller (70° of sweep) primarily utilize the vortex lift phenomenon due to highly swept leading edges and are more aligned with the shape of slender delta wings (typically having more than 65° of sweep).

The addition of LEVCON improves the overall airflow over the main delta wing to a certain extent. Induced vortex flow patterns enhance the spanwise flow, delaying the stall occurrence beyond the half wingspan of the main wing, unlike the leading-edge stall that affects the entire surface of the main wing, as observed with LERX. For angles of attack $\alpha =(20,25)°$, a LEVCON deflection of $\Lambda =10°$ proves to be the most effective in terms of energizing the airflow over the main delta wing and delaying the stall, as evident in Figure 17d,e. In these configurations, full separation occurs somewhere around 5.8 m along the wingspan. However, for $\alpha =31°$, this deflection angle shows considerably worse results, stalling at the 3.3 m section in relation to the wingspan. The deflection of $\Lambda =20°$ closely follows the behavior of $\Lambda =10°$ in the range of $\alpha =(20,25)°$, albeit in a weaker form (Figure 17g,h), as the stall occurs at sections 5.4 and 5.3 m along the wingspan, respectively. This deflection provides the best results in terms of delaying stall at $\alpha =31°$, with fully separated flow observed only after the 5.4 m section of the wingspan (Figure 17i). However, the highest deflection, as shown in Figure 17j,k, does not provide meaningful gains, as explained in Section 3.1.2. This configuration has the weakest stall delay capabilities at $\alpha =(20,25)°$, with separation fully forming at sections 4.8 and 4 m in relation to the wing span, respectively. As the aircraft approaches stall, specifically at $\alpha =31°$, a LEVCON deflection of $\Lambda =30°$ is found to be a middle ground between the two other deflections, as depicted in Figure 17l, where full separation occurs at the outboard section of 4.2 m.

Despite these differences between the configurations, the outer portions of the wing still experience the tip stall phenomenon. One effective aerodynamic technique to mitigate tip stall is the implementation of washout, which involves designing the wing with a twist, gradually decreasing the angle of incidence from the wing root towards the wingtip. Consequently, the wingtip stalls at a higher angle of attack than it would without washout. This approach is often employed in fighter jet aircraft to delay stall at the wingtip. The aircraft used in this study incorporates a wing twist of −7$°$ at the tip, corresponding to ${\alpha }_{tip}=(14,19,25)°$ at angles of attack $\alpha =(20,25,31)°$ respectively, as the main wing of the aircraft also maintains an incidence angle of 1$°$. However, this method proved ineffective in countering tip stall, indicating the need for additional wing devices to address the unfavorable flow in the wingtip region.

While LEVCON significantly enhances lift and stall characteristics, further comprehensive examination, considering its shape and sizing, as well as the incorporation of additional vortex and high-lift devices, is necessary. Leading-edge slats and flaps and trailing-edge flaps or flaperons, commonly used in modern fighter jets, can play a crucial role in improving lift and preventing stalls [1,2,8]. Although these possibilities are acknowledged, they require a dedicated case study beyond the scope of this paper. This study exclusively focuses on the preliminary analysis of how LEVCONs influence the aerodynamic characteristics of a fighter jet. It is important to note that while the potential influence of additional devices is acknowledged, exploring their impact in conjunction with LEVCONs warrants a separate case study. The analysis also points towards the future direction of CFD research. The introduction of LEVCON accelerates the airflow to such an extent that the local Mach number surpasses Ma = 0.3, which means that the future investigations should also take compressibility effects into the consideration.

4. Discussion

Certainly, the shape of the leading-edge root extension, as well as the entire aircraft, could be further improved and refined to achieve an optimal velocity profile for the airflow around the designed airframe. The absence of high-lift devices, such as leading-edge flaps, does not present this aerodynamic solution in its best light. However, a comparative basis had to be established, and a clean configuration of the airplane model was chosen for this purpose. It is apparent that in the LERX configuration, the vortex dissipates rapidly at high angles of attack, suggesting that utilizing a steeper sweep angle, a thinner airfoil, or a sharper leading-edge might enhance the performance of this airframe.

LEVCON changes the overall airflow around the aircraft, producing more energized vortices, which strengthen each other and are induced onto the main wing. This in turn improves the flow across the wing, delaying separation and increasing lift over a wide spectrum of $\alpha$. The gains in generated lift are noticeable at $\alpha$ = 20–40°, averaging at 8.5–10% depending on the configuration, while the peak gain being $19.4\%$. We were hoping to achieve more in the lower area of angles of attack, mostly due to increased surface area of the LEVCON, but the gains were lower than expected. The critical angle of attack has been increased from $\alpha =33°$ to $\alpha =35°$, which is a welcome growth, but not as high to call it a major improvement. On the other hand, a more flat stall characteristic has been achieved with the addition of LEVCON, which is an important aspect for highly maneuverable aircraft. As is the case with most wing devices, this aerodynamic solution also has its drawback in form of increased drag and this is especially harming for lower range of $\alpha$ = 0–15°, where it produces an average of 3.5–6% more drag, depending on the configuration, while the peak increase of drag being $13.3\%$. All of that, while producing <1% more lift. Subsequently, the lift-to-drag ratio deteriorated more in the lower range of $\alpha$, than it improved in the higher range of $\alpha$. This leads to the conclusion that this device is tailored more towards aircraft utilizing flight with high angle of attack, as is the case of fighter aircraft. Of coarse, the generated lift could be improved further and the effect of drag could be lessened with the use of the optimization process. Though for such complex shapes, where many geometrical aspects take place, it is a very tedious task. The simulation results proved that there are far more LEVCON sizing aspects than just its overall shape, such as the airfoil, leading-edge sweep angle or surface area. Inner sweep angle, leading-edge sharpness, mounting position and gap sizing between the fuselage and the device itself are equally as important. On top of that, there is the aspect of optimal deflection angle, which gives far more combinations than just 10, 20 or 30 degrees. The research presented in this work has shown that the Leading-Edge Vortex Controller is a capable device, but the conceptualization of its shape requires further investigation, as the geometry proposed in this article is certainly sub-optimal, meaning more geometric variations should be tested in the future. Another aspect that could be investigated is the usage of other high-lift and vortex devices in combination with LEVCONs, as perhaps they could positively influence each other, possibly expanding their capabilities. Most importantly, LEVCONs are movable surfaces, which can deflect symmetrically and asymmetrically in a dynamic matter, similar to ailerons or flaperons, meaning there is far more to evaluate regarding the flight dynamics of this device, than just steady-state aerodynamics.

This is where CFD as a research method really proves to be a very capable alternative to a physical wind tunnel, as it is possible to create virtually any variation of shape in the digital CAD environment and input those geometries to CFD code, such as OpenFOAM, in order to conduct a preliminary investigation of a problem without significant financial effort. This is not the case with experimental research, where we would have to 3D print or create physical copies of each of the tested configurations to investigate the problem at a basic level. The OpenFOAM 8 software proved to be extremely easy to work with, and thanks to its code, we were able to design around 100 numerical grids by using bash scripts, which partially automated the grid creation process. On a final note, we believe that the research provided in this work should be subject to experimental verification at a later stage when the topic of LEVCON shape optimization is further investigated. Future research should utilize experimental methods, such as wind tunnel testing on a scaled model of the fighter aircraft, in order to compare the numerical results with the experimental results. This, in turn, would require scaled 3D printed aircraft models, preferably with an actively controlled LEVCON mechanism, or at least a version of it in which the deflection angle could be easily adjusted between the testing sessions. Another experimental method is water tunnel testing, which would provide significant insight into the investigation of vortex structures’ behavior by using either dye visualization or Particle Image Velocimetry (PIV). Numerical research hinted at a possible location of dye injection openings on the top surface of the vortex controller, where significant suction persists due to vortex forming in that area. The dynamic behavior of vortex creation and breakdown could also be visualized in the water tunnel by introducing and combining motions, such as pitch, yaw, and roll.

5. Conclusions

The introduction of the leading-edge vortex controller (LEVCON) into the studied fighter jet geometry marked a significant improvement in lift generation and stall delay. Thanks to computational fluid dynamics (CFD) simulations, the impact of various LEVCON deflection angles could be explored, shedding light on their transformative influence on the aircraft’s aerodynamic characteristics. One of the most striking findings was the substantial increase in lift achieved with the incorporation of LEVCON. In the range of angles of attack $\alpha$ = (20–40)$°$, the generated lift underwent significant improvement due to the phenomenon known as vortex lift. Lift gains ranged from 8.5% to 10% on average, with a peak gain of 19.4%. The energized vortices induced by these devices effectively improved the airflow over the main delta wing, ensuring that the wing maintained lift even at higher angles of attack. Furthermore, the incorporation of LEVCON played a pivotal role in delaying the stall. At high angles of attack, typically around $\alpha$ = (20–35)$°$, the aerodynamic performance of the aircraft equipped with LEVCON far surpassed that of the configurations without this device. The vortices generated by LEVCON altered the airflow patterns, reinforcing the airflow on the main wing. This phenomenon significantly delayed the separation of airflow over the wing upper surface, allowing the aircraft to operate at higher angles of attack before experiencing stall conditions. Due to the introduction of LEVCON, the critical angle of attack was also raised from $\alpha =33°$ to $\alpha =35°$. Additionally, the stall characteristic of the aircraft was improved, as it became more gradual and predictable, resembling a flatter stall profile. In summary, the incorporation of LEVCON into an existing delta wing aircraft led to a substantial increase in lift coefficients, ranging from 8.5% to 10% on average, and increased the critical angle of attack to $\alpha =35°$. Unfortunately, as is the case with most wing devices, this aerodynamic solution also has its drawback in the form of increased drag. Nevertheless, the obtained results prove that LEVCON may pose a significant improvement to aircraft utilizing vortex flow aerodynamics.

The conducted analysis highlights the need for considering compressibility effects and employing compressible solvers. The accelerated airflow induced by LEVCON reaches such high velocities that the local Mach number surpasses the incompressible regime at Ma = 0.3. Furthermore, we emphasize the importance of subjecting the research presented in this work to experimental verification in subsequent investigations focused on LEVCON shape optimization. To comprehensively understand the complex aerodynamic phenomena associated with LEVCON, future research should incorporate experimental techniques. Specifically, wind tunnel testing using a scaled model of the fighter aircraft is essential to compare and validate the numerical findings. Additionally, employing water tunnel testing would yield insights into the behavior of vortex structures. These experimental approaches are vital for advancing our understanding of the dynamics involved in LEVCON.