Methodology for the Optimization of a Novel Hydro Turbine with a Case Study
Abstract
:1. Introduction
2. Previous Attempts to Optimize Design Parameters
2.1. Description of the Pelton and Turgo turbines
2.1.1. Pelton Turbine
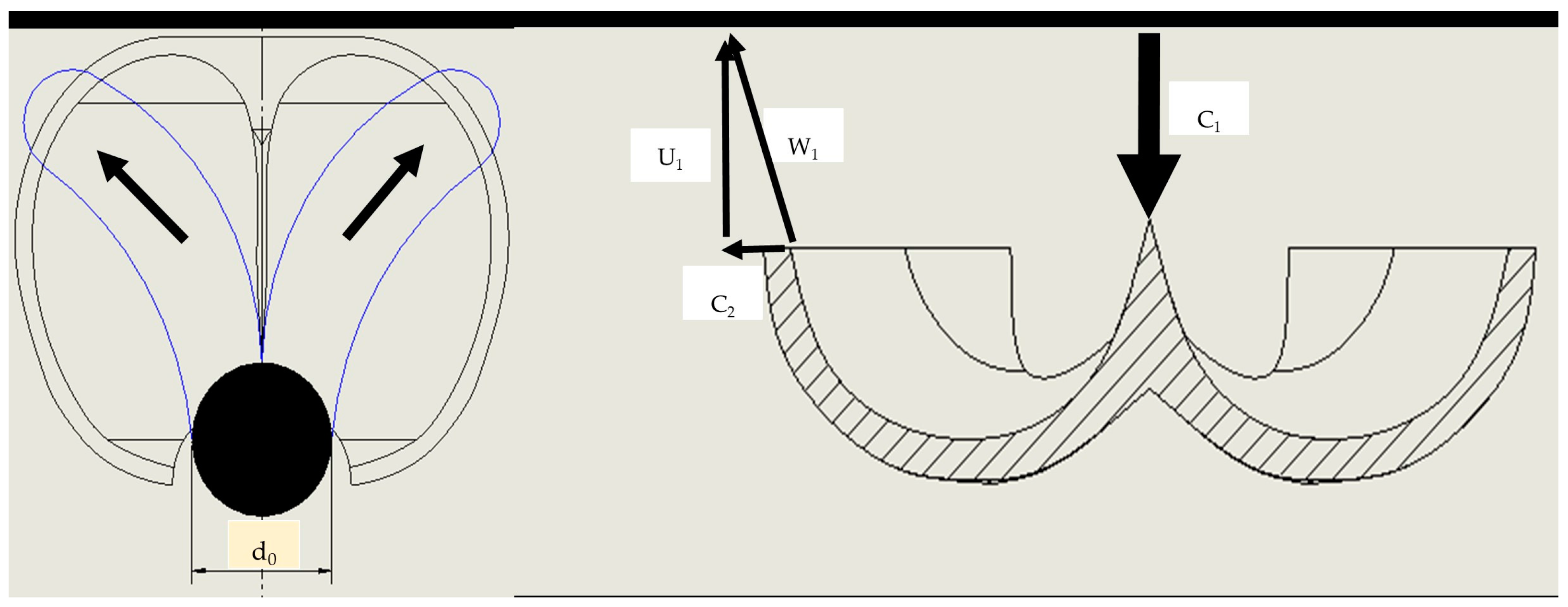
2.1.2. Turgo Turbine
2.2. Research to Date
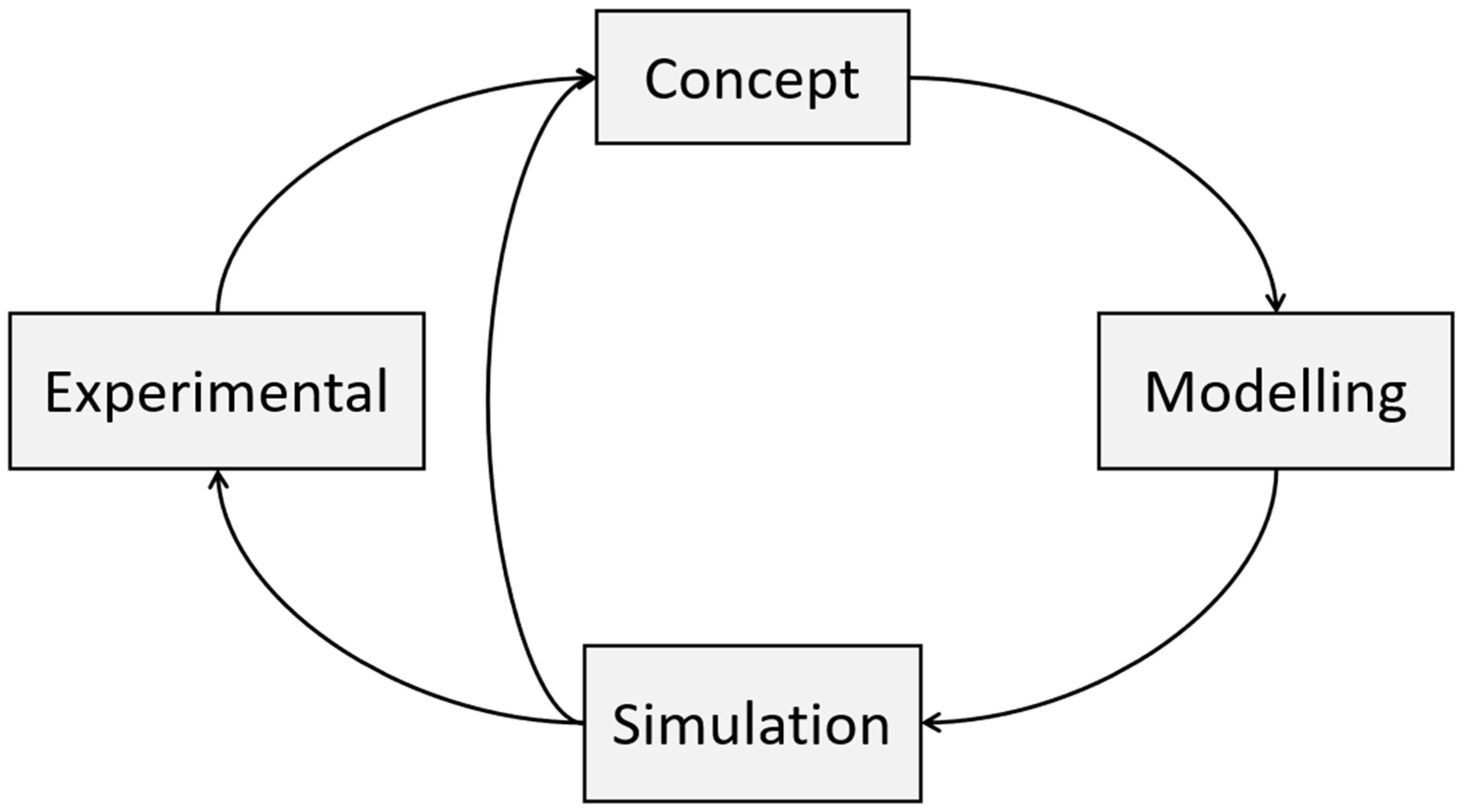
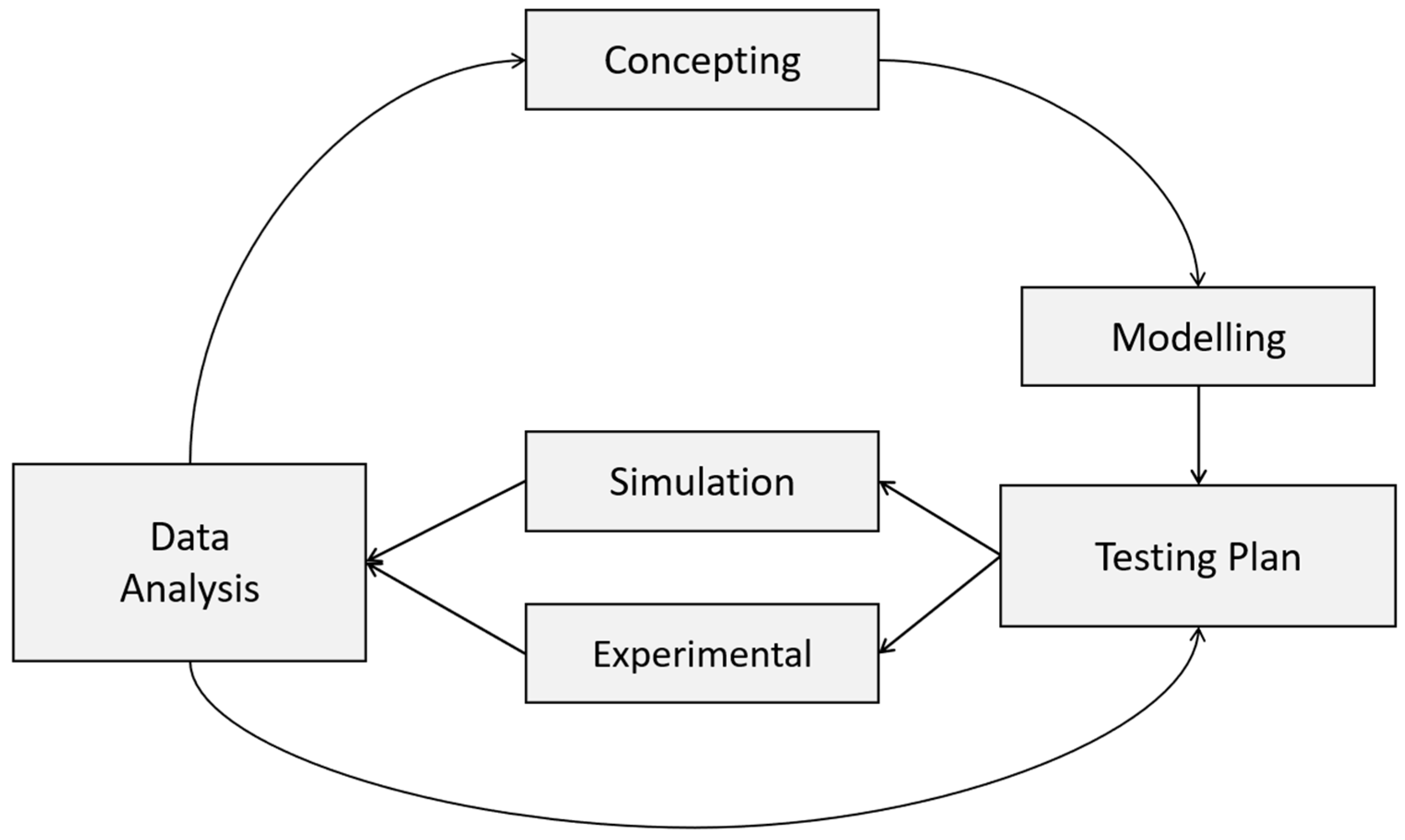
3. Overview of Workflow
4. Comparison of Numerical and Experimental Results for Pelton Turbines
5. Case Study
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pickston, D.; Orritt, S.; Wilmot, L.; Burtenshaw, L.; Dubois, M.; Prigov, G.; Aggidis, G. Experimental and Computational Development of a Novel High Head Impulse Turbine. Master’s Thesis, Lancaster University, Lancaster, UK, 2023. [Google Scholar]
- Pelton and Turgo Turbines. Renewables First. 2015. Available online: https://www.renewablesfirst.co.uk/hydropower/hydropower-learning-centre/pelton-and-turgo-turbines/ (accessed on 13 April 2023).
- Chazarra, M.; Pérez-Díaz, J.I.; García-González, J. Economic Viability of Pumped-Storage Power Plants Equipped with Ternary Units and Considering Hydraulic Short-Circuit Operation. J. Phys. Conf. Ser. 2017, 813, 012013. [Google Scholar] [CrossRef]
- Nag, S.; Lee, K.Y.; Suchitra, D. A Comparison of the Dynamic Performance of Conventional and Ternary Pumped Storage Hydro. Energies 2019, 12, 3513. [Google Scholar] [CrossRef]
- A Brief History of Hydropower. iha. 2022. Available online: https://www.hydropower.org/iha/discover-history-of-hydropower (accessed on 28 May 2023).
- An Ultimate Guide to Francis Turbine. Linquip Technews. 27 June 2022. Available online: https://www.linquip.com/blog/what-is-francis-turbine/ (accessed on 5 May 2023).
- Breeze, P. Chapter 8—Hydropower. In Power Generation Technologies, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 173–201. [Google Scholar]
- Francis Turbine Cross Section. saVREE. 2023. Available online: https://savree.com/en/encyclopedia/francis-turbine-cross-section#:~:text=History,with%20an%20efficiency%20exceeding%2090%25 (accessed on 14 April 2023).
- Lewis, B.J.; Cimbala, J.M.; Wouden, A.M. Major historical developments in the design of water wheels and Francis hydroturbines. IOP Conf. Ser. Earth Environ. Sci. 2014, 22, 012020. [Google Scholar] [CrossRef]
- Solemslie, B.W. Experimental Methods and Design of a Pelton Bucket; NTNU: Trondheim, Norway, 2016. [Google Scholar]
- Abgottspon, A.; Staubli, T.; Felix, D. Erosion of Pelton Buckets and Changes in Turbine Efficiency Measured in the HPP Fieschertal. Earth Environ. Sci. 2016, 49, 122008. [Google Scholar] [CrossRef]
- Padhy, M.; Saini, R. Study of Silt Erosion Mechanism in Pelton Turbine Buckets. Energy 2012, 39, 286–293. [Google Scholar] [CrossRef]
- Abgottspon, A.; Staubli, T.; Felix, D.; Albayrak, I.; Boes, R.M. Hydro-Abrasive Erosion of Pelton Buckets and Suspended Sediment Monitoring. 2013. Available online: https://www.researchgate.net/publication/291339891_Hydro-Abrasive_Erosion_of_Pelton_Buckets_and_Suspended_Sediment_Monitoring/citation/download (accessed on 4 June 2023).
- Pelton Turbine. saVRee. 2023. Available online: https://savree.com/en/encyclopedia/pelton-turbine#:~:text=Pelton%20Turbine%20Components,as%20torque%20prior%20to%20discharge (accessed on 15 April 2023).
- Pelton Turbine. Energy Education. 2023. Available online: https://energyeducation.ca/encyclopedia/Pelton_turbine (accessed on 15 April 2023).
- Bellis, M. Lester Allan Pelton and the Invention of Hydroelectric Power. ThoughtCo. 19 December 2019. Available online: https://www.thoughtco.com/lester-allan-pelton-hydroelectric-power-4074158#:~:text=Pelton%C2%B4s%20turbine%20proved,manufacture%20his%20new%20water%20turbine (accessed on 15 April 2023).
- Crawford, M. Lester Allan Pelton. The American Society of Mechanical Engineers. 12 June 2012. Available online: https://www.asme.org/topics-resources/content/lester-allan-pelton (accessed on 13 April 2023).
- Židonis, A.; Aggidis, G.A. State of the art in numerical modelling of Pelton turbines. Renew. Sustain. Energy Rev. 2015, 45, 135–144. [Google Scholar] [CrossRef]
- Turgo Turbines. Energy Education. 2023. Available online: https://energyeducation.ca/encyclopedia/Turgo_turbine (accessed on 17 April 2023).
- Turbinesinfo. Turgo Turbines. Turbines Info. 22 February 2020. Available online: https://www.turbinesinfo.com/turgo-turbines/ (accessed on 17 April 2023).
- Benzon, D.; Aggidis, G.; Anagnostopoulos, J. Development of the Turgo Impulse turbine: Past and present. Appl. Energy 2016, 166, 1–18. [Google Scholar] [CrossRef]
- Team, L. What Is Turgo Turbine and How Does It Work? Linquip Technews. 1 February 2021. Available online: https://www.linquip.com/blog/turgo-turbine/ (accessed on 17 April 2023).
- Chung, T. Computation Fluid Dynamics, 1st ed.; Cambridge University Press: Huntsville, Alabama, 2002. [Google Scholar]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications; Elsevier: Sankt Augustin, Germany, 2015. [Google Scholar]
- Wendt, J.F. Computational Fluid Dynamics: An Introduction; Springer: Rhode-Saint-Genese, Belgium, 1992. [Google Scholar]
- Scherer, G.; Kreiss, H.O. Finite Element and Finite Difference Methods for Hyperbolic Partial Differential Equations. In Mathematical Aspects of Finite Elements in Partial Differential Equations; Elsevier: Madison, WI, USA, 1974; pp. 195–212. [Google Scholar]
- Ashgriz, N.; Mostaghimi, J. An Introduction to Computational Fluid Dynamics. In Fluid Flow Handbook; McGraw-Hill Education: Toronto, ON, Canada, 2002; pp. 1–49. [Google Scholar]
- Marfurt, K.J. Accuracy of finite-difference and finite-element modelling of the scalar and elastic wave equations. Geophysics 1984, 49, 493–682. [Google Scholar] [CrossRef]
- Gupta, K.K.; Meek, J.L. A Brief History of The Beginning of The Finite Element Method. Int. J. Numer. Methods Eng. 1994, 39, 3761–3774. [Google Scholar] [CrossRef]
- Liu, G.R.; Quek, S.S. The Finite Element Method: A Practical Course; Elsevier: Cincinnati, OH, USA, 2014. [Google Scholar]
- Dhatt, G.; Touzot, G.; Lefrancois, E. Finite Element Method; Wiley: London, UK, 2012. [Google Scholar]
- Leveque, R.J. Finite Volume Methods for Hyperbolic Problems; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Jeong, W.; Seong, J. Comparison of effects on technical variances of computational fluid dynamics (CFD) software based on finite element and finite volume methods. Int. J. Mech. Sci. 2014, 78, 19–26. [Google Scholar] [CrossRef]
- Penta Precision. Your Guide to Aluminium Bronze Machining. 2023. Available online: https://www.pentaprecision.co.uk/material-resources/bronze-resources/aluminium-bronze-machining (accessed on 4 June 2023).
- The Piping Mart. Advantages and Disadvantages of Aluminium Bronze. 2022. Available online: https://blog.thepipingmart.com/metals/advantages-and-disadvantages-of-aluiminium-bronze/ (accessed on 4 June 2023).
- Erazo, J.; Barragan, G.; Pérez-Sánchez, M.; Tapia, C.; Calahorrano, M.; Hidalgo, V. Geometrical Optimization of Pelton Turbine Buckets forEnhancing Overall Efficiency by Using a ParametricModel—A Case Study: Hydroelectric Power Plant “Illuchi N2”from Ecuador. Energies 2022, 15, 9052. [Google Scholar] [CrossRef]
- Kumashiro, T.; Fukuhara, H.; Tani, K. Unsteady CFD simulation for bucket design optimization of Pelton turbine runner. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 022003. [Google Scholar] [CrossRef]
- Židonis, A.; Panagiotopoulos, A.; Aggidis, G.A.; Anagnostopoulos, J.S.; Papantonis, D.E. Parametric optimisation of two Pelton turbine runner designs using CFD*. J. Hydrodyn. 2015, 27, 403–412. [Google Scholar] [CrossRef]
- Camuffo, D. Microclimate for Cultural Heritage, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Bhattarai, S.; Vichare, P.; Dahal, K.; Al Makky, A.; Olabi, A. Novel Trends in Modelling Techniques of Pelton Turbine Bucketfor Increased Renewable Energy Production. Renew. Sustain. Energy Rev. 2019, 112, 87–101. [Google Scholar] [CrossRef]
- Perrig, A.; Avellan, F.; Farhat, M.; Parkinson, E.; Kueny, J.-L. Flow in a Pelton Turbine Bucket: Numerical and Experimental Investigation. J. Fluids Eng. 2006, 128, 350–358. [Google Scholar] [CrossRef]
- Wille, R.; Fernholz, H. Report on the first European Mechanics Colloquium, on the Coanda effect. J. Fluid Mech. 1965, 23, 801–819. [Google Scholar] [CrossRef]
- Aggidis, G.; Zidonis, A. Pelton turbine: Identifying the optimum number of buckets using CFD. J. Hydrodyn. 2016, 28, 75–83. [Google Scholar]
- Budiarso, W.; Lubis, M.; Adanta, D. Performance of a Low Cost Spoon-Based Turgo Turbine for Pico Hydro Installation. Energy Procedia 2018, 156, 447–451. [Google Scholar] [CrossRef]
- Farge, T.Z.; Owaid, A.J.; Qasim, M.A.K. Effect of Flow Parameters on Pelton Turbine Performance by using different nozzles. Int. J. Model. Optim. 2017, 7, 128–133. [Google Scholar]
- Židonis, A.; Petley, S.; Aggidis, G.; Benzon, D. Experimental investigation and analysis of the spear valve. In HYDRO 2017; Researchgate: Seville, Spain, 2017. [Google Scholar]
- Gudukeya, L.K.; Mbohwa, C. Improving the Efficiencies of Pelton Wheel in MicroHydro Power Plants. In Proceedings of the International Conference on Industrial Engineering and Operations Management, Bogota, Colombia, 25–26 October 2017. [Google Scholar]
- Leman, O.Y.; Wulandari, R.; Bintara, R. Optimization of Nozzle Number, Nozzle Diameter and Number of Bucket of Pelton Turbine using Computational Fluid Dynamics and Taguchi Methods. IOP Conf. Ser. Mater. Sci. Eng. 2019, 694, 012017. [Google Scholar] [CrossRef]
- Srirekha, A.; Bashetty, A. Infinite to Finite: An overview to finite element analysis. Indian J. Dent. Res. 2010, 21, 425. [Google Scholar] [CrossRef]
- Dar, F.H.; Meakin, J.R.; Aspden, R.M. Statistical Methods in Finite Element Analysis. J. Biomech. 2002, 35, 1155–1161. [Google Scholar] [CrossRef] [PubMed]
- Petrolo, M.; Carrera, E.; Cinefra, M.; Zappino, E. Finite Element Analysis of Structures through Unified Formulation; John Wiley and Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- ANSYS. Measuring Rotation in Ansys Mechanical Application (Workbench). 2018. Available online: https://forum.ansys.com/forums/topic/measuring-rotation-in-ansys-mechanical-application-workbench/ (accessed on 4 June 2023).
- Bhavikatti, S. Finite Element Analysis, 1st ed.; New Age International (P) Publishers: New Delhi, India, 2005. [Google Scholar]
- Costen, E. FEA Mesh Elements & Nodes Guide|Intro to FEA. 2019. Available online: https://asrengineering.com/2019/09/23/FEA-MESH-ELEMENTS-NODES-GUIDE-INTRO-TO-FEA/ (accessed on 4 June 2023).
- Michelmann, M.; Khim, J. Finite Elements. Available online: https://brilliant.org/wiki/finite-elements/ (accessed on 4 June 2023).
- Gardiner, J. Finite Element Analysis Convergence and Mesh Independence. 2017. Available online: https://www.xceed-eng.com/FINITE-ELEMENT-ANALYSIS-CONVERGENCE-AND-MESH-INDEPENDENCE/ (accessed on 4 June 2023).
- Kunaporn, S.; Ramulu, M.; Jenkins, M.G.; Hashish, M. Residual stress induced by waterjet peening: A finite element analysis. Press. Vessel. Technol. 2004, 126, 333–340. [Google Scholar] [CrossRef]
- Egusquiza, M.; Egusquiza, E.; Valentin, D.; Valero, C.; Presas, A. Failure Investigation of a Pelton Turbine Runner. Eng. Fail. Anal. 2017, 81, 234–244. [Google Scholar] [CrossRef]
- Chavez, J.; Valencia, J.; Jaramillo, G.; Coronado, J.; Rodriguez, S. Failure Analysis of a Pelton Impeller. Eng. Fail. Anal. 2015, 48, 297–307. [Google Scholar] [CrossRef]
- Mesh Quality. ANSYS. 29 January 2009. Available online: https://www.afs.enea.it/project/neptunius/docs/fluent/html/ug/node167.htm#:~:text=A (accessed on 15 March 2023).
- PA12. Designerdata. 2023. Available online: https://designerdata.nl/materials/plastics/thermo-plastics/polyamide-12 (accessed on 10 January 2023).
- Overview of Materials for Nylon 12. MatWeb. 2023. Available online: https://www.matweb.com/search/DataSheet.aspx?MatGUID=0e37a459c4eb452faa9d92659f9a0ccc&ckck=1 (accessed on 10 January 2023).
- CableOrganizer. Materials Spotlight: The Properties of Nylon 12. CableOrganizer. 2023. Available online: https://www.cableorganizer.com/learning-center/articles/materials-nylon12.php (accessed on 2 June 2023).
- Duquesnoy, M.; Lombardo, T.; Chouchane, M.; Primo, E.N.; Franco, A.A. Data-driven assessment of electrode calendering process by combining experimental results, in silico mesostructures generation and machine learning. J. Power Sources 2020, 480, 229103. [Google Scholar] [CrossRef]
- Hill, T.P.; Miller, J. How to combine independent data sets for the same quantity. Chaos 2011, 21, 033102. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Wang, Z.; Zhang, J.; Zeng, C.; Yan, Z. Numerical and Experimental Analysis of the Hydraulic Performance of a Prototype Pelton Turbine. Proc. Inst. Mech. Eng. Part A J. Power Energy 2014, 228, 46–55. [Google Scholar] [CrossRef]
- Petley, S.; Aggidis, G.A. Transient CFD and experimental analysis for improved Pelton turbine casing designs. IOP Conf. Ser. Earth Environ. Sci. 2019, 240, 022005. [Google Scholar] [CrossRef]


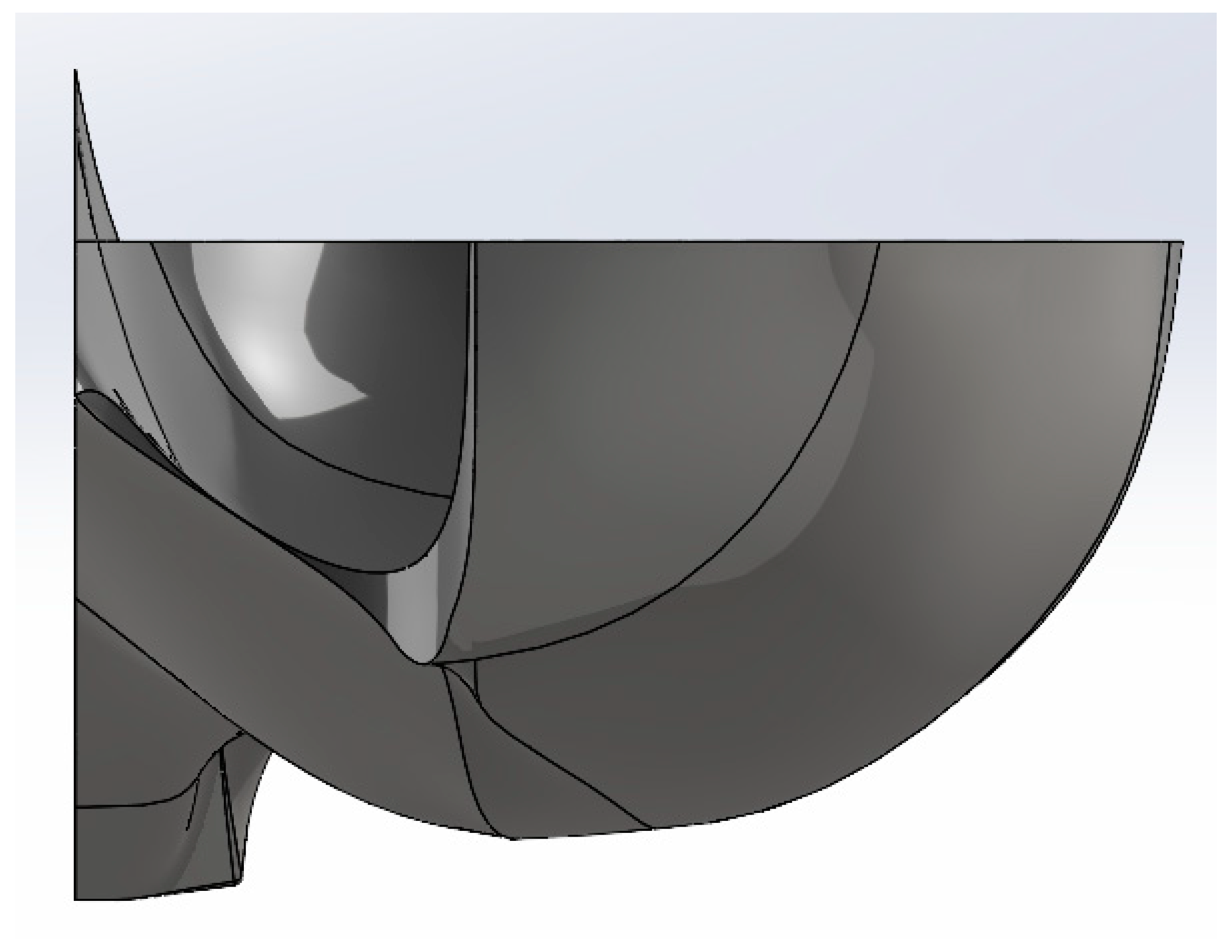
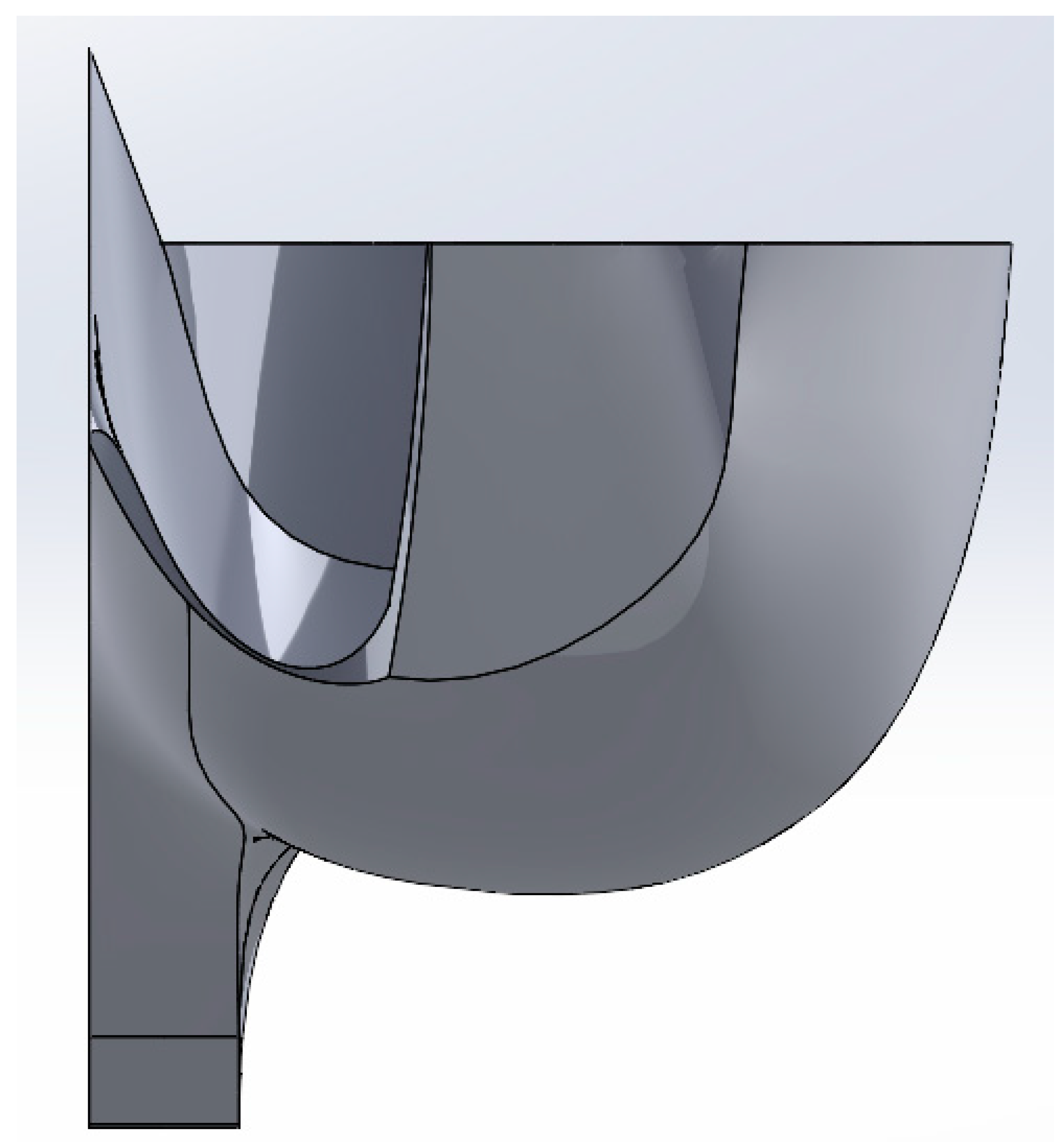
| Paper | Publication Year | Optimization Method | Parameters Investigated | Results | Comments |
|---|---|---|---|---|---|
| Pelton Turbine Bucket Optimizations | |||||
| Pickston et al. (Project Report Paper) [1] | 2023 | Numerical, CFD (ANSYS CFX) |
| 6.73% efficiency increase | The biggest increase in efficiency came from the increase in bucket depth and the updated internal geometry |
| Erazo et al. [36] | 2022 | Numerical, CFD (ANSYS 2019 R2) |
| 3.14% efficiency increase | Exit angle had the largest influence on the efficiency of the Pelton turbine. Both B/do and L/do are inversely proportional |
| Kumashiro et al. [37] | 2016 | Numerical, CFD (ANSYS CFX) |
| 2–3% Variation | Reduction in both Bucket Width and Length caused an increase in turbine efficiency |
| Židonis et al. [38] | 2015 | Numerical, CFD (ANSYS CFX) |
| 0.9% efficiency increase | An overall improvement of 0.9% was achieved by extending the bucket length and depth and adjusting the exit angle to match these changes |
| Additional Pelton Turbine Optimizations | |||||
| Židonis and Aggidis [43] | 2016 | Numerical, CFD (ANSYS CFX) |
| 0.8% efficiency increase | Increased runner efficiency by 0.8% under single jet operation when reducing the number of buckets from 18 to 15 |
| Farge et al. [45] | 2017 | Experimental |
| 60% efficiency variation between nozzle diameters | The best performance of the Pelton turbine was obtained by the nozzle with an outlet diameter of 8.87 mm, which had a 60% increase in efficiency compared to another nozzle with an outer diameter of 5.19 mm. |
| Židonis et al. [46] | 2017 | Numerical, CFD (ANSYS Fluent) |
| 1% increase | Steeper nozzle and spear tip angles produce higher efficiencies than the standard design. A gain of about 1% in efficiency was achieved at the BEP of the turbine |
| Gudukeya and Mbohwa [47] | 2017 | Experimental |
| 20–25% efficiency increase | The use of stainless steel resulted in the least rough finish. Gave an overall increase of 20–25% on the turbine efficiencies |
| Leman et al. [48] | 2019 | Numerical, CFD (ANSYS Fluent) |
| 42.97% efficiency variation between nozzle diameters | The most optimal experimental variation was the variation with the number of bucket 27 and a double nozzle with a diameter of 5.5 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aggidis, G.; Židonis, A.; Burtenshaw, L.; Dubois, M.; Orritt, S.; Pickston, D.; Prigov, G.; Wilmot, L. Methodology for the Optimization of a Novel Hydro Turbine with a Case Study. Energies 2023, 16, 7591. https://doi.org/10.3390/en16227591
Aggidis G, Židonis A, Burtenshaw L, Dubois M, Orritt S, Pickston D, Prigov G, Wilmot L. Methodology for the Optimization of a Novel Hydro Turbine with a Case Study. Energies. 2023; 16(22):7591. https://doi.org/10.3390/en16227591
Chicago/Turabian StyleAggidis, George, Audrius Židonis, Luke Burtenshaw, Marc Dubois, Stephen Orritt, Dominic Pickston, George Prigov, and Luke Wilmot. 2023. "Methodology for the Optimization of a Novel Hydro Turbine with a Case Study" Energies 16, no. 22: 7591. https://doi.org/10.3390/en16227591
APA StyleAggidis, G., Židonis, A., Burtenshaw, L., Dubois, M., Orritt, S., Pickston, D., Prigov, G., & Wilmot, L. (2023). Methodology for the Optimization of a Novel Hydro Turbine with a Case Study. Energies, 16(22), 7591. https://doi.org/10.3390/en16227591







