Prediction of CO2 in Public Buildings
Abstract
:1. Introduction
1.1. Motivation
1.2. State of the Art
1.3. Paper Contributions
- It is widely accepted that white-box or physical models lack precision for short-time prediction; however, the benefits that data-based models may provide in comparison are not well studied. In this work, we compare machine learning algorithms with a physics-based model to appreciate the actual advantage of the first class of methodologies;
- In addition, we compare a range of data-based algorithms, starting from a simple regression algorithm, continuing with a more advanced KNN method, and finally with a sophisticated LSTM neural network, to evaluate the needs and advantages of more complex machine learning approaches;
- Finally, our case study is different from the others, as our CO2 predictions are performed by exploiting both available historical data, as most of the other references do, but also other measured variables, such as the opening and closure of doors/windows and the full, partial, or non-utilization of mechanical ventilation devices.
2. Methodology
2.1. Physical Model
2.2. Data-Based Models
2.2.1. A Simple Regression Algorithm
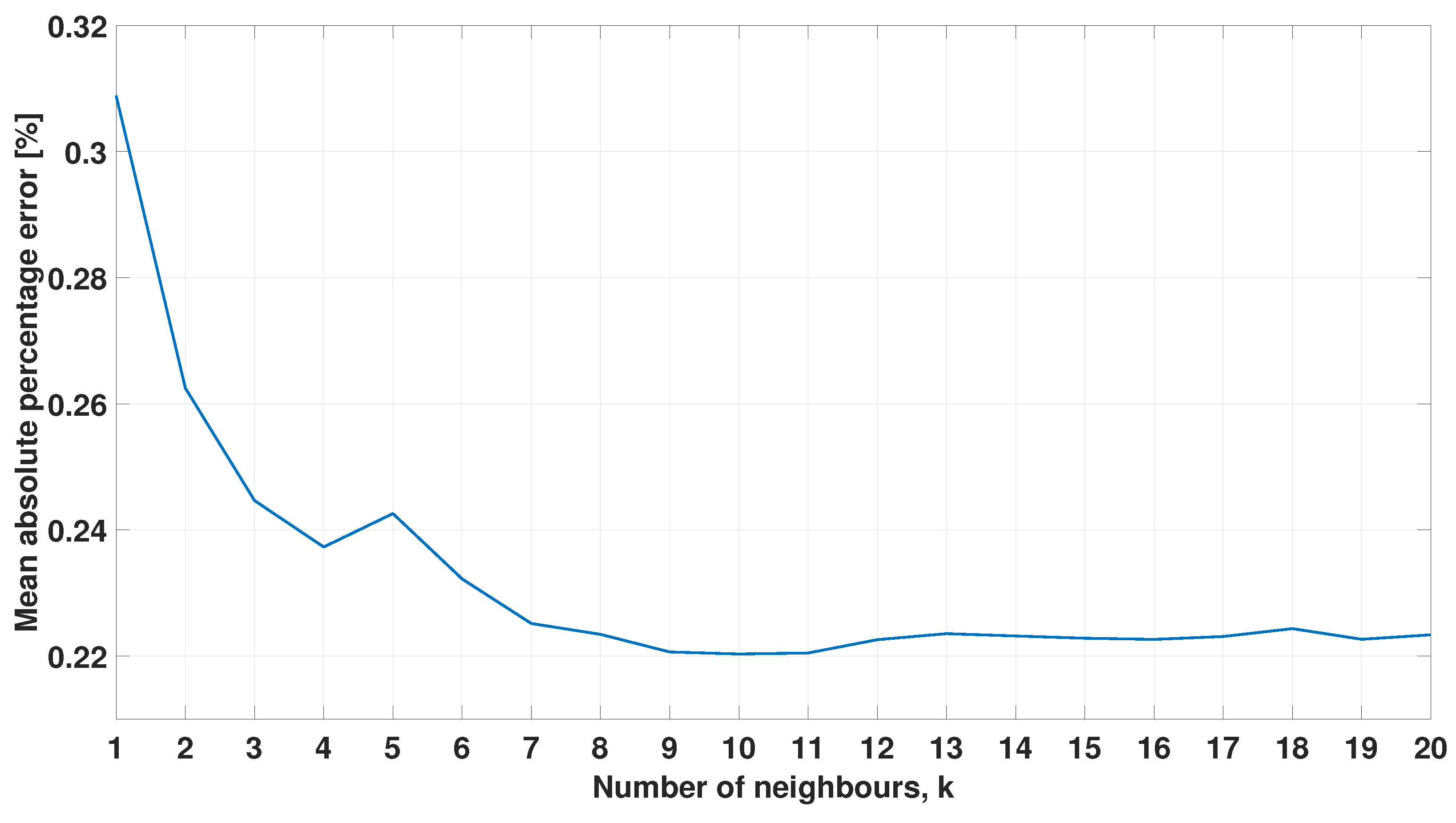
2.2.2. k-Nearest Neighbor
- Choose a number of neighbors, k, which will participate in forming the new prediction. The choice of k is not trivial, and it significantly influences the performance of the algorithm [21].
- Calculate the distance between the explanatory variables in the target case and other values in the training dataset. The classic choice as a distance measure for continuous variables is the Euclidean distance, which, for vectors and , of length n, may be computed in terms of their components, and , as follows:In our application, the explanatory variables are the number of occupants in a room, whether doors/windows are open, and whether the mechanical ventilation is switched on or off (or in partial operation).
- Choose the k closest neighbors, according to the list of distances calculated in step (2), and assign weights.
- Form the prediction, by taking the average of the CO2 measured values in the selected k historical instances. The average has to be taken in a weighted fashion, using the weights (and the neighbors) computed in step (3).
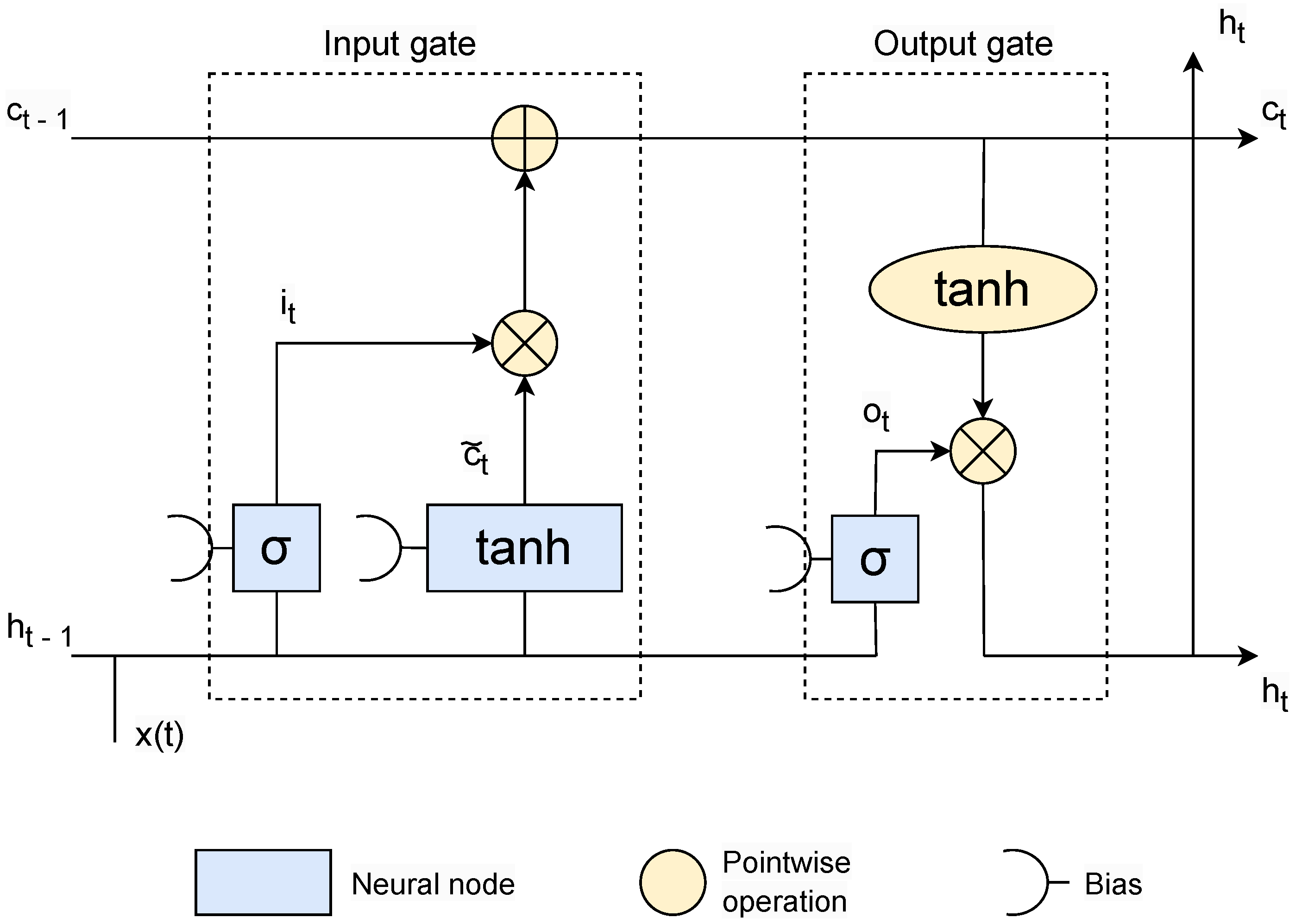
2.2.3. LSTM
3. Case Study
- Multisensor 9 in 1 SmartDHOME: It measures temperature (°C), brightness (lx), CO2 (ppm), humidity (%), particulate matter (g/m), volatile organic compounds (ppb), noise pollution (dB), movements, and the presence of smoke.
- Multisensor 4 in 1 SmartDHOME: It measures temperature (°C), luminosity (lx), humidity (%), and movements.
3.1. Algorithm Setup and Model Training
- The initial concentration of CO2 at the beginning of the day;
- The time series of the state of the doors during the morning. This information is coded as a real number equal to ‘0’ if all doors are closed, as ‘1’ if they are open, and as ‘0.5’ if only one door is open;
- The time series of the state of the windows during the whole number. Similar to the doors, it is coded with a real number, ranging from 0 to 1;
- The time series of the number of people in the room during the whole morning;
- The sequence of the state of the ventilation system, which again is coded with a real number ranging from 0 to 1, depending on the rate of the ventilation system’s operation power. Here, ‘0’ corresponds to the mechanical ventilation switched off.
3.2. Evaluation Metrics
- Root mean square error (RMSE):
- Mean absolute percentage error (MAPE):
- Coefficient of determination (R2):
4. Results and Discussion
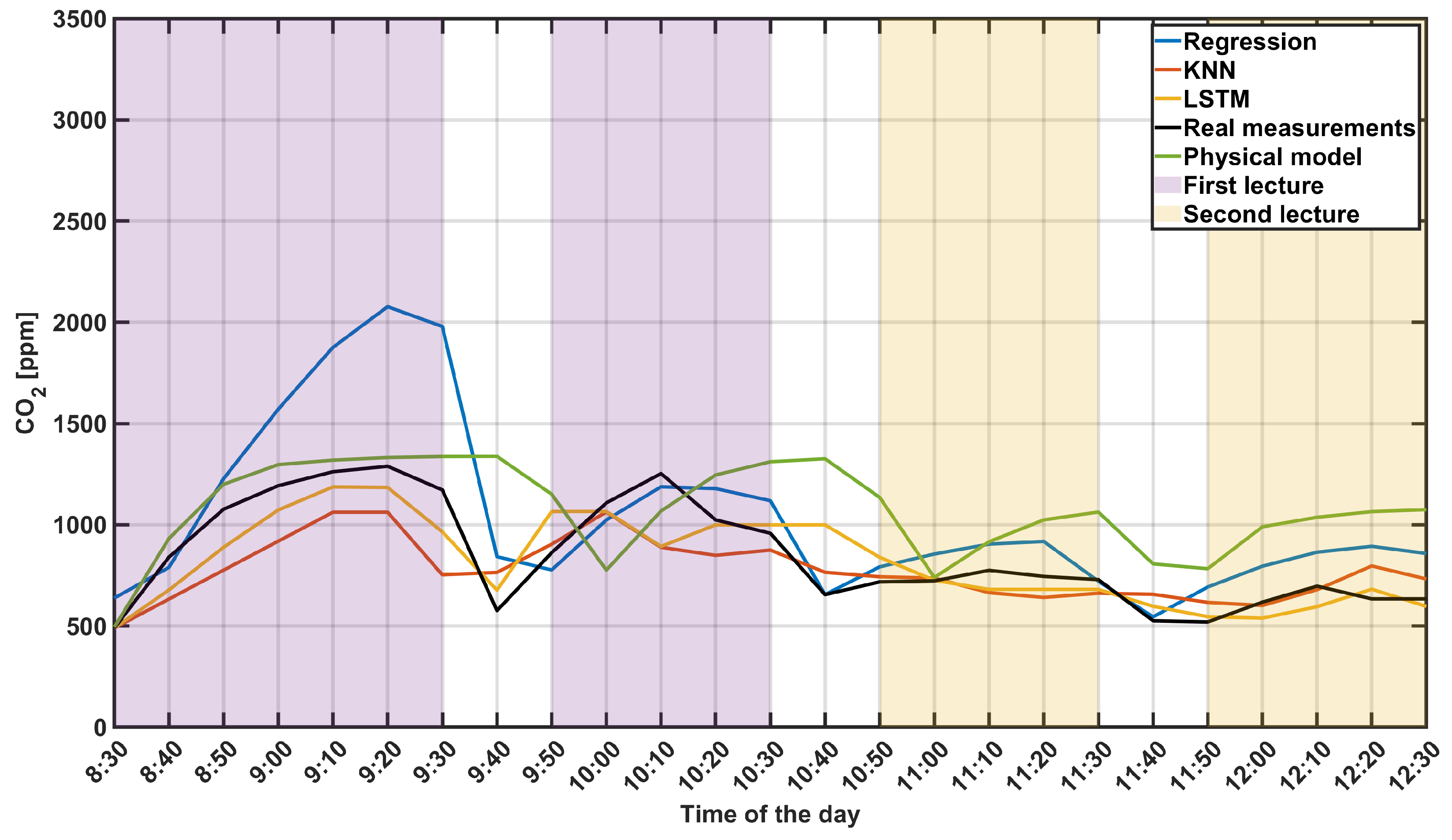
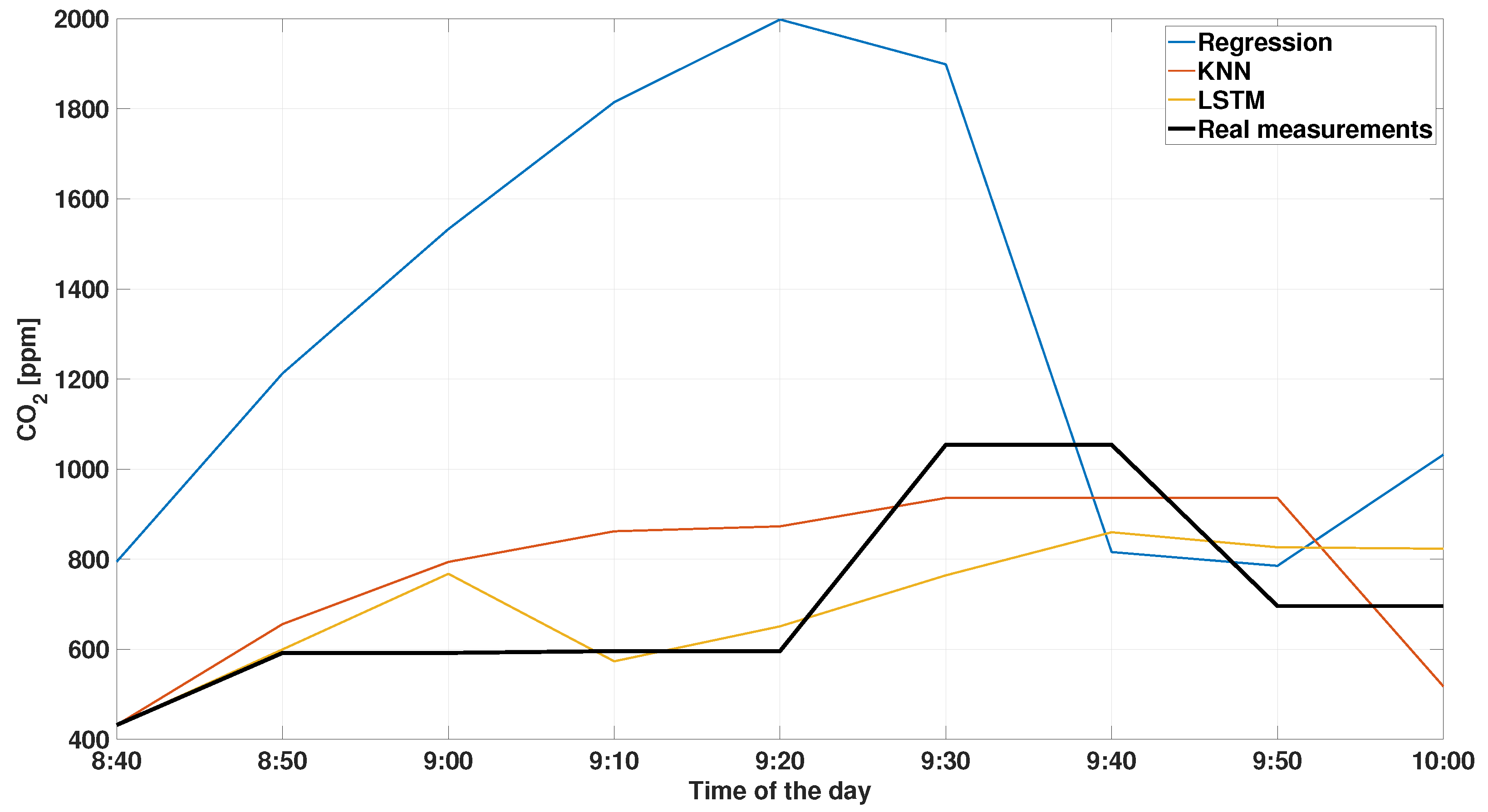
4.1. Machine Learning Algorithms Outperform the Physical Model
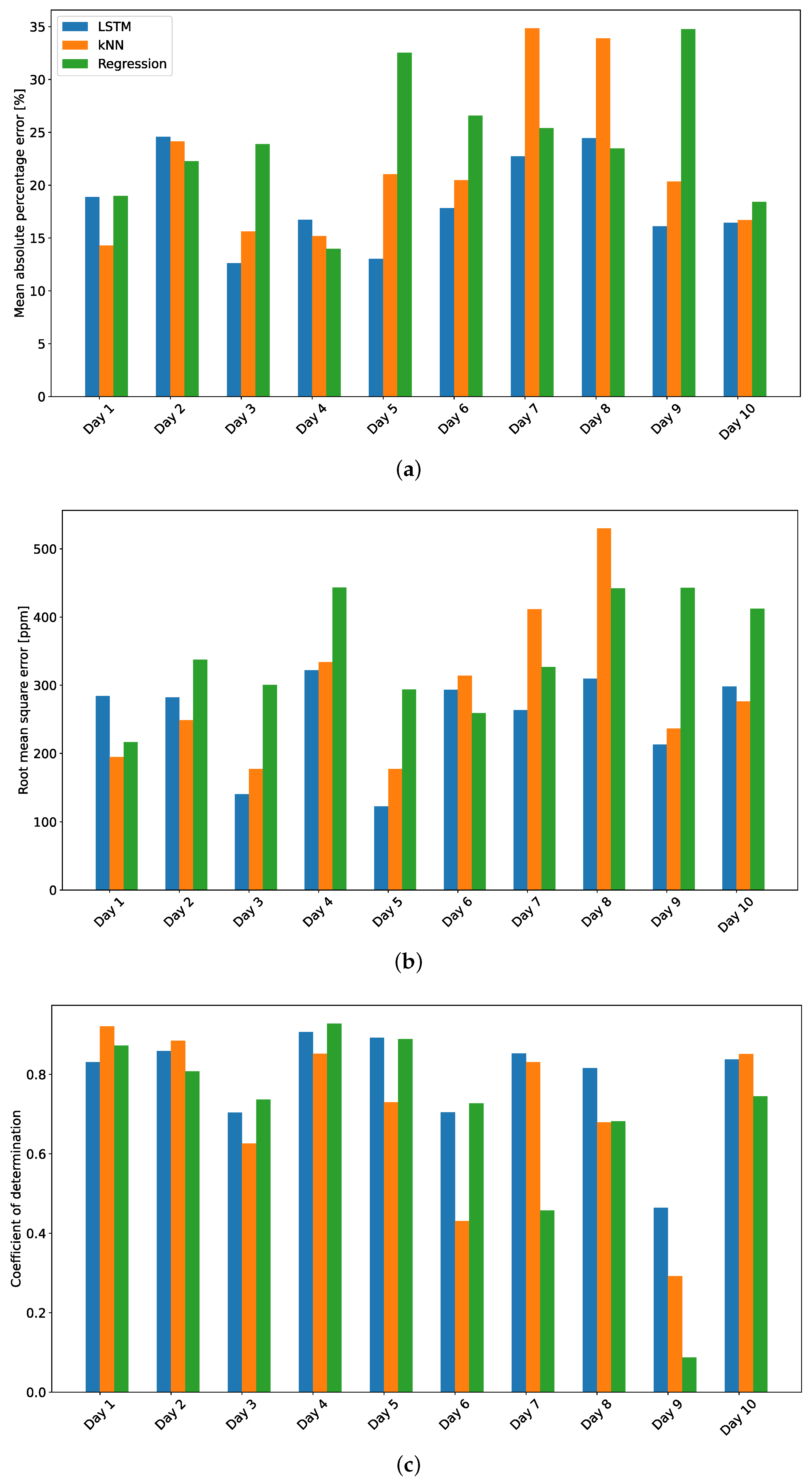
4.2. Comparison between LSTM, KNN, and Regression
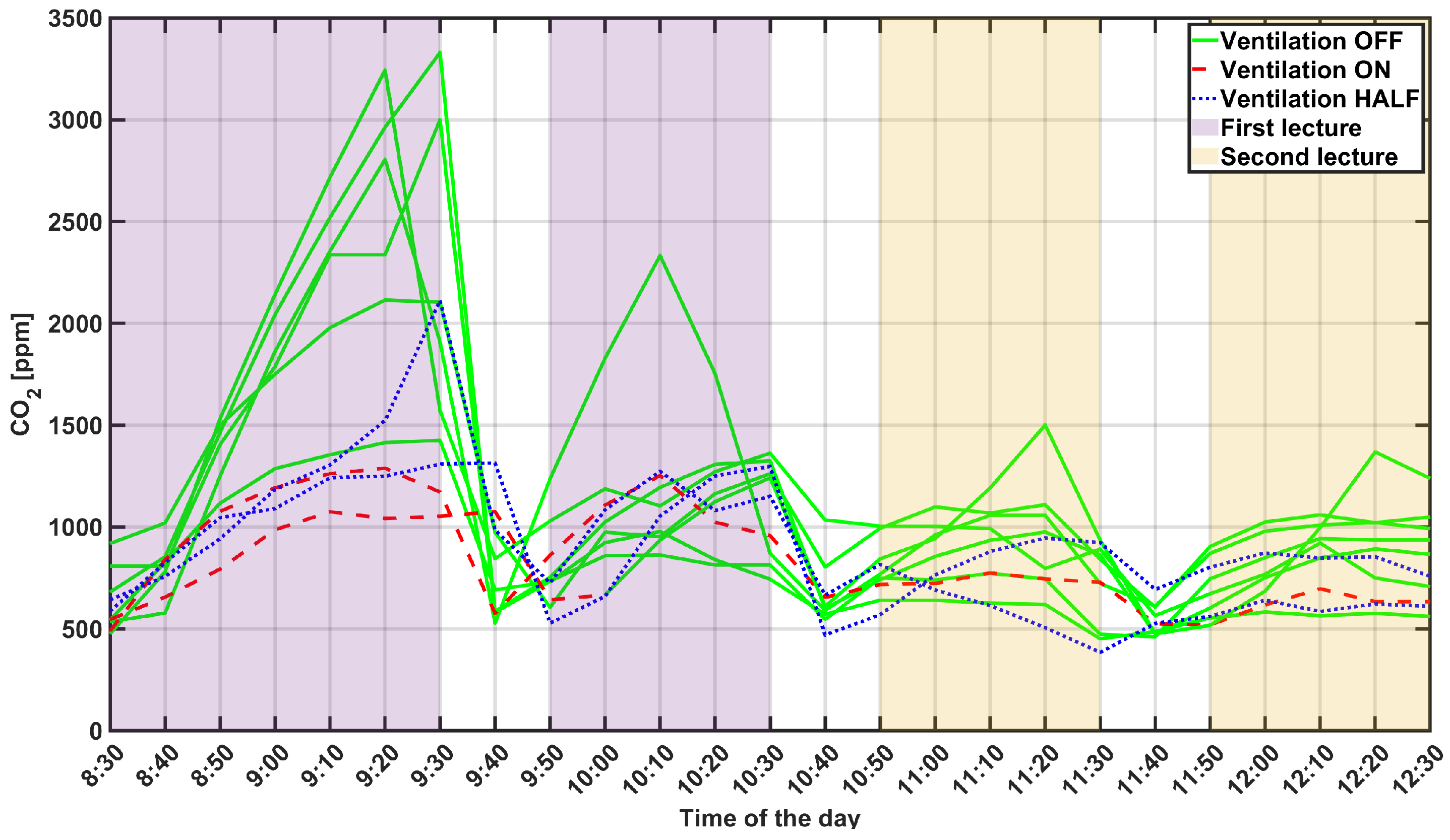
4.3. A Comparison of Different Environmental Conditions
4.4. Final Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moghadam, T.T.; Ochoa Morales, C.E.; Lopez Zambrano, M.J.; Bruton, K.; O’Sullivan, D.T.J. Energy efficient ventilation and indoor air quality in the context of COVID-19—A systematic review. Renew. Sustain. Energy Rev. 2023, 182, 113356. [Google Scholar] [CrossRef] [PubMed]
- Franco, A.; Crisostomi, E. HVAC Systems Operation Control Based on Indirect Occupant-Centric Method for Ensuring Safety Conditions and Reducing Energy Use in Public Buildings after COVID-19. Available online: https://ssrn.com/abstract=4440539 (accessed on 2 July 2023). [CrossRef]
- Ventilation in Buildings. Available online: https://www.cdc.gov/coronavirus/2019-ncov/community/ventilation.html (accessed on 1 August 2023).
- Lim, A.Y.; Yoon, M.; Kim, E.H.; Kim, H.A.; Lee, M.J.; Cheong, H.K. Effects of mechanical ventilation on indoor air quality and occupant health status in energy-efficient homes: A longitudinal field study. Sci. Total. Environ. 2021, 785, 147324. [Google Scholar] [CrossRef]
- Franco, A.; Schito, E. Definition of optimal ventilation rates for balancing comfort and energy use in indoor spaces using CO2 concentration data. Buildings 2020, 10, 135. [Google Scholar] [CrossRef]
- Taheri, S.; Razban, A. Learning-based CO2 concentration prediction: Application to indoor air quality control using demand-controlled ventilation. Build. Environ. 2021, 205, 108164. [Google Scholar] [CrossRef]
- Li, C.; Cui, C.; Li, M. A proactive 2-stage indoor CO2-based demand-controlled ventilation method considering control performance and energy efficiency. Appl. Energy 2023, 329, 120288. [Google Scholar] [CrossRef]
- Franco, A.; Crisostomi, E.; Hammoud, M. Advanced Monitoring Techniques for Optimal Control of Building Management Systems for Reducing Energy Use in Public Buildings. Int. J. Sustain. Dev. Plan. 2023, 18, 2025–2035. [Google Scholar] [CrossRef]
- Lu, X.; Pang, Z.; Fu, Y.; O’Neill, Z. The nexus of the indoor CO2 concentration and ventilation demands underlying CO2-based demand-controlled ventilation in commercial buildings: A critical review. Build. Environ. 2022, 218, 109116. [Google Scholar] [CrossRef]
- Kapoor, N.R.; Kumar, A.; Kumar, A.; Kumar, A.; Mohammed, M.A.; Kumar, K.; Kadry, S.; Lim, S. Machine Learning-Based CO2 Prediction for Office Room: A Pilot Study. Wirel. Commun. Mob. Comput. 2022, 2022, 9404807. [Google Scholar] [CrossRef]
- Kallio, J.; Tervonen, J.; Räsänen, P.; Mäkynen, R.; Koivusaari, J.; Peltola, J. Forecasting office indoor CO2 concentration using machine learning with a one-year dataset. Build. Environ. 2021, 187, 107409. [Google Scholar] [CrossRef]
- Tagliabue, L.C.; Re Cecconi, F.; Rinaldi, S.; Ciribini, A.L.C. Data driven indoor air quality prediction in educational facilities based on IoT network. Energy Build. 2021, 236, 110782. [Google Scholar] [CrossRef]
- Dai, H.; Huang, G.; Wang, J.; Zeng, H. VAR-tree model based spatio-temporal characterization and prediction of O3 concentration in China. Ecotoxicol. Environ. Saf. 2023, 257, 114960. [Google Scholar] [CrossRef] [PubMed]
- Duhirwe, P.N.; Ngarambe, J.; Yun, G.Y. Energy-efficient virtual sensor-based deep reinforcement learning control of indoor CO2 in a kindergarten. Front. Archit. Res. 2023, 12, 394–409. [Google Scholar] [CrossRef]
- Zhu, Y.; Al-Ahmed, S.A.; Shakir, M.Z.; Olszewska, J.I. LSTM-Based IoT-Enabled CO2 Steady-State Forecasting for Indoor Air Quality Monitoring. Electronics 2023, 12, 107. [Google Scholar] [CrossRef]
- Yang, G.; Yuan, E.; Wu, W. Predicting the long-term CO2 concentration in classrooms based on the BO–EMD–LSTM model. Build. Environ. 2022, 224, 109568. [Google Scholar] [CrossRef]
- Martínez-Comesaña, M.; Eguia-Oller, P.; Martinez-Torres, J.; Febrero-Garrido, L.; Granada-Álvarez, E. Optimisation of thermal comfort and indoor air quality estimations applied to in-use buildings combining NSGA-III and XGBoost. Sustain. Cities Soc. 2022, 80, 103723. [Google Scholar] [CrossRef]
- Wang, X.; Yan, J.; Wang, X.; Wang, Y. Air quality forecasting using GRU model based on multiple sensors nodes. IEEE Sensors Lett. 2023, 7, 6003804. [Google Scholar] [CrossRef]
- Khazaei, B.; Shiehbeigi, A.; Haji Molla Ali Kani, A. Modeling indoor air carbon dioxide concentration using artificial neural network. Int. J. Environ. Sci. Technol. 2019, 16, 729–736. [Google Scholar] [CrossRef]
- Emmerich, S.J.; Persily, A.K. State-of-the-Art Review of CO2 Demand Controlled Ventilation Technology and Application. Nist Interagency/Internal Rep. (NISTIR) 2001, 12, 1–43. [Google Scholar]
- Zhang, Z. Introduction to machine learning: k-Nearest neighbors. Ann. Transl. Med. 2016, 4, 218. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Eyben, F.; Weninger, F.; Squartini, S.; Schuller, B. Real-life voice activity detection with LSTM Recurrent Neural Networks and an application to Hollywood movies. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013. [Google Scholar]
- Ren, B. The use of machine translation algorithm based on residual and LSTM neural network in translation teaching. PLoS ONE 2020, 15, e0240663. [Google Scholar] [CrossRef] [PubMed]
- Karevan, Z.; Suykens, J.A.K. Transductive LSTM for time-series prediction: An application to weather forecasting. Neural Netw. 2020, 125, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Yassein, M.B.; Mardini, W.; Khalil, A. Smart homes automation using Z-Wave protocol. In Proceedings of the 2016 International Conference on Engineering & MIS (ICEMIS), Agadir, Morocco, 22–24 September 2016. [Google Scholar]
- SmartDHOME. Available online: https://www.smartdhome.com/ (accessed on 1 August 2023).
- Keras: Deep Learning for Humans. Available online: https://keras.io/ (accessed on 1 April 2023).


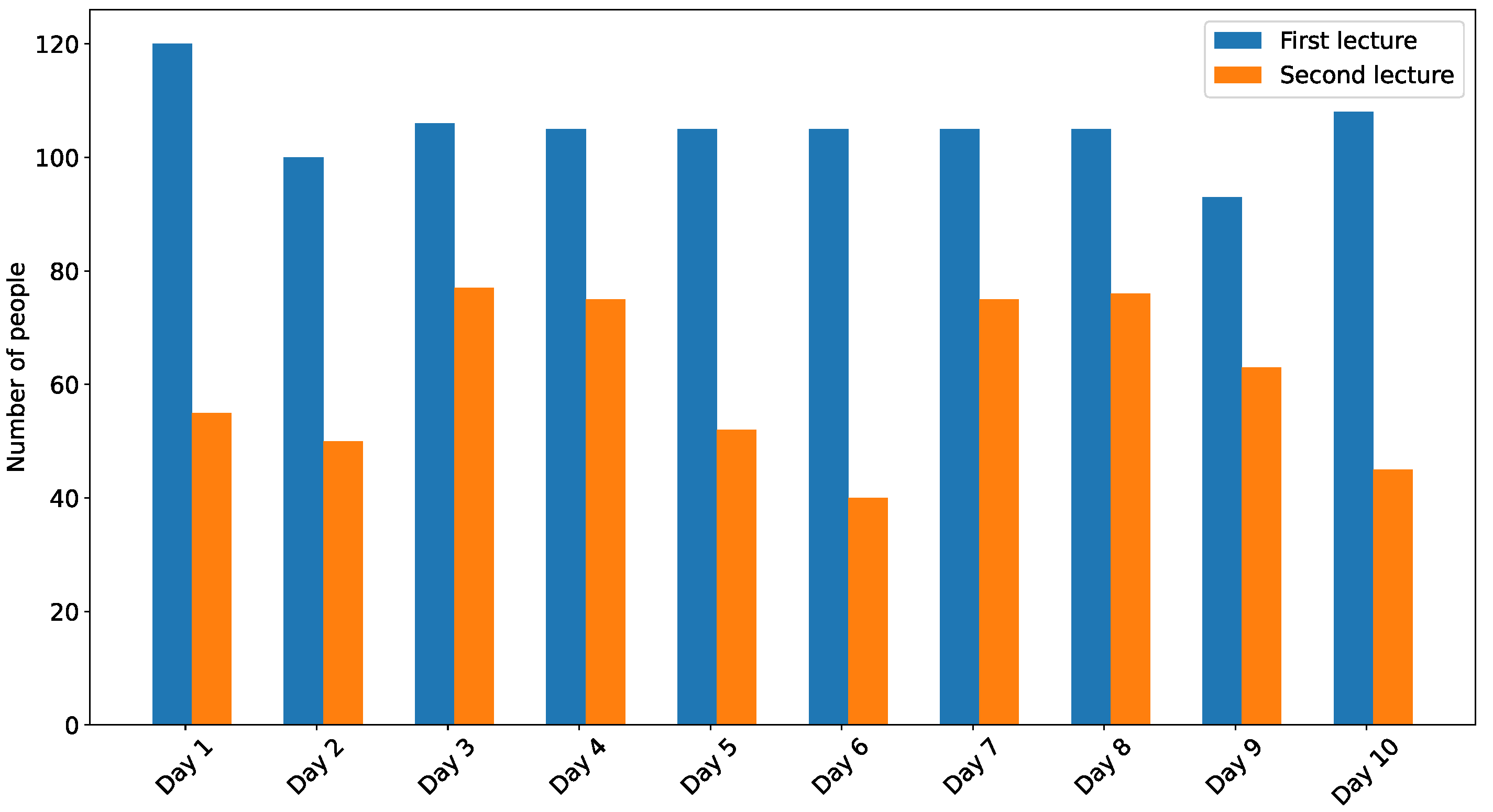

| Type of Indoor Activity | CO2 Production Rate per Person ( in m/s/person) |
|---|---|
| Adult people reading, seated | 0.0044 |
| Adult people seated | 0.0052 |
| or involved in light-intensity activities | |
| Adult people standing | 0.0063 |
| or operating at medium physical activity | |
| High-intensity physical activity | 0.0174 |
| MAPE, % | RMSE, ppm | R2 | |
|---|---|---|---|
| Regression | 24 | 347 | 0.69 |
| LSTM | 18 | 253 | 0.79 |
| KNN | 22 | 290 | 0.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dudkina, E.; Crisostomi, E.; Franco, A. Prediction of CO2 in Public Buildings. Energies 2023, 16, 7582. https://doi.org/10.3390/en16227582
Dudkina E, Crisostomi E, Franco A. Prediction of CO2 in Public Buildings. Energies. 2023; 16(22):7582. https://doi.org/10.3390/en16227582
Chicago/Turabian StyleDudkina, Ekaterina, Emanuele Crisostomi, and Alessandro Franco. 2023. "Prediction of CO2 in Public Buildings" Energies 16, no. 22: 7582. https://doi.org/10.3390/en16227582
APA StyleDudkina, E., Crisostomi, E., & Franco, A. (2023). Prediction of CO2 in Public Buildings. Energies, 16(22), 7582. https://doi.org/10.3390/en16227582








