Prediction of Lithium Battery Health State Based on Temperature Rate of Change and Incremental Capacity Change
Abstract
:1. Introduction
- (1)
- By analyzing the characteristics of the temperature difference (DT) curve, the capacity increment (IC) curve, and the differential voltage analysis (DVA) curve, five features were extracted from each of the three curves as the health factors, respectively, and the correlation with lithium battery SOH was analyzed using the Pearson correlation coefficient.
- (2)
- For the problem of the random initialization of Elman neural network weights and thresholds, the whale optimization algorithm (WOA) is used for optimization to find the best weights and thresholds. Meanwhile, for the problem that the number of hidden layers is set artificially, which leads to unsatisfactory training results, the same whale optimization algorithm is used to obtain the optimal number of hidden layers.
- (3)
- For the problem of machine learning models relying on different information sources, a weighted average method can be used to fuse the data, which improves the overall estimation accuracy and robustness, and effectively avoids the differences in prediction results due to different sources of data.
2. Feature Extraction
2.1. Oxford Dataset
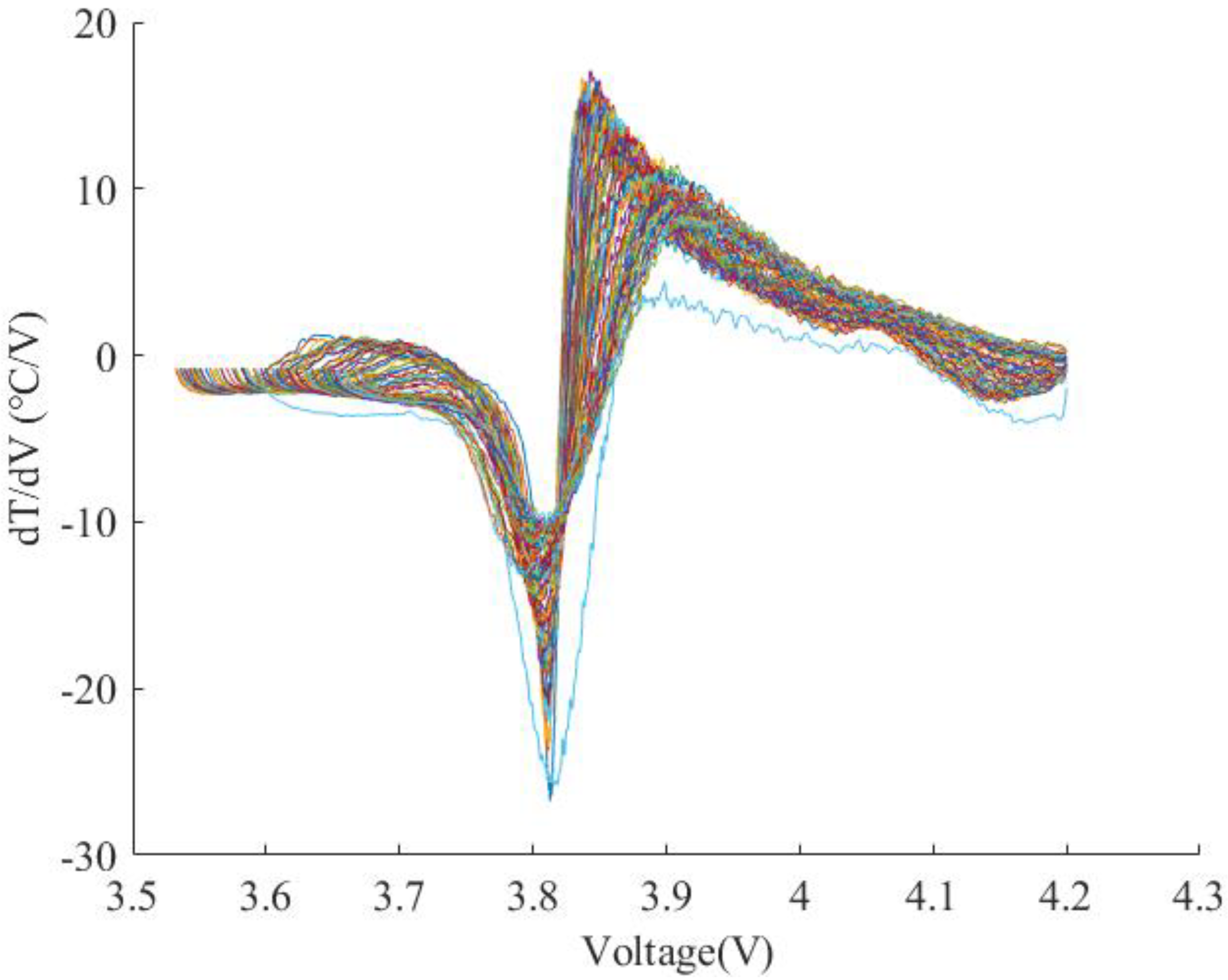
2.2. Temperature Difference Curve
DT Curve Feature Extraction
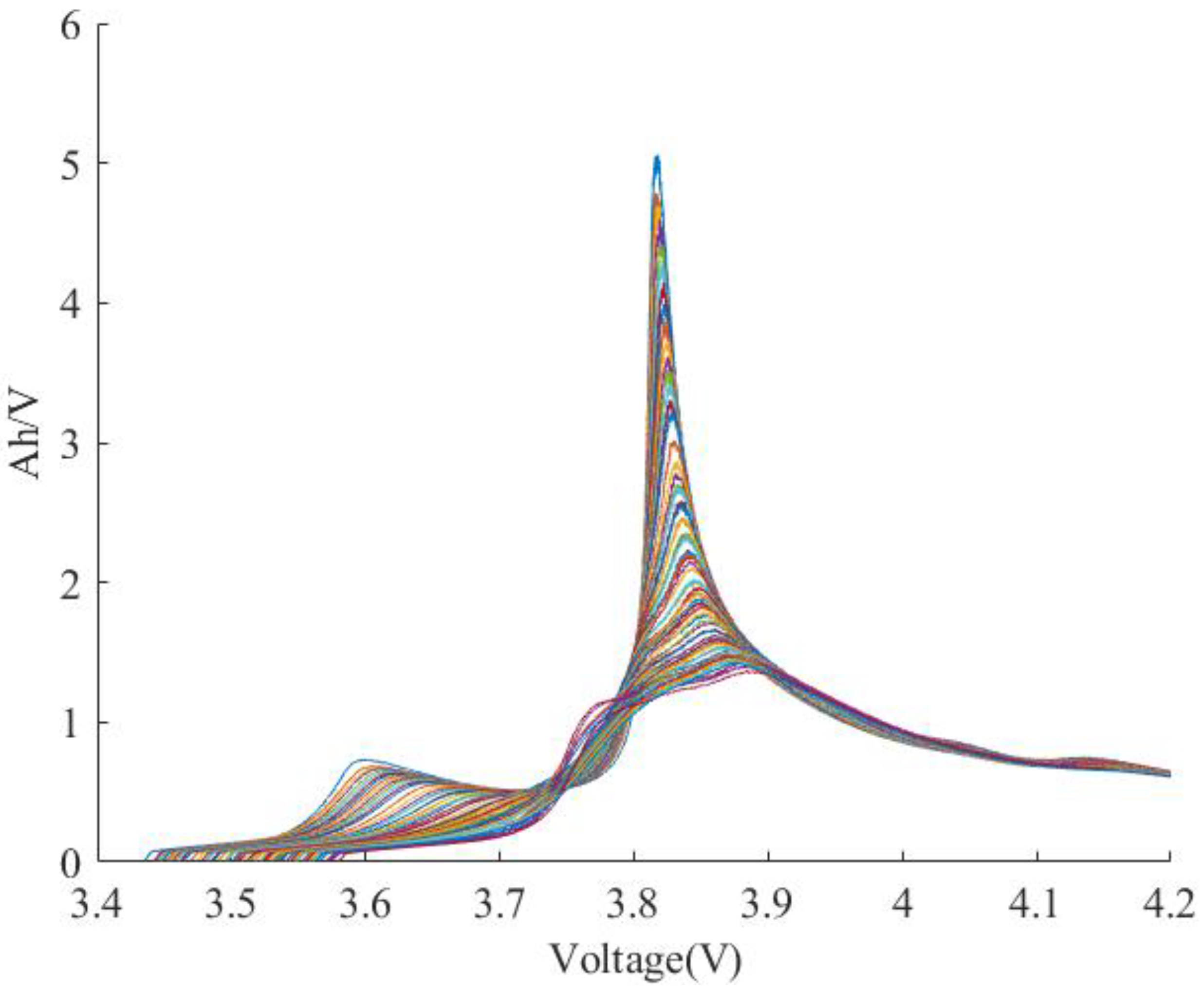
2.3. Incremental Capacity Analysis
IC Curve Feature Extraction
2.4. Differential Voltage Analysis
DVA Curve Feature Extraction
3. Elman Neural Network
Whale Optimization Algorithm (WOA)
4. Evaluation Indicators
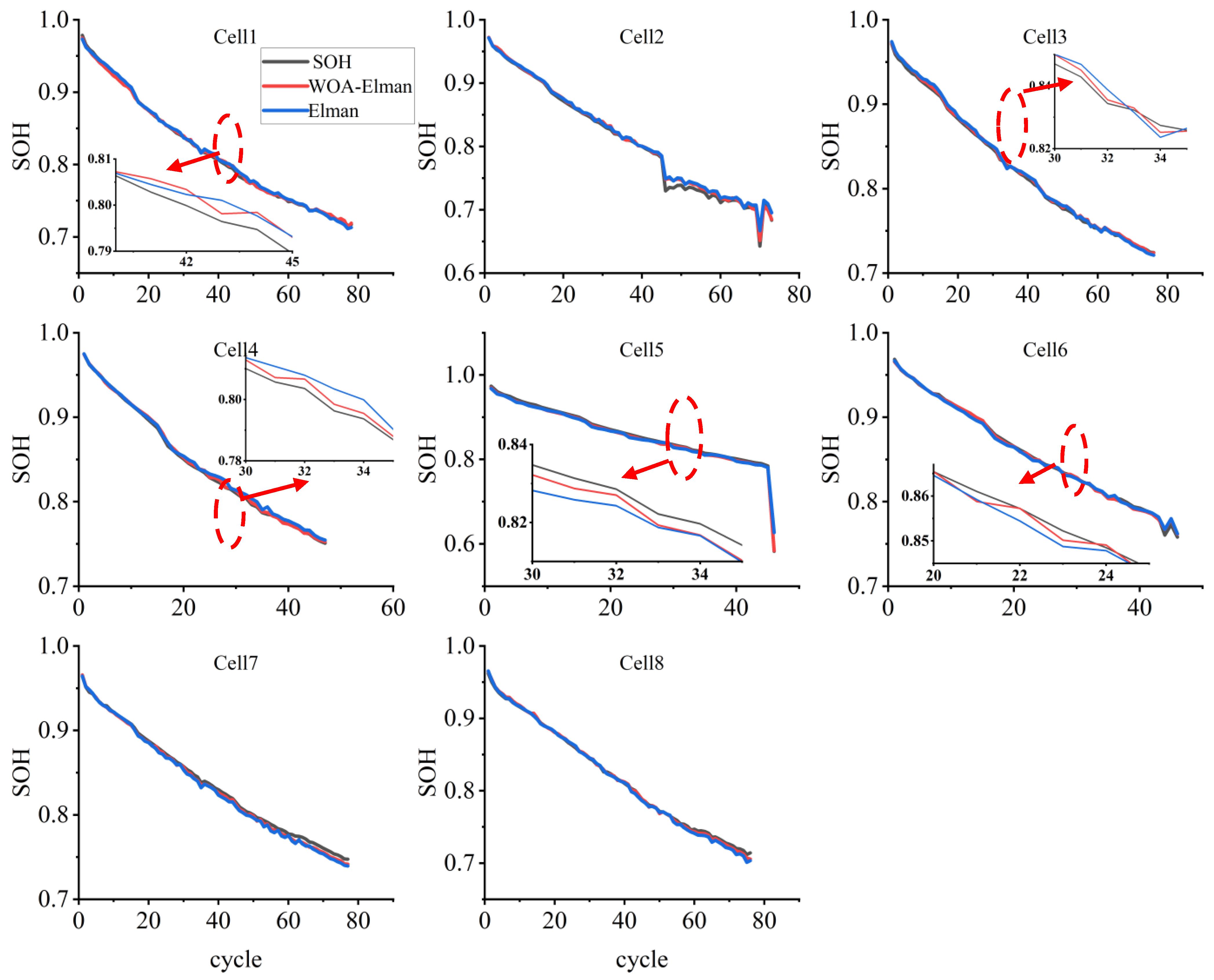
5. Projected Results
5.1. DT Forecast Results
5.2. IC Forecast Results
5.3. DVA Forecast Results
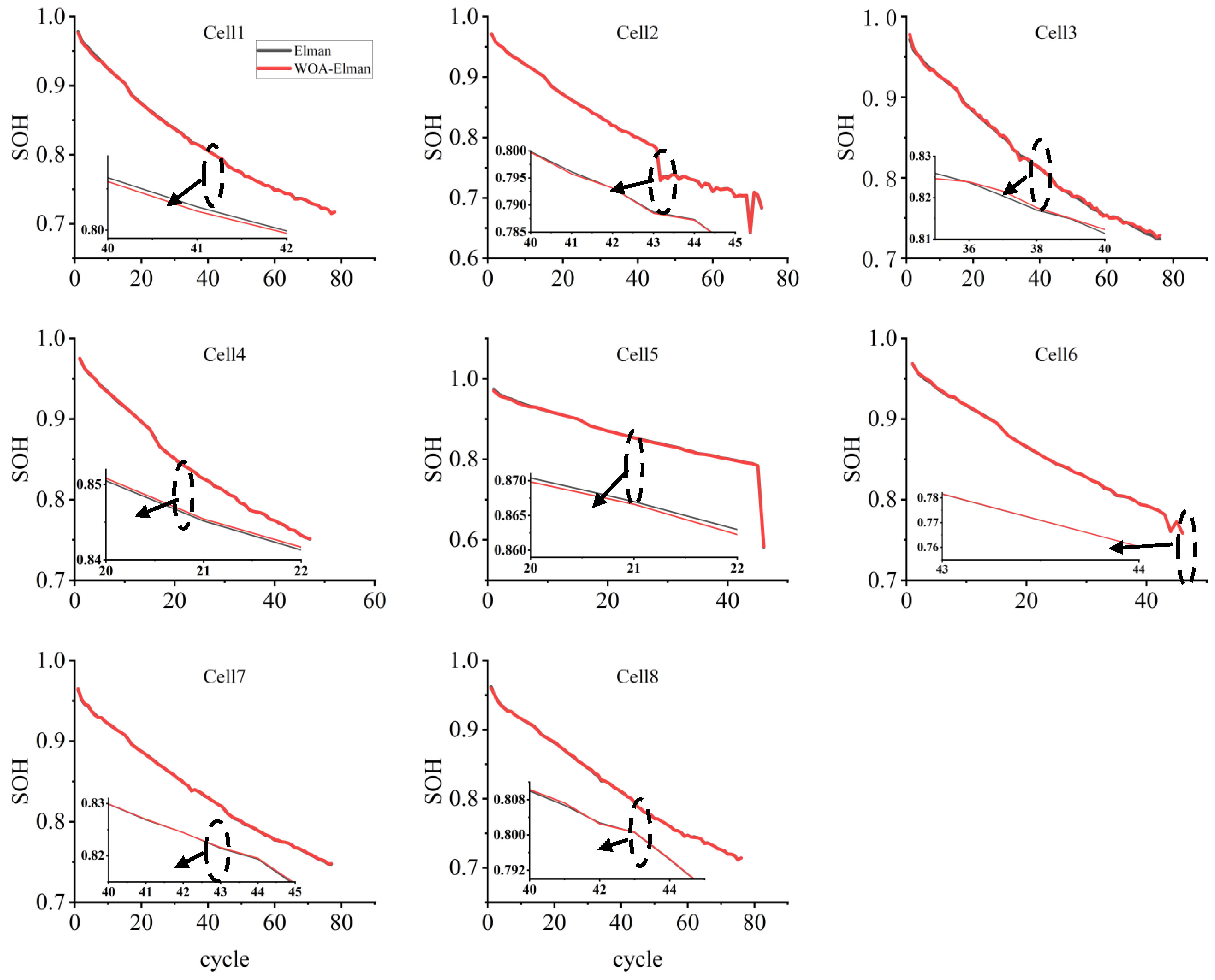
6. Weighted Average Method
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, X.; Li, Z.; Wang, X.; Li, C. Technology Development of Electric Vehicles: A Review. Energies 2020, 13, 90. [Google Scholar] [CrossRef]
- Yang, F.; Wang, D.; Zhao, Y.; Tsui, K.-L.; Bae, S.J. A study of the relationship between coulombic efficiency and capacity degradation of commercial lithium-ion batteries. Energy 2018, 145, 486–495. [Google Scholar] [CrossRef]
- Song, L.; Zhang, K.; Liang, T.; Han, X.; Zhang, Y. Intelligent state of health estimation for lithium-ion battery pack based on big data analysis. J. Energy Storage 2020, 32, 101836. [Google Scholar] [CrossRef]
- Xu, J.; Ma, J.; Zhao, X.; Chen, H.; Xu, B.; Wu, X. Detection Technology for Battery Safety in Electric Vehicles: A Review. Energies 2020, 13, 4636. [Google Scholar] [CrossRef]
- Petzl, M.; Danzer, M.A. Nondestructive detection, characterization, and quantification of lithium plating in commercial lithium-ion batteries. J. Power Sources 2014, 254, 80–87. [Google Scholar] [CrossRef]
- Leonori, S.; Baldini, L.; Rizzi, A.; Mascioli, F.M.F. A Physically Inspired Equivalent Neural Network Circuit Model for SoC Estimation of Electrochemical Cells. Energies 2021, 14, 7386. [Google Scholar] [CrossRef]
- Liu, B.; Tang, X.; Gao, F. Joint estimation of battery state-of-charge and state-of-health based on a simplified pseudo-two-dimensional model. Electrochim. Acta 2020, 344, 136098. [Google Scholar] [CrossRef]
- Chen, Y.; He, Y.; Li, Z.; Chen, L.; Zhang, C. Remaining Useful Life Prediction and State of Health Diagnosis of Lithium-lon Battery Based on Second-Order Central Difference Particle Filter. IEEE Access 2020, 8, 37305–37313. [Google Scholar] [CrossRef]
- Jokar, A.; Rajabloo, B.; Desilets, M.; Lacroix, M. Review of simplified Pseudo-two-Dimensional models of lithium-ion batteries. J. Power Sources 2016, 327, 44–55. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, X.; Zhang, X. Multi-objective decision analysis for data-driven based estimation of battery states: A case study of remaining useful life estimation. Int. J. Hydrogen Energy 2020, 45, 14156–14173. [Google Scholar] [CrossRef]
- Wu, L.; Fu, X.; Guan, Y. Review of the remaining useful life prognostics of vehicle lithium-ion batteries using data-driven methodologies. Appl. Sci. 2016, 6, 166. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H.; Pecht, M.G. Lithium-ion battery remaining useful life prediction with box-cox transformation and Monte Carlo simulation. IEEE Trans. Ind. Electron. 2018, 66, 1585–1597. [Google Scholar] [CrossRef]
- Ding, W.L.; Lu, Y.; Peng, X.L.; Dong, H.; Chi, W.J.; Yuan, X.; Sun, Z.Z.; He, H. Accelerating evaluation of the mobility of ionic liquid-modulated PEDOT flexible electronics using machine learning. J. Mater. Chem. 2021, 9, 25547–25557. [Google Scholar] [CrossRef]
- Huang, H.; Meng, J.; Wang, Y.; Cai, L.; Peng, J.; Wu, J.; Xiao, Q.; Liu, T.; Teodorescu, R. An enhanced data-driven model for Lithium-ion battery state-of-health estimation with optimized features and prior knowledge. Automot. Innov. 2022, 5, 134–145. [Google Scholar] [CrossRef]
- Pang, X.; Huang, R.; Wen, J.; Shi, Y.; Jia, J.; Zeng, J. A lithium-ion battery RUL prediction method considering the capacity regeneration phenomenon. Energies 2019, 12, 2247. [Google Scholar] [CrossRef]
- Ng, M.F.; Zhao, J.; Yan, Q.; Conduit, G.J.; Seh, Z.W. Predicting the state of charge and health of batteries using data-driven machine learning. Nat. Mach. Intell. 2020, 2, 161–170. [Google Scholar] [CrossRef]
- Chaoui, H.; lbe-Ekeocha, C.C. State of charge and state of health estimation for lithium batteries using recurrent neural networks. IEEE Trans. Veh. Technol. 2017, 66, 8773–8783. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, X.; Zhou, C.; Zou, Y.; Du, Z.; Sun, M.; Ouyang, Y.; Yang, D.; Liao, Q. State-of-health estimation of batteries in an energy storage system based on the actual operating parameters. J. Power Sources 2021, 506, 230162. [Google Scholar] [CrossRef]
- Li, Q.; Li, D.; Zhao, K.; Wang, L.; Wang, K. State of health estimation of lithium-ion battery based on improved ant lion optimization and support vector regression. J. Energy Storage 2022, 50, 104215. [Google Scholar] [CrossRef]
- Jia, J.; Liang, J.; Shi, Y.; Wen, J.; Pang, X.; Zeng, J. SOH and RUL Prediction of Lithium-Ion Batteries Based on Gaussian Process Regression with Indirect Health Indicators. Energies 2020, 13, 375. [Google Scholar] [CrossRef]
- Vidal, C.; Malysz, P.; Kollmeyer, P.; Emadi, A. Machine learning applied to electrified vehicle battery state of charge and state of health estimation: State-of-the-art. IEEE Access 2020, 8, 52796–52814. [Google Scholar] [CrossRef]
- Bian, X.; Liu, L.; Yan, J.; Zou, Z.; Zhao, R. An open circuit voltage-based model for state-of-health estimation of lithium-ion batteries: Model development and validation. J. Power Sources 2020, 448, 227401. [Google Scholar] [CrossRef]
- Tian, J.; Xiong, R.; Shen, W. State-of-health estimation based on differential temperature for lithium-ion batteries. IEEE Trans. Power Electron. 2020, 35, 10363–10373. [Google Scholar] [CrossRef]
- Hu, X.; Che, Y.; Lin, X.; Onori, S. Battery health prediction using fusion-based feature selection and machine learning. IEEE Trans. Transp. Electrif. 2021, 7, 382–398. [Google Scholar] [CrossRef]
- Bian, X.; Wei, Z.; Li, W.; Pou, J.; Sauer, D.U.; Liu, L. State-of-health estimation of lithium-ion batteries by fusing an open circuit voltage model and incremental capacity analysis. IEEE Trans. Power Electron. 2022, 37, 2226–2236. [Google Scholar] [CrossRef]
- Liu, D.; Kim, C. High-Voltage Lithium-Ion Battery Using Substituted LiCoPO4: Electrochemical and Safety Performance of 1.2 Ah Pouch Cell. Materials 2020, 7, 4450. [Google Scholar] [CrossRef]
- Fetanat, M.; Stevens, M. Fully Elman Neural Network: A Novel Deep Recurrent Neural Network Optimized by an Improved Harris Hawks Algorithm for Classification of Pulmonary Arterial Wedge Pressure. IEEE Trans. Biomed. Eng. 2022, 69, 1733–1744. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Zhang, R. Multistrategy Improved Whale Optimization Algorithm and Its Application. Comput. Intell. Neurosci. 2022, 27, 3418269. [Google Scholar] [CrossRef]
- Brodzicki, A.; Piekarski, M.; Jaworek-Korjakowska, J. The Whale Optimization Algorithm Approach for Deep Neural Networks. Sensors 2021, 21, 8003. [Google Scholar] [CrossRef]
- Tsai, Y.-S.; Fang, T.-P.; Chi, C.-C. A scale for measuring evidence-searching capability: A development and validation study. J. Eval. Clin. Pract. 2019, 24, 678–681. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, S.I.; Sanad, M.M.S. Maghemite-based anode materials for Li-Ion batteries: The role of intentionally incorporated vacancies and cation distribution in electrochemical energy storage. J. Alloys Compd. 2021, 861, 157962. [Google Scholar] [CrossRef]
- Moustafa, M.G.; Sanad, M.M.S.; Hassaan, M.Y. NASICON-type lithium iron germanium phosphate glass ceramic nanocomposites as anode materials for lithium ion batteries. J. Alloys Compd. 2020, 845, 156338. [Google Scholar] [CrossRef]
- Sanad, M.M.S.; Rashad, M.M.; Powers, K. Enhancement of the electrochemical performance of hydrothermally prepared anatase nanoparticles for optimal use as high capacity anode materials in lithium ion batteries (LIBs). Appl. Phys. A 2015, 118, 655–674. [Google Scholar] [CrossRef]





| Battery | HF1 | HF2 | HF3 | HF4 | HF5 |
|---|---|---|---|---|---|
| Cell 1 | 0.7812 | −0.7768 | −0.8952 | 0.8792 | 0.8397 |
| Cell 2 | 0.8875 | −0.8436 | −0.9696 | 0.9531 | 0.9624 |
| Cell 3 | 0.8811 | −0.8080 | −0.9647 | 0.9306 | 0.9480 |
| Cell 4 | 0.9441 | −0.7911 | −0.9776 | 0.9415 | 0.9609 |
| Cell 5 | 0.7046 | −0.8104 | −0.9064 | 0.9159 | 0.91552 |
| Cell 6 | 0.8457 | −0.8247 | −0.9666 | 0.9450 | 0.9779 |
| Cell 7 | 0.8681 | −0.7692 | −0.9700 | 0.9248 | 0.9347 |
| Cell 8 | 0.8983 | −0.9174 | −0.9774 | 0.9724 | 0.9849 |
| Battery | HF1 | HF2 | HF3 | HF4 | HF5 |
|---|---|---|---|---|---|
| Cell 1 | 0.9633 | −0.9625 | 0.9794 | 0.9524 | 0.9711 |
| Cell 2 | 0.9451 | −0.9682 | 0.9722 | 0.9156 | 0.9652 |
| Cell 3 | 0.9671 | −0.9707 | 0.9806 | 0.9606 | 0.9717 |
| Cell 4 | 0.9771 | −0.9731 | 0.9839 | 0.9756 | 0.9775 |
| Cell 5 | 0.9048 | −0.9917 | 0.9448 | 0.8724 | 0.9303 |
| Cell 6 | 0.9741 | −0.9832 | 0.9816 | 0.9733 | 0.9736 |
| Cell 7 | 0.9704 | −0.9728 | 0.9836 | 0.9665 | 0.9724 |
| Cell 8 | 0.9656 | −0.9698 | 0.9811 | 0.9547 | 0.9736 |
| Battery | HF1 | HF2 | HF3 | HF4 | HF5 |
|---|---|---|---|---|---|
| Cell 1 | −0.9863 | 0.2285 | −0.9878 | −0.2221 | −0.9867 |
| Cell 2 | −0.9708 | 0.7995 | −0.9755 | −0.8056 | −0.9588 |
| Cell 3 | −0.9874 | 0.3447 | −0.9785 | −0.3081 | −0.9843 |
| Cell 4 | −0.9863 | 0.2873 | −0.9895 | −0.2430 | −0.9841 |
| Cell 5 | 0.9048 | 0.6261 | −0.9673 | −0.6233 | −0.9521 |
| Cell 6 | −0.9829 | 0.1944 | −0.9892 | −0.2928 | −0.9819 |
| Cell 7 | −0.9837 | 0.6072 | −0.9887 | −0.2071 | −0.9833 |
| Cell 8 | −0.9849 | 0.3157 | −0.9878 | −0.2140 | −0.9842 |
| Test Set | MAE | RMSE | MAPE |
|---|---|---|---|
| Cell 1 | 0.0010254 | 0.0012192 | 0.12462% |
| Cell 2 | 0.00025247 | 0.0003664 | 0.030107% |
| Cell 3 | 0.0015656 | 0.0021123 | 0.18437% |
| Cell 4 | 0.00023486 | 0.00035171 | 0.027124% |
| Cell 5 | 0.00064367 | 0.00091341 | 0.073228% |
| Cell 6 | 0.00059183 | 0.00076863 | 0.067114% |
| Cell 7 | 0.00033889 | 0.00043897 | 0.039798% |
| Cell 8 | 0.00039627 | 0.00057397 | 0.047694% |
| Test Set | MAE | RMSE | MAPE |
|---|---|---|---|
| Cell 1 | 0.0039592 | 0.0044058 | 0.45667% |
| Cell 2 | 0.0016823 | 0.0020586 | 0.21423% |
| Cell 3 | 0.0090102 | 0.010912 | 1.1042% |
| Cell 4 | 0.0015892 | 0.0018576 | 0.18737% |
| Cell 5 | 0.0017174 | 0.0019943 | 0.20165% |
| Cell 6 | 0.001516 | 0.001828 | 0.17711% |
| Cell 7 | 0.0012513 | 0.0015811 | 0.1518% |
| Cell 8 | 0.002599 | 0.0029838 | 0.32145% |
| Test Set | MAE | RMSE | MAPE |
|---|---|---|---|
| Cell 1 | 0.0015355 | 0.0019628 | 0.186% |
| Cell 2 | 0.0036111 | 0.0053521 | 0.48069% |
| Cell 3 | 0.0017421 | 0.0020672 | 0.20905% |
| Cell 4 | 0.0012496 | 0.0015615 | 0.15047% |
| Cell 5 | 0.0027543 | 0.0029526 | 0.32258% |
| Cell 6 | 0.0015464 | 0.0020215 | 0.1853% |
| Cell 7 | 0.0024968 | 0.0028942 | 0.30831% |
| Cell 8 | 0.0017175 | 0.0022618 | 0.22121% |
| Test Set | MAE | RMSE | MAPE |
|---|---|---|---|
| Cell 1 | 0.0020832 | 0.0027034 | 0.25851% |
| Cell 2 | 0.0044156 | 0.0062386 | 0.58832% |
| Cell 3 | 0.0028335 | 0.0031952 | 0.33774% |
| Cell 4 | 0.0029127 | 0.0036651 | 0.3591% |
| Cell 5 | 0.0046339 | 0.0077523 | 0.58816% |
| Cell 6 | 0.0019521 | 0.002523 | 0.23102% |
| Cell 7 | 0.0041325 | 0.0048961 | 0.51481% |
| Cell 8 | 0.0027281 | 0.0037465 | 0.33547% |
| Test Set | MAE | RMSE | MAPE |
|---|---|---|---|
| Cell 1 | 0.0022685 | 0.0029795 | 0.28117% |
| Cell 2 | 0.0048903 | 0.0079513 | 0.66421% |
| Cell 3 | 0.0024732 | 0.0037361 | 0.30522% |
| Cell 4 | 0.0027153 | 0.0032519 | 0.32872% |
| Cell 5 | 0.0036418 | 0.0042333 | 0.42154% |
| Cell 6 | 0.0016742 | 0.0024906 | 0.19799% |
| Cell 7 | 0.001477 | 0.0017831 | 0.17052% |
| Cell 8 | 0.001571 | 0.001917 | 0.1962% |
| Test Set | MAE | RMSE | MAPE |
|---|---|---|---|
| Cell 1 | 0.0021908 | 0.0036268 | 0.27287% |
| Cell 2 | 0.0084709 | 0.013501 | 1.1566% |
| Cell 3 | 0.0038561 | 0.0058704 | 0.41307% |
| Cell 4 | 0.0037689 | 0.0069539 | 0.46528% |
| Cell 5 | 0.0032137 | 0.0080635 | 0.43145% |
| Cell 6 | 0.002645 | 0.0032587 | 0.3141% |
| Cell 7 | 0.0028182 | 0.0034156 | 0.33942% |
| Cell 8 | 0.0023898 | 0.0041675 | 0.30402% |
| Battery | HF1 | HF2 | HF3 | HF4 | HF5 |
|---|---|---|---|---|---|
| Cell 1 | 0.8848 | −0.7813 | −0.8953 | 0.8754 | 0.9740 |
| Cell 2 | 0.9827 | −0.8479 | −0.9697 | 0.9515 | 0.9734 |
| Cell 3 | 0.9460 | −0.8132 | −0.9649 | 0.9274 | 0.9759 |
| Cell 4 | 0.9801 | −0.7945 | −0.9777 | 0.9392 | 0.9821 |
| Cell 5 | 0.8851 | −0.8139 | −0.9066 | 0.9139 | 0.9387 |
| Cell 6 | 0.9403 | −0.8273 | −0.9667 | 0.9431 | 0.9800 |
| Cell 7 | 0.9414 | −0.7745 | −0.9701 | 0.9224 | 0.9751 |
| Cell 8 | 0.9457 | −0.9194 | −0.9775 | 0.97714 | 0.9794 |
| Test Set | MAE | RMSE | MAPE |
| Cell 1 | 0.00055622 | 0.00083431 | 0.06454% |
| Cell 2 | 0.00044995 | 0.00058576 | 0.058233% |
| Cell 3 | 0.00121419 | 0.0019488 | 0.15269% |
| Cell 4 | 0.00026275 | 0.00039682 | 0.030537% |
| Cell 5 | 0.00082164 | 0.0011593 | 0.093373% |
| Cell 6 | 0.00034954 | 0.00047364 | 0.039561% |
| Cell 7 | 0.0003449 | 0.00042638 | 0.041071% |
| Cell 8 | 0.00036636 | 0.00049316 | 0.043783% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Wang, Y.; Ma, R.; Zhao, Y.; Shi, M.; Qu, W. Prediction of Lithium Battery Health State Based on Temperature Rate of Change and Incremental Capacity Change. Energies 2023, 16, 7581. https://doi.org/10.3390/en16227581
Zhang T, Wang Y, Ma R, Zhao Y, Shi M, Qu W. Prediction of Lithium Battery Health State Based on Temperature Rate of Change and Incremental Capacity Change. Energies. 2023; 16(22):7581. https://doi.org/10.3390/en16227581
Chicago/Turabian StyleZhang, Tao, Yang Wang, Rui Ma, Yi Zhao, Mengjiao Shi, and Wen Qu. 2023. "Prediction of Lithium Battery Health State Based on Temperature Rate of Change and Incremental Capacity Change" Energies 16, no. 22: 7581. https://doi.org/10.3390/en16227581
APA StyleZhang, T., Wang, Y., Ma, R., Zhao, Y., Shi, M., & Qu, W. (2023). Prediction of Lithium Battery Health State Based on Temperature Rate of Change and Incremental Capacity Change. Energies, 16(22), 7581. https://doi.org/10.3390/en16227581





