Abstract
Changes are being implemented in the electrical power grid to accommodate the increased penetration of renewable energy sources interfaced with grid-connected inverters. The grid-forming (GFM) control paradigm of inverters in active power grids has emerged as a technique through which to tackle the effects of the diminishing dominance of synchronous generators (SGs) and is preferred to the grid-following (GFL) control for providing system control and stability in converter-dominated grids. Therefore, the development of the GFM control is important as the grid advances towards 100% inverter-based grids. In this paper, therefore, we aim to review the changing grid scenario; the behaviour of grid-connected inverter control paradigms and major GFM inverter controls, including their modifications to tackle low inertia, reduced power quality, fault-ride through capability, and reduced stability; and the state-of-the-art GFM models that are pushing the universality of GFM inverter control.
1. Introduction
The increased integration of power electronics-interfaced energy resources into the power grid is driven by the need for renewable energy, following the sustainability paradigm to combat climate change. It is expected that this trend will proceed towards a 100% inverter-based power grid as synchronous generators (SGs) are replaced, and the characteristics of the grid are adapted to inverters [,,,,].
A GFL control operates optimally in stiff voltage systems, dominated conventionally by SGs, wherein it tracks the voltage phasor using a synchronisation unit, normally the phase-locked loop (PLL) []. The effects of the integration of inverters into the power grid include reduced fault levels and the loss of directly coupled inertia, exacerbating voltage and frequency stability, and resulting in GFL inverters integrating grid-supporting capabilities as a grid code requirement [].
GFL and grid-supporting inverters operate as dispatchable power sources, prioritising the injection of current into the grid, while other functionalities are secondary []. Unlike GFL, GFM control is designed primarily to provide a stiff voltage, while meeting the power demand through voltage source operation to intrinsically maintain its voltage output level, which represents an attractive feature for weak power systems []. In this paper, we review the changing paradigm of the power grid as more inverters are deployed to replace SGs, considering grid strength as quantified with the short circuit ratio (SCR), and inertia, which represents a form of primary energy storage through which to mitigate frequency deviations in a power system.
The GFM control is attractive because it provides fast control dynamics, coupled with voltage source characteristics that are attractive for low-inertia, high-dynamics grids, with a decreasing number of SGs [,,]. Various control approaches implementing GFM are therefore reviewed, including: droop control, power synchronisation methods based on synchronous machine (SM) emulations, oscillator-based controls, and the electronic matching of SMs. This article also discusses state-of-the-art GFM implementations, including hybrid approaches that incorporate conventional current source and voltage source behaviour, advanced oscillator-based methods, universal controllers designed to operate under all grid scenarios without mode changes, multivariable GFM designs for uncertain systems, and methods based on interoperability. We also discuss the factors affecting GFM controllers, such as power coupling and fault protection, given their effects on the behaviour and stability of any GFM control approach.
Therefore, the major contribution of this paper is in the presentation of research efforts towards GFM primary control design, geared towards universal and unified control in grid-connected inverters and interoperability—an aspect that defines major performance guidelines without giving away vendor intellectual property—of control design in the certainty of an inverter-dominated grid.
The remainder of the article is summarised as follows: Section 2 reviews the changing dynamics of the grid. Section 3 tackles the classifications of control used for grid-connected inverters—the GFL and GFM. Section 4 reviews the primary GFM control approaches used to implement voltage source behaviour in inverters. Section 5 illustrates the construction of state-of-the-art GFM controller designs. Lastly, Section 6 addresses power coupling and overcurrent protection paradigms as the major issues faced in the construction of controllers. The paper concludes with a discussion of the evolution of GFM inverter control as the grid heads towards a 100% inverter-based scenario.
2. The Changing Dynamics of the Grid
The SG dominates the conventional electrical power system and is controlled based on both its physical and electrical properties []. In Figure 1, this kind of grid is shown as “Present”. SGs present ideal voltage source characteristics, with low impedance and automatic voltage control, synchronous voltage and frequency control from their exciter and governor controls, and inertia from their spinning mass.
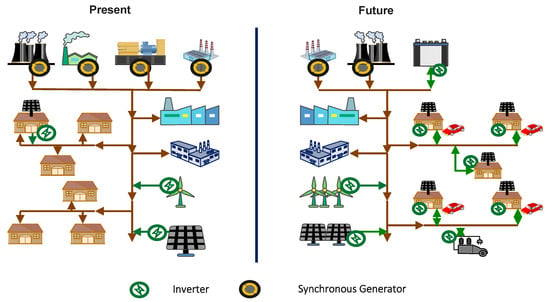
Figure 1.
The changing trend of the grid towards majority inverter-interfaced generating resources.
Power electronics are utilised by non-synchronous generators in the integration of renewable energy sources, like solar and wind, into the power grid. These generators are known as grid-connected inverters. Inverter controllers are digitally implemented, which provides them greater flexibility and speed compared to SG controllers, which are constrained by the mechanical and electrical qualities of their physical constructions []. As shown in Figure 1, inverter penetration in the grid is anticipated to increase in the future, due to factors related to climate change and the need for sustainable energy. It is expected that momentary penetration levels will reach 100% in certain regions of Europe, due to the accelerated deployment of distributed solar systems and large-scale wind projects [].
When synchronous generators are the dominant power source, grid-connected inverters operate in GFL control topologies, in which the controllers rigorously follow the slower machine dynamics through their inherently faster controls. The PLL is used to track the rigid grid voltage signals in order to synchronise with the grid. As the penetration of inverters rises, the dynamics of the grid change, due to the faster controllers’ increasing influence and the slower SG controllers’ dwindling influence, resulting in low-inertia grids, more frequent frequency variations, and weak voltage that is vulnerable to collapse. In this situation, GFL inverters would be required to operate faster to keep up with the changing grid state. As a result, the integration of inverter-based resource (IBR) control cannot depend on GFL control; rather, GFM control is suggested as the method through which to address the problems caused by the changing electric power grid.
2.1. SCR and Grid Strength
Grid strength is related to the ability of a power system to maintain its voltage and frequency within acceptable limits following an external disturbance. In this case, the grid is expected to operate as an ideal voltage source with automatic regulation of both frequency and voltage. Therefore, the definition of grid strength in this instance can be approached either in terms of voltage stability and sensitivity, in which case the grid impedance is considered [,,], or in terms of frequency stability, which is determined by the amount of synchronous inertia available to prevent frequency anomalies during transient periods. Traditional grids, dictated by the characteristics of the synchronous generator, can be simplified with the Thevenin equivalent model, shown in Figure 2.
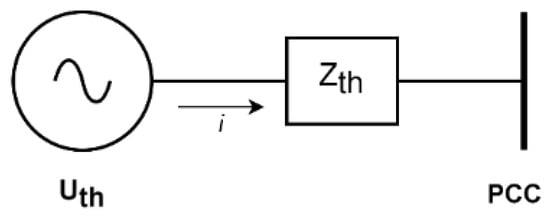
Figure 2.
Thevenin equivalent circuit for an arbitrary system.
When a current is injected into the network, the voltage at the point of common coupling (PCC) changes through , where is the equivalent Thevenin impedance, and is the terminal voltage of the source. When a short circuit is considered at a bus of the PCC, the short circuit power is delivered to the fault at that location from the generator, in terms of and . Let be the short circuit current, and the short circuit power; then, and ,
The SCR, which is used to describe the strength of a grid [], can be described as the ratio of the short circuit fault level, , to the power rating of the component connected at that point. Let be the rated power of the generator in Figure 2. The SCR is shown to be proportional to the impedance of the network []. If and are base values, such that:
Power grids are typically considered strong or stiff with SCR values greater than 3, and weak with SCR values lower than 3 [].
The SCR is also dependent on the duration of a fault current during a fault. In both steady-state and fault scenarios, SGs preserve their electrical properties and can provide up to five times their rated current. Due to the physical constraints of solid-state technology’s ability to maintain high levels of current, as well as their device protection mechanisms in case of current overloads, fault current levels are decreasing as inverter-interfaced sources become more and more prevalent within the electrical grid [].
2.2. Low-Inertia Systems
The resistance of the grid to frequency variations when a sudden load change occurs is correlated with inertia [,,]. Since frequency is a gauge of the balance between load and generation, frequency variations result in oscillations and system instability. The frequency nadir, or the lowest point the system frequency reaches because of the disturbance, and the rate of change of frequency (RoCoF) are the measures used to quantify frequency stability []. These relationships are shown in Figure 3a.
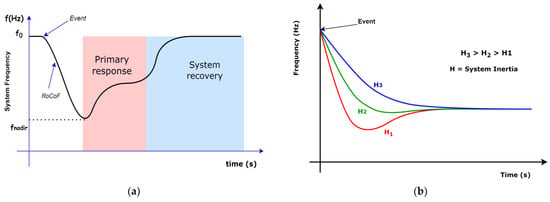
Figure 3.
(a) Frequency control showing the RoCoF and frequency nadir []. (b) System frequency response for different inertia constants [].
The RoCoF is derived from the swing equation of the synchronous machine, such that:
where is the differential active power between the input and output, is the system’s nominal frequency, is the rated power of the system, and is the system inertia constant.
Inertia is related to the stored kinetic energy in the rotating masses and is synchronised in the network through the synchronous torque, expressed as follows:
where is the moment of inertia of the machine , and is the angular synchronous frequency.
According to Equation (3), the higher the system inertia, the lower the RoCoF, and vice versa. Inertia provides the primary response to disturbances, as shown in Figure 3a. Then, controllers operate in the system recovery region of the figure, following delays in their algorithms.
Figure 3b shows the frequency response of systems with different inertia constants, showing that a low-inertia constant results in a lower-frequency nadir.
The mechanical-to-electrical energy conversion system of an SG immediately couples the spinning mass to the grid, giving it an instantaneous inertial reaction, as opposed to the measurement delays in power electronic controllers. Therefore, the loss of mechanically associated inertia worsens frequency excursions and lowers the frequency nadir, which has an impact on the stability of the electrical power system. A power system is set with the minimum synchronous inertia necessary to reduce frequency excursions in the presence of SGs. Therefore, the suitable design of the inverter controllers would make it possible for the GFM inverters to provide grid support and replace synchronous machines in low-inertia grids.
In function and design, inverters are power processing devices, whereas synchronous generators incorporate the energy source through mechanical inputs, energy storage through the rotor, and a power converter through electromechanical operations []. Inverters, therefore, decouple the energy source from the grid and can only emulate inertia using energy storage, with controller designs emulating synchronous machines and other novel methods [].
A completely autonomous inverter-based electrical system was considered in []. The power–frequency analysis considered the number of inverters to be operated in GFM and GFL controls for autonomous grid operation. For the GFM inverters, the analysis determines the size of the converter, its location in the power grid, the distance between subsequent generators, and the required control aspects of the inertia constant and virtual impedance. The results showed that large grid-forming inverters should be used for relatively reliable power sources, such as battery storage or wind; smaller grid-forming units should be designed with low inertia constants and fast controls; and inertia is best suited for grid-following inverters designed to take part in frequency regulation. The analysis is performed using positive root mean square simulation models to identify the interactions between grid-forming inverters.
Distributed inverter-based generators in a power system necessitate system-wide control paradigms through which to optimise the operation of all low-inertia systems. A synchronous virtual power plant method was proposed in [] to provide adjustable inertia throughout a system of grid-forming inverters operating in a virtual synchronous generator (VSG) control scheme. An online learning-based method was designed to coordinate the multiple VSGs in order to provide the required frequency response through adjustable system inertia. The online learning approach was preferred to a mathematical model of constant inertia, due to the dynamic nature of a low-inertia system with an uneven distribution of moments of inertia.
The analogy between mechanical systems and electrical systems in the synchronisation mechanisms of a connected system was shown in [,]. In [], the mechanical synchronisation in a system of pendulums connected in a system was replicated in electrical converters, thus obtaining coordination without communication. The impedance and mobility analogies were used to derive synchronisation in parallel and series connections of inverters. In [], a system of generators with mechanical heterogeneity was shown to achieve synchronisation, which was replicated in a system of 100% inverter-interfacing resources, in which the system inertia was reduced and generator damping was shown to be the main factor driving synchronisation.
A microgrid power and current reference management scheme was proposed in [] to achieve voltage control and provide the required frequency response through their virtual inertia functionalities. The control scheme achieved concurrent voltage and frequency management, while taking care of the limitations of devices and considering other parameters of the grid. The proposed method applies to both traditional grids and microgrids. In [], a method to improve power quality was proposed, showing the need for voltage control when large loads are connected to a weak point in the grid, which is an issue likely to be faced with inverter-based grids.
Some challenges faced with low-inertia grids dominated by inverters include controller interactions, as well as with synchronous generators and line dynamics that cause sustained oscillations and sub-synchronous oscillations, thus leading to instabilities []. Differential equations of system components—the generator, lines, loads, and inverters—were developed in [] to capture the dynamics of low-inertia systems. By using participation factor and parameter sensitivity methods, the most vulnerable segments were identified in a test grid, and the effects of controller interactions in different timescales and with line dynamics were studied, providing insights into low-inertia system stability and approaches through which to improve. This study was further extended in [] to capture the scenario of a 100% inverter-based system, which revealed that a purely inverter-based grid has better small-signal stability than a hybrid low-inertia system and emphasised the importance of modelling the study of controller interactions in low-inertia systems.
An inverter is always susceptible to resonance and loss of control, resulting from transient overloads and current saturation during operations. Faults on the grid and grid changes also cause oscillatory behaviour, particularly affecting protection coordination. Therefore, the inverter control structure is of paramount importance.
Virtual inertia emulation is not the most effective operation of electronic converters, given that it operates based on measured quantities of frequency, power, and voltage, which introduce measurement delays in the fast-actuating controllers driving power electronics and cause significant performance issues, unlike in slow-actuating synchronous machine controllers. The operation of inertia requires a post-contingency current overload, which is not replicable in power electronics, whose solid-state construction limits conductible currents. The future of the electrical power grid is decentralised, with low inertia and fast control, characterised by clusters of producers and consumers in microgrids.
3. Grid-Connected Inverter Control Classification
Grid-connected inverters are DC-to-AC power converters that interface power sources and are tasked with the injection of local voltage and current into active AC power grids. Unlike in synchronous machines, whose mechanical and electrical characteristics dictate their controller limits, in power converters, the controller configuration is the main determinant of control to obtain the desired electrical performance [,].
Controllers are required to have high bandwidth and performance that guarantees quick response, to participate in load sharing with other generators under normal operating conditions, and to maintain system stability in transient situations following a disturbance. The formulation of inverter power control principles is derived from basic active power control, considered in Figure 4, which shows an ideal power system containing a source coupled to a load through an impedance and the subsequent phasor diagram.
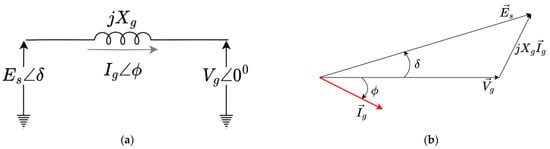
Figure 4.
(a) A simple power system schematic presenting a source and receiving end voltage across an inductive load and its phasor diagram. (b) Phasor diagram of the simple power system.
The active power at the grid side can be expressed through Equation (5)(i) and (ii), while Equation (5)(iii) expresses the relationships among , , and .
Based on the expressions in Equation (5), the active power can be controlled by managing the source current, , or the source voltage, , while the grid voltage, , is a control variable to be kept constant.
3.1. GFL Control
When the active power supplied by an inverter is primarily controlled through the injected current, ,while the grid voltage and phase are inputs via the synchronisation unit, Equation (5)(i) expresses the active power, and the inverter control is grid following. The internal inverter voltage, , is then calculated using Equation (5). The operation of the synchronising unit keeps the injected current, , in phase with the grid voltage, . This control represents current source operation, while the grid voltage phasor is tracked via measurements in the synchronisation unit, implemented through phase-locked loops (PLLs) or frequency-locked loops (FLLs).
The control schematic is equivalent to a current source behind a high impedance, as shown in Figure 5a. The control block diagram shows that the major inputs to this inverter are the set power points of the active power () and reactive power (), as required to dispatch maximum power and to support the grid profile at the PCC.
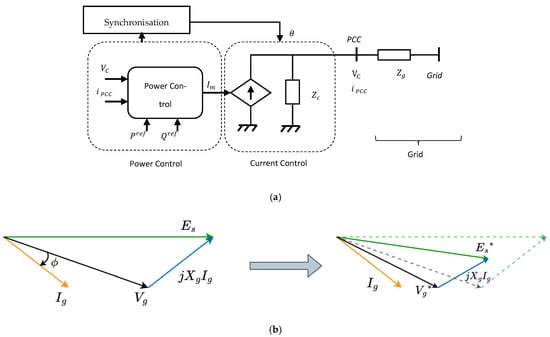
Figure 5.
(a) The basic layout of GFL control. (b) Phasor diagram showing the performance of the GFL controller under a small disturbance.
In the phasor diagram in Figure 5b, the current supplied to the grid, , is kept constant in phase and magnitude when a small disturbance in the grid voltage causes a change in the phase and magnitude of the grid voltage. Consequently, the controller voltage, , is adjusted to in response to the new grid voltage before resynchronisation occurs to restore , in following .
3.2. GFM Control
The control of active power supplied by an inverter based on the autonomous control of the source voltage , and its modulation angle , based on Equation (5)(ii), forms the basis of grid-forming inverter control. The inverter voltage, , is regulated to maintain a stiff PCC voltage, with reference value , while the power angle is determined by the power control unit through its power synchronisation loop, with a reference angular frequency maintained at . This basic schematic of the GFM controller is shown in Figure 6a, with the grid-forming inverter depicted as a controlled voltage source behind a low impedance.
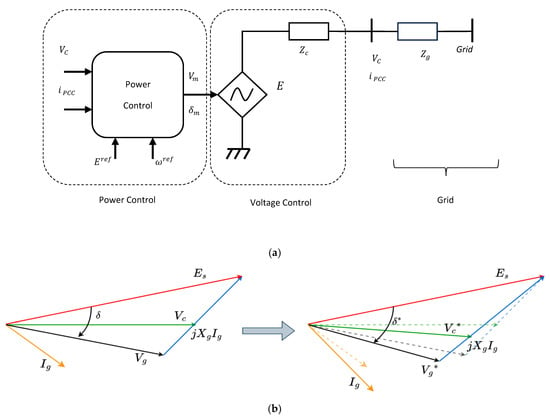
Figure 6.
(a) Basic schematic layout of GFM control. (b) Phasor diagram showing the performance of the GFM controller under a small disturbance.
Figure 6b shows the response of the GFM controller when subjected to an external disturbance. The voltage phasor is regulated in a near-constant manner by the reference , while the power angle changes according to the nature of the disturbance before the power synchronisation unit determines its new value in the steady state. This behaviour of the grid-forming inverter is therefore attractive in supporting the grid voltage and, consequently, its stability, due to voltage source operation.
3.3. Comparison between Grid-Following and Grid-Forming Inverter Control
While both the GFL and GFM control are used as grid-connected inverters, their inherent current source and voltage source characteristics, respectively, differentiate their operation. The major difference between GFM and GFL control is their behaviours under step phase changes in the voltage phasors, whereby GFM control maintains a stiff voltage operation, while GFL control may face voltage violations before resynchronisation with the grid voltage state. Generally, GFLs are designed to operate within the limits of the system’s strength, with measures such as disconnection or power runback taken in cases of reduced strength to maintain the stability of the grid. Their general impact on the grid is a reduction in its voltage stiffness, unless it is designed to support voltage, or if the grid voltage is compensated using synchronous condensers or FACTS devices. GFMs behave as voltage sources during the steady state, offering a stiff voltage at their terminals. However, their behaviour during fault conditions is affected by the current saturation mechanisms implemented to protect solid-state devices from high-fault currents [,,]. A summarised comparison of the GFL and GFM configurations of inverters is presented in Table 1.

Table 1.
Comparison between the performances of the GFL and GFM controls.
4. GFM Control Approaches
Generally regarded, the GFM structure is made up of inner control loops for voltage and current and an outer power synchronisation loop that implements the grid-forming control mechanism, depending on the method of preference [,]. A current-limiting algorithm may be implemented between the voltage control and the current control to prevent current overloads and keep the solid-state devices within allowable operational margins. The general controller layout of the GFM is shown in Figure 7.
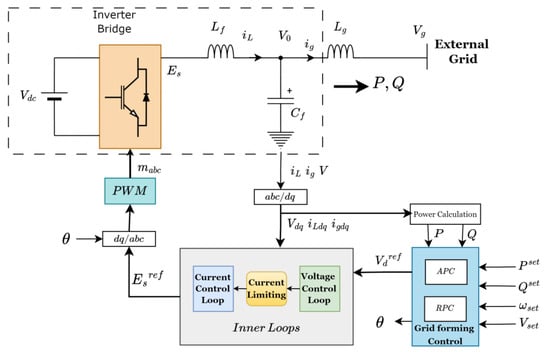
Figure 7.
The general structure of GFM inverter control.
The inner control loops of the GFM may be implemented in single-loop, multi-loop, or open-loop frameworks []. When implemented in a multi-loop framework, the voltage and current loops are implemented, serving different purposes. The voltage loop regulates converter voltage and incorporates virtual impedance, while the current loop regulates the damping of LC filters, as well as overcurrent limitation []. Multi-loop control loops implement better harmonic rejection, resonance damping, fault-handling ride-through capability, and mode transition capability, compared to single-loop or open-loop implementations [] The design of controllers strives to achieve a large control bandwidth and phase margins, which guarantee stable performance over a wide range. The adoption of each implementation framework has its merits over the others. For example, in [], triple loops were used to provide the converter with a large bandwidth; in [], the single-loop implementation was shown to perform better in motor inrush current mitigation, when compared to double-loop GFM controllers.
These controllers are preferably designed in the synchronous reference frame or the stationary frame (, to transform a sinusoidal tracking problem into a DC tracking problem, which provides a robust design of controllers with suitable fidelity, bandwidth, and small errors, achievable with a simple controller design [,].
The primary structure of GFM control should provide dynamic synchronisation ability to an arbitrary grid and maintain the voltage magnitude and phase at the PCC for the entire range of load demands from the grid, without loss of synchronisation within the electrical and thermal limits of the inverter and its storage capacity [].
4.1. Droop Control
Droop control is the simplest control adopted for connecting parallel inverters in active power networks, through adopting the steady-state power-sharing droop capabilities of SGs [,] Droop control depends on the steady-state relationships of active power and angular frequency, and reactive power and voltage difference in a predominantly inductive network, and may suffer instability due to power coupling in highly resistive networks, unless they are designed with alternative behaviours. This is further illustrated in Section 6.1.
Droop control emulates synchronous generator governor control in the frequency control of inverters, establishing a negative feedback relationship between real power and frequency, and may incorporate a degree of inertia [,] The droop law is shown in Equation (6).
where is the instantaneous angular frequency, is the angular frequency reference, is the power output of the converter, is the reference power, is the droop coefficient, and is the power angle.
Given the relationship between angular frequency and power angle, shown in Equation (6)(ii), active power may be drooped with angular frequency or power angle . Angle droop has been adopted in some applications, due to the limits imposed on frequency in frequency regulation in a network with frequent load changes []. In the case of angle droop,
where is the set value of the power angle, is the real power output of the inverter, is the reference power value, and is the droop coefficient.
The voltage droop is established to ensure reactive power sharing in the voltage magnitude loop, also imposing a negative feedback relationship between the reactive power and the voltage magnitude, according to Equation (8), as follows:
where is the instantaneous voltage, is the voltage reference, is the instantaneous reactive power, and is the reference reactive power.
Figure 8a shows the simplified droop controller implementation, with the active power control loop (APC) and the reactive power control loop (RPC).
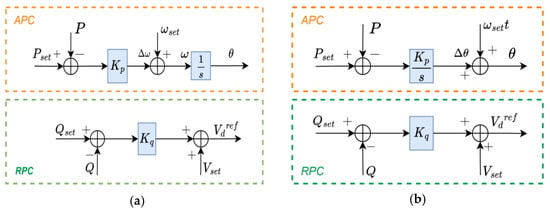
Figure 8.
(a) Droop control. (b) Power synchronisation control (PSC).
When the controller is set in the , the and components of the voltage are defined according to Equation (9), as follows:
The value of is set to zero to assume that the frame is aligned with the stationary reference frame at the PCC. The reactive power loop prevents the circulation of reactive current between inverters while maintaining a predefined voltage magnitude, according to the droop Equation (8).
Droop control is related to virtual synchronous machine control in a steady-state system [] and has been proven to emulate inertia using low-pass filters in its power loops []. Correlations between angle droop, virtual impedance, and frequency droop were derived in [], showing that angle droop is effectively a virtual inductance method, virtual inductance is a frequency droop method with derivative feedback, and virtual inductance and frequency droop, when combined, enhance oscillation damping in a proportional derivative manner. A comparison of the performance of single-loop and multi-loop droop controllers was performed in [], showing the better performance of single-loop over multi-loop controllers in small-signal stability, due to the larger inner coupling reactance of the controller.
Droop controllers may face inaccuracy issues with power sharing, in highly loaded and high-impedance systems with varied line impedances between controllers, which may lead to the prioritisation of frequency and voltage regulation over power droop operation. To address this issue, the droop controllers in a microgrid were optimised in [] following a multi-objective evolutionary algorithm to obtain a frontier of optimisation, from which the solution was chosen using the fuzzy affiliation function.
Droop variants proposed in the literature address the limitations of conventional droop that arise due to assumptions in its formulation, which include purely inductive network (high X/R ratio) coupling, decoupled voltage and frequency control, and simple networks with constant impedances. Therefore, controllers may be optimised using heuristic algorithms [] or variants of the conventional droop used. In [], the various droop control variants present in the literature were compared, including transient droop, angle power feedforward droop, and the virtual frame transformation droop.
Droop control used for steady-state power sharing in electrical grids [] is implicitly incorporated in all grid-forming control techniques in their steady state [], regardless of their unique designs and transient characteristics.
4.2. Power Synchronisation Control (PSC)
First presented in [], this control mechanism was designed to use the transient power transfer mechanism of synchronous generators in voltage source converters (VSCs) to achieve active power control in weak grid HVDC applications [,]. The principle employs the relationship between the change in power (and torque) at the generator output and the angular frequency of the voltage phasor (and hence phase angle) when synchronous generators restore their synchronism after a disturbance in a connected system.
The PSC control law is as follows:
where is the electrical angle, is the controller gain, is the instantaneous active power, and is the reference of active power.
The PSC controller contains a high-pass filter and an embedded current controller that limits current during transients, which grants it a preferable advantage to operate in weak grids, as initially designed []. The PSC primary controller implementations for both the APC and RPC are shown in Figure 8b.
The transient stability of the PSC is related to the power angle dynamics of a converter, which affect the gain and bandwidth of the controller. Therefore, a PSC faces transient instability in weak grids, due to the higher power angle dynamics affecting its gain and bandwidth []. The PSC was designed for VSCs operated in weak grids, but faced operational challenges under those conditions, due to the large load angles, and needed to run a low controller bandwidth to maintain a stability margin. The challenge of achievable bandwidth was further proven through the analysis methods in []. This challenge was also addressed in [], in which the active power loop was cascaded with the DC-link voltage loop design for a desirable bandwidth and stability margins, following a robust design that quantified the closed-loop transfer function, allowing for the design of the gain of the DC-link control loop. The design was reported to provide controller stability for all grid strengths and operational conditions.
The problems of low bandwidth and synchronous frequency resonance in PSCs operating in inductive grids was addressed in []. Using small-signal stability analysis, the dynamics of grid impedance on the power loops revealed that a slight resistance in the grid impedance and the non-minimum effect of loop gains on the phase caused synchronous frequency resonance. The conjugate pair poles in the open loop, due to the grid impedance, were eliminated using the analytics branch method in the power loops, which stabilised the controller by nullifying the non-minimum phase effect of the loop gains. The proposed method was reported to perform better than virtual resistance methods.
In [], the transient stability of a PSC was performed using the phase portrait method. The system was modelled as a first-order system and was observed to possess better transient dynamics, as compared to SGs. The overdamped nature of the PSC grants it stability after a disturbance if equilibrium points exist. However, in cases for which no equilibrium points exist, and the VSC loses synchronism due to a fault, resynchronisation is possible after one cycle if the fault is cleared after the critical clearing time.
In [], a deep neural network machine learning approach was used to detect the transient stability of a PSC using voltage sag severity and duration, the grid characteristics, and the operating point of the converter as data points for the learning process. This detection system was incorporated into the power synchronisation loop and fitted with a corrective mechanism that freezes the phase to keep the converter synchronised during faults.
An internal model with a one-degree-of-freedom structure was adopted for the PSC in [] to minimise the plant error in the small-signal model of the controller to deal with the effects of non-minimal phase dynamics that affect the stability of a PV-based converter. This resulted in better tracking capabilities of the controller in weak grids, with seamless transitioning between island and grid-connected modes.
The control of a PSC using proportional-integral-derivative (PID) controllers was proposed in [] to eliminate non-minimum phase phenomena in the small-signal model of the controller. This PID was tuned for robustness during voltage imbalances and frequency oscillations by adopting the power–frequency swing equation of the synchronous generator and a high-pass filter.
4.3. Synchronous Machine Emulation Controllers
To facilitate the seamless operation of controllers in a machine-dominated grid, controllers are designed to resemble the performance aspects of synchronous machines. The full-scale machine model is a high-order electrical and mechanical model that is not fully replicable in controllers, with only the relevant components for frequency and voltage regulation used in the required application. The power synchronisation loop is designed for machine emulation to provide the angular frequency (and power angle) by incorporating control algorithms used in the SG excitation, governor, and rotor. In this article, we address the virtual synchronous generator and the synchronverter controllers.
4.3.1. Virtual Synchronous Generator (VSG) Control
The VSG was proposed to combat the high RoCoF effect observed in grids with increased penetration of inverter-based resources. To replace the rotating masses of synchronous machines, the emulation of rotor dynamics through electronic controllers was proposed first in []. The VSG, therefore, emulates the rotor (swing equation) and governor dynamics of the SG.
The formulation of VSG control includes governor dynamics that establish the necessary steady-state droop characteristics and a rotor dynamic that includes damping and inertia coefficients whose implementations are pertinent to the behaviour of the design [,,,,]. The VSG dynamics are obtained through Equation (11), as follows:
where is the angular frequency, is the set value of angular frequency, is the electrical angle, is the inertia constant, is the damping coefficient of the rotor dynamics, is governor stiffness factor, is the electrical power supplied, is the set value of power, and is a variable calculated in the controller, derived as shown in Figure 9.
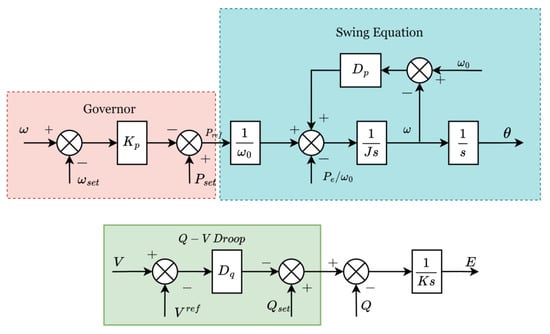
Figure 9.
The virtual synchronous generator (VSG) controller.
The reactive power regulation is dictated through the following relationship:
where is the voltage integral gain, is the instantaneous reactive power and its set value, and is the droop coefficient of the controller.
The VSG is a virtual inertia implementation of the conventional droop function and uses this inertia derivable from energy storage to enhance the stability of the grid [].
The limitations of the VSG stem from the implementation of mechanical control dynamics in an electronic setup. For example, SGs use the power system stabiliser unit for oscillation damping, whereas VSGs face oscillations when connected to the grid []. The advantage of using the VSG is its controllability, shown in the flexibility of designing the coefficients and for the desired inertia and damping responses, unlike the SG, which is limited by its physical characteristics [].
The steady-state, transient, and synchronisation stability characteristics of the VSG are of interest, given that it is an attractive GFM control through which to combat the issue of reduced inertia in grids [], with areas such as damping [], resonance and oscillations in weak grids [], virtual resistance [], system representation [,], decoupling for oscillation mitigation [], and the effects of grid conditions [] being investigated extensively.
4.3.2. Synchronverter
In the initial design of grid-connected inverters, the motivation was to design a controller whose interaction with the power grid was minimal. The synchronverter is, therefore, designed to mimic the SG by emulating the governor, rotor, and exciter dynamics to provide controllability to factors that affect performance, such as inertia, friction, damping, and inductance, which the electronic control provides when compared to the rigid control of the SG [].
The synchronverter is defined in Equation (13), as follows:
where is the electrical angle, with , ; is the moment of inertia, is the damping factor, also designed for droop functionality []; is the mechanical torque; is the electrical torque; represents the inner product; is the mutual inductance; is the excitation current of the stator; is the electromotive force; is the real power; is the reactive power; and is the stator current.
The power synchronisation loop of this controller [] is as follows:
where and are the nominal values for real power and angular frequency.
The synchronverter controller is shown in Figure 10, where the voltage error, , multiplied by droop coefficient , and added to the reactive power tracking error, , forms the input to an integrator of gain to produce the magnetic flux . is the grid voltage, and is the grid current.
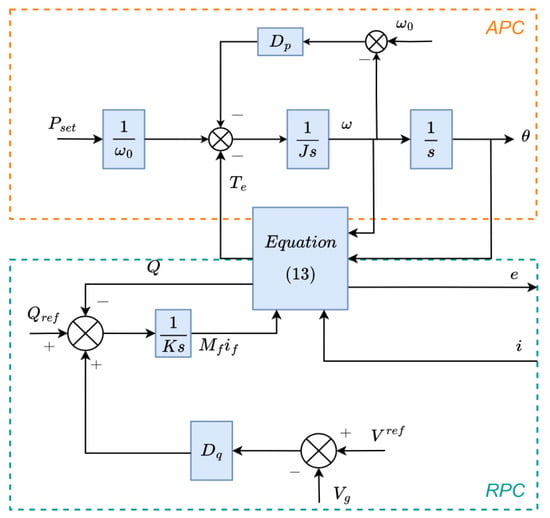
Figure 10.
The basic synchronverter controller [].
Initial synchronverter designs included a synchronisation unit, such as a PLL, to provide grid frequency and voltage references. A self-synchronising synchronverter is proposed in [] through the introduction of a switching algorithm in the controller structure, operated to eliminate the synchronising unit, thus making the synchronverter structure simple. The stability of the synchronverter in [] was improved in [] through modification of the field current control for fault handling, improved filters for better grid connection, changes in the torque to incorporate losses and provide better power tracking, and incorporation of a virtual capacitor to filter DC components. A detailed analysis of a 5th-order synchronverter connected to an infinite bus was carried out in [], investigating the necessary conditions for its local asymptotic stability using equilibrium points in the two-dimensional power plane.
The modification of the synchronverter, the effects of its parameters, and its applications were addressed in [], presenting the effects of parameter tuning, based on proposed methods in the literature, on the eigenvalue-based analysis of stability. A synchronverter was designed in [] to mitigate voltage imbalance in STATCOMs through supplying oscillating power locally in order to compensate for negative sequence voltage, illustrating the use of GFM inverters to improve power quality.
4.4. Matching Control
While power synchronising controllers assume decoupled DC and AC sides of a DC-to-AC power converter [], with their synchronisation based on active power transfer emulating SGs, matching control is developed upon the measurement of the DC voltage at the DC bus of the inverter to indicate frequency balance on the AC side, which effectively couples the control of the AC frequency to the DC voltage []. The DC bus voltage, a form of energy storage in an inverter, fluctuates to indicate power transfer, and the control thereof can be utilised to effectively control active power transfer. Matching control is therefore designed to utilise the device-level similarities between power converters and synchronous machines [].
By considering the averaged 3-phase model of a converter, given as a linear AC and DC circuit coupled with a nonlinear modulation block representing the 6-switch 2-level inverter, as shown in Figure 11, and matching its dynamics to those of a single pole pair, non-salient rotor SG excited externally, with both systems represented in the frame, the converter model below can be derived [,]. Let represent the modulation signal, so that and .
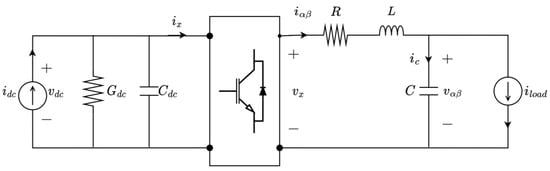
Figure 11.
Equivalent inverter model in frame, used in the analysis.
The inverter model for the closed-loop system in Figure 11 is as follows:
where for an arbitrary variable .
The generator model in [] is as follows:
where M is the rotor inertia, is the damping coefficient, is the mechanical torque, is mutual inductance of the machine, is rotor current, is the electrical angle, is the capacitance at the output, and are the output inductance current and output voltage expressed in the frame, is the load current, is the stator inductance, is the stator resistance, and is the angular frequency.
The matching of the two sets of models in Equations (15) and (16) is derived through relating similarities in the two equations. Let the modulation , where is the amplitude gain constant. Let angular frequency , whereby the virtual angle resembles the rotor angle, with . Then, and . By comparing these terms in Equations (15) and (16), it is deduced that .
By letting , the matched converter model becomes the following:
From Equation (17)(i), in the converter relates to the mechanical torque of the machine and controls the active power set point, while the primary energy source is controlled by the voltage .
The controller implementing matching control is shown in Figure 12.
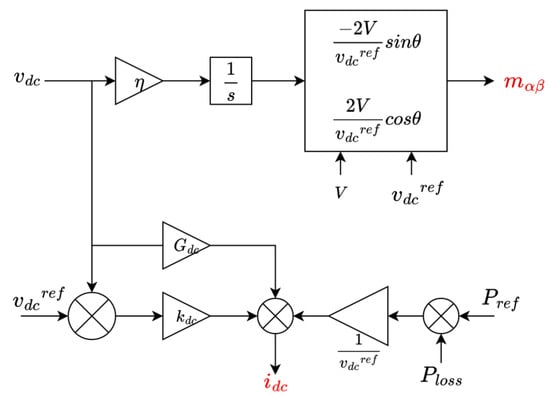
Figure 12.
The basic controller implementing matching control [,].
In Figure 12, is the amplitude of the AC side voltage, is the voltage reference, is the DC-side conductance, and is the compensator gain. The use of power loss in the calculation of compensates for the losses in the converter, ensuring that accurately tracks the set points of power. The controller model represents an inner loop, and outer loops can be incorporated to produce the desired performance, such as inertia, voltage, and frequency regulation through the modulation of , , and . A droop controller can be incorporated to control the relationship between the DC voltage and the frequency .
Matching control is attractive because it harnesses the interaction between the AC and DC sides of the converter, removing the need for the measurement delays used in feedback loops in other control approaches. In [], the electronic synchronous machine concept was further illustrated, showing that the relationship between the DC bus voltage and the angular frequency of the AC side constitutes a matching of machine dynamics and power flow in the converter. Energy functions of designed converter control features, such as synchronisation, power tracking, and voltage controller are used to formulate the GFM or GFL behaviour of the controller.
4.5. Virtual Oscillator Control (VOC)
The synchronisation ability of a network of coupled oscillators in a nonlinear dynamic network is used to implement the VOC model. Therefore, VOC utilises the dynamics of non-linear, weakly coupled oscillators to achieve a stable grid synchronisation mechanism in a limited-communication environment while regulating the voltage and frequency with proportional load-sharing capabilities [,,,].
VOC is a non-machine-emulating technique that does not require phasor measurements, or the calculation of quantities in a predefined synchronous state [], but rather, achieves system-wise synchronisation stability of the local measurements in the underlying network in the real-time domain without direct communication. While loads may vary within a grid, VOC minimises any frequency deviations that threaten system stability and maintains the voltage with a droop capability in the steady state, a property that has been demonstrated in [].
The basic VOC model, shown in Figure 13a, is built upon the dead zone oscillator, and is composed of the following features:
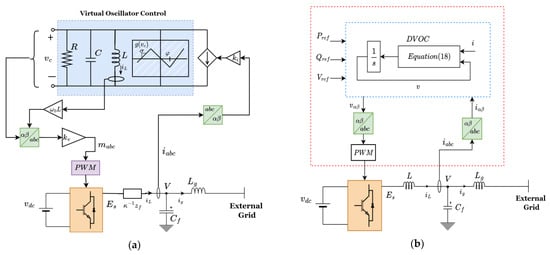
Figure 13.
(a) Basic diagram of the virtual oscillator controller (VOC) []. (b) The dispatchable VOC (DVOC) model [].
- Parallel tank, which determines the resonant frequency that sets the system frequency.
- represents a voltage-dependent source. The value of its maximum slope, , is related to the resistance, used for damping.
- The constant is the voltage scaling factor related to the grid RMS value, and and are used to ensure that the voltage of the inverter is within the limits for safe supply to load. is related to the power rating of the GFM in proportion to other inverters within the network.
Global synchronisation is based on the filter impedance, , the effective impedance of the parallel branch in the oscillator, and the scaling factors and .
A Van der Pol (VDP)-based VOC model was proposed in [], designed using linear control methods to synthesise the required sinusoidal behaviour for application in AC power grids, with the capability for proportional power-sharing and droop characteristics in the steady state. The VDP-VOC structure deploys a current source with a cubic function of voltage obtained through , while its general structure resembles that described for the basic VOC model, with replaced with a negative conductance element. The droop law embedded in the non-linearity of the VDP oscillator is shown through averaging methods in a slow timescale, and its stability in resistive networks is demonstrated through the global convergence of voltage in [].
The nonlinearity of VOC laws leads to harmonics in the voltage output that require careful filter design to mitigate their effects. A modification of the cubic voltage function of the traditional VOC is addressed in [], in which an improved VOC law was proposed to eliminate the third-order harmonic component in the voltage output, eliminating the need for notch filters, while making VOC faster in load response and synchronisation. A harmonic suppression method was proposed in []; using a virtual inductance control and current feedback from the network side of the output filter, compared to converter side current feedback in traditional methods, it led to simple implementation for grid-connected VOC inverters in the required performance region of passivity.
VDP-based VOC regulation of power flow in the grid-connected mode is constrained due to the lack of power control, and this issue was addressed in [], in which a parameter was derived that describes voltage and power injection and could decouple real and active power; a controller was then designed to derive this parameter for different power references.
The dispatchable virtual oscillator control (dVOC) law was proposed in [,] to address the power control limitation of VOC-programmed inverters, while ensuring system-wide synchronisation.
The dVOC law [] is as follows:
where is the terminal voltage in the frame, is the measured inverter current, are positive constants, and , , , and where is the Euclidean norm. , , and are the active power, reactive power, and voltage set points, respectively. caters for the line parameters, i.e., 0 for resistive and for inductive lines. The dVOC controller is shown in Figure 13b.
By expressing as , dVOC, the non-linear droop relationships are obtained as follows:
Assuming (for inductive impedance) and for small voltage deviations in the steady state,
The authors of [] tested the validity of the dVOC approach for inverters, showing its abilities for dynamic synchronisation, droop characteristics, black start, voltage regulation, and dynamic load sharing in an inverter-dominated grid.
A variant of the dVOC, proposed in [], was based on the dynamics of the Andronov–Hopf oscillator (AHO), which is suitable for three-phase systems because of intrinsic orthogonal signal generation and performs better dynamically as compared to the traditional VOC, demonstrating better harmonic elimination. The controller is composed of an LC resonant tank of natural resonant frequency and nonlinear state-dependent voltage and current sources modelled after the nonlinear harmonic oscillators.
A benchmarking study on VOC oscillator implementations was carried out in [], showing that the Andronov–Hopf-based dVOC is more suitable for grid applications, due to its superior dynamic and harmonic performance as compared to other implementations of VOC. A single-phase dVOC model, based on the VDP oscillator, was implemented in [] to regulate power in a system of controlled and uncontrolled inverters, connected in parallel using tuneable proportional-integral (PI) controllers in the controlled inverters and proportional autonomous power sharing in the uncontrolled inverters, to supply a fixed load.
Nonlinear droop behaviour in frequency and voltage regulation was reported in [] for the AHO-VOC inverter with decentralised and autonomous control for a system of interconnected inverters. The stability conditions for this nonlinear behaviour are addressed in [], showing that nonlinear droop, also termed complex droop, presents better properties than conventional droop in the stable operation of the grid.
Despite VOC’s fast primary control, facilitated by instantaneous time-domain operation, it is difficult to incorporate into a hierarchical grid control, which is often required for both grid and island operation. The authors of [] proposed a hierarchical secondary controller to facilitate the seamless transition of VOC in all modes of microgrid operation, with parameter regulation and synchronisation in island mode and power reference tracking in grid-tied modes.
VOC has been shown to operate in series-connected inverters in island mode, for which it offers decentralised synchronisation and control of inverters in a communication-free approach []. A port-Hamiltonian passivity-based VOC method for dealing with unknown grid conditions while ensuring synchronous stability was proposed in [], satisfying a condition that is necessary for integration with systems of varied SCR values and disturbances.
Other limitations of VOC include inertia emulation for low-inertia systems, fault management, and fault ride-through capability in the grid-connected mode. Inertia emulation was proposed in [], in which the power set point of dVOC was adjusted to enable the injection or absorption of power according to the differential power causing frequency deviation. Another implementation of the virtual inertia concept, using a proportional derivative controller approach to emulate inertia, was proposed in []. The fault ride-through capability of VOC was addressed in the unified virtual oscillator controller in [], in which a fast overcurrent limiting mechanism was implemented (see Section 5.2). Current limiting is also proposed in a reduced dVOC model in [] for overcurrent protection suitable for all grid impedances.
A system-level VOC control method was presented in []; termed sequence component-based VOC (S-VOC), it introduced improved control to encompass synchronisation of all sequence voltage components. This enabled VOC to deal with unbalanced voltages, integrating both single-phase and three-phase inverters, while accurately sharing power in hybrid structures with linear and nonlinear loads. This implementation was further improved in [], in which S-VOC was combined with nested inner loops to decouple phases, improving the handling of unbalanced voltages with a feedback modification to the VOC that improved its unbalanced fault ride-through synchronous stability.
Table 2 shows the summarised characteristics of the GFM controllers covered in this article, regarding the basic operation metrics for a controller and including basic operation, salient controller parameters, inertia support, fault ride-through capability, and the associated transient stability.

Table 2.
Comparison of the ideal GFM characteristics of controllers.
5. State-of-the-Art GFM Controller Designs
This section details inverter controllers, designed primarily as GFM controllers that augment additional characteristics based on modifications of the basic GFM control approaches addressed in Section 4, thereby presenting state-of-the-art designs of inverters for a wide range of grid conditions.
5.1. Hybrid Synchronisation Control
GFM inverters generally utilise power synchronisation (or oscillators) with internal voltage phasor generation, while GFL models utilise voltage phase synchronisation through the PLL, with internal current control for required performance.
The hybrid synchronisation control augments modifications in PSC and vector current control (VCC), used in GFL, into a single universally operating GFM and GFL controller []. These modifications are derived from the similarities present in the structures of PSC and VCC, as shown in Figure 14.
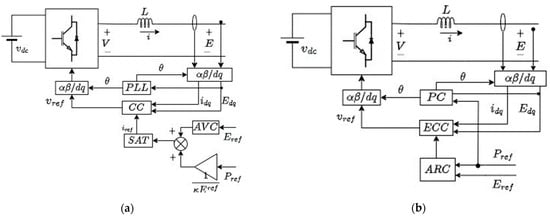
Figure 14.
(a) Basic structure of VCC. (b) Basic structure of PSC.
The parameters above, and , are vectors in the frame, representing converter voltage and PCC voltage, respectively. In the steady state, it is assumed that the is aligned to the PCC so that . and are reference values for voltage and active power in both diagrams of Figure 14.
The VCC in Figure 14a contains a current control (CC) mechanism, whose input is passed through a saturator, SAT, and which is augmented with a PLL for synchronisation. The alternating bus voltage controller (AVC) provides a rigid voltage input. The PSC in Figure 14b contains the active-resistance control (ARC), which is placed in cascade with an embedded current controller (ECC). The power controller (PC) contains the mechanism through which to generate the electric angle , according to the power synchronisation control law.
The hybridisation of VCC, using modifications in PSC, is summarised below:
- PC and PLL integration
The PSC law is as follows:
where is the power angle, is the nominal angular frequency, is controller gain, and and are the nominal and instantaneous real active power.
The PLL control law is as follows:
where is PLL gain constant, and is the component of voltage.
The hybrid synchronisation controller is formulated by augmenting Equations (21) and (22) to obtain the control law, presented in Equation (23).
The basic controller implementing Equation (23) is shown in Figure 15.
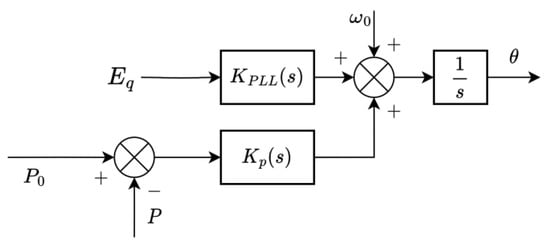
Figure 15.
The hybrid synchronisation controller.
- 2.
- Modification of AVC
In VCC,
where and are reference values of voltage and current; and are PCC voltage and current vectors, represents the component of the in Figure 14, and is the nominal angular frequency. represents the saturation operation of the controller. is a feedforward filter that prevents overcurrent by eliminating disturbances in . Equation (24)(ii) defines an open-loop active power control for VCC, which is later modified.
The term AVC, obtained through Equation (25), is constructed to assign the component of the reference current that is fed to the current controller using the real component of the control error as the input. This grants it an asymmetric characteristic.
where is a gain function that depends on the grid impedance.
The modification of VCC using PSC formulates an alternative AVC that presents a symmetrical coupling by introducing a real part in in Equation (25) to form the PSC-AVC. This is developed through three implementations: the modification of the PCC voltage orientation (Equation (26)(i)), the use of a feedforward closed-loop system to obtain current reference, and the replacement of embedded current control through a saturation operation on stiff voltage reference. These modifications result in Equation (26), providing new expressions and .
is formed by adding the term from Equation (26)(ii) to AVC from Equation (25) to incorporate PSC into VCC. This provides VCC robustness and enables GFM voltage control.
is a controller gain obtained through Equation (27) and depends on the filters and controller characteristics. represents the closed-loop gain, with as the closed-loop bandwidth, is the filter bandwidth for the low-pass filter of PSC, and is the active resistance of PSC in Equation (27).
The term can then be designed to provide the controller with the preferred control: GFL for , or GFM for .
The controller implementing the modifications to include in the generation of the components of is shown in Figure 16.
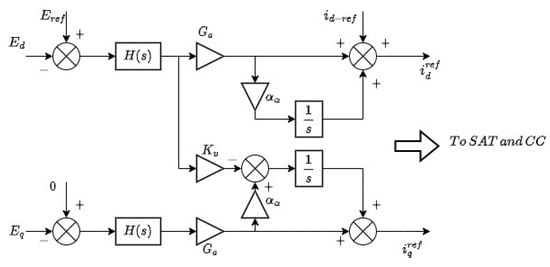
Figure 16.
The modified controller to generate current reference according to Equation (26) [].
The HSC was further modified in [] to eliminate PLL in HSC, replacing it with the swing equation emulation of the PLL, suggested in [], thereby eliminating the effects of PLL instability in operation. In Equation (23), the coefficient operates on . To eliminate the PLL, and assume swing equation operation, the PLL term is modified to have the same effect as , effectively making proportional to . This is achieved by creating a coupling effect between the and loops in the controller AVC. By including the term , the AVC of Equation (26)(ii) becomes the following:
The term is a cascade of susceptance gain, , and a low-pass filter. Through steady-state derivations,
This effectively modifies HSC to yield a PLL-based GFM controller.
A critique of the HSC was proposed in [], in which the gain of the AVC is a major concern to providing the necessary step response time when the grid SCR is below 1, even though the proposed control in [], and its improvement in [], provides robustness to the VCC and an effective GFM technique. To this end, the authors of [] proposed a modified method for eliminating the complexity of the vector voltage control introduced with the coupling modifications suggested in [,] and the PLL and replacing it with an active susceptance for damping in the traditional PSC with the standard VCC. This approach was reported to provide robustness under SCR conditions.
HSC is a power synchronisation mechanism that embeds voltage-based synchronisation through the inclusion of the PLL, thereby offering frequency damping, which increases the transient stability of GFM controllers []. To further enhance this characteristic, the droop control is preferable to PI controllers.
The stability of HSC was compared to that of PSC in [], showing that HSC is more stable around the fundamental frequency. Controller loop interactions in multi-loop HSC, incorporating virtual admittance, inner current loops, and AVC, were studied in [,,] to identify oscillation modes and the effects of damping coefficients on the stability of the controller; a design-oriented sensitivity analysis was then presented for robust controller design. The small-signal stability of HSC with virtual admittance was studied in [], through modelling in the and frames, showing that the HSC modelled in the frame has a better stability response than that in the frame.
5.2. Unified Virtual Oscillator Controller (uVOC)
The uVOC, built upon the dVOC presented in Section 4.5, addresses the fault ride-through capability of oscillator controllers while offering robust synchronisation, without the need for an external unit with both GFL and GFM modes of operation []. The basic principle of the uVOC is based on the state vector oscillator as the primary synchronisation unit.
Let the voltage vector, , where is the power angle and is the voltage magnitude. The time derivative of is as follows:
where the term is the instantaneous frequency, and is the normalised rate of change in voltage magnitude, .
Based on Equation (30), control laws are defined for GFL and GFM operations.
- GFL operation
The control law below is proposed as follows:
where and are vectors in the synchronous reference frame. is the instantaneous voltage, is the instantaneous current, is the current reference, is nominal oscillator frequency, is the current reference, is the instantaneous current, is a design parameter, and is the rotational angle that represents the grid impedance.
By using the instantaneous power theorem, is expressed as follows:
where and are the real and reactive power set points, and are the components of the voltage in the frame, and is the number of phases.
Comparing the arbitrary space vector derivative in Equation (30) with Equation (31), and expressing through Equation (32), the uVOC control law dynamics on the and axis are expressed as follows:
where and are instantaneous values of real and reactive power. Equation (33) provides the instantaneous frequency and voltage magnitude. Accurate power tracking and the droop characteristic of the instantaneous frequency are achieved based on on the or axis. Current control is achieved through the current reference , following the space vector voltage, .
- b.
- GFM operation
The control law for GFM uVOC is proposed as follows:
where the terms , , and represent the harmonic oscillator, the voltage magnitude correction, and the synchronisation terms, respectively. is the set point of the voltage magnitude, . Self-synchronisation is achieved through their collective operation.
is a mode determinant parameter for either GFL or GFM.
As with the GFL case, using the instantaneous power theorem to express and comparing Equations (30) and (34), the uVOC control law for GFM dynamics on the and axes is expressed as follows:
The relationships above show an inherent droop characteristic, depending on the choice of the parameter representing the line impedance. Subsequently, the corresponding coupling between and is achieved for . A nonlinear voltage droop is observed from Equation (35).
Figure 17 shows the uVOC implementation in the stationary reference frame, used for both the GFL and GFM controllers. The parameter is used as the determinant for the mode of operation, whereby it is assigned the value 0 for GFL mode.
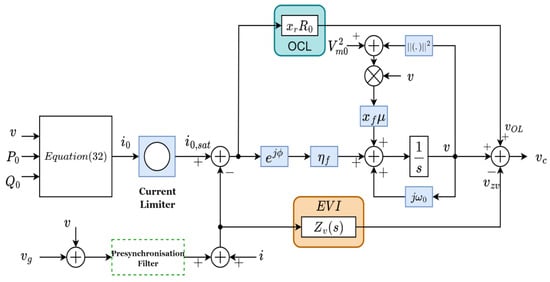
Figure 17.
The controller implemented for universal virtual oscillator control [].
The controller in Figure 17 is composed of emulated virtual impedance, , which is designed with a resonant component and virtual resistance, with limited bandwidth to provide sufficient harmonic compensation and cater for whether the feedback is taken from the converter-side or grid-side current. The fault management system consists effectively of three signals: for overcurrent limiting (OCL), for fault detection and synchronisation gain, and its complement, , which caters for the magnitude error correction. These are activated when a fault (overcurrent) is detected.
The OCL operates series compensation, where is control bandwidth, and and are converter filter inductance and grid side inductance, respectively. has a ramp after-fault clearance to cater for smooth after-fault transients. is the output of a circular current magnitude limiter that limits the current below a threshold, but keeps its phase.
The resynchronisation element ensures the converter connection to the load or grid without large transients and consists of a virtual low-pass filter.
The controller is also set to support voltage and reactive power regulation at the PCC while conducting the allowable maximum current of the device during a fault. The pre-synchronisation module of the controller is a first-order low-pass filter, implemented using a virtual network.
To implement the asynchronous fault ride-through capability of the uVOC, a double synchronous uVOC was implemented in [], implementing decoupled sequence component synchronisation in the steady state for symmetrical and asymmetrical currents and incorporating current limiting in both sequences to tackle unbalanced grid faults.
5.3. Universal Control Scheme (UniCon)
This scheme is built on the principle of operating the inverters to cater for the unpredictability of a power system without a change in operation mode. While most inverter designs are tailored to a single view of the grid and may have to change their operational modes to cater for any changes, the UniCon is proposed to operate several functions in order to obtain the desired system performance, veering away from the local performance-oriented design of the inverter.
This control strategy was proposed in [] and demonstrated in [] to showcase the need for collaborative and autonomous operation of inverters in the grid-connected mode for future grids. The controller was designed to tackle the problematic inverter-based grids faced with low inertia, controller interactions, instabilities, failure susceptibility, resonances, network dynamics, and transient overloads. The design aimed to ensure that systems are oblivious to the vendors’ intellectual property, inverter inner controls, and protection schemes, and it was designed with the objective of operating under varied inverter topologies and applications.
The major control features of the controller are as follows:
5.3.1. Rapid Phase Jump Algorithm
The algorithm was built on the inductor voltage and current of the converter output, with the current being controlled for fast phase movement in order to control phase shifting situations, as well as current overshoots.
The general inverter equations are as follows:
where is the inverter voltage amplitude, is the inverter terminal voltage, is defined by the frequency loop, is defined by the angle loop, is the inductor current with amplitude , is the inductance, and constant is a design parameter that yields the desired exponential behaviour of Equation (36)(iii).
The collective behaviour of Equation (36) describes the phase jump algorithm. The operation of the angle loop control exponentially limits the current to a threshold at which the frequency loop, operating adaptively, converges on the frequency without excursions.
5.3.2. Fault Ride-through Capability
- Overcurrent protection mechanism:
This contains a fast overcurrent protection that operates a virtual resistance to limit the instantaneous overcurrent at p.u. The virtual resistance is as follows:
where is the overcurrent gain, and is the maximum allowable current.
- Dynamic virtual impedance:
This is operated to limit the current total harmonic distortion (THD) after the operation of the overcurrent fault protection, keep the current sinusoidal, and limit the current at a nominal value of 1.25 p.u. after a fault is detected. Virtual admittance is used for virtual impedance, with a proportional resonant controller providing the required decoupling of reactive and active power at an ratio of 5. This is achieved by expressing virtual resistance, and inductance, , obtained through
where is a dynamic gain responsible for varying the virtual impedance using the expression in Equation (39).
where is the sampling time, and is the controller gain.
- Fault recovery:
When a fault occurs, the frequency loop is frozen to maintain synchronism by keeping frequencies relatively close. It is then reactivated when the inverter’s voltage crosses a threshold, which also initiates the lowering of virtual impedance to its nominal value.
5.3.3. Variable Inertia and Damping
The inertia is designed to have a high value during a small-signal state and adopts a small value to support large signal stability, using the expression , where represents the disturbance magnitude.
The damping scheme is obtained through , where , and is the effective inductance. The controller implementation is represented in Figure 18.
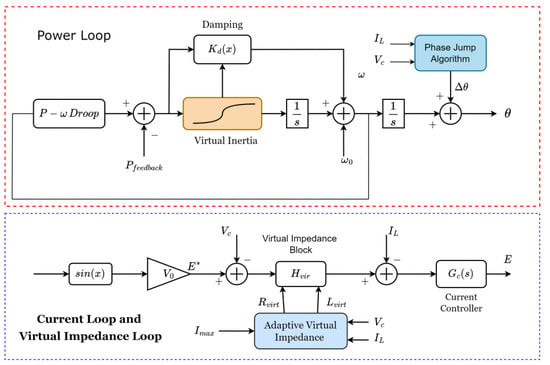
Figure 18.
The power loop and current loop representations for UniCon [].
5.4. Multiple Input–Multiple Output (MIMO) GFM Converters
The growing complexity of inverter parameter design using conventional control theory methods, such as the root locus, in multivariable nonlinear systems, has led to the idea of MIMO-based control design, which enables the use of suitable methods for uncertain systems, such as synthesis, wherein optimisation can be utilised [,,,]. Given the variety of GFM controls in the developing area of inverter-based systems towards a 100% inverter-based grid, the design of GFM controllers, as covered in Section 4, is expanding in scope, and undergoing a variety of modifications to provide ideal performance to support grid connection.
Traditional GFM design assumes a simplistic structure of the controller, with decoupled AC and DC control in the converter structure, APC and RPC decoupling in the power synchronisation loop, and negligible effects of line dynamics. This, however, is not the case, because interactions that affect performance have been observed in controller performance, leading to complex controller designs to accommodate the uncertainties.
A unification approach is also being proposed for GFM control design, motivated by the need to conjure a vendor-independent approach for interoperability [] and to satisfy the requirements desired for GFM operation.
A generalised GFM control model, following the MIMO model, as illustrated in [], was derived and could represent a generic controller or combination of controllers designed to achieve the collective performance attributes of all of the traditional GFM methods, which may include droop, PSC, matching control, VSG, and VOC. The representation is summarised in a matrix of linear and nonlinear signals, whose formulation does not assume any decoupling, but considers the natural dynamics of coupling in converters.
Consider the circuit in Figure 19, whose parameters are used in the derivation.
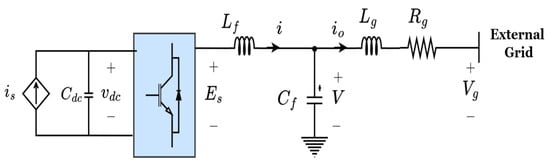
Figure 19.
Circuit schematics showing the major variables used in a converter system.
The DC source in Figure 19 is modelled as a controlled current source and a parallel capacitor [], having arbitrary values of current, , and capacitance, .
Let be the phase difference between the inverter’s internal voltage and the grid voltage , such that and . is the filter inductor current, is the filter capacitor voltage, is the output current, is the filter inductance, is the filter capacitance, and and comprise the grid-side filter impedance. The adopted dynamic electrical models used, considering coupling, are represented in the frame in Equation (40) [,].
where is converter frequency, and is the frequency base.
The AC-side and DC-voltage dynamics are represented through Equation (40). For the MIMO systems, the outputs considered for a GFM model are the DC bus voltage , the voltage magnitude , the converter output frequency , and the active and reactive power and .
Let the vectors and represent the state, control, output, and disturbance vectors of the system, such that
The output can be expressed as a function, with , which depends on the state variables and the control variables.
Equation (40) can be summarised as a function operation of the state variable, the disturbance, and the control variables, represented as .
By establishing a closed-loop system of the GFM, with set points for the control variables obtained through and determined according to the design preference and the reference values of the output variables , the general schematic of the MIMO GFM control is represented in Figure 20.
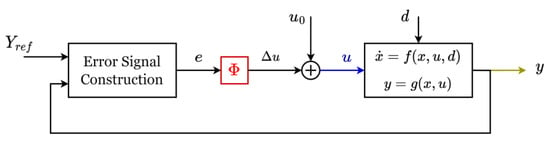
Figure 20.
General MIMO schematic for a closed-loop configuration [].
The GFM controller determines the formulation of the error vector matrix and the control transfer matrix , a 3 × 5 matrix independent of the modelling frame.
The matrix represents the generalised GFM, whose parameters can be designed according to preference. Notably, control matrices for all of the GFM methods can be constructed in the generalised form of , and their improvements are implemented through the addition of the elements therein. This formulation allows for the consideration of coupling between the active power, reactive power, and DC and AC control loops, which would otherwise be assumed non-existent in conventional controller design. The control transfer matrix also shows that nonlinear and higher-order controllers can be integrated with variable controls to improve the performance of GFM controllers.
Another area in which improvements in GFM can be devised is in the formulation of the error , which can take up a linear or nonlinear concept. This method is used to formulate the GFM block in the overall converter schematic and does not account for inner controllers and virtual impedance, but can be included as per the design preference.
In [] a controller was proposed based on full-state error feedback, using the MIMO design principle, which allows for the assignment of closed-loop eigenvalues for desired performance, without any special line conditions. This idea was expanded in [], in which the controllability of an error-based model using the MIMO concept was investigated, and a full-state feedback design concept was used for a predefined time domain performance of GFM, with only local measurements developed.
5.5. Other Methods
Interoperability is a concept that was proposed in [] to create an all-encompassing environment for the design of GFM control schemes that are universally incorporated into the grid, without much concern for the manufacturer of the product. Given that the GFM is a rather new concept for grid-connected inverters, major industrial players protect their innovations [] as intellectual property. The design of inverters following the interoperability paradigm, therefore, seeks to tackle this challenge and propose a universally accepted inverter model that can be adopted and incorporated into power grids, regardless of manufacturer, so that grid modelling, which remains a concern for grid-connected inverters, can be streamlined.
In [], a unified model was proposed that encompasses multiple conventional controllers, whose properties are augmented to form one controller that can universally be considered a GFM one. This design was derived from the similarities that exist between conventional controls, such as droop, virtual synchronous machine, and VOC.
Table 3 outlines the major features of the state-of-the-art approaches addressed in Section 5, stating the improvements from their derivatives.

Table 3.
A summary of state-of-the-art GFM controllers.
6. Issues Affecting Inverter Controllers and Their Mitigation Approaches
6.1. Power Coupling in Inverter Controls
The APC and RPC are integral in GFM control for the regulation of frequency and voltage and are conventionally decoupled to achieve desired performance through the use of decoupling reactance or impedance angle transformation. These loops form the outer loops of a GFM control, which may also have inner loops consisting of current and voltage loops. In conventional power system modelling, it is assumed that line dynamics and inner controllers operate at faster timescales compared to outer loops, and power dynamics that are based on synchronous machine dynamics around the fundamental grid frequency are therefore ignored in converter modelling. However, interactions among inverter controllers, grid dynamics, and power controls have been observed, especially in low-impedance systems and high SCR grids for grid-forming inverters [].
Instabilities in GFMs in strong grids are derived from power surges and oscillations, which have been attributed to controller interactions within loops and within the grid. Power synchronisation loop controllers have a smaller bandwidth of operation when compared to oscillator-dependent controllers and therefore face coupling issues that affect their performance. To maintain the reactance as inductive, virtual impedance techniques are used and are implemented through a differential current term implementing virtual impedance or virtual admittance [].
Consider the schematic of the power system in Figure 21, used to derive coupling between the active and reactive control loops [].
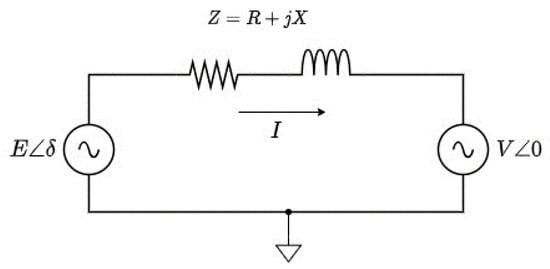
Figure 21.
A simple power system, with two sources coupled through an impedance Z.
In Figure 21, E represents the source voltage, while V is the receiving end voltage, at an angle , out of phase with each other. The impedance Z represents the impedance of the line coupling between the voltages.
Equation (42) shows the general expression for real power, P, and reactive power, Q, delivered to the grid.
Droop relations between , and , can be derived from Equation (42), depending on the ratio of the grid impedance, under the assumption that the angle is small, such that and .
For an inductive grid, . The Equation (42) is simplified as follows:
which shows that P depends on , and Q depends on the voltage difference, in predominantly inductive grids.
For a resistive grid, , Equation (42) is simplified as follows:
showing that P is related to the voltage difference, , while Q is related to angle in predominantly resistive grids.
Preferably, the inductive characteristics of the impedance are designed with the impedance within a suitable range for a linear relationship, which results in a linear relationship of and [,].
Power coupling is attributed to the violation of assumptions in the control laws that govern GFM characteristics, namely the small power angle approximations and predominantly inductive impedance between the source voltage, , and the grid voltage, , for the system simplified in Figure 21. Line resistance in stiff grids distorts the ideal inductive grid characteristics and imposes a small power angle, which increases the controller gain, an undesirable trait for normal operation in GFM controllers, leading to power overshoots []. The presence of resistance in the impedance of the grid therefore brings about coupling in the APC and RPC []. The coupling of controllers in the active and reactive power loops affects their dynamic performance, restricting converter stability margins and the upper bound of the controller bandwidth.
Power coupling is categorised according to its effect on both the steady-state stability and the dynamic performance during transients and post-disturbance [], with various methods designed to decouple the APC and RPC in converters to improve either the steady-state stability or the dynamic performance. Virtual inductance, which alters the converter inductance, thereby reducing the effect caused by the grid impedance and SCR and phase compensation, is an example of a method used to improve steady-state stability.
In [], a virtual power-based method was proposed that utilised phase angle rotation to tackle power coupling and guarantee stability through the Routh stability criterion in droop controllers. In [], a virtual power decoupling method was proposed to deal with harmonic control, as well as provide droop control. A time-domain approach was used to instantiate a converter–filter system with a virtual source consisting of a Thevenin equivalent of the system in parallel to a current source and the subsequent system designed with a virtual impedance. The finite output impedance voltage source operates with a modified frequency–phase angle droop and a voltage–current droop in the time domain to supply the required active and reactive power.
A method that suppresses coupling and creates decoupling paths to cancel conjugate poles was derived and experimentally proven for GFMs in a strong grid. The undesirable coupling between and was effectively cancelled out in the small-signal model by counter couplings designed to compensate the sub-synchronous resonances, online virtual resistance, and inverter impedance adjustment, based on grid impedance estimation, which reshaped the effective power synchronisation control plant into linearly separated APC and RPC loops for effective implementation of the desirable phase margin and extended controller bandwidth. This method was effective for dealing with both weak grids and ultra-strong grids.
Table 4 summarises these decoupling methods in GFM models to achieve both steady-state stability and dynamic performance.

Table 4.
A summary of power decoupling methods used in GFM control.
6.2. Overcurrent Protection in GFMs
Fault protection in grid-forming inverters is required to protect the device from high levels of current during grid short-circuit events. Their effectiveness depends on timely operation during events of frequency disturbances and voltage sags, applicability over varied SCRs, and post-fault stability. An ideal protection scheme must, therefore, operate for its assigned fault type (voltage and frequency disturbances), under all SCR conditions, and have an instantaneous response to a fault, while ensuring post-fault stability. The methods used for protection are summarised below.
6.2.1. Mode-Switching
The controller adopts a current-oriented operation mode during fault situations to protect the device from overloads []. This mechanism requires a fault detection mechanism before mode transition is activated, which may damage the device when large currents are conducted within the measurement delay period before transition. The post-fault stability is complicated by the integrator wind-up phenomenon of the controller.
6.2.2. Power Angle Limiting
In [,], active power limitation through a virtual angle algorithm was proposed. In this method, the power angle was implemented in the APC loop and fitted with a high-bandwidth PLL, which measures the angle between the reference voltage and the PCC voltage. The use of angle limiting ensures that the power synchronisation law is conserved during the transient periods, using the expression of the power angle in Equation (45), passed through an angle-limiting block, as shown in Figure 22.
Figure 22.
Power angle limiter [].
Therefore, by limiting the power angle, both active power, , and current through the inverter are limited. By utilising Equation (45), relating power angle and real power, inverter protection can be implemented appropriately.
In the figure, is the output of the power controller, is the output of the PLL, tracking the voltage at the PCC. A virtual angle, is used instead of the power angle that is not easily known explicitly in grid-connected operation.
During normal operation, the angle-limiting block does not affect the virtual angle, which is limited within the range , as shown in the flat sections of the phase angle limiter in Figure 22, where is the maximum virtual power angle, yielding . Under abnormal conditions, the virtual power angle is limited to , thereby limiting the output power and the current.
6.2.3. Virtual Impedance
A virtual impedance algorithm block is inserted between the voltage and current loops in Figure 7 to limit the current reference generated for modulation. This method effectively adjusts the impedance between the inductor and the grid to limit current flow. Virtual impedance may be affected by changes in grid impedance, requiring adaptive approaches [,] through which to mitigate the changes in grid impedance. This method also causes transient instability, due to sudden adjustments in impedance that produce oscillations when the fault-limiting algorithm is activated.
Virtual admittance is a variation in the virtual impedance, with better transient performance when compared to the derivative implementation of the virtual impedance, which is prone to noise disturbance.
6.2.4. Reference Parameter Limiting
The power references are reduced to limit the power supplied during fault conditions to within the limits of the converter. This approach is normally utilised when inverters are required to supply specific current (active or reactive), due to the grid code for low-voltage ride-through requirements []. In [], a controller was designed to maximise the converter capacity while meeting the LVRT requirement, with an algorithm designed to generate current references for the negative and positive sequence currents under fault conditions.
6.2.5. Voltage-Based Frequency Feedforward
This approach consists of the addition of a frequency feedforward term in the droop power synchronisation controller, using the q-component voltage in the -modelled controller to mitigate harmonic effects, phase, and gain margins for enhanced stability in weak grids [].
6.2.6. Current Saturation
A current saturation mechanism that limits the allowable current through the device during its transient period was introduced in the controller, which is usually fitted with allowable ranges of current during normal operation and is levelled during overcurrent periods. Equation (46) defines the algorithm defined for [,].
where and are the inputs to the current controller, while and are the outputs of the voltage controller in the GFM of Figure 7. is the maximum allowable current magnitude of the converter.
In [], reactive power synchronisation was proposed, fitted with a saturation trigger ability for the voltage controller’s anti-wind, and facilitated a low-voltage ride-through using reactive power sags, while current saturation was used for current protection. In [] a current limitation and post-fault synchronisation stability method was proposed, using the direct voltage control of a lead–lag filter, based droop-controlled GFM, to operate under balanced and unbalanced grid conditions and a current-control loop, whose threshold was activated at the inception of a fault to limit the current and ensure that post-fault synchronisation was guaranteed.
7. Discussion
GFM control of inverters has emerged as the solution through which to tackle the dynamics of low-inertia power grids, caused by the continued adoption and integration of converter-based renewable energy, and leading to a 100% IBR scenario in the foreseeable future. GFM control, therefore, is designed to overcome reduced system inertia, interactions of controller dynamics, fast system dynamics, resonances and oscillations, and transient overloads.
GFM control approaches include droop control, PSC, VSG, synchronverters, matching control, and VOC. Matching control, unlike the SG-derived control, eliminates the use of delay measurements by directly coupling inverter AC and DC sides. VOC is a fast control, due to its instantaneous time-domain operation, and has been varied to be dispatchable and capable of fault management. These primary inverter controls achieve only portions of the spectrum of the requirements of the GFM controller and have continued to be modified.
Inverters in power systems still face various challenges, including standard modelling in simulations and at the utility end. This is attributed to the multiple GFM control paradigms, which have a range of characteristics as compared to SGs, which have been well studied and therefore easily modelled. Universal, generic, hybrid, and unified controllers are emerging concepts in GFM inverter design to deal with the need for interoperability, broad grid conditions, simplified designs, and flexibility in control modifications. In this framework, controllers are designed to augment the advantages of conventional approaches through integration, emulation, and augmentation, in order to achieve compounded advantages of control, given the controllability attributed to the electronic control of inverters. These state-of-the-art designs are, therefore, attractive approaches towards achieving the standardisation of controllers for ease of modelling.
Therefore, it is expected that the formulation of the GFM control will achieve interoperability to allow various private research firms to protect their intellectual property while maintaining the GFM functionality of inverters used in the market. This is a direction suggested as a future roadmap for GFM control.
8. Conclusions
While the integration of inverter-based power resources into the grid is on the rise, the need for grid-forming inverters is on a parallel trajectory for their voltage-stabilising ability within the changing grid paradigm. GFM control is shifting from machine emulation techniques, which use the power-synchronising behaviour of synchronous generators, towards generic and universal designs that fully utilise the fast control and modular nature of power converters.
In this paper, we discussed the issues facing the changing grid paradigm, i.e., low inertia and varying grid strength expressed in SCR; compared the operations of the GFM and GFL inverters; and addressed the major GFM control approaches, their formulations, control variables, and variations, as presented in the literature. The advancements in the development of new grid-forming approaches that modify and improve conventional methods were discussed. Hybrid and state-of-the-art controllers and methods, which encapsulate capabilities for both GFM and GFL operations, were also discussed.
In addition, universal control approaches through which to tackle grid uncertainties were reviewed. The generalised MIMO method for the design of a GFM model with which to accommodate parameters for any desired inverter performance was addressed, as well as the design for interoperability, mentioned for its role towards a vendor-independent GFM model. Finally, issues affecting inverter performance—power coupling and overcurrent protection—were also addressed, and the varied methods used to achieve desired performances were also addressed. The issues addressed in this article encompass the advancements in grid-forming inverters as grids evolve towards 100% converter-based systems.
Author Contributions
All authors contributed equally to the paper; E.E. was responsible for writing the initial manuscript, for data collection, and for idea conceptualisation. O.A.-R. and D.-E.A.M. were responsible for supervising, idea conceptualisation, organising and revising the paper. M.S. and S.M.A. were mainly responsible for supervising and revising the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
The abbreviations below are used in this paper.
| GFL | Grid following |
| GFM | Grid forming |
| VSC | Voltage source converter |
| IBR | Inverter-based resources |
| SCR | Short circuit ratio |
| SG | Synchronous generator |
| SM | Synchronous machine |
| PLL | Phase-locked loop |
| FLL | Frequency-locked loop |
| APC | Active power control |
| RPC | Reactive power control |
| PSC | Power synchronisation control |
| MIMO | Multiple input–multiple output |
| RoCoF | Rate of change of frequency |
| VOC | Virtual oscillator control |
| dVOC | Dispatchable virtual oscillator control |
| uVOC | Unified virtual oscillator control |
| VSG | Virtual synchronous generator |
| HSC | Hybrid synchronisation control |
| AC | Alternating current |
| DC | Direct current |
| RMS | Root mean square |
| PCC | Point of common coupling |
| FACTS | Flexible AC transmission systems |
| HVDC | High-voltage direct current |
| VDP | Van der Pol oscillator |
| VCC | Vector current control |
| PC | Power controller |
| CC | Current controller |
| AVC | Alternating bus voltage controller |
| UniCon | Universal control scheme |
References
- Cohn, J. The Grid: Biography of an American Technology. 27 September 2021. Available online: https://youtu.be/rJSR-Pt5tOI (accessed on 2 July 2023).
- Abdel-Rahim, O.; Chub, A.; Vinnikov, D.; Blinov, A. DC Integration of Residential Photovoltaic Systems: A Survey. IEEE Access 2022, 10, 66974–66991. [Google Scholar] [CrossRef]
- International Energy Agency. Net Zero by 2050—A Roadmap for the Global Energy Sector. International Energy Agency, Special Report. Available online: https://www.iea.org/reports/net-zero-by-2050 (accessed on 12 June 2023).
- Wang, H.; Abdel-Rahim, O. Five-level one-capacitor boost multilevel inverter. IET Power Electron. 2020, 13, 2245–2251. [Google Scholar] [CrossRef]
- Kroposki, B.; Johnson, B.; Zhang, Y.; Gevorgian, V.; Denholm, P.; Hodge, B.-M.; Hannegan, B. Achieving a 100% Renewable Grid: Operating Electric Power Systems with Extremely High Levels of Variable Renewable Energy. IEEE Power Energy Mag. 2017, 15, 61–73. [Google Scholar] [CrossRef]
- Simpson-Porco, J.W.; Dörfler, F.; Bullo, F. Voltage collapse in complex power grids. Nat. Commun. 2016, 7, 10790. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Song, Y.; Zhu, L.; Hill, D.J. Stability and Control of Power Grids. Annu. Rev. Control Robot. Auton. Syst. 2022, 5, 689–716. [Google Scholar] [CrossRef]
- Ramasubramanian, D.; Baker, W.; Matevosyan, J.; Pant, S.; Achilles, S. Asking for fast terminal voltage control in grid following plants could provide benefits of grid forming behavior. IET Gener. Transm. Distrib. 2023, 17, 411–426. [Google Scholar] [CrossRef]
- Ackermann, T.; Prevost, T.; Vittal, V.; Roscoe, A.J.; Matevosyan, J.; Miller, N. Paving the Way: A Future Without Inertia Is Closer Than You Think. IEEE Power Energy Mag. 2017, 15, 61–69. [Google Scholar] [CrossRef]
- Lin, Y.; Eto, J.H.; Johnson, B.B.; Flicker, J.D.; Lasseter, R.H.; Pico, H.N.V.; Seo, G.-S.; Pierre, B.J.; Ellis, A.; Miller, J.; et al. Pathways to the Next-Generation Power System with Inverter-Based Resources: Challenges and recommendations. IEEE Electrif. Mag. 2022, 10, 10–21. [Google Scholar] [CrossRef]
- Abdel-Rahim, O.; Funato, H.; Haruna, J. A comprehensive study of three high-gain DC-DC topologies based on Cockcroft-Walton voltage multiplier for reduced power PV applications. IEEJ Trans. Electr. Electron. Eng. 2018, 13, 642–651. [Google Scholar] [CrossRef]
- Anttila, S.; Döhler, J.S.; Oliveira, J.G.; Boström, C. Grid Forming Inverters: A Review of the State of the Art of Key Elements for Microgrid Operation. Energies 2022, 15, 5517. [Google Scholar] [CrossRef]
- de Leon, F.; de Leon, F. The future belongs to dc: Edison will beat Tesla after all. IEEE Power Energy Mag. 2023, 21, 78–80. [Google Scholar] [CrossRef]
- Mahmoud, K.; Astero, P.; Peltoniemi, P.; Lehtonen, M. Promising Grid-Forming VSC Control Schemes Toward Sustainable Power Systems: Comprehensive Review and Perspectives. IEEE Access 2022, 10, 130024–130039. [Google Scholar] [CrossRef]
- Matevosyan, J.; Badrzadeh, B.; Prevost, T.; Quitmann, E.; Ramasubramanian, D.; Urdal, H.; Achilles, S.; MacDowell, J.; Huang, S.H.; Vital, V.; et al. Grid-Forming Inverters: Are They the Key for High Renewable Penetration? IEEE Power Energy Mag. 2019, 17, 89–98. [Google Scholar] [CrossRef]
- CIGRÉ. Connection of Wind Farms to Weak AC Networks; CIGRÉ: Paris, France, 2016. [Google Scholar]
- Abdel-Rahim, O.; Furiato, H. Switched inductor quadratic boosting ratio inverter with proportional resonant controller for grid-tie PV applications. In Proceedings of the IECON 2014—40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 5606–5611. [Google Scholar]
- Gomis-Bellmunt, O.; Song, J.; Cheah-Mane, M.; Prieto-Araujo, E. Steady-state impedance mapping in grids with power electronics: What is grid strength in modern power systems? Int. J. Electr. Power Energy Syst. 2022, 136, 107635. [Google Scholar] [CrossRef]
- Mitsugi, Y.; Baba, J. Phaser-Based Transfer Function Analysis of Power Synchronization Control Instability for a Grid Forming Inverter in a Stiff Grid. IEEE Access 2023, 11, 42146–42159. [Google Scholar] [CrossRef]
- Harnefors, L.; Hinkkanen, M.; Riaz, U.; Rahman, F.M.M.; Zhang, L. Robust Analytic Design of Power-Synchronization Control. IEEE Trans. Ind. Electron. 2019, 66, 5810–5819. [Google Scholar] [CrossRef]
- IEEE Guide for Planning DC Links Terminating at AC Locations Having Low Short-Circuit Capacities; IEEE: New York, NY, USA, 1997. [CrossRef]
- Bikdeli, E.; Islam, R.; Rahman, M.; Muttaqi, K.M. State of the Art of the Techniques for Grid Forming Inverters to Solve the Challenges of Renewable Rich Power Grids. Energies 2022, 15, 1879. [Google Scholar] [CrossRef]
- Ratnam, K.S.; Palanisamy, K.; Yang, G. Future low-inertia power systems: Requirements, issues, and solutions—A review. Renew. Sustain. Energy Rev. 2020, 124, 109773. [Google Scholar] [CrossRef]
- Faragalla, A.; Abdel-Rahim, O.; Orabi, M.; Abdelhameed, E.H. Enhanced Virtual Inertia Control for Microgrids with High-Penetration Renewables Based on Whale Optimization. Energies 2022, 15, 9254. [Google Scholar] [CrossRef]
- Todorovic, I.; Isakov, I.; Reljic, D.; Jerkan, D.G.; Dujic, D. Mitigation of Voltage and Frequency Excursions in Low-Inertia Microgrids. IEEE Access 2023, 11, 9351–9367. [Google Scholar] [CrossRef]
- Ahmed, F.; Al Kez, D.; McLoone, S.; Best, R.J.; Cameron, C.; Foley, A. Dynamic grid stability in low carbon power systems with minimum inertia. Renew. Energy 2023, 210, 486–506. [Google Scholar] [CrossRef]
- Rezkalla, M.; Pertl, M.; Marinelli, M. Electric power system inertia: Requirements, challenges and solutions. Electr. Eng. 2018, 100, 2677–2693. [Google Scholar] [CrossRef]
- Milano, F.; Dörfler, F.; Hug, G.; Hill, D.J.; Verbič, G. Foundations and Challenges of Low-Inertia Systems (Invited Paper). In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; pp. 1–25. [Google Scholar] [CrossRef]
- Yehia, D.M.; Taha, I.B.M. Application of Superconducting Fault Current Limiter as a Virtual Inertia for DC Distribution Systems. IEEE Access 2021, 9, 135384–135391. [Google Scholar] [CrossRef]
- Ippolito, M.G.; Musca, R.; Sanseverino, E.R.; Zizzo, G. Frequency Dynamics in Fully Non-Synchronous Electrical Grids: A Case Study of an Existing Island. Energies 2022, 15, 2220. [Google Scholar] [CrossRef]
- Hu, Q.; Han, R.; Quan, X.; Wu, Z.; Tang, C.; Li, W.; Wang, W. Grid-Forming Inverter Enabled Virtual Power Plants with Inertia Support Capability. IEEE Trans. Smart Grid 2022, 13, 4134–4143. [Google Scholar] [CrossRef]
- Dalboni, M.; Soldati, A. On the Synchronization of Parallel Power Converters via Emulation of Linear Mechanical Oscillators. In IEEE/ASME Transactions on Mechatronics; IEEE: New York, NY, USA, 2023; pp. 1–12. [Google Scholar] [CrossRef]
- Sajadi, A.; Kenyon, R.W.; Hodge, B.-M. Synchronization in electric power networks with inherent heterogeneity up to 100% inverter-based renewable generation. Nat. Commun. 2022, 13, 2490. [Google Scholar] [CrossRef]
- Matter, E.M.; Mahmoud, E.S.; El-Sayed, M. Power Quality Improvement Considering Voltage Sag and Unbalance Using DVR. J. Al-Azhar Univ. Eng. Sect. 2023, 18, 83–97. [Google Scholar] [CrossRef]
- Perera, U.; Oo, A.M.T.; Zamora, R. Sub Synchronous Oscillations under High Penetration of Renewables—A Review of Existing Monitoring and Damping Methods, Challenges, and Research Prospects. Energies 2022, 15, 8477. [Google Scholar] [CrossRef]
- Markovic, U.; Stanojev, O.; Vrettos, E.; Aristidou, P.; Hug, G. Understanding Stability of Low-Inertia Systems. engrXiv 2019. [Google Scholar] [CrossRef]
- Markovic, U.; Stanojev, O.; Aristidou, P.; Vrettos, E.; Callaway, D.S.; Hug, G. Understanding Small-Signal Stability of Low-Inertia Systems. IEEE Trans. Power Syst. 2021, 36, 3997–4017. [Google Scholar] [CrossRef]
- Abdel-Rahim, O.; Orabi, M.; Ahmed, M.E. Development an efficient photovoltaic (PV) configuration for low power applications. In Proceedings of the 2010 IEEE International Conference on Power and Energy (PECon), Kuala Lumpur, Malaysia, 29 November–1 December 2010; pp. 622–627. [Google Scholar] [CrossRef]
- Abdel-Rahim, O.; Takeuchi, M.; Funato, H.; Junnosuke, H. T-type three-level neutral point clamped inverter with model predictive control for grid connected photovoltaic applications. In Proceedings of the 2016 19th International Conference on Electrical Machines and Systems (ICEMS), Chiba, Japan, 13–16 November 2016; pp. 1–5. [Google Scholar]
- Li, Y.; Gu, Y.; Green, T.C. Revisiting Grid-Forming and Grid-Following Inverters: A Duality Theory. IEEE Trans. Power Syst. 2022, 37, 4541–4554. [Google Scholar] [CrossRef]
- Gao, X.; Zhou, D.; Anvari-Moghaddam, A.; Blaabjerg, F. A Comparative Study of Grid-Following and Grid-Forming Control Schemes in Power Electronic-Based Power Systems. Power Electron. Drives 2023, 8, 1–20. [Google Scholar] [CrossRef]
- Pattabiraman, D.; Lasseter, R.H.; Jahns, T.M. Comparison of Grid Following and Grid Forming Control for a High Inverter Penetration Power System. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Rosso, R.; Wang, X.; Liserre, M.; Lu, X.; Engelken, S. Grid-Forming Converters: Control Approaches, Grid-Synchronization, and Future Trends—A Review. IEEE Open J. Ind. Appl. 2021, 2, 93–109. [Google Scholar] [CrossRef]
- Li, Z. Advanced Control of Grid-Forming Inverters under Uncertain Operating Conditions in AC Microgrids. Ph.D. Thesis, The Hong Kong Polytechnic University, Hongkong, China, 2021. Available online: https://theses.lib.polyu.edu.hk/handle/200/11693 (accessed on 17 July 2023).
- Dokus, M.; Mertens, A. On the Coupling of Power-Related and Inner Inverter Control Loops of Grid-Forming Converter Systems. IEEE Access 2021, 9, 16173–16192. [Google Scholar] [CrossRef]
- Pereira, A.T.; Pinheiro, H. Inner Loop Controllers for Grid-Forming Converters. In Proceedings of the 2022 14th Seminar on Power Electronics and Control (SEPOC), Santa Maria, Brazil, 12–15 November 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Buso, S.; Caldognetto, T.; Liu, Q. Analysis and Experimental Characterization of a Large-Bandwidth Triple-Loop Controller for Grid-Tied Inverters. IEEE Trans. Power Electron. 2019, 34, 1936–1949. [Google Scholar] [CrossRef]
- Gursoy, M.; Mirafzal, B. Direct vs. Indirect Control Schemes for Grid-Forming Inverters–Unveiling a Performance Comparison in a Microgrid. IEEE Access 2023, 11, 75023–75036. [Google Scholar] [CrossRef]
- Pogaku, N.; Prodanovic, M.; Green, T.C. Modeling, Analysis and Testing of Autonomous Operation of an Inverter-Based Microgrid. IEEE Trans. Power Electron. 2007, 22, 613–625. [Google Scholar] [CrossRef]
- Yazdani, A.; Iravani, R. Voltage-Sourced Converters in Power Systems: Modeling, Control, and Applications; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Unruh, P.; Nuschke, M.; Strauß, P.; Welck, F. Overview on Grid-Forming Inverter Control Methods. Energies 2020, 13, 2589. [Google Scholar] [CrossRef]
- Zhang, H.; Xiang, W.; Lin, W.; Wen, J. Grid Forming Converters in Renewable Energy Sources Dominated Power Grid: Control Strategy, Stability, Application, and Challenges. J. Mod. Power Syst. Clean Energy 2021, 9, 1239–1256. [Google Scholar] [CrossRef]
- Abdel-Rahim, O.; Funato, H.; Junnosuke, H. Droop method based on model predictive control for DC microgrid. In Proceedings of the 2016 19th International Conference on Electrical Machines and Systems (ICEMS), Chiba, Japan, 13–16 November 2016; pp. 1–6. [Google Scholar]
- Majumder, R.; Ledwich, G.; Ghosh, A.; Chakrabarti, S.; Zare, F. Droop Control of Converter-Interfaced Microsources in Rural Distributed Generation. IEEE Trans. Power Deliv. 2010, 25, 2768–2778. [Google Scholar] [CrossRef]
- D’Arco, S.; Suul, J.A. Virtual Synchronous Machines—Classification of Implementations and Analysis of Equivalence to Droop Controllers for Microgrids. In Proceedings of the 2013 IEEE Powertech Grenoble Conference, Grenoble, France, 16–20 June 2013; pp. 1–7. [Google Scholar] [CrossRef]
- D’Arco, S.; Suul, J.A. Equivalence of Virtual Synchronous Machines and Frequency-Droops for Converter-Based MicroGrids. IEEE Trans. Smart Grid 2013, 5, 394–395. [Google Scholar] [CrossRef]
- Sun, Y.; Hou, X.; Yang, J.; Han, H.; Su, M.; Guerrero, J.M. New Perspectives on Droop Control in AC Microgrid. IEEE Trans. Ind. Electron. 2017, 64, 5741–5745. [Google Scholar] [CrossRef]
- Du, W.; Chen, Z.; Schneider, K.P.; Lasseter, R.H.; Nandanoori, S.P.; Tuffner, F.K.; Kundu, S. A Comparative Study of Two Widely Used Grid-Forming Droop Controls on Microgrid Small-Signal Stability. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 963–975. [Google Scholar] [CrossRef]
- Shi, Y.; Gu, X.; Yin, X.; Feng, S.; Zhang, S. Design of droop controller in islanded microgrids using multi-objective optimisation based on accurate small-signal model. IET Power Electron. 2022, 15, 1093–1109. [Google Scholar] [CrossRef]
- Eberlein, S.; Rudion, K. Small-signal stability modelling, sensitivity analysis and optimization of droop controlled inverters in LV microgrids. Int. J. Electr. Power Energy Syst. 2021, 125, 106404. [Google Scholar] [CrossRef]
- Eberlein, S.; Rudion, K. Optimisation, benchmark testing and comparison of droop control variants in microgrids. IET Smart Grid 2021, 4, 536–548. [Google Scholar] [CrossRef]
- Belal, E.K.; Yehia, D.M.; Azmy, A.M. Effective Power Management of DC Microgrids Using Adaptive Droop Control. In Proceedings of the 2018 Twentieth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 18–20 December 2018; pp. 905–910. [Google Scholar] [CrossRef]
- Gurugubelli, V.; Ghosh, A.; Panda, A.K.; Rudra, S. Implementation and comparison of droop control, virtual synchronous machine, and virtual oscillator control for parallel inverters in standalone microgrid. Int. Trans. Electr. Energy Syst. 2021, 31, e12859. [Google Scholar] [CrossRef]
- Zhang, L.; Harnefors, L.; Nee, H.-P. Power-Synchronization Control of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Syst. 2010, 25, 809–820. [Google Scholar] [CrossRef]
- Ahmed, H.Y.; Abdel-Rahim, O.; Ali, Z.M. New High-Gain Transformerless DC/DC Boost Converter System. Electronics 2022, 11, 734. [Google Scholar] [CrossRef]
- Zhang, L.; Harnefors, L.; Nee, H.-P. Interconnection of Two Very Weak AC Systems by VSC-HVDC Links Using Power-Synchronization Control. IEEE Trans. Power Syst. 2011, 26, 344–355. [Google Scholar] [CrossRef]
- Sepehr, A.; Gomis-Bellmunt, O.; Pouresmaeil, E. Employing Machine Learning for Enhancing Transient Stability of Power Synchronization Control During Fault Conditions in Weak Grids. IEEE Trans. Smart Grid 2022, 13, 2121–2131. [Google Scholar] [CrossRef]
- Zhang, L.; Nee, H.-P.; Harnefors, L. Analysis of Stability Limitations of a VSC-HVDC Link Using Power-Synchronization Control. IEEE Trans. Power Syst. 2011, 26, 1326–1337. [Google Scholar] [CrossRef]
- Xiong, X.; Zhou, Y.; Luo, B.; Cheng, P.; Blaabjerg, F. Analysis and Suppression Strategy of Synchronous Frequency Resonance for Grid-Connected Converters with Power-Synchronous Control Method. IEEE Trans. Power Electron. 2023, 38, 6945–6955. [Google Scholar] [CrossRef]
- Wu, H.; Wang, X. Design-Oriented Transient Stability Analysis of Grid-Connected Converters with Power Synchronization Control. IEEE Trans. Ind. Electron. 2019, 66, 6473–6482. [Google Scholar] [CrossRef]
- Yazdani, S.; Davari, M.; Ferdowsi, M.; Shamsi, P. Internal Model Power Synchronization Control of a PV-Based Voltage-Source Converter in Weak-Grid and Islanded Conditions. IEEE Trans. Sustain. Energy 2021, 12, 1360–1371. [Google Scholar] [CrossRef]
- Yazdani, S.; Ferdowsi, M.; Shamsi, P. Power Synchronization PID Control Method for Grid-Connected Voltage-Source Converters. In Proceedings of the 2020 IEEE Kansas Power and Energy Conference (KPEC), Manhattan, KS, USA, 13–14 July 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Driesen, J.; Visscher, K. Virtual synchronous generators. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–3. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Bevrani, H.; Ise, T. Enhanced Virtual Synchronous Generator Control for Parallel Inverters in Microgrids. IEEE Trans. Smart Grid 2017, 8, 2268–2277. [Google Scholar] [CrossRef]
- Li, B.; Zhou, L.; Yu, X.; Zheng, C.; Liu, J. Improved power decoupling control strategy based on virtual synchronous generator. IET Power Electron. 2017, 10, 462–470. [Google Scholar] [CrossRef]
- Shuai, Z.; Shen, C.; Liu, X.; Li, Z.; Shen, Z.J. Transient Angle Stability of Virtual Synchronous Generators Using Lyapunov’s Direct Method. IEEE Trans. Smart Grid 2019, 10, 4648–4661. [Google Scholar] [CrossRef]
- Chen, M.; Zhou, D.; Blaabjerg, F. Enhanced Transient Angle Stability Control of Grid-Forming Converter Based on Virtual Synchronous Generator. IEEE Trans. Ind. Electron. 2022, 69, 9133–9144. [Google Scholar] [CrossRef]
- Xiong, X.; Wu, C.; Hu, B.; Pan, D.; Blaabjerg, F. Transient Damping Method for Improving the Synchronization Stability of Virtual Synchronous Generators. IEEE Trans. Power Electron. 2021, 36, 7820–7831. [Google Scholar] [CrossRef]
- Sadeque, F.; Fateh, F. On Control Schemes for Grid-Forming Inverters. In Proceedings of the 2022 IEEE Kansas Power and Energy Conference (KPEC), Manhattan, KS, USA, 25–26 April 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Shintai, T.; Miura, Y.; Ise, T. Oscillation Damping of a Distributed Generator Using a Virtual Synchronous Generator. IEEE Trans. Power Deliv. 2014, 29, 668–676. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, H.; Hu, X.; Hou, X.; Su, C.; Sun, K. Adaptive Inertia and Damping Coordination (AIDC) Control for Grid-Forming VSG to Improve Transient Stability. Electronics 2023, 12, 2060. [Google Scholar] [CrossRef]
- Cheema, K.M.; Chaudhary, N.I.; Tahir, M.F.; Mehmood, K.; Mudassir, M.; Kamran, M.; Milyani, A.H.; Elbarbary, Z.S. Virtual synchronous generator: Modifications, stability assessment and future applications. Energy Rep. 2022, 8, 1704–1717. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.; Du, Z.; Xu, Z.; Dong, Z. Damping Turning Rule of Virtual Synchronous Generator for Global Stability. IEEE Trans. Power Deliv. 2023, 38, 2650–2660. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.; Cao, Y.; Wang, L.; Blaabjerg, F.; Dragicevic, T. Frequency and Voltage Stability Analysis of Grid-Forming Virtual Synchronous Generator Attached to Weak Grid. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2662–2671. [Google Scholar] [CrossRef]
- Chen, S.; Sun, Y.; Han, H.; Fu, S.; Luo, S.; Shi, G. A Modified VSG Control Scheme with Virtual Resistance to Enhance Both Small-Signal Stability and Transient Synchronization Stability. IEEE Trans. Power Electron. 2023, 38, 6005–6014. [Google Scholar] [CrossRef]
- Miranbeigi, M.; Kandula, P.; Divan, D. A New Representation based on Virtual Capacitor for Virtual Synchronous Generators. In Proceedings of the 2020 IEEE 11th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Dubrovnik, Croatia, 28 September–1 October 2020; pp. 205–210. [Google Scholar] [CrossRef]
- Suvorov, A.; Askarov, A.; Bay, Y.; Maliuta, B.; Achitaev, A.; Suslov, K. Comparative small-signal stability analysis of voltage-controlled and enhanced current-controlled virtual synchronous generators under weak and stiff grid conditions. Int. J. Electr. Power Energy Syst. 2023, 147, 108891. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, J.; Li, C.; Zhang, W.; Wu, Q.; Wen, M.; Blaabjerg, F. A New Virtual Inductance Control Method for Frequency Stabilization of Grid-Forming Virtual Synchronous Generators. IEEE Trans. Ind. Electron. 2023, 70, 441–451. [Google Scholar] [CrossRef]
- Lu, S.; Zhu, Y.; Dong, L.; Na, G.; Hao, Y.; Zhang, G.; Zhang, W.; Cheng, S.; Yang, J.; Sui, Y. Small-Signal Stability Research of Grid-Connected Virtual Synchronous Generators. Energies 2022, 15, 7158. [Google Scholar] [CrossRef]
- Zhong, Q.-C.; Weiss, G. Synchronverters: Inverters that mimic synchronous generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Tayyebi, A.; Dörfler, F.; Kupzog, F.; Miletic, Z.; Hribernik, W. Grid-Forming Converters—Inevitability, Control Strategies and Challenges in Future Grids Application. In Proceedings of the CIRED 2018 Ljubljana Workshop, Ljubljana, Slovenia, 7–8 June 2018. [Google Scholar] [CrossRef]
- Rosso, R.; Engelken, S.; Liserre, M. A Generalized Formulation of Active Power Synchronization Based Control Algorithms for Grid Connected Converters. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 883–888. [Google Scholar] [CrossRef]
- Zhong, Q.-C.; Nguyen, P.-L.; Ma, Z.; Sheng, W. Self-Synchronized Synchronverters: Inverters Without a Dedicated Synchronization Unit. IEEE Trans. Power Electron. 2014, 29, 617–630. [Google Scholar] [CrossRef]
- Natarajan, V.; Weiss, G. Synchronverters with Better Stability Due to Virtual Inductors, Virtual Capacitors, and Anti-Windup. IEEE Trans. Ind. Electron. 2017, 64, 5994–6004. [Google Scholar] [CrossRef]
- Lorenzetti, P.; Kustanovich, Z.; Shivratri, S.; Weiss, G. The Equilibrium Points and Stability of Grid-Connected Synchronverters. IEEE Trans. Power Syst. 2022, 37, 1184–1197. [Google Scholar] [CrossRef]
- Vasudevan, K.R.; Ramachandaramurthy, V.K.; Babu, T.S.; Pouryekta, A. Synchronverter: A Comprehensive Review of Modifications, Stability Assessment, Applications and Future Perspectives. IEEE Access 2020, 8, 131565–131589. [Google Scholar] [CrossRef]
- Gomes, L.D.N.; Abrantes-Ferreira, A.J.G.; Dias, R.F.d.S.; Rolim, L.G.B. Synchronverter-Based STATCOM With Voltage Imbalance Compensation Functionality. IEEE Trans. Ind. Electron. 2022, 69, 4836–4844. [Google Scholar] [CrossRef]
- Remon, D.; Cantarellas, A.M.; Rakhshani, E.; Candela, I.; Rodriguez, P. An active power synchronization control loop for grid-connected converters. In Proceedings of the IEEE Power & Energy Society General Meeting, National Harbor, MD, USA, 27–31 July 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Arghir, C.; Jouini, T.; Dörfler, F. Grid-forming control for power converters based on matching of synchronous machines. Automatica 2018, 95, 273–282. [Google Scholar] [CrossRef]
- Curi, S.; Gross, D.; Dorfler, F. Control of low-inertia power grids: A model reduction approach. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, VIC, Australia, 12–15 December 2017; pp. 5708–5713. [Google Scholar] [CrossRef]
- Jouini, T.; Arghir, C.; Dörfler, F. Grid-Friendly Matching of Synchronous Machines by Tapping into the DC Storage. IFAC-Pap. Online 2016, 49, 192–197. [Google Scholar] [CrossRef]
- Arghir, C.; Dorfler, F. The Electronic Realization of Synchronous Machines: Model Matching, Angle Tracking, and Energy Shaping Techniques. IEEE Trans. Power Electron. 2020, 35, 4398–4410. [Google Scholar] [CrossRef]
- Mahamedi, B.; Fletcher, J.E. The Equivalent Models of Grid-Forming Inverters in the Sequence Domain for the Steady-State Analysis of Power Systems. IEEE Trans. Power Syst. 2020, 35, 2876–2887. [Google Scholar] [CrossRef]
- Dörfler, F.; Chertkov, M.; Bullo, F. Synchronization in complex oscillator networks and smart grids. Proc. Natl. Acad. Sci. USA 2013, 110, 2005–2010. [Google Scholar] [CrossRef]
- Torres, L.A.B.; Hespanha, J.P.; Moehlis, J. Synchronization of Identical Oscillators Coupled Through a Symmetric Network with Dynamics: A Constructive Approach with Applications to Parallel Operation of Inverters. IEEE Trans. Autom. Control 2015, 60, 3226–3241. [Google Scholar] [CrossRef]
- Johnson, B.B.; Dhople, S.V.; Hamadeh, A.O.; Krein, P.T. Synchronization of Parallel Single-Phase Inverters with Virtual Oscillator Control. IEEE Trans. Power Electron. 2014, 29, 6124–6138. [Google Scholar] [CrossRef]
- Dhople, S.V.; Johnson, B.B.; Hamadeh, A.O. Virtual Oscillator Control for voltage source inverters. In Proceedings of the 2013 51st Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 2–4 October 2013; pp. 1359–1363. [Google Scholar] [CrossRef]
- Aghdam, S.A.; Agamy, M. Virtual oscillator-based methods for grid-forming inverter control: A review. IET Renew. Power Gener. 2022, 16, 835–855. [Google Scholar] [CrossRef]
- Sinha, M.; Dorfler, F.; Johnson, B.B.; Dhople, S.V. Virtual Oscillator Control subsumes droop control. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 2353–2358. [Google Scholar] [CrossRef]
- Lu, M.; Dutta, S.; Purba, V.; Dhople, S.; Johnson, B. A Grid-compatible Virtual Oscillator Controller: Analysis and Design. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 2643–2649. [Google Scholar] [CrossRef]
- Johnson, B.B.; Sinha, M.; Ainsworth, N.G.; Dorfler, F.; Dhople, S.V. Synthesizing Virtual Oscillators to Control Islanded Inverters. IEEE Trans. Power Electron. 2016, 31, 6002–6015. [Google Scholar] [CrossRef]
- Sinha, M.; Dorfler, F.; Johnson, B.B.; Dhople, S.V. Uncovering Droop Control Laws Embedded Within the Nonlinear Dynamics of Van der Pol Oscillators. IEEE Trans. Control Netw. Syst. 2017, 4, 347–358. [Google Scholar] [CrossRef]
- Luo, S.; Wu, W.; Koutroulis, E.G.; Chung, H.S.-H.; Blaabjerg, F.G. A New Virtual Oscillator Control Without Third-Harmonics Injection For DC/AC Inverter. IEEE Trans. Power Electron. 2021, 36, 10879–10888. [Google Scholar] [CrossRef]
- Awal, M.A.; Yu, H.; Husain, I.; Yu, W.; Lukic, S.M. Selective Harmonic Current Rejection for Virtual Oscillator Controlled Grid-Forming Voltage Source Converters. IEEE Trans. Power Electron. 2020, 35, 8805–8818. [Google Scholar] [CrossRef]
- Raisz, D.; Thai, T.T.; Monti, A. Power Control of Virtual Oscillator Controlled Inverters in Grid-Connected Mode. IEEE Trans. Power Electron. 2019, 34, 5916–5926. [Google Scholar] [CrossRef]
- Colombino, M.; Gros, D.; Dorfler, F. Global phase and voltage synchronization for power inverters: A decentralized consensus-inspired approach. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, VIC, Australia, 12–15 December 2017; pp. 5690–5695. [Google Scholar] [CrossRef]
- Colombino, M.; Groz, D.; Brouillon, J.-S.; Dorfler, F. Global Phase and Magnitude Synchronization of Coupled Oscillators with Application to the Control of Grid-Forming Power Inverters. IEEE Trans. Autom. Control 2019, 64, 4496–4511. [Google Scholar] [CrossRef]
- Seo, G.-S.; Colombino, M.; Subotic, I.; Johnson, B.; Gros, D.; Dorfler, F. Dispatchable Virtual Oscillator Control for Decentralized Inverter-dominated Power Systems: Analysis and Experiments. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 561–566. [Google Scholar] [CrossRef]
- Lu, M.; Dhople, S.V.; Johnson, B. Benchmarking Nonlinear Oscillators for Grid-Forming Inverter Control. IEEE Trans. Power Electron. 2022, 37, 10250–10266. [Google Scholar] [CrossRef]
- Ali, M.; Nurdin, H.I.; Fletcher, J.E. Dispatchable Virtual Oscillator Control for Single-Phase Islanded Inverters: Analysis and Experiments. IEEE Trans. Ind. Electron. 2021, 68, 4812–4826. [Google Scholar] [CrossRef]
- Lu, M. Virtual Oscillator Grid-Forming Inverters: State of the Art, Modeling, and Stability. IEEE Trans. Power Electron. 2022, 37, 11579–11591. [Google Scholar] [CrossRef]
- He, X.; Haberle, V.; Subotic, I.; Dorfler, F. Nonlinear Stability of Complex Droop Control in Converter-Based Power Systems. IEEE Control Syst. Lett. 2023, 7, 1327–1332. [Google Scholar] [CrossRef]
- Awal, M.A.; Yu, H.; Tu, H.; Lukic, S.M.; Husain, I. Hierarchical Control for Virtual Oscillator Based Grid-Connected and Islanded Microgrids. IEEE Trans. Power Electron. 2020, 35, 988–1001. [Google Scholar] [CrossRef]
- Lu, M.; Dutta, S.; Johnson, B. Self-Synchronizing Cascaded Inverters with Virtual Oscillator Control. IEEE Trans. Power Electron. 2022, 37, 6424–6436. [Google Scholar] [CrossRef]
- Kong, L.; Xue, Y.; Qiao, L.; Wang, F. Enhanced Synchronization Stability of Grid-Forming Inverters with Passivity-Based Virtual Oscillator Control. IEEE Trans. Power Electron. 2022, 37, 14141–14156. [Google Scholar] [CrossRef]
- Li, J.; Fletcher, J.E.; Holmes, D.; McGrath, B. Developing a machine equivalent inertial response for a Virtual Oscillator Controlled Inverter in a machine-inverter based microgrid. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 4314–4321. [Google Scholar] [CrossRef]
- Awal, M.A.; Husain, I. Unified Virtual Oscillator Control for Grid-Forming and Grid-Following Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 4573–4586. [Google Scholar] [CrossRef]
- Ajala, O.; Lu, M.; Johnson, B.B.; Dhople, S.V.; Dominguez-Garcia, A. Model Reduction for Inverters with Current Limiting and Dispatchable Virtual Oscillator Control. IEEE Trans. Energy Convers. 2022, 37, 2250–2259. [Google Scholar] [CrossRef]
- Ghosh, R.; Tummuru, N.R.; Rajpurohit, B.S. Modified VOC Using Three Symmetrical Components for Grid-Supporting Operation During Unbalanced Grid Voltages and Grid-Forming Operation in Hybrid Single-Phase/Three-Phase Microgrid. IEEE Trans. Ind. Electron. 2023, 70, 11276–11286. [Google Scholar] [CrossRef]
- Ghosh, R.; Tummuru, N.R.; Rajpurohit, B.S. A New Virtual Oscillator-Based Grid-Forming Controller with Decoupled Control Over Individual Phases and Improved Performance of Unbalanced Fault Ride-Through. IEEE Trans. Ind. Electron. 2023, 70, 12465–12474. [Google Scholar] [CrossRef]
- Harnefors, L.; Kukkola, J.; Routimo, M.; Hinkkanen, M.; Wang, X. A Universal Controller for Grid-Connected Voltage-Source Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5761–5770. [Google Scholar] [CrossRef]
- Harnefors, L.; Schweizer, M.; Kukkola, J.; Routimo, M.; Hinkkanen, M.; Wang, X. Generic PLL-Based Grid-Forming Control. IEEE Trans. Power Electron. 2021, 37, 1201–1204. [Google Scholar] [CrossRef]
- Wang, X.; Taul, M.G.; Wu, H.; Liao, Y.; Blaabjerg, F.; Harnefors, L. Grid-Synchronization Stability of Converter-Based Resources—An Overview. IEEE Open J. Ind. Appl. 2020, 1, 115–134. [Google Scholar] [CrossRef]
- Zhao, F.; Wang, X.; Zhou, Z.; Sun, Y.; Harnefors, L.; Zhu, T. Robust Grid-Forming Control with Active Susceptance. IEEE Trans. Power Electron. 2023, 38, 2872–2877. [Google Scholar] [CrossRef]
- Liu, T.; Wang, X. Physical Insight into Hybrid-Synchronization-Controlled Grid-Forming Inverters Under Large Disturbances. IEEE Trans. Power Electron. 2022, 37, 11475–11480. [Google Scholar] [CrossRef]
- Pan, R.; Liu, S.; Gu, H.; Liu, D.; Zhu, L.; Chen, E. Stability analysis of hybrid synchronization controller based grid forming control. Energy Rep. 2023, 9, 1291–1298. [Google Scholar] [CrossRef]
- Gong, H.; Wang, X. Design-Oriented Analysis of Grid-Forming Control with Hybrid Synchronization. In Proceedings of the 2022 International Power Electronics Conference (IPEC-Himeji 2022-ECCE Asia), Himeji, Japan, 15–19 May 2022; pp. 440–446. [Google Scholar] [CrossRef]
- Abdel-Rahim, O.; Funato, H. Model Predictive Control based Maximum Power Point Tracking technique applied to Ultra Step-Up Boost Converter for PV applications. In Proceedings of the 2014 IEEE Innovative Smart Grid Technologies—Asia (ISGT ASIA), Kuala Lumpur, Malaysia, 20–23 May 2014; pp. 138–142. [Google Scholar] [CrossRef]
- Gong, H.; Wang, X. Interaction analysis and enhanced design of grid-forming control with hybrid synchronization and virtual admittance loops. iEnergy 2023, 2, 71–84. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, X.; Gong, H.; Jin, Z. Stability Impact of Hybrid Synchronization Strategy on Virtual-Admittance-Based Grid-Forming Inverters. In Proceedings of the 2023 IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 19–23 March 2023; pp. 2735–2740. [Google Scholar] [CrossRef]
- Awal, M.A.; Rachi, R.K.; Yu, H.; Husain, I.; Lukic, S. Double Synchronous Unified Virtual Oscillator Control for Asymmetrical Fault Ride-Through in Grid-Forming Voltage Source Converters. IEEE Trans. Power Electron. 2023, 38, 6759–6763. [Google Scholar] [CrossRef]
- Miranbeigi, M.; Kandula, P.; Divan, D. Unified Control (UniCon) Strategies for Grid-Connected Inverters. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; pp. 3000–3006. [Google Scholar] [CrossRef]
- Benzaquen, J.; Miranbeigi, M.; Kandula, P.; Divan, D. Collaborative Autonomous Grid-Connected Inverters: Flexible grid-forming inverter control for the future grid. IEEE Electrification Mag. 2022, 10, 22–29. [Google Scholar] [CrossRef]
- Rafiee, A.; Batmani, Y.; Bevrani, H.; Kato, T. Robust MIMO Controller Design for VSC-Based Microgrids: Sequential Loop Closing Concept and Quantitative Feedback Theory. IEEE Trans. Smart Grid 2022, 13, 129–138. [Google Scholar] [CrossRef]
- Alamir, N.; Abdel-Rahim, O.; Ismeil, M.; Orabi, M.; Kennel, R. Fixed Frequency Predictive MPPT for Phase-Shift Modulated LLC Resonant Micro-Inverter. In Proceedings of the 2018 20th European Conference on Power Electronics and Applications (EPE’18 ECCE Europe), Riga, Latvia, 17–21 September 2018; pp. 1–9. [Google Scholar]
- Abdel-Rahim, O.; Funato, H. A novel model predictive control for high gain switched inductor power conditioning system for photovoltaic applications. In Proceedings of the 2014 IEEE Innovative Smart Grid Technologies—Asia (ISGT ASIA), Kuala Lumpur, Malaysia, 20–23 May 2014; pp. 170–174. [Google Scholar] [CrossRef]
- Huang, L.; Xin, H.; Dorfler, F. H∞-Control of Grid-Connected Converters: Design, Objectives and Decentralized Stability Certificates. IEEE Trans. Smart Grid 2020, 11, 3805–3816. [Google Scholar] [CrossRef]
- Johnson, B.; Roberts, T.G.; Ajala, O.; Dominguez-Garcia, A.; Dhople, S.; Ramasubramanian, D.; Tuohy, A.; Divan, D.; Kroposki, B. A Generic Primary-control Model for Grid-forming Inverters: Towards Interoperable Operation & Control. In Proceedings of the Hawaii International Conference on System Sciences, Maui, HI, USA, 4–7 January 2022. [Google Scholar] [CrossRef]
- Chen, M.; Zhou, D.; Tayyebi, A.; Prieto-Araujo, E.; Dorfler, F.; Blaabjerg, F. Generalized Multivariable Grid-Forming Control Design for Power Converters. IEEE Trans. Smart Grid 2022, 13, 2873–2885. [Google Scholar] [CrossRef]
- Tayyebi, A.; Groß, D.; Anta, A.; Kupzog, F.; Dörfler, F. Interactions of Grid-Forming Power Converters and Synchronous Machines. arXiv 2019, arXiv:1902.10750. Available online: http://arxiv.org/abs/1902.10750 (accessed on 20 July 2023).
- Kroutikova, N.; Hernandez-Aramburo, C.; Green, T. State-space model of grid-connected inverters under current control mode. IET Electr. Power Appl. 2007, 1, 329–338. [Google Scholar] [CrossRef]
- Mo, O.; D’Arco, S.; Suul, J.A. Evaluation of Virtual Synchronous Machines with Dynamic or Quasi-Stationary Machine Models. IEEE Trans. Ind. Electron. 2017, 64, 5952–5962. [Google Scholar] [CrossRef]
- Chen, M.; Zhou, D.; Blaabjerg, F. Power Control of Grid-Forming Converters Based on Full-State Feedback. In Proceedings of the IECON 2022—48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 17–20 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, M.; Zhou, D.; Tayyebi, A.; Prieto-Araujo, E.; Dörfler, F.; Blaabjerg, F. On Power Control of Grid-Forming Converters: Modeling, Controllability, and Full-State Feedback Design. IEEE Trans. Sustain. Energy 2023, 1–12. [Google Scholar] [CrossRef]
- Lin, Y.; Eto, J.H.; Johnson, B.B.; Flicker, J.D.; Lasseter, R.H.; Pico, H.N.V.; Seo, G.-S.; Pierre, B.J.; Ellis, A. Research Roadmap on Grid-Forming Inverters’, National Renewable Energy Laboratory, Technical Report NREL/TP-5D00-73476. Available online: https://www.nrel.gov/docs/fy21osti/73476.pdf (accessed on 15 September 2023).
- Musca, R.; Vasile, A.; Zizzo, G. Grid-forming converters. A critical review of pilot projects and demonstrators. Renew. Sustain. Energy Rev. 2022, 165, 112551. [Google Scholar] [CrossRef]
- Ferreira, A.J.G.A.; Oliveira, A.C.; Lima, A.M.N. A Unified Control Framework for Grid-Forming Inverters. EasyChair, 2022; preprint. [Google Scholar]
- Wu, T.; Liu, Z.; Liu, J.; Wang, S.; You, Z. A Unified Virtual Power Decoupling Method for Droop-Controlled Parallel Inverters in Microgrids. IEEE Trans. Power Electron. 2016, 31, 5587–5603. [Google Scholar] [CrossRef]
- Rodriguez, P.; Candela, I.; Citro, C.; Rocabert, J.; Luna, A. Control of grid-connected power converters based on a virtual admittance control loop. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–10. [Google Scholar] [CrossRef]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodríguez, P. Control of Power Converters in AC Microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Du, W.; Lasseter, R.H.; Khalsa, A.S. Survivability of Autonomous Microgrid During Overload Events. IEEE Trans. Smart Grid 2019, 10, 3515–3524. [Google Scholar] [CrossRef]
- Rathnayake, D.B.; Akrami, M.; Phurailatpam, C.; Me, S.P.; Hadavi, S.; Jayasinghe, G.; Zabihi, S.; Bahrani, B. Grid Forming Inverter Modeling, Control, and Applications. IEEE Access 2021, 9, 114781–114807. [Google Scholar] [CrossRef]
- Zhao, F.; Wang, X.; Zhu, T. Power Dynamic Decoupling Control of Grid-Forming Converter in Stiff Grid. IEEE Trans. Power Electron. 2022, 37, 9073–9088. [Google Scholar] [CrossRef]
- Li, M.; Wang, Y.; Hu, W.; Shu, S.; Yu, P.; Zhang, Z.; Blaabjerg, F. Unified Modeling and Analysis of Dynamic Power Coupling for Grid-forming Converters. IEEE Trans. Power Electron. 2021, 37, 2321–2337. [Google Scholar] [CrossRef]
- De Brabandere, K.; Bolsens, B.; Van den Keybus, J.; Woyte, A.; Driesen, J.; Belmans, R. A Voltage and Frequency Droop Control Method for Parallel Inverters. IEEE Trans. Power Electron. 2007, 22, 1107–1115. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.W. Power Management of Inverter Interfaced Autonomous Microgrid Based on Virtual Frequency-Voltage Frame. IEEE Trans. Smart Grid 2011, 2, 30–40. [Google Scholar] [CrossRef]
- Gong, Z.; Liu, C.; Gui, Y.; da Silva, F.F.; Bak, C.L. Power Decoupling Method for Voltage Source Inverters Using Grid Voltage Modulated Direct Power Control in Unbalanced System. IEEE Trans. Power Electron. 2023, 38, 3084–3099. [Google Scholar] [CrossRef]
- Wen, T.; Zou, X.; Zhu, D.; Guo, X.; Peng, L.; Kang, Y. Comprehensive perspective on virtual inductor for improved power decoupling of virtual synchronous generator control. IET Renew. Power Gener. 2020, 14, 485–494. [Google Scholar] [CrossRef]
- Long, B.; Long, B.; Zhu, S.; Zhu, S.; Rodriguez, J.; Rodriguez, J.; Guerrero, J.M.; Guerrero, J.M.; Chong, K.T.; Chong, K.T. Enhancement of Power Decoupling for Virtual Synchronous Generator: A Virtual Inductor and Virtual Capacitor Approach. IEEE Trans. Ind. Electron. 2023, 70, 6830–6843. [Google Scholar] [CrossRef]
- Rathnayake, D.B.; Bahrani, B. Multivariable Control Design for Grid-Forming Inverters with Decoupled Active and Reactive Power Loops. IEEE Trans. Power Electron. 2023, 38, 1635–1649. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, J.; Bi, D.; Wen, Y.; Dai, Y.; Yin, X.; Shen, J. Droop Control Strategy Incorporating Coupling Compensation and Virtual Impedance for Microgrid Application. IEEE Trans. Energy Convers. 2019, 34, 277–291. [Google Scholar] [CrossRef]
- Gong, Z.; Liu, C.; Shang, L.; Lai, Q.; Terriche, Y. Power Decoupling Strategy for Voltage Modulated Direct Power Control of Voltage Source Inverters Connected to Weak Grids. IEEE Trans. Sustain. Energy 2023, 14, 152–167. [Google Scholar] [CrossRef]
- Yan, X.; Zhang, Y. Power coupling analysis of inverters based on relative gain method and decoupling control based on feedforward compensation. In Proceedings of the International Conference on Renewable Power Generation (RPG 2015), Beijing, China, 17–18 October 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Oureilidis, K.O.; Demoulias, C.S. A Fault Clearing Method in Converter-Dominated Microgrids with Conventional Protection Means. IEEE Trans. Power Electron. 2016, 31, 4628–4640. [Google Scholar] [CrossRef]
- Huang, L.; Wu, C.; Zhou, D.; Blaabjerg, F. A Power Angle Limiting Method for Improving Stability of Grid-Forming Inverter Under Overcurrent Condition. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Huang, L.; Wu, C.; Zhou, D.; Blaabjerg, F. A Power-Angle-Based Adaptive Overcurrent Protection Scheme for Grid-Forming Inverter Under Large Grid Disturbances. IEEE Trans. Ind. Electron. 2023, 70, 5927–5936. [Google Scholar] [CrossRef]
- Liu, B.; Liu, Z.; Liu, J.; An, R.; Zheng, H.; Shi, Y. An Adaptive Virtual Impedance Control Scheme Based on Small-AC-Signal Injection for Unbalanced and Harmonic Power Sharing in Islanded Microgrids. IEEE Trans. Power Electron. 2019, 34, 12333–12355. [Google Scholar] [CrossRef]
- Zhong, C.; Zhang, Z.; Zhu, A.; Liang, B. An Adaptive Virtual Impedance Method for Grid-Connected Current Quality Improvement of a Single-Phase Virtual Synchronous Generator under Distorted Grid Voltage. Sensors 2023, 23, 6857. [Google Scholar] [CrossRef]
- Azizi, A.; Banaiemoqadam, A.; Hooshyar, A.; Patel, M. A Blind Spot in the LVRT Current Requirements of Modern Grid Codes for Inverter-Based Resources. IEEE Trans. Power Deliv. 2023, 38, 319–334. [Google Scholar] [CrossRef]
- Garnica Lopez, M.A.; de Vicuna, J.L.G.; Miret, J.; Castilla, M.; Guzmán, R. Control Strategy for Grid-Connected Three-Phase Inverters During Voltage Sags to Meet Grid Codes and to Maximize Power Delivery Capability. IEEE Trans. Power Electron. 2018, 33, 9360–9374. [Google Scholar] [CrossRef]
- Xu, J.; Xie, S.; Tang, T. Improved control strategy with grid-voltage feedforward for LCL-filter-based inverter connected to weak grid. IET Power Electron. 2014, 7, 2660–2671. [Google Scholar] [CrossRef]
- Deng, H.; Qi, Y.; Fang, J.; Debusschere, V.; Tang, Y. A Low-Voltage-Ride-Through Strategy for Grid-Forming Converters Based on Reactive Power Synchronization. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Huang, L.; Xin, H.; Wang, Z.; Zhang, L.; Wu, K.; Hu, J. Transient Stability Analysis and Control Design of Droop-Controlled Voltage Source Converters Considering Current Limitation. IEEE Trans. Smart Grid 2019, 10, 578–591. [Google Scholar] [CrossRef]
- Deng, H.; Qi, Y.; Fang, J.; Tang, Y.; Debusschere, V. A Robust Low-Voltage-Ride-Through Strategy for Grid-Forming Converters Based on Reactive Power Synchronization. IEEE Trans. Power Electron. 2023, 38, 346–357. [Google Scholar] [CrossRef]
- Qoria, T.; Wang, X.; Kadri, R. Grid-forming control VSC-based including current limitation and re-synchronization functions to deal with symmetrical and asymmetrical faults. Electr. Power Syst. Res. 2023, 223, 109647. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).