Two models, one simple 1D and one more complicated 2D axis-symmetric CFD model, were constructed in an attempt to reproduce the phenomenon. The models mimic suspended drops; in that, there is neither shape oscillation nor temporal increase in air speed.
3.1. Theory Common to Both Models
Liquid evaporates from the parent drop, and vapour is transported by diffusion and convection. Where this vapour reaches sufficiently high supersaturation, critical nuclei form. Critical nuclei are assemblages of molecules of the condensing compound, which are just large enough that the vapour pressure adjacent to their surface is smaller than that in the surrounding vapour. It is thus thermodynamically favourable for these nuclei to grow via condensation. As the concentration of dust and other heterogeneous nucleation sites are sufficiently low in the experiments, only homogenous nucleation is considered. Classical nucleation theory (CNT) [
12] is used to determine nucleation rate and critical nucleus size. CNT has known flaws [
13], including predicting non-zero formation energy for a single vapour molecule, which is theoretically impossible [
12]. CNT is also known to underpredict the nucleation rate of alcohols [
14,
15]. However, CNT is simple, widely used, and, as will be seen, produces satisfactory results. The inadequacies of CNT are noted, but the main goal of these models was simply to see if the cyclic phenomenon could be reproduced with a limited set of physics.
In CNT, the radius
of a critical nucleus is given by Equation (1):
where
is the surface tension,
is the liquid density,
is the specific gas constant,
is the local gas-phase temperature, and
is the saturation ratio, given by Equation (2):
where
is the partial pressure of the volatile compound in the bulk vapour and
is the vapour pressure of a saturated mixture of that compound at the local gas temperature.
The nucleation rate
(number of critical nuclei formed per second per unit volume) is given by Equation (3):
In this implementation,
includes a factor of
in accordance with [
12].
is Boltzmann’s constant,
is the molar mass of the volatile compound,
is Avogadro’s constant, and
is the Zeldovich factor given by Equation (4) [
16]:
In the present model, a single pure volatile species (1,3-propanediol) is considered. It is assumed that air is insoluble in the liquid and both air and liquid are free of water. Humidity is present in the experiments and affects the final droplet size due to hygroscopic growth but it is neglected here since the effect is slight, and the models are only concerned with the early stage of growth. It is thus assumed that the vapour phase consists only of 1,3-propanediol and air and is treated as an ideal gas. Instantaneous adiabatic mixing is assumed. Laminar flow is assumed, as the experiments suggest that spatial and temporal aerosol patterns need laminar conditions at the nucleation zone, and that turbulence quickly destroys cyclic nucleation patterns.
The rate of change in the number of droplets in each finite volume cell (of volume
) is given by Equation (5):
Once the critical nuclei are formed, vapour molecules diffuse to the surface of these nuclei, causing them to grow by condensation into droplets, which continue to grow until the vapour is sufficiently depleted that the vapour density adjacent to the curved droplet surfaces,
, equals that in the bulk vapour.
over an aerosol droplet of radius
is given using the Kelvin equation (Equation (6)):
This is used to determine the mass fraction of volatile compound in the vapour above the droplet surface, and thus the mass flux due to diffusion.
The rate of change in liquid mass in a cell containing aerosol is given by Equation (7):
where, on the right-hand side, the first term is the rate of mass gain due to nucleation, and the second is the rate of mass gain due to droplet growth.
Mass and heat flux between parent drop and vapour, and nucleated aerosol droplets and vapour, are modelled as quasi-steady, spherically symmetric diffusion between the liquid surface and an infinite, homogeneous far field (far field properties indicated by the subscript ). The aerosol droplets are assumed to be travelling at the same velocity as the vapour immediately surrounding them (no slip). This is reasonable since the droplets are formed from that vapour. Therefore, there is no convective heat or mass transfer.
Mass diffusion is unimolar since the inert compound (air) does not diffuse towards or away from the droplet. The mass flow rate of the volatile compound from far field to the droplet equals the mass gain rate of the droplet
is given by Equation (8):
where
is the diffusion coefficient of the volatile compound in air,
the mean gas phase density,
the mass fraction of volatile compound at the droplet surface, and
the mass fraction of the volatile compound in the far field. This constitutes the Stefan–Fuchs droplet growth model [
17], in the special case that there is no slip between the droplet and surrounding gas. This special case is identical to the Maxwell model [
18].
The droplet is assumed to be of uniform temperature throughout. The droplet surface gas phase is in vapour–liquid equilibrium with the droplet’s liquid. Radiative heat loss is assumed negligible due to the low temperature difference with the surroundings.
The steady-state rate of heat flow
from a single droplet to the far field is given by Equation (9):
where
is the gas-phase heat conductivity;
is the droplet radius;
is the latent heat;
is the specific heat of the volatile compound in its vapour state at constant pressure;
is the droplet temperature (assumed uniform); and
is the local gas-phase temperature.
Latent heat released upon condensation was deposited into the liquid and in the vapour in the surrounding cell in proportion to their heat capacities.
When the droplet is at a quasi-steady equilibrium temperature, the rate of release of latent heat is equal to the heat flow (Equation (10)):
For a suspended parent drop, as the liquid temperature is close to the boiling point, the enthalpy flux at the liquid/vapour interface can be very high, and this can lead to a non-negligible temperature difference between the heated copper core
and the liquid/vapour interface temperature
. A simple model of heat transfer via a liquid layer of constant thickness
was introduced, assuming heat transfer by heat conduction and evaporation only, with conduction only perpendicular to the surface. With known mass flux
of the evaporating volatile compound, and to the gas phase
calculated from a previous estimate of the temperature gradient, the temperature difference across the liquid layer is given by Equation (11):
where
is the thermal conductivity of the liquid. This approach was only used in the 1D model as the suspended drop was not modelled with CFD. The model assumes a single value of layer thickness
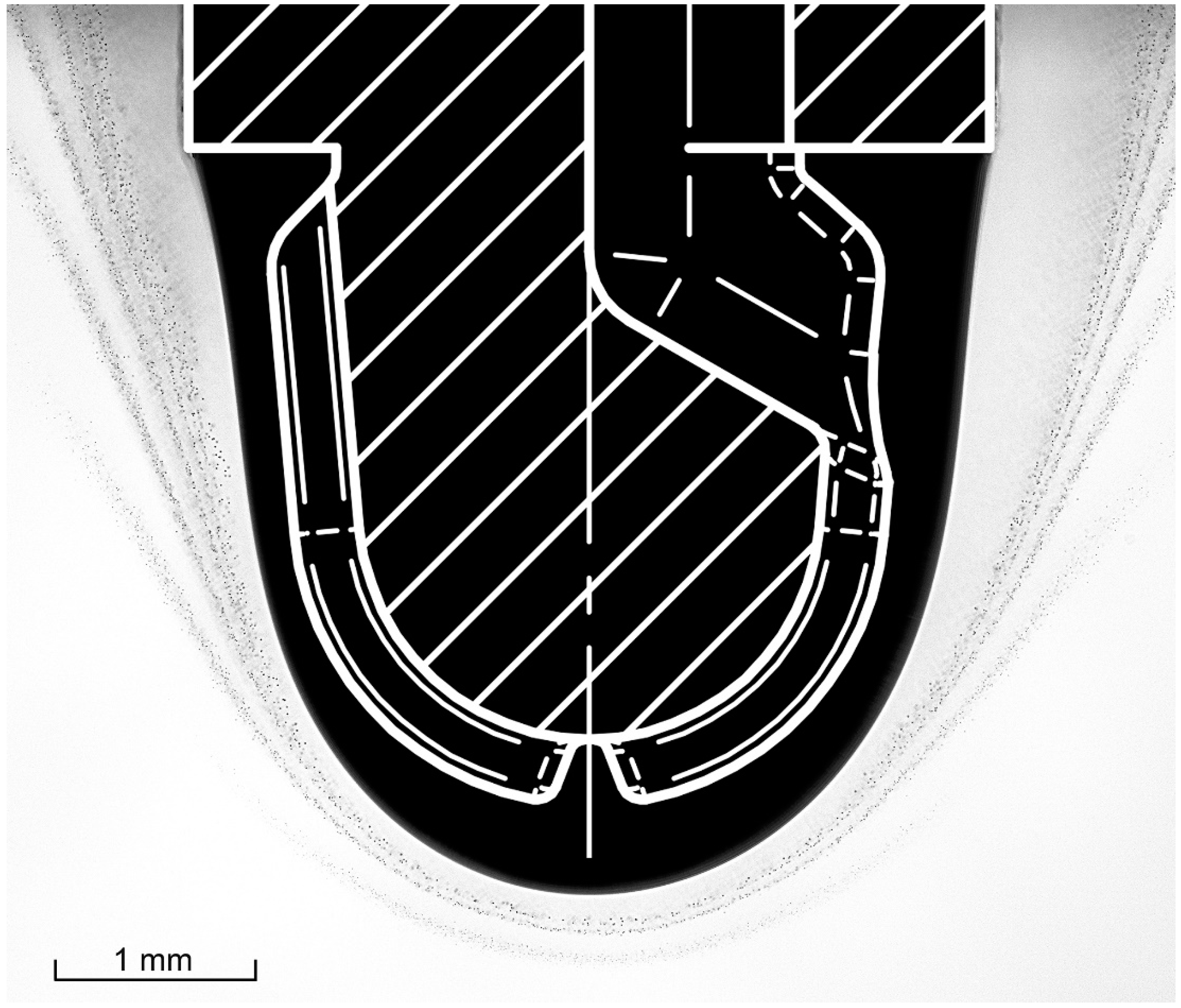
, but in the experiments, it varied with a position on the tip (
Figure 5) from 0.2 to 0.6 mm. Simulations were carried out with
= 0 (i.e., the surface of the liquid at core temperature), and with
= 0.3, 0.4, and 0.5 mm. These results are presented later.
The surface temperature of the parent drop is an additional state variable which is adjusted in order to meet the balance of heat flux via the liquid layer and the heat flux transmitted to the gas phase. A time constant in the millisecond range was arbitrarily chosen for the dynamic thermal behaviour of the liquid layer, assuming that—once the surface temperature has reached equilibrium—this time constant is of little further impact. Heat flux via the liquid layer leads to liquid/air surface temperatures up to 55 K below the temperature of the heated core for the range of used here.
The value of the latent heat is determined at the drop surface temperature. Other properties are determined at an intermediate temperature
and volatile compound mass fraction
, both of which lie between that of the droplet and far field. Following [
19], the 1/3 rule is used (Equations (12) and (13)):
The mass fraction of volatile compound at the droplet’s surface is given by a partial pressure rule (Equation (14)):
where
and
are the molar masses of the volatile compound and air, respectively.
The diffusion coefficient of vapour in air
was estimated using the method of Fuller, Schettler, and Giddings [
20]. The special atomic diffusion volume used by this method was found by fitting the method to data for the diffusion of propanediol in air at 25 °C [
21]. The Fuller, Schettler, and Giddings method [
20] was then used to calculate the diffusivity at other temperatures. For the thermal conductivity
of the air/propanediol gas phase, the mixing rule of [
22] and [
23] was applied. Other properties were taken from the VDI Heat Atlas [
24].
The droplets in a single control volume are assumed to all be the same size, as well as spherical, so their diameter can be calculated from the droplet mass density and number density.
Aerosol is, of course, not a continuum on a microscopic scale. A threshold is applied to the nucleation rate, which prevents droplets from forming if there is less than a given threshold. A similar threshold could be applied to the droplet number density instead of the nucleation rate, but the nucleation rate was chosen as it was considered to be less prone to historical effects. The threshold model proved necessary to predict spatially stratified aerosol and stable temporally cyclic nucleation. Otherwise, only single poorly defined aerosol layers developed, or cyclic nucleation decayed within a few periods after the start of the simulation. The threshold value could be varied over a wide range, showing only moderate impact on nucleation frequency and thickness of layers.
3.2. Simple 1D Numerical Model
A simple finite volume model of cyclic nucleation was constructed using axis-symmetric potential flow solutions for the velocity field of the suspended drop. The coordinate system is spherical for the approaching flow, with the origin at the centre of curvature of the body’s windward face. Only the flow along the stagnation line is modelled, as this sets the nucleation frequency. Nucleation, growth, and heat transfer to the aerosol droplets were solved using a finite volume approach. Nucleation rate, droplet growth, and droplet-vapour heat transfer are computed in each cell. The computational cells move with the bulk mass (
Figure 8). Thus, no convectional transport across the boundaries needs to be calculated, only diffusion. As the cell boundary at the surface is the only one not moving with bulk mass, the transfer of heat and the volatile compound’s mass is calculated according to unimolar transfer from the surface to the first cell’s centre. It is assumed that heat and mass transport within the boundary layer are dominant in the one coordinate which is used for discretization. Cells are split or merged to keep their size within 0.4 to 1.5 times their initial width. Splitting occurs in the cell closest to the evaporating surface as it constantly gains mass. Merging occurs in the approaching flow simulation due to the mass and enthalpy sinks, which are used to generate the flow pattern.
The velocity field is generated using a potential flow solution. For a suspended drop with vapour approaching at speed
, the local vapour velocity
can be estimated from the superposition of a parallel flow and
discrete point sources of strength
placed at positions
on the
x-axis according to Equation (15):
The factor
is used to keep the contour constant at different approach velocities. The suspended drop contour used for the simulations (
Figure 5) can be approximated by
sources with the values given in
Table 1. The values of
and
were determined to approximate the desired body contour, by finding optimal values using the MATLAB
TM (MathWorks, Natick, MA, USA) release R2022a multidimensional minimization algorithm
fminsearch.
The superposition of the velocity field was carried out implicitly by mass and enthalpy sinks in each calculation cell in a way that without unimolar diffusion from the surface, the cell boundaries move with the given velocities
according to Equations (16) and (17):
where
x is the corresponding cell’s centre location and
is the radius of the tip. Cell locations are determined by masses and cell volumes. Therefore, this step requires the calculation of cell volumes and locations from the actual state variables first, as follows.
In each cell, the model solves for the state variable’s total enthalpy (including liquid and vapour), mass of air , mass of volatile compound in the vapour phase , mass of volatile compound in the liquid state (in the form of aerosol droplets), and number of droplets . The temperatures of the gas phase and droplets are found using a numerical search for values which satisfying the quasi-steady-state temperature model and the enthalpy sum. Once the temperatures are known, cell volumes and locations of the cell centres can be calculated and used for discretization of the heat and mass diffusion between cells. Droplet diameters and vapour phase composition are then calculated, followed by nucleation rates and mass condensation rates of the volatile compound, and the above-mentioned mass and enthalpy sink rates (Equations (16) and (17)).
All derivatives at cell boundaries are calculated to be first order. The model was solved in MATLAB as an ordinary differential equation (ODE), using the ODE113-solver with variable order method and variable timestep. The splitting and merging of cells were triggered by event handling, which required intermission of the solution at each event since the state vector had to be adjusted to the change in cell number and according to state variables numbers.
At the surface of the droplet, or the wetted parts of the suspended drop apparatus, the boundary conditions are that the surface temperature is the bulk temperature, the partial pressure of the volatile compound is equal to the saturation vapour pressure at this temperature, and the mass flux of air is zero.
The nucleation rate threshold was one droplet per cube of side 100 or 30 μm per 10 μs. This was chosen based on observed droplet–droplet distances in the order of 10 μm. Cell sizes were 2 to 5 μm, although stable simulations could be carried out up to 40 μm for the 2.8 mm diameter drop.
Each cell is initialized with air at 20 °C, with no volatile compound and no droplets present.
In order to reduce computation time, the model uses constant material properties over the whole boundary layer, except for the latent heat
and vapour pressure
of the volatile compound. For the latter, temperature dependency was modelled using Equation (18):
with constants
A and
B fitted across the temperature range from ambient air to bulk liquid.
With constant specific heat capacities
and
of the volatile compound in the vapour and liquid phase, the latent heat is linear with temperature (Equation (19)):
Equations (9) and (10) are used to determine droplet temperature .
Results from the Simple 1D Model
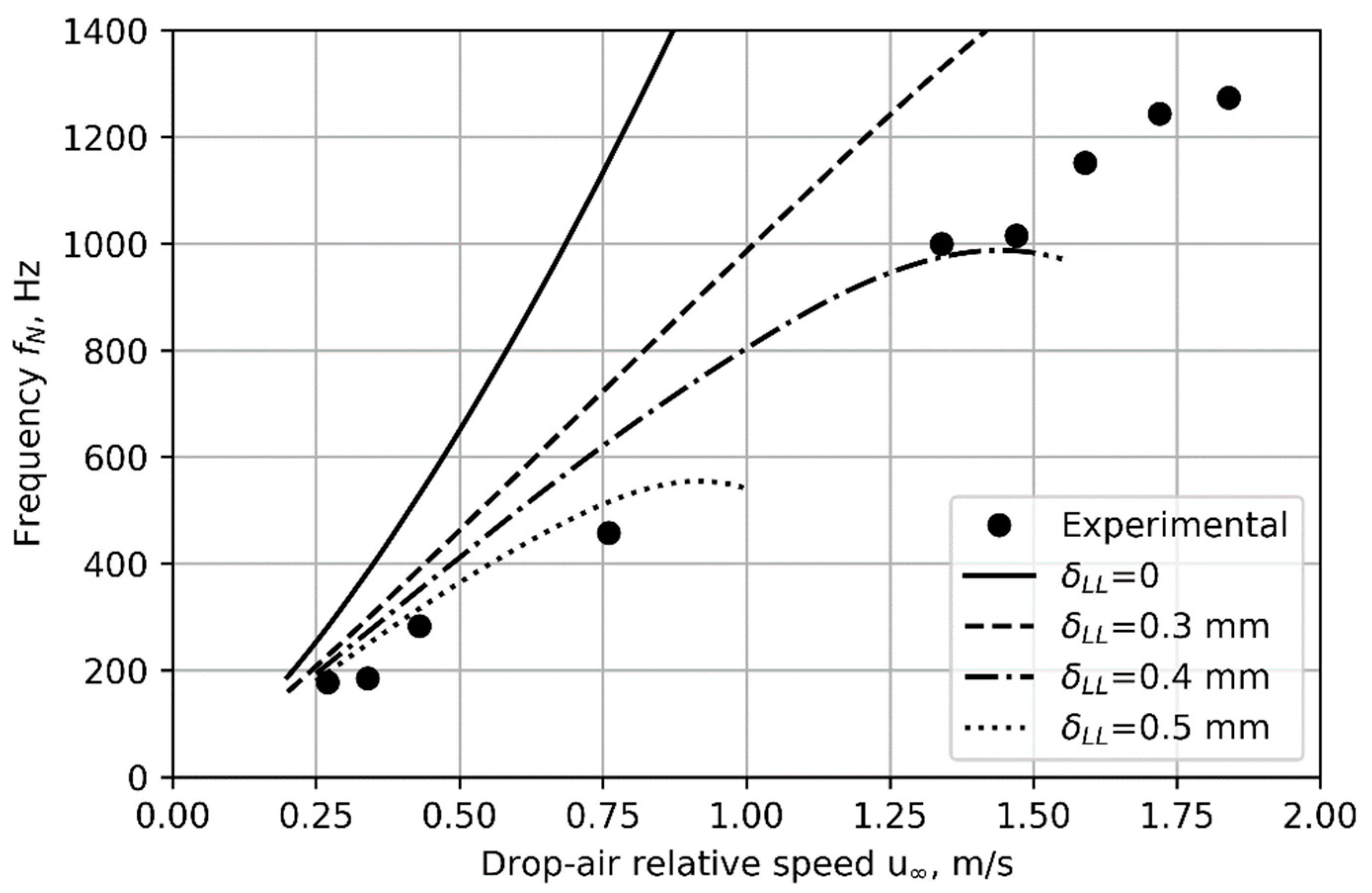
The frequency of nucleation predicted by the model, for a nozzle core temperature of 190 °C, and for liquid layer thicknesses of
= 0 (liquid/air interface at nozzle core temperature) and
= 0.3, 0.4, and 0.5 mm are compared to experimental results in
Figure 9. A liquid layer thickness
between 0.3 and 0.5 mm fits the experimental data best. The model is imperfect. No single value of
predicts the nucleation frequency correctly across the whole range of air speeds. The model predicts a drop in frequency (at
> 1.3 m/s for
= 0.4 mm), which is not seen in the experiment. Nevertheless, the most important observation is that the model does predict cyclic nucleation, indicating that it includes the physics necessary to explain the phenomenon. Further, it predicts nucleation frequency to better than order-of-magnitude accuracy.
3.3. CFD Model
Transient flow, nucleation, vapour transport, and growth were modelled using ANSYS Fluent 2020 R2 (ANSYS, Canonsburg, PA, USA) for spherical parent drops at a fixed speed, replicating the windward conditions of a suspended drop. ANSYS Fluent is a general-purpose code for solving computational fluid dynamics and heat transfer calculations, suitable for problems involving evaporation and condensation, as illustrated in [
25]. The parent drop was 2.8 mm in diameter, with liquid surface temperatures of 180 °C, chosen to compare with the 190 °C nozzle core temperature, allowing for a reduced surface temperature due to heat loss to the surrounding air.
Two-dimensional axis-symmetric meshes were created with ANSYS Meshing using quad- and tri-elements. Mesh convergence was checked by monitoring nucleation frequency. Meshes of 104,242 elements, 350,755 elements, and 581,913 elements were chosen with the finest mesh selected for generating the results shown here. The finest mesh produced nucleation frequencies within 15% of the intermediate mesh. Further refinement was not carried out due to limitations in computing resources. This mesh had a minimum cell volume of 2.4 × 10−11 m3, a maximum cell volume of 1.8 × 10−10 m3, and a minimum orthogonal quality of 0.398.
Dry air at 20 °C approaching the drop was set at a velocity from 0.2 to 0.8 m/s (Re = 37 to 150) using a velocity inlet boundary. All other external boundaries were outflow. The boundary of the droplet had a specified temperature of 180 °C and a 1,3-propanediol vapour mass fraction of 0.343.
Two user-defined scalars were defined to model the aerosol population: one to model the droplet number and one to model the droplet mass. These scalars were modified using two user-defined functions within Fluent.
The timestep was fixed at 10−6 s, which produced nucleation at the same times and locations as runs with adaptive timestep. Residuals were converged to 10−3 at each timestep. The calculation ran until five oscillations of nucleation were completed.
The second-order implicit transient scheme was used with the coupled solver. Pressure–velocity coupling used the ‘coupled’ option. No turbulence model was used, i.e., the flow was forced to be laminar. Gradient spatial discretization was least-squares and cell-based. Pressure, momentum, species, energy, and scalar droplet number density were discretized using second-order schemes. Aerosol mass density was discretized using the first-order scheme.
The nucleation rate threshold was one droplet in a volume equivalent to a cube of sides 40 µm, per 10−6 s.
The workstation used had an Intel i7-10700 CPU running at 2.9 GHz with eight cores and 64 GB RAM. Computation took 1–3 weeks depending on the inlet velocity, as a lower velocity produced a lower nucleation frequency.
Results from the CFD
The model successfully reproduced the cyclic nucleation phenomenon at all three speeds.
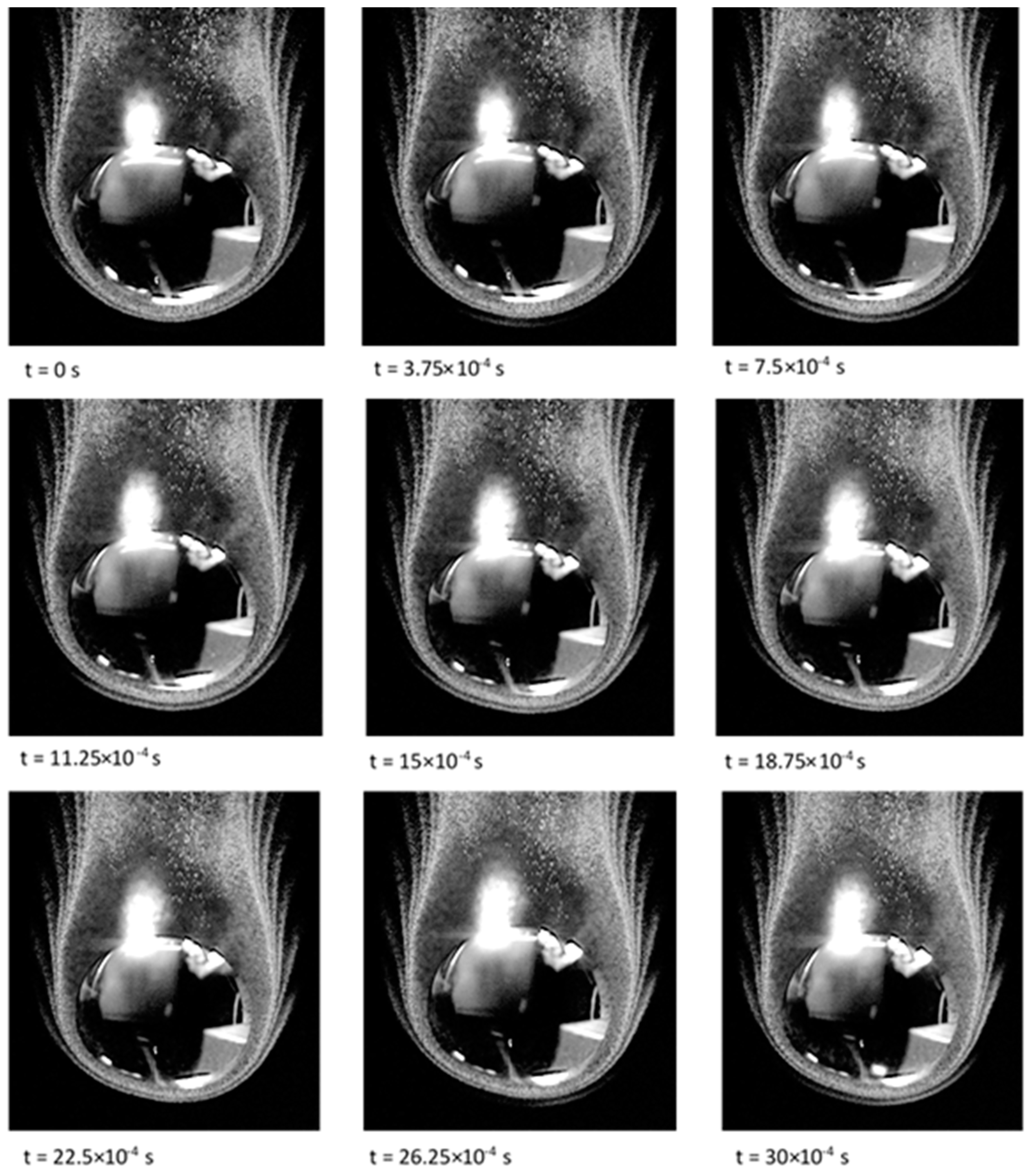
Figure 10 shows plots of droplet number density. Nucleation first appears in an arc on the windward side of the parent drop. The ends of this arc grow in the streamwise direction. Aerosol droplets formed by this nucleation grow and deplete the vapour surrounding them, which stops further nucleation from occurring. The arc of nucleated droplets moves closer to the drop surface until the concentration of aerosol decreases as it is pushed around the side of the droplet. This allows vapour to diffuse away from the upstream face of the droplet until the concentration increases enough to allow another arc of aerosol to form. The development of the bands of aerosol in
Figure 10 closely resembles the experimental observations in
Figure 1.
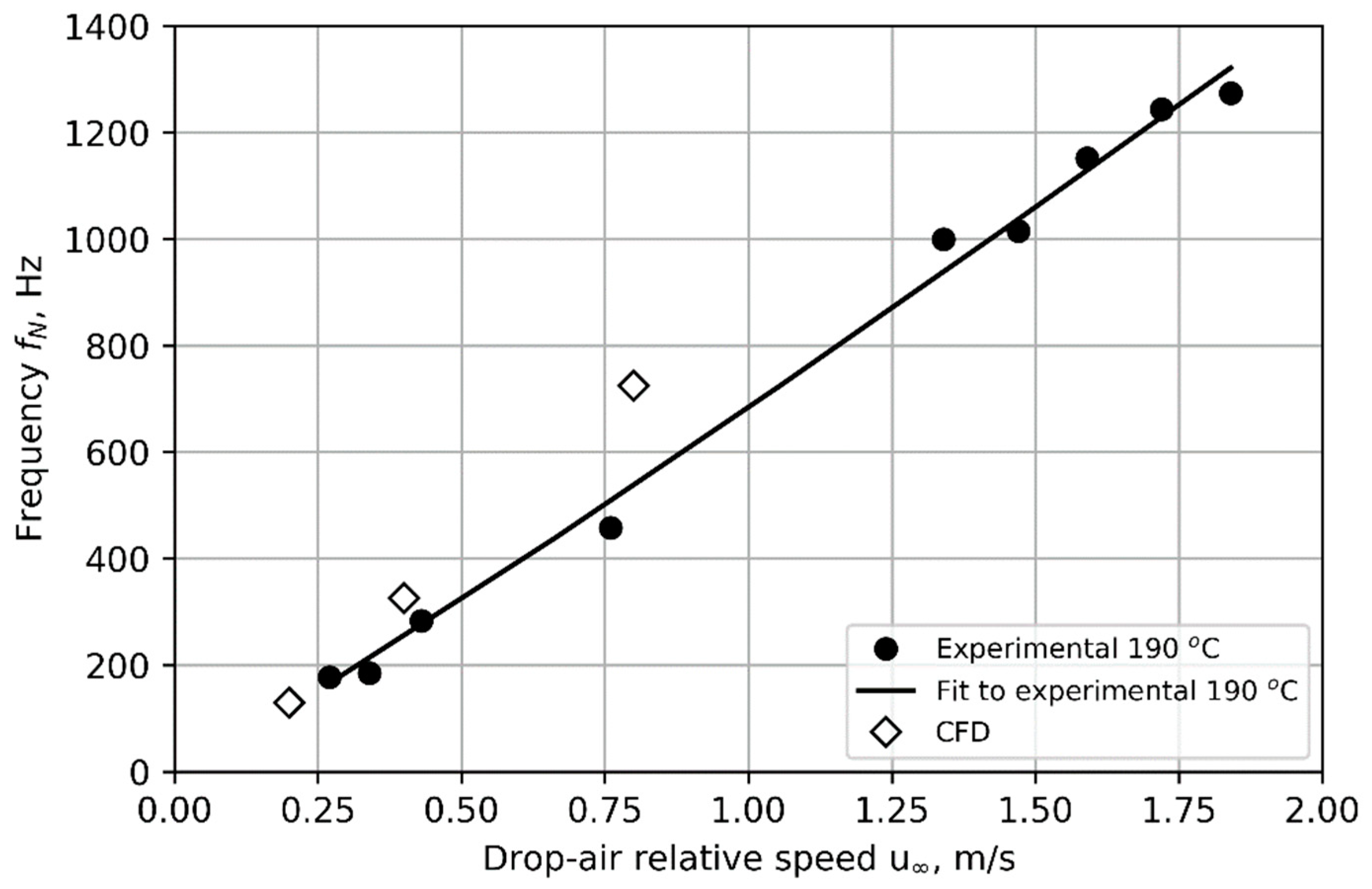
Figure 11 compares the frequency of cyclic nucleation predicted by the CFD model to experimental results with a nozzle core temperature of 190 °C. The trend observed in the experiment of nucleation frequency increasing with drop–air relative velocity
is successfully reproduced by the model. A power law (Equation (20)) fits the CFD predictions well, albeit with coefficients differing from the fit to experimental data (
A = 975,
B = 1.24 for the CFD with
f in Hz and
u in m/s).
The aerosol droplet diameter predicted by the model was approximately 5 µm, which is in reasonable agreement with the photographic observations between 3 µm and 6 µm.