Abstract
The use of innovative methods for the design of heating, cooling, and heat storage devices has been mainly oriented in the last decade toward the use of nanofluids, metal foams coupled with working fluids, or phase change materials (PCMs). A network of nine Italian universities achieved significant results and innovative ideas on these topics by developing a collaborative project in the last four years, where different approaches and investigation techniques were synergically employed. They evaluated the quantitative extent of the enhancement in the heat transfer and thermal performance of a heat exchanger or thermal energy storage system with the combined use of nanofluids, metal foams, and PCMs. The different facets of this broad research program are surveyed in this article. Special focus is given to the comparison between the mesoscopic to macroscopic modeling of heat transfer in metal foams and nanofluids, as well as to the experimental data collected and processed in the development of the research.
1. Introduction
In recent decades, substantial effort has been devoted to the investigation of the thermal behavior of foams, PCM (Phase Change Materials), and nanoparticles in PCM and fluids mainly focused on the development of heat exchangers with foams, gas, and/or nanofluids, as working fluid, for several heat loads varying in a dimensional analysis from 1–3 cm3 to 0.2–0.6 m3, for example, related to thermal control for electronic components and condensers or evaporators in heat pumps or refrigeration systems, or as a thermal energy storage with PCMs in foams, without or with nanoparticles. The devices are also integrated into a building wall to realize an energy-equipped wall or a system of electronic cooling. The possibility of designing such devices led to a joint research work among nine different Italian universities, as indicated in the affiliations, in the last five years. The main results of this collaboration are the subject of this review paper.
The analysis of thermal stability and transition to instability in fluid-saturated porous media has been the goal of a broad research work. When modeling Darcy–Bénard instability, the momentum balance is usually given by Darcy’s law [1]. This instability phenomenon was first investigated by considering a fluid at rest while being heated from below at constant, uniform, and unequal temperatures at the solid boundaries. The restriction of a basic rest state is relaxed in the so-called Prats problem [2], where a uniform and horizontal throughflow is included. Surveys on the main results obtained in this field can be found in [2]. Transport phenomena in a foam are highly affected by its microstructure. Using tomography-based and Kelvin foam geometries, Ambrosio et al. [3] found that convection in a foam can be optimized if the foam is manufactured with a low porosity and circular shapes. The effects of the morphology of Kelvin-foam cells on effective thermal conductivity and convection heat transfer were studied by Pusterla et al. [4,5]. The influence of the cell inclination angle, the cell radius at the junction, and the strut tapering on effective thermal conductivity was highlighted in [4]. Their effect on pressure drop and heat transfer efficiency was shown in [5]. The heat transfer efficiency accounted for the combined effects of convection heat transfer and pressure drop. Recently, Yang et al. [6] showed that the effect of strut shape on the effective thermal conductivity was not remarkable.
Thermal storage systems are utilized in a variety of applications and, in particular, in renewable energy systems, as they ensure the decoupling between the generation and consumption of energy [7]. On the basis of this, Thaker et al. [8] proposed an application for solar energy systems, whereas Yang et al. [9] experimentally investigated a geothermal heat pump with an integrated thermal energy storage system. Other authors [10] have focused on the application of thermal storages in buildings in order to improve their energy performances.
The accomplishment of the new environmental laws establishes the use of eco-friendly refrigerants and innovative solutions for heat exchangers to be implemented in refrigeration and air conditioning systems and in devices for cooling electronics. In this context, research has been focused on the study of air flow on new heat transfer surfaces and of new fluids during flow boiling and condensation through/over enhanced surfaces in more-compact heat exchangers with reduced refrigerant charge [11]. Also, innovative solutions for refrigeration and air conditioning systems rely on melting and solidifying a PCM inserted in a heat exchanger for efficient operation [12,13]. The use of a PCM as the storage medium provides a high energy density due to the ability to store thermal energy as latent heat during the phase transition; however, the charge and discharge rate is limited by the low thermal conductivity of the PCM. The insertion of a metal or graphite foam or a 3D-printed metal structure within the PCM can increase the rate of charge–discharge and decrease the downtime of the cooling device [14,15].
Investigations of heat transfer augmentation by the use of nanoparticles and PCM as well as nanofluids and foams is developing very quickly. The need to evaluate the thermal properties of nanofluid mixtures is important to enable their use in engineering applications [16,17]. The use of nanofluids is increasing in various applications such as electronic cooling [18]. However, colloidal suspensions have been extensively investigated for a long time due to their ubiquitous presence in many engineering applications [19]. In particular, the DLVO theory, named after Derjaguin, Landau, Verwey, and Overbeek, explains the stability of colloidal suspensions by using a continuum simplified model. Unfortunately, this classical theory is not sufficient for describing the discrete effects emerging in nanoparticles (with approximate diameters below 100 nm); hence, proper extensions must still be developed for providing more realistic predictions [20]. Moreover, the combined use of nanofluids with microchannels, foams, or honeycombs and nanoparticles with PCM (nanoPCM), foams and PCM, or nanoPCM and foams provides possible ways to significantly improve the heat transfer performances [21,22]. However, it should be underlined that a reference with a review of the direct integration of phase change materials (PCMs) with metal foams and/or nanofluids or with microchannels and nanofluids seems not to be present in the open literature. In the present paper, this gap is filled by reviewing (considering) the activity developed in the research project PRIN2017 with the title “Heat Transfer and Thermal Energy Storage Enhancement by Foams and Nanoparticles”, which involved nine Italian universities, as indicated in the affiliations. Moreover, the collaboration among the teams has enabled an elaboration on the topics with different methodologies, which are experimental, numerical, or theoretical, at different scales from the nanoscale to the macroscale, as underlined in the review.
The review is organized such that the first section describes the analysis from nano/microscales to mesoscale as related to nanofluids, microchannels, and metal foam structures. Subsequently, the macroscale models are considered to investigate the metal foams and nanofluids in order to make a comparison with the lower-scales data. Several engineering applications are considered to evaluate the heat transfer enhancement due to the use of metal foams, microchannels, and nanofluids as well as their possible combinations. The applications are mainly related to innovative heat exchangers and thermal energy storage systems as well as thermal control, thermal recovery using a thermoelectric generator (TEG), and refrigerant use.
2. Mesoscale Flow Characteristics of Fluid-Saturated Metal Foams
Heat transfer in open-cell foams can be investigated by using pore-scale (or mesoscale) approaches or volume-averaged (or macroscale) approaches [23], whereas the latter consists in writing governing equations using the volume-averaging approach [24]. With this approach, variables are averaged over a representative elementary volume of the foam whose characteristics are representative of the whole porous medium [25]. It has been widely shown that mesoscale approaches are preferable if one wants to obtain data at the pore levels, while macroscale approaches are better if the computational domain is as large as requiring substantial computational effort. With the latter, variables like pressure drop in an engineering device or, for instance, thermal efficiency can still be obtained with a certain accuracy. It is also important to underline that to close volume-average equations, some pieces of information that could be derived from a pore-scale analysis might be required.
2.1. Use of μCT Images for Single-Phase Flow Simulations
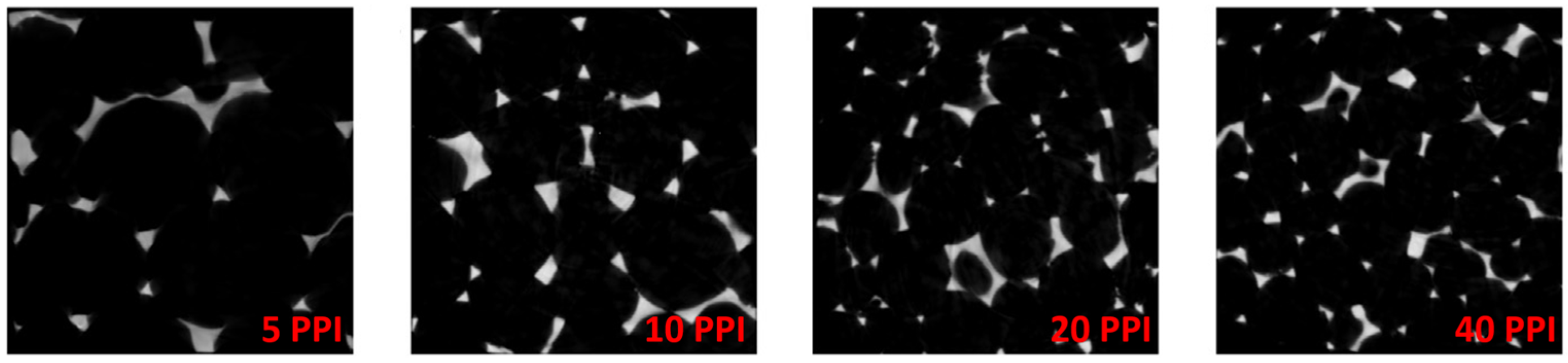
Micro computed tomography (μCT) allows for the reconstruction of the real complex structures. Its applications span from the medical field to the industrial one. μCT was implemented by Diani et al. [26] to reconstruct the real structures of four copper foams having 5, 10, 20, and 40 PPI, with a porosity between 93.4% and 93.6%, and at a scan resolution of 20 μm. The scanned copper foams were elaborated and meshed with the commercial software Simpleware v2012. A greyscale threshold value was selected during the reconstruction of the real foams in order to match the effective porosity of the specimens. An example of the scanned Images is reported in Figure 1.
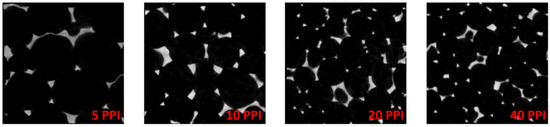
Figure 1.
Examples of μCT scanning.
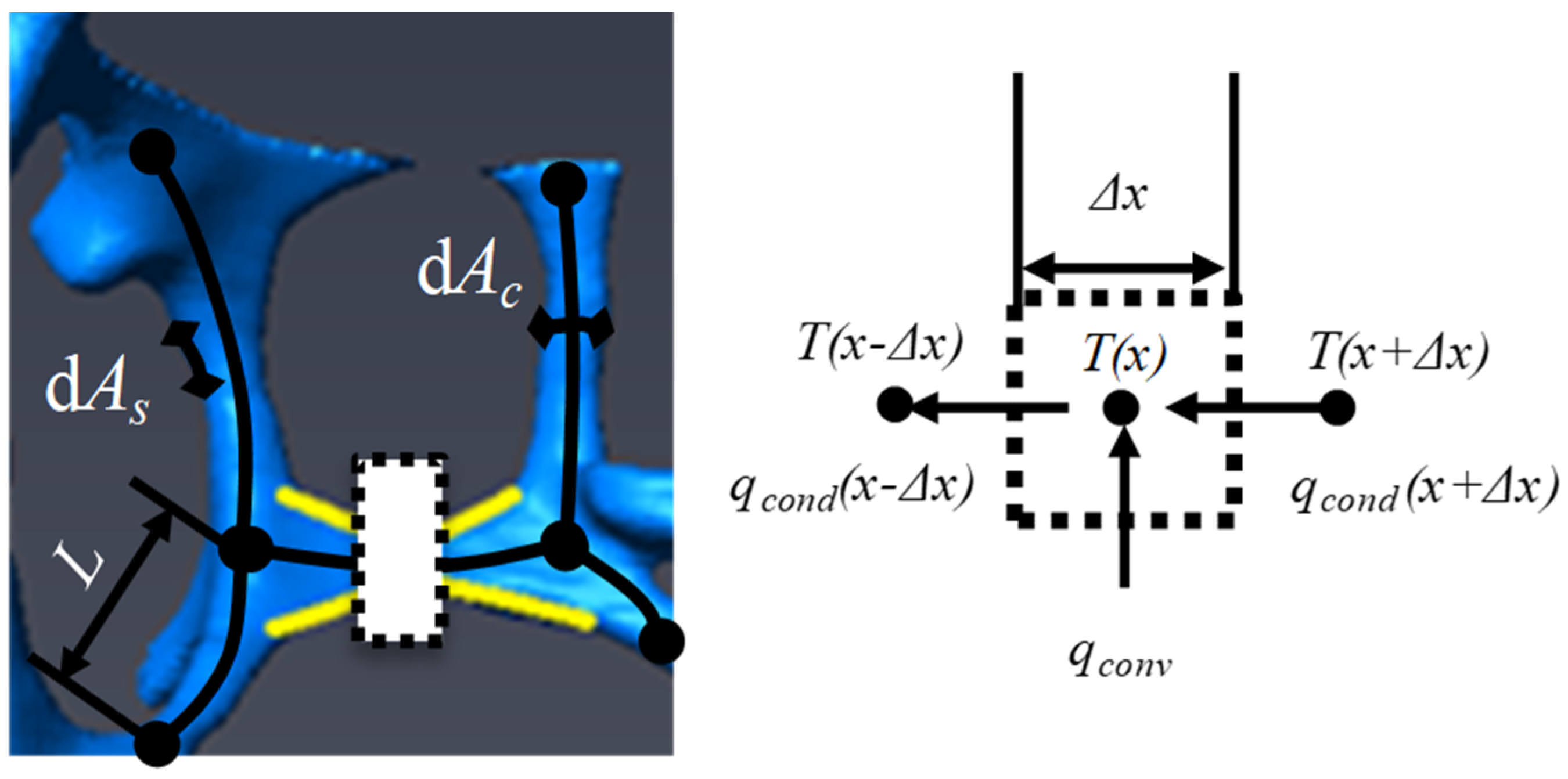
Heat conduction within open-cell foams has been investigated using different approaches on different structures. With references to the so-called real foams, for example, casted foams to be reconstructed with techniques like computed tomography, the effective thermal conductivity has been derived with two different approaches. In the first, one assumes that the foam is a fins network, where conventional fins equations can be applied to derive the temperature field within the solid phase [27]. Since a 1D approach is used, with the coordinate always taken as the ligament axial coordinate, the computational effort is far smaller than that of the other approaches like finite-element-based ones, as also underlined in similar studies based on the electrochemical fin theory [28]. A sketch that illustrates the employed technique is presented in Figure 2. Each ligament axis is assumed to be a fin, with the strut-cross-section variation accounted for within the governing equation by assuming that the decay follows an exponential law [28]. For each infinitesimal portion, an energy balance is then written by assuming continuity between the various ligaments. At the top/bottom of the whole tomographic scan, a uniform temperature boundary condition is assumed to compute the overall effective thermal conductivity.
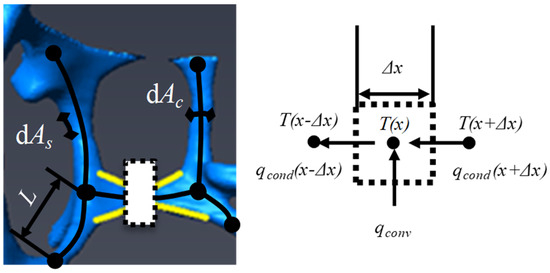
Figure 2.
The thermal fin theory model with an energy balance performed on an elementary portion (Δx).
Starting from tomographic scans, a throughout analysis of the anisotropy in open cell foams was carried out in [29]. Anisotropy is a phenomenon that might arise because of manufacturing routes [30] affected by gravity or viscosity; anisotropy can also be artificially included via additive manufacturing techniques. By assuming that a single foam cell presents three main axes, to be computed as Feret diameters, it has been shown that such foam cells can present a certain elongation. Secondly, this elongation has been linked to effective thermal conductivity, showing that the higher the cell diameters ratio, the higher the difference between effective thermal conductivities computed along different axes. This might be attributed to the fact that a stretched cell behaves like a purely parallel heat transfer porous medium. In particular, the cell size ratio can reach 1.4, while the effective thermal conductivity ratio would reach about 1.8. This means that some effort should be made if one wants to consider anisotropy effects within thermal conduction computations in foams.
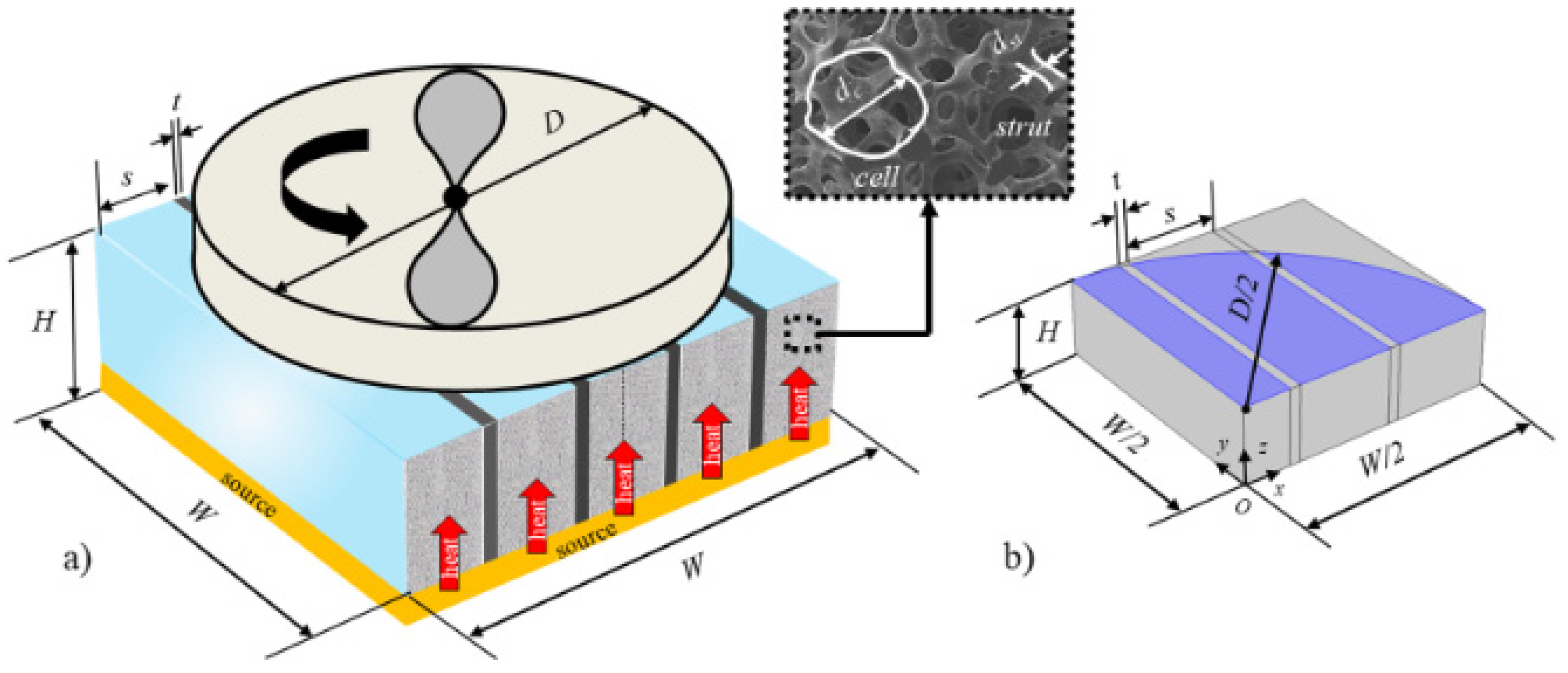
The same metal foams studied in [26] were experimentally tested in a wind tunnel by Mancin et al. [31]. These foams were arranged in a sandwich-like structures: two plates, each one 10 mm thick, were brazed to the top and bottom sides of each foam whose height was either 20 mm or 40 mm. The experimental tests permitted the evaluation of the heat transfer coefficient and pressure drop during an air forced convection. The experimental tests also enabled the development of an empirical correlation for the estimation of the air forced convection heat transfer coefficient. Specimens were experimentally heated from the bottom using an electrical heater connected to a DC power supplier, whereas the top plate was in adiabatic conditions. As a result, the foam structure experienced an increased efficiency. Since, due to computational constraints, it was not possible to simulate the foams along their entire height, a constant heat flux boundary condition was applied to computational domains smaller than the experimental counterpart. Preliminary simulations were performed to find the proper number of pores in the flow direction to be simulated.
Simulations were run with the commercial software Ansys Fluent release 13 (2010). A direct comparison in terms of experimental and numerical pressure drops was performed by Diani et al. [26]. Considering all the four samples, a mean relative and absolute deviation of −3.8% and 5.4%, respectively, were obtained. The interfacial heat transfer coefficients evaluated from the numerical simulations with the constant heat flux boundary condition were compared against the values estimated by the empirical correlation developed by Mancin et al. [31], which was fitted from the experimental data during air forced convection inside the same structures. The empirical model estimates both the heat transfer coefficient and the finned efficiency of the foam. Both the numerical interfacial heat transfer coefficient and the product between interfacial heat transfer coefficient and foam efficiency were in very good agreement with the empirical/experimental counterpart.
After the studies on conduction [29,30], where it was shown that anisotropy arises in computing the effective thermal conductivity, and that the anisotropy is related to the cell elongation, similar outcomes have been found for convection. In [32], a throughout analysis of the anisotropy within open-cell foams in terms of heat transfer coefficient was carried out. Starting from the same samples shown in [29], the heat transfer coefficients were computed by assuming that air flows along each of the three main directions. It was shown that the heat transfer coefficient presents a reverse proportionality with the cell elongation; in other words, the more elongated the cell, the lower the heat transfer coefficient. The authors attributed this to some thermally developing effects that also arise in foams, as shown in similar previous articles [33]. Eventually, a Nusselt–Reynolds number correlation that accounts for anisotropic effect—i.e., the cell size as the characteristic length is computed along an axis—was carried out.
2.2. Two-Phase Heat Transfer inside Microfinned Tubes
Among the different approaches for modeling porous materials and their characteristics, the capillary models consist in the representation of the porous structure as a bundle of multiple straight mini channels. Besides being a representation of porous media, small-sized channels have a wide range of different applications, ranging from air conditioning and refrigeration systems to electronic cooling applications. Furthermore, as widely proved in the literature, the implementation of microfins on the inner surface of the channels enhances the heat transfer, not only due to an augmented heat transfer area, but also due to a greater turbulence induced by the microfins. In addition, in the case of a two-phase flow, the presence of microfins causes the transition from stratified to annular flow at a lower vapor quality and mass velocity compared to a smooth channel with the same inner diameter; moreover, in the case of flow boiling, the microfins cause the onset of a dryout at higher vapor qualities.
In this context, Diani and Rossetto [34], Liu et al. [35], and Diani et al. [36,37] tested microfin tubes having outer diameters of 3.0 mm, 4.0 mm, and 7.0 mm during both condensation and flow boiling with different low-GWP refrigerants, such as R513A, R450A, R515B, and R1234ze(E). The experimental tests were run in a wide range of working conditions, aiming at highlighting their effects on both the heat transfer coefficient and the frictional pressure drop. Considering all the tests, mass velocity was varied from 50 to 800 kg m−2 s−1, saturation temperature was set in the range of 20–40 °C, and, in the case of flow boiling, the applied heat flux was varied between 10 and 60 kW m−2.
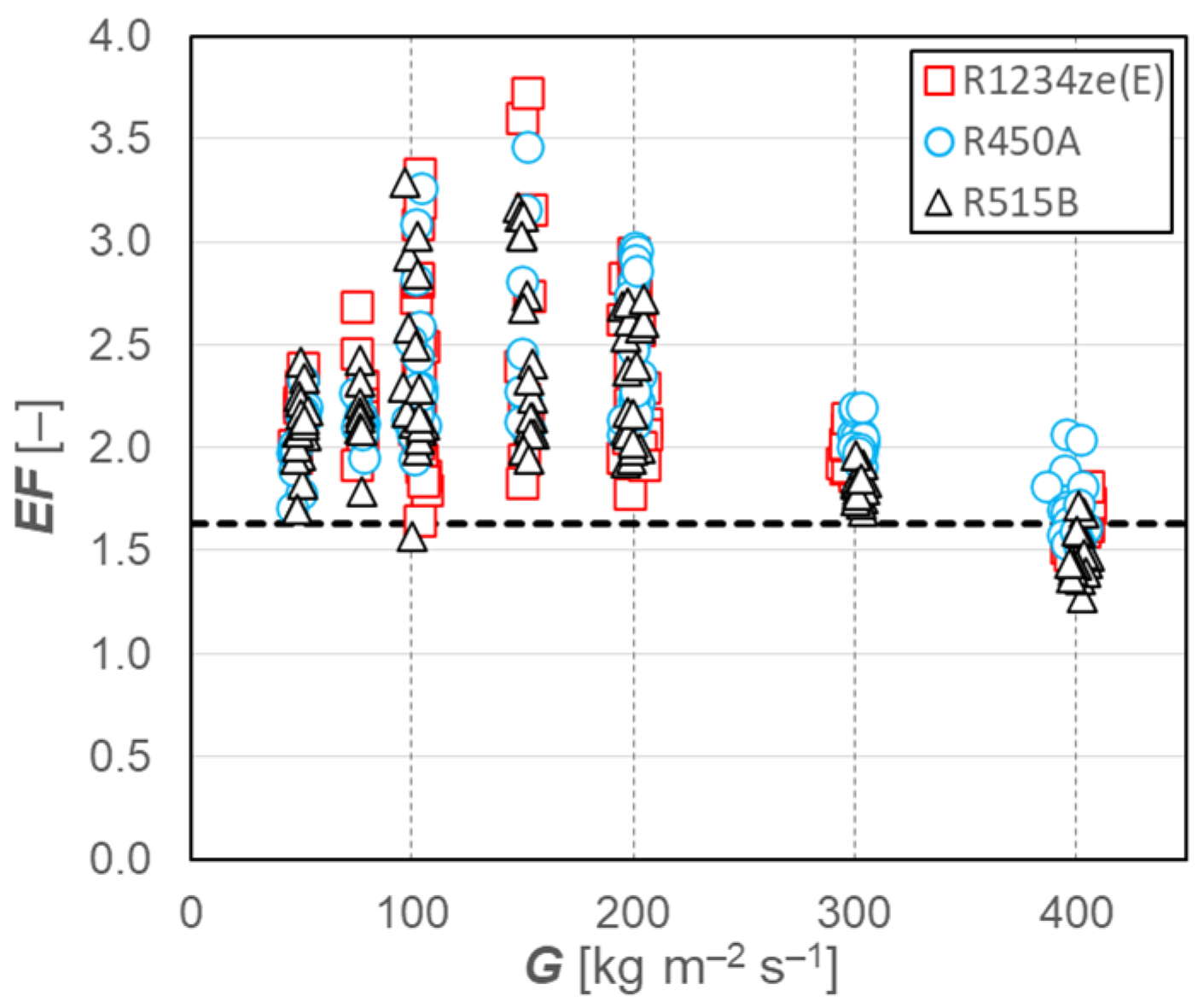
Compared to equivalent smooth tubes having the same inner diameters, the microfin tubes revealed their higher thermal performance in terms of heat transfer coefficient. As an example, Figure 3 shows the enhancement factor (EF), which is the heat transfer coefficient experienced by the microfin tubes divided by the one for the smooth tube under the same working conditions in the case of condensation tests with the microfin tube having 7 mm as its outer diameter. The dotted line represents the geometry enhancement factor, Rx, which is the heat transfer area of the microfin tube divided by that of the equivalent smooth tube. Rx is equal to 1.63 for the microfin tube considered. The highest values of EF are shown as mass velocities in the range of 100–200 kg m−2 s−1: in these operative conditions, most of the data for the microfin tube are in an annular flow regime (to which higher heat transfer coefficients are associated), whereas the counterparts for the smooth tube are in a stratified flow regime.
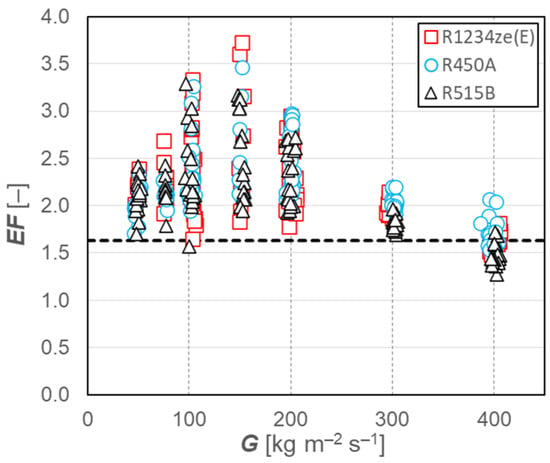
Figure 3.
Enhancement factor vs. mass velocity for the OD 7 mm microfin tube during condensation.
2.3. Metal Foams as an Engineered Periodic Structure
The typical structure of a metal foam crafted as a random porous medium presents difficulty in reproducing it both virtually and experimentally. Despite this randomness, there is evidence that the metal foam pores may be described by periodic structures [38]. Different types of structures may be employed to reproduce this periodicity. As suggested in the literature [39], one may employ the triply periodic minimal surfaces (TPMSs). These surfaces are particularly convenient since they are a combination of trigonometric functions, and they can also be produced by employing metal additive manufacturing 3D printing techniques [40]. One potential application of this technology is the production of an innovative TPMS metal foam-based heat exchanger. There are many possible choices for the type of TPMS to be employed. Here, we focus on three surfaces called gyroid, diamond, and primitive. The three-dimensional surfaces are expressed as the following functions:
where the subscripts G, D, and P stand for gyroid, diamond, and primitive, respectively, while is the spatial periodicity of the TPMS in the direction. The case of yields an isotropic medium. Figure 4 shows the three different surfaces for an isotropic case and a single period, . The surfaces are plotted for , and an arbitrary thickness is added to qualitatively simulate the metallic foam.
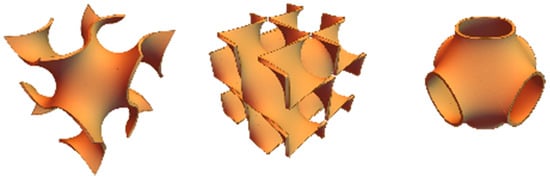
Figure 4.
Gyroid, diamond, and primitive TPMS drawn for an isotropic medium.
A relevant characteristic of the TPMS based metal foams, beside the thermal properties, is how they respond to mechanical stresses. The mechanical properties of several different types of engineered metal foams were investigated in [41] by employing thermomechanical simulations: the influence of residual stress on the mechanical properties of the TPMS was evaluated for selective laser melting (SLM)-produced metal foams. Novak et al. [42] investigated both experimentally and numerically how a diamond TPMS filled tube reacts under compressive loading: the energy absorption was proved to be enhanced for both axial and transversal loading directions when TPMSs are employed compared to free tubes. They also proved that the specific energy absorption enhancement of TPMS-filled tubes was higher compared to those presented in previous work for different types of foam-filled tubes [43,44,45].
Besides the mechanical properties, the investigation of the heat and mass transfer performances of a TPMS is also relevant. The numerical simulation of the heat and mass transfers for this type of engineered metal foam is reported in [46], where the analysis of the thermal entrance region in a gyroid TPMS based channel is carried out. The flow model employed for the local momentum balance equation is based on the Navier–Stokes equations while, for the local energy balance, it is based on a convection/conduction equation. A sketch of the channel is presented in Figure 5.

Figure 5.
Square section channel filled with a fluid-saturated engineered metal foam based on gyroid TPMS [46].
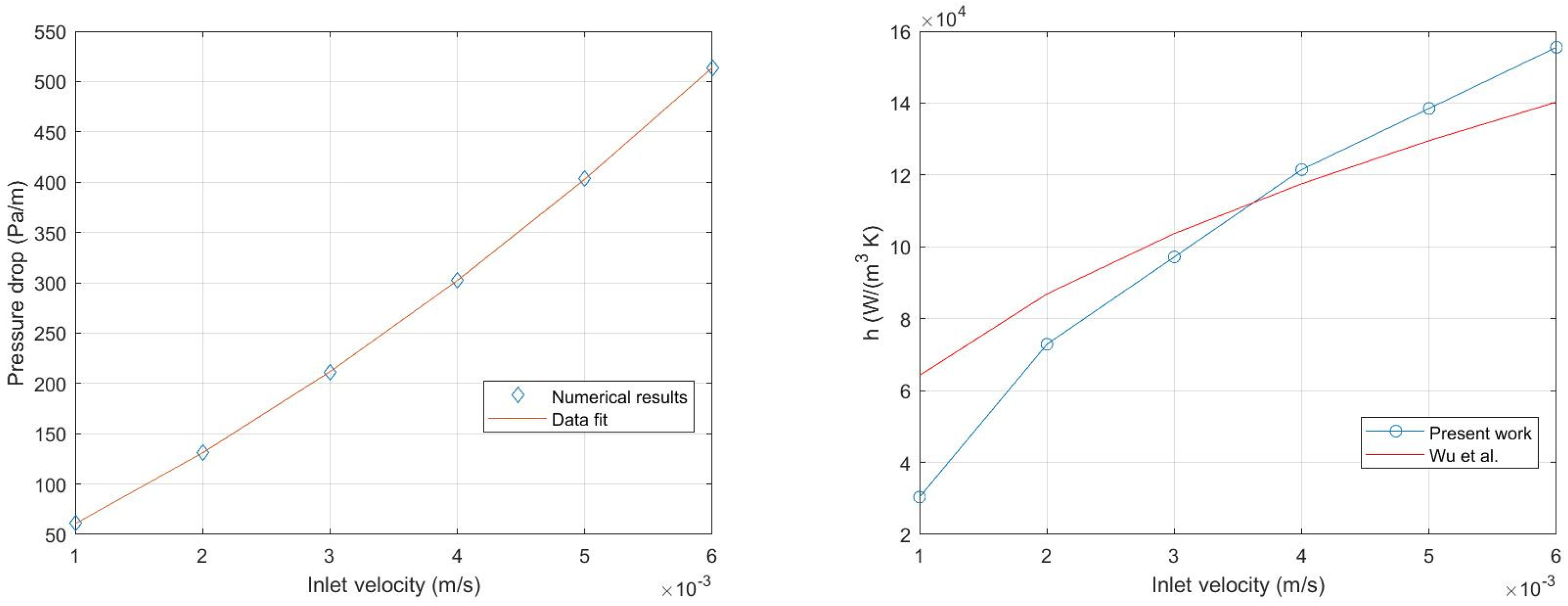
A high-conductivity metal foam is assumed such that the solid structure is considered as being isothermal. The pressure drop and the volumetric interphase heat transfer coefficient are evaluated as functions of the inlet velocity as displayed in Figure 6. It is worth noting that the dependence of the pressure drop on the velocity reported in Figure 6 matches the Darcy–Forchheimer [1] averaged macroscopic model for an equivalent porous medium.
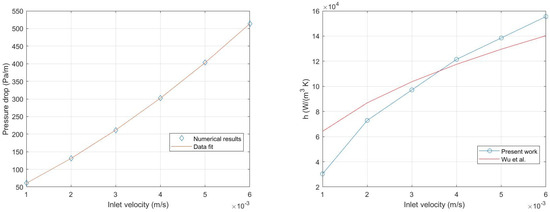
Figure 6.
Pressure drop, left hand side frame; and volumetric interphase heat transfer coefficient, (compared with the paper by [47]) right hand side frame; as functions of the inlet velocity [46].
The investigation of a structured metal foam at the cell scale level is reported in [48,49], considering mixture, water, and Al2O3 as a working fluid to evaluate both the fluid dynamic and thermal characteristics such as the permeability and the local heat transfer coefficient. The analysis also includes the entropy generation inside the system of cells with different pore densities [50]. The main entropy generation is due to the thermal irreversibility, but for a high pore density, the mechanical irreversibility due to the friction increases significantly. The first study on the slip condition in the Kelvin cells is reported in [51], with an estimation of the effect on the permeability and the heat transfer coefficient at the cell/pore scale. Variable permeability and porosity and the porosity related to the melting of Kelvin cells to simulate the phase change from solid to liquid of an ice-structured system was examined in [52].
3. Macroscale Flow Models in Metal Foams and Comparison with Mesoscale Data
3.1. Metal Foams and Local Thermal Non-Equilibrium
The metal foam is a solid matrix, which is typically characterized by a high thermal conductivity compared to the fluid that saturates the matrix. This feature yields, for intense thermal loads, a Local Thermal Non-Equilibrium (LTNE) between the solid and the fluid phases [53]. Regarding the stability analysis of the horizontal flow in a saturated porous layer, the LTNE has a destabilizing effect on the onset of both convective and absolute instabilities, independently of the Péclet number associated with the horizontal flow rate and the aspect ratio [54]. This non-equilibrium can be investigated by employing a two-temperature model. This model prescribes two different local energy balance equations, one for the solid and one for the fluid. We recall that the meaning of “local quantity”, when the metal foam is treated as a porous medium, must be intended as the average value of the given quantity evaluated in a Reference Elementary Volume (REV). A REV is a small volume, which is also large enough, such that the definition of the main fields average value is meaningful [1]. The two energy balance equations for the two-temperature model are, thus, the following:
where the subscripts s and f refer to the solid and fluid phases, respectively. Moreover, is the density, is the specific heat capacity, is the porosity of the solid phase (metal foam), is the temperature, is the time, is the thermal conductivity, is the volumetric interphase heat transfer, and is the velocity vector.
When the porous medium is assumed to have a high thermal conductivity compared to the conductivity of the saturating fluid, the governing equations in their dimensionless form may be simplified. By substituting the relations
into Equations (4) and (5), one obtains the dimensionless governing balance equations, namely:
where is the reference length, is a suitable reference temperature, and is a typical temperature difference of the system investigated. The dimensionless group numbers employed in Equations (7) and (8) are defined as
When an ideal metal foam is considered, the thermal conductivity of the solid phase is much larger than that of the fluid phase; thus, and, since from Equation (9), one has and , the energy balance equation for the solid simplifies to
The energy balance equation for the solid phase, Equation (10), may be solved analytically and yields, for the boundary conditions at the wall, an isothermal solid phase at . This conclusion also simplifies the fluid energy balance equation (8) to
An example to allow for the possible use of LTE with a reasonable approximation for the case of rectangular porous fins is given in [55]. In the investigation, the porous fin was studied in LTNE. The analysis provides the same criteria for the possible use of the LTE model.
3.2. Additive-Manufactured Porous Media Impregnated with PCMs
Phase change materials (PCMs) are a class of materials that are used to store or release latent thermal energy at fixed values of temperatures. Among the existing PCMs, paraffins are a mixture of hydrocarbon molecules whose melting temperature can be properly selected depending on the studied application. The main drawback is their low thermal conductivity, which may result in high temperatures and/or a long needed to complete the melting/solidification process. To overcome this issue, metal inserts, such as metal foams, can be implemented to enhance the overall thermal conductivity of the system. The recent developments in the field of the additive manufacturing technology allow for customizing the solid media to be impregnated with the PCMs.
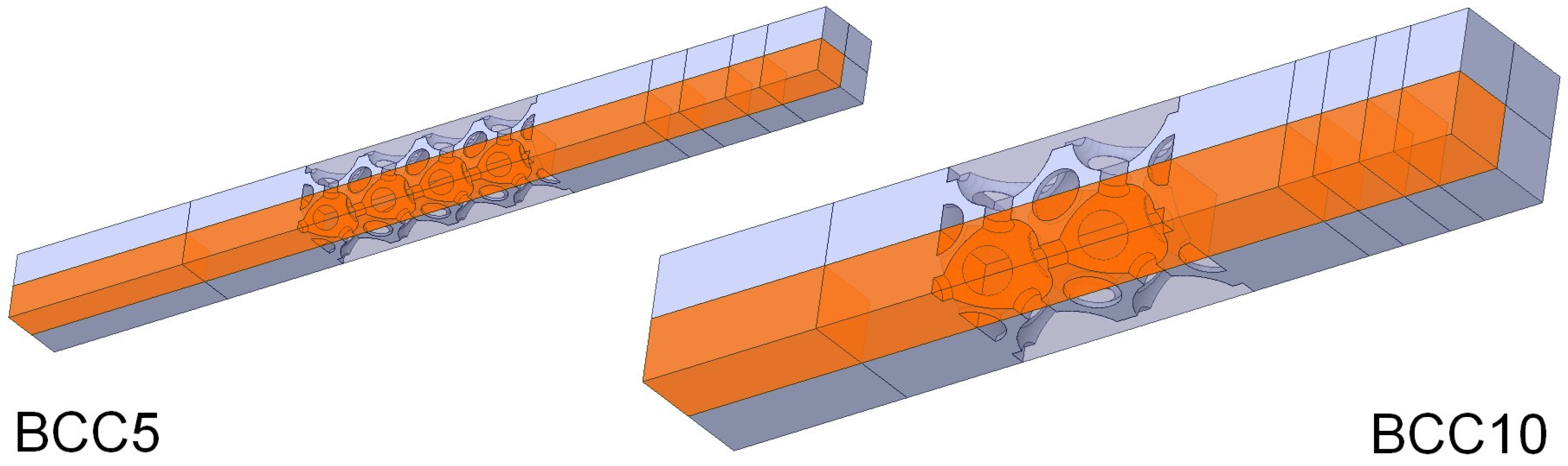
Modified body centered cubic (BCC) cells were fabricated through selective laser melting and experimentally tested by Diani et al. [56]. Cells with an edge of 5 mm (BCC5) and 10 mm (BCC10) were considered. Samples were made of AlSi10Mg, which is an aluminum alloy with a thermal conductivity of 175 W m−1 K−1, whose value has been measured in [57] with the hot disk technique. Samples were fabricated together with two plates of the same material, each plate being 10 mm thick, in order to install T-type thermocouples. Two Bakelite plates and a Teflon housing completed the experimental module. Three different paraffin waxes supplied by Rubitherm and named RT42, RT55, and RT64HC (the number that appears in the commercial names represents the characteristic melting temperature) were tested during melting by laterally applying three different heat fluxes (10, 15, and 20 kW m−2), with the samples vertically positioned. A frontal glass window was used to observe how the melting process propagated inside the structure, and the electric heater was turned off as soon as all the paraffin inside the metal structure was melted.
Since the results of the experimental tests had indicated that the effects of natural convection on the melted PCM were negligible, it was possible to use the data thus obtained to validate a purely conductive numerical model developed using the commercial code Ansys Fluent release 17.0 (2016). Indeed, the nonlinear transient heat conduction equation was solved using the apparent specific heat method to account for phase change enthalpy [56]. This approach allowed for a description of the phase change enthalpy variation with temperature that is more accurate than that allowed by the enthalpy–porosity formulation available in Fluent, which can only account for a linear enthalpy variation within the melting range.
The computational domains are represented by repetitive units that can be identified in the test modules and that correspond to the orange portions depicted in Figure 7. To allow for a more accurate reproduction of the experimental results, which depend not only on the heat flux applied to the heated surface, but also on the dispersions to the ambient and thermal inertia of the part of the insulating structures not represented in the simplified model, convection boundary conditions were also applied to the lateral surfaces of the computational domain that geometrically correspond to the symmetry planes. In addition, the heat capacity of Teflon was suitably increased.
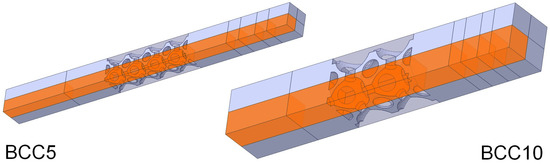
Figure 7.
Computational domains (orange) used for numerical simulations concerning the BCC5 and BCC10 structures [56] (reproduced from [56] with permission from Diani et al., Applied Thermal Engineering; published by Elsevier, 2022).
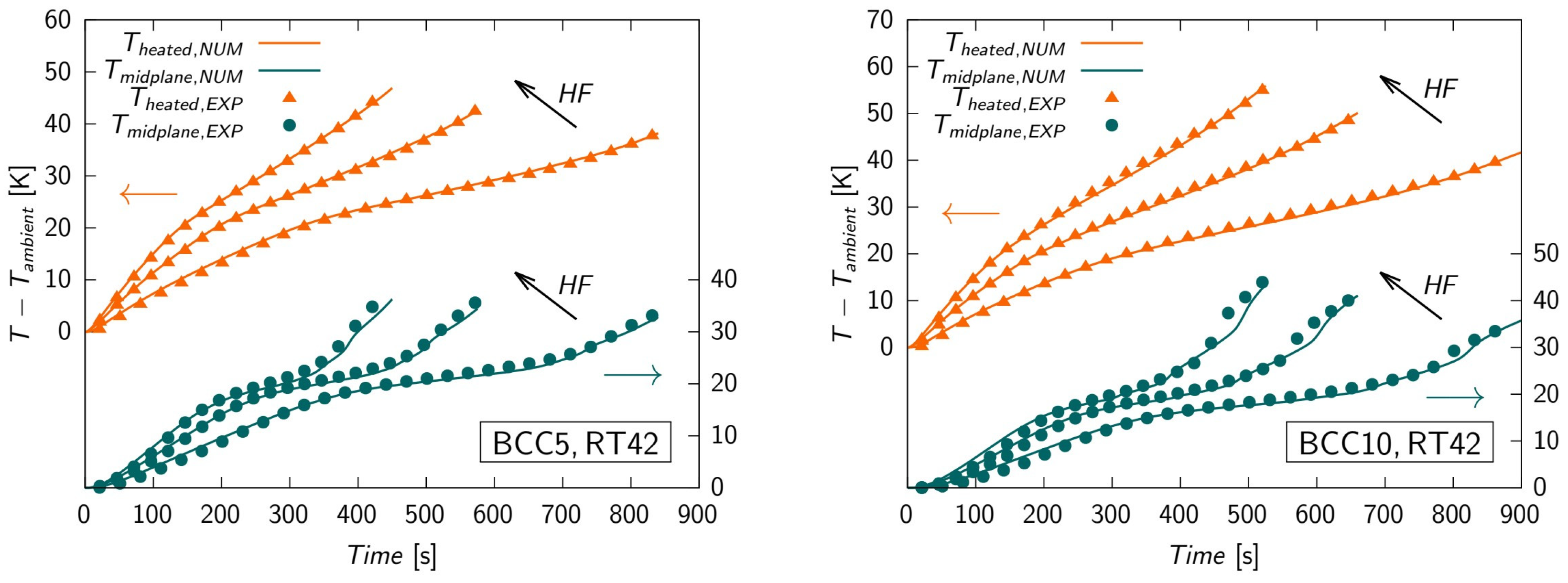
The validity of the model thus developed is demonstrated by the excellent agreement between the experimental results and those of the numerical simulations for all test cases. Figure 8 shows, as an example, comparisons of the temperature trends of the heated surfaces and midplanes of the test modules for the BCC5 and BCC10 structures and one of the three paraffins considered (RT42). From a practical point of view, the availability of a reliable simplified model such as the one proposed by Diani et al. [56] is particularly useful for verifying and comparing the thermal performance of PCM-impregnated metal structures with a computational effort that is only a small fraction of what would be required in the case of a model that also accounts for possible convective flows in the molten PCM. An example of an application reported in [56] consists in the verification of the rate of thermal energy storage in the considered PCM-impregnated structures (BCC5 and BCC10) with the RT42 wax, also considering two different metallic materials (AlSi10Mg and copper), when the temperature, and not the heat flux, is imposed on the heated surface as a boundary condition. Then, the same analysis was performed by Nonino et al. [58], with reference to RT55 and RT64HC paraffins.
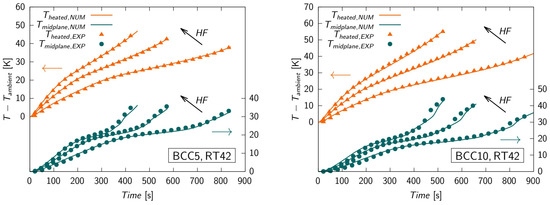
Figure 8.
Sample comparisons of experimental and numerical results for three values of the heat flux HF [56].
In order to evaluate the effect of volume extension on the melting of PCM inside a structure with Kelvin cells of different cell densities, a numerical study on two different volumes was performed in [59]. The investigation highlighted the effect of the volume on the melting rate. It increases for the greatest volume at the same cell density, whereas it decreases for the lowest volume with increasing cell density.
4. Nanofluids: Models and Experimental Data at Nanoscale and Macroscale
Physical Properties of Nanofluids
This section presents recent models for calculating the thermophysical properties of nanofluids, including density, specific heat, thermal conductivity, and viscosity. The local concentration of nanoparticles in the base fluid is a key factor in determining these properties, but other effects such as temperature or particle shape must be taken into account. It is worth noting that the concentration of nanoparticles can be affected by gravitational sedimentation, and the stability of nanofluids is a critical issue for their applicability [60]. Various models have been proposed to describe the thermophysical properties of nanofluids, ranging from simple models that only consider the dependence on nanoparticle concentration to more complex models that incorporate factors such as nanoparticle size, shape, Brownian motion, and temperature. The theoretical classic models are re presented in [61]. One of the main problems is the evaluation of thermophysical properties, as underlined in [62].
The activity on models at different scales, from nanoscale to macroscale, becomes very important to identify the main characteristics of thermophysical properties. Due to their intrinsic multiscale nature, thermophysical properties of nanofluids show a non-trivial dependence on particle composition and shape, agglomeration phenomena, presence of surfactants, etc. Such phenomena have been typically handled by theoretical and empirical analytical expressions [63], which can only partly model the necessary complexity. As such, recent approaches have introduced novel possibilities to reproduce the dynamics of the self-assembly of suspended nanoparticles in aqueous solutions. These approaches are still challenging, even for the modelling community, because of the wide range of scales involved and the complexity of the chemical features needed for catching realistic systems. In the following paragraphs, some remarkable features are discussed, namely, self-assembly, surfactants, and interactions with complex structures, which are critical for the fundamental understanding of nanofluids at the molecular level.
In [64], a new multiscale approach was proposed to understand the dynamics of self-assembly of suspended nanoparticles in aqueous media. This approach incorporates nanoscale phenomena into the dynamics of suspended nanoparticles and bridges the gap between the nanoscopic and macroscopic scales. The researchers used all-atom molecular dynamics simulations to evaluate the potentials of mean force (PMFs) between several nanoparticles in aqueous solutions. They then defined ad hoc coarse-grained (CG) force fields to carry out stochastic dynamics (SD) simulations and predict the stability of nanoparticle suspensions and the kinetics of the underlying aggregation processes over different regimes. A representation of the new multiscale modeling approach for nanofluids is shown in Figure 9, in which a matrix form is used to provide a useful summary of the different multiscale steps involved.
It was found that the traditional van der Waals and electrostatic interactions, derived in the context of the DLVO theory, may fail in accurately describing inter-particle interactions due to the underlying molecular details. Atomistic-simulation-based strategies are, therefore, recommended for computing the interaction potential between NPs, which allow for capturing the attractive van der Waals and the repulsive electrostatic interactions as well as entropic effects that are particularly important at the nanoscale (see Figure 9c).
The calculated PMF curves were then used to simulate the Langevin dynamics of suspended NPs in aqueous media. The results showed that the potential energy barrier plays a crucial role in yielding well-dispersed NP suspensions. The addition of surfactants and the adjusting of the NP surface charge density were found to have great potential to stabilize NP suspensions. In the case of purely attractive interactions, rapid aggregation of single-dispersed NPs occurred, and nano-dispersions possessing lower particle volume fractions showed a higher propensity for stability (see Figure 9d).
Finally, focusing on alumina nanoparticle, the overall thermal properties of nanofluids were estimated using cluster analysis and, thus, not relying upon prior assumptions about the shape and size of the resulting NP aggregates, with the goal to predict the thermal conductivity of the nanofluids and, more generally, to pave the way toward new design strategies of nanofluids.
Subsequently, the above approach was further extended to titania nanoparticles in [65]. Here, the coordinates of the atoms forming the NPs were retrieved from quantum calculations. MD simulations of pairs of NPs were performed to calculate their interaction potential (PMF) using Umbrella Sampling. The results obtained were compared with the theoretical PMF predicted using the DLVO theory, showing finding significant discrepancies and justifying the proposed approach. The PMF was used to perform Brownian Dynamics (BD) simulations with dozens of thousands of NPs at a relatively low computational cost. The aggregation kinetics obtained via BD simulations were compared with the classic Smoluchowski theory, observing larger deviations for smaller NPs at higher volume fractions. The traditional theory was time-discretized and modified to relate the aggregation kinetic to the instantaneous average cluster size, including two numerical coefficients to be fitted on the simulation data, obtaining excellent agreement.
Another crucial aspect related to the stability of nanofluids and nanosuspension is the impact of possible amphiphilic molecules (i.e., surfactants). In a recent paper [66,67], the coupling of steered molecular dynamics (SMD) enhanced-sampling algorithm with the Langmuir theory was proposed to predict the surfactant adsorption isotherm and provide more insightful guidelines for designing nanosuspensions (see Figure 9a). Such model has been proven to match experimental data well in the low-concentration regime, where the solution is highly diluted and the surfactants are not self-assembled. This study also elucidated the important role of both entropic and enthalpic effects on surfactant (here Sodium Dodecyl Sulfate—SDS) and NP interactions. The reported results suggest that the presence of repulsive interactions between SDS and a coated NP arises mainly from entropic effects. The NP curvature effect and heterogeneities in the NP surface morphology were found to facilitate the splitting of free energy landscapes corresponding to diverse possible sites of adsorption, which may result in asymmetric dislocation of the adsorption sites. Interestingly, the proposed model translates nanoscale interfacial phenomena into a continuum theory of adsorption and provides design rules for engineering NP aqueous suspensions suitable for a wide range of applications.
In line with the above work, the mechanism of the self-assembling of biomolecules, as a paradigmatic example of complex structures, on suspended nanoparticles in water has been investigated in [67,68]. Here, specifically focusing on gold NP (AuNP), atomistic MD simulations showed that PLGA oligomers first self-assembled in larger clusters and then aggregated on the AuNP surface. Machine-learning algorithms have been used to confirm that the rate of cluster formation is higher at higher PLGA concentrations (see Figure 9b). This study also revealed the anisotropic nature of PLGA coating, with the {1 1 1} crystal plane of the AuNP resulting more favorable for adsorption than the {1 0 0} plane. The enthalpic nature of the anisotropic adsorption was revealed using Umbrella Sampling. This study shows—at least conceptually—that the adsorption mechanisms of surfactants on NPs can be controlled using a rational and functional design of the particle topology.
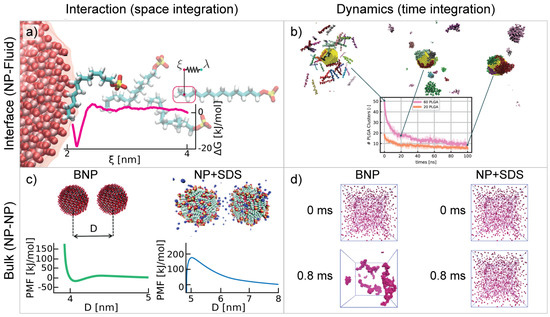
Figure 9.
The multi-panel figure depicts multiscale modeling of nanofluids and outlines the various steps involved in nanoscale characterization and macroscale properties of nanoparticle suspensions, namely: (a) the study of nanoscale interactions with nanoparticle interfaces from De Angelis et al. [66] (Reprinted/adapted with permission from Ref. [66] Copyright 2019, American Chemical Society); (b) the analysis of interaction with nanoparticles in a fluid at the absorption scale from Cappabianca et al. [67] (Reprinted/adapted with permission from Ref. [67] Copyright 2022, American Chemical Society); (c) the study of particle–particle interaction; and (d) finally coarse-grained modeling to predict the behavior of several nanoparticle suspensions from Cardellini et al. [64] (Reprinted/adapted with permission from Ref. [64] Copyright 2019, Royal Society of Chemistry). Panels (a,c) illustrate interaction phenomena, demonstrating the use of molecular dynamics simulation to evaluate the energetic interactions between several nanoparticles in aqueous solution. The analysis can be upscaled using coarse graining to evaluate and compare the interaction between bare or coated particles. Panels (b,d) display the dynamics of suspended nanoparticles, showing the time evolution of the aggregation processes over different regimes. The researchers investigated the kinetics of the phenomena, shedding light on what can accelerate aggregation, such as a more concentrated system. Also, they can exhibit the stability of several coated nanoparticle suspensions over time.
Figure 9.
The multi-panel figure depicts multiscale modeling of nanofluids and outlines the various steps involved in nanoscale characterization and macroscale properties of nanoparticle suspensions, namely: (a) the study of nanoscale interactions with nanoparticle interfaces from De Angelis et al. [66] (Reprinted/adapted with permission from Ref. [66] Copyright 2019, American Chemical Society); (b) the analysis of interaction with nanoparticles in a fluid at the absorption scale from Cappabianca et al. [67] (Reprinted/adapted with permission from Ref. [67] Copyright 2022, American Chemical Society); (c) the study of particle–particle interaction; and (d) finally coarse-grained modeling to predict the behavior of several nanoparticle suspensions from Cardellini et al. [64] (Reprinted/adapted with permission from Ref. [64] Copyright 2019, Royal Society of Chemistry). Panels (a,c) illustrate interaction phenomena, demonstrating the use of molecular dynamics simulation to evaluate the energetic interactions between several nanoparticles in aqueous solution. The analysis can be upscaled using coarse graining to evaluate and compare the interaction between bare or coated particles. Panels (b,d) display the dynamics of suspended nanoparticles, showing the time evolution of the aggregation processes over different regimes. The researchers investigated the kinetics of the phenomena, shedding light on what can accelerate aggregation, such as a more concentrated system. Also, they can exhibit the stability of several coated nanoparticle suspensions over time.
5. Applications of Metal Foams, Microchannels, and Nanofluids to PCM Thermal Energy Storage Devices and Heat Exchangers
5.1. Metal Foams Applications
Metal foams are employed in several engineering applications with a specific interest in heat transfer. The main effect is related to their porous-media nature, which allows for them to pass from a surface heat transfer to a quasi-bulk-volume heat transfer. This significantly increases the heat transfer, and the use of a metal foam can be very useful in heat exchangers, thermal control, and thermal energy storage. Some examples are described below.
In order to simulate engineering devices, i.e., higher spatial scales, the volume-averaging (macroscale) approach is required. This approach can be employed if one is interested in variables that are not affected by the space-scale level of the simulation performed. With references to metal foams, heat sinks that might be used for electronic cooling have been simulated and optimized using the genetic algorithm to obtain predictions in acceptable times.
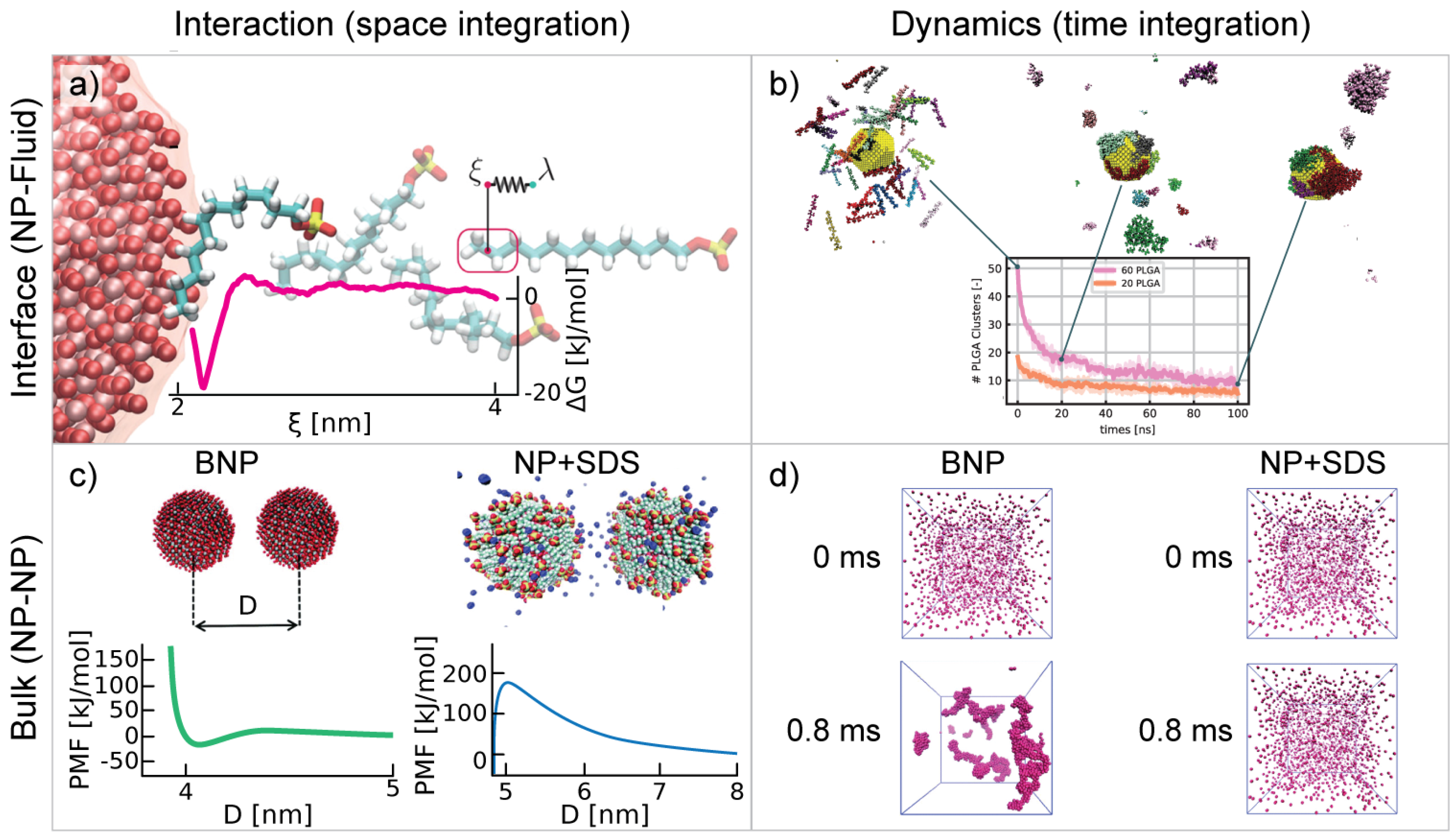
An impinging-flow heat sink equipped with both metal foam and fins was optimized in [68]. A sketch of the device is shown in Figure 10. After writing volume-averaged equations, because of the lack of closure coefficients for this specific case, say impinging flows in metal foams, a calibration with available experiments was carried out by assuming that the closure functions behaved like the well-known Žukauskas correlations for cross-flows in tube banks. The multi-objective function comprised pumping power and heat rate, whereas the latter was obtained by assuming that the plate temperature was uniform. The design variables were the heat sink geometry—at a constrained base size—and foam morphology. The results showed that the heat to be dissipated—at constrained pumping power—could be higher by 3.3–3.5 times if the finned foam configuration was used instead of the foam configuration. By comparing the results with a similar study from the literature [69], the heat to be dissipated increased by a factor of 2.5–3 or 5–6 for foams or finned-foam devices, respectively. This highlights the importance of running multi-objective optimization for engineering devices. An additional improvement to the use of metal foam in impinging jets was obtained using nanofluids [70].
Figure 10.
(a) Finned-foam heat sink under impinging flow conditions (reproduced from [68] with permission from Bianco et al., Applied Thermal Engineering; published by Elsevier, 2021) and (b) domain used for computations.
Heat exchangers with metal foams present interesting behaviors as underlined in [71], where a review of crossflow heat exchangers is given. A numerical model to examine the fluid dynamic and thermal performance parameters in aluminum-foam compact-heat exchangers was developed in [72]. A more recent application of metal foams is related to the heat recovery along the automotive exhaust line to improve the performance of thermoelectric generators (TEGs) [73,74].
5.2. Effects of Non-Uniform Flow Distribution in Cross-Flow Double-Layered Microchannel Heat Sinks
The use of liquid-cooled microchannel heat sinks (MCHSs) represents a well-established method for the thermal control of electronic components. In the past decades, MCHSs have been proposed first in single-layer (SL-MCHS) and then in counter-flow double-layer (DL-MCHS) configurations. The latter allow for better temperature uniformity, albeit at the expense of greater complications in the header design because two inlets and two outlets are required. An extensive review on the subject was recently conducted by He et al. [74].
A survey of the literature shows that the two-layer cross-flow configuration has been almost totally neglected despite the greater simplicity in piping it can offer compared to the counter-flow configuration. In fact, only Nonino and Savino [75] explored the potential of this type of MCHS configuration using an in-house numerical procedure based on the finite element method (FEM), which had been previously developed for the analysis of the thermal and hydraulic performance of cross-flow micro heat exchangers [76,77,78].
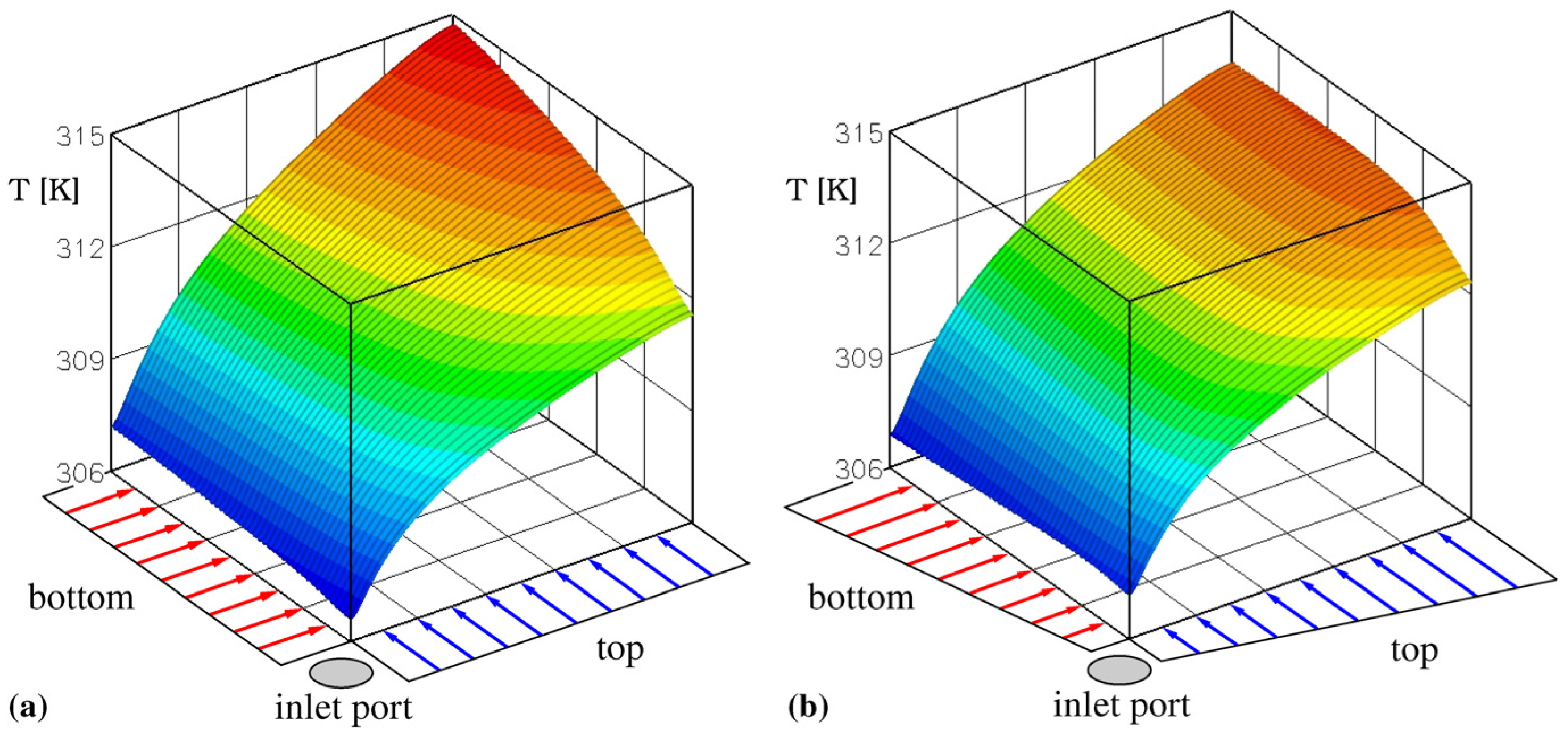
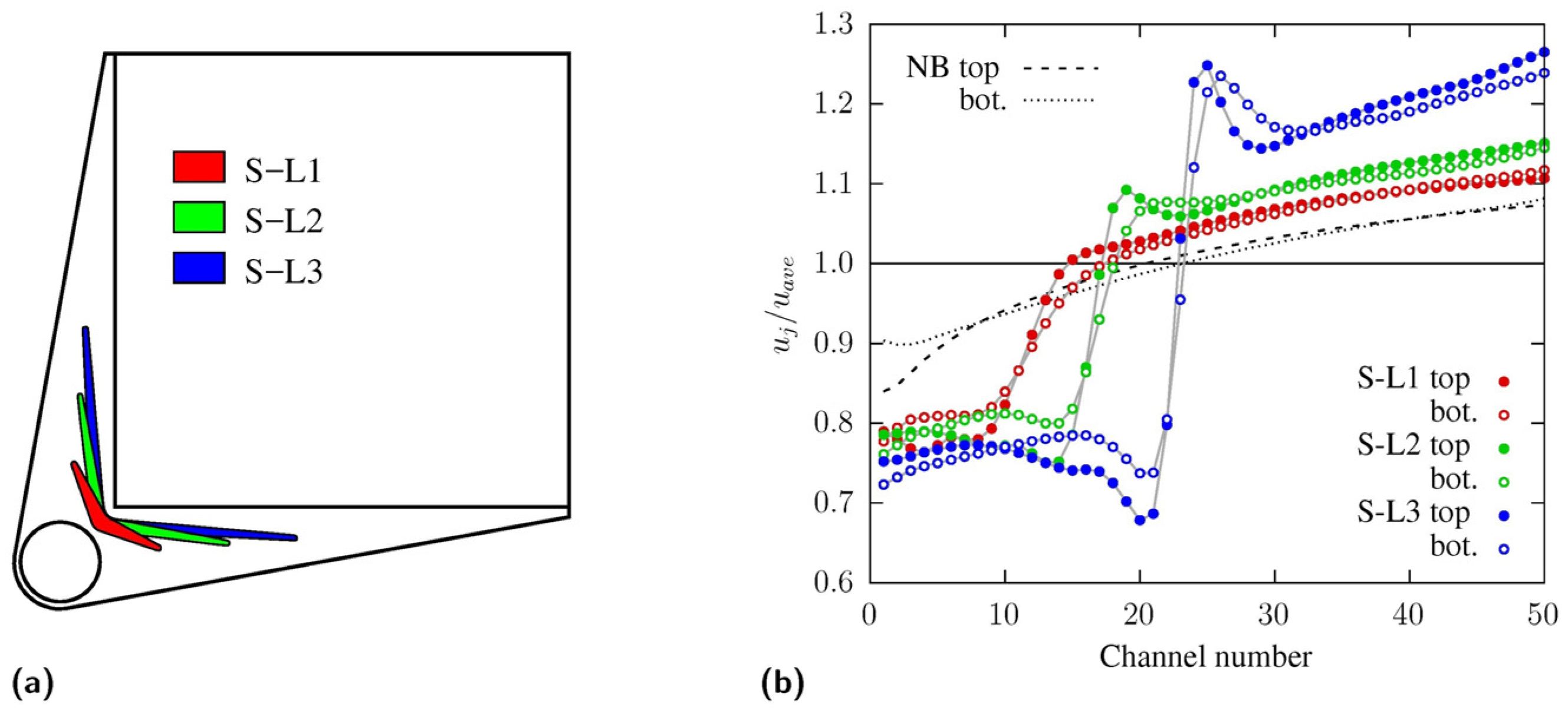
The study by Nonino and Savino [75] pointed out that an unavoidable consequence resulting from the adoption of a cross-flow configuration is the appearance of a hotspot on the heated surface of the MCHS at the corner formed by the sides where the microchannel outlets are located. This effect clearly appears in Figure 11a, where a typical temperature distribution on the heated base of a cross-flow DL-MCHS is shown.
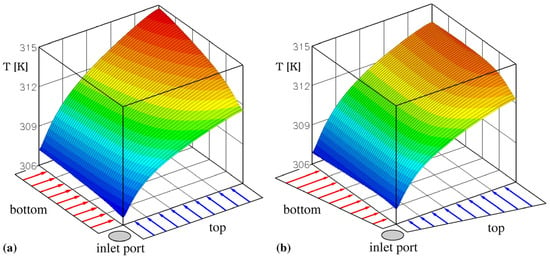
Figure 11.
Examples of temperature distributions on the heated base of square cross-flow DL-MCHSs: (a) uniform microchannel velocity; (b) microchannel velocities varying linearly along the sides [79].
The situation described above, however, refers to an ideal condition in which the velocity distribution in the microchannels is uniform, but this is unlikely to occur in practice since some degree of velocity unevenness is unavoidable, while in general, flow maldistribution negatively affects the performance of thermal devices; in the case of cross-flow DL-MCHSs, instead, it can be exploited to achieve more uniform temperature distributions and reductions in thermal resistance [75]. This happens if the microchannel velocity non-uniformity is such that it results in an increase in the flow rate in the hotspot region, as shown in the example depicted in Figure 11b.
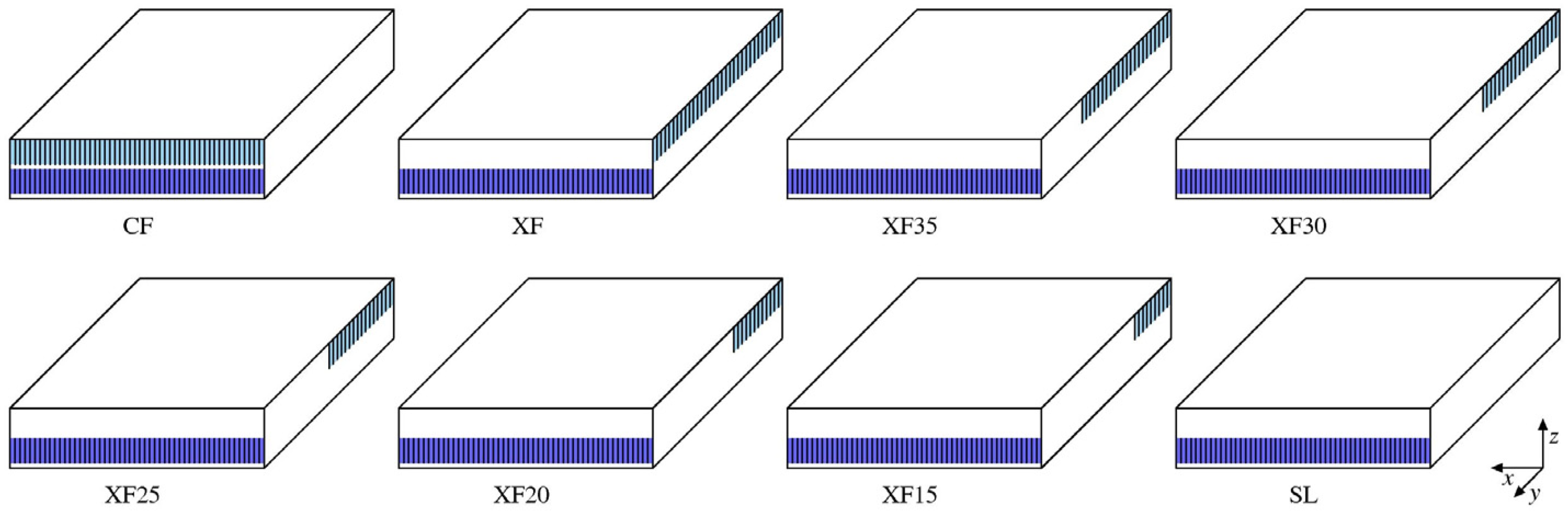
Possible methods for achieving a non-uniform microchannel velocity distribution that would allow for hotspot mitigation were studied by Savino and Nonino [79], who proposed the use of an angled baffle positioned in the inlet header to obtain the desired increase in flow rate in the microchannels closest to the outlet header, as illustrated in Figure 12. In their analysis, which was conducted using the commercial software Ansys Fluent (release 17.0, 2016), they considered various options resulting from the combination of baffles of different lengths and heights, possibly also consisting, in whole or in part, of porous material.
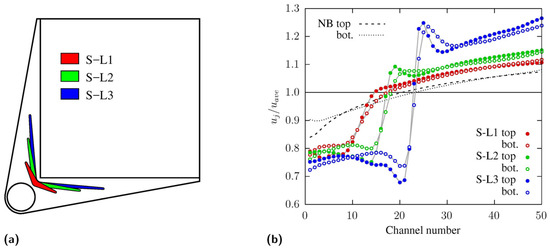
Figure 12.
Inlet header with a baffle: (a) schematic representation of baffles of different lengths; (b) examples of non-uniform normalized microchannel velocity distributions [79].
Thermal resistances and temperature uniformity of the heated surface similar to those achievable with appropriate velocity non-uniformity can also be attained with cross-flow DL-MCHSs in which the number of channels in the upper layer is smaller than that in the lower layer. This was demonstrated by Nonino and Savino [80], who analyzed the configurations schematized in Figure 13, which refer to the case where there are 50 microchannels in the lower layer, while in the upper layer, the number varies between a minimum of 15 and a maximum of 50. The analysis, which was conducted using the same numerical FEM procedure employed in [75], concluded that, at least with some of the configurations considered, acceptable temperature uniformity and thermal resistances can be achieved with a much simpler collector design than that required by counter-flow DL-MCHSs. In addition, in the case where the thermal flux applied to the heated base is not uniform, an appropriate orientation of a cross-flow DL-MCHS can allow for more effective thermal management of the electronic devices than that possible with other configurations.
Figure 13.
Schematic representations of the MCHS configurations considered in [80].
5.3. Effects of Nanofluids in Heat Transfer Applications
Applications of nanofluids for enhanced heat transfer applications are disparate, and the applications drastically influence the goals, the approaches, and the trade-offs for their optimization. In the following paragraphs, we briefly review some representative examples. For instance, in Ref. [81], the authors report a comprehensive review that aimed at highlighting the potential of nanofluids for automotive cooling applications. The work first provides a detailed description of the state of the art in nanofluids, including their synthesis, thermo-physical properties, and dependency on various factors such as particle material, size, shape, volume concentration, base fluid pH, and surfactant concentration. Furthermore, this review also suggests that future research should focus on investigating the optimal nanofluid aggregate morphologies that lead to the best combination of thermal conductivity, viscosity, and stability.
As far as less conventional applications of nanosuspensions are concerned, it is worth mentioning the interesting possibility of engineering optical properties of nanofluids for solar energy collection. In this respect, in Ref. [82], Moradi et al. report on the potential benefits of using direct solar absorption in solar thermal collectors for residential and small commercial applications. Here, nanofluids are suggested as a promising option due to their high absorption coefficient and stability at moderate temperatures. In particular, the use of carbon nanohorns is investigated, as they are expected to exhibit a lower toxicity compared to other carbon nanoparticles. In particular, the study presents a three-dimensional model of the absorption process in nanofluids within a cylindrical tube.
One major issue with the use of nanofluids is the possible toxicity of the adopted nanomaterials. In order to alleviate this aspect, in Ref. [83], Alberghini et al. present, for the first time [84], a study that investigates the photo-thermal properties of a sustainable, stable, and inexpensive colloid based on coffee and utilized for direct solar energy collection. Here, the nano-colloid was composed of distilled water, Arabica coffee, glycerol, and copper sulphate, which enhanced its properties and biocompatibility. The researchers found that the coffee-based colloids show competitive optical and thermal properties for direct solar absorption, similar to traditional indirect absorption based on selective surfaces.
5.4. Use of Phase Change Materials in Thermal Control and Thermal Energy Storage
Moving to thermal energy storage applications, the idea of using (nano)additivities within phase change materials (PCMs) or microporous sorbents for latent and/or thermochemical energy storage applications has also attracted significant attention in the literature as recently reviewed in [85,86].
In particular, using nano-additivities of PCMs is certainly an effective approach to enhance the thermophysical properties of PCMs (e.g., the effective thermal conductivity). At the same time, there is still a lack of understanding regarding the optimal use of additives to design PCMs with desired properties. One reason for this is the impact of thermal resistances at the filler-matrix interface, which limits heat transport within the material. Hence, further experiments and theoretical analyses are required to improve the design of PCMs for thermal energy storage applications [85].
As a future perspective, in the context of enhanced heat transfer techniques, it appears interesting to explore the combined effect of nanofluids and/or nano-additivated PCMs with emerging and more flexible manufacturing techniques (e.g., 3d metal printing, laser etching) [87,88,89,90,91,92].
Another example of a combined system with a finned foam heat sink equipped with a PCM, as shown in Figure 14, was analyzed and optimized in [93]. After setting up the model, in which the enthalpy–porosity approach was used to describe the liquid PCM motion, the optimization problem was set up by considering a cost/operation time multi-objective function, with the foam and finned surface geometrical variables as the design variables. The outcomes showed that the optimized device can cost between about EUR 200 and EUR 250, with an operation time—obtained by assuming 90 °C as the survival temperature for the base plate—between about 2000 and 6000 s.
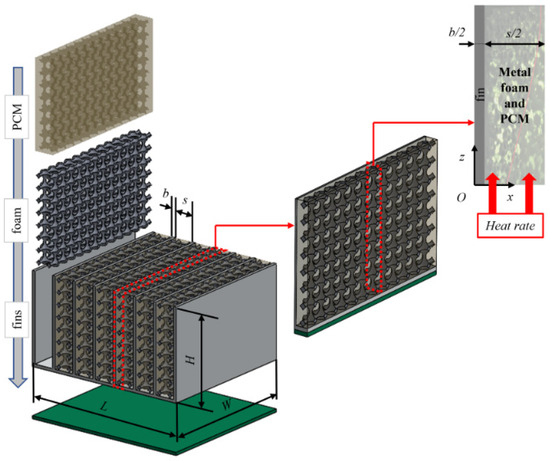
Figure 14.
Finned-foam heat sink equipped with a phase change material for thermal management [93] (reproduced from [93] with permission from Bianco et al., Applied Thermal Engineering; published by Elsevier, 2021).
With references to simpler engineering devices, say only channels or boxes, studies have been carried out to optimize the foam morphology distribution within a heated rectangular channel [94], as shown in Figure 15a, as well as to describe the melting evolution in a foam/PCM box [95], as shown in Figure 15b. Graded foams can be obtained with manufacturing techniques [30], by sintering foam layers [96], or with additive manufacturing. An optimization analysis to understand how to distribute the foam material—at a constrained average porosity or cell size—was carried out in [94], and a sketch of the foam device analyzed is shown in Figure 15a. After setting up the predictive model by using the volume-average approach, different sets of objective functions were analyzed, which was also by considering different power-law variations of porosity and/or cell size within the foam domain. For the multi-objective optimization problem, Nusselt vs. friction factor and similar objective functions have been considered; on the other hand, the mono-objective analysis was carried out by using the performance evaluation criteria [97,98]. By considering different foam morphology distributions, a PEC of 1.51 computed with references to the uniform foam case was reached, demonstrating that one could increase thermal performances by 51% at a constrained pumping power if the foam morphology is varied.
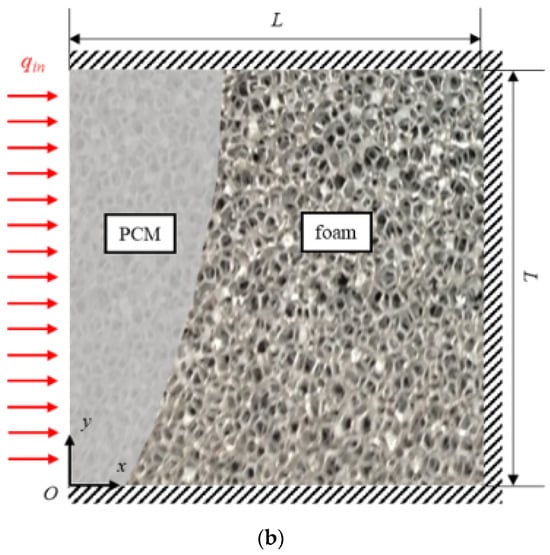
Figure 15.
Graded-foam channel for an optimization analysis (a) and PCM/foam composite box (b) investigated in [94] and [95] (reproduced from [95] with permission from Iasiello et al., Applied Thermal Engineering; published by Elsevier, 2021), respectively.
A foam/PCM composite box was analyzed with both numerical and experimental approaches in [95], and a sketch is presented in Figure 15b. The numerical model was set up by using volume-averaged equations together with the enthalpy porosity method. On the other hand, experiments were run by including the composite within several boxes to guarantee thermal insulation and to monitor the melting front evolution with both LCD and IR cameras. The melting front evolution was then monitored with the IR camera and mutually validated with numerical results, showing that using an IR camera is a real option to investigate the melting front position at each time for this kind of problem. Different orientations, porosities, and PPIs were investigated, also showing that lower porosities have the highest impact on the melting front velocity, while orientation and PPIs do not considerably affect this aspect.
The advantage of the use of a metal foam in a PCM to improve the melting rate in a thermal energy storage (TES) is a strong interest, as recently reviewed by Sehrawat et al. [99]. Some examples are provided in [100,101] for shell and tube latent heat TESs with PCM partially filled with a metal foam. The analysis was accomplished on an adiabatic TES [100] and on a TES with external heat losses [101]. Moreover, latent heat thermal energy storages can be combined with a solar system such as the solar chimney in a building [102].
6. Conclusions and Future Developments
Using metal foams and nanofluids in a heat exchanger and in a thermal energy storage system offers several advantages primarily related to the enhanced heat transfer rate and efficiency. This review paper has discussed in detail some key benefits of incorporating these materials into the heat exchanger design as a result of the wide collaborative research program carried out on this topic, which involved nine Italian universities in the last four years. The Universities are Alma Mater Studiorum University of Bologna, Polytechnic of Torino, University of Genoa, University of Campania Luigi Vanvitelli, University of Napoli Federico II, University of Napoli Parthenope, University of Padova, University of Pisa, and University of Udine.
It has been shown that the comparison between the mesoscopic approach, at the nanoparticle scale, or at the pore scale with the macroscopic approach based on suitable volume averages provides a correct evaluation of the material parameters, such as the metal foam permeability and interphase heat transfer coefficient, or the average conductivity of the nanofluid. In detail, metal foams have a highly porous structure with interconnected pores. This structure provides a large surface area for heat transfer, which significantly increases the convective heat transfer coefficient. This means that heat can be transferred more efficiently between the fluid and the solid material, leading to an improved thermal performance. Due to their high porosity, metal foams can have relatively low pressure drop characteristics. This allows for an efficient fluid flow through the heat exchanger without requiring excessive pumping power. On the other hand, nanofluids are engineered suspensions of nanoparticles in a base fluid. The addition of nanoparticles, which have a much higher thermal conductivity than the base fluid, increases the overall thermal conductivity of the nanofluid. This results in an improved heat transfer rate in the heat exchanger. With their enhanced heat transfer properties, nanofluids can enable the design of smaller and more compact heat exchangers for the same heat transfer rate. It has also been pointed out that PCMs play a crucial role in enhancing energy efficiency, reducing greenhouse gas emissions, and promoting sustainable energy solutions in various sectors by efficiently storing and releasing thermal energy. Their continued development and integration into metal foams and nanofluid-based devices hold significant promise for the future of thermal energy storage.
Despite the broad results achieved within the framework of the research program, there are several aspects yet to be exploited and further pursued. Among the future perspectives, relative to the enhanced heat transfer techniques, it must be mentioned that there is a combined effect of nanofluids and/or nano-additivated PCMs on innovative and more flexible manufacturing techniques, which include 3d metal printing and laser etching. There are also several topics regarding the physical and mathematical analyses of the microfluidics and microscale heat transfer processes that offer a possible focus for future developments. In fact, the accurate modeling of such processes is of paramount importance with respect to the prediction of the properties and the performance of both the metal foams and the nanofluids. The manifold microscopic processes deserving a special attention include the Brownian motion of diffusing nanoparticles or solute substances inside the porous matrix of the metal foam with trapping or Levy flight events leading to departures from the standard diffusion such as subdiffusion or superdiffusion. The convection flows and the heat transfer rates can be significantly affected by such phenomena to an extent that has not yet been determined in the existing literature. The numerical models for the simulation of the small-scale flow and heat transfer offer many possibilities for future developments, especially relative to the interaction with the methods of additive manufacturing. A key topic is the design of metal foams with geometries displaying optimized performances for heat transfer and pressure drop characteristics, which are also suitable for efficient and economically competitive manufacturing.
More experimental data are needed to better understand the advantages and feasibility of using nanofluids and metal foams in various applications. It is important to note that nanofluids face challenges related to stability and potential environmental and health effects. These issues can be addressed by using biocompatible nanoparticles in nanofluid mixtures and hybrid nanofluids. However, the relatively high costs associated with nanofluids and metal foams have limited their widespread adoption despite the significant benefits they offer in enhancing heat transfer and increasing heat transfer density.
The ongoing trend toward miniaturization in various industries is expected to lead to a decrease in the costs of nanofluids and metal foams, which, in turn, will likely increase their use. This suggests that more research should be dedicated to exploring the combined utilization of metal foams, micro/mini channels, nanofluids, and phase change materials to further improve thermal efficiency in various applications.
Funding
This research was funded by MIUR (Ministero dell’Istruzione, dell’Università e della Ricerca), grant number PRIN-2017F7KZWS.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nield, D.A.; Bejan, A. Convection in Porous Media, 4th ed.; Springer: New York, NY, USA, 2013; ISBN 978-1-4899-9822-4. [Google Scholar]
- Barletta, A. Thermal Instabilities in a Fluid Saturated Porous Medium. In Heat Transfer in Multi-Phase Materials; Öchsner, A., Murch, G.E., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 381–414. ISBN 978-3-642-04403-8. [Google Scholar]
- Ambrosio, G.; Bianco, N.; Chiu, W.K.S.; Iasiello, M.; Naso, V.; Oliviero, M. The Effect of Open-Cell Metal Foams Strut Shape on Convection Heat Transfer and Pressure Drop. Appl. Therm. Eng. 2016, 103, 333–343. [Google Scholar] [CrossRef]
- Pusterla, S.; Ortona, A.; D’Angelo, C.; Barbato, M. The Influence of Cell Morphology on the Effective Thermal Conductivity of Reticulated Ceramic Foams. J. Porous Mater. 2012, 19, 307–315. [Google Scholar] [CrossRef]
- Pusterla, S.; Barbato, M.; Ortona, A.; D’Angelo, C. Numerical Study of Cell Morphology Effects on Convective Heat Transfer in Reticulated Ceramics. Int. J. Heat Mass Transf. 2012, 55, 7902–7910. [Google Scholar] [CrossRef]
- Yang, X.H.; Bai, J.X.; Yan, H.B.; Kuang, J.J.; Lu, T.J.; Kim, T. An Analytical Unit Cell Model for the Effective Thermal Conductivity of High Porosity Open-Cell Metal Foams. Transp. Porous Media 2014, 102, 403–426. [Google Scholar] [CrossRef]
- Hast, A.; Rinne, S.; Syri, S.; Kiviluoma, J. The Role of Heat Storages in Facilitating the Adaptation of District Heating Systems to Large Amount of Variable Renewable Electricity. Energy 2017, 137, 775–788. [Google Scholar] [CrossRef]
- Thaker, S.; Olufemi Oni, A.; Kumar, A. Techno-Economic Evaluation of Solar-Based Thermal Energy Storage Systems. Energy Convers. Manag. 2017, 153, 423–434. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, H.; Liang, X. Experimental Performance Evaluation and Parametric Study of a Solar-Ground Source Heat Pump System Operated in Heating Modes. Energy 2018, 149, 173–189. [Google Scholar] [CrossRef]
- Dincer, I. On Thermal Energy Storage Systems and Applications in Buildings. Energy Build. 2002, 34, 377–388. [Google Scholar] [CrossRef]
- Deng, D.; Wan, W.; Qin, Y.; Zhang, J.; Chu, X. Flow Boiling Enhancement of Structured Microchannels with Micro Pin Fins. Int. J. Heat Mass Transf. 2017, 105, 338–349. [Google Scholar] [CrossRef]
- Dhumane, R.; Mallow, A.; Qiao, Y.; Gluesenkamp, K.R.; Graham, S.; Ling, J.; Radermacher, R. Enhancing the Thermosiphon-Driven Discharge of a Latent Heat Thermal Storage System Used in a Personal Cooling Device. Int. J. Refrig. 2018, 88, 599–613. [Google Scholar] [CrossRef]
- Son, K.N.; Weibel, J.A.; Kumaresan, V.; Garimella, S.V. Design of Multifunctional Lattice-Frame Materials for Compact Heat Exchangers. Int. J. Heat Mass Transf. 2017, 115, 619–629. [Google Scholar] [CrossRef]
- Mancin, S.; Diani, A.; Doretti, L.; Hooman, K.; Rossetto, L. Experimental Analysis of Phase Change Phenomenon of Paraffin Waxes Embedded in Copper Foams. Int. J. Therm. Sci. 2015, 90, 79–89. [Google Scholar] [CrossRef]
- Mallow, A.; Abdelaziz, O.; Graham, S. Thermal Charging Performance of Enhanced Phase Change Material Composites for Thermal Battery Design. Int. J. Therm. Sci. 2018, 127, 19–28. [Google Scholar] [CrossRef]
- Taylor, R.; Coulombe, S.; Otanicar, T.; Phelan, P.; Gunawan, A.; Lv, W.; Rosengarten, G.; Prasher, R.; Tyagi, H. Small Particles, Big Impacts: A Review of the Diverse Applications of Nanofluids. J. Appl. Phys. 2013, 113, 011301. [Google Scholar] [CrossRef]
- Lomascolo, M.; Colangelo, G.; Milanese, M.; de Risi, A. Review of Heat Transfer in Nanofluids: Conductive, Convective and Radiative Experimental Results. Renew. Sustain. Energy Rev. 2015, 43, 1182–1198. [Google Scholar] [CrossRef]
- Colangelo, G.; Favale, E.; Milanese, M.; de Risi, A.; Laforgia, D. Cooling of Electronic Devices: Nanofluids Contribution. Appl. Therm. Eng. 2017, 127, 421–435. [Google Scholar] [CrossRef]
- Israelachvili, J.N. (Ed.) Intermolecular and Surface Forces. In Intermolecular and Surface Forces, 3rd ed.; Academic Press: Boston, MA, USA, 2011; p. iii. ISBN 978-0-12-391927-4. [Google Scholar]
- Cardellini, A. Modelling of Multi-Scale Phenomena in Nanoparticle Suspensions. Ph.D. Thesis, Politecnico di Torino, Torino, TO, Italy, 2017. [Google Scholar]
- Liu, C.; Rao, Z.; Zhao, J.; Huo, Y.; Li, Y. Review on Nanoencapsulated Phase Change Materials: Preparation, Characterization and Heat Transfer Enhancement. Nano Energy 2015, 13, 814–826. [Google Scholar] [CrossRef]
- Ercole, D.; Manca, O.; Vafai, K. An Investigation of Thermal Characteristics of Eutectic Molten Salt-Based Nanofluids. Int. Commun. Heat Mass Transf. 2017, 87, 98–104. [Google Scholar] [CrossRef]
- Feng, S.; Shi, M.; Li, Y.; Lu, T.J. Pore-Scale and Volume-Averaged Numerical Simulations of Melting Phase Change Heat Transfer in Finned Metal Foam. Int. J. Heat Mass Transf. 2015, 90, 838–847. [Google Scholar] [CrossRef]
- Stephen, W. Advances in Theory of Fluid Motion in Porous Media. Ind. Eng. Chem. 1969, 61, 14–28. [Google Scholar] [CrossRef]
- Hill, R. Elastic Properties of Reinforced Solids: Some Theoretical Principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Diani, A.; Bodla, K.K.; Rossetto, L.; Garimella, S.V. Numerical Investigation of Pressure Drop and Heat Transfer through Reconstructed Metal Foams and Comparison against Experiments. Int. J. Heat Mass Transf. 2015, 88, 508–515. [Google Scholar] [CrossRef]
- Iasiello, M.; Savarese, C.; Damian, P.J.; Bianco, N.; Andreozzi, A.; Chiu, W.K.S.; Naso, V. Modeling Heat Conduction in Open-Cell Metal Foams by Means of the Three-Dimensional Thermal Fin Theory. J. Phys. Conf. Ser. 2019, 1224, 012009. [Google Scholar] [CrossRef]
- Nelson, G.J.; Nakajo, A.; Cassenti, B.N.; Degostin, M.B.; Bagshaw, K.R.; Peracchio, A.A.; Xiao, G.; Wang, S.; Chen, F.; Chiu, W.K.S. A Rapid Analytical Assessment Tool for Three Dimensional Electrode Microstructural Networks with Geometric Sensitivity. J. Power Sources 2014, 246, 322–334. [Google Scholar] [CrossRef]
- Iasiello, M.; Bianco, N.; Chiu, W.K.S.; Naso, V. Thermal Conduction in Open-Cell Metal Foams: Anisotropy and Representative Volume Element. Int. J. Therm. Sci. 2019, 137, 399–409. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 2014; p. 510. [Google Scholar]
- Mancin, S.; Zilio, C.; Diani, A.; Rossetto, L. Air Forced Convection through Metal Foams: Experimental Results and Modeling. Int. J. Heat Mass Transf. 2013, 62, 112–123. [Google Scholar] [CrossRef]
- Iasiello, M.; Bianco, N.; Chiu, W.K.S.; Naso, V. Anisotropic Convective Heat Transfer in Open-Cell Metal Foams: Assessment and Correlations. Int. J. Heat Mass Transf. 2020, 154, 119682. [Google Scholar] [CrossRef]
- Iasiello, M.; Bianco, N.; Chiu, W.K.S.; Naso, V. Anisotropy Effects on Convective Heat Transfer and Pressure Drop in Kelvin’s Open-Cell Foams. J. Phys. Conf. Ser. 2017, 923, 012035. [Google Scholar] [CrossRef]
- Diani, A.; Rossetto, L. Characteristics of R513A Evaporation Heat Transfer inside Small-Diameter Smooth and Microfin Tubes. Int. J. Heat Mass Transf. 2020, 162, 120402. [Google Scholar] [CrossRef]
- Liu, Y.; Rossetto, L.; Diani, A. Flow Boiling of R450A, R515B, and R1234ze(E) Inside a 7.0 Mm OD Microfin Tube: Experimental Comparison and Analysis of Boiling Mechanisms. Appl. Sci. 2022, 12, 12450. [Google Scholar] [CrossRef]
- Diani, A.; Brunello, P.; Rossetto, L. R513A Condensation Heat Transfer inside Tubes: Microfin Tube vs. Smooth Tube. Int. J. Heat Mass Transf. 2020, 152, 119472. [Google Scholar] [CrossRef]
- Diani, A.; Liu, Y.; Wen, J.; Rossetto, L. Experimental Investigation on the Flow Condensation of R450A, R515B, and R1234ze(E) in a 7.0 Mm OD Micro-Fin Tube. Int. J. Heat Mass Transf. 2022, 196, 123260. [Google Scholar] [CrossRef]
- Ranut, P.; Nobile, E.; Mancini, L. High Resolution Microtomography-Based CFD Simulation of Flow and Heat Transfer in Aluminum Metal Foams. Appl. Therm. Eng. 2014, 69, 230–240. [Google Scholar] [CrossRef]
- Iasiello, M.; Cunsolo, S.; Bianco, N.; Chiu, W.K.S.; Naso, V. Developing Thermal Flow in Open-Cell Foams. Int. J. Therm. Sci. 2017, 111, 129–137. [Google Scholar] [CrossRef]
- Frazier, W.E. Metal Additive Manufacturing: A Review. J. Mater. Eng. Perform. 2014, 23, 1917–1928. [Google Scholar] [CrossRef]
- Ahmed, N.; Barsoum, I.; Abu Al-Rub, R.K. Numerical Investigation on the Effect of Residual Stresses on the Effective Mechanical Properties of 3D-Printed TPMS Lattices. Metals 2022, 12, 1344. [Google Scholar] [CrossRef]
- Novak, N.; Kytyr, D.; Rada, V.; Doktor, T.; Al-Ketan, O.; Rowshan, R.; Vesenjak, M.; Ren, Z. Compression Behaviour of TPMS-Filled Stainless Steel Tubes. Mater. Sci. Eng. A 2022, 852, 143680. [Google Scholar] [CrossRef]
- Duarte, I.; Krstulović-Opara, L.; Vesenjak, M. Characterisation of Aluminium Alloy Tubes Filled with Aluminium Alloy Integral-Skin Foam under Axial Compressive Loads. Compos. Struct. 2015, 121, 154–162. [Google Scholar] [CrossRef]
- Duarte, I.; Vesenjak, M.; Krstulović-Opara, L.; Ren, Z. Static and Dynamic Axial Crush Performance of In-Situ Foam-Filled Tubes. Compos. Struct. 2015, 124, 128–139. [Google Scholar] [CrossRef]
- Duarte, I.; Vesenjak, M.; Krstulović-Opara, L.; Ren, Z. Compressive Performance Evaluation of APM (Advanced Pore Morphology) Foam Filled Tubes. Compos. Struct. 2015, 134, 409–420. [Google Scholar] [CrossRef]
- Pulvirenti, B.; Celli, M.; Barletta, A. Flow and Convection in Metal Foams: A Survey and New CFD Results. Fluids 2020, 5, 155. [Google Scholar] [CrossRef]
- Wu, Z.; Caliot, C.; Flamant, G.; Wang, Z. Numerical simulation of convective heat transfer between air flow and ceramic foams to optimise volumetric solar air receiver performances. Int. J. Heat Mass Transf. 2011, 54, 1527–1537. [Google Scholar] [CrossRef]
- Buonomo, B.; di Pasqua, A.; Manca, O.; Nappo, S.; Nardini, S. Analysis at Cell Scale of Porosity Effect on Forced Convection with Nanofluids in Porous Structures with Kelvin Cells. Int. J. Thermofluids 2022, 16, 100215. [Google Scholar] [CrossRef]
- Buonomo, B.; Pasqua, A.D.; Manca, O.; Sekrani, G.; Poncet, S. Numerical Analysis on Pressure Drop and Heat Transfer in Nanofluids at Pore Length Scale in Open Metal Porous Structures with Kelvin Cells. Heat Transf. Eng. 2021, 42, 1614–1624. [Google Scholar] [CrossRef]
- Buonomo, B.; di Pasqua, A.; Manca, O.; Nappo, S.; Nardini, S. Entropy Generation Analysis of Laminar Forced Convection with Nanofluids at Pore Length Scale in Porous Structures with Kelvin Cells. Int. Commun. Heat Mass Transf. 2022, 132, 105883. [Google Scholar] [CrossRef]
- Sabet, S.; Barisik, M.; Buonomo, B.; Manca, O. Thermal and Hydrodynamic Behavior of Forced Convection Gaseous Slip Flow in a Kelvin Cell Metal Foam. Int. Commun. Heat Mass Transf. 2022, 131, 105838. [Google Scholar] [CrossRef]
- Buonomo, B.; Cinquegrana, D.; Ferraiuolo, M.; Manca, O.; Nardini, S.; Plomitallo, R.E. Numerical Investigation on Thermal and Fluid Dynamic Behaviours in Ice Melting at Pore Scale. Case Stud. Therm. Eng. 2023, 47, 103117. [Google Scholar] [CrossRef]
- Mahjoob, S.; Vafai, K. A Synthesis of Fluid and Thermal Transport Models for Metal Foam Heat Exchangers. Int. J. Heat Mass Transf. 2008, 51, 3701–3711. [Google Scholar] [CrossRef]
- Freitas, R.B.; Brandão, P.V.; Alves, L.S.D.B.; Celli, M.; Barletta, A. The Effect of Local Thermal Non-Equilibrium on the Onset of Thermal Instability for a Metallic Foam. Phys. Fluids 2022, 34, 034105. [Google Scholar] [CrossRef]
- Buonomo, B.; Cascetta, F.; Manca, O.; Sheremet, M. Heat Transfer Analysis of Rectangular Porous Fins in Local Thermal Non-Equilibrium Model. Appl. Therm. Eng. 2021, 195, 117237. [Google Scholar] [CrossRef]
- Diani, A.; Nonino, C.; Rossetto, L. Melting of Phase Change Materials inside Periodic Cellular Structures Fabricated by Additive Manufacturing: Experimental Results and Numerical Simulations. Appl. Therm. Eng. 2022, 215, 118969. [Google Scholar] [CrossRef]
- Diani, A.; Moro, L.; Rossetto, L. Melting of Paraffin Waxes Embedded in a Porous Matrix Made by Additive Manufacturing. Appl. Sci. 2021, 11, 5396. [Google Scholar] [CrossRef]
- Nonino, C.; Diani, A.; Rossetto, L. Numerical Analysis of the Thermal Energy Storage in Cellular Structures Filled with Phase-Change Material. J. Phys. Conf. Ser. 2022, 2385, 012024. [Google Scholar] [CrossRef]
- Sabet, S.; Buonomo, B.; Sheremet, M.A.; Manca, O. Numerical Investigation of Melting Process for Phase Change Material (PCM) Embedded in Metal Foam Structures with Kelvin Cells at Pore Scale Level. Int. J. Heat Mass Transf. 2023, 214, 124440. [Google Scholar] [CrossRef]
- Misale, M.; Bocanegra, J.A.; Marchitto, A. Long-Term Experimental Study on Gravitational Sedimentation of Water Aluminum Oxide Nanofluid at Different Volumetric Concentrations. Int. J. Sediment Res. 2023, 38, 303–315. [Google Scholar] [CrossRef]
- Younes, H.; Mao, M.; Sohel Murshed, S.M.; Lou, D.; Hong, H.; Peterson, G.P. Nanofluids: Key Parameters to Enhance Thermal Conductivity and Its Applications. Appl. Therm. Eng. 2022, 207, 118202. [Google Scholar] [CrossRef]
- Bobbo, S.; Buonomo, B.; Manca, O.; Vigna, S.; Fedele, L. Analysis of the Parameters Required to Properly Define Nanofluids for Heat Transfer Applications. Fluids 2021, 6, 65. [Google Scholar] [CrossRef]
- Cardellini, A.; Fasano, M.; Bozorg Bigdeli, M.; Chiavazzo, E.; Asinari, P. Thermal Transport Phenomena in Nanoparticle Suspensions. J. Phys. Condens. Matter 2016, 28, 483003. [Google Scholar] [CrossRef]
- Cardellini, A.; Alberghini, M.; Govind Rajan, A.; Misra, R.P.; Blankschtein, D.; Asinari, P. Multi-Scale Approach for Modeling Stability, Aggregation, and Network Formation of Nanoparticles Suspended in Aqueous Solutions. Nanoscale 2019, 11, 3925–3932. [Google Scholar] [CrossRef]
- Mancardi, G.; Alberghini, M.; Aguilera-Porta, N.; Calatayud, M.; Asinari, P.; Chiavazzo, E. Multi-Scale Modelling of Aggregation of TiO2 Nanoparticle Suspensions in Water. Nanomaterials 2022, 12, 217. [Google Scholar] [CrossRef]
- De Angelis, P.; Cardellini, A.; Asinari, P. Exploring the Free Energy Landscape to Predict the Surfactant Adsorption Isotherm at the Nanoparticle-Water Interface. ACS Cent. Sci. 2019, 5, 1804–1812. [Google Scholar] [CrossRef] [PubMed]
- Cappabianca, R.; De Angelis, P.; Cardellini, A.; Chiavazzo, E.; Asinari, P. Assembling Biocompatible Polymers on Gold Nanoparticles: Toward a Rational Design of Particle Shape by Molecular Dynamics. ACS Omega 2022, 7, 42292–42303. [Google Scholar] [CrossRef] [PubMed]
- Bianco, N.; Iasiello, M.; Mauro, G.M.; Pagano, L. Multi-Objective Optimization of Finned Metal Foam Heat Sinks: Tradeoff between Heat Transfer and Pressure Drop. Appl. Therm. Eng. 2021, 182, 116058. [Google Scholar] [CrossRef]
- Feng, S.S.; Kuang, J.J.; Wen, T.; Lu, T.J.; Ichimiya, K. An Experimental and Numerical Study of Finned Metal Foam Heat Sinks under Impinging Air Jet Cooling. Int. J. Heat Mass Transf. 2014, 77, 1063–1074. [Google Scholar] [CrossRef]
- Bianco, V.; Buonomo, B.; di Pasqua, A.; Manca, O. Heat Transfer Enhancement of Laminar Impinging Slot Jets by Nanofluids and Metal Foams. Therm. Sci. Eng. Prog. 2021, 22, 100860. [Google Scholar] [CrossRef]
- Hassan, A.M.; Alwan, A.A.; Hamzah, H.K. Metallic Foam with Cross Flow Heat Exchanger: A Review of Parameters, Performance, and Challenges. Heat Transf. 2023, 52, 2618–2650. [Google Scholar] [CrossRef]
- Buonomo, B.; di Pasqua, A.; Manca, O.; Nardini, S. Evaluation of Thermal and Fluid Dynamic Performance Parameters in Aluminum Foam Compact Heat Exchangers. Appl. Therm. Eng. 2020, 176, 115456. [Google Scholar] [CrossRef]
- Buonomo, B.; Cascetta, F.; di Pasqua, A.; Manca, O. Performance Parameters Enhancement of a Thermoelectric Generator by Metal Foam in Exhaust Automotive Lines. Therm. Sci. Eng. Prog. 2023, 38, 101684. [Google Scholar] [CrossRef]
- He, Z.; Yan, Y.; Zhang, Z. Thermal Management and Temperature Uniformity Enhancement of Electronic Devices by Micro Heat Sinks: A Review. Energy 2021, 216, 119223. [Google Scholar] [CrossRef]
- Nonino, C.; Savino, S. Effects of Non-Uniform Flow Distribution in Double-Layered Cross-Flow Microchannel Heat Sinks. In Proceedings of the Second Pacific Rim Thermal Engineering Conference PRTEC2019, Maui, HI, USA, 13–17 December 2019; pp. 24191.1–24191.5. [Google Scholar]
- Nonino, C.; Savino, S.; Giudice, S.D. FEM for the 3-D Analysis of Conjugate Conduction-Convection Heat Transfer in Cross-Flow Micro Heat Exchangers. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 1322–1339. [Google Scholar] [CrossRef]
- Nonino, C.; Savino, S. Numerical Investigation on the Performance of Cross-Flow Micro Heat Exchangers. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 745–766. [Google Scholar] [CrossRef]
- Nonino, C.; Savino, S. Effects of Flow Maldistribution on the Thermal Performance of Cross-Flow Micro Heat Exchangers. J. Phys. Conf. Ser. 2016, 745, 032099. [Google Scholar] [CrossRef]
- Savino, S.; Nonino, C. Header Shape Effect on the Inlet Velocity Distribution in Cross-Flow Double-Layered Microchannel Heat Sinks. Fluids 2022, 7, 7. [Google Scholar] [CrossRef]
- Nonino, C.; Savino, S. Temperature Uniformity in Cross-Flow Double-Layered Microchannel Heat Sinks. Fluids 2020, 5, 143. [Google Scholar] [CrossRef]
- Bigdeli, M.B.; Fasano, M.; Cardellini, A.; Chiavazzo, E.; Asinari, P. A Review on the Heat and Mass Transfer Phenomena in Nanofluid Coolants with Special Focus on Automotive Applications. Renew. Sustain. Energy Rev. 2016, 60, 1615–1633. [Google Scholar] [CrossRef]
- Moradi, A.; Sani, E.; Simonetti, M.; Francini, F.; Chiavazzo, E.; Asinari, P. Carbon-Nanohorn Based Nanofluids for a Direct Absorption Solar Collector for Civil Application. J. Nanosci. Nanotechnol. 2015, 15, 3488–3495. [Google Scholar] [CrossRef]
- Alberghini, M.; Morciano, M.; Bergamasco, L.; Fasano, M.; Lavagna, L.; Humbert, G.; Sani, E.; Pavese, M.; Chiavazzo, E.; Asinari, P. Coffee-Based Colloids for Direct Solar Absorption. Sci. Rep. 2019, 9, 4701. [Google Scholar] [CrossRef]
- Balakin, B.V.; Struchalin, P.G. Corrigendum to “Eco-Friendly and Low-Cost Nanofluid for Direct Absorption Solar Collectors”. Mater. Lett. 2023, 340, 134211. [Google Scholar] [CrossRef]
- Ribezzo, A.; Falciani, G.; Bergamasco, L.; Fasano, M.; Chiavazzo, E. An Overview on the Use of Additives and Preparation Procedure in Phase Change Materials for Thermal Energy Storage with a Focus on Long Term Applications. J. Energy Storage 2022, 53, 105140. [Google Scholar] [CrossRef]
- Aghemo, L.; Lavagna, L.; Chiavazzo, E.; Pavese, M. Comparison of Key Performance Indicators of Sorbent Materials for Thermal Energy Storage with an Economic Focus. Energy Storage Mater. 2023, 55, 130–153. [Google Scholar] [CrossRef]
- Morciano, M.; Alberghini, M.; Fasano, M.; Almiento, M.; Calignano, F.; Manfredi, D.; Asinari, P.; Chiavazzo, E. 3D Printed Lattice Metal Structures for Enhanced Heat Transfer in Latent Heat Storage Systems. J. Energy Storage 2023, 65, 107350. [Google Scholar] [CrossRef]
- Fasano, M.; Ventola, L.; Calignano, F.; Manfredi, D.; Ambrosio, E.P.; Chiavazzo, E.; Asinari, P. Passive Heat Transfer Enhancement by 3D Printed Pitot Tube Based Heat Sink. Int. Commun. Heat Mass Transf. 2016, 74, 36–39. [Google Scholar] [CrossRef]
- Ventola, L.; Robotti, F.; Dialameh, M.; Calignano, F.; Manfredi, D.; Chiavazzo, E.; Asinari, P. Rough Surfaces with Enhanced Heat Transfer for Electronics Cooling by Direct Metal Laser Sintering. Int. J. Heat Mass Transf. 2014, 75, 58–74. [Google Scholar] [CrossRef]
- Chiavazzo, E.; Ventola, L.; Calignano, F.; Manfredi, D.; Asinari, P. A Sensor for Direct Measurement of Small Convective Heat Fluxes: Validation and Application to Micro-Structured Surfaces. Exp. Therm. Fluid Sci. 2014, 55, 42–53. [Google Scholar] [CrossRef]
- Ventola, L.; Scaltrito, L.; Ferrero, S.; Maccioni, G.; Chiavazzo, E.; Asinari, P. Micro-Structured Rough Surfaces by Laser Etching for Heat Transfer Enhancement on Flush Mounted Heat Sinks. J. Phys. Conf. Ser. 2014, 525, 012017. [Google Scholar] [CrossRef]
- Alberghini, M.; Morciano, M.; Giardino, M.; Perrucci, F.; Scaltrito, L.; Janner, D.; Chiavazzo, E.; Fasano, M.; Asinari, P. Textured and Rigid Capillary Materials for Passive Energy-Conversion Devices. Adv. Mater. Interfaces 2022, 9, 2200057. [Google Scholar] [CrossRef]
- Bianco, N.; Busiello, S.; Iasiello, M.; Mauro, G.M. Finned Heat Sinks with Phase Change Materials and Metal Foams: Pareto Optimization to Address Cost and Operation Time. Appl. Therm. Eng. 2021, 197, 117436. [Google Scholar] [CrossRef]
- Mauro, G.M.; Iasiello, M.; Bianco, N.; Chiu, W.K.S.; Naso, V. Mono-and Multi-Objective CFD Optimization of Graded Foam-Filled Channels. Materials 2022, 15, 968. [Google Scholar] [CrossRef]
- Iasiello, M.; Mameli, M.; Filippeschi, S.; Bianco, N. Metal Foam/PCM Melting Evolution Analysis: Orientation and Morphology Effects. Appl. Therm. Eng. 2021, 187, 116572. [Google Scholar] [CrossRef]
- Xu, Z.G.; Zhao, C.Y. Experimental Study on Pool Boiling Heat Transfer in Gradient Metal Foams. Int. J. Heat Mass Transf. 2015, 85, 824–829. [Google Scholar] [CrossRef]
- Webb, R.L.; Eckert, E.R.G. Application of Rough Surfaces to Heat Exchanger Design. Int. J. Heat Mass Transf. 1972, 15, 1647–1658. [Google Scholar] [CrossRef]
- Yilmaz, M.; Comakli, O.; Yapici, S.; Sara, O.N. Performance Evaluation Criteria for Heat Exchangers Based on First Law Analysis. J. Enhanc. Heat Transf. 2005, 12, 121–157. [Google Scholar] [CrossRef]
- Sehrawat, R.; Sahdev, R.K.; Tiwari, S. Heat Storage Material: A Hope in Solar Thermal. Environ. Sci. Pollut. Res. 2022, 30, 11175–11198. [Google Scholar] [CrossRef] [PubMed]
- Buonomo, B.; Manca, O.; Nardini, S.; Plomitallo, R.E. Numerical Study on Latent Heat Thermal Energy Storage System with PCM Partially Filled with Aluminum Foam in Local Thermal Equilibrium. Renew. Energy 2022, 195, 1368–1380. [Google Scholar] [CrossRef]
- Buonomo, B.; Manca, O.; Nardini, S.; Plomitallo, R.E. Numerical Investigation on Shell and Tube Latent Heat Thermal Energy Storage with External Heat Losses Partially Filled with Metal Foam. J. Phys. Conf. Ser. 2022, 2385, 012023. [Google Scholar] [CrossRef]
- Buonomo, B.; Golia, M.R.; Manca, O.; Nardini, S. A Numerical Study on an Integrated Solar Chimney with Latent Heat Thermal Energy Storage in Various Arrangements. Int. J. Sustain. Dev. Plan. 2022, 17, 1693–1698. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).