Abstract
The world is facing many challenges to keep up with growing energy demand and greenhouse gas and pollutant emissions. A possible solution is to integrate renewable energy sources (RESs) into residences and create energy management systems (EMSs) that reduce consumption and relieve the main grid in critical hours. This paper is focused on analyzing different EMSs using solar photovoltaic (PV) modules and three energy storage systems (ESSs) to increase savings without affecting the user’s needs, with thirty-three power consumption profiles and three energy tariffs over a 25-year investment to compare which solution presents the best economic result in each of the 297 analyzed scenarios. The results show that the higher the overall daily consumption values, the greater the profits for all EMSs. The lowest demand profiles lead to the best self-consumption and self-sufficiency results. PV-only systems with a tri-hourly tariff have the best overall results. In the case of battery operation, each case should be carefully analyzed in order to choose the correct technologies and tariff. The results also allowed us to verify that even though having more PV modules generates more energy, it can make a project less economically desirable.
1. Introduction
The world has been struggling to meet shared climate goals since the global energy-related CO2 emissions reached their highest ever level, according to the IEA’s Global Energy Review for 2021 [1]. Shared energy goals, like the ones set in the Paris Agreement, have also been jeopardized because fuel markets were already showing signs of hardship [2,3]. This crisis has resulted from a combination of supply and demand factors that gradually constricted markets over the course of the past years. Lower investment in fossil fuel solutions has made the supply of these energies more vulnerable to the unpredictable situations seen at present. Lower-than-expected levels of supply have pushed up the prices [4]. As a result of this instability, energy prices in 2021–2022 sky-rocketed [5].
As Luthander et al. (Uppsala University) stated in their work, renewable energy sources (RESs) such as solar photovoltaic (PV) or wind power are variable power generation solutions, and their intermittent charging patterns can lead to several problems in the grid such as increasingly higher demand peaks, high voltage, load fluctuations and overgeneration [6].
According to the IEA data on electricity consumption by sector in Europe during 1990–2019, the residential sector has consistently been the second highest electricity consumer, only falling behind the industrial sector [7]. Residences were responsible for 29% of European electricity consumption in 2019, and reports suggest that energy consumption of residential and commercial buildings might increase by over 20% [8]. It is important to note that offices and commercial buildings also play a big role in electricity consumption, hence the need to re-evaluate current energy-saving solutions and improve this sector’s efficiency. This sector was also one of the biggest polluters since, according to Ritchie et al., it is responsible for 17.5% of global greenhouse gas emissions, making it an attractive platform for energy reform [9]. In fact, in the year of 2006, the European Commission issued its “Action Plan for Energy Efficiency”, in which it was estimated that the EU-wide energy-saving potential of households is approximately 27% [10].
According to studies conducted by Shakeri et al. (The National University of Malaysia) and Leitão et al. (University of Coimbra), with the development of a smart grid, households can now be aware of their consumption habits via home energy management systems (HEMSs) [11,12]. Smart buildings use automated processes to control several linked systems: lighting, air conditioning, elevators and even the charging of electric vehicles (EVs). Benefits include energy savings, a positive sustainability impact and even employee-productivity gains (when used in office buildings). These energy management systems (EMSs) are technologies that are reactive to certain conditions and can fully function without any human interaction, although they are increasingly focused on user preference. Olsen et al. and Luo et al. analyzed how HEMSs can shift or cut down the electricity demand in response to electricity prices while maintaining human comfort, thus optimizing electricity consumption at peak hours and relieving the power grid [13,14]. For optimal resource allocation using RESs, energy storage systems (ESSs), EVs and shifting loads, a new concept was created: the microgrid (MG). Microgrids can operate in grid-connected or islanded modes.
Many smart house solutions integrate solar PV electricity generation. This sector had an increase of 45% in the 2019–2021 period, as per the IEA’s 2021 Global Energy Review [15].
The objective of this work was to study and assess the energy management of a household and improve savings without compromising the user’s needs. An evaluation was carried out using different measures on whether the application of either of the three management systems in each consumption case is economically justifiable with any energy tariff and, if so, which combination of them works best.
The use of different electricity tariffs applied to different consumption profiles is not sufficiently explored in the current literature. Moreover, the great potential of Portugal as a location for residential PV projects is not nearly enough explored. To fill these gaps, this work contributes with the creation of two hundred ninety-seven consumption scenarios using three energy tariffs in a 25-year long investment in Portugal.
The structure of this paper is as follows: Section 2 contains a brief overview of the relevant literature on this subject. Section 3 describes the chosen equipment, data collection and treatment and provides information on tariffs, costs and on the instruments used to analyze the results. Section 4 contains the proposed EMSs and the adopted strategies for each one. In Section 5, the main results are gathered and discussed. Section 6 presents an extensive sensitivity analysis of a particular consumption scenario and the conclusions it leads to. Section 6.6 gathers the most important conclusions made based on the studied data.
2. Literature Review
Companies like Smart Home Company, IntelSity, MiMi Smart, IQDim, 1 m-Smart home, Gira, etc., offer smart house solutions based on the end user’s specific needs. Some devices like Google Nest or Amazon Alexa can be bought for under EUR 50, while other, more comprehensive, solutions may set customers back by thousands of euros. The key difference in prices is related to the capabilities of each product. The most affordable ones control lighting with user activation, for example, while more expensive solutions can passively control appliances with a user-defined strategy. To achieve higher levels of customizability and obtain more strategies to save energy, more complex systems are required.
The first approach to address the previously mentioned problems is to rethink and redesign how buildings are placed in a city. As backed by Söeren Schöebel’s (Technical University of Munich) findings, the current electricity distribution design considers home and working environments as isolated and passive individual units, which disregards the potential of homes, offices and commercial buildings to be seen as a collaborative network where buildings are situated and intelligently managed within their external environment as active communities that collaborate with their broader environment [16]. Hence, Hussain et al. analyzed smart houses’ interactions with the possibility to negotiate with customers and suppliers in the grid [17]. This is possible with technological developments such as in-house EMSs that rely on real-time user feedback and tariffs to better control appliances’ utilization and communicate with the grid operators and energy suppliers to ensure real-time flexibility of resource usage. Other works, such as the one developed by Pelekis and authors from the National Technical University of Athens, studied aggregation software that clusters smart buildings for better service usage [18].
To attain minimum electricity costs without jeopardizing human comfort, two methods can be used, as per Liu et al.: predictive energy management and consumption or real-time energy management [19]. The first method was used by Gomes et al. in a community in Portugal and consists of a mixed integer linear programming (MILP) algorithm, which is easier to implement than a nonlinear one, although it sacrifices human comfort conditions the most to reduce electricity bills [20]. Salari et al. implemented real-time energy management algorithms in their work [21].
HEMSs are often considered as multi-objective optimization arrangements, since they have several features intended to solve multiple problems in order to improve energy efficiency including cost minimization, user comfort, etc. Several algorithms can be used to solve these problems, such as the commonly used genetic algorithms developed by Yang et al. or the particle swarm optimization algorithms proposed by Cao et al. (Shanghai University of Electric Power) [22,23]. Other less explored alternatives in the current literature include the cuckoo search algorithm and strawberry algorithm studied by Aslam et al. and the ant colony algorithm analyzed by Güven et al. [24,25].
HEMSs consist of multiple solutions (devices, sensors, actuators) integrated into one management system, as per Tulenkov et al. (National Technical University of Zaporizhzhia). Modern HEMS technologies started to incorporate wireless connectivity as well as different topologies and protocols for SHSs meeting basic requirements: simple installation and usage, high degree of data protection and minimum costs [26].
Some particularly important works were studied in depth so as to obtain a better understanding of HEMSs. They are categorized in Table 1 in terms of the solutions they offer and are analyzed ahead.

Table 1.
Collection of studied works and the solutions analyzed in each of them.
Alfarveh et al. (University of Hertfordshire) proposed a HEMS in which demand is shifted during peak hours, thus decreasing electricity bills since shiftable loads are changed to off-peak hours. This is achieved using pre-established appliance functioning priority orders, thus preserving the users’ needs and preferences. This HEMS was simulated using the MATLAB/Simulink software (Matlab R2022a version) and is rather simple. However, it managed to reduce power consumption by around 30% [27].
Zakeri et al. (International Institute for Applied Systems Analysis) analyzed the impact of different incentive mechanisms on the profitability of solar PV power generation and an ESS for a residential consumer. Yearly savings of 25% to 35% were attained when standalone storage was used and 41% to 74% savings when it was combined with an ESS, compared to a PV-only arrangement. These results, however, were not enough to achieve an economic payback on the investment. Hence, three policies were created for consumers: solar PV power self-consumption bonus, dynamic retail pricing mechanisms and a storage policy where consumers are rewarded for discharging their electricity to the grid in times of need [28].
Shakeri et al. created a HEMS capable of managing the operation of electrical appliances based on the state of charge of an energy storage battery, on the power consumption and on the price of electricity received the day before from the utility company. The utilized software predicted the potential to reduce electricity bills to be up to 20 percent per day, also meaning that there is potential for lower production costs across the energy grid since consumption during peak hours is reduced [11].
Three scenarios were created by Kermanshah University of Technology’s researchers Hemmati and Saboori, in which the smart home buys or sells energy to the grid, or it operates independently, only sending energy to the upstream network. The results of this work point to a reduction of 27.8 percent of the annual electricity bill of the designed home based on three scenarios put into place. This flexibility of operation caused a significant cost reduction. The net-zero energy mode of operation is not only feasible but profitable, an important conclusion on energy and environmental sustainability [29].
Yang et al. and Aslam et al. used bidirectional energy flows via an ESS and an EV to help the HEMS to schedule the operation of shiftable appliances [37,38]. These works, according to Hou et al. (Xihua University), fail to demonstrate the potential of the ESS and EV strategy in a comprehensive HEMS model to reduce costs and battery degradation. Therefore, the authors developed a MILP-based model including a HEMS, RES, ESS, EV and domestic appliances to achieve a solution with the lowest cost using bidirectional energy methods for the ESS and PEV, a real-time pricing mechanism and ESS and PEV strategies. What sets this work apart is that it resulted in higher economic revenue for the user and the prolonged life of batteries without hurting the user’s comfort or travel needs with the EV [30].
A HEMS was developed by Mohammad et al. with PV power generation, an ESS and an EV to minimize costs, peak-to-average ratios and user discomfort by minimizing the difference in operating hours when loads are shifted. Generated power charges the ESS and EV and is used in appliances while leftover power is sold to the grid. The results showed a reduction of around 52% in operating costs and in total costs of over 29% and significant improvements in peak-to-average ratios and in the user satisfaction index [31].
Amer et al. (Qatar University) introduced the distribution transformer condition (loss-of-life, LoL) by preventing its prolonged overloading. Considering PV power generation, an EV, an ESS and shiftable appliances based on the pricing scheme used, the authors concluded that electricity costs are reduced by 31%, demand peak is reduced by 18%, and the transformer’s LoL is reduced by 28% via thermal management [32].
Ouramdane et al. studied an MG with an RES, ESS and EV, in which the EV is used as an additional energy storage device over its available hours. Comparisons between the two cases show that integration of V2H/V2G reduces costs, improves energy self-sufficiency and the continuity of electrical service, while also alleviating the main grid [33].
Abdalla et al. (Hohai University) used a PV system with an EV and a HEMS to improve grid stability in this MG, reduce costs and flatten the load curve. The usage of the EV takes into consideration parameters most authors do not use, like arrival and departure times. The results showed a reduction in daily costs of over 16%, and a flattening of the power load profile is achieved when compared to an MG with an EV and without PV power generation however [34].
Zafar and Slama also used a PV installation combined with an electric vehicle with V2H possibility to create a HEMS. The created software works with a predefined household consumption scenario, thus not allowing the loads to shift. However, these authors innovated in this field by considering the distance travelled by the EV as well as different weather conditions and several subsidies to create optimum purchasing prices for smart homes in different scenarios [35].
In a world where information is kept mostly in digital systems, privacy has become a key concern. Hence, Rong et al. studied a home energy management system with a demand response possibility that not only lowers power cost but is also privacy-aware [36].
A very interesting and different study was conducted by Tuomela et al., who did not simulate the behavior of smart houses, like most of the previous works in this field. Rather, these investigators analyzed real-life changes in the energy consumption profiles of 10 households which adopted a proposed HEMS. Their study also addressed the discrepancy between prioritizing comfort and saving energy. The results showed that even families that valued comfort above energy efficiency gained savings, as savings increased at the cost of small to no degree of a discomfort increase [39].
All the previous work in this field focuses on simulating one or few more households using just one electricity tariff. Consequently, the effects of using different electricity tariffs for different consumption profiles are not explored enough in the current literature. Furthermore, there is limited research about Portugal, which has an annual average sunshine of 2799 h, which, combined with one of the highest annual average solar irradiation values in Europe, makes it a great platform for residential investment in PV power generation [40,41]. These are the reasons why this study uses 33 different power consumption profiles and three different electricity tariffs to simulate as many situations as possible in Portugal (297 in total), making it unlike any other analyzed work and of importance to the energy transition field of knowledge.
To fill the gaps in the current literature, this works contributes with the following methodology: PV power generation data for the past 15 years were collected from the PVGIS software (PVGIS version 5) for the chosen location, and a generic generation year was compiled in the Python software (Python version 3.9.7). With the data from a study conducted in several households, different types of consumption profiles were created. Using three different energy tariffs, a 25-year investment was simulated using three different systems to manage energy with distinct algorithms: (1) a PV system with house-to-grid capability (H2G); (2) a PV system with a battery energy storage system (BESS) without charge/discharge rate limitations and with H2G; (3) a PV system with a BESS and a limit on the charge/discharge rate and with H2G. The results were compared using economic measures (net present value (NPV), internal rate of return (IRR) and payback period) and also the self-consumption and self-sufficiency of the houses. A thorough sensitivity analysis is performed in order to analyze the most important variables in the designed system.
3. Methodology
This is a research article focused on analyzing different renewable energy investment scenarios. This section consists of the details of the created scenarios and the tools that were used to compare them. Primary data were collected on the power generation by PV modules over 25 years, and secondary data were gathered on the consumption profiles of each consumer for that period. With this quantitative data and a developed energy optimization model, simulations were run for all the gathered consumption profiles, from which conclusions were drawn.
3.1. Chosen Location and Equipment
A 500 watt solar panel was chosen to generate power in this MG. It takes up 2.02 m2 and has a degradation rate of 0.5% [42].
For the analytic and economic analysis, a generic house with a rooftop of 100 m2 was considered. The chosen location for this home is in Lisbon, Portugal. The considered rooftop can physically hold 49 panels, but it is common practice to leave about 50% of space cleared out for accessibility purposes during maintenance procedures. Therefore, during this report, the maximum number of used panels was set at 25, associated with a maximum power capacity of 12.5 kWp (the installed capacity will be discussed in Section 3.5.2).
In order to store the potential surplus of generated energy, a 5 kWh lithium-ion battery was chosen [43]. This battery offers a high charge/discharge efficiency of 98% which means every time this device charges or discharges, 98% of the sent energy reaches its destiny.
Each technology has an average lifetime that can be seen in Table 2. This is considered to be a 25-year investment since it is the chosen duration of the PV modules, although some panels may still be usable after 25–26 years with a lower capacity. The degradation rate of the PV modules is responsible for progressively lowering power generation each year. Since the degradation rate of the selected PV module is 0.5%, after 25 years its output has already decreased to 88% of the original value. Batteries and inverters, due to their lower lifetimes, must be replaced twice during the 25 years.

Table 2.
Lifetime of PV modules, inverter and battery.
3.2. PVGIS and Data Treatment
The photovoltaic geographical information system, or PVGIS, provides information about solar radiation and photovoltaic (PV) system performance for several locations across the globe [44]. This software can provide electricity generation options for different PV modules and configurations, solar radiation and temperature as monthly or daily profiles in a full time series of hourly values. For this work, a time series of hourly values from 2005 to 2020 of power generated by a single 0.5 kWp crystalline silicon panel was calculated using the PVGIS-SARAH2 radiation database with the following options: fixed panel, optimized slope and azimuth and a reference 14% system loss factor that accounts for losses in cables, power inverters, as well as losses due to dirt and other factors.
The output given from the PVGIS software (PVGIS version 5) was treated using the Python software (Python version 3.9.7), so as to group the 15 years of data into different years. Subsequently, the values were separated into different seasons. According to the meteorological definition, seasons begin on the first day of the months that include equinoxes and solstices. As Lisbon is located in the Northern Hemisphere: spring runs from 1 March to 31 May, summer runs from 1 June to 31 August, fall (autumn) runs from 1 September to 30 November, and winter runs from 1 December to 28/9 February. Once the data were grouped by seasons, each season’s hourly power generation values (in watts) were averaged to show four average power generation profiles in Figure 1. Since solar irradiance and power generation are directly correlated in PV systems, Figure 1 also indirectly represents the average seasonal incident irradiance rate. These hourly power values were used throughout this work as generic days for each season so that a full year of consumption could be simulated. Therefore, to attain yearly consumption, the winter-type values in Figure 1 were used for 90 days; the spring-type values were used for 92 days; the summer-type values were used for 92 days; and the remaining 91 days consisted of the autumn-type generation values.
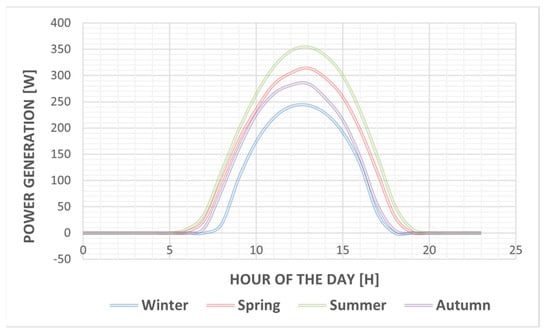
Figure 1.
Power generation (in watts) per PV module for each season’s calculated generic day.
3.3. Power Consumption Load Curves
To simulate several power consumption load curves, we used the consumption data from a study in which power consumption curves for various types of family and home were discretized in hourly values for different days of the week [45]. This study was divided into the following categories: apartments, houses without electrical heating and houses with electrical heating. Each of those was then described using the types of family and the ages associated with each of them, as shown in Table 3. For each of the situations, there were three different types of consumption: weekends, workdays and “all days” which is the merge of the previous two. Each of these consumption scenarios was used (33 total) as a constant load for every day of the 25-year period. All the previously mentioned power consumption curves were studied in this work, and their results are analyzed in Section 5, which is divided as follows: Section 5.1 refers to all the results for the apartments; Section 5.2 contains the results for the houses without electrical heating; and Section 5.3 includes the results for the houses with electrical heating.

Table 3.
Types of families studied in [45], demonstrated schematically.
3.4. Tariffs
In Portugal, EDP Comercial is one of the main electricity suppliers, so this work features EDP energy tariffs [46]. Three different tariffs are offered: tri-hourly, bi-hourly and daily. Using the EDP website, all the previously mentioned tariffs were determined for a contracted power of 6.9 kVA in May 2022 and are shown in Table 4 [47]. Values in the tri-hourly tariff differ between the peak (most expensive), shoulder and off-peak (least expensive) periods. Prices in the bi-hourly tariff vary between the peak and off-peak periods, while the values for the daily option are fixed throughout the day. All of the above-mentioned tariffs have a fixed daily cost as well, and none of these costs includes value-added tax (VAT), which was added in the calculations and is reflected in the results. For low voltage contracts up to a contracted power of 6.9 kVA, a 13% markup was applied for the consumption of up to 100 kWh. Consequently, this was the applied VAT rate throughout the calculations of the energy purchases from the grid.

Table 4.
Pricing of all the tariffs, in euros, per day and per kWh.
According to the Portuguese Decree Law 162/2019 [48] which regulates self-consumption, electricity can be sold at 0.035 EUR/kWh to the Portuguese grid; hence, this value was utilized in this work whenever surplus energy was sold.
The daily and bi-hourly tariffs have a constant format all year round. The bi-hourly tariff has its lowest energy prices (0.1669 EUR/kWh) from 22 h at night to 7 h in the morning. From 7 h to 22 h, peak values of 0.1865 EUR/kWh are paid. The tri-hourly tariff, however, has a summer format and a winter format which differ from each other. The summer format makes consumers pay off-peak values (0.1561 EUR/kWh) from 22 h at night to 8 h in the morning and from 14 h to 19 h. Shoulder values (0.1686 EUR/kWh) are paid from 8 h to 10 h and from 13 h to 14 h. Peak values (0.2724 EUR/kWh) are paid in the remaining hours. In the winter format, off-peak values are paid from 22 h to 8 h. Shoulder values are applied from 8 h to 9 h, from 11 h to 18 h and from 21 h to 22 h. Peak values are used in the remaining hours of the day.
These formats are related to daylight savings, not the seasons. In 2022, daylight savings started at the March 27th, during spring and ended on October 30th, mid-autumn. Consequently, calculations in this work are affected by the summer–winter shift in pricing schedules. Spring is composed of 27 days of winter tariff and the remaining of summer tariff. Autumn has 60 days of summer tariff and the remaining of winter tariff. As such, only the winter and summer seasons have a fixed tariff structure.
3.5. Assessment Tools
This subsection contains all the costs of the investment, as well as the explanation of the tools that were used to analyze and compare the results: NPV, IRR payback time, self-sufficiency (SS) and self-consumption (SC).
3.5.1. Savings
The savings for each situation () were calculated for every year of the investment using Equation (1), which subtracts the cost of the reference situation (), where all energy is bought from the grid, from each management system’s cost (). This way, even if an EMS has a negative profit, but it is less than the cost of buying from the grid, savings are positive.
Every year, the savings are lesser than those in the previous year due to the 0.5% degradation factor of the panels, which decreases energy production on a yearly basis.
3.5.2. Costs
In the first year, all the equipment must be bought: PV modules, the inverter and the battery, depending on the chosen EMS. A lot of indirect costs are related to the purchase and installation of a PV system: permitting, inspection, sales tax, installation labor, etc. All of these costs were modelled by the National Renewable Energy Laboratory in [49] and are displayed in Table 5 and Table 6. As Feldman et al. used a 7000 Wp PV installation, so did the authors of this work [49]. Consequently, 14 of the selected PV modules were used in this work, which is well below the rooftop’s physical limit of 25 modules.

Table 5.
Cost breakdown for EMS1 as per [49].

Table 6.
Cost breakdown for EMS2/3 as per [49].
Every 10 years, the inverter and battery are replaced, as their lifetime cycles are between 10 and 12 years, while the PV modules have lifetimes of 25 or more years (as seen in Table 2).
Yearly operation and maintenance costs were calculated by Feldman et al. and, for residential applications, were set at 25.85 EUR/kWp/year. These include property taxes, inverter and module replacement, cleaning, etc.
Table 5 refers to the costs of EMS1. Since no battery is used, it is less costly than EMS2 and EMS3, which have their costs described in Table 6. The cost benchmark taken from Feldman et al. already includes all the costs of a residential solar PV investment; however, Table 5 and Table 6 display other costs, like the cost of inverters and the battery since these must be replaced by the middle of the investment period. The used maintenance cost was calculated for a variety of equipment in the mentioned reference; consequently, the costs per year may be overestimated, making this work’s conclusions more conservative.
The investment amount for the initial investment period is calculated using Equation (2), depending on the cost of used PV power and BESS.
3.5.3. Net Present Value and Internal Rate of Return
All the net profit values between an EMS and the reference situation in which all energy is bought from the grid () were calculated as per Equation (3). One must first calculate the cash flows: subtract the costs incurred in in year n () from that year’s savings () over the lifetime of the investment. After that, the cash flows can be discounted with the selected discount rate, and the NPV is obtained. Grant Thornton conducted a survey to help to determine the discount rate of renewable energy projects across the world [50]. In Europe, the discount rate for solar projects was calculated to be at under 6%. Hence, the selected discount rate for this project is r = 6%.
When the NPV of an investment becomes positive, an economic payback is reached. The time this takes to happen (if it ever happens within the 25-year time period of the investment) is called the payback period, which will be discussed in Section 5. A simple payback approach was utilized to calculate the payback months. To exemplify, if an investment’s NPV increases from EUR −10,000 in one year to EUR 30,000 in the next year, the payback is considered to be attained in (or 3 months).
The internal rate of return (IRR) was calculated using the method described in Equation (4), as well as the discount rate required for an investment to achieve a net present value of zero. A higher IRR value is a good indicator of profitability of an investment since it is the discount rate that would make the NPV null.
3.5.4. Self-Sufficiency and Self-Consumption
Energy self-sufficiency (SS) is the quality of being able to produce enough energy to meet demands without the grid. Energy self-consumption (SC) measures the amount of energy used that is produced in-house (without the grid).
These values were calculated using Equations (5) and (6) in which “Grid In” represents energy bought from the grid. It is not uncommon for SS values to surpass 100%. The SC cannot be higher than 100% since this would be the situation in which only generated energy is used, and the grid is not required.
4. Energy Management Systems
In order to study the energy flows of the households, it is necessary to predetermine the behavior of energy in each of them. To achieve the said objective, thee different energy management systems were created: the first one with PV power generation, the second with a BESS and the third with a BESS with a charge/discharge rate constraint. Each of the EMSs’ values are calculated in comparison to a reference scenario. All of the aforementioned EMSs are described in this section.
4.1. Reference
In this EMS, no renewable energy solutions are used, instead it consists of buying all demanded energy from the grid. Consequently, it is not an energy management system, but rather it was created to compare other EMSs to it and see if the solutions were viable or not by analyzing the generated savings.
4.2. EMS1
The first energy management system uses 14 PV modules (7000 Wp installation) to generate energy to meet demands and, whenever possible, sell the remainder to the grid. During the night and early morning, when generation is null, this system purchases its energy demand from the grid.
4.3. EMS2
EMS2 involves 14 PV modules (7000 Wp installation) and a battery to store energy. All of the following conditions govern EMS2 and are disposed in Equation (7): the battery’s state of charge at any hour ”h” () is limited between = 20% and = 80%; if demand () exceeds generation (), and the battery is not yet at , it will be discharged until it reaches its minimum value, only then will it require grid energy to be purchased; if generation exceeds demand, and the battery is not yet at , it will charge until it reaches the maximum value, and only then will it sell the surplus to the grid. Every day, at 22 h, the system evaluates the battery’s SOC. If SOC is not at , at 23 h, the system buys energy from the grid so as to guarantee that the following day has a = . All battery charges/discharges are subject to the 98% charge/discharge efficiency (CDE).
4.4. EMS3
EMS3 differs from the previous management system in the battery’s charge/discharge rate (| − |) since it is limited to 1 kW per hour. Even though the charge and discharge values are limited to 1 kW per hour, the system buys whatever energy is necessary from the grid at 23 h just like in EMS2 because energy prices do not vary during the night and this is, consequently, a mere simplification to this work. All the equations used for EMS2 in Equation (7) are applicable for EMS3 as well, with the addition of the charge/discharge rate constraint, as seen in Equation (8).
5. Results
5.1. Apartments
The NPV results for the apartments’ consumption patterns are gathered in the histogram in Figure 2. Each tariff was analyzed using the consumption scenarios listed in Table 3, which are divided into three different types of consumption (weekends, workdays and “all days”). Moreover, for each of the latter, three EMSs are used generating 45 different load profiles and thus 45 different NPV results for each tariff. Figure 2 is a visual representation of how the NPV results are distributed for each tariff.
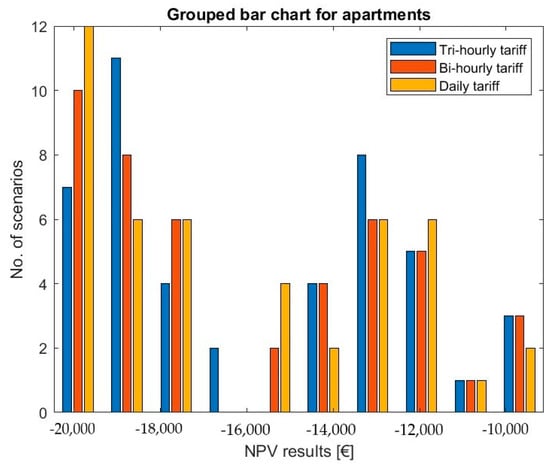
Figure 2.
Histogram of the NPV results achieved for apartments—all types of consumption profiles.
Note: It is important to mention that PV-only systems always perform better than EMS2/EMS3 in terms of the NPV and IRR parameters. The battery-operated systems always perform better than EMS1 in terms of SS and SC.
5.1.1. NPV
The apartment households never achieve a positive NPV. Couples without children aged 26 to 64 years have higher NPVs than those for aged 64 and older. Families aged 26 to 64 years, with the highest consumption profile for the apartments, have the highest NPVs in this sample group however; the highest net present value is EUR–9117.
For all situations, using a PV-only system is beneficial, as EMS1 has NPVs 30+% higher compared to the battery-operated systems.
When using EMS1, the tri- and bi-hourly tariffs are almost equal to one another, and they always perform better than the daily tariff. EMS2 and EMS3 have identical results, and their tariffs have a clear ranking: tri-hourly works best, followed by the bi-hourly tariff and only then the daily tariff.
5.1.2. IRR
No value of internal rate of return was positive, which reinforces the poor results obtained by these housing consumption profiles.
5.1.3. Payback Period
No positive NPVs are achieved; hence, no economic payback occurs in either situation.
5.1.4. Self-Sufficiency
The highest demand scenario (family aged 26–64 years) achieves the lowest SS values of around 200% and the lowest demand scenario (single person aged 64 years or older) reaches values of SS of almost 700%. This means that the PV system generates two and seven times more electricity than the house requires in that consumption scenario, respectively.
5.1.5. Self-Consumption
SC reaches the highest values in the lower demand scenarios, of over 90%, since the PV system generation covers for almost all of the house’s energy needs and surplus energy is sold to the grid during most of the day. In the majority of these low demand scenarios, the only time energy is bought from the grid is at night to ensure the battery is at SOCmin in the morning since this is a nonoptimized algorithm. For some scenarios, realistically, self-consumption could reach 100% since the battery could withstand the night and morning demand and recharge during the day, with the PV system meaning the house could be disconnected from the grid (or connected unilaterally, as an energy producer).
5.2. Houses without Electrical Heating
The results for the consumption patterns of the houses without electrical heating are shown in Figure 3. Each tariff was analyzed using the consumption scenarios in Table 3, which are all divided into three different types of consumption (weekends, workdays and “all days”). Moreover, for each of the latter, three EMSs are used generating 27 different load profiles and thus 27 different NPV results for each tariff. Figure 2 is a visual representation of how the NPV results are distributed for each tariff.
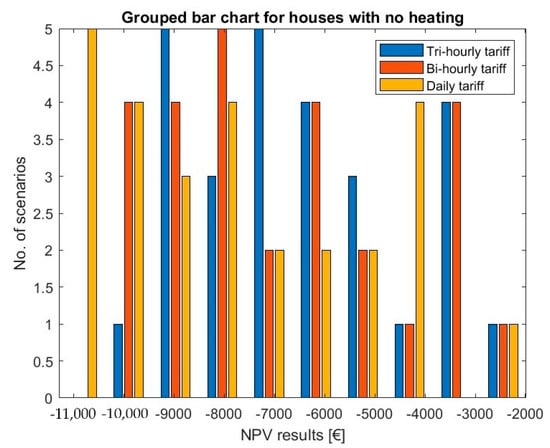
Figure 3.
Histogram of the NPV results achieved for houses without electrical heating—all types of consumption profiles.
Note: It is important to mention that the PV-only systems always perform better than EMS2/EMS3 in terms of the NPV and IRR parameters. The battery-operated systems always perform better than EMS1 in terms of SS and SC.
5.2.1. NPV
All NPVs are negative in this housing situation, although they achieve closer-to-zero values than in Section 5.1.
The best overall values are related to 26–64-year-old couples without children using EMS1 and the tri-hourly tariff (NPV = EUR −1975. This is a particular consumption scenario in which the consumption of EMS1 is 2.7 times higher than that of EMS2 and 3.1 times higher than that of EMS3.
EMS1 is the best management system in all consumption profiles by 30% to 50+%. EMS3 has the lowest NPVs of the studied management systems for the grand majority of the scenarios.
The tri-hourly tariff results in the highest NPVs, and the daily tariff in the worst NPVs.
5.2.2. IRR
All obtained IRR values for this Section are lower than 4.5%. With the selected discount rate of 6%, investments for these housing types is not economically attractive.
5.2.3. Payback Period
In line with Section 5.1 above, no positive NPVs are achieved; thus, no economic payback occurs.
5.2.4. Self-Sufficiency
The SS values are more moderate than those in Section 5.1, since none of them surpasses 100%; hence, no household can theoretically sustain its energy needs. In fact, the highest SS value is reached with the lowest consumption profile, in houses inhabited by couples without children aged 64 years or older with “weekend” consumption and the SS values as high as 93%. Interestingly, the same household in an “all days” scenario achieves the lowest value of self-sufficiency at 38%.
Unlike in some of the apartments, as explained in Section 5.1, these households cannot be disconnected from the main grid, since their energy demand during the night and morning is higher than what the capacity of the chosen battery can sustain without PV power generation. Power generation is still high enough so as to still sell surplus energy to the grid during the day.
5.2.5. Self-Consumption
Most of the achieved SC values range from 40% to 60%, a result lower than the one achieved for the apartments in Section 5.1 which account for the SC values close to 90% due to their lower energy demand.
5.3. Houses with Electrical Heating
The results for the consumption patterns of the houses with electrical heating are shown in Figure 4. Each tariff was analyzed using the consumption scenarios in Table 3, which are all divided into three different types of consumption (weekends, workdays and “all days”). Moreover, for each of the latter, three EMSs are used generating 27 different load profiles and thus 27 different NPV results for each tariff. Figure 2 is a visual representation of how the NPV results are distributed for each tariff.
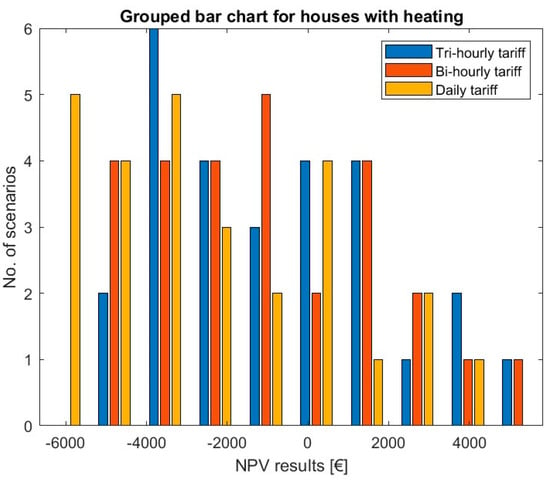
Figure 4.
Histogram of the NPV results achieved for houses with electrical heating—all types of consumption profiles.
Note: It is important to mention that the PV-only systems always perform better than EMS2/EMS3 in terms of the NPV and IRR parameters. The battery-operated systems always perform better than EMS1 in in terms of SS and SC.
5.3.1. NPV
This is the only housing scenario in which positive NPVs are attained.
The PV-only system has a clear dominance in NPV calculations, being up to four times higher than EMS2-related NPVs and more than four times higher than EMS3-related NPVs which present the lowest values for most situations.
For EMS1 and EMS2, there is a clear ranking in the utilized tariffs: tri-hourly is the best one and the daily tariff is the worst tariff to use. For EMS3, however, the bi-hourly tariff performs the best of the three when consumption increases (for 26–64-year-old couples without children and especially for 26–64-year-old families—the highest consumption profile).
It is important to note that EMS2 and EMS3 only achieve a positive NPV in the highest consumption profile of this work (26–64-year-old families). Using the tri-hourly tariff, EMS2 achieves a fairly high NPV of EUR 1584, while EMS3 barely breaks even with an NPV of EUR 72. Using the bi-hourly tariff, EMS2 and EMS3 have closer values ( = EUR 1280 and = EUR 1355). The daily tariff narrowly avoids economic failure with and has a negative (and low) value of NPV for EMS3.
The highest NPVs (of the whole work) are achieved for a family aged 26 to 64 years with a “weekend” type of consumption, specifically using the tri-hourly tariff. This scenario is, in fact, characterized by the highest power consumption based on the utilized data. The lowest values of NPV relate to a couple without children aged 64 years or older with “workday” consumption (the lowest power consumption of the houses with electrical heating) using the daily tariff.
More conclusions on the relation between the consumption and the value of the investment will be drawn in Section 6.6.
5.3.2. IRR
The IRR values for this housing scenario range from 2.4% to 10.1%, and 33% of the IRR values are equal to or greater than the selected 6% discount rate. The tariff that generally presents the best IRR values is the tri-hourly, followed by the bi-hourly.
Once again, for all situations, EMS1 is the most advantageous when looking at the internal rate of return, although considerations between EMS2 and EMS3 must be made when choosing an EMS and a tariff, since these present some rank reversals when using the bi-hourly tariff. For the other tariffs, nevertheless, EMS1 is always ranked first, EMS2 second and EMS3 third.
5.3.3. Payback Period
For all situations, there is a clear ranking of preferable tariffs: the tri-hourly is always the best one, the bi-hourly is the second best, and the daily tariff is the worst tariff for all studied scenarios. There is, however, a single situation in which it is preferable to use EMS3 with the bi-hourly tariff rather than the tri-hourly one.
The lowest payback period values are obtained from the highest demand scenario and are about 14 years and 1 month (54% into the investment). The worst (yet achieved) payback periods come in just under the 25-year limit which is related to lower consumption profiles.
Most scenarios, however, still do not achieve an economic payback after 25 years and most battery-operated systems are far from the break-even point.
5.3.4. Self-Sufficiency
Demand values in this section are high enough so as not to have any SS over 31% and to have several negative self-sufficiency values, meaning that those households do not generate enough power to provide for their energy needs (they buy more energy from the grid than they produce with their PV system).
The highest value of self-sufficiency is 31%, which is achieved for the lowest consumption profile; however, the lowest value of SS (achieved with the highest consumption) is −10%, which is very low. This happens since this last household must rely on the grid for 17.5% more energy than it generates when using EMS1.
Adding battery operation helps to improve the SS value by 6%.
5.3.5. Self-Consumption
As for the SC values, SC is at its lowest value in this section due to the higher demands in these housing scenarios.
The best SC values (for the lowest consumption scenario) are 32%, a notable decrease from the results achieved in Section 5.2 (houses without electrical heating) where the worst value of SC was 35% and an even greater one when comparing to the results of Section 5.1 (apartments) in which the worst value was 76%. As explained in the SS values, once again, there are negative SC values (as low as −24% for the higher consumption profiles) since, according to Equations (5) and (6) if a household buys more energy than it produces, its SS and SC values will both fall below zero.
6. Sensitivity Analysis
A sensitivity analysis with a deviation of ±20% was performed to obtain a better comprehension of how certain variables affect the results. This high deviation value was chosen to emphasize the variation in the obtained results, or the lack thereof. The selected case for this study was a house with electrical heating inhabited by a family aged 26–64 years with a “weekend” type of consumption, whose power consumption curve is shown in Figure 5. This scenario was chosen since, as show the results in Table 7, there are positive and negative NPVs, and some of these values are close to zero; hence, after changing the variable under study, negative NPVs may reach the break-even point, and positive NPVs may become unreliable. Table 7 consequently represents the reference scenario for Section 6.
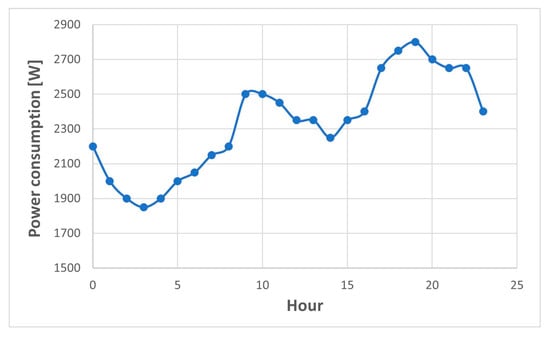
Figure 5.
Structure of the hourly load curve for houses with electrical heating and families aged 26–64 years with weekend consumption.

All variables except the one under study were kept as described in Section 3.
6.1. Energy Price Fluctuation
As per Figure 6, a drop in energy prices of 20% negatively impacts this investment to a great extent, making battery-operated management systems not viable by far and EMS1 barely breaking even with the tri-hourly and bi-hourly tariffs and not feasible at all for the daily tariff.
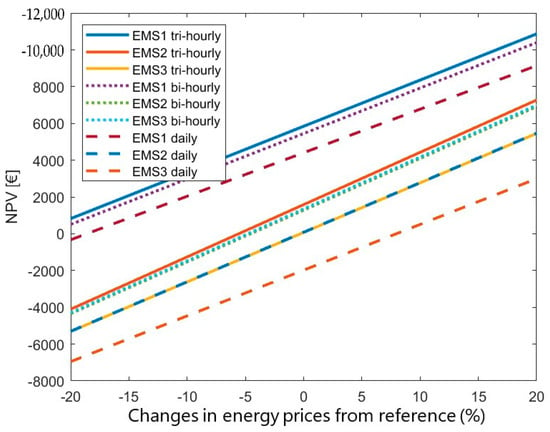
Figure 6.
NPV sensitivity to energy price changes.
If there is an increase of 20% in energy prices, this investment is advisable for all tariffs and all management systems. Notable increases occur in the NPV and IRR which achieve their best values for EMS1 with the tri-hourly tariff, the solution that an investor should select when also looking for the quickest payback period.
6.2. Number of PV Modules
If the number of PV modules increases to 17, all economic comparison measures are worsened (only EMS1 achieves a payback) and the opposite occurs if the number of PV modules decreases from the initial value of 14 to 11, making the investment economically better, since almost all EMS achieve a payback.
There are significant variations in NPV, as can be seen in Figure 7, which is also true for the IRR, payback period and self-sufficiency; since generation values are affected directly. Using less PV modules, the self-sufficiency is lower than the reference one in Table 7. When the number of PV modules increases to 17, they provide slightly more energy than demanded by the household. Nevertheless, the extra generation does not make up for the investment in extra modules even though surplus energy is sold to the grid.
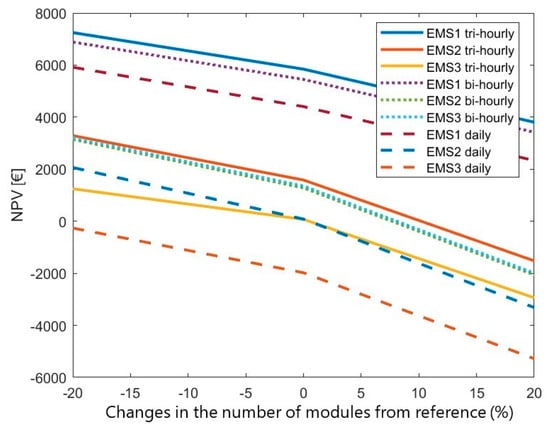
Figure 7.
NPV sensitivity to changes in the number of modules.
So that more conclusions can be drawn, the behavior of this investment was also studied for a variable number of PV modules (5, 10, 15, 20) and the rooftop’s maximum of 25. The analytical results show that, for all tariffs, utilizing more than 10 PV modules was not beneficial for this investment (this specific type of consumption). The maximum NPV is reached when using 10 modules, which means that in the reference situation as described in Section 3 and visualized in Table 7, using 14 panels is not the optimal allocation of resources. The best overall tariff to be chosen is the tri-hourly since it achieves the highest NPVs.
When using 10 panels and the bi-hourly tariff, the results are similar to those of the tri-hourly tariff when using EMS1 and EMS2. Nonetheless, far better results are obtained when using EMS3 with the bi-hourly tariff.
6.3. Battery (kWh)
EM1 is not affected by battery operation, so it will not be analyzed.
As seen in Figure 8 decreasing the battery’s capacity by −20% almost halves the NPVs and adds almost a year to the payback period. EMS2 becomes unreliable with the daily tariff, and EMS3 only achieves a payback with the bi-hourly tariff. If, however, the battery’s capacity were to be increased by +20%, NPVs would increase by over 20% and payback periods would decrease up to over a year.
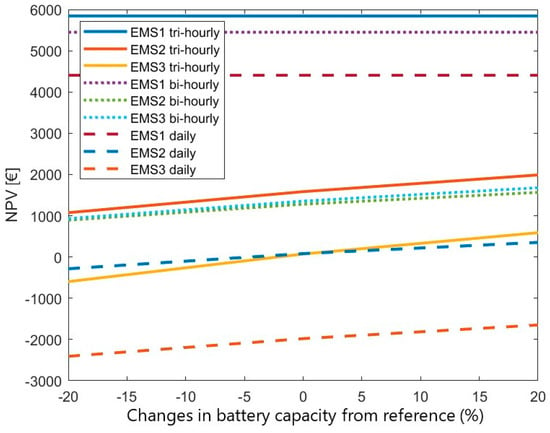
Figure 8.
NPV sensitivity to changes in battery capacity.
The SS and SC values almost remain constant, with slight increases when the battery’s capacity also increases, and vice versa.
6.4. and
EM1 is not affected by battery operation, so it will not be analyzed.
The achieved results for a variation of ±20% in the and are almost equal to the ones in Section 6.3. Hence, the drawn conclusions on the previous section remain true in this one.
Although a 20% increase in and provides better results, using higher values of the depth of discharge is correlated with a lower life cycle in lithium-ion batteries. Hence, this solution would imply the replacement of the batteries earlier than expected.
6.5. Power Generation
If the generated power were to decrease by 20%, no battery-operated management system would prove to be sufficiently robust to be profitable. EMS1, nevertheless, still achieves payback periods shorter than 19 years and some hefty NPVs. As Figure 9 shows, the exact opposite occurs for 20% higher power generation: all tariffs and all EMSs are profitable and worthy of investment as they achieve positive NPVs and payback periods as low as 12 years and 6 months.
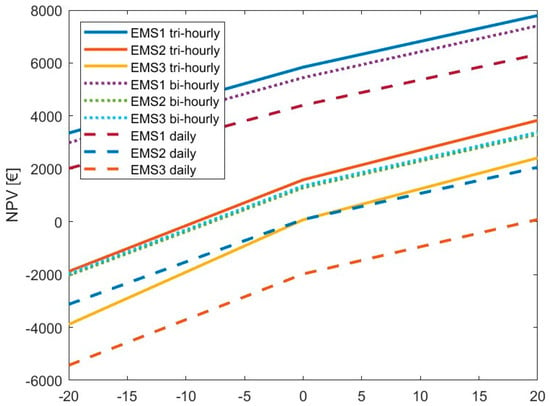
Figure 9.
NPV sensitivity to changes in power generation by PV modules.
As the equations that calculate the SS and SC values (Equations (5) and (6)) directly involve energy generation, these measures are both expected to change and, in fact, they do. The SS value drops a little when power generation decreases by 20% and increases by 20% if power generation also has an increase of 20%. Self-consumption, on the other hand, is very much affected by power generation, as it rises 13% with the referred power generation increase, but it crashes down by more than 40% when power generation falls by 20%.
6.6. Power Consumption
If power consumption values were to decrease, the investment shown in Figure 10 would become unreliable for the battery-operated management systems while still profitable for EMS1. Figure 10 also shows that for a variation of +20% in power consumption, this investment gains significant value, since almost all EMSs prove to have good NPVs, higher IRRs and the payback periods as low as 11 years and 10 months.
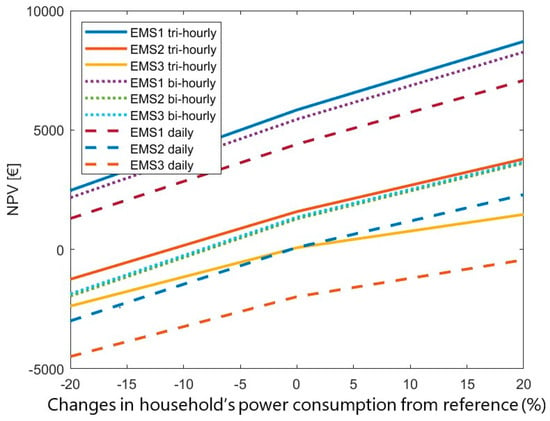
Figure 10.
NPV sensitivity to changes household’s power consumption.
The self-consumption values increase by almost 20% when power consumption decreases, but the SC values decrease to as low as −49% for a 20% increase in consumption, meaning that a lot more energy must be bought from the grid. The SS values do not change much when increasing the power consumption, although they do increase by 25+% if power consumption decreases, since demand suffers a big drop.
Figure 10 shows the existent dynamics between the power consumption and the NPVs of the investment. Values of power consumption from 50% to 250% were used to show that for higher values of power consumption, so does the net present value of the project grow. EMS1 and EMS2 seem to achieve an upper NPV limit after the 200% mark in power consumption. EMS2 reaches a maximum at 150% then drops when using the tri-hourly and daily tariffs; however, this management system pairs so well with the bi-hourly tariff that it does not drop after the 150% consumption mark using this tariff.
7. Conclusions
In this work, a comparison of the created value for three EMSs of 33 different consumption profiles was carried out using three different energy tariffs, creating a total of 297 scenarios. Conclusions were drawn on the profitability of these investments using NPV, IRR, payback time, self-consumption and self-sufficiency parameters. A thorough sensitivity analysis was carried out on the most important variables of this work. The results indicate that higher consumption profiles benefit the most from this type of investment; nevertheless, these are the ones that have the lowest self-consumption and self-sufficiency values. The tri-hourly tariff was the most profitable for most scenarios. The option of battery operation should be carefully analyzed for each scenario, since with the correct combination of the tariff and number of modules some consumers achieve profitable and energy-efficient battery-operated investments. The correct number of modules must be determined beforehand to maximize profitability. Therefore, investing in renewable energy solutions and smart energy systems is economically viable for certain scenarios. A careful analysis of the household’s load, the installed capacity of a PV module and BESS, the type of tariff and other factors should be conducted to determine the monetary viability of the investment.
The highest NPVs were achieved for the houses with electrical heating because of their highest consumption (the highest overall value of = EUR 5843 for a family’s weekend consumption using the tri-hourly tariff), and the lowest NPVs were attained for the apartments (the lowest overall value of = −EUR 20,471 for weekend consumption of a single person aged 64 years or older using the daily tariff). The conducted sensitivity analysis also pointed in the same direction, as it shows that higher consumption profiles lead to higher NPVs ( = EUR 8710).
For all studied scenarios, the PV-only operation was the best option, especially when using the tri-hourly tariff. The daily tariff proved to be the worst overall tariff. The inclusion of three different tariffs proved to be important if an investor is keen on using battery energy storage (whose systems were always responsible for the best results in terms of self-sufficiency and self-consumption). By reducing the number of PV panels to 10, for example, the house studied in the sensitivity analysis can double its NPVs for the tri- and bi-hourly tariffs, not for the daily tariff. Hence, a close look at each tariff and every other characteristic of the investment should be considered beforehand.
For the apartments, no positive NPVs are ever achieved, which makes these investments an economically unacceptable decision. Consumption patterns are too low, and the required investment is still too high. These households have the best self-sufficiency and self-consumption values: a house inhabited by a single person aged 64 years or older with weekend consumption can consume only 6% of grid electricity and produces seven times its total energy consumption. For the houses without electrical heating, the results are better than the ones achieved for the apartments, although investing in a RES of any sort is strongly unadvised. For the houses with electrical heating, the chosen system should always be PV-only. When demand increases within these housing situations, a BESS may become profitable. Such households have the lowest self-sufficiency and self-consumption values.
The sensitivity analysis allowed us to conclude that the optimum number of PV modules can be found at which the NPV is optimized. Having more PV modules can improve self-sufficiency and self-consumption. Another important factor was discovered to be higher energy prices which, if continue to increase, make investing in RESs and ESSs more attractive.
This work did not include any optimization techniques for the modelled EMSs, which used fixed mechanisms and do not reflect the potential of dynamic pricing mechanisms, for example. Future work could include a model of a HEMS able to forecast energy consumption and power generation and manage the energy flows of a smart house with PV power generation, an ESS and an EV using software that can maximize savings while maintaining the energetic needs of the household.
The macroeconomic and political scenario in which a renewable energy investment takes place can deeply affect the possibility for a country’s average citizen to invest. Thus, future work can include a comparative analysis of different countries based not only on the acquisition cost of RESs but also on the average salary of each country.
Author Contributions
Conceptualization, N.R., R.C. and C.S.S.; methodology, N.R., R.C. and C.S.S.; software, N.R.; validation, N.R., R.C. and C.S.S.; formal analysis, N.R., R.C. and C.S.S.; investigation, N.R.; resources, R.C. and C.S.S.; data curation, N.R.; writing—original draft preparation, N.R.; writing—review and editing, R.C. and C.S.S.; visualization, R.C. and C.S.S.; supervision, R.C. and C.S.S.; project administration, R.C. and C.S.S.; funding acquisition, R.C. and C.S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by national funds through FCT, Fundação para a Ciência e a Tecnologia, under project UIDB/50021/2020 and LA/P/0083/2020 (LA LARSyS – IN+).
Data Availability Statement
Data are unavailable due to privacy restrictions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- IEA. Global Energy Review: CO2 Emissions in 2021—Analysis. 2022. Available online: https://www.iea.org/reports/global-energy-review-co2-emissions-in-2021-2 (accessed on 18 May 2022).
- IEA. Statement on Recent Developments in Natural Gas and Electricity Markets—News. 2021. Available online: https://www.iea.org/news/statement-on-recent-developments-in-natural-gas-and-electricity-markets (accessed on 18 May 2022).
- Birol, D.F.; IEA. What Does the Current Global Energy Crisis Mean for Energy Investment?—Analysis. 2022. Available online: https://www.iea.org/commentaries/what-does-the-current-global-energy-crisis-mean-for-energy-investment (accessed on 18 May 2022).
- Alvarez, C.F.; Molnar, G.; IEA. What is Behind Soaring Energy Prices and What Happens Next?—Analysis. 2021. Available online: https://www.iea.org/commentaries/what-is-behind-soaring-energy-prices-and-what-happens-next (accessed on 18 May 2022).
- Birol, D.F.; IEA. Europe and the World Need to Draw the Right Lessons from Today’s Natural Gas Crisis—Analysis. 2022. Available online: https://www.iea.org/commentaries/europe-and-the-world-need-to-draw-the-right-lessons-from-today-s-natural-gas-crisis (accessed on 18 May 2022).
- Luthander, R.; Shepero, M.; Munkhammar, J.; Widen, J. Photovoltaics and opportunistic electric vehicle charging in the power system—A case study on a swedish distribution grid. IET Renew. Power Gener. 2019, 13, 710–716. [Google Scholar] [CrossRef]
- IEA. Europe—Countries Regions—IEA. 2022. Available online: https://www.iea.org/regions/europe (accessed on 18 May 2022).
- Yahia, Z.; Pradhan, A. Optimal load scheduling of household appliances considering consumer preferences: An experimental analysis. Energy 2018, 163, 15–26. [Google Scholar] [CrossRef]
- Ritchie, H.; Roser, M.; Rosado, P. CO2 and Greenhouse Gas Emissions. 2020. Available online: https://ourworldindata.org/co2-and-other-greenhouse-gas-emissions (accessed on 24 June 2022).
- European Parliament and Council. European End-Use Energy Efficiency and Energy Services Directive; Directive nr. 2006/32/EC; European Parliament and Council: Brussels Belgium, 2006. [Google Scholar]
- Shakeri, M.; Shayestegan, M.; Abunima, H.; Reza, S.S.; Akhtaruzzaman, M.; Alamoud, A.R.M.; Sopian, K.; Amin, N. An intelligent system architecture in home energy management systems (hems) for efficient demand response in smart grid. Energy Build. 2017, 138, 154–164. [Google Scholar] [CrossRef]
- Leitao, J.; Gil, P.; Ribeiro, B.; Cardoso, A. A survey on home energy management. IEEE Access 2020, 8, 5699–5722. [Google Scholar] [CrossRef]
- Olsen, D.J.; Sarker, M.R.; Ortega-Vazquez, M.A. Optimal penetration of home energy management systems in distribution networks considering transformer aging. IEEE Trans. Smart Grid 2018, 9, 3330–3340. [Google Scholar] [CrossRef]
- Luo, F.; Ranzi, G.; Kong, W.; Dong, Z.Y.; Wang, F. Coordinated residential energy resource scheduling with vehicle-to-home and high photovoltaic penetrations. IET Renew. Power Gener. 2018, 12, 625–632. [Google Scholar] [CrossRef]
- IEA. Electricity—Global Energy Review 2021—Analysis. Available online: https://www.iea.org/reports/global-energy-review-2021/electricity (accessed on 20 June 2022).
- Schöebel, S. Space, Place, and Energy: Perspectives on the Energetic Design of Cities and Regions. In Urban Energy Transition; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar] [CrossRef]
- Hussain, S.; Lai, C.; Eicker, U. Flexibility: Literature review on concepts, modeling, and provision method in smart grid. Sustain. Energy Grids Netw. 2023, 35, 101113. [Google Scholar] [CrossRef]
- Pelekis, S.; Pipergias, A.; Karakolis, E.; Mouzakitis, S.; Santori, F.; Ghoreishi, M.; Askounis, D. Targeted demand response for flexible energy communities using clustering techniques. Sustain. Energy Grids Netw. 2023, 36, 101134. [Google Scholar] [CrossRef]
- Liu, Y.; Qiu, B.; Fan, X.; Zhu, H.; Han, B. Review of smart home energy management systems. Energy Procedia 2016, 104, 504–508. [Google Scholar] [CrossRef]
- Gomes, I.L.R.; Ruano, M.G.; Ruano, A.E. MILP-based model predictive control for home energy management systems: A real case study in Algarve, Portugal. Energy Build. 2023, 281, 112774. [Google Scholar] [CrossRef]
- Salari, A.; Ahmadi, S.E.; Marzband, M.; Zeinali, M. Fuzzy Q-learning-based approach for real-time energy management of home microgrids using cooperative multi-agent system. Sustain. Cities Soc. 2023, 95, 104528. [Google Scholar] [CrossRef]
- Yang, J.; Liu, J.; Fang, Z.; Liu, W. Electricity scheduling strategy for home energy management system with renewable energy and battery storage: A case study. IET Renew. Power Gener. 2018, 12, 639–648. [Google Scholar] [CrossRef]
- Cao, Y.; Liu, G.; Sun, J.; Bavirisetti, D.P.; Xiao, G. PSO-Stacking improved ensemble model for campus building energy consumption forecasting based on priority feature selection. J. Build. Eng. 2023, 72, 106589. [Google Scholar] [CrossRef]
- Aslam, S.; Javaid, N.; Khan, F.A.; Alamri, A.; Almogren, A.; Abdul, W. Towards efficient energy management and power trading in a residential area via integrating a grid-connected microgrid. Sustainability 2018, 10, 1245. [Google Scholar] [CrossRef]
- Güven, A.F.; Yörükeren, N.; Samy, M.M. Design optimization of a stand-alone green energy system of university campus based on Jaya-Harmony Search and Ant Colony Optimization algorithms approaches. Energy 2022, 253, 124089. [Google Scholar] [CrossRef]
- Tulenkov, A.; Parkhomenko, A.; Sokolyanskii, A.; Stepanenko, A.; Zalyubovskiy, Y. The features of wireless technologies application for smart house systems. In Proceedings of the 2018 IEEE 4th International Symposium on Wireless Systems within the International Conferences on Intelligent Data Acquisition and Advanced Computing Systems (IDAACS-SWS), Lviv, Ukraine, 20–21 September 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Alfaverh, F.; Denai, M.; Alfaverh, K. Demand-response based energy advisor for household energy management. In Proceedings of the 2019 Third World Conference on Smart Trends in Systems Security and Sustainablity (WorldS4), London, UK, 30–31 July 2019. [Google Scholar] [CrossRef]
- Zakeri, B.; Cross, S.; Dodds, P.E.; Gissey, G.C. Policy options for enhancing economic profitability of residential solar photovoltaic with battery energy storage. Appl. Energy 2021, 290, 116697. [Google Scholar] [CrossRef]
- Hemmati, R.; Saboori, H. Stochastic optimal battery storage sizing and scheduling in home energy management systems equipped with solar photovoltaic panels. Energy Build. 2017, 152, 290–300. [Google Scholar] [CrossRef]
- Hou, X.; Wang, J.; Huang, T.; Wang, T.; Wang, P. Smart home energy management optimization method considering energy storage and electric vehicle. IEEE Access 7 2019, 7, 144010–144020. [Google Scholar] [CrossRef]
- Mohammad, A.; Zuhaib, M.; Ashraf, I.; Alsultan, M.; Ahmad, S.; Sarwar, A.; Abdollahian, M. Integration of electric vehicles and energy storage system in home energy management system with home to grid capability. Energies 2021, 14, 8557. [Google Scholar] [CrossRef]
- Amer, A.; Shaban, K.; Gaouda, A.; Massoud, A. Home energy management system embedded with a multi-objective demand response optimization model to benefit customers and operators. Energies 2021, 14, 257. [Google Scholar] [CrossRef]
- Ouramdane, O.; Elbouchikhi, E.; Amirat, Y.; Gall, F.; Sedgh Gooya, E. Home energy management considering renewable resources, energy storage, and an electric vehicle as a backup. Energies 2022, 15, 2830. [Google Scholar] [CrossRef]
- Abdalla, M.A.A.; Min, W.; Mohammed, O.A.A. Two-stage energy management strategy of ev and pv integrated smart home to minimize electricity cost and flatten power load profile. Energies 2020, 13, 6387. [Google Scholar] [CrossRef]
- Zafar, B.; Slama, S.A. PV-EV integrated home energy management using vehicle-to-home (V2H) technology and household occupant behaviors. Energy Strategy Rev. 2022, 44, 101001. [Google Scholar] [CrossRef]
- Rong, J.; Liu, W.; Jiang, F.; Cheng, Y.; Li, H.; Peng, J. Privacy-aware optimal load scheduling for energy management system of smart home. Sustain. Energy Grids Netw. 2023, 34, 101039. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y.; Zhao, B.; Huang, F.; Chen, Y.; Ren, S. Optimal energy flow control strategy for a residential energy local network combined with demand-side management and real-time pricing. Energy Build. 2017, 150, 177–188. [Google Scholar] [CrossRef]
- Aslam, S.; Javaid, N.; Asif, M.; Iqbal, U.; Iqbal, Z.; Sarwar, M.A. A mixed integer linear programming based optimal home energy management scheme considering grid-connected microgrids. In Proceedings of the 2018 14th International Wireless Communications & Mobile Computing Conference (IWCMC), Limassol, Cyprus, 25–29 June 2018. [Google Scholar] [CrossRef]
- Tuomela, S.; de Castro Tomé, M.; Iivari, N.; Svento, R. Impacts of home energy management systems on electricity consumption. Appl. Energy 2021, 299, 117310. [Google Scholar] [CrossRef]
- Current Results. Average Sunshine a Year in Portugal. Available online: https://www.currentresults.com/Weather/Portugal/annual-sunshine.php (accessed on 14 October 2021).
- Cavaco, A.; Silva, H.; Canhoto, P.; Neves, S.; Neto, J.; Pereira, M.C. Annual Average Value of Solar Radiation and its Variability in Portugal. Workshop On Earth Sciences 2016. 2016. Available online: https://www.researchgate.net/publication/311680456_Annual_Average_Value_of_Solar_Radiation_and_its_Variability_in_Portugal (accessed on 22 October 2023).
- Greenice. Painel AS SOLAR 500W Monaovidroinao 144 Celulas Tier 1. Available online: https://greenice.com/pt/modulos-solares/18452-painel-solar-risen-410w-monocrystalline-144-cells-8445152004971.html?currency=EUR&wt_ga=101787014103_443947817426&wt_kw=_101787014103_&gclid=Cj0KCQjw5JSLBhCxARIsAHgO2Sd5Glv8H28n9PpS2LiaY3hv94WxHHMJlEmpprno8eFRYncOF6QiHdsaAmWAEALw_wcB (accessed on 10 October 2021).
- OSM Battery. 5kwh 48v Battery Bank 100Ah Lithium Iron LFP Home Powerwall Modules. Available online: https://osmbattery.com/products/48v-100ah-5kwh-bess-battery-energy-storage-system/ (accessed on 9 June 2022).
- Photovoltaic Geographical Information System. Available online: https://re.jrc.ec.europa.eu/pvg_tools/en/ (accessed on 14 May 2022).
- Zimmermann, J.P.; Swedish Energy Agency. End-Use Metering Campaign in 400 Households In Sweden—Assessment of the Potential Electricity Savings. Available online: https://www.enertech.fr/wp-content/uploads/modules/catalogue/pdf/54/consommations%20usages%20electrodomestiques%20en%20Suede_2009.pdf (accessed on 23 May 2022).
- EDP in Portugal. Available online: https://portugal.edp.com/en/edp-portugal (accessed on 10 June 2022).
- EDP. Tarifarios de Eletricidade e Gas Natural para Particulares. Available online: https://www.edp.pt/particulares/energia/tarifarios/ (accessed on 2 June 2022).
- Presidencia do Conselho de Ministros. Decreto-Lei n.o 162/2019, de 25 de Outubro. Diario da Republica n.o 206/2019. Series I; 25 October 2019; pp. 45–62. Available online: https://dre.pt/dre/detalhe/decreto-lei/162-2019-125692189 (accessed on 12 April 2023).
- David Feldman, R.F.A.R.J.D.; Vignesh Ramasamy & Margolis, R.U.S. Solar Photovoltaic System and Energy Storage Cost Benchmark: Q1 2020. Available online: https://www.nrel.gov/docs/fy21osti/77324.pdf (accessed on 7 August 2023).
- Grant Thornton Australia Limited. Renewable Energy Discount Rate Survey 2018. Available online: https://www.grantthornton.com.au/insights/publications/renewable-energy-discount-rate-survey-2018/ (accessed on 2 April 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).