Abstract
This paper presents a detailed literature review on the thermal management issue faced by electronic devices, particularly concerning uneven heating and overheating problems. Special focus is given to the design and structural optimization of heat sinks for efficient single-phase liquid cooling. Firstly, the paper highlights the common presence and detrimental consequences of electronics overheating resulting from multiple heat sources, supported by various illustrative examples. Subsequently, the emphasis is placed on single-phase liquid cooling as one of the effective thermal management technologies for power electronics, as well as on the enhancement of heat transfer in micro/mini channel heat sinks. Various studies on the design and structural optimization of heat sinks are then analyzed and categorized into five main areas: (1) optimization of channel cross-section shape, (2) optimization of channel flow passage, (3) flow distribution optimization for parallel straight channel heat sinks, (4) optimization of pin-fin shape and arrangement, and (5) topology optimization of global flow configuration. After presenting a broad and complete overview of the state of the art, the paper concludes with a critical analysis of the methods and results from the literature and highlights the research perspectives and challenges in the field. It is shown that the issue of uneven and overheating caused by multiple heat sources, which is commonly observed in modern electronics, has received less attention in the literature compared to uniform or single-peak heating. While several design and structural optimization techniques have been implemented to enhance the cooling performance of heat sinks, topology optimization has experienced significant advancements in recent years and appears to be the most promising technology due to its highest degree of freedom to treat the uneven heating problem. This paper can serve as an essential reference contributing to the development of liquid-cooling heat sinks for efficient thermal management of electronics.
1. Introduction
The rapid advancement of computing and information technologies in recent decades has made remarkable contributions to the progress witnessed in human society. Electronics, being crucial components, have become indispensable in almost every sector of daily life. To meet the escalating demand for smaller, faster, and more powerful electronic devices, it has become customary to enclose an increasing number of functional components within a compact volume. However, this prevailing practice has resulted in a significant increase in power density and the consequential generation of excessive heat. Hence, the implementation of effective thermal management assumes a vital role in tackling the increasingly urgent challenge of overheating in modern electronics.
In many instances, it is commonly assumed that the heating surface of electronics exhibits a uniform heat flux for the purpose of simplification. However, in practical applications, a multiple-peak shape of heat flux is frequently encountered when several functional elements, acting as heat sources, are concentrated within a small volume of the package or arranged in an array on a panel. In comparison to uniform heating surfaces, this non-uniform heating, characterized by multiple-peak heat flux, places higher demands on the effectiveness of thermal management devices. The objective is to mitigate potential detrimental consequences, such as reduced lifetime, material damage, or thermal runaway.
Numerous techniques have been developed and employed to address the thermal management challenges in the field of electronics [1]. Among these techniques, single-phase liquid cooling has emerged as one of the most widely adopted approaches, primarily due to its advantageous attributes, such as simplicity, compactness, safety, and superior cooling performance [2]. A heat sink, functioning as a device for this purpose, is commonly attached to the heat-generating surface of an electronic device. It incorporates miniaturized channel structures to circulate the cooling fluid. Using forced convection heat transfer, this flowing coolant is expected to efficiently remove the generated heat, ensuring an optimal working temperature range for the electronics.
The cooling performance of a heat sink is subject to the influence of several factors, with the internal structure or channel configuration assuming a pivotal role in determining flow path patterns and facilitating heat transfer. Therefore, careful design and structural optimization considerations are essential in achieving enhanced cooling performance [3]. Extensive research efforts have been devoted to this objective, categorized into three levels: size optimization, shape optimization, and topology optimization (TO). These levels progressively offer greater degrees of freedom for morphing and sophistication, allowing for more refined improvements in cooling performance [4].
In the existing body of literature, there appears to be a noticeable oversight and limited attention given to the issue of uneven heating and overheating caused by multiple heat sources, which is indeed a common occurrence in modern electronics. Although various studies have been conducted on heat sink design and optimization, a clear classification and analysis of these optimization practices within the available literature are still lacking. Therefore, the primary objective of this paper is to present a comprehensive review of the design and structural optimization of heat sinks for efficient single-phase liquid cooling of electronic devices, with a specific emphasis on addressing the challenges posed by heterogeneous heating. The rest of the paper is organized as follows. Section 2 will commence by enumerating the detrimental consequences of electronics overheating resulting from multiple heat sources, incorporating several illustrative examples. Subsequently, in Section 3, an extensive survey of the state-of-the-art will explore different practices and advancements related to heat sink design and structural optimization. Finally, Section 4 will provide conclusions, future research perspectives, and challenges to overcome.
2. Overheating Problem of Electronics under Multiple Peak Heat Flux
In this section, we present several cases where electronic devices exhibit multiple-peak heat flux. We provide an overview of the packing/arranging structure and the resulting shape of the heat flux in each case. Examples of such devices include Lithium-ion battery packs for electric vehicles, arrays of multiple light-emitting diodes (LEDs), power electronics (such as Insulated-gate bipolar transistors and diodes: IGBTs), multi-chip modules (MCMs), and multi-junction high concentrator photovoltaics (HCPVs), among others. It is essential for these devices to operate normally within a typical acceptable temperature range. However, the presence of uneven heat generation significantly increases the likelihood of device overheating issues.
2.1. Lithium-Ion Battery Packs
Li-ion batteries are extensively employed as energy storage units in electric vehicles, primarily due to their high capacity and lightweight nature. The packaging of Li-ion batteries can be classified into two main types based on the shape of the battery cell: cylindrical type (Figure 1a) and prismatic type (Figure 1b). In both packaging types, multiple battery cells are arranged in an array layout to fulfill the desired storage capacity, ensuring the maximum mileage range for electric vehicles.
Figure 1c,d show measured temperature contours of a prismatic battery cell at its initial and final stage of discharging, respectively. Notably, distinct temperature gradients are observed between the upper region (hotspot) and the bottom at the initial stage of discharging, as well as between the middle upper region (hotspot) and the bottom at the final stage of discharging. The array arrangement of the unit cells in the battery package leads to the emergence of a multiple-peak heat flux pattern. Handling this uneven heating surface with multiple hotspots poses greater complexity compared to a uniform heating surface, necessitating the use of appropriate thermal management techniques. For instance, Figure 1b illustrates the use of a thermal conductive pad along with a liquid cooling plate [5].
Although Lithium-ion batteries typically operate within a temperature range of −20–60 °C [6], their capacity during normal charge and discharge is highly sensitive to temperature variations. It has been reported [7] that the capacity fade of these batteries can increase from 28.0% to 51.0% as the battery temperature rises from 21 °C to 45 °C. Moreover, when insufficient cooling leads to overheating, the chemical components within the battery packages are susceptible to decomposing and subsequent exothermic reactions. This may result in the sudden generation and release of excessive heat and gaseous products, triggering thermal runaway or even explosion [8].
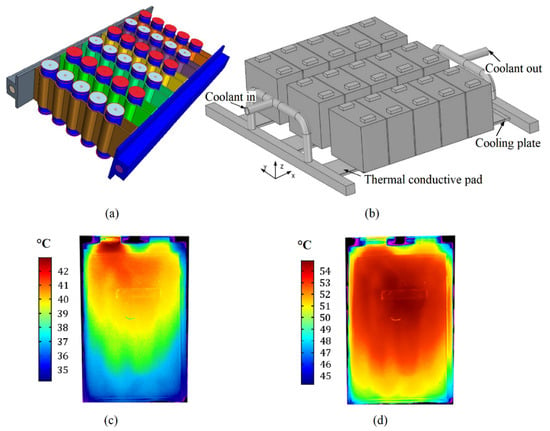
Figure 1.
Lithium-ion battery package with array arrangement of battery cells. (a) cylindrical type [9]; (b) prismatic type [5]; camera-measured temperature contours of the single battery cell (c) at the initial stage of discharging and (d) at the end of discharging, under a constant current [10]. Reprinted/adapted with permission from Refs. [5,9,10], October 2023, Elsevier.
2.2. Multiple LED Arrays
LED packages find widespread usage in various industrial and residential sectors [11] due to their numerous advantages, including low energy consumption, high photoelectric conversion efficiency, high luminous flux, and long lifespan. Typically, individual LED chips are arranged in an array configuration (Figure 2a), connected to the silicon die using Au-Si bonding, and then bonded to a heat spreader (Figure 2b).
Research has indicated that approximately 60% to 70% of the power supplied to LEDs is converted into excess heat. This heat generation can lead to delamination within the electronics packages and hinder the dissipation of heat, posing a significant risk to their proper functioning [12]. A numerical study conducted by Zhang et al. [13] demonstrates that even when a microchannel heat sink is employed for liquid cooling of the LED package, temperature hotspots may persist, as shown in Figure 2c. This exacerbates the issue of package overheating, where localized temperatures may approach or exceed the upper limit (e.g., 85 °C [14]) for normal operation, potentially resulting in device damage.
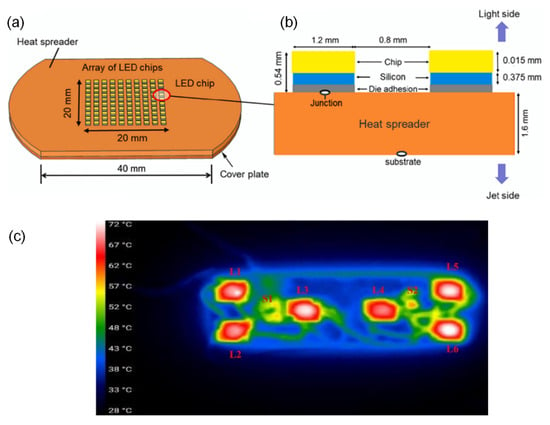
Figure 2.
LED package. (a,b) array arrangement of LED chips and layer structure [15]; (c) temperature distribution on the surface of a microchannel heat sink [16]. Reprinted/adapted with permission from Refs. [15,16], October 2023, Elsevier.
2.3. Power Electronics
An insulated-gate bipolar transistor (IGBT) is a power semiconductor device with three terminals that serves as an electronic switch in high-power applications such as variable-frequency drives, electric vehicles, trains, variable-speed refrigerators, lamp ballasts, arc-welding machines, and air conditioners [17]. Figure 3a presents an actual example of an IGBT module (Infineon FF225R17ME4), which consists of three sub-modules with diagonally arranged diodes and IGBT chips. The temperature limits for IGBT modules range from 125 °C to 150 °C, depending on the rated voltage [18]. To ensure efficient heat dissipation, an air-cooled heat sink equipped with multiple intermediate layers of different materials (as shown in Figure 3c) is employed.
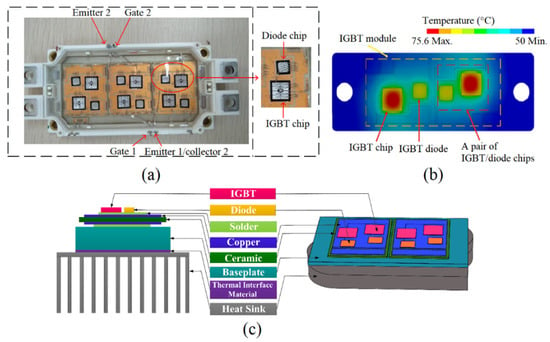
Figure 3.
Thermal management for IGBT module. (a) a real opened IGBT module [19]; (b) simulated temperature distribution of IGBT module [20]; (c) air-cooling of IGBT module using a heat sink [21].
As power electronics continue to advance, there is a growing demand for highly compact IGBTs that experience non-uniform and high heat flux generation [21]. Figure 3b illustrates a simulated temperature contour of an IGBT module based on the power loss of the IGBT diode chips, with a heat sink simplified as an aluminum block. It is evident that temperature hotspots appear at the chip locations, with a temperature difference of up to 25.6 °C, indicating high thermal gradients. This phenomenon becomes even more significant in densely packaged powerful IGBT modules containing hundreds of chips. According to Choi et al. [22], semiconductor-related failures account for 34% (the highest proportion among all failure causes) in power converter systems of IGBT modules, with solder failures induced by high temperatures comprising nearly 60% of these failures [23].
2.4. Single-Chip Modules (SCMs) and Multi-Chip Modules (MCMs)
Central processing unit (CPU) chips play an essential role in modern society. Depending on the number of integrated chips, CPUs can be classified into single-chip modules (SCMs) and multi-chip modules (MCMs). An SCM typically consists of a substrate, a CPU chip (also known as a die), a thermal interface material (TIM-1) between the integrated heat spreader (IHS) and the chip, and another TIM-2 between the heat sink and the IHS, as illustrated in Figure 4a. On the other hand, an MCM consists of multiple chips in a package, which can be arranged in a 3D stack or multiple 3D stacks, as shown in Figure 4b.
Figure 4.
Thermal management issue for CPU chips. (a) an SCM with a heat sink [24]; (b) multiple-peak heat generation [25]. Reprinted/adapted with permission from Refs. [24,25], October 2023, Elsevier.
During operation, both SCMs and MCMs can generate heat flux with a multiple-peak shape (Figure 4c). This occurs due to the varying locations of transistors within an SCM and the presence of multiple chips in an MCM. However, as the demand for performance and compactness of next-generation processors continues to rise, the heat density generated by the chips increases, leading to more severe overheating issues. SCMs and MCMs have specified normal working temperatures (ideally below 50 °C) to ensure optimal efficiency, security, and lifespan. Most CPUs should operate at temperatures below 85–90 °C, such as the case of an Intel Core i5-12600K processor cooled by a suitable dual heat sink air cooler, where the junction temperature should not exceed 70 °C [26]. It is important to note that for every 10 °C increase in junction temperature, the device failure rate doubles [27]. Exceeding the upper limit (105–110 °C) [28] for a certain period may trigger self-protective shutdown mechanisms to prevent material damage and related issues.
2.5. Multi-Junction High Concentrator Photovoltaics (HCPVs)
The utilization of solar photovoltaic systems for renewable electricity generation has experienced significant growth in recent years [29]. Conventional single-junction solar cells face the limitation of low maximum theoretical efficiency of sunlight conversion (32–33%) [30]. In contrast, multi-junction solar cells offer the potential to significantly increase the theoretical conversion efficiency, reaching up to 45%. This is achieved by the stacking of multiple solar cells [31] and by increasing the band gaps to harness a broader solar spectrum while minimizing transmission and thermalization losses [32].
Figure 5a shows the operational principle of an HCPV system. Incident sunlight is reflected by the non-imaging dish concentrator to the crossed compound parabolic concentrator (CCPC) lens array, which is composed of 8 × 10 CPV cells. The detailed structure of a single CCPC lens is depicted in the right part of Figure 5a. The CPV module is affixed to a water-cooled heat sink via Artic Silver Adhesive. Figure 5b presents the solar flux contour on such CPV cells array, displaying multiple peak profiles reaching a maximum of 2.940 106 Wm−2. This non-uniform distribution of solar flux inevitably leads to heterogeneous heat generation and large temperature gradients on the CPV board. Numerous studies have highlighted the consequences of CPV cells exposed to high and non-uniform solar concentration ratios. For instance, the open circuit voltage of CPV cells is inversely proportional to their temperature, thereby reducing the power conversion efficiency [33]. The effects of high temperature become particularly significant at concentration levels approaching 1000 suns, even for a brief duration of a few milliseconds [33].
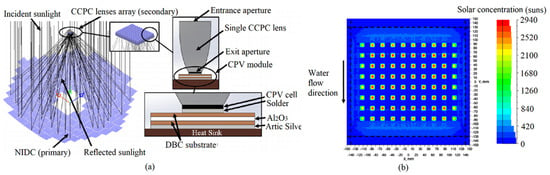
Figure 5.
High concentrator photovoltaics (HCPV) system cooled by a liquid multi-channel heat sink [34]. (a) schematic diagram and working principle of HCPV; (b) power map of an array of CPV cell modules. Reprinted/adapted with permission from Ref. [34], October 2023, Elsevier.
2.6. Short Summary
The aforementioned examples demonstrate that modern electronic devices have specific normal operating temperatures and maximum temperature limits. The former ensures optimal performance and a guaranteed device lifetime, while the latter prevents shutdown, material damage, and thermal runaway. However, the increasing demand for smaller, multifunctional, faster, and more powerful electronics has led to a significant rise in heat generation, resulting in more frequent occurrences of overheating.
Furthermore, the pursuit of higher capacity and performance has driven the rapid development of electronic packages or boards with increased integration levels. The arrangement of functional elements in these integrated packages, such as arrays or stacks, inevitably leads to uneven heat generation with multiple-peak heat flux shapes. This amplifies the temperature gradient, posing additional challenges for efficient cooling compared to cases of uniform heating or single heat source. Besides the examples presented in the above text, similar problems can also be found in motor inverters in electric vehicles [35], in GaN high-electron-mobility-transistors (HEMTs) [36], and in many other modern electronic devices. Consequently, efficient thermal management technologies have become particularly needed to address the issues of overheating and uneven heating caused by multiple-peak heat flux in electronics. This problem remains inadequately addressed in the current literature, underscoring the need for further research in this area.
3. Heat Sink Design and Structural Optimization
A variety of techniques have been developed and utilized for thermal management in electronics [1]. One prominent method is single-phase liquid cooling using forced convection. This technique offers numerous advantages and has gained widespread adoption. In this section, our focus will be on the pivotal component of liquid cooling systems: the heat sink.
Heat sinks for electronic cooling typically feature compact and miniaturized structures, with characteristic channel lengths ranging from hundreds of micrometers to several millimeters. The cooling performance of heat sinks is strongly influenced by the geometries and topologies of the flow channels, i.e., how the flow paths of the cooling fluid are arranged and organized. Therefore, this section will provide a comprehensive examination of the design and structural optimization of heat sinks, offering detailed insights into their characteristics and performance.
3.1. Heat Sink Design—Basic Structures and Variants
A typical heat sink for liquid cooling consists of an entrance part (inlet tube/manifold), an exit part (outlet tube/manifold), and the main domain with flow paths in the middle. Heat sinks can be classified into several basic types based on the flow channel configuration: parallel-channels type, pin-fin type, and complex type. Examples and variants of these heat sink types are illustrated in Figure 6.
The parallel straight channels type heat sink is one of the most common and conventional structures. Its main domain comprises multiple straight channels arranged in parallel, with thin solid walls separating neighboring channels (Figure 6a). Some variants in this category include wavy/serpentine channel shapes (Figure 6b) [37], cavities channels (Figure 6d), or ribbed channels (Figure 6e) [38,39]. Compared to the basic parallel straight channel type, these variants can generally create the secondary flow, local vortices, and recirculation near the enhancement elements (cf. Figure 7), which then disturb the establishment of thermal boundary in the channel. The heat transfer could thereby be enhanced but at the expense of higher pressure drop (pumping power). Numerous studies have focused on optimizing the size and/or shape of the unit enhancement elements, such as ridges, cavities, and obstacles, to obtain an improved thermal-hydraulic performance of the heat sink. For more detailed information, readers are invited to refer to the review papers [3,40], and Section 3.2.2.
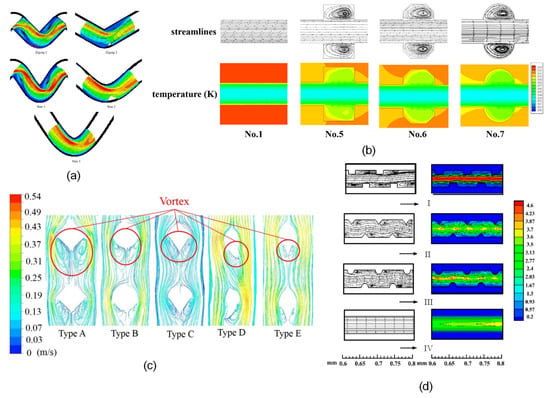
Figure 7.
Local flow disturbance generated by different channel structuration for heat transfer enhancement. (a) zigzag and wary channel [44]; (b) cavity channel [45]; (c) ribs on the bottom walls [46]; (d) ribs on the side walls [47]. Reprinted/adapted with permission from Refs. [44,46], October 2023, Elsevier.
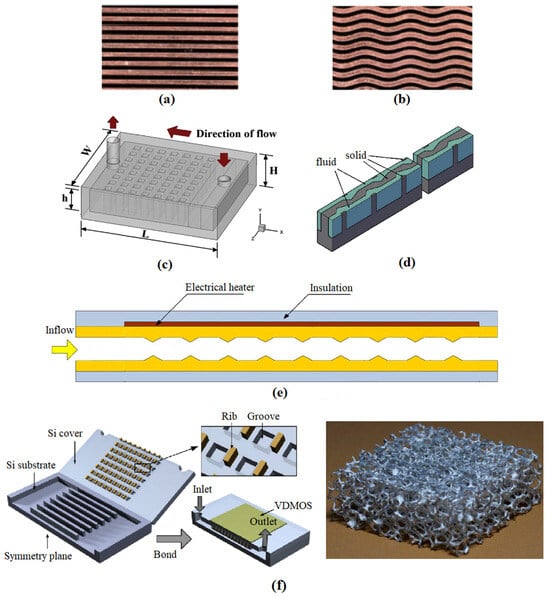
Figure 6.
Different categories and variants of heat sink for liquid cooling. (a) parallel straight channel [37]; (b) parallel wavy channel [37]; (c) pin-fin structure [41]; (d) straight channel with cavities [38]; (e) straight channel with ribs [39]; (f) Complex (hybrid) structure [42,43]. Reprinted/adapted with permission from Refs. [37,38,39,41,42,43], October 2023, Elsevier.
In parallel channel-type heat sinks, another factor that greatly affects their thermal and hydraulic performances is the flow (mal)distribution, which is closely related to the inlet/outlet position(s) and the shape of the distributor and collector [48,49]. While uniform flow distribution is often the target to achieve for cooling a uniform heat-generating surface, the heterogeneous heat-generating surface, due to the presence of multiple heat sources, changes and complicates the rule. Research on flow distribution in this context will be further reviewed and analyzed in Section 3.2.3. Additionally, the channel cross-sectional shape can also be subjected to optimization, and relevant studies will be summarized in Section 3.2.1.
The pin-fin heat sink (Figure 6c) is another common category for liquid cooling purposes, where the flow domain is a cavity filled with an array of fins usually having the same height. Various fin shapes have been considered, including rectangular, triangular, circular, or others. The shape, the spacing, and the arrangement of fins all impact the heat sink’s performance and are therefore subjected to optimization. Section 3.2.4 will further introduce studies on pin-fin structure optimization.
The last category of the heat sink combines two or more of the aforementioned enhancement structures. Examples include a combination of cavity, rib, and parallel-straight channels or the use of porous medium (such as metal foam) in general, as shown in Figure 6f. Despite offering better cooling performance, these complex heat sink structures should consider the associated increase in pressure drop as an important factor. It is worth noting that a new trend has emerged, where the global flow channel configuration of these complex heat sinks is not based on some predefined geometries but is typically the result of topology optimization (TO). More discussion on this topic will be provided in Section 3.2.5.
3.2. Structural Optimization of Heat Sinks for Liquid Cooling
This sub-section presents in detail the structural optimization of heat sinks for electronic cooling, which are categorized into five main areas: (1) optimization of channel cross-section shape, (2) optimization of channel flow passage, (3) flow distribution optimization for parallel-straight channel heat sinks, (4) optimization of pin-fin shape and arrangement, and (5) TO of global flow channel configuration. Note that emphasis is given to the optimization approach used, the level of complexity and flexibility (size, shape, or topology), and the applicability and prospects to address the problem of uneven heating with multiple-peak heat flux. Regarding performance comparison of different studied heat sinks and their tested conditions, readers are invited to refer to specific review papers such as [40,50,51,52,53,54].
3.2.1. Channel Cross-Section Optimization
The structural optimization of parallel-straight channel heat sinks often involves optimizing the cross-sectional shape of the channel. The optimized shape is then extended along the flow direction to form the entire channel length without further modifications of the channel passage (to be introduced in Section 3.2.2). Based on the design parametrizations, the studies in this category could be classified into three classes, as shown in Figure 8: (a) optimization of single channel cross-section size/parameter based on a predefined simple geometry [55,56,57,58,59,60,61,62,63,64,65]; (b) optimization of single channel cross-section shape [66,67]; and (c) TO of the entire cross-section of the heat sink [68]. The key step in the optimization is establishing the relationship between the design variables and the objective function, either by direct physics analysis or by constructing a surrogate function.
Figure 8.
Cross-section optimization of straight channel heat sinks. (a) single channel cross-section geometrical parameters optimization [59]; (b) single channel cross-section shape optimization [67]; (c) entire cross-section topology optimization [68]. Reprinted/adapted with permission from Refs. [67,68], October 2023, Elsevier.
The size/parameter optimization of channel cross-section has received a lot of attention due to its predefined and simple geometry, allowing for the establishment of explicit analytical relations between the design variables and the objective function. For instance, Shao et al. [55] optimized the number, width, height of microchannels, and thickness of solid separating walls for a conventional parallel-straight microchannel heat sink using a genetic algorithm (GA). Other studies in this line have also been conducted (e.g., [69]), often assuming fully developed laminar flow pattern and simplified heating boundaries (e.g., constant Nusselt number). When dealing with more complex heat sink geometries or under real operating conditions, the use of surrogate functions becomes necessary. Response Surface Analysis (RSA) is a commonly applied approach for this purpose [56,70,71]. The global thermal resistance is typically considered as the (single) objective criterion, with constraint(s) such as fixed pressure drop or pumping power. The conjugate-gradient method is often used [60,61,62,63], considering design variables such as the number of channels, the channel aspect ratio, and the channel-to-pitch ratio. When multiple objectives (thermal resistance, pressure drop/pumping power, weight, etc.) are involved, the non-dominated sorting genetic algorithms (NSGA-II) coupled with CFD simulations are frequently used (e.g., [57,58,72,73]) to determine optimal values of design variables. Recent advancements include the application of “Jaya” algorithm proposed by Rao et al. [64], showing promising effectiveness in heat sink optimization. Machine learning (ML) techniques have also been introduced for cross-section optimization purposes. Shaeri et al. [74] utilized an artificial neural network (ANN) for multi-objective optimization of an air-cooled heat sink, achieving significant weight reduction and pressure drop reduction with a negligible decrease in heat transfer coefficient.
Relatively fewer studies have focused on evolving the shape of channel cross-section beyond a predefined geometry. Foli et al. [66] used a multi-objective genetic algorithm (MOGA) to optimize the thermo-hydraulic performance of a heat exchanger by utilizing non-uniform Rational B-splines (NURBS) as design parameters. Ge et al. [67] employed MOGA and multi-objective particle swarm optimization (MOPSO) to optimize the cross-section shape described by six variables (Figure 8b). Their results indicated that modifying the rectangular cross-section shape to a curvy boundary shape yielded effectively reduced pumping power without a significant increase in thermal resistance. Pai and Weibel [75] developed ML-based surrogate models to predict the Nusselt number (Nu) and the friction factor under fully developed internal flow in channels with arbitrary cross-section. The optimized channel cross-section for different objective functions using ML-based models has been demonstrated.
TO of heat sink cross-sections has been explored in two studies to the best of the authors’ knowledge. Dokken and Fronk [68] discretized the heat sink cross-section into bit arrays (Figure 8c) and used a micro-GA to generate optimal shapes that minimize the system’s entropy generation rate. Lee et al. [76] developed a TO method to minimize the thermal resistance under the constraint of fixed pumping power. This approach enables the design of lighter heat sinks with higher thermal performance for practical applications. It is important to note that both studies address the problem of localized (multiple) heat sources rather than simplified uniform heating surfaces, highlighting the superiority of TO in treating electronic cooling problems under multiple-peak heat flux. However, this approach differs from the TO of the global channel configuration to be discussed in Section 3.2.5, as it maintains the same optimized cross-section topology throughout the channel length (flow direction). Actually, this optimization approach focuses on the mass flow distribution inside the heat sink without presetting parallel channels, providing prospects for tailoring flow distribution to address multiple-peak heat flux cases (cf. Section 3.2.3).
3.2.2. Channel Flow Passage Optimization
Different from the channel cross-section optimization, this category focuses on modifying the channel geometry along the flow passage direction to disturb the development of the thermal boundary layer and enhance heat transfer.
Many studies in this category concentrate on the basic straight channel-type heat sinks and involve modifications to the shape of channel side walls (cf. Figure 9a). For example, Khudhur et al. [77] numerically investigated the channel walls with added or subtracted pins. They found that among various fin shapes, the semicircular fins exhibited the best thermal performance, with Nu number increasing by about 21% (added) and 32% (subtracted) compared with smooth straight channels. Rajalingam and Chakraborty [78] studied the effect of gradual and sudden variation of the channel cross-sectional area on the thermohydraulic performance of a heat sink. They reported that a combination of alternating large and small cross-sectional areas along the channel length achieved the best performance at high Reynolds numbers (Re). Similarly, Zhu et al. [79] proposed periodic gradual-expansion and sudden-constriction cross-sections by incorporating backward right-angled trapezoidal grooves in the channel side walls. This channel passage shape resulted in an increase in 1.31–2.14 times in the Nu number and 1.02–1.45 times in the pressure drop compared to the smooth straight microchannels. Similar results were also reported by Samadi et al. [80], who investigated the groovy structures. Chen et al. [81] proposed a cross-rib microchannel to induce self-rotation of the coolant to enhance the cooling capacity (cf. Figure 8c), achieving an increase in 28.6% or 14.3% compared to rectangularly or horizontally ribbed microchannels, respectively. While these mentioned studies generally examined the effects of some channel geometrical parameters on the thermo-hydraulic performance of the heat sink, they did not employ specific optimization algorithms to determine the optimal design. In contrast, Wang and Chen [82] used a cantor fractal baffle on the microchannel side walls and performed structural optimization using GA to minimize the global thermal resistance. Zhang et al. [83] numerically tested various split-and-recombine type microchannels and used the NSGA-II algorithm to obtain optimal channel configuration parameters. Other studies on modification and optimization of channel side walls have also been reported, employing machine learning surrogates [84], fuzzy grey approach [85], etc.
A few other studies work on the channel bottom wall closer to the heating surface, adding pins or altering the channel height, as shown in Figure 9b,e. For example, Cao et al. [86] proposed adding straight-slot fins with different aspect ratios to the channel base walls. Rajalingam and Chakraborty [87] compared various shapes of micro-ribs on the channel bottom wall and found that aerofoil and reversed aerofoil micro-ribs improved heat transfer and reduced the pressure drop, respectively. Zhang et al. [88] studied a countercurrent flow mini-channel heat sink with cavity structures (zigzag, square-wavy, and wavy) on the bottom wall. Numerical results showed that zigzag cavities yielded the lowest wall temperature and the best wall temperature uniformity.
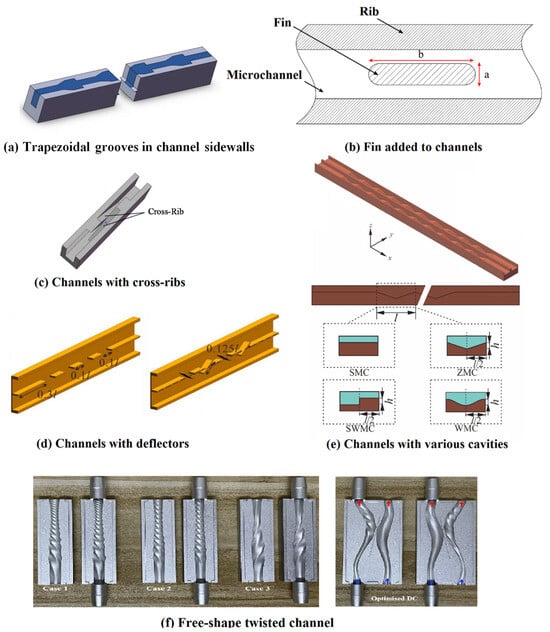
Figure 9.
Different types of heat sink channel flow passage optimization. (a) backward right-angled trapezoidal grooves in channel sidewalls [79]; (b) channels added with fins [86]; (c) channels with cross-rib [81]; (d) channels with deflectors [89]; (e) Channels with various cavities [88]; (f) free-shape twisted channel [90]. Reprinted/adapted with permission from Refs. [79,88,89,90], October 2023, Elsevier.
More complex channel flow passage geometries have also been studied, e.g., by structuring both the side walls and the bottom wall. Narendran and Gnanasekaran [91] explored the potential of ribs and inertial-based spillway channels to enhance heat transfer and overcome flow maldistribution, a critical issue that will be further addressed in Section 3.2.3. Tan et al. [92] introduced multi-jet twisted square microchannels and observed a 16.48% increase in Nu with a small rise in pressure drop. Jiang and Pan [93] proposed trapezoidal cavity channels and solid/slotted oval pins to enhance heat transfer. Design variables such as aspect ratio, distance from the center of the oval pin to the center of the cavity, and slot thickness were optimized using GA and BP (backpropagation) neural networks. Shen et al. [89] employed deflectors (cf. Figure 9d) to induce mixing flow between the channels of the heat sink. A 7 °C decrease in the substrate peak temperature could be achieved compared to traditional straight channel heat sinks. Tian et al. [90] used conventional and rational Bernstein–Bézier functions to define and optimize the passage pattern, cross-section, and twist of the channel (cf. Figure 9f). The optimized design could bring the highest drop in average temperature and root mean square temperature of the heating surface.
It should be noted that this category of channel structure optimization acts on disturbing the establishment of thermal boundary layer along the flow direction. Once the channel flow passage is optimized, the same geometry of the channel will be multiplied into a parallel arrangement. Therefore, it is less applicable to address the unevenly heating problem due to the existence of multiple heat sources on the heating surface.
3.2.3. Flow Distribution Investigation/Optimization on Parallel Straight Channels
The presence of the coolant flow maldistribution among the parallel channels can lead to thermal performance deterioration of the heat sink and the formation of localized temperature hot spots in electronic devices [94]. Therefore, achieving proper delivery and distribution of cooling fluid across the parallel micro/mini channels is a crucial issue for optimizing the cooling performance of the heat sink. Plenty of research has been devoted to achieving uniform flow distribution for an evenly heating surface. These researches can be categorized into three main approaches: (1) arrangement of heat sink inlet/outlet positions or injecting angle; (2) design and structuration of the manifolds (headers); and (3) shape modification of the parallel channels.
Studies have investigated the effect of flow inlet angle between the inlet port and parallel channels [95], as well as the locations of inlet/outlet positions [96,97] (cf. Figure 10). Kumar and Singh [94] reported that an I-type flow arrangement provided better thermal performance for uniform heating compared to a D-type heat sink having a more uniform flow distribution. Chen et al. [98] reported the best cooling performance of an air-cooled battery thermal management system with the inlet and outlet located in the middle of the plenums.
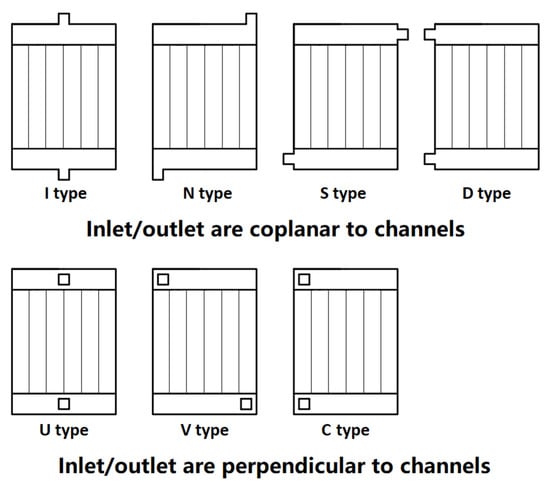
Figure 10.
Different arrangements of global inlet-outlet position for parallel straight channel heat sink [99]. Reprinted/adapted with permission from Ref. [99], October 2023, Elsevier.
Additionally, the design and shape of headers have been examined by Manikanda Kumaran et al. [96], with triangular inlet headers and trapezoidal outlet headers shown to provide better flow uniformity. Many other novel header designs [96,100,101,102] have also been proposed and tested, as summarized in the review paper by Ghani et al. [54]. Besides modifying the inlet/outlet header shapes, studies have been performed on adding obstacles inside the header to address the issue of flow maldistribution, including staggered pin-fin array (Figure 11a) [103], non-uniform-sized mini-inlet baffle (Figure 11b) [104,105], thin layers of porous media [106], and optimized manifold configurations (Figure 11c) [107].
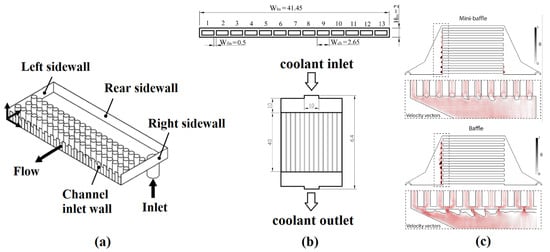
Figure 11.
Design and structuration of the manifolds (headers) by (a) pin-fin structure [103], (b) baffle [104], and (c) baffle and mini-baffle [107]. Reprinted/adapted with permission from Refs. [103,104,107], October 2023, Elsevier.
The geometry of the heat sink channel has also been considered as a design parameter to adjust flow distribution. Studies have shown that decreasing the header/channel area ratio [108], using parallel channels with variable channel height [109], optimizing geometry parameters (number of channels, channel width, and channel length) [110,111], and adjusting channel height, width, length, header length, and connection tube diameter [112] can improve the flow distribution uniformity.
Most studies aim to achieve uniform flow distribution under the assumption of uniform heat flux at the base wall of the heat sink. However, for more realistic scenarios with heterogeneous heating surfaces and multiple-peak heat flux, intentional non-uniform flow distribution may be desirable for better cooling of local hotspots. This aligns with observations in the literature (e.g., [113,114]), indicating that optimal flow distribution is typically non-uniform and follows certain trends based on defined optimization objectives and constraints. Kumar and Singh [94] emphasized the importance of aligning the flow arrangement and actual flow distribution with the heat flux shape to achieve lowered peak temperature and thermal resistance. Li et al. [99] optimized the channel inlet sizes of parallel mini-channel heat sinks under a non-uniform multiple-peak heat flux. The flow distribution was tailored step by step according to the temperature distribution on the heating surface, resulting in reduced peak temperature. Annapurna et al. [115] used MOGA to determine suitable orifice diameters to reach the target flow distribution (uniform or non-uniform) among parallel channels. These effective practices underscore that optimizing the flow distribution among parallel channels constitutes a simple but practical approach to tackle the cooling issue of unevenly heating surfaces with multiple-peak heat flux. The simpler geometry and the fewer number of design variables to handle could largely save the required computational resources and costs compared to the TO approach.
3.2.4. Fin-Shape and Arrangement Optimization for Pin-Fin Heat Sinks
Pin-fin structures are widely employed in heat sinks due to their large fluid-solid contacting surface area for heat transfer. Conventional pin-fin heat sinks typically feature simple, regular, and uniformly distributed fins. Numerous studies have been conducted to optimize the geometry of pin-fins in order to enhance the cooling performance. These studies primarily focus on size or shape optimization of pin fins and their arrangement, either based on a predefined geometry or through mathematical parametrization (cf. Figure 12). More recently, there have been advances in the TO of pin-fin structures.
The size optimization of the pin-fin structures is relatively straightforward and relies on simple pin geometry, such as a cuboid or cylinder, which remains unchanged during optimization. Design variables often include the number, height, width/length (or diameter), or the spacing/pitch of the pins [116]. Various optimization algorithms have been employed, utilizing simplified physical models or assisted by CFD simulations. For example, Ahmadian-Elmi et al. [116] reported that a rise in the number and diameter of pin-fin would increase both the heat transfer coefficient and pressure drop while increasing the fin height and transverse pitch had the opposite effect. Huang et al. [117] used the Levenberg–Marquardt Method to optimize the heights and widths of non-uniform fins, while Yang et al. [118] employed the Taguchi method or GA-RSA method [119]. It has been found that better thermal performance could be achieved with increased fin height and inter-fin spacing of outer fins. However, the effects of those geometrical parameters could be decayed at a high Reynolds number. Chen et al. [120] applied the direction-based GA to search for the optimal fin design variables for lowered entropy generation rate and material cost. A similar approach has been adopted by Wang et al. [121]. Jiang and Pan [122] used the orthogonal test, NSGA-II, and k-mean clustering methods for multi-objective optimization of rectangular fins. Their results showed that a non-uniform fin array with higher pin heights (at the second and fourth row) and thinner fin thicknesses (along the direction of flow) could reduce the thermal resistance of the heat sink. Multi-objective optimization is frequently performed using algorithms like NSGA-II [123,124,125]. Some studies have explored factors beyond geometry, such as pin-fin porosity and location angle with respect to the flow direction [41] or heat sinks with staggered diamond-shaped pin-fin arrays [126]. Chen et al. [127] optimized the structure of a sinusoidal wavy plate-fin heat sink with crosscut using the Bayesian Optimization (BO) algorithm. Machine-learning techniques have also been applied in this area, with ANN used to optimize the geometry of tapered squared cross-section pin-fins [128] and elliptical pin-fin microchannel heat sinks [129]. Most of these studies focus on uniform heating surfaces, with the exception of Yang and Mills [130], who optimized pin arrangement and geometry for localized heat sources using a CFD-assisted GA method.
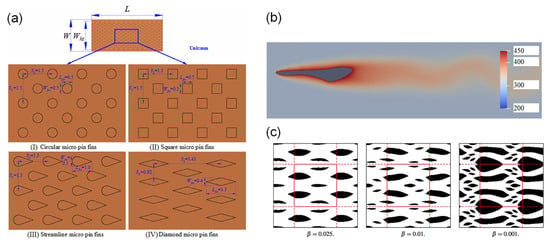
Figure 12.
Structural optimization of pin-fin type heat sinks. (a) pin-fin size and spacing optimization [131]; (b) single fin-shape optimization [132]; (c) topology optimization [133]. Reprinted/adapted with permission from Refs. [131,132], October 2023, Elsevier.
Shape optimization of pin-fin heat sinks involves modifying the boundary of a predefined or non-predefined pin geometry using optimization methods. Ismayilov et al. [134] utilized CFD-assisted MOGA to vary the shape of hydrofoil pin-fins, while Keramati et al. [132] employed composite Bézier curve parameterized by control points (Figure 12b) and optimized it using Deep Neural Network (DNN). Huang et al. [135] proposed extracting the wake flow contours in the channels as pin-fin geometry contours to enhance the thermo-hydraulic performances of micro-pin-fin heat sinks. In terms of TO, Ghasem and Elham [133] utilized a gradient-based method for multi-objective TO of pin-fin heat sinks, demonstrating improved cooling performance with optimized hydrofoil-shaped fins (cf. Figure 12c) compared to conventional (circular) in-line and staggered fins as well as those after sizing optimization.
However, the complexity of CFD simulation and optimization often limits these studies on pin-fin shape optimization to a single pin shape or, at best, a single slice along the flow direction. Consequently, research addressing shape or topology optimization for the cooling of an entire heat-generating surface remains relatively scarce. Additionally, the inherent geometry simplicity and array arrangement of pin-fin structures may restrict the design flexibility and diversity regarding uneven heating due to the existence of multiple heat sources. In this regard, more efforts on the TO of pin-fin heat sinks are still needed.
3.2.5. Topology Optimization (TO) of Global Flow Configuration
Unlike the size or shape optimization methods that always start from a predefined geometry, the TO approach acts directly on the spatial distribution of materials and their connectivity within a design domain. The topology that minimizes/maximizes the objective function(s) could be determined by running an optimization algorithm under specific constraints. Particularly for thermal-fluid problems in the structural optimization of heat sinks, the TO of global flow channel configuration enables the flexible organization and arrangement of both fluid and solid elements, allowing for the creation of solid islands or flow paths without predetermined geometries. Holding the highest degrees of freedom for the design, this approach has gained significant attention from academia and industry owing to its ability to obtain innovative designs of heat sinks (or heat exchangers in a general sense) with greatly improved effectiveness. Some illustrative examples of TO-derived designs are shown in Figure 13.
The TO process typically comprises four basic stages [4]: (1) design parametrization, (2) heat transfer modeling, (3) optimization process, and (4) final realization. Based on the design parametrization, the TO for single-phase heat sinks can be classified into three types: density-based, level-set, and direct explicit. These methods differ in their representation of the relationship between design variables and physical properties, such as the density distribution used to describe the flow paths in the density-based method [136]. Once parametrized, the design variables are mapped, interpolated, and updated iteratively to approach the optimum configuration. This process involves modeling heat transfer in both fluid and solid domains coupled with fluid flow to compute the distribution of state variables (pressure, velocity, and temperature) at each optimization iteration. Various solvers have been implemented over the years, including the finite element method (FEM), the finite volume method (FVM), and the Lattice Boltzmann Method (LBM), typically assuming laminar, incompressible, and steady-state flow [137,138,139]. Regarding the optimizer, both gradient-based and non-gradient-based approaches can be employed. The gradient method calculates the objective function’s gradient and its stagnant point, often using the adjoint method [140]. Currently, a combination of the density-based method, FEM, and gradient-based optimizer represents the mainstream approach for TO of heat sinks/heat exchangers [4]. This approach has demonstrated good efficacy in handling optimization problems with a high number of design variables [141]. More detailed information about these methods and relevant studies can be found in recent review papers [4,142]. However, the implementation of such a TO strategy may encounter difficulties in handling numerical artifacts, describing clear solid-fluid interfaces, and, more importantly, avoiding local optima [143]. Conversely, novel, gradient-free approaches, such as GA and BO, have emerged as alternative ways to overcome these limitations and converge towards a global optimum.
There have been few attempts to perform TO of global flow channel configuration in heat sinks using the non-gradient approaches. This is primarily due to the complexity of modeling conjugate heat transfer and fluid flow, the challenges in formulating the optimizer, and the high computational costs involved. Among these attempts, Yoshimura et al. [144] proposed a Kriging surrogate model-assisted GA method on single-/multi-objective TO of cooling flow channel configurations. Later, the NSGA-II method was coupled with the Kriging surrogate model to search for better designs of lattice-structured heat sinks in terms of thermal performance and material cost [145]. Mekki et al. [146,147] developed and tested a GA-based TO method for thermo-fluid equipment in aerospace applications, focusing on elementary fin shapes using voxel representation (cf. Figure 13c). Weber et al. [148] also employed a GA method to optimize the shape/topology of a heat exchanger fin, achieving optimal designs when coupled with free-form deformation. Yaji et al. [149] proposed a hybrid data-driven multi-fidelity topology design that combines density-based methods for low-fidelity TO and NSGA-II for selecting the optimal Pareto front. However, the majority of the mentioned TO studies deal with simplified 2D or pseudo-3D design domains (e.g., [150]). Among studies with 3D parametrization (e.g., [151,152]), most are performed under uniform heating conditions, with only a few exceptions addressing more complex but realistic heating boundaries involving multiple heat sources [153,154] or shifted thermal loads [155]. Notably, Li et al. [154] developed a GA-based TO method (GATO) for convective cooling of a heating surface with multiple heat sources. The design domain was represented as a binary matrix, where each element was considered either as fluid or as solid. The allocation determining the global flow channel configuration in the heat sink was optimized using GA. The results demonstrated that the optimized flow channel configuration, being dependent on the design and operating parameters, consistently led to improved performance compared to the parallel straight channel configuration. Zhang et al. [156] also tried to address the cooling problem of a non-uniform heating surface by optimizing the topology of the regenerative cooling channel. In particular, the influence of different heat flux distributions on the heat transfer efficiency of the TO design has been investigated. Wang et al. [157] proposed a multiphysics TO for the conformal cooling channel design of the injection molding process. The overall cooling channel layout has been optimized based on the non-uniform thermal load distribution in the design domain, leading to both low-pressure drop and high heat transfer rate. These attempts show the superiority and flexibility of the TO approach in the situation of non-uniform and/or unsteady heat boundaries, highlighting its broad prospect in handling the general thermal-fluid structural optimization problems.
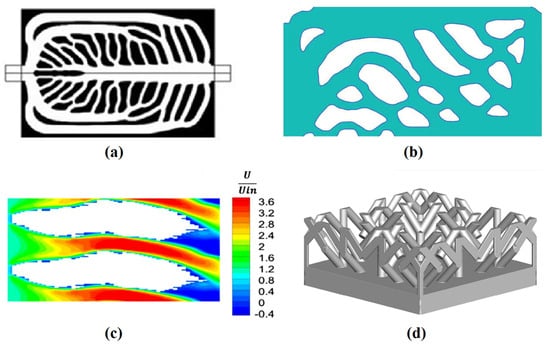
Figure 13.
TO of global channel configuration of heat sinks. (a) flow channel generation by density-based gradient adjoint optimizer [158]; (b) level-set TO for thermal-fluid problem [159]; (c) non-gradient GA-based TO approach [147]; (d) non-gradient Bayesian method for TO of heat sink in natural convection [145]. Reprinted/adapted with permission from Refs. [147,158], October 2023, Elsevier; from Ref. [159], October 2023, John Wiley and Sons.
4. Conclusions and Perspectives
This paper provides a comprehensive literature review on thermal management for electronic devices facing uneven heating and overheating issues, with a specific focus on the design and structural optimization of heat sinks for efficient single-phase liquid cooling. The key conclusions can be summarized as follows:
- In electronic devices, non-uniform heating with multiple heat sources is a common occurrence due to the stacking/array arrangement of functional units for increased power or capacity. This multiple-peak heat flux condition poses a greater risk of overheating compared to uniform heating or single-peak heating, leading to detrimental consequences such as reduced efficiency, device shutdown, decreased lifespan, irreversible component damage, or even thermal runaway. Therefore, an efficient thermal management approach is crucial for cooling non-uniform heating surfaces with multiple heat sources.
- Conventional heat sinks for single-phase cooling can be categorized into parallel channel, pin-fin, and complex types, with different variants proposed to enhance heat transfer performance. Notably, structural optimization can be performed using size, shape, or TO methods. Research efforts have been directed towards optimizing (1) the shape of the channel cross-section, (2) the channel flow passages, (3) flow distribution uniformity or adaptability in parallel-channel heat sinks, (4) the shape and arrangement of pin-fins, and (5) the topology of global flow channel configuration in heat sinks.
- The TO of global flow channel configurations involves allocating and organizing the fluid and solid phases within the design domain of a heat sink without geometry presetting. Offering the highest design flexibility, this approach shows promise in addressing the cooling challenges posed by non-uniform heating with multiple heat sources, surpassing the limitations of size or shape optimization methods. Currently, the most popular TO method for heat sink structural optimization combines density-based design parametrization, FEM for heat transfer modeling and gradient-based optimizers. While this TO strategy is efficient and straightforward, it also faces limitations such as local optimum trapping, vague fluid-solid boundary, inaccuracy in modeling conjugate heat transfer modeling, non-physical topologies obtained, etc.
Several research gaps and challenges arise from the inadequate attention given to the multiple-peak heat flux issue, which is, in fact, commonly encountered in modern electronics but insufficiently addressed in the literature. These gaps and challenges highlight the key issues in current research and development:
- (1)
- The majority of heat sink design and structural optimization studies are still based on simplified uniform heating conditions. Some very recent work has started to consider more realistic non-uniform heating boundaries in the optimization, which should be prioritized in future studies. More adapted design guidelines and optimization approaches also need to be developed specifically for the cooling of uneven heating surfaces caused by multiple heat sources.
- (2)
- The limitations of the current density-based methods for TO of global flow channel configuration have been identified. More efforts should be directed towards improving the effectiveness and applicability of these methods. Additionally, there is a significant need to explore and develop gradient-free approaches (e.g., GA, BO) as promising alternatives.
- (3)
- ML technique has recently emerged and has been applied in the structural optimization of heat sinks. Currently, ML shows interesting applications when combined with size or shape optimization approaches, either for accelerating the modeling process by improving the prediction of thermo-hydraulic performances or for enhancing the optimization algorithms. ML-assisted TO approaches [160] for heat sink/heat exchangers, although still rare, hold great promise and represent a ground-breaking direction for future research.
- (4)
- The majority of TO studies rely only on CFD simulations, while experimental validation is indispensable for verifying simulation results and assessing the optimization effectiveness. The rapid development of additive manufacturing technologies offers promising ways for the realization of topologically optimized heat sinks with complex internal structures [161,162]. Therefore, additional efforts are needed to conduct experimental testing and performance comparisons of heat sinks optimized using different characterization methods.
Addressing these research gaps and challenges will significantly contribute to advancing the field of heat sink design and optimization, enabling more efficient cooling of electronic devices with multiple-peak heat flux conditions.
Funding
This work is supported by the Chinese Scholarship Council (CSC) with the scholarship for Y.L. (No. 201908070033).
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| ANN | Artificial Neural Network |
| BO | Bayesian Optimization |
| CCPC | Crossed Compound Parabolic Concentrator |
| CFD | Computational Fluid Dynamics |
| CPV | Concentrator Photovoltaics |
| CPU | Central Processing Unit |
| DNN | Deep Neural Network |
| FEM | Finite Element Method |
| FVM | Finite Volume Method |
| GA | Genetic Algorithm |
| HCPV | High Concentrator Photovoltaics |
| HEMTs | High Electron Mobility Transistors |
| IGBT | Insulated-Gate Bipolar Transistor and Diodes |
| IHS | Integrated Heat Spreader |
| LBM | Lattice Boltzmann Method |
| LED | Light-Emitting Diode |
| MCM | Multi-Chip Modules |
| ML | Machine Learning |
| MOGA | Multi-Objective Genetic Algorithm |
| MOPSO | Multi-Objective Particle Swarm Optimization |
| NSGA | Non-Dominated Sorting Genetic Algorithm |
| PSO | Particle Swarm Optimization |
| RSA | Response Surface Analysis |
| SCM | Single-Chip Module |
| TIM | Thermal Interface Material |
| TO | Topology Optimization |
References
- Zhang, Z.; Wang, X.; Yan, Y. A review of the state-of-the-art in electronic cooling. e-Prime 2021, 1, 100009. [Google Scholar] [CrossRef]
- Xia, G.; Ma, D.; Zhai, Y.; Li, Y.; Liu, R.; Du, M. Experimental and numerical study of fluid flow and heat transfer characteristics in microchannel heat sink with complex structure. Energy Convers. Manag. 2015, 105, 848–857. [Google Scholar] [CrossRef]
- Ahmed, H.E.; Salman, B.H.; Kherbeet, A.S.; Ahmed, M.I. Optimization of thermal design of heat sinks: A review. Int. J. Heat Mass Transf. 2018, 118, 129–153. [Google Scholar] [CrossRef]
- Fawaz, A.; Hua, Y.; Le Corre, S.; Fan, Y.; Luo, L. Topology optimization of heat exchangers: A review. Energy 2022, 252, 124053. [Google Scholar] [CrossRef]
- Shang, Z.; Qi, H.; Liu, X.; Ouyang, C.; Wang, Y. Structural optimization of lithium-ion battery for improving thermal performance based on a liquid cooling system. Int. J. Heat Mass Transf. 2019, 130, 33–41. [Google Scholar] [CrossRef]
- Ma, S.; Jiang, M.; Tao, P.; Song, C.; Wu, J.; Wang, J.; Deng, T.; Shang, W. Temperature effect and thermal impact in lithium-ion batteries: A review. Prog. Nat. Sci. Mater. Int. 2018, 28, 653–666. [Google Scholar] [CrossRef]
- Ehrlich, G.M. Handbook of Batteries, 3rd ed.; Linden, D., Reddy, T.B., Eds.; McGraw-Hill: New York, NY, USA, 2002; ISBN 0-07-135978-8. [Google Scholar]
- Zhao, R. Overheating Prediction and Management of Lithium-Ion Batteries; Carleton University: Ottawa, ON, Canada, 2018. [Google Scholar]
- Basu, S.; Hariharan, K.S.; Kolake, S.M.; Song, T.; Sohn, D.K.; Yeo, T. Coupled electrochemical thermal modelling of a novel Li-ion battery pack thermal management system. Appl. Energy 2016, 181, 1–13. [Google Scholar] [CrossRef]
- Goutam, S.; Nikolian, A.; Jaguemont, J.; Smekens, J.; Omar, N.; Van Dan Bossche, P.; Van Mierlo, J. Three-dimensional electro-thermal model of li-ion pouch cell: Analysis and comparison of cell design factors and model assumptions. Appl. Therm. Eng. 2017, 126, 796–808. [Google Scholar] [CrossRef]
- Tang, Y.; Luo, Y.; Du, P.; Wang, H.; Ma, H.; Qin, Y.; Bai, P.; Zhou, G. Experimental investigation on active heat sink with heat pipe assistance for high-power automotive LED headlights. Case Stud. Therm. Eng. 2021, 28, 101503. [Google Scholar] [CrossRef]
- Hu, J.; Yang, L.; Whan Shin, M. Mechanism and thermal effect of delamination in light-emitting diode packages. Micro. J. 2007, 38, 157–163. [Google Scholar] [CrossRef]
- Zhang, X.; Li, R.-C.; Zheng, Q. Analysis and simulation of high-power LED array with microchannel heat sink. Adv. Manuf. 2013, 1, 191–195. [Google Scholar] [CrossRef][Green Version]
- Effects Of Temperature On LED Lights. Available online: https://ledlightsunlimited.net/2020/09/15/effects-of-temperature-on-led-lights/ (accessed on 6 September 2023).
- Gatapova, E.Y.; Sahu, G.; Khandekar, S.; Hu, R. Thermal management of high-power LED module with single-phase liquid jet array. Appl. Therm. Eng. 2021, 184, 116270. [Google Scholar] [CrossRef]
- Rammohan, A.; Ramesh Kumar, C.; Chandramohan, V.P. Experimental analysis on estimating junction temperature and service life of high power LED array. Microelectron. Reliab. 2021, 120, 114121. [Google Scholar] [CrossRef]
- Bose, B.K. Power Electronics and Variable Frequency Drives: Technology and Applications; Bose, B.K., Ed.; Wiley-IEEE Press: New York, NY, USA, 1997; ISBN 9780470545553. [Google Scholar]
- Schlapbach, U.; Rahimo, M.; von Arx, C.; Mukhitdinov, A.; Linder, S. 1200 V IGBTs operating at 200 °C? An investigation on the potentials and the design constraints. In Proceedings of the 19th International Symposium on Power Semiconductor Devices and IC’s, Jeju, Republic of Korea, 27–31 May 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 9–12. [Google Scholar]
- Hu, Z.; Ge, X.; Xie, D.; Zhang, Y.; Yao, B.; Dai, J.; Yang, F. An Aging-Degree Evaluation Method for IGBT Bond Wire with Online Multivariate Monitoring. Energies 2019, 12, 3962. [Google Scholar] [CrossRef]
- An, N.; Du, M.; Hu, Z.; Wei, K. A High-Precision Adaptive Thermal Network Model for Monitoring of Temperature Variations in Insulated Gate Bipolar Transistor (IGBT) Modules. Energies 2018, 11, 595. [Google Scholar] [CrossRef]
- Yahyaee, A.; Bahman, A.; Blaabjerg, F. A Modification of Offset Strip Fin Heatsink with High-Performance Cooling for IGBT Modules. Appl. Sci. 2020, 10, 1112. [Google Scholar] [CrossRef]
- Choi, U.-M.; Blaabjerg, F.; Lee, K.-B. Study and Handling Methods of Power IGBT Module Failures in Power Electronic Converter Systems. IEEE Trans. Power Electron. 2015, 30, 2517–2533. [Google Scholar] [CrossRef]
- Qiu, X.Z.; Zhang, G.R.; Chen, W.J.; Yu, T.; Hou, X.M.; Zhang, Q.Z.; Xu, G.Q. Review of IGBT Junction Temperature Extraction and Estimation Methods. IOP Conf. Ser. Mater. Sci. Eng. 2020, 774, 012091. [Google Scholar] [CrossRef]
- Hao, X.; Peng, B.; Xie, G.; Chen, Y. Efficient on-chip hotspot removal combined solution of thermoelectric cooler and mini-channel heat sink. Appl. Therm. Eng. 2016, 100, 170–178. [Google Scholar] [CrossRef]
- Nan, G.; Xie, Z.; Guan, X.; Ji, X.; Lin, D. Constructal design for the layout of multi-chip module based on thermal-flow-stress coupling calculation. Microelectron. Reliab. 2021, 127, 114417. [Google Scholar] [CrossRef]
- What is the safe CPU temperature range? Available online: https://levvvel.com/what-is-the-safe-cpu-temperature-range/ (accessed on 6 September 2023).
- Manoj Siva, V.; Pattamatta, A.; Das, S.K. Effect of flow maldistribution on the thermal performance of parallel microchannel cooling systems. Int. J. Heat Mass Transf. 2014, 73, 424–428. [Google Scholar] [CrossRef]
- Will Overheating My CPU Cause any Real Damage? Available online: https://www.pcgamer.com/cpu-temperature-overheat/#:~:text=Overclocking (accessed on 6 September 2023).
- IEA. Renewable Electricity Growth Is Accelerating Faster than Ever Worldwide, Supporting the Emergence of the New Global Energy Economy; IEA: Paris, France, 2021. [Google Scholar]
- Yamaguchi, M.; Dimroth, F.; Geisz, J.F.; Ekins-Daukes, N.J. Multi-junction solar cells paving the way for super high-efficiency. J. Appl. Phys. 2021, 129, 240901. [Google Scholar] [CrossRef]
- Multijunction III-V Photovoltaics Research. Available online: https://www.energy.gov/eere/solar/multijunction-iii-v-photovoltaics-research (accessed on 6 September 2023).
- Philipps, S.P.; Bett, A.W. III-V Multi-junction solar cells and concentrating photovoltaic (CPV) systems. Adv. Opt. Technol. 2014, 3, 469–478. [Google Scholar] [CrossRef]
- Braun, A.; Hirsch, B.; Vossier, A.; Katz, E.A.; Gordon, J.M. Temperature dynamics of multijunction concentrator solar cells up to ultra-high irradiance. Prog. Photo. Res. Appl. 2013, 21, 202–208. [Google Scholar] [CrossRef]
- Tan, W.-C.; Chong, K.-K.; Tan, M.-H. Performance study of water-cooled multiple-channel heat sinks in the application of ultra-high concentrator photovoltaic system. Sol. Energy 2017, 147, 314–327. [Google Scholar] [CrossRef]
- Han, F.; Guo, H.; Ding, X. Design and optimization of a liquid cooled heat sink for a motor inverter in electric vehicles. Appl. Energy 2021, 291, 116819. [Google Scholar] [CrossRef]
- Hua, Y.-C.; Li, H.-L.; Cao, B.-Y. Thermal Spreading Resistance in Ballistic-Diffusive Regime for GaN HEMTs. IEEE Trans. Electron Devices 2019, 66, 3296–3301. [Google Scholar] [CrossRef]
- Cui, P.; Liu, Z. Enhanced flow boiling of HFE-7100 in picosecond laser fabricated copper microchannel heat sink. Int. J. Heat Mass Transf. 2021, 175, 121387. [Google Scholar] [CrossRef]
- Li, Y.F.; Xia, G.D.; Ma, D.D.; Jia, Y.T.; Wang, J. Characteristics of laminar flow and heat transfer in microchannel heat sink with triangular cavities and rectangular ribs. Int. J. Heat Mass Transf. 2016, 98, 17–28. [Google Scholar] [CrossRef]
- Promvonge, P.; Chompookham, T.; Kwankaomeng, S.; Thianpong, C. Enhanced heat transfer in a triangular ribbed channel with longitudinal vortex generators. Energy Convers. Manag. 2010, 51, 1242–1249. [Google Scholar] [CrossRef]
- Singh, S.; Malik, A.; Mali, H.S. A critical review on single-phase thermo-hydraulic enhancement in geometrically modified microchannel devices. Appl. Therm. Eng. 2023, 235, 121729. [Google Scholar] [CrossRef]
- Zhao, J.; Huang, S.; Gong, L.; Huang, Z. Numerical study and optimizing on micro square pin-fin heat sink for electronic cooling. Appl. Therm. Eng. 2016, 93, 1347–1359. [Google Scholar] [CrossRef]
- Wang, G.; Niu, D.; Xie, F.; Wang, Y.; Zhao, X.; Ding, G. Experimental and numerical investigation of a microchannel heat sink (MCHS) with micro-scale ribs and grooves for chip cooling. Appl. Therm. Eng. 2015, 85, 61–70. [Google Scholar] [CrossRef]
- Paknezhad, M.; Rashidi, A.M.; Yousefi, T.; Saghir, Z. Effect of aluminum-foam heat sink on inclined hot surface temperature in the case of free convection heat transfer. Case Stud. Therm. Eng. 2017, 10, 199–206. [Google Scholar] [CrossRef]
- Dai, Z.; Fletcher, D.F.; Haynes, B.S. Impact of tortuous geometry on laminar flow heat transfer in microchannels. Int. J. Heat Mass Transf. 2015, 83, 382–398. [Google Scholar] [CrossRef]
- Li, H.; Li, Y.; Huang, B.; Xu, T. Numerical Investigation on the Optimum Thermal Design of the Shape and Geometric Parameters of Microchannel Heat Exchangers with Cavities. Micromachines 2020, 11, 721. [Google Scholar] [CrossRef]
- Zhou, F.; Zhou, W.; Zhang, C.; Qiu, Q.; Yuan, D.; Chu, X. Experimental and numerical studies on heat transfer enhancement of microchannel heat exchanger embedded with different shape micropillars. Appl. Therm. Eng. 2020, 175, 115296. [Google Scholar] [CrossRef]
- Wang, G.-L.; Yang, D.-W.; Wang, Y.; Niu, D.; Zhao, X.-L.; Ding, G.-F. Heat Transfer and Friction Characteristics of the Microfluidic Heat Sink with Variously-Shaped Ribs for Chip Cooling. Sensors 2015, 15, 9547–9562. [Google Scholar] [CrossRef]
- Tang, S.; Zhao, Y.; Diao, Y.; Quan, Z. Effects of various inlet/outlet positions and header forms on flow distribution and thermal performance in microchannel heat sink. Microsyst. Technol. 2018, 24, 2485–2497. [Google Scholar] [CrossRef]
- Saeed, M.; Kim, M.H. Header design approaches for mini-channel heatsinks using analytical and numerical methods. Appl. Therm. Eng. 2017, 110, 1500–1510. [Google Scholar] [CrossRef]
- Zhang, X.; Ji, Z.; Wang, J.; Lv, X. Research progress on structural optimization design of microchannel heat sinks applied to electronic devices. Appl. Therm. Eng. 2023, 235, 121294. [Google Scholar] [CrossRef]
- Zhou, W.; Dong, K.; Sun, Q.; Luo, W.; Zhang, B.; Guan, S.; Wang, G. Research progress of the liquid cold plate cooling technology for server electronic chips: A review. Int. J. Energy Res. 2022, 46, 11574–11595. [Google Scholar] [CrossRef]
- Sadique, H.; Murtaza, Q. Samsher Heat transfer augmentation in microchannel heat sink using secondary flows: A review. Int. J. Heat Mass Transf. 2022, 194, 123063. [Google Scholar] [CrossRef]
- He, Z.; Yan, Y.; Zhang, Z. Thermal management and temperature uniformity enhancement of electronic devices by micro heat sinks: A review. Energy 2021, 216, 119223. [Google Scholar] [CrossRef]
- Ghani, I.A.; Che Sidik, N.A.; Kamaruzzaman, N.; Jazair Yahya, W.; Mahian, O. The effect of manifold zone parameters on hydrothermal performance of micro-channel HeatSink: A review. Int. J. Heat Mass Transf. 2017. [CrossRef]
- Baodong, S.; Lifeng, W.; Jianyun, L.; Heming, C. Multi-objective optimization design of a micro-channel heat sink using adaptive genetic algorithm. Int. J. Numer. Methods Heat Fluid Flow 2011, 21, 353–364. [Google Scholar] [CrossRef]
- Karathanassis, I.K.; Papanicolaou, E.; Belessiotis, V.; Bergeles, G.C. Multi-objective design optimization of a micro heat sink for Concentrating Photovoltaic/Thermal (CPVT) systems using a genetic algorithm. Appl. Therm. Eng. 2013, 59, 733–744. [Google Scholar] [CrossRef]
- Normah, G.-M.; Oh, J.-T.; Chien, N.B.; Choi, K.-I.; Robiah, A. Comparison of the optimized thermal performance of square and circular ammonia-cooled microchannel heat sink with genetic algorithm. Energy Convers. Manag. 2015, 102, 59–65. [Google Scholar] [CrossRef]
- Halelfadl, S.; Adham, A.M.; Mohd-Ghazali, N.; Maré, T.; Estellé, P.; Ahmad, R. Optimization of thermal performances and pressure drop of rectangular microchannel heat sink using aqueous carbon nanotubes based nanofluid. Appl. Therm. Eng. 2014, 62, 492–499. [Google Scholar] [CrossRef]
- Lin, D.; Kang, C.-H.; Chen, S.-C. Optimization of the Micro Channel Heat Sink by Combing Genetic Algorithm with the Finite Element Method. Inventions 2018, 3, 32. [Google Scholar] [CrossRef]
- Hung, T.-C.; Yan, W.-M.; Wang, X.-D.; Huang, Y.-X. Optimal design of geometric parameters of double-layered microchannel heat sinks. Int. J. Heat Mass Transf. 2012, 55, 3262–3272. [Google Scholar] [CrossRef]
- Wang, X.-D.; An, B.; Xu, J.-L. Optimal geometric structure for nanofluid-cooled microchannel heat sink under various constraint conditions. Energy Convers. Manag. 2013, 65, 528–538. [Google Scholar] [CrossRef]
- Wang, X.-D.; An, B.; Lin, L.; Lee, D.-J. Inverse geometric optimization for geometry of nanofluid-cooled microchannel heat sink. Appl. Therm. Eng. 2013, 55, 87–94. [Google Scholar] [CrossRef]
- Leng, C.; Wang, X.-D.; Wang, T.-H.; Yan, W.-M. Optimization of thermal resistance and bottom wall temperature uniformity for double-layered microchannel heat sink. Energy Convers. Manag. 2015, 93, 141–150. [Google Scholar] [CrossRef]
- Rao, R.V.; More, K.C.; Taler, J.; Ocłoń, P. Dimensional optimization of a micro-channel heat sink using Jaya algorithm. Appl. Therm. Eng. 2016, 103, 572–582. [Google Scholar] [CrossRef]
- Yin, H.; Ooka, R. Shape optimization of water-to-water plate-fin heat exchanger using computational fluid dynamics and genetic algorithm. Appl. Therm. Eng. 2015, 80, 310–318. [Google Scholar] [CrossRef]
- Foli, K.; Okabe, T.; Olhofer, M.; Jin, Y.; Sendhoff, B. Optimization of micro heat exchanger: CFD, analytical approach and multi-objective evolutionary algorithms. Int. J. Heat Mass Transf. 2006, 49, 1090–1099. [Google Scholar] [CrossRef]
- Ge, Y.; Wang, S.; Liu, Z.; Liu, W. Optimal shape design of a minichannel heat sink applying multi-objective optimization algorithm and three-dimensional numerical method. Appl. Therm. Eng. 2019, 148, 120–128. [Google Scholar] [CrossRef]
- Dokken, C.B.; Fronk, B.M. Optimization of 3D printed liquid cooled heat sink designs using a micro-genetic algorithm with bit array representation. Appl. Therm. Eng. 2018, 143, 316–325. [Google Scholar] [CrossRef]
- Khan, W.A.; Kadri, M.B.; Ali, Q. Optimization of Microchannel Heat Sinks Using Genetic Algorithm. Heat Transf. Eng. 2013, 34, 279–287. [Google Scholar] [CrossRef]
- Husain, A.; Kim, K.-Y. Optimization of a microchannel heat sink with temperature dependent fluid properties. Appl. Therm. Eng. 2008, 28, 1101–1107. [Google Scholar] [CrossRef]
- Kulkarni, K.; Afzal, A.; Kim, K.-Y. Multi-objective optimization of a double-layered microchannel heat sink with temperature-dependent fluid properties. Appl. Therm. Eng. 2016, 99, 262–272. [Google Scholar] [CrossRef]
- Shang, X.; Li, Q.; Cao, Q.; Li, Z.; Shao, W.; Cui, Z. Mathematical modeling and multi-objective optimization on the rectangular micro-channel heat sink. Int. J. Therm. Sci. 2023, 184, 107926. [Google Scholar] [CrossRef]
- Alperen, Y.; Sertac, C. Multi objective optimization of a micro-channel heat sink through genetic algorithm. Int. J. Heat Mass Transf. 2020, 146, 118847. [Google Scholar] [CrossRef]
- Shaeri, M.R.; Sarabi, S.; Randriambololona, A.M.; Shadlo, A. Machine learning-based optimization of air-cooled heat sinks. Therm. Sci. Eng. Prog. 2022, 34, 101398. [Google Scholar] [CrossRef]
- Pai, S.S.; Weibel, J.A. Machine-learning-aided design optimization of internal flow channel cross-sections. Int. J. Heat Mass Transf. 2022, 195, 123118. [Google Scholar] [CrossRef]
- Lee, G.; Lee, I.; Kim, S.J. Topology optimization of a heat sink with an axially uniform cross-section cooled by forced convection. Int. J. Heat Mass Transf. 2021, 168, 120732. [Google Scholar] [CrossRef]
- Khudhur, D.S.; Al-Zuhairy, R.C.; Kassim, M.S. Thermal analysis of heat transfer with different fin geometry through straight plate-fin heat sinks. Int. J. Therm. Sci. 2022, 174, 107443. [Google Scholar] [CrossRef]
- Rajalingam, A.; Chakraborty, S. Estimation of the thermohydraulic performance of a microchannel heat sink with gradual and sudden variation of the flow passage. Int. J. Heat Mass Transf. 2022, 190, 122776. [Google Scholar] [CrossRef]
- Zhu, Q.; Su, R.; Hu, L.; Chen, J.; Zeng, J.; Zhang, H.; Sun, H.; Zhang, S.; Fu, D. Heat transfer enhancement for microchannel heat sink by strengthening fluids mixing with backward right-angled trapezoidal grooves in channel sidewalls. Int. Commun. Heat Mass Transf. 2022, 135, 106106. [Google Scholar] [CrossRef]
- Samadi, H.; Hosseini, M.J.; Ranjbar, A.A.; Pahamli, Y. Thermohydraulic performance of new minichannel heat sink with grooved barriers. Int. Commun. Heat Mass Transf. 2023, 144, 106753. [Google Scholar] [CrossRef]
- Chen, H.; Chen, C.; Zhou, Y.; Yang, C.; Song, G.; Hou, F.; Jiao, B.; Liu, R. Evaluation and Optimization of a Cross-Rib Micro-Channel Heat Sink. Micromachines 2022, 13, 132. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Chen, X. Numerical simulation of heat transfer and flow of Al2O3-water nanofluid in microchannel heat sink with cantor fractal structure based on genetic algorithm. Anal. Chim. Acta 2022, 1221, 339927. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; He, Y.; Wang, C.; Liang, B.; Zhu, Y.; Gou, H.; Xiao, K.; Lu, F. A new type of liquid-cooled channel thermal characteristics analysis and optimization based on the optimal characteristics of 24 types of channels. Int. J. Heat Mass Transf. 2023, 202, 123734. [Google Scholar] [CrossRef]
- Sikirica, A.; Grbčić, L.; Kranjčević, L. Machine learning based surrogate models for microchannel heat sink optimization. Appl. Therm. Eng. 2023, 222, 119917. [Google Scholar] [CrossRef]
- Cheng, Y.; Luo, X.; Wang, P.; Yang, Z.; Huang, J.; Gu, J.; Zhao, W. Multi-objective optimization of thermal-hydraulic performance in a microchannel heat sink with offset ribs using the fuzzy grey approach. Appl. Therm. Eng. 2022, 201, 117748. [Google Scholar] [CrossRef]
- Cao, Y.; Abbas, M.; El-Shorbagy, M.A.; Gepreel, K.A.; Dahari, M.; Le, V.V.; Badran, M.F.; Huynh, P.H.; Wae-hayee, M. Thermo-hydraulic performance in ceramic-made microchannel heat sinks with an optimum fin geometry. Case Stud. Therm. Eng. 2022, 36, 102230. [Google Scholar] [CrossRef]
- Rajalingam, A.; Chakraborty, S. Microchannel heat sink with microstructured wall—A critical study on fluid flow and heat transfer characteristics. Therm. Sci. Eng. Prog. 2023, 38, 101613. [Google Scholar] [CrossRef]
- Zhang, Q.; Feng, Z.; Zhang, J.; Guo, F.; Huang, S.; Li, Z. Design of a mini-channel heat sink for high-heat-flux electronic devices. Appl. Therm. Eng. 2022, 216, 119053. [Google Scholar] [CrossRef]
- Shen, H.; Xie, G.; Wang, C.-C.; Liu, H. Experimental and numerical examinations of thermofluids characteristics of double-layer microchannel heat sinks with deflectors. Int. J. Heat Mass Transf. 2022, 182, 121961. [Google Scholar] [CrossRef]
- Tian, X.-W.; Sun, C.; Zeng, X.; Qian, S.-H.; Li, C.-F.; Cai, Y.-Z.; Chen, Y.; Wang, W. Free-shape modeling and optimization for straight channel of cold plate involving passage pattern, cross-section, and twist of channel. Int. J. Heat Mass Transf. 2022, 184, 122299. [Google Scholar] [CrossRef]
- Narendran, G.; Gnanasekaran, N. Investigation on novel inertial minichannel to mitigate maldistribution induced high temperature zones. Energy Convers. Manag. 2022, 271, 116300. [Google Scholar] [CrossRef]
- Tan, Z.; Jin, P.; Zhang, Y.; Xie, G. Flow and thermal performance of a multi-jet twisted square microchannel heat sink using CuO-water nanofluid. Appl. Therm. Eng. 2023, 225, 120133. [Google Scholar] [CrossRef]
- Jiang, M.; Pan, Z. Optimization of micro-channel heat sink based on genetic algorithm and back propagation neural network. Therm. Sci. 2023, 27, 179–193. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, P.K. A novel approach to manage temperature non-uniformity in minichannel heat sink by using intentional flow maldistribution. Appl. Therm. Eng. 2019, 163, 114403. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, P.K. Effects of flow inlet angle on flow maldistribution and thermal performance of water cooled mini-channel heat sink. Int. J. Therm. Sci. 2019, 138, 504–511. [Google Scholar] [CrossRef]
- Manikanda Kumaran, R.; Kumaraguruparan, G.; Sornakumar, T. Experimental and numerical studies of header design and inlet/outlet configurations on flow mal-distribution in parallel micro-channels. Appl. Therm. Eng. 2013, 58, 205–216. [Google Scholar] [CrossRef]
- Chein, R.; Chen, J. Numerical study of the inlet/outlet arrangement effect on microchannel heat sink performance. Int. J. Therm. Sci. 2009, 48, 1627–1638. [Google Scholar] [CrossRef]
- Chen, K.; Wu, W.; Yuan, F.; Chen, L.; Wang, S. Cooling efficiency improvement of air-cooled battery thermal management system through designing the flow pattern. Energy 2019, 167, 781–790. [Google Scholar] [CrossRef]
- Li, Y.; Roux, S.; Castelain, C.; Luo, L.; Fan, Y. Tailoring the fluid flow distribution in a parallel mini-channel heat sink under multiple-peak heat flux. Therm. Sci. Eng. Prog. 2022, 29, 101182. [Google Scholar] [CrossRef]
- Dąbrowski, P. Mitigation of Flow Maldistribution in Minichannel and Minigap Heat Exchangers by Introducing Threshold in Manifolds. J. Appl. Fluid Mech. 2020, 13, 815–826. [Google Scholar] [CrossRef]
- Liu, H.; Li, P.; Van Lew, J.; Juarez-Robles, D. Experimental study of the flow distribution uniformity in flow distributors having novel flow channel bifurcation structures. Exp. Therm. Fluid Sci. 2012, 37, 142–153. [Google Scholar] [CrossRef]
- Zhou, J.; Ding, M.; Bian, H.; Zhang, Y.; Sun, Z. Characteristics of flow distribution in central-type compact parallel flow heat exchangers with modified inlet and header. Appl. Therm. Eng. 2020, 166, 114636. [Google Scholar] [CrossRef]
- Song, J.Y.; Hah, S.; Kim, D.; Kim, S.M. Enhanced flow uniformity in parallel mini-channels with pin-finned inlet header. Appl. Therm. Eng. 2019, 152, 718–733. [Google Scholar] [CrossRef]
- Liu, X.; Yu, J. Numerical study on performances of mini-channel heat sinks with non-uniform inlets. Appl. Therm. Eng. 2016, 93, 856–864. [Google Scholar] [CrossRef]
- Hou, Q.; Xuan, Y.; Lian, W.; Xu, Y.; Ma, Y. A novel approach for suppressing flow maldistribution in mini-channel heat exchangers. Int. J. Therm. Sci. 2023, 184, 108020. [Google Scholar] [CrossRef]
- Fatahian, H.; Jouybari, N.F.; Nimvari, M.E.; Fatahian, E.; Zhang, W. Improving the flow uniformity in compact parallel-flow heat exchangers manifold using porous distributors. J. Therm. Anal. Calorim. 2022, 147, 12919–12931. [Google Scholar] [CrossRef]
- Gilmore, N.; Hassanzadeh-Barforoushi, A.; Timchenko, V.; Menictas, C. Manifold configurations for uniform flow via topology optimisation and flow visualisation. Appl. Therm. Eng. 2021, 183, 116227. [Google Scholar] [CrossRef]
- Dhahad, H.A.; Alfayydh, E.M.; Fahim, K.H. Effect of flow field design and channel/header ratio on velocity distribution: An experimental approach. Therm. Sci. Eng. Prog. 2018, 8, 118–129. [Google Scholar] [CrossRef]
- Mu, Y.T.; Chen, L.; He, Y.L.; Tao, W.Q. Numerical study on temperature uniformity in a novel mini-channel heat sink with different flow field configurations. Int. J. Heat Mass Transf. 2015, 85, 147–157. [Google Scholar] [CrossRef]
- Hao, X.; Wu, Z.; Chen, X.; Xie, G. Numerical analysis and optimization on flow distribution and heat transfer of a U-type parallel channel heat sink. Adv. Mech. Eng. 2015, 7, 672451. [Google Scholar] [CrossRef]
- Mitra, I.; Ghosh, I. Mini-channel heat sink parameter sensitivity based on precise heat flux re-distribution. Therm. Sci. Eng. Prog. 2020, 20, 100717. [Google Scholar] [CrossRef]
- Song, J.-Y.; Senguttuvan, S.; Choi, W.-W.; Kim, S.-M. Effects of manifold design parameters on flow uniformity in parallel mini-channels. Int. J. Mech. Sci. 2022, 234, 107694. [Google Scholar] [CrossRef]
- Milman, O.O.; Spalding, D.B.; Fedorov, V.A. Steam condensation in parallel channels with nonuniform heat removal in different zones of heat-exchange surface. Int. J. Heat Mass Transf. 2012, 55, 6054–6059. [Google Scholar] [CrossRef]
- Wei, M.; Fan, Y.; Luo, L.; Flamant, G. Fluid flow distribution optimization for minimizing the peak temperature of a tubular solar receiver. Energy 2015, 91, 663–677. [Google Scholar] [CrossRef]
- Annapurna, S.; Varughese, S.; Niranjanappa, A.; Reddy, K.H. A Design of Experiments Approach Towards Desired Flow Distribution Through Manifolds in Electronics Cooling. Def. Sci. J. 2022, 72, 516–525. [Google Scholar] [CrossRef]
- Ahmadian-Elmi, M.; Mashayekhi, A.; Nourazar, S.S.; Vafai, K. A comprehensive study on parametric optimization of the pin-fin heat sink to improve its thermal and hydraulic characteristics. Int. J. Heat Mass Transf. 2021, 180, 121797. [Google Scholar] [CrossRef]
- Huang, C.-H.; Chen, Y.-H. An optimal design problem in determining non-uniform fin heights and widths for an impingement heat sink module. Appl. Therm. Eng. 2014, 63, 481–494. [Google Scholar] [CrossRef]
- Yang, Y.T.; Peng, H.S.; Hsu, H.T. Numerical Optimization of Pin-Fin Heat Sink with Forced Cooling. Int. J. Electron. Commun. Eng. 2013, 7, 884–891. [Google Scholar] [CrossRef]
- Yang, Y.-T.; Lin, S.-C.; Wang, Y.-H.; Hsu, J.-C. Numerical simulation and optimization of impingement cooling for rotating and stationary pin–fin heat sinks. Int. J. Heat Fluid Flow 2013, 44, 383–393. [Google Scholar] [CrossRef]
- Chen, C.-T.; Chen, H.-I. Multi-objective optimization design of plate-fin heat sinks using a direction-based genetic algorithm. J. Taiwan Inst. Chem. Eng. 2013, 44, 257–265. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Liu, D. The application of genetic algorithm for pin-fin heat sink optimization design. In Proceedings of the 2009 4th IEEE Conference on Industrial Electronics and Applications, Xi’an, China, 25–27 May 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 2816–2821. [Google Scholar]
- Jiang, M.; Pan, Z. Optimization of open micro-channel heat sink with pin fins by multi-objective genetic algorithm. Therm. Sci. 2022, 26, 3653–3665. [Google Scholar] [CrossRef]
- Nemati, H.; Moghimi, M.A.; Sapin, P.; Markides, C.N. Shape optimisation of air-cooled finned-tube heat exchangers. Int. J. Therm. Sci. 2020, 150, 106233. [Google Scholar] [CrossRef]
- Polat, M.E.; Ulger, F.; Cadirci, S. Multi-objective optimization and performance assessment of microchannel heat sinks with micro pin-fins. Int. J. Therm. Sci. 2022, 174, 107432. [Google Scholar] [CrossRef]
- Ge, Y.; He, Q.; Lin, Y.; Yuan, W.; Chen, J.; Huang, S.-M. Multi-objective optimization of a mini-channel heat sink with non-uniform fins using genetic algorithm in coupling with CFD models. Appl. Therm. Eng. 2022, 207, 118127. [Google Scholar] [CrossRef]
- Polat, M.E.; Cadirci, S. Artificial neural network model and multi-objective optimization of microchannel heat sinks with diamond-shaped pin fins. Int. J. Heat Mass Transf. 2022, 194, 123015. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, H.; Zeng, H.; Zhu, J.; Chen, K.; Cui, Z.; Wang, J. Structural optimization design of sinusoidal wavy plate fin heat sink with crosscut by Bayesian optimization. Appl. Therm. Eng. 2022, 213, 118755. [Google Scholar] [CrossRef]
- Ismail, O.A.; Ali, A.M.; Hassan, M.A.; Gamea, O. Geometric optimization of pin fins for enhanced cooling in a microchannel heat sink. Int. J. Therm. Sci. 2023, 190, 108321. [Google Scholar] [CrossRef]
- Yu, C.; Zhu, X.; Li, Z.; Ma, Y.; Yang, M.; Zhang, H. Optimization of elliptical pin-fin microchannel heat sink based on artificial neural network. Int. J. Heat Mass Transf. 2023, 205, 123928. [Google Scholar] [CrossRef]
- Yang, W.; Mills, J.K. Optimization of Pin Arrangement and Geometry in EV and HEV Heat Sink Using Genetic Algorithm Coupled With CFD. In Proceedings of the 2021 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 8–11 August 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 332–337. [Google Scholar]
- Wan, W.; Deng, D.; Huang, Q.; Zeng, T.; Huang, Y. Experimental study and optimization of pin fin shapes in flow boiling of micro pin fin heat sinks. Appl. Therm. Eng. 2017, 114, 436–449. [Google Scholar] [CrossRef]
- Keramati, H.; Hamdullahpur, F.; Barzegari, M. Deep reinforcement learning for heat exchanger shape optimization. Int. J. Heat Mass Transf. 2022, 194, 123112. [Google Scholar] [CrossRef]
- Ghasemi, A.; Elham, A. Multi-objective topology optimization of pin-fin heat exchangers using spectral and finite-element methods. Struct. Multidiscip. Optim. 2021, 64, 2075–2095. [Google Scholar] [CrossRef]
- Ismayilov, F.; Akturk, A.; Peles, Y. Systematic micro heat sink optimization based on hydrofoil shape pin fins. Case Stud. Therm. Eng. 2021, 26, 101028. [Google Scholar] [CrossRef]
- Huang, Y.; Xu, M.; Li, H.; Shen, S.; Song, X.; Liu, H.; Waili, A.; Zhao, L.; Wei, W. Novel thermal design of micro-bream-fin heat sink using contour-extraction-based (CEB) method. Int. J. Therm. Sci. 2021, 165, 106952. [Google Scholar] [CrossRef]
- Yoon, G.H. Topological design of heat dissipating structure with forced convective heat transfer. J. Mech. Sci. Technol. 2010, 24, 1225–1233. [Google Scholar] [CrossRef]
- Dong, X.; Liu, X. Multi-objective optimal design of microchannel cooling heat sink using topology optimization method. Numer. Heat Transf. Part A Appl. 2020, 77, 90–104. [Google Scholar] [CrossRef]
- Subramaniam, V.; Dbouk, T.; Harion, J.-L. Topology optimization of conjugate heat transfer systems: A competition between heat transfer enhancement and pressure drop reduction. Int. J. Heat Fluid Flow 2019, 75, 165–184. [Google Scholar] [CrossRef]
- Yaji, K.; Yamada, T.; Yoshino, M.; Matsumoto, T.; Izui, K.; Nishiwaki, S. Topology optimization in thermal-fluid flow using the lattice Boltzmann method. J. Comput. Phys. 2016, 307, 355–377. [Google Scholar] [CrossRef]
- Sun, S.; Liebersbach, P.; Qian, X. Large Scale 3D Topology Optimization of Conjugate Heat Transfer. In Proceedings of the 2019 18th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), Las Vegas, NV, USA, 28–31 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Alexandersen, J. Efficient Topology Optimisation of Multiscale and Multiphysics Problems; University of Southern Denmark: Odense, Denmark, 2016. [Google Scholar]
- Alexandersen, J.; Andreasen, C.S. A Review of Topology Optimisation for Fluid-Based Problems. Fluids 2020, 5, 29. [Google Scholar] [CrossRef]
- Sigmund, O.; Petersson, J. Numerical instabilities in topology optimization: A survey on procedures dealing with checkerboards, mesh-dependencies and local minima. Struct. Optim. 1998, 16, 68–75. [Google Scholar] [CrossRef]
- Yoshimura, M.; Shimoyama, K.; Misaka, T.; Obayashi, S. Topology optimization of fluid problems using genetic algorithm assisted by the Kriging model. Int. J. Numer. Methods Eng. 2017, 109, 514–532. [Google Scholar] [CrossRef]
- Shimoyama, K.; Komiya, A. Multi-objective Bayesian topology optimization of a lattice-structured heat sink in natural convection. Struct. Multidiscip. Optim. 2022, 65, 1. [Google Scholar] [CrossRef]
- Mekki, B.S.; Lynch, S.P. Voxel-Based Topology Optimization of Heat Exchanger Fins. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2022. [Google Scholar]
- Mekki, B.S.; Langer, J.; Lynch, S. Genetic algorithm based topology optimization of heat exchanger fins used in aerospace applications. Int. J. Heat Mass Transf. 2021, 170, 121002. [Google Scholar] [CrossRef]
- Weber, J.; Huckaby, E.D.; Straub, D. Comparison of Shape Optimization Methods for Heat Exchanger Fins Using Computational Fluid Dynamics. Int. J. Heat Mass Transf. 2023, 207, 124003. [Google Scholar] [CrossRef]
- Yaji, K.; Yamasaki, S.; Fujita, K. Data-driven multifidelity topology design using a deep generative model: Application to forced convection heat transfer problems. Comput. Methods Appl. Mech. Eng. 2022, 388, 114284. [Google Scholar] [CrossRef]
- Joo, Y.; Lee, I.; Kim, S.J. Topology optimization of heat sinks in natural convection considering the effect of shape-dependent heat transfer coefficient. Int. J. Heat Mass Transf. 2017, 109, 123–133. [Google Scholar] [CrossRef]
- Dilgen, S.B.; Dilgen, C.B.; Fuhrman, D.R.; Sigmund, O.; Lazarov, B.S. Density based topology optimization of turbulent flow heat transfer systems. Struct. Multidiscip. Optim. 2018, 57, 1905–1918. [Google Scholar] [CrossRef]
- Sun, S.; Liebersbach, P.; Qian, X. 3D topology optimization of heat sinks for liquid cooling. Appl. Therm. Eng. 2020, 178, 115540. [Google Scholar] [CrossRef]
- Yu, M.; Wang, X.; Gu, J.; Ruan, S.; Li, Z.; Qian, S.; Zhang, J.; Shen, C. A synergic topology optimization approach on distribution of cooling channels and diverse-intensity heat sources for liquid-cooled heat sink. Struct. Multidiscip. Optim. 2022, 65, 48. [Google Scholar] [CrossRef]
- Li, Y.; Roux, S.; Cathy, C.; Luo, L.; Fan, Y. A genetic algorithm-based topology optimization method for convective cooling of a heating surface with multiple-peak heat flux. In Proceedings of the Congrès Français de Thermique SFT, 30ième Congrès SFT, Valenciennes, France, 31 May 2022. [Google Scholar]
- Ozguc, S.; Pan, L.; Weibel, J.A. Topological optimization of flow-shifting microchannel heat sinks. Int. J. Heat Mass Transf. 2023, 207, 123933. [Google Scholar] [CrossRef]
- Zhang, T.; Jing, T.; Qin, F.; Sun, X.; Li, W.; He, G. Topology optimization of regenerative cooling channel in non-uniform thermal environment of hypersonic engine. Appl. Therm. Eng. 2023, 219, 119384. [Google Scholar] [CrossRef]
- Wang, M.L.; Zheng, L.J.; Bae, S.; Kang, H.W. Comprehensive performance enhancement of conformal cooling process using thermal-load-based topology optimization. Appl. Therm. Eng. 2023, 227, 120332. [Google Scholar] [CrossRef]
- Chen, F.; Wang, J.; Yang, X. Topology optimization design and numerical analysis on cold plates for lithium-ion battery thermal management. Int. J. Heat Mass Transf. 2022, 183, 122087. [Google Scholar] [CrossRef]
- Lin, Y.; Zhu, W.; Li, J.; Ke, Y. A stabilized parametric level-set XFEM topology optimization method for thermal-fluid problem. Int. J. Numer. Methods Eng. 2022, 123, 924–952. [Google Scholar] [CrossRef]
- Maksum, Y.; Amirli, A.; Amangeldi, A.; Inkarbekov, M.; Ding, Y.; Romagnoli, A.; Rustamov, S.; Akhmetov, B. Computational Acceleration of Topology Optimization Using Parallel Computing and Machine Learning Methods–Analysis of Research Trends. J. Ind. Inf. Integr. 2022, 28, 100352. [Google Scholar] [CrossRef]
- Dbouk, T. A review about the engineering design of optimal heat transfer systems using topology optimization. Appl. Therm. Eng. 2017, 112, 841–854. [Google Scholar] [CrossRef]
- Liu, J.; Gaynor, A.T.; Chen, S.; Kang, Z.; Suresh, K.; Takezawa, A.; Li, L.; Kato, J.; Tang, J.; Wang, C.C.L.; et al. Current and future trends in topology optimization for additive manufacturing. Struct. Multidiscip. Optim. 2018, 57, 2457–2483. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).