Abstract
This article presents an approach to locating wind farms based on open-source data, GIS software (QGiS v.3.32 Lima), and multicriteria decision-making methods such as AHP, TOPSIS and Borda. The article aims to check the availability of the most suitable sites for wind farms in Podlaskie Voivodeship, Poland. After the site-selection process, 704 plots were selected after three stages of exclusion (technical–natural, social, and economic). These plots cover a total area of 32.50 km2, about 0.16% of the region’s area. The results show that Podlaskie Voivodeship has the most considerable clustering of suitable sites for wind farm construction in three districts, with a total area of 21.53 km2. The first district is in the southwestern part of the region, with an area of 14.84 km2; the second district is in the southeastern part of the region, with an area of 5.59 km2; and the third district is in the northern part of the region, with an area of 1.1 km2. A selected area of 32.50 km2 for wind farms and single turbines could increase the power capacity by 62% with 131.5 MW. The GIS and multicriteria decision analysis (MCDA) methodology is repeatable and can be used for further research in other voivodeships in Poland and other countries. International and Polish investors and renewable energy sources (RESs) developers can use the research results to select new locations for investments that fit their strategy in the local market.
1. Introduction
The world is shifting towards sustainable energy sources, and wind energy significantly contributes to reducing greenhouse gas emissions and combating climate change [1]. This is indicated in research by Chaurasiya and Kuo, emphasising the importance of reducing greenhouse gas emissions. Wind farms are installed rapidly, e.g., by 33% in the EU in 2022 [2]. More than 38,000 large offshore wind turbines will be installed across the globe by 2036, significantly adding to the world’s renewable energy capacity. By the end of 2023, the industry will reach a historic milestone—1 terawatt of wind energy installed worldwide [3,4]. However, the question of where to place new wind farms has become a topic of intense scientific research and public discussion due to the increasing demand for clean energy [5,6].
As we work towards a sustainable energy future, it is crucial to identify suitable locations for wind farms. Factors such as wind resource potential (wind speed) [7,8], land availability (land cover classification) [9], impacts on nature and humans (the aesthetic of the landscape, acoustic environment, shadow flickering, and wind turbines electromagnetic interference) [10], social acceptance (survey with the use of the questionnaire and the analysis of the content of strategic documents of the voivodeships) [11,12], and grid integration (distance to the power grid and roads) [13,14] all play an essential role in the successful development and operation of wind power projects.
Studies have been conducted on different aspects of this topic to overcome the difficulties related to wind farm localisation. One area of research has focused on finding more accurate ways to assess wind resources, which has helped pinpoint the best locations for wind farm development. Łaska [15] analysed nine multicriteria analyses based on nine criteria (environmental, social, and economic) for siting 15 turbines in Northeastern Poland. Santos-Alamillos et al. [16] utilised the principal component analysis (PCA) to examine the spatiotemporal balancing of wind energy resources and evaluated the ideal wind farm location to minimise fluctuations in wind power. Additionally, advanced computer modelling and geospatial analysis tools have been utilised to analyse the potential effects of wind farms on wildlife, habitats, and visual landscapes, making it easier to choose sustainable locations that minimise environmental impacts [17,18].
Apart from environmental protection, local communities’ approval of wind farms is crucial. Some communities welcome wind energy as a chance for economic growth [19,20] and decreasing greenhouse gas emissions [21]. A 2 MW wind turbine with a hub height from 80 m to 120 m and a 20-year lifespan will reduce greenhouse gas emissions from 3.1 × 106 kg CO2 to 3.57 × 106 kg CO2, respectively, compared with traditional fossil fuel [1]. Meanwhile, others analysed visual beauty [22,23] and potential effects on property values [24,25]. Also, an important factor is an acoustic environment with an acoustic noise level of 50 dB at nighttime and 55 dB during the day [26]. To reach this goal, the acousticians and the power engineers are looking for the best wind turbine model with a low acoustic emission [27]. Based on the simulations conducted by Ruggiero et al. [28], the noise levels near the turbines are around 55 dBA with average wind speed conditions, while the noise levels in the surrounding area are lower. It is considered compatible with daily human agricultural activity.
Experts are evaluating how changes in Polish law regarding renewables in 2023 will impact the Polish market [29]. The capacity of onshore wind power has been steadily increasing over the years, with a growth of 10.6% recorded in 2022, rising from 6.61 GW to 7.31 GW [30]. In addition, energy production also significantly increased by 28%, from 14,234 GWh to 18,305 GWh, according to the Polish Energy Regulatory Office [31]. By the end of March 2023, the capacity of onshore wind power increased by 17.9% to 8.57 GW [32], now representing 10% of the total energy produced in Poland [29].
Another critical factor is the distance to the urban areas, where, after changes in the ACT on investments in wind power plants of 9 March 2023, liberalisation from the 10H rule to 700 m was made [33]. Experts say that reducing the limits from 700 m to 500 m to the urban areas could give 7–8% of the area with a theoretical power capacity of 6 GW [34]. They consider that it gives an extra 4–5% of new areas for further investments with a theoretical power capacity of 4–5 GW [35].
While there is a growing demand for clean energy and the rapid expansion of wind farms globally, the specific process of selecting optimal sites in the Podlaskie Voivodeship using GIS and multicriteria decision-making methods has not been thoroughly explored.
Finding locations that balance clean energy production with environmental protection [36,37], economic feasibility [38], and social acceptance [39] is crucial as the demand for renewable energy like wind power grows [40].
The novelty of the research is a holistic approach to site selection by integrating a set of criteria and using GIS and multicriteria decision analysis (MCDA) methods. This approach allows for spatial analysis and data-driven decision making, enhancing the accuracy and objectivity of the site selection process. The research focuses on a specific region, Podlaskie Voivodeship, providing localised insights into the potential for wind farm development. The study offers practical implications for international and Polish investors, renewable energy developers, and local authorities. Identifying 704 potential plots and three specific districts with high suitability for wind farm construction provides actionable information for stakeholders looking to invest in clean energy projects.
Mathematical modelling was conducted using a set of 11 criteria and three multicriteria decision methods: AHP, TOPSIS, and Borda. The article also presents a map of appropriate sites for further investigation created in the QGiS program.
2. Materials and Methods
2.1. Materials
In the analysis of potential wind farm locations, we utilised data from various databases:
- The National Database of Topographic Objects with a resolution of 1:10,000 (BDOT10k) [41,42,43];
- A digital elevation model (DEM) [44,45];
- Surface forms of nature protection in Poland managed by the General Directorate for Environmental Protection (GDOŚ) [46];
- The land cover classification gridded map managed by the European Space Agency and Copernicus Services (the Earth observation component of the European Union’s space programme) [47];
- The land cover table used for the land cover classification gridded map [48];
- The flood hazard areas map (ISOK project), powered by the Institute of Meteorology and Water Management (IMGW) [49,50];
- Maps of mean wind speed and power density of air at 100 m managed by Global Wind Atlas [51];
- Locations of currently built wind farms in the region from OpenStreetMap [52].
In the analysis of wind farm locations, the BDOT10k layers were used with data about communication networks, water networks, land development, land cover, etc (Table 1). Various factors were taken into account in the study, such as distances to water bodies and wetlands, protected nature areas and forests due to ecological, distances to urban areas due to legal, distances to roads, power grids, and the minimal area for one wind turbine due to technical and economic restrictions. To eliminate hilly terrain, mountains, and areas with extensive earthworks, a slopes map was generated using DEM data. The analysis also excludes areas of natural hazard related to floods.

Table 1.
GIS layers from BDOT10k were used in the analysis of potential wind farm locations.
2.2. Methods
The multicriteria decision analysis (MCDA) allows for a set of admissible solutions to be determined and, based on a defined set of criteria for evaluating individual results, allows for the optimal solution to be found. These methods are among the multicriteria optimisation methods in which the domain of the decision variables is a finite set of values. Decision variables are to be understood as quantities that influence the value of the synthetic evaluation index of individual solutions [53,54]. The result of conducting a multicriteria analysis is the selection of the best solution from among a number of alternatives. The selection is based on various criteria that significantly impact the solution’s implementation and performance. The criteria are like factors designed to increase or decrease the suitability of a particular decision option. Different criteria are assigned different preferences, thus effecting the final outcome of the multicriteria analysis. The criteria that form the basis of decision making are measured or evaluated. Individual options are qualified or excluded during the decision-making process due to the requirement to consider specific constraints [53].
In solving decision-making problems, consideration is given to the following:
- A set of options from which the best one is chosen;
- A set of decision criteria;
- The set of weights assigned to the decision criteria;
- A decision matrix containing the values obtained by the variants in light of each criterion.
The criteria in multicriteria analyses are either “hard” or “soft” in nature [53,55]. The analysis of the problem in the case of “hard” criteria leads to a solution that is the sum or product of events. The “hard” criteria allow for a map to be created showing the areas that match or do not match the accepted conditions. The combination of “hard” criteria makes it possible to find a common part. The “soft” criteria make it possible to determine the degree of suitability of the areas in question for the stated purpose of the analysis. Soft criteria are used when the decision criteria are very heterogeneous in nature. The results with “soft” criteria are less clear-cut than with “hard” criteria [53].
MCDA methods are applied in many fields; they are used, among others, in the creation of structural and spatial classifications of specific areas, in the valorisation of areas, in the development of optimal strategies for the development of territorial units, in determining the suitability of land for specific functions (mixed, service, industrial, protective, and natural), in the management of environmental resources, in the assessment of the impact of planned investments and activities on the environment, and in the resolution of conflict situations in spatial management [53,56,57].
We divide multicriteria decision support into utility functions, relationship outranking, distances, and decision support methods (Figure 1).
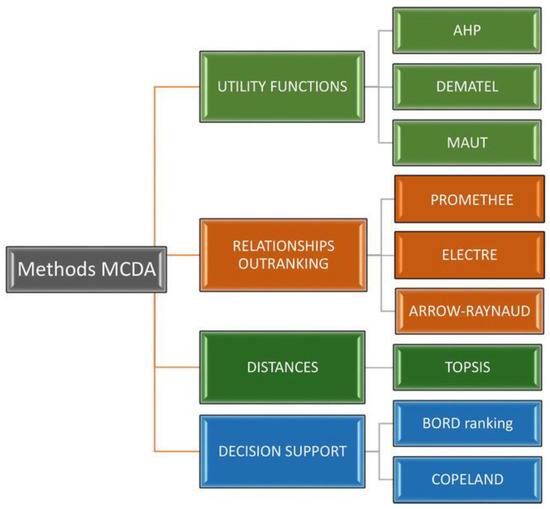
Figure 1.
Division of MCDA methods [15].
2.2.1. The AHP Method
The AHP method is a versatile tool for solving many decision-making problems. In the analysed method, the evaluations of the options or criteria are generally subjective in nature, as they indicate the different preferences of the decision-maker. The final result of the multicriteria analysis often depends on the stated objectives and preferences of the decision-maker. The advantage of the AHP method is the ease of combining evaluations of criteria of a quantitative and qualitative nature. It is used, among other things, in marketing research and management decision support, in product attractiveness rankings, in the analysis of market competitiveness factors, in supporting the selection of bidders or suppliers, or in supporting the selection of the best alternative [53,58,59].
The AHP method allows users to determine the mutual importance of criteria or decision alternatives in relation to individual criteria by comparing criteria in pairs and comparing decision alternatives in pairs in light of the criteria adopted for their evaluation. The method uses a relative rating scale defined by Saaty [60] (pp. 5–7).
The AHP method is characterised by not assigning weights to the adopted criteria and decision options directly. The method operates only on the relative ratings determined in pairwise comparisons; as a result, this procedure allows the weights to be determined [53]. The calculation procedure in the AHP method is based on three principles [61]:
- The principle of “constructing a hierarchy”;
- The “prioritisation” principle;
- The principle of “logical” consistency [60].
The AHP method is implemented in five steps [53]:
- The construction of a hierarchical model, including decomposition into components and determining the hierarchy of criteria.
- A pairwise comparison evaluation involves creating quadratic matrices for each hierarchy level. These matrices, known as preference matrices, exhibit pairwise consistency (1):
The creation of the comparison matrix is performed by initially determining the ratings according to the Saaty scale [60] (the value determining the degree of dominance of one element over the other in each pair of elements being compared (i) and (j)) and then completing the comparison matrix:
- When (i) = (j), then = 1 is assumed;
- When (i) ≠ (j), then = 1/ is taken;
- When there is no evaluation, then = is taken.
- 3.
- Global and local preferences are determined by the components of the eigenvector (w) of the comparison matrix, P, which is associated with the maximum eigenvalue, . The determination of preferences from the pairwise comparison matrix is performed by various methods, including the following:
- The column averaging method of the evaluation matrix (the so-called Saaty method);
- The power method;
- The right-hand eigenmatrix method.
The method of averaging the columns of the rating matrix (P) consists of two steps: the normalisation of the rating matrix (P 🡪 ) and the determination of preferences based on the elements of the normalised matrix. The normalisation of the matrix consists of summing the elements contained in each column and dividing by the resulting sum the subsequent elements of the column [53]. Subsequently, preferences are determined as values that are the arithmetic mean of the elements, , in the individual rows ((i) = 1, 2, …, (m)) of the normalised matrix (2):
The power method involves raising the rating matrix (P) to successive powers and determining, in each successive step, the arithmetic averages of the individual rows of the resulting matrix, which is a successive power of the initial matrix. The normalised values are obtained by dividing the values of these averages by their sum, creating a potential vector of weights/preferences (w) of the individual attributes whose pairwise comparison formed the basis for the creation of the matrix, P. The process of normalising the components of the vector of weights makes it possible to obtain successive approximations that are comparable with each other [53].
The right-hand eigenmatrix method is recommended by Saaty [62] for determining preferences. It is one of the complex methods for which it is necessary to use appropriate numerical computing systems [53].
- 4.
- Verify the rating consistency from pairwise comparisons and calculate the consistency index (CI) to assess the quality of subjective assessments (3). The (CI) determines transitivity in dominance assessment. The consistency ratio (CR) is then computed by dividing the (CI) by the (RI) value (4):
- 5.
- Decision options are classified by calculating the aggregate utility function value for each option, resulting in a final ranking.
2.2.2. The Borda Method
The Borda method involves applying the adopted ordinal scale to all criteria and considering the options in light of successive criteria numbered from 1 to n in order from best to worst. When several variants rank equally in a particular ranking, it is permissible to apply a score averaging for them [53,63,64,65]. The best variant has the highest value of the so-called Borda number (5):
where is the order of option (i) in light of criterion (j), with (i) = 1, 2, …, (m), (j) = 1, 2, …, (n).
In order to take into account the importance of each criterion, the Borda number can be modified by using a weighted SAR summation index, which, in the case of the Borda number, has the following form (6):
with restrictions (7):
2.2.3. Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS)
TOPSIS is a user-friendly method, thus making it easy to comprehend and utilise [66,67]. Another major advantage of TOPSIS is its capacity to incorporate both quantitative and qualitative factors, making it a versatile solution for various decision-making scenarios. However, it is worth noting that this method may not be the most suitable choice for all situations, as it can be sensitive to changes in criteria weights and relies on certain assumptions about linear relationships. Despite these limitations, TOPSIS has proven to be an effective solution in many fields, including project selection, supplier evaluation, product design, environmental management, and healthcare.
The TOPSIS method is implemented in seven steps:
- Create a decision matrix with alternatives and criteria. It is an m x n matrix, where m is the alternatives and n is the criteria, showing each alternative’s performance on specific criteria.
- Normalise the decision matrix to equalise criteria weights. This step eliminates scale differences between criteria. Normalise each element using Equation (8), as specified:
- 3.
- Determine the weighted normalised decision matrix by assigning weights to criteria based on their relative importance (summing up to 1). Multiply each element of the normalised decision matrix by its corresponding weight to obtain the weighted normalised decision matrix (9):
- 4.
- Calculate the ideal and negative–Ideal solutions to represent the best and worst performances on each criterion. Identify the maximum and minimum values among all alternatives for each criterion. Ideal solution (10):
Negative–ideal solution (11):
- 5.
- Calculate the Euclidean distances between each alternative and the ideal and negative–ideal solutions. This measures the similarity between an alternative and the ideal or negative–ideal solutions. Ideal solution (12):
Negative–ideal solution (13):
where and are the Euclidean distances of the (i)-th alternative from the ideal and negative–ideal solutions, respectively.
- 6.
- Calculate the relative closeness to the ideal solution by finding the ratio of the Euclidean distance from the negative–ideal solution to the sum of the distances from both the ideal and negative–ideal solutions for each alternative (14):
- 7.
- Rank the alternatives based on their relative closeness values. The alternative with the highest relative closeness is considered the best choice.
3. Results
3.1. Area of Potential Investments
Poland experiences constant changes in territorial division. Compared to 2021, the area of Poland has increased by 15.05 km2 (from 312,705.25 km2 to 312,720.30 km2), of which 12.04 km2 concerns the Pomorskie Voivodeship. It is the result of adjusting the borders of territorial units to the baseline of the territorial sea [68]. The total area of the Podlaskie Voivodeship decreased by 0.17 km2 [69]. Poland has 16 voivodeships. Podlaskie Voivodeship is the East region of Poland, with a population of 1.143 mln and a total area of 20,180 km2 [69,70]. This region has the 14th position according to population, the 6th position according to the total area, and the 10th position by the level of urbanisation [71]. The Podlaskie Voivodeship presents an excellent opportunity for additional investment in renewable energy thanks to its optimal combination of urbanisation, population, and region size (Figure 2).
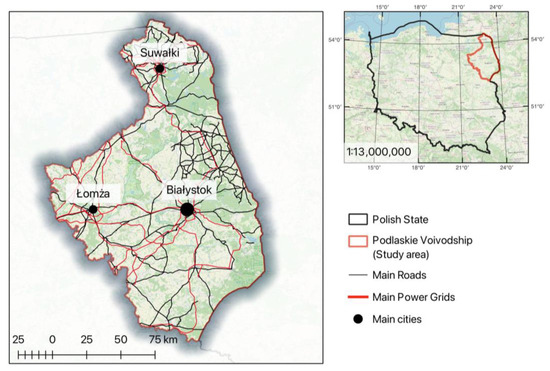
Figure 2.
Area of potential investments and its location in Poland.
3.2. Mathematical Modelling
Before the spatial analysis, mathematical modelling was performed. The mathematical models use a group of 11 criteria for the six variants. These variants represent potential setups of criteria that RES developers could use as a template under the first phase of investment (Table 2). The criteria were chosen and adapted to Polish conditions because of the previous work of authors [72] and Szurek [13]. Three criteria, such as protected nature areas, urban areas, and water bodies, are groups and contain sub-criteria. Each sub-criterion has the same value as the main criterion of the group (urban areas and water network). Sub-criteria of the protected nature areas group have different values because of legal restrictions in Poland. The value for the protected nature areas in Table 2 represents the distances to Natura 2000 areas. All the criteria and sub-criteria values used in the analysis are presented in Section 3.3.

Table 2.
Variants with criteria and their values for mathematical modelling.
The article uses three MCDA methods (AHP, Borda, and TOPSIS). It is necessary to avoid mistakes during the calculation process and for comparing results. If the results of all three methods are the same or consistent, the result (i.e., variant from 1 to 6) will be used in the spatial planning.
3.2.1. AHP Method Results
In this research, the AHP method was used because the hierarchy of evaluation criteria and most criteria for evaluating the considered options are subjective, and a small part of the criteria is quantitative options. A hierarchical model was created for the decision problem under consideration, and then a comparison matrix was built to determine global and local preferences. Subsequently, a synthetic score was determined for each decision option, ranking the considered variety. For pairwise comparison, the preference matrix was created (Supplementary Table S1). After pairwise comparison, the preference matrix was normalised. The weights and the λ were calculated (Table 3).

Table 3.
Criteria weights and λ values for the AHP method.
Based on the 11 criteria, the (RI) value is 1.51. If the maximum eigenvalue () is 11.23, the consistency index (CI) is 0.023, and the consistency ratio (CR) is 0.016 < 0.1, then the matrix is considered consistent. By calculating the value of the aggregate utility function for each option, a final ranking is produced (Table 4). Table 4 shows that Variant 6 is the best for further spatial analysis. Variant 6 implicates the location of wind farms with a 200 m distance from monuments of nature and 2000 m to Natura 2000; 100 m distance to the forests, water surfaces, and roads; 200 m distance to the power grid; and 700 m distance to the urban areas.

Table 4.
Ranking of variants according to scores, using the AHP method.
3.2.2. Borda Method Results
The Borda number and SAR summation index show that Variant 6 is the best for further spatial analysis because of the highest value of the Borda number and the weighted SAR summation index (Table 5). The weights for calculating the weighted SAR summation index were taken from the AHP method. Variant 6 is the same as the result in the AHP method.

Table 5.
The Borda number and the weighted SAR summation index, using the Borda method.
3.2.3. TOPSIS Method Results
The final results of calculations, such as the Euclidean distance of each variant to the ideal and negative–ideal solutions and the relative closeness values, are presented below (Table 6). Variant 3 is the best, with the highest relative closeness value. Due to the slight difference of 4.5% between Variants 3 and 6 and the results of previous mathematical models (AHP and Borda ranking), Variant 6 is selected for further spatial analysis.

Table 6.
The Euclidean distances and the final ranking of variants, using the TOPSIS method.
3.3. Spatial Analysis
The spatial analysis was performed using open-source GIS programs: QGiS and SAGAGIS.
The spatial analysis was conducted in three stages. The initial stage involved eliminating areas that did not meet the criteria for wind farm placement. There are protected nature areas with monuments of nature, forests, water networks, and permanent crops; urban areas; power grids and roads; and areas around already-built wind turbines. A safety buffer was added for each of these areas (Table 7).

Table 7.
GIS layers with buffer zones, their area, and their share for spatial analysis.
As a result, from the total area of the Podlaskie Voivodeship (20,180 km2), the overlayed area of 19,911 km2 was eliminated. This number includes protected natural areas with monuments of nature (3867 km2). There are 4 national parks, 94 reserves, 3 landscape parks, 13 protected landscape areas, and 37 areas of Natura 2000 (25 SOO; 12 OSO), in addition to other forms of protected natural areas [73]. Next, areas such as ecological corridors (10,009 km2), forests (11,749 km2), water networks (5021 km2), permanent crops (136 km2), urban areas (14,422 km2), power grids (278 km2), roads (6296 km2), and areas around already-built wind turbines (63.2 km2) were eliminated (Table 7).
After the initial stage of exclusion, a total of 4556 plots were selected, covering a combined area of 269 km2. These plots represent approximately 1.33% of the total area in the west, southwest, and south parts of Podlaskie Voivodeship (Figure 3).
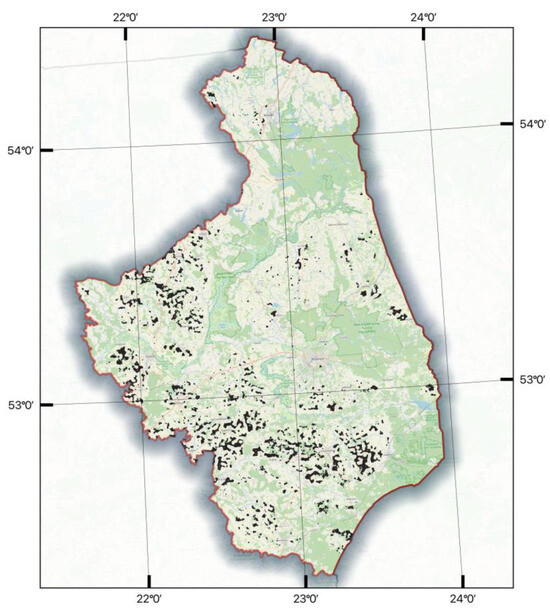
Figure 3.
Area of investments with potential sites for wind farms after the initial stage of exclusion (black colour—selected plots after exclusion).
The second stage involved eliminating areas which were not included in the mathematical model. There are areas which are fragmented in the Podlaskie Voivodeship: sacred complex and cemetery (11.6 km2), historic and historical complexes (4.02 km2), city borders (951.15 km2), and excavations and heaps (30.43 km2). Figure 4a presents a map with prohibited areas before exclusion.
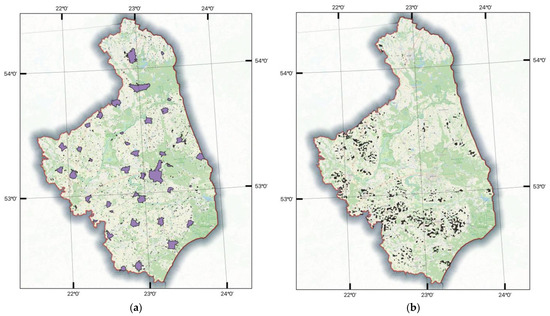
Figure 4.
Area of potential investments, with (a) a map with prohibited areas before exclusion (violet colour—prohibited areas) and (b) a resulting map with potential sites after the second stage of exclusion (black colour—selected plots after exclusion).
After the second stage of exclusion, a total of 4344 plots were selected, covering a combined area of 255.41 km2. These plots represent approximately 1.26% of the total area in the west, southwest, and south parts of Podlaskie Voivodeship (Figure 4b).
Before the final (third) exclusion, single plots with an area of less than 400 m2 were deleted because of the required minimum area for one wind turbine foundation.
The third stage involved eliminating areas which did not meet the economic criteria (Figure 5) according to Variant 6 (Table 2):
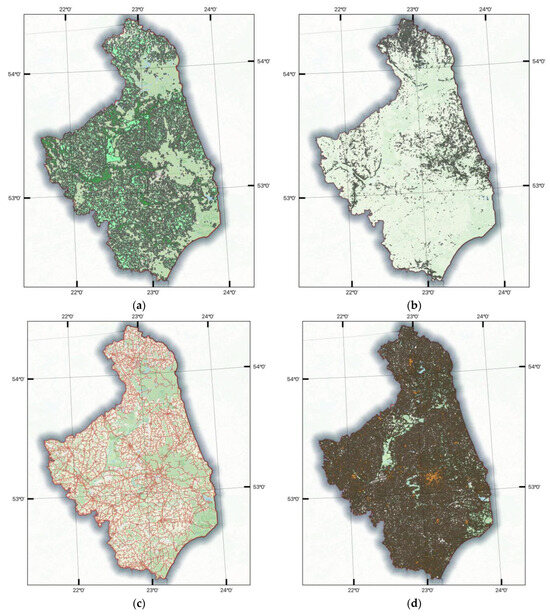
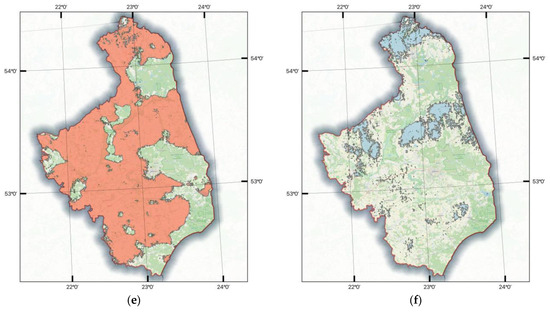
Figure 5.
Area of potential investments with criteria during the final exclusion: (a) the map of roughness classes with a value from 1 to 2 (green colour—roughness class with a value 1; light green colour—roughness class with a value 2); (b) the map of the slope with a value from 0° to 3° (light green colour—the slope with a value 0°; grey colour—the slope with a value 3°); (c) the map of the power grid with 200 m buffer (red colour—power grid with 200 m buffer); (d) the map of roads with 100 m buffer (black and orange colour—roads with 100 m buffer); (e) the map of mean wind speed on 100 m high with a value from 7 to 8 m/s (orange colour—mean wind speed with a value from 7 to 8); and (f) the map of the power density of air with a value from 450 to 500 W/m2 (light blue colour—power density of air with a value from 450 to 500).
- Roughness class from 1 to 2;
- Slope from 0° to 3°;
- Power grid with 200 m buffer;
- Roads with 100 m buffer;
- Mean wind speed from 7 to 8 m/s;
- Power density of air from 450 to 500 W/m2.
During the third stage, the last six criteria were overlayed to eliminate unsuitable sites. There are six maps: the map of roughness (11,520.19 km2), the map of slope (19,108.04 km2), the map of the power grid with a 200 m zone (4869.6 km2), the map of roads with a 100 m zone (10,875.2 km2), the map of mean wind speed of 100 m high (13,791.1 km2), and the map of the power density of air (2412.9 km2).
After the third stage of exclusion, a total of 704 plots were selected, covering a combined area of 32.50 km2. These plots represent approximately 0.16% of the total area in the west, southwest, and south parts of Podlaskie Voivodeship (Figure 6).
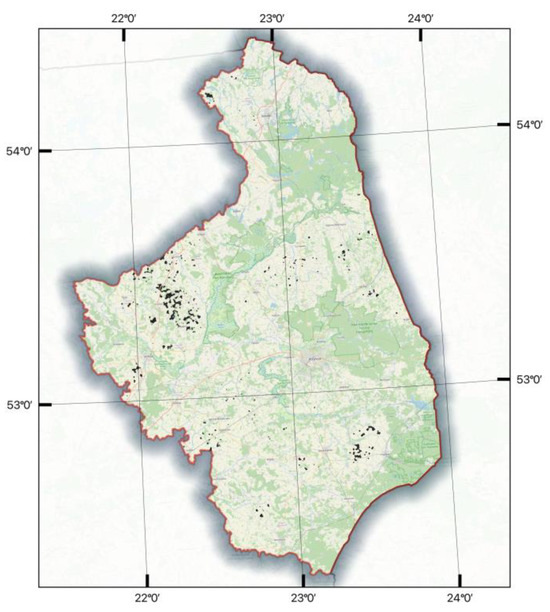
Figure 6.
Area of potential investments with potential sites for wind farms after the final stage of exclusion (black colour—selected plots after exclusion).
Through a thorough site-selection process, 704 plots covering a total area of 32.50 km2 were identified as potential locations for wind farms and single turbine development. The final exclusion also shows that Podlaskie Voivodeship has the largest clustering of suitable sites for wind farm construction in three districts, with a total area of 21.53 km2. The first district has 240 plots between Stawiski and Jedwabne cities (14.84 km2). This district is in the eastern part of Kolneński County, in the northern part of Łomżyński County and in the southern part of Grajewski County. This district crosses seven communes (Grabowo, Wąsosz, Radziłów, Mały Płock, Stawiski, Przytuły, and Jedwabne). The second district has 79 plots between Bielsk Podlaski and Hajnowka Cities (5.59 km2). This district is in the eastern part of Bielski County and in the western part of Hajnówski County. This district crosses five communes (Bielsk Podlaski, Czyże, Narew, Hajnowka, and Orla). The third district has 20 plots close to Garbas Drugi village (1.1 km2). This district is in the western part of Suwałski County in Filipów Commune.
4. Discussion
The selected area (about 0.16% of the region) offers significant opportunities for international and Polish investors and renewable energy developers to select new sites that align with their strategies in the local market. Podlaskie Voivodeship has seven wind farms, according to open-source data (Augustowo, Grajewo, Orla, Rajgrod, Piecki, Suwałki, and Taciewo), with a total power capacity of 211.9 MW. These wind farms use 52.35 km2 of land, with a 250 m radius around each turbine because of the inefficiency of air turbulence and power production. Adding 32.50 km2 of selected areas could theoretically increase the power capacity by 62%, with 131.5 MW, if wind farms and single wind turbines are built. Adding 21.53 km2 of selected areas in three districts for building wind farms could increase the power capacity by 41%, with 87.2 MW. This assumption is based on averaged data from constructed wind farms in the region and should be refined during further stages of assessing the potential of the selected site for wind farms. The results (about 0.16% of the region’s area) can be considered satisfactory. Diaz [74] reports that up to 0.03% (143.5 km2 of the considered area) has good potential for offshore wind farms.
The use of GIS and MCDA methods allows for a comprehensive assessment of various criteria, including wind resource potential, land availability, environmental restrictions, and grid integration, among others. Considering these factors, the study provides valuable insights for spatial energy planning and the efficient deployment of onshore wind farms.
The article shows that the TOPSIS method is reasonably objective, helping to analyse complex sets of criteria. Konstantinos [18] states that TOPSIS is well suited for complex analyses in combination with other methods, like AHP. The TOPSIS method is suitable for finding locations for wind farms, considering a criterion such as social acceptance. Lozano-Minguez [75] says that the TOPSIS method was applied to obtain an objective methodology for the comparative analysis of different support structure options for offshore wind farms, considering engineering, economic, and environmental criteria.
The most used method is AHP [72]. It was used in the article because of the simplicity of the structuring and expanding of the mathematical model. According to Watróbski [76], the AHP method allows for an intuitive dialogue with decision-makers and simplifies organising and enhancing models. It can also be used in various areas of wind energy production. Aras [77] indicates that the AHP is widely used and can be easily applied to determine possible construction locations of wind observation stations. Also, the AHP method can be used for surveying local people and analysing based on it. Latinopoulos [78] says it is possible to carry out the AHP method comparative analyses with different groups of people, e.g., residents, experts, and wind farm developers.
The Borda method produces equivalent outcomes to the AHP method, allowing for an impartial comparison of criteria that are viewed as equal. Despite its infrequent use in mathematical modelling due to the absence of criteria standardisation and weight assignment, the Borda method treats all criteria with equal significance, as noted by Łaska [79]. Ultimately, the method delivers an objective outcome that hinges on the wind farm’s specific localisation criteria.
In scientific papers, different methods such as VIKOR, ANP, DEMATEL, ELECTRE, PROMETHEE, and others are utilised [72]. While each method has its advantages and disadvantages, combining them increases the accuracy of mathematical modelling and geospatial analysis [5], avoids uncertainties in the estimation processes of the weight and score of criteria [17], and eliminates vagueness in decision matrices [74]. Ultimately, using a combination of methods helps to achieve better and more precise outcomes in an analysis.
GIS layers of different types of topography used in the article have the maximum accuracy for Poland. Ławniczak [80] presented the results for the BDOT10k database comparing the location and shape of selected lakes. The geometric accuracy of the object size estimated is about 2% different than the field measurement. BDOT10k is countrywide topographic data with a level of detail and thematic scope corresponding to the civilian maps at a 1:10,000 scale. Mierzwiak [81] says that the primary source of spatial data for the study in Poland is BDOT10k, provided by the Central Geodetic and Cartographic Documentation Centre.
The digital elevation model provided by the Head Office of Geodesy and Cartography (GUGiK) is a state database for the representation of the elevation of the terrain, together with an interpolation algorithm that allows for the calculation of the elevation at any point in the area for which the model was built. It helps users obtain such layers as the elevation (relief) and slope of the chosen area. Kozłowska [82] says that an essential part of their approach was the cartometric analysis of the DEM, which provided detailed information about the relief of the valley bottom and the slopes limiting it, which allowed for a precise determination of the flood range.
Using a surface form of the nature protection database that is managed by the General Directorate for Environmental Protection (GDOŚ) is obligatory because it is necessary to know the exact boundaries of all forms of nature protection to fulfil the restrictions that are specified in the law on investments in wind energy installations [33].
To minimise the risk of flooding, the ISOK map was utilised, which identifies areas with a 0.2% occurrence probability. The ISOK map, provided by the Institute of Meteorology and Water Management (IMGW), allows authors to use it on a country scale in future work. Kozłowska [82] also says that one of the main tasks was comparing the results with the flood risk zones determined in the ISOK project and the flooded area in 1997. Thanks to this, it can be presumed that the presented area of flood risk could occur with a probability of 0.1%, which means that the determined flood extent can statistically happen once in 1000 years.
In the article for creating a roughness map, we use the land cover classification gridded map managed by the European Space Agency and Copernicus Services based on the methodology presented by Floors [48]. For now, Poland does not have data which can be used for creating roughness maps. Using the Polish digital land cover model to create a roughness map is also impossible because it covers only part of the country, is outdated, and is presented as tiles of 5 km2.
The article uses wind data such as maps of mean wind speed and power density of air from the Global Wind Atlas. These data allow authors to use it on a country scale without losing the accuracy of the results. Murcia [83] says that the combination of ERA5 and the Global Wind Atlas shows good agreement with measured country-level generation data. In future work, authors will collect regional wind data to compare them with the wind data from the Global Wind Atlas.
Seasonal wind variability is a critical factor to consider when constructing a wind farm. However, it is just one of many criteria involved in a comprehensive analysis. After identifying several suitable locations for wind farms, a thorough examination of the seasonal wind variability is necessary. In upcoming research, the analysis will focus on a smaller scale, such as one of the three districts outlined in the current study. This type of research is becoming increasingly important, as Weber [84] notes an increase in seasonal wind variability in most of Central, Northern, and Northwestern Europe.
Large companies’ investment planning departments evaluate future wind farms’ economic efficiency. Their objective is to achieve maximum profitability while minimising expenses. The key factors that impact the end outcome are the wind turbine purchase cost, wind speed, and wind stability throughout the year (measured in hours of operation) [85]. According to [72,86], the investment payback period lasts approximately 15.5 years.
This article strengthens the drive towards sustainable energy sources and reducing greenhouse gas emissions. Using wind turbines with varying hub heights (80 m to 120 m), rated power (2 MW to 3 MW), and a 20-year lifespan could significantly decrease greenhouse gas emissions compared to traditional coal plants [1,87].
They also highlight the importance of strategic site selection based on rigorous analysis and stakeholder engagement. With the increasing demand for clean energy, identifying suitable locations for wind parks becomes crucial to ensure successful project development and operation.
The sensitivity analysis was performed in the SuperDecisions program (Supplementary File S2). The sensitivity analysis results for the AHP method show that they are stable, with Variant 6 remaining the best option after the 11 criteria have been correctly considered, regardless of the criteria in question and changes in the values of its weights (Figure 7).
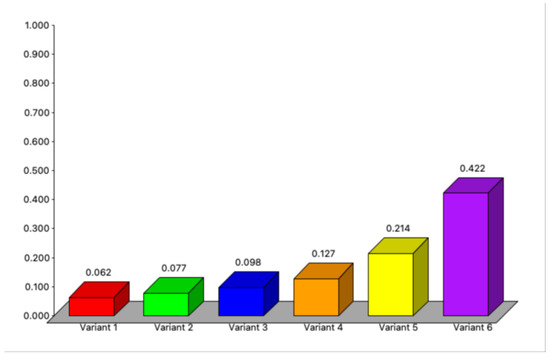
Figure 7.
Sensitivity analysis of criteria for the AHP method.
On the other hand, the sensitivity analysis of each variant indicated that the variants are sensitive with a p-value > 0.64. With such a p-value, each variant will rank first and better than Variant 6. However, choosing one of the variants when it is better than Variant 6 will not allow the wind farm to be built due to non-compliance with the regulations for constructing wind farms in Poland (Figure 8).
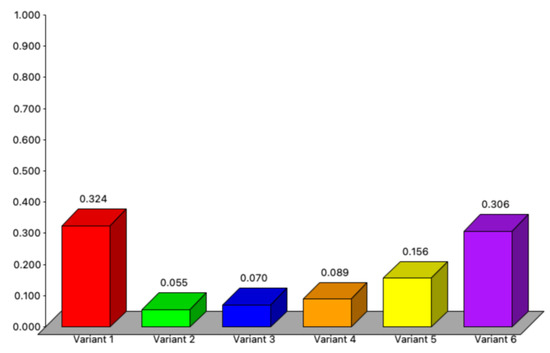
Figure 8.
Sensitivity analysis of criteria for the AHP method with a p-value > 0.64.
5. Conclusions
This article demonstrates the effectiveness of GIS and MCDA tools in the context of wind farm localisation. The results can inform decision-making processes for wind energy investments in Podlaskie Voivodeship and serve as a foundation for further research and development in the field of renewable energy planning and implementation in other voivodeships and countries. The most important conclusions from the article are as follows:
- The selected area, constituting approximately 0.16% of the region, offers significant opportunities for international and Polish investors and renewable energy developers. These opportunities align with the current market strategies and may result in the establishment of new wind farms or individual wind turbines.
- By adding 32.50 km2 of selected areas, the power capacity could increase by 62%, reaching 131.5 MW. Additionally, adding 21.53 km2 of selected areas in three districts could increase the power capacity by 41%, amounting to 87.2 MW. These estimates are based on averaged data and may be improved in future assessments.
- The study used Geographic Information Systems (GIS) and multicriteria decision analysis (MCDA) methods to comprehensively assess criteria such as wind resource potential, land availability, environmental restrictions, and grid integration for wind farm site selection.
- The Analytic Hierarchy Process (AHP) is the most commonly used wind farm site selection method due to its simplicity and effectiveness in structuring mathematical models. The Borda method is mentioned as providing impartial comparisons of criteria. The TOPSIS method, in combination with other methods, like AHP, is highlighted as effective for complex analyses.
- The article suggests that combining various methods, such as AHP, TOPSIS, Borda, VIKOR, ANP, DEMATEL, ELECTRE, and PROMETHEE, can enhance the accuracy of mathematical modelling and geospatial analysis.
- Accurate spatial data sources, such as the BDOT10k database, digital elevation models, nature protection databases, and flood risk maps, are crucial for making informed decisions in wind farm site selection.
- Seasonal wind variability is acknowledged as a critical factor in wind farm construction, and future research will focus on analysing it on a smaller scale.
- Large companies’ investment planning departments consider wind turbine cost, wind speed, and wind stability to evaluate wind farm economic efficiency.
- Wind turbines with varying specifications are highlighted to reduce greenhouse gas emissions compared to traditional coal plants, contributing to sustainable energy sources.
- Strategic site selection based on rigorous analysis and stakeholder engagement is crucial for successful wind park development, especially when considering the increasing demand for clean energy.
- Sensitivity analysis results for the AHP method indicate stability, with Variant 6 consistently being the best option. However, other variants are sensitive, and choosing an option better than Variant 6 may lead to non-compliance with Polish regulations for wind farm construction.
The study has several limitations. Limitations in the accuracy and currency of the GIS data could introduce uncertainties in the site selection process. The projected power capacity increase is based on assumptions about the efficiency of wind farms and turbine placement. Because of that, the actual performance may vary. This study did not comprehensively assess the potential ecological impact of wind farm construction, which may require more detailed investigations. Wind energy regulations and policies can change over time. This study assumes compliance with current regulations, but future changes in legislation could affect the feasibility and permitting of wind farm projects. The study mentions the importance of social acceptance. However, it needs to delve deeper into the complexities of community engagement and potential opposition to wind farm development, which can be a significant challenge.
The study has several perspectives. Regular updates and continuous data collection on wind patterns, environmental conditions, and land use could enhance the accuracy of future site selection processes. Future research could benefit from applying advanced modelling techniques, including machine learning and AI algorithms, to refine site selection based on historical data and real-time inputs. Future studies could explore integrating wind energy with other renewable sources, such as solar or hydroelectric power, to create more comprehensive and resilient energy systems. Comparative studies across different regions or countries can provide valuable insights into the best practices for wind farm site selection and regulatory frameworks. As climate change impacts wind patterns, future research should consider how these changes may affect the long-term viability of wind energy projects.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/en16207107/s1, Table S1: The comparison matrix with the ratings according to the Saaty fundamental scale; File S2: Sensitivity analysis for AHP.
Author Contributions
Conceptualisation, A.A.; methodology, A.A. and G.Ł.; software, A.A.; validation, A.A. and G.Ł.; formal analysis, A.A.; investigation, A.A.; resources, A.A. and G.Ł.; data A.A.; writing—original draft preparation, A.A.; writing—review and editing, A.A. and G.Ł.; visualisation, A.A.; project administration, G.Ł. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Education and Science of Poland, grant number WZ/WB-IIS/4/2023.
Data Availability Statement
Data are contained within the article or Supplementary Materials.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chaurasiya, P.K.; Patidar, H.; Shende, V.; Rajak, U.; Verma, T.N.; Dwivedi, G. Evaluation of the Reduction in Greenhouse Gas Emissions Attributable to Wind Energy: A Retrospective Evaluation of Indian Offshore and Coastal Site. Ocean Eng. 2023, 281, 114665. [Google Scholar] [CrossRef]
- EU Wind Installations up by a Third Despite Challenging Year for Supply Chain. Available online: https://windeurope.org/newsroom/press-releases/eu-wind-installations-up-by-a-third-despite-challenging-year-for-supply-chain/ (accessed on 18 July 2023).
- Wind Industry Predicts Bounceback and Rapid Growth in 2023. Available online: https://www.nbcnews.com/science/environment/wind-industry-predicts-bounceback-rapid-growth-2023-rcna76795 (accessed on 18 July 2023).
- More Than 38,000 Offshore Wind Turbines Are to Be Installed by 2036. Available online: https://www.linkedin.com/pulse/more-than-38000-offshore-wind-turbines-installed-2036 (accessed on 18 July 2023).
- Azizi, A.; Malekmohammadi, B.; Jafari, H.R.; Nasiri, H.; Amini Parsa, V. Land Suitability Assessment for Wind Power Plant Site Selection Using ANP-DEMATEL in a GIS Environment: Case Study of Ardabil Province, Iran. Environ. Monit. Assess. 2014, 186, 6695–6709. [Google Scholar] [CrossRef]
- Resak, M.; Rogosz, B.; Szczepiński, J.; Dziamara, M. Legal Conditions for Investments in Renewable Energy in the Overburden Disposal Areas in Poland. Sustainability 2022, 14, 1065. [Google Scholar] [CrossRef]
- Baban, S.M.J.; Parry, T. Developing and Applying a GIS-Assisted Approach to Locating Wind Farms in the UK. Renew. Energy 2001, 24, 59–71. [Google Scholar] [CrossRef]
- Sotiropoulou, K.F.; Vavatsikos, A.P. Onshore Wind Farms GIS-Assisted Suitability Analysis Using PROMETHEE II. Energy Policy 2021, 158, 112531. [Google Scholar] [CrossRef]
- Nitsch, F.; Turkovska, O.; Schmidt, J. Observation-Based Estimates of Land Availability for Wind Power: A Case Study for Czechia. Energy Sustain. Soc. 2019, 9, 1–13. [Google Scholar] [CrossRef]
- Katsaprakakis, D. Al A Review of the Environmental and Human Impacts from Wind Parks. A Case Study for the Prefecture of Lasithi, Crete. Renew. Sustain. Energy Rev. 2012, 16, 2850–2863. [Google Scholar] [CrossRef]
- Witkowska-Dabrowska, M.; Świdyńska, N.; Świdyńska, S.; Napiórkowska-Baryła, A.; Zakeri, B.; Marks-Bielska, R. Attitudes of Communities in Rural Areas towards the Development of Wind Energy. Energies 2021, 14, 8052. [Google Scholar] [CrossRef]
- Horzela, I.; Gromadzki, S.; Gryz, J.; Kownacki, T.; Nowakowska-Krystman, A.; Piotrowska-Trybull, M.; Wisniewski, R. Energy Portfolio of the Eastern Poland Macroregion in the European Union. Energies 2021, 14, 8426. [Google Scholar] [CrossRef]
- Szurek, M.; Blachowski, J.; Nowacka, A. GIS-Based Method for Wind Farm Location Multi-Criteria Analysis. Min. Sci. 2014, 21, 65–81. [Google Scholar] [CrossRef]
- Sliz-Szkliniarz, B.; Vogt, J. GIS-Based Approach for the Evaluation of Wind Energy Potential: A Case Study for the Kujawsko–Pomorskie Voivodeship. Renew. Sustain. Energy Rev. 2011, 15, 1696–1707. [Google Scholar] [CrossRef]
- Łaska, G. Wind Energy and Multicriteria Analysis in Making Decisions on the Location of Wind Farms: A Case Study in the North-Eastern of Poland. In Modeling, Simulation and Optimization of Wind Farms and Hybrid Systems; Maalawi, K., Ed.; IntechOpen: London, UK, 2020; pp. 1–18. [Google Scholar]
- Santos-Alamillos, F.J.; Pozo-Vázquez, D.; Ruiz-Arias, J.A.; Lara-Fanego, V.; Tovar-Pescador, J. A Methodology for Evaluating the Spatial Variability of Wind Energy Resources: Application to Assess the Potential Contribution of Wind Energy to Baseload Power. Renew. Energy 2014, 69, 147–156. [Google Scholar] [CrossRef]
- Li, M.; Xu, Y.; Guo, J.; Li, Y.; Li, W. Application of a GIS-Based Fuzzy Multi-Criteria Evaluation Approach for Wind Farm Site Selection in China. Energies 2020, 13, 2426. [Google Scholar] [CrossRef]
- Konstantinos, I.; Georgios, T.; Garyfalos, A. A Decision Support System Methodology for Selecting Wind Farm Installation Locations Using AHP and TOPSIS: Case Study in Eastern Macedonia and Thrace Region, Greece. Energy Policy 2019, 132, 232–246. [Google Scholar] [CrossRef]
- Standar, A.; Kozera, A.; Satoła, Ł. The Importance of Local Investments Co-Financed by the European Union in the Field of Renewable Energy Sources in Rural Areas of Poland. Energies 2021, 14, 450. [Google Scholar] [CrossRef]
- Wind Turbines as an Opportunity for Polish Local Communities. Available online: https://trendywenergetyce.pl/en/wind-turbines-as-an-opportunity-for-polish-local-communities (accessed on 18 July 2023).
- Ligus, M. Evaluation of Economic, Social and Environmental Effects of Low-Emission Energy Technologies Development in Poland: A Multi-Criteria Analysis with Application of a Fuzzy Analytic Hierarchy Process (FAHP). Energies 2017, 10, 1550. [Google Scholar] [CrossRef]
- Badora, K. Farmy Wiatrowe Jako Elementy Determinujące Strukturę i Funkcjonowanie Krajobrazu Wiejskiego. Archit. Krajobrazu 2013, 2, 58–77. [Google Scholar]
- Nõ Lvak, H.; Truu, J.; Limane, B.; Truu, M.; Cepurnieks, G.; Bartkevičs, V.; Juhanson, J.; Muter, O. Visual Impact Assessment of Wind Turbines and Their Farms on Landscape of Kretinga Region (Lithuania) and Grobina Townscape (Latvia). J. Environ. Eng. Landsc. Manag. 2015, 23, 39–49. [Google Scholar] [CrossRef][Green Version]
- Jensen, C.U.; Panduro, T.E.; Lundhede, T.H.; Sofie, A.; Nielsen, E.; Dalsgaard, M.; Thorsen, B.J. The Impact of On-Shore and Off-Shore Wind Turbine Farms on Property Prices. Energy Policy 2018, 116, 50–59. [Google Scholar] [CrossRef]
- Vyn, R.J.; Mccullough, R.M. The Effects of Wind Turbines on Property Values in Ontario: Does Public Perception Match Empirical Evidence? Can. J. Agric. Econ./Rev. Can. d’Agroeconomie 2014, 62, 365–392. [Google Scholar] [CrossRef]
- Obwieszczenie Marszałka Sejmu Rzeczypospolitej Polskiej z Dnia 1 Grudnia 2022 r. w Sprawie Ogłoszenia Jednolitego Tekstu Ustawy—Prawo Ochrony Środowiska. Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU20220002556 (accessed on 9 August 2023).
- Wolniewicz, K.; Zagubień, A.; Wesołowski, M. Energy and Acoustic Environmental Effective Approach for a Wind Farm Location. Energies 2021, 14, 7290. [Google Scholar] [CrossRef]
- Ruggiero, A.; Quartieri, J.; Guarnaccia, C.; Hloch, S. Noise Pollution Analysis of Wind Turbines in Rural Areas. Int. J. Environ. Res. 2015, 9, 1277–1286. [Google Scholar] [CrossRef]
- Po Drugiej Stronie Ustawy Odległościowej. Available online: https://www.teraz-srodowisko.pl/aktualnosci/po-drugiej-stronie-ustawy-odleglosciowej-13555.html#ntrack=c3BlY2lhbGV8NjM%3D[MzY0NDA0] (accessed on 21 June 2023).
- Najwięksi Inwestorzy w Energetyce Wiatrowej w Polsce. Available online: https://cleanerenergy.pl/2022/02/14/najwieksi-inwestorzy-w-energetyce-wiatrowej-w-polsce-liderem-jest-grupa-pge/ (accessed on 21 June 2023).
- Sprawozdania—BIP—Urząd Regulacji Energetyki. Available online: https://bip.ure.gov.pl/bip/o-urzedzie/zadania-prezesa-ure/sprawozdania/800,Sprawozdania.html (accessed on 21 June 2023).
- Moc Zainstalowana Farm Wiatrowych w Polsce. Available online: https://www.rynekelektryczny.pl/moc-zainstalowana-farm-wiatrowych-w-polsce/ (accessed on 21 June 2023).
- Ustawa z Dnia 9 Marca 2023, r. o Zmianie Ustawy o Inwestycjach w Zakresie Elektrowni Wiatrowych Oraz Niektórych Innych Ustaw. Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU20230000553 (accessed on 19 July 2023).
- Poland Onshore Wind Energy 10H Distance Rule Liberalized. Available online: https://www.trade.gov/market-intelligence/poland-onshore-wind-energy-10h-distance-rule-liberalized (accessed on 21 June 2023).
- Nowe Odległości Farm Wiatrowych Od Domów—Ustawa Wiatrakowa Obowiązuje. Available online: https://www.muratorplus.pl/biznes/prawo/nowe-odleglosci-farm-wiatrowych-od-domow-ustawa-wiatrakowa-obowiazuje-aa-3pnA-gW7q-uxk4.html (accessed on 27 June 2023).
- Gao, C.K.; Na, H.M.; Song, K.H.; Dyer, N.; Tian, F.; Xu, Q.J.; Xing, Y.H. Environmental Impact Analysis of Power Generation from Biomass and Wind Farms in Different Locations. Renew. Sustain. Energy Rev. 2019, 102, 307–317. [Google Scholar] [CrossRef]
- Dai, K.; Bergot, A.; Liang, C.; Xiang, W.N.; Huang, Z. Environmental Issues Associated with Wind Energy—A Review. Renew. Energy 2015, 75, 911–921. [Google Scholar] [CrossRef]
- Shaahid, S.M.; Al-Hadhrami, L.M.; Rahman, M.K. Economic Feasibility of Development of Wind Power Plants in Coastal Locations of Saudi Arabia—A Review. Renew. Sustain. Energy Rev. 2013, 19, 589–597. [Google Scholar] [CrossRef]
- Enevoldsen, P.; Sovacool, B.K. Examining the Social Acceptance of Wind Energy: Practical Guidelines for Onshore Wind Project Development in France. Renew. Sustain. Energy Rev. 2016, 53, 178–184. [Google Scholar] [CrossRef]
- Wind Power’s Explosive Growth Is Blowing Past Green Energy Goals. Available online: https://reasonstobecheerful.world/texas-wind-power-renewables-future/ (accessed on 15 September 2023).
- Baza Danych Obiektów Topograficznych-BDOT10k. Available online: https://dane.gov.pl/pl/dataset/2030,dane-obiektow-topograficznych-o-szczegolowosci-zap (accessed on 28 June 2023).
- Topographic Objects Database (BDOT10k). Available online: https://www.geoportal.gov.pl/dane/baza-danych-obiektow-topograficznych-bdot (accessed on 28 June 2023).
- Geoportal.Gov.Pl. Available online: https://mapy.geoportal.gov.pl/imap/Imgp_2.html (accessed on 28 June 2023).
- Numeryczny Model Terenu o Interwale Siatki Co Najmniej 100 m. Available online: https://dane.gov.pl/pl/dataset/792,numeryczny-model-terenu-o-interwale-siatki-co-najmniej-100-m (accessed on 28 June 2023).
- Digital Elevation Model (DEM). Available online: https://www.geoportal.gov.pl/dane/numeryczny-model-terenu (accessed on 28 June 2023).
- Dostęp Do Danych Geoprzestrzennych—Generalna Dyrekcja Ochrony Środowiska. Available online: https://www.gov.pl/web/gdos/dostep-do-danych-geoprzestrzennych (accessed on 28 June 2023).
- ESA/CCI Viewer. Available online: http://maps.elie.ucl.ac.be/CCI/viewer/download.php (accessed on 29 June 2023).
- Floors, R.; Badger, M.; Troen, I.; Grogan, K.; Permien, F.H. Satellite-Based Estimation of Roughness Lengths and Displacement Heights for Wind Resource Modelling. Wind Energy Sci. 2021, 6, 1379–1400. [Google Scholar] [CrossRef]
- INSPIRE. Available online: https://isok.gov.pl/inspire.html (accessed on 28 June 2023).
- METEOIMGW-PIB. Available online: https://meteo.imgw.pl/ (accessed on 28 June 2023).
- Global Wind Atlas. Available online: https://globalwindatlas.info/en/ (accessed on 1 July 2023).
- Poland Wind Power Plants. Available online: https://openinframap.org/stats/area/Poland/plants?source=wind (accessed on 29 June 2023).
- Kobryń, A. Wielokryterialne Wspomaganie Decyzji w Gospodarowaniu Przestrzenią; Difin: Warszawa, Poland, 2014; ISBN 9788379304691. [Google Scholar]
- Findeisen, W.; Szymanowski, J. Teoria i Metody Obliczeniowe Optymalizacji, 2nd ed.; Państwowe Wydawnictwo Naukowe: Warszawa, Poland, 1980. [Google Scholar]
- Lindfors, A. Developing a Multi-Criteria Method for Sustainability Assessment of Socio-Technical Systems. Ph.D. Thesis, Linköping University, Linköping, Sweden, 2022. [Google Scholar]
- Calixto Figueiroa, A.; de Souza de Lima, A.; Eymael Garcia Scherer, M.; Bonetti, J. How to Choose the Best Category for a Protected Area? A Multicriteria Analysis Method Based on Ecosystem Services Conservation. Environ. Monit. Assess. 2020, 192, 1–14. [Google Scholar] [CrossRef]
- Marques, M.; Reynolds, K.M.; Marto, M.; Lakicevic, M.; Caldas, C.; Murphy, P.J.; Borges, J.G. Multicriteria Decision Analysis and Group Decision-Making to Select Stand-Level Forest Management Models and Support Landscape-Level Collaborative Planning. Forests 2021, 12, 399. [Google Scholar] [CrossRef]
- Trzaskalik, T. Multiple Criteria Decision Making ’05; The Karol Adamiecki University of Economics: Katowice, Poland, 2006; ISBN 8372468435. [Google Scholar]
- Goodwin, P.; Wright, G. Analiza Decyzji; Wydawnictwo Nieoczywiste: Siedliska, Poland, 2016; ISBN 9788363391065. [Google Scholar]
- Saaty, T.L.; Vargas, L.G. Models, Methods, Concepts & Applications of the Analytic Hierarchy Process; International Series in Operations Research & Management Science; Springer: Boston, MA, USA, 2001; Volume 34, ISBN 978-1-4613-5667-7. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process; Golden, B.L., Wasil, E.A., Harker, P.T., Eds.; Springer: Berlin/Heidelberg, Germany, 1989; ISBN 978-3-642-50246-0. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation; McGraw-Hill: New York, NY, USA, 1980; Volume 9, ISBN 9780070543713. [Google Scholar]
- Erdamar, B.; Luis Garcia-Lapresta, J.; Pérez-Roman, D. Measuring Consensus in a Preference-Approval Context. Inf. Fusion 2012, 17, 2012–2023. [Google Scholar] [CrossRef]
- Bouyssou, D.; Marchant, T.; Pirlot, M.; Tsoukiàs, A.; Vincke, P. Evaluation and Decision Models with Multiple Criteria, 1st ed.; Springer: New York, NY, USA, 2006; Volume 86. [Google Scholar]
- Zimmermann, H.-J.; Gutsche, L. Einführung in Die Allgemeine Entscheidungs-Theorie. In Heidelberger Lehrtexte Wirtschaftswissenschaften; Springer: Berlin, Germany, 1991; pp. 2–10. [Google Scholar]
- Hwang, C.-L.; Yoon, K. Multiple Attribute Decision Making, 1st ed.; Lecture Notes in Economics and Mathematical Systems; Springer: Berlin, Germany, 1981; Volume 186, ISBN 978-3-540-10558-9. [Google Scholar]
- Hwang, C.L.; Lai, Y.J.; Liu, T.Y. A New Approach for Multiple Objective Decision Making. Comput. Oper. Res. 1993, 20, 889–899. [Google Scholar] [CrossRef]
- Rozporządzenie Rady Ministrów z Dnia 13 Stycznia 2017 r. w Sprawie Szczegółowego Przebiegu Linii Podstawowej, Zewnętrznej Granicy Morza Terytorialnego Oraz Zewnętrznej Granicy Strefy Przyległej Rzeczypospolitej Polskiej. Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU20170000183 (accessed on 9 August 2023).
- Powierzchnia i Ludność w Przekroju Terytorialnym w 2022 Roku. Available online: https://stat.gov.pl/obszary-tematyczne/ludnosc/ludnosc/powierzchnia-i-ludnosc-w-przekroju-terytorialnym-w-2022-roku,7,19.html (accessed on 21 June 2023).
- Ludność. Stan i Struktura Ludności Oraz Ruch Naturalny w Przekroju Terytorialnym. Available online: https://stat.gov.pl/obszary-tematyczne/ludnosc/ludnosc/ludnosc-stan-i-struktura-ludnosci-oraz-ruch-naturalny-w-przekroju-terytorialnym-stan-w-dniu-31-grudnia,6,34.html (accessed on 21 June 2023).
- Lista Województw w Polsce (Spis Województw, Mapa Województw, Liczba Ludności, Powierzchnia, Stopa Urbanizacji). Available online: https://www.polskawliczbach.pl/Wojewodztwa (accessed on 23 June 2023).
- Amsharuk, A.; Łaska, G. A Review: Existing Methods for Solving Spatial Planning Problems for Wind Turbines in Poland. Energies 2022, 15, 8957. [Google Scholar] [CrossRef]
- CRFOP. Available online: https://crfop.gdos.gov.pl/CRFOP/search.jsf (accessed on 9 August 2023).
- Díaz, H.; Soares, C.G. A Multi-Criteria Approach to Evaluate Floating Offshore Wind Farms Siting in the Canary Islands (Spain). Energies 2021, 14, 865. [Google Scholar] [CrossRef]
- Lozano-Minguez, E.; Kolios, A.J.; Brennan, F.P. Multi-Criteria Assessment of Offshore Wind Turbine Support Structures. Renew. Energy 2011, 36, 2831–2837. [Google Scholar] [CrossRef]
- Watróbski, J.; Ziemba, P.; Jankowski, J.; Ziolo, M. Green Energy for a Green City-A Multi-Perspective Model Approach. Sustainability 2016, 8, 702. [Google Scholar] [CrossRef]
- Aras, H.; Erdoǧmuş, Ş.; Koç, E. Multi-Criteria Selection for a Wind Observation Station Location Using Analytic Hierarchy Process. Renew. Energy 2004, 29, 1383–1392. [Google Scholar] [CrossRef]
- Latinopoulos, D.; Kechagia, K. A GIS-Based Multi-Criteria Evaluation for Wind Farm Site Selection. A Regional Scale Application in Greece. Renew. Energy 2015, 78, 550–560. [Google Scholar] [CrossRef]
- Łaska, G. Wind Energy and Multi-Criteria Analysis in Making Decisions on the Location of Wind Farms. Procedia Eng. 2017, 182, 418–424. [Google Scholar] [CrossRef]
- Ławniczak, R.; Kubiak, J. Geometric Accuracy of Topographical Objects at Polish Topographic Maps. Geod. Cartogr. 2016, 65, 55–66. [Google Scholar] [CrossRef]
- Mierzwiak, M.; Calka, B. Multi-Criteria Analysis for Solar Farm Location Suitability. Rep. Geod. Geoinform. 2017, 104, 20–32. [Google Scholar] [CrossRef]
- Kozłowska, A. Floodplain Delineation Based on Analysis of Digital Elevation Model, Soil Maps and Occurrence of Quaternary Formations. Arch. Fotogrametrii Kartografii Teledetekcji 2019, 31, 29–47. [Google Scholar] [CrossRef]
- Murcia, J.P.; Koivisto, M.J.; Luzia, G.; Olsen, B.T.; Hahmann, A.N.; Sørensen, P.E.; Als, M. Validation of European-Scale Simulated Wind Speed and Wind Generation Time Series. Appl. Energy 2022, 305, 117794. [Google Scholar] [CrossRef]
- Weber, J.; Wohland, J.; Reyers, M.; Moemken, J.; Hoppe, C.; Pinto, J.G.; Witthaut, D. Impact of Climate Change on Backup Energy and Storage Needs in Wind-Dominated Power Systems in Europe. PLoS ONE 2018, 13, 0201457. [Google Scholar] [CrossRef]
- Kuczyński, W.; Wolniewicz, K.; Charun, H. Analysis of the Wind Turbine Selection for the Given Wind Conditions. Energies 2021, 14, 7740. [Google Scholar] [CrossRef]
- Gnatowska, R.; Was, A. Wind Energy in Poland—Economic Analysis of Wind Farm. E3S Web Conf. 2017, 14, 01013. [Google Scholar] [CrossRef]
- Kuo, Y.-M.; Fukushima, Y. Photovoltaic and Wind Power Introduction Considering Interactions among Technologies in Taiwan. J. Air Waste Manag. Assoc. 2012, 59, 360–372. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).