Abstract
Current stratospheric airships generally employ photovoltaic cycle energy systems. Accurately calculating their power generation is significant for airships’ overall design and mission planning. However, the power generation of solar arrays on stratospheric airships is challenging to model and calculate due to the dynamic nature of the airships’ flight, resulting in continuously changing radiation conditions on the curved surface of the airships. The power generated by the airship solar array was modeled herein through a combination of the flight attitude, spatial position, time, and other influencing factors. Additionally, the model was modified by considering the variation in photovoltaic conversion efficiency based on the radiation incidence angle, as well as the state of charge and power consumption of the energy storage battery pack. This study compared the measurement data of power generation in real flight tests with the calculation results of the model. The comparison showed that the results of the calculated model were highly consistent with the actual measured data. An average normalized root-mean-square error of 2.47% validated the accuracy of the newly built model. The generalizability and rapidity of the model were also tested, and the results showed that the model performed well in both metrics.
1. Introduction
A stratospheric airship is a new type of high-altitude platform (HAP) that can transport payloads equipped with communication devices [1], scientific equipment [2], and remote sensing instruments [3] to work at the bottom of the stratosphere at around 20 km altitude, or even carry rockets to the stratosphere for launching [4]. Stratospheric airships have become one of the leading flight vehicles for exploiting and utilizing atmospheric space, since this altitude is higher than that reachable by most aircraft but lower than the minimum orbital altitude of satellites. These features have led stratospheric airships to attract significant attention from research institutions and commercial companies [5,6,7].
However, a prolonged energy supply must be guaranteed to allow stratospheric airships to maintain long-term flight. The adoption of photovoltaic cycle energy systems for stratospheric airships is a feasible solution in the current development trend due to the high solar radiation in the stratospheric region and the absence of weather phenomena such as clouds, rain, or fog [8]. In the airship photovoltaic energy system, the solar energy received by the solar array is converted into electrical energy for the propulsion, avionics, and battery systems. The power generation model of the solar array can be used for flight simulation, which is of great significance for airship design and mission planning.
In the field of energy, accurate modeling of the system under study is very important and is the basis for analysis and optimization of the system [9,10]. Stratospheric airships differ from ground-based photovoltaic energy systems in that they dynamically change their flight status, resulting in continuously changing radiation conditions for the solar array laid on the curved surface of the airship, causing continuous fluctuations in output power and making it challenging to model and analyze the power generation.
Several studies on stratospheric airship energy generation have investigated solutions to challenging issues in solar vehicle research and the problems related to designing a sustainable energy supply. Garg et al. [11] proposed a method to estimate and optimize the area of solar panels on stratospheric airships, aiming to maximize the solar energy yield per unit panel area. Zhu et al. [12] applied genetic algorithms to solar array layout optimization and proposed layout schemes for four common airship flight conditions. Du et al. [13] presented a conceptual design of a rotatable solar array for airships to enhance the solar array’s power generation. Zhang et al. [14] devised attitude planning strategies for a stratospheric airship with a rotatable solar array. They conducted an analysis of the energy balance for strato-spheric solar-powered airships across various flight dates. Liu et al. [15] developed models for solar irradiation and energy reception tailored to crystalline silicon arrays. Their study assessed the impact of factors such as array shape, location, and module size on energy absorption at different flight latitudes. Additionally, they introduced an enhanced genetic algorithm for optimizing array geometry. Tang et al. [16] examined the most effective solar array layouts for different flight conditions. Their research demonstrated that higher latitudes led to larger solar-powered airships and expanded solar array areas. Moreover, they identified varying optimal solar layouts and associated central angles.
One of the key factors directly related to the success or failure of the mission of solar aircraft is whether the balance between energy generation and energy consumption can be maintained. Therefore, accurately estimating power generation capacity is crucial for solar vehicle designers. Zhu et al. [17] analyzed the relative positions of the solar aircraft and the Sun. Gupta et al. [18] discretized the surface of an airship into contours to calculate the power generation of the solar array and analyzed the effect of wind-induced oscillations. Pande et al. [19] conducted an analysis using three types of solar cells to assess the in-fluence of wind speed and solar irradiance on the solar array size of a solar-powered airship. Dai et al. [20] introduced a conceptual design method emphasizing the thermal and power characteristics of the energy system for stratospheric airships. They examined the impact of the solar array’s thermal behavior on the energy system, ultimately obtaining an optimized case that considered the thermal behaviors of power supply unit, helium, and solar array. For a more precise calculation of the stratospheric airship solar array’s output power, Wang et al. [21] factored in temperature effects and employed a support vector machine to predict the solar array temperature. Wang et al. [22] proposed a numerical method to estimate the power generated by a curved solar array on a stratospheric airship. They also investigated the influence of the airship’s attitude on the solar panels’ output performance. However, they considered the solar cells’ photovoltaic conversion efficiency as being constant.
More and more previously overlooked factors are being taken into account to obtain more accurate models. Jiang et al. [23] conducted a parametric sensitivity analysis. They discussed the effect of the solar cells’ installation angle on the output power of the stratospheric airship solar array when the airship was in cruising flight. Li et al. [24] analyzed the output power of a stratospheric airship solar array by considering thermal effects. Li et al. [25] investigated the impact of factors such as latitude, wind speed, and solar array area on the power generated by stratospheric airships. Du et al. [26] further considered the loss of solar cell power generation capacity by considering the angle of incidence. The results showed that the angular loss could effectively correct the overestimation problem of power generation calculation. However, all the above studies discussed only the results of numerical simulations, which were not validated by experiments. Moreover, they failed to discuss the impact of the state of the battery pack on power generation.
According to the experience of previous flight trials, the photovoltaic conversion efficiency of solar cells is attenuated when the incidence angle of solar radiation is large. Moreover, the output power of the solar array is coupled with the state of charge (SOC) and power consumption of the energy storage battery pack. Therefore, accurate solar cell power generation calculations should consider these two factors.
This study meticulously constructs a model for calculating the power generation of the solar array on stratospheric airship. This study provides the following main contributions:
- Based on the actual stratospheric airship solar array layout model, a calculation model of real-time solar radiation power received by the stratospheric airship solar array is obtained by comprehensively considering kinematic factors such as airship flight attitude, position, time, and date.
- We construct a high-precision calculation model for real-time power generation for the stratospheric airship solar array. Model corrections are conducted for the case where the photovoltaic conversion efficiency of solar cells varies with the radiation incidence angle and the case of the constant-voltage charging stage in the energy storage battery pack.
- The calculation results of the constructed model are compared and analyzed with the power generation measured in an actual flight test, and the accuracy of the model calculation is validated.
The rest of the article is organized as follows: Section 2 constructs a basic power generation calculation model that treats the photovoltaic conversion efficiency of solar cells as a constant. Section 3 models the angular loss of solar cell photovoltaic conversion efficiency and the coupled matching relationship between the storage battery pack state, power consumption, and power generation to correct the calculation error of the base model. Section 4 compares and analyzes the model-calculated results with the actual measured data from the flight tests. Section 5 presents the conclusions.
2. Basic Calculation Model for Power Generation
2.1. Model Variables Associated with Flight Date
Airships can remain aloft within the Earth’s atmosphere and receive radiation from the Sun. The Earth follows an elliptical orbit around the Sun, with the Sun located at one of the foci, and the Sun–Earth distance varies around one astronomical unit (AU) with the year’s date. The conversion relationship between astronomical units and kilometers is as follows:
The Sun-Earth distance varies, being greater in summer and smaller in winter. These fluctuations directly impact the intensity of extraterrestrial solar radiation, which is inversely proportional to the square of the distance. The Sun–Earth distance correction factor is introduced to correct this variation, defined as follows:
is calculated with high accuracy, as shown by [27]:
where is the day angle. is calculated in radians:
The term in Equation (4) represents the day number of the year, ranging from 1 on January 1 to either 365 or 366, depending on whether it is a leap year or not.
The ecliptic plane is the plane of the Earth’s orbit around the Sun. The Earth revolves around the Sun while rotating around its polar axis. The polar axis is normal to the ecliptic plane at an angle of approximately 23.43°, causing the Sun’s direct point on the Earth’s surface to change periodically with the date. The latitudinal position of the Sun’s direct point equals the solar declination angle, calculated in radians [28]:
When the solar rays hit the equator directly, the solar declination angle becomes 0 at the vernal and autumnal equinoxes. The solar rays hit the Tropic of Cancer and the Tropic of Capricorn on the summer and winter solstices, on which the solar declination angles are 23.43° and −23.43°, respectively, reaching their maximum absolute value. Figure 1 shows the changes in the Sun–Earth distance and the declination angle of the Sun over the year.
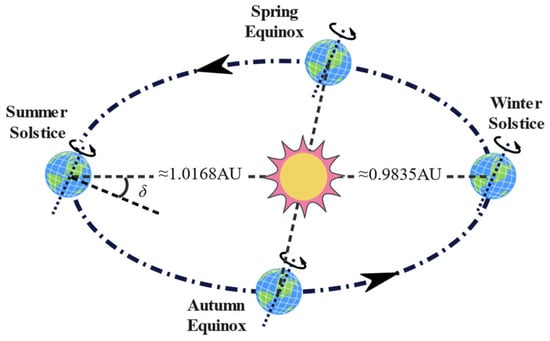
Figure 1.
Solar declination angle and changes in the Sun–Earth distance within a year.
The solar day also varies with the date in the year. A solar day is the time interval showing how the Sun completes one cycle as a stationary observer on Earth. However, this is not necessarily 24 h, delivering a maximum 16 min deviation. The time of deviation in minutes is calculated using the following expression [28]:
where may be positive or negative.
The solar day duration is calculated as follows:
The airship can receive solar radiation during sunshine hours only, which are longer in summer and shorter in winter. The duration of sunlight is as follows:
The term in Equation (8) is the sunset hour angle. Stratospheric airships operate at an altitude of approximately 20 km, where sunset is later than sunset at sea level. The sunset hour angle at altitude is given (in radians) as follows:
where is the latitude of the flight position, and is the Earth’s radius.
The following two equations can be used to obtain the sunrise time and sunset time :
2.2. The Relative Positions of the Airship and the Sun
To describe the relative position between the airship and the Sun, we established both ground and body-fixed coordinate systems, both of which are right-handed. The ground coordinate system adopts the north–east–down inertial coordinate system, with the positive directions of the -axis, -axis, and -axis pointing the Earth’s north, east, and center, respectively. The origin of the body coordinate system coincides with the center of mass of the airship. The x-axis positive direction points to the nose, and the y-axis positive direction points to the right side of the airship (observed from the tail towards the nose). The z-axis positive direction is directed downward, perpendicular to the body of the airship. The rotation relationship between the body-fixed coordinate system and the ground coordinate system is described by three Euler angles: yaw , pitch , and roll . The axis positive direction of the ground coordinate system coincides with that of the body-fixed coordinate system if the ground coordinate system rotates , , and along the positive direction (clockwise along the positive direction of the axis) around the -axis, -axis, and -axis, respectively. Figure 2 shows the relative positions of the ground and body-fixed coordinate systems and the sun direction vectors in the two coordinate systems.
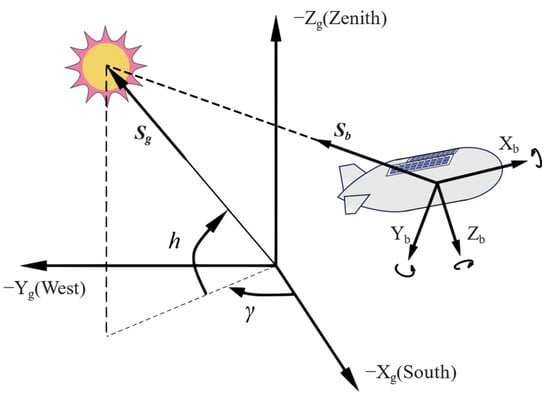
Figure 2.
Sun direction vectors in the ground and body-fixed coordinate systems.
The Sun’s coordinate position in the ground coordinate system varies with time during the day and is usually determined using the local apparent solar time, . However, data measurement is usually recorded in local standard time, . The conversion relationship between the two is done when measured in hours, as follows:
where is the longitude of the standard meridian for the local time zone (in degrees), and is the local longitude.
The solar hour angle is obtained (in degrees) [29]:
In terms of solar time, the solar time angle is positive in the morning, negative in the afternoon, and zero at noon. Together, the solar elevation angle and the solar azimuth angle determine the solar direction vector’s coordinates in the ground coordinate system. The solar elevation angle represents the angle between the Sun’s rays and the horizontal plane, while the solar azimuth is defined as the angle between the projection of the Sun’s rays on the ground and the due south direction. The solar azimuth is measured negatively to the east and positively to the west. and are calculated [30] as follows:
where is the flight latitude and is the hour angle.
In the ground coordinate system, the coordinates of the solar direction vector are as follows:
The coordinate conversion matrix from the ground coordinate system to the body-fixed coordinate system is expressed as follows:
In the body-fixed coordinate system, the coordinates of the solar direction vector are obtained as follows:
2.3. Radiation Model
The solar constant given by the World Radiation Center in 1980 [31] is as follows:
representing the rate of total solar energy incident on an extraterrestrial unit area, ex-posed normally to rays of the Sun at one AU, encompassing all wavelengths.
The Sun–Earth distance varies with the date, causing a change in the normal extraterrestrial intensity of solar radiation, expressed as follows:
Since the atmosphere is very thin at an altitude of 20 km, with little atmospheric dust and no weather phenomena such as clouds, rain, or fog, we have mainly considered the effect of atmospheric transmittance at different solar elevation angles. As sunlight passes through the atmosphere, the solar radiation intensity at this altitude is attenuated compared with that in the upper atmosphere due to scattering and absorption. The atmospheric transmittance was introduced to describe this attenuation quantitatively and given by [32] as follows:
where is the air mass when sunlight passes through the atmosphere. This was given by [33] as follows:
In Equation (22), and are the values of atmospheric pressure at altitude and sea level, respectively. The solar elevation angle is in degrees.
For altitudes above 11,000 m, the atmospheric pressure at flight altitude , using the International Standard Atmospheric Model, was expressed by [34] as follows:
where Pa; m/s2; m; m2/K·s2; K.
The direct solar radiation intensity at the flight altitude of the airship is as follows:
It is unnecessary to consider the scattered and reflected radiation when calculating the power generation of the solar array on stratospheric airships; only direct solar radiation needs to be considered. The reason for this is that the flexible solar cell array of the airship is paved on the upper surface of the curved fuselage. At the same time, the reflected radiation falls on the lower half surface of the fuselage and does not participate in the photovoltaic conversion of the solar cell. Despite the scattered radiation, only the downward scattering above the solar cell can participate in the photovoltaic conversion. The atmosphere is thin at the flight altitude of 20 km, and the intensity of downward scattered radiation from above the solar array is less than 1% of the intensity of direct radiation, meaning that it can be ignored [32].
Modern airships usually have a curved solar array on their upper surface for converting solar radiation into electrical energy. The curved solar array consists of a flexible substrate and numerous semi-flexible solar modules. Each solar cell module consists of numerous brittle crystalline silicon solar cells and can therefore only be bent to a small extent. To calculate the solar radiation flux of the solar array, the solar array of the case-study airship was meshed into a planar grid with solar cells as the meshing unit. The radiation flux of each grid cell is calculated one by one, and the radiation flux on the entire solar array is the sum of that on each grid cell, as shown in Figure 3.
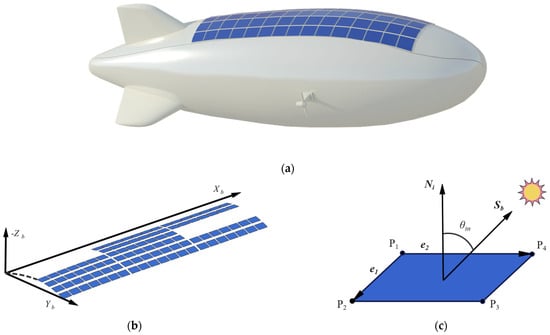
Figure 3.
Solar radiation flux calculation model: (a) A render graph of an airship with a solar array on its upper surface; (b) The meshing of the curved solar array on the case-study airship; (c) Model of a grid cell receiving solar radiation.
For a certain grid cell , the coordinates of its four vertices are , , , and .
The edge vectors of grid cell are as follows:
The outward normal vector of grid cell is obtained as the cross-product of the grid edge vectors as follows:
The solar radiation flux received by grid cell is related to the incidence angle of the solar rays, which is calculated as follows:
Then, the solar radiation flux of grid cell is obtained as
where is the area of a single grid cell.
Note that the solar radiation flux is only calculated when the angle of incidence is acute. Otherwise, the solar radiation will be blocked by the fuselage.
The solar radiation flux on the whole solar array is obtained as follows:
where is the number of grid cells.
The power generation is the product of the total radiation flux and the photovoltaic conversion efficiency :
3. Model Correction
3.1. Angular Loss Correction
Subject to the physical characteristics of the solar cell itself, the solar cell’s photovoltaic conversion efficiency will decline when the solar radiation irradiates the solar cell at a large incidence angle. Several studies have reported such a reduction in photovoltaic conversion efficiency with the angle, which has been referred to as angular loss or Kelly cosine characteristics [26,35,36,37,38,39]. Angular loss typically occurs when the radiation incidence angle surpasses about 47.5°, diminishing to zero beyond 80° [40]. The photovoltaic conversion efficiency decay factor (PCEDF) is introduced to correct the impact of the radiation incidence angle on the photovoltaic conversion efficiency of the solar cells, and the solar radiation incidence angle determines its value, as follows:
Figure 4 illustrates the dependence of the photovoltaic conversion efficiency decay factor on the solar radiation incidence angle. For angles less than 47.5°, the PCEDF remains at 1, indicating no decline in electric conversion efficiency. Beyond 47.5°, the PCEDF decreases rapidly, and when the angle exceeds 80°, it reaches zero. This implies that electricity generation ceases for angles beyond 80°. The photovoltaic conversion efficiency is given by
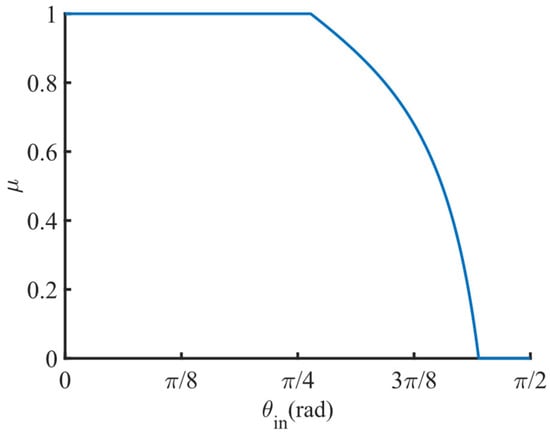
Figure 4.
The incidence angle dependence of the photovoltaic conversion efficiency decay factor.
3.2. Model Correction for an Energy Storage Battery Pack in Constant-Voltage Charging Stage
Figure 5 depicts the conceptual design of the energy system for stratospheric airships. In the presence of light, power generated by the solar array is optimized through the maximum power point tracking (MPPT) system. This power is then distributed to various loads, including propulsion motors, radars, and avionics equipment, through the power controller, simultaneously charging the lithium-ion battery pack. In the absence of light, the lithium-ion battery pack supplies power to the load via the power controller.
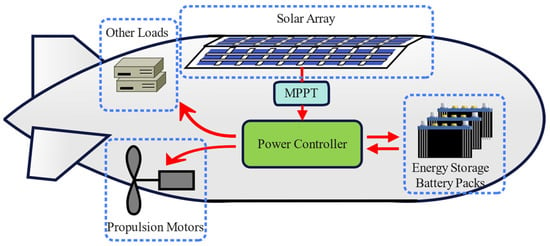
Figure 5.
Impression drawing of the energy system of a stratospheric airship.
When the lithium-ion battery pack is close to full, usually when the SOC reaches about 90%, its charging process enters a constant-voltage charging stage [41]. During the constant-voltage charging process, the charging voltage remains constant, with the charging current gradually decreasing to 0 and the charging power falling to 0. As shown in Figure 6, the SOC of the energy storage battery pack conversely increases to about 100% until the end of the charging process.
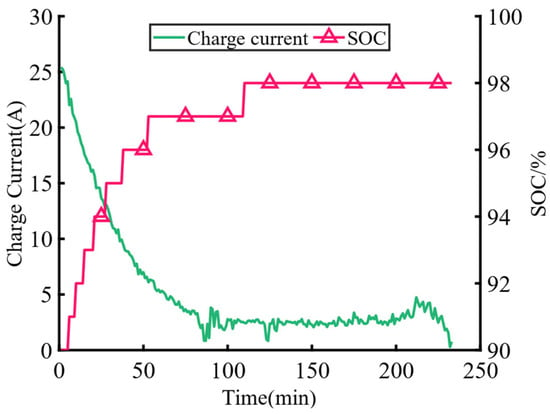
Figure 6.
Changes in charging current and SOC during a constant-voltage charging phase.
When the SOC reaches 90%, the energy storage battery enters the constant-voltage charging stage. When the SOC is higher than 98%, the charging is completed. The charging voltage is kept constant in the constant-voltage charging stage, and the charging current is approximately linear with the SOC. A first-order linear fit algorithm is used to fit the relationship between and SOC as follows:
The coefficients and were determined by the least squares method as −3.7 and 359.9, respectively, in the following case study in Section 4. The charging power is obtained as follows:
After the storage battery pack enters the constant-voltage charging stage, the MPPT system shifts the tracking of the maximum power point (MPP) to match the total power consumption level if the maximum power generated by the solar array meets the charging demand of the battery pack and the power consumption of other loads.
When the MPPT system shifts the MPP tracking, the relationship of power generated being equal to the radiated power multiplied by the photovoltaic conversion efficiency no longer holds; instead, the following relationship is satisfied:
where is the power consumed by the load other than the energy storage battery, and is the efficiency of the power controller.
Consequently, the expression for the power generation from the solar array considering the energy storage battery in the constant-voltage charging stage is given by
4. Experimental Validation
The attitude angle, position, power consumption, and SOC measured during the actual flight test were substituted into the basic calculation model and the corrected model to obtain the output results, validate the modeling accuracy, and analyze the improvement of model correction in Section 3. Then, the model outputs were compared with the sampled power generation during the actual flight. Figure 7 shows the validation workflow. Table 1 shows the nominal parameters of the photovoltaic cells installed on the case-study airship. Figure 8 shows the measured data in the actual flight, which were used as inputs to validate the model’s output. Figure 9 shows the comparative results.
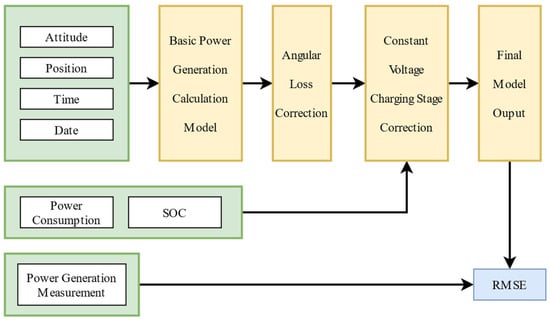
Figure 7.
Workflow of the validation experiment.

Table 1.
Nominal parameters of the photovoltaic modules installed on the case-study airship.
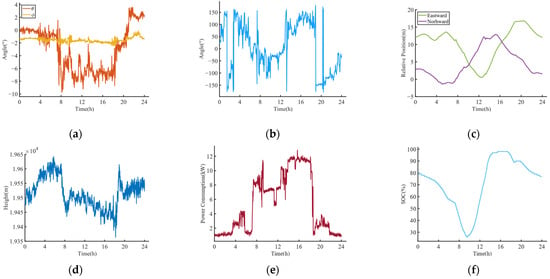
Figure 8.
Measured data from the actual flight: (a) Pitch and roll; (b) Yaw; (c) Relative Position; (d) Height; (e) Power Consumption; (f) SOC.
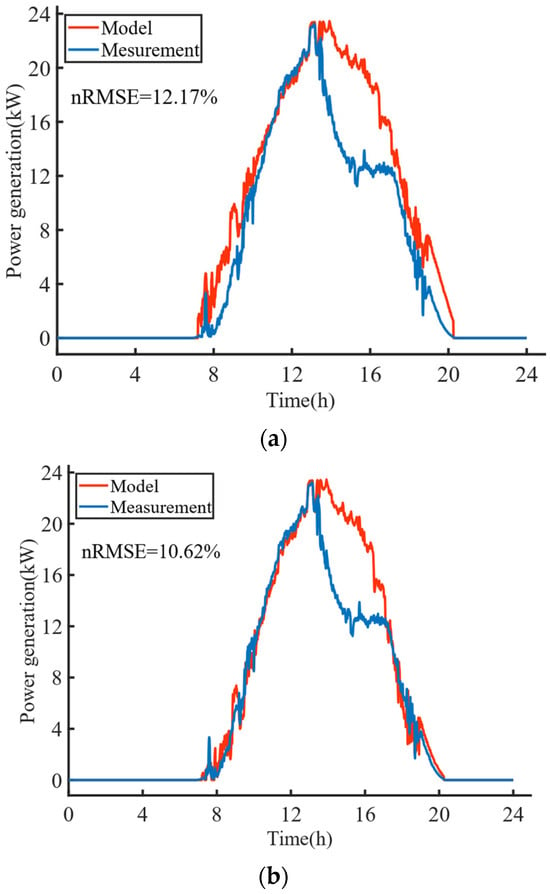
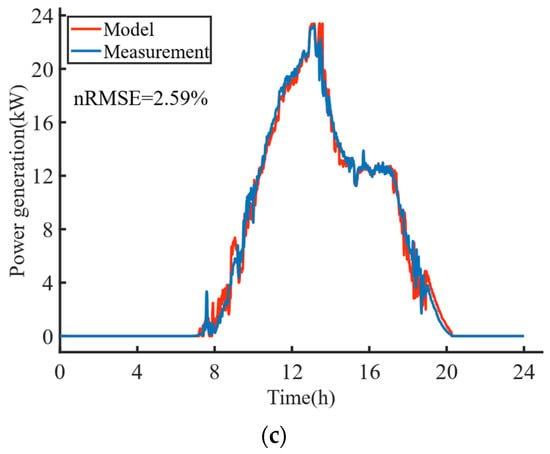
Figure 9.
Comparison between the basic and corrected model outputs and the sampled data: (a) Comparison of the model output with the sampled data for a constant value of photovoltaic conversion efficiency; (b) Comparison of model output and sampled data after angular loss correction; (c) Comparison of model output and sampled data after constant-charging stage correction and angular loss correction.
Figure 9 demonstrates a comparison of different extents of correction models with the flight measured data. The measurement data were obtained from sensors mounted on the case-study airship. A data sampling unit in the avionics system of the airship collected the sensor data and then downlinked them via network to the ground for storage. The quantitative evaluation criterion for the degree of conformity between the model output results and the actual measurement results was the normalized root-mean-square error (nRMSE), shown as follows:
where is the number of data; is the -th model output value; is the -th measured value; is the maximum measured value; and is the minimum measured value.
In Figure 9, the basic model with a constant photovoltaic conversion efficiency, as described in Section 2, underwent no corrections during the constant-voltage charging stage. Large deviations were observed in the model’s output and the actual measurements during hours with a low solar elevation angle (around 8:00–10:00 and 18:00–20:00) and during the constant-voltage charging stage of the storage battery pack (around 13:00–16:00), with nRMSEs of 13.03% and 27.24%, respectively. The overall 24 h nRMSE was 12.17%. After correcting for the angular loss, the model calculation error was significantly reduced in the hours with a lower solar elevation angle. The nRMSE was reduced from 13.03% to 4.73% during the hours of 8:00–10:00 and 18:00–20:00. The overall 24 h nRMSE was reduced to 10.62%. However, a significant error was observed between the model output results and the measured data when the energy storage battery pack was in the constant-voltage charging stage at around 13:00–16:00. The calculation result of the basic model at this stage represents the theoretical maximum power generated from the solar array. To generate this theoretical maximum power, the MPPT system must track the MPP. However, at this stage, due to the decrease in charging power of the energy storage battery pack, the MPPT system shifts the MPP tracking to match the overall energy storage demand and power consumption level of the airship, resulting in a significant error between the calculated results and the actual measurement results. After correcting for this constant-voltage charging stage, the nRMSE at 13:00–16:00 decreased from 27.11% to 3.59%. After the two corrections, the overall nRMSE decreased from 12.17% to 2.59%, significantly improving the conformity between the model calculation results and the actual measurement. Table 2 summarizes the changes in nRSME after different corrections.

Table 2.
Changes in nRSME after different corrections.
The computational model complexity is a key concern for application scenarios that usually require large-scale iterative computation, such as flight trajectory planning and solar array layout optimization. Excessive computational complexity is unacceptable because of the time required for massive iterations. Table 3 shows the computing environment used for the model calculation. In this environment, the time required for a 24 h simulation step of 0.01 h was 0.092 s. The average single-point calculation time was 3.8 × 10−5 s, which can be applied to large-scale iterative optimization algorithms or fast simulation models.

Table 3.
The computing platform used for model testing.
A study similar to that in this paper was conducted in [29], where the average nRMSE of their proposed model output compared to the experimental data was 12.32%. In contrast, our constructed model has a higher computational accuracy. No other models are available for comparison since few studies have calculated power generation with a near-space vehicle as the research object and supported their research with experimental data.
To further verify the model’s generalizability, the model’s calculated results were validated with more dates of flight data, as shown in Figure 10. We randomly selected measured data from three flight dates to test the model’s generalizability: 7 September, 23 September, and 29 September. The measured data for all three random flight dates showed high consistency with the model calculations. The average nRMSE of the multi-day comparison results was 2.47%, indicating that the model has high accuracy and good generalizability.
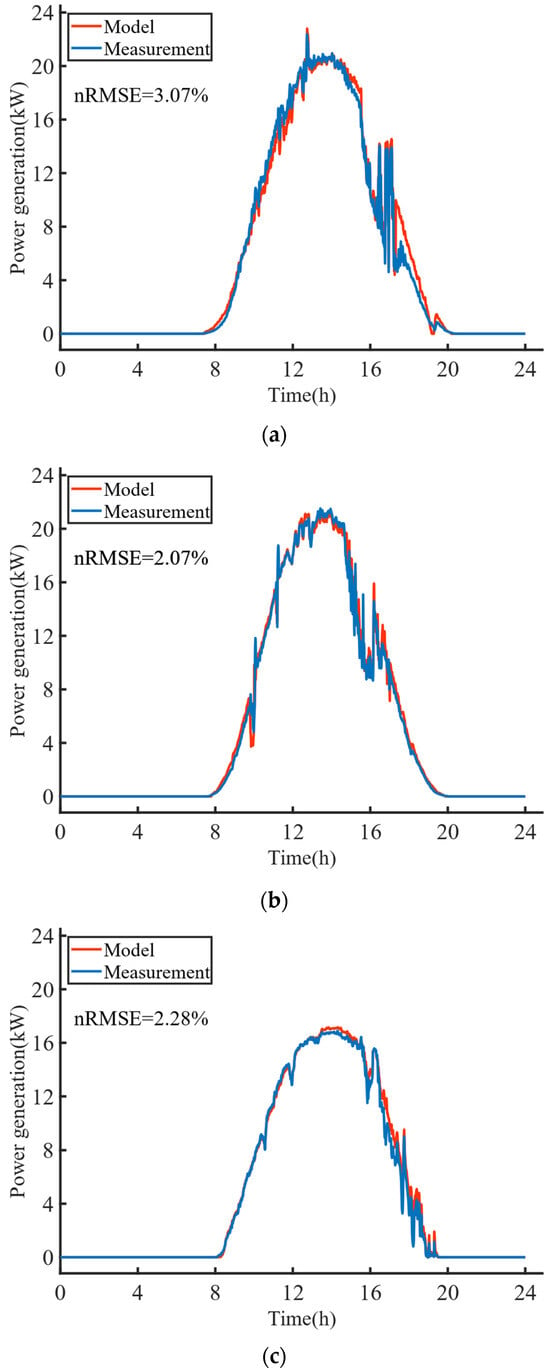
Figure 10.
Comparison of power generation model calculation results and measured results from different flight dates: (a) 7 September; (b) 23 September; (c) 29 September.
5. Conclusions
The model presented herein incorporates critical parameters, including the attitude angle, geographic coordinates, and flight date, among other influencing factors, to accurately represent an airship’s power generation process. Significantly, adjustments were made to consider angular loss and storage battery behavior during constant-voltage charging. The comparative analysis of model outputs and experimental data yielded the following key observations:
- Correcting for angular loss and optimizing the storage battery pack during the constant-voltage charging stage substantially improved the accuracy of the overall power generation calculation model. This refinement reduced the normalized root-mean-square error from 12.17% to 2.59%.
- The model developed in this study demonstrates low computational complexity, making it suitable for integration into iterative optimization algorithms and rapid simulation models.
- Comparative analysis of the model calculation results across multiple flight dates with corresponding experimental data demonstrated the newly established power generation model’s commendable computational precision and robust generalization capabilities, evidenced by an average normalized root-mean-square error of 2.47%.
Author Contributions
Conceptualization, K.S. and Y.Z.; methodology, K.S.; software, K.S.; validation, X.W., G.X. and Z.L.; formal analysis, Y.Z. and Z.L.; investigation, K.S.; resources, Z.L. and X.W.; data curation, Y.Z.; writing—original draft preparation, K.S.; writing—review and editing, X.Z., Y.Z. and Z.L.; visualization, K.S.; supervision, Z.L., Y.Z. and G.X.; project administration, Z.L.; funding acquisition, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Youth Innovation Promotion Association of the Chinese Academy of Science (No. 313320010D).
Data Availability Statement
The authors do not have permission to share data.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Symbols | |||
| The coordinate conversion matrix from the ground coordinate system to the body-fixed coordinate system. | Sunrise time | ||
| The duration of sunlight | Local apparent solar time | ||
| The Sun–Earth distance correction factor | Sunset time | ||
| The deviation of the solar day from 24 h | The charging voltage of the storage battery packs | ||
| The flight altitude | The solar azimuth angle | ||
| The intensity of the extraterrestrial normal solar radiation | The solar declination angle | ||
| The solar constant | The photovoltaic conversion efficiency under standard conditions | ||
| The charging current of storage battery packs | The efficiency of the power controller | ||
| The intensity of direct solar radiation | The photovoltaic conversion efficiency | ||
| The longitude of the standard meridian for the local time zone | The pitch angle of the airship | ||
| The solar day duration | The solar radiation incidence angle | ||
| The local longitude | The day angle | ||
| The normal outward vector of the mesh grid | The air mass | ||
| The atmospheric pressure at flight altitude | The photovoltaic conversion efficiency decay factor | ||
| The charging power | The atmospheric transmittance | ||
| The power generation | The roll angle of the airship | ||
| The power consumption | The flight latitude | ||
| The coordinates of the solar direction vector in the body-fixed coordinate system | The yaw angle of the airship | ||
| The coordinates of the solar direction vector in the ground coordinate system | The solar hour angle | ||
| Local standard time | The sunset hour angle at flight altitude | ||
| Abbreviations | |||
| AU | Astronomical unit | ||
| HAP | High-altitude platform | ||
| MPP | Maximum power point | ||
| MPPT | Maximum power point tracking | ||
| nRMSE | Normalized root-mean-square error | ||
| PCEDF | Photovoltaic conversion efficiency decay factor | ||
| SOC | State of charge | ||
References
- Ilcev, S.D. Stratospheric communication platforms as an alternative for space program. Aircr. Eng. Aerosp. Technol. 2011, 83, 105–111. [Google Scholar] [CrossRef]
- Miller, S.H.; Fesen, R.; Hillenbrand, L.; Rhodes, J.; Baird, G.; Blake, G.; Booth, J.; Carlile, D.E.; Duren, R.; Edworthy, F.G.; et al. Airships: A new horizon for science. arXiv 2014, arXiv:14026706. [Google Scholar] [CrossRef]
- Song, Q.; Zhang, H.-H.; Liang, F.-L.; Li, Y.-H.; Zhou, Z.-M. Results from an airship-mounted ultra-wideband synthetic aperture radar for penetrating surveillance. In Proceedings of the 2011 3rd International Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Seoul, Republic of Korea, 26–30 September 2011; pp. 1–4. [Google Scholar]
- Wan, L. Stratospheric-airship-assisted orbital payload launching system. In Proceedings of the AIAA SPACE and Astronautics Forum and Exposition, Orlando, FL, USA, 17–19 September 2018; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. [Google Scholar]
- Liao, L.; Pasternak, I. A review of airship structural research and development. Prog. Aerosp. Sci. 2009, 45, 83–96. [Google Scholar] [CrossRef]
- Manikandan, M.; Pant, R.S. Research and advancements in hybrid airships—A review. Prog. Aerosp. Sci. 2021, 127, 100741. [Google Scholar] [CrossRef]
- Shuichi, S.; Yukio, M.; Masaaki, N.; Kazutoshi, I. Ongoing research on disaster monitoring UAV at JAXA’s Aviation Program Group. In Proceedings of the 2008 SICE Annual Conference, Chofu, Japan, 20–23 August 2008; IEEE: New York, NY, USA, 2008. [Google Scholar]
- Lv, M.; Li, J.; Zhu, W.; Du, H.; Meng, J.; Sun, K. A theoretical study of rotatable renewable energy system for stratospheric airship. Energy Convers. Manag. 2017, 140, 51–61. [Google Scholar] [CrossRef]
- Hoseinzadeh, S.; Yargholi, R.; Kariman, H.; Heyns, P.S. Exergoeconomic analysis and optimization of reverse osmosis desalination integrated with geothermal energy. Environ. Prog. Sustain. Energy. 2020, 39, e13405. [Google Scholar] [CrossRef]
- Yargholi, R.; Kariman, H.; Hoseinzadeh, S.; Bidi, M.; Naseri, A. Modeling and advanced exergy analysis of integrated reverse osmosis desalination with geothermal energy. Water Supply 2020, 20, 984–996. [Google Scholar] [CrossRef]
- Garg, A.; Burnwal, S.; Pallapothu, A.; Alawa, R.; Ghosh, A. Solar panel area estimation and optimization for geostationary stratospheric airships. In Proceedings of the 11th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference, Virginia Beach, VA, USA, 20–22 September 2011; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2011. [Google Scholar]
- Zhu, W.; Xu, Y.; Li, J.; Du, H.; Zhang, L. Research on optimal solar array layout for near-space airship with thermal effect. Sol. Energy 2018, 170, 1–13. [Google Scholar] [CrossRef]
- Du, H.; Li, J.; Zhu, W.; Yao, Z.; Cui, E.; Lv, M. Thermal performance analysis and comparison of stratospheric airships with rotatable and fixed photovoltaic array. Energy Convers. Manag. 2018, 158, 373–386. [Google Scholar] [CrossRef]
- Zhang, L.; Li, J.; Wu, Y.; Lv, M. Analysis of attitude planning and energy balance of stratospheric airship. Energy 2019, 183, 1089–1103. [Google Scholar] [CrossRef]
- Liu, S.; Sun, K.; Gao, J.; Liang, H. Receiving energy analysis and optimal design of crystalline silicon solar cell array on solar airship. Energy 2023, 282, 128988. [Google Scholar] [CrossRef]
- Tang, J.; Xie, W.; Zhou, P.; Yang, H.; Zhang, T.; Wang, Q. Multidisciplinary Optimization and Analysis of Stratospheric Airships Powered by Solar Arrays. Aerospace 2023, 10, 43. [Google Scholar] [CrossRef]
- Zhu, X.; Hou, Z.; Zhang, J.; Liu, D.; Zhu, B. Sun-seeking eternal flight of solar-powered airplane. J. Aerosp. Eng. 2014, 27, 06014004. [Google Scholar] [CrossRef]
- Gupta, S.; Duttagupta, S.P.; Vachhani, L.; Mitra, M. Attitude control of LTA platform for generation of a non-oscillatory solar power. Sol. Energy 2019, 189, 131–150. [Google Scholar] [CrossRef]
- Pande, D.; Verstraete, D. Impact of solar cell characteristics and operating conditions on the sizing of a solar powered nonrigid airship. Aerosp. Sci. Technol. 2018, 72, 353–363. [Google Scholar] [CrossRef]
- Dai, Q.; Xing, D.; Fang, X.; Zhao, Y. Conceptual Design of an Energy System for High Altitude Airships Considering Thermal Effect. Energies 2021, 14, 4204. [Google Scholar] [CrossRef]
- Wang, X.; Li, Z.; Zhang, Y. Model for Predicting the Operating Temperature of Stratospheric Airship Solar Cells with a Support Vector Machine. Energies 2021, 14, 1228. [Google Scholar] [CrossRef]
- Wang, H.; Song, B.; Zuo, L. Effect of high-altitude airship’s attitude on performance of its energy system. J. Aircr. 2007, 44, 2077–2080. [Google Scholar] [CrossRef]
- Jiang, Y.; Lv, M.; Sun, K. Effects of installation angle on the energy performance for photovoltaic cells during airship cruise flight. Energy 2022, 258, 124982. [Google Scholar] [CrossRef]
- Li, J.; Lv, M.; Tan, D.; Zhu, W.; Sun, K.; Zhang, Y. Output performance analyses of solar array on stratospheric airship with thermal effect. Appl. Therm. Eng. 2016, 104, 743–750. [Google Scholar] [CrossRef]
- Li, J.; Liao, J.; Liao, Y.; Du, H.; Luo, S.; Zhu, W.; Lv, M. An approach for estimating perpetual endurance of the stratospheric solar-powered platform. Aerosp. Sci. Technol. 2018, 79, 118–130. [Google Scholar] [CrossRef]
- Du, H.; Zhu, W.; Wu, Y.; Zhang, L.; Li, J.; Lv, M. Effect of angular losses on the output performance of solar array on long-endurance stratospheric airship. Energy Convers. Manag. 2017, 147, 135–144. [Google Scholar] [CrossRef]
- Ran, H.; Thomas, R.; Mavris, D. A comprehensive global model of broadband direct solar radiation for solar cell simulation. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2007. [Google Scholar]
- Iqbal, M. An Introduction to Solar Radiation; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Liu, Q.; Xu, G.; Li, Z.; Gao, Y.; Yang, Y.; Li, Y.; Du, H. A rapid prediction model of photovoltaic power generation for autonomous long-duration aerostat. IET Renew. Power Gener. 2023, 17, 1597–1608. [Google Scholar] [CrossRef]
- Yang, X.; Liu, D. Renewable power system simulation and endurance analysis for stratospheric airships. IET Renew. Power Gener. 2017, 113, 1070–1076. [Google Scholar] [CrossRef]
- Li, H.; Lian, Y.; Wang, X.; Ma, W.; Zhao, L. Solar constant values for estimating solar radiation. Energy 2011, 36, 1785–1789. [Google Scholar] [CrossRef]
- Kreith, F.; Kreider, J.F. Numerical Prediction of the Performance of High Altitude Balloons; No. NCAR/TN-65+STR; National Center for Atmospheric Research: Boulder, CO, USA, 1974. [Google Scholar]
- Kasten, F.; Young, A.T. Revised optical air mass tables and approximation formula. Appl. Opt. 1989, 28, 4735. [Google Scholar] [CrossRef] [PubMed]
- International Civil Aviation Organization. Manual of the ICAO Standard Atmosphere—Extended to 80 Kilometres (262,500 Feet); Doc 7488/3; International Civil Aviation Organization: Montreal, QC, Canada, 1993. [Google Scholar]
- Martin, N.; Ruiz, J.M. Calculation of the PV modules angular losses under field conditions by means of an analytical model. Sol. Energy Mater. Sol. Cells 2001, 70, 25–38. [Google Scholar] [CrossRef]
- Sun, B.; Lu, L.; Yuan, Y.; Ocłoń, P. Development and validation of a concise and anisotropic irradiance model for bifacial photovoltaic modules. Renew Energ. 2023, 209, 442–452. [Google Scholar] [CrossRef]
- John, J.J.; Rajasekar, V.; Boppana, S.; Chattopadhyay, S.; Kottantharayil, A.; TamizhMani, G. Quantification and modeling of spectral and angular losses of naturally soiled PV modules. IEEE J. Photovolt. 2015, 5, 1727–1734. [Google Scholar] [CrossRef]
- Mustafa, F.I.; Shakir, S.; Mustafa, F.F.; Naiyf, A.T. Simple design and implementation of solar tracking system two axis with four sensors for Baghdad city. In Proceedings of the 9th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 20–22 March 2018; IEEE: New York, NY, USA, 2018; pp. 1–5. [Google Scholar]
- Song, T.-B.; Chen, Q.; Zhou, H.; Jiang, C.; Wang, H.-H.; Yang, M.Y.; Liu, Y.; You, J.; Yang, Y. Perovskite solar cells: Film formation and properties. J. Mater. Chem. A 2015, 3, 9032–9050. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, Y. Design and verification of an integrated panoramic sun sensor atop a small spherical satellite. Sensors 2022, 22, 8130. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Li, Z.; Zhang, Y.; Wang, X.; Gao, Y. An optimization model based on temperature field and series–parallel structure for battery-package of a stratospheric airship. Energy Sci. Eng. 2022, 10, 1986–1997. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).