A Two-Terminal Directional Protection Method for HVDC Transmission Lines of Current Fault Component Based on Improved VMD-Hilbert Transform
Abstract
1. Introduction
2. Basic Principles of Improving VMD-Hilbert Transform
2.1. Algorithmic Principles of the VMD-Hilbert Transform
2.2. Parameter Optimization of the VMD Algorithm
3. DC Line Fault Discrimination Based on an Improved VMD-Hilbert Transform
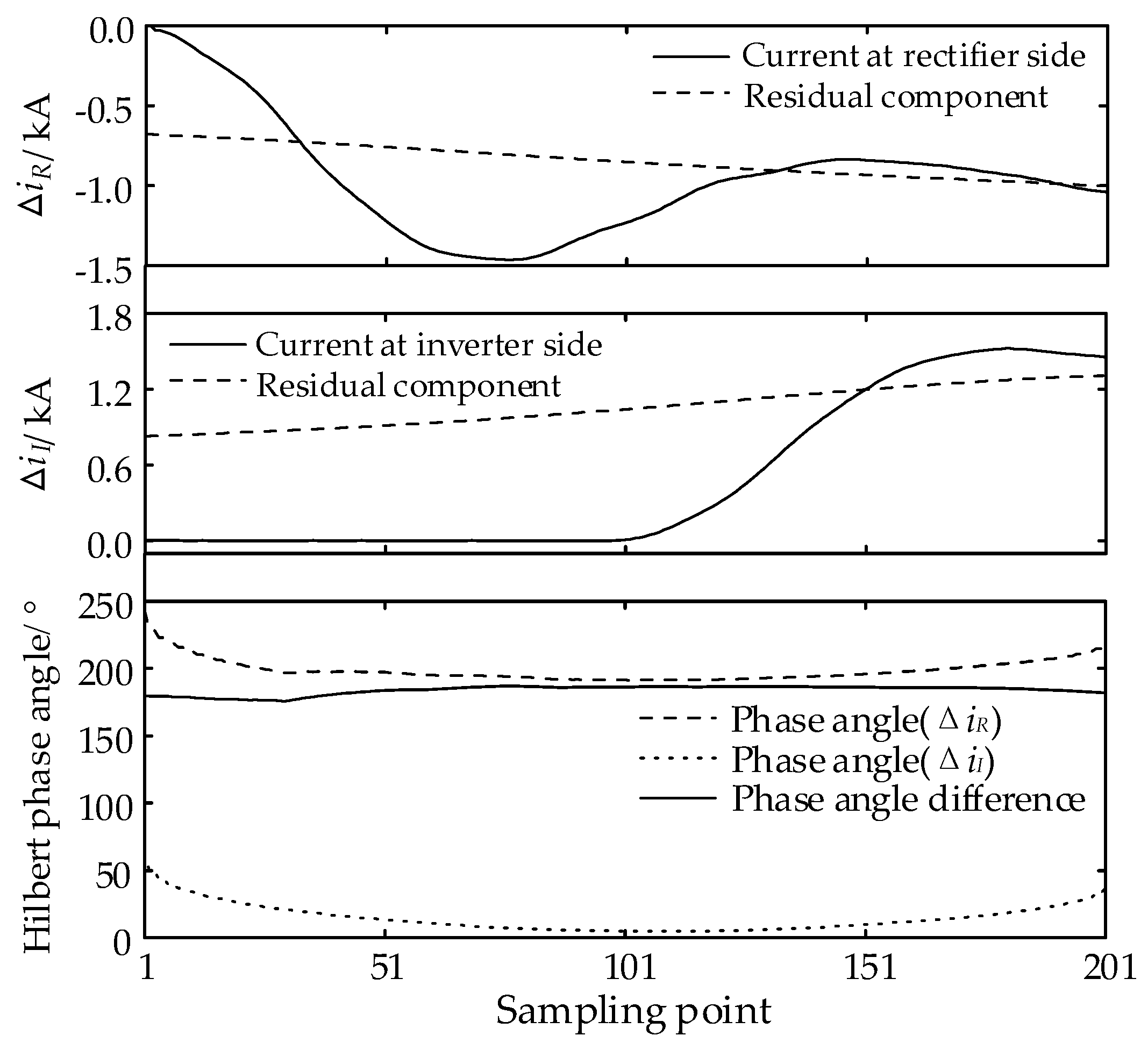
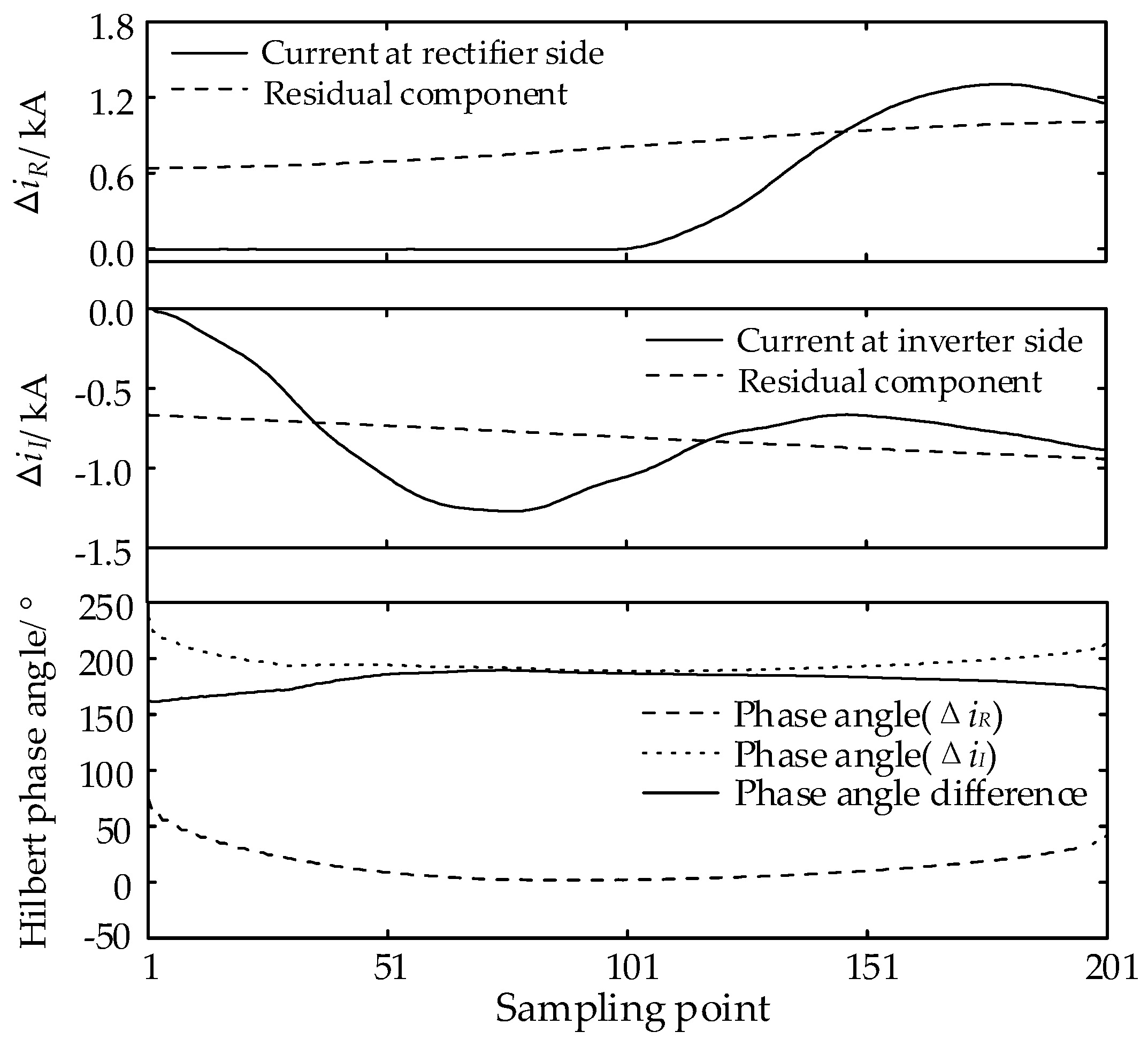
3.1. Analysis of the Direction Characteristics of the Current Fault Component
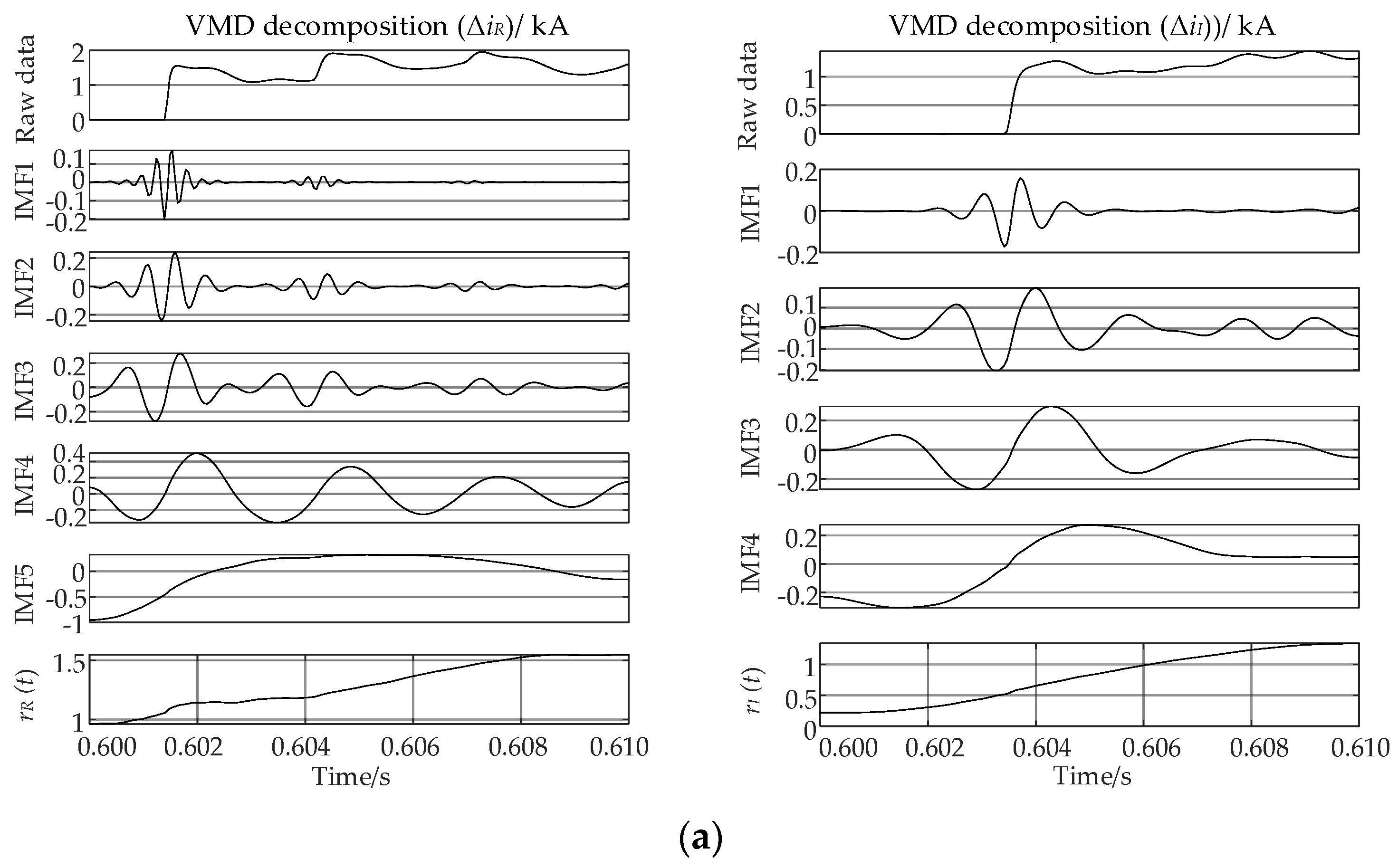
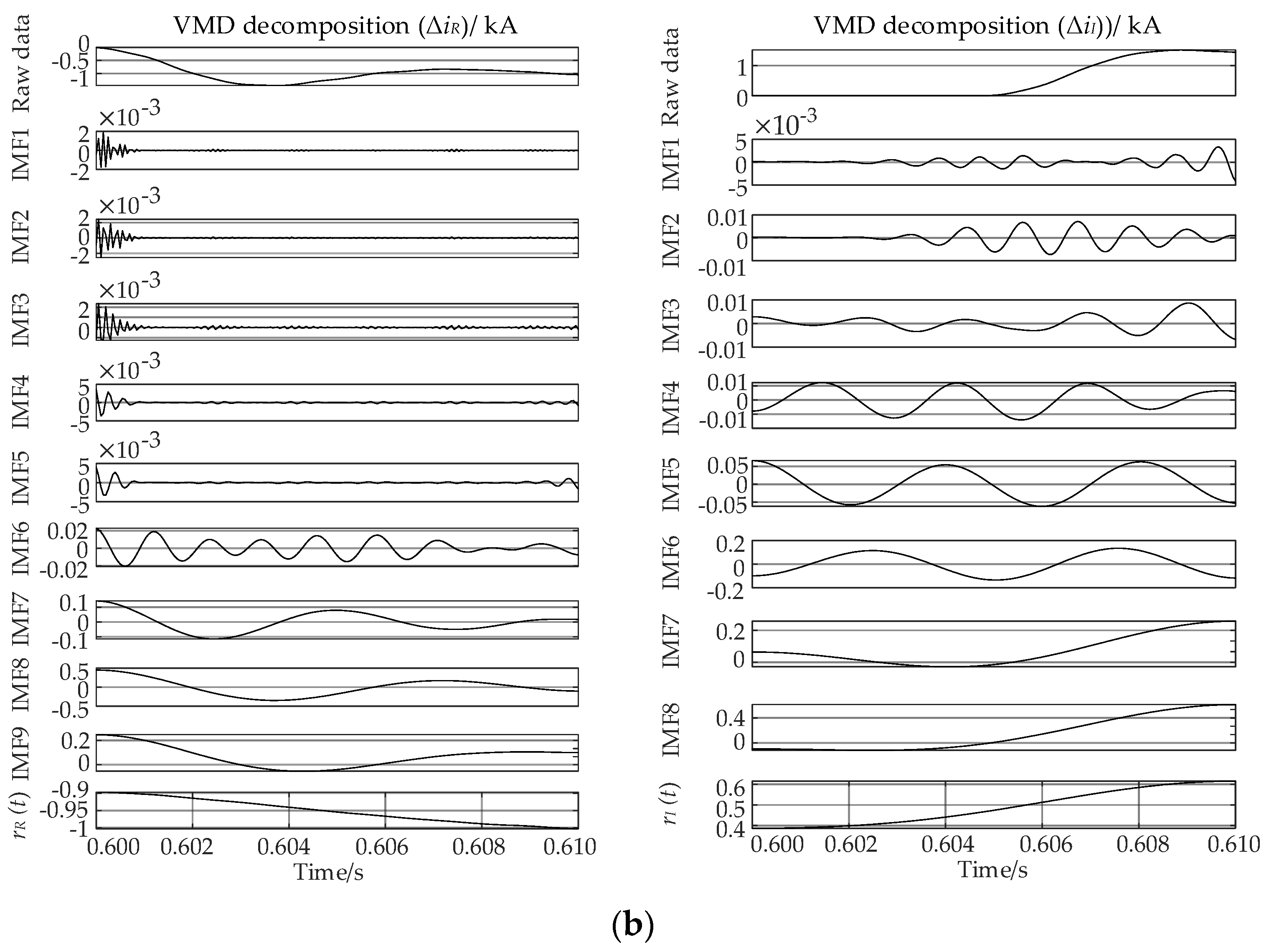
3.2. SSA-VMD Extraction of Residual Components
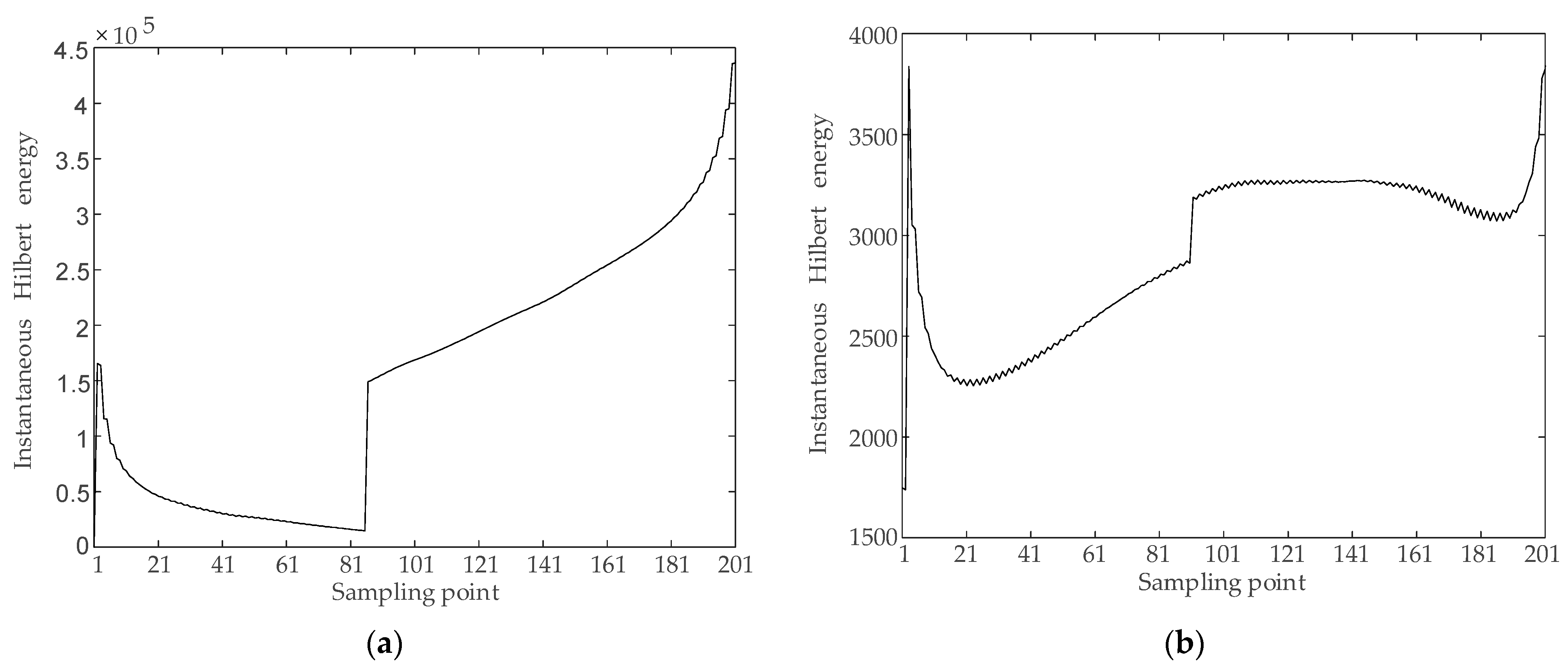
3.3. Directional Determination Based on Phase Angle Difference of Hilbert Transform
3.4. Directional Protection Criterion of the Current Fault Component Based on an Improved VMD-Hilbert Transform
- Start criterion:
- 2.
- Action criterion:
- 3.
- Fault pole selection criterion
4. Simulation Analysis of the Experiments
4.1. Simulation Model of the HVDC Transmission System
4.2. Simulation of Internal Faults in the Line Area
- (1)
- Under different fault distances and transition resistances, the protection can correctly determine the fault section and fault pole.
- (2)
- The Hilbert phase angle difference Δθ2 gradually increases from the midpoint of the line to both ends and when the distance to both ends is 100 km or less, the frequency oscillation of the current fault component causes Δθ2 to increase faster, which is significantly more on the rectifier side than on the inverter side.
- (3)
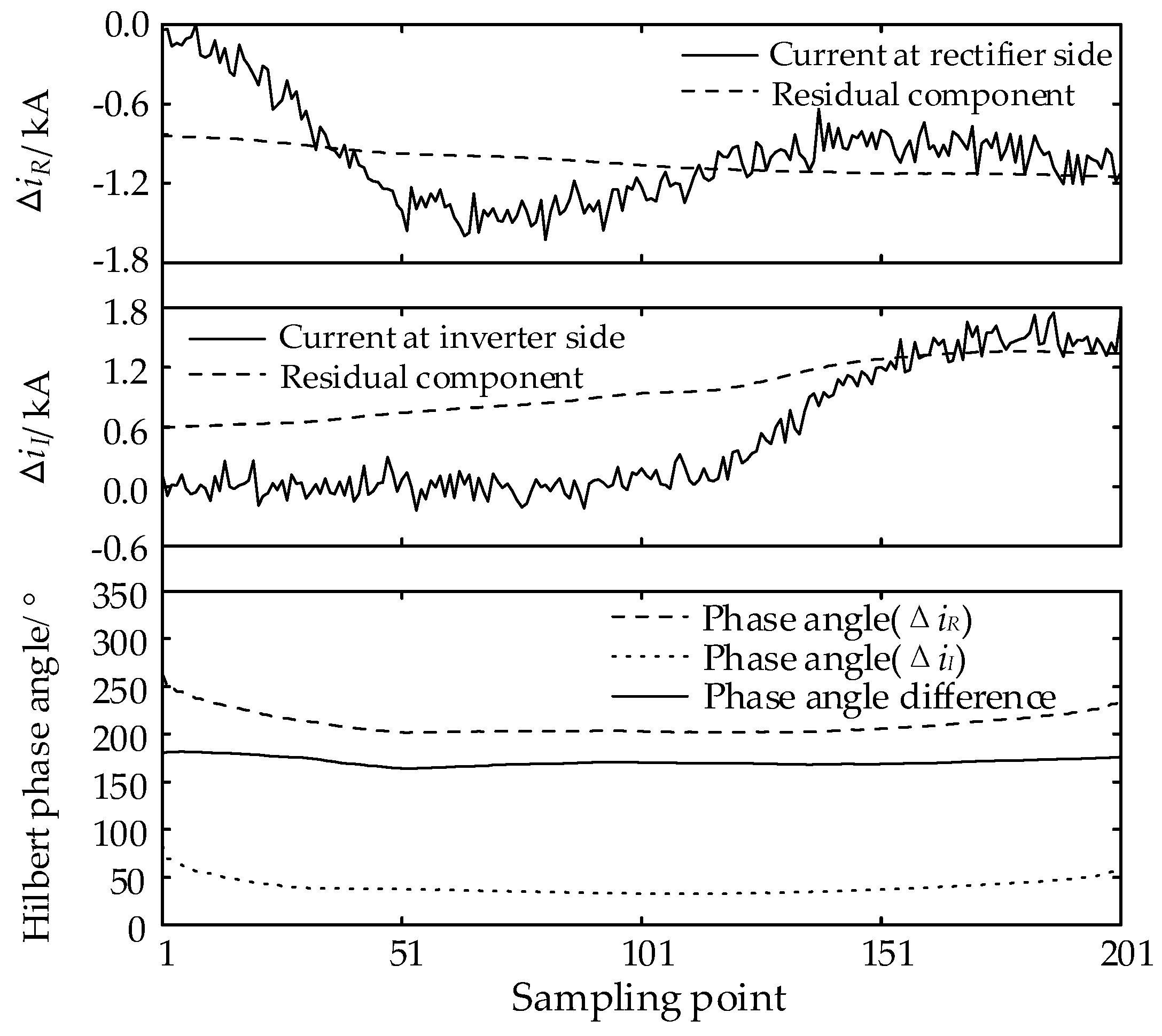
- SSA-VMD of the current fault component eliminates the effects of line distribution capacitance and communication noise, and reliably identifies faults at both ends of the line.
4.3. Simulation of External Faults in the Line Area
4.4. Examination of Anti-Noise Interference Performance
4.5. Analysis of Protection Action Time
5. Conclusions
- (1)
- VMD combines the features of SSA solving speed and and selects the average envelope entropy as the fitness function to adaptively determine the best selection parameters of VMD, which effectively solves the problem of difficult selection of VMD parameters. Nevertheless, optimization for large-scale complex problems should also be evaluated and tuned on a case-by-case basis.
- (2)
- SSA-VMD can eliminate the influence of line distributed capacitance and communication noise on the current fault component at both ends of the line, obtain the residual component characterizing the direction of change at both ends, and then calculate the Hilbert phase angle difference through Hilbert transform to determine the directional relationship of the current fault component at both ends of the line. Meanwhile, the ratio of multi-band Hilbert energy sum of single-ended voltage fault component at both poles can be obtained by improving the VMD-Hilbert transform to effectively identify the fault poles.
- (3)
- Compared with the existing DC differential protection and pilot protection, the proposed protection is not affected by the distributed capacitance and does not depend on the boundary conditions. As verified by simulation, the method does not require a high sampling device and has fast action speed, can reliably identify the internal and external faults, has good tolerance to transition resistance and anti-noise interference, and better meets the backup protection needs of HVDC transmission lines.
- (4)
- The two-terminal backup protection method proposed in this paper can also be used as the main protection without considering the communication delay and the calculation amount, and can be combined with each other for further analysis in the future. Since the scheme is based on theoretical analysis and simulation verification, it needs to be further combined with actual engineering to verify the applicability of the scheme. At the same time, based on the research in this article, further research can be conducted on this method in related fields of power systems such as lightning strike identification, fault location, fault intelligent algorithm, transient signal analysis, and power quality analysis.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

Appendix B

References
- Perez-Molina, M.J.; Larruskain, D.M.; Lopez, P.E.; Buigues, G.; Valverde, V. Review of Protection Systems for Multi-terminal High Voltage Direct Current Grids. Renew. Sustain. Energy Rev. 2021, 144, 111037. [Google Scholar]
- Radwan, M.; Azaz, S.P. Protection of Multi-Terminal HVDC Grids: A Comprehensive Review. Energies 2022, 15, 9552. [Google Scholar]
- Bahrman, M.P.; Johnson, B.K. The ABCs of HVDC Transmission Technologies. IEEE Power Energy Mag. 2007, 5, 32–44. [Google Scholar] [CrossRef]
- Muniappan, M. A comprehensive Review of DC Fault Protection Methods in HVDC Transmission Systems. Prot. Control. Mod. Power Syst. 2021, 6, 1. [Google Scholar]
- Zhang, Y.; Tai, N.L.; Xu, B. Fault Analysis and Traveling-Wave Protection Scheme for Bipolar HVDC Lines. IEEE Trans. Power Deliv. 2012, 27, 1583–1591. [Google Scholar] [CrossRef]
- Gao, B.F.; Zhang, R.X.; Zhang, X.W. A Novel Procedure for Protection Setting in an HVDC System Based on Fault Quantities. J. Electr. Eng. Technol. 2017, 12, 513–521. [Google Scholar] [CrossRef][Green Version]
- Gao, S.P.; Liu, Q.; Song, G.B. Current Differential Protection Principle of HVDC Transmission System. IET Gener. Transm. Distrib. 2017, 11, 1286–1292. [Google Scholar] [CrossRef]
- Lin, S.; Gao, S.; He, Z.Y.; Deng, Y.J. A Pilot Directional Protection for HVDC Transmission Line Based on Relative Entropy of Wavelet Energy. Entropy 2015, 17, 5257–5273. [Google Scholar] [CrossRef]
- Li, Z.; Zou, G.B.; Du, T.; Yang, W.J. S-Transform Based Pilot Protection Method for HVDC Transmission Lines. In Proceedings of the 2015 5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Changsha, China, 26–29 November 2015; pp. 1667–1672. [Google Scholar]
- Shu, H.C.; Tian, X.C. Entire-line Instant Protection Based on PCA Clustering for 800kV HVDC Transmission Line. Electr. Power Autom. Equip. 2016, 36, 51–59. [Google Scholar]
- Gong, Y.L.; Cao, B.H.; Zhang, H.; Sun, F.S.; Fan, M.B. Terahertz Based Thickness Measurement of Thermal Barrier Coatings Using Hybrid Machine Learning. Nondestruct. Test. Eval. 2023, 47, 1–18. [Google Scholar] [CrossRef]
- Weingessel, A.; Hornik, K. Local PCA Algorithms. IEEE Trans. Neural Netw. 2000, 11, 1242–1250. [Google Scholar] [PubMed]
- Qi, G.Q.; Wang, Z.P. Directional Pilot Protection Method of Fault Component for HVDC Transmission Lines Based on Hilbert-Huang Transform. Power Syst. Prot. Control. 2017, 45, 92–99. [Google Scholar]
- Liu, Z.G.; Gui, Y.; Li, W.H. A Classification Method for Complex Power Quality Disturbances Using EEMD and Rank Wavelet SVM. IEEE Trans. Smart Grid 2015, 6, 1678–1685. [Google Scholar] [CrossRef]
- Zhan, L.W.; Li, C.W. A Comparative Study of Empirical Mode Decomposition-Based Filtering for Impact Signal. Entropy 2016, 19, 13. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Salim, L. Comparative Study of ECG Signal Denoising by Wavelet Thresholding in Empirical and Variational Mode Decomposition Domains. Healthc. Technol. Lett. 2014, 1, 104–109. [Google Scholar]
- Wang, Y.X.; Markert, R.; Xiang, J.W. Research on Variational Mode Decomposition and its Application in Detecting Rub-impact Fault of the Rotor System. Mech. Syst. Signal Process. 2015, 60, 243–251. [Google Scholar] [CrossRef]
- Yang, H.B.; Liu, S.L.; Zhang, H.L. Adaptive Estimation of VMD Modes Number Based on Cross Correlation Coefficient. J. Vibroengineering 2017, 19, 1185–1196. [Google Scholar] [CrossRef]
- Viswanath, A.; Jose, K.J.; Krishnan, N.; Kumar, S.S.; Soman, K.P. Spike Detection of Disturbed Power Signal Using VMD. Procedia Comput. Sci. 2015, 46, 1087–1094. [Google Scholar] [CrossRef]
- Wang, L.; Liu, H.; Dai, L.V.; Liu, Y.W. Novel Method for Identifying Fault Location of Mixed Lines. Energies 2018, 11, 1529. [Google Scholar] [CrossRef]
- Xu, Y.C.; Gao, Y.K.; Li, Z.H.; Lu, M. Detection and Classification of Power Quality Disturbances in Distribution Networks Based on VMD and DFA. Csee J. Power Energy Syst. 2019, 6, 122–130. [Google Scholar]
- Luo, D.R.; Wu, T.; Li, M.; Yi, B.S.; Zuo, H.B. Application of VMD and Hilbert Transform Algorithms on Detection of the Ripple Components of the DC Signal. Energies 2020, 13, 935. [Google Scholar] [CrossRef]
- Wang, L.; He, Y.G.; Li, L. A Single-Terminal Fault Location Method for HVDC Transmission Lines Based on a Hybrid Deep Network. Electronics 2021, 10, 255. [Google Scholar] [CrossRef]
- Song, S.D.; Yao, Z.C.; Wang, X.N. The summary of Hilbert-Huang transform. In Proceedings of the 2013 5th International Symposium on Photoelectronic Detection and Imaging (ISPDI)—Infrared Imaging and Applications, Beijing, China, 25–27 June 2013. [Google Scholar]
- Paternina, M.R.A.; Tripathy, R.K.; Zamora-Mendez, A.; Dotta, D. Identification of Electromechanical Oscillatory Modes Based on Variational Mode Decomposition. Electr. Power Syst. Res. 2019, 167, 71–85. [Google Scholar] [CrossRef]
- Xiao, G.; Xu, F.; Tong, L.H.; Xu, H.R.; Zhu, P.W. A Hybrid Energy Storage System Based on Self-adaptive Variational Mode Decomposition to Smooth Photovoltaic Power Fluctuation. J. Energy Storage 2022, 55, 105509. [Google Scholar] [CrossRef]
- Zhang, Q.; Ma, W.H.; Li, G.L.; Ding, J.J.; Xie, M. Fault Diagnosis of Power Grid Based on Variational Mode Decomposition and Convolutional Neural Network. Electr. Power Syst. Res. 2022, 208, 107871. [Google Scholar] [CrossRef]
- Yue, Y.G.; Cao, L.; Lu, D.W.; Hu, Z.Y.; Xu, M.H. Review and Empirical Analysis of Sparrow Search Algorithm. Artif. Intell. Rev. 2023, 56, 10867–10919. [Google Scholar]
- Yan, X.A.; Jia, M.P.; Xiang, L. Compound Fault Diagnosis of Rotating Machinery Based on OVMD. Meas. Sci. Technol. 2016, 27, 075002. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, T.T.; Wang, Y.; Wang, K.W.; Shen, Y. A Parameter Optimized Variational Mode Decomposition Method for Rail Crack Detection Based on Acoustic Emission Technique. Nondestruct. Test. Eval. 2020, 36, 411–439. [Google Scholar] [CrossRef]
- Zheng, X.X.; Wang, S.; Qian, Y.Q. Fault Feature Extraction of Wind Turbine Gearbox under Variable Speed Based on Improved Adaptive Variational Mode Decomposition. Proc. Inst. Mech. Eng. Part A J. Power Energy 2019, 234, 848–861. [Google Scholar] [CrossRef]
- Song, G.B.; Chu, X.; Gao, S.P.; Kang, X.N.; Jiao, Z.B. A New Whole-Line Quick-Action Protection Principle for HVDC Transmission Lines Using One-end Current. IEEE Trans. Power Deliv. 2014, 30, 599–607. [Google Scholar] [CrossRef]



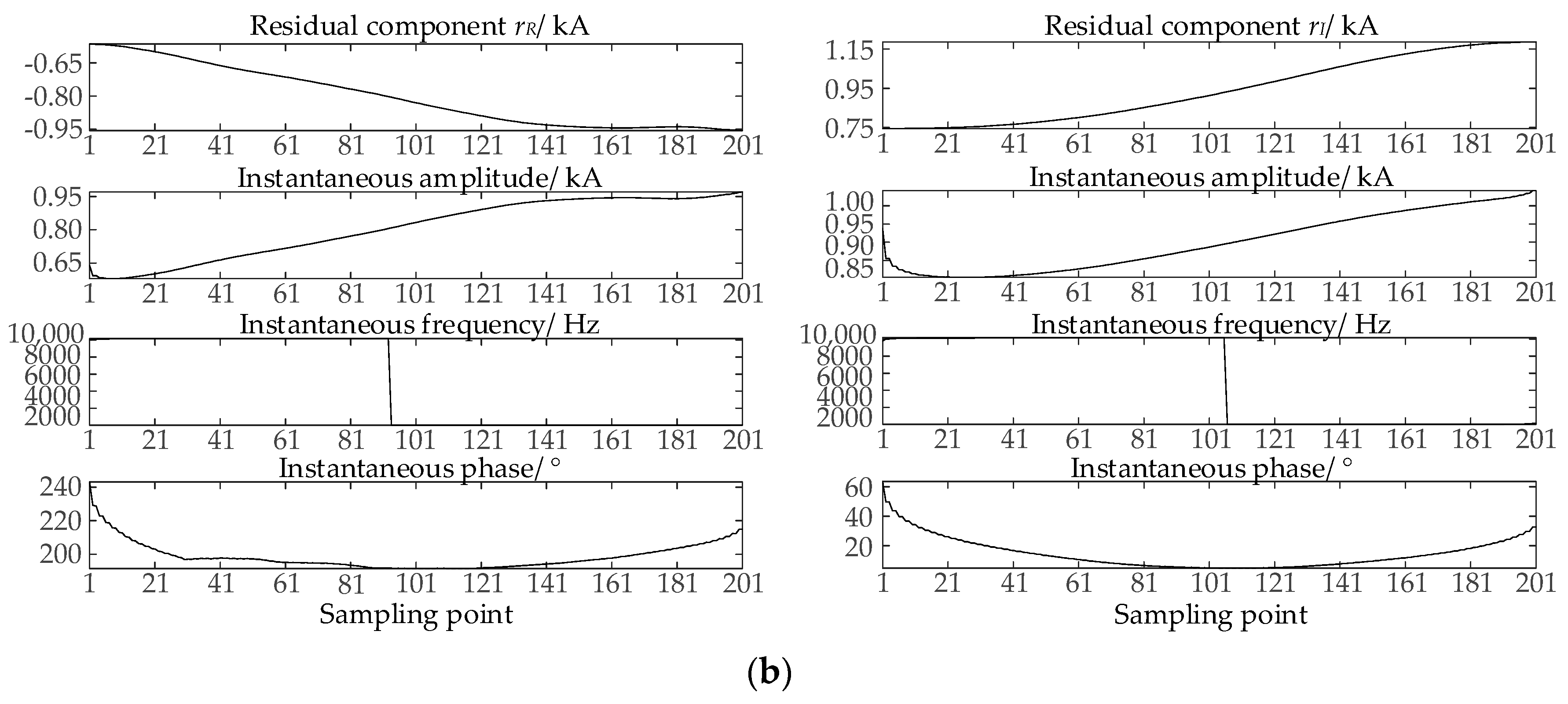

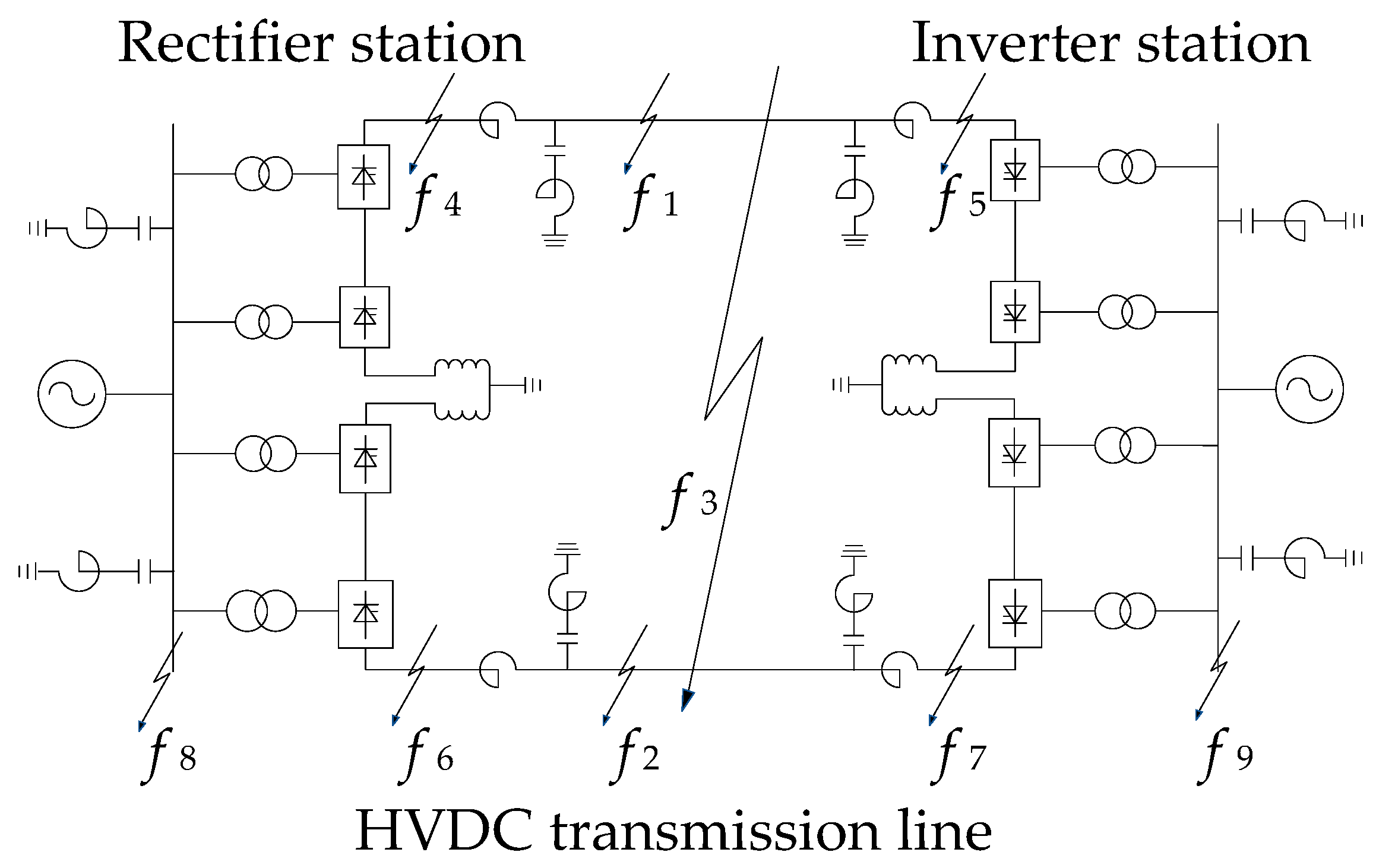
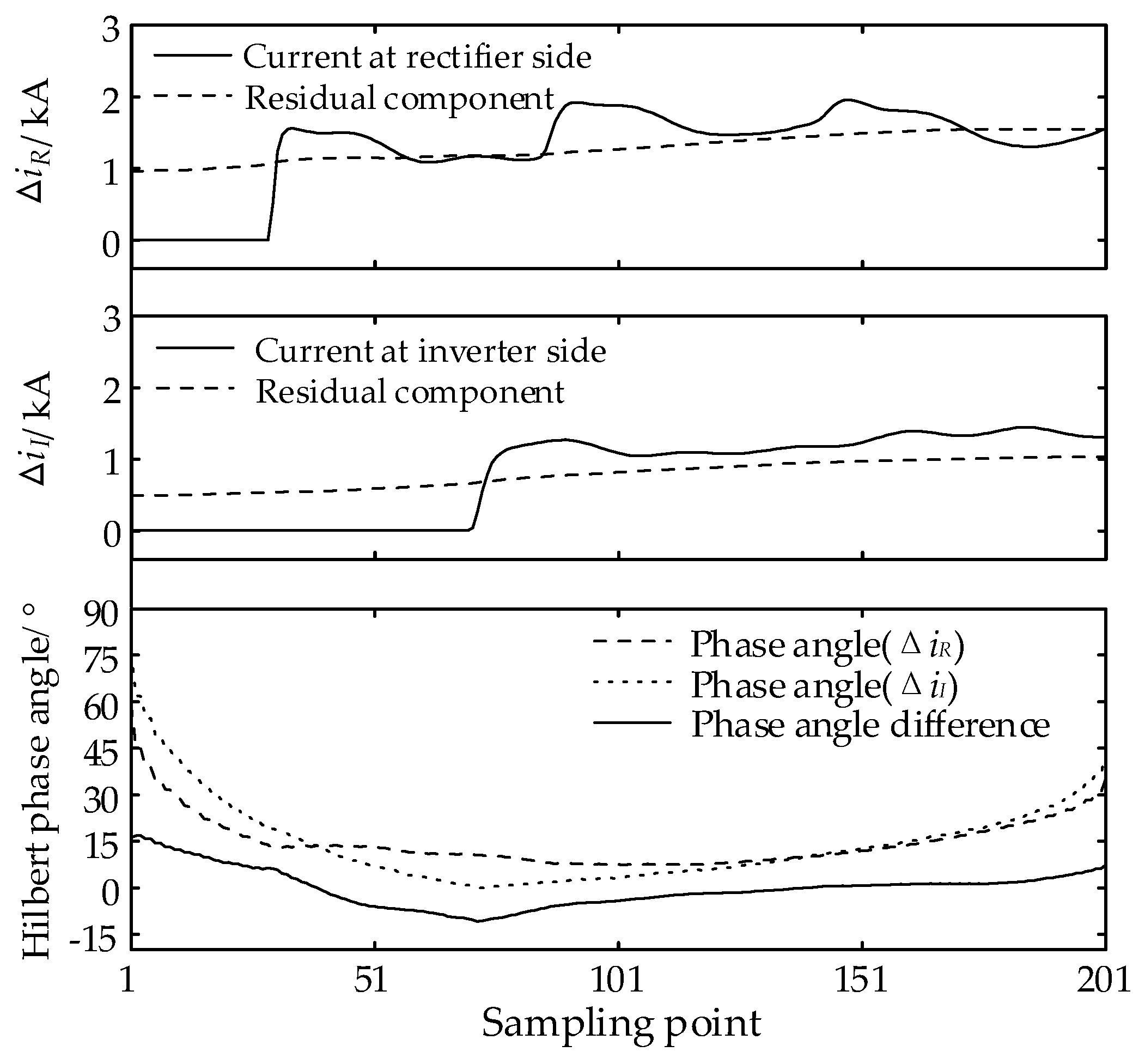
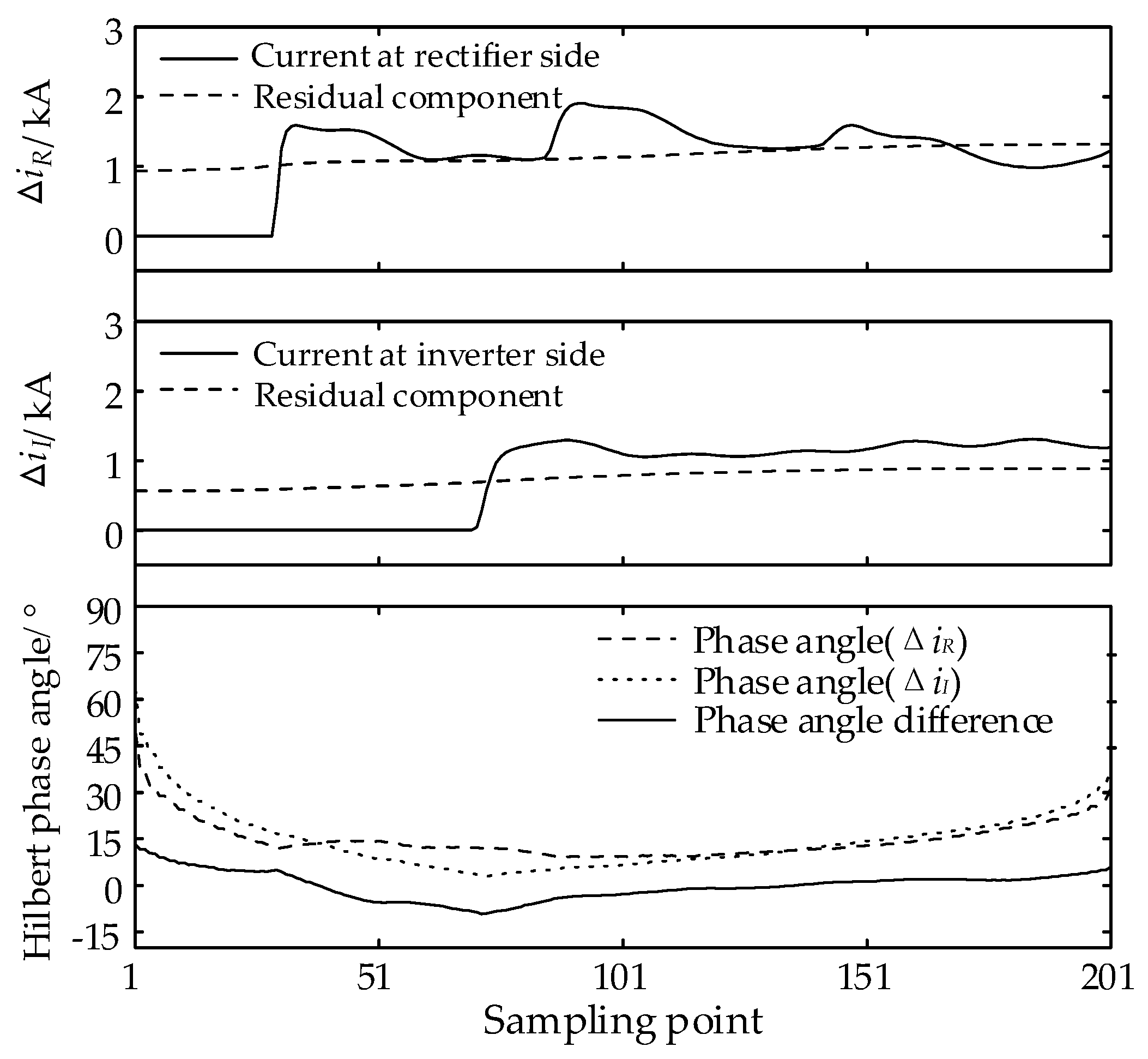

| Type of Fault | Fault Distance/km | Transition Resistance/Ω | ) | ) |
|---|---|---|---|---|
| Internal fault in the line area | 400 | 10 | (7, 173) | (6, 78) |
| 100 | (6, 345) | (5, 89) | ||
| 300 | (6, 107) | (5, 35) | ||
| 700 | 10 | (4, 341) | (5, 183) | |
| 100 | (4, 210) | (4, 155) | ||
| 300 | (4, 97) | (4, 104) | ||
| 1300 | 10 | (7, 241) | (8, 541) | |
| 100 | (6, 99) | (8, 346) | ||
| 300 | (6, 153) | (7, 301) | ||
| External fault on rectifier valve side | – | 10 | (10, 2251) | (9, 211) |
| – | 100 | (11, 1544) | (9, 194) | |
| External fault on inverter valve side | – | 10 | (8, 351) | (10, 658) |
| – | 100 | (8, 222) | (9, 514) | |
| Three-phase failure of the AC bus on the rectifier side | – | – | (9, 189) | (7, 58) |
| Three-phase fault of the AC bus on the inverter side | – | – | (7, 115) | (7, 258) |
| Fault Position | Transition Resistance/Ω | Hilbert Phase Angle Difference Δθ2/° | Electrode Selection Factor P | Identification Result |
|---|---|---|---|---|
| 20 km | 10 | 38.0279 | 0.0416 | Negative internal fault |
| 100 | 36.4295 | 0.0223 | Negative internal fault | |
| 300 | 34.1124 | 0.0719 | Negative internal fault | |
| 100 km | 10 | 26.7622 | 0.0693 | Negative internal fault |
| 100 | 25.2729 | 0.0545 | Negative internal fault | |
| 300 | 23.6231 | 0.0414 | Negative internal fault | |
| 300 km | 10 | 14.1787 | 0.0294 | Negative internal fault |
| 100 | 22.5746 | 0.0202 | Negative internal fault | |
| 300 | 22.4879 | 0.0583 | Negative internal fault | |
| 700 km | 10 | 1.0162 | 0.0192 | Negative internal fault |
| 100 | 0.1877 | 0.0361 | Negative internal fault | |
| 300 | 0.3662 | 0.0682 | Negative internal fault | |
| 1300 km | 10 | 13.3134 | 0.0634 | Negative internal fault |
| 100 | 12.8028 | 0.1125 | Negative internal fault | |
| 300 | 18.3977 | 0.1265 | Negative internal fault |
| Fault Position | Transition Resistance/Ω | Hilbert Phase Angle Difference Δθ1/° | Hilbert Phase Angle Difference Δθ2/° | Identification Result |
|---|---|---|---|---|
| f4 | 10 | 185.2359 | 173.6549 | External fault |
| 100 | 187.3681 | 177.6515 | External fault | |
| 300 | 182.8825 | 173.3255 | External fault | |
| f5 | 10 | 182.1298 | 170.6549 | External fault |
| 100 | 181.8433 | 176.2542 | External fault | |
| 300 | 180.5513 | 178.9875 | External fault | |
| f8 | – | 183.4566 | 176.4587 | External fault |
| f9 | – | 181.1287 | 173.5422 | External fault |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Han, K.; Li, H.; Zhang, T.; Chen, F. A Two-Terminal Directional Protection Method for HVDC Transmission Lines of Current Fault Component Based on Improved VMD-Hilbert Transform. Energies 2023, 16, 6987. https://doi.org/10.3390/en16196987
Liu S, Han K, Li H, Zhang T, Chen F. A Two-Terminal Directional Protection Method for HVDC Transmission Lines of Current Fault Component Based on Improved VMD-Hilbert Transform. Energies. 2023; 16(19):6987. https://doi.org/10.3390/en16196987
Chicago/Turabian StyleLiu, Shuhao, Kunlun Han, Hongzheng Li, Tengyue Zhang, and Fengyuan Chen. 2023. "A Two-Terminal Directional Protection Method for HVDC Transmission Lines of Current Fault Component Based on Improved VMD-Hilbert Transform" Energies 16, no. 19: 6987. https://doi.org/10.3390/en16196987
APA StyleLiu, S., Han, K., Li, H., Zhang, T., & Chen, F. (2023). A Two-Terminal Directional Protection Method for HVDC Transmission Lines of Current Fault Component Based on Improved VMD-Hilbert Transform. Energies, 16(19), 6987. https://doi.org/10.3390/en16196987







