A Control Design Technology of Isolated Bidirectional LLC Resonant Converter for Energy Storage System in DC Microgrid Applications
Abstract
:1. Introduction
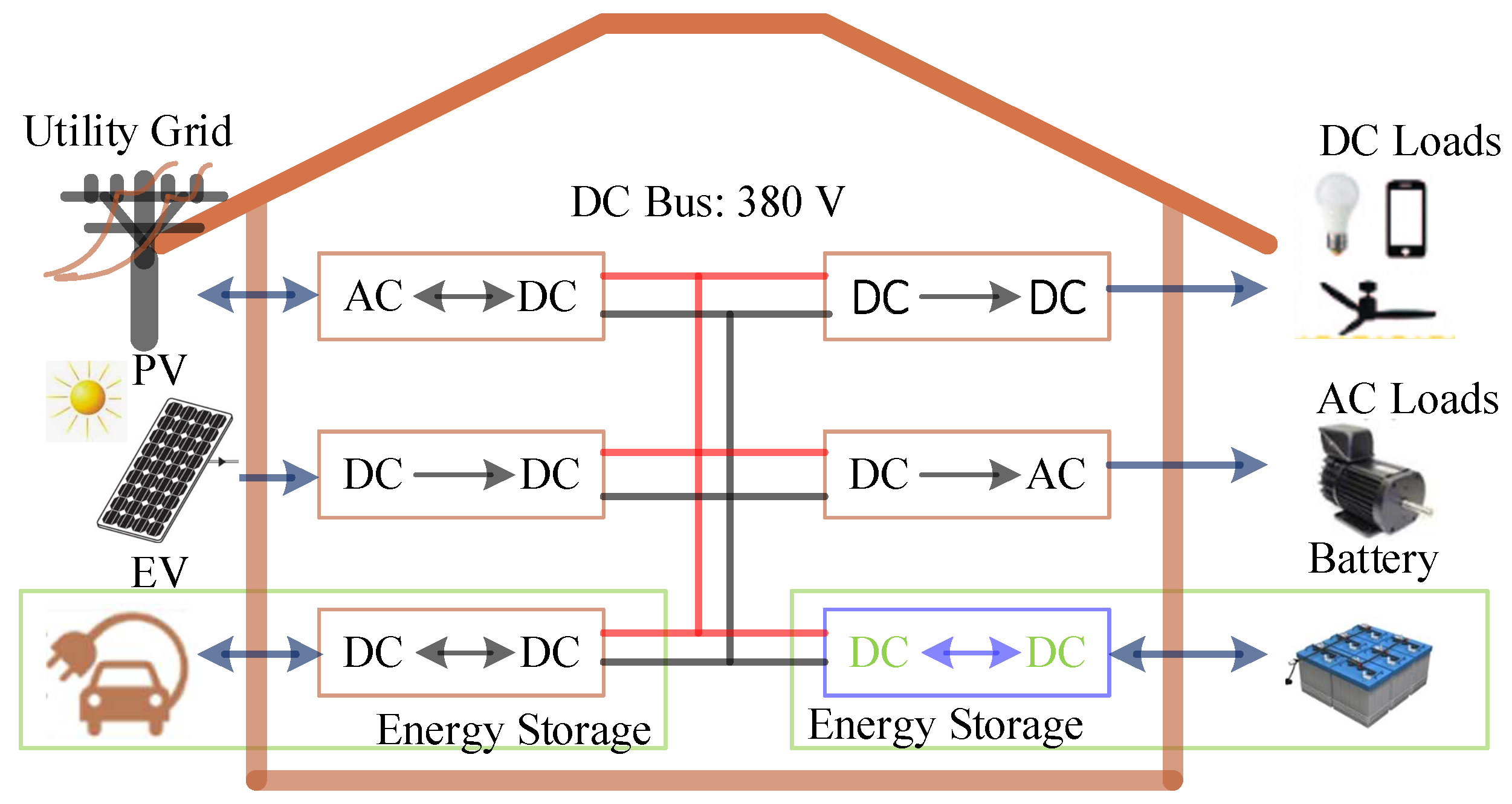
1.1. Overview
1.2. Detailed Analysis
1.3. Motivation
- The low voltage side is defined as the primary side, whereas the high voltage side is defined as the secondary side;
- All switches have ZVS turn-on, and the body diodes of the primary-side switches have ZCS turn-off, thus reducing switching losses and improving overall efficiency;
- Compared with the half-bridge structure, the primary side is driven by the low-side gate drivers, so no floating gate drivers are needed, thus simplifying the design of the drive circuit and reducing costs;
- The switching duty cycle is maintained at about 0.5 to obtain the maximum component utilization;
- The series connection of a resonant capacitor can isolate the DC current to avoid the magnetic escape of the transformer.
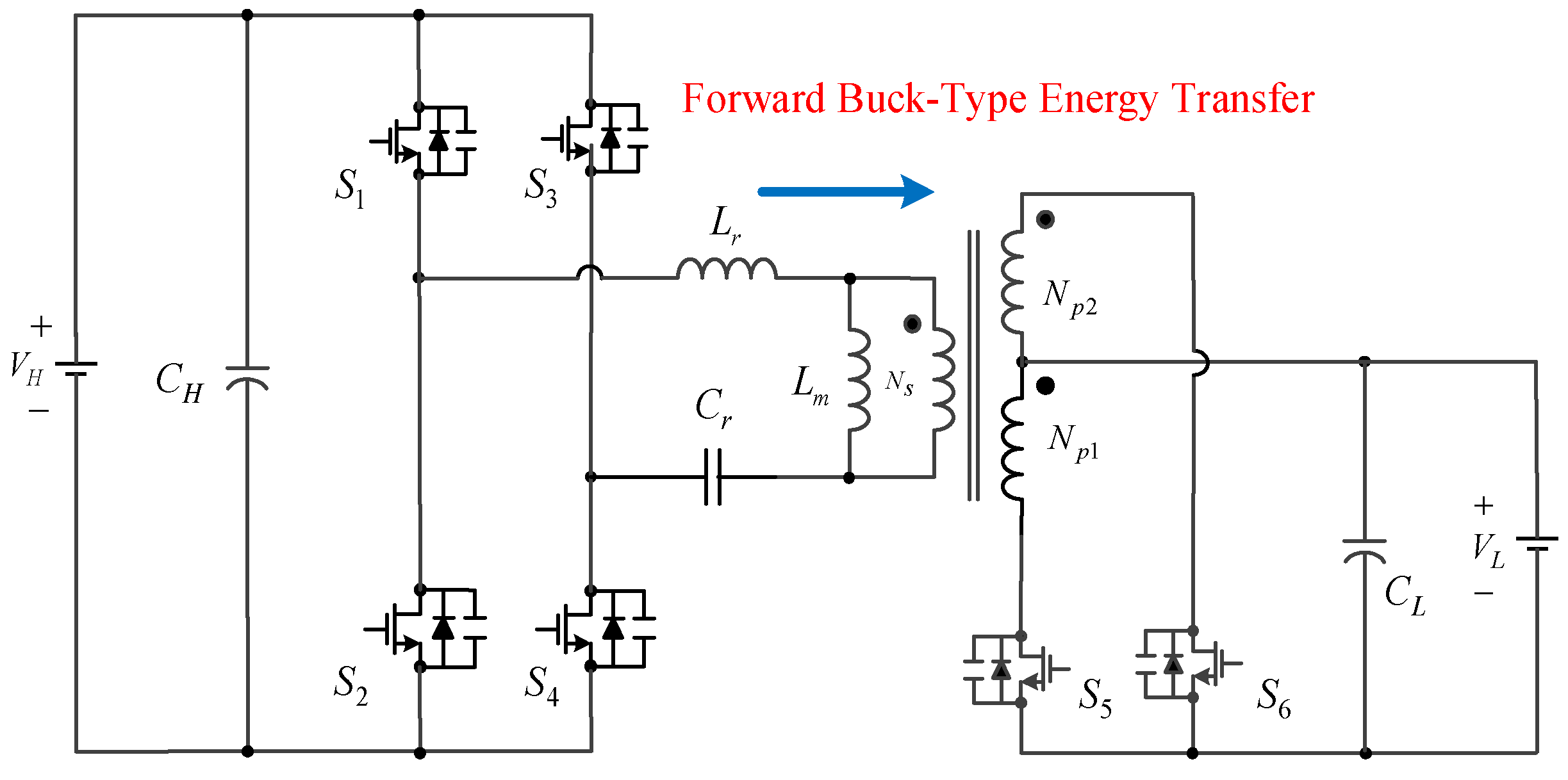
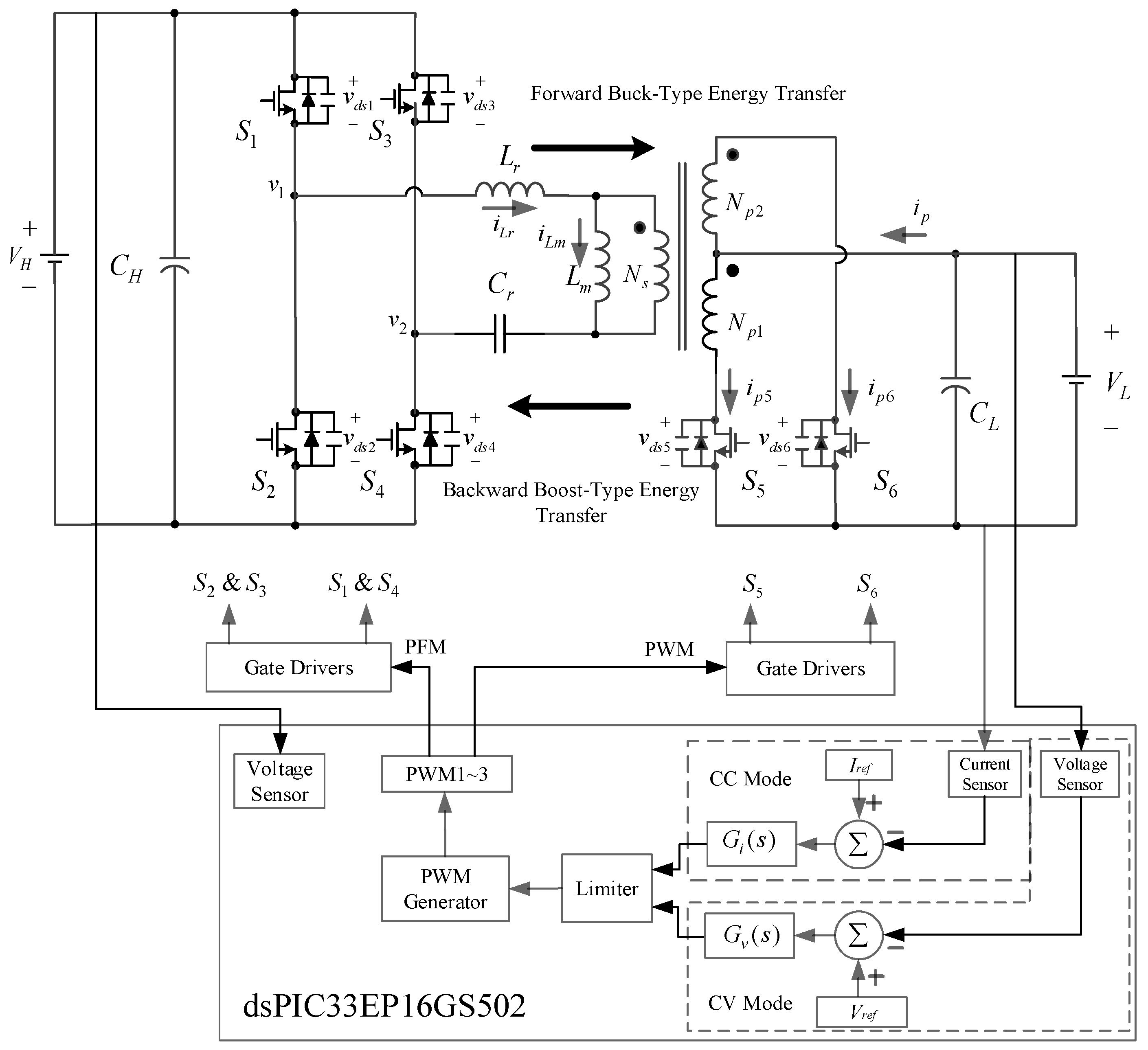
2. Topology Description
2.1. Forward Buck-Type Energy Transfer
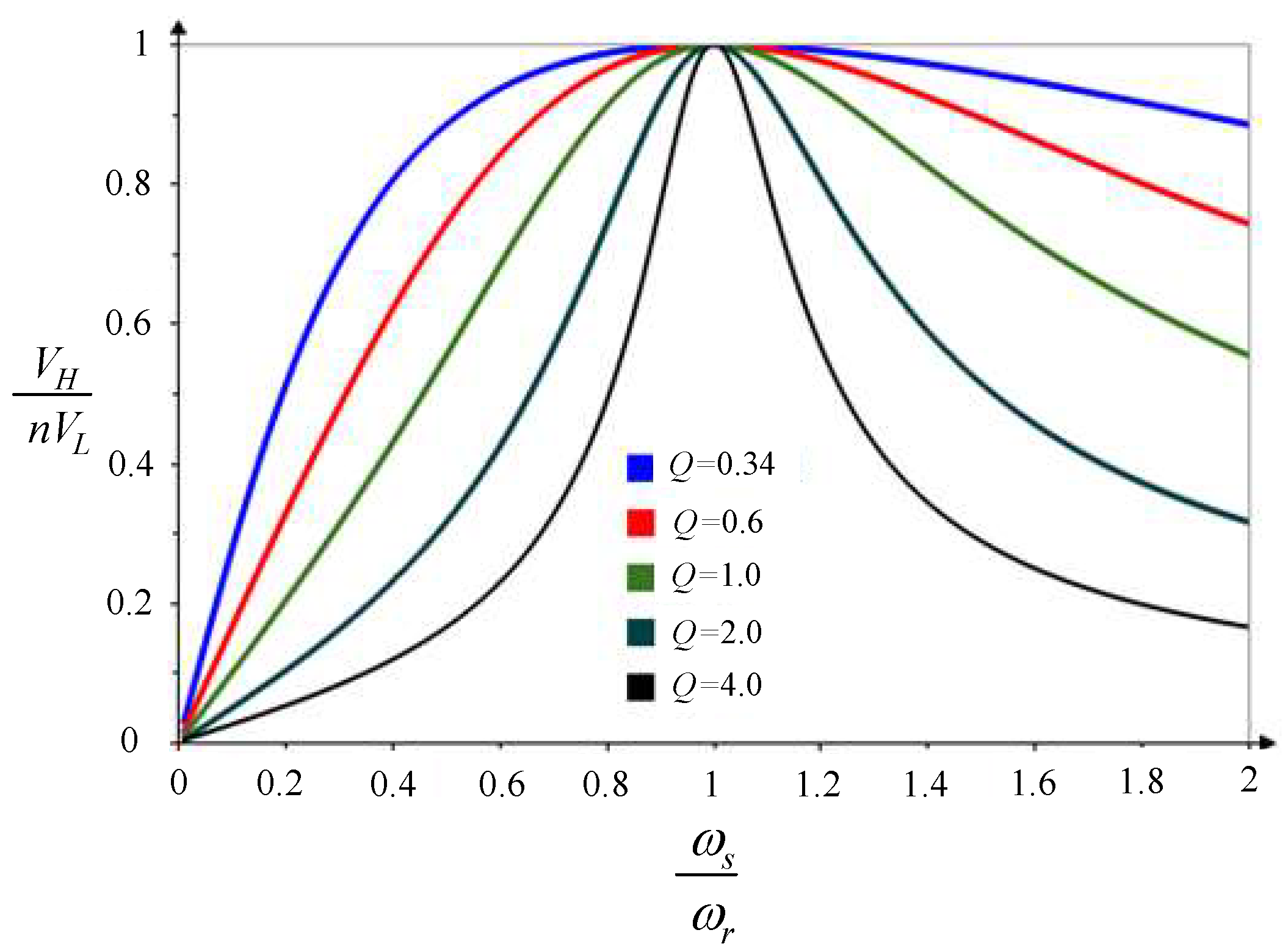
2.1.1. Voltage Gain under the Turns Ratio Equal to One
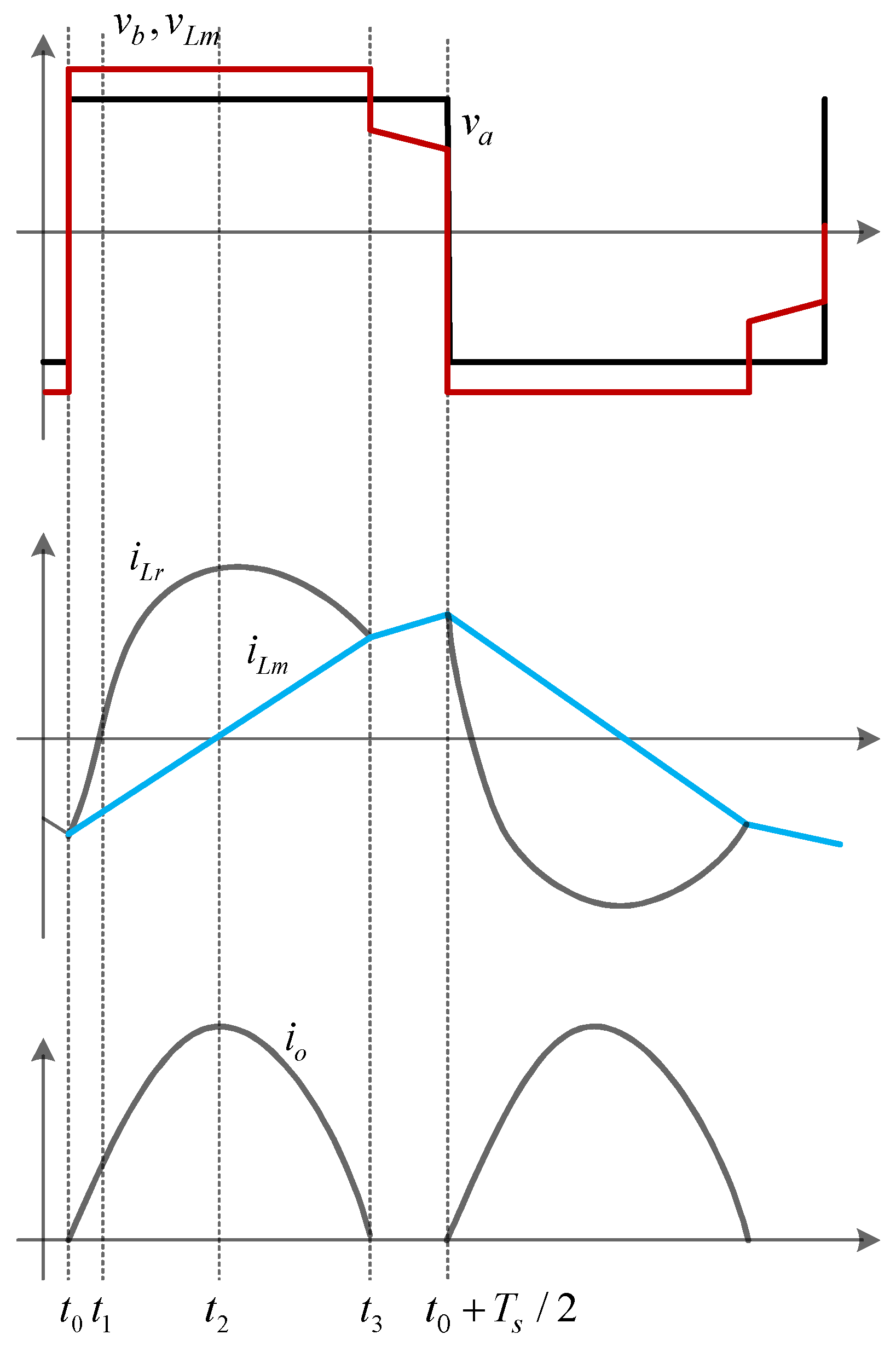
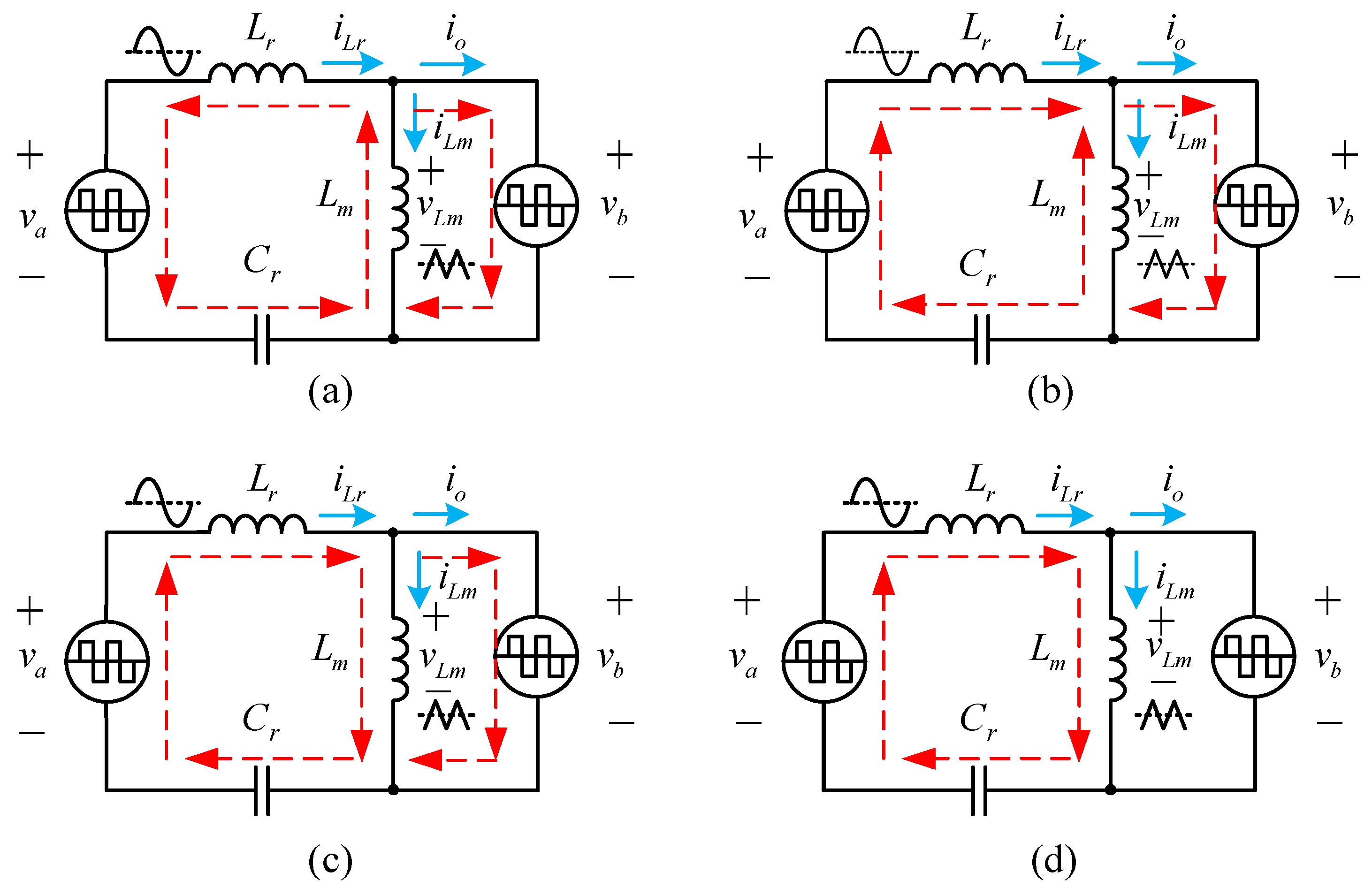
2.1.2. Operating Principles
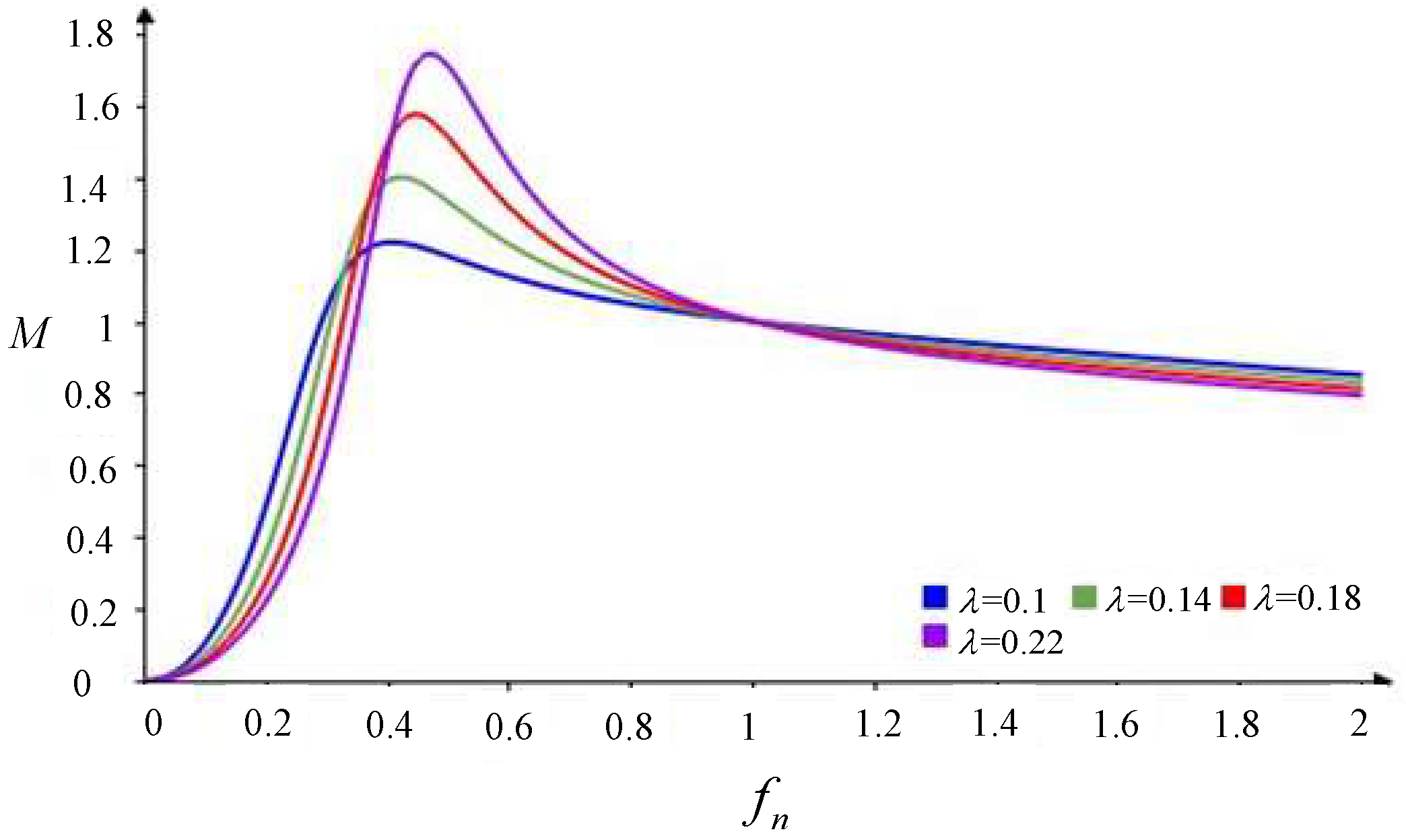
Case 1: Switching Frequency Equal to Resonant Frequency (fs = fr1)
Case 2: Switching Frequency Greater than Resonant Frequency (fs > fr1)
Case 3: Switching Frequency Less than Resonant Frequency (fs < fr1)
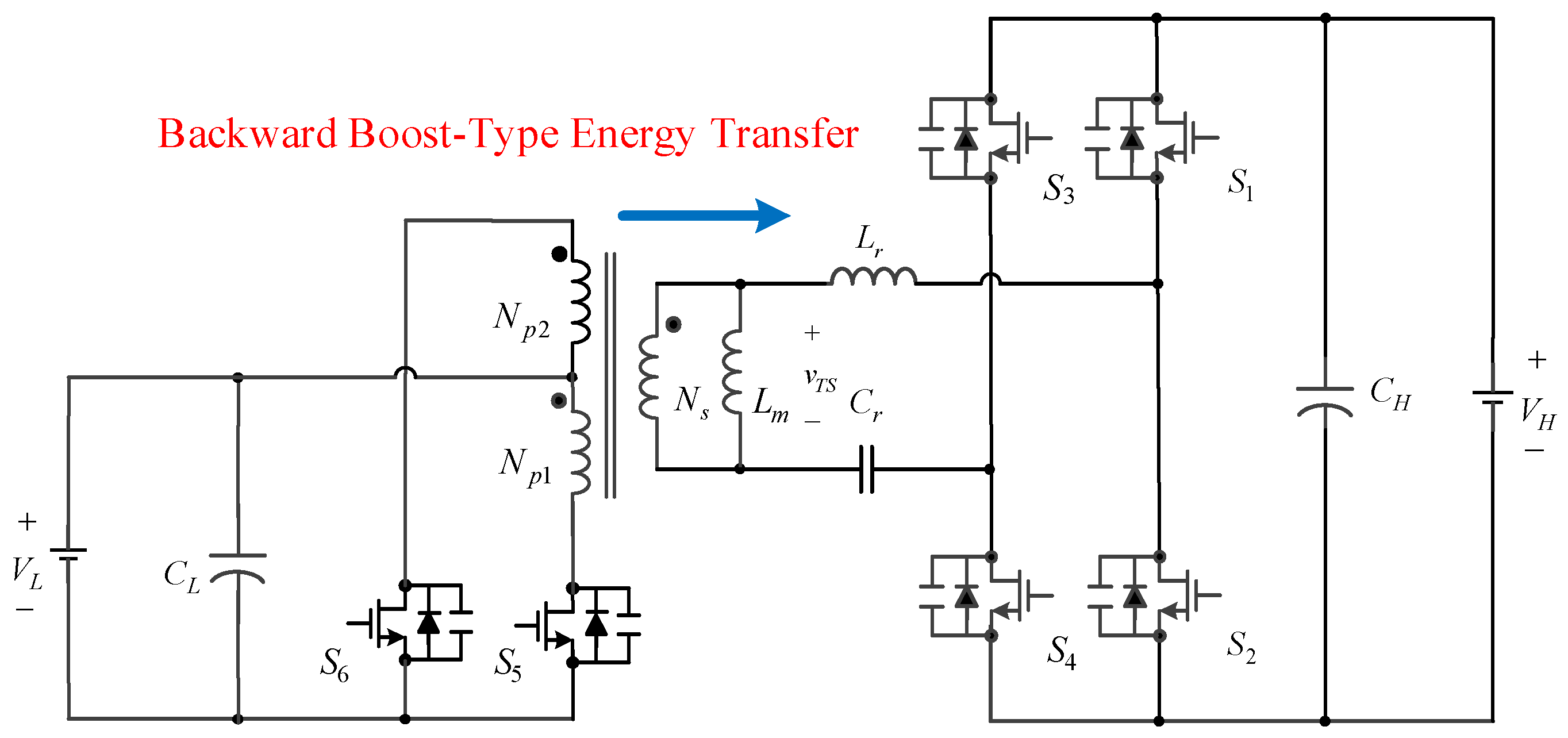
2.2. Backward Boost-Type Energy Transfer
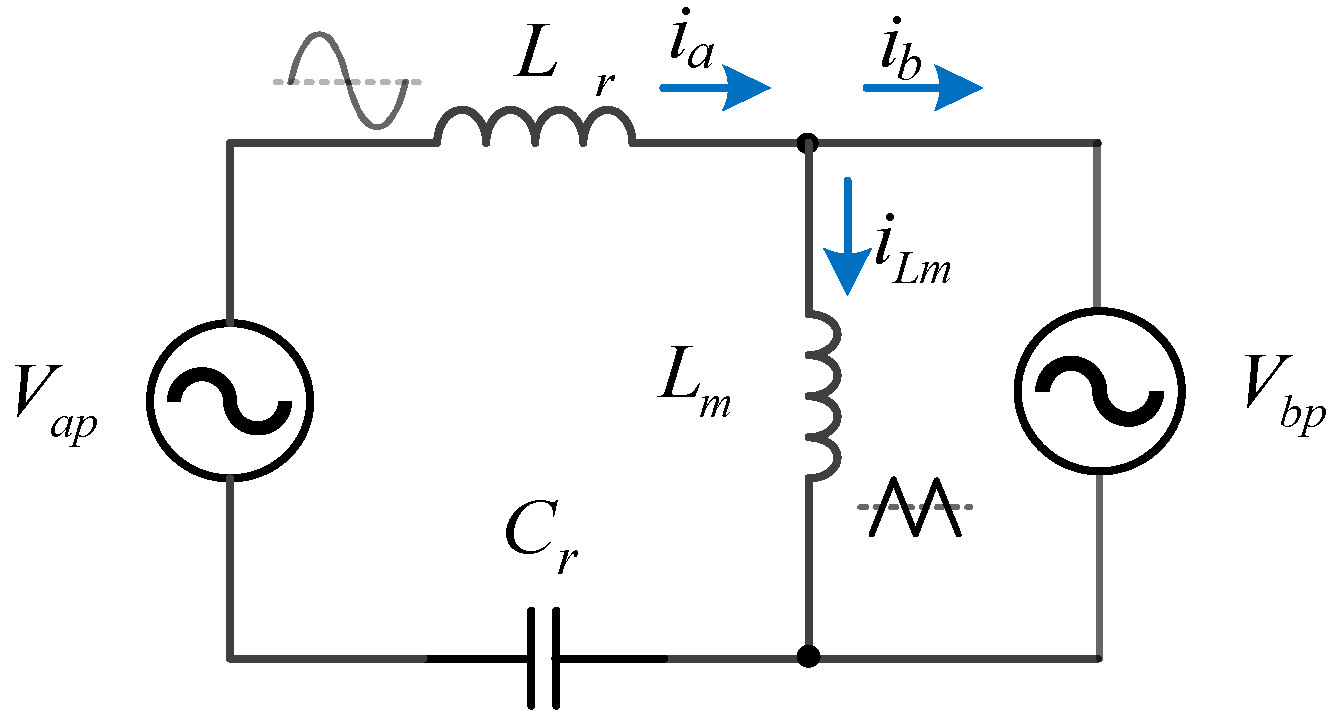
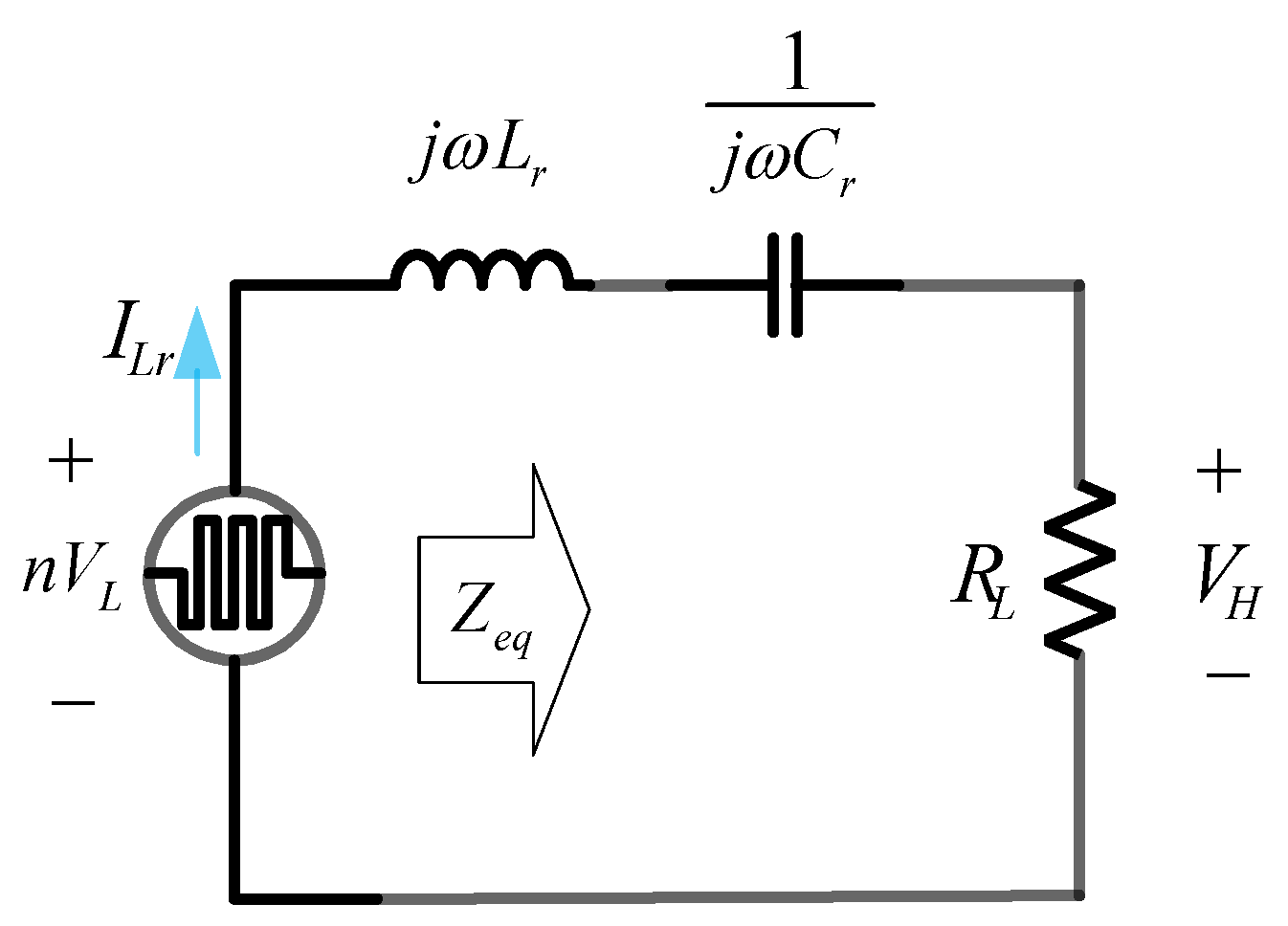
2.2.1. Series Load Resonant Converter Analysis
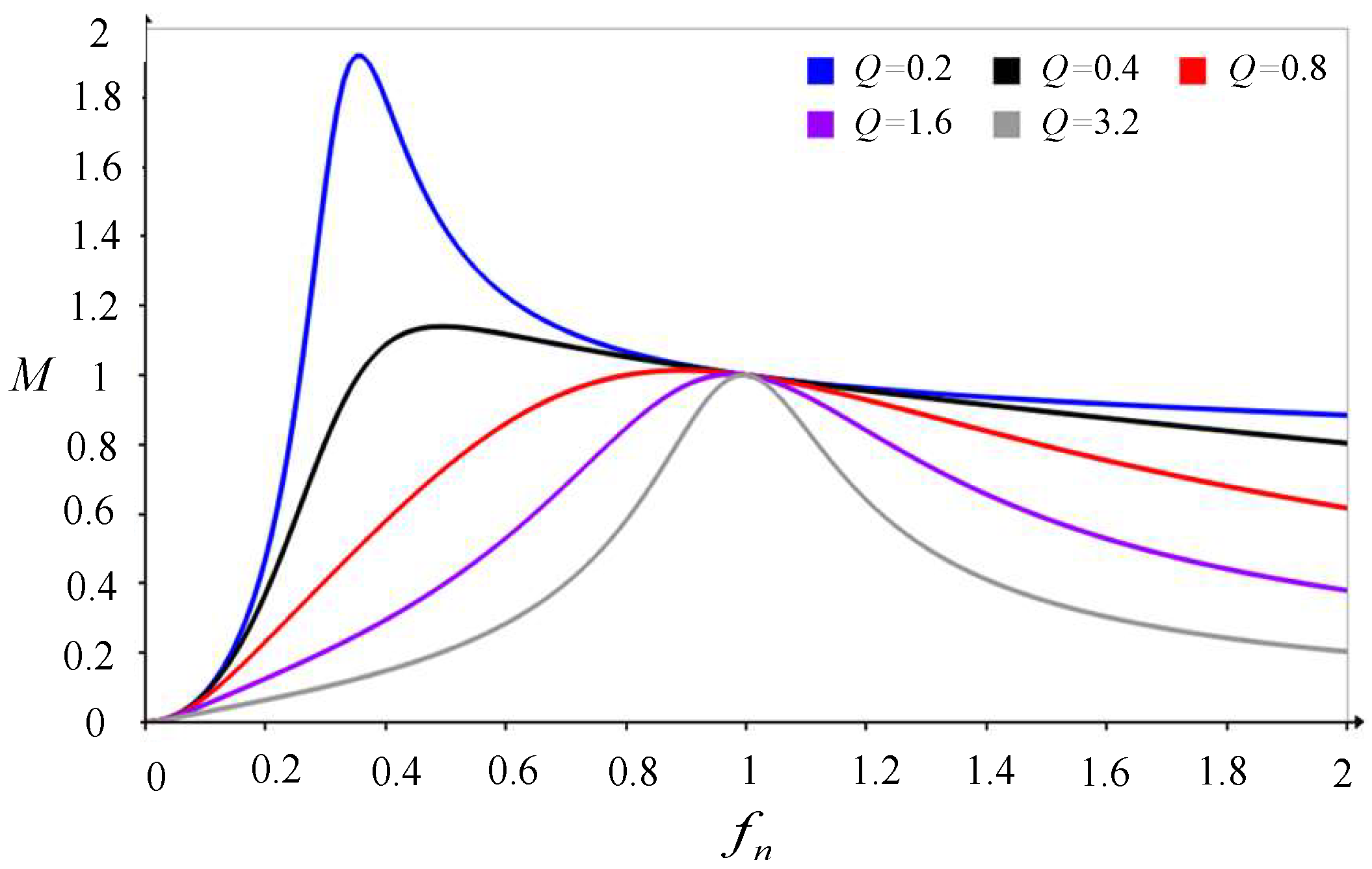
2.2.2. Voltage Gain
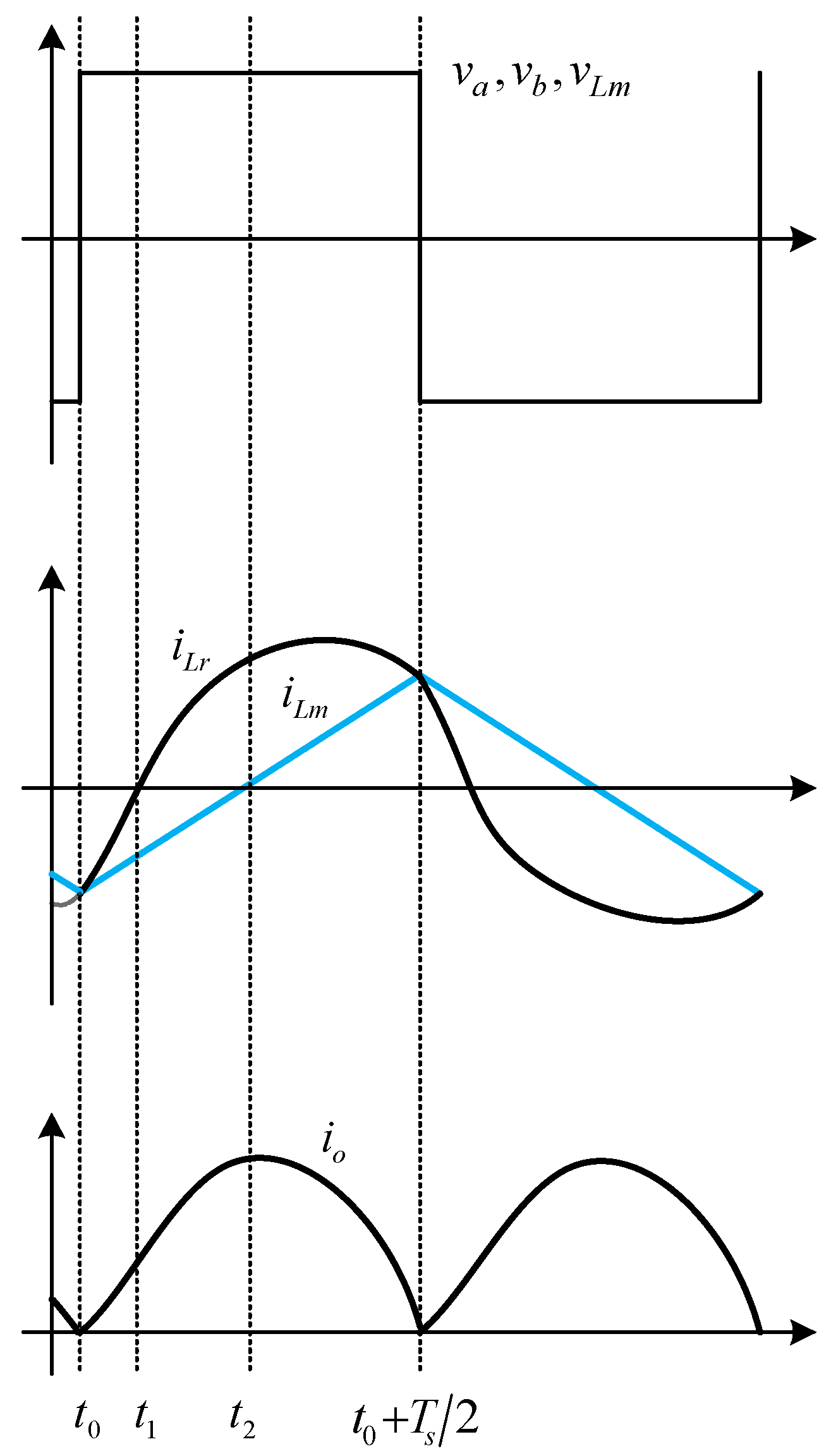
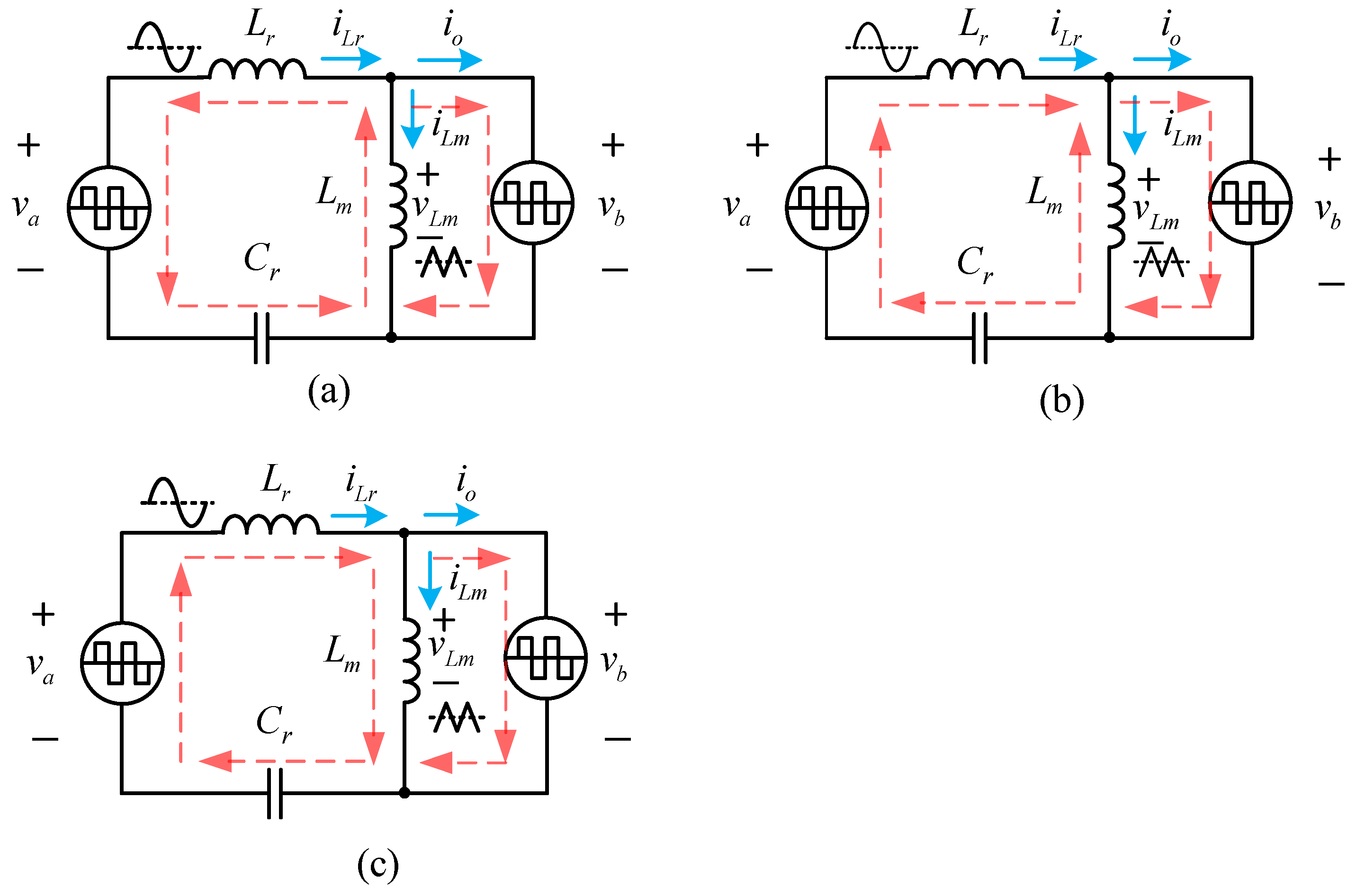
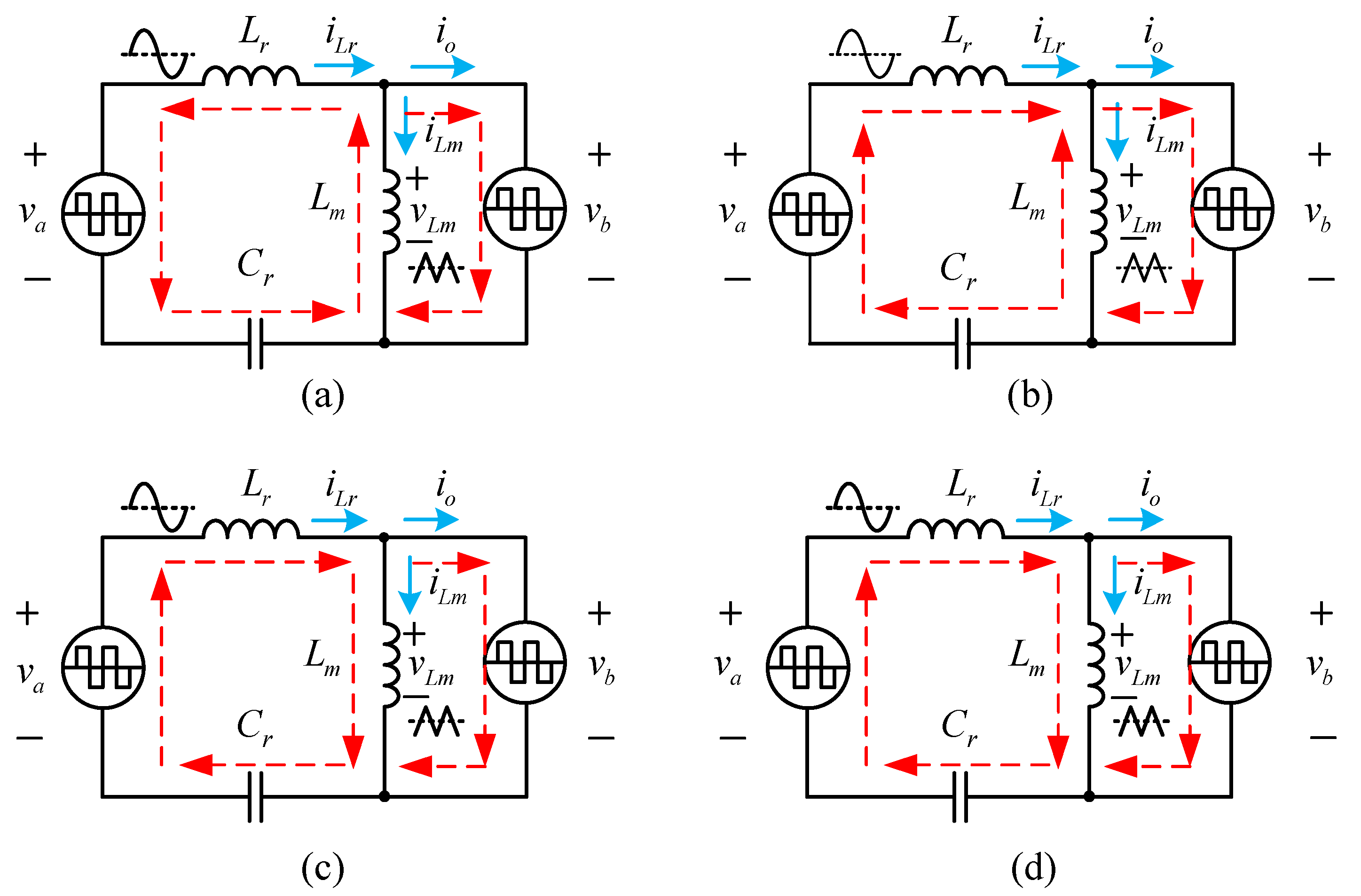
2.2.3. Operating Principles
3. Design Procedure for Bidirectional Converter
3.1. Forward Converter Design
3.1.1. Transformer Turns Ratio Determination
3.1.2. Magnetizing Inductance Lm Design
3.1.3. Determining Resonant Circuit Equivalent Load Resistance Rac
3.1.4. Designing Resonant Inductance Lr and Capacitance Cr
3.1.5. Transformer T Design
3.2. Backward Converter Design
4. Battery Charge/Discharge Control Method
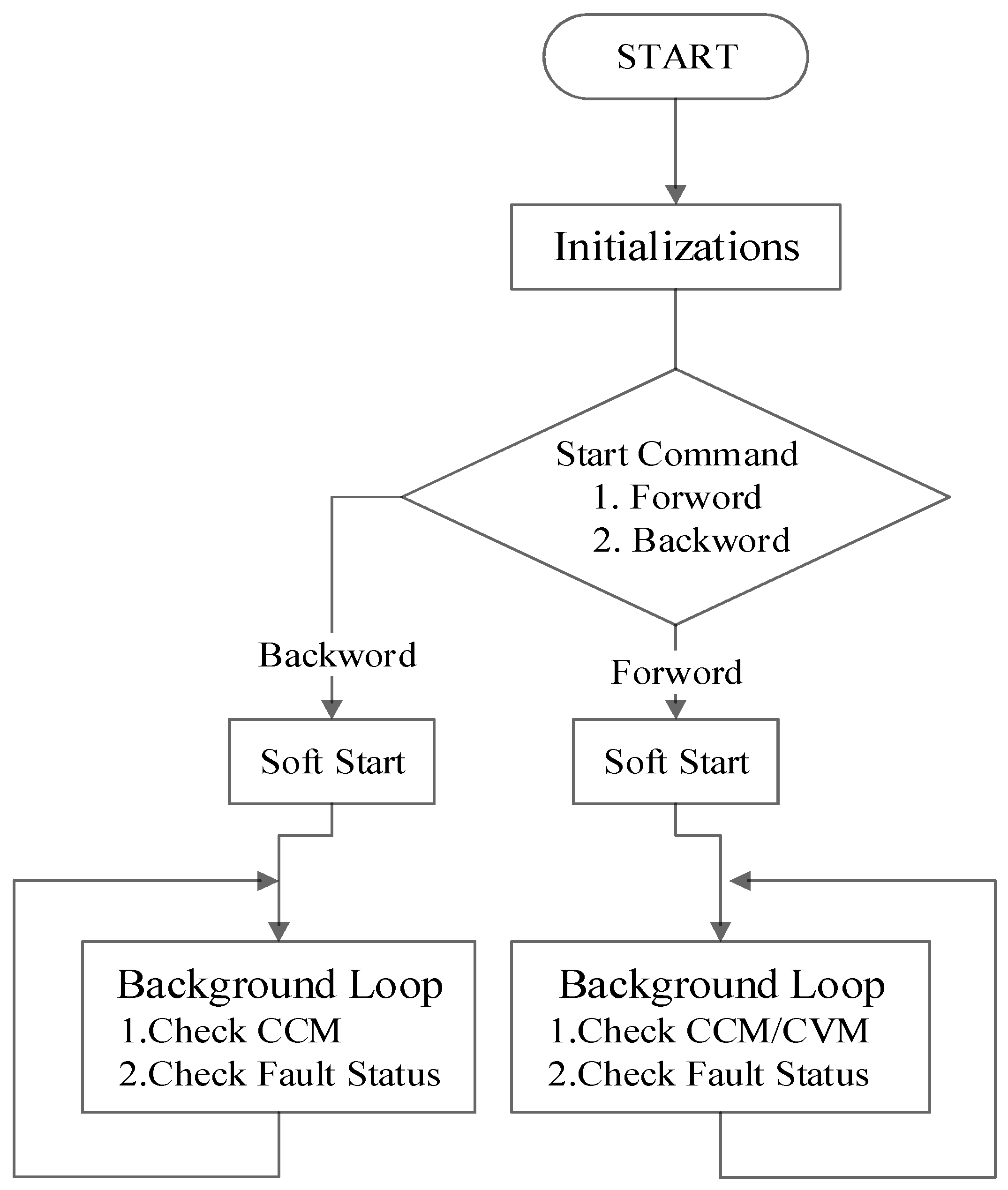
4.1. Software Planning Process
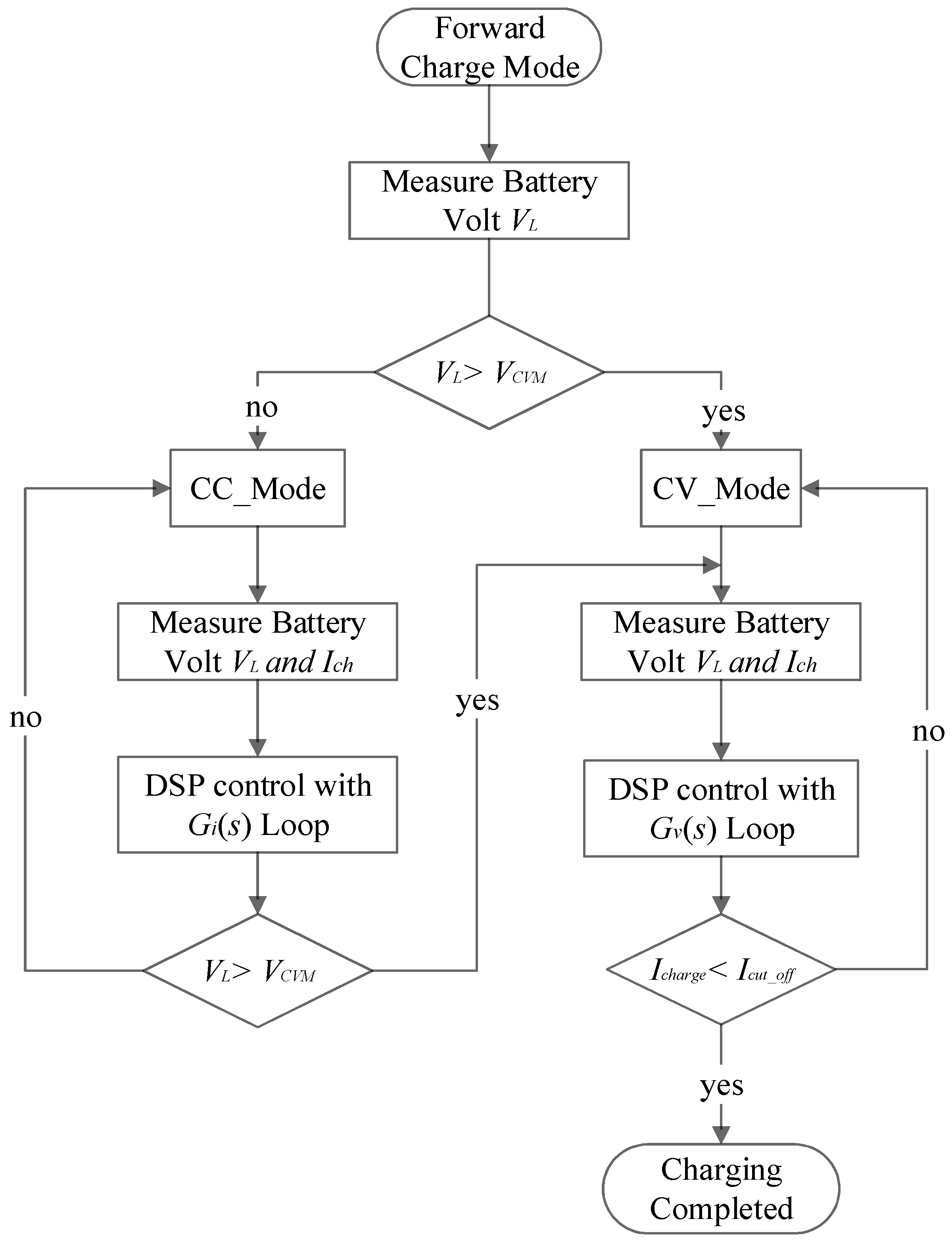
4.2. Forward Charge Mode
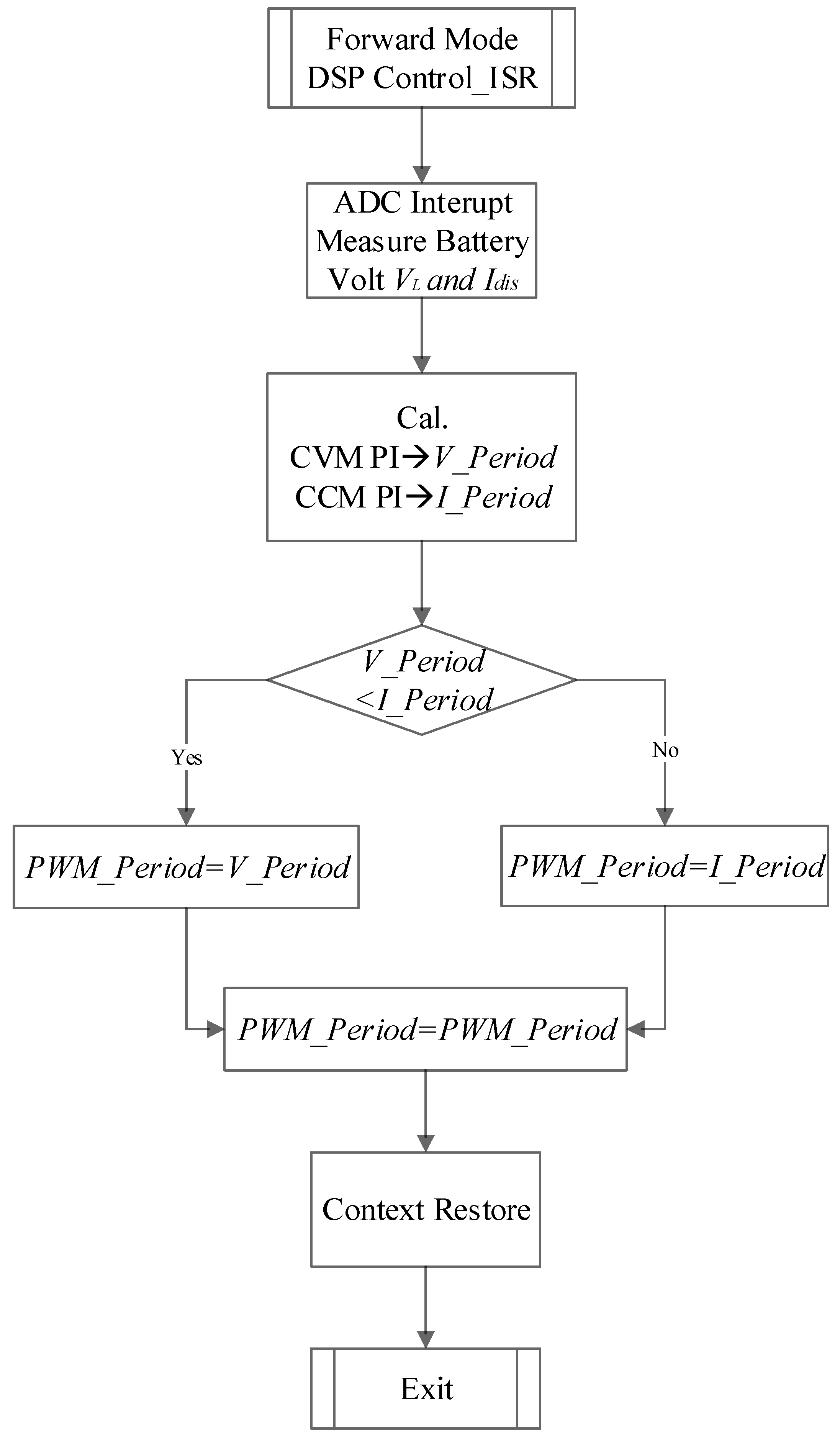
4.3. Forward-Mode DSP Control ISR
4.4. Backward Discharge Mode
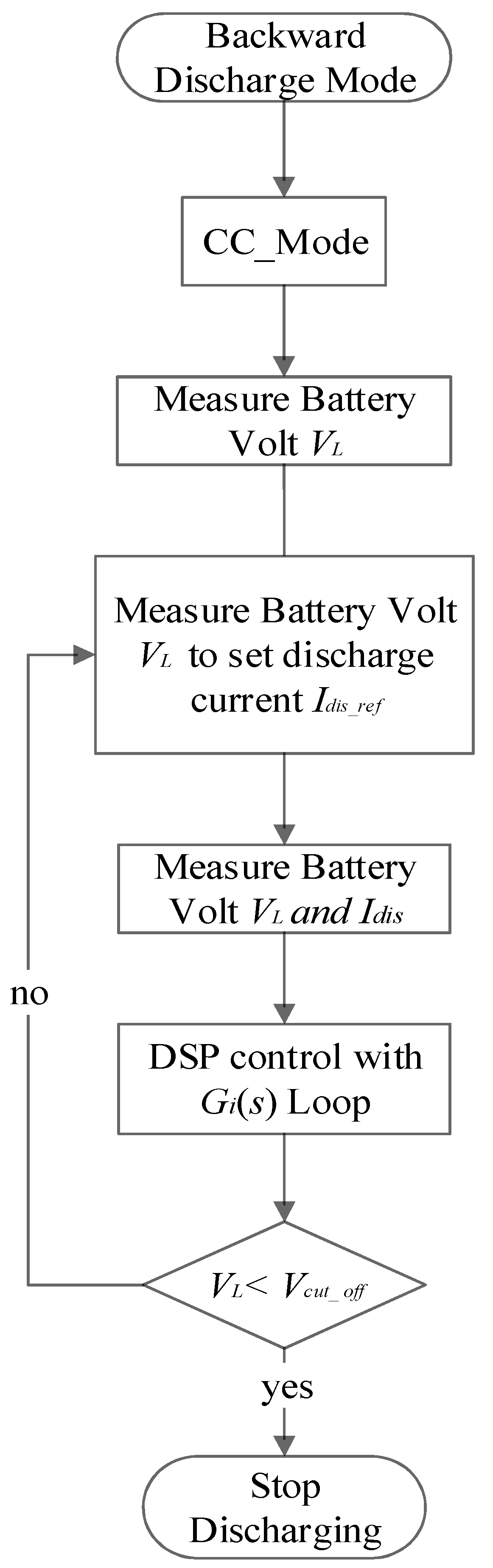
4.5. Backward-Mode DSP Control ISR
5. Experimental Results
5.1. Instrumentation Configuration
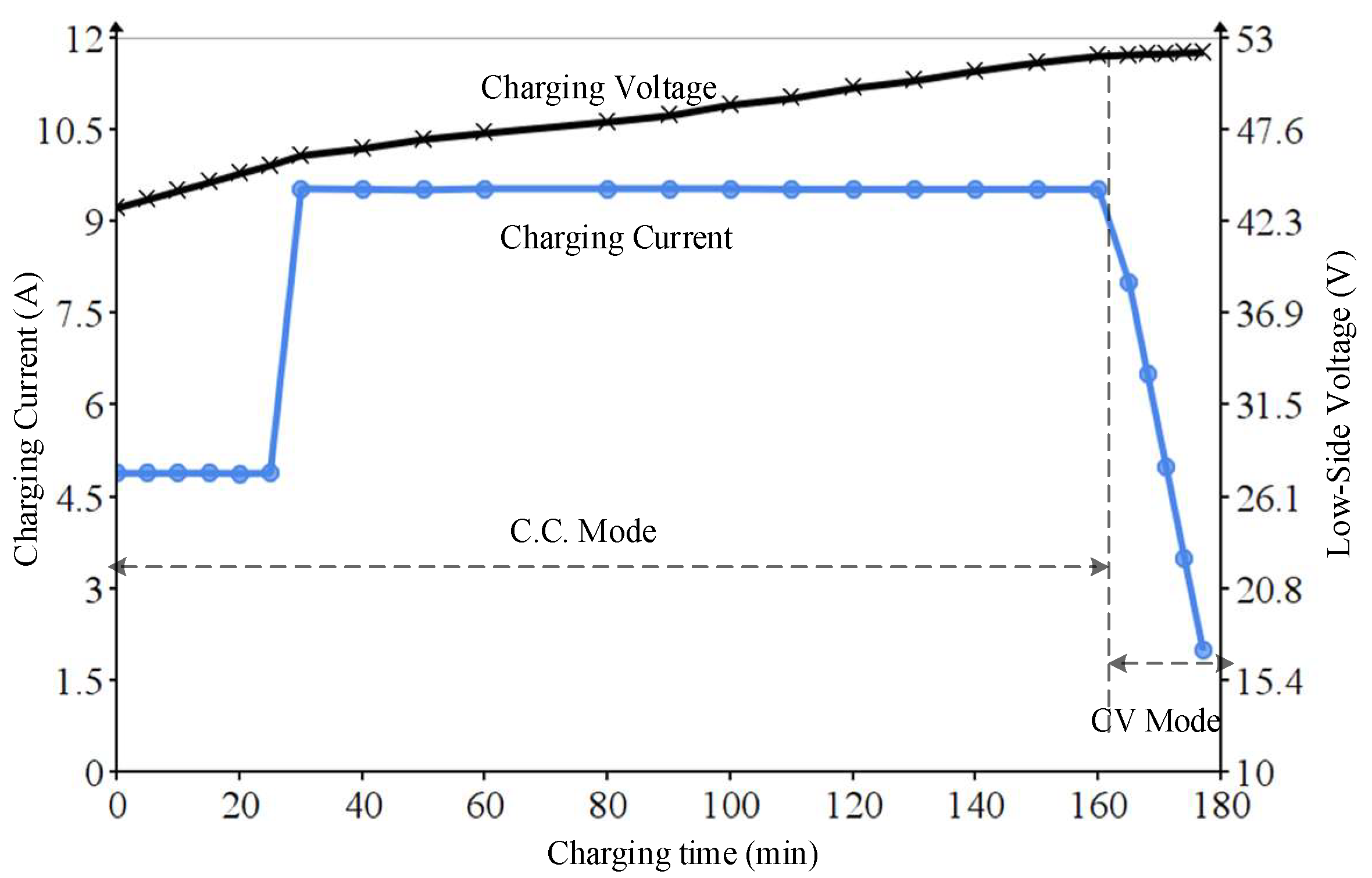
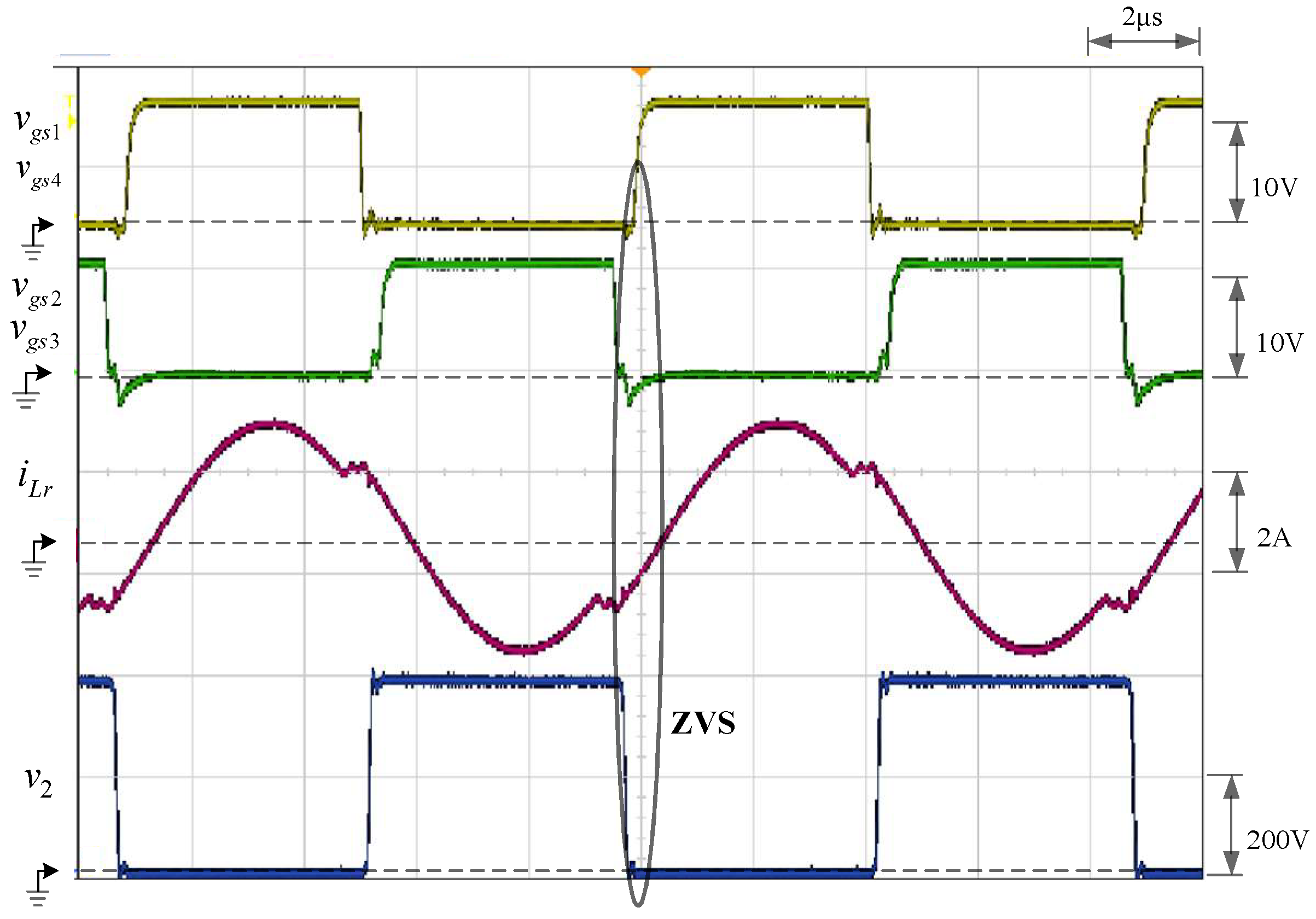
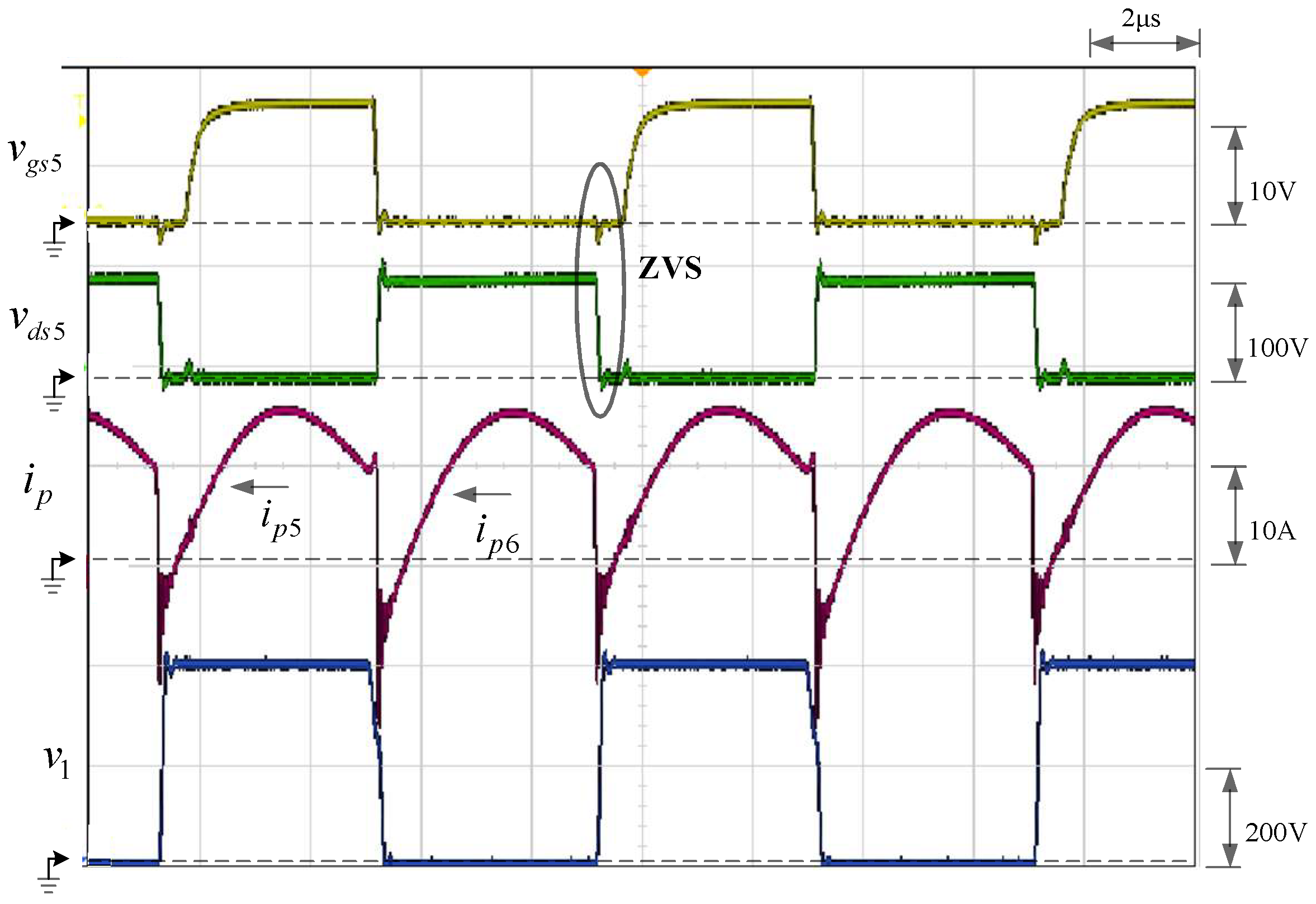
5.2. Forward Charge Mode
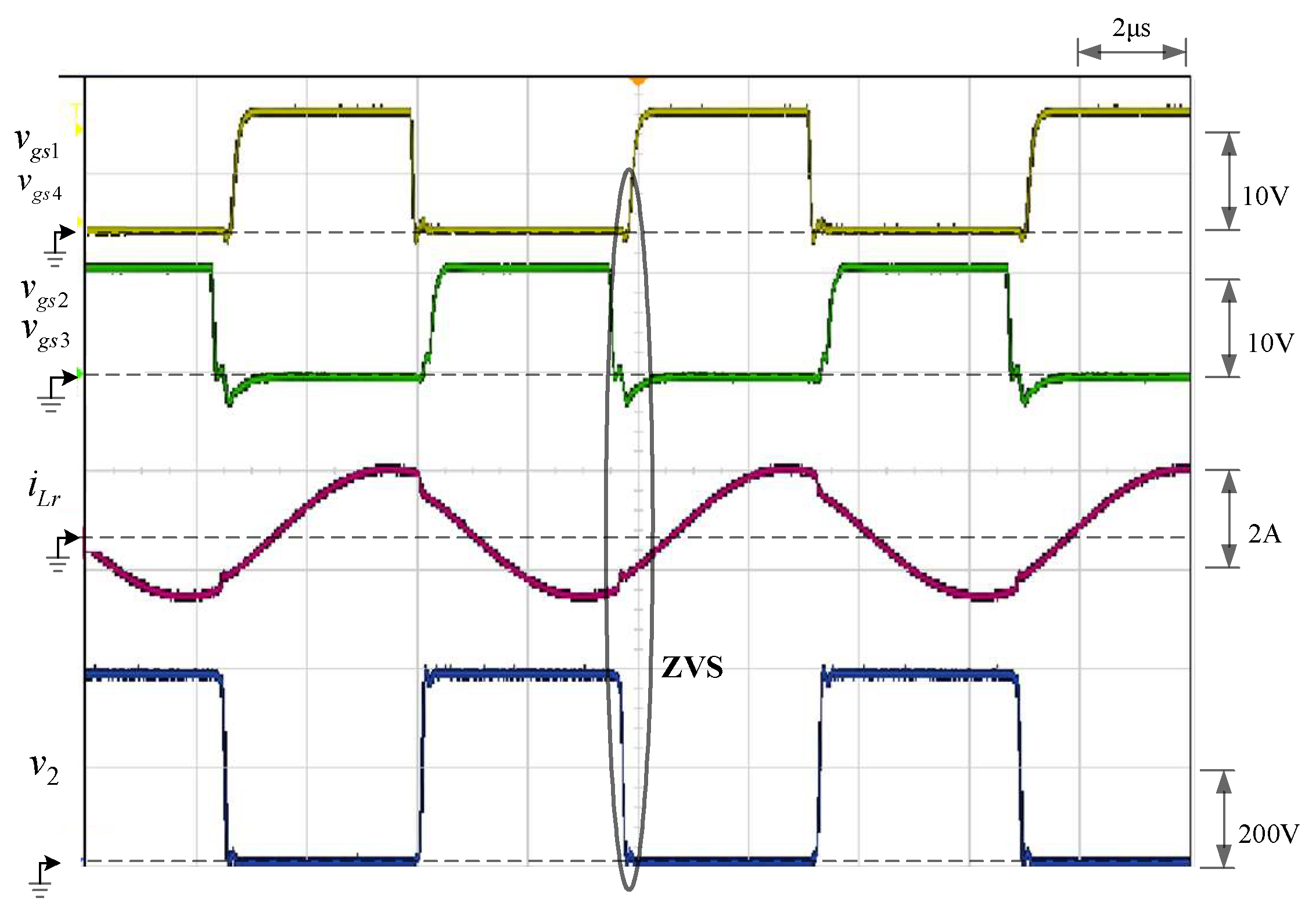
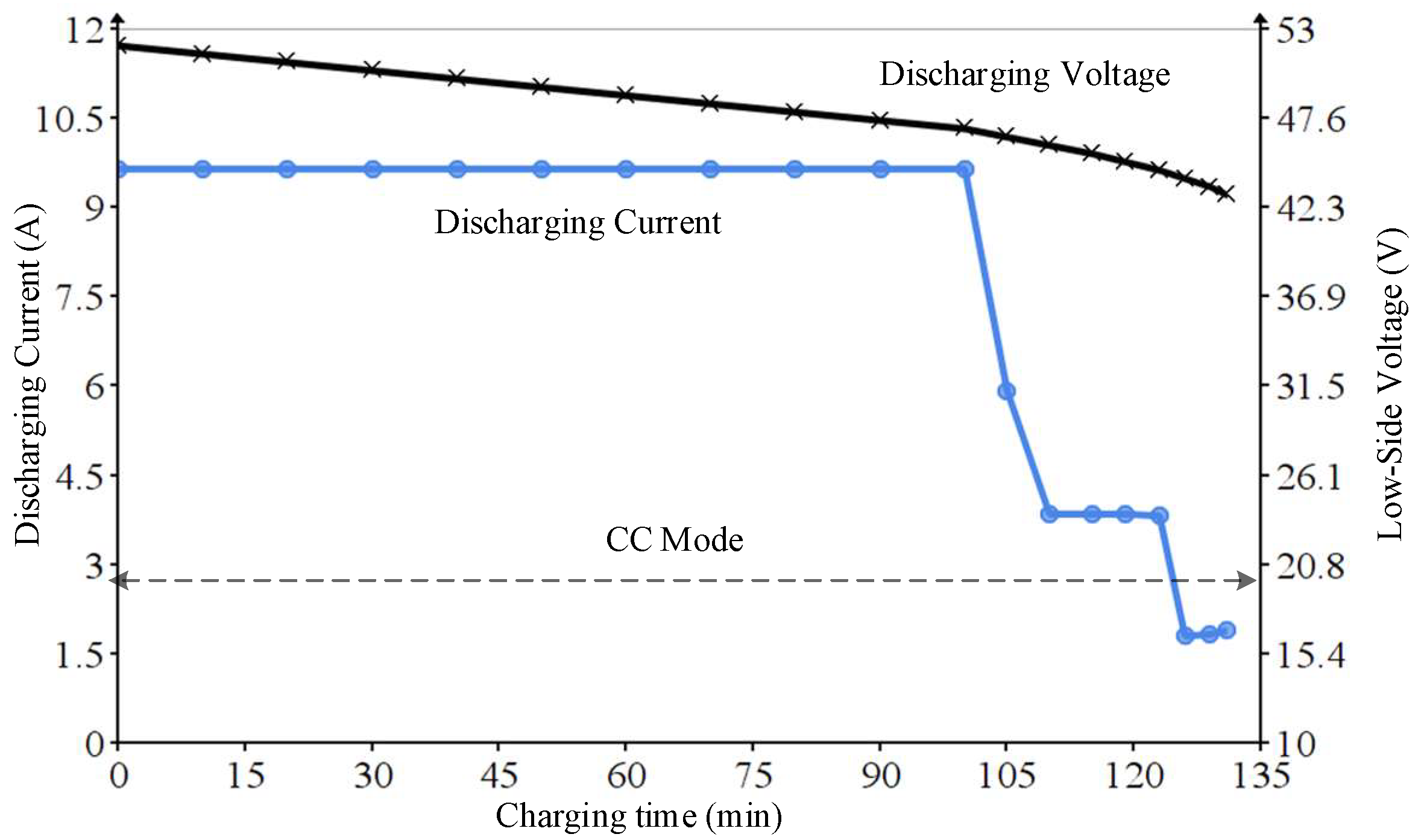
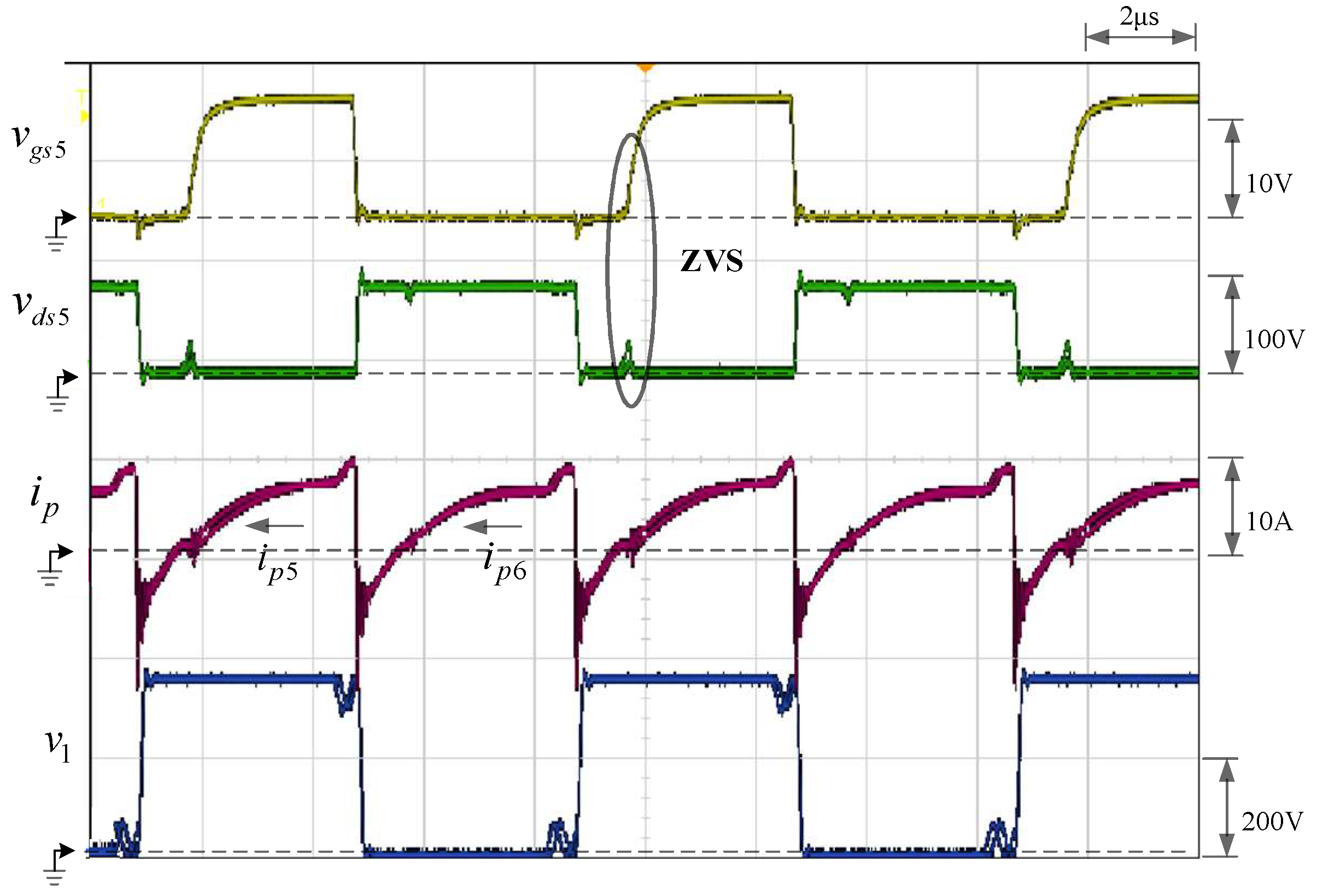
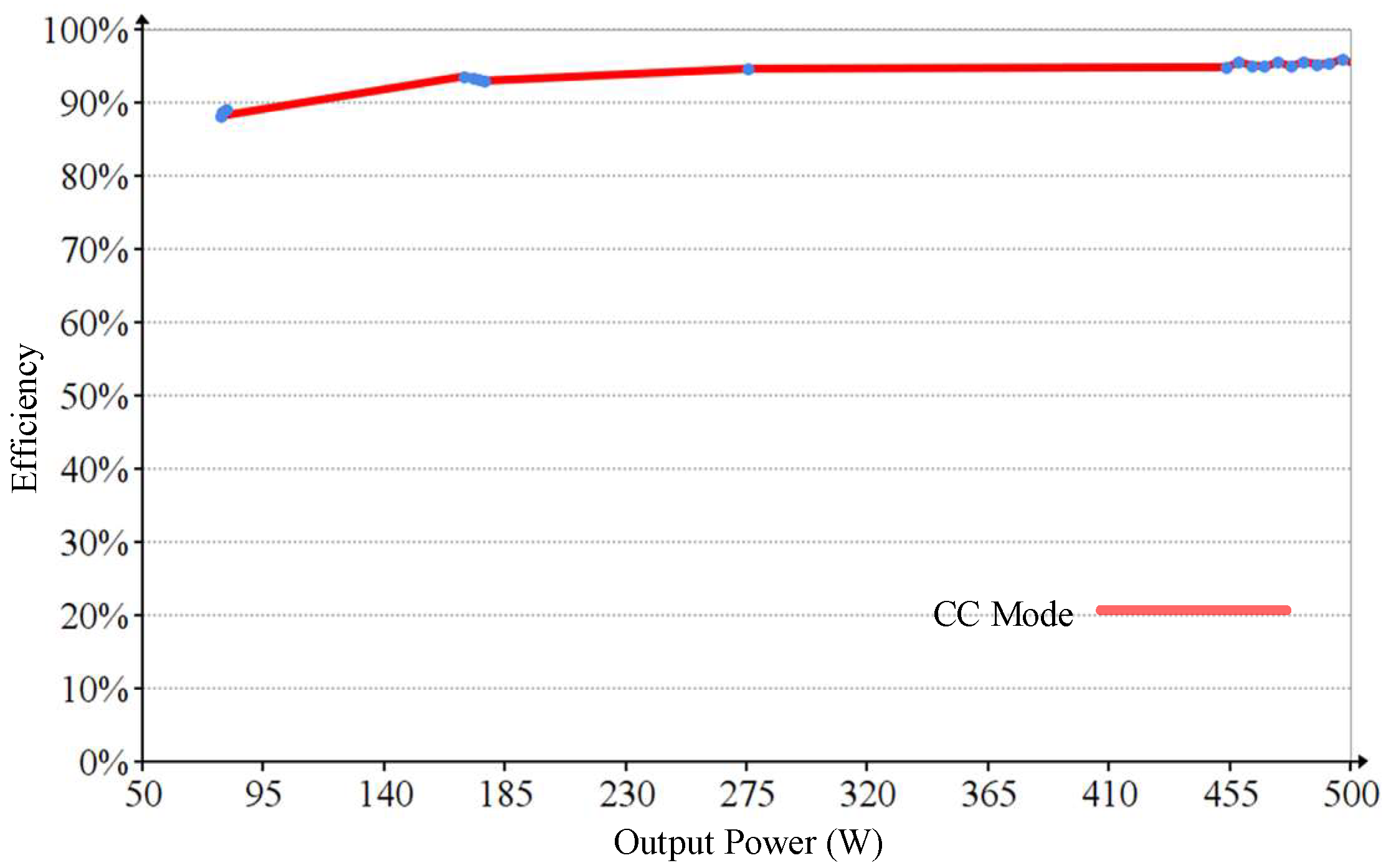
5.3. Backward Discharge Mode
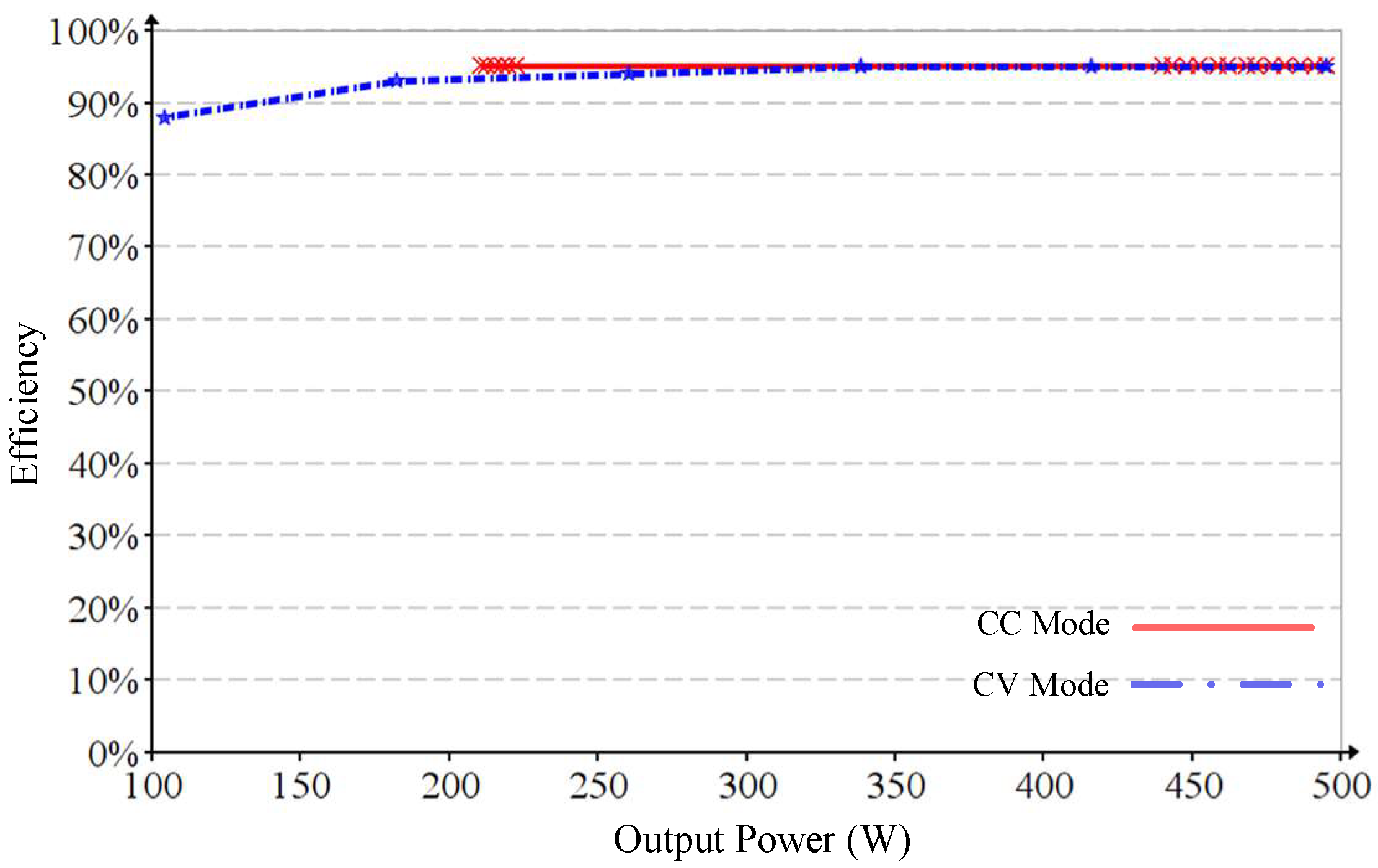
5.4. Experimental Summarization
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mohtasham, J. Review article-renewable energies. Energy Procedia 2015, 74, 1289–1297. [Google Scholar] [CrossRef]
- Lawder, M.T.; Suthar, B.; Northrop, P.W.C.; De, S.; Hoff, C.M.; Leitermann, O.; Crow, M.L.; Santhanagopalan, S.; Subramanian, V.R. Battery Energy Storage System (BESS) and Battery Management System (BMS) for Grid-Scale Applications. Proc. IEEE 2014, 102, 1014–1030. [Google Scholar] [CrossRef]
- Rachid, A.; Fadil, H.E.; Gaouzi, K.; Rachid, K.; Lassioui, A.; Idrissi, Z.E.; Koundi, M. Electric vehicle charging systems: Comprehensive review. Energies 2023, 16, 255. [Google Scholar] [CrossRef]
- Attar, H.A.; Hamida, M.A.; Ghanes, M.; Taleb, M. LLC dc-dc converter performances improvement for bidirectional electric vehicle charger application. World Electr. Veh. J. 2022, 13, 2. [Google Scholar] [CrossRef]
- Al-Ismail, F.S. Dc microgrid planning, operation, and control: A comprehensive review. IEEE Access 2021, 9, 36154–36172. [Google Scholar] [CrossRef]
- Lowder, T.; Xu, K. The Evolving U.S. Distribution System: Technologies, Architectures, and Regulations for Realizing a Transactive Energy Marketplace; Technical Report; National Renewable Energy Laboratory: Golden, CO, USA, 2020. [Google Scholar]
- Gorji, S.A.; Sahebi, H.G.; Ektesabi, M.; Rad, A.B. Topologies and control schemes of bidirectional dc-dc power converters: An overview. IEEE Access 2019, 7, 117997–118019. [Google Scholar] [CrossRef]
- Alatai, S.; Salem, M.; Ishak, D.; Das, H.S.; Nazari, M.A.; Bughneda, A.; Kamarol, M. A review on state-of-the-art power converters: Bidirectional, resonant, multilevel converters and their derivatives. Appl. Sci. 2021, 11, 10172. [Google Scholar] [CrossRef]
- Tytelmaier, K.; Husev, O.; Veligorskyi, O.; Yershov, R. A review of non-Isolated bidirectional dc-dc converters for energy storage systems. In Proceedings of the 2016 II International Young Scientists Forum on Applied Physics and Engineering (YSF), Kharkiv, Ukraine, 10–14 October 2016. [Google Scholar]
- Xu, W.; Chan, H.L.; Or, S.W.; Ho, S.L.; Chan, K.W. A new control method for a bidirectional phase-shift-controlled dc-dc converter with an extended load range. Energies 2017, 10, 1532. [Google Scholar] [CrossRef]
- Pellitteri, F.; Miceli, R.; Schettino, G.; Viola, F.; Schirone, L. Design and realization of a bidirectional full bridge converter with improved modulation strategies. Electronics 2020, 9, 724. [Google Scholar] [CrossRef]
- Nene, H.; Zaitsu, T. Bidirectional PSFB dc-dc converter with unique PWM control schemes and seamless mode transitions using enhanced digital control. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 3229–3233. [Google Scholar]
- Babokany, A.S.; Jabbari, M.; Shahgholian, G.; Mahdavian, M. A review of bidirectional dual active bridge converter. In Proceedings of the 9th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology, Phetchaburi, Thailand, 16–18 May 2012; pp. 1–4. [Google Scholar]
- Kumar, B.M.; Kumar, A.; Bhat, A.H.; Agarwal, P. Comparative study of dual active bridge isolated dc to dc converter with single phase shift and dual phase shift control techniques. In Proceedings of the Recent Developments in Control, Automation & Power Engineering (RDCAPE), Noida, India, 26–27 October 2017; pp. 453–458. [Google Scholar]
- Huang, J.; Wang, Y.; Li, Z.; Lei, W. Unified triple-phase-shift control to minimize current stress and achieve full soft-switching of isolated bidirectional dc-dc converter. IEEE Trans. Ind. Electron. 2016, 64, 4169–4179. [Google Scholar] [CrossRef]
- Jung, J.H.; Kim, H.S.; Ryu, M.H.; Baek, J.W. Design methodology of bidirectional CLLC resonant converter for high-frequency isolation of dc distribution systems. IEEE Trans. Power Electron. 2013, 28, 1741–1755. [Google Scholar] [CrossRef]
- Yan, Y.H.; Cheng, H.L.; Chan, S.Y.; Chen, Y.D.; Chang, Y.N. Design of an isolated bidirectional symmetric resonant converter. Appl. Sci. 2020, 10, 8144. [Google Scholar]
- Zahid, Z.U.; Dalala, Z.M.; Chen, R.; Chen, B.; Lai, J.S. Design of bidirectional dc-dc resonant converter for vehicle-to-grid (V2G) applications. IEEE Trans. Transp. Electrif. 2015, 1, 232–244. [Google Scholar] [CrossRef]
- Reddy, R.M.; Das, M. Reconfigurable bidirectional dc-dc converter for electric vehicle onboard charging applications. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; pp. 1–6. [Google Scholar]
- Lin, B.R. Bidirectional resonant converter for dc microgrid applications. Processes 2021, 9, 1664. [Google Scholar] [CrossRef]
- Zong, S.; Fan, G.; Yang, X. Double voltage rectification modulation for bidirectional dc/dc resonant converters for wide voltage range operation. IEEE Trans. Power Electron. 2019, 34, 6510–6521. [Google Scholar] [CrossRef]
- Li, H.; Wang, S.; Zhang, Z.; Zhang, J.; Zhu, W.; Ren, X.; Hu, C. A bidirectional synchronous/asynchronous rectifier control for wide battery voltage range in SiC bidirectional LLC chargers. IEEE Trans. Power Electron. 2022, 37, 6090–6101. [Google Scholar] [CrossRef]
- Xu, J.; Yang, J.; Xu, G.; Jiang, T.; Su, M.; Sun, Y.; Wang, H.; Zheng, M. PWM modulation a control strategy for LLC-DCX converter to achieve bidirectional power flow in facing with resonant parameters variation. IEEE Access 2021, 7, 54693–54704. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, J.; Wu, X.; Sheng, K.; Wang, Y. A bidirectional LLC resonant converter with automatic forward and backward mode transition. IEEE Trans. Power Electron. 2015, 30, 757–770. [Google Scholar] [CrossRef]
- Xie, D.; Wang, L.; Zhang, Z.; Wang, S.; Kang, L.; Yao, J. Photovoltaic energy storage system based on bidirectional LLC resonant converter control technology. Energies 2022, 15, 6436. [Google Scholar] [CrossRef]
- Jaiswal, V.K.; Ghoshal, A. A design methodology of bidirectional LLC resonant converter for energy storage systems. In Proceedings of the 2019 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Jeju, Republic of Korea, 8–10 May 2019; pp. 1–6. [Google Scholar]
- Rahman, A.N.; Chiu, H.J.; Hsieh, Y.C. Design of wide input voltage range high step-up dc-dc converter based on secondary-side resonant tank full bridge LLC. In Proceedings of the 3rd International Conference on Intelligent Green Building and Smart Grid (IGBSG), Yilan, Taiwan, 22–25 April 2018; pp. 1–6. [Google Scholar]
- Chen, W.; Lu, Z.; Zhang, X.; Ye, S. A novel ZVS step-up push-pull type isolated LLC series resonant dc-dc converter for UPS systems and its topology variations. In Proceedings of the Twenty-Third Annual IEEE Applied Power Electronics Conference and Exposition, Austin, TX, USA, 24–28 February 2008; pp. 1073–1078. [Google Scholar]
- Ma, X.; Wang, P.; Bi, H.; Wang, Z. A bidirectional LLCL resonant dc-dc converter with reduced resonant tank currents and reduced voltage stress of the resonant capacitor. IEEE Access 2020, 8, 125549–125564. [Google Scholar] [CrossRef]
- Yan, Y.H.; Chang, Y.N.; Peng, Z.X. Design of a bidirectional CL3C full-bridge resonant converter for battery energy storage systems. Energies 2022, 15, 412. [Google Scholar] [CrossRef]









| Ref. No. | [12] | [15] | [17] | [20] | [25] | |
|---|---|---|---|---|---|---|
| Parameter | ||||||
| Input voltage | 12 V | 70–110 V | 280–403 V | 400 V | 30–50 V | |
| Output voltage | 400 V | 60 V | 400 V | 200–450 V | 350 V | |
| Output power | 300 W | 300 W | 1 kW | 1 kW | 3 kW | |
| Max. efficiency | <90% | <96% | 94.6% | 93.5% | 95.6% | |
| Topology | PSFB | DAB | CLLC | CLLC | L-LLC | |
| Control technique | Phase control | Phase control | PFM | PFM | PFM | |
| No. of main switches | 6 | 8 | 8 | 10 | 8 | |
| No. of inductors/ transformers/ capacitors | 2/1/0 | 1/1/0 | 2/1/2 | 2/1/2 | 2/1/1 | |
| Parameter | Symbol | Specification |
|---|---|---|
| Low-side voltage | VL | 43~52 V |
| High-side voltage | VH | 360~410 V |
| Output power | Po | 100~500 W |
| Resonant frequency | fr | 125 kHz |
| PFM switching frequency | Fllc_s | 96~160 kHz |
| PWM switching frequency | Fpp_s | 125 kHz |
| Duty cycle | D | 0.36~0.46 |
| Transformer turns ratio | Np1:Np2:Ns | 4:4:36 |
| Magnetizing inductance | Lms | 586 µH |
| Leakage inductance | Llk (Lr) | 114 µH |
| Resonant capacitance | Cr | 14.1 nF |
| Transformer core | T1 | PC40 (LP2930) |
| Primary-side switches | S1, S2, S3, S4 | IPP60R120P7 |
| Secondary-side switches | S5, S6 | IPP200N15N3G |
| DSP microcontroller | DSP | dsPIC33EP16GS502 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tai, Y.-K.; Hwu, K.-I. A Control Design Technology of Isolated Bidirectional LLC Resonant Converter for Energy Storage System in DC Microgrid Applications. Energies 2023, 16, 6877. https://doi.org/10.3390/en16196877
Tai Y-K, Hwu K-I. A Control Design Technology of Isolated Bidirectional LLC Resonant Converter for Energy Storage System in DC Microgrid Applications. Energies. 2023; 16(19):6877. https://doi.org/10.3390/en16196877
Chicago/Turabian StyleTai, You-Kun, and Kuo-Ing Hwu. 2023. "A Control Design Technology of Isolated Bidirectional LLC Resonant Converter for Energy Storage System in DC Microgrid Applications" Energies 16, no. 19: 6877. https://doi.org/10.3390/en16196877
APA StyleTai, Y.-K., & Hwu, K.-I. (2023). A Control Design Technology of Isolated Bidirectional LLC Resonant Converter for Energy Storage System in DC Microgrid Applications. Energies, 16(19), 6877. https://doi.org/10.3390/en16196877








