Application of Clustering Techniques for Improved Energy Benchmarking on Deep-Level Mines

Abstract

The South African mining industry relies on coal-based energy to run operations, with the sector utilising 29.6 terawatt-hours of energy in 2018. However, energy availability constraints and swelling electricity prices in the country have instilled a greater emphasis on energy management practices to reduce waste and maintain profitability. Energy benchmarking is a popular and effective energy management method applied in industry, but the current methods in the mining sector use the average energy usage of various mining shafts over different intervals to develop benchmarks. This may lead to skewed benchmarks when anomalous energy usage is present within the interval or when vastly different energy users are aggregated. However, clustering-based benchmarking techniques have been applied successfully in other industries to compare similar energy users accurately. This study developed and applied a clustering-based benchmarking method to evaluate the performance of different mining shafts at a deep-level gold mine in South Africa. The K-means unsupervised learning clustering algorithm was used to group similar energy users and benchmark different mining shafts using ordinary least squares regression equations. Compared to traditional methods, the benefit of clustered energy usage benchmarks is shown by more accurately evaluating energy performance and facilitating focused energy management responses.

1. Introduction

1.1. Background

The mining industry is a crucial contributor to the South African economy, accounting for 8.6% (ZAR 481 billion; USD 1 = ZAR 19.04 (15 September 2023)) of the gross domestic product (GDP) in 2021 [1]. A reliable energy supply is essential for mining operations, with the sector using 29.6 terawatt-hours (TWh) in the form of electricity in 2018 [2]. However, the energy availability factor (EAF) has decreased from above 70% in 2019 to below 50% at the start of 2023 [3].

Contrary to the availability, the cost of electricity for mines has increased from 15.07 c/kWh in 2003 to 130.62 c/kWh in 2021/22 [4], a trend that deviates considerably from the consumer price index (CPI) [5], as depicted in Figure 1.

Due to the declining EAF and the importance of maintaining a stable electrical grid to avoid a national blackout [6,7], load curtailment measures have been implemented to reduce demand to match the decreasing supply. Load curtailment requires large energy users such as mines to reduce their energy usage for a specified period of time.

The procedure and associated rules of load curtailment are set out in the NRS 048-9: 2019 document from the National Energy Regulators of South Africa (NERSA) [8]. The stages of load curtailment and the corresponding load reduction percentages are shown in

Table 1. Load curtailment stages.

Stage	Reduction (%)
2	10
3	15
4	20

.

The escalating electricity costs and expanding constraints on mines’ production caused by load curtailment have placed immense pressure on mining companies to manage their energy consumption and sustain profitable operations for all stakeholders. Consequently, continuous energy management and monitoring strategies are of great concern in the mining sector to minimise energy wastage and improve overall operational efficiency.

A review of energy management techniques in large industries by Schulze et al. [9] examined concepts considered in energy management studies and found that there are five main energy management themes covered in the literature; namely, strategy and planning, implementation and operational, control, organisational, and cultural.

The control theme includes different categories, such as energy accounting, performance measurement, and benchmarking. Control as an energy management theme is common in the mining industry, with studies on energy auditing [10,11], performance evaluation [12], and benchmarking [13,14,15].

Benchmarking is the process of comparing a performance metric of a system or process to a standard to identify opportunities for improvement and to measure progress over time [16,17]. Benchmarking is valuable when comparing performance between related systems via external benchmarking [18] or against a system’s previous or intended performance with internal benchmarking [19].

The scale of energy usage in the mining industry and its vital role in the South African economy highlight the value of applying this type of energy management method. The use of energy benchmarking may help to accurately measure energy performance and identify energy-saving opportunities leading to more efficient operations. Therefore, energy benchmarking was chosen for this study, focusing on improving the current methods in the mining industry by applying methods found in the literature.

1.2. Literature Review of Energy Benchmarking Methods

A study by Cilliers [14] developed a method to benchmark electricity usage in the mining industry by analysing five high-electricity-usage systems’ correlations with different mining variables. The mining variables were used to develop equations for average- and best-practice monthly expected electricity usage benchmarks for each system for various mining shafts.

Another study on mines developed energy-intensity benchmarks representing the energy input to system output ratio across different mining shafts. Several different benchmarks were calculated, taking the average at various intervals, including months, weekdays, Saturdays, Sundays, and different mining shifts [15].

An important but often overlooked problem with mine energy benchmarking is that mines host an ever-changing (dynamic) environment, often with daily fluctuations in energy usage. Mining shafts are also very different, with diverse mining methods and high-energy-usage machinery. When benchmarks are based on averaging energy usage of different mining shafts over various intervals, such as weekdays, they may depend on aggregating vastly different energy usages.

Therefore, these benchmarks, which may consist of non-representative energy usage, fail to accurately depict the mining operations, resulting in a skewed performance evaluation.

However, benchmarking studies on buildings in various sectors have studied the importance of concurrently categorising different energy usage types for more accurate and representative benchmarks. These studies used clustering techniques to find the underlying energy usage patterns to classify energy users into groups for more informative energy benchmarks [20,21,22,23,24,25,26,27,28,29].

For example, in [29], the authors propose a method to cluster different buildings based on multiple building features to develop representative benchmarks. The study used ordinary least squares (OLS) step-wise regression to select the most relevant features that play a role in a building’s energy use intensity (EUI).

The K-means clustering algorithm was used to group the buildings based on the most relevant features to discover four clusters where the centroid EUIs of each cluster represented the benchmarks.

The energy efficiency ratio (EER), which is the ratio of the building EUI to the centroid EUI, was used to develop a benchmark score. The EER was compared to the Energy Star method, which compares buildings by primary space use, and it was found that the Energy Star method may over- and under-predict the EUI benchmark when there are large differences in the magnitude of building features, resulting in skewed performance evaluation.

The clustering-based approach is robust to different magnitudes as it groups buildings with similar characteristics, more accurately representing the benchmark. This makes this approach attractive for the mining industry as the mining shafts may have varying energy usage and associated energy drivers.

The benefit of exploring this method in the mining sector is emphasised by comparing the energy usage of a building to that of a deep-level gold mine. The energy usage in one study conducted on a building was reported to be 754 megawatt-hours (MWh) per annum [22], which pales in comparison to the 364 gigawatt-hours (GWh) recorded at a single South African mining shaft for 2021. The improvement of energy efficiency and identification of energy savings in the mining sector will make a more significant contribution to improving the country’s overall energy outlook.

1.3. Problem Statement

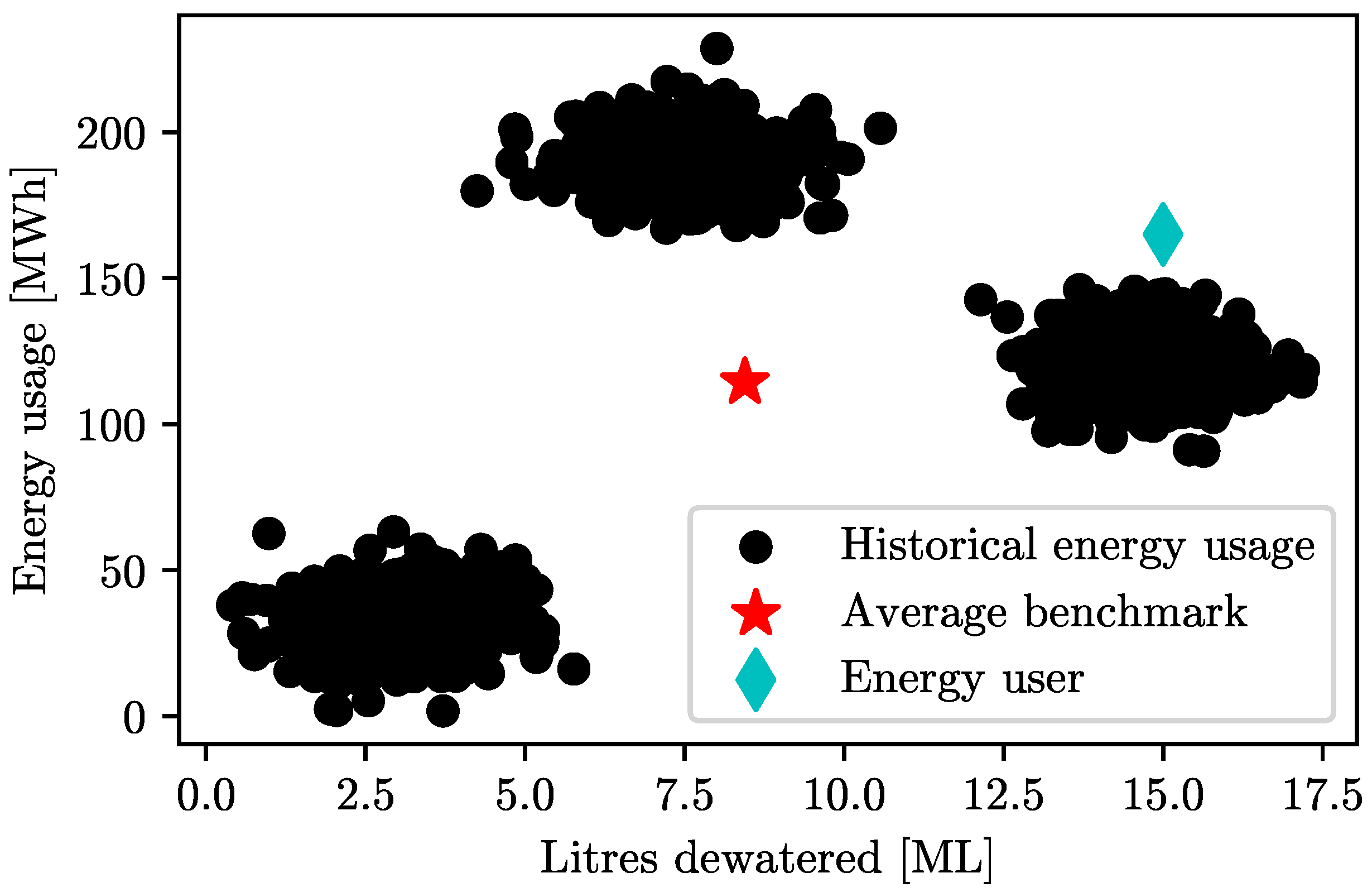
To create benchmarks, current benchmarking methods in the mining industry analyse different mining shafts and group energy usage at different frequencies, such as by month, weekday, or shift. These methods may result in inaccurate performance evaluations when there is a significant mismatch between the energy users aggregated to develop the benchmark and the energy user that is being benchmarked.

In Figure 2, the average benchmark taken from the historical energy usage is shown with the red star. Evaluating the energy user (blue diamond) against this benchmark will lead to a skewed representation of performance and will not effectively identify the scope for improvement.

1.4. Aim

This research aimed to adapt and apply a clustering-based benchmarking method to a mining complex to identify similar groups of energy users for improved benchmarking. These new benchmarks were used for performance evaluation and the detection of abnormal energy usage across different shafts. The results were compared to the traditional benchmark approach.

1.5. Scope

A South African deep-level gold-mining complex was selected as a case study, where four production shafts were used as the dataset to implement and evaluate the applicability of the clustering-based benchmarking method in the mining industry.

This study was concerned with applying the method in the context of external benchmarking. Therefore, the mining shafts were benchmarked against each other to identify energy wastage and areas for improvement.

2. Method

The method proposed in this study was constructed using attributes of the benchmarking methods applied to the mining industry with the clustering-based methods used in the building sector.

2.1. Data Collection

This study considered multiple data sources, including data from underground power meters and data regarding mining parameters, such as compressed air, water flow, and hoisted tonnes. The energy and flow data were extracted half-hourly from different databases while the production data were manually recorded in Excel spreadsheets by mining personnel and uploaded to a centralised database with the rest of the data.

2.2. Data Pre-Processing

2.2.1. Reshaping the Data

The energy, flow, and production data had to be combined into a single dataset. The production data had a daily frequency; thus, the energy and flow data were aggregated into daily readings by summing the total energy usage and averaging the daily flows.

The dataset then had to be reshaped to comprise daily readings for each variable and the related mining shaft. The reshaped dataset consisted of the date, shaft, daily average compressed air flow, daily average dewatering flow rate, tonnes of ore hoisted, and total energy used.

2.2.2. Data Cleaning

A data cleaning step removed outliers that may have affected the analysis results. Due to the large differences in the magnitudes of the mining parameters contributing to energy usage, the columns were screened individually for extreme values. This was done by calculating the z-scores for each entry using the corresponding column’s mean and standard deviation, as in Equation (1) [30].

$$z_{ij}=\frac{x_{ij}-{\mu }_j}{{\sigma }_j},$$

(1)

where $z_{ij}$ is the z-score of the ith row in the jth column, and $x_{ij}$ is the corresponding value for which the z-score is calculated. The ${\mu }_j$ and ${\sigma }_j$ represent the jth column’s mean and standard deviation. The ith row is removed if the z-score exceeds three [31,32].

2.2.3. Data Normalisation

Due to the diverse variables in the shaft energy usage dataset and the significant differences in the magnitudes of some of the parameters, the data had to be normalised so that the clustering analysis did not place any artificial importance on any of the parameters.

To ensure each feature was on the same scale, the columns were normalised individually using min-max normalisation, which scales each entry between 0 and 1 using Equation (2) [30].

$$x_{scaled}=\frac{x-x_{min}}{x_{max}-x_{min}},$$

(2)

where $x_{scaled}$ represents the new scaled value; x is the unscaled, original value; and $x_{max}$ and $x_{min}$ are the maximum and minimum values of the dataset of each column.

2.3. Algorithm Comparison and Selection

The clustering algorithms considered in this study were selected based on the review of energy benchmarking studies in the building sector. The commonly used algorithms in the literature were implemented and compared in this study [33,34]:

• K-means clustering;
• Bisecting K-means;
• Gaussian mixture models;
• Hierarchical clustering;
• Self-organising maps.

The algorithms were compared by combining three common clustering validation metrics. The Calinski–Harabasz index (CHI) [35], Davies–Bouldin index (DBI) [36], and the silhouette coefficient [37] were used to compare the different clustering algorithms [38].

These clustering metrics use different equations to evaluate the quality of the clusters in terms of their grouping and how distant each cluster is from the rest. The combined index is shown in Equation (3).

$$Combined Index=\frac{Silhoutte coefficient\ast CHI}{DBI},$$

(3)

The index takes the product of the CHI and silhouette coefficient and divides it by the DBI. A larger CHI and silhouette coefficient are associated with a better fit, whilst a smaller DBI indicates a better fit. Therefore, the higher the combined index is, the better the algorithm can cluster the data into distinct groups.

The algorithm was chosen if it performed best across most cluster numbers or achieved the highest combined index score.

2.4. Number of Clusters

Once the best algorithm was chosen, the number of clusters into which the data had to be split was selected. The clustering metrics were again used with a plot of the within-cluster sum of squares (WCSS) and analysed individually to determine the ideal number of clusters.

2.5. Identification of Benchmarks

Multiple variables were considered for each of the mining shafts and, thus, benchmarking methods such as OLS regression could be employed to discover functions related to the expected energy usage. These functions were developed for each cluster to evaluate energy usage more accurately. The expected energy usage from each cluster’s equation was used as a benchmark against which the actual energy usage was compared.

2.6. Verification of Benchmarks

The cluster-based OLS regression models were evaluated in terms of the ability to predict the actual energy usage based on the mining variables. To verify the cluster-based equations, they were compared to the current method of developing a single OLS regression equation for the entire dataset from which all energy users were benchmarked [14].

The clustered datasets were split into a training and test set to evaluate the predictive ability of the regression equations. Popular error metrics were used to evaluate the accuracy of the prediction, including the RMSE and the MAE, as shown in Equations (4) and (5).

$$\mathrm{RMSE}=\frac{1}{n}{\mathrm{\Sigma }}_i^n\sqrt{{(y_i-\widehat{y_i})}^2},$$

(4)

where n is the number of data points, $y_i$ is the ith actual data point, and $\widehat{y_i}$ is the ith model’s prediction;

$$\mathrm{MAE}=\frac{1}{n} {\mathrm{\Sigma }}_i^n |y_i-\widehat{y_i}|,$$

(5)

where the error term is taken as an absolute value and not squared, making it less sensitive to outliers.

2.7. Daily Benchmarking

Daily energy benchmarking evaluates energy performance and prioritises different energy-saving initiatives. The daily benchmarking process is divided into three steps:

1.

Assign new energy users to clusters;

2.

Identify abnormal energy usage through outlier detection;

3.

Benchmark energy performance based on the assigned cluster benchmarks.

2.7.1. Cluster Assignment

The cluster in which most of the shaft’s energy usage was classified in the training dataset was seen as the shaft’s dominant cluster and its typical mode of operation.

Each shaft’s new daily energy usage was assigned to the shaft’s dominant cluster and benchmarked using the associated expected energy equation.

2.7.2. Identifying Outliers

Once the energy user was assigned to the related cluster, possible excessive energy usage was flagged. The actual energy usage was compared to the distribution of the energy usage of the assigned cluster.

If the energy usage exceeded three standard deviations from the mean, it was flagged as excessive wastage for further examination [31,32].

2.7.3. Cluster Benchmarking

Once the new daily energy user was assigned to a cluster based on the dominant cluster and had been screened for excessive wastage, the energy user could be evaluated against the cluster benchmarks.

The OLS regression equations within each cluster were based on the recorded daily mining parameters, allowing for dynamic benchmarks that vary for different operating conditions.

A benchmarking score based on the EER was calculated to compare energy performance between different shafts. The EER benchmark scores were calculated using Equation (6)

$$Benchmark score=\frac{E_{actual}}{E_{benchmark}}\ast 100,$$

(6)

where $E_{actual}$ is the daily energy usage being benchmarked, and $E_{benchmark}$ is the predicted energy usage from the OLS regression. The score is converted to a percentage by multiplying by 100.

An EER benchmark score below 100% indicates that the energy user is performing better than the benchmark based on the expected energy usage benchmark determined using the associated mining variables. Conversely, a score above 100% highlights poor performance.

When comparing different mining shafts, the EER benchmark score allows the energy management team to identify and investigate poor performance and adjust energy management strategies accordingly.

3. Case Study: Application on a Deep-Level Gold Mining Complex

The four production shafts from the case study consumed 1073 GWh of energy and extracted 1,671,025 tonnes of ore in 2021. These shafts have different characteristics and different mining methods. A summary of the energy usage and hoisted tonnes for each shaft is shown in

Table 2. Mining shaft energy usage and production in 2021.

Shaft	Energy Usage (GWh)	Hoisted Tonnes (t)
Shaft A	398.48	603,932
Shaft B	338.72	569,002
Shaft C	274.66	180,187
Shaft D	66.31	317,904

.

Shaft A has a compressor house and uses compressed air for drilling. The shaft has refrigeration plants, an underground network of pumps, and ventilation fans. Shaft B uses hydro-power drills and thus only uses compressed air, which it receives from shaft A’s compressor house, for underground refuge bays. There are pumps, refrigeration plants, and ventilation fans. Shaft C has its own compressor house and uses compressed air for drilling. The mining shaft has pumps, refrigeration plants, and ventilation fans. Shaft D receives its compressed air from shaft A and uses it for drilling. The shaft has pumps and ventilation fans but requires no secondary cooling from refrigeration plants.

3.1. Data Collection

The common variables amongst all the shafts that contribute to the shafts’ energy usage were collected for the analysis.

The daily average compressed air usage was considered because the compressed air usage is associated with the compressor energy consumption. The daily average flow rate through the dewatering column was recorded because the dewatering flow is related to the pumping system’s energy consumption. The daily hoisted tonnes was recorded as it is the direct output of the mine and is the reason why the mine uses high-energy systems. The daily total energy usage for each shaft was recorded as this was the parameter being benchmarked based on the other mining variables.

The data were collected for each shaft for 2021 and 2022 for the training dataset (excluding five months in 2022 due to labour action). The same variables for the first five months of 2023 were collected and used for the evaluation dataset from which the daily energy usage was benchmarked.

An example of the raw dataset is shown in

Table 3. The first four rows of the raw training dataset.

Date	Time	TagID	TagUnit	TagName	TagValue
1 January 2021	00:00	630f253	kWh	Shaft_A_Energy	889,902
1 January 2021	00:00	630f254	kg/h	Shaft_A_Air	53,963
1 January 2021	00:00	630f255	L/s	Shaft_A_Water	129.5
1 January 2021	00:00	630f256	t	Shaft_A_tonnes	0

, where each of the daily parameters is stored in a TagValue column with the associated TagName, TagUnit, TagID, and Time.

3.2. Data Pre-Processing

3.2.1. Reshaping the Dataset

The first step of pre-processing was to remove unnecessary columns such as Time, TagUnit, and TagID. The time is not required for daily readings, and the unit and ID did not play any role in the analysis.

The dataset was then reshaped to consist of daily readings of each parameter for each shaft. Two new columns were created by extracting information from the TagName column. The first column showed the parameter being recorded for the type of variable (CA_flow, Water_flow, hoisted tonnes, energy usage), while the second column showed the shaft name (Shaft A, Shaft B, Shaft C, Shaft D).

The TagName column was subsequently removed before pivoting the data so that they consisted of the date, shaft, and shaft variables, as shown in

Table 4. The first four rows of the reshaped training dataset.

Date	Shaft	CA (kg/h)	Water (L/s)	Hoisted (t)	Energy (kWh)
1 January 2021	Shaft A	53,963	129.5	0	889,902
1 January 2021	Shaft B	28.26	264.6	0	861,194
1 January 2021	Shaft C	79,921	145.3	0	684,658
1 January 2021	Shaft D	16,218	110.5	0	103,889

.

3.2.2. Data Cleaning

The reshaped training dataset consisted of 2308 rows and six columns. The z-scores were calculated for each entry in all the columns to remove outliers using Equation (1).

The z-scores for this dataset were all below the threshold of three; thus, no outlier rows were removed.

However, there were 26 negative and 87 missing values due to erroneous or faulty meter readings. These entries were dropped from the dataset, leaving the final cleaned dataset with 2195 rows of data.

3.2.3. Data Normalisation

The data in each column were normalised using Equation (2) to scale the data between 0 and 1.

Table 5. The maximum and minimum values used for normalising each variable.

	CA (kg/h)	Water (L/s)	Hoisted Tonnes (t)	Energy (MWh)
Minimum	0	0	0	0
Maximum	193,332.10	754.63	4114.00	1366.05

highlights each parameter’s minimum and maximum values.

3.3. Clustering Algorithm Comparison and Selection

Four of the algorithms were implemented using Scikit-learn [33], a popular machine learning library in Python, while the self-organising maps algorithm was implemented using the minisom Python library [34]. A one-dimensional network of nodes was used for the self-organising map implementation to compare its performance to the other algorithms effectively.

The result of the comparison between clustering algorithms using the combined index is shown in Figure 3.

The K-means, self-organising maps, and bisecting K-means showed similar performance between cluster numbers two and four, where the bisecting K-means’ and self-organising maps’ performance dropped off. Hierarchical clustering had a similar trend to K-means until after cluster four, where the score remained slightly lower than K-means, while Gaussian mixture models showed the worst performance across all cluster numbers.

The K-means clustering algorithm was selected as the best-suited algorithm to group the data because it performed best across all cluster numbers and had the highest overall combined index score.

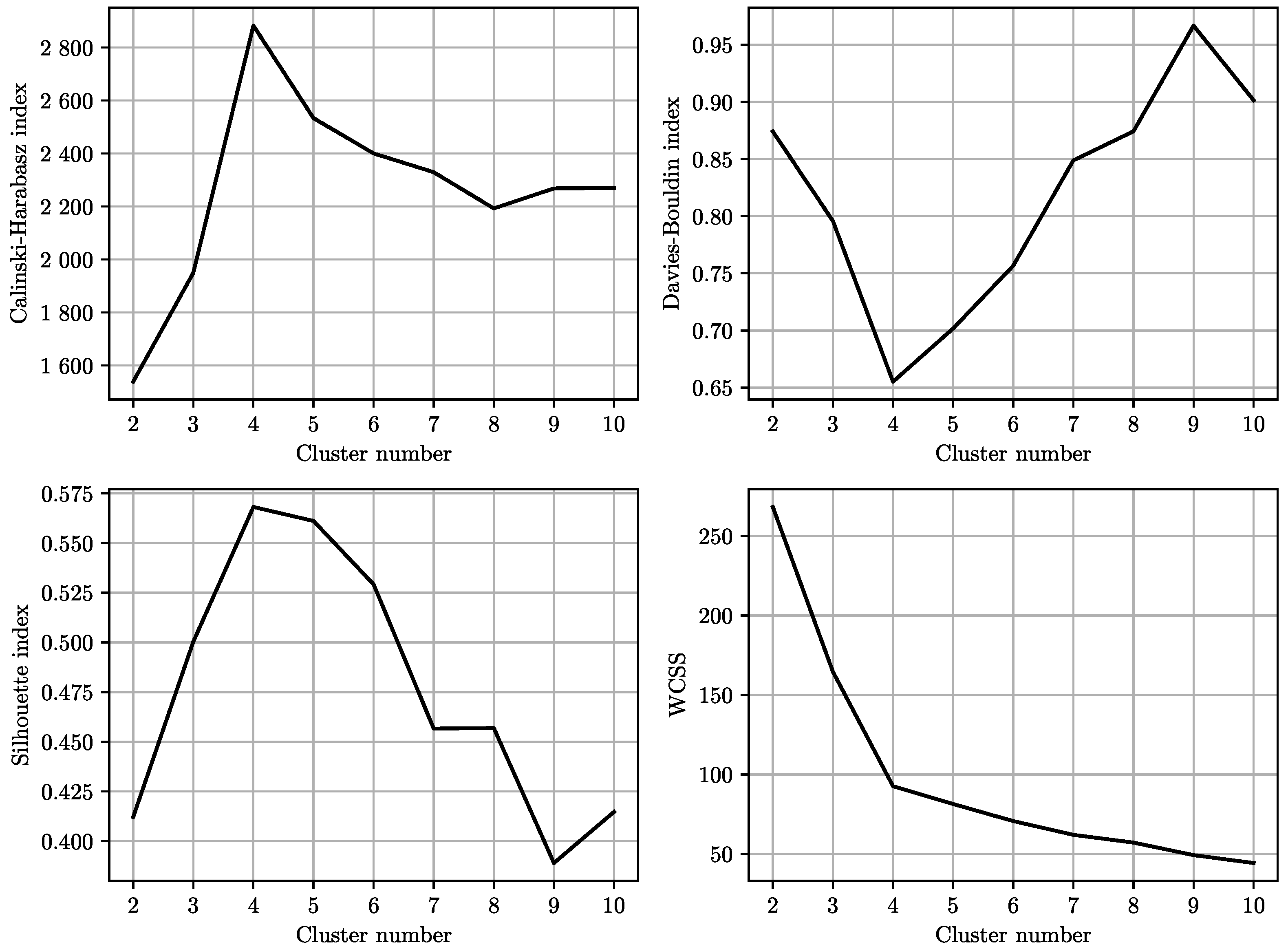
3.4. Number of Clusters

The clustering metrics were used to examine the optimal number of clusters to partition the dataset into based on the variables in the dataset. The CHI, DBI, silhouette coefficient, and the elbow method on the WCSS plot were considered. The results of the clustering metrics are illustrated in Figure 4.

From all the metrics, it is clear that the ideal number of clusters was four. The CHI and silhouette coefficient had sharp increases at cluster number four before decreasing gradually for higher cluster numbers. Conversely, the DBI sharply decreased at cluster number four and progressively increased for higher cluster numbers. The plot of the WCSS showed a distinct elbow at cluster number four, where there were diminishing returns for an increasing number of clusters.

The number of clusters identified and the number of shafts being analysed were the same, and this emphasised that there may have been very distinct operating variables among them.

3.5. Identification of Cluster Benchmarks

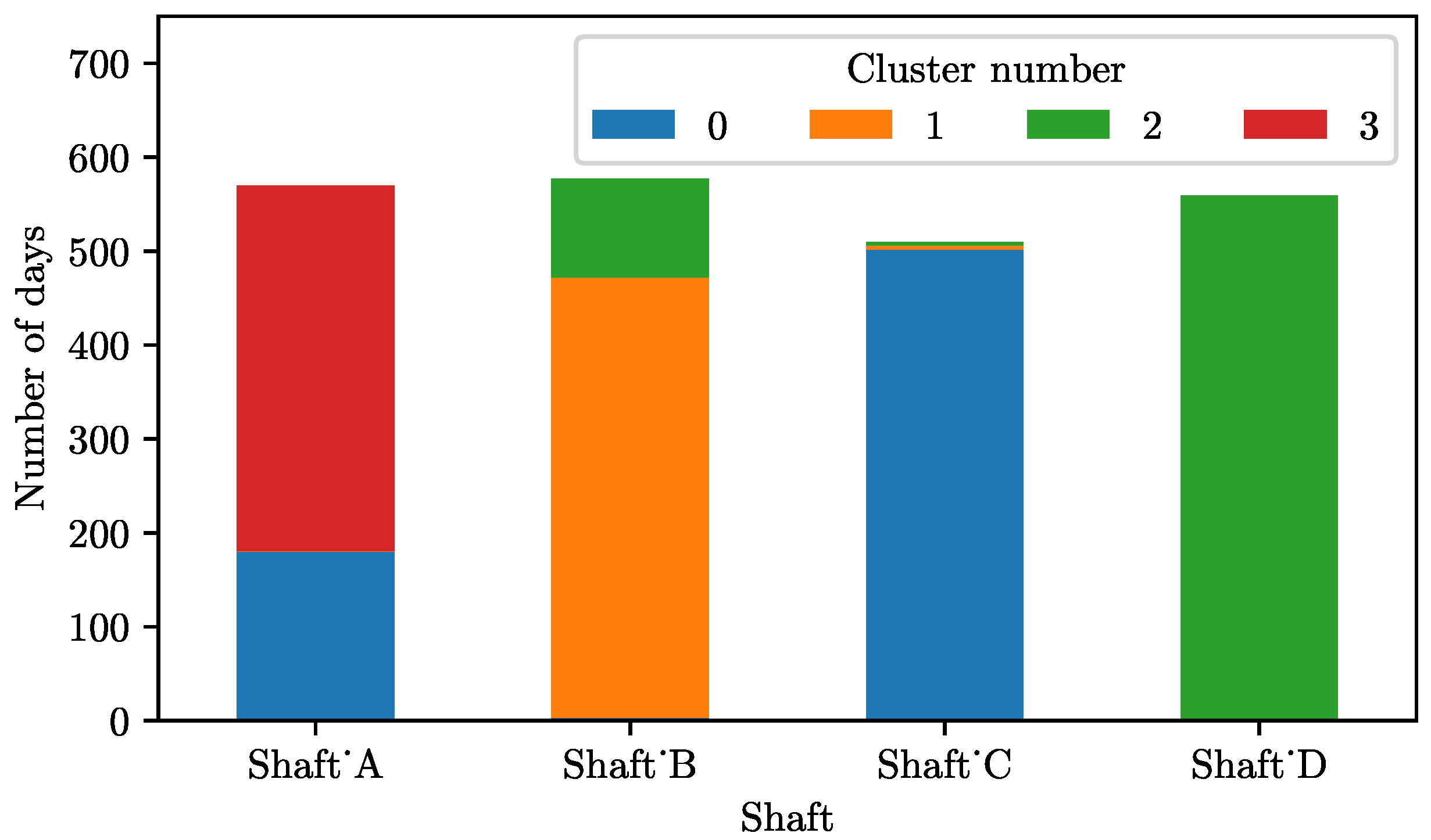
The K-means clustering algorithm was implemented on the dataset with the cluster number set to four. Each day was assigned to a cluster based on the similarity in its daily compressed air usage, litres dewatered, hoisted tonnes, and overall energy usage.

The number of days assigned to each cluster for the shafts is illustrated in Figure 5, which highlights the difference between the operations at the different shafts, each with a distinct cluster.

Shaft A had the most diverse mode of operation, with 31.6% of the days classified as cluster zero and 68.4% classified as cluster three. Shaft B also had two main modes of operation, with 81.3% in cluster one, 18.2% in cluster two, and a small portion in cluster zero.

Shafts C and D had far more distinct modes of operation with single dominant clusters. Shaft C operated in cluster zero 98.4% of the time, while Shaft D exclusively operated in cluster two.

The shafts each had a dominant cluster where more than 50% of the days were assigned to a single cluster. The dominant clusters are summarised in

Table 6. The shafts’ dominant clusters.

Shaft	Cluster
Shaft A	3
Shaft B	1
Shaft C	0
Shaft D	2

.

The OLS benchmarking method was applied to each cluster in the original dataset with no normalisation to develop functions that returned an expected energy usage based on the features. This served as a dynamic benchmark depending on the daily compressed air usage, water dewatered, and hoisted tonnes for future daily energy benchmarking. The clustered datasets each had their own associated OLS regression functions.

The matrix of the resulting function coefficients is highlighted in

Table 7. A matrix of each cluster’s function coefficients.

Cluster	CA	Water	Hoisted	Intercept
0	−1.25	468.04	35.67	747,102.65
1	1.40	326.47	90.48	570,826.37
2	−1.00	−824.89	−12.85	330,998.87
3	0.73	850.23	11.12	892,810.67

.

3.6. Verification of Cluster Benchmarks

The use of the cluster-based benchmarks was verified by testing the predictive capabilities of each cluster’s regression model against the currently used method employing a single model derived from the full, unclustered dataset [14]. The predictive capabilities were tested using the error metrics discussed in Section 2.6.

A summary of the RMSE, MAE, and $R^2$ for each cluster and the overall dataset is shown in

Table 8. A summary of each cluster’s regression model performance.

Cluster	RMSE	MAE	${\mathit{R}}^2$
0	73,530	52,220	0.055
1	128,438	91,501	−0.014
2	73,290	42,781	0.336
3	62,335	46,012	0.340
Average	84,398	58,128	0.179
Full dataset	266,605	206,207	0.556

.

The clustered regression models had excellent predictive accuracy, with each error metric showing comparatively lower scores than the full dataset model. However, the $R^2$ values were far lower in the clustered datasets than in the full dataset. This was due to the nature of clustering algorithms, which aim to reduce the variance within each cluster and ensure that the clusters are distinct. The $R^2$ value illustrates the proportion of variance explained by the model in the dependent variable, which by design was low in the clustered datasets [39].

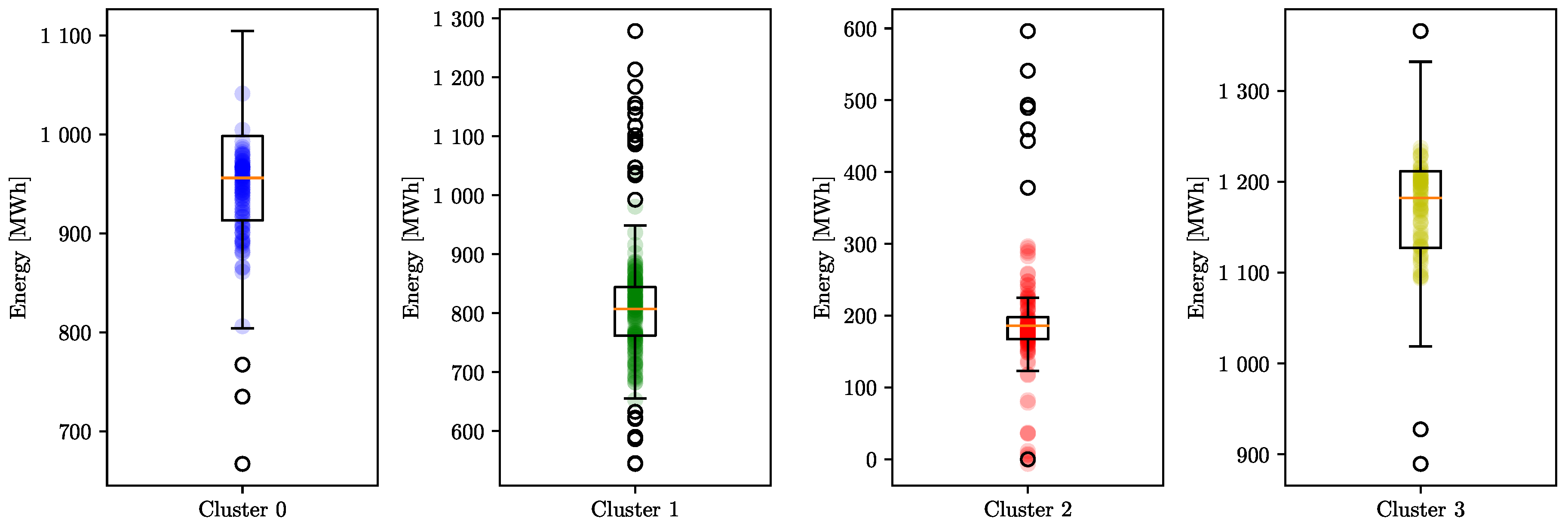
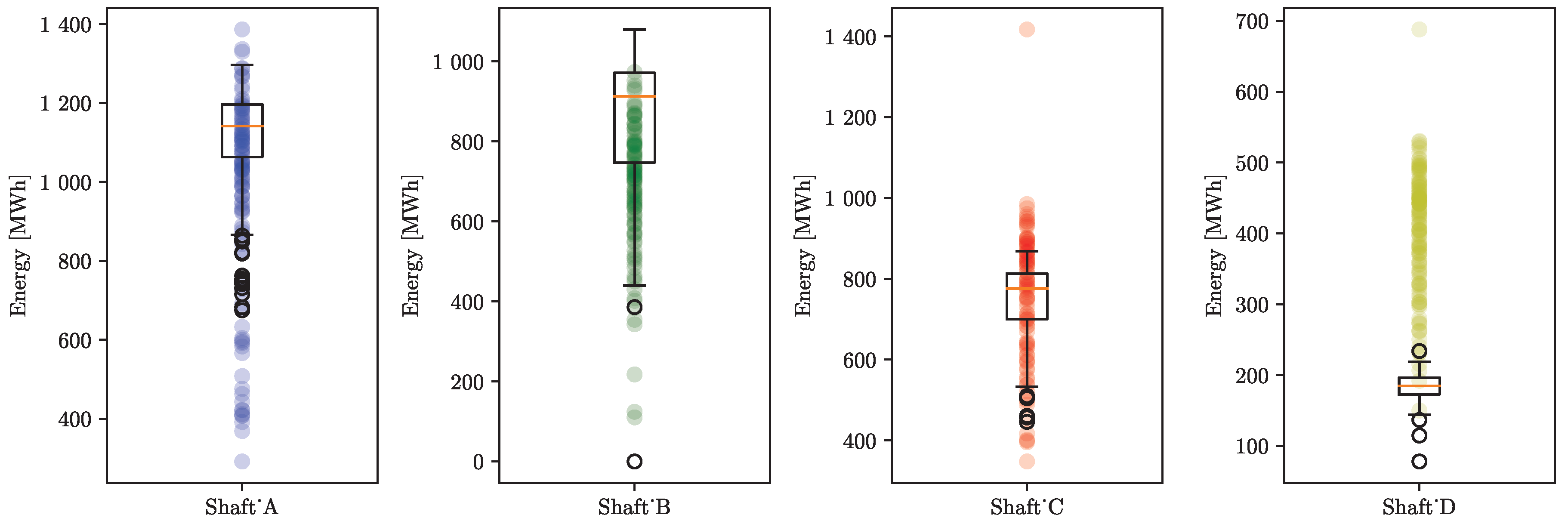
The distribution of the actual recorded energy usage for the test set and the spread of the predicted energy are highlighted in Figure 6. The distribution of the actual energy usage is shown with a box plot with a scatter plot overlayed with the predicted energy usage.

Cluster zero had a symmetric distribution with low-energy-usage outliers on a few days. Similarly, cluster one showed symmetric distribution but with many outliers with higher and lower energy usage. Cluster two had a narrow but symmetric distribution with a few outliers. Cluster three showed a wide symmetric distribution with a few outliers.

The predicted energy usage based on the output of the OLS equations for each cluster was very well centred within the distribution of actual energy usage, emphasising the accuracy of the OLS regression models in predicting actual energy usage.

Figure 7 shows the results for the single OLS regression model on the test set. Each shaft’s results are shown separately to compare them with the clustered results, which predominantly represented a single shaft.

From Figure 7, it is clear that the accuracy of the single OLS regression model favoured some shafts’ energy usage, especially when the magnitude of the energy usage varied.

Shaft A had very dispersed predictions with high and low outlier energy predictions. However, most of the energy usage predictions were within the range of the actual energy usage distribution. Shaft B had slightly better predictions, with only a few low-energy-usage outlier predictions and most predictions within the actual energy distribution. Similarly, Shaft C had good predictions with a few outliers.

Shaft D showed the worst predictions, with almost all the energy usage predictions falling outside the actual energy usage distribution. This emphasises how a change in energy usage may lead to inaccurate benchmarks when using a single OLS regression equation to capture vastly different energy users.

3.7. Daily Benchmarking

3.7.1. Cluster Assignment

The new daily energy usage was assigned to the cluster representing the associated shaft’s dominant mode of operation from Table 6.

3.7.2. Identifying Outliers

The mean and standard deviation of each cluster’s energy usage were calculated for the training set to develop an outlier threshold to flag excessive energy usage in the evaluation dataset.

Table 9. A summary of each cluster’s outlier thresholds.

Cluster	Mean (MWh)	Std. Deviation (MWh)	Threshold (MWh)
0	942.14	79.04	1179.28
1	801.58	139.54	1220.19
2	171.64	92.47	449.06
3	1166.57	77.43	1398.86

summarises the outlier thresholds.

The daily entries in the evaluation dataset were compared to each of the associated thresholds based on the cluster that they were assigned to, resulting in no outliers being flagged.

3.7.3. Cluster Benchmarking

The expected energy usage for each of the entries in the evaluation dataset was calculated based on the equations in Table 7 depending on the assigned cluster for each shaft. The expected energy usage served as the dynamic benchmark based on the variables recorded on the day. The actual energy usage for each day was evaluated against these benchmarks.

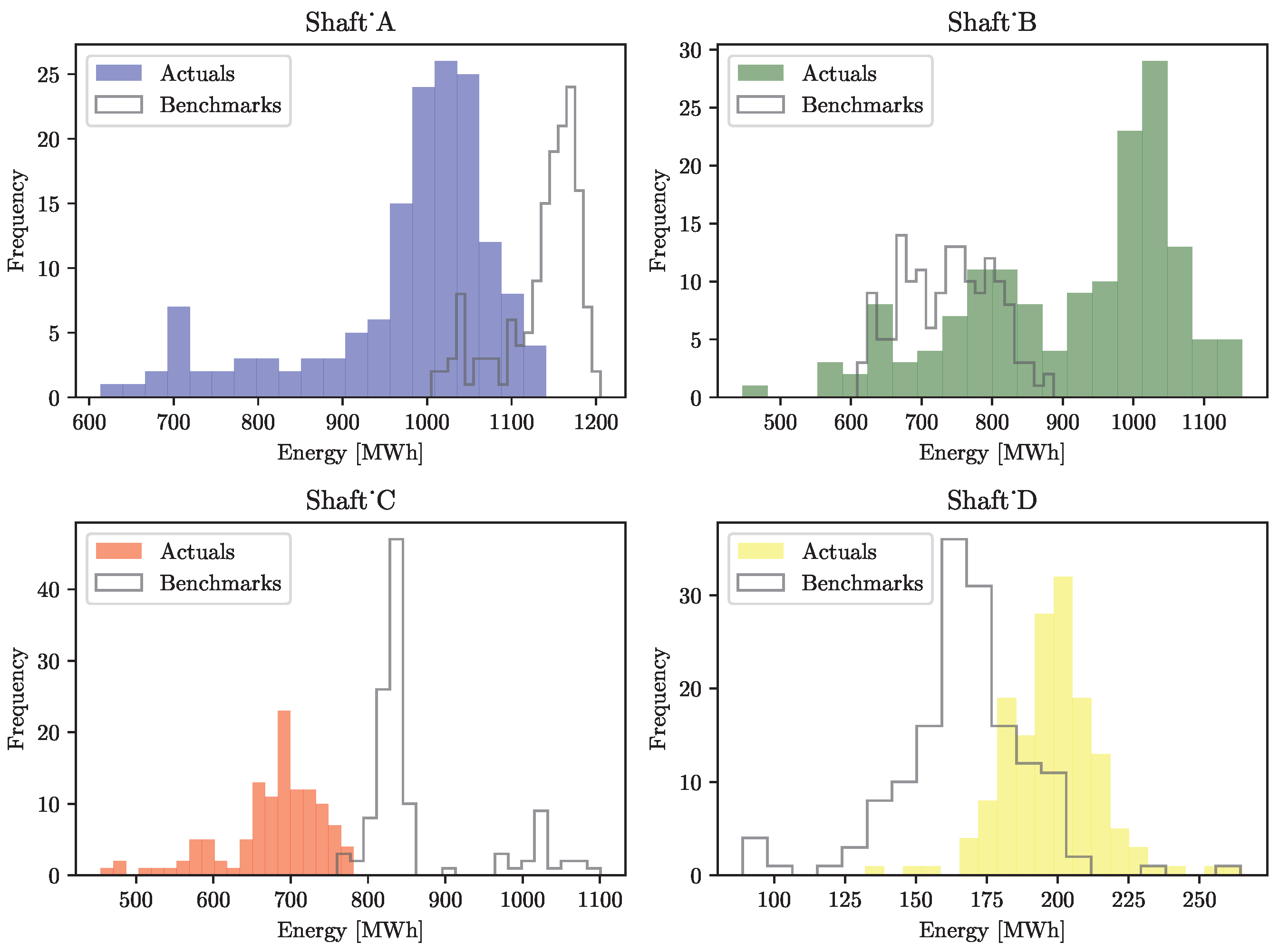
Histograms showing the spread of the actual and benchmark energy usage for each of the shafts in the evaluation set are illustrated in Figure 8.

Shafts A and C had actual energy usage that was mostly below the benchmarks, showing improved performance compared to the benchmarks, while Shafts B and D showed a larger overlap in the distribution of actual and benchmark energy usage, but the actual energy usage peak was higher, illustrating that the performance had deteriorated compared to the benchmarks.

To compare the performance of the different mining shafts, the monthly EER benchmark scores were calculated using Equation (6) and are shown in

Table 10. The cluster-based EER benchmarking scores for each shaft for the evaluation dataset.

Month	Shaft A Score (%)	Shaft B Score (%)	Shaft C Score (%)	Shaft D Score (%)
Jan	85.12	131.78	77.52	130.15
Feb	83.35	130.92	83.35	116.09
Mar	88.30	129.71	76.89	115.17
Apr	85.86	119.71	75.02	123.90
May	84.80	111.71	78.88	125.72
Average	85.43	123.77	78.84	122.01

.

Shaft A scored consistently over the five months with an average monthly score of 85.43%. This highlights that, based on the compressed air, dewatered litres, and hoisted tonnes, the shaft performed better than the expected energy usage benchmarks.

Shaft B showed very poor performance at the start of the year, with benchmark scores above 130% for the first two months. This performance improved throughout the year, with consecutively decreasing benchmark scores. The increase in performance is positive, and the scores should continue to be monitored for any changes that should be investigated.

Shaft C showed the best overall performance, with an average score of 78.84%. There were, however, months where the score increased, indicating a drop in performance, which may be further investigated to ensure that any future decline in performance is avoided.

Similarly to Shaft B, Shaft D started the year with a benchmark score greater than 130%. The performance improved for the next two months but then declined again. This performance should be monitored over time, and days with large benchmark scores should be studied to implement savings initiatives and return to better energy performance.

4. Discussion

For the evaluation period, mining shafts B and D both had poor performance, with average EER scores of 123.77% and 122.01%, respectively. Implementing focused energy-saving initiatives to return these poor-performing shafts to their respective benchmarks could result in 201 MWh of energy savings over the evaluation period.

The current method implemented in [14] employed a single OLS regression model for the full dataset containing all the shaft’s variables. To compare this research with the current mining energy benchmarking method, an OLS regression function was found for the full dataset, as shown in Equation (7).

$$E_{expected}=1.91\ast CA+1523.52\ast Water+105.20\ast Hoisted+170656.66,$$

(7)

where CA, Water, and Hoisted represent the variables, of which each is multiplied by a coefficient to give the expected energy usage ($E_{expected})$.

The evaluation metrics of this regression model are shown in Table 8, which highlights that Equation (7) was inferior to the individual cluster models in predicting the expected energy usage when evaluated on the test portion of the training dataset.

The actual and benchmark energy distributions for each shaft are shown in Figure 9. Shaft A had an actual energy distribution that overlapped with the upper end of the wide benchmark distribution, which shows that it performed slightly worse than the benchmarks. Shaft B had an actual energy distribution with higher energy usage than the benchmark distribution, highlighting poor performance. Shaft C showed a narrow actual energy distribution slightly higher than the peak of the wide benchmark distribution, illustrating slightly worse performance than the benchmarks. Shaft D had a very narrow actual energy distribution that was completely separate from the benchmark distribution, which means it outperformed the benchmarks by a large margin.

Equation (6) was used to compare the shafts using the associated EER benchmark scores. The resulting benchmark scores from the entire dataset model are summarised for each shaft in

Table 11. The full dataset’s EER benchmarking scores for each shaft.

Month	Shaft A Score (%)	Shaft B Score (%)	Shaft C Score (%)	Shaft D Score (%)
Jan	125.31	146.58	116.55	35.81
Feb	109.90	137.16	125.35	38.75
Mar	110.60	137.16	99.98	39.32
Apr	109.04	148.00	112.40	37.11
May	105.21	125.34	100.13	34.65
Average	111.91	138.03	111.70	37.06

.

The benchmark scores in Table 11 show that shaft D was the best-performing shaft and the only shaft with scores below the corresponding benchmarks throughout the year. Shafts A and C performed similarly, with benchmark scores on average 11% above the benchmark, while shaft B was seen as the worst performing shaft, with scores consistently above 135%.

As in Section 3.7.3, the benchmark score for shaft B indicated the worst performance, and shaft C showed similar scores to shaft A, which was a similar finding as in Table 10; however, both of the shafts showed poor performance using this method, unlike in Table 10.

Shaft D showed the most significant difference between the two methods. The single OLS regression equation showed benchmark scores that were far below the benchmark expected energy usage, demonstrating that it was the best-performing shaft and the daily variables indicated a 63.94% increase in performance compared to the benchmark. In Section 3.7.3, shaft D benchmark scores indicated poor performance, with scores 22.01% above the benchmark.

The difference in the benchmark scores between the two methods is explained by the poor predictive capabilities of Equation (7), as shown in Table 8 and Figure 7, which illustrates that the single equation model had the most inaccurate predictions for shaft D, leading to its incorrect performance evaluation.

Using the entire dataset of diverse energy users to develop a single OLS regression equation may lead to skewed benchmarks favouring certain energy users that do not cater for the considerable variation in the shaft variables.

This study showcased an important shift in energy benchmarking in the mining industry by revealing that tailored benchmarks, derived through clustering techniques, lead to precise performance evaluations. This breakthrough enhances our understanding of energy consumption and paves the way for substantial energy savings within the mining sector.

It is estimated that, by extrapolating the application of this method to the 526 mines in South Africa (https://safacts.co.za/list-of-mines-in-south-africa/, accessed on 26 September 2023) and identifying poor-performing shafts, potential energy savings of at least 10% (2.96 TWh) of the sector’s energy usage may be realised.

Ultimately, reducing energy wastage in the mining sector may alleviate the constraints on energy availability in the country, leading to sustainable mining operations and long-lasting contributions to the South African economy.

5. Conclusions

This study developed and implemented a clustering-based benchmarking method for the mining industry to explore whether adding clustering techniques improves the accuracy of the energy benchmarks.

The K-means clustering algorithm was implemented to discover four dominant clusters without prior knowledge of the dataset. The mining shafts each had distinct modes of operation with predominantly single-cluster energy usage.

An OLS regression was performed on each cluster to develop equations that predicted the energy usage based on variables from the mining shafts. Popular error metrics were used to compare these cluster-based equations to the traditional methods.

The cluster-based benchmarks were far superior at predicting energy usage when evaluated on the test set and were thus better able to describe each shaft’s energy usage, leading to a more accurate evaluation of performance across the gold-mining complex.

The more accurate EER benchmarking scores allow for a fair comparison between shafts and indicate where the energy-saving initiatives should be focused. Investigating and addressing the shortcomings of worst-performing shafts would result in energy savings of 201 MWh for the period considered in this study.

The daily reporting of the benchmark score allows for swift adjustments to the energy management strategy, ensuring that the mining sector can accurately monitor and manage its energy performance and continue to make important contributions to the South African economy.

This study boasts the first-known implementation of cluster-based energy benchmarking in the mining sector. The additional step of clustering energy users improves the accuracy of the resulting benchmarks and allows for improved energy management strategies. The successful application of the method to a case-study gold-mining complex with an annual energy usage of 1073 GWh emphasises the importance of the method in the context of energy benchmarking and energy management as a whole.

Although the results illustrate the benefits of applying clustering techniques for improved energy benchmarking, the list of algorithms explored is not exhaustive. Additionally, only a single benchmarking method was adopted within the discovered clusters. Therefore, future research in this area may benefit from exploring different clustering algorithms, mining variables, and benchmarking methods within different high-energy-usage industries.