Abstract
Variable-cross-section beams have better mass and strength distribution compared with constant cross-section beams, which can optimize the harvesting power of piezoelectric vibration energy harvesters, which are widely used in self-supplied and low-power electronic devices, providing more convenience and innovation for the development of micromechanical intelligence and portable mobile devices. This paper proposes a piezoelectric energy harvester with a tristable-exponential-decay cross section, which optimizes the strain distribution of the cantilever beam through exponential decay changes to improve the harvesting efficiency of the harvester in low-frequency environments. First, the nonlinear magnetic force is obtained based on the magnetic dipole, and the dynamic model is established by using the Euler–Bernoulli beam theory and Lagrangian equation. The influence of the structural parameters of the harvester on the system dynamics and output characteristics is analyzed in the two dimensions of time and frequency, and the influence of the exponential decay coefficient on the system dynamic response and output power is deeply studied. The research shows that the exponential decay section can reduce the first natural frequency of the cantilever beam; by changing the amplitude, frequency, d and dg of the excitation acceleration, the switching of the monostable, tristable and bistable states of the system can be realized. With a decrease in the exponential decay coefficient, under a low-frequency excitation of 0–7 Hz, the output power of the cantilever beam per unit volume is significantly improved, and under a 4 Hz low-frequency excitation, the acquisition output power per unit volume of the cantilever beam is increased by 7 times, thus realizing low-frequency, high-efficiency energy harvesting.
1. Introduction
A piezoelectric vibration energy harvester directly harvests mechanical energy from environmental excitations and converts it into electrical energy by utilizing the positive piezoelectric effect of PZT patches. It has the advantages of a simple structure, a small size and high energy efficiency performance and is widely used in wireless sensor networks, remote monitoring devices, the low power consumption of devices and other scenarios [1,2,3]. By harvesting vibrational energy in the environment, microelectronic devices can be self-powered, reducing or eliminating the need for conventional battery replacement [4], thereby reducing device maintenance costs and increasing device reliability and lifetime. Therefore, harvesting energy directly from the environment is a perfect solution for powering microelectronic devices in the future and has great value in research and application [5,6].
Linear piezoelectric energy harvesters are usually limited to a narrow frequency band, making it difficult to efficiently generate electrical power at low frequencies [7,8]. Nonlinear piezoelectric vibration energy harvesters seem to have better harvesting performance and can generally be classified into four categories: monostable [9], bistable [10], tristable [11] and multistable [12]. Many scholars have done a lot of research on the nonlinear multi-stable state. Erturk and Inman et al. [13,14] experimentally verified that the nonlinear transition behavior induces high-energy interwell oscillations of the bistable energy harvester under a harmonic excitation, which greatly improves the energy harvesting performance. Singh et al. [15] proposed an accurate model of the bistable sensor using a nonlinear extraction circuit, and the average power obtained in the experiment was more than 100 times higher than the extraction power reported in the similar literature. Cao et al. [16,17] studied the nonlinear dynamic characteristics of magnetically coupled broadband energy harvesters under low-frequency excitation. Experiments proved that rotating, magnetically coupled energy harvesters have available frequency bandwidths for a wide range of low-frequency excitations. Energy harvesting is dominated by high-energy chaotic attractors and inter-trap oscillations. In [18], the influence of excitation parameters and magnet spacing on the output power of the bistable harvester was investigated in the time–frequency domain. The bistable motion not only widens the frequency bandwidth of the system but also increases the average power of the system.
However, bistable large-amplitude well-to-well oscillations require stronger excitation triggers. Zhou et al. [19,20] were the first to carry out theoretical modeling and experimental research on the nonlinear-broadband, bistable energy harvester. The experimental results show that compared with the bistable energy harvester, the tristable energy harvester has a shallower potential well and can produce higher energy output in a wider frequency range. Zhou and Zou [21] used the harmonic balance method to study the asymmetric tristable energy harvester and found that the potential barrier is the key factor determining the orbital height of the high-energy interwell oscillation. Li et al. [22] studied the influence of parameters such as the distance between the magnets at the fixed end on the nonlinear response characteristics of the tristable harvester. Wang et al. [23] and Li et al. [24] investigated geometric nonlinearity, gravity models and ladder-trap tristable energy harvesters, respectively, to increase the output voltage under weak random excitation. Since then, Zhou and Qin have studied the tetrastable [25] and even pentastable [26] systems and found that the more potential wells, the more uniform the potential energy distribution is and the lower the potential barrier between the potential wells, but the structure becomes more complicated.
The above research mainly focuses on the piezoelectric vibration energy harvester of the rectangular cross-section cantilever beam. Because the bending stress of the rectangular cantilever beam changes along the length, the maximum power output of the bending stress is the highest at the fixed end, and the minimum power output tends to zero at the free end. The variable-cross-section beam vibration energy harvester can optimize the uniform distribution of a PZT patch strain along the length of the piezoelectric beam well and improve the power generation power of the piezoelectric sheet pasted on both sides of the cantilever beam root [27,28].
In order to obtain the higher output performance of piezoelectric energy harvesters, scholars also studied triangular, trapezoidal, concave and arc-shaped beam structures [8]. Baker et al. [29] found that linearly varying the cross section of the beam along its length increased the output power density of the energy harvester by up to 30%. Shan et al. [30] found that for the same volume of piezoelectric material, the maximum output power of the triangular piezoelectric structure is more than three times higher than that of the rectangular structure. Wang et al. [31] studied the structure of a triangular-cross-section cantilever beam piezoelectric energy harvester and experimentally proved that the output power is higher as the width of the end becomes narrower. Ma et al. [32] and Tan et al. [33] studied the trapezoidal-cross-section cantilever piezoelectric energy harvester and proved that the stress distribution in the trapezoidal cantilever is more uniform than that in the rectangular cantilever, and the trapezoidal-cantilever piezoelectric energy harvester has a higher voltage output. He et al. [27] compared trapezoidal and rectangular piezoelectric vibration energy harvesters. The piezoelectric vibration energy harvester with a concave beam shape has a uniform surface stress distribution and performs the best output.
The above studies on the cross section of the cantilever show that by optimizing the cross section of the nonlinear vibration cantilever structure, better strain distribution, lower resonance frequency and higher output power density can be obtained. Finding a more suitable cantilever-cross-section optimization function is the biggest challenge to achieving better performance.
In order to describe the dynamic vibration response of a piezoelectric energy harvester, it is necessary to obtain an accurate solution of the kinetic equation of the cantilever beam. The distributed parametric model (DPM) can give an accurate solution for the uniform-cross-section cantilever beam, and the dynamic characteristics of the energy harvester can be easily obtained [34,35]. However, the derivation of DPM for cantilever beams with linear changes in cross section is more complicated. Ismail [36] uses the finite element method to establish the finite element model of a linear-gradient piezoelectric cantilever beam, which improves the solution accuracy of the concentrated parametric model (LPM). For energy harvesters with exponentially changing cross sections, Salmani [37] studied piezoelectric energy harvesters with exponential cross sections and tip mass, proving that exponential gradients can increase the power density of piezoelectric beams, but did not study the dynamic characteristics of collectors with external magnets.
In summary, among many optimized piezoelectric energy harvesters with variable sections, although exponential-attenuation piezoelectric energy harvesters show potential advantages in theory, it is difficult to comprehensively evaluate their performance in practical engineering applications due to the lack of research on the dynamic, steady-state characteristics of exponential piezoelectric energy harvesters under the action of a multi-magnet, nonlinear magnetic force, as well as the influence of different optimization exponential attenuation coefficients and system structure parameters on their dynamic characteristics, energy conversion efficiency and numerical output power. This limits the development and application of models in real-world engineering applications. Therefore, further research in these areas will help to fully reveal the potential and application areas of these energy harvesters.
In order to study the geometric structure of a variable-cross-section cantilever beam piezoelectric energy harvester with better energy harvesting performance, a variable-exponential-cantilever-beam piezoelectric energy harvester is proposed in this paper. The distributed parameter force–magnetism–electricity-coupled dynamics model of the variable-exponential-cross-section, tristable, piezoelectric vibration energy harvester was established by the Euler–Bernoulli beam theory and Lagrange equation. The time–frequency dynamics and energy output characteristics were studied through experimental simulation; the influence of the main structural parameters of the harvester on its nonlinear dynamic response and voltage output performance was numerically investigated, and the variable exponential coefficient on the output was analyzed. The mapping relationship of power density is expected to provide a reference for the geometric structure design and optimization of variable-cross-section cantilever piezoelectric energy harvesters.
2. Energy Harvester Structure
As shown in Figure 1, the Euler–Bernoulli beam is a cantilever beam of equal thickness, gradually narrowing exponentially along the length direction, with Young’s modulus E, density ρ, length L, thickness h, fixed end and free end widths wA and wB, respectively, and the concentrated mass at the end being Mt.
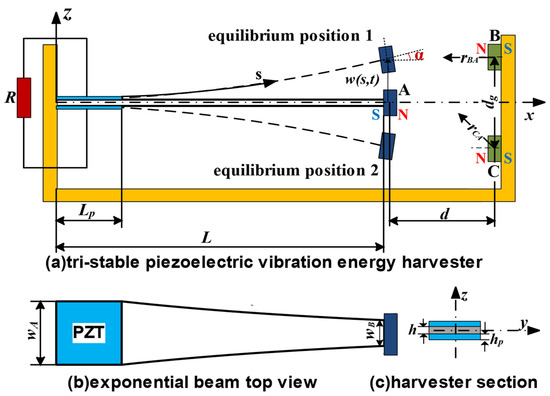
Figure 1.
Tristable, exponential-cross-section piezoelectric energy harvester.
As shown in Figure 1b, its cross-sectional shape parameters , cross section with length variation and moment of inertia are
where and . and are the cross-sectional area and the moment of inertia of the fixed end.
3. Establishment of Dynamic Model of Energy Harvester
3.1. Modeling of Nonlinear Magnetic Potential Energy
The vibration of a cantilever beam with a PZT patch is affected by the nonlinear magnetic force of the end magnet. The model based on the magnetic dipole is usually used to analyze the nonlinear magnetic force relationship between the end magnet A and the fixed-end magnets B and C. The geometric relationship is shown in Figure 1, and the magnetic flux density of the end magnet B at A can be expressed as
where is the vacuum permeability, is the vector gradient, and are the magnetic moments of dipole A and dipole B, respectively, , is the magnetization of magnet B, is the volume of magnet B, and is the direction vector of distance from magnet B to magnet A. The potential energy between magnet A and magnet B is
Substitute (2) into (3) to get
From the geometric relationship in Figure 1, we can get
Because , can get
Substituting Equations (5) and (6) into Equation (4), the nonlinear magnetic potential energy can be obtained as
Similarly, the nonlinear potential energy of magnet C at magnet A is given by
From (7) and (8) the total nonlinear potential energy can be obtained as
The total nonlinear magnetic force on the end magnet A is
3.2. Electromechanical Dynamic Model
Neglecting the gravity effect and rotation effect of the beam, according to the Cartesian coordinate system shown in Figure 1, the -axis is located at the neutral axis of the beam, the -axis is along the width direction of the beam, the -axis is along the thickness direction of the beam, and the -axis is the arc coordinate along the length direction of the beam.
Assuming that the fixed end is subjected to the transverse harmonic displacement excitation to generate a nonlinear bending vibration, Figure 1a is the deformation diagram of the micro-segment at the coordinate . The deformation of the micro-segment includes the horizontal displacement along the x-axis and the lateral displacement along the y-axis. The displacement of the micro-segment in the figure can be expressed as
Among them, the axial displacement of the micro-element segment and lumped mass are, respectively, expressed as
In the above formula, is a virtual symbol, and the velocity of the micro-element section can be obtained by calculating the first derivative of the Formula (12):
Similarly, the velocity of the concentrated mass is
In the above formula, (·) represents the partial derivative with respect to time, and (′) represents the partial derivative with respect to distance.
When the cantilever beam vibrates under external excitation, its kinetic energy is
Similarly, the kinetic energy, , of the concentrated mass, , can be expressed as
The kinetic energy of the PZT patch can be expressed as
The bending moment of the cantilever beam during vibration is
The bending potential energy of the beam is
Substituting (17) into (18), omitting the high-order small quantity, we can get
The elastic potential energy of the PZT patch can be expressed as
In the formula, .
The potential energy generated by the PZT patch can be expressed as
3.3. Lagrange Equation
Using the Lagrange equation, we can establish the motion equation of the tristable-pressure, variable-exponential-cross-section electric cantilever harvester, that is,
Using the Lagrange equation
where and are the generalized coordinates and generalized velocity of the system, respectively, and is the Lagrange function, where . The dissipation function of the system can be expressed as
Substituting Equations (14)–(16), (18)–(20) and (21) into Equations (23) and (24), the system vibration nonlinear differential equation is as below.
In the formula
3.4. Mode Function
In order to solve Equation (26), it is first necessary to solve the expression of the mode vibration shape, , function. Based on the Euler–Bernoulli beam theory, this paper first solves the free vibration equation of the constant-section beam:
where the variables and are the transverse bending stiffness and linear density, respectively, and is the transverse deflection function of the beam.
The piezoelectric cantilever works effectively under low-frequency vibration conditions, so its first-order bending vibration mode has the most significant impact on the dynamic response characteristics of the system. In this frequency range, the vibration response of the cantilever beam is dominated by the first-order bending mode, while the influence of other vibration modes is relatively small, and its vibration displacement can be written as
In the formula, is the generalized modal coordinate, and is the first-order mode shape of the bimorph piezoelectric cantilever beam, which can be written as
In the formula, is the first-order bending mode shape of beam with bimorph and is the first-order bending mode shape of beam without bimorph, and the mode function is expressed as
and
In the formula, , and are the linear densities of the PZT patch and the cantilever beam, respectively, and are the bending stiffnesses of the PZT patch and the cantilever beam, respectively.
The following boundary conditions are satisfied at the root and free end of the cantilever beam
There are the following boundary conditions at the junction of the two beams
In the formula, , , is the negligible moment of inertia of the center of mass of the end magnet, and is the mass of the end magnet.
Convert the above formula into vector form, we can get
where is the coefficient matrix of the modal equation, .
The solution of Formula (26) can be obtained by solving the determinant of , from which the first-order natural frequency and mode shape function of the system can be determined, and then the vibration displacement can be obtained.
4. Analysis of System Dynamic Response
In this paper, a variable-section cantilever beam with length L = 0.07 m and initial width b0 = 0.01 m is studied. The length of the PZT patch is Lp = 0.01 m and the initial width is also b0 = 0.01 m. Preliminary, the exponential coefficient p = −0.5 is seleted. For specific physical parameters, Table A1 of Appendix A can be referred to.
The 4th–5th order Rungekuta algorithm ODE45 is used to solve the electrolinear coupling equation of the piezoelectric vibration energy harvester represented by Equation (26) in the MATLAB simulation software, and the time-domain solution of the system under different initial conditions and different system parameters is obtained, such as vibration displacement, vibration velocity, output voltage and phase diagram. Here we uniformly default the initial condition to (0,0,0).
4.1. Potential Energy Analysis of Harvester
The interaction between magnets A, B and C is the main cause of the nonlinearity of the system. According to the Formulas (7)–(10), the distance dg between the fixed-end magnets and the horizontal distance d between the end magnets and the fixed-end magnets jointly determine the distribution of the magnetic field and the magnitude of the magnetic force of the tristable energy harvester system, thus affecting the potential energy of the energy harvester.
Figure 2 shows the distribution curves of the magnetic potential energy and total potential energy of the harvester when d = 17 mm and dg is 13 mm, 17 mm and 50 mm, respectively. It can be seen from the figure that as dg gradually increases, the harvester successively experienced a bistable state, monostable state and tristable state. When dg = 13 mm, the magnetic potential energy at the central position is the largest, so that the total potential energy forms two potential barriers at symmetrical positions on both sides, with the largest width and the harvester presents a bistable state; as dg increases to 17 mm, the magnetic potential energy is in the two short potential barriers formed on both sides, the magnetic potential energy at the center is concave, and the total potential energy appears at three stable equilibrium points, the potential well at the center becomes deeper and the harvester moves in a tristable state; as dg further increases to 50 mm, the horizontal distance between the magnets is too large, the total potential energy only has a potential well in the center and the harvester degenerates into monostable state.
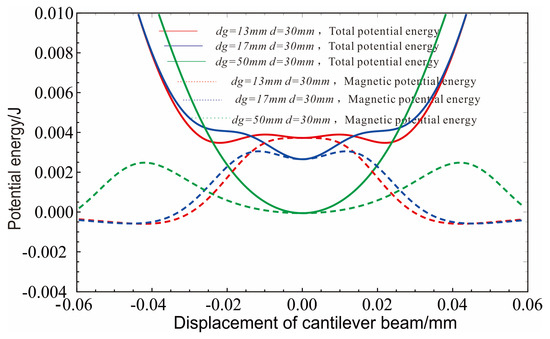
Figure 2.
When d = 30 mm and dg = 13, 17, 50 mm, the total potential energy and magnetic potential energy of the harvester.
Figure 3 shows the distribution curves of the magnetic potential energy and total potential energy of the harvester when dg = 17 mm and d is 30 mm, 35 mm and 50 mm, respectively. It can be seen from the figure that as dg gradually decreases, the magnetic potential energy at the center gradually increases, and the total potential energy also changes with this law. When d = 50 mm, because the distance between the end magnet and the fixed-end magnet is too large, the magnetic potential energy is small, the total potential energy curve is slightly affected and there is only one equilibrium position, which is in monostable state. As d increases to 35 mm, the potential energy of the magnetic field increases significantly, and a potential well begins to appear, which is still in a monostable state; when d = 30 mm, the potential energy of the magnetic field continues to increase, two potential wells appear, the center of the total potential energy well becomes deeper and the harvester begins to appear in three equilibrium positions at this time, forming a tristable structure. The case of d = 30 mm is consistent with Figure 2.

Figure 3.
When dg = 17 mm and d = 30, 35, 50 mm, the total potential energy and magnetic potential energy of the harvester.
4.2. Influence of Acceleration Amplitude on Dynamic Characteristics
Under the magnet distances d = 30 mm and dg = 17 mm, the excitation frequency f = 4 Hz is constant, and the excitation acceleration amplitude A is used as the bifurcation parameter to draw the bifurcation diagram. The tristable system exhibits a variety of nonlinear phenomena, as shown in Figure 4a.

Figure 4.
Bifurcation diagram and effects of different exciting acceleration amplitudes on energy harvester dynamics and output characteristics.
When the acceleration amplitude A < 2.4 g, the system cannot cross the potential barrier, makes small periodic oscillations in a single potential well and performs only monostable motion. Figure 4b shows the displacement velocity of the system when A = 1 g, the phase diagram and the output voltage response. The output voltage of the harvester is 0.5 mV. When the acceleration amplitude A = 2.4 g, the system crosses the potential barrier, and then the vibration amplitude and output voltage of the system continue to increase, and there is a tristable motion, and the output voltage can reach 6 mV, as shown in Figure 4c, A = 3 g. As the acceleration amplitude increases to 3.5~4.2 g, the system begins to exhibit a large-scale chaotic motion and there is a strange attractor (indicated by the red line in the Figure 4), which represents the acyclical, disordered system state in the chaotic system. The voltage output jumps rapidly, as shown in Figure 4d. By further increasing the excitation acceleration, the system crosses the next potential barrier until A = 5 g, the system behaves as a bistable single-cycle vibration, and the motion amplitude and output voltage amplitude are both large, as shown in Figure 4e. As the excitation acceleration amplitude is further increased, the system response alternates between chaotic, quasi-periodic and periodic motions.
4.3. Influence of Excitation Frequency on System Response Characteristics
Keeping the acceleration excitation amplitude at 2 g, the bifurcation diagram of the system with respect to the excitation frequency, f, is drawn. Changing the excitation frequency also causes chaos, as shown in Figure 5a.
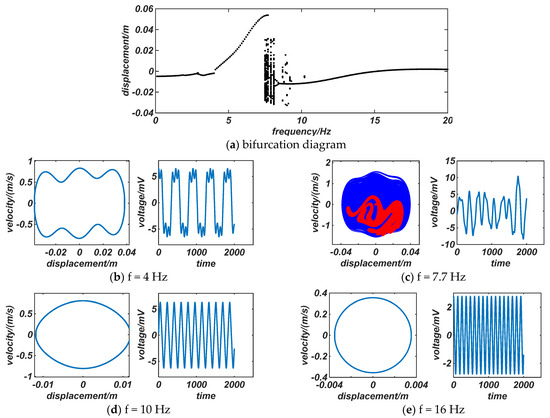
Figure 5.
Bifurcation diagram and effects of different excitation frequencies on energy harvesters’ dynamics and output characteristics.
In the low-frequency range f = 0~7.5 Hz, the harvester response shows a single-cycle motion whose amplitude gradually increases. Figure 5b shows the motion phase diagram when f = 4 Hz, and the maximum output voltage of the acquisition is 6 mV at this time; when the frequency comes to f = 7.6~8.1 Hz, the system responds to chaotic motion, and the output voltage jumps rapidly with time. Figure 5c shows the Poincaré diagram and output voltage of the system at f = 7.7 Hz; Figure 5d shows that within f = 8.2~15 Hz, the system initially exhibits a small-amplitude, double-periodic motion and some chaotic motion. As the excitation frequency is increased, the system gradually stabilizes and the motion amplitude gradually decreases. When entering the high-frequency region f > 15 Hz, the system has only a very small-amplitude, monostable periodic vibration, and the output voltage is only 3 mV, as shown in Figure 5e.
4.4. Influence of Magnet Spacing d on System Dynamics
Under the condition that the frequency f = 4 Hz, the excitation amplitude A = 2 g and the distance between the fixed magnets dg = 17 mm remain unchanged, the distance d between the terminal magnet and the fixed magnet is 30 mm, 35 mm and 50 mm, respectively, and an energy harvester is manufactured. The phase diagram and voltage output diagram are shown in Figure 6.

Figure 6.
Effects of different magnet horizontal distance d on dynamics and output characteristics.
It can be seen from Figure 6a that when d = 50 mm, due to the large horizontal distance between the end magnet and the fixed-end magnet, the nonlinear magnetic force has little effect on the harvester, and the harvester performs monostable periodic motion, and the output voltage of the harvester is 4 mV. When the distance between the end magnet and the fixed-end magnet is reduced to 40 mm, it can be seen from the phase diagram of the reaper movement that the magnetic force received by the end magnet increases, the speed of the reaper in the equilibrium position increases significantly, and the output voltage of the harvester reaches 5 mV, as shown in Figure 6b.
When the horizontal distance between the end magnet and the fixed-end magnet decreases to d = 35 mm, the nonlinear magnetic force between the magnets increases, the constraint of the nonlinear magnetic force on the energy harvester becomes larger and the motion state of the harvester jumps from monostable to tristable. In this state, an equilibrium position is formed at the central equilibrium position and at both ends, but the potential wells between each steady state are relatively shallow, and the acquisition voltage reaches 5.6 mV, as shown in Figure 6c.
When the horizontal distance between the end magnet and the fixed-end magnet is further reduced to d = 30 mm, the influence of the nonlinear magnetic force on the end magnet becomes more obvious, the tristable motion of the harvester becomes more obvious, and the potential well between the steady states becomes deeper, forming three stable equilibrium states, and the acquisition voltage reaches 6.2 mV, as shown in Figure 6d.
4.5. Influence of Magnet Spacing dg on System Dynamics
Through the analysis in Section 4.4, when the horizontal distance between the magnets is d = 30 mm, the influence of the nonlinear magnetic force on the system is more obvious. In the case when the frequency f = 4 Hz, the excitation amplitude A = 2 g and d = 30 mm, the distance of the end magnet from the fixed magnet, dg, is 13 mm, 17 mm and 50 mm, respectively, and the phase diagram and voltage output diagram of the energy harvester are shown in Figure 7. The harvester performs monostable, tristable and bistable motion, respectively, as dg decreases.

Figure 7.
Effects of different magnet distances, dg, on dynamics and output characteristics.
It can be seen from Figure 7a that when dg = 50 mm, because the distance between the end magnet and the fixed-end magnet is too large, the effect of the fixed-end magnet on the harvester is almost negligible, the harvester moves in a monostable state, the phase diagram is approximately circular, the system degenerates into a linear system and the output voltage of the harvester drops to 2 mV. When the distance of the fixed end magnet is reduced to 25 mm, the magnetic force of the end magnet increases, the movement of the harvester is irregular under the action of a nonlinear magnetic force and the output voltage of the harvester reaches 1 mV, which is 10 times higher than when dg = 50 mm, as shown in Figure 7b.
When the distance between the fixed-end magnets is reduced to dg = 17 mm, the distance between the fixed-end magnets and the end magnets decreases, the nonlinear magnetic force increases, the constraint of the nonlinear magnetic force on the energy harvester becomes larger, the motion state of the harvester changes from the monostable state to the tristable state, the potential well between the stable points is deep, forming three stable equilibrium states and the detection voltage reaches 6 mV, as shown in Figure 7c. When the distance between the fixed-end magnets is further reduced to d = 13 mm, the influence of the nonlinear magnetic force on the end magnets becomes more obvious, the tristable motion of the harvester degenerates into a bistable state, and the two fixed-end magnets are equivalent. For the magnet at the center of the fixed end, the essentially double magnetic force makes the potential well between the stable points deeper, and the acquisition voltage can reach 8 mV, as shown in Figure 7d.
4.6. Influence of Exponential Decay Coefficient on System Dynamics
Studies have shown that narrowing the cantilever beam with a variable cross section can reduce the resonant frequency of the cantilever and improve the performance of the harvester [30]. In this section, four exponential sections with p = −0.5, p = −0.8, p = −1 and p = −1.5 are selected, as shown in Figure 8, and the first-order natural frequencies of the four-section cantilever beam structure are obtained as shown in Table 1. It can be seen from the table that the natural frequency of the rectangular section beam is the largest. For the exponential section cantilever beam, as p decreases, the natural frequency of the cantilever beam structure gradually decreases, and when the excitation frequency of the external environment reaches the natural frequency of the cantilever beam, the piezoelectric cantilever beam has the best energy-harvesting performance. Therefore, the energy-harvesting performance of the exponential cantilever is better at low frequencies.

Figure 8.
Cantilever beams with different exponential decay coefficient sections.

Table 1.
The first natural frequency under different decay coefficient p.
When the excitation frequency = 4 Hz, the excitation acceleration amplitude is A = 2 g, the horizontal distance between the magnets is d = 30 mm, and the distance between the magnets at the fixed end is dg = 17 mm, the harvesters with five cross sections can be tristable. The phase diagram and voltage output diagram of the exponential decay section of the energy harvester are shown in Figure 9.

Figure 9.
Dynamics and output characteristics of energy harvesters with different exponential decay coefficients.
According to Figure 9, after the variable exponential section of the harvester reaches the tristable state; the motion amplitudes in the left and right steady states are much larger than that of the rectangular beam. As for the output voltage, the output voltages of the four kinds of exponential cantilever beams are all higher than those of the rectangular beams, and the output voltage of the exponential cantilever beams gradually increases with the decrease in the exponential decay coefficient due to the excessive concentration of the piezoelectric patches attached to the fixed end of the cantilever, and the exponentially changing section changes the strain distribution of the cantilever beam, making the stress distribution of the cantilever beam more uniform on the whole beam, and the PZT patches can better generate the piezoelectric effect and increase the output voltage.
If the excitation frequency is reduced to f = 3 Hz and f = 2 Hz and other conditions are kept unchanged, the phase diagram and voltage output diagram of the energy harvester with an exponential decay cross section are shown in Figure 10.

Figure 10.
Dynamics and output characteristics of exponentially decaying energy harvesters at different frequencies.
When f = 3 Hz, the cantilever beam with exponent coefficient p = −1.5 is first excited to tristable motion, and the output voltage remains the highest. This is related to its lowest natural frequency, and it is precisely because of its high energy harvesting efficiency at low frequencies that its use in harvesting voltage in the environment is greatly improved, and it has high research value. As the excitation frequency is reduced to f = 2 Hz, the rectangular-cross-section energy harvester moves in the well with low frequency and small amplitude, and the voltage of the energy harvester is much lower than that of the exponential-cross-section harvester. At the same time, the peak voltage of the exponential attenuation section of the harvester has the widest frequency band, which is three times that of the rectangular section of the cantilever beam.
In order to further study the performance of the exponentially changing cross section on the harvesting voltage and power of the piezoelectric cantilever, a power sweep analysis of five energy harvesters was carried out. According to the research in Section 4.1, Section 4.2, Section 4.3, Section 4.4 and Section 4.5, the parameters d = 30 mm and dg = 17 mm are selected, f is gradually increased from 0 Hz to 15 Hz and the average output power of each energy harvester at the current frequency is calculated at the same time.
In this paper, the time-domain voltage output of the voltage signal changing with time can be obtained through the ODE45 algorithm. The energy harvesting circuit is completely composed of a load resistor with R = 1 MΩ. The output of the energy harvester is completely consumed on the load resistor, and the instantaneous power can be obtained by multiplying the voltage and current values at each time step.
Since it is a purely resistive circuit, the time-domain output current can be expressed as:
where V(t) is a function of voltage over time and I(t) is a function of current over time.
Therefore, at each time t, the time-domain power, P(t), can be calculated as:
Figure 11 is the frequency–power sweep response graph of five energy harvesters. Figure 12 shows the frequency–power sweep response of five energy harvesters at low frequency.

Figure 11.
Frequency–power sweep response diagrams of five types of energy harvesters.

Figure 12.
Low-frequency–power sweep response diagrams of five types of energy harvesters.
It can be seen from Figure 11 that the average power of the exponential cantilever is higher than that of the rectangular cantilever. In the mid-frequency band, each cantilever reaches the resonance frequency correspondingly, the power increases sharply, and the average power of the exponential cantilever is higher than that of the rectangular cantilever. In the high-frequency band, the power of the four exponential cantilever beams has the opposite relationship to the low-frequency band, which is related to its natural frequency, and the power gradually decreases as the decay coefficient becomes smaller.
It can be seen from Figure 12 that the average power of the exponential cantilever is always higher than that of the rectangular cantilever in the low-frequency band, the average power gradually increases as the decay coefficient decreases and the power of the cantilever with the decay coefficient p = −1.5 is always the highest.
In order to better study the energy harvesting performance of exponentially attenuated cantilever beams under low-frequency excitation, Table 2 shows the average power and peak voltage of five piezoelectric energy harvesters under several low-frequency excitations. It can be found from Table 2 that under an f = 2, 3, 4, 5 Hz excitation, the peak voltage of the energy harvester at the exponential decay section increases by 1.51–88.24 times, and the average power increases by 1.22–7.03 times. This also verifies that the exponential decay section has better performance than the constant section of the cantilever beam.

Table 2.
Output characteristics of cantilever beams with different exponential cross sections under different low-frequency excitations.
In order to compare the performance of each energy harvester more directly, the data visualization in Table 2 is shown in Figure 13.

Figure 13.
Output characteristics of cantilever beams with different exponential cross sections under different low-frequency excitations.
5. Discussion
This study shows that narrowing the cross section can improve the energy harvesting performance of piezoelectric energy harvesters and increase the energy output power. At the same time, this paper studies the influence of external influence and internal structure on the piezoelectric energy harvester. Research shows that for external influences, the acceleration amplitude and excitation frequency of the external excitation can change the motion amplitude of the energy harvester. By adjusting the excitation acceleration amplitude to A = 2–3.5 g and the excitation frequency to f = 4–7.5 Hz, a larger and more stable voltage output can be obtained when the harvester is in a state of large-amplitude motion.
For the internal structure of the harvester, the settings of parameters such as the horizontal magnet distance d and the fixed-end magnet distance dg directly determine the steady state of the harvester. When d = 30 mm and dg = 17 m are set, the piezoelectric vibration energy harvester is made to move in a tristable state, respectively, which can increase the frequency bandwidth and output power of the peak voltage.
The article further studies the output characteristics of the cantilever beam with different exponential decay coefficient sections and finds that the exponential decay section can optimize the stress distribution of the cantilever beam. Through the power sweep analysis, in the low-frequency band f = 0–7 Hz, the output power of the section with coefficient p = −1.5 is up to 7.03 times that of the rectangular section. In the mid-frequency band f = 7–12 Hz, the output power of each harvester can reach two times more than that of the rectangular cantilever. In the high-frequency band above f = 12 Hz, the energy harvesting power of the exponential cantilever is still higher than that of the rectangular cantilever.
Table 3 shows the energy harvesting data for other energy harvesters with different structures. Through comparison, it can be found that under low-frequency excitation (0–10 Hz), the tristable exponential section of the piezoelectric energy harvester proposed in this paper has greater advantages at the highest power density. However, this result can be influenced by a variety of factors, including the material of the cantilever and PZT and the amplitude parameter of the applied excitation. It is important to note that while increasing the applied force results in a higher voltage output, it can also lead to more microstructural cracks, which reduce the life expectancy of the energy harvester.

Table 3.
Harvested performance in the present study and the reported data in the literature.
In practical applications, we have to make a trade-off between lifetime and power density. Even as we pursue higher power densities, we need to consider the challenge of crack generation, which can affect the long-term performance and reliability of the harvester. Therefore, when designing and optimizing the harvester, these factors need to be considered comprehensively to ensure the best performance and lifetime in specific application scenarios.
In general, the cantilever beam with an exponential decay cross section investigated in this paper has high research value in the field of low-frequency micromechanics. This paper carries a meaningful exploration on the determination of the optimal section parameters of the future piezoelectric cantilever beam under certain environmental excitations.
6. Conclusions
In this paper, a cantilever beam piezoelectric energy harvester with an exponential decay section is proposed, and a dynamic model for the tristable, exponential piezoelectric energy harvester is established. The influence of the dynamic characteristics of the system is investigated, and the influence of different exponential decay coefficients on the output voltage and harvester power is studied. In the paper, we come to the following conclusions:
- Increasing the excitation acceleration amplitude can quickly make the system overcome the potential barrier, enter a state of large vibration, and increase the output voltage of the harvester; increasing the excitation frequency can also make the system enter a state of large vibration in the low-frequency range f = 0~7.5 Hz. However, after entering the medium- and high-frequency range f > 7.5 Hz, increasing the excitation frequency only will make the system enter a chaotic state and a state of small vibration;
- Adjusting the horizontal distance between the magnets can change the monostable and tristable motion states of the system; adjusting the fixed-end magnet distance can realize the transition of the system from monostable to tristable and bistable. The potential well of the system state is shallower and has a higher output voltage than the monostable and bistable states;
- The beam with an exponential decay section can reduce the first natural frequency of the system. As the exponential decay gradually decreases, the cantilever beam with the smaller decay coefficient, p, has higher voltage and power in the low-frequency region. This research shows that under low-frequency excitation with the exponential decay coefficient p = −1.5, the output power of the energy harvester with an exponential cross section is up to seven times higher than that of the cantilever beam with a rectangular cross section. Improving the power density of piezoelectric beams provides a new idea for optimizing the performance of energy harvesters.
Author Contributions
Conceptualization, Z.C. and K.Z.; methodology, K.Z.; software, Z.C. and K.Z.; validation, Z.C., K.Z. and T.Y.; formal analysis, T.Y.; investigation, S.H.; data curation, Z.C. and K.Z.; writing—original draft preparation, Z.C.; writing—review and editing, Z.C. and K.Z.; visualization, T.Y.; supervision, S.H.; funding acquisition, S.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 12072234.
Data Availability Statement
Datasets are available upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Main physical parameters of piezoelectric energy harvesters.
Table A1.
Main physical parameters of piezoelectric energy harvesters.
| Physical Parameters | Symbols and Units | Value |
|---|---|---|
| Cantilever length | L/mm | 70 |
| Cantilever width | b/mm | 10 |
| Cantilever thickness | h/mm | 0.15 |
| Cantilever density | ρs/(kg/m3) | 7800 |
| Cantilever elastic modulus | Es/GPa | 212 |
| PZT patch length | Lp/mm | 10 |
| PZT patch width | bp/mm | 10 |
| PZT patch thickness | hp/mm | 0.5 |
| PZT patch density | ρp/(kg/m3) | 7450 |
| PZT patch elastic modulus | Ep/GPa | 21.45 |
| PZT material constants | e31/(C·m−1) | −4.08 |
| Magnet density | ρm/(kg/m3) | 7500 |
| Magnet volume | VA, VB, VC/m3 | 0.55 × 10−6 |
| Magnet magnetization strength | MA, MB, MC/(A/m) | 1.19 × 106 |
References
- Yang, T.; Zhou, S.; Cao, Q.; Zhang, W.; Chen, L. Some advances in nonlinear vibration energy harvesting technology. Chin. J. Theor. Appl. Mech. 2021, 53, 2894–2909. [Google Scholar]
- Sun, Y.; Li, Y.Z.; Yuan, M. Requirements, challenges, and novel ideas for wearables on power supply and energy harvesting. Nano Energy 2023, 115, 108715. [Google Scholar] [CrossRef]
- Jiang, J.; Liu, S.; Feng, L.; Zhao, D. A review of piezoelectric vibration energy harvesting with magnetic coupling based on different structural characteristics. Micromachines 2021, 12, 436. [Google Scholar] [CrossRef] [PubMed]
- Man, D.W.; Bai, Y.Y.; Hu, Q.N.; Xu, H.M.; Xu, G.Z.; Tang, L.P. Dynamic characteristic analysis of tri-stable piezoelectric energy harvester with double elastic amplifiers. J. Intell. Syst. Control 2023, 2, 54–69. [Google Scholar] [CrossRef]
- Bairagi, S.; Shahadat, M.; Mulvihill, D.M.; Ali, W. Mechanical energy harvesting and self-powered electronic applications of textile-based piezoelectric nanogenerators: A systematic review. Nano Energy 2023, 111, 108414. [Google Scholar] [CrossRef]
- Fan, F.R.; Tang, W.; Wang, Z.L. Flexible nanogenerators for energy harvesting and self-powered electronics. Adv. Mater. 2016, 28, 4283–4305. [Google Scholar] [CrossRef]
- Li, X.; Upadrashta, D.; Yu, K.; Yang, Y. Sandwich piezoelectric energy harvester: Analytical modeling and experimental validation. Energy Convers. Manag. 2018, 176, 69–85. [Google Scholar] [CrossRef]
- Li, H.; Tian, C.; Deng, Z.D. Energy harvesting from low frequency applications using piezoelectric materials. Appl. Phys. Rev. 2014, 1, 4. [Google Scholar] [CrossRef]
- Daqaq, M.F. Response of uni-modal duffing-type harvesters to random forced excitations. J. Sound Vib. 2010, 329, 3621–3631. [Google Scholar] [CrossRef]
- Ziying, W.; Wenteng, Y.; Qiang, L. Research on the superharmonic effects of bistable electromagnetic vibration energy harvester. Chin. J. Comput. Mech. 2017, 43, 623–630. [Google Scholar]
- Wang, G.; Wu, H.; Liao, W.H.; Cui, S.; Zhao, Z.; Tan, J. A modified magnetic force model and experimental validation of a tri-stable piezoelectric energy harvester. J. Intell. Mater. Syst. Struct. 2020, 31, 967–979. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Q.; Wang, W.; Feng, J. A low-frequency, wideband quad-stable energy harvester using combined nonlinearity and frequency up-conversion by cantilever-surface contact. Mech. Syst. Signal Process. 2018, 112, 305–318. [Google Scholar] [CrossRef]
- Erturk, A.; Hoffmann, J.; Inman, D.J. A piezomagnetoelastic structure for broadband vibration energy harvesting. Appl. Phys. Lett. 2009, 94, 254102. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Broadband piezoelectric power generation on high-energy orbits of the bistable Duffing oscil-lator with electromechanical coupling. J. Sound Vib. 2011, 330, 2339–2353. [Google Scholar] [CrossRef]
- Singh, K.A.; Kumar, R.; Weber, R.J. A broadband bistable piezoelectric energy harvester with nonlinear high-power ex-traction. IEEE Trans. Power Electron. 2015, 30, 6763–6774. [Google Scholar] [CrossRef]
- Cao, J.; Zhou, S.; Inman, D.J.; Chen, Y. Chaos in the fractionally damped broadband piezoelectric energy generator. Nonlinear Dyn. 2015, 80, 1705–1719. [Google Scholar] [CrossRef]
- Cao, J.; Zhou, S.; Inman, D.J.; Lin, J. Nonlinear dynamic characteristics of variable inclination magnetically coupled pie-zoelectric energy harvesters. J. Vib. Acoust. 2015, 137, 021015. [Google Scholar] [CrossRef]
- Zhao, Z.X.; Wang, G.Q.; Tan, J.P. Dynamic characteristics in time-frequency domain and experimental research of the bi-stable piezoelectric vibration energy harvester. Chin. J. Sens. Actuators 2019, 32, 1200–1208. [Google Scholar]
- Zhou, S.; Cao, J.; Inman, D.J.; Lin, J.; Liu, S.; Wang, Z. Broadband tristable energy harvester: Modeling and experiment verification. Appl. Energy 2014, 133, 33–39. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Lin, J.; Wang, Z. Exploitation of a tristable nonlinear oscillator for improving broadband vibration energy harvesting. Eur. Phys. J.-Appl. Phys. 2014, 67, 30902. [Google Scholar] [CrossRef]
- Zhou, S.; Zuo, L. Nonlinear dynamic analysis of asymmetric tristable energy harvesters for enhanced energy harvesting. Commun. Nonlinear Sci. Numer. Simul. 2018, 61, 271–284. [Google Scholar] [CrossRef]
- Li, Y.; Ju, Y.; Tan, J. Dynamic Modeling, simulation and experimental study of a tristable piezoelectric vibration energy harvester. Chin. J. Sens. Actuators 2020, 33, 1098–1109. [Google Scholar]
- Wang, G.; Zhao, Z.; Liao, W.H.; Tan, J.; Ju, Y.; Li, Y. Characteristics of a tri-stable piezoelectric vibration energy harvester by considering geometric nonlinearity and gravitation effects. Mech. Syst. Signal Process. 2020, 138, 106571. [Google Scholar] [CrossRef]
- Hai-Tao, L.; Hu, D.; Xing-Jian, J.; Wei-Yang, Q.; Li-Qun, C. Improving the performance of a tri-stable energy harvester with a staircase-shaped potential well. Mech. Syst. Signal Process. 2021, 159, 107805. [Google Scholar] [CrossRef]
- Zhou, Z.; Qin, W.; Zhu, P. Harvesting performance of quad-stable piezoelectric energy harvester: Modeling and experiment. Mech. Syst. Signal Process. 2018, 110, 260–272. [Google Scholar] [CrossRef]
- Zhou, Z.; Qin, W.; Yang, Y.; Zhu, P. Improving efficiency of energy harvesting by a novel penta-stable configuration. Sens. Actuators A Phys. 2017, 265, 297–305. [Google Scholar] [CrossRef]
- He, X.; Li, D.; Zhou, H.; Hui, X.; Mu, X. Theoretical and experimental studies on MEMS variable cross-section cantilever beam based piezoelectric vibration energy harvester. Micromachines 2021, 12, 772. [Google Scholar] [CrossRef] [PubMed]
- Benasciutti, D.; Moro, L.; Zelenika, S.; Brusa, E. Vibration energy scavenging via piezoelectric bimorphs of optimized shapes. Microsyst. Technol. 2010, 16, 657–668. [Google Scholar] [CrossRef]
- Baker, J.; Roundy, S.; Wright, P. Alternative geometries for increasing power density in vibration energy scavenging for wireless sensor networks. In Proceedings of the 3rd International Energy Conversion Engineering Conference, San Francisco, CA, USA, 15 August 2005. [Google Scholar]
- Shan, X.B.; Yuan, J.B.; Xie, T.; Chen, W.S. Modeling and test of piezoelectric cantilever generators with different shapes. J. Vib. Shock 2010, 29, 177–180. [Google Scholar]
- Wang, J.J.; Cao, D.X.; Yao, M.H. Dynamic characteristic analysis of piezoelectric energy harvester with variable cross-section cantilever beam. Piezoelectr. Acoustooptics 2018, 40, 727–731. [Google Scholar]
- He, T.; Ma, J.; Liu, Y.; Li, B.; Chu, J. Study on an energy harvester based on trapezoidal piezoelectric cantilever. Yadian Yu Shengguang 2012, 34, 872–876. [Google Scholar]
- Tan, Y.K.; Gao, S.Q.; Zhang, G.Y. Study on the characteristics of trapezoidal cantilever piezoelectric energy harvester. Piezoelectr. Acoustooptics 2016, 38, 579–583. [Google Scholar]
- Erturk, A.; Inman, D.J. A distributed parameter electromechanical model for cantilevered piezoelectric energy harvesters. J. Vib. Acoust. 2008, 130, 041002. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations. Smart Mater. Struct. 2009, 18, 025009. [Google Scholar] [CrossRef]
- Ismail, M.R.; Omar, F.K.; Ajaj, R.; Ghodsi, M. Correction factor of lumped parameter model for linearly tapered piezoelectric cantilever. J. Intell. Mater. Syst. Struct. 2022, 33, 474–488. [Google Scholar] [CrossRef]
- Salmani, H.; Rahimi, G.H.; Hosseini Kordkheili, S.A. An exact analytical solution to exponentially tapered piezoelectric energy harvester. Shock Vib. 2015, 2015, 426876. [Google Scholar] [CrossRef]
- Wu, Y.; Qiu, J.; Zhou, S.; Ji, H.; Chen, Y.; Li, S. A piezoelectric spring pendulum oscillator used for multi-directional and ultra-low frequency vibration energy harvesting. Appl. Energy 2018, 231, 600–614. [Google Scholar] [CrossRef]
- Ghodsi, M.; Mohammadzaheri, M.; Soltani, P. Analysis of Cantilever Triple-Layer Piezoelectric Harvester (CTLPH): Non-Resonance Applications. Energies 2023, 16, 3129. [Google Scholar] [CrossRef]
- Mohamed, K.; Elgamal, H.; Kouritem, S.A. An experimental validation of a new shape optimization technique for piezoelectric harvesting cantilever beams. Alex. Eng. J. 2021, 60, 1751–1766. [Google Scholar] [CrossRef]
- Ma, T.; Ding, Y.; Wu, X.; Chen, N.; Yin, M. Research on piezoelectric vibration energy harvester with variable section circular beam. J. Low Freq. Noise Vib. Act. Control 2021, 40, 753–771. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).