Rock Typing Approaches for Effective Complex Carbonate Reservoir Characterization
Abstract
:1. Introduction
- -
- Macropores (2 µm < R35 < 10 µm);
- -
- Mesopores (0.5 µm < R35 < 2 µm);
- -
- Micropores (0.1 µm < R35 < 0.5 µm).
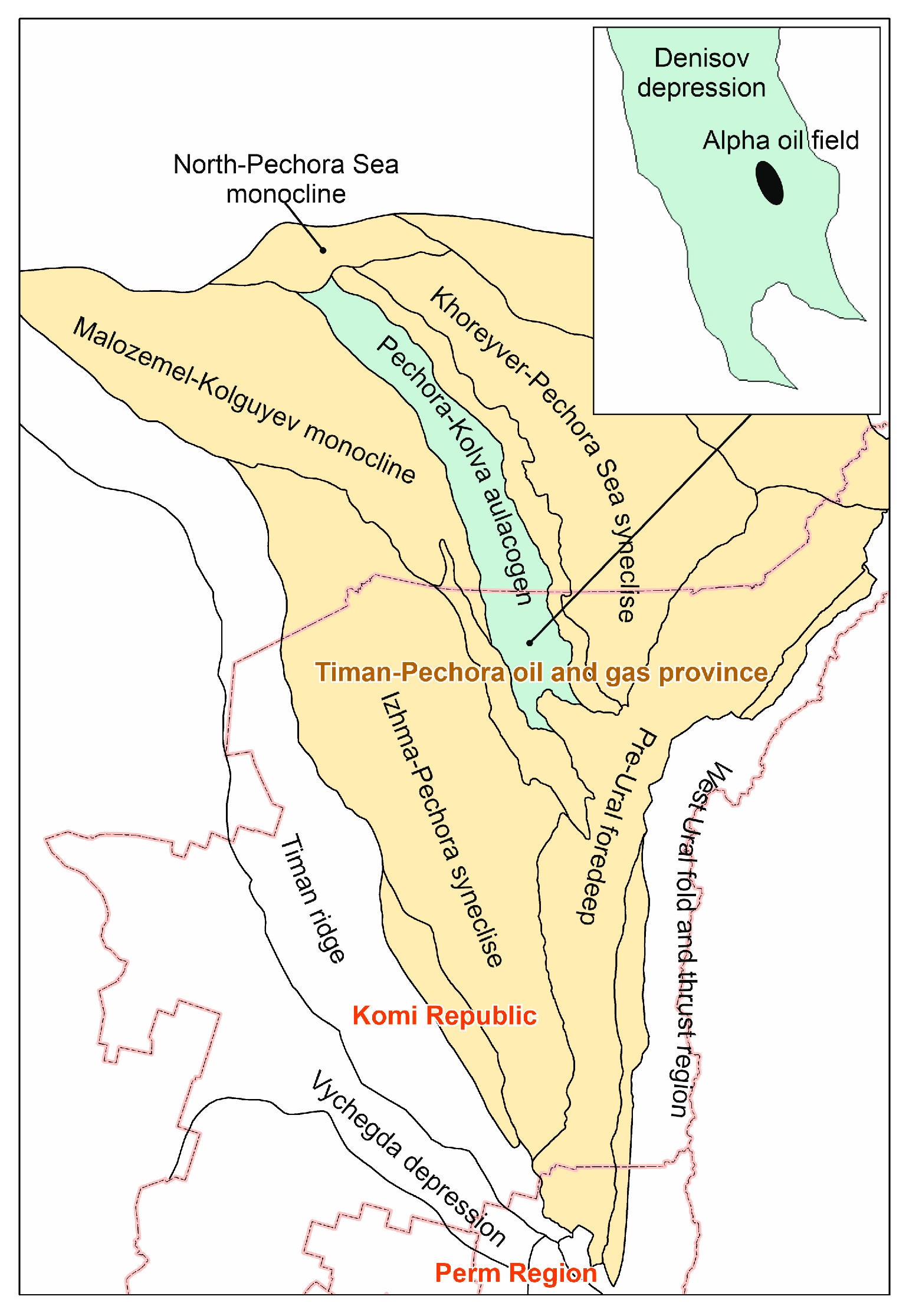
2. Geological Settings
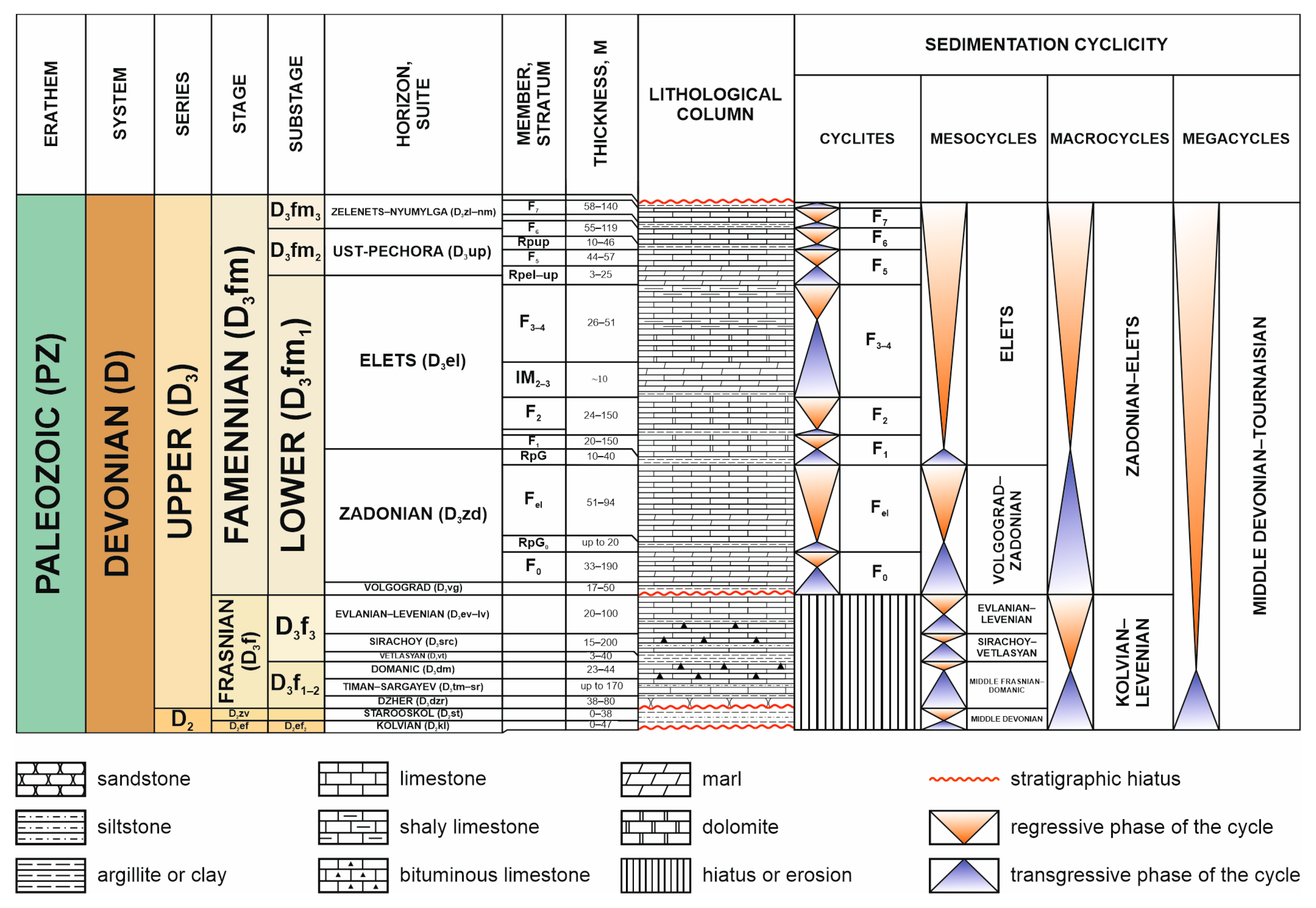
3. Materials and Methods
4. Results
- Class 1—micropores (0.1 µm < R35 < 0.5 µm);
- Class 2—mesopores (0.5 µm < R35 < 2 µm);
- Class 3—macropores (2 µm < R35 < 10 µm);
- Class 0—caverns (>10 µm).
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tavakoli, V. Carbonate Reservoir Heterogeneity: Overcoming the Challenges; Springer International Publishing: Tehran, Iran, 2019; pp. 1–108. [Google Scholar]
- Sharifi-Yazdi, M.; Rahimpour-Bonab, H.; Nazemi, M.; Tavakoli, V.; Gharechelou, S. Diagenetic impacts on hydraulic flow unit properties: Insight from the Jurassic carbonate Upper Arab Formation in the Persian Gulf. J. Pet. Explor. Prod. Technol. 2020, 10, 1783–1802. [Google Scholar] [CrossRef]
- Tabrizinejadas, S.; Fahs, M.; Hoteit, H.; Younes, A.; Ataie-Ashtiani, B.; Simmons, C.; Carrayrou, J. Effect of temperature on convective-reactive transport of CO2 in geological formations. Int. J. Greenh. Gas Control 2023, 128, 103944. [Google Scholar] [CrossRef]
- Al-Otaibi, M.; Abdullah, E.; Hanafy, S. Prediction of Permeability from Logging Data Using Artificial Intelligence Neural Networks. In Proceedings of the SPE Western Regional Meeting, Anchorage, AK, USA, 22–25 May 2023. [Google Scholar] [CrossRef]
- Mustafa, R.; Sameera, H. Studying the Effect of Permeability Prediction on Reservoir History Matching by Using Artificial Intelligence and Flow Zone Indicator Methods. Iraqi Geol. J. 2023, 56, 9–21. [Google Scholar] [CrossRef]
- Zolotukhin, A.B.; Gayubov, A.T. Machine learning in reservoir permeability prediction and modelling of fluid flow in porous media. IOP Conf. Ser. Mater. Sci. Eng. 2019, 700, 012023. [Google Scholar] [CrossRef]
- Efremova, E.I.; Putilov, I.S. On the question of hydraulic flow units use in terrigenous deposits taking into account facies (on the example of the Sof’inskoye field in the Perm Krai). J. Pet. Min. Eng. 2022, 22, 52–57. [Google Scholar]
- Antoniuk, V.; Bezrodna, I.; Petrokushyn, O. Multiple regressions and ann techniques to predict permeability from pore structure for terrigenous reservoirs, west-shebelynska area. Eur. Assoc. Geosci. Eng. 2019, 2019, 1–5. [Google Scholar] [CrossRef]
- Srinivasan, S.; Leung, J.Y. Petroleum Reservoir Modeling and Simulation: Geology, Geostatistics, and Performance Prediction, 1st ed.; McGraw Hill: New York, NY, USA, 2022; Available online: https://www.accessengineeringlibrary.com/content/book/9781259834295 (accessed on 1 February 2023).
- Haddad, A.; Lathion, R.; Courgeon, S.; Fabre, G.; Martinuzzi, V.; Pedraza, S.; Hauvette, L.; Games, F. Multi-Scale Karstic Reservoir Characterization: An Innovative Approach to Improve Reservoir Model Predictions and Decision Making. In Proceedings of the International Petroleum Technology Conference, Riyadh, Saudi Arabia, 21–23 February 2022. [Google Scholar] [CrossRef]
- Mulyanto, B.; Dewanto, O.; Yuliani, A.; Yogi, A.; Wibowo, R. Porosity and permeability prediction using pore geometry structure method on tight carbonate reservoir Porosity and permeability prediction using pore geometry structure method on tight carbonate reservoir. In Proceedings of the 9th International Conference on Theoretical and Applied Physics (ICTAP), Bandar Lampung, Indonesia, 15 July 2020. [Google Scholar] [CrossRef]
- Krivoshchekov, S.; Kochnev, A.; Kozyrev, N.; Ozhgibesov, E. Factoring Permeability Anisotropy in Complex Carbonate Reservoirs in Selecting an Optimum Field Development Strategy. Energies 2022, 15, 8866. [Google Scholar] [CrossRef]
- Lathion, R.; Courgeon, S.; Martinuzzi, V.; Fabre, G.; Haddad, A.; Games, F. Identification and integrated characterization of large-scale karstic network: Critical impact on reservoir understanding and modeling. In Proceedings of the 8ème Congrès Français de Sédimentologie—ASF 2022, Brest, Belarus, 28–30 September 2022. [Google Scholar]
- Shishaev, G.; Demyanov, V.; Arnold, D.; Vygon, R. History Matching and Uncertainty Quantification of Reservoir Performance with Generative Deep Learning and Graph Convolutions. In Proceedings of the International Petroleum Technology Conference, Riyadh, Saudi Arabia, 21–23 February 2022. [Google Scholar] [CrossRef]
- Robail, F.; Sanyal, S.; Azudin, A.; Koh, K.; Nizar, F.; Rosli, U. Machine Learning for Facies Distribution of Large Carbonate Reservoir Models—A Case Study. In Proceedings of the International Petroleum Technology Conference, Bangkok, Thailand, 1–3 March 2023. [Google Scholar] [CrossRef]
- Elarouci, F.; Maalouf, C.; Espinoza, I.; Al-jaberi, S.; Amer, M.; Smith, S.; Jalalh, A. Integrated Reservoir Characterization to Approach the Carbonate Permeability Distribution Challenges: Case Study from Offshore Abu Dhabi. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 7–10 November 2016. [Google Scholar] [CrossRef]
- Albreiki, M.; Geiger, S.; Corbett, P. Impact of modelling decisions and rock typing schemes on oil in place estimates in a giant carbonate reservoir in the Middle East. Pet. Geosci. 2021, 28, 1–21. [Google Scholar] [CrossRef]
- Palabiran, M.; Sesilia, N.; Akbar, M.N.A. An Analysis of Rock Typing Methods in Carbonate Rocks For Better Carbonate Reservoir Characterization: A Case Study of Minahaki Carbonate Formation, Banggai Sula Basin, Central Sulawesi. In Proceedings of the 41th Scientific Annual Meeting of Indonesian Association of Geophysicists, Lampung, Indonesian, 26–29 September 2016. [Google Scholar]
- Archie, G.E. Classification of Carbonate Reservoir Rocks and Petrophysical Considerations. AAPG Bull. 1952, 36, 278–298. [Google Scholar] [CrossRef]
- Raznicyn, A.; Putilov, I. Development of a Methodological Approach to Identifying Petrophysical Types of Complicated Carbonate Rocks According to Laboratory Core Studies. Perm J. Pet. Min. Eng. 2021, 21, 109–116. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Lake, L.; Sahimi, M. Insights Into Rock Typing: A Critical Study. SPE J. 2018, 24, 230–242. [Google Scholar] [CrossRef]
- Ellabad, Y.; Corbett, P.W.M.; Straub, R. Hydraulic Units approach conditioned by well testing for better permeability modeling in a North African Oil Field. In Proceedings of the 2001 International Symposium of the Society of Core Analysts, Edinburgh, UK, 17–19 September 2001. [Google Scholar]
- Lazim, S.A.; Hamd-Allah, S.M.; Jawad, A. Permeability Estimation for Carbonate Reservoir (Case Study/South Iraqi Field). Iraqi J. Chem. Pet. Eng. 2018, 19, 41–45. [Google Scholar] [CrossRef]
- El-Sawy, M.Z.; Abuhagaza, A.A.; Nabawy, B.; Lashin, A. Rock typing and hydraulic flow units as a successful tool for reservoir characterization of Bentiu-Abu Gabra sequence, Muglad basin, southwest Sudan. J. Afr. Earth Sci. 2020, 171, 103961. [Google Scholar] [CrossRef]
- Nabawy, B.; Rashed, M.; Mansour, A.; Afifi, W. Petrophysical and microfacies analysis as a tool for reservoir rock typing and modeling: Rudeis Formation, off-shore October Oil Field, Sinai. Mar. Pet. Geol. 2018, 97, 260–276. [Google Scholar] [CrossRef]
- Irawan, D.; Wihdany, F.I.; Idea, K. Permeability Anisotropy Effect in Reservoir Characterization: New Rock Typing Approach. In Proceedings of the Forty-Third Annual Convention & Exhibition, Jakarta, Indonesia, 4–6 September 2019. [Google Scholar]
- Kolodzie, S. Analysis of pore throat size and use of the Waxman–Smits equation to determine OOIP in Spindle Field, Colorado. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 21 September 1980. [Google Scholar] [CrossRef]
- Pittman, E.D. Relationship of porosity and permeability to various parameters derived from mercury injection-capillary pressure curves for sandstone. Am. Assoc. Pet. Geol. Bull. 1992, 76, 191–198. [Google Scholar] [CrossRef]
- Sousa, A.M.; Ines, N.; Bizarro, P.; Ribeiro, M.T. Improving Carbonate Reservoir Characterization and Modelling through the Definition of Reservoir Rock Types by Integrating Depositional and Diagenetic Trends. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 10–13 November 2014. [Google Scholar] [CrossRef]
- Permadi, P.; Susilo, A. Permeability Prediction and Characteristics of Pore Structure and Geometry as Inferred from Core Data. In Proceedings of the 2009 SPE/EAGE Reservoir Characterization and Simulation Conference, Abu Dhabi, United Arab Emirates, 19–21 October 2009. [Google Scholar] [CrossRef]
- Choquette, P.W.; Pray, L.C. Geologic Nomenclature and Classification of Porosity in Sedimentary Carbonates. Am. Assoc. Pet. Geol. Bull. 1970, 54, 207–250. [Google Scholar] [CrossRef]
- Dunham, R.J. Classification of Carbonate Rocks According to Depositional Texture. In Classification of Carbonate Rocks—A Symposium; The American Association of Petroleum Geologists: Tulsa, OK, USA, 1962; pp. 108–121. [Google Scholar]
- Repina, V.A.; Galkin, V.I.; Galkin, S.V. Complex petrophysical correction in the adaptation of geological hydrodynamic models (on the example of Visean pool of Gondyrev oil field). J. Min. Inst. 2018, 231, 268–274. [Google Scholar] [CrossRef]
- Galkin, V.I.; Ponomareva, I.N.; Repina, V.A. Study of the process of oil recovery in reservoirs of various types of voids using multivariate statistical analysis. Bull. Perm Natl. Res. Polytech. Univ. Geol. Oil Gas Eng. Min. 2016, 15, 145–154. [Google Scholar]
- Putilov, I.; Kozyrev, N.; Demyanov, V.; Krivoshchekov, S.; Kochnev, A. Factoring in Scale Effect of Core Permeability at Reservoir Simulation Modeling. SPE J. 2022, 27, 1930–1942. [Google Scholar] [CrossRef]
- Galvao, P.; Halihan, T.; Hirata, R. The karst permeability scale effect of Sete Lagoas, MG, Brazil. J. Hydrol. 2016, 532, 149–162. [Google Scholar] [CrossRef]
- Corbett, P.W.M.; Potter, D.K. Petrotyping: A basemap and atlas for navigating through permeability and porosity data for reservoir comparison and permeability prediction. In Proceedings of the International Symposium of the Society of Core Analysts, Abu Dhabi, United Arab Emirates, 5–9 September 2004. [Google Scholar]
- Garrouch, A.A.; Al-Sultan, A.A. Exploring the link between the flow zone indicator and key open-hole log measurements: An application of dimensional analysis. Pet. Geosci. 2019, 25, 219–234. [Google Scholar] [CrossRef]
- Lake, L.; Jensen, J. A review of heterogeneity measures used in Reservoir Characterisation. In Situ 1991, 15, 409–440. [Google Scholar]
- Gunter, G.W.; Finneran, J.M.; Hartmann, D.J.; Miller, J.D. Early Determination of Reservoir Flow Units Using an Integrated Petrophysical Method. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 5 October 1997. [Google Scholar] [CrossRef]
- Korablev, N.M.; Fomichev, A.A. K-means data clustering using artificial immune systems. Bionics Intell. Sci. Mag. 2011, 3, 102–106. [Google Scholar]
- Mirkin, B.G. Clustering for Data Mining. A Data recovery Approach; Chapman and Hall/CRC: New York, NY, USA, 2005; pp. 269–296. [Google Scholar] [CrossRef]
- Bradley, P.S.; Fayyad, U.M. Refining Initial Points for K-Means Clustering. In Proceedings of the International Conference on Machine Learning, San Francisco, CA, USA, 24–27 July 1998. [Google Scholar]
- Cherezov, D.S.; Tukachev, N.A. Classification and clasterization base methods review. Bull. Voronezh State Univ. Ser. Syst. Anal. Inf. Technol. 2009, 2, 25–29. [Google Scholar]



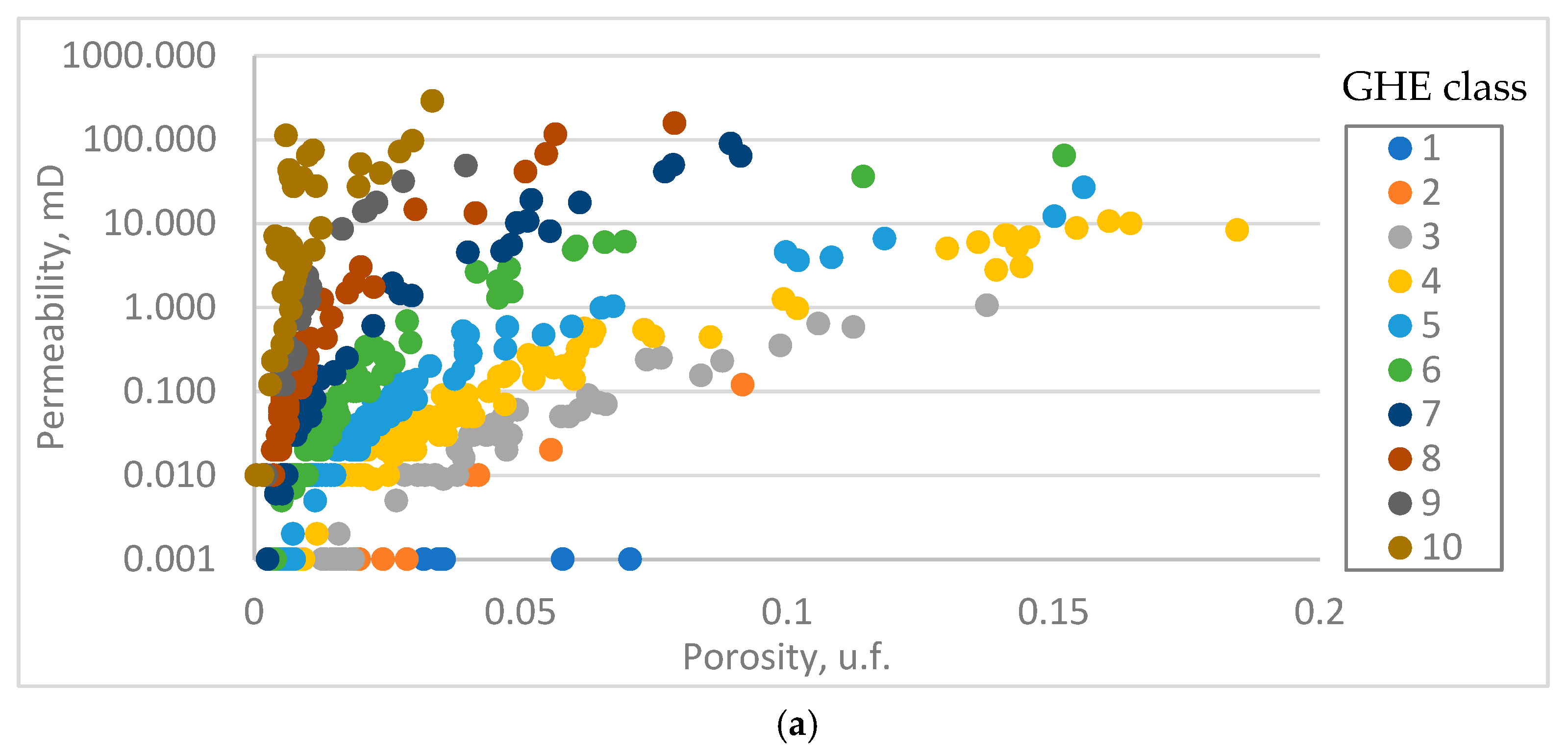

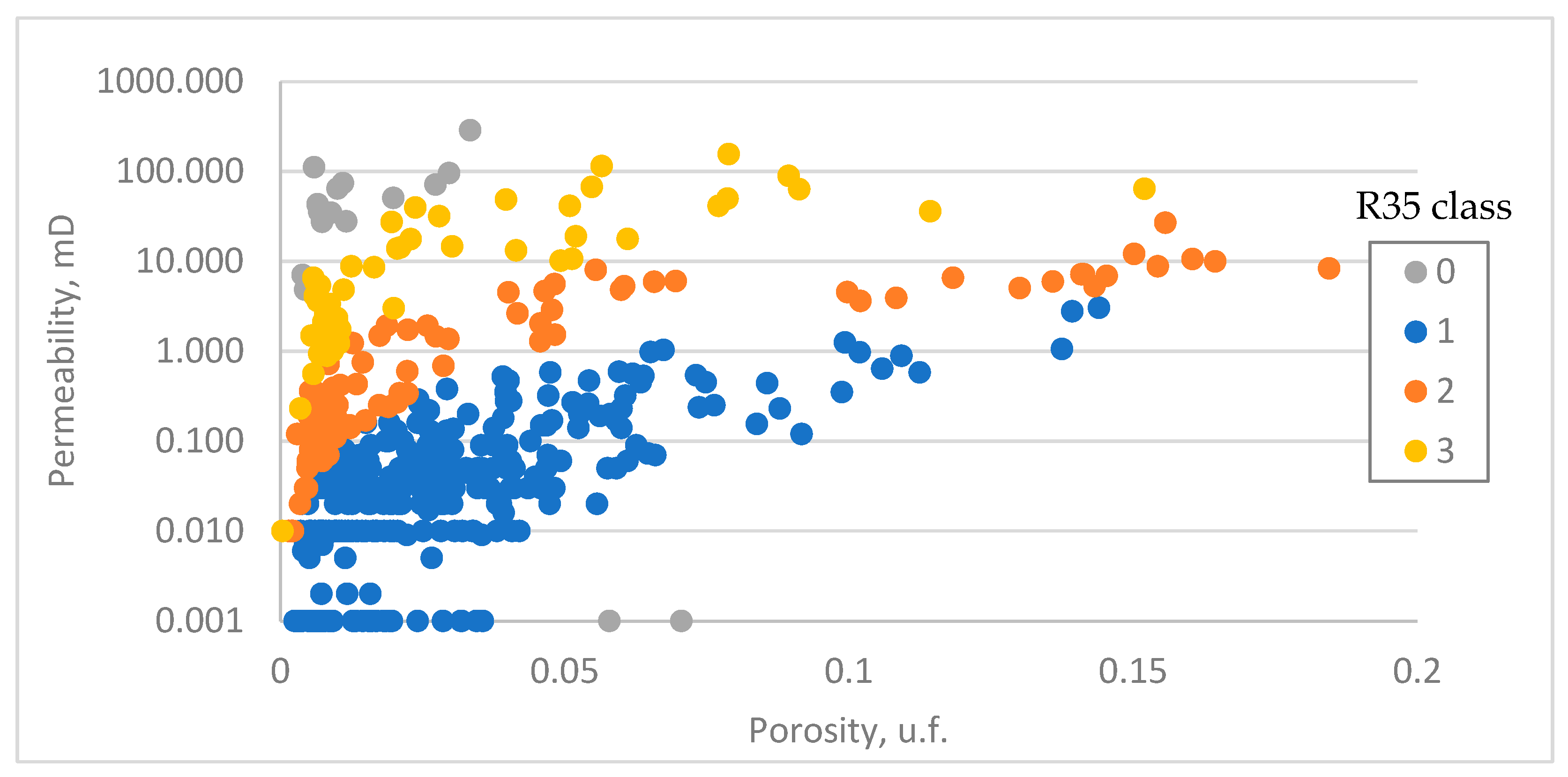
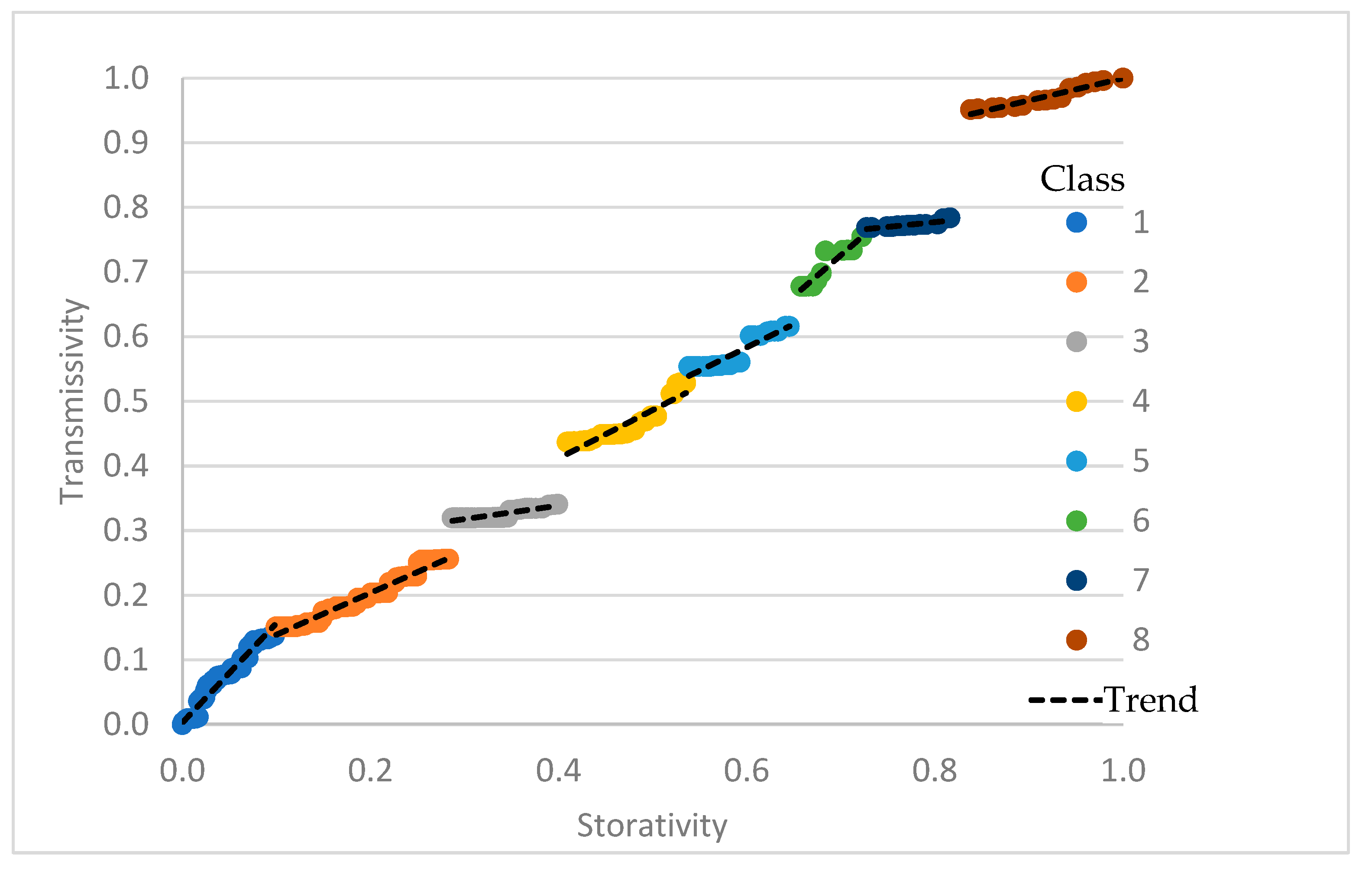
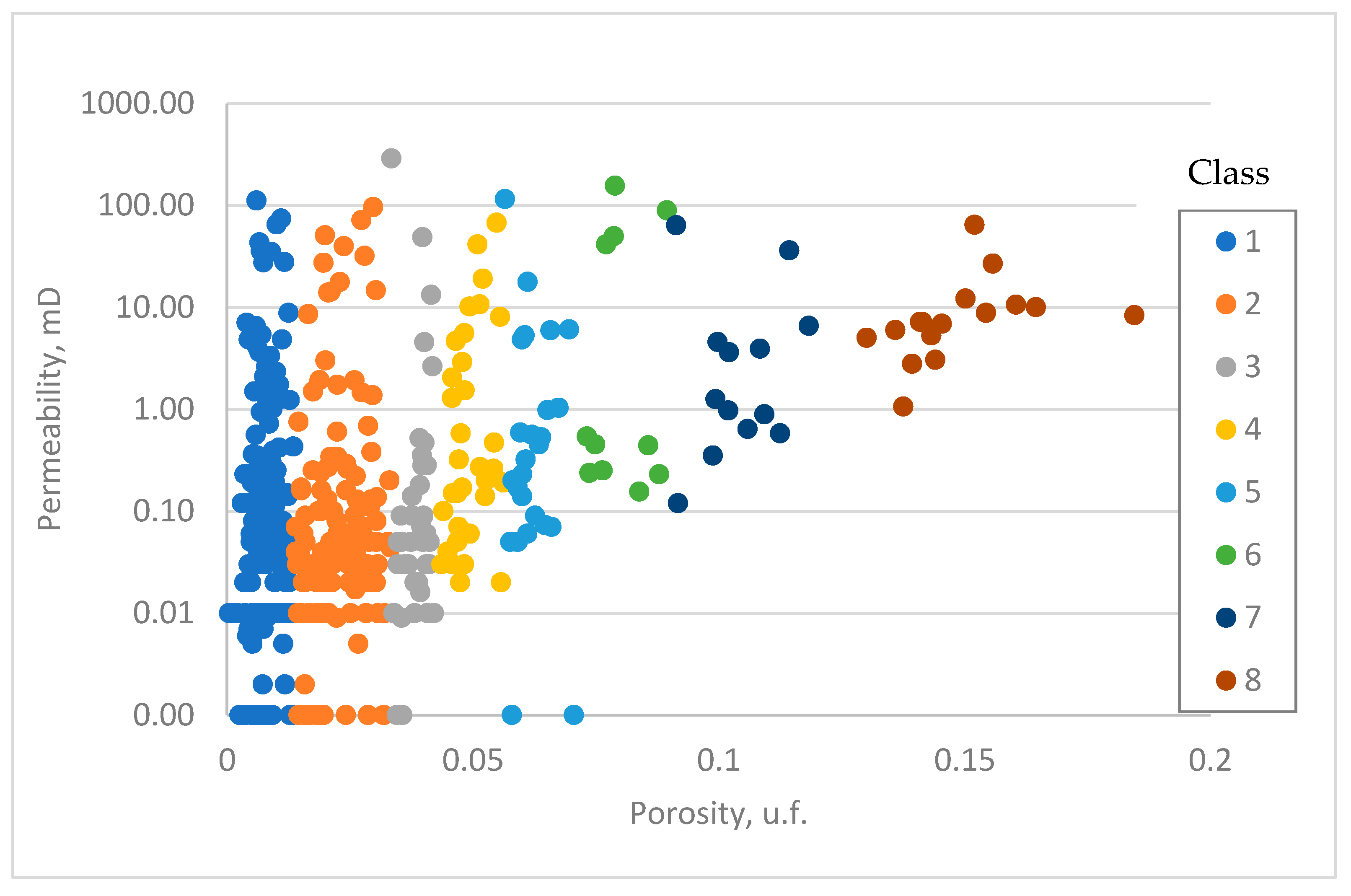
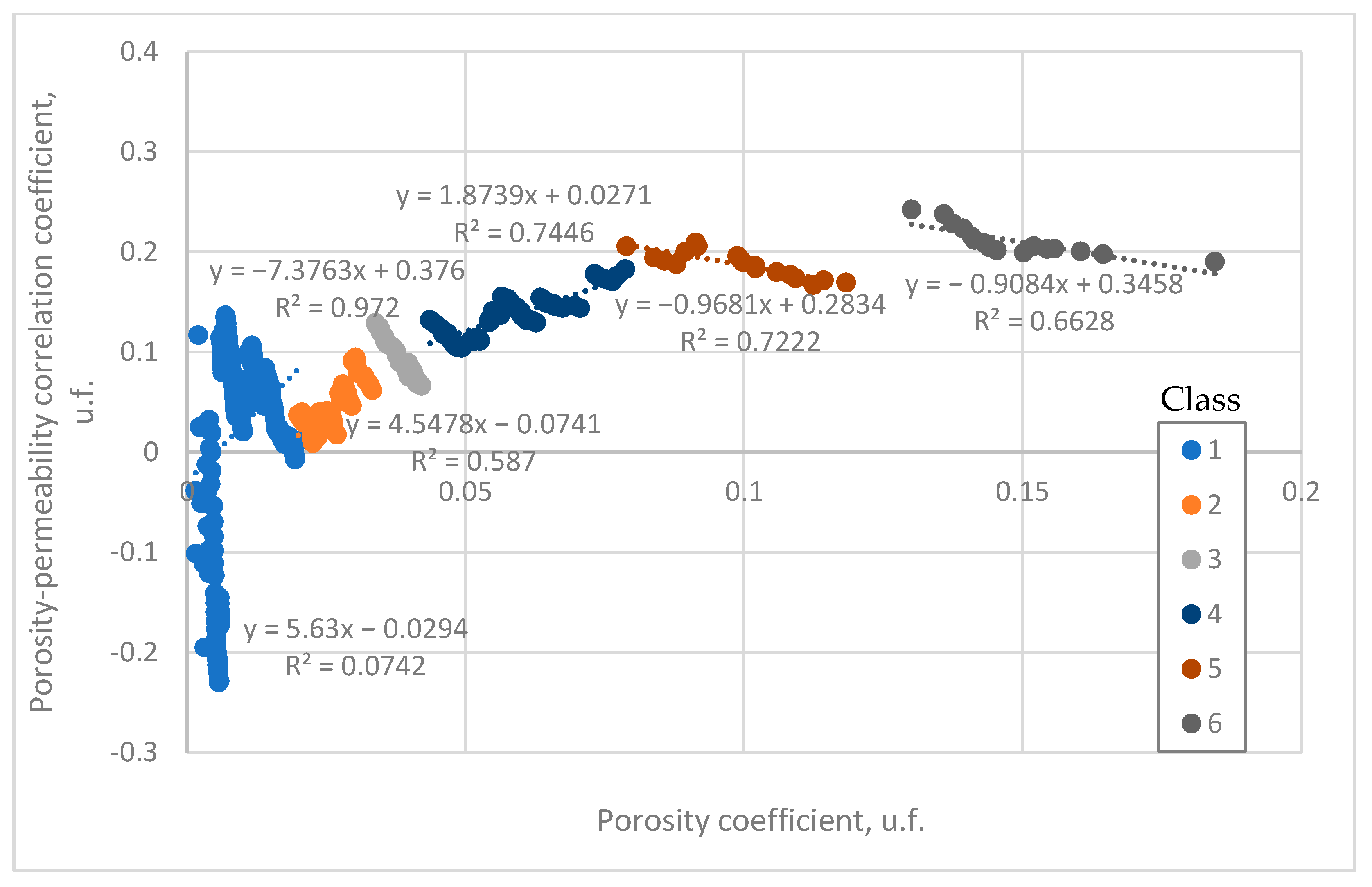
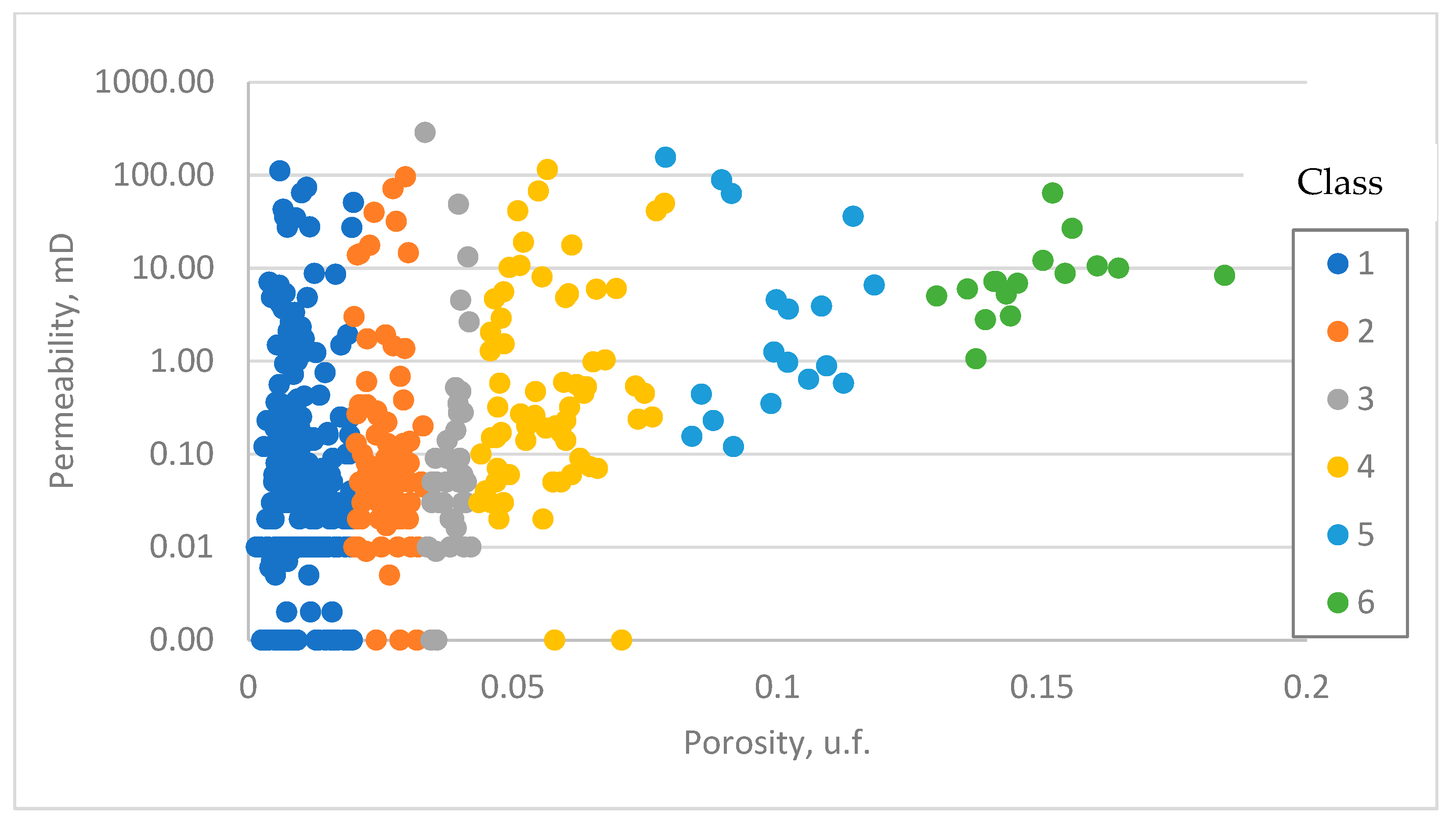
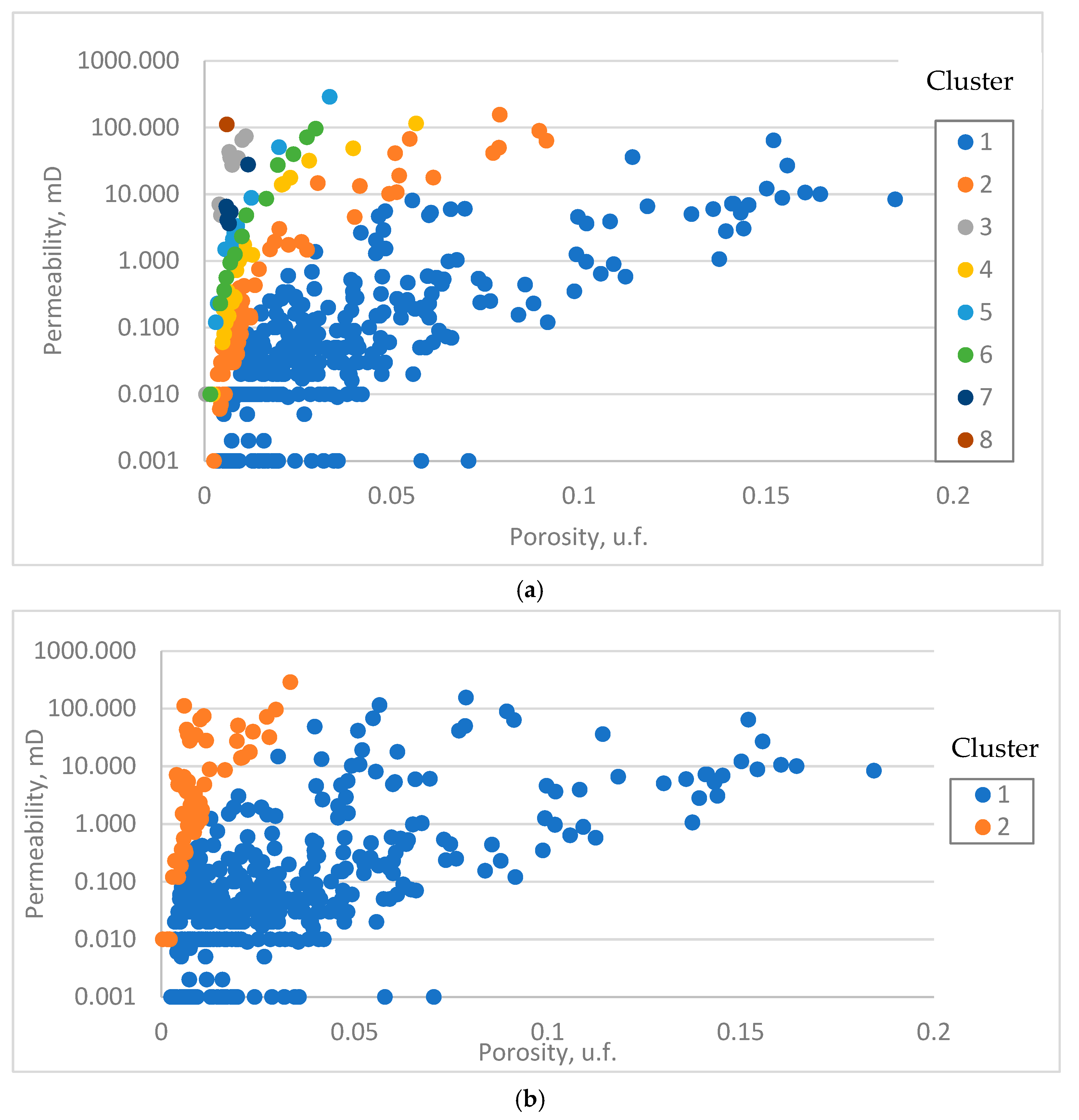
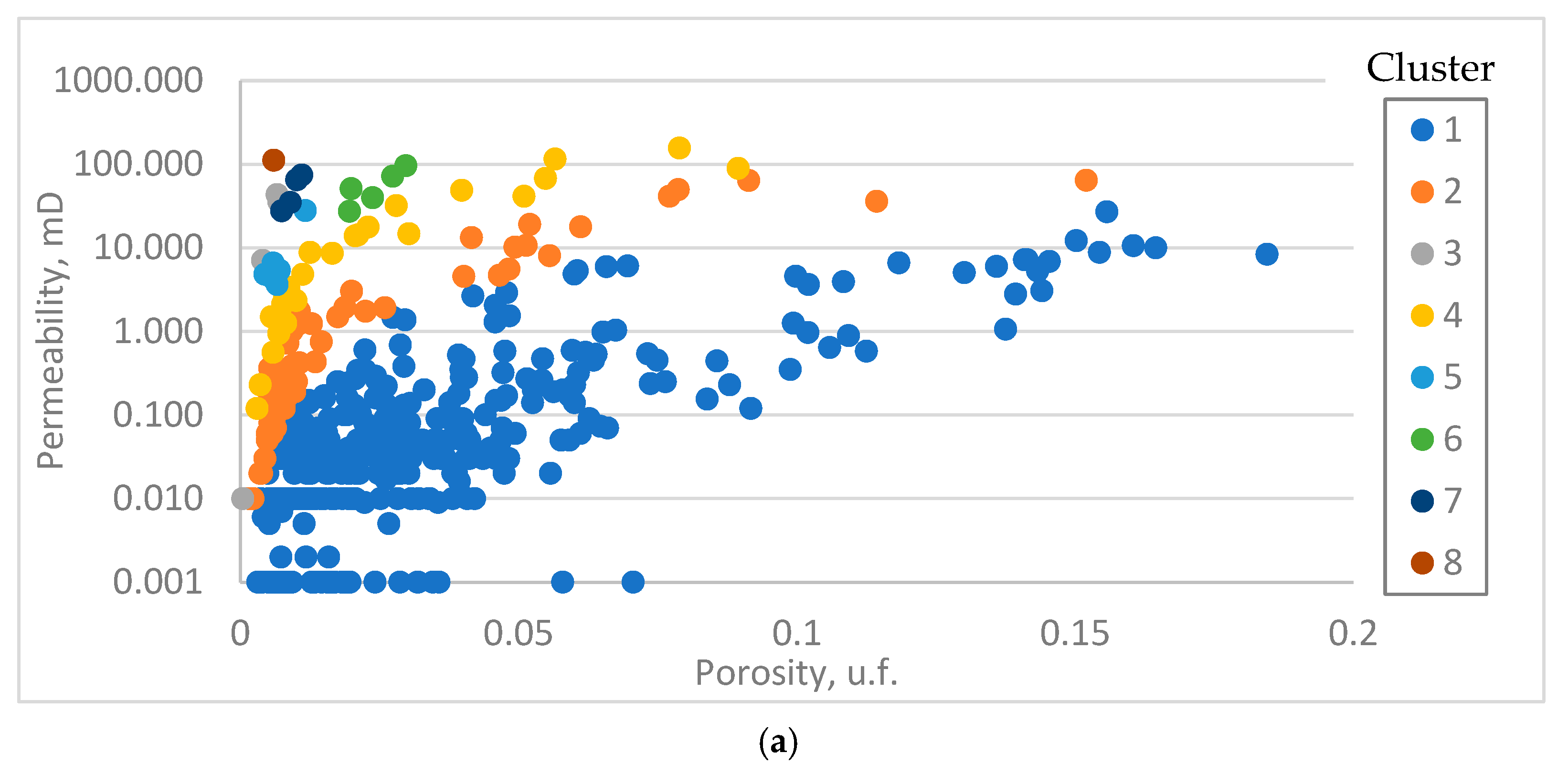
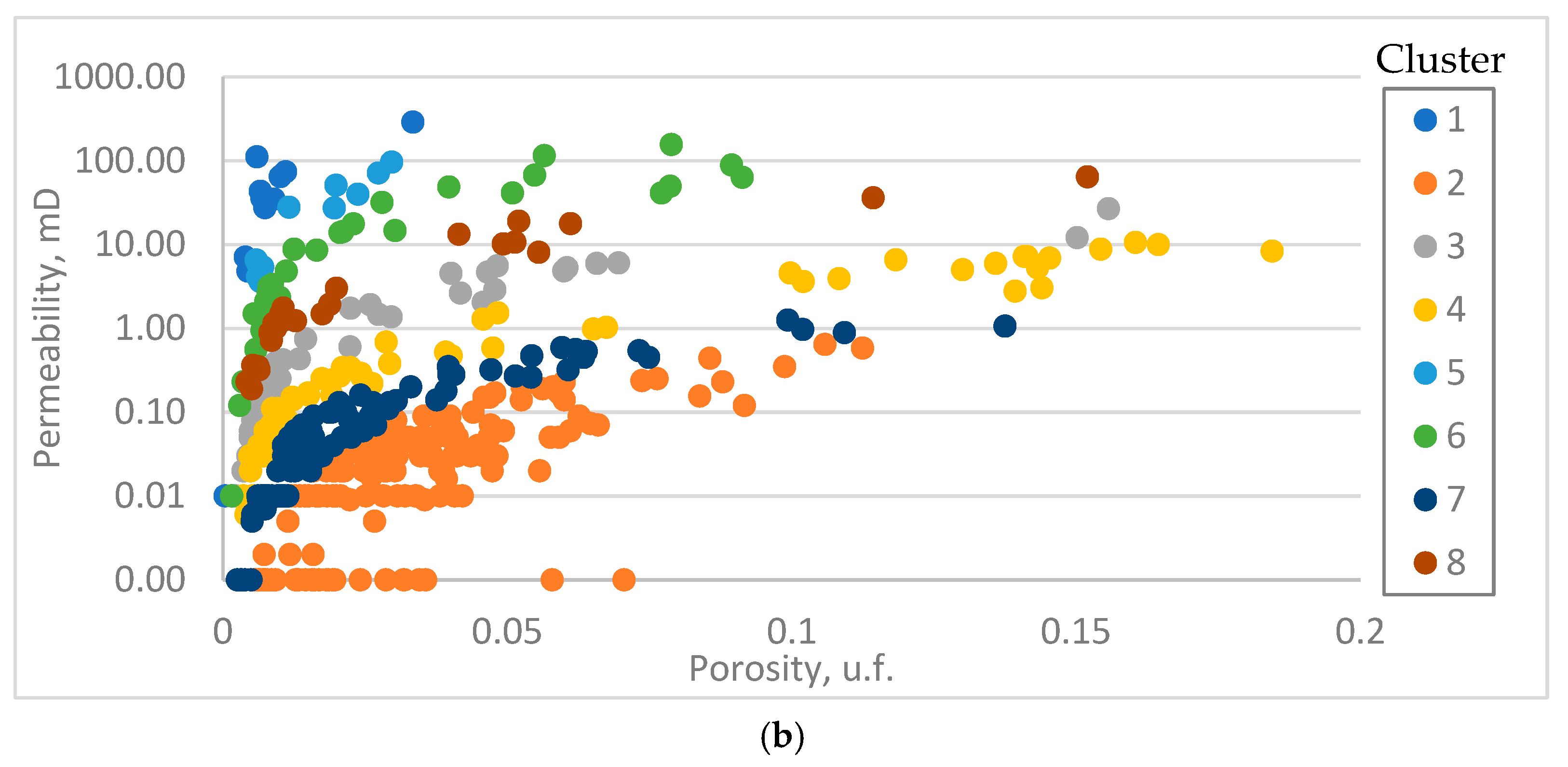

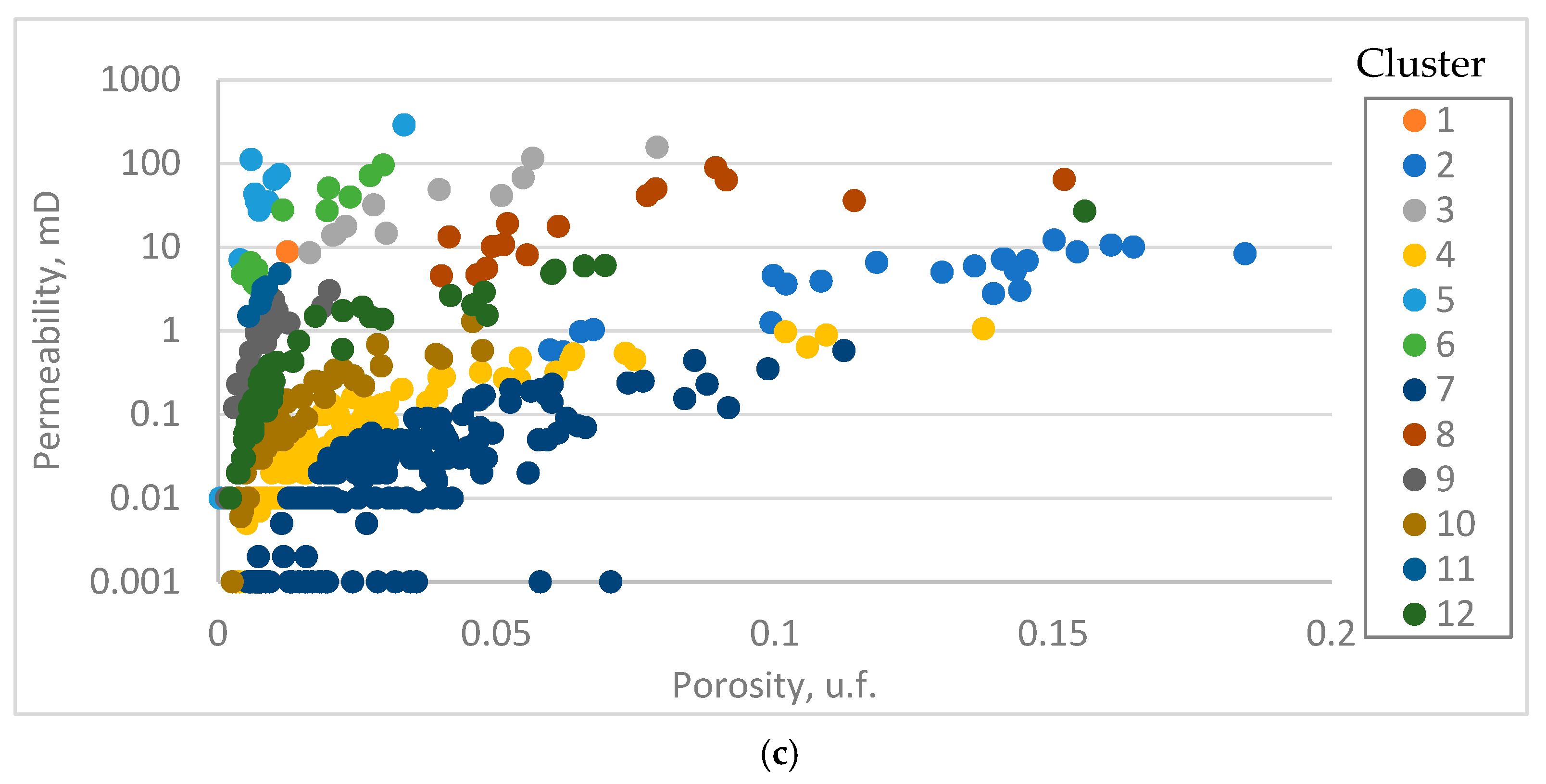
| GHE Classification | DRT Classification | ||||
|---|---|---|---|---|---|
| Class | Regression Dependence | Determination Coefficient | Class | Regression Dependence | Determination Coefficient |
| 2 | y = 0.0003 × e71.888x | R2 = 0.98 | 4 | y = 0.0001 × e96.725x | R2 = 0.93 |
| 3 | y = 0.0008 × e66.062x | R2 = 0.72 | 5 | y = 0.0007 × e64.187x | R2 = 0.85 |
| 4 | y = 0.0065 × e49.341x | R2 = 0.55 | 6 | y = 0.0037 × e50.779x | R2 = 0.90 |
| 5 | y = 0.0047 × e70.066x | R2 = 0.91 | 7 | y = 0.005 × e54.849x | R2 = 0.85 |
| 6 | y = 0.0118 × e83.039x | R2 = 0.78 | 8 | y = 0.0049 × e68.011x | R2 = 0.92 |
| 7 | y = 0.0151 × e112.92x | R2 = 0.81 | 9 | y = 0.0103 × e76.634x | R2 = 0.98 |
| 8 | y = 0.0417 × e135.73x | R2 = 0.61 | 10 | y = 0.0107 × e105.42x | R2 = 0.89 |
| 9 | y = 0.0748 × e220.27x | R2 = 0.65 | 11 | y = 0.015 × e110.85x | R2 = 0.82 |
| 10 | y = 0.506 × e224.47x | R2 = 0.78 | 12 | y = 0.0328 × e135.02x | R2 = 0.83 |
| - | - | - | 13 | y = 0.0444 × e162.76x | R2 = 0.88 |
| - | - | - | 14 | y = 0.0386 × e293.85x | R2 = 0.80 |
| - | - | - | 15 | y = 0.2359 × e224.17x | R2 = 0.97 |
| - | - | - | 16 | y = 0.0865 × e523.56x | R2 = 0.90 |
| - | - | - | 17 | y = 0.3076 × e506.17x | R2 = 0.98 |
| - | - | - | 18 | y = 0.0451 × e890.15x | R2 = 0.58 |
| Cluster | 8 Clusters | 10 Clusters | 12 Clusters | |||
|---|---|---|---|---|---|---|
| Equation | R2 | Equation | R2 | Equation | R2 | |
| 1 | y = 8902.5x − 17.533 | R2 = 0.88 | y = 0.3547 × e47.106x | R2 = 0.77 | (1 value) | (1 value) |
| 2 | y = 3.3793x − 0.0587 | R2 = 0.61 | y = 0.002 × e60.971x | R2 = 0.68 | y = 0.2162 × e23.336x | R2 = 0.57 |
| 3 | y = 122.08x − 0.9967 | R2 = 0.85 | y = 0.0335 × e42.529x | R2 = 0.87 | y = 5.6505 × e45.206x | R2 = 0.86 |
| 4 | y = 48.027x − 0.5159 | R2 = 0.89 | y = 3.7495 × e181.16x | R2 = 0.85 | y = 8.0369x − 0.0742 | R2 = 0.95 |
| 5 | y = 3120.9x − 15.714 | R2 = 0.88 | y = 5.9112 × e26.089x | R2 = 0.91 | y = 3.7495 × e181.16x | R2 = 0.85 |
| 6 | y = 1099.4x − 4.7463 | R2 = 0.70 | y = 1557.2x − 12.372 | R2 = 0.82 | y = 2.6719 × e124.16x | R2 = 0.93 |
| 7 | y = 9.0492x − 0.083 | R2 = 0.92 | y = 0.0571 × e34.385x | R2 = 0.65 | y = 0.0018 × e63.192x | R2 = 0.58 |
| 8 | y = 383.7x − 3.6482 | R2 = 0.94 | y = 0.3547 × e47.106x | R2 = 0.77 | y = 649.79x − 16.278 | R2 = 0.58 |
| 9 | - | - | y = 9.0622x − 0.0838 | R2 = 0.92 | y = 153.37x − 0.3226 | R2 = 0.82 |
| 10 | - | - | y = 2.6729 × e124.89x | R2 = 0.93 | y = 18.335x − 0.0983 | R2 = 0.80 |
| 11 | - | - | - | - | y = 0.4716 × e214.35x | R2 = 0.94 |
| 12 | - | - | - | - | y = 0.1061 × e53.025x | R2 = 0.86 |
| Method | Rock Types Numbers | Mean R2 | Min R2 | Max R2 | Variance | St. Deviation | Variation Coefficient |
|---|---|---|---|---|---|---|---|
| DRT | 18 | 0.73 | 0.58 * | 0.98 | 0.12 | 0.35 | 47.64 |
| GHE | 10 | 0.68 | 0.61 * | 0.99 | 0.07 | 0.27 | 40.31 |
| EM (8 clusters) | 8 | 0.83 | 0.61 | 0.94 | 0.01 | 0.11 | 14.01 |
| EM (10 clusters) | 10 | 0.82 | 0.65 | 0.93 | 0.009 | 0.09 | 12.02 |
| EM (12 clusters) | 12 | 0.73 | 0.57 * | 0.95 | 0.07 | 0.27 | 36.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krivoshchekov, S.; Kochnev, A.; Kozyrev, N.; Botalov, A.; Kochneva, O.; Ozhgibesov, E. Rock Typing Approaches for Effective Complex Carbonate Reservoir Characterization. Energies 2023, 16, 6559. https://doi.org/10.3390/en16186559
Krivoshchekov S, Kochnev A, Kozyrev N, Botalov A, Kochneva O, Ozhgibesov E. Rock Typing Approaches for Effective Complex Carbonate Reservoir Characterization. Energies. 2023; 16(18):6559. https://doi.org/10.3390/en16186559
Chicago/Turabian StyleKrivoshchekov, Sergey, Alexander Kochnev, Nikita Kozyrev, Andrey Botalov, Olga Kochneva, and Evgeny Ozhgibesov. 2023. "Rock Typing Approaches for Effective Complex Carbonate Reservoir Characterization" Energies 16, no. 18: 6559. https://doi.org/10.3390/en16186559
APA StyleKrivoshchekov, S., Kochnev, A., Kozyrev, N., Botalov, A., Kochneva, O., & Ozhgibesov, E. (2023). Rock Typing Approaches for Effective Complex Carbonate Reservoir Characterization. Energies, 16(18), 6559. https://doi.org/10.3390/en16186559






