Failure Mechanism of Integrity of Cement Sheath under the Coupling Effect of Formation Creep and Temperature during the Operation of Salt Rock Gas Storage
Abstract
:1. Introduction
2. Establishment of FEM Model for Casing–Cement Sheath–Creep Formation Combination
2.1. Salt Rock Creep Model
2.2. Feasibility Verification of Salt Rock Creep Simulation in FEM
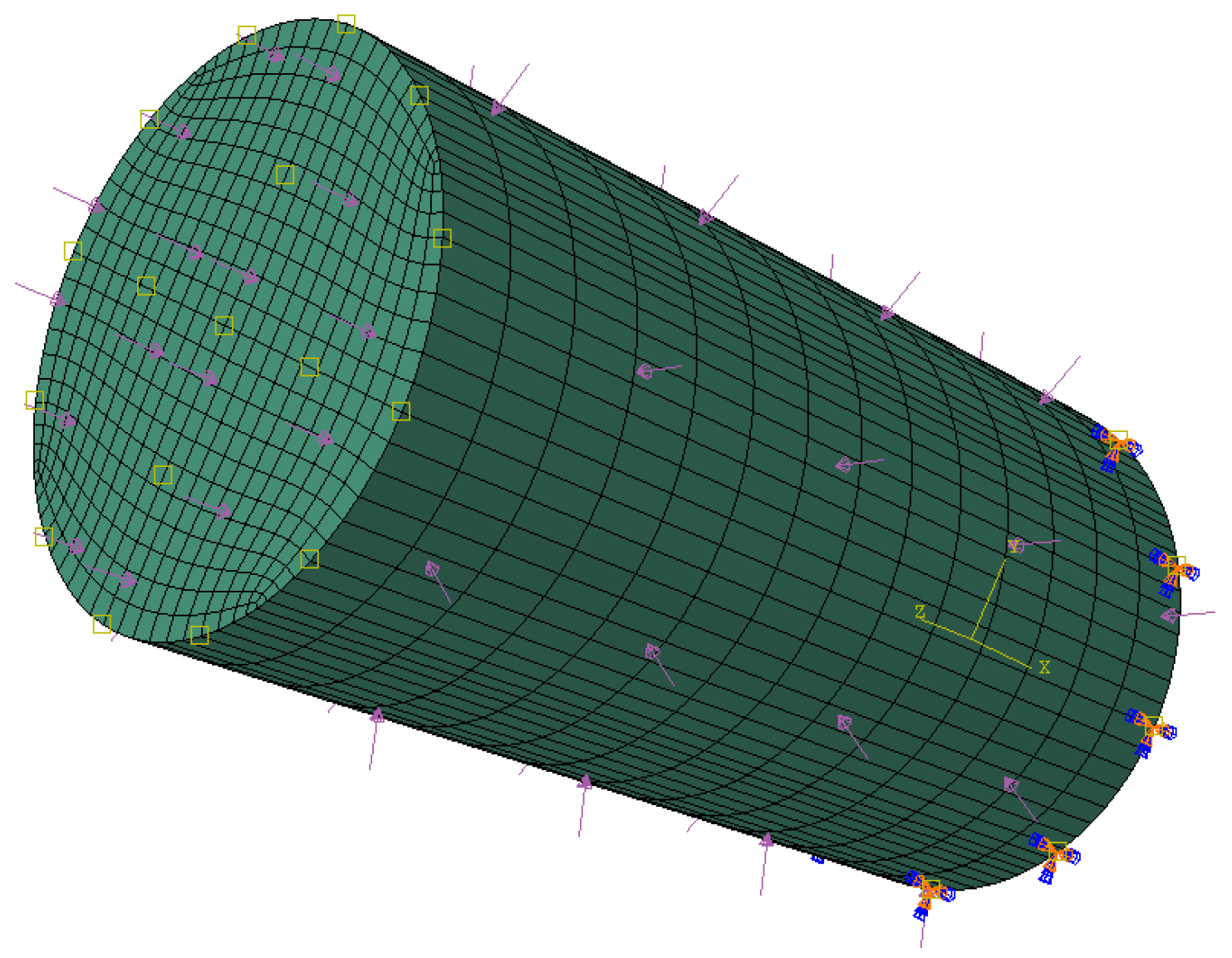
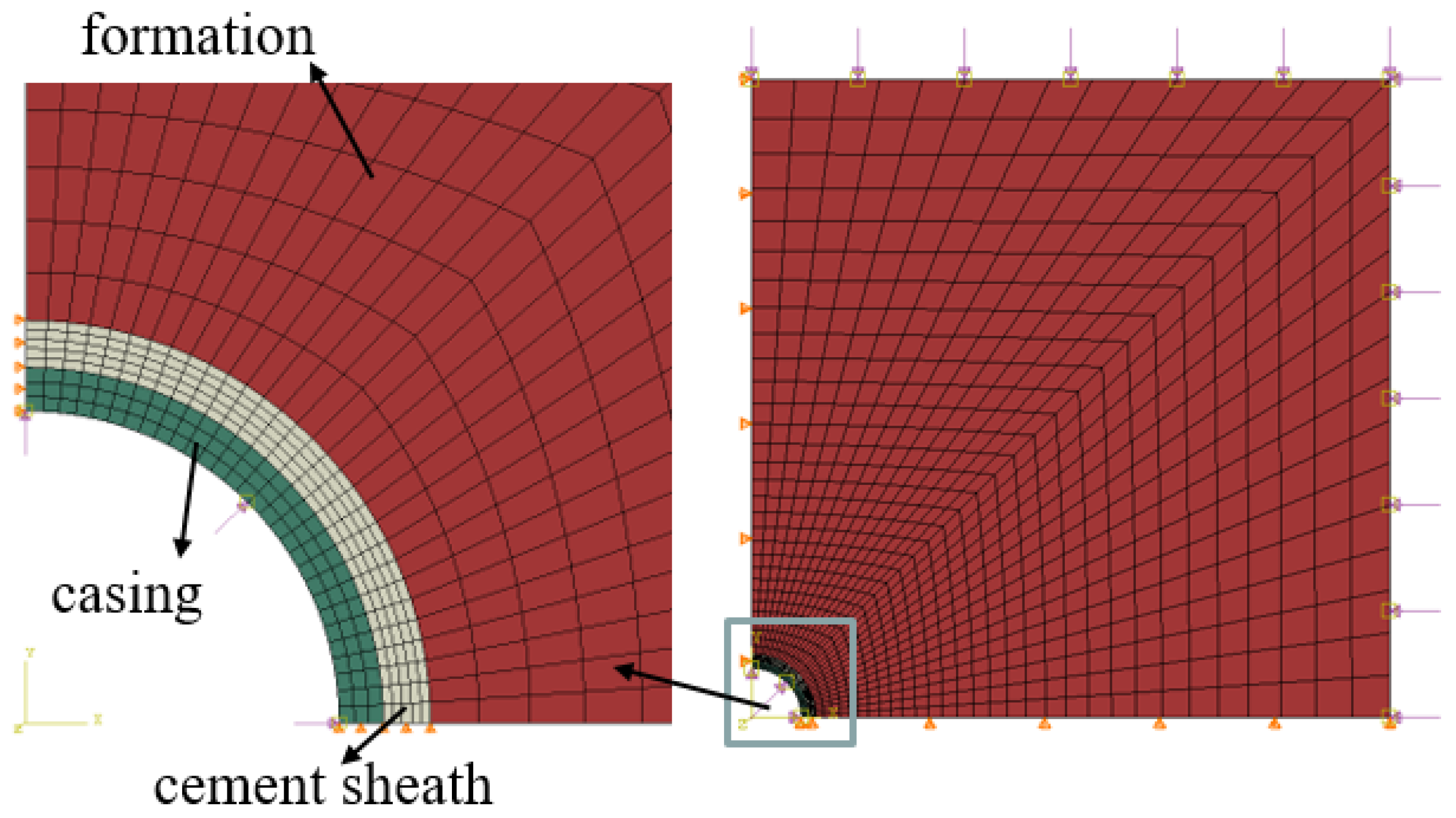
2.3. FEM Model of Casing–Cement Sheath–Creep Formation Combination
3. Results and Discussion
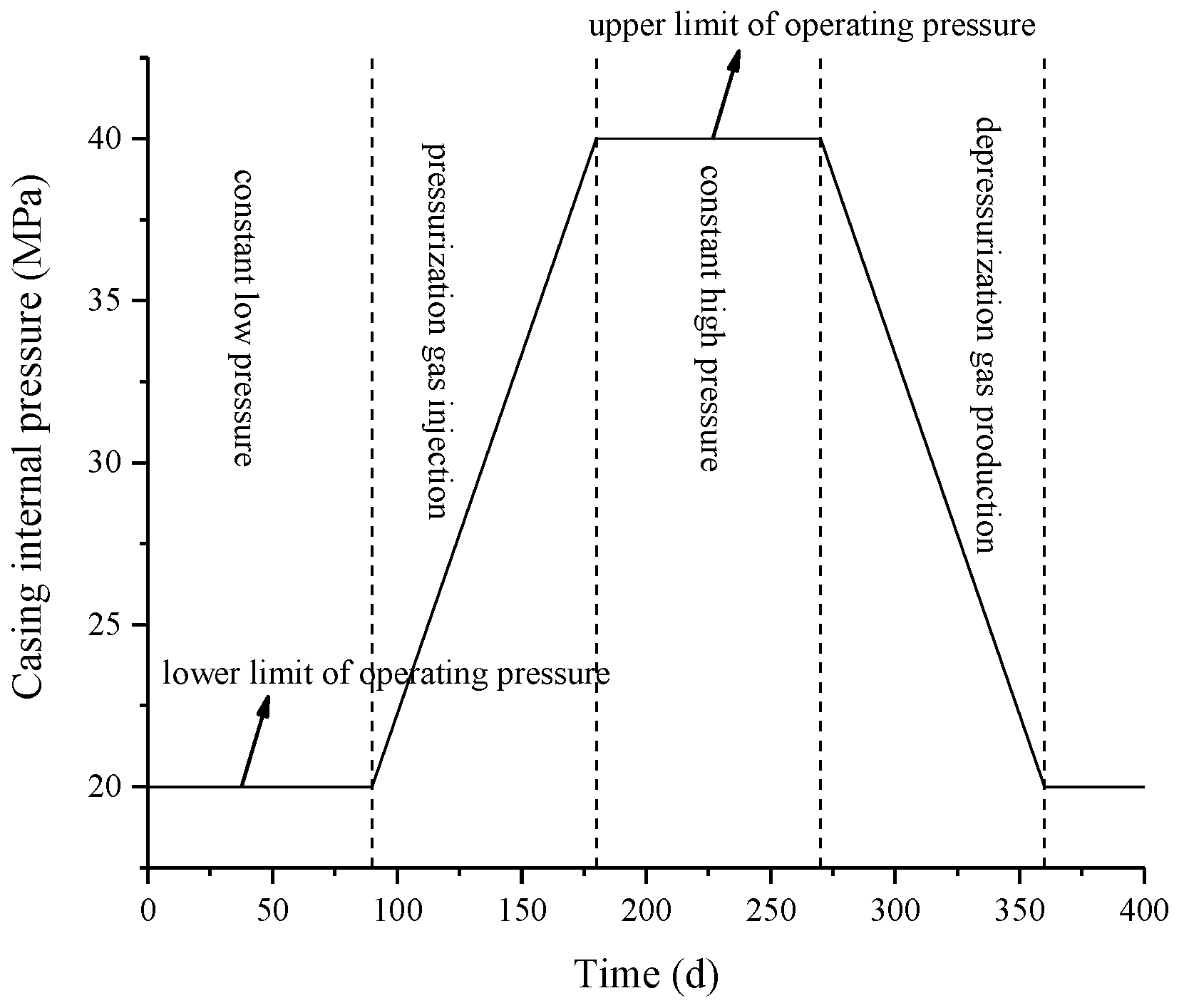
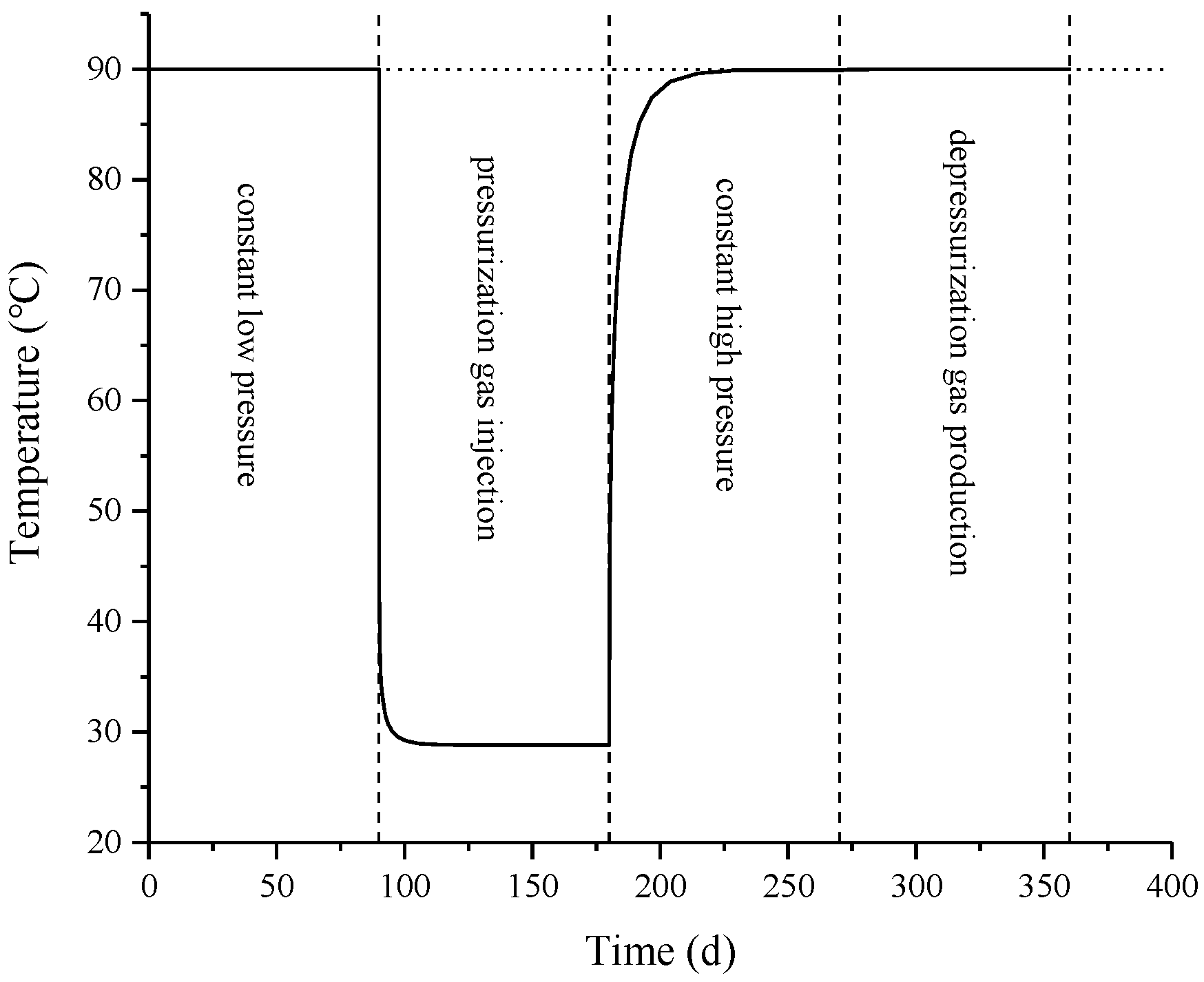
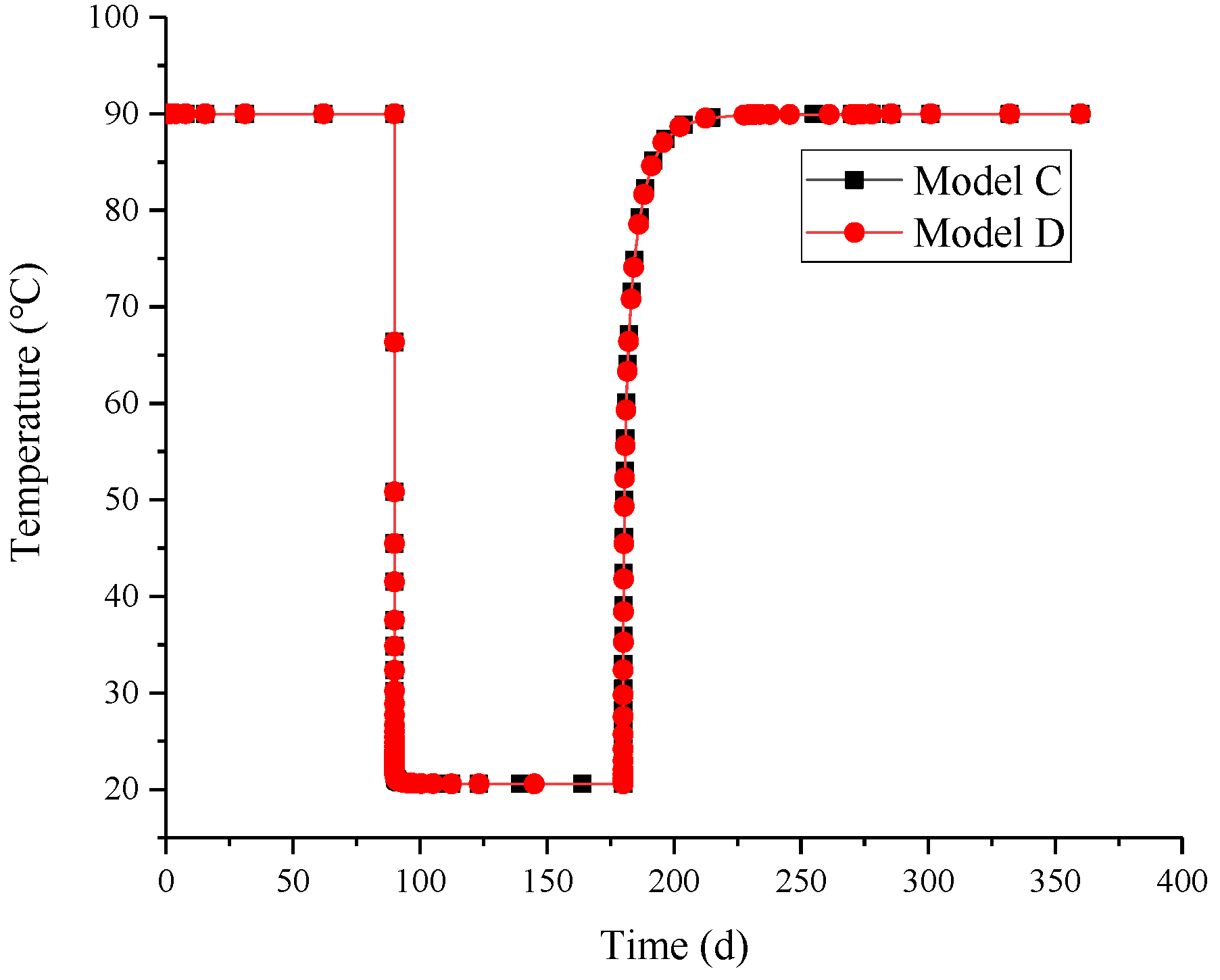
3.1. Variation of Formation Temperature and Stress during Operation of UGS
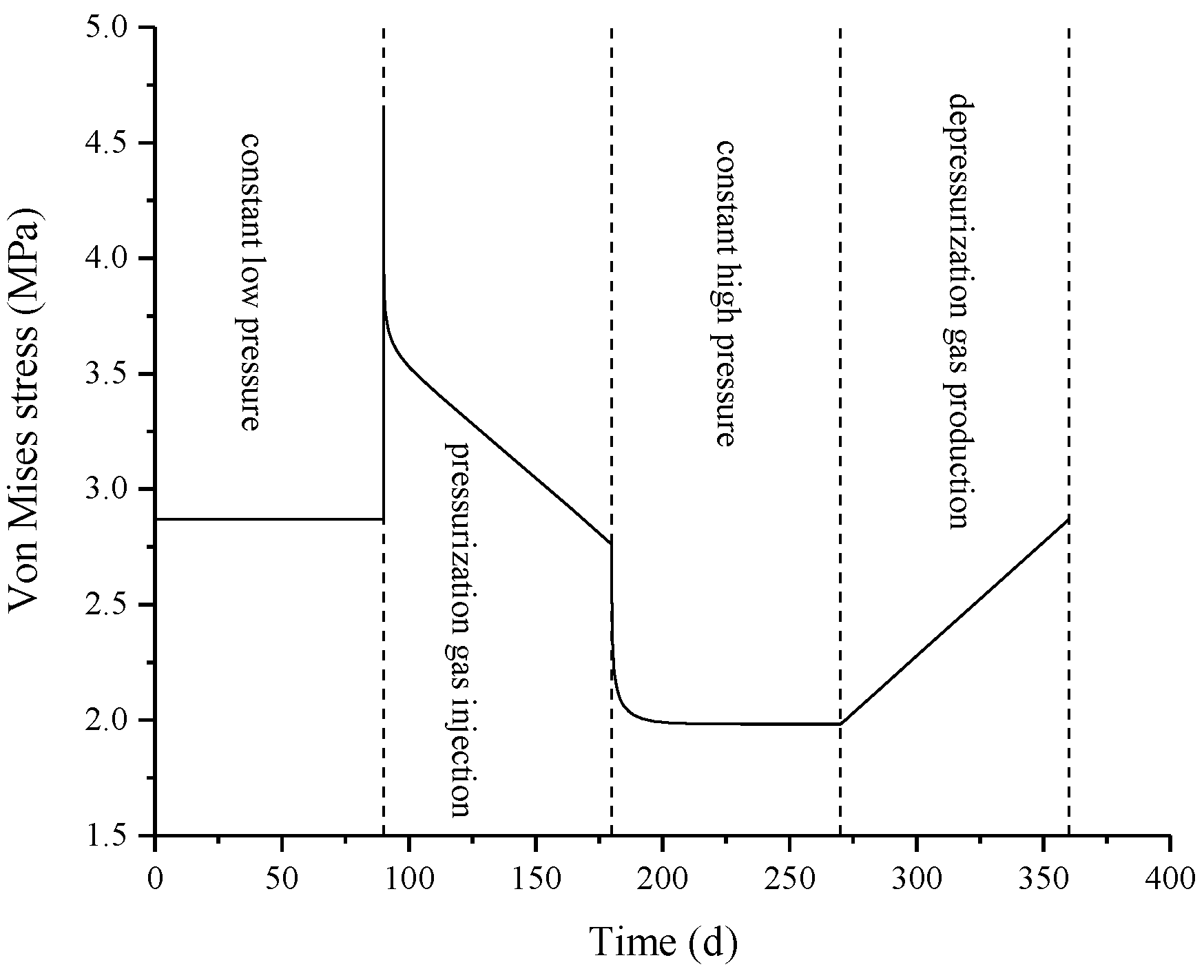
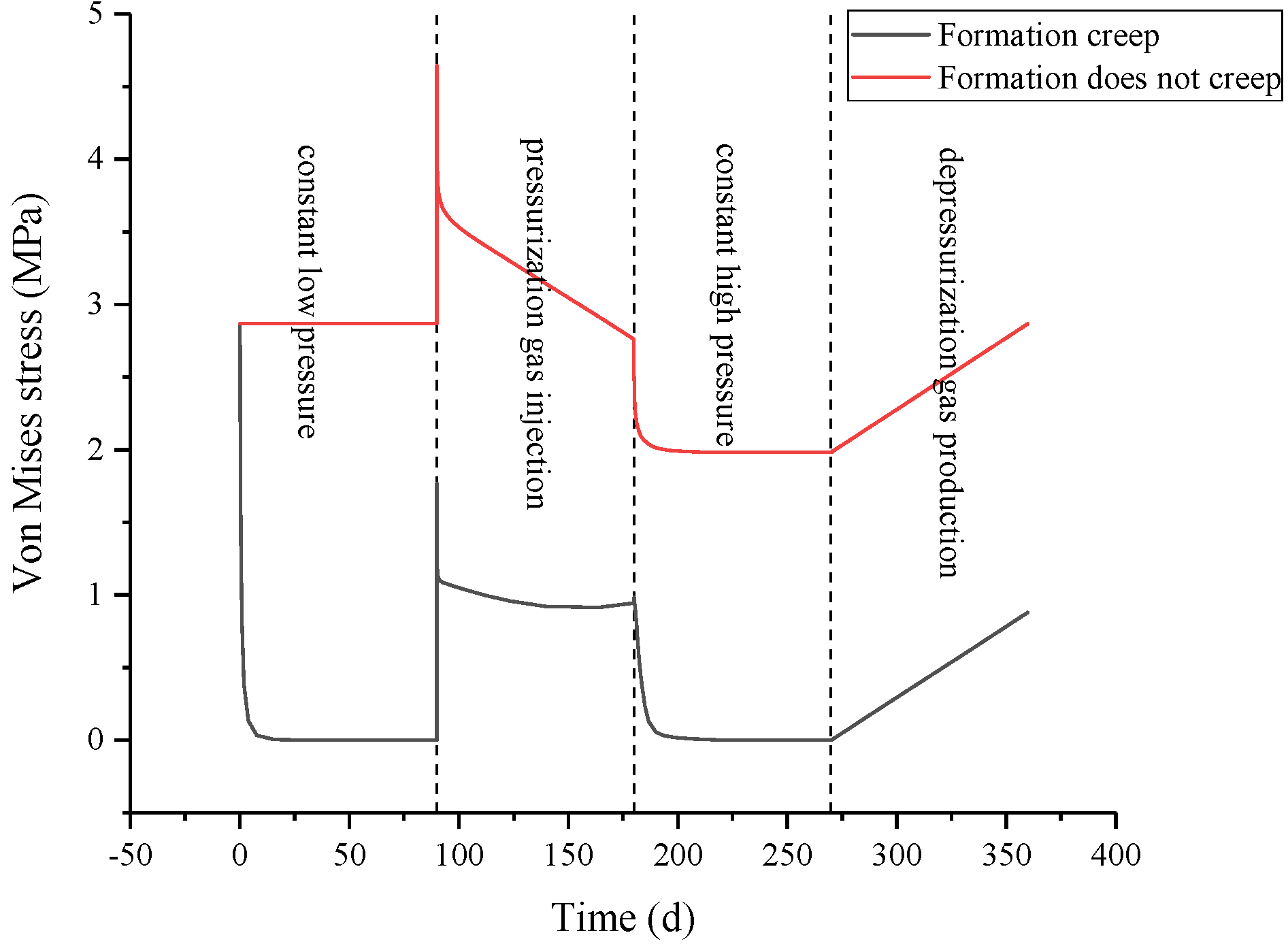
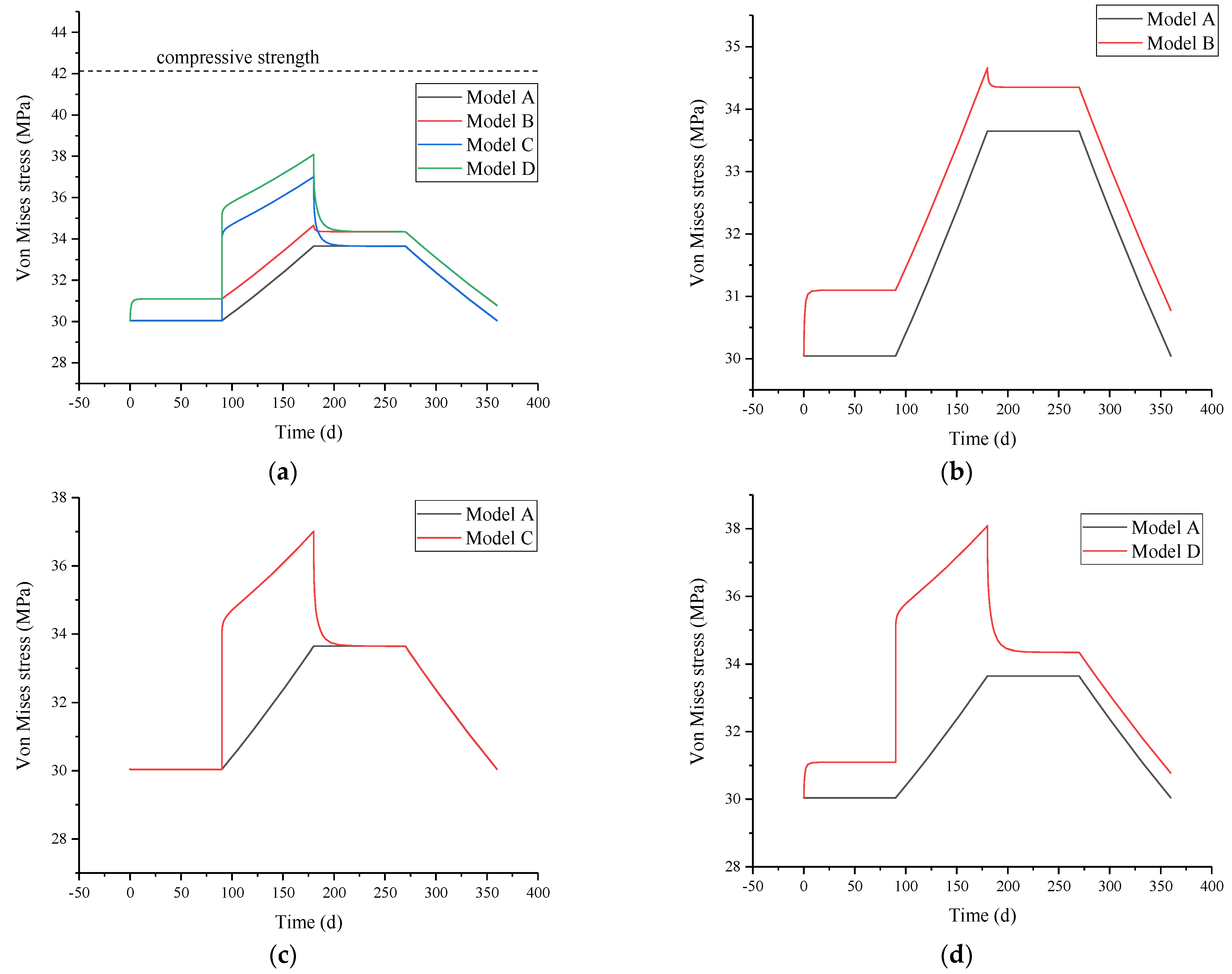
3.2. Effects of Downhole Temperature Changes and Formation Creep on Integrity Failure of Cement Sheath
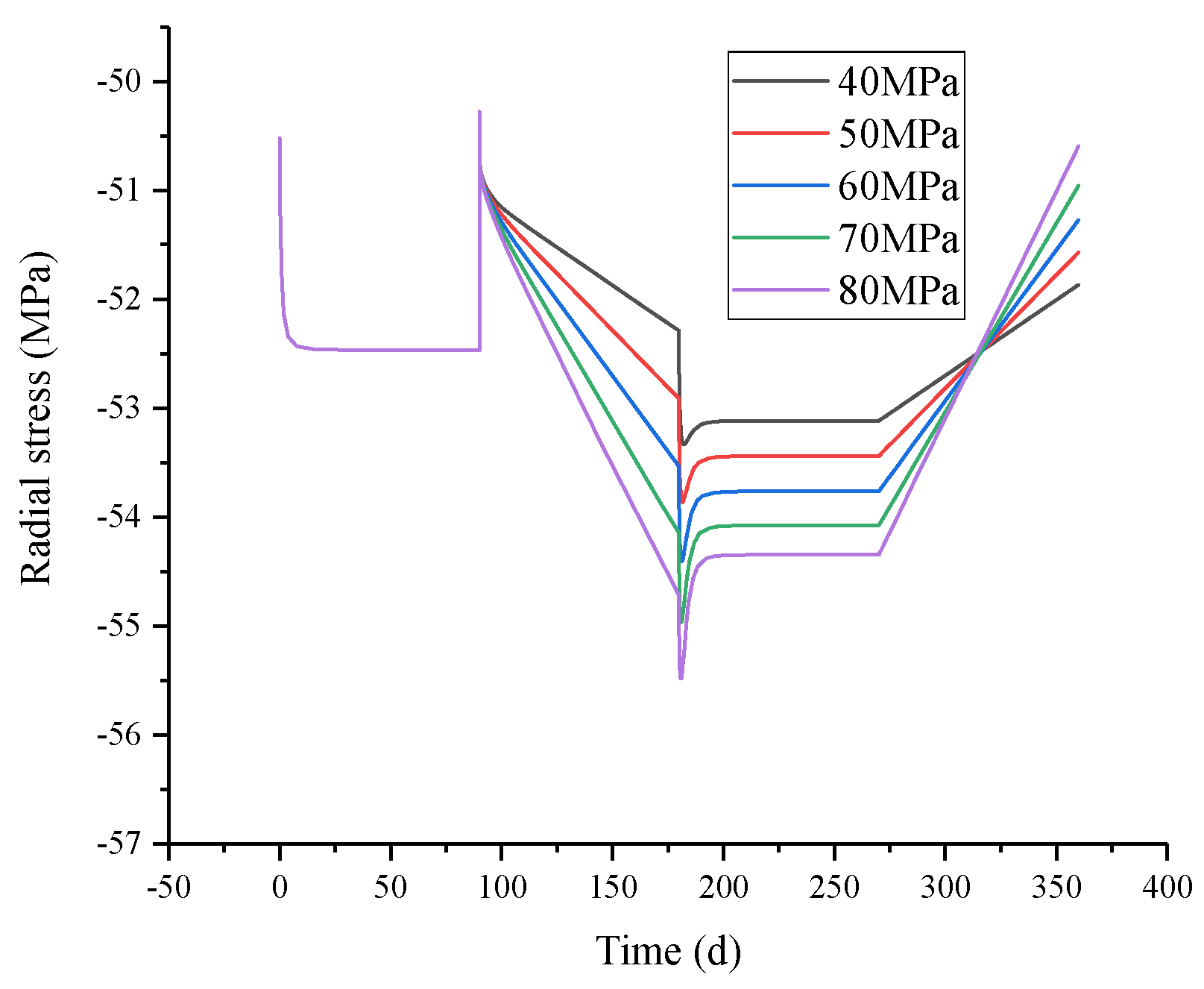
3.3. The Influence of the Upper Limit of Operating Pressure of UGS on the Integrity of Cement Sheath
3.4. Measure to Prevent the Integrity Failure of Cement Sheath
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
References
- Yang, C.; Daemen, J.J.K.; Yin, J.H. Experimental investigation of creep behavior of salt rock. Int. J. Rock Mech. Min. Sci. 1999, 36, 233–242. [Google Scholar] [CrossRef]
- Yang, H.; Bu, Y.; Guo, S.; Liu, H.; Du, J.; Cao, X. Effects of in-situ stress and elastic parameters of cement sheath in salt rock formation of underground gas storage on seal integrity of cement sheath. Eng. Fail. Anal. 2021, 123, 105258. [Google Scholar] [CrossRef]
- Yin, F.; Hou, D.; Liu, W.; Deng, Y. Novel assessment and countermeasure for micro-annulus initiation of cement sheath during injection/fracturing. Fuel 2019, 252, 157–163. [Google Scholar] [CrossRef]
- Bu, Y.; Du, J.; Guo, S.; Liu, H.; Liang, Y.; Su, Z.; Li, Y. Effects of formation water influx on the bonding strength between oil well cement and the formation. Constr. Build. Mater. 2020, 251, 118989. [Google Scholar] [CrossRef]
- De Andrade, J.; Sangesland, S. Cement Sheath Failure Mechanisms: Numerical Estimates to Design for Long-Term Well Integrity. J. Pet. Sci. Eng. 2016, 147, 682–698. [Google Scholar] [CrossRef]
- Bu, Y.; Yang, H.; Zhao, L.; Guo, S.; Liu, H.; Ma, X. Stress concentration of perforated cement sheath and the effect of cement sheath elastic parameters on its integrity failure during shale gas fracturing. Front. Mater. 2022, 9, 980920. [Google Scholar] [CrossRef]
- He, T.; Wang, T.; Wang, D.; Xie, D.; Daemen, J. Failure mechanism of gas storage salt cavern cement sheath under the coupling effect of plasticity and fatigue damage. Constr. Build. Mater. 2022, 354, 129179. [Google Scholar] [CrossRef]
- Zhao, L.; Yang, H.; Wei, Y.; Bu, Y.; Jing, S.; Zhou, P. Integrity and Failure Analysis of Cement Sheath Subjected to Coalbed Methane Fracturing. Fluid Dyn. Mater. Process. 2023, 19, 329–344. [Google Scholar] [CrossRef]
- Jandhyala, S.R.K.; Barhate, Y.R.; Anjos, J.; Fonseca, C.E.; Ravi, K. Cement Sheath Integrity in Fast Creeping Salts: Effect of Well Operations. In Proceedings of the SPE Offshore Europe Oil and Gas Conference and Exhibition, Aberdeen, UK, 3–6 September 2013; Society of Petroleum Engineers: Alexandria, VA, USA. [Google Scholar] [CrossRef]
- Tian, L.; Bu, Y.; Liu, H.; Lu, C.; Guo, S.; Xu, H.; Ren, Y. Effects of the mechanical properties of a cement sheath and formation on the sealing integrity of the cement-formation interface in shallow water flow in deep water. Constr. Build. Mater. 2023, 369, 130496. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, R.; Zeng, H.; Zeng, Y.; Zhang, L.; Zhang, J.; Li, X. Mechanical characteristics of well cement under cyclic loading and its influence on the integrity of shale gas wellbores. Fuel 2019, 250, 132–143. [Google Scholar] [CrossRef]
- Li, C.; Guan, Z.; Zhao, X.; Yan, Y.; Zhang, B.; Wang, Q.; Sheng, Y. A new method to protect the cementing sealing integrity of carbon dioxide geological storage well: An experiment and mechanism study. Eng. Fract. Mech. 2020, 236, 107213. [Google Scholar] [CrossRef]
- Yang, H.; Bu, Y.; Jing, S.; Guo, S.; Liu, H. Adaptability of Different Shear Failure Criteria in Shear Failure Evaluation of Cement Sheaths. Arab. J. Sci. Eng. 2023, 1–10. [Google Scholar] [CrossRef]
- Patel, H.; Salehi, S. Development of an Advanced Finite Element Model and Parametric Study to Evaluate Cement Sheath Barrier. J. Energy Resour. Technol.-Trans. ASME 2019, 141, 092902. [Google Scholar] [CrossRef]
- Patel, H.; Salehi, S. Structural integrity of liner cement in oil & gas wells: Parametric study, sensitivity analysis, and risk assessment. Eng. Fail. Anal. 2021, 122, 105203. [Google Scholar] [CrossRef]
- Zhang, H.; Shen, R.; Yuan, G.; Ba, Z.; Hu, Y. Cement sheath integrity analysis of underground gas storage well based on elastoplastic theory. J. Pet. Sci. Eng. 2017, 159, 818–829. [Google Scholar] [CrossRef]
- Yan, X.; Jun, L.; Gonghui, L.; Qian, T.; Wei, L. A new numerical investigation of cement sheath integrity during multistage hydraulic fracturing shale gas wells. J. Nat. Gas Sci. Eng. 2018, 49, 331–341. [Google Scholar] [CrossRef]
- Liu, K.; Gao, D.; Zeng, J.; Wang, Z. Study on Cement Sheath Integrity in Horizontal Wells during Hydraulic Fracturing Process. In Proceedings of the 52nd U.S. Rock Mechanics/Geomechanics Symposium, Seattle, WA, USA, 17–20 June 2018. [Google Scholar]
- Bagheri, M.; Shariatipour, S.M.; Ganjian, E. Parametric study on the integrity of wellbores in CO2 storage sites. Constr. Build. Mater. 2021, 268, 121060. [Google Scholar] [CrossRef]
- Liu, K.; Gao, D.; Taleghani, A.D. Analysis on integrity of cement sheath in the vertical section of wells during hydraulic fracturing. J. Pet. Sci. Eng. 2018, 168, 370–379. [Google Scholar] [CrossRef]
- Guo, S.; Bu, Y.; Yang, X.; Wang, C.; Guo, B.; Sun, B. Effect of casing internal pressure on integrity of cement ring in marine shallow formation based on XFEM. Eng. Fail. Anal. 2020, 108, 104258. [Google Scholar] [CrossRef]
- Han, X.; Feng, F.; Zhang, J. Study on the whole life cycle integrity of cement interface in heavy oil thermal recovery well under circulating high temperature condition. Energy 2023, 278, 127873. [Google Scholar] [CrossRef]
- Chu, W.; Shen, J.; Yang, Y.; Li, Y.; Gao, D. Calculation of micro-annulus size in casing-cement sheath-formation system under continuous internal casing pressure change. Pet. Explor. Dev. 2015, 42, 414–421. [Google Scholar] [CrossRef]
- Bu, Y.; Tian, L.; Guo, B.; Wang, C.; Sun, B. Experiment and simulation on the integrity of cement ring interface in deep water shallow formation. J. Pet. Sci. Eng. 2020, 190, 107127. [Google Scholar] [CrossRef]
- Liu, X.; Birchwood, R.; Hooyman, P.J. A new analytical solution for wellbore creep in soft sediments and salt. In Proceedings of the 45th U.S. Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 26–29 June 2011; American Rock Mechanics Association: Alexandria, VA, USA, 2011. [Google Scholar]
- Orlic, B.; Buijze, L. Numerical modeling of wellbore closure by the creep of rock salt caprocks. In Proceedings of the 48th U.S. Rock Mechanics/Geomechanics Symposium, Minneapolis, MN, USA, 1–4 June 2014; American Rock Mechanics Association: Alexandria, VA, USA, 2014. [Google Scholar]
- Orlic, B.; Thienen-Visser, V.; Schreppers, G. Numerical estimation of structural integrity of salt cavern wells. In Proceedings of the 50th US Rock Mechanics/Geomechanics Symposium, Houston, TX, USA, 26–29 June 2016; American Rock Mechanics Association: Alexandria, VA, USA, 2016. [Google Scholar]
- Melo, D.; Fountoura, S.A.B.; Inoue, N.; Anjos, J.L.R. Finite Element Analysis of Casing-in-Casing Integrity due to Annulus Pressurization by means of Salt Creep. In Proceedings of the 49th US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 28 June–1 July 2015; American Rock Mechanics Association: Alexandria, VA, USA, 2015. [Google Scholar]
- Yu, B.; Hardy, M.P.; Zhao, H. Laboratory Testing of Casing-Cement Interface and Multi-Scale Modeling of Casing Integrity Within Salt. In Proceedings of the 51st US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 25–28 June 2017; American Rock Mechanics Association: Alexandria, VA, USA, 2017. [Google Scholar]
- Velilla, J.; Fountoura, S.A.B.; Inoue, N.; Anjos, J.L.R. Numerical modelling of casing integrity in salt layers including the effects of dissolution and creep. In Proceedings of the 49th US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 28 June–1 July 2015; American Rock Mechanics Association: Alexandria, VA, USA, 2015. [Google Scholar]
- Gholami, R.; Aadnoy, B.; Fakhari, N. A thermo-poroelastic analytical approach to evaluate cement sheath integrity in deep vertical wells. J. Pet. Sci. Eng. 2016, 147, 536–546. [Google Scholar] [CrossRef]
- Jenab, A.; Taheri, A.K.; Jenab, K. The Use of ANN to Predict the Hot Deformation Behavior of AA7075 at Low Strain Rates. J. Mater. Eng. Perform. 2013, 22, 903–910. [Google Scholar] [CrossRef]
- Erisov, Y.; Surudin, S.; Grechnikov, F. Hot Deformation Behavior of Al-Cu-Li-Mg-Zn-Zr-Sc Alloy in As-Cast and Hot-Rolled Condition. Mater. Sci. Forum 2018, 920, 244–249. [Google Scholar] [CrossRef]
- Maia, C.A.; Poiate, E., Jr.; Falcao, J.L.; Coelho, L.F.M. Triaxial Creep Tests in Salt Applied in Drilling Through Thick Salt Layers in Campos Basin-Brazil. In Proceedings of the SPE/IADC Drilling Conference, Amsterdam, The Netherlands, 23–25 February 2005. [Google Scholar]
- Poiate, E., Jr.; Costa, A.M.; Falcao, J.L. Well Design for Drilling Through Thick Evaporite Layers in Santos Basin—Brazil. In Proceedings of the IADC/SPE Drilling Conference, Miami, FL, USA, 21–23 February 2006. [Google Scholar]
- da Costa, A.; Amaral, C.; Poiate, E.; Pereira, A.; Martha, L.; Gattass, M.; Roehl, D. Underground storage of natural gas and CO2 in salt caverns in deep and ultra-deep water offshore Brazil. In Proceedings of the 12th ISRM Congress, Beijing, China, 16–21 October 2011; pp. 1659–1664. [Google Scholar] [CrossRef]
- Costa, A.M.; Roehl, D.; da Costa, A.M.; Amaral, C.d.S.; Poiate, E., Jr. Rock Mechanics and Computer Modeling Applied in the Design of Underground Salt Caverns Opened by Solution Mining for Brine Production and Natural Gas Storage. In Proceedings of the 13th ISRM International Congress of Rock Mechanics, Montreal, QC, Canada, 10–13 May 2015. [Google Scholar]
- Da Costa, A.M.; Costa, P.V.M.; Miranda, A.C.O.; Goulart, M.B.R.; Bergsten, A.; Meneghini, J.R.; Nishimoto, K.; Assi, G.R.S.; Sampaio, C.M.; Ebecken, N.F.F.; et al. Well Design for the Construction and Operation of an Experimental Salt Cavern Built Offshore in Ultra-Deep Water for CCS in Brasil. In Proceedings of the 54th U.S. Rock Mechanics/Geomechanics Symposium, Physical Event Cancelled, 28 June–1 July 2020. [Google Scholar]
- Fan, M.; Liu, G.; Li, J.; Guo, L.; He, M.; Li, B. Study on Micro-gap Generation Mechanism of Cement Ring Interface Under Thermal Alternating Pressure. Sci. Technol. Eng. 2016, 16, 72–76. [Google Scholar]
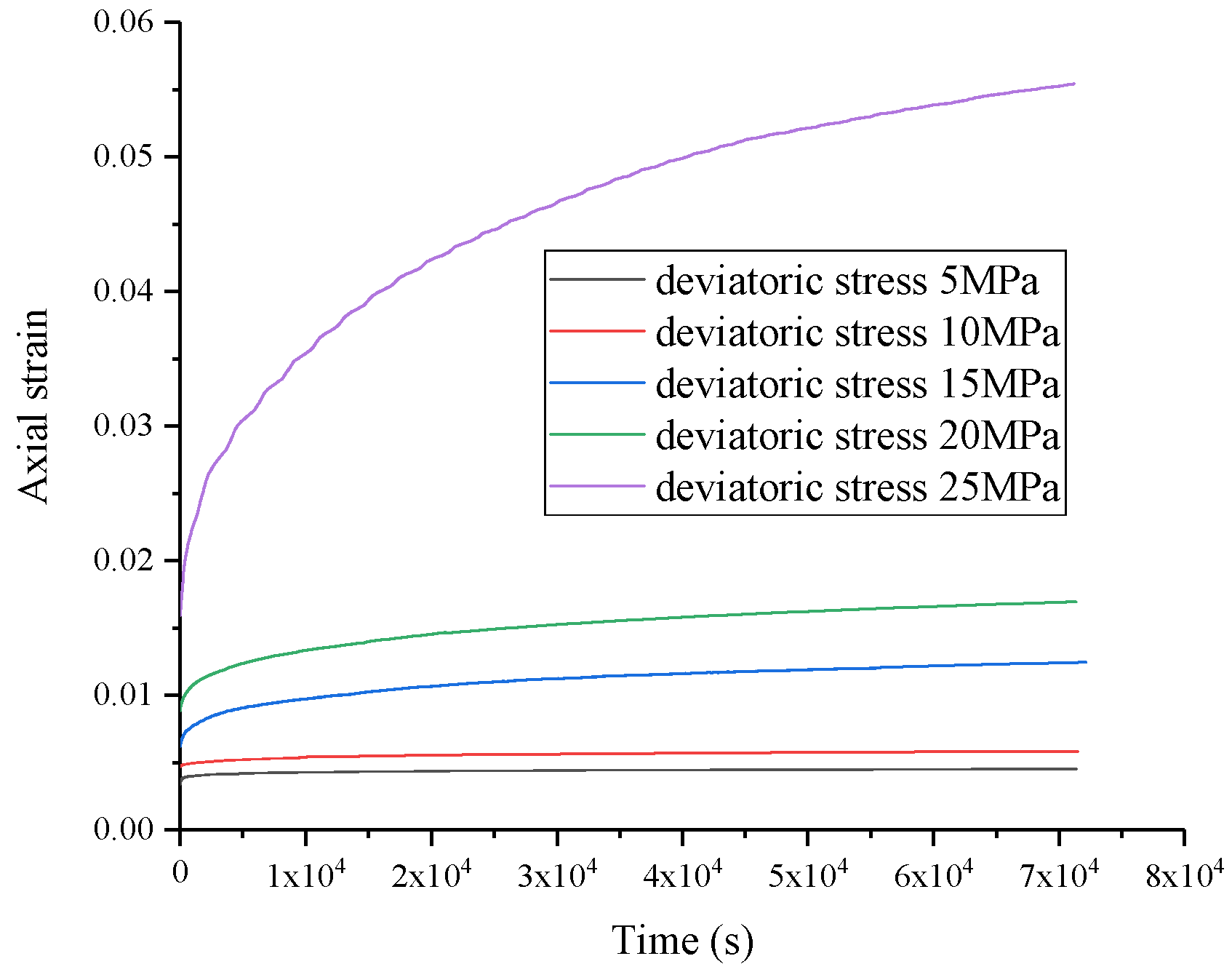
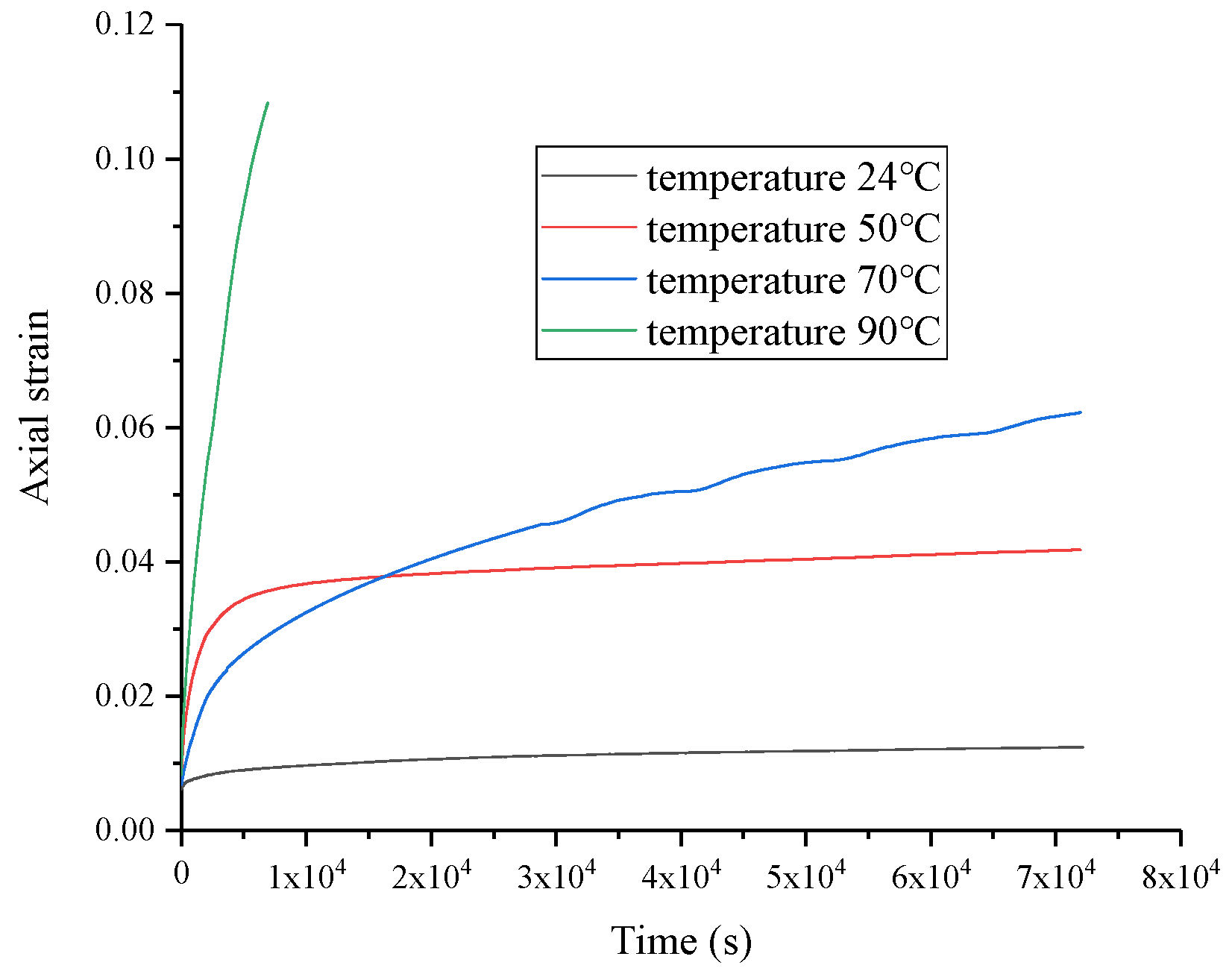







| Sample Number | Confine Pressure/MPa | Axial Pressure/MPa | Deviatoric Stress/MPa | Temperature/°C |
|---|---|---|---|---|
| 1 | 5 | 30 | 25 | 24 |
| 2 | 10 | 30 | 20 | 24 |
| 3 | 15 | 30 | 15 | 24 |
| 4 | 20 | 30 | 10 | 24 |
| 5 | 25 | 30 | 5 | 24 |
| 6 | 15 | 30 | 15 | 50 |
| 7 | 15 | 30 | 15 | 70 |
| 8 | 15 | 30 | 15 | 90 |
| Sample Number | Steady-State Creep Rate/s−1 |
|---|---|
| 1 | 1.782 × 10−7 |
| 2 | 1.192 × 10−7 |
| 3 | 4.199 × 10−8 |
| 4 | 3.687 × 10−8 |
| 5 | 2.543 × 10−9 |
| 6 | 6.655 × 10−8 |
| 7 | 3.753 × 10−7 |
| 8 | 8.534 × 10−6 |
| Material | Inner Diameter/mm | Outer Diameter/mm |
|---|---|---|
| Casing | 247.94 | 282.58 |
| Cement sheath | 282.58 | 320 |
| Formation | 320 | 3200 × 3200 |
| Material | Elastic Modulus/GPa | Poisson’s Ratio | Density/(kg·m−3) | Coefficient of Expansion /10−5 °C−1 | Specific Heat/ (J kg−1·°C−1) | Thermal Conductivity/ (W·m−1·°C−1) |
|---|---|---|---|---|---|---|
| Casing | 210 | 0.3 | 7800 | 1.22 | 460 | 45 |
| Cement sheath | 10.61 | 0.22 | 1800 | 1.05 | 865 | 0.9 |
| Formation | 1.80 | 0.38 | 2300 | 1.03 | 896 | 2.2 |
| Model | Formation Creep | Downhole Temperature Change |
|---|---|---|
| Model A | × | × |
| Model B | ✓ | × |
| Model C | × | ✓ |
| Model D | ✓ | ✓ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Bu, Y.; Jing, S.; Guo, S.; Liu, H. Failure Mechanism of Integrity of Cement Sheath under the Coupling Effect of Formation Creep and Temperature during the Operation of Salt Rock Gas Storage. Energies 2023, 16, 7089. https://doi.org/10.3390/en16207089
Yang H, Bu Y, Jing S, Guo S, Liu H. Failure Mechanism of Integrity of Cement Sheath under the Coupling Effect of Formation Creep and Temperature during the Operation of Salt Rock Gas Storage. Energies. 2023; 16(20):7089. https://doi.org/10.3390/en16207089
Chicago/Turabian StyleYang, Heng, Yuhuan Bu, Shaorui Jing, Shenglai Guo, and Huajie Liu. 2023. "Failure Mechanism of Integrity of Cement Sheath under the Coupling Effect of Formation Creep and Temperature during the Operation of Salt Rock Gas Storage" Energies 16, no. 20: 7089. https://doi.org/10.3390/en16207089
APA StyleYang, H., Bu, Y., Jing, S., Guo, S., & Liu, H. (2023). Failure Mechanism of Integrity of Cement Sheath under the Coupling Effect of Formation Creep and Temperature during the Operation of Salt Rock Gas Storage. Energies, 16(20), 7089. https://doi.org/10.3390/en16207089










