Influence of Cooling Water Parameters on the Thermal Performance of the Secondary Circuit System of a Modular High-Temperature Gas-Cooled Reactor Nuclear Power Plant
Abstract
:1. Introduction
2. Model and Validation
2.1. Description of the Model
2.2. Model Validation
3. Mathematical Model
3.1. Condenser
3.2. Pump
3.3. Evaluation Index
3.4. Prerequisite
- (1)
- Eight operating conditions (100%, 90%, 80%, 70%, 60%, 50%, 40%, and 30% RC) were selected for research. Under the same operating conditions, the thermal power input to the secondary circuit system and main steam mass flow rate remained constant.
- (2)
- The pipeline pressure loss at extraction point I was set to 3%, whereas that for extraction points II, III, IV, and V was assumed to be 5% based on engineering experience.
- (3)
- Water and steam thermal properties were determined according to the IAPWS-IF97 standard [32].
- (4)
- Heat dissipation to the external environment from other components was neglected, in addition to the main steam header and condenser. The main steam underwent a reduction in temperature and pressure from 571 °C and 13.9 MPa at the steam generator outlet to 566 °C and 13.24 MPa, respectively, at the steam turbine inlet.
4. Results and Discussion
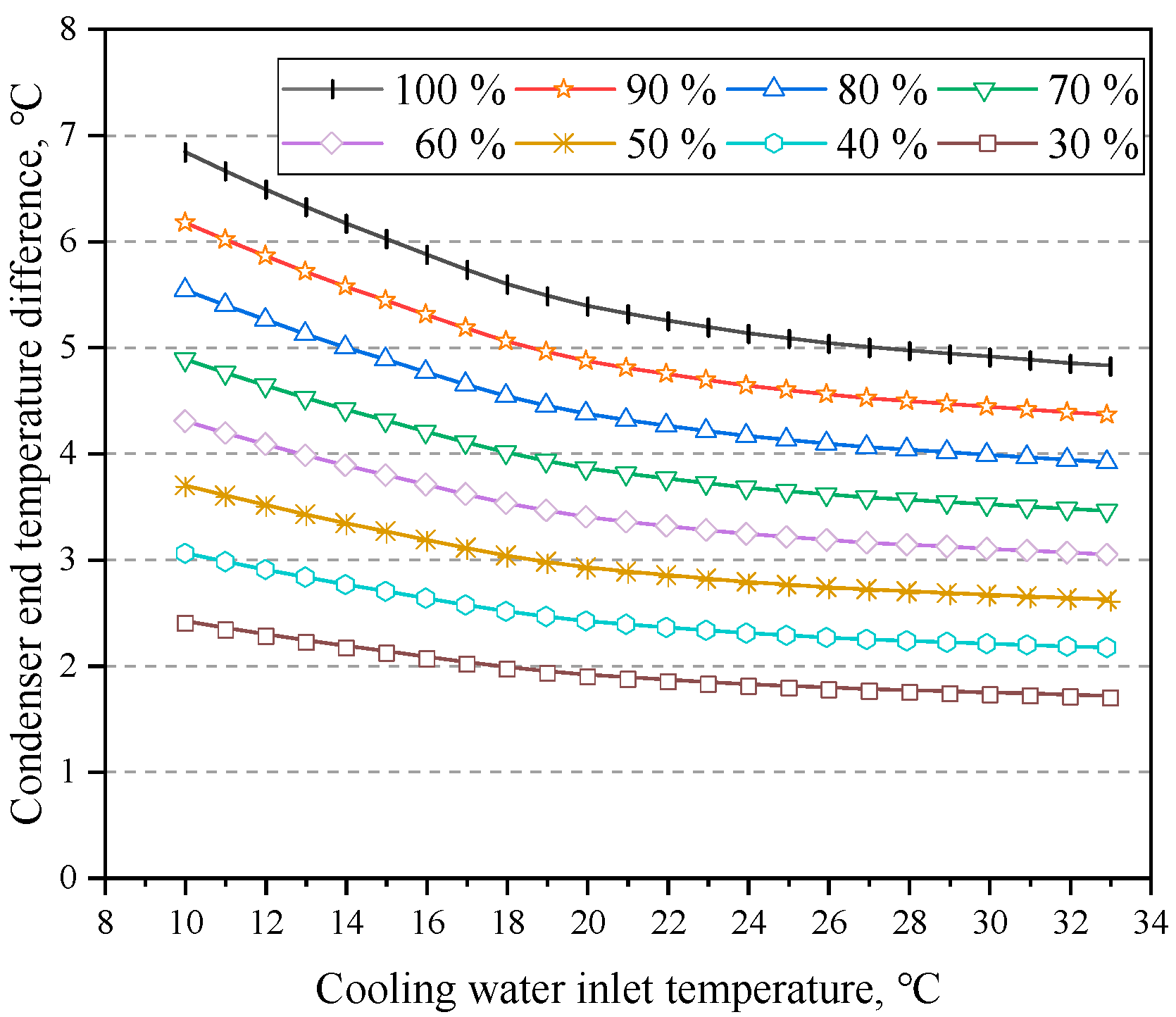
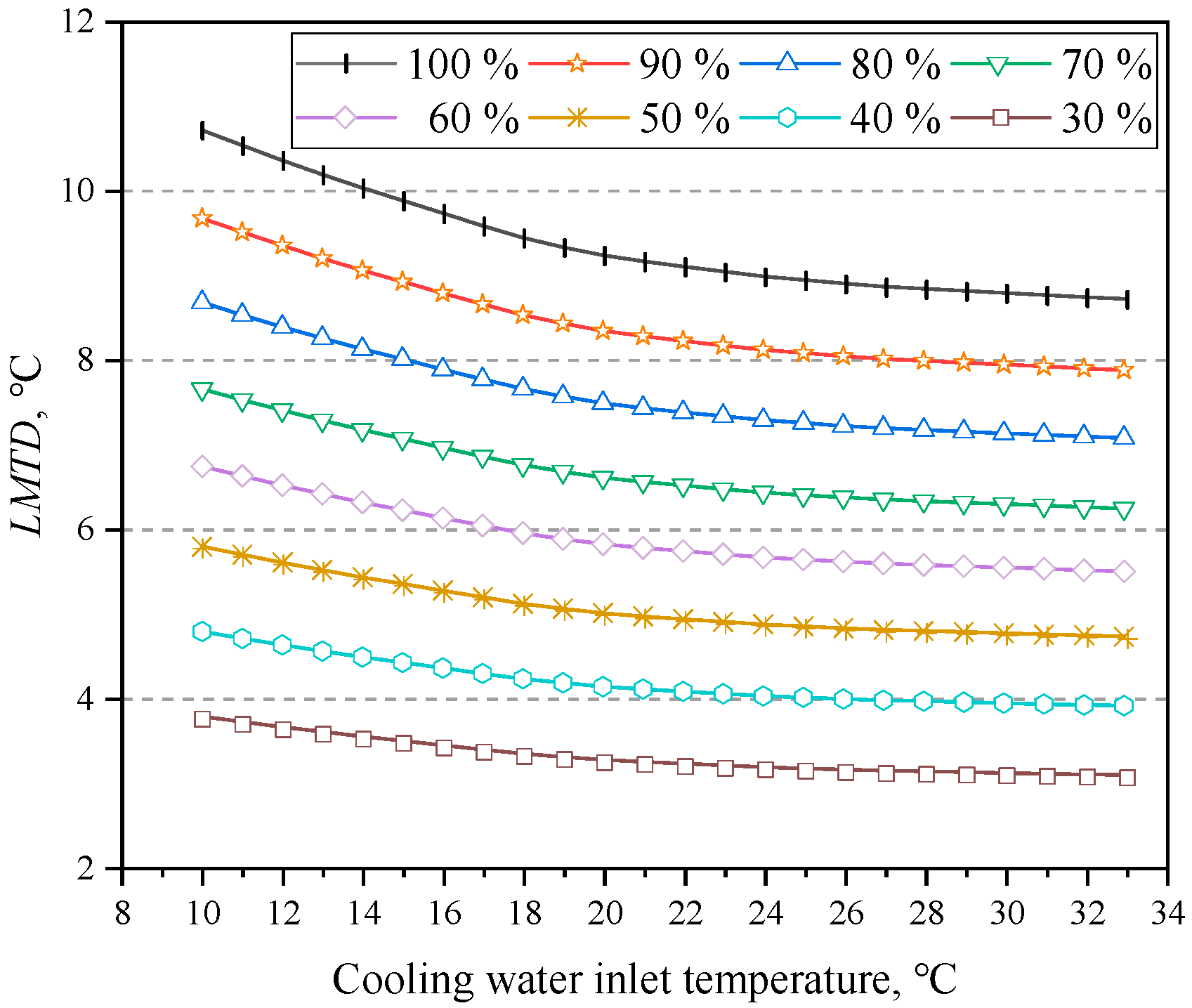
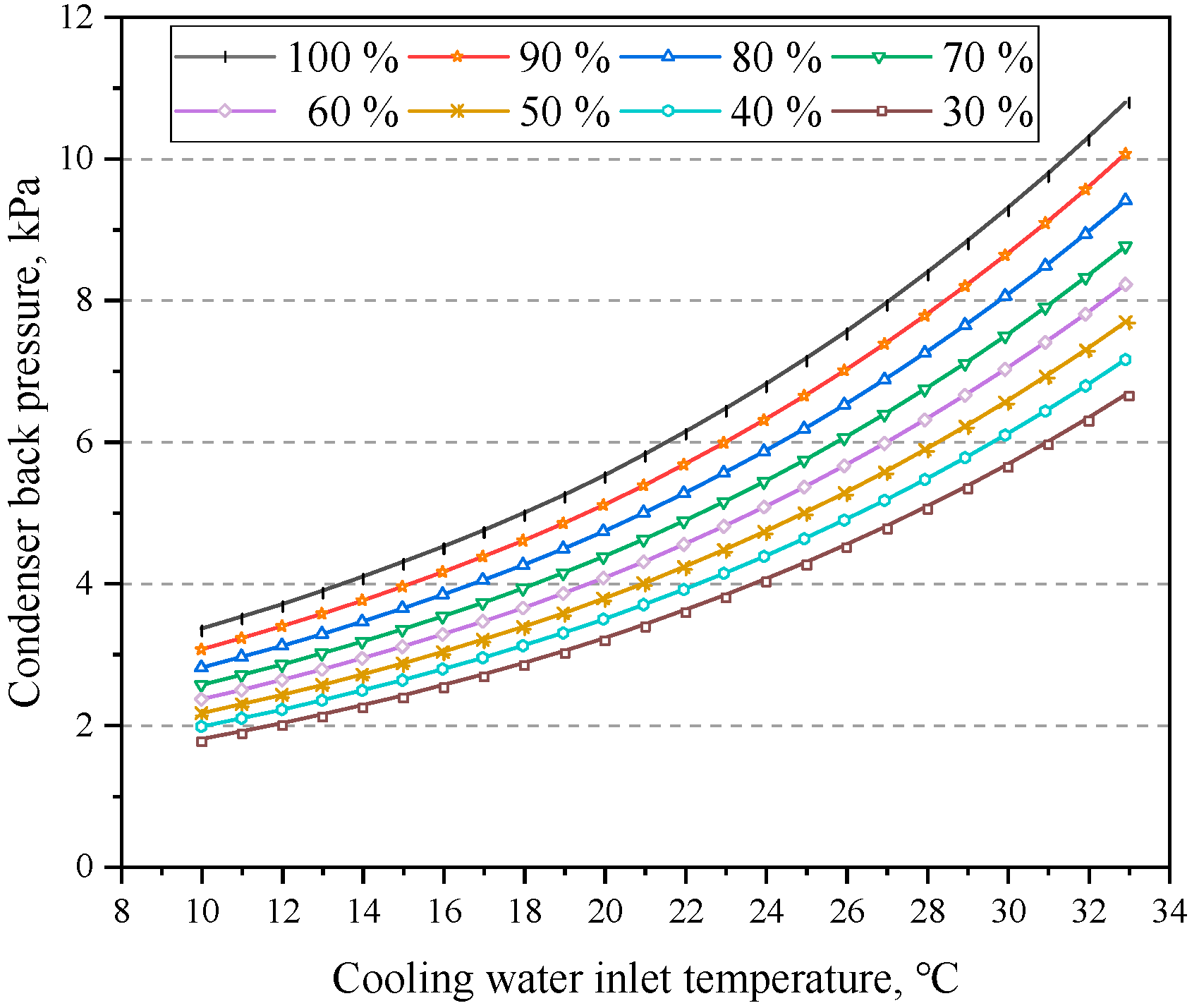
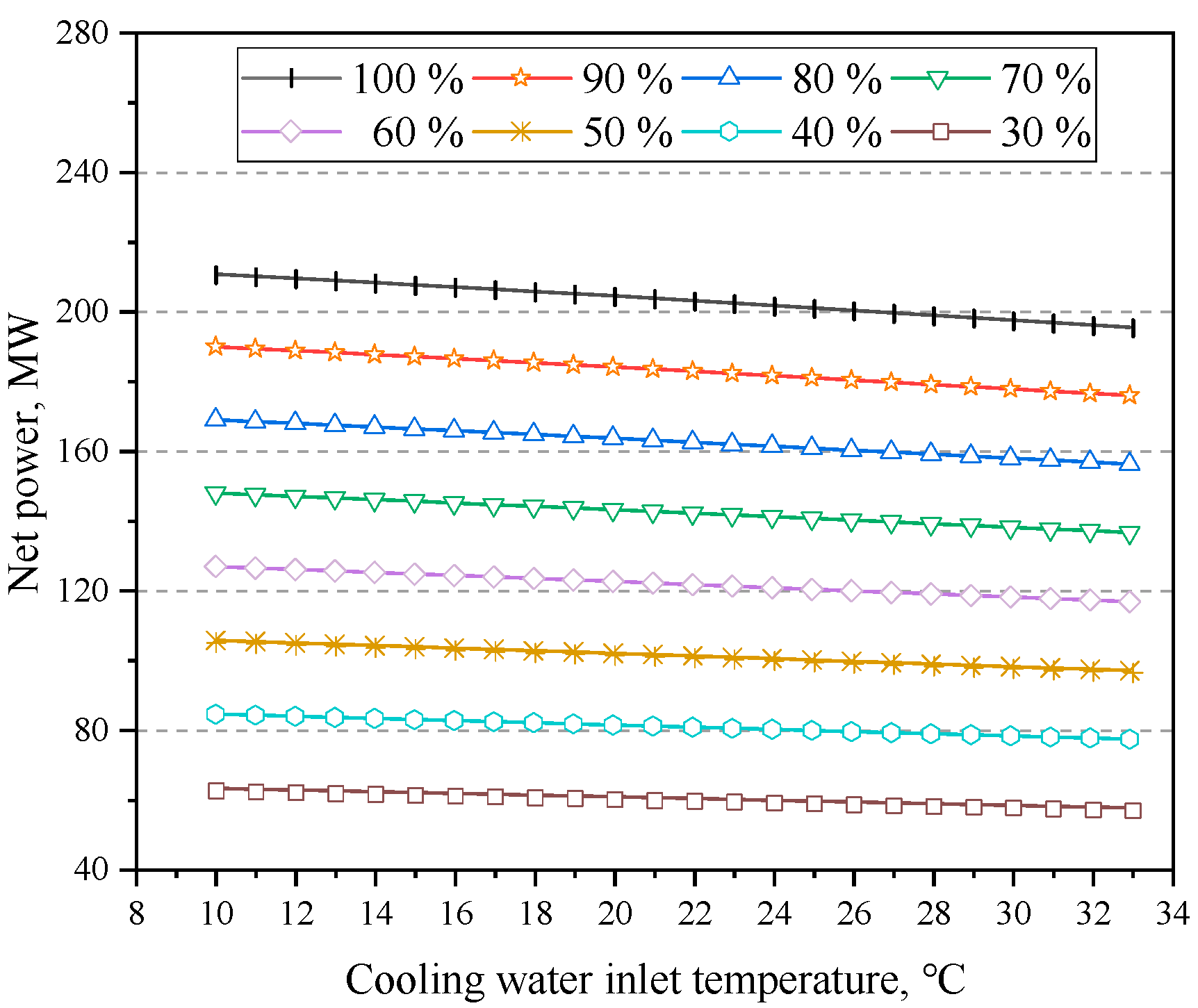
4.1. Influence of Cooling Water Inlet Temperature
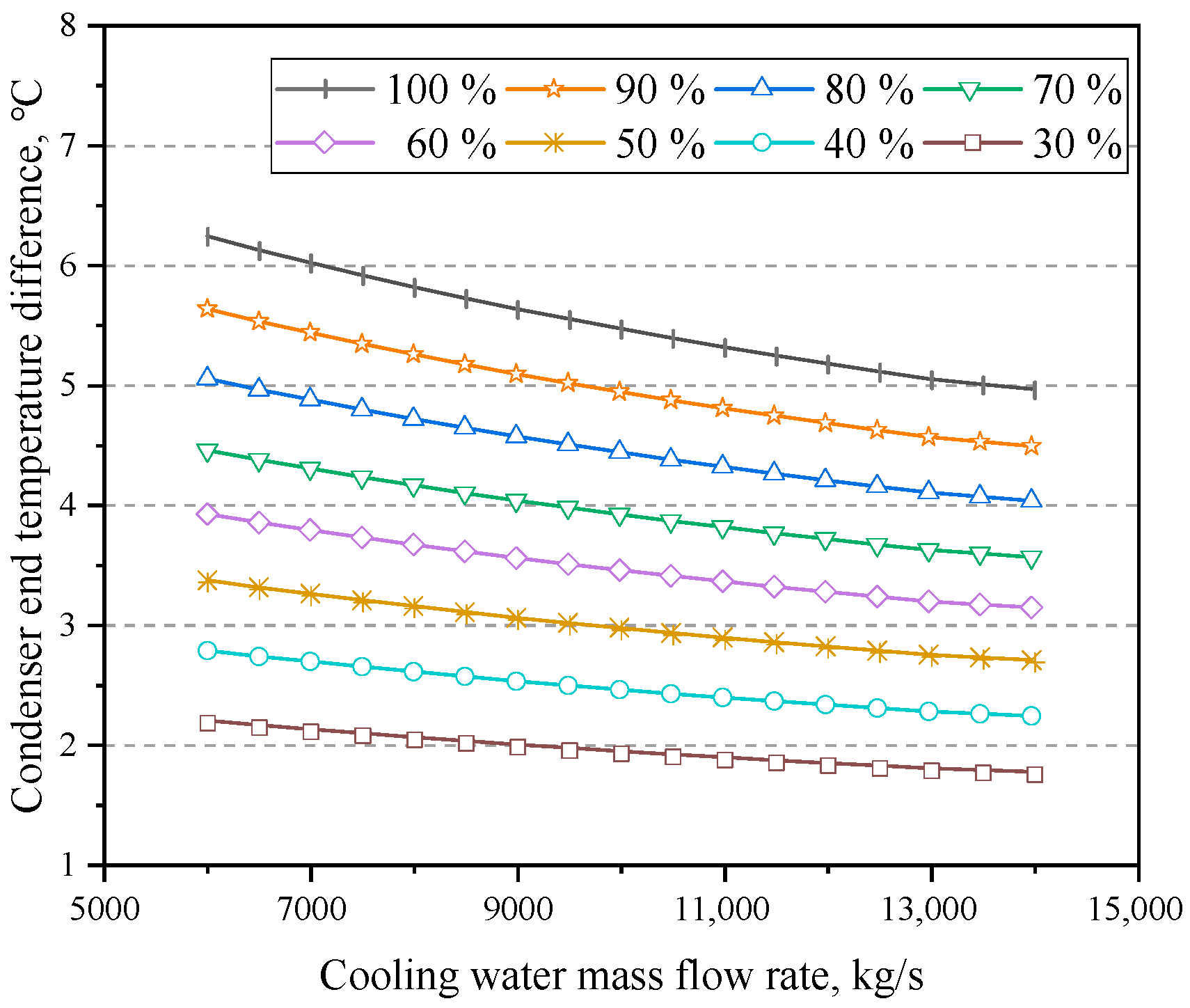
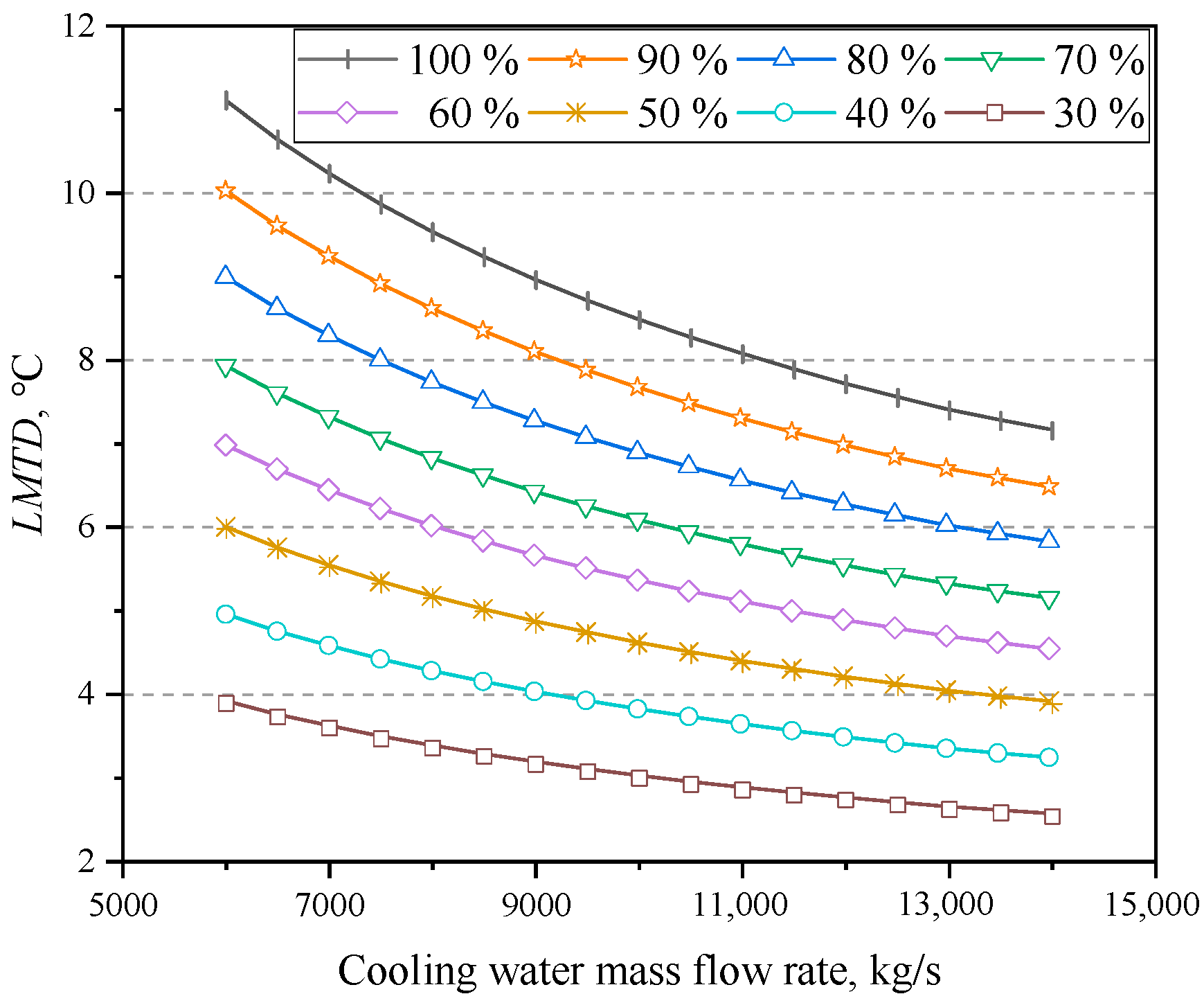
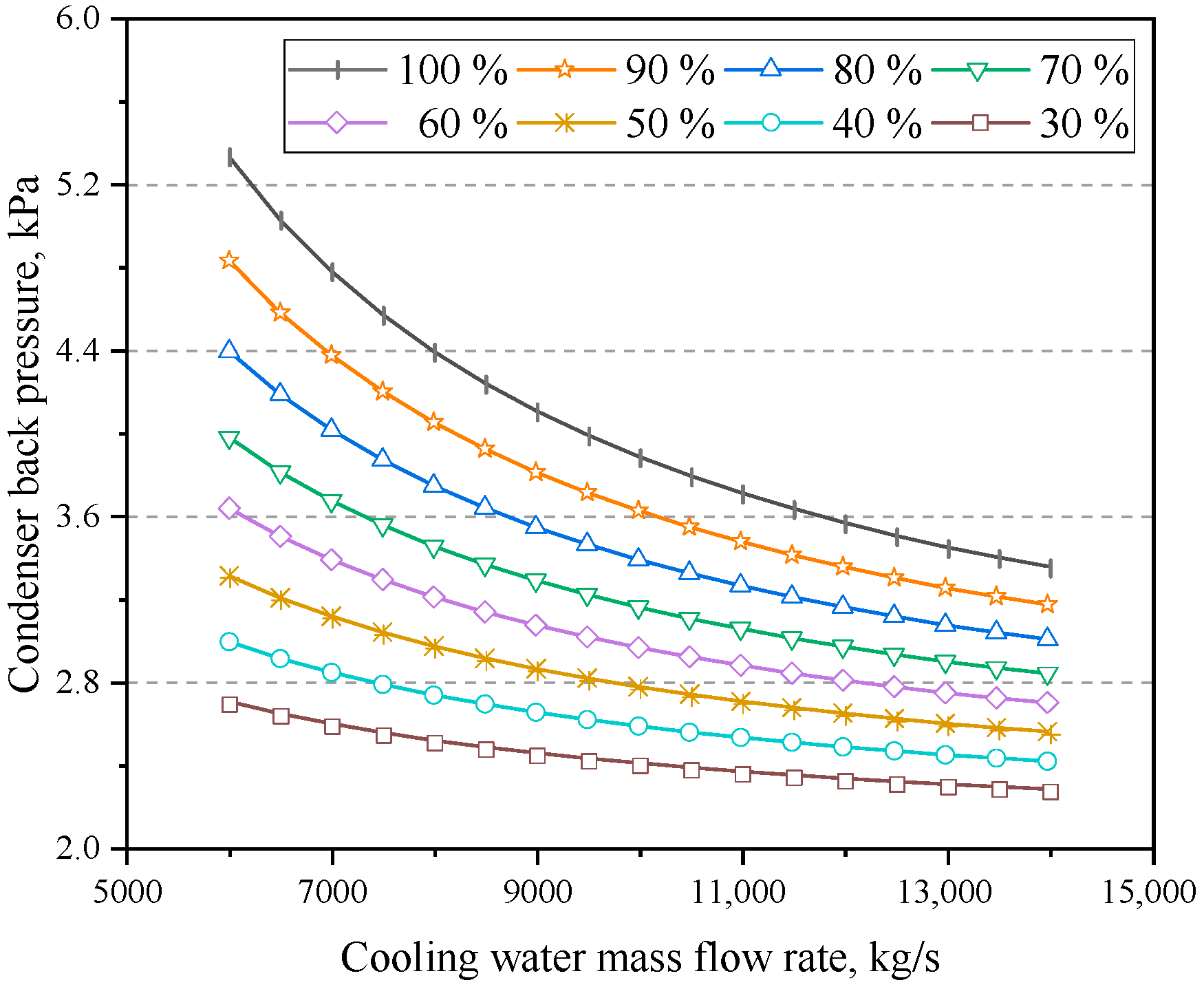
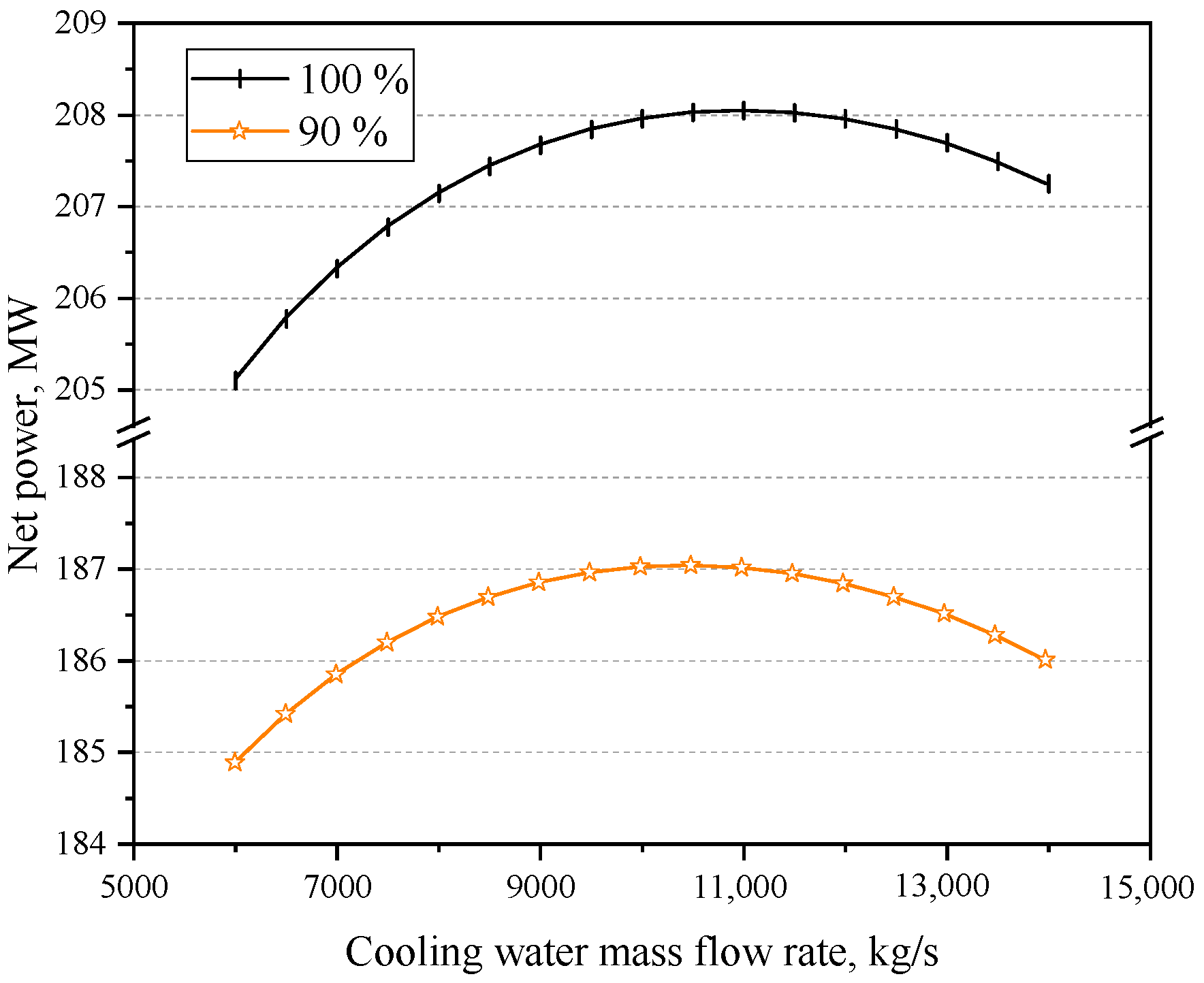
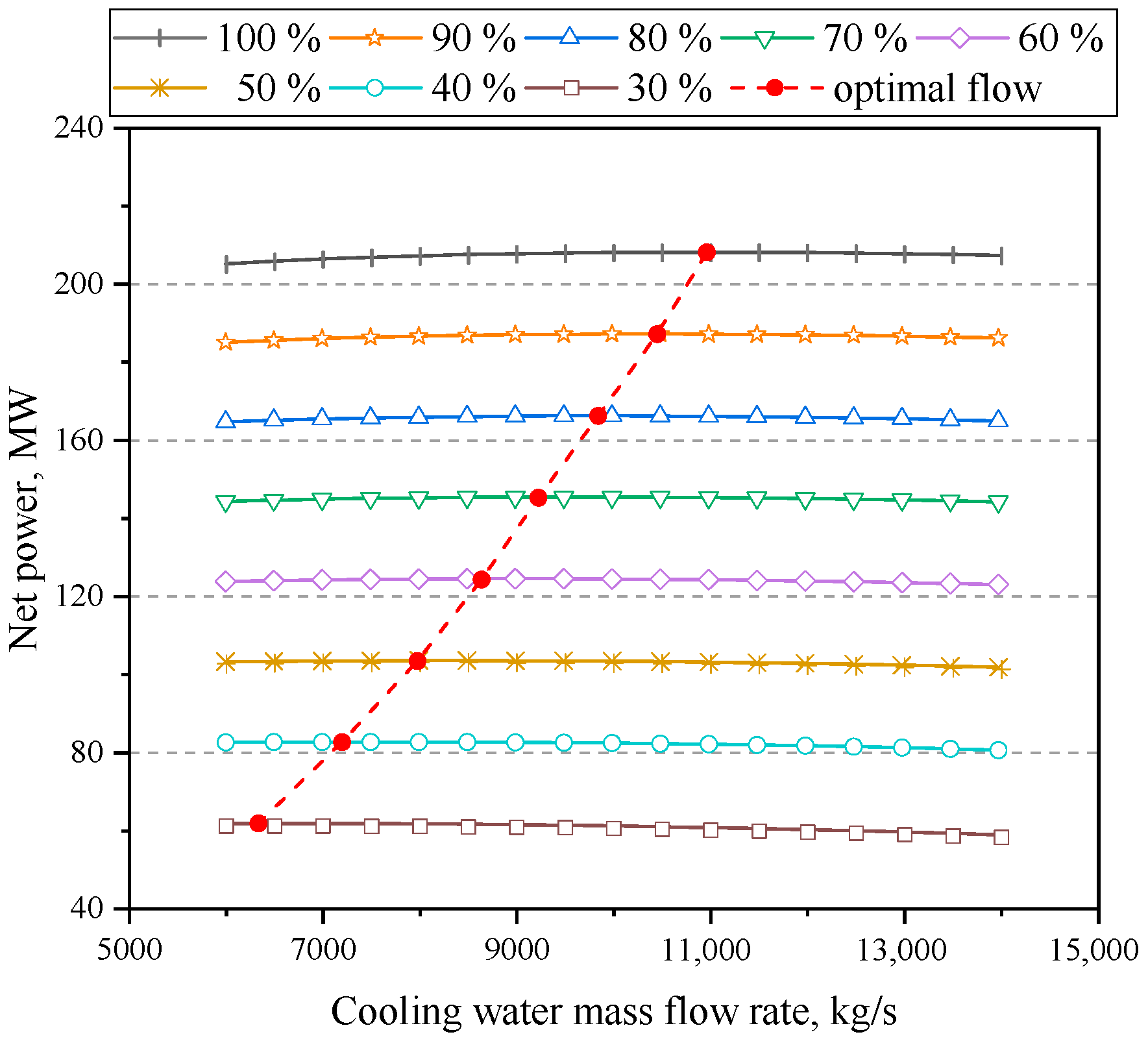
4.2. Influence of Cooling Water Mass Flow Rate
5. Conclusions
- (1)
- Excessive cooling water inlet temperature causes a substantial elevation in condenser back pressure, resulting in a decline in the thermal performance of the unit. Particularly, at a cooling water inlet temperature of 33 °C, the condenser back pressure reached 10.8 kPa, which surpasses the design parameter of 4.5 kPa by a considerable 139.79%. Additionally, under both 100% and 30% RC, the net power decreased by 11.64 and 4.18 MW, respectively, and the cycle efficiencies decreased by 2.36% and 2.57%, respectively. Moreover, the heat consumption rate increased by 510.84 and 702.70 kJ/(kW·h). Furthermore, under 100% RC, a rise in the inlet temperature from 10 °C to 33 °C led to a reduction in the net power and cycle efficiency of the system by 0.67 MW and 0.14%, respectively, with the heat consumption rate escalating by 28.72 kJ/(kW·h) for every 1 °C increment.
- (2)
- Within a certain range, the net power of the system first increased and then decreased as the cooling water mass flow rate increased. By considering the maximum net power as the optimisation goal, the optimal cooling water mass flow rate for various operating conditions can be determined. The findings indicated a nonlinear decrease in the optimal cooling water mass flow rate as the power level decreased.
- (3)
- At a higher power level, appropriately increasing the cooling water mass flow rate can significantly increase the net power, whereas, at a lower power level, the cooling water mass flow rate must be reduced correspondingly to increase the net power. Taking cooling water inlet temperatures of 16 °C and 33 °C, respectively, when the mass flow rate increased from the design value to the optimal value under 100% RC, the net power increased by 1119.49 and 1032.96 kW, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| specific enthalpy, [kJ/kg] | |
| logarithmic mean temperature difference, [°C] | |
| mass flow rate, [kg/s] | |
| temperature, [°C] | |
| steam saturation temperature in condenser, [°C] | |
| pressure, [Pa] | |
| condenser back pressure, [kPa] | |
| specific entropy, [] | |
| heat consumption rate, [] | |
| net power, [] | |
| gross power generation, [] | |
| power consumption, [] | |
| condenser heat transfer rate, [] | |
| thermal power input to the secondary circuit system, [] | |
| Abbreviations | |
| high-pressure | |
| low-pressure | |
| rated condition | |
| Greek letters | |
| cycle efficiency of the system, [%] | |
| isentropic efficiency of the pump, [%] | |
| condenser end temperature difference, [°C] | |
| Subscripts | |
| cycle | |
| condenser | |
| cooling water | |
| isentropic process | |
| inlet | |
| outlet | |
| pump | |
References
- Doe, U.S. A Technology Roadmap for Generation IV Nuclear Energy Systems. In Nuclear Energy Research Advisory Committee and the Generation IV International Forum; Doene: Berryville, VA, USA, 2002; pp. 9–11. [Google Scholar]
- Kugeler, K.; Zhang, Z. Modular High-Temperature Gas-Cooled Reactor Power Plant; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Wang, J.; Ding, M.; Yang, X.; Wang, J. Performance comparison and optimization of two configurations of (Very) high temperature gas-cooled reactors combined cycles. Ann. Nucl. Energy 2016, 94, 279–287. [Google Scholar] [CrossRef]
- Qu, X.; Zhao, G.; Wang, J. Thermodynamic evaluation of hydrogen and electricity cogeneration coupled with very high temperature gas-cooled reactors. Int. J. Hydrogen Energy 2021, 46, 29065–29075. [Google Scholar] [CrossRef]
- Ni, H.; Qu, X.; Peng, W.; Zhao, G.; Zhang, P. Study of two innovative hydrogen and electricity co-production systems based on very-high-temperature gas-cooled reactors. Energy 2023, 273, 127206. [Google Scholar] [CrossRef]
- Haneklaus, N.; Schröders, S.; Zheng, Y.; Allelein, H.-J. Economic evaluation of flameless phosphate rock calcination with concentrated solar power and high temperature reactors. Energy 2017, 140, 1148–1157. [Google Scholar] [CrossRef]
- Gao, Q.; Zhang, P.; Sun, Q.; Zhang, P.; Chen, S.; Peng, W. Experimental and numerical investigation of sulfuric acid decomposition for hydrogen production via iodine–sulfur cycle. Energy Convers. Manag. 2023, 289, 117167. [Google Scholar] [CrossRef]
- Lin, X.; Song, H.; Wang, L.; Guo, Y.; Liu, Y. Cold-end integration of thermal system in a 1000 MW ultra-supercritical double reheat power plant. Appl. Therm. Eng. 2021, 193, 116982. [Google Scholar] [CrossRef]
- Wang, C.; Liu, M.; Zhao, Y.; Qiao, Y.; Chong, D.; Yan, J. Dynamic modeling and operation optimization for the cold end system of thermal power plants during transient processes. Energy 2018, 145, 734–746. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, R. Optimization for steam turbine cold-end system of a nuclear power plant and sensitivity analysis. J. Nucl. Eng. Radiat. Sci. 2017, 3, 014501. [Google Scholar] [CrossRef]
- Ahmad, A.; Covatariu, A.; Ramana, M.V. A stormy future? Financial impact of climate change-related disruptions on nuclear power plant owners. Util. Policy 2023, 81, 101484. [Google Scholar] [CrossRef]
- EDF. Annual Results 2022 Presentation. Available online: https://www.edf.fr/sites/groupe/files/2023-04/annual-results-2022-presentation-2023-02-17-v3-2.pdf (accessed on 28 July 2023).
- Laskowski, R.; Theibech, M.; Uzunow, N. The effect of cooling water temperature on the performance of a BWR nuclear power plant. Mod. Eng. 2021, 3, 5–13. Available online: https://mengineering.eu/index.php/me/article/view/85/81 (accessed on 28 July 2023).
- Attia, S.I. The influence of condenser cooling water temperature on the thermal efficiency of a nuclear power plant. Ann. Nucl. Energy 2015, 80, 371–378. [Google Scholar] [CrossRef]
- Durmayaz, A.; Sogut, O.S. Influence of cooling water temperature on the efficiency of a pressurized-water reactor nuclear-power plant. Int. J. Energy Res. 2006, 30, 799–810. [Google Scholar] [CrossRef]
- Laković, M.S.; Stojiljković, M.M.; Laković, S.V.; Stefanović, V.P.; Mitrović, D.D. Impact of the cold end operating conditions on energy efficiency of the steam power plants. Therm. Sci. 2010, 14, 53–66. [Google Scholar] [CrossRef]
- Ahmadi, G.R.; Toghraie, D. Energy and exergy analysis of Montazeri Steam Power Plant in Iran. Renew. Sustain. Energy Rev. 2016, 56, 454–463. [Google Scholar] [CrossRef]
- Medica-Viola, V.; Pavković, B.; Mrzljak, V. Numerical model for on-condition monitoring of condenser in coal-fired power plants. Int. J. Heat Mass Transf. 2018, 117, 912–923. [Google Scholar] [CrossRef]
- Harish, R.; Subhramanyan, E.E.; Madhavan, R.; Vidyanand, S. Theoretical model for evaluation of variable frequency drive for cooling water pumps in sea water based once through condenser cooling water systems. Appl. Therm. Eng. 2010, 30, 2051–2057. [Google Scholar] [CrossRef]
- Xia, L.; Liu, D.; Zhou, L.; Wang, P.; Chen, Y. Optimization of a seawater once-through cooling system with variable speed pumps in fossil fuel power plants. Int. J. Therm. Sci. 2015, 91, 105–112. [Google Scholar] [CrossRef]
- Wang, W.; Liu, J.; Zeng, D.; Lin, Z.; Cui, C. Variable-speed technology used in power plants for better plant economics and grid stability. Energy 2012, 45, 588–594. [Google Scholar] [CrossRef]
- Zhang, W.; Ma, L.; Jia, B.; Zhang, Z.; Liu, Y.; Duan, L. Optimization of the circulating cooling water mass flow in indirect dry cooling system of thermal power unit using artificial neural network based on genetic algorithm. Appl. Therm. Eng. 2023, 223, 120040. [Google Scholar] [CrossRef]
- Laskowski, R.; Smyk, A.; Lewandowski, J.; Rusowicz, A.; Grzebielec, A. Selecting the cooling water mass flow rate for a power plant under variable load with entropy generation rate minimization. Energy 2016, 107, 725–733. [Google Scholar] [CrossRef]
- Wu, T.; Wei, H.; Ge, Z.; Yang, L.; Du, X. Cooling water mass flow optimization for indirect dry cooling system of thermal power unit under variable output load. Int. J. Heat Mass Transf. 2019, 133, 1–10. [Google Scholar] [CrossRef]
- Btaszczyk, A.; Gfuch, J.; Gardzilewicz, A. Operating and economic conditions of cooling water control for marine steam turbine condensers. Pol. Mar. Res. 2011, 18, 48–54. [Google Scholar] [CrossRef]
- Laskowski, R.; Smyk, A.; Rusowicz, A.; Grzebielec, A. Optimization of the cooling water mass flow rate under variable load of a power unit. Appl. Therm. Eng. 2021, 191, 116874. [Google Scholar] [CrossRef]
- Dong, L.; Zhou, Z. Simulation study on the condensing system of high-temperature reactor demonstration power station HTR-PM 200 based on Vpower. Shenyang Inst. Eng. (Nat. Sci.) 2011, 7, 16–19. [Google Scholar] [CrossRef]
- Laskowski, R. Relations for steam power plant condenser performance in off-design conditions in the function of inlet parameters and those relevant in reference conditions. Appl. Therm. Eng. 2016, 103, 528–536. [Google Scholar] [CrossRef]
- Laskowski, R.; Smyk, A.; Rusowicz, A.; Grzebielec, A. A useful formulas to describe the performance of a steam condenser in off-design conditions. Energy 2020, 204, 117910. [Google Scholar] [CrossRef]
- Yang, T.; Wang, W.; Zeng, D.; Liu, J.; Cui, C. Closed-loop optimization control on fan speed of air-cooled steam condenser units for energy saving and rapid load regulation. Energy 2017, 135, 394–404. [Google Scholar] [CrossRef]
- Feng, H.; Wang, M.; Wang, N.; Xu, Y.; He, S.; Gao, M. Influence of environmental parameters on the cold-end and thermal system of coal-fired power plant based on Ebsilon simulation. Therm. Sci. Eng. Prog. 2022, 32, 101340. [Google Scholar] [CrossRef]
- IAPWS-IF97; Revised Release on the IAPWS Industrial Formulation 1997 for the Thermodynamic Properties of Water and Steam. The International Association for the Properties of Water and Steam: Oakville, ON, Canada, 2007.
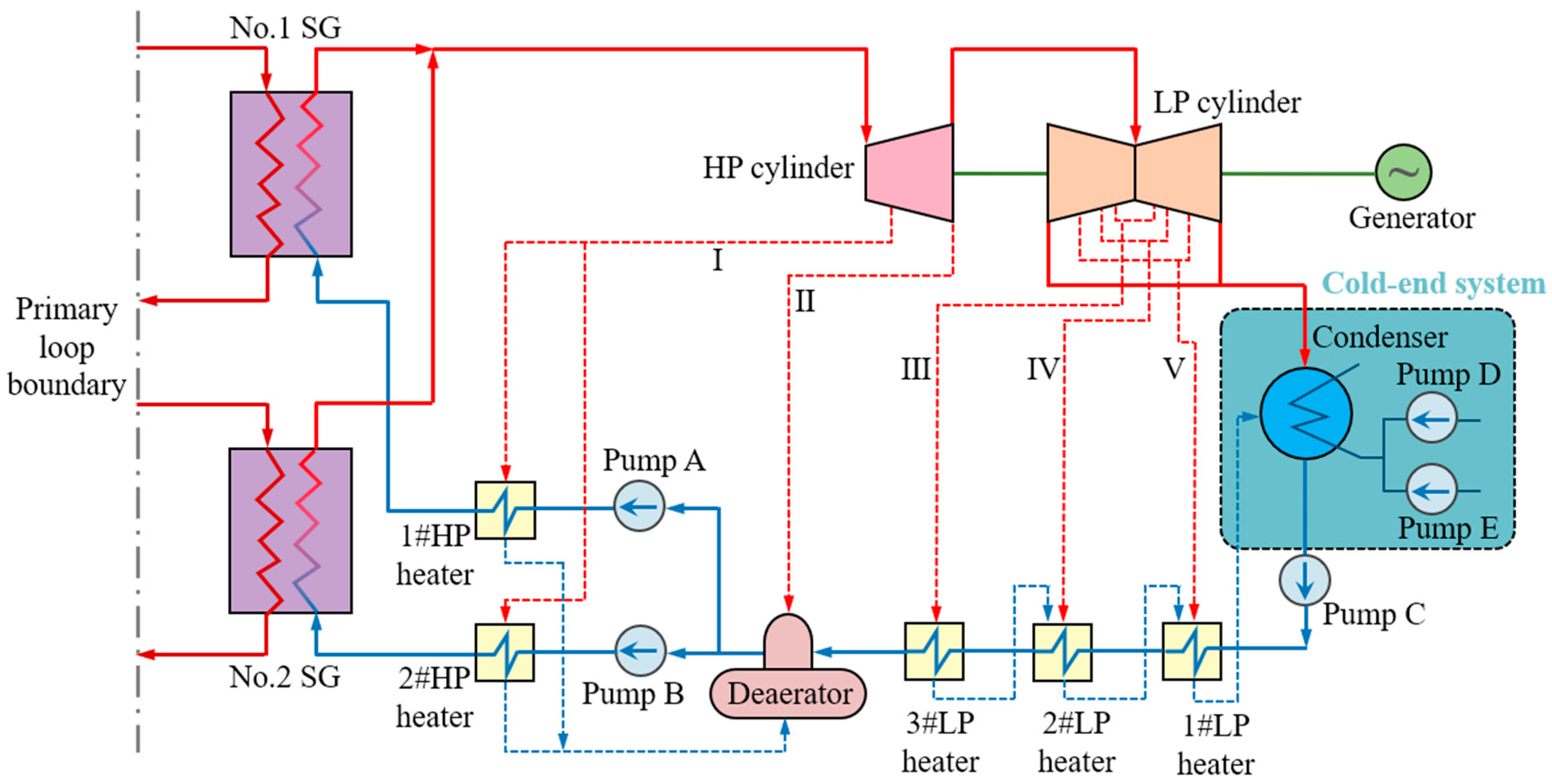
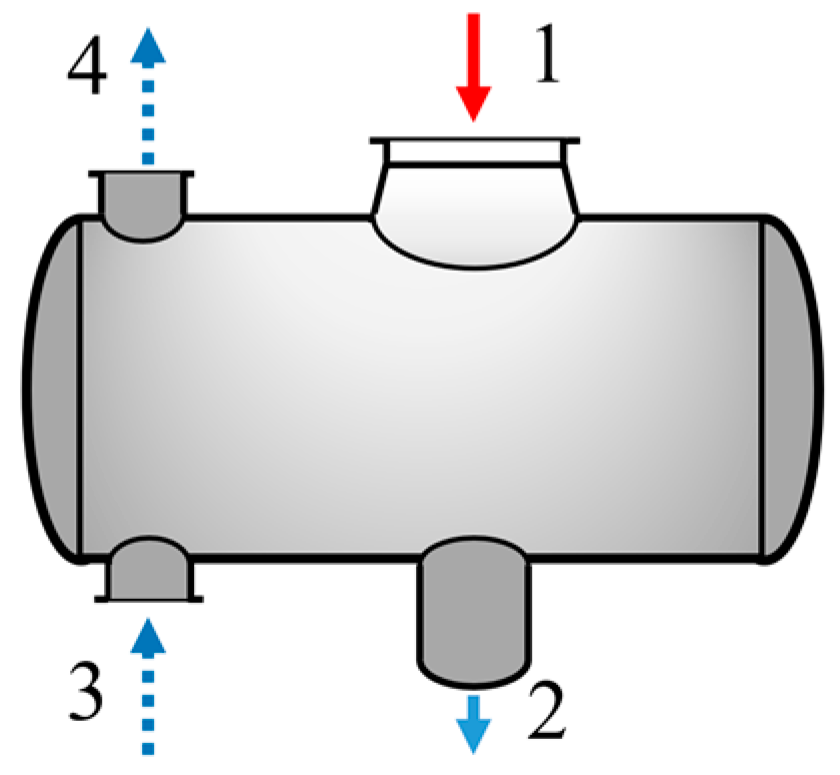


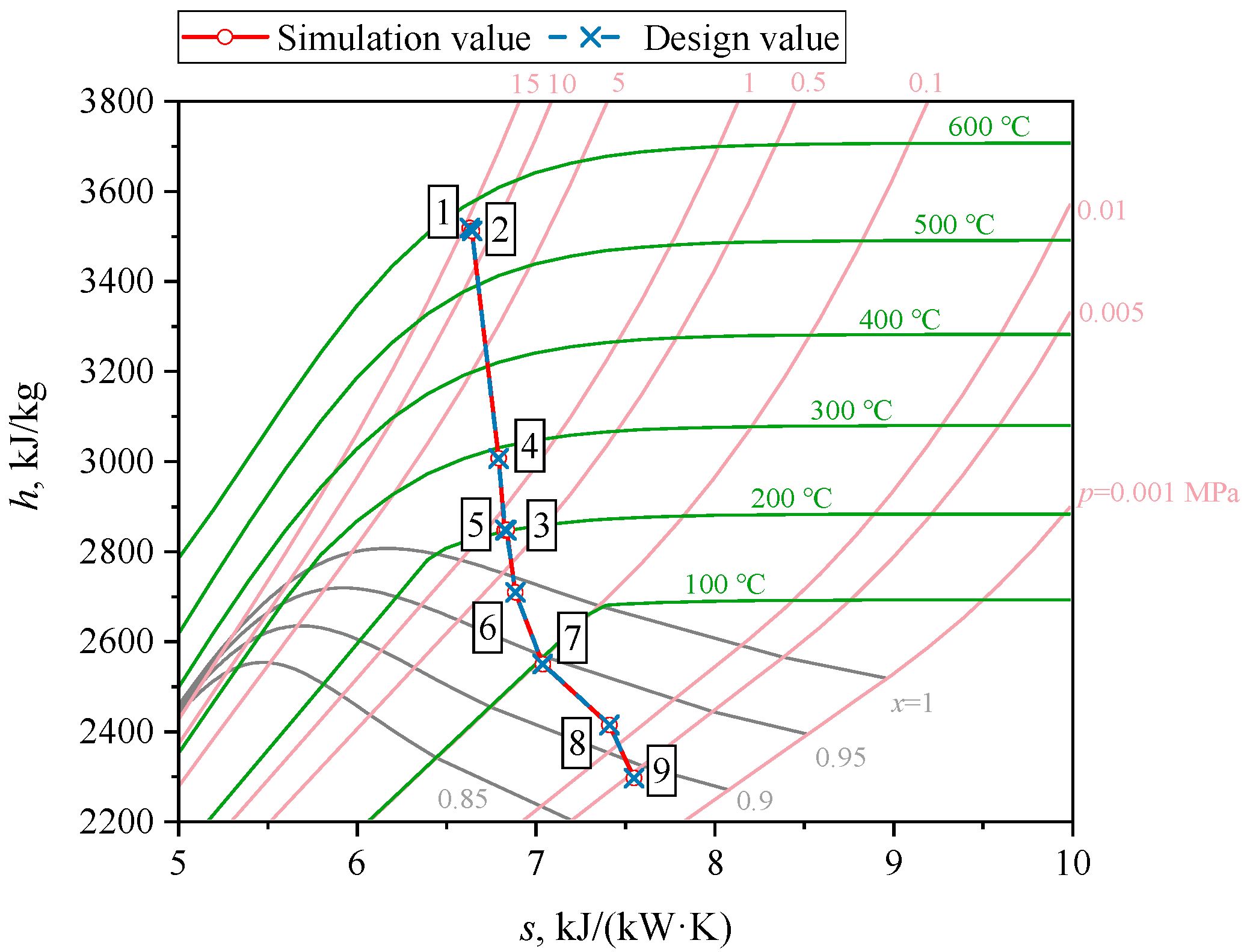

| Parameter | Unit | Value |
|---|---|---|
| Thermal power of reactor module | MWth | 250 |
| Number of reactor modules | - | 2 |
| Main steam temperature | °C | 566 |
| Main steam pressure | MPa | 13.24 |
| Main feed water temperature | °C | 205 |
| Condenser back pressure | kPa | 4.5 |
| Item | Unit | Value |
|---|---|---|
| Tube material | - | titanium |
| Heat transfer surface area | m2 | 12,000 |
| Tube outer diameter | mm | 28 |
| Tube inner diameter | mm | 27 |
| Length of tubes | mm | 1084 |
| Cooling water inlet temperature | °C | 16 |
| Maximum cooling water inlet temperature | °C | 33 |
| Cleanliness factor | - | 0.85 |
| Cooling water mass flow rate | kg/s | 7697.61 |
| Operating Condition, % RC | Relative Error, % | ||
|---|---|---|---|
| Main Steam Mass Flow Rate, kg/s | Main Feed Water Temperature, °C | Deaerator Pressure, MPa | |
| 100 | 0 | −0.01 | 0.00 |
| 90 | −0.13 | −0.04 | −0.13 |
| 75 | −0.56 | −0.14 | −0.38 |
| 50 | −0.69 | 0.18 | 0.8 |
| 30 | −2.98 | −0.19 | −0.57 |
| Extraction Point | Relative Error, % | ||
|---|---|---|---|
| Mass Flow Rate, kg/s | Pressure, MPa | Specific Enthalpy, kJ/kg | |
| I | −0.88 | −0.54 | −0.01 |
| II | −0.37 | −0.38 | 0.00 |
| III | −0.69 | −0.51 | 0.00 |
| IV | −1.03 | −0.48 | −0.11 |
| V | 0.11 | 2.42 | 0.06 |
| Operating Condition, % RC | Cooling Water Inlet Temperature, °C | Cycle Efficiency, % | Heat Consumption Rate, kJ/(kW·h) | Net Power, MW |
|---|---|---|---|---|
| 100 | 10 | 0.75 | −149.66 | 3.68 |
| 33 | −2.36 | 510.84 | −11.64 | |
| 30 | 10 | 0.90 | −224.55 | 1.47 |
| 33 | −2.57 | 702.70 | −4.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhao, G.; Qu, X.; Yang, X.; Wang, J.; Wang, P. Influence of Cooling Water Parameters on the Thermal Performance of the Secondary Circuit System of a Modular High-Temperature Gas-Cooled Reactor Nuclear Power Plant. Energies 2023, 16, 6560. https://doi.org/10.3390/en16186560
Wang X, Zhao G, Qu X, Yang X, Wang J, Wang P. Influence of Cooling Water Parameters on the Thermal Performance of the Secondary Circuit System of a Modular High-Temperature Gas-Cooled Reactor Nuclear Power Plant. Energies. 2023; 16(18):6560. https://doi.org/10.3390/en16186560
Chicago/Turabian StyleWang, Xin, Gang Zhao, Xinhe Qu, Xiaoyong Yang, Jie Wang, and Peng Wang. 2023. "Influence of Cooling Water Parameters on the Thermal Performance of the Secondary Circuit System of a Modular High-Temperature Gas-Cooled Reactor Nuclear Power Plant" Energies 16, no. 18: 6560. https://doi.org/10.3390/en16186560
APA StyleWang, X., Zhao, G., Qu, X., Yang, X., Wang, J., & Wang, P. (2023). Influence of Cooling Water Parameters on the Thermal Performance of the Secondary Circuit System of a Modular High-Temperature Gas-Cooled Reactor Nuclear Power Plant. Energies, 16(18), 6560. https://doi.org/10.3390/en16186560





