A Current Control Method for Grid-Connected Inverters
Abstract
:1. Introduction
- (1)
- By introducing the compensation unit, the proposed control method can greatly enhance the system’s phase margin and stability. Also, a mathematical model is constructed, and the system bode diagrams for the conventional and proposed controls are compared.
- (2)
- The effect of two parameters in the compensation unit is investigated. Furthermore, an optimization method is proposed to determine optimal parameters.
- (3)
- To handle weak-grid conditions, the proposed scheme is expanded by including the compensation unit in the grid’s feed-forward loop.
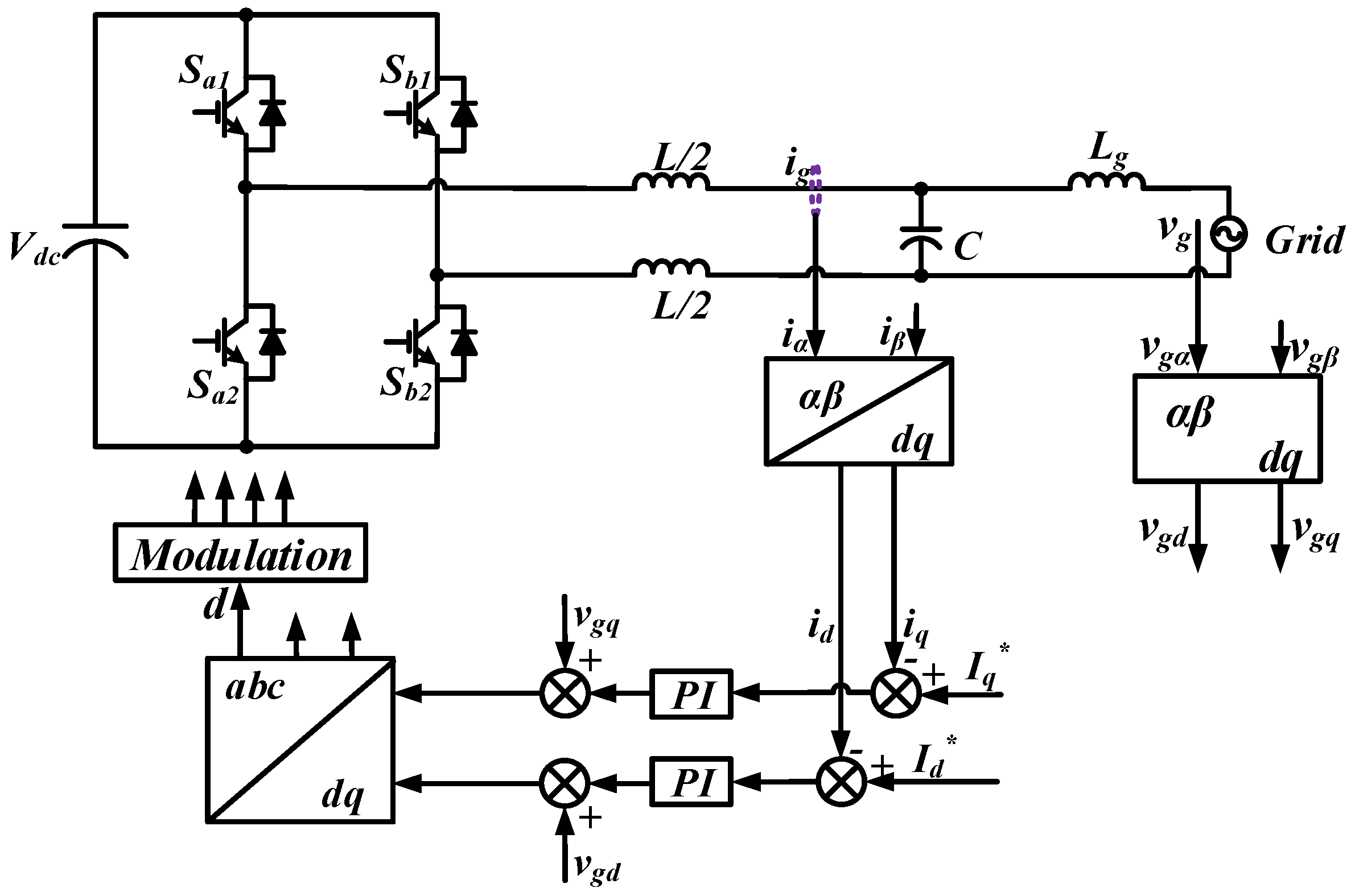
2. System Setup and Method
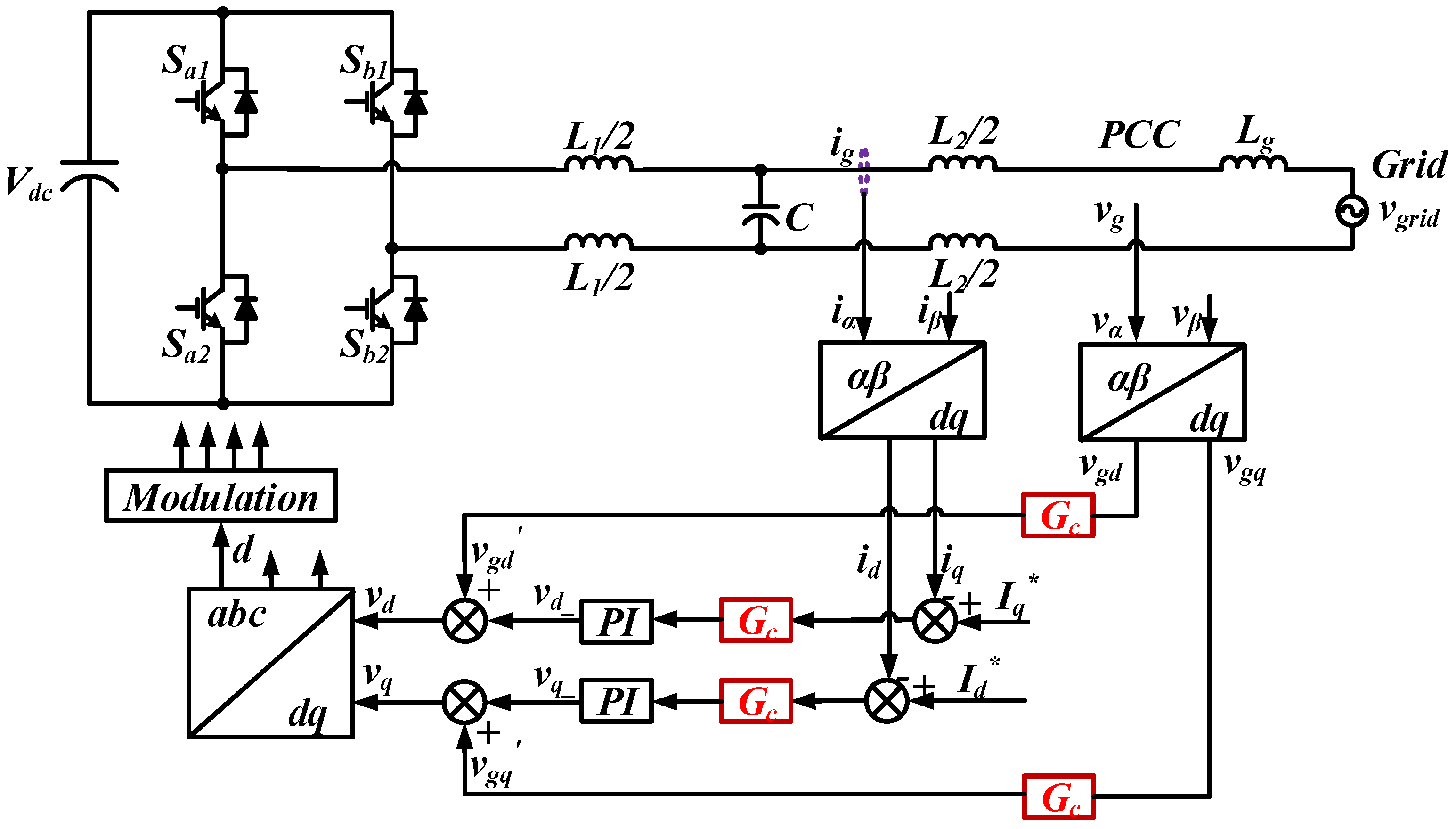
2.1. System Setup and Conventional Control Method
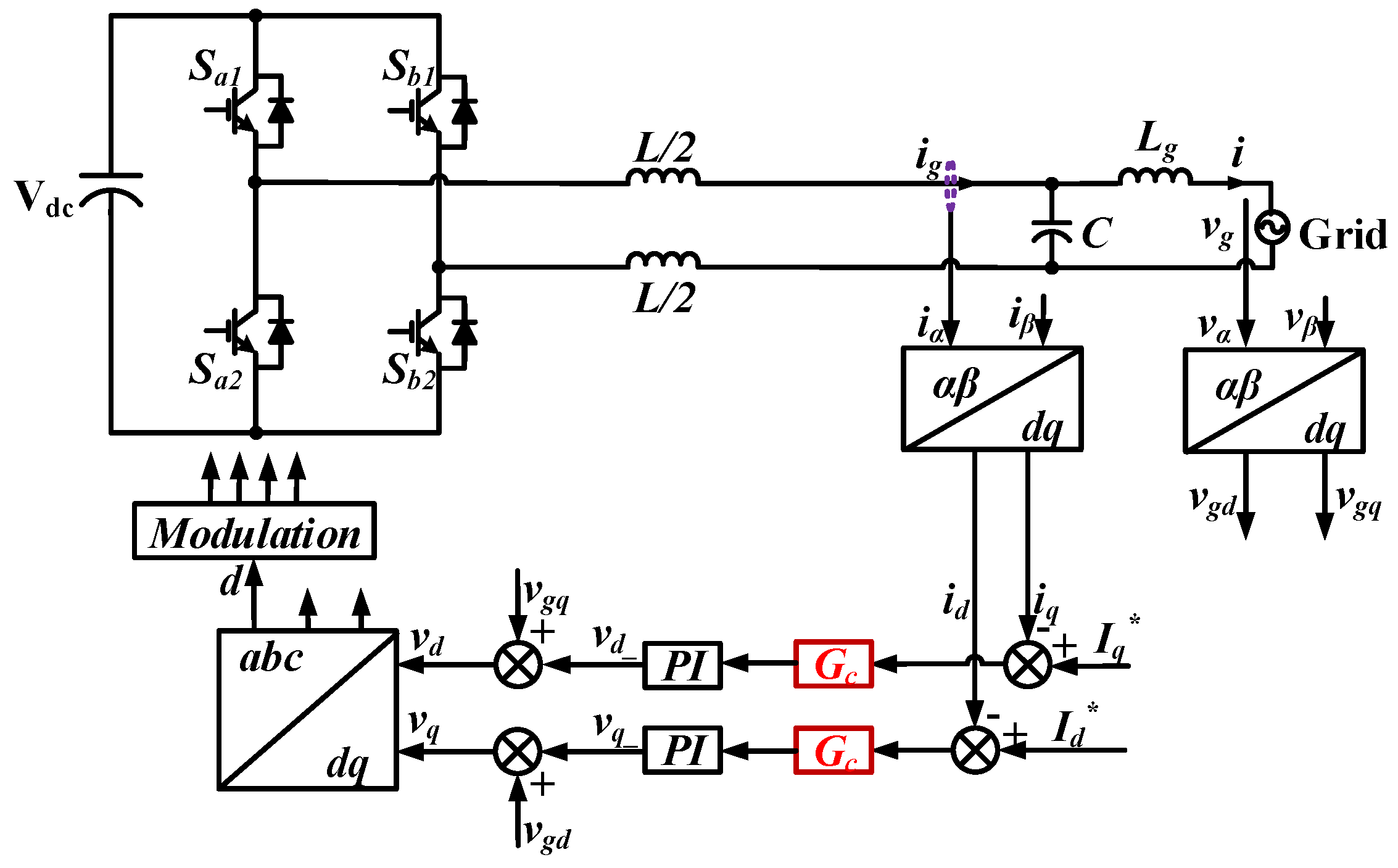
2.2. Proposed Control Method
3. Results and Discussion
3.1. Simulation Result Comparison
3.2. Discussion on Impact of Compensation Unit Parameters
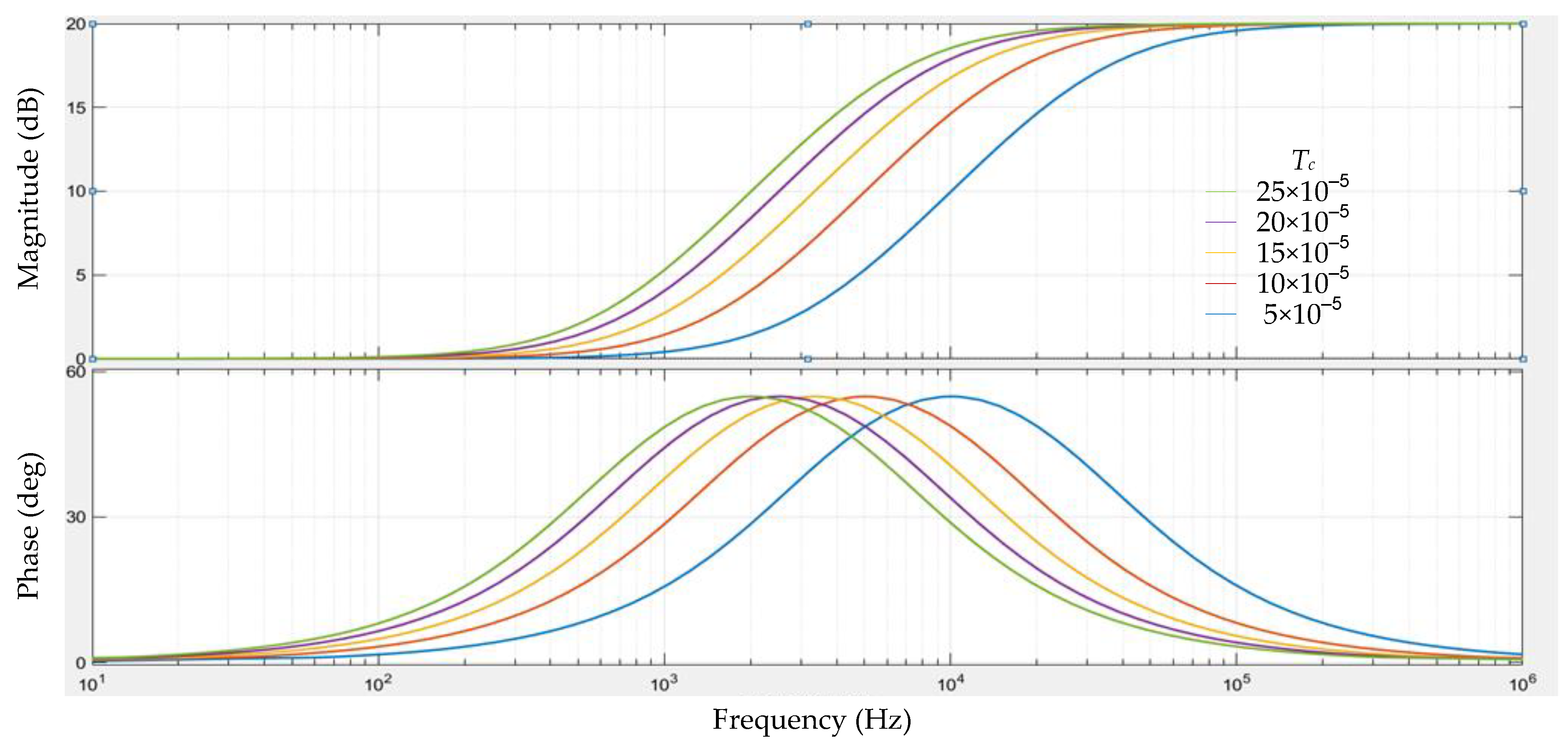
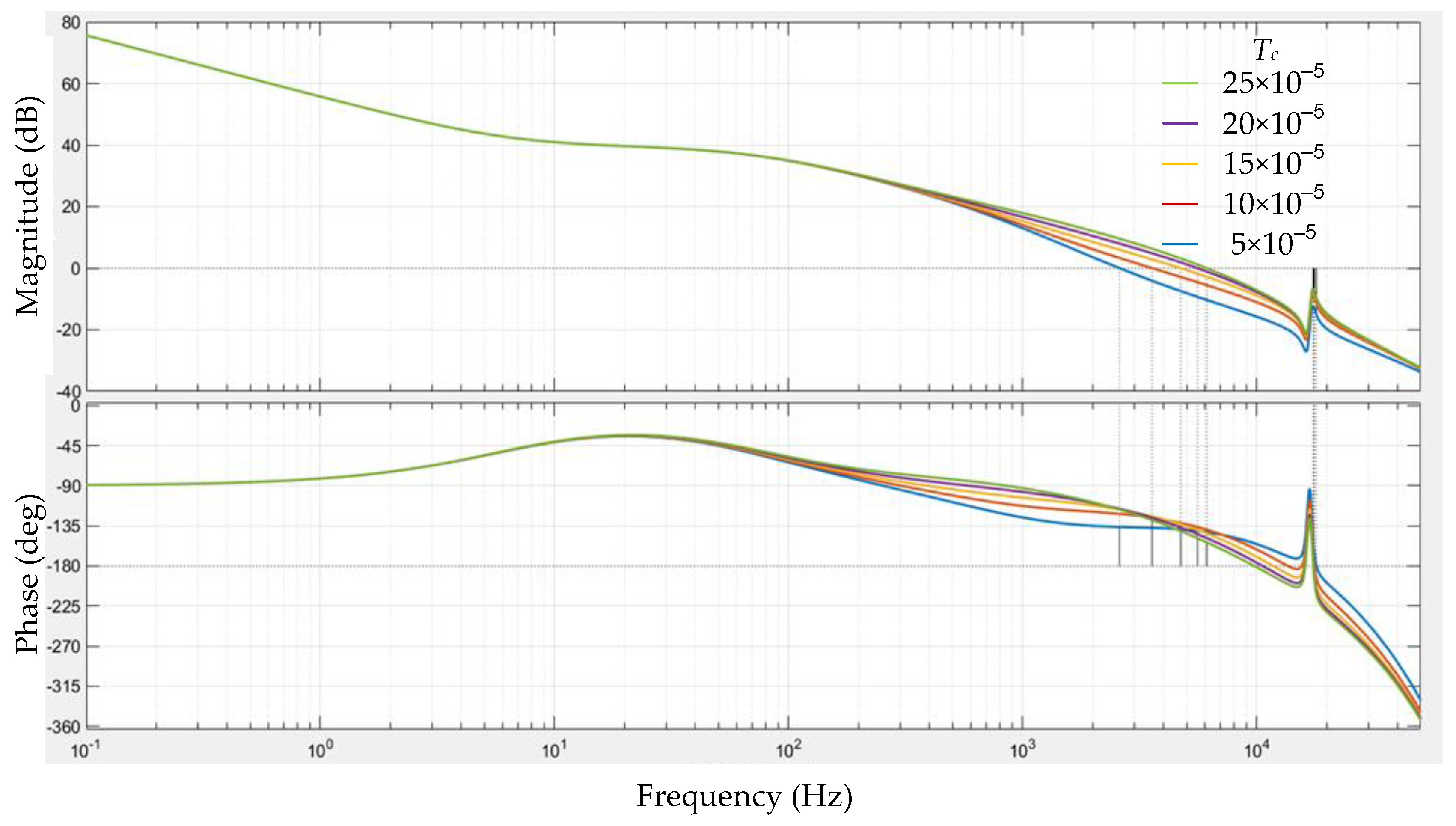
3.2.1. Tc Varies
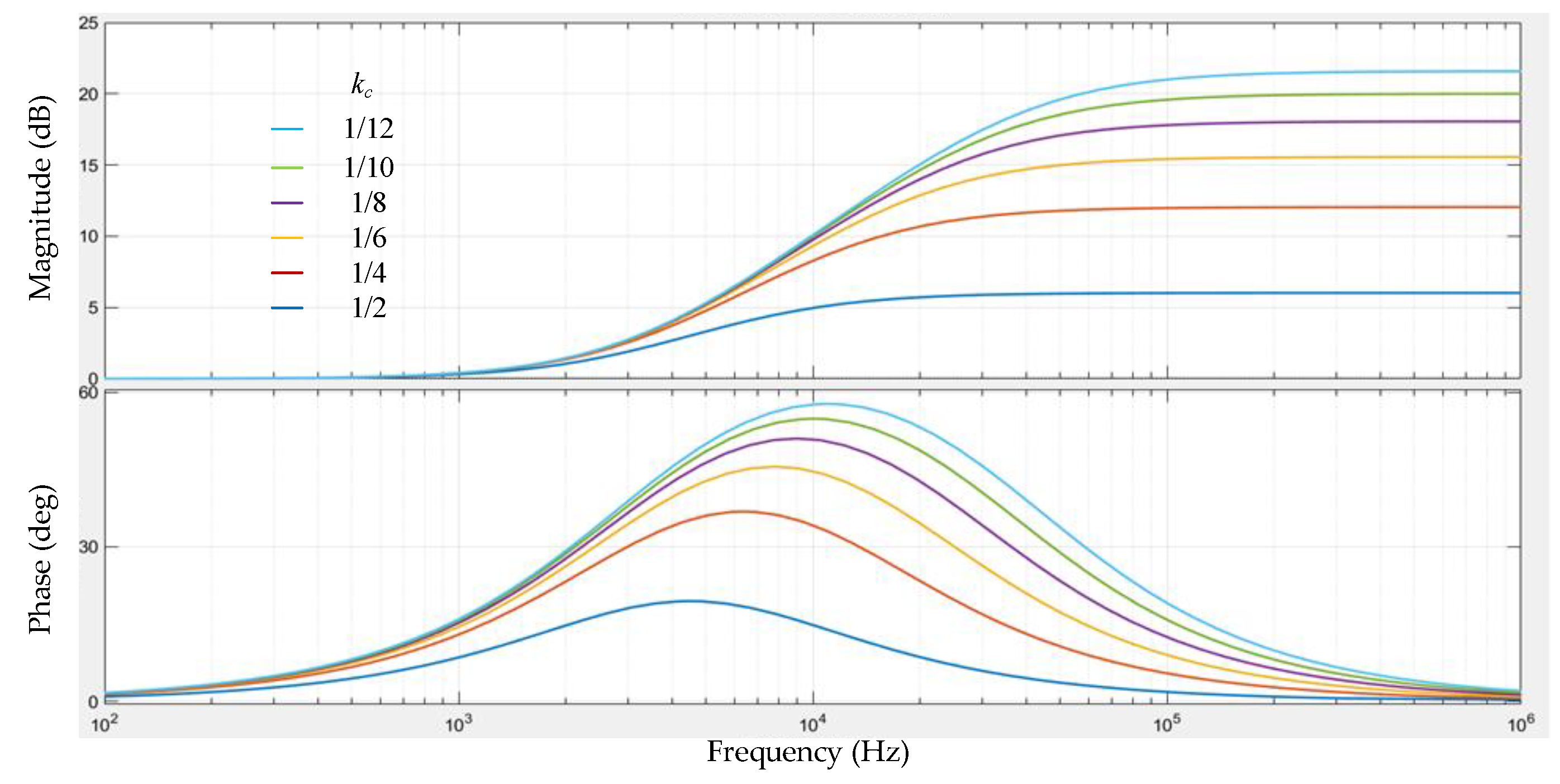
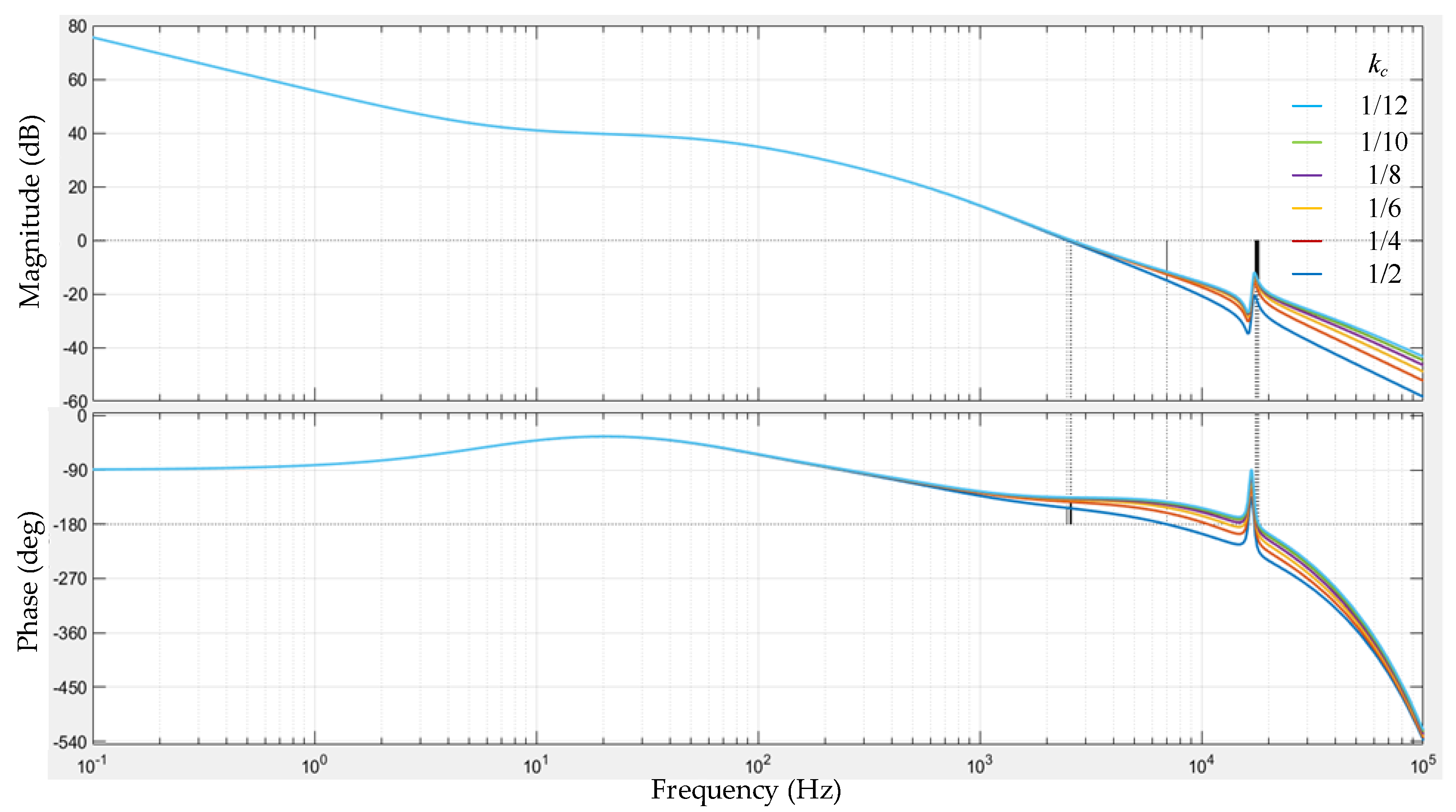
3.2.2. kc Varies
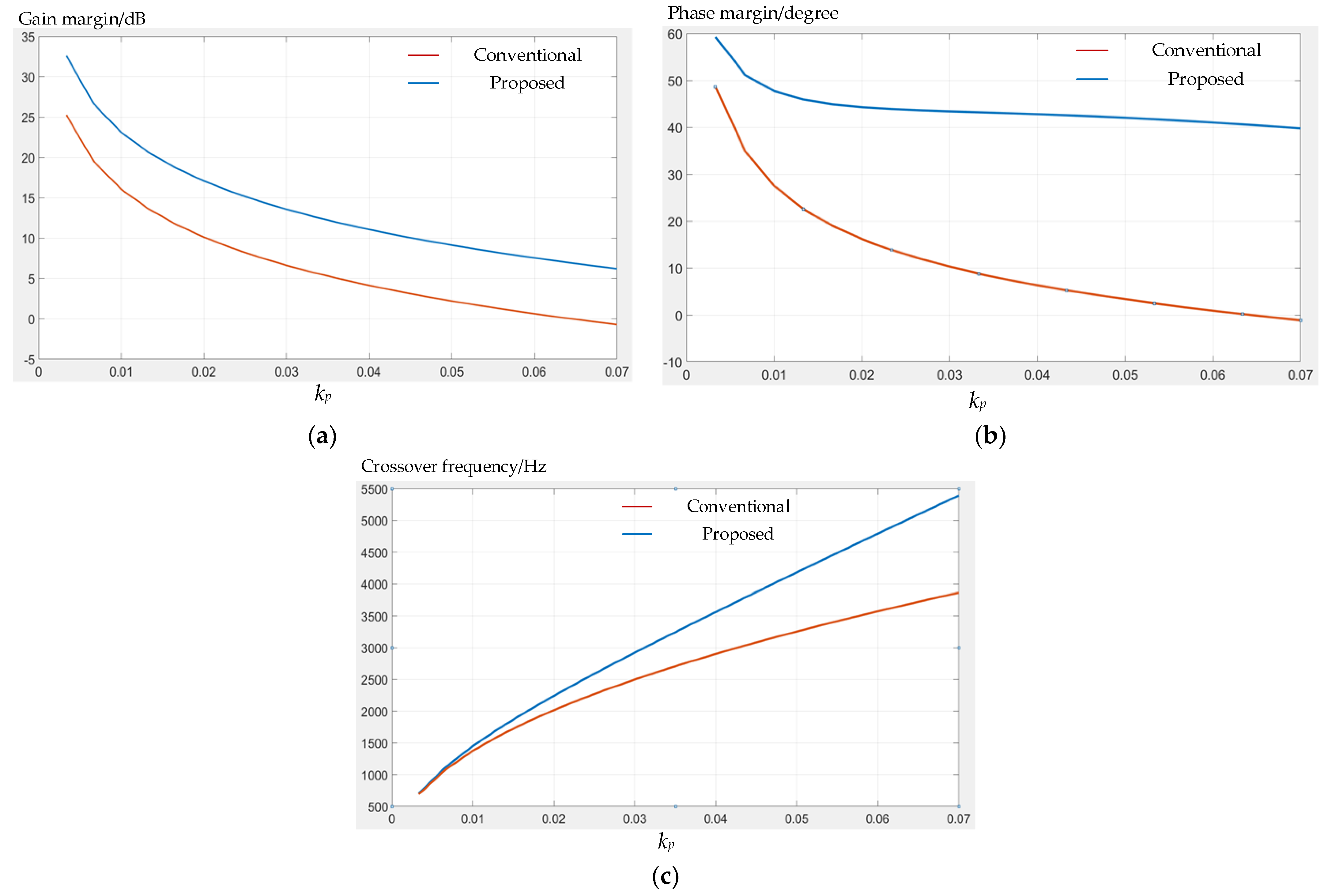
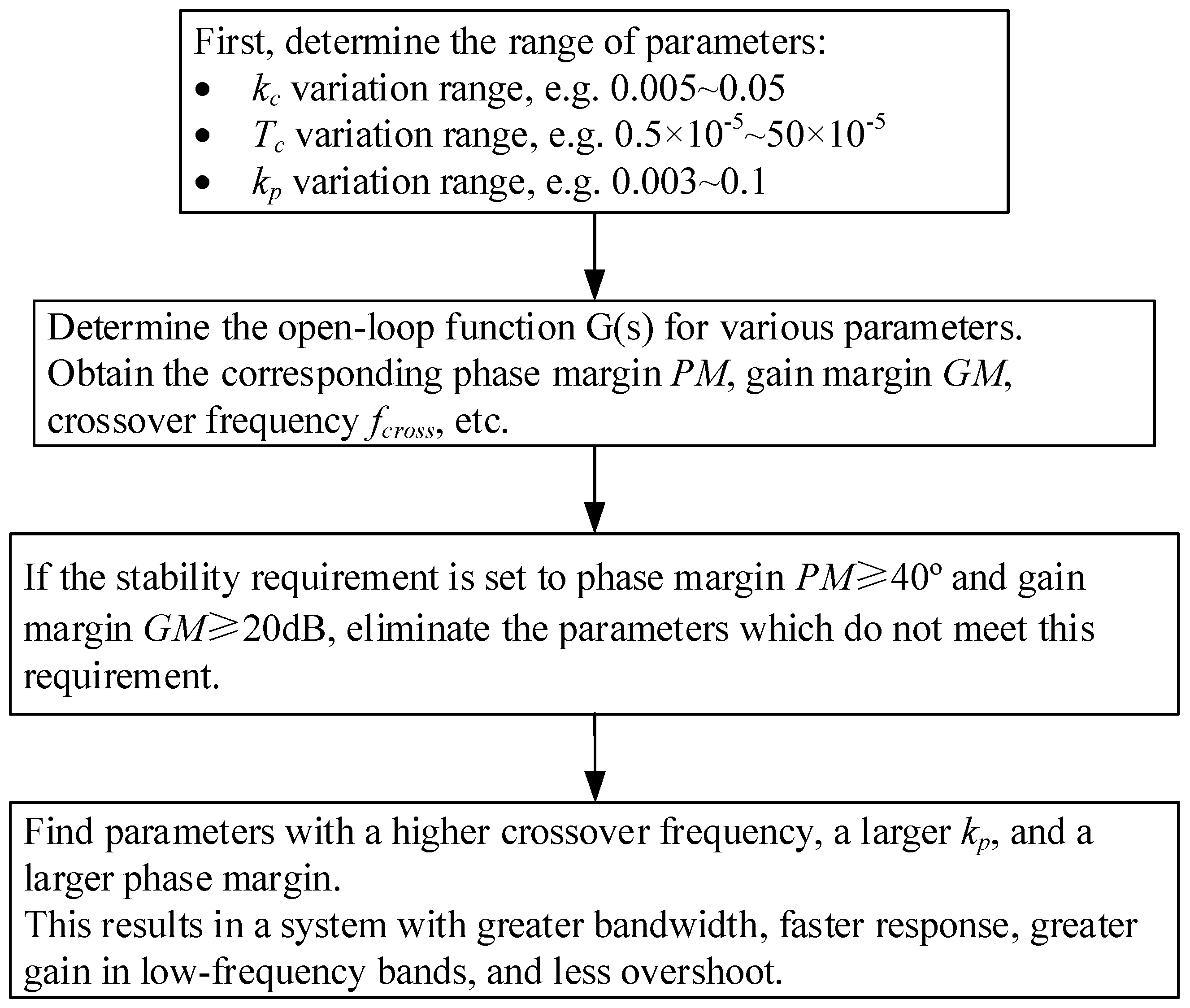
3.3. Discussion on Parameter Optimization
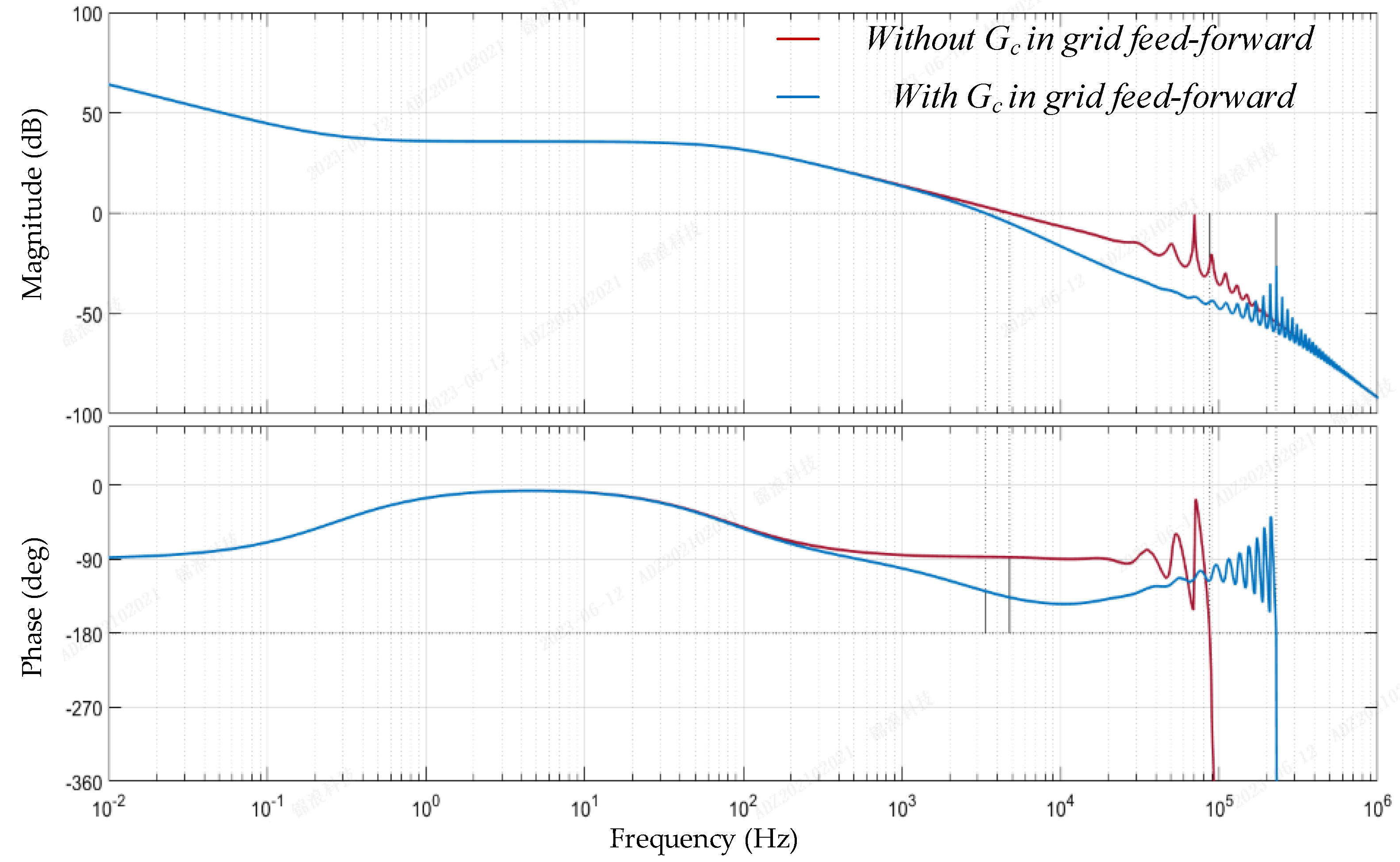
4. Method Extension for Weak-grid Conditions
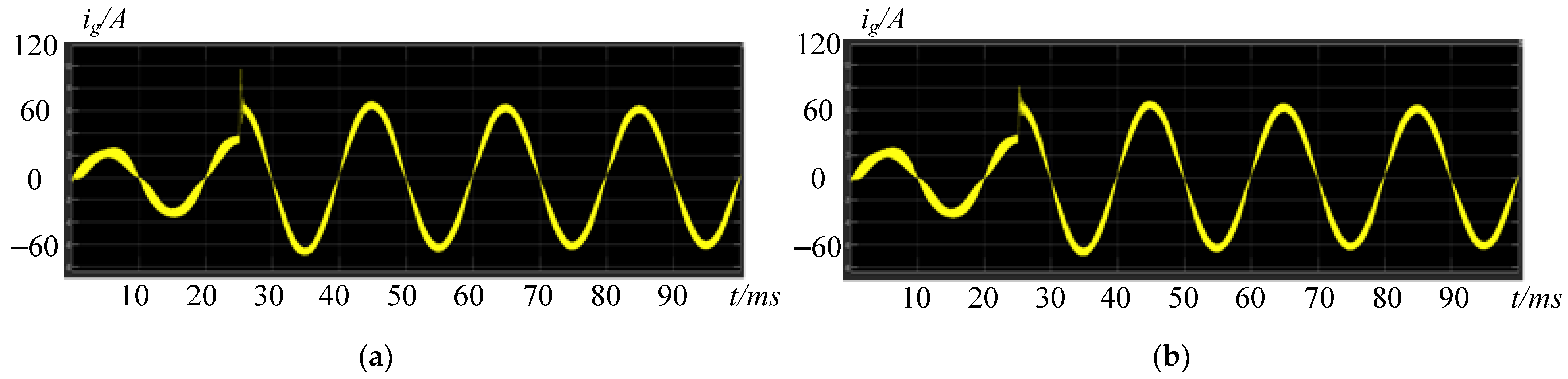
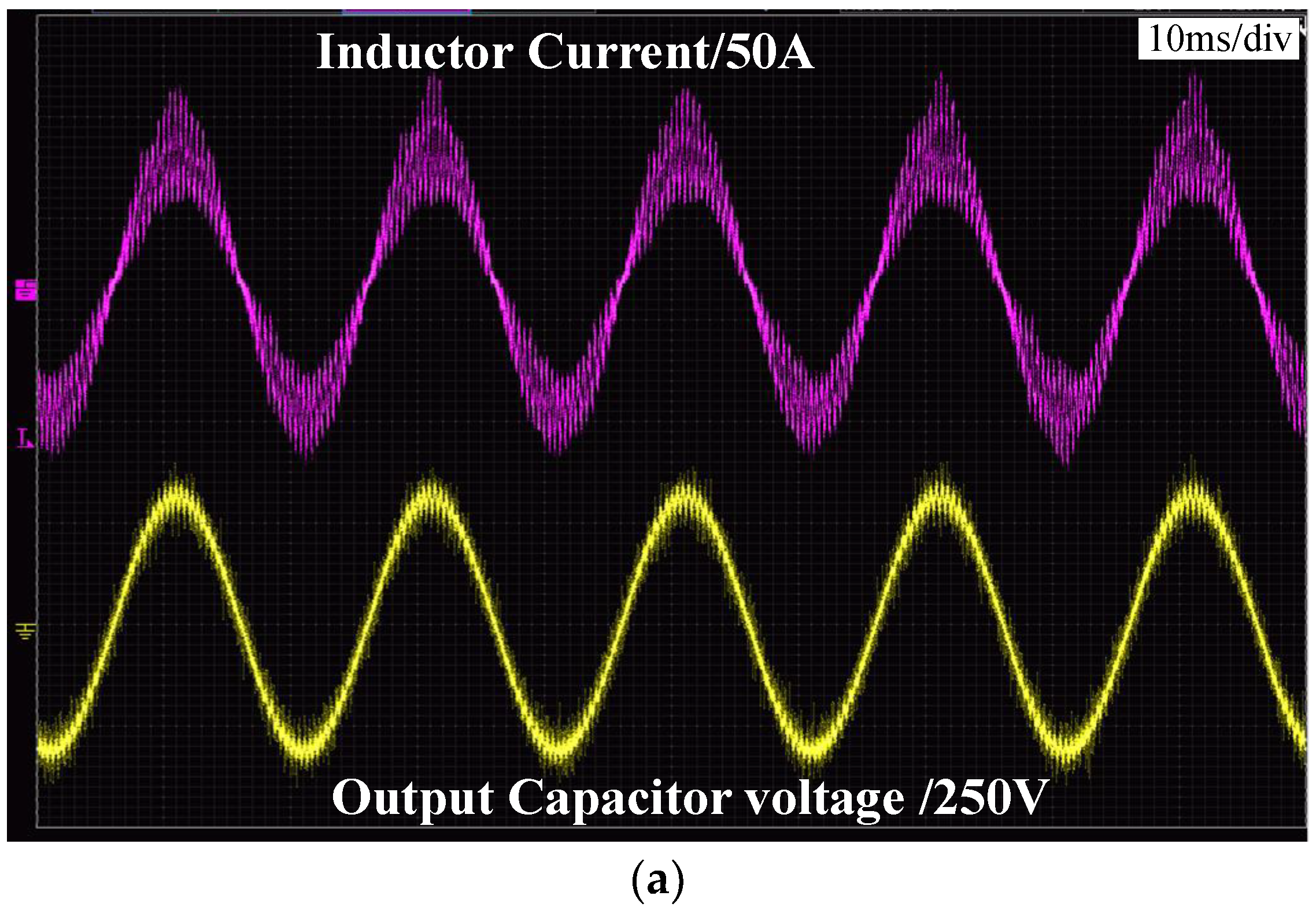
5. Experimental Verifications
6. Conclusions
- The system bode diagrams for the conventional and proposed controls are compared. From it, the compensation unit can effectively compensate the system’s phase around the crossover frequency, greatly enhancing the system’s phase margin and stability.
- The effect of two parameters, kc and Tc, is investigated. From the analysis, the change trend of parameters does not have a simple monotonic relationship with the system performance indexes and cannot be determined directly.
- An optimization method is proposed to determine optimal parameters for the compensation unit and PI controller. From the results, after optimization, the crossover frequency and the low frequency band’s gain can be increased.
- To handle weak-grid conditions, the proposed scheme is expanded by including the compensation unit in the grid’s feed-forward loop. From the analysis, the system reliability and performance can be enhanced by incorporating the compensation unit.
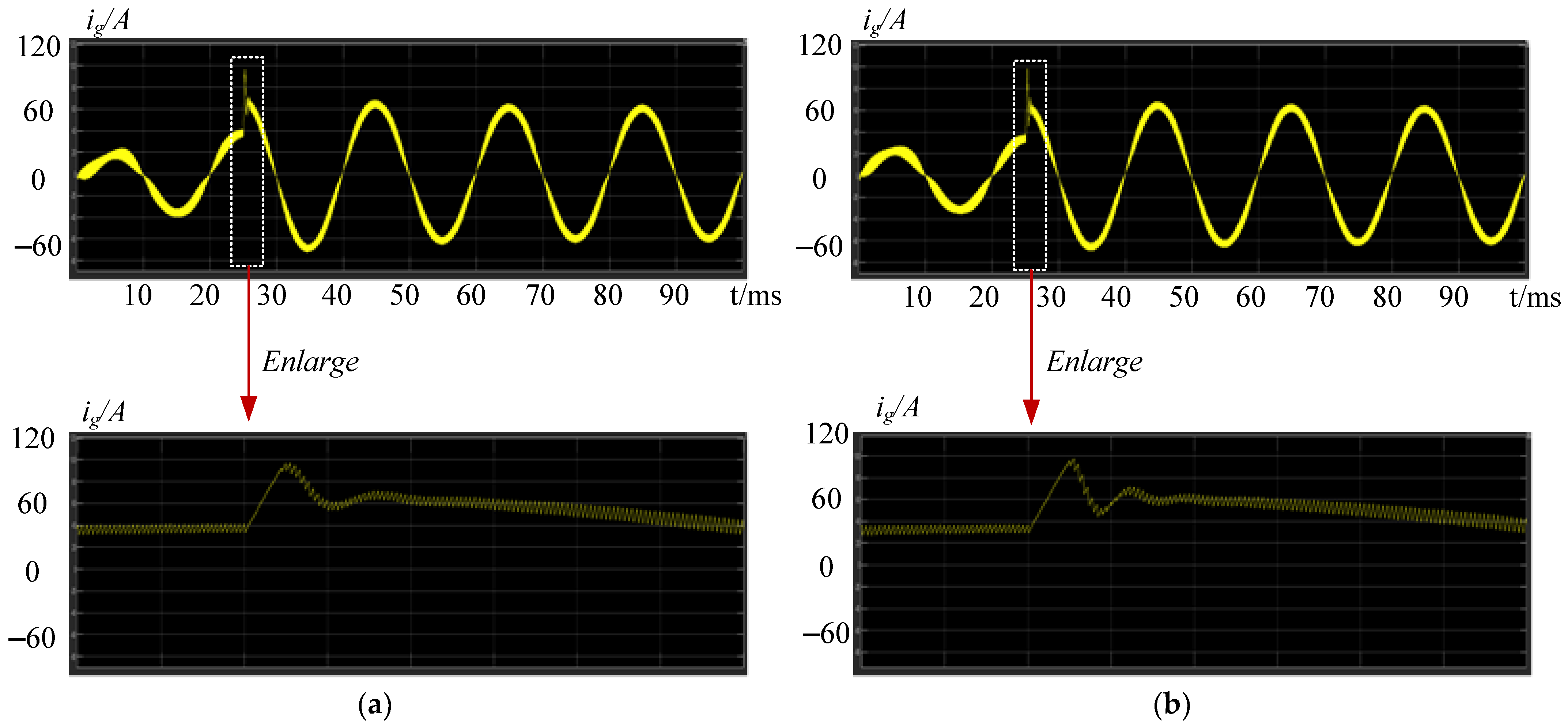
- Finally, an experimental platform is constructed. From the experimental results, the system is unstable when the conventional control is used and there are large oscillations in the current and voltage. When the proposed control is applied, the system is stable, and the output current is of good quality. Therefore, the proposed control method can greatly enhance the system’s stability and performance.
- In the future, as renewable energy becomes more popular, more and more grid-connected inverters will be applied. This proposed method incorporates a simple compensation unit into the control loop, which greatly improves system performance. This can increase the inverters’ robustness, allowing them to adapt to more complex operating scenarios. Furthermore, weak-grid conditions are becoming more common, and this control method allows the grid-connected inverters to be more adaptable to weak grids.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tang, J.; Ni, H.; Peng, R.-L.; Wang, N.; Zuo, L. A review on energy conversion using hybrid photovoltaic and thermoelectric systems. J. Power Sources 2023, 562, 232785. [Google Scholar] [CrossRef]
- Xu, X.; Yao, W.; Xie, G. A Damping Control Strategy to Improve the Stability of Multi-Parallel Grid-Connected PCSs. Energies 2023, 16, 4633. [Google Scholar] [CrossRef]
- Wang, X.; Taul, M.G.; Wu, H.; Liao, Y.; Blaabjerg, F.; Harnefors, L. Grid-synchronization stability of converter-based re-sources_An overview. IEEE Open J. Ind. Appl. 2020, 1, 115–134. [Google Scholar] [CrossRef]
- Paikray, P.; Swain, S.C.; Dash, R.; Panda, P.C. A review on current control techniques for inverter for three phase grid connected renewable sources. In Proceedings of the 2017 Innovations in Power and Advanced Computing Technologies (i-PACT), Vellore, India, 21–22 April 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Pal, B.; Sahu, P.K.; Mohapatra, S. A review on feedback current control techniques of grid-connected PV inverter system with LCL filter. In Proceedings of the 2018 Technologies for Smart-City Energy Security and Power (ICSESP), Bhubaneswar, India, 28–30 March 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Elhassan, G.; Zulkifli, S.A.; Iliya, S.Z.; Bevrani, H.; Kabir, M.; Jackson, R.; Khan, M.H.; Ahmed, M. Deadbeat Current Control in Grid-Connected Inverters: A Comprehensive Discussion. IEEE Access 2021, 10, 3990–4014. [Google Scholar] [CrossRef]
- Simek, P.; Bejvl, M.; Valouch, V. Power Control for Grid-Connected Converter Based on Generalized Predictive Current Control. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 7072–7083. [Google Scholar] [CrossRef]
- Dannehl, J.; Wessels, C.; Fuchs, F.W. Limitations of Voltage-Oriented PI Current Control of Grid-Connected PWM Rectifiers with LCL Filters. IEEE Trans. Ind. Electron. 2009, 56, 380–388. [Google Scholar] [CrossRef]
- Liang, X.; Andalib-Bin-Karim, C. Harmonics and Mitigation Techniques Through Advanced Control in Grid-Connected Renewable Energy Sources: A Review. IEEE Trans. Ind. Appl. 2018, 54, 3100–3111. [Google Scholar] [CrossRef]
- Dannehl, J.; Liserre, M.; Fuchs, F.W. Filter-Based Active Damping of Voltage Source Converters with LCL Filter. IEEE Trans. Ind. Electron. 2011, 58, 3623–3633. [Google Scholar] [CrossRef]
- Bahrani, B.; Vasiladiotis, M.; Rufer, A. High-Order Vector Control of Grid-Connected Voltage-Source Converters With LCL-Filters. IEEE Trans. Ind. Electron. 2014, 61, 2767–2775. [Google Scholar] [CrossRef]
- Bao, C.; Ruan, X.; Wang, X.; Li, W.; Pan, D.; Weng, K. Step-by-Step Controller Design for LCL-Type Grid-Connected Inverter with Capacitor–Current-Feedback Active-Damping. IEEE Trans. Power Electron. 2014, 29, 1239–1253. [Google Scholar] [CrossRef]
- Pan, D.; Ruan, X.; Bao, C.; Li, W.; Wang, X. Capacitor-Current-Feedback Active Damping with Reduced Computation Delay for Improving Robustness of LCL-Type Grid-Connected Inverter. IEEE Trans. Power Electron. 2014, 29, 3414–3427. [Google Scholar] [CrossRef]
- Shen, G.; Xu, D.; Cao, L.; Zhu, X. An Improved Control Strategy for Grid-Connected Voltage Source Inverters with an LCL Filter. IEEE Trans. Power Electron. 2008, 23, 1899–1906. [Google Scholar] [CrossRef]
- Shen, G.; Zhu, X.; Zhang, J.; Xu, D. A New Feedback Method for PR Current Control of LCL-Filter-Based Grid-Connected Inverter. IEEE Trans. Ind. Electron. 2010, 57, 2033–2041. [Google Scholar] [CrossRef]
- Mohammed, N.; Zhou, W.; Bahrani, B. Comparison of PLL-Based and PLL-Less Control Strategies for Grid-Following Inverters Considering Time and Frequency Domain Analysis. IEEE Access 2022, 10, 80518–80538. [Google Scholar] [CrossRef]
- Gui, Y.; Wang, X.; Wu, H.; Blaabjerg, F. Voltage-Modulated Direct Power Control for a Weak Grid-Connected Voltage Source Inverters. IEEE Trans. Power Electron. 2019, 34, 11383–11395. [Google Scholar] [CrossRef]
- Mansour, M.Z.; Ravanji, M.H.; Karimi, A.; Bahrani, B. Linear Parameter-Varying Control of a Power-Synchronized Grid-Following Inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2547–2558. [Google Scholar] [CrossRef]
- Reyes, M.; Rodriguez, P.; Vazquez, S.; Luna, A.; Teodorescu, R.; Carrasco, J.M. Enhanced Decoupled Double Synchronous Reference Frame Current Controller for Unbalanced Grid-Voltage Conditions. IEEE Trans. Power Electron. 2012, 27, 3934–3943. [Google Scholar] [CrossRef]
- Song, G.; Cao, B.; Chang, L. Review of Grid-forming Inverters in Support of Power System Operation. Chin. J. Electr. Eng. 2022, 8, 1–15. [Google Scholar] [CrossRef]
- Maganti, S.; Padhy, N.P. Analysis and Design of PLL Less Current Control for Weak Grid-Tied LCL-Type Voltage Source Converter. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 4026–4040. [Google Scholar] [CrossRef]
- Jayathilaka, I.; Lakpriya, L.; De Alwis, D.; Jayakody, G.; Hemapala, K.; Karunadasa, J.; Lakshika, H. DQ Transform Based Current Controller for Single-Phase Grid Connected Inverter. In Proceedings of the 2018 2nd International Conference on Electrical Engineering (EECon), Colombo, Sri Lanka, 28 September 2018; pp. 32–37. [Google Scholar] [CrossRef]
- Mnider, A.M.; Atkinson, D.J.; Dahidah, M.; Armstrong, M. A simplified DQ controller for single-phase grid-connected PV inverters. In Proceedings of the 2016 7th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 22–24 March 2016; pp. 1–6. [Google Scholar] [CrossRef]






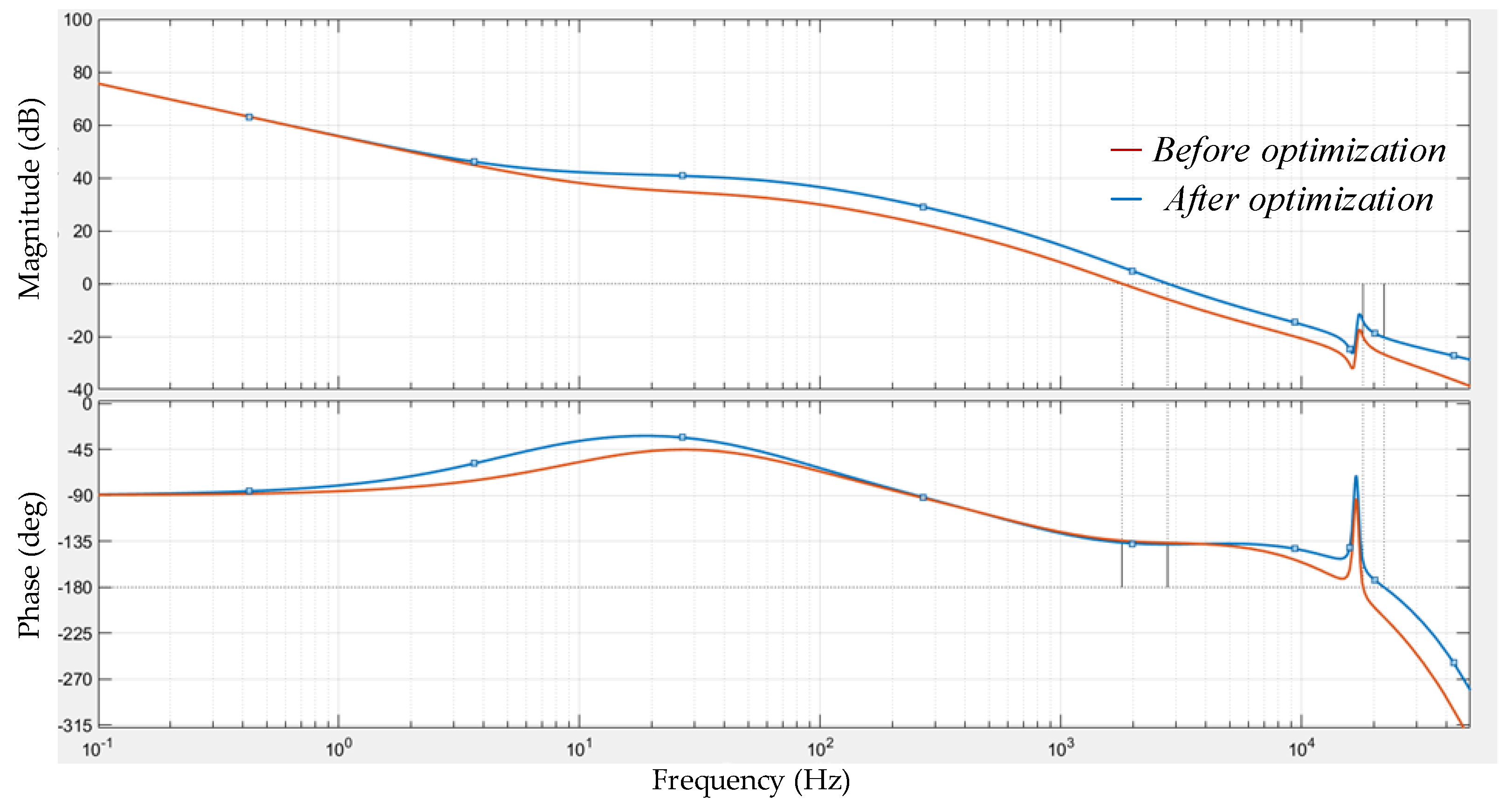





| Items | Before Optimization | After Optimization |
|---|---|---|
| Parameters | kc = 0.1, Tc = 5 × 10−5, kp = 0.014, ki = 1 | kc = 0.01, Tc = 4 × 10−5, kp = 0.03, ki = 1 |
| Phase Margin | 45.7° | 42° |
| Gain Margin | 20.2 dB | 20.4 dB |
| Crossover frequency | 1790 Hz | 2770 Hz |
| Gain at 150 Hz | 27.1 dB | 33.7 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Wang, Y.; Xu, P.; Li, D.; Liu, B. A Current Control Method for Grid-Connected Inverters. Energies 2023, 16, 6558. https://doi.org/10.3390/en16186558
Zhang W, Wang Y, Xu P, Li D, Liu B. A Current Control Method for Grid-Connected Inverters. Energies. 2023; 16(18):6558. https://doi.org/10.3390/en16186558
Chicago/Turabian StyleZhang, Wenping, Yiming Wang, Po Xu, Donghui Li, and Baosong Liu. 2023. "A Current Control Method for Grid-Connected Inverters" Energies 16, no. 18: 6558. https://doi.org/10.3390/en16186558
APA StyleZhang, W., Wang, Y., Xu, P., Li, D., & Liu, B. (2023). A Current Control Method for Grid-Connected Inverters. Energies, 16(18), 6558. https://doi.org/10.3390/en16186558






