1. Introduction
Fossil fuels accelerated a prodigious era of prosperity and advancement for human civilization in the past two centuries. Still, today, the entire world heavily relies on fossil fuels to fulfill about 80% of its energy demands and to generate vast quantities of adopted fuels and vital commodities [
1]. However, the amount of fossil fuel accessible to us is limited and can be diminished in coming decades. This is because developed and developing nations deliberately expanded the use of fossil fuel in various sectors over the last few decades; consequently, the price of fuel rose unreasonably at the same time. Simultaneously, an excessive use of fossil fuels has led to a devastating increase in greenhouse gas emissions, which leads to global warming.
Carbon dioxide (CO
2), carbon monoxide (CO), and methane (CH
4) gases are considered the key contributors to greenhouse gases [
2,
3]. Flue gases (FG) emitted from coal or natural gas-based thermal power plants is one of the major sources of CO
2, which is approximately 40% of total CO
2 emissions [
4]. On the other hand, the steel and iron industry are responsible for 7% of total CO
2 emissions globally, which is around 30% of the worldwide industrial sector emissions [
5]. Coke oven gas (COG) is another industrial waste gas: a major by-product of the coking process of the steel and iron industry, it contains around 55–60 mol% of H
2, 23–27 mol% of CH
4, 5–8 mol% of CO, 3–5 mol% of N
2, and other impurities in small proportions [
6].
In light of environmental concerns related to greenhouse gas emissions and the expanding global population, the foremost challenge facing societies is meeting the rising global energy demand while minimizing reliance on fossil fuels to reduce greenhouse gas emissions. Therefore, it is very urgent to develop processes that decrease/utilize the fossil fuel-based CO2 emissions and produce value-added chemicals simultaneously. Since we cannot avoid using fossil fuels, thus, an integrated processing approach is needed to control the emissions of greenhouse gases such as CO2, CO, and CH4 from FG and COG.
As a part of an integrated processing approach, value-added fuels and chemicals can be produced from greenhouse gases of industrial waste gases. For instance, the synthesis of methanol (MeOH) from industrial waste gases (FG and COG) can be a viable solution as it not only controls the emissions of greenhouse gases but also has the potential to make alternative renewable energy. Although the energy density of methanol (20.1 MJ kg
−1) is half that of gasoline (44.3 MJ kg
−1) [
7], a higher-octane number of MeOH (108) relative to gasoline (95) makes it a potential fuel. In addition, it has a higher compression ratio than gasoline, resulting in a more efficient combustion, which can consequently reduce the greenhouse gas emissions [
8].
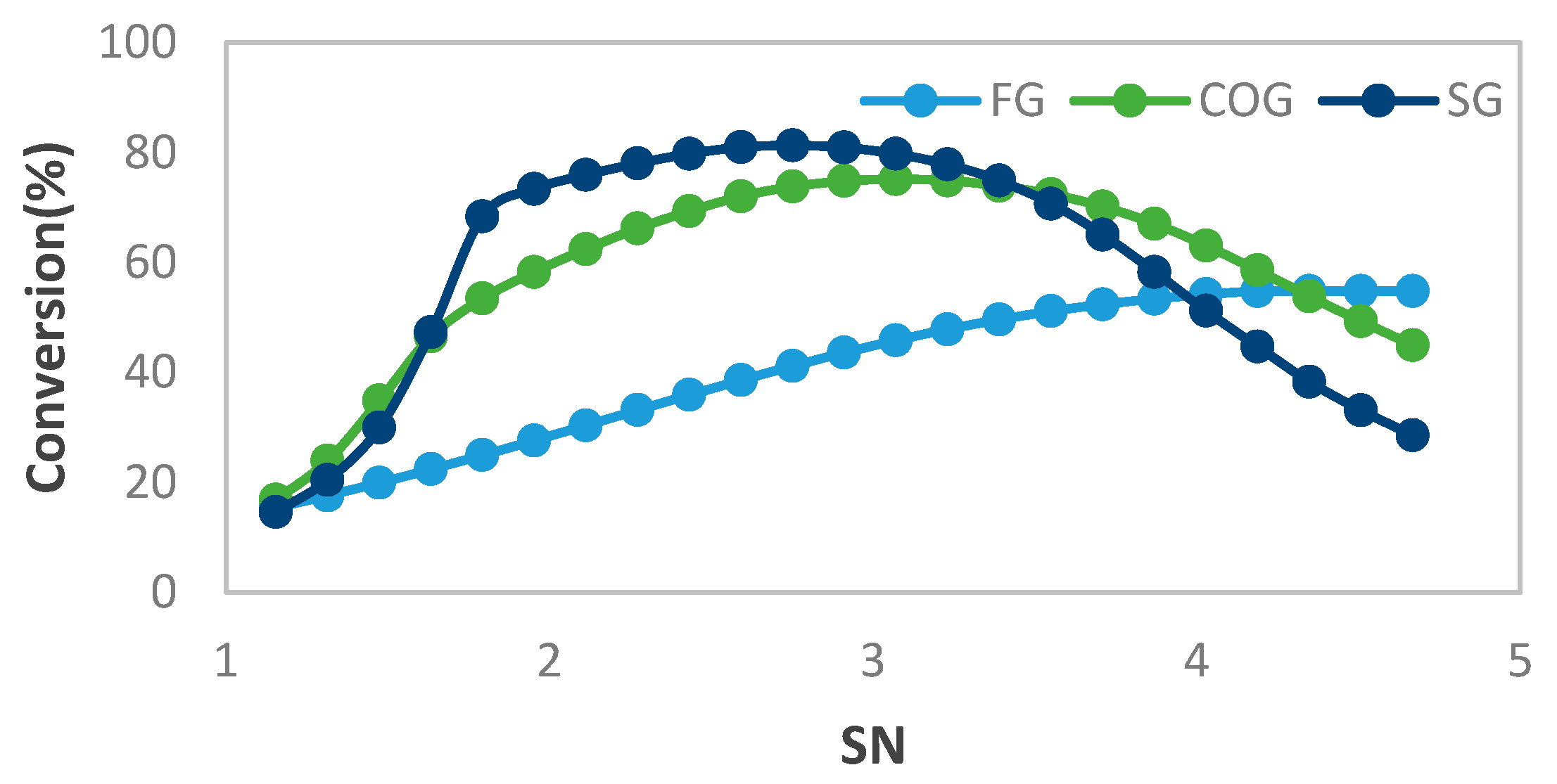
In this regard, the aim of this paper is to study the systematic approach of MeOH production from industrial waste gases (FG and COG) that are considered a great threat to the environment. The specific objective is to analyze the impact of process parameters, including dimensional parameters and operational parameters, over the MeOH synthesis by Aspen Plus. Another specific goal is to maximize heat recovery by exchanging process heat between cold and hot streams while minimizing the required external heating and cooling utilities. To achieve this goal, pinch analysis principles are followed to perform heat integration. Since syngas (SG) is the main feedstock in industry for MeOH production, firstly, a base case MeOH production from the SG model is developed in Aspen Plus. Based on the SG composition and stoichiometric reaction, a stoichiometric number (SN) is calculated for the base case model. Later, MeOH synthesis process models for FG and COG industrial waste gases are developed based on the optimized base case model.
2. Theoretical Background
The reaction mechanisms of methanol synthesis have been studied by several authors, and they have suggested the following microkinetic mechanisms [
9]:
The microkinetic mechanism includes several reaction steps among the adsorbed species, and about 50 reactions have been proposed. The Langmuir–Hinshelwood (L-H) and Eley–Rideal (E-R) mechanisms are usually adopted, and one or more of the steps are considered to be the rate-determining step (RDS) for MeOH synthesis. MeOH production mainly depends on the composition of SG, which is a mixture of CO, CO
2, and H
2. The composition of SG can be best described by SN. The SN can be expressed by the following equation:
The SN can be calculated from the stoichiometric equations (Equations (1)–(3)), and the SN value is assumed to be 2 [
10] under the ideal condition. But several authors suggested that SN should remain slightly higher than 2 for better results, and the optimum value of SN is recommended as 2–2.1 [
10,
11]. In addition, to have a better yield of MeOH, the H
2 to CO ratio is suggested to remain within 2.4–3.0 [
11]. According to Sahibzada et al. [
12], around 4% CO
2 in SG can help increase MeOH production. But based on different types of biomass and different reforming/gasification processes, the composition of SG varies, and none of the SG composition falls within the suggested range of SN value (2–2.1) and H
2 to CO ratio (2.4–3.0) as reported by Arashiro et al. [
13] and AlNouss et al. [
14]. As the development of the pretreatment process of SG is not the main aim of this study, therefore, a hypothetical SG composition is considered in the subsequent analysis. The composition of SG is considered as 28.5978% CO, 2.7675% CO
2 and 68.6347% H
2, and we assumed that there is no presence of inert gases such as CH
4, N
2, etc. Based on these hypothetical values, the SN of HSG comes up as 2.1 and H
2/CO as 2.4.
To synthesize MeOH from FG and COG, pretreatment is also necessary for better yield, which can be completed in various ways. According to Abdelaziz et al. [
15], FG can be pretreated by capturing CO
2 for subsequent steps, which is economically more efficient than other processes [
15]. As FG contains no hydrogen gas, an external source of hydrogen is required to produce MeOH from FG. Among various established methods, the water electrolysis method is suggested as the source of hydrogen [
16]. Abdelaziz et al. [
15] recommended an optimum composition of FG for MeOH synthesis, which is considered in this study and presented in
Table 1. In addition, the present study has adopted the iron-molybdenum hydro-desulfurization pretreatment process for COG, which was proposed by Kim et al. [
17] for effective desulfurization and providing optimum proportion of H
2, CO, and others in the COG for MeOH synthesis.
Table 1 states the composition of the reactor feed for SG, FG, and COG for MeOH production [
17].
A different kinetic model is proposed for the methanol synthesis [
18,
19,
20]. Among the different established kinetic models, the most frequently used models are those of Graaf et al. [
21] and Bussche and Froment [
22]. To predict the performance of the MeOH synthesis reactor, Langmuir–Hinshelwood–Hougen–Watson (LHHW)-based kinetic models have been proposed (Equation (5)) by Bussche and Froment [
22].
In this model, it is assumed that CO
2 hydrogenation produces methanol as well as CO, and a reverse water gas shift (rWGS) reaction occurs simultaneously (Equations (2) and (3)). To determine the kinetic parameters for this model, experiments have been performed at a range of pressure and temperature on an industrial catalyst Cu/ZnO/Al
2O
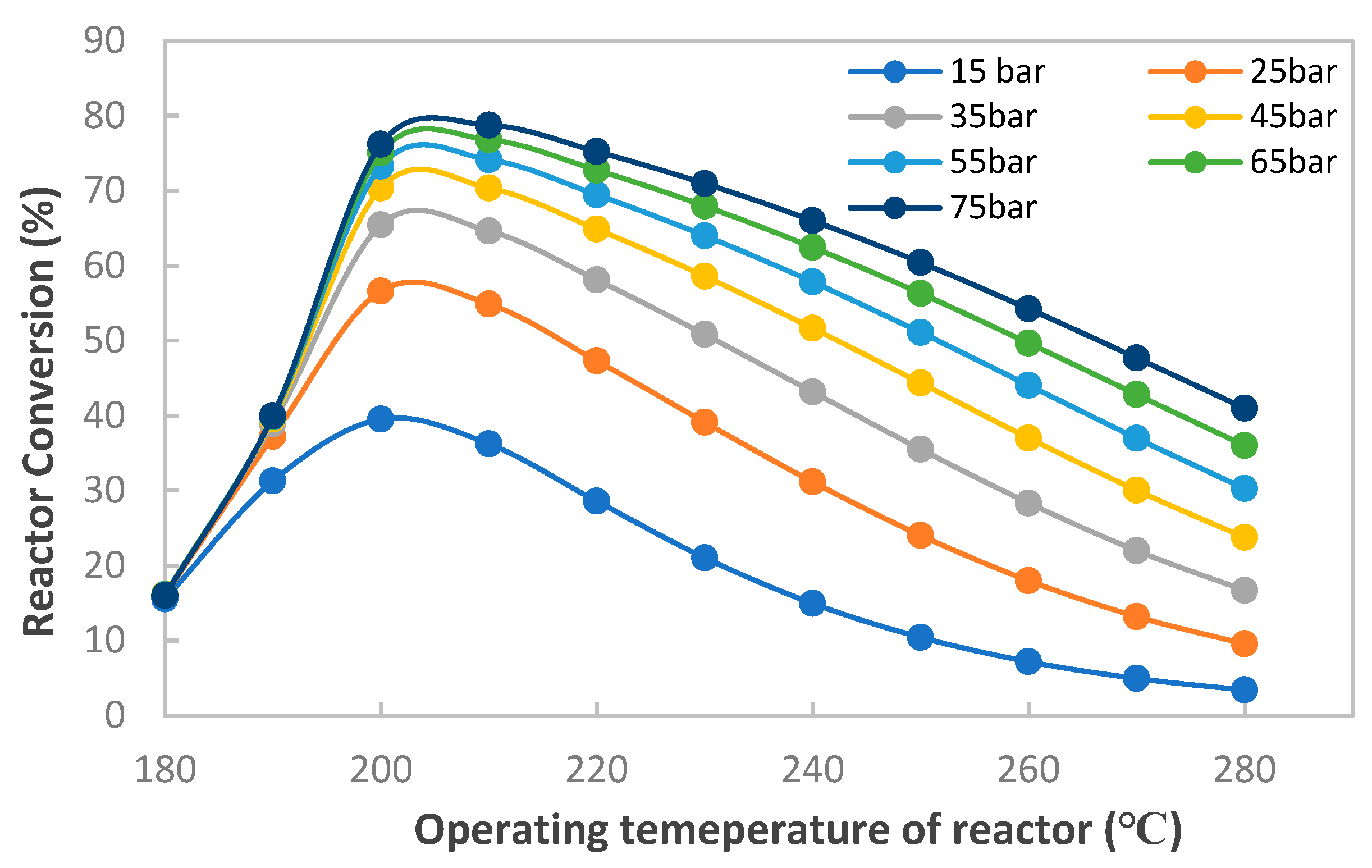
3. The validated range of this kinetic model is 15 to 51 bar and 180 to 280 °C. For a better representation of these experimental data, Mignard and Pritchard readjusted the activation energy [
23], which expanded the application range of the model up to 75 bar. The kinetic model of Bussche and Froment with readjusted parameters of Mignard and Pritchard are given by the following expressions (Equations (6) and (7)):
Methanol synthesis reaction:
Reverse water gas shift reaction:
where
reaction rate
;
kinetic factor ( or ;
partial pressure ;
equilibrium constant [−] or ;
adsorption constant .
Arrhenius law is used to calculate the kinetic constants of Equations (6) and (7) [
22], and
Table 2 summarizes the constants.
Thermodynamic equilibrium constants (
and
) are adapted from Graaf et al. [
24] by Equations (8) and (9), whereas the pressure drop within the reactor is calculated by Ergun Equation [
25,
26].
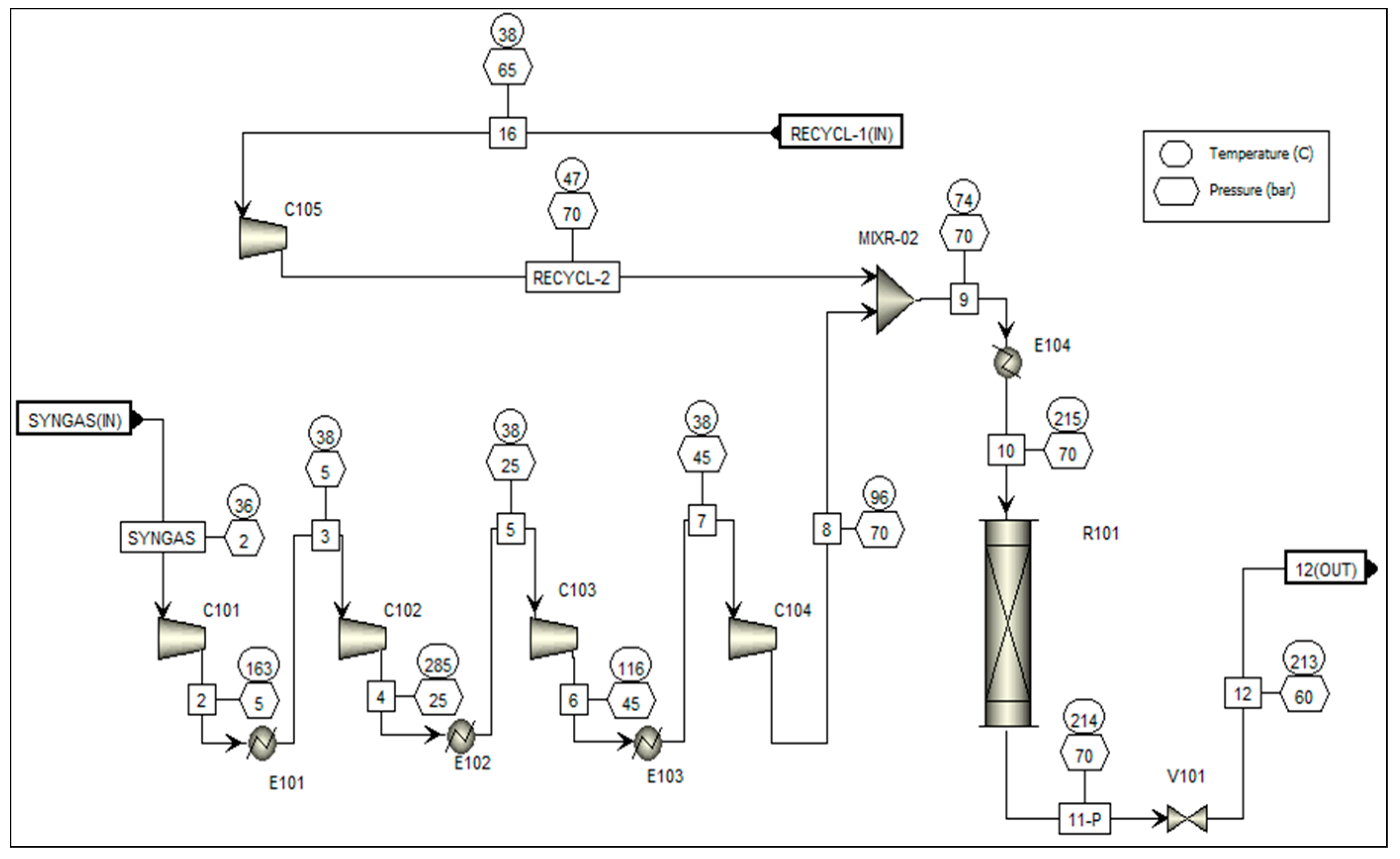
However, to design, analyze, and optimize a chemical process, simulations are largely implicated in evaluating different process scenarios. To achieve the objective of this study, Aspen ONE™ (Advanced System for Process Engineering) v10.0 software was used. Here, process design and heat integration were accomplished using Aspen Plus and Aspen energy analyzer (AEA), respectively. To create the process flowsheet, several key assumptions were taken into consideration [
27]. Firstly, it was assumed that there is negligible dispersion in the axial direction. Secondly, radial mixedness is presumed to be at its maximum. Ad-ditionally, concentration, velocity, and temperature profiles were assumed to remain constant in the radial direction. Furthermore, the feasibility activities of the process were carried out in steady-state mode, employing a pseu-do-homogeneous model. It was also assumed that the catalyst’s effectiveness remains constant, with negligible catalyst deactivation. Finally, side reactions, excluding the rWGS (reverse water-gas shift) reaction, were deemed to be negligible.
5. Conclusions
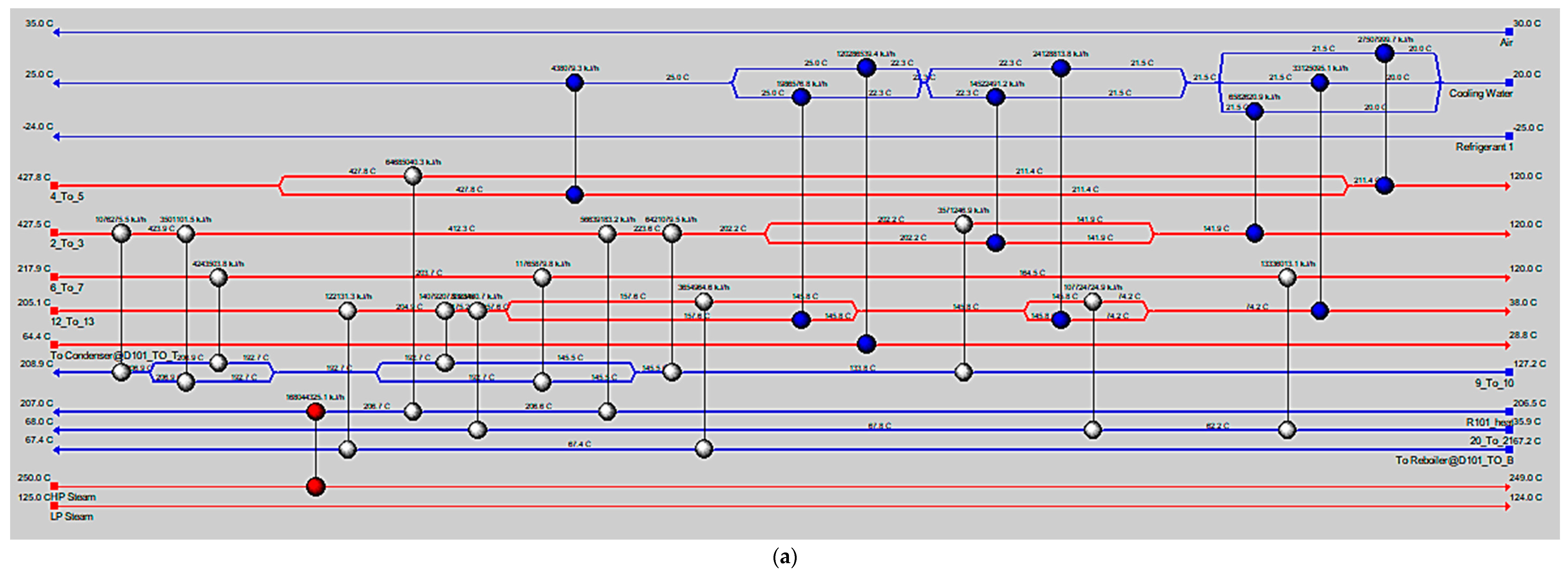
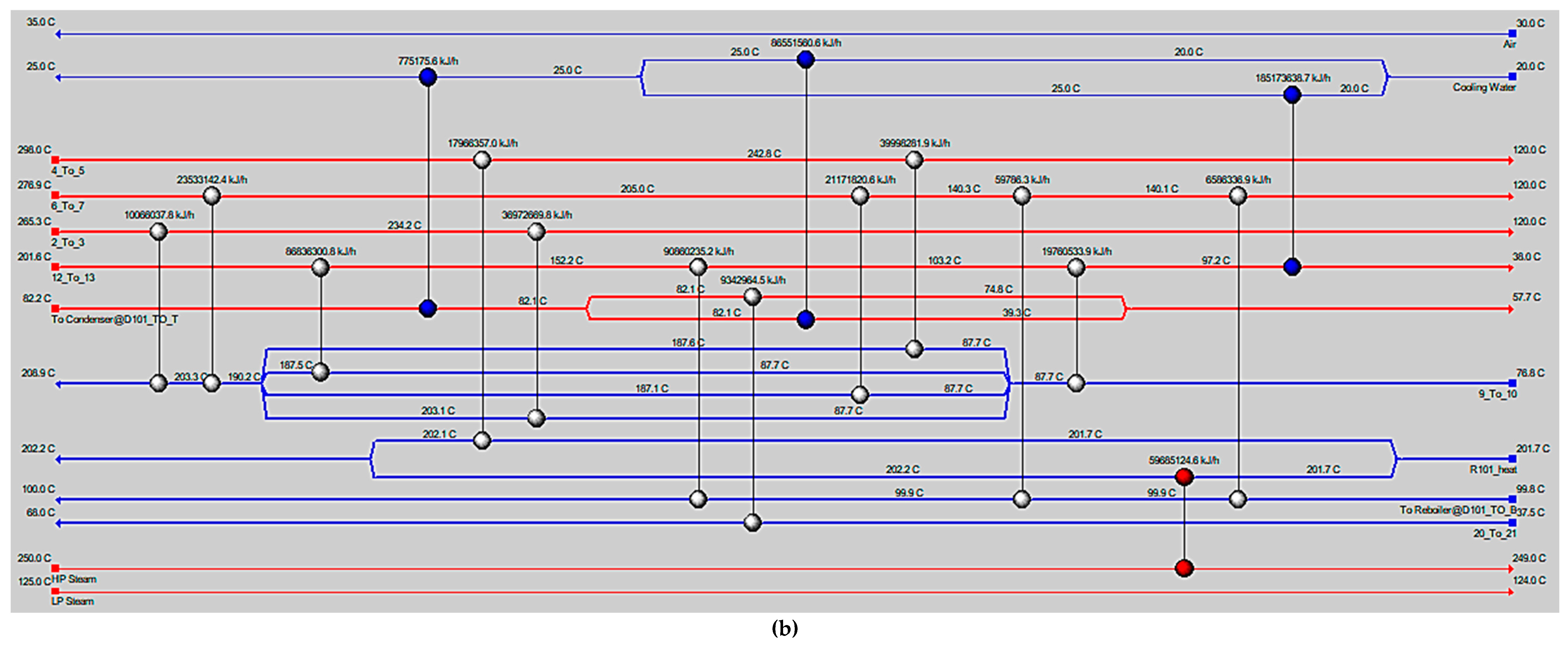
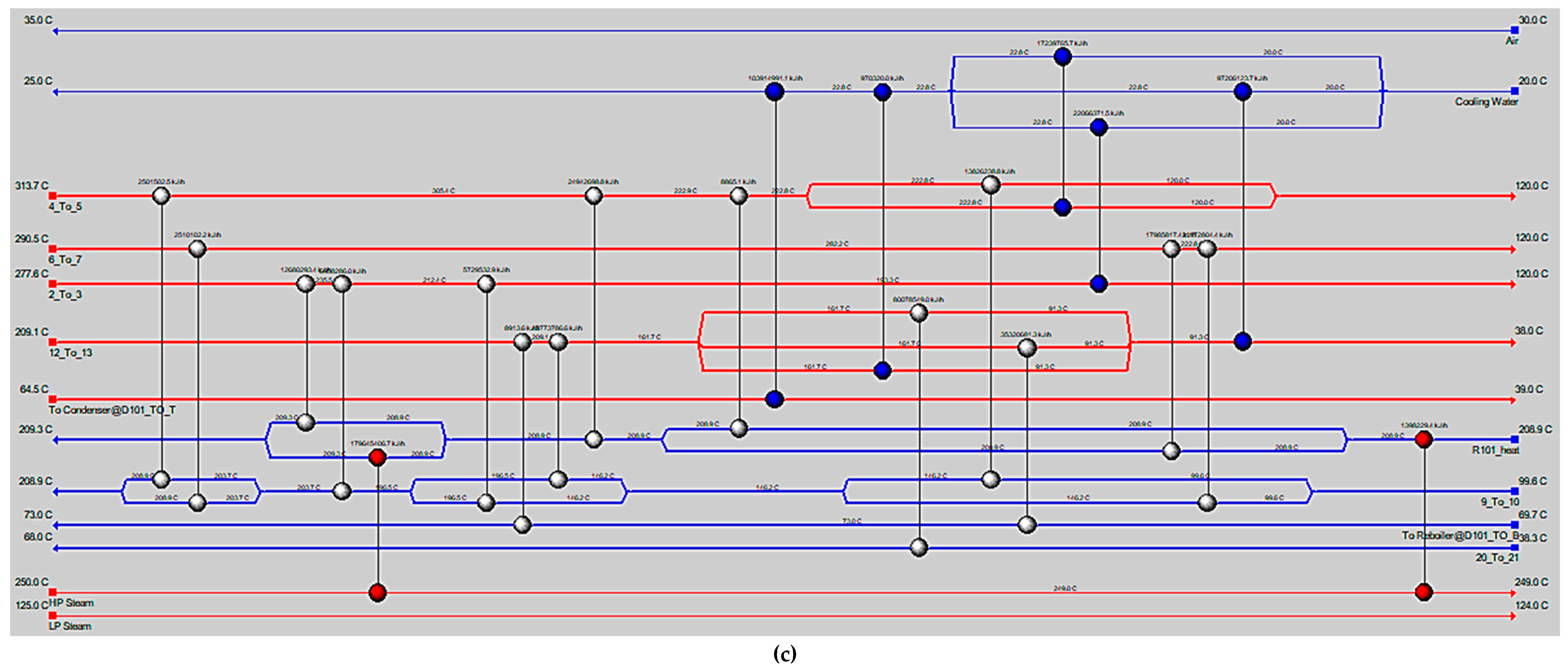
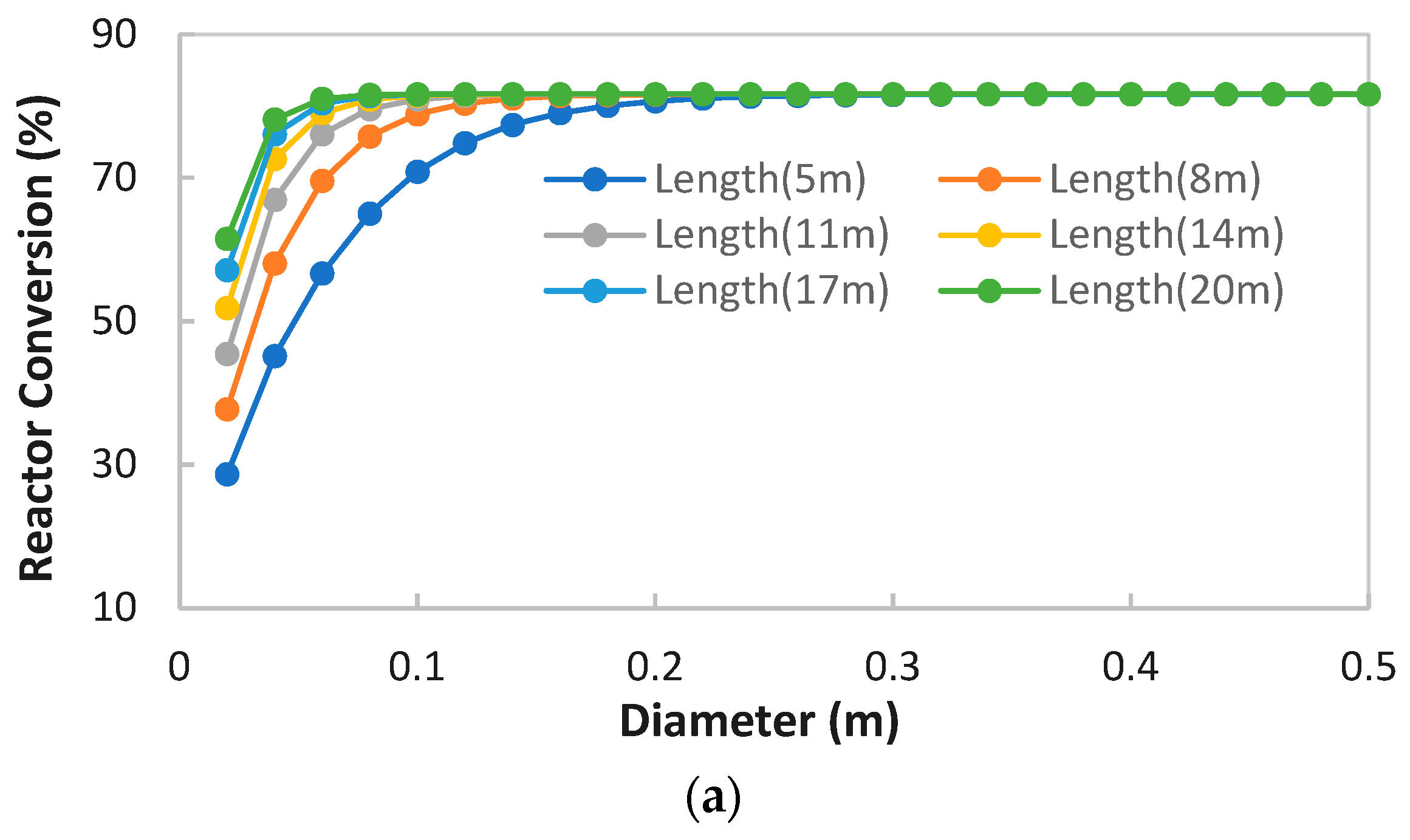
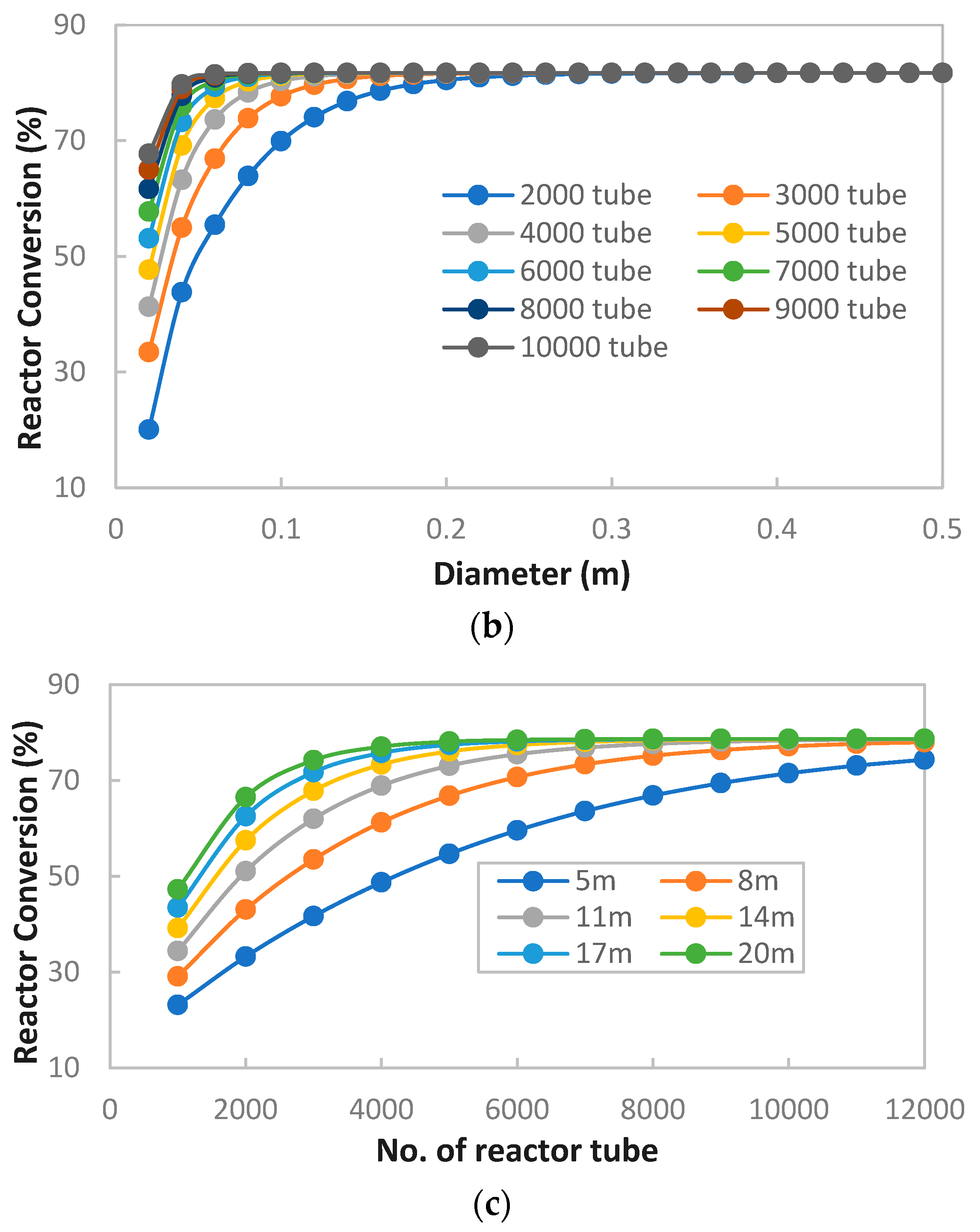
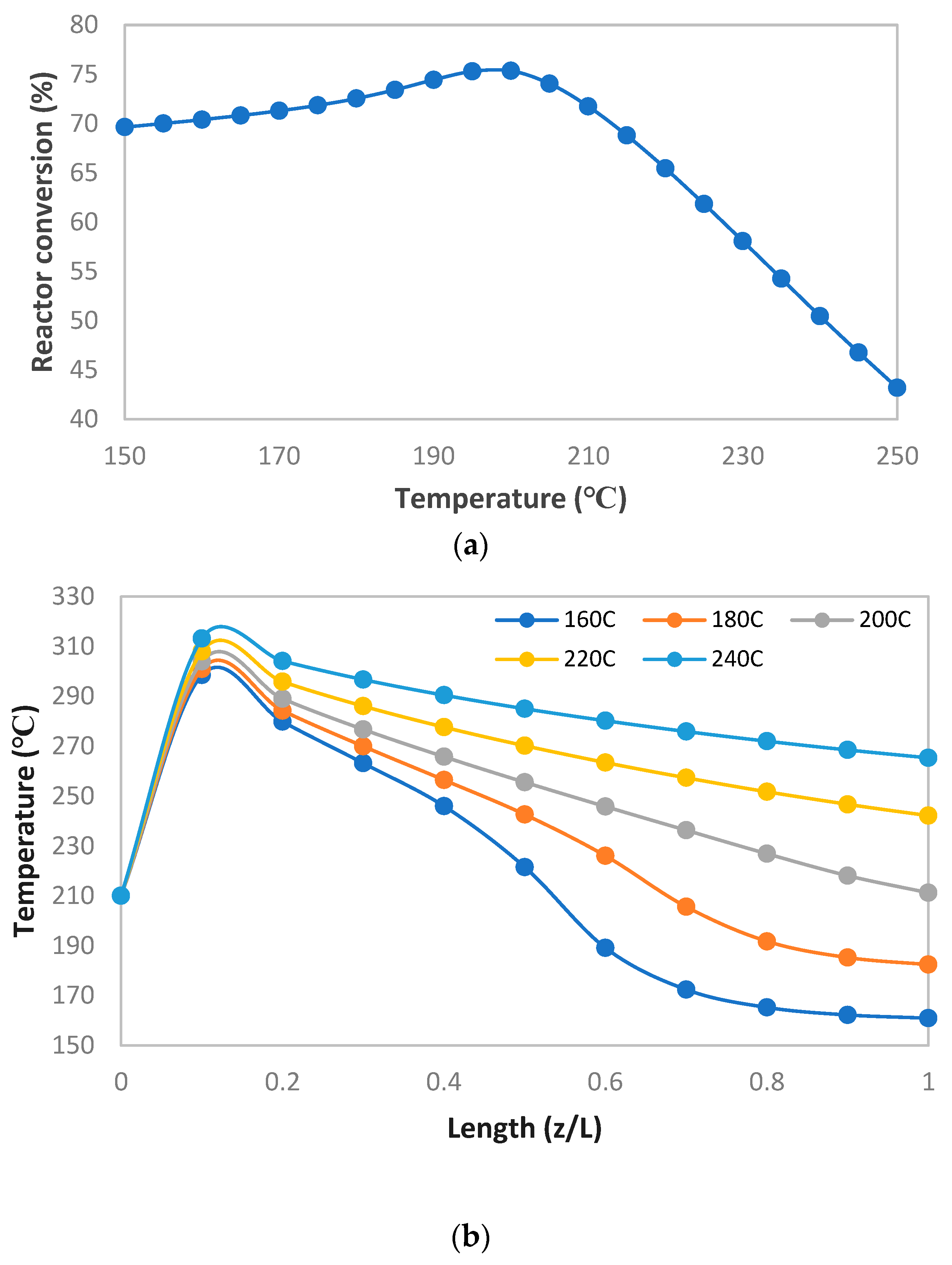
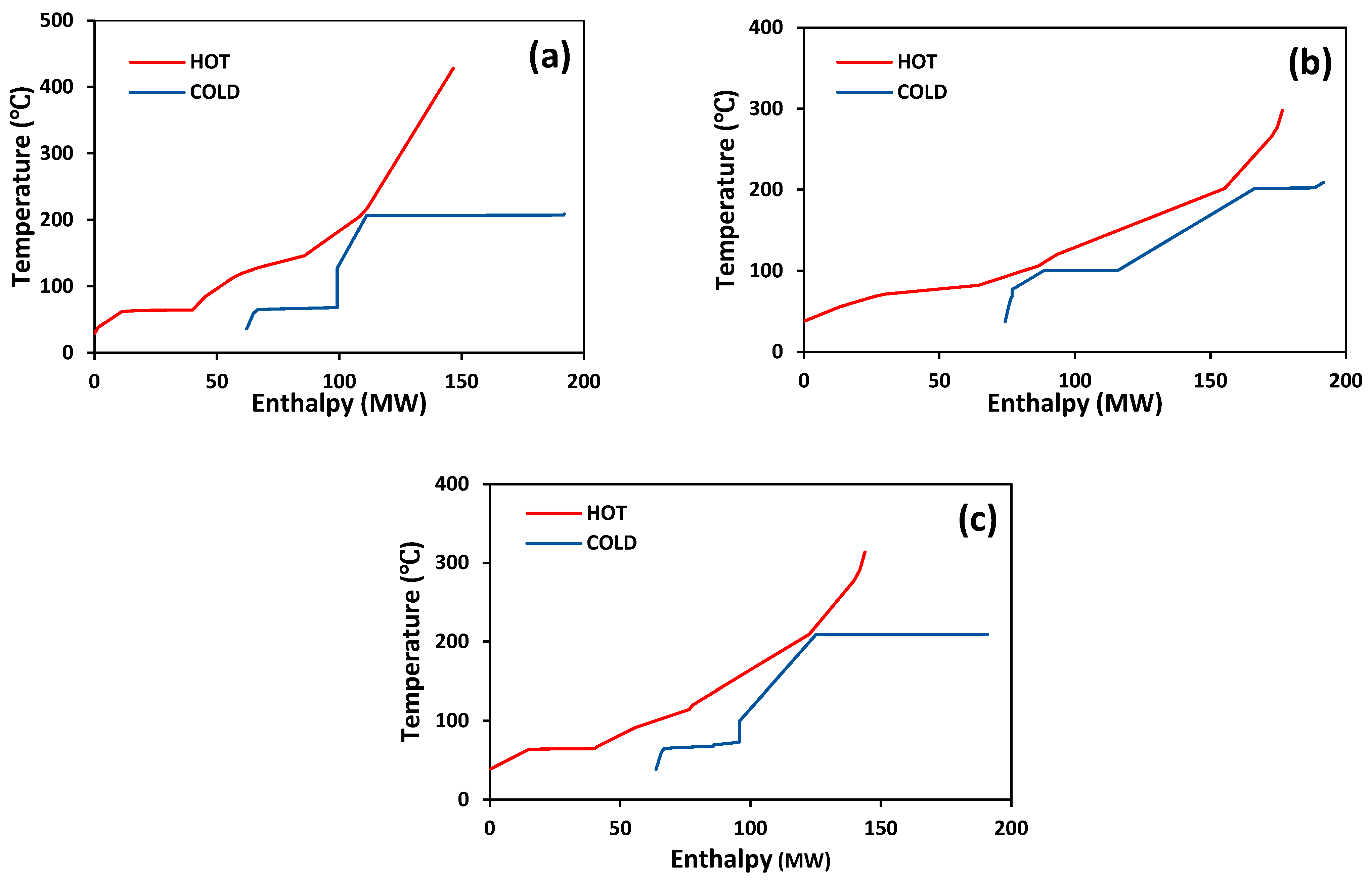
MeOH production based on SG feedstock was developed by the modified LHHW kinetic model in Aspen Plus. Later, Aspen Plus process models were optimized for both dimensional and operating parameters for MeOH production. Optimization results showed that 5000 tubes, each with a 12 m length and 0.06 m diameter, resulted in the optimum 75.39% PFR conversion. To achieve the similar conversion from the SG feedstock, the optimum operational parameters for the RFR were 209 °C, 70 bar, and thermal fluid circulating at 196 °C. However, the variations in conversion and MeOH production were observed when the feedstock material was replaced with the FG and COG within the optimized process for SG. It was found that FG resulted in significantly lower MeOH production with a reactor conversion of only 15.5% compared to other feedstocks. SG and COG-based MeOH production processes achieved conversions of 75.39% and 74.01%, correspondingly. The lower conversion of FG feedstock can be improved up to 21.72% by increasing the SN value to 4.5. In addition, a higher recycle ratio of 7.14 can also increase the conversion of FG-based MeOH synthesis. Finally, composite curve analyses showed that all three MeOH synthesis processes have interprocess heat-exchanging capability with a cost of adding the heat transfer area. To utilize the heat-exchanging capability, an optimized HEN was designed for each process. It was found that a comparatively lower number of heat exchangers (12), heaters (1), and coolers (3) were required for the SG feedstock for interprocess heat exchanging relative to SG and COG-based MeOH synthesis processes.