ML-Based Intermittent Fault Detection, Classification, and Branch Identification in a Distribution Network
Abstract
:1. Introduction
- High-resolution data collection: MATLAB/Simulink is used to generate realistic high-sampling-frequency voltage and current waveform data. These data were collected under different scenarios such as different fault durations (sub-cycle and multi-cycle) and deploying dynamic loads to generate harmonics into waveforms.
- High fault impedances: Very few studies investigated incipient fault identification [10,11] or incipient fault location [12]. However, they did not consider high-impedance faults. The proposed method is capable of detecting, classifying, and identifying faults with impedances ranging from 0.01–100 Ω.
- A method for fault detection and identification: Eight supervised learning methods are used, and their performances are compared to find the best model for incipient fault detection. Moreover, a distinction between the faulty and non-faulty phases is achieved, thus identifying the fault type: single-phase (LG), two-phase (LL-LLG), or three-phase faults (LLLL-LLLG).
- A method for faulty branch identification: ML classifiers are used to define the faulty branch.
- Topology-independent: The proposed approach for fault detection, identification, and location are generalizable and applicable to different grid topologies. Particularly, the method can be trained in a specific grid topology and employed in a different one.
2. Incipient Fault Definition and Simulation Approach
2.1. Characterization of Intermittent Faults
- These faults typically start near the positive or negative peak of the voltage waveform and end at the zero-crossing of the current waveform;
- They are typically self-clearing;
- No overcurrent protective device operates because of the short duration and self-clearance;
- The frequency of intermittent fault occurrence increases over time until permanent failure occurs;
- They are precursors to permanent failures;
- Intermittent faults can have a high impedance, meaning that an arc voltage may be present [12].
2.2. Simulation
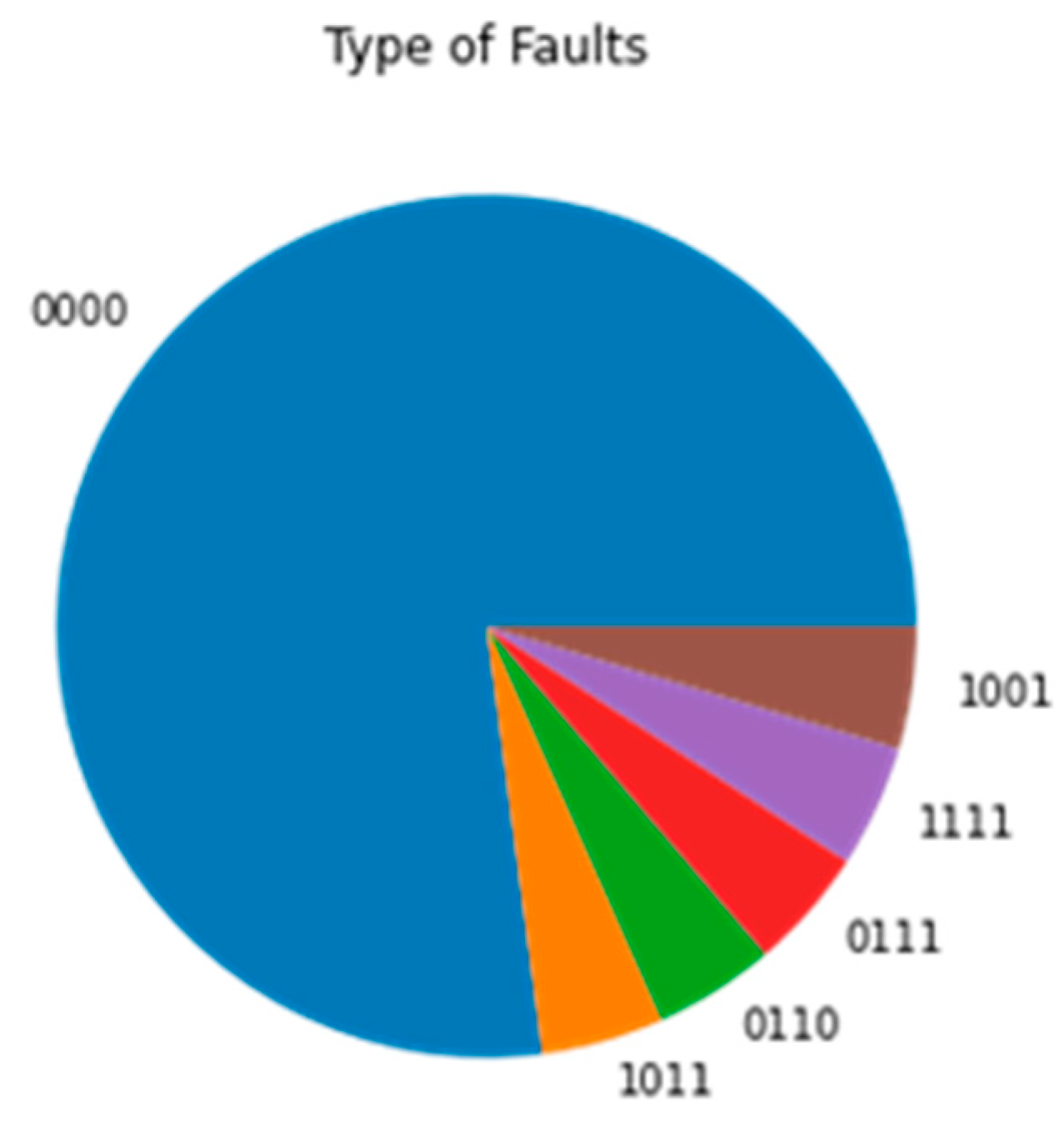
- Fault types: All possible electrical faults are considered in this research; LG, LL, LLG, LLL, and LLLG.
- Fault resistance: As explained in the motivation, very few studies were reported in the literature that covers HIFs in distribution systems. In this case, nine different fault impedances were investigated: 0.01, 1, 3, 5, 10, 25, 50, 75, and 100 Ω, covering the full spectrum of faults, both low- and high-impedance ones.
- Fault duration: Two different fault durations were considered, 5 ms and 50 ms, to represent sub-cycle and multi-cycle intermittent faults.
- Harmonics: To generate the harmonics in current and voltage waveforms, non-linear loads were used in this simulation.
- Imbalanced network: An imbalanced three-phase system is considered in this study to distinguish between LLL and LLLG.
- Faults have a more significant impact on current than voltage waveforms.
- When fault impedance increases, the amplitude of the fault current will reduce and be closer to the regular current waveforms. As a result, it is more difficult to detect these faults.
- Current and voltage waveforms for LLL and LLLG are close to each other. Therefore, it is not easy to distinguish them from each other, especially for multi-cycle faults.
2.3. Fault Detection and Identification
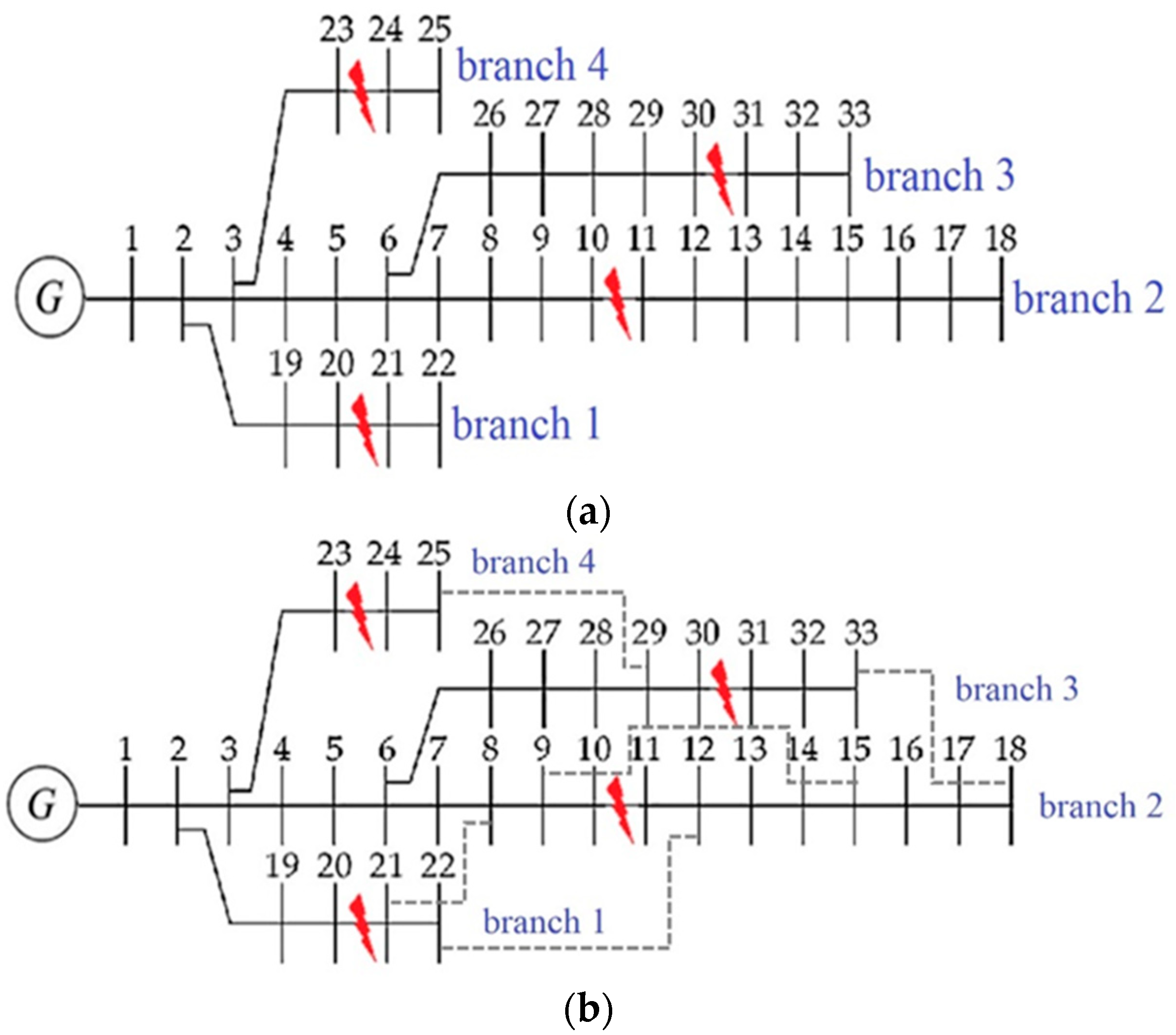
2.4. Branch Identification
2.5. Training
2.6. Evaluation and Model Selection
3. ML Tools
3.1. Linear Regression (LiRe)
3.2. Logistic Regression (LoRe)
3.3. Multi-Layer Perceptron (MLPC)
3.4. Naive Bayes (NB)
3.5. Decision Tree (DT)
3.6. KNN
3.7. GB
3.8. Random Forest (RF)
4. Results and Discussion
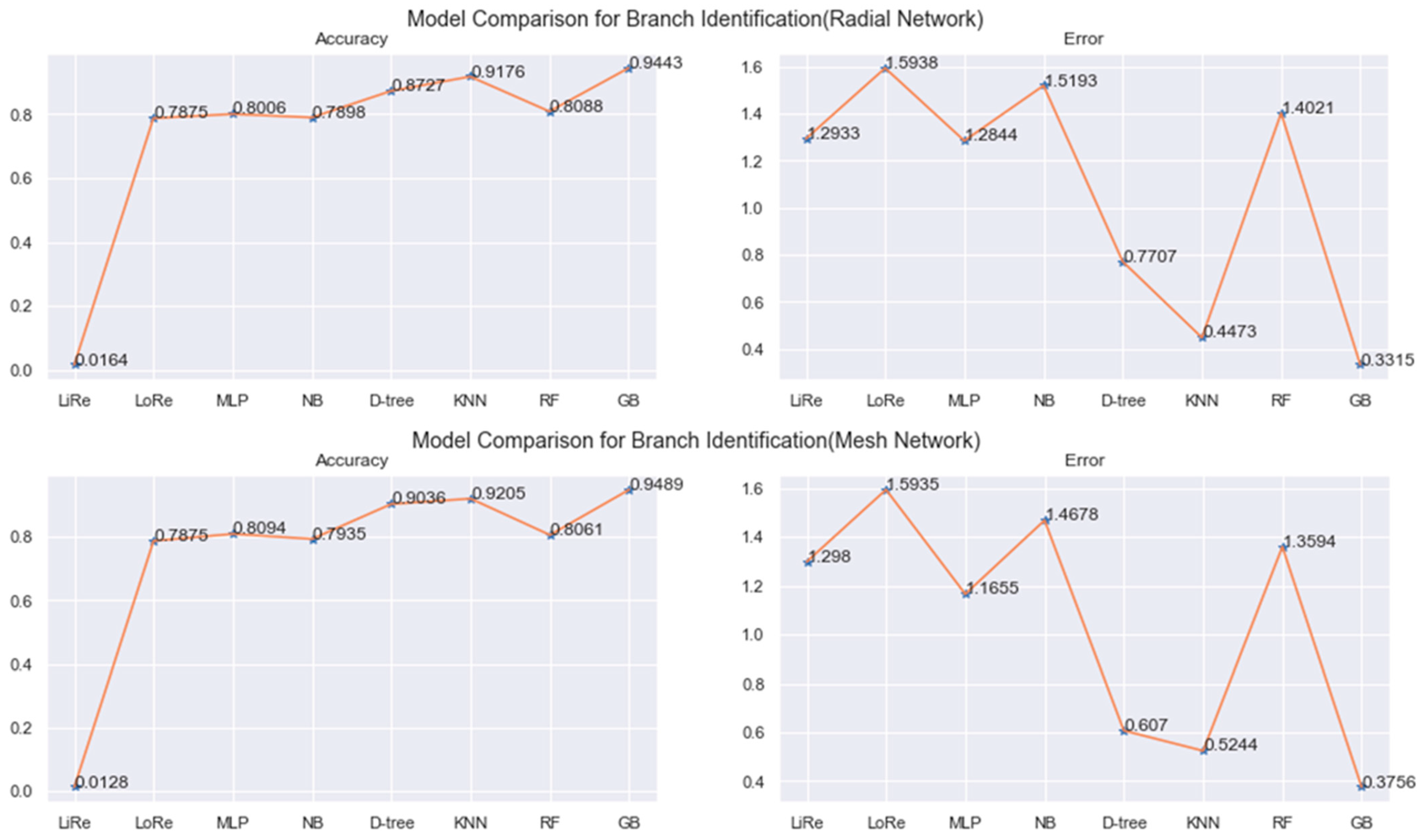
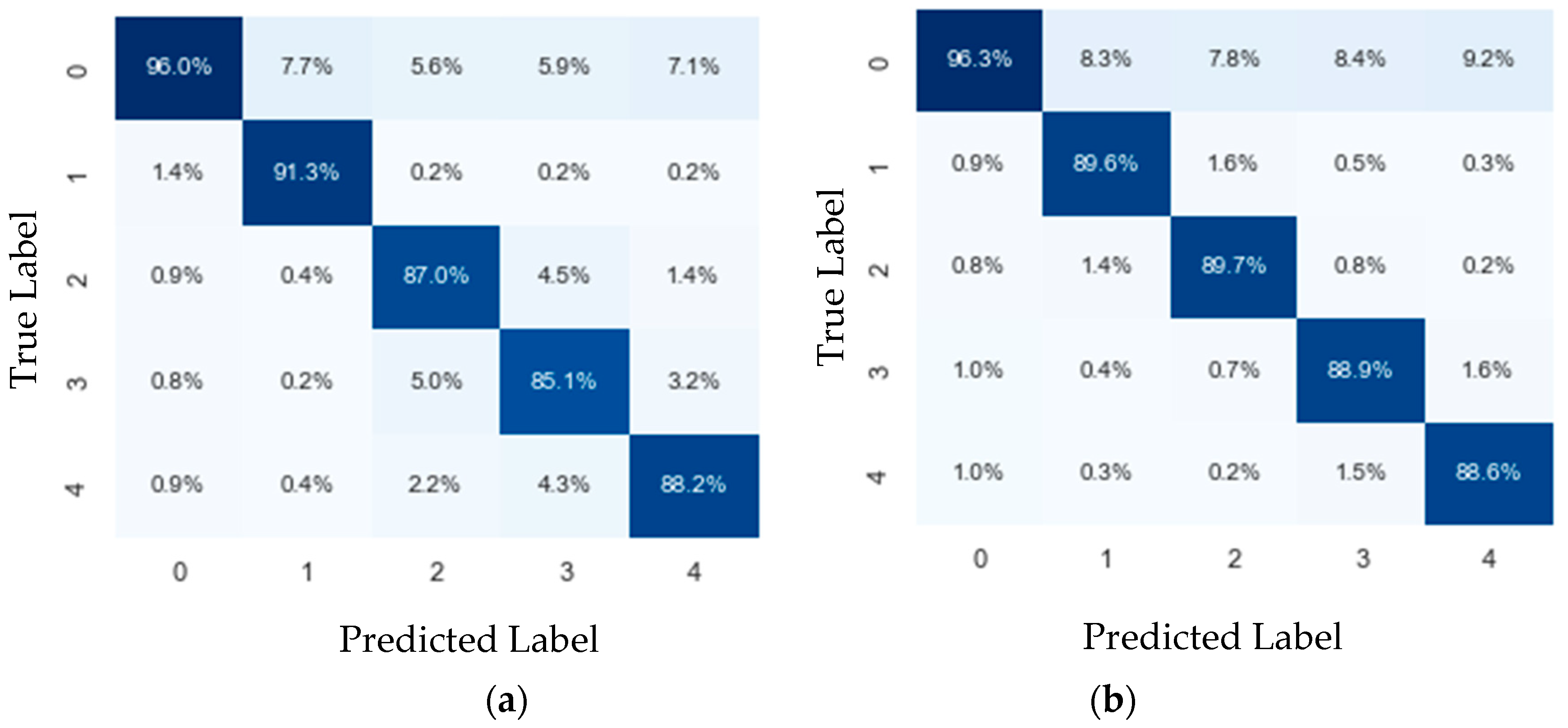
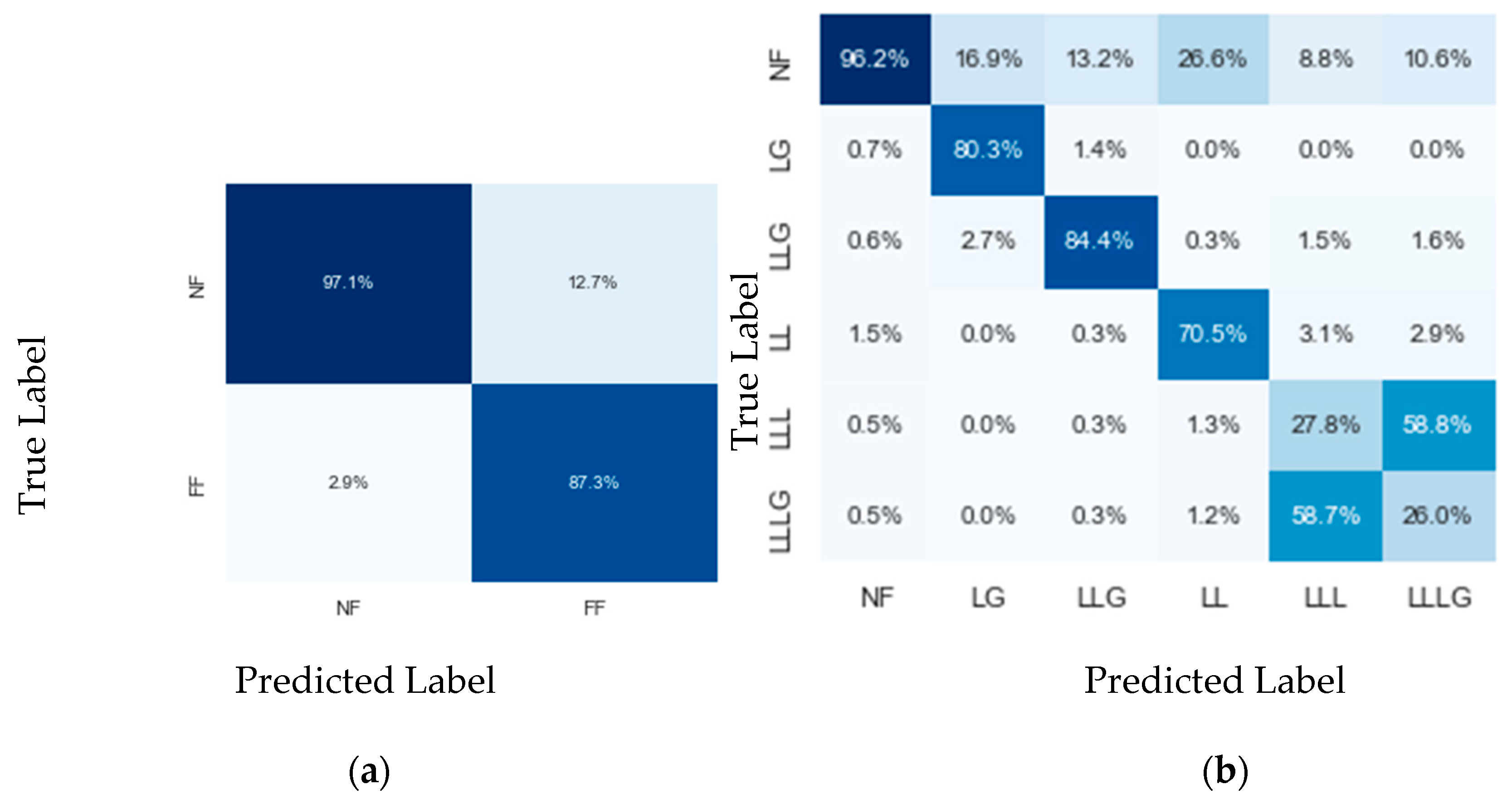
4.1. Branch Identification
4.2. Fault Detection and Fault-Type Identification
4.3. Performance Comparison
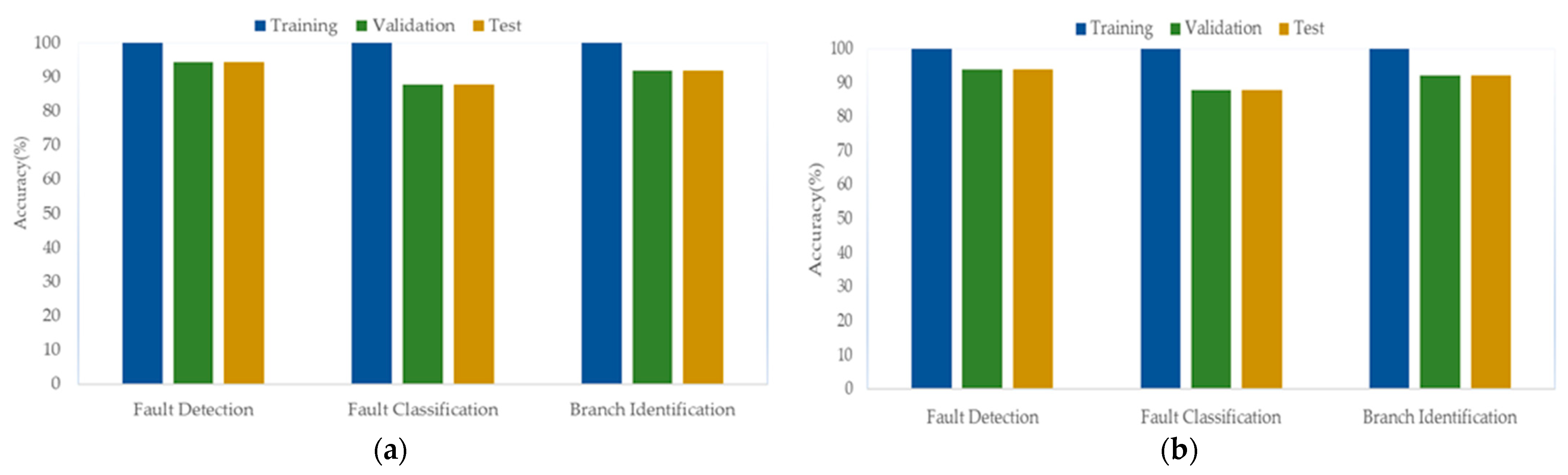
4.4. Overfitting
4.5. Comparison with Literature Methods
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Roberts, D.; Lees, M. Foresight Project; EA Technology: Chester, UK, 2021. [Google Scholar]
- Mamuya, Y.D.; Der, L.Y.; Shen, J.W.; Shafiullah, M.; Kuo, C.C. Application of machine learning for fault classification and location in a radial distribution grid. Appl. Sci. 2020, 10, 4965. [Google Scholar] [CrossRef]
- Teimourzadeh, H.; Moradzadeh, A.; Shoaran, M.; Mohammadi, B.; Razzaghi, R. High impedance single-phase faults diagnosis in transmission lines via deep reinforcement learning of transfer functions. IEEE Access 2021, 9, 15796–15809. [Google Scholar] [CrossRef]
- Bon, N.N.; Van, D.L. Fault identification, classification, and location on transmission lines using combined machine learning methods. Int. J. Eng. Technol. Innov. 2022, 12, 91–109. [Google Scholar] [CrossRef]
- Shahriar, R.F.; Yeahia, S.; Omar, K.I.; Subrata, K.S. An Intelligent Approach of Fault Classification and Localization of a Power Transmission Line. In Proceedings of the 2019 IEEE International Conference on Power, Electrical, and Electronics and Industrial Applications (PEEIACON), Dhaka, Bangladesh, 29 November–1 December 2019; pp. 53–56. [Google Scholar]
- Sapountzoglou, N.; Lago, J.; De Schutter, B.; Raison, B. A generalizable and sensor-independent deep learning method for fault detection and location in low-voltage distribution grids. Appl. Energy 2020, 276, 115299. [Google Scholar] [CrossRef]
- Sapountzoglou, N.; Lago, J.; Raison, B. Fault diagnosis in low voltage smart distribution grids using gradient boosting trees. Electr. Power Syst. Res. 2020, 182, 106254. [Google Scholar] [CrossRef]
- Baicong, S.; Hengxu, Z.; Fang, S. Machine Learning Based Fault Type Identification in the Active Distribution Network. In Proceedings of the 2019 IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC 2019), Chengdu, China, 15–17 March 2019; pp. 1330–1334. [Google Scholar]
- Asman, S.H.; Ab Aziz, N.F.; Amirulddin, U.A.; Ab Kadir, M.Z.A. Transient fault detection and location in power distribution network: A review of current practices and challenges in Malaysia. Energies 2021, 14, 2988. [Google Scholar] [CrossRef]
- Xiong, S.; Liu, Y.; Fang, J.; Dai, J.; Luo, L.; Jiang, X. Incipient fault identification in power distribution systems via human-level concept learning. IEEE Trans. Smart Grid 2020, 11, 5239–5248. [Google Scholar] [CrossRef]
- Zhang, C.; Song, N.; Li, Y. Incipient fault identification of distribution networks based on feature matching of power disturbance data. Electr. Eng. 2021, 103, 2447–2457. [Google Scholar] [CrossRef]
- Herrera-Orozco, A.R.; Bretas, A.S.; Orozco-Henao, C.; Iurinic, L.U.; Mora-Flórez, J. Incipient fault location formulation: A time-domain system model and parameter estimation approach. Int. J. Electr. Power Energy Syst. 2017, 90, 112–123. [Google Scholar] [CrossRef]
- Lukowicz, M.; Rebizant, W.; Kereit, M. New approach to intermittent earth fault detection with admittance criteria. Int. J. Electr. Power Energy Syst. 2020, 123, 106271. [Google Scholar] [CrossRef]
- Hojabri, M.; Kellerhals, S.; Upadhyay, G.; Bowler, B. IoT-based PV array fault detection and classification using embedded supervised learning methods. Energies 2022, 15, 2097. [Google Scholar] [CrossRef]
- Scikit-Learn. Available online: https://scikit-learn.org/ (accessed on 24 March 2023).
- GeegkforGeeks. Available online: https://www.geeksforgeeks.org/ (accessed on 28 July 2023).
- Towards Data Science. Available online: https://towardsdatascience.com/introduction-to-logistic-regression-66248243c148 (accessed on 28 July 2023).
- Codecademy. Available online: https://www.codecademy.com/learn/machine-learning-k-nearest-neighbors/modules/knn-classification-course/cheatsheet (accessed on 28 July 2023).
- IBM. What Is Random Forest? Available online: https://www.ibm.com/topics/random-forest (accessed on 28 July 2023).
- Lago, J.; Ridder, F.D.; Vrancx, P.; Schutter, B.D. Forecasting day-ahead electricity prices in Europe: The importance of considering market integration. Appl. Energy 2018, 211, 890–903. [Google Scholar] [CrossRef]
- Moloi, K.; Davidson, I. High impedance fault detection protection scheme for power distribution systems. Mathematics 2022, 10, 4298. [Google Scholar] [CrossRef]





| Fault Type | Output | |||
|---|---|---|---|---|
| G | C | B | A | |
| No fault | 0 | 0 | 0 | 0 |
| LG | 1 | 0 | 0 | 1 |
| LL | 0 | 0 | 1 | 1 |
| LLG | 1 | 0 | 1 | 1 |
| LLL | 0 | 1 | 1 | 1 |
| LLLG | 1 | 1 | 1 | 1 |
| Model | Model Hyperparameters | ||
|---|---|---|---|
| Fault Detection | Fault Classification | Branch Identification | |
| MLP | solver = ‘adam’, alpha = 1e-5, hidden_layer_sizes = (5, 2), random_state = 1,max_iter = 700 | solver = ‘adam’, alpha = 1e-5, hidden_layer_sizes = (10, 6), random_state = 1,max_iter = 1500 | solver = ‘adam’, alpha = 1e-5, hidden_layer_sizes = (10, 6), random_state = 1,max_iter = 1500 |
| NB | var_smoothing = 1.2328467394420635e-09 | var_smoothing = 8.111308307896856e-09 | var_smoothing = 2.310129700083158e-07 |
| DT | criterion = ‘entropy’, max_depth = 20, min_samples_leaf = 5, random_state = 42 | criterion = ‘entropy’, max_depth = 20, min_samples_leaf = 5, random_state = 42 | criterion = ‘entropy’, max_depth = 20, min_samples_leaf = 5, random_state = 42 |
| KNN | metric = ‘manhattan’, n_neighbors = 2, weights = ‘distance’ | metric = ‘manhattan’, n_neighbors = 5, weights = ‘distance’ | metric = ‘manhattan’, n_neighbors = 5, weights = ‘distance’ |
| RF | max_depth = 6, min_samples_leaf = 2, min_samples_split = 5, n_estimators = 56, bootstrap = ‘False’,max_features = ‘sqrt’ | max_depth = 6, min_samples_leaf = 1, min_samples_split = 5, n_estimators = 72, bootstrap = ‘False’,max_features = ‘sqrt’ | max_depth = 6, min_samples_leaf = 1, min_samples_split = 2, n_estimators = 41, bootstrap= True, max_features= ‘sqrt’ |
| GB | n_estimators = 100, learning_rate = 1.0, max_depth = 20 | n_estimators = 50, learning_rate = 1.0, max_depth = 20 | n_estimators = 100, learning_rate = 0.1, max_depth = 20, random_state = 0 |
| Parameters | [6] | [7] | This Case Study |
|---|---|---|---|
| Grid voltage (kV) | 0.4 | 0.4 | 12.66 |
| Method | DNNs | GBT | GB, KNN |
| Fault types | LG, LLL | LG, LLL | LG, LLG, LLLG, LLL, LL |
| Accuracy | 100 | 84.1-95.8 | 93.9–94.9 |
| Sample frequency (kHz) | NA | NA | 10 |
| Fault characteristic | permanent | permanent | intermittent |
| Fault resistance (Ω) | 0.1–1000 | 0.1, 0.5, 1, 3, 5, 7.5, 10, 30, 50, 75, 100, 300, 500, 750, 1000 | 0.01, 1, 3, 5, 10, 25, 50, 75, 100 |
| Parameters | [5] | [21] | This Case Study |
|---|---|---|---|
| Grid voltage (kV) | 11 | 22 | 12.66 |
| Method | ANN | SVM, NN, DT | KNN |
| Fault types | LG, LLG, LLLG | LG, LLG, LLLG, LLL, LL | LG, LLG, LLLG, LLL, LL |
| Accuracy | 84.5 | 83-97.6 | 87.8 |
| Sample frequency (kHz) | NA | 12.5 | 10 |
| Fault characteristic | permanent | permanent | intermittent |
| Fault resistance (Ω) | LIF | LIF | 0.01, 1, 3, 5, 10, 25, 50, 75, 100 |
| Parameters | [6] | [7] | This Case Study |
|---|---|---|---|
| Grid voltage (kV) | 0.4 | 0.4 | 12.66 |
| Method | deep learning | GBT | GB, KNN |
| Fault types | LG, LLL | LG, LLL | LG, LLG, LLLG, LLL, LL |
| Accuracy | 83.5 | 91.7-93.8 | 91.8-94.9 |
| Sample frequency (kHz) | NA | NA | 10 |
| Fault characteristic | permanent | permanent | intermittent |
| Fault resistance (Ω) | 0.1, 0.5, 1, 3, 5, 7.5, 10, 30, 50, 75, 100, 300, 500, 750, 1000 | 0.1, 0.5, 1, 3, 5, 7.5, 10, 30, 50, 75, 100, 300, 500, 750, 1000 | 0.01, 1, 3, 5, 10, 25, 50, 75, 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hojabri, M.; Nowak, S.; Papaemmanouil, A. ML-Based Intermittent Fault Detection, Classification, and Branch Identification in a Distribution Network. Energies 2023, 16, 6023. https://doi.org/10.3390/en16166023
Hojabri M, Nowak S, Papaemmanouil A. ML-Based Intermittent Fault Detection, Classification, and Branch Identification in a Distribution Network. Energies. 2023; 16(16):6023. https://doi.org/10.3390/en16166023
Chicago/Turabian StyleHojabri, Mojgan, Severin Nowak, and Antonios Papaemmanouil. 2023. "ML-Based Intermittent Fault Detection, Classification, and Branch Identification in a Distribution Network" Energies 16, no. 16: 6023. https://doi.org/10.3390/en16166023
APA StyleHojabri, M., Nowak, S., & Papaemmanouil, A. (2023). ML-Based Intermittent Fault Detection, Classification, and Branch Identification in a Distribution Network. Energies, 16(16), 6023. https://doi.org/10.3390/en16166023








