Power Quality Measurement Results for a Configurable Urban Low-Voltage DC Microgrid

Abstract

The growing use of renewable energy sources and sustainable technologies has increased the attractiveness of low-voltage DC distribution grids. Despite initial research and standardization work, the definition of power quality (PQ) issues and their related compatibility levels in DC grids and the related measurement techniques remain in their infancy. The lack of available measurement results obtained in real-world situations is a major shortcoming. In this paper, the results of a measurement campaign obtained in a configurable bipolar 350 V/700 V DC microgrid in an urban environment are presented. Voltage and current signals were registered continuously at different positions in the microgrid with a sampling rate of 500 kSa/s while changing the configuration of the microgrid; the resulting data were analyzed afterwards, with a focus on DC voltage and current variation, ripple, and spectral analysis. The measurements were taken with custom-designed metrology-sound measurement equipment. The measurement results provide input to the development of DC PQ analysis tools and the standardization of DC PQ measurement methods. Furthermore, the experience obtained will be beneficial for utility companies and regulatory authorities for reliable planning-level and compatibility-level surveys.

1. Introduction

Despite the inefficient power conversion required, local DC power distribution was proposed and investigated as a clean and reliable supply system for AC industrial applications two decades ago [1]. LED lighting, photovoltaic cells, and electric vehicles (EVs) are fundamentally DC, which means they require power conversion when connected to traditional AC grids. As a result, the growing use of renewable and sustainable technologies has increased the attractiveness of low-voltage (LV) DC microgrids as local extensions of the traditional AC grid [2] or potentially even replacing the existing AC grid infrastructure with DC distribution grids [3]. Several DC grid trials are currently underway to investigate the potential benefits and challenges of these systems. The first DC test grid experiments have been reported, with a focus on power flow monitoring [4], energy management and harmonics control [5], and efficiency, losses, and potential energy savings [6].

A lot of research has been conducted on DC microgrids focusing on control strategies and stabilization techniques [7], system architectures and related aspects [8], and planning and implementation challenges [9]. An important difference between AC and DC grids is in droop control, which facilitates the operation of multiple power sources in parallel. The droop control of AC electrical power generators reduces their output power as the line frequency increases and vice versa, even if communication is lost. In DC systems, there is no frequency, and therefore a voltage regulation circuit is used to intentionally increase or decrease the output voltage as it needs to provide lower or higher current, respectively. Distributed energy sources such as photovoltaic (PV) panels and micro wind turbines with variable output will be common in future DC grids. Hence, the switching of power delivery between multiple sources should be extremely smooth to avoid transient voltages and system instabilities.

The present focus of the standardization of DC grid control is on installation, safety, voltage levels, and the detection of faults [10]. However, the implementation of DC microgrids introduces new measurement challenges including current and voltage ripple, inrush currents, voltage fluctuations, short circuit events, and other power quality (PQ) issues. The magnitudes, durations, and dynamics of these DC PQ issues differ from those in AC grids because, for example, zero-crossings do not exist in DC. In particular, switching events can lead to very high voltage transients [11] and arching effects [12] that may lead to severe damage. Furthermore, lower-frequency harmonics can enter the DC microgrid by rectifiers in the AC-DC converters when linked to an AC grid, and higher-frequency distortions caused by converter switching at resonance frequencies are potentially harmful as well [13] and might cause extensive heating of components such as capacitors, batteries, and cables [14].

Many PQ standards already exist for AC, such as those setting PQ limits for European public electricity grids [15], providing guidance on monitoring PQ in electrical power systems [16], or defining the methods for measurement and interpretation of results for PQ parameters [17] and harmonics and interharmonics in particular [18]. However, the standardization of measurement methods and definitions for DC PQ phenomena and events is still largely missing. The problem of defining PQ indices for LV DC grids was discussed more than a decade ago [19]. Statistical DC PQ indicators were proposed in [4] based on current waveforms measured at the DC power supply of various household applications. Specific DC PQ phenomena have been considered for DC microgrids [20], smart grids [21], and railway systems [22] and reviewed in the context of existing standards [23] and international regulations [24]. This and other related information was recently compiled in a standardization technical report [25], which states that some of the technical items have yet to be fully explained and that some gaps have been identified for future work. A recent overview of PQ phenomena in the context of standards and proposed metrics for DC grids is provided in Ref. [14]. From this overview, it is concluded that the measurement method for ripple and frequency analysis is an important aspect of DC microgrids that still needs further investigation. A significant shortcoming in this regard is the lack of available measurement data and their interpretation in real-world DC grids with renewable energy sources implemented.

The European metrology project “20NRM03 DC grids” addresses these needs by investigating the distortions that occur in real LV DC grids and by developing reference measurement systems [26]. The aim is to contribute to new or improved standards regarding the definitions, measurement methods, and compatibility levels of PQ in DC grids, and to suggest suitable test waveforms for DC electricity meter testing. Measurement campaigns have been planned for existing LV DC grid trials, such as in Malaga Smart City [27]. Furthermore, initial reference systems for DC power [28] and electricity meter testing in the presence of AC distortions [29] have been developed.

In this paper, we present the preliminary results of the continuous wideband voltage and current monitoring in an experimental LV DC microgrid in an urban environment. The purpose of the measurement campaign was to investigate the level and type of distortions occurring in different DC grid configurations for frequencies up to 150 kHz, with a focus on ripple magnitude and frequency content. This frequency range was chosen based on the behavior of power electronics and the ongoing trend towards higher switching frequencies and smaller passive components, leading to new measurements [30] and related challenges [31] as well as to a new standardization of PQ for AC power systems [32]. As a demonstration of the importance of standardized definitions, the ripple magnitude is calculated using various signal processing parameter settings. The measurement results are valuable input for the development of DC PQ analysis tools and standards on measurement methods. Furthermore, the experience obtained will be beneficial for utility companies and regulatory authorities for reliable planning-level and compatibility-level surveys.

From the network topology point of view, this work should be considered a case study rather than representing a benchmark LV microgrid such as for AC [33]. Rather than using simulations or a detailed analysis of the DC microgrid and its components, using Kirchhoff’s voltage and current laws and Tellegen’s theorem for instantaneous power to explain the origin of the observed PQ distortions, the focus of this work is on the occurrence of PQ phenomena in a real DC grid in operation and how to measure them, regardless of their origin.

2. Experimental Procedure

2.1. Description of the DC Microgrid

A PQ measurement campaign was performed at an experimental LV DC microgrid designed, installed, and operated by DC Opportunities R&D (DCO). The microgrid is installed in The Green Village, which is a field lab at the Campus of the Technical University of Delft for sustainable innovation in the urban environment. Due to its experimental status, it is exempt from standard rules and regulations, which makes it a unique site to investigate the behavior, benefits, and challenges of DC grids in a real-world urban environment.

The DC microgrid is a bipolar grid that can be operated at a nominal voltage of 350 V or 700 V; for the experiments described in this paper, it was operated at 350 V and can be connected to the 230 V AC distribution grid by means of a unipolar AC/DC converter. A PV converter with nominal power of 6 kW with MPPT (Maximum Power Point Tracking) delivers solar energy to the grid. The MPPT system regulates the voltage level at the output of the PV converter; when the power consumption is lower than the available power, the voltage level will increase to a maximum of 380 V (no-load condition). Currently, the main load consists of externally controlled dimmable LED streetlights, with a maximum power consumption of approximately 1.5 kW in total. Additionally, a custom-developed dimmable LED streetlight is connected, which is redesigned and operated by DCO with a power curtailment system that automatically reduces the power consumption when the voltage level decreases below 325 V. The streetlights and the custom DCO LED are connected to the positive polarity conductor. The negative polarity conductor was not in use for the experiments described in this paper. In the future, a DC electric vehicle charging station and a battery storage system will be implemented. The 230 V AC mains power was still available for supplying the measurement equipment and auxiliary instrumentation.

Solid-state circuit breakers are installed to disconnect the AC/DC converter providing the link to the AC grid or the loads (streetlights and DCO LED). The MPPT control electronics can be used to turn off the PV system. This allows the microgrid to be reconfigured while the measurements are being performed. In particular, it can be operated in grid-connected mode, i.e., connected to the AC grid through the AC/DC converter, or in island mode, i.e., disconnected from the AC grid and fully powered by the PV and MPPT system.

A schematic diagram of the LV DC grid and the sensors connected to it is shown in Figure 1. The actual power during the experiments was lower than the maximum 1.5 kW because the streetlights were dimmed externally and the solar energy generation on a cloudy winter day is low. Therefore, the expected currents are in the order of amperes or less and the voltage drop over the main conductor is negligible. The voltage is measured close to the circuit breaker controlling the link with the AC grid, such that it still measures the voltage if the AC grid voltage is disconnected. Since the voltage is more or less the same everywhere, more voltage measurement points are not required, although at the highest frequencies of concern (up to 150 kHz), differences in magnitude might exist due to the voltage drop over the inductive component of the conductor impedance. Even though no loads of interest are connected to the negative pole, for comparison, the voltage is measured both at the positive and the negative pole (not shown in the figure).

Since there are no loads connected to the negative pole, only the current through the positive-polarity conductors is measured. Three current transducers are installed for measurements: current sensors 1, 2, and 3 are connected in series with the AC/DC converter positive output, in between the loads and sources, and at the MPPT positive output, respectively. The current sensors are positioned such that their currents should add up to zero in agreement with Kirchhoff’s current law.

2.2. Measurement Equipment

The experiments described here were carried out using metrology-sound, high-precision measurement equipment. Hioki type 9322 voltage transducers were used, which are 2 kV, 1000:1, 10 MHz differential voltage probes. The current transducers used are Hioki type CT6862-05, which are 50 A, 40 mV/A, 1 MHz AC/DC pass-through current sensors. Due to the expected low current levels (in the order of amperes or less when measuring only part of the maximum 1.5 kW power of the loads and the low power generation of the PV system on a cloudy winter day at a voltage level of 350 V), the current wires were wound ten times through the current sensors to increase the current level by a factor of ten. A well-characterized waveform recorder originally designed by VSL for AC applications [34] has been adapted for use in DC grids. It is based on a Picoscope 4824 oscilloscope, which is an 8-channel, 12-bit, 20 MHz digitizer. The uncertainty of the voltage sensors at 350 V, the current sensors at 10 A, and the digitizer unit input channels in the 1 V range, as determined by direct measurement with a calibrated precision calibrator, is well within 0.1% over the entire frequency range up to 150 kHz; a more accurate calibration can be performed using, for instance, the method presented in [35], if required. A minicomputer is built in for running the data acquisition software and an external solid-state drive is connected for local storage of the raw measurement data.

The output signals of the five transducers were recorded with a sampling rate of 500 kSa/s. Therefore, the Nyquist frequency (i.e., half the sampling rate) is lower than the analog bandwidth of the equipment used, which means that signals occurring at frequencies higher than 250 kHz will show up as frequency content below 250 kHz due to aliasing. However, the majority of the distortions are expected to occur at frequencies below a few kilohertz and not many distortions are expected in the hundreds-of-kilohertz range. Therefore, no anti-aliasing filter was used.

The raw samples were stored in files consisting of subsequent gapless windows of 2 s. For a measurement time of one hour, this provides a dataset of about 100 GB. To reduce the amount of data to be stored during longer measurement periods, trigger mechanisms could be implemented, such as those used for the onsite detection of current distortions causing errors in static electricity meters [36]. However, at this stage, there is no indication of the level and type of distortions to be expected, so no suitable trigger mechanisms could be defined. Therefore, it was decided to store all raw measurement data unconditionally to be investigated for the presence of PQ distortions afterwards. The consequence is that we cannot store and analyze data over periods of 24 h or even a week. Instead, we reconfigured the grid by switching on or off specific parts on a timescale of minutes, thus mimicking different situations that might occur during 24 h or even longer. Continuing the measurements for a longer period might give other values of the voltage or current and perhaps other amplitudes of the ripple or spectra, but is not expected to provide us with significantly different PQ phenomena.

2.3. Measurand Definitions: Ripple

The primary focus of our measurements was to investigate the occurrence of ripple for different grid configurations. Usually, ripple is used to indicate distortions dominated by single-frequency tones caused by rectifiers in, for instance, AC/DC converters [8], but it can be applied to any broadband signal. In our investigations, the following definitions are used. The data from the five different transducers is represented by five sets of samples {$x_i$}, i being the sample number. These sets represent the positive and negative voltages $V_{+,i}$ and $V_{-,i}$, and the signals registered with the three current sensors, $I_{1,i},I_{2,i},$ and $I_{3,i}$, respectively. For each of these datasets, the average value $x_{\mathrm{DC}}$ was determined as follows:

$$x_{\mathrm{DC}}=\frac{1}{N}{\sum }_{i=0}^{N-1}{x}_i,$$

(1)

where N = 1,000,000 denotes the number of samples in each 2 s time window. Likewise, the root-mean-square (RMS) value $x_{\mathrm{RMS}}$ was determined as follows:

$$x_{\mathrm{RMS}}=\sqrt{\frac{1}{N}{\sum }_{i=0}^{N-1}{x_i}^2}$$

(2)

The ripple content $x_{\mathrm{ripple}}$, which is a measure of the total AC contribution of the spectral content of the signal $x_i$ in each 2 s time window, including noise and electromagnetic interference, can be determined from (2) and (3) as follows:

$$x_{\mathrm{ripple},\mathrm{RMS}}=\sqrt{{x_{\mathrm{RMS}}}^2-{x_{\mathrm{DC}}}^2}$$

(3)

The ripple content defined this way is similar to the conventional standard deviation of a random variable $x$ and can be considered an integral component representing the RMS deviation from the DC value. For a single-tone ripple signal of 1 V RMS magnitude, sampled with a sampling rate equal to an integer multiple of the signal frequency for a time period equal to an integer number of cycles, this definition indeed provides a ripple with a magnitude of 1 V. Similarly, multitone signals consisting of equal magnitude components with 1 V magnitude also provide a ripple content of 1 V.

An alternative definition that is sometimes used instead is based on the difference between the maximum and minimum observed values, $x_{\max }$ and $x_{\min }$, respectively, in the dataset under consideration:

$$x_{\mathrm{ripple},\max -\min }=\frac{1}{2}·(x_{\max }-x_{\min })$$

(4)

Obviously, this latter definition will give significantly higher values for the ripple than the first definition (3). For example, for single-tone signals, Equation (4) provides a √2 ≈ 1.4 times higher ripple value than Equation (3), but when adding other single-tone distortions, the difference between the two ripple definitions further increases, depending on the phase and magnitude of the individual tones. In the case of distortions dominated by white noise, the difference is typically a factor of more than 3.

It should be emphasized that this parameter is only useful for stationary signals; in the case of transients, switching events, or even gradually varying DC voltage, it can provide unexpected and unreliable values, or at least less meaningful information. In particular, the second definition (4) is very vulnerable to randomness and very short-time phenomena, which might be useful for certain applications. For this reason, the time window of 2 s might be reduced to 10 ms to be in line with the AC PQ definition of voltage values being updated every half-cycle at 50 Hz [17], with additional averaging over 200 ms (equivalent to 10 cycles of 50 Hz) and aggregated every 3 s.

The ripple parameter, as defined in Equation (3), has been investigated before [37] as a measure of the amount of distortion measured by the different transducers and has already been suggested in preliminary standardization [25]. Further details on determining this parameter for different voltage and current signals, as well as alternative approaches, were considered in Ref. [38].

An alternative definition in terms of spectral components is discussed in the next subsection. Other definitions have been proposed as well [14], but in this paper, we primarily focus on the time-domain RMS value because in DC grids, the heating of components due to ripple is supposed to be the major issue. Most alternative definitions differ mainly in multiplication factors, which are less relevant for the purpose of this paper, in which we are investigating the influence of the measurement conditions on the results of the calculations. Furthermore, we neglect metrics based on quantiles [14] that can be considered a mixture of, or a compromise between, definitions (3) and (4).

2.4. Spectral Analysis

Apart from the DC voltage and current magnitudes and the corresponding ripple content, to investigate the spectral components caused by the different systems connected to the grid, Fourier analysis of the data was performed. To reduce the calculation time, the frequency resolution was limited to 5 Hz for frequencies up to 2 kHz, in line with the AC PQ harmonic analysis defined in the IEC 61000-4-7 [18]. For higher frequencies, as suggested in the IEC 61000-4-30 [17], a resolution of 200 Hz was used. To accomplish this, each 2 s time window was divided into 10 or 400 equal sub-windows of 200 ms or 5 ms each. The Discrete Fourier Transform (DFT) {$X_k$},

$$X_k=\frac{1}{N}{\sum }_{i=0}^{N-1}{x}_i·e^{-\frac{j2\pi }{N}kn},$$

(5)

was calculated for each of these sub-windows, with k representing the frequency; the resulting 10 or 400 DFTs were averaged such that one single averaged DFT represents the whole 2 s time window. The normalization factor 1/N ensures that the k = 0 component represents the DC voltage defined in Equation (1).

Apart from the methods suggested in the IEC 61000-4-30 [17], several alternative methods for the detection of emission or measurement of compatibility levels in the frequency range from 2 kHz to 150 kHz exist [39], including the quasi-peak detection method of CISPR-16-1-1 [40] for frequencies above 9 kHz. The latter is designed for laboratory testing, but has recently been modified [41] and tested [42] for grid applications. However, for the purpose of this paper, we will use the straightforward approach of Equation (5) described in the previous paragraph over the whole frequency range.

At this stage, it should be mentioned that the ripple content can also be defined in the frequency domain using the Fourier components of Equation (5),

$$x_{\mathrm{ripple},\mathrm{DFT}}=\sqrt{{\sum }_{k=1}^{N-1}{X_k}^2},$$

(6)

where the summation excludes the k = 0 component representing the DC voltage [25]. Note that as a direct consequence of Parseval’s theorem, calculating the ripple in the frequency domain through (6) or in the time domain through (3) yields the same result. Though mathematically not as simple as (3) or (4), using the definition in (6) has the advantage that the bandwidth considered can be easily reduced by lowering the upper index of the summation (in which case Equations (3) and (6) no longer provide the same results). The drawback is that it is significantly more calculation intensive, which might cause problems in the actual implementation into future DC PQ analyzers, particularly when considering a bandwidth of 150 kHz with the related high sampling rates required.

2.5. Measurement Procedure

Before performing any measurements, as an initial check, the AC/DC converter, loads, and PV converter were switched on subsequently. While doing so, the voltage and current sensors were read out using the Picoscope digitizer and its oscilloscope software to verify whether all voltage and current levels were as expected. After that, data storage began while changing the grid configuration settings as described in

Table 1. Different grid configurations investigated during the measurement campaign. X means disconnected, whereas 0 and 1 mean connected and switched on and off, respectively.

Config.	Description	Time (s)	AC Link	MPPT	Lighting	LED DCO
1	Experiment started	0	1	1	1	default
2	Reduced-intensity LED DCO	434	1	1	1	reduced
3	LED DCO switched off	584	1	1	1	0
4	Streetlights switched off	790	1	1	0	0
5	MPPT switched off	1076	1	0	0	0
6	Switched on loads	1298	1	0	1	default
7	LED DCO at max power	1548	1	0	1	max
8	Switched on MPPT	1730	1	1	1	max
9	Switched off MPPT	2082	1	0	1	max
10	Switched off loads	2130	1	0	0	0
11	AC link and streetlights disconnected	2208	X	0	X	0
12	Reconnected AC	2538	1	0	X	0
13	Switched on LED DCO	2596	1	0	X	default
14	Switched on MPPT	2692	1	1	X	default
15	Dimmed LED DCO	2834	1	1	X	reduced
16	Switched off AC link, islanding mode	2952	0	1	X	reduced
17	Increased LED DCO	3090	0	1	X	increased
18	Minimum power LED DCO	3226	0	1	X	min
19	Increased demand LED DCO	3326	0	1	X	increased
20	Further increased LED DCO	3412	0	1	X	high
21	De-islanding, reconnected AC	3484	1	1	X	high
22	Switched off MPPT	3556	1	0	X	high
23	Switched off LED DCO	3638	1	0	X	0
24	Switched off AC/DC	3660	0	0	X	0
25	Experiment completed	3722	X	X	X	X

. The link to the AC grid, the PV and MPPT system, and the loads could all be switched on or off independently. When preparing for operation in island mode, in configuration 11, the streetlights were disconnected manually because they draw more power than was available from the PV converter on the cloudy winter day of the measurements. In islanding mode, the negative pole of the MPPT was also switched off.

The MPPT system regulating the voltage level was realized both in grid-connected mode and in island mode, i.e., with or without a connection to the AC grid, by controlling the power consumption to a level that is higher or lower than the available power from the PV converter, respectively. The DCO LED power demand was set manually, but the operation of the built-in power curtailment system was investigated in island mode when the power was fully generated by the PV converter and the power consumption was higher than the available power. Therefore, even though little variation in PV power was obtained during the measurements, by varying the configurations according to Table 1, all relevant scenarios were investigated. For instance, in grid-connected mode, high solar radiation resulted in a surplus of available power, a scenario that we obtained by disconnecting the streetlights (configuration no. 4). Similarly, in islanding mode, the DCO LED demand was reduced from a value greater than to a value less than the power available from the PV converter (configuration no. 18).

3. Results

The specific grid configurations, described in Table 1, were selected primarily to observe a variety of distortions, in particular with different amplitudes of the ripple signal and the corresponding DC component. The output signals of the two voltage and three current transducers, obtained for successive 2 s time windows using Equations (1)–(3), were investigated as a function of time while changing the configuration. The measurement results obtained with the different transducers are summarized in

Table 2. Typical voltage and current levels measured for the different measurement configurations and the magnitudes of their corresponding ripple content.

Config.	${\mathit{V}}_{\mathit{D}\mathit{C}}^{+}$ (V)	${\mathit{V}}_{\mathit{r}\mathit{i}\mathit{p}\mathit{p}\mathit{l}\mathit{e}}^{+}$ (V)	${\mathit{V}}_{\mathit{D}\mathit{C}}^{-}$ (V)	${\mathit{V}}_{\mathit{r}\mathit{i}\mathit{p}\mathit{p}\mathit{l}\mathit{e}}^{-}$ (V)	${\mathit{I}}_{1,\mathit{D}\mathit{C}}$ (A)	${\mathit{I}}_{1,\mathit{r}\mathit{i}\mathit{p}\mathit{p}\mathit{l}\mathit{e}}$ (A)	${\mathit{I}}_{2,\mathit{D}\mathit{C}}$ (A)	${\mathit{I}}_{2,\mathit{r}\mathit{i}\mathit{p}\mathit{p}\mathit{l}\mathit{e}}$ (A)	${\mathit{I}}_{3,\mathit{D}\mathit{C}}$ (A)	${\mathit{I}}_{3,\mathit{r}\mathit{i}\mathit{p}\mathit{p}\mathit{l}\mathit{e}}$ (A)
1	350	50	380	56	1.08 1	0.40 1	1.21	0.21	0.13 1	0.16 1
2	350	50	380	56	0.95 1	0.36 1	1.05	0.20	0.10 1	0.14 1
3	350	50	380	56	0.81 1	0.33 1	0.91	0.19	0.09 1	0.12 1
4	380	40	380	44	−0.03	0.01	0.00	0.01	0.03	0.01
5	350	16	350	19	0.00	0.02	0.00	0.00	0.00	0.00
6	350	19	350	24	1.06	0.28	1.06	0.20	0.00	0.00
7	350	19	350	25	1.32	0.30	1.32	0.21	0.00	0.00
8	350	50	380	53	1.20	0.38 1	1.32	0.21	0.12 1	0.15 1
9	350	19	350	26	1.32	0.30	1.32	0.00	0.00	0.00
10	350	16	350	19	0.00	0.02	0.00	0.00	0.00	0.00
11	0	12	0	13	−0.02	0.00	0.00	0.00	0.00	0.00
12	350	16	350	19	0.00	0.02	0.00	0.02	0.00	0.00
13	350	16	350	19	0.15	0.08	0.15	0.02	0.00	0.00
14	350	35	350	41	0.04	0.07	0.15	0.02	0.11 1	0.04
15	380	38	350	43	−0.02	0.01	0.07	0.02	0.09	0.01
16	350 1	35	350	39	−0.02	0.01	0.07	0.02	0.09 1	0.01
17	325	36	350	41	−0.02	0.01	0.10	0.02	0.12 1	0.01
18	380	34	350	40	−0.02	0.01	0.01	0.02	0.03	0.01
19	325	36	350	41	−0.02	0.01	0.12 1	0.01	0.14 1	0.01
20	325 1	36	350	41	−0.02	0.01	0.11 1	0.02	0.13 1	0.01
21	350	35	350	40	0.04	0.07	0.15	0.02	0.11 1	0.04
22	350	13	350	14	0.15	0.08	0.15	0.02	0.00	0.00
23	350	13	350	14	0.00	0.01	0.00	0.02	0.00	0.00
24	0	13	0	14	−0.02	0.00	0.00	0.00	0.00	0.00

¹ Values are not stable, but vary over time.

in terms of typical voltage and current levels and their respective ripple content for each configuration.

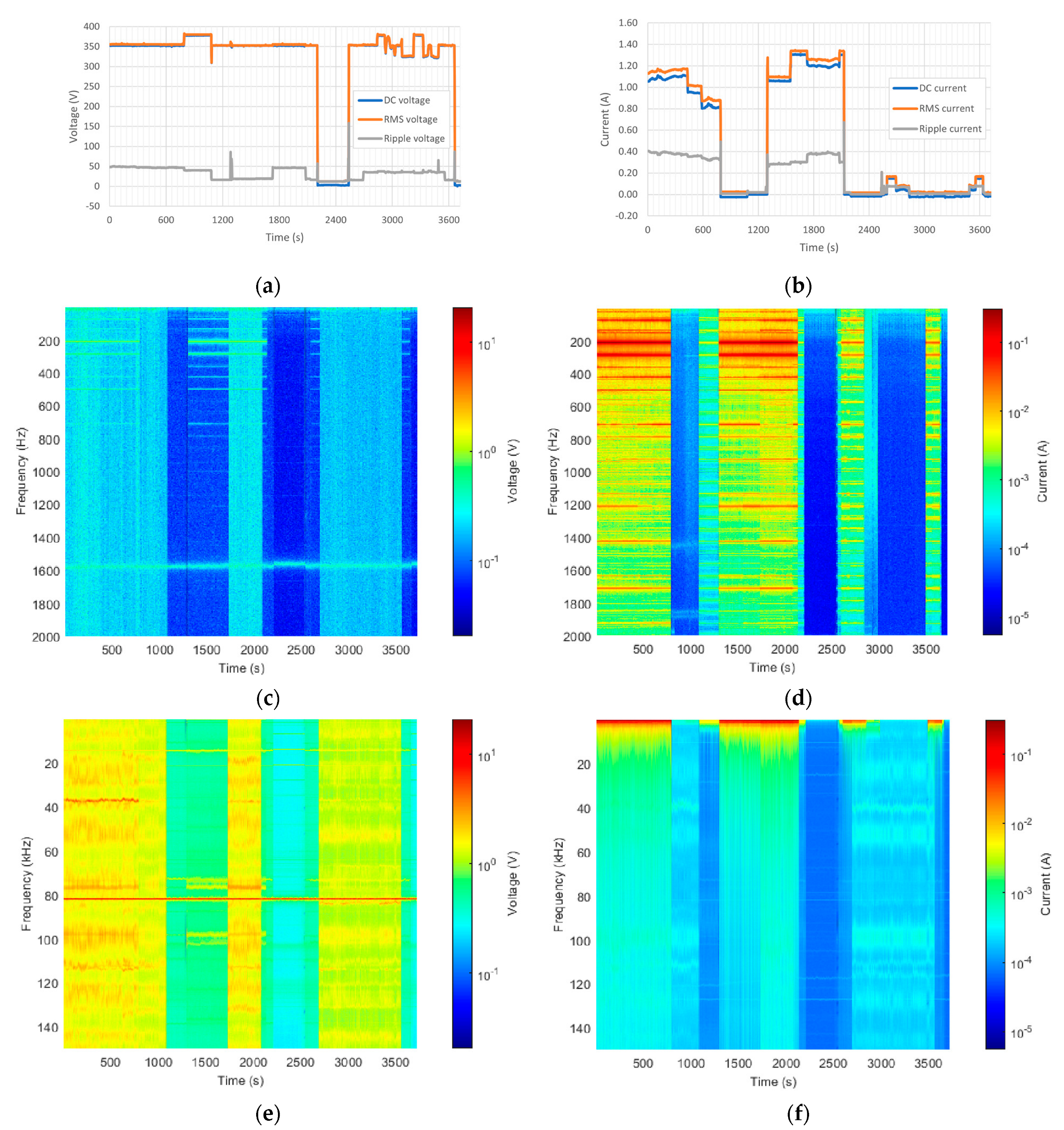
The measured DC, RMS, and ripple signals as a function of time and their corresponding DFTs, presented as two-dimensional (2D) density charts for frequencies up to 2 kHz with 5 Hz resolution and for frequencies up to 150 kHz with 200 Hz resolution, respectively, are presented in Figure 2 for the voltage at the positive pole and the current at the AC/DC converter. The measurement results for the other sensors look similar, but do not add much to the present paper. The figures for each of the two selected parameters are presented such that they are aligned vertically with the same time axis because this makes it easier to compare the different analyses.

3.1. DC Voltage and Current Levels

From Table 2, it can be observed that connecting or disconnecting a specific element does not automatically imply that all signals are changing. For instance, when switching to island mode (from configuration no. 15 to no. 16), all power was already provided by the PV generator, so switching off the AC link does not make a difference in the current signals. However, from that moment, the voltage level starts varying due to changes in solar irradiation and MPPT efficiency. On the other hand, the corresponding ripple signal is nevertheless constant.

Table 2 also shows that the voltage on the negative pole does not simply follow the voltage at the positive pole. For instance, at the start of the experiments (configuration no. 1), the voltage is 380 V rather than 350 V, whereas in island mode (starting with configuration no. 16 at t = 2952 s in Figure 2), the voltage remains constant at 350 V while at the positive pole, with only the custom DCO LED as a load, the voltage level is no longer stable at 350 V. As can be seen from Figure 2a, in that case, the voltage varies between the lower and upper limits of 325 V and 380 V, defined by the DCO LED’s built-in power curtailment system and by the MPPT, respectively.

Sometimes, negative currents are registered at the output of the AC/DC converter, for instance, when all loads are disconnected (configuration no. 4), indicating that the MPPT is feeding current into the AC/DC converter. For two configurations (i.e., configuration nos. 11 and 24), the currents of the three sensors do not add up to zero. Apparently, in that case, the negative current does not come from the MPPT. These two configurations correspond to situations where all parts are disconnected, so the negative currents observed might be caused by capacitor discharging after disconnecting the MPPT or the AC/DC converter.

3.2. Voltage Spikes

When carefully considering the voltage at the positive pole in Figure 2a, several spikes can be observed. Many of these spikes are correlated to the intentional switching events described in Table 1, for example, the one occurring at t = 790 s (configuration 4), when the circuit breaker connecting the sources to the loads is disconnected and the MPPT becomes grid-forming; at t = 1076 s (configuration 5), the MPPT is switched off and the AC/DC converter becomes grid-forming. Changing from grid-following to grid-forming takes some time for the system to recover because the supplies are not designed to recover so quickly, which results in the voltage spikes before the voltage recovers.

Other spikes, such as the ones below t = 300 s, are not related to such intentionally induced changes in the grid configuration. These “spontaneous” spikes might be caused by switching events occurring in the AC grid, which are transmitted to the DC microgrid through the AC/DC converter. This is in agreement with the observation in Figure 2a that they do not show up in island mode, i.e., between t = 2952 s and t = 3484 s.

The size, duration, and dynamics of the spikes, which might be considered transients or rapid voltage changes in the language of the IEC 61000-4-30 standard for AC PQ [17], are beyond the scope of this paper.

3.3. Voltage and Current Ripple

Although the positive and negative pole voltage levels do not follow the same pattern, the ripple voltage does, albeit with a slightly different magnitude. This is due to the fact that the voltage ripple is induced by the generators symmetrically because of the converter designs [8]. Furthermore, the current ripple seems to be correlated with the voltage ripple, although it is not a one-to-one relation. For instance, after the streetlights were switched off (configuration no. 4), the current ripple reduced from well above 0.10 A to about 0.01 A for all three sensors, whereas the voltage ripple also reduced, but remained at a relatively high level.

From Table 2, one can also observe that most of the time, the ripple content of the three sensors does not add up to zero. This is because by using Equation (3), the contributions of different spectral components are combined for each individual sensor irrespective of their phase, even if the individual spectral components of the three sensors do add up to zero. Furthermore, capacitive leakage might cause the higher-frequency components to escape from the measurement system.

3.4. Frequency Spectra

The DFT patterns of Figure 2c,e for voltage on the one hand, and Figure 2d,f for current on the other, appear to follow the patterns of the ripple voltage and current presented in Figure 2a,b over time. However, in island mode, the voltage ripple remains relatively high and stable, while the current ripple magnitude is rather low, whereas the Fourier spectra of the same measurement data show that when switching to island mode, the distinct peaks disappear, whereas the background noise level changes with the setting of the load (i.e., the DCO LED).

Although Table 2 shows that the voltage ripple magnitude measured at the positive and negative poles show the same pattern, only the voltage at the positive pole show a few distinct lower-frequency peaks, in particular at 210 Hz and 290 Hz, with magnitudes up to a few volts (colored orange in Figure 2c, i.e., order of 1% at 350 V); no such peaks were observed for the negative pole. Distinct peaks show up, for instance, at frequencies of 75 Hz, 210 Hz, 290 Hz, and higher, but no clear harmonics of 50 Hz can be observed that might be caused by the rectifiers in the AC/DC converter. For current, typically the same frequency components were found as for voltage, though much more pronounced; magnitudes up to several tenths of amperes were observed (i.e., order of 10% and higher at 1 A). Furthermore, much more distinct lower-frequency components can be observed for the current signal.

Another remarkable frequency component of the order of 10 V can be observed in Figure 2e at 36.8 kHz below t = 790 s and between t = 1730 s and t = 2082 s. These time windows correspond to configurations during which both the AC/DC converter and the MPPT were operational (see Table 1); apparently, the interaction between the two devices causes this frequency component to show up if they need to deliver power. Many other stable or fluctuating frequency components can be observed over the whole frequency range up to 150 kHz that can be traced to specific devices or combinations of devices.

A persistent frequency component at 1.6 kHz with a magnitude of a few tenths of a volt (order of 0.1 %) can be observed for all grid topologies for the voltage signal in Figure 2c, which was not significant for current (Figure 2d). A similar persistent isolated tone was observed at 82 kHz for voltage (Figure 2e) with a magnitude of several volts (about 1 % of the nominal voltage); the same tone was not clearly visible for the current measured at the AC/DC converter (Figure 2f), but did show up clearly for the two other sensors at the MPPT and at the loads, respectively. These persistent tones might indicate the pick-up of electromagnetic interference with our measurement system that is not directly caused by any of the equipment connected to the LV DC grid.

4. Discussion

4.1. DC PQ Analysis Considerations: Voltage Dips, Swells, and Fluctuations

The voltage level in the DC microgrid under test was regulated by the operation of the AC/DC converter, the MPPT system, and the power curtailment system of the DCO LED. Dependent on which system was grid-forming, the voltage was 350 V, as set by the AC/DC converter, or fluctuating around that value with a maximum of 380 V, dependent on weather conditions and load demand. In island mode, the minimum voltage of 325 V was defined by the DCO LED regulating the demand. These upper and lower limits can be set by manufacturers and should be defined by standards. The definition of the duration of voltage variations could be defined in a way equivalent to definitions for AC PQ [17], though the question is whether this is useful. After all, the measurements presented in Figure 2a confirm the expectation that DC microgrids have a much higher voltage variation than AC grids, due to more severe load changing and the variable power available from renewable energy sources (PV or wind turbines).

4.2. DC PQ Analysis Considerations: Ripple Magnitude

From the results in Table 2 and Figure 2a, the magnitude of the voltage ripple in particular appears to be quite high: up to about 50 V for a nominal voltage of 350 V. This leads to the question of whether this level is influenced by the measurement settings or the processing of the data. To answer this question, we investigated how changing the time window and frequency bandwidth affected the ripple value when using the definitions of Equations (3) and (4).

4.2.1. Time Window

First, the influence of the selected time window of 2 s was investigated. Rather than considering a window of 2 s, the corresponding 1,000,000 measurement points can be subdivided into sub-windows of, for instance, 500 ms, 200 ms, 100 ms, 50 ms, 20 ms, and 10 ms, and the ripple can be calculated for all of the sub-windows. This analysis was performed for a time window during which the voltage was stationary, i.e., containing no spikes and no noticeable drift.

The result of this analysis was that the magnitude of the voltage ripple did not significantly change with window size, which is to be expected because the definition in Equation (3) is similar to an ordinary standard deviation of the measurement data (rather than the standard deviation of the mean, which does depend on the number of measurements). For the ripple based on maxima and minima in (4), the result is also marginal because, for large statistical ensembles, the value of the highest or lowest few values will be close. However, it should be noted that for non-stationary voltage, decreasing the window size significantly increases the level of details observed. Therefore, we propose a window size of 10 ms, which is in line with the half-cycle update rate defined at 50 Hz for AC PQ [17], with additional averaging over 200 ms and aggregated every 3 s. Note that for 60 Hz systems, a half-cycle equivalence would mean a time window of 8.33 ms, but a decadic value seems more appropriate for standardization.

4.2.2. Frequency Bandwidth

Another parameter of interest is the frequency bandwidth of the measurement equipment. In the case of ripple signals consisting of a single tone or a limited number of frequency components, the frequency bandwidth should have no influence as long as it is higher than the highest frequency component. However, if the ripple is dominated by white noise, the RMS voltage magnitude, by definition, scales with the square root of the frequency bandwidth, such as for Johnson–Nyquist noise $V_{\mathrm{RMS}}=\sqrt{4k_{\mathrm{B}}TR∆f}$ caused by a resistance R at temperature T. The exact relation between the noise level and frequency bandwidth depends on the type of noise, but it is clear that for ripple signals with significant noise contribution, the frequency bandwidth might be very important.

For illustration purposes, from the available dataset obtained during our experiments, measurements performed with equipment with an analog bandwidth n times smaller than the equipment used in the present paper can be simulated digitally by averaging each non-overlapping subsequent set of n of successive samples. These averaged values should then be used as input for the ripple analysis of Equations (3) and (4), with the number N of samples to be considered reduced by a factor of n.

Figure 3 shows the influence of this averaging on the voltage ripple magnitude for a typical 2 s time window recorded during configuration 1 when using both Equations (3) and (4). The number of points averaged varies from 1 (i.e., no averaging) to 1000, the latter corresponding to an effective sampling frequency of 500 Sa/s or an effective bandwidth of 250 Hz. For comparison, a trendline visualizing the inverse dependence on the square root of the number of measurement points used for averaging, 1/√n, is also shown. This proportionality is to be expected for a spectrum dominated by white noise that is averaged out by this method. As we can see, the max–min ripple values deviate more from the 1/√n behavior than the RMS-based ripple values, which is in line with the expectation.

For the highest number of averaging points, the RMS-based ripple is slightly higher than the trendline, indicating that the lower-frequency components only have a significant impact on the ripple value when reducing the bandwidth to a sufficiently low bandwidth; only then would the largest low-frequency components observed in Figure 2a become clearly visible in the time domain. The observed isolated higher-frequency components in Figure 2e do not contribute to the ripple because they are dominated by the higher noise level at higher frequencies. This result suggests that a ripple analysis in terms of the frequency components beyond the noise floor using Equation (5) would make more sense than a time-domain definition, as in Equation (3), although the result is the same and Figure 3 looks quite similar when plotting the ripple as a function of the frequency reduction factor. A major advantage of the frequency-domain definition of Equation (5) is that it is easy to limit the frequency bandwidth mathematically to well-defined values such as 2 kHz, 9 kHz, or 150 kHz. Alternatively, if a time-domain approach is to be preferred, in order to avoid aliasing, we suggest limiting the analog bandwidth instead. The specific bandwidth might be dependent on the application, but an obvious choice would be to be in line with the existing standards for AC, i.e., to use, for instance, 9 kHz [18] or 150 kHz [32].

4.2.3. Different Metrics

The focus of this paper is on the time-domain RMS value as defined in Equation (3) because this parameter is the relevant one for the heating of particular components such as capacitors, batteries, or cables. However, for some applications, it might be useful to consider Equation (4) using the maximum and minimum rather than the RMS values of data subsets. The discussion on time window or frequency bandwidth for the two methods is very similar: a smaller time window leads to more details, but does not change the values significantly, whereas generally speaking, reducing the frequency bandwidth leads to the loss of information due to low-pass filtering and, consequently, to a reduction in the ripple value.

The definition in Equation (6) in terms of spectral components leads to exactly the same values as Equation (3). However, reducing the frequency bandwidth is very simple by just reducing the upper limit of the summation in (6). However, the drawback is the computational burden on the DC PQ analyzer on which the algorithm needs to be installed.

Ripple metrics based on quantiles can be considered a compromise between the RMS and max–min definition. Due to their dependence on statistics alone rather than measurement principles, the calculations are independent of the measurement method, although it is of utmost importance that the correct measurement data are considered, obtained using well-defined conditions.

4.3. DC PQ Analysis Considerations: Fourier Analysis

The conclusion obtained for the influence of bandwidth on the ripple magnitudes is not expected for the DFT. However, when using Equation (4), increasing the frequency resolution has no effect on the magnitudes of single or isolated frequency components, but frequency components that are sufficiently close (as for the noise floor) are combined, resulting in higher magnitudes. This increased noise floor is clearly visible when comparing Figure 2e,f (with 200 Hz resolution) to Figure 2c,d (with 5 Hz resolution). Another example of this effect is in the persistent frequency component of 82 kHz observed in Figure 2e, which was analyzed with a resolution of 200 Hz; if we use a resolution of 5 Hz instead, the apparent single peak seems to consist of several peaks at slightly different frequencies, as shown in Figure 4. The corresponding maximum magnitude of the recalculated spectrum is only about 3.2 V, whereas the related magnitude determined using the original 200 Hz resolution is about 9.1 V.

An obvious choice for the lower-frequency range (also followed in this paper) is to use a resolution of 5 Hz, which means a spectral analysis of time traces of 200 ms, in line with the definition of harmonics for AC power systems [18]. However, one might argue that for DC, there is no fundamental frequency component of 50 Hz or 60 Hz and spectral leakage might lead to incomparable results, an effect that would be reduced when analyzing larger time windows such as 1 s leading to a frequency resolution of 1 Hz. For higher frequencies, as suggested in the IEC 61000-4-30 for AC [17], a resolution of 200 Hz or multiples of that value would be more convenient, depending on the level of detail required and the calculational burden of the instrumentation used.

The calculation of the Fourier spectrum of all current and voltage signals considering the full 150 kHz bandwidth with a resolution of 200 Hz over a time window of 2 s using a MATLAB routine on a typical modern laptop takes only a few milliseconds. A few milliseconds every 2 s could be considered appropriate when implementing this in a dedicated DC PQ analyzer, but it would set considerable constraints on its computational power. Instead, one could reduce the sampling rate to 300 kHz and the frequency resolution to multiples of 200 Hz, or only analyze parts of the successive time windows.

4.4. Uncertainty Considerations

As mentioned in Section 2, the uncertainty of the measurement equipment and, therefore, of the measured voltage and current signals is in the order of 0.1%. For straightforward measurement parameters such as voltage variations, including dips and swells, when expressed in volts, the uncertainties will be in the order of 0.1% as well, but when defined as a percentage relative to another measured voltage level (i.e., as $V_1/V_2$), uncertainties due to the gain factors of the voltage measurement will cancel out and the overall uncertainty will even be lower.

For more complex measurement parameters such as ripple or Fourier components, the situation is different. As discussed in Section 4.2.2 and Section 4.3 and shown Figure 3 and Figure 4, the values of the calculated parameters can strongly depend on the parameter definitions—in this case, the frequency bandwidth of the measurement equipment for the calculation of the ripple and the selected frequency resolution for the calculation of the Fourier components, respectively. However, it should be emphasized that the dependence on parameter definitions is an intrinsic property that should not be considered uncertainty.

In itself, as long as a well-defined metric is used, the conversion of measurement data into parameters such as ripple or Fourier spectra is a very highly accurate mathematical exercise that does not add significantly to the total uncertainty of the measurement parameter. However, if the definitions rely on particular measurement conditions such as the frequency bandwidth of the measurement equipment, the implementation leads to increased uncertainty. In particular, the brick-wall filter realized by limiting the number of Fourier components in the ripple calculation using Equation (6) is rather straightforward and does not add any measurement uncertainty, but an analog low-pass filter that is required when using the time-domain definition of Equation (3) will lead to an extra uncertainty, which can easily be in the order of percents; perhaps this could be somewhat improved with a digital higher-order low-pass filter in combination with a proper anti-aliasing filter. Furthermore, the ripple definition of Equation (4) in terms of maximum and minimum values is intrinsically more fluctuating than an RMS calculation. Dependent on the type of signal, this can lead to an additional uncertainty in the order of many percents.

These considerations lead to the conclusion that a ripple definition in terms of Fourier components is preferred for the lowest measurement uncertainties. For well-defined bandwidth-limited ripple values in terms of time-domain RMS calculation, as in Equation (3), the measurement uncertainty will be a few percent; using the maximum and minimum values, as in (4), it will be in the order of ten percent or more; when using Fourier components, as in (6), it will be in the order of a percent. However, it should be noted that these uncertainties depend on the type of signal as well and might be lower if the ripple is mainly dominated by only a few frequency components.

5. Conclusions and Further Work

In this paper, we have presented measurement results obtained during a PQ measurement campaign performed in an experimental bipolar 350 V DC microgrid in an urban environment, focusing on voltage and current levels and their related ripple content and spectral components. Due to its experimental nature, this microgrid is a very convenient site to perform such measurements because the grid configuration and load demand can be manually controlled and varied while conducting the measurements. The metrology-grade measurement equipment used was developed specifically for this purpose.

Broadband voltage and current signals were recorded continuously during the whole measurement period with a 500 kSa/s sampling rate; the unprocessed measurement data were analyzed afterwards using 2 s time windows. However, to increase the level of detail and to be in line with PQ definitions for AC [17], it is suggested that 10 ms time windows (equivalent to values updated every half-cycle for 50 Hz systems) be used with additional averaging over 200 ms, aggregated every 3 s. For spectral analysis, it is suggested to use a frequency resolution of 5 Hz for frequencies below 2 kHz or 200 Hz for higher frequencies up to 150 kHz, respectively. However, it should be noted that when using larger frequency bins, individual frequency components might become merged, thus overlooking details that might be relevant for specific applications.

The voltage was observed to vary between levels of 325 V and 380 V, limited by the electronic components connected to the microgrid. The definition of voltage dips and swells for such voltage variations could be similar to AC PQ definitions [17], but the usefulness is questionable due to the intrinsic voltage variations of renewable energy sources and load variations in DC microgrids. A distinction in standardization could be made between DC grids operating in grid-connected or island mode.

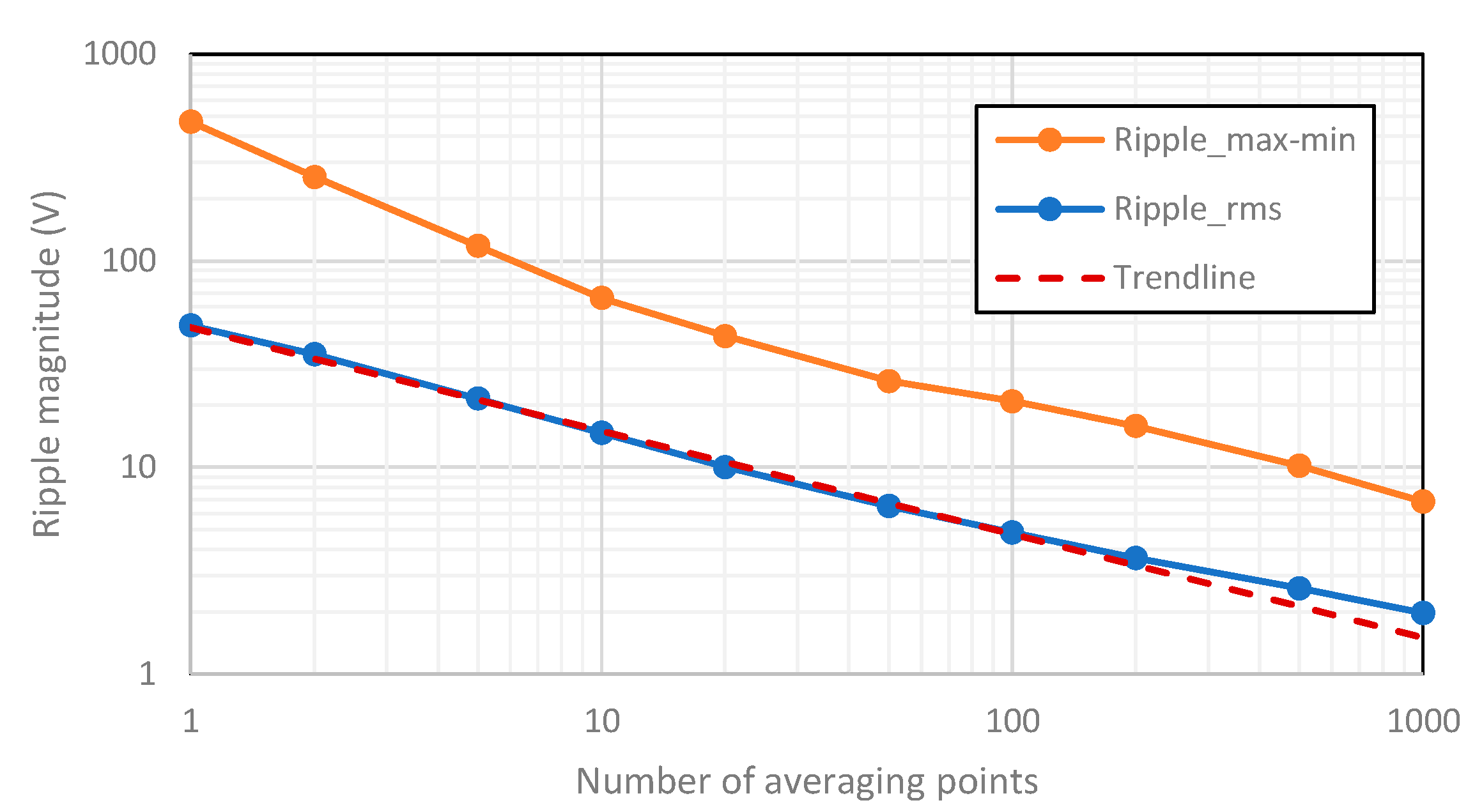
Distortions have been observed with a ripple content as large as 50 V for a nominal DC voltage of 350 V, equivalent to about 15%, and 0.40 A for a DC current of about 1.20 A, equivalent to about 30%. However, considerations on the analysis of the magnitude of the voltage ripple voltage show that the definitions and measurement conditions (particularly the bandwidth considered) have a huge impact on the ripple magnitude. For instance, one could define bandwidths of 2 kHz, 9 kHz, or 150 kHz depending on the application. Limiting the bandwidth would drastically reduce the ripple magnitudes presented in this paper. This is confirmed by the fact that the observed frequency spectrum of the voltage signal was dominated by white noise, which is, by definition, dependent on the frequency bandwidth, and showed just a few peaks with magnitudes at the level of volts. Obviously, from the ripple value alone, one has very limited information on the measured distortions, and Fourier or other analyses is necessary to obtain more detailed information.

For well-defined measurement conditions and calculation settings, the ripple value can be determined with the lowest measurement uncertainty when calculated in terms of Fourier components. However, this might lead to a significant computational burden on the equipment used to measure the ripple signal.

Sincere voltage spikes were observed related to intentional switching events, during which the configuration of the microgrid was changed. Smaller “spontaneous” spikes were observed during operation in grid-connected mode, but not in island mode. Investigating the details and dynamics of voltage spikes is beyond the scope of this paper and is left for future work.

The measurement results and conclusions obtained from this study provide valuable information that can serve as input for further investigations and that can lead to new definitions of measurement methods, analysis tools, and compatibility levels for PQ parameters in DC supply grids. Further analysis of the data obtained during this measurement campaign might lead to new results and conclusions. Furthermore, the experience and results obtained during this measurement campaign will be beneficial for utility companies and regulatory authorities for reliable planning-level and compatibility-level surveys.