1. Introduction
Due to problems such as pollution, energy crisis and sustainable development, the use of offshore energy is being driven by the global quest for renewable energy. For almost 2.4 billion people [
1], corresponding to 40% of the world’s population, living within 100 km of the coast, ocean energy presents a convenient solution to tackle climate change while contributing to a more sustainable future. Coastal areas provide renewable energy sources in the form of wind, ocean currents, and waves. The theoretical resource potential of ocean energy could meet present and projected global electricity demand, as it is about 130,000 TWh of electricity per year [
2], more than twice the current global electricity demand. Different technologies have been developed to harness renewable offshore energy. Wave and offshore wind energy are examples of marine renewables that could play an important role in the EU’s electricity mix. They are expected to meet 15% of European electricity demand by 2050 and up to 20% of national demand in some countries [
3]. Emissions are planned to be reduced by at least 55% compared to 1990 levels, as defined in the 2030 climate target, while biodiversity will be protected [
4]. Indeed, Europe has an offshore wind energy industry that has achieved remarkable developments throughout its supply chain, with large marine areas facing 89,000 km of coastline. Today’s installed offshore wind capacity is 12 GW and the European Commission estimates that an installed capacity of 300 GW for offshore and 40 GW for marine energy should be reached by 2050 [
5]. EU policy also supports the development of an offshore renewable energy industry. For example, the “NextgenerationEU” Economic Recovery Plan has allocated 37% of EUR 672.5 billion for the green transition to a more sustainable future [
6].
There are different types of support structures for offshore wind turbines: ground-fixed and floating support structures [
7]. The floating support structure has the advantage that it can be used in water depths of more than 50 m where a larger amount of energy can be harvested [
8]. The fixed bottom structure is replaced by the floating structure, which is cheaper in deep waters and can be deployed in a larger permitted marine space. However, FOWTs are usually subject to significant motions that can affect the aerodynamic performance of the turbine and cause additional structural loads [
9]. One possible solution to this problem could be the use of damping systems [
10] that passively dissipate the energy induced by the waves and improve the stability of the whole platform. Another solution is not to dissipate the energy induced by the waves, but to absorb the wave loads through wave energy converters (WECs) [
11] and integrate them into the offshore wind power structure.
It has been proven that the combination of wave and wind energy:
brings better utilization of marine space;
reduces shared costs, such as installation and maintenance costs;
reduces offshore floater motion;
increases overall power generation, improving the use of the natural resource;
reduces the variability of the energy generated, as waves have less variability and are more predictable than wind [
12].
Several commercial projects for hybrid wind and wave systems have been developed, such as Floating Power Plant’s Poseidon project, which consists of a floating triangular foundation [
13], in which multiple pivoting absorbers convert energy into rotational energy. The WECs activate hydraulic cylinders that drive an electric generator, while the large stable platform is used as a floating foundation for wind turbines. Another floating hybrid system project is the W2Power power plant developed by Pelagic Power AS [
14]. A triangular floating structure supports 3 MW wind turbines at each corner in the front while multiple oscillating body WECs placed on the three sides of the structure produce around 2–3 MW. The Kriso semi-submersible multiunit floating offshore wind turbine is another type of platform, which is quadrangular and equipped with four offshore wind turbines and wave energy converters (WECs) buoys on the sides [
15]. The WEC buoys move vertically along the waves to absorb the energy, thereby producing electrical power from the hydrodynamic loads. SeaForLife [
16] is developing an innovative device that combines a bottom-fixed wind turbine with a gravitational wave energy absorber named WEGA. The WindWaveFloat is another type of hybrid device that combines the WindFloat floating wind turbine developed by Principle Power with different types of WECs [
17]. However, a preliminary investigation in 2011 showed that the wave energy conversion hardly affected the motion of the platform. Finally, the DualSub, developed by Marine Power Systems Ltd., captures both wind and wave energy from a single wind turbine and the orbital motion of three submerged floats. The first commercial DualSub platform is estimated to have a rated power of about 15 to 20 MW as wave energy and wind turbine technology evolves [
18].
Numerical modelling of marine technologies can range from high fidelity models to low fidelity models. In general, there is also a trade-off between accuracy and computational cost. Computational Fluid Dynamics (CFD) are often very accurate, but are used to analyse local effects and do not consider a large number of simulations. For example, the winglet aerodynamics of the NACA 0017 aerofoil were analysed in [
19], while the blades of a vertical axis wind turbine (VAWT) were analysed in [
20]. More complex systems, such as a tidal array layout, could be also analysed with CFD, but at the expense of some approximations, such as assuming the turbines as generalized actuator disks [
21]. Other approximations such as the use of a linear potential flow theory for estimating hydrodynamic loads can be also assumed, especially in optimisation studies and complex multi-body systems in which a low computational cost is required [
22,
23,
24].
The integration of wind and wave technologies has also been explored in several scientific publications. Peiffer and Roddier [
25] provided a detailed description of the numerical modelling and experimental testing of the hybrid platform consisting of the Wind Float structure and an Oscillating Wave Surge Converter (OWSC). Michailides et al. [
26,
27,
28] proposed a combined semi-submersible flap system and performed an integrated time-domain numerical analysis of this system and related experiments. Muliawan et al. [
29] demonstrated the benefits in total capital cost and power generation by installing an axi-symmetric WEC on a floating wind turbine. This approach also led to the patent for the Spar Torus Combination WEC [
30]. Lee et al. [
31] investigated in the frequency domain the performance of multiple heaving WECs placed on a floating semi-submersible platform that can be used as a support structure for multiple wind turbine. In [
32,
33], the WindWEC system combining the spar floating wind turbine and an oscillating WEC buoy was proposed and numerically investigated in the time domain. Finally, the Windfloat platform was investigated in combination with multiple heave point absorbers in [
34]. The WECs were found to reduce the maximum horizontal force and the pitch moment on the platform, while increasing the maximum heave force.
Previous works [
25,
26,
27,
28,
29,
30,
31,
32,
33] show that a hybrid system can increase the energy output of the system and actively reduce the global motions of the platform in general. Since the WECs use the same infrastructure, lower grid connection and mooring system costs can be expected for the same amount of energy from a FOWT. This paper proposes a preliminary assessment of a novel hybrid offshore wind and wave energy system that combines the Nautilus FOWT with four heave point absorbers. The preliminary assessment shows the feasibility of the proposed new technology, which makes this new concept very interesting for further investigation. This paper also provides an estimate of the energy production of the Belmullet site, where the WECs are optimised for optimal performance. The proposed methodology based on linear potential flow theory and an aero-hydro-servo time-domain model is particularly suitable for the large number of simulations required for this study. The hybrid system has several advantages compared to a pure FOWT, such as higher stability of the platform, higher power generation and cost sharing.
The paper is organized as follows: the Materials and Methods (
Section 2) describes the floating foundation and integration of WEC. The Methodology (
Section 2.2) explains the chosen design process. In particular,
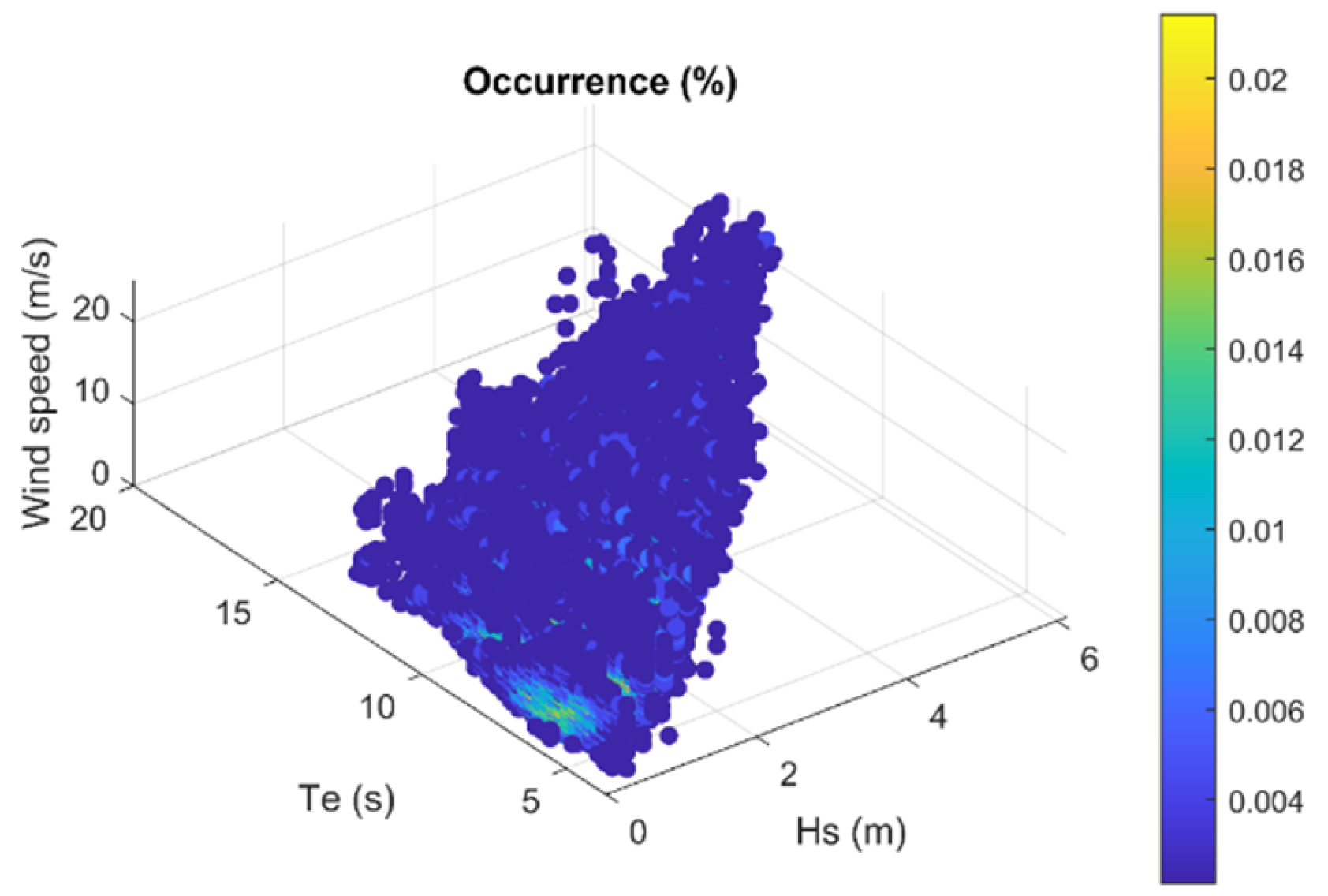
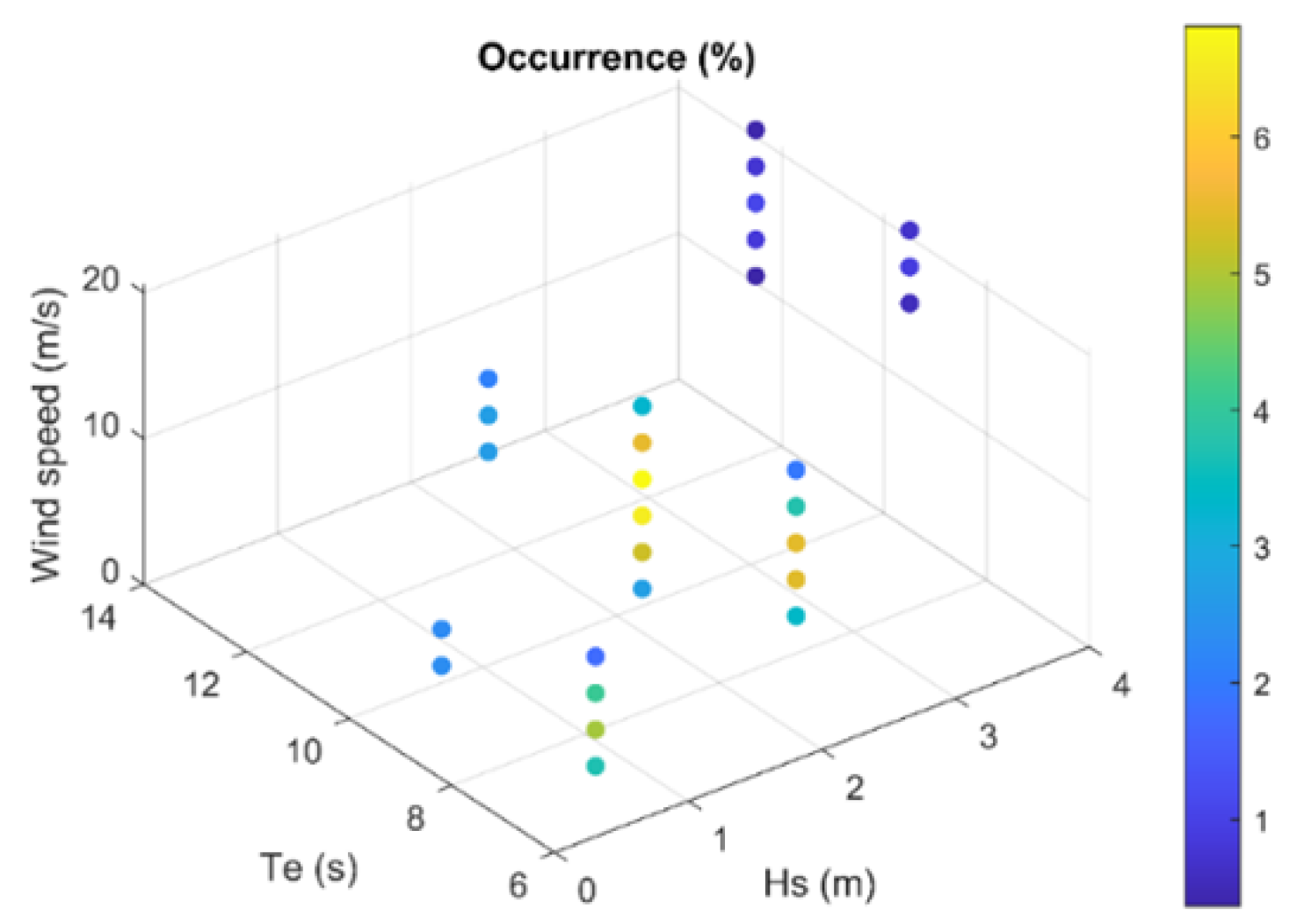
Section 2.2.2 describes the method of data extraction used to obtain the environmental conditions;
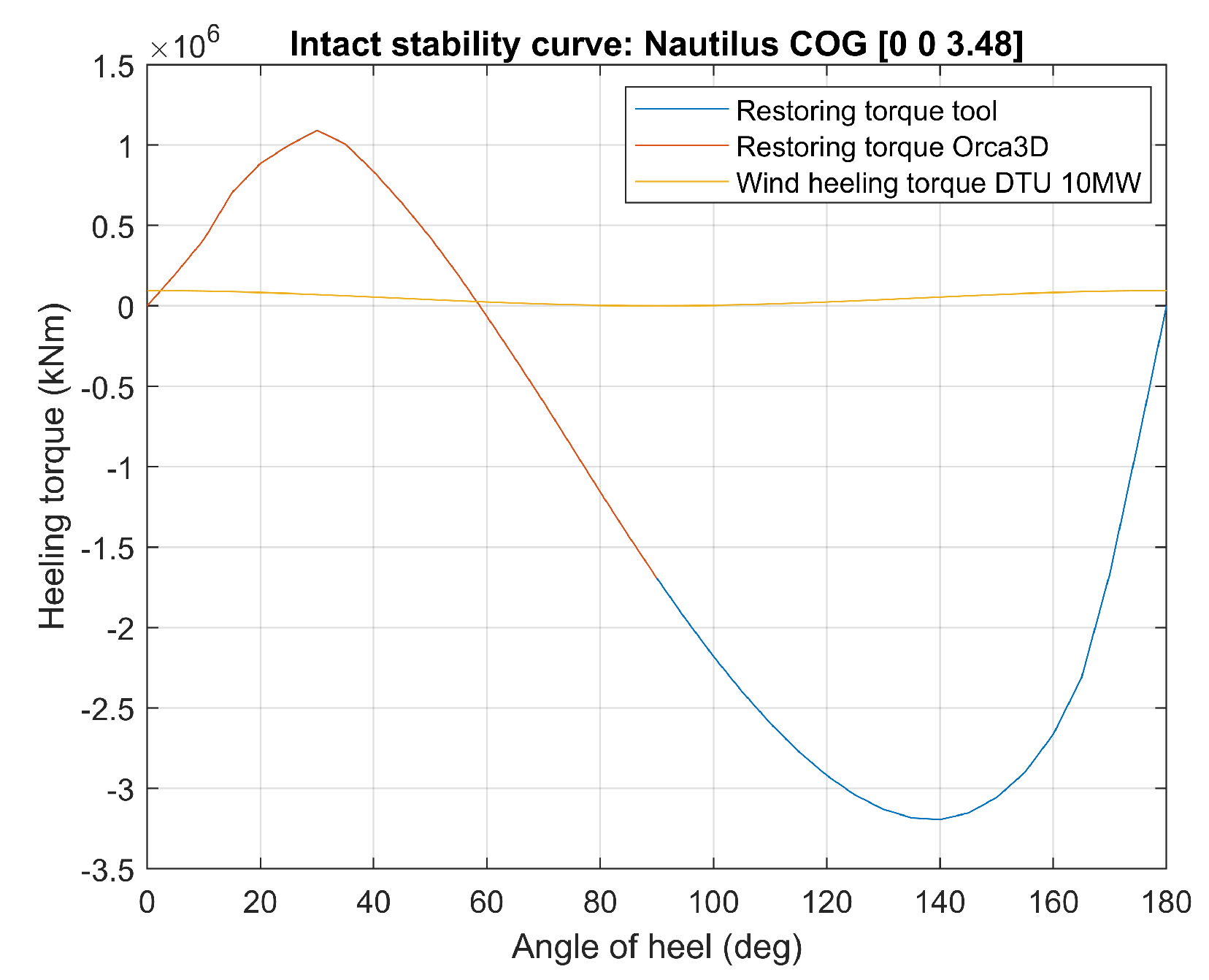
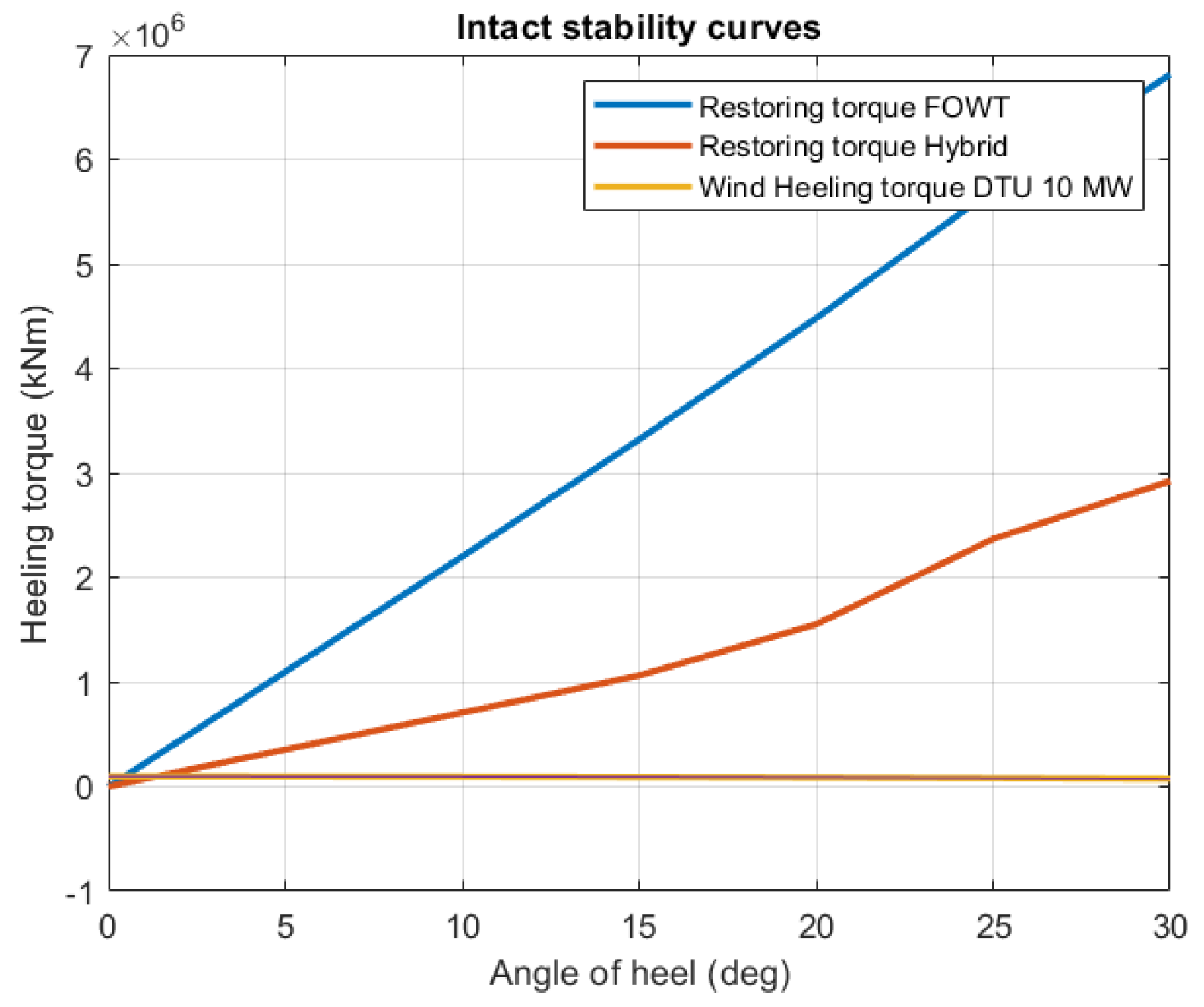
Section 2.2.3 shows the modeling framework to verify the static stability;
Section 2.2.6 addresses the hydrodynamic modelling of the hybrid system;
Section 2.2.7 analyses the mooring loads acting on the floating platform;
Section 2.2.8 explains the method used for the control and for the calculation of the aerodynamic loads;
Section 2.2.5 describes the time-domain modelling of the device; and, lastly,
Section 2.2.9 describes the economic analysis.
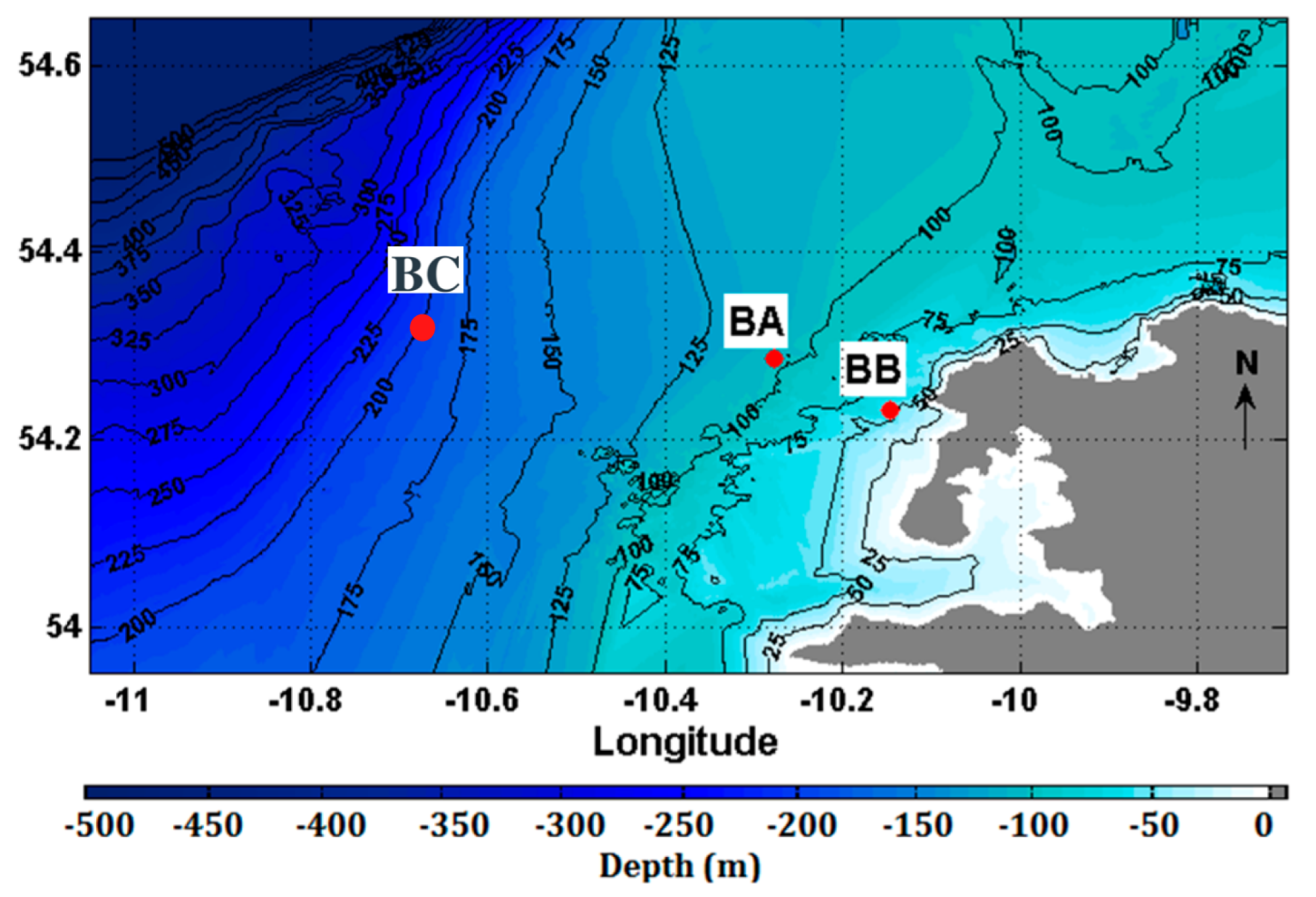
Section 2.2.1 provides the basis for determining the installation site;
Section 3.2 describes the results of the data extraction;
Section 3.3 and
Section 3.4 compares the hybrid and the FOWT in terms of dynamic stability, power extraction and economic assessment.
Section 4 discusses the limitations of the study and compares it with other studies. Finally,
Section 5 provides some conclusions.
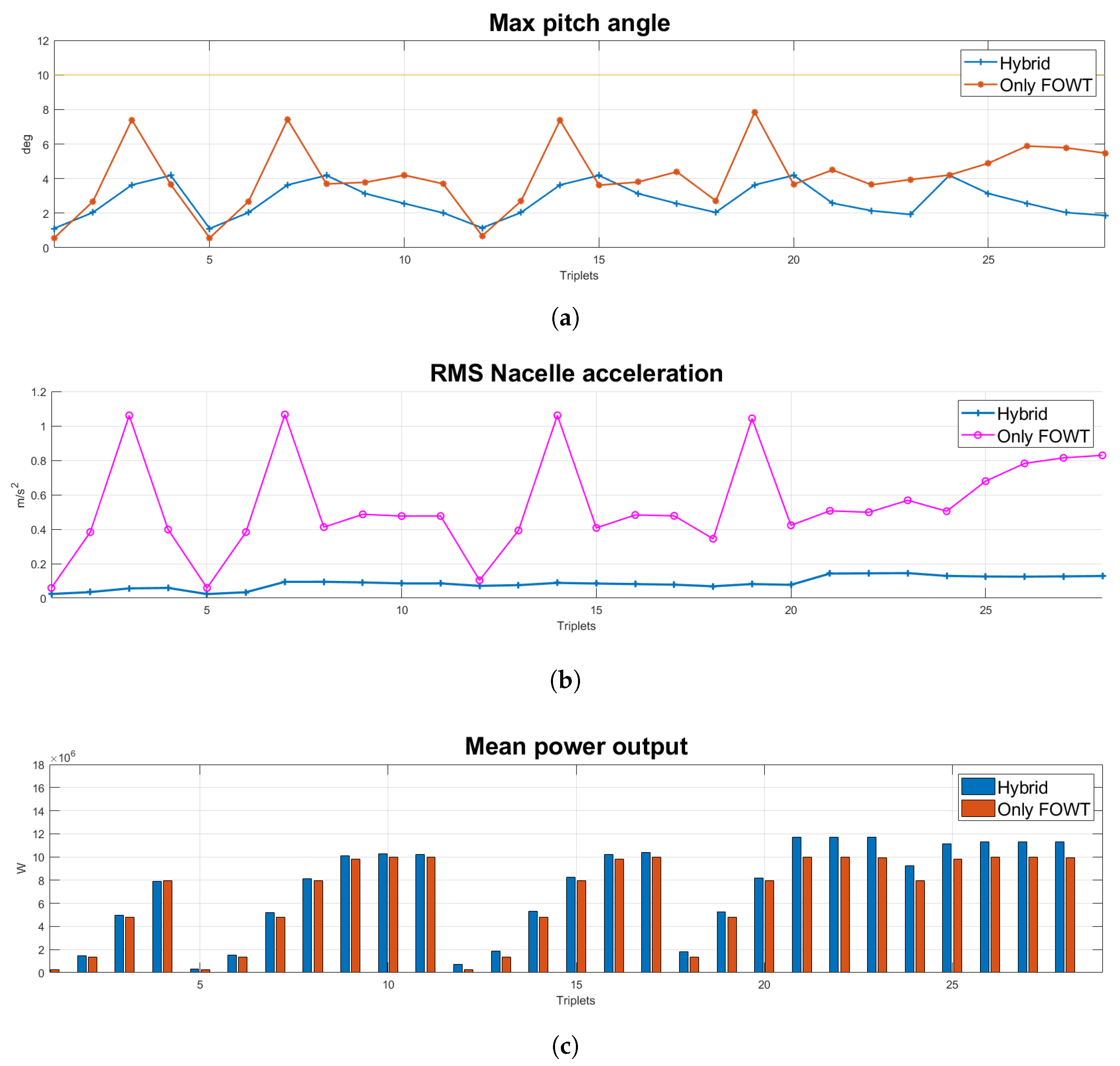
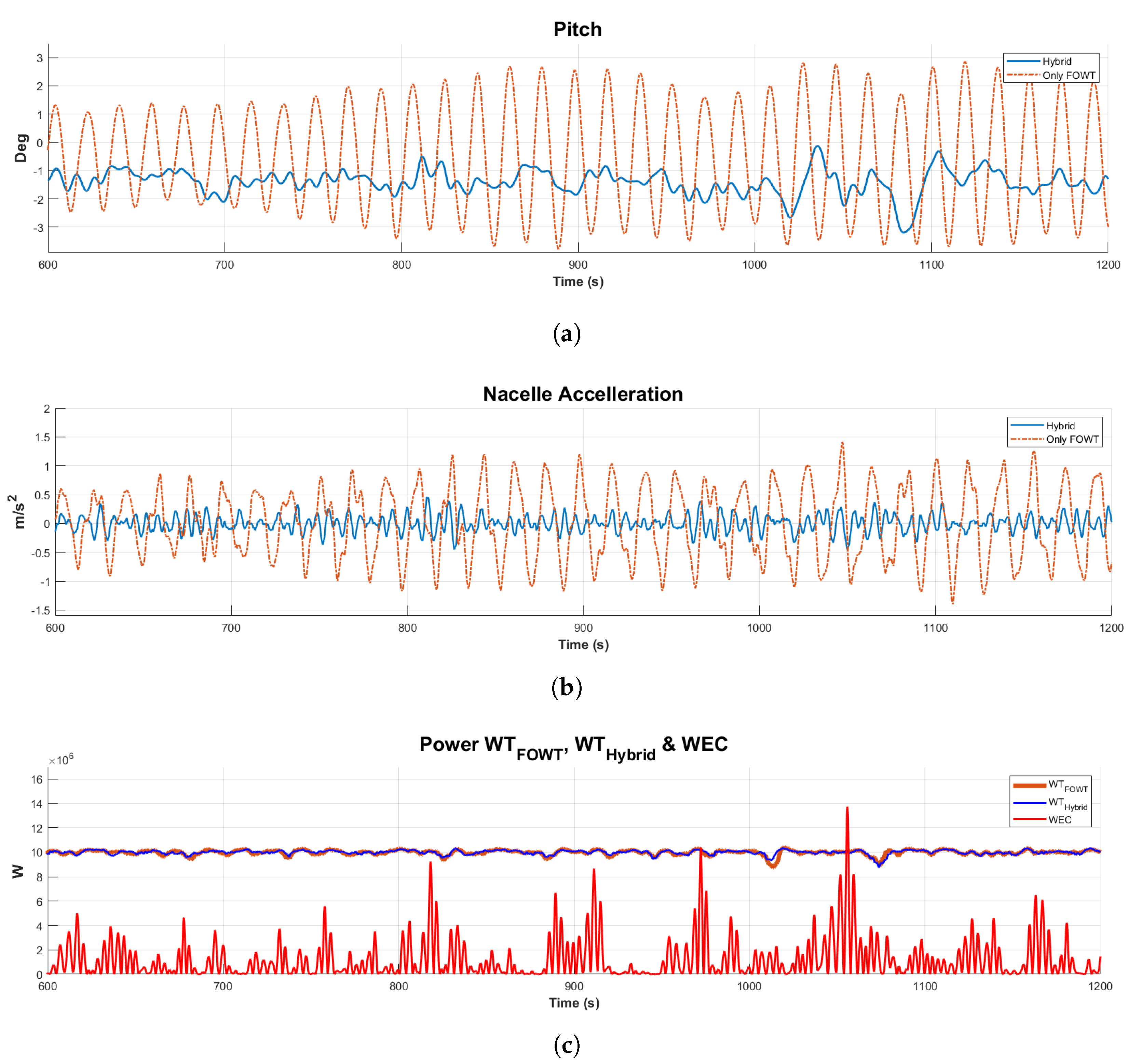
4. Discussion
Preliminary evaluation of the hybrid solution presented in this study showed improved performance compared to a floating wind turbine alone. Our results are in good agreement with previous studies in which WECs help to reduce the motion of the platform. In [
34], for example, the addition of WECs in the floating WindFloat structure helped to reduce the horizontal force and pitching moment of the platform.
The potential synergy of a wave energy converter on the floating WindFloat platform is also described in [
25], while in [
26,
33] a power increase of 1–8% was identified for the hybrid system. A combined concept involving a spar-type FOWT and an axi-symmetric two-body WEC not only reduced the total capital cost but also increased the total electricity production [
29]. However, another study [
30] shows that the heave response of a hybrid platform of four 3 MW wind turbines is only slightly affected by the PTO damping of the WECs.
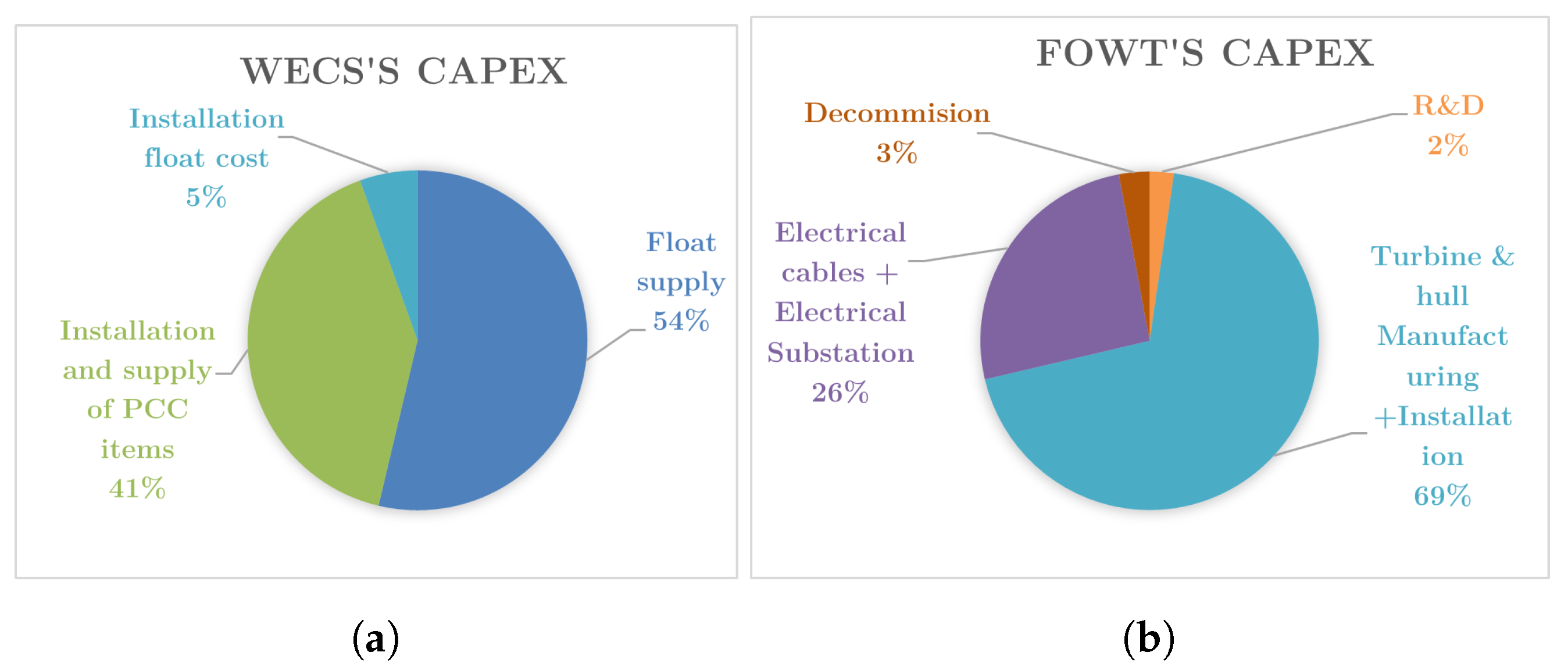
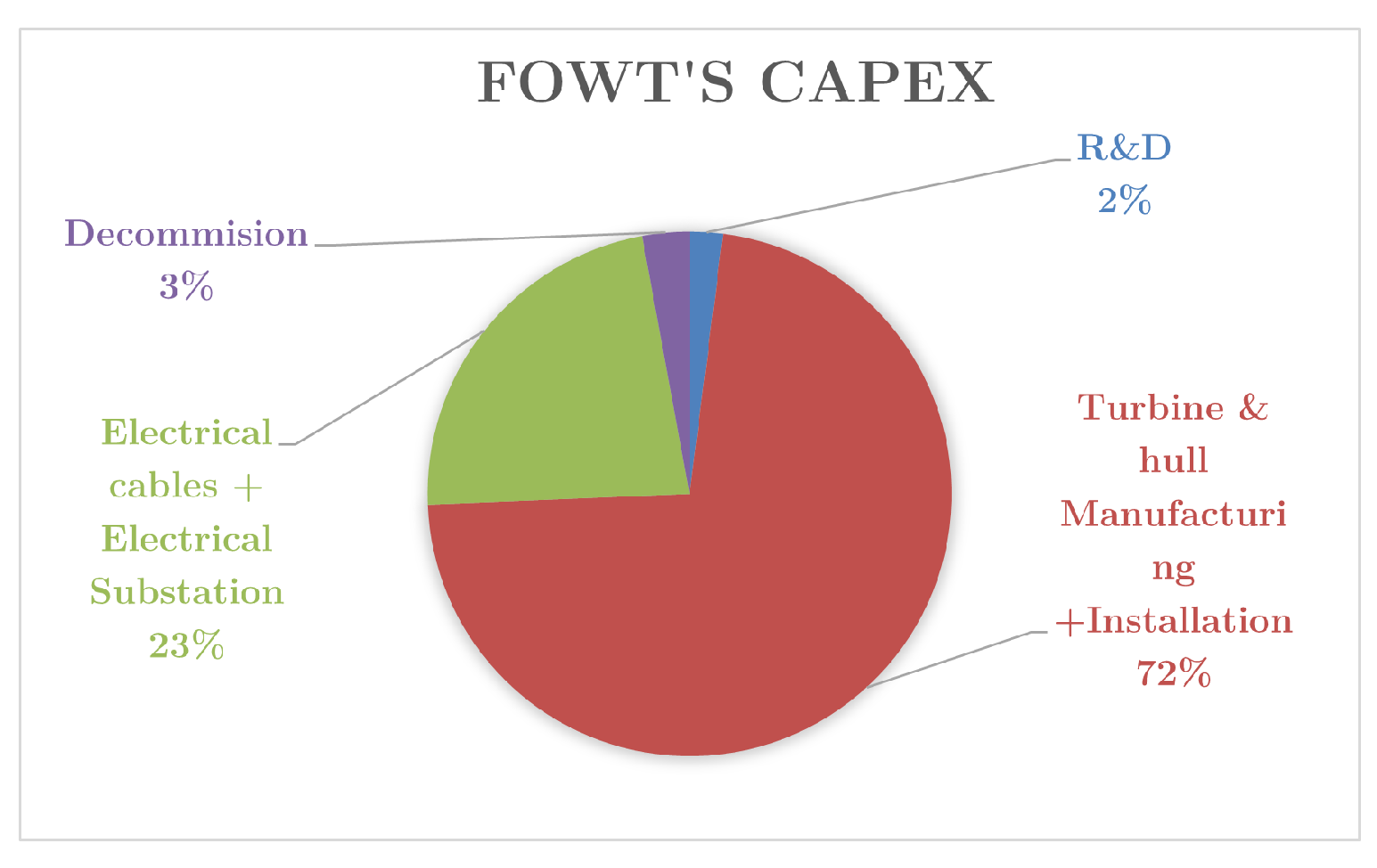
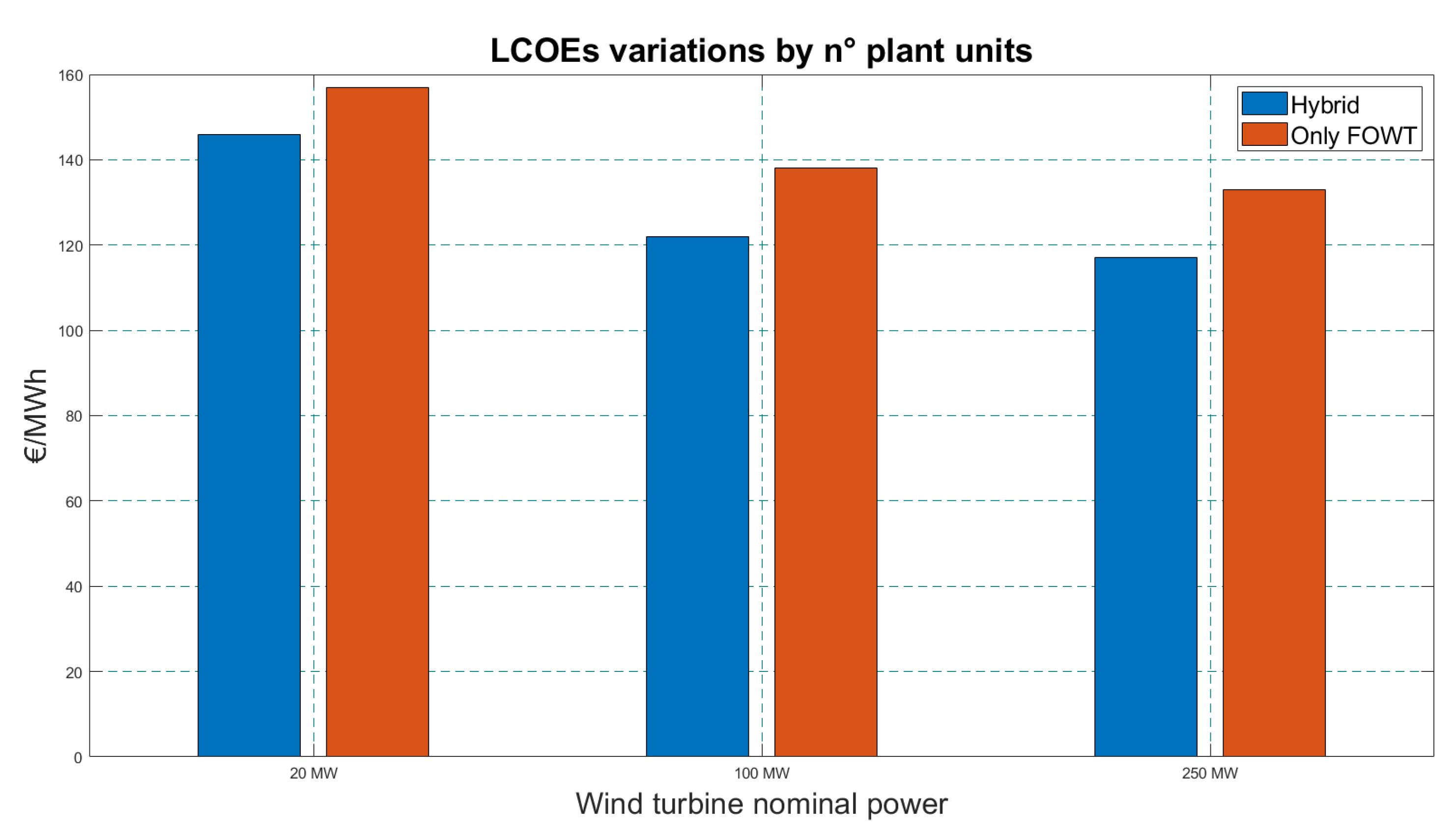
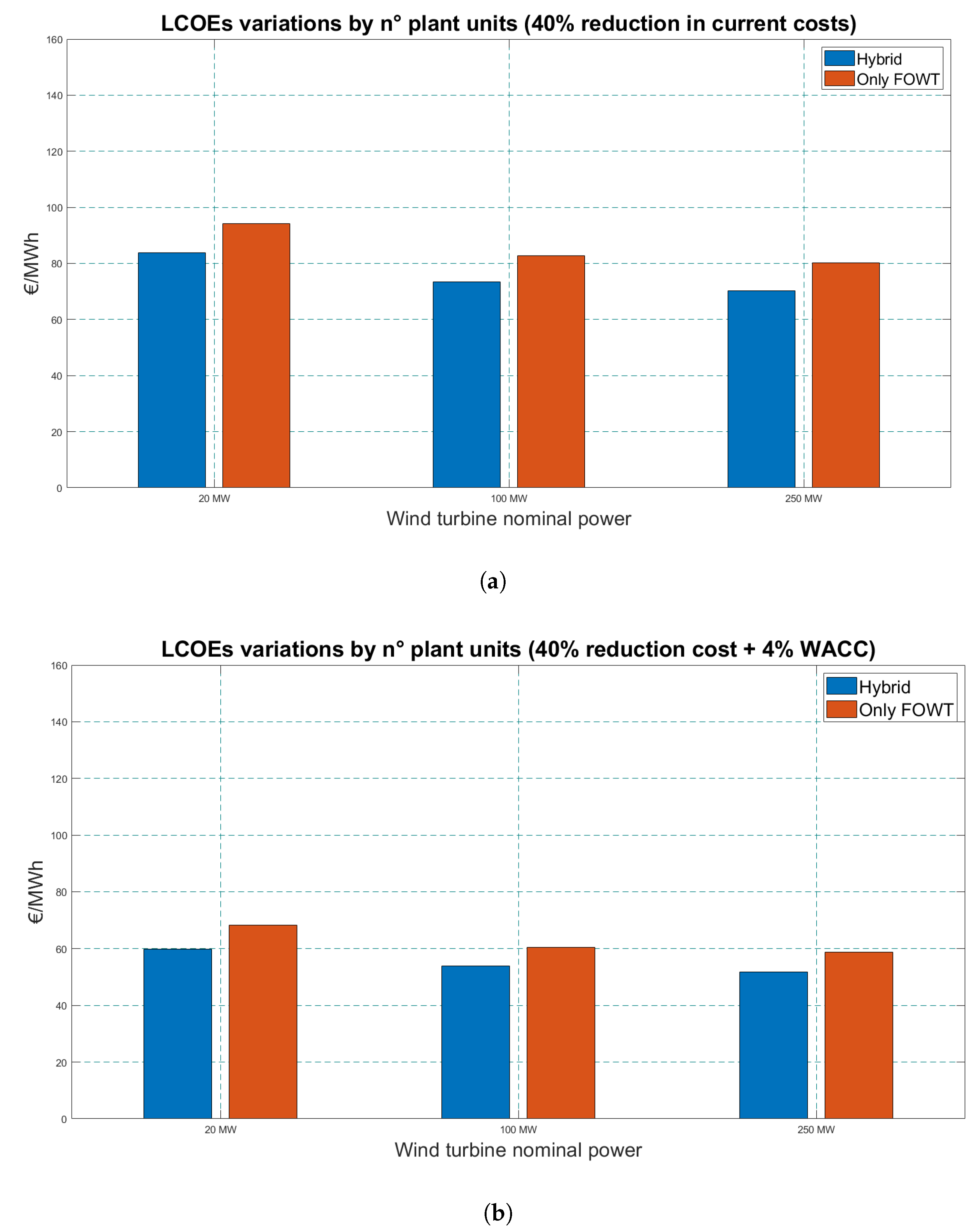
The LCOE of the hybrid solution from this study was 10% lower than that of the traditional system. The capital cost was 3% higher for the hybrid system, but the wind turbines contributed significantly to the power generated with a maximum relative difference of 151% for the hybrid system. However, some studies such as in [
83] show that the best alternative regarding life-cycle costs and LCOE was the FOWT. The best alternatives for hybrid systems were given by Poseidon and W2Power for large and small systems, respectively.
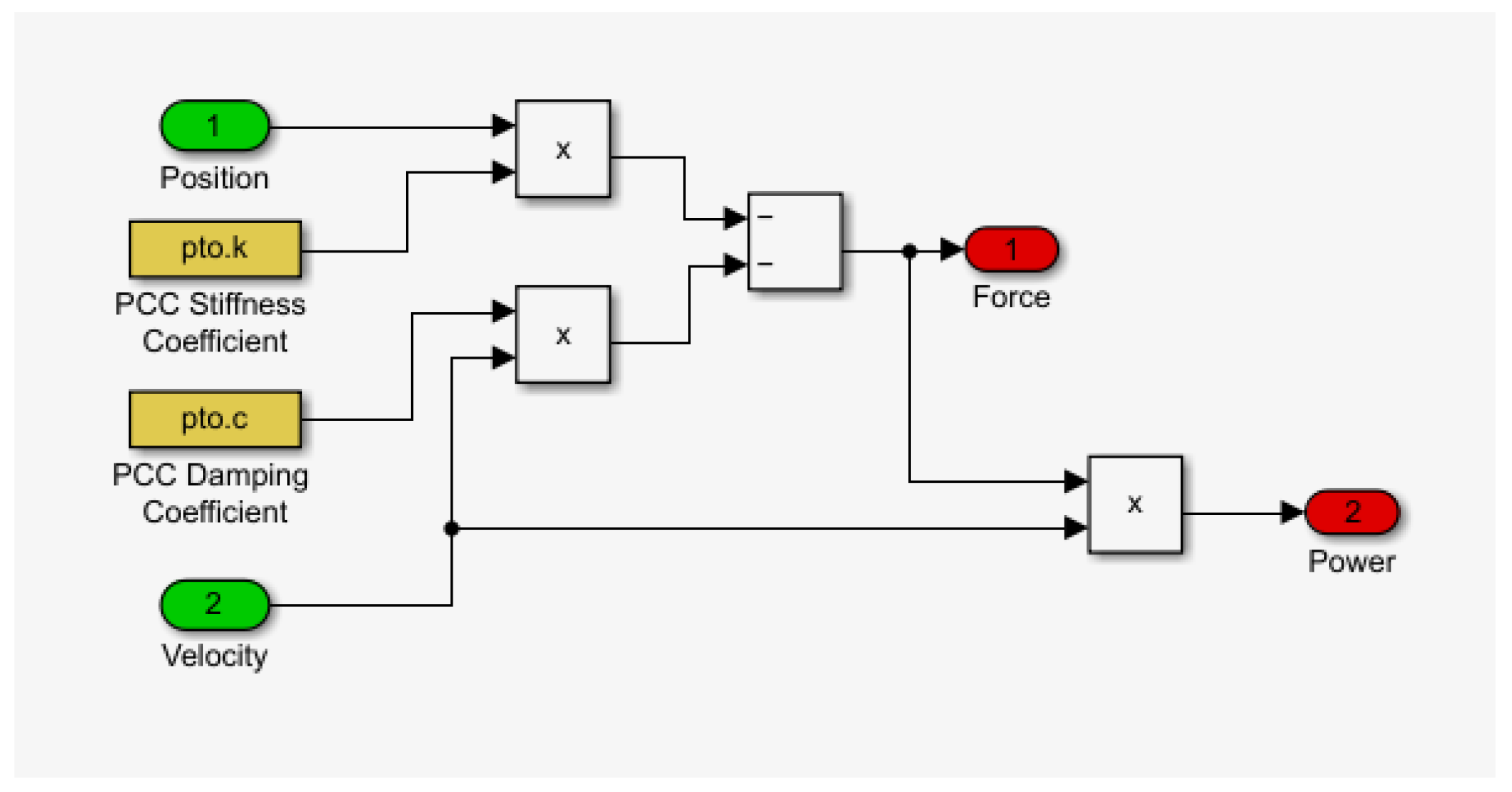
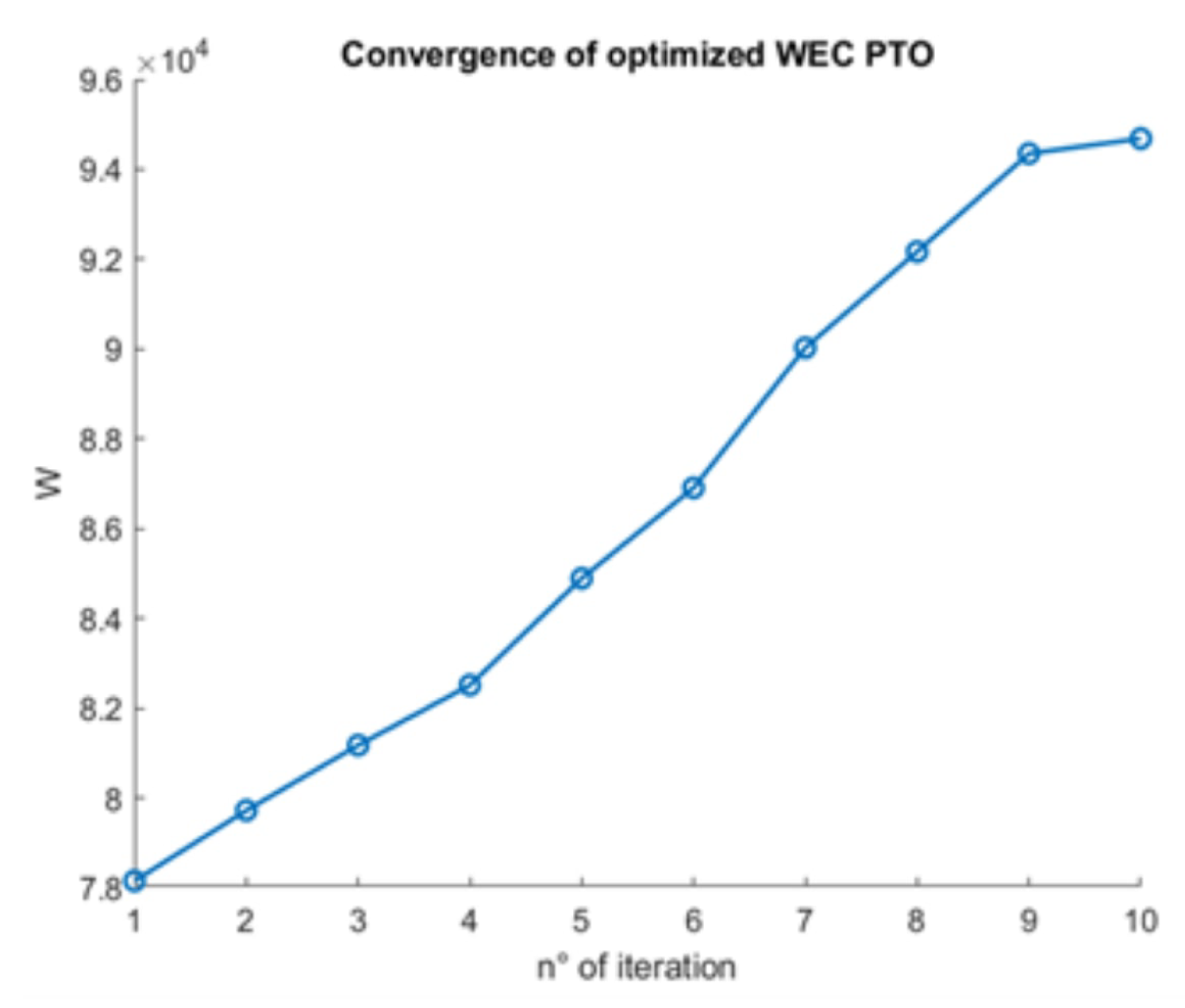
The first limitation of this study is the PTO of the WECs. A linear model was assumed to simulate their behaviour. This assumption was required to reduce computational time for the simulations. In fact, it was necessary to optimise the WECs for each environmental condition in order to obtain a realistic estimate of the energy generated. Linear PTO was also used in [
45,
84] to simulate the RM3 device, where similar energy production was obtained for similar wave conditions. A more realistic PTO is beyond the scope of this study.
Another limitation is related to the environmental conditions considered in a narrow range of triplets. The sensitivity of the generated energy at a wider range of triplets could be investigated in a further study to understand the influence on the results of this work. For example, in [
45,
84] a wider range of sea states was covered, giving more accurate results for AEP. The results of this work are also very sensitive to the site chosen. These results only apply to sites characterised by sufficient energy resource, where both wind and waves maximise the performance of the wind turbine and WECs. The design of the WECs is particularly limited to energetic sites, as their geometry has to be tuned to the sea conditions. Finally, the LCOE was estimated for a different number of devices. The reduction of costs due to an increased number of devices in the farm are assumed from [
36]. The entire system has not been simulated in the time domain (due to the enormous computational effort and time required), so the interaction between devices is not accounted for in terms of energy. As a rule of thumb, it was assumed that the distance between the devices of the farm is equal to 6 times the rotor diameter to justify the absence of the wake effect [
85].
5. Conclusions
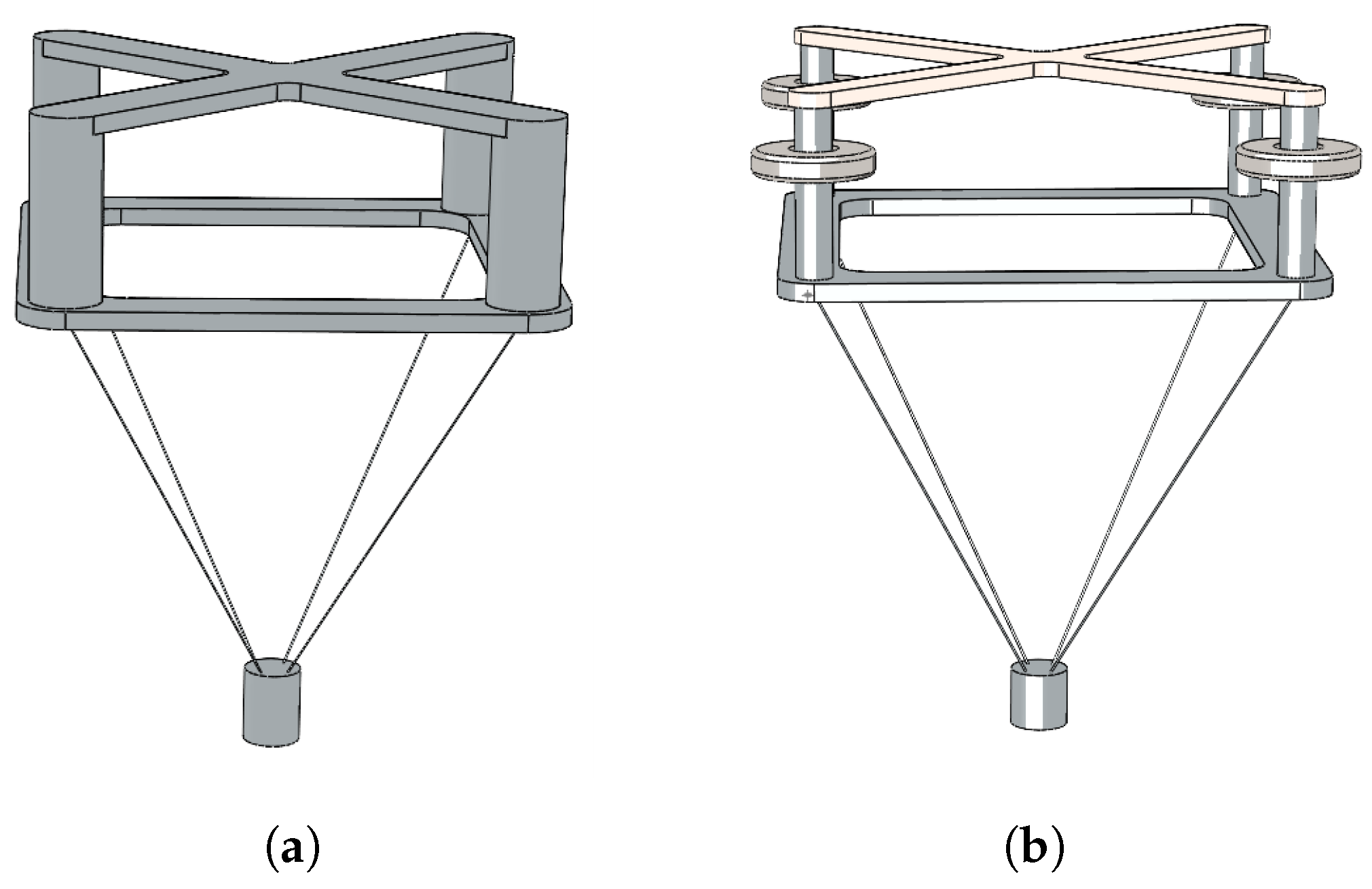
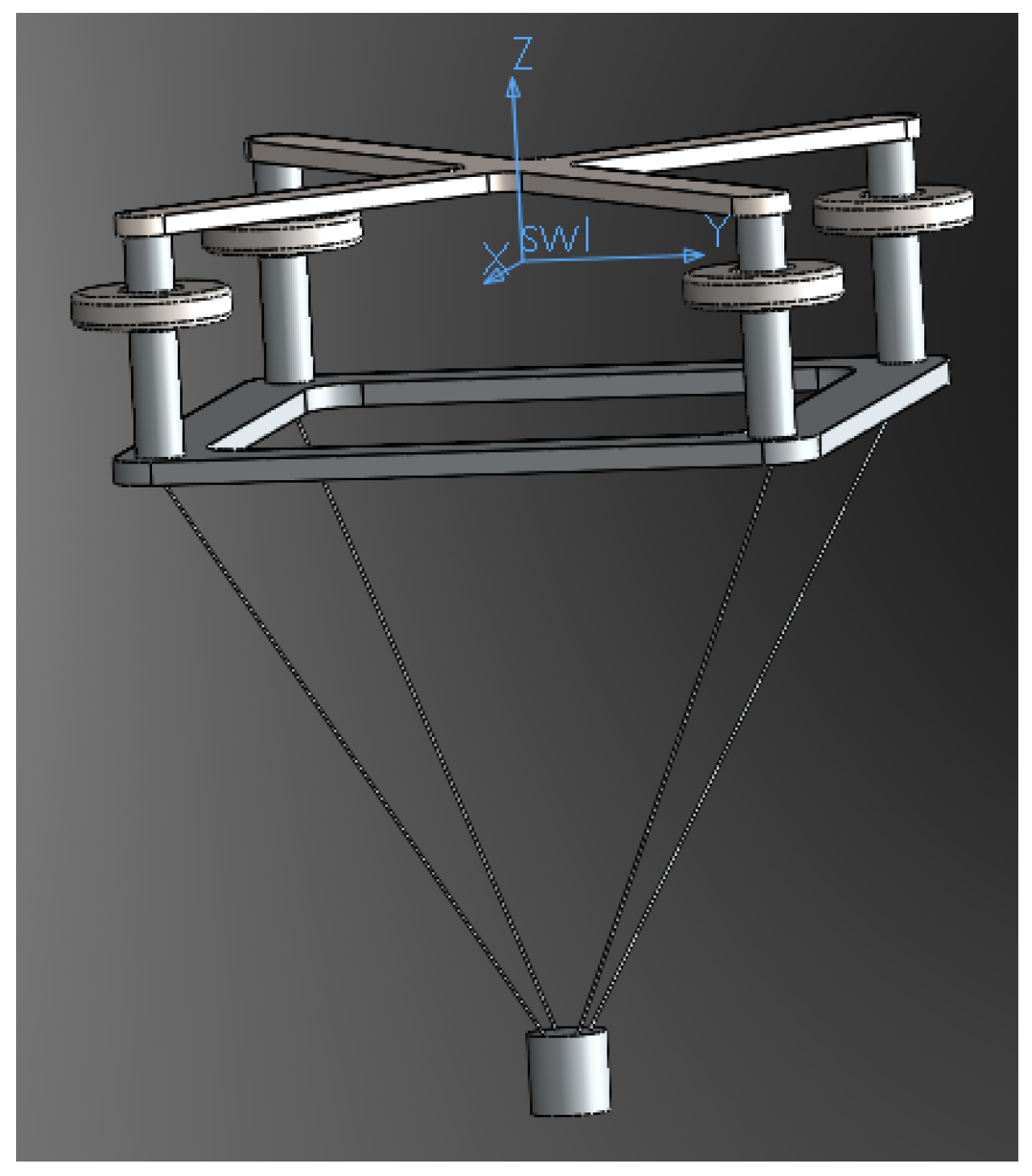
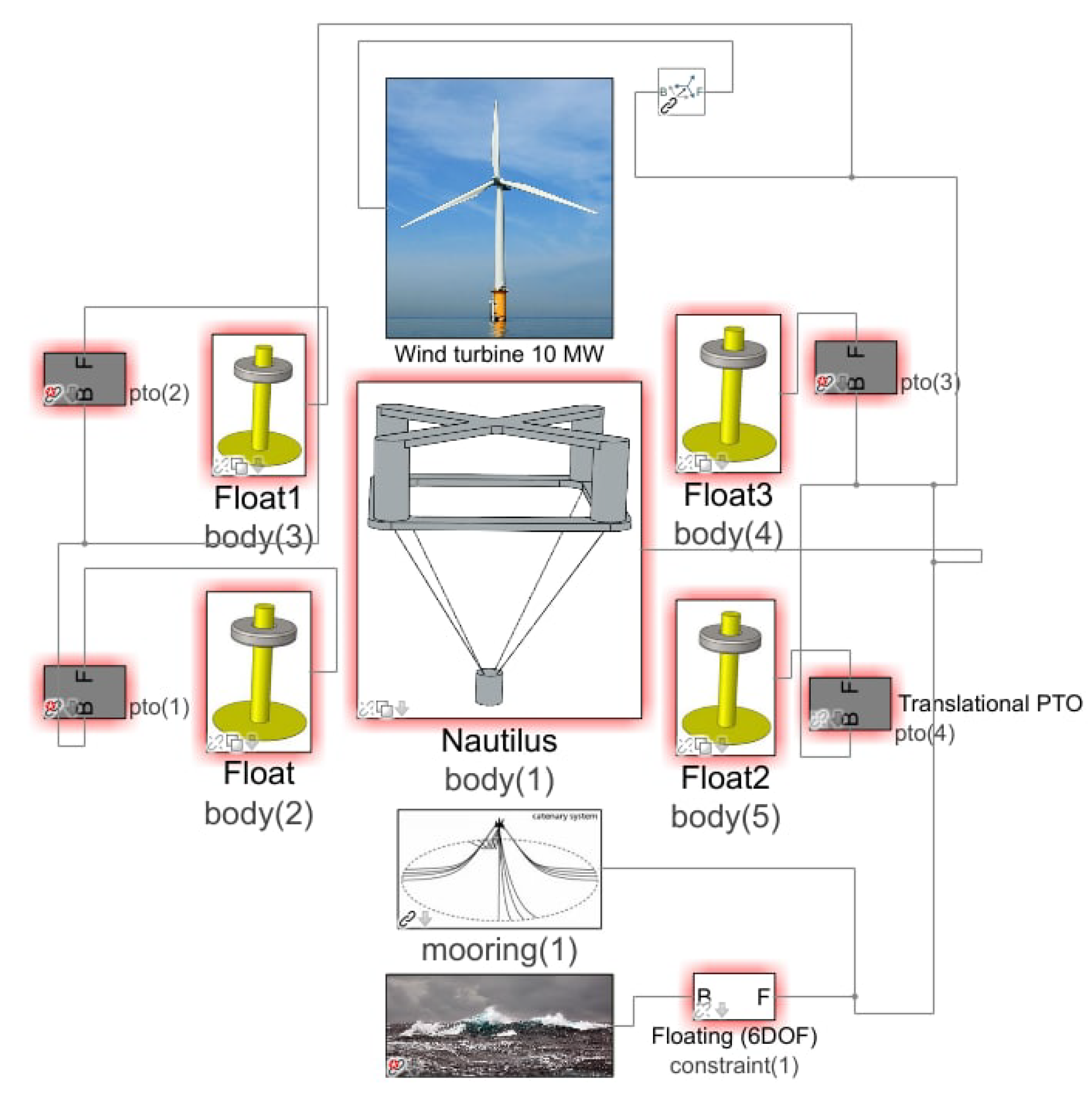
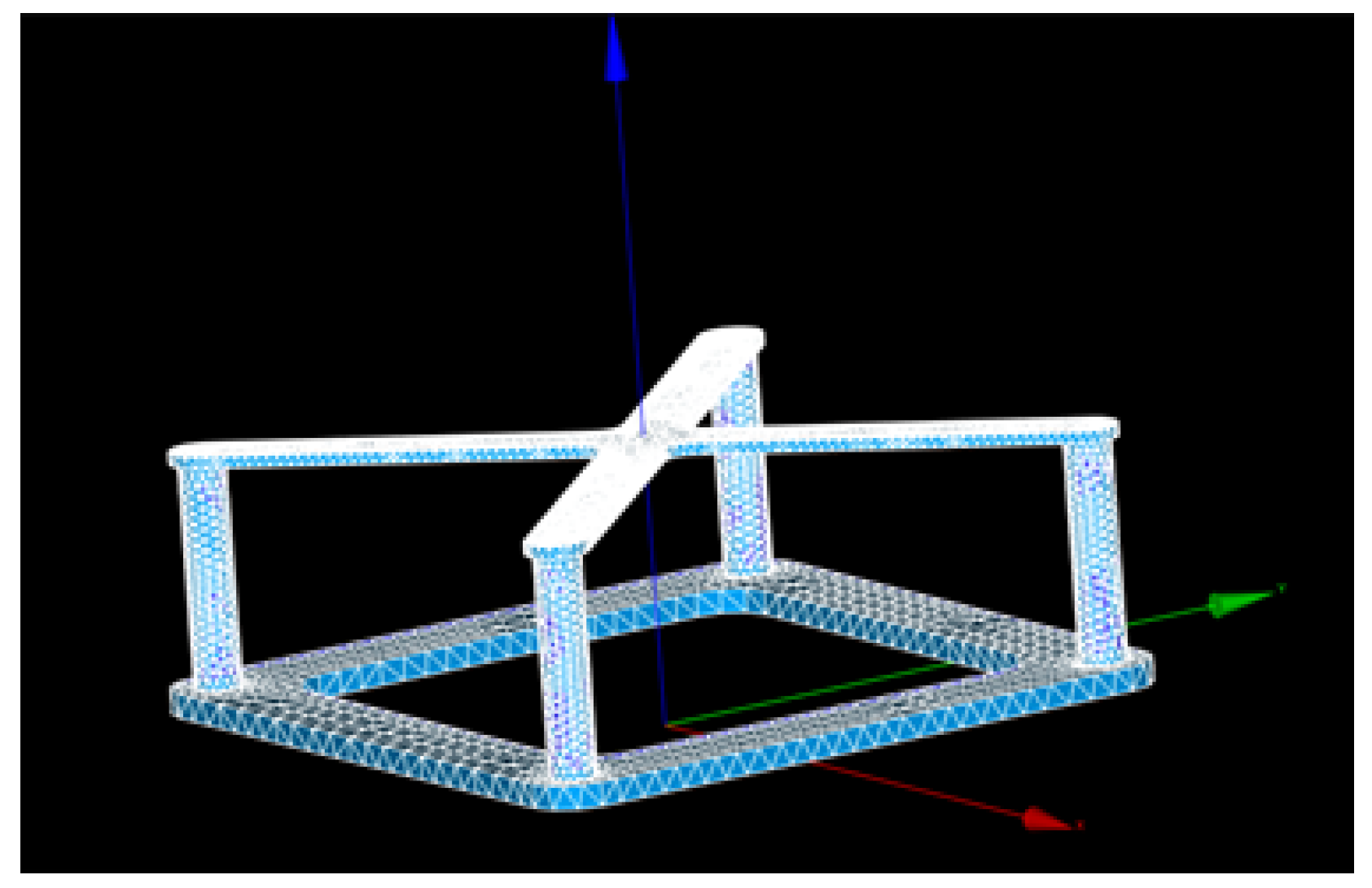
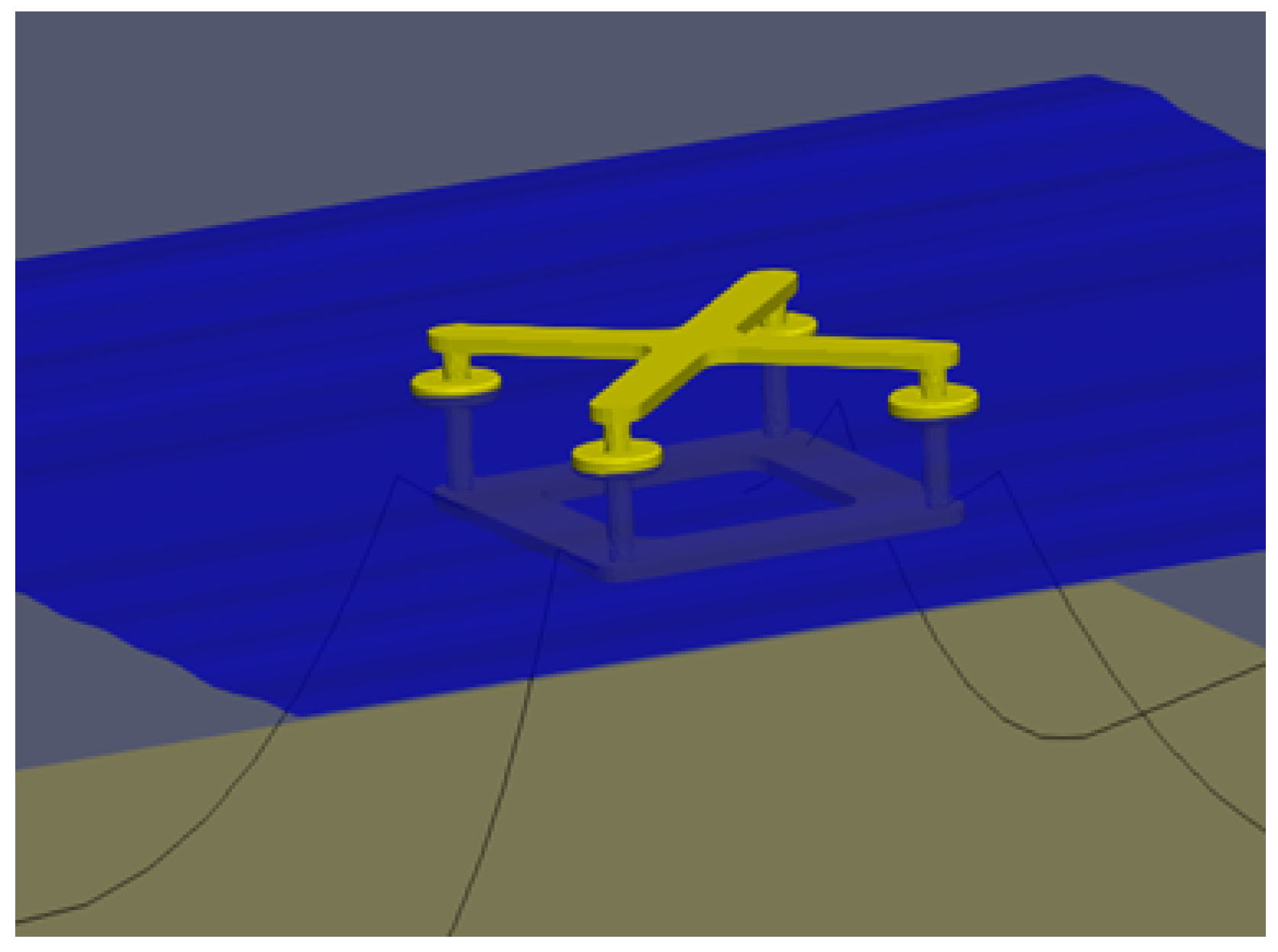
In this study, the novel hybrid concept of the Nautilus platform and four-point absorbers WECs was investigated. First, the various advantages of a multi-purpose platform combining wind and wave energy were discussed in comparison to a simple floating wind turbine. The different components of the hybrid system were identified: Wind turbine, WECs and the support platform. They were replicated individually and combined in the final hybrid system concept. Therefore, the single FOWT system was modelled using the same turbine and floating platform concept to compare the results of the hybrid system.
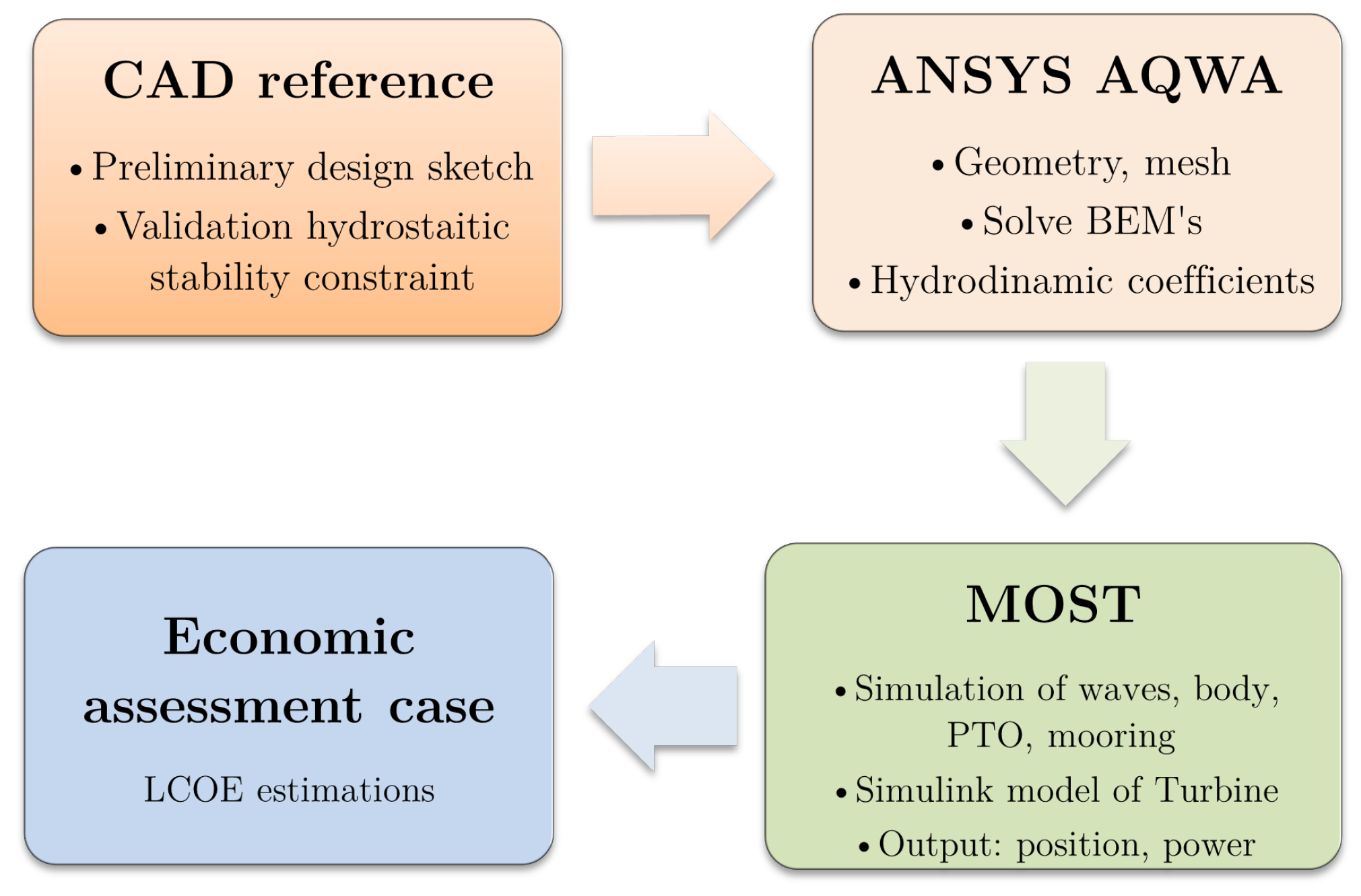
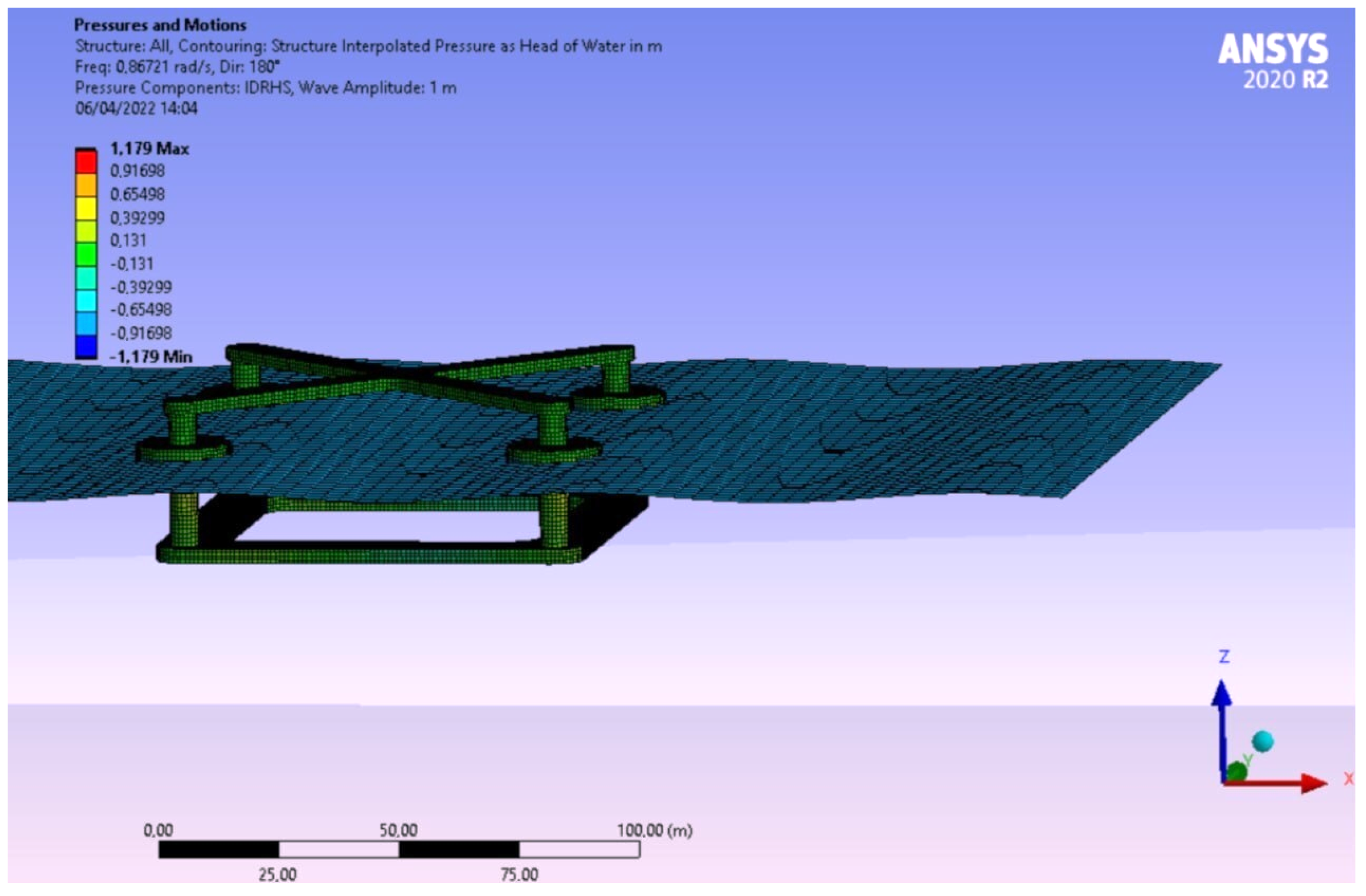
Both systems were designed in accordance with DNV regulations. The design model was created using the software package ANSYS AQWA, with the hydrodynamic coefficients extracted from the frequency domain analysis. The latter were imported into WEC-Sim, which can simulate hydrodynamic bodies and their interaction. A Simulink wind turbine model (WT) was coupled with the rest of the component system modelled in WEC-Sim (mooring lines, point absorbers, floating platform) to simulate the coupled dynamic system. The mooring lines are simulated in WEC-Sim in particular with the open source software Moordyn. The performance of the WECs was optimised as it is strongly influenced by the PTO parameters. Finally, the analysis of the Irish case study Belmullet was taken into account when estimating the energy production required for the techno-economic analysis. Environmental conditions were extracted from ERA5 using wind speed and wave parameters. The results show the CAPEX and the LCOE for the hybrid and the FOWT solution, as well as the key performance indicators (KPIs), such as pitch angle and nacelle acceleration. In summary, the hybrid solution is better in terms of both economic competitiveness and stability. The synergy of sources could be one of the best solutions for the future of the ocean energy sector and the energy transition.
Futher Work
Floating offshore wind turbines include a variety of physical components that can be designed to tune dynamic performance and energy productivity. Consequently, many aspects have not been addressed in this work such as: the implementation of a control system for the WEC devices that could improve energy production; simulation with a wide range of meta-oceanic data that could allow a more accurate evaluation of WEC performance.
It would also be helpful to define more accurate cost functions that take into account the manufacturing process and pure material costs. Operating and maintenance costs also need to be further investigated to obtain more accurate LCOE.