Forecasting Solar Home System Customers’ Electricity Usage with a 3D Convolutional Neural Network to Improve Energy Access
Abstract
:1. Introduction
2. Literature Review
2.1. Common Load Forecasting Models
2.2. Intervention Research
2.3. Gaps in Literature
3. Materials and Methods
3.1. Time Series Analysis
3.2. CNN
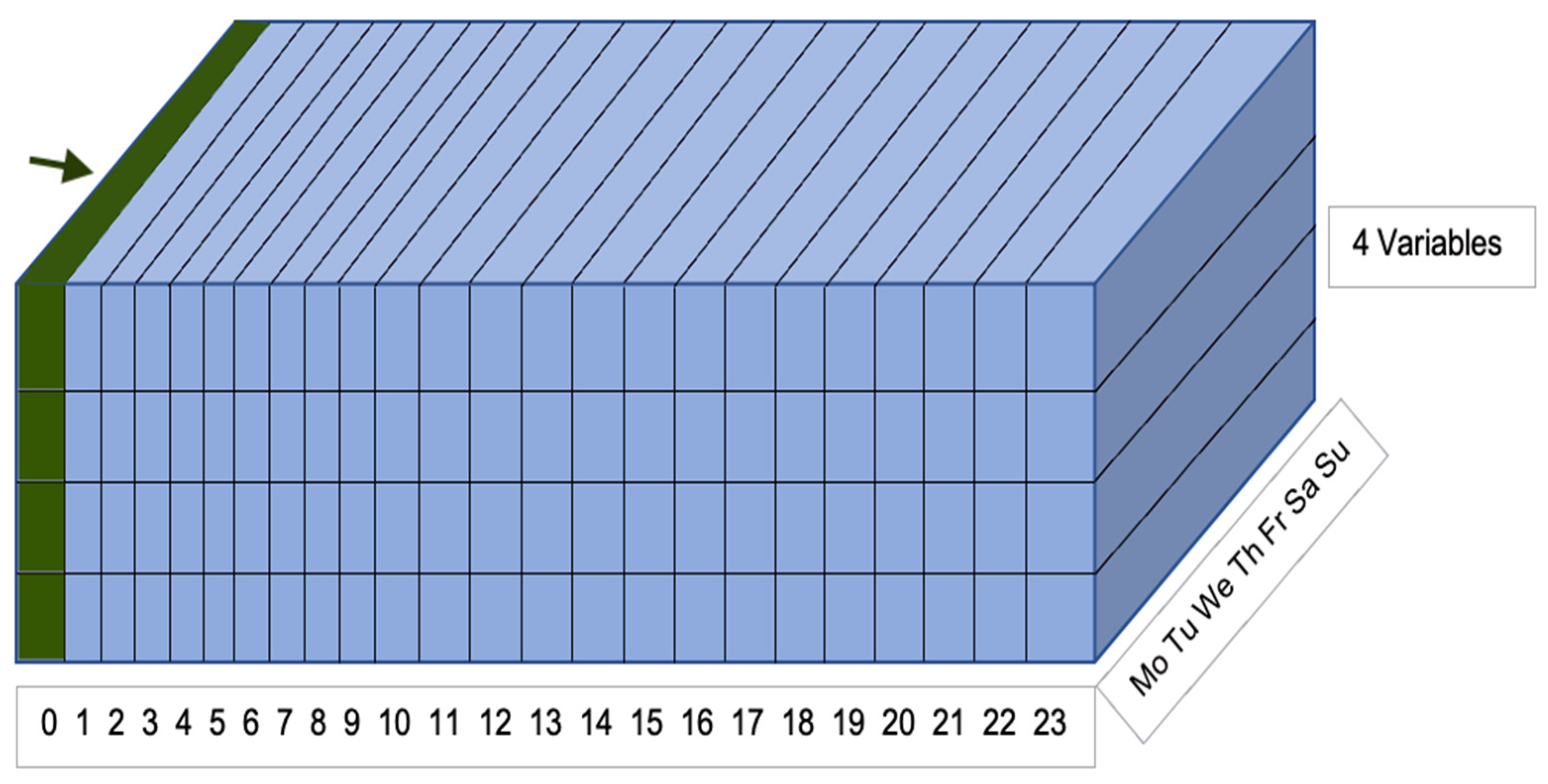
3.2.1. CNN Architecture
3.2.2. Scenarios
3.2.3. Used Variables
4. Results and Discussion
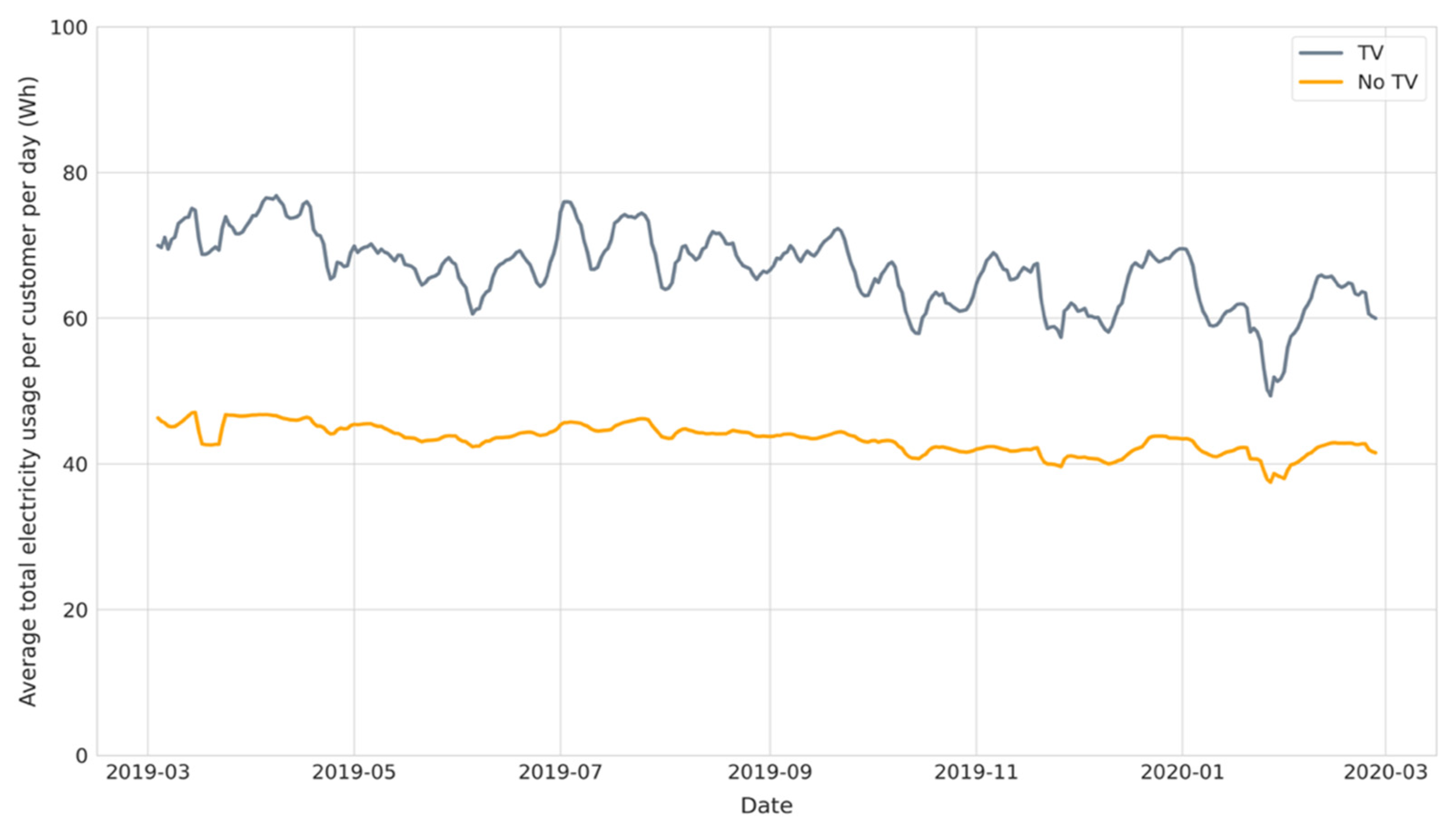
4.1. Yearly Usage
4.2. Usage across a Year
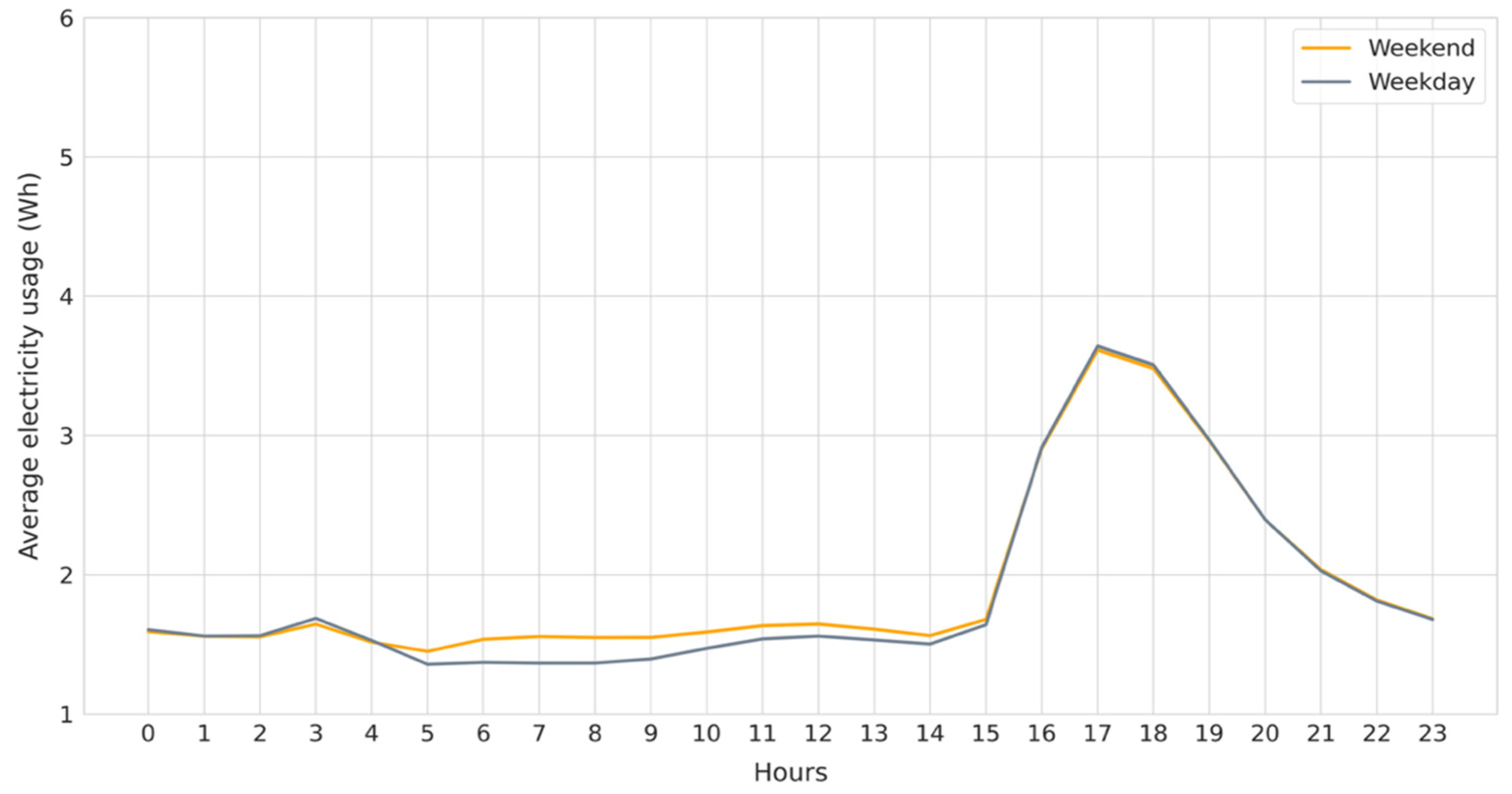
4.3. Daily Usage
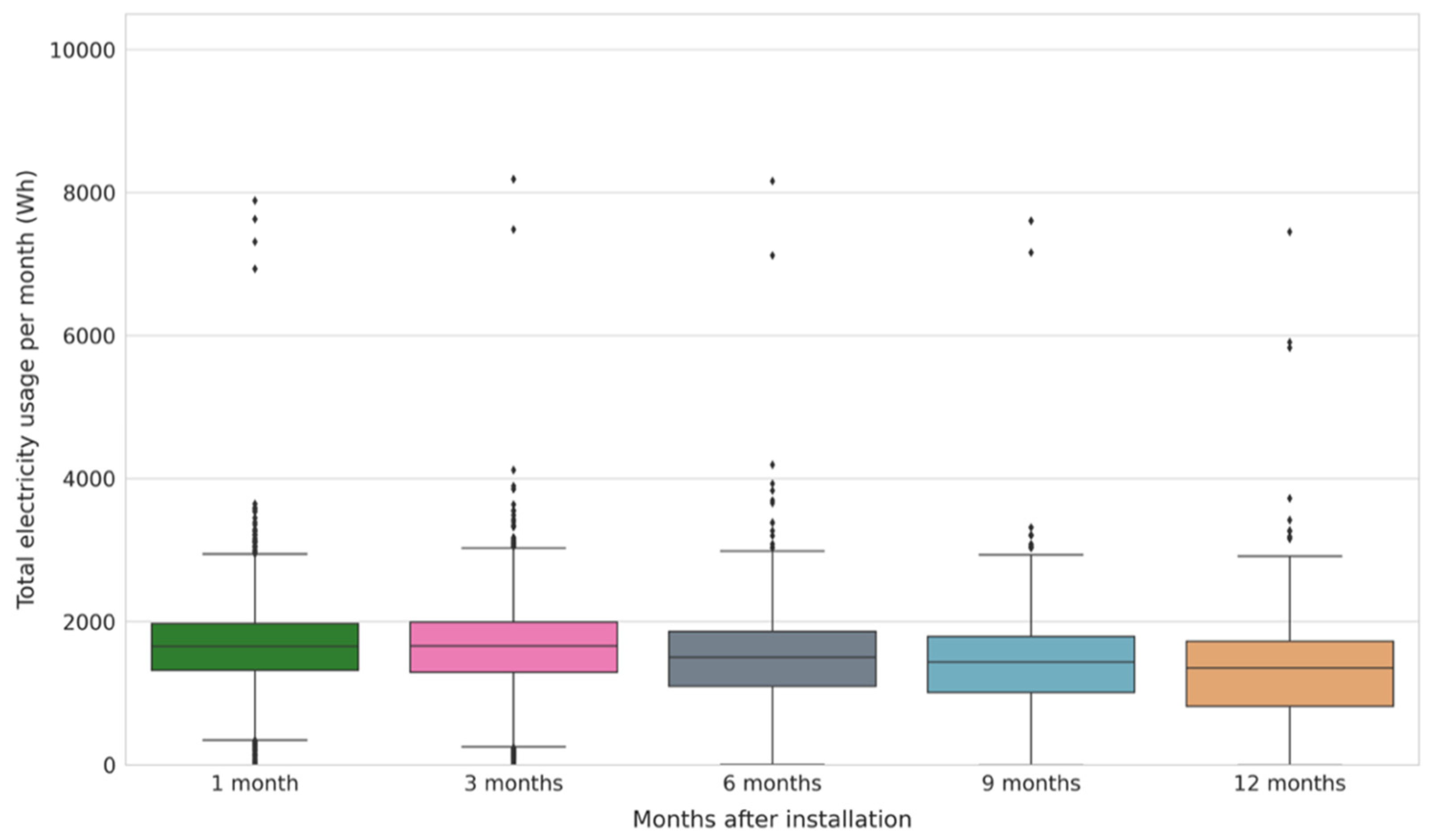
4.4. Usage Change per Customer
4.5. CNN Results
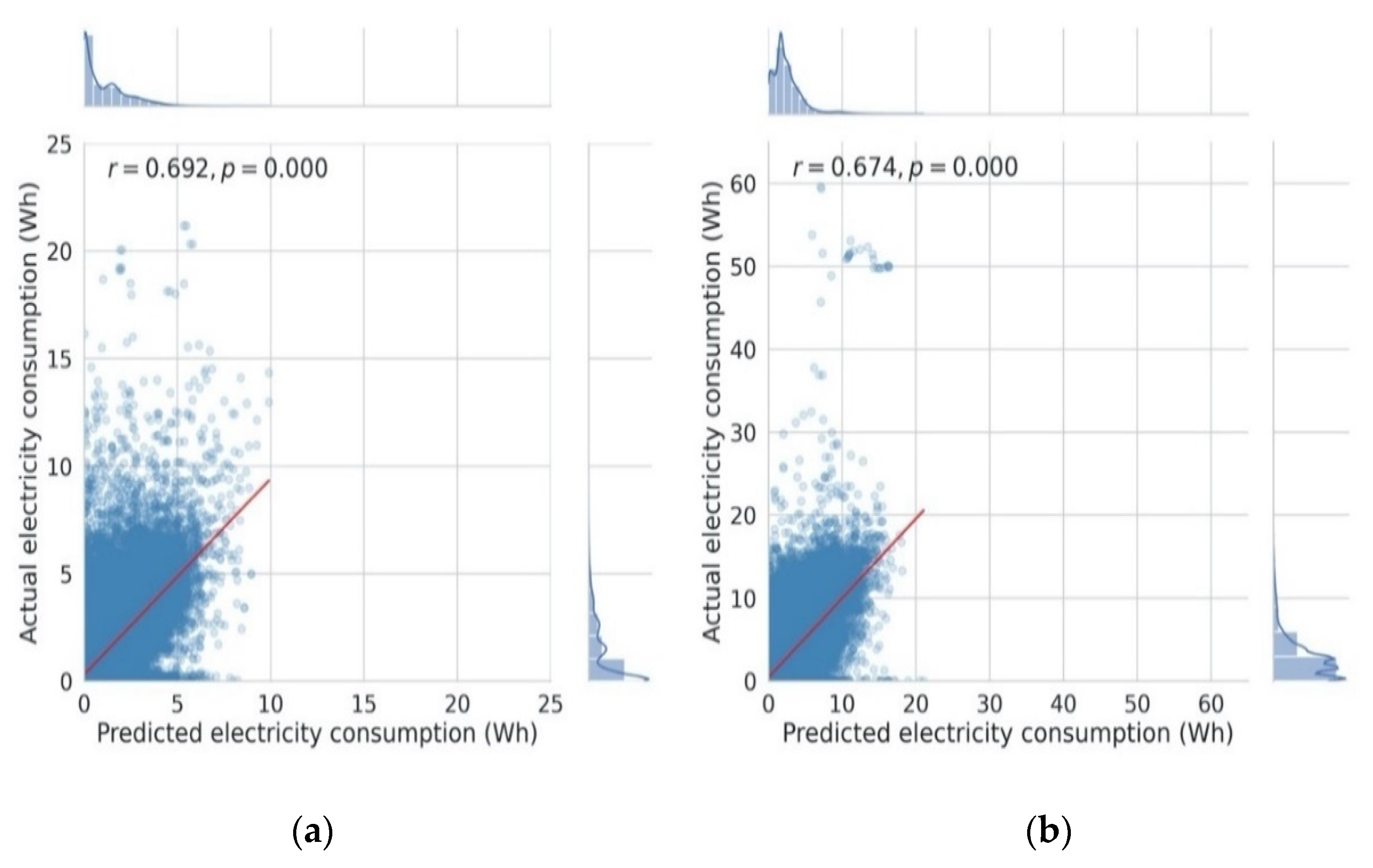
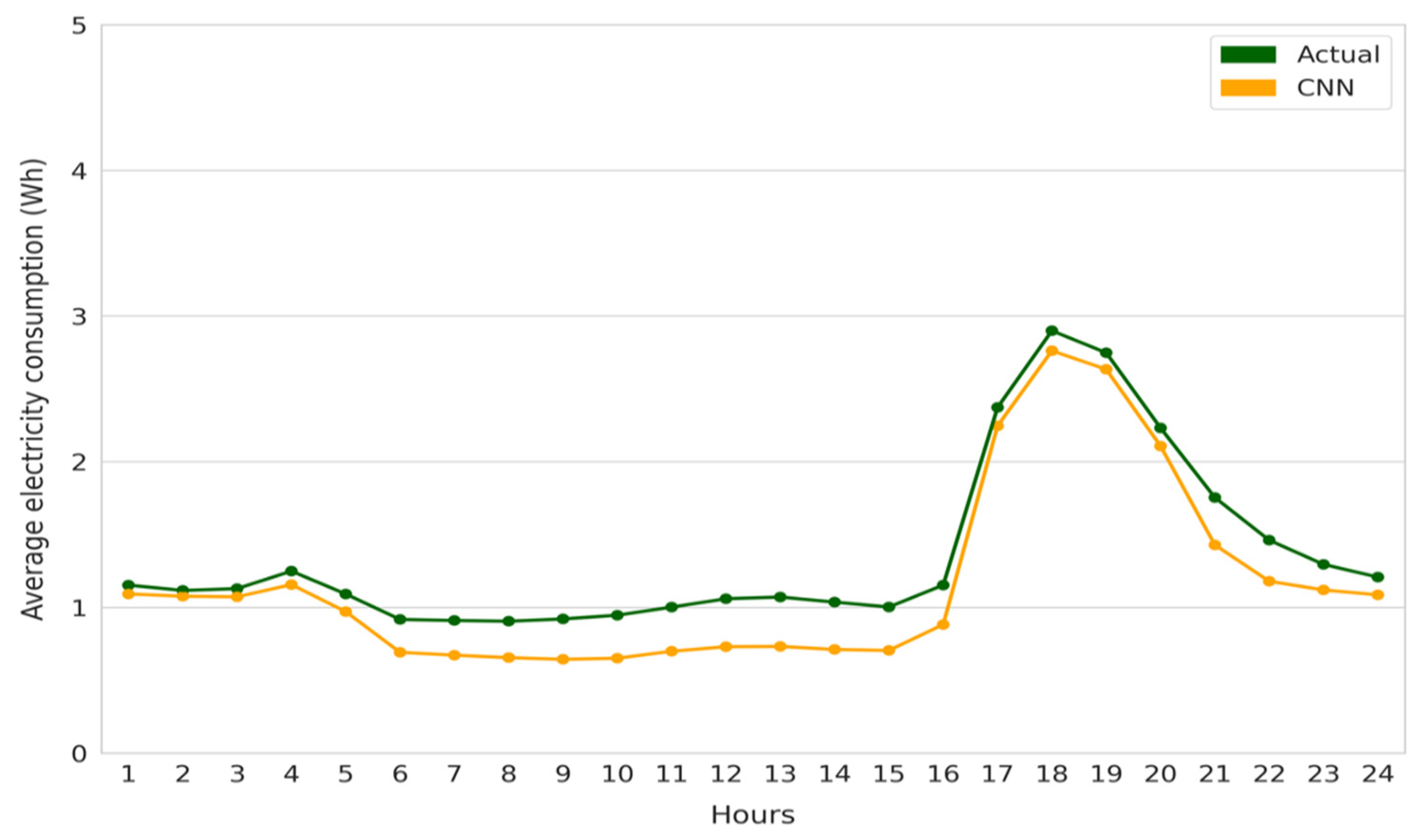
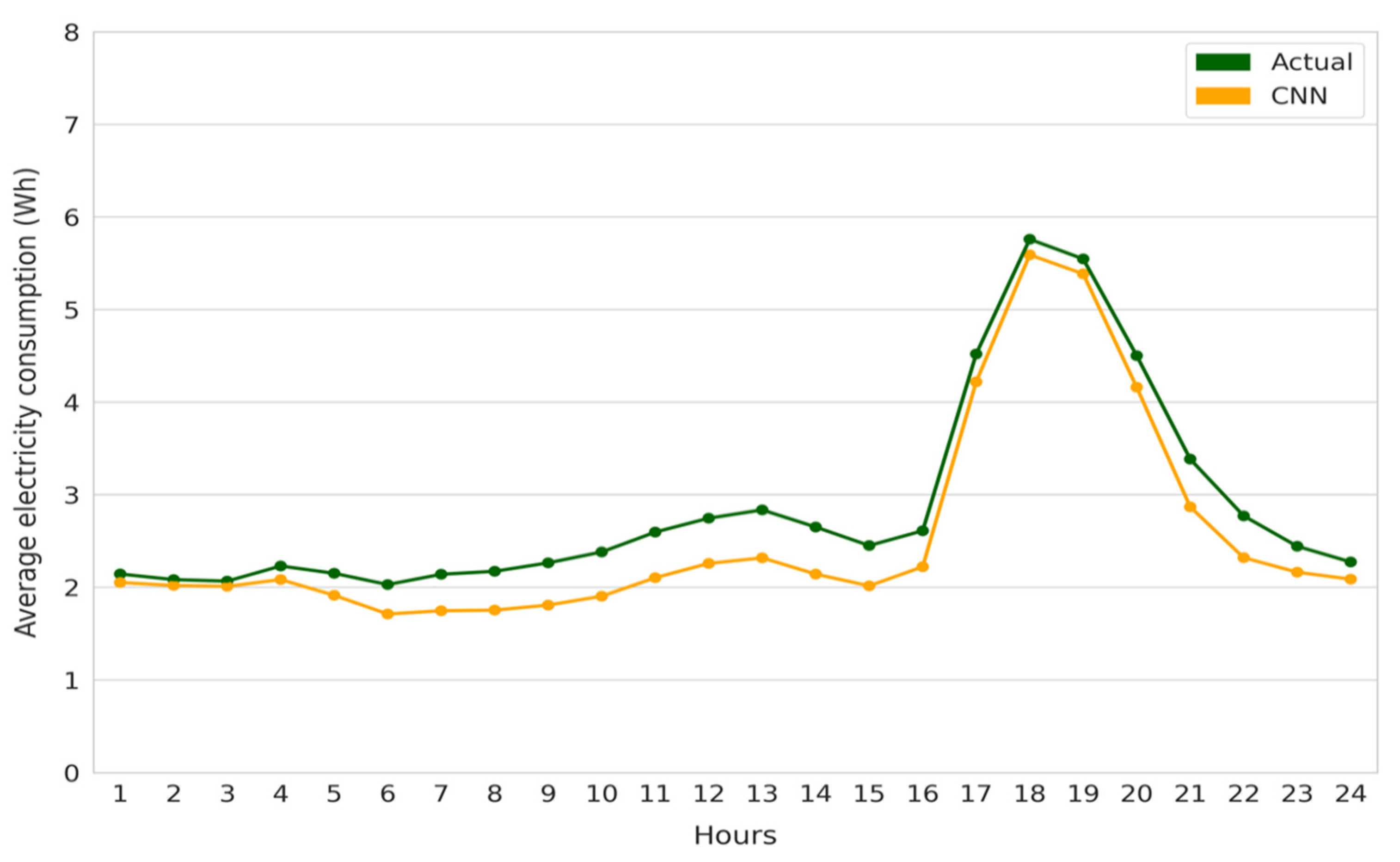
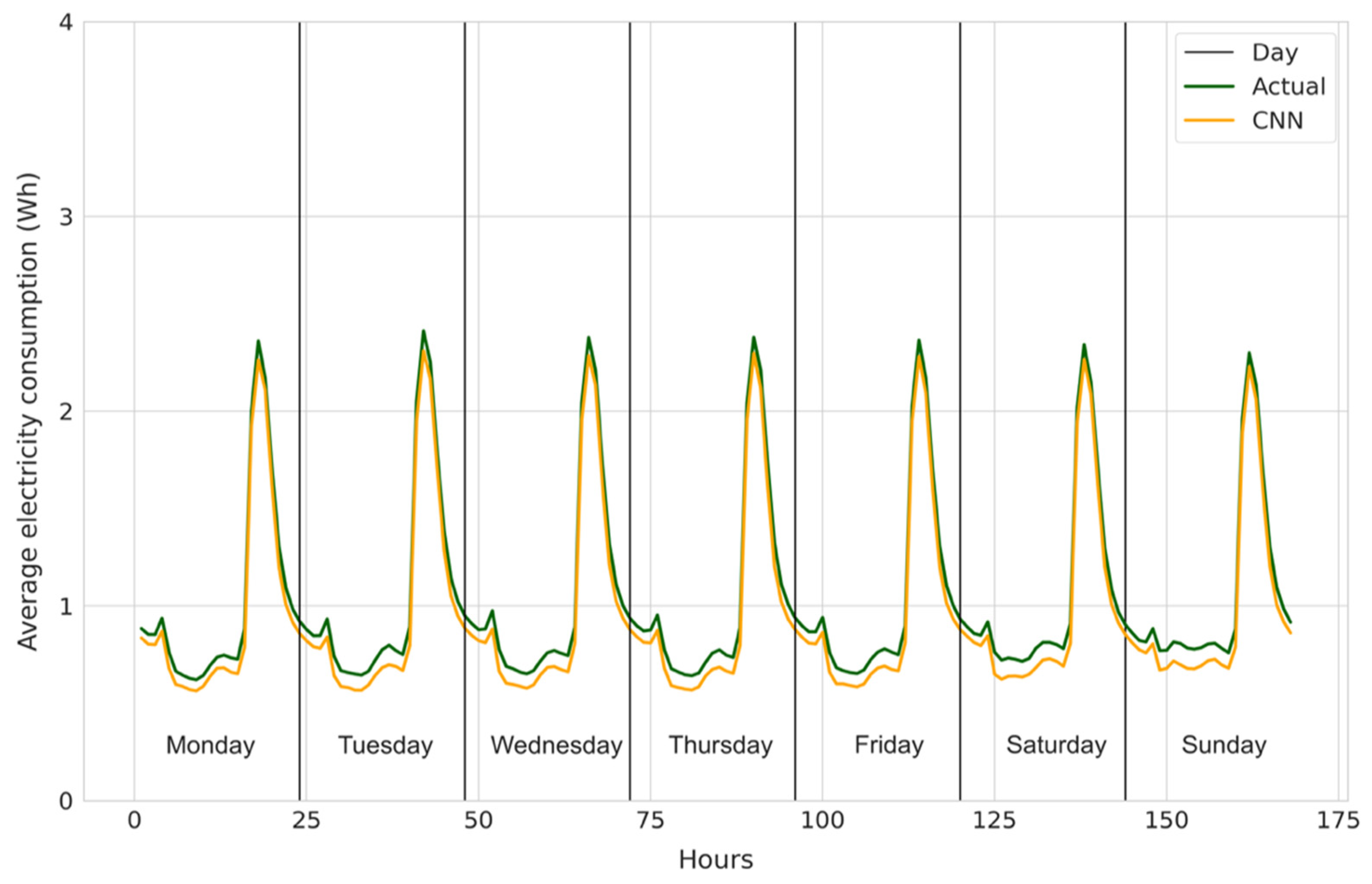
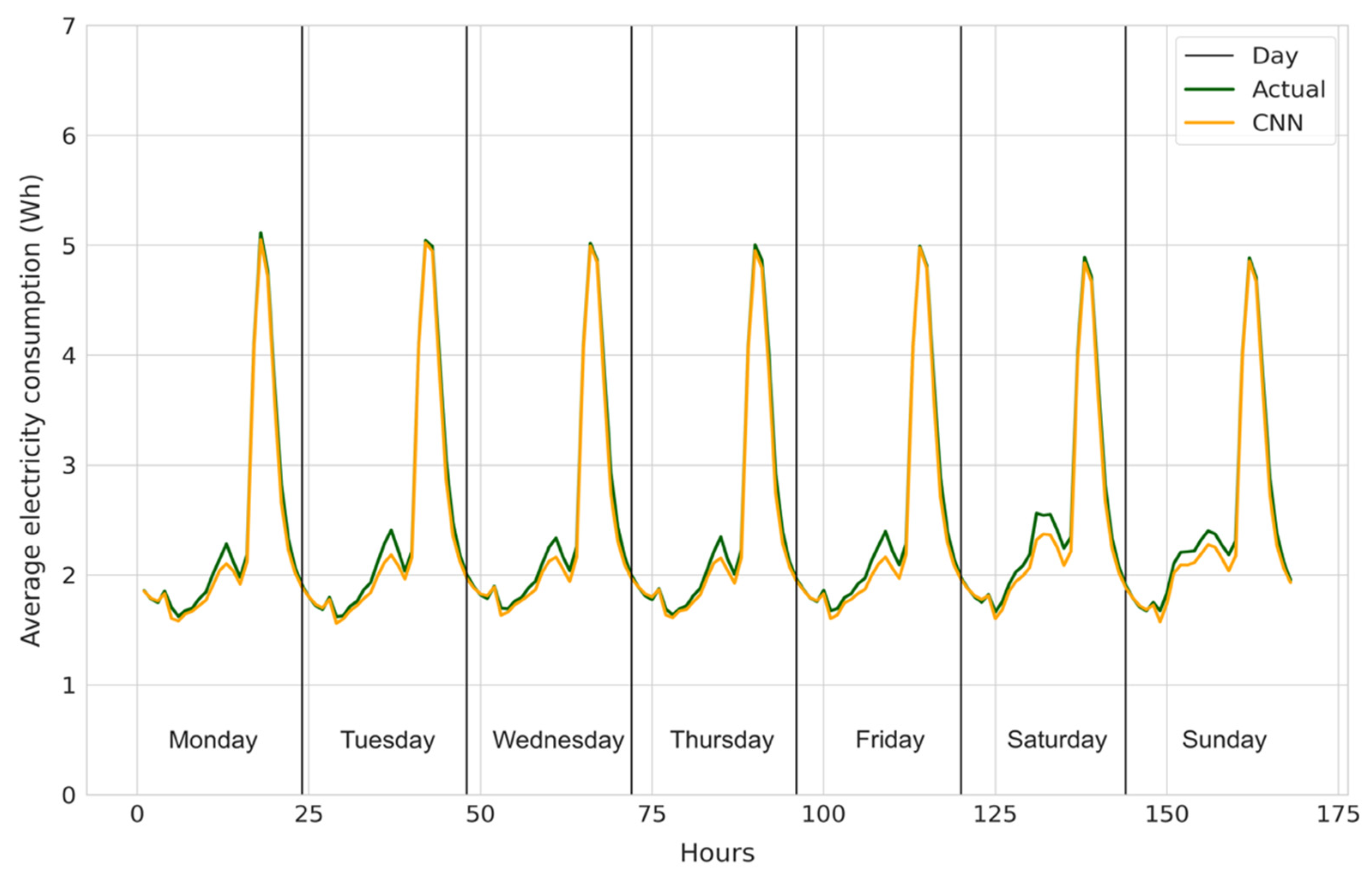
4.5.1. Scenario 1: 24 Hours
4.5.2. Scenario 2: 7 Daily Sums
4.5.3. Scenario 3: Usage across 3 Months
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IEA Access to Electricity Database, Electronic Dataset, IEA, Paris. 2020. Available online: https://www.iea.org/reports/sdg7-data-and-projections/access-to-electricity (accessed on 19 June 2021).
- United Nations The Sustainable Development Goals Report 2016; United Nations Publications: New York, NY, USA, 2016.
- Zerriffi, H. Innovative business models for the scale-up of energy access efforts for the poorest. Curr. Opin. Environ. Sustain. 2011, 3, 272–278. [Google Scholar] [CrossRef]
- Lighting Global; GOGLA; ESMAP. Off-Grid Solar Market Trends Report 2020; Lighting Global Program: Washington, DC, USA, 2020. [Google Scholar]
- Narayan, N.; Chamseddine, A.; Vega-Garita, V.; Qin, Z.; Popovic-Gerber, J.; Bauer, P.; Zeman, M. Exploring the boundaries of Solar Home Systems (SHS) for off-grid electrification: Optimal SHS sizing for the multi-tier framework for household electricity access. Appl. Energy 2019, 240, 907–917. [Google Scholar] [CrossRef]
- Koo, B.B.; Rysankova, D.; Portale, E.; Angelou, N.; Keller, S.; Padam, G. Rwanda: Beyond Connections; World Bank: Washington, DC, USA, 2018. [Google Scholar]
- IEA Africa Energy Outlook 2019; IEA Publications: Paris, France, 2019.
- Gustavsson, M. With time comes increased loads—An analysis of solar home system use in Lundazi, Zambia. Renew. Energy 2007, 32, 796–813. [Google Scholar] [CrossRef]
- Opoku, R.; Obeng, G.Y.; Adjei, E.A.; Davis, F.; Akuffo, F.O. Integrated system efficiency in reducing redundancy and promoting residential renewable energy in countries without net-metering: A case study of a SHS in Ghana. Renew. Energy 2020, 155, 65–78. [Google Scholar] [CrossRef]
- Bisaga, I.; Parikh, P. To climb or not to climb? Investigating energy use behaviour among Solar Home System adopters through energy ladder and social practice lens. Energy Res. Soc. Sci. 2018, 44, 293–303. [Google Scholar] [CrossRef] [Green Version]
- Bhatti, S.; Williams, A. Estimation of surplus energy in off-grid solar home systems. Renew. Energy Environ. Sustain. 2021, 6, 25. [Google Scholar] [CrossRef]
- Manur, A.; Marathe, M.; Manur, A.; Ramachandra, A.; Subbarao, S.; Venkataramanan, G. Smart Solar Home System with Solar Forecasting. Proceedings of 2020 IEEE International Conference on Power Electronics, Smart Grid and Renewable Energy (PESGRE2020), Cochin, India, 2–4 January 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Andersen, F.M.; Larsen, H.V.; Boomsma, T.K. Long-term forecasting of hourly electricity load: Identification of consumption profiles and segmentation of customers. Energy Convers. Manag. 2013, 68, 244–252. [Google Scholar] [CrossRef]
- Aung, Z.; Toukhy, M.; Williams, J.R.; Sanchez, A.; Herrero, S. Towards Accurate Electricity Load Forecasting in Smart Grids. In Proceedings of the DBKDA 2012: The Fourth International Conference on Advances in Databases, Knowledge, and Data Applications, Reunion Island, France, 1 March 2012; IARIA: Saint Gilles, Brussels, 2012. [Google Scholar]
- Humeau, S.; Wijaya, T.K.; Vasirani, M.; Aberer, K. Electricity load forecasting for residential customers: Exploiting aggregation and correlation between households. In Proceedings of the 2013 Sustainable Internet and ICT for Sustainability SustainIT, Palermo, Italy, 30–31 October 2013; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Schultz, P.W.; Estrada, M.; Schmitt, J.; Sokoloski, R.; Silva-Send, N. Using in-home displays to provide smart meter feedback about household electricity consumption: A randomized control trial comparing kilowatts, cost, and social norms. Energy 2015, 90, 351–358. [Google Scholar] [CrossRef] [Green Version]
- Gajowniczek, K.; Zabkowski, T. Short term electricity forecasting using individual smart meter data. Procedia Comput. Sci. 2014, 35, 589–597. [Google Scholar] [CrossRef] [Green Version]
- Efficiency for Access Coalition. The State of the Off-Grid Appliance Market; Efficiency for Access Coalition, 2019. [Google Scholar]
- Practical Action. Poor People’s Energy Outlook 2014; Practical Action Publishing: Rugby, UK, 2014. [Google Scholar]
- Wang, Q.; Li, S.; Li, R. Forecasting energy demand in China and India: Using single-linear, hybrid-linear, and non-linear time series forecast techniques. Energy 2018, 161, 821–831. [Google Scholar] [CrossRef]
- Kuster, C.; Rezgui, Y.; Mourshed, M. Electrical load forecasting models: A critical systematic review. Sustain. Cities Soc. 2017, 35, 257–270. [Google Scholar] [CrossRef]
- Lazzeri, F. Machine Learning for Time Series Forecasting with Python; John Wiley & Sons, Inc.: Indianapolis, Indiana, 2020. [Google Scholar]
- Dostál, P. Forecasting of Time Series with Fuzzy Logic. In Prediction, Modeling and Analysis of Complex Systems. Advances in Intelligent Systems and Computing; Zelinka, I., Chen, G., Rössler, O., Snasel, V.A.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- González, P.A.; Zamarreño, J.M. Prediction of hourly energy consumption in buildings based on a feedback artificial neural network. Energy Build. 2005, 37, 595–601. [Google Scholar] [CrossRef]
- Nielsen, M.A. A visual proof that neural nets can compute any function. In Neural Networks and Deep Learning; Determination Press: San Francisco, CA, USA, 2015. [Google Scholar]
- Pujari, P.; Sewak, M.; Rezaul Karim, M. Practical Convolutional Neural Networks; Packt Publishing: Birmingham, UK, 2018; ISBN 978-1-78839-230-3. [Google Scholar]
- Amran, N.A.; Soltani, M.D.; Yaghoobi, M.; Safari, M. Deep Learning Based Signal Detection for OFDM VLC Systems. In Proceedings of the 2020 IEEE International Conference on Communications Workshops (ICC Workshops), Online, 7–10 June 2020; pp. 1–6. [Google Scholar]
- Acharya, S.K.; Wi, Y.M.; Lee, J. Short-term load forecasting for a single household based on convolution neural networks using data augmentation. Energies 2019, 12, 3560. [Google Scholar] [CrossRef] [Green Version]
- Amarasinghe, K.; Marino, D.L.; Manic, M. Deep neural networks for energy load forecasting. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017; pp. 1483–1488. [Google Scholar] [CrossRef]
- Lang, C.; Steinborn, F.; Steffens, O.; Lang, E.W. Electricity load forecasting—An evaluation of simple 1D-CNN network structures. arXiv 2019, arXiv:1911.11536. [Google Scholar]
- Koprinska, I.; Wu, D.; Wang, Z. Convolutional Neural Networks for Energy Time Series Forecasting. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Heo, J.; Song, K.; Han, S.; Lee, D.-E. Multi-channel convolutional neural network for integration of meteorological and geographical features in solar power forecasting. Appl. Energy 2021, 295, 1–13. [Google Scholar] [CrossRef]
- Kiguchi, Y.; Heo, Y.; Weeks, M.; Choudhary, R. Predicting intra-day load profiles under time-of-use tariffs using smart meter data. Energy 2019, 173, 959–970. [Google Scholar] [CrossRef]
- Mack, B.; Tampe-Mai, K.; Kouros, J.; Roth, F.; Taube, O.; Diesch, E. Bridging the electricity saving intention-behavior gap: A German field experiment with a smart meter website. Energy Res. Soc. Sci. 2019, 53, 34–46. [Google Scholar] [CrossRef]
- Komatsu, H.; Kimura, O. Peak demand alert system based on electricity demand forecasting for smart meter data. Energy Build. 2020, 225, 1–14. [Google Scholar] [CrossRef]
- Guo, Z.; Zhou, K.; Zhang, C.; Lu, X.; Chen, W.; Yang, S. Residential electricity consumption behavior: Influencing factors, related theories and intervention strategies. Renew. Sustain. Energy Rev. 2018, 81, 399–412. [Google Scholar] [CrossRef]
- Bonan, J.; Adda, G.; Mahmud, M.; Said, F. The Role of Flexibility and Planning in Repayment Discipline: Evidence from a Field Experiment on Pay-as-You-Go Off-Grid Electricity; Working Paper: Milan, Italy, 2020. [Google Scholar]
- Zhang, X.M.; Grolinger, K.; Capretz, M.A.M.; Seewald, L. Forecasting Residential Energy Consumption: Single Household Perspective. In Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; pp. 110–117. [Google Scholar] [CrossRef]
- Gans, W.; Alberini, A.; Longo, A. Smart meter devices and the effect of feedback on residential electricity consumption: Evidence from a natural experiment in Northern Ireland. Energy Econ. 2013, 36, 729–743. [Google Scholar] [CrossRef] [Green Version]
- Dominicis, S. De; Sokoloski, R.; Jaeger, C.M.; Schultz, P.W. Making the smart meter social promotes long-term energy conservation. Palgrave Commun. 2019, 5, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Gajowniczek, K.; Ząbkowski, T. Electricity forecasting on the individual household level enhanced based on activity patterns. PLoS One 2017, 12, 1–26. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, C.; Cook, D.J. Behavior-Based Home Energy Prediction. In Proceedings of the 2012 Eighth International Conference on Intelligent Environments (IE ’12), Guanajuato, Mexico, 26–29 June 2012; IEEE Computer Society: Washington, DC, USA, 2012; pp. 57–63. [Google Scholar]
- Chitsaz, H.; Shaker, H.; Zareipour, H.; Wood, D.; Amjady, N. Short-term electricity load forecasting of buildings in microgrids. Energy Build. 2015, 99, 50–60. [Google Scholar] [CrossRef]
- Kizilcec, V.; Parikh, P. Solar Home Systems: A comprehensive literature review for Sub-Saharan Africa. Energy Sustain. Dev. 2020, 58, 78–89. [Google Scholar] [CrossRef]
- Opiyo, N.N. How basic access to electricity stimulates temporally increasing load demands by households in rural developing communities. Energy Sustain. Dev. 2020, 59, 97–106. [Google Scholar] [CrossRef]
- Bisaga, I.; Puźniak-Holford, N.; Grealish, A.; Baker-Brian, C.; Parikh, P. Scalable off-grid energy services enabled by IoT: A case study of BBOXX SMART Solar. Energy Policy 2017, 109, 199–207. [Google Scholar] [CrossRef] [Green Version]
- Abdul-Salam, Y.; Phimister, E. Modelling the impact of market imperfections on farm household investment in stand-alone solar PV systems. World Dev. 2019, 116, 66–76. [Google Scholar] [CrossRef]
- Adwek, G.; Boxiong, S.; Ndolo, P.O.; Siagi, Z.O.; Chepsaigutt, C.; Kemunto, C.M.; Arowo, M.; Shimmon, J.; Simiyu, P.; Yabo, A.C. The solar energy access in Kenya: A review focusing on Pay-As-You-Go solar home system. Env. Dev Sustain. 2019, 22, 3897–3938. [Google Scholar] [CrossRef]
- Lay, J.; Ondraczek, J.; Stoever, J. Renewables in the energy transition: Evidence on solar home systems and lighting fuel choice in Kenya. Energy Econ. 2013, 40, 350–359. [Google Scholar] [CrossRef] [Green Version]
- Witten, I.H.; Frank, E.; Hall, M.A.; Pal, C.J. Data Mining, 4th ed.; Morgan Kaufmann: Cambridge, MA, USA, 2017; ISBN 978-0-12-804291-5. [Google Scholar]
- Agrawal, T. Hyperparameter Optimization in Machine Learning: Make Your Machine Learning and Deep Learning Models More Efficient; Apress Standard: New York, NY, USA, 2021; ISBN 978-1-4842-6578-9. [Google Scholar]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 2nd ed.; OTexts: Melbourne, Australia, 2018. [Google Scholar]
- Khan, S.I.; Raihan, S.A.; Habibullah, M.; Abrar, S.F. Reducing the cost of solar home system using the data from data logger. In Proceedings of the 2017 IEEE International Conference on Smart Grid and Smart Cities (ICSGSC), Singapore, 23–26 July 2017; pp. 37–41. [Google Scholar]
- Soltowski, B.; Bowes, J.; Strachan, S.; Anaya-Lara, O.L. A Simulation-Based Evaluation of the Benefits and Barriers to Interconnected Solar Home Systems in East Africa. In Proceedings of the 2018 IEEE PES/IAS PowerAfrica, Cape Town, South Africa, 28–29 June 2018; pp. 491–496. [Google Scholar] [CrossRef] [Green Version]
- van der Plas, R.J.; Hankins, M. Solar electricity in Africa: A reality. Energy Policy 1998, 26, 295–305. [Google Scholar] [CrossRef]
- Heeten, T. Den; Narayan, N.; Diehl, J.; Verschelling, J.; Silvester, S.; Popovic-Gerber, J.; Bauer, P.; Zeman, M. Understanding the present and the future electricity needs: Consequences for design of future Solar Home Systems for off-grid rural electrification. In Proceedings of the 2017 International Conference on the Domestic Use of Energy (DUE), Cape Town, South Africa, 4–5 April 2017; pp. 8–15. [Google Scholar]
- Adeoye, O.; Spataru, C. Modelling and forecasting hourly electricity demand in West African countries. Appl. Energy 2019, 242, 311–333. [Google Scholar] [CrossRef]
- Marszal-Pomianowska, A.; Heiselberg, P.; Larsen, O.K. Household electricity demand profiles—A high-resolution load model to facilitate modelling of energy flexible buildings. Energy 2016, 103, 487–501. [Google Scholar] [CrossRef]
- Laicane, I.; Blumberga, D.; Blumberga, A.; Rosa, M. Evaluation of Household Electricity Savings. Analysis of Household Electricity Demand Profile and User Activities. Energy Procedia 2015, 72, 285–292. [Google Scholar] [CrossRef] [Green Version]
- Soares, L.J.; Medeiros, M.C. Modeling and forecasting short-term electricity load: A comparison of methods with an application to Brazilian data. Int. J. Forecast. 2008, 24, 630–644. [Google Scholar] [CrossRef]
- McLoughlin, F.; Duffy, A.; Conlon, M. A clustering approach to domestic electricity load profile characterisation using smart metering data. Appl. Energy 2015, 141, 190–199. [Google Scholar] [CrossRef] [Green Version]
- Kizilcec, V.; Parikh, P.; Bisaga, I. Examining the Journey of a Pay-as-You-Go Solar Home System Customer: A Case Study of Rwanda. Energies 2021, 14, 330. [Google Scholar] [CrossRef]
- Sedgwick, P. Pearson’s correlation coefficient. BMJ 2012, 345, 1. [Google Scholar] [CrossRef] [Green Version]
- Fischer, C. Feedback on household electricity consumption: A tool for saving energy? Energy Effic. 2008, 1, 79–104. [Google Scholar] [CrossRef]
- Karjalainen, S. Consumer preferences for feedback on household electricity consumption. Energy Build. 2011, 43, 458–467. [Google Scholar] [CrossRef]
- Zeyringer, M.; Pachauri, S.; Schmid, E.; Schmidt, J.; Worrell, E.; Morawetz, U.B. Analyzing grid extension and stand-alone photovoltaic systems for the cost-effective electrification of Kenya. Energy Sustain. Dev. 2015, 25, 75–86. [Google Scholar] [CrossRef]









| Models | Feature | Advantages | Disadvantages |
|---|---|---|---|
| Regression-based | Find out influencing factors; build the regression equation between factors and objectives | Good at analysing multi-factor models; provide error checking of model estimation parameters; easy to calculate | Does not consider the un-testability of certain influence factors; results cannot reflect periodic wave |
| ARIMA | Established by regression of the dependent variable only for its lag value and the present value of the random error term | The mathematical model requires only endogenous variables without resorting to exogenous variables | Require timing data to be stable; cannot reflect non-linear relationships; the determination of model parameters is complicated |
| Fuzzy Logic | Perform fuzzy judgment for systems with unknown models; reasoning solves the regular fuzzy information problem that is difficult to deal with by conventional methods | High accuracy in reflecting uncertainty qualitative knowledge; good at uncertain situation prediction of input variables | Lack of specific prediction formulas; cannot reflect the relationship between predicted values and historical data |
| Artificial Neural Networks | It abstracts the human brain neural network from the perspective of information processing; usually a logical expression of some kind of algorithm in nature. | Provide self-learning function and high-speed search for optimal solutions; fully approximate any arbitrarily complex non-linear relationship; can learn and adapt to unknown or uncertain systems | No ability to explain reasoning process and reasoning basis; cannot work when data is insufficient; turning all reasoning into numerical calculations results in the loss of information |
| Support Vector Regression | Find the best compromise between the complexity of the model and the learning ability based on limited sample information | Can solve machine learning and non-linear problems in the case of small samples; simplify the usual classification and regression issues; can improve generalization performance; less parameters to solve | Sensitive to missing data; difficult to implement large-scale training samples; difficult to solve multiple classification problem |
| Models | Data Trend Characteristics | Forecast Period | Number of Variables | Most Applied Case in Energy Field | |||
|---|---|---|---|---|---|---|---|
| Linear | Non-Linear | Long-Term | Short-Term | Multivariate | Univariate | ||
| Regression-based |  |  |  | Short-term load forecasting | |||
| ARIMA |  |  |  | Electricity price/energy consumption | |||
| Fuzzy Logic |  |  |  | Short-term electricity consumption | |||
| Artificial Neural Networks |  |  |  | Electricity price/energy consumption | |||
| Support Vector Regression |  |  |  | Hourly/daily/monthly load demand | |||
 symbol means the relative superiority of predictive performance.
symbol means the relative superiority of predictive performance.| Method | Dates | Number of Customers |
|---|---|---|
| Time series analysis | 1 March 2019–29 Feburary 2020 | 63,299 |
| CNN | 11 Feburary 2019–29 December 2019 | 48,485 |
| Groups | Customers | Percent (%) | Mean Daily Electricity Usage (Wh) |
|---|---|---|---|
| No television | 56,166 | 90 | 43.2 |
| Television | 6291 | 10 | 66.3 |
| 62,457 | 100 |
| Low Energy Users (<2.1 Wh) | High Energy Users (≥2.1 Wh) | |
|---|---|---|
| Training | 25,973 | 7308 |
| Validation | 5018 | 2561 |
| Test | 5054 | 2571 |
| 36,045 | 12,440 |
| Scenario | CNN Forecast Interval | CNN’s Output | Naïve Baseline |
|---|---|---|---|
| 1 | 24 h | 24 | Previous 24 h |
| 2 | 1 week (daily sum) | 7 | Previous 1 week (daily sum) |
| 3 | 3 months (hourly mean over a week) | 168 | Previous 4 weeks (hourly sum) |
| Variables | Description | Unit of Measurement | Average % Difference to Control Value | |
|---|---|---|---|---|
| 1 | Hourly power usage | Mean power usage per hour per customer, where: power = current × voltage | Wh | N.A. |
| 2 | Mean power | Mean weekly power values over the entire training period | Wh | 1.059% |
| 3 | Days until month end | The number of days until the end of the month | Integer | 0.926% |
| 4 | Province | Province in which the SHS is installed. Categories: Eastern, Southern, Western, Northern, Kigali City | Text | 0.744% |
| 5 | Number of torches | Number of torches per customer | Integer | 0.433% |
| 6 | Age | Customer age | Integer | 0.405% |
| 7 | Number of bulbs | Number of bulbs per customer | Integer | 0.337% |
| 8 | Maximum power | Maximum weekly power values over the entire training period | Wh | 0.336% |
| 9 | Temperature | Hourly temperature recorded per SHS, i.e., customer | Celsius | 0.346% |
| 10 | Number of TVs | Number of televisions per customer | Integer | 0.340% |
| 11 | How heard about Bboxx | Method through which customer first heard about Bboxx. Categories: sales agent, flyer, other client, radio, shop, tv, other | Text | 0.325% |
| 12 | Days from month start | The number of days from the start of the month | Integer | 0.307% |
| 13 | Number of radios | Number of radios per customer | Integer | 0.147% |
| 14 | Previous lighting source | Previous light or energy source used by customer. Categories: candles, batteries, lantern, other | Text | 0.001% |
| Hyperparameter | Min to Max Value Range | Value Used |
|---|---|---|
| Batch size | 128–256 | 256 |
| Dropout | 0–0.7 | 0.5 |
| Input neurons | 128–2048 | 900 |
| Batch normalisation momentum | 0.6–0.99 | 0.65 |
| Learning rate start Learning rate patience Learning rate weight decay Learning rate minimum | 0.01–0.05 3–5 1 × 10−5–1 × 10−3 0.0005–0.002 | 0.02 5 1 × 10−4 0.001 |
| Scenario | Forecast Interval | Type of Energy User | Baseline MSE | CNN MSE | Percentage Difference |
|---|---|---|---|---|---|
| 1 | 24 h | Low | 2.788 | 1.386 | 50.3% |
| High | 8.052 | 4.577 | 43.2% | ||
| 2 | 1 week (sum per day) | Low | 0.669 (385) 1 | 0.382 (220) 1 | 42.9% |
| High | 2.014 (1160) 1 | 1.265 (729) 1 | 37.2% | ||
| 3 | 3 months (hourly mean) | Low | 0.768 | 0.369 | 52.0% |
| High | 2.568 | 1.194 | 53.5% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kizilcec, V.; Spataru, C.; Lipani, A.; Parikh, P. Forecasting Solar Home System Customers’ Electricity Usage with a 3D Convolutional Neural Network to Improve Energy Access. Energies 2022, 15, 857. https://doi.org/10.3390/en15030857
Kizilcec V, Spataru C, Lipani A, Parikh P. Forecasting Solar Home System Customers’ Electricity Usage with a 3D Convolutional Neural Network to Improve Energy Access. Energies. 2022; 15(3):857. https://doi.org/10.3390/en15030857
Chicago/Turabian StyleKizilcec, Vivien, Catalina Spataru, Aldo Lipani, and Priti Parikh. 2022. "Forecasting Solar Home System Customers’ Electricity Usage with a 3D Convolutional Neural Network to Improve Energy Access" Energies 15, no. 3: 857. https://doi.org/10.3390/en15030857
APA StyleKizilcec, V., Spataru, C., Lipani, A., & Parikh, P. (2022). Forecasting Solar Home System Customers’ Electricity Usage with a 3D Convolutional Neural Network to Improve Energy Access. Energies, 15(3), 857. https://doi.org/10.3390/en15030857







