1. Introduction
Recent policy for climate and energy leans towards reducing greenhouse gas emissions and reaching energy systems without a significant carbon footprint. Electricity generation and consumption are at the forefront of this change. Therefore, currently used distribution and transmission grids will have to inevitably meet the above-mentioned requirements and a key solution in achieving carbon-neutral smart grids seem to be wide usage of microgrid solutions [
1]. To reach that neutrality, a vast amount of renewable energy sources is vital and transition to such means of energy production is already taking place. Unfortunately, as pinpointed in [
2], the adoption of renewable energy sources pose various challenges arising from user demands and fluctuate profiles of renewable energy generation far different from traditional means of energy generation. The structural solution to those new challenges is splitting the electrical network into smaller units based on distributed resources. Every smaller segment, the so-called microgrid, manages the local loads, generation and is equipped with storage capabilities. Moreover, it possesses means of connecting to and disconnecting from other segments, as well as can exchange energy with them. This approach significantly improves possibilities of remedying the instability of renewable sources and allows for fuller utilization of available renewable energy. In addition, small independent networks capable of island-mode operation tend to be incomparably more reliable in terms of continuity of supply and, with appropriate control strategies, offer economical benefits not only in remote regions.
According to [
3], when considering complex microgrid control solutions, hierarchical control is mainly selected. Such systems consist of three distinguishable levels. Primary control stabilizes system frequency and voltage in response to rapid load changes, thus operating on the smallest timescale. Secondary control focuses on nullifying grid parameters deviations in steady-state and synchronizing with the public grid after the transition to grid-connected operation. Lastly, tertiary control is responsible for power flow control between microgrid elements or between microgrid clusters and upstream, public grid. Additionally, it introduces further functionalities in form of large-scale planning or economic optimization. As reported in [
4], microgrid management is often associated with optimal control or optimization. Such optimization may concern economic, environmental, or technical objectives and optimal operation can be achieved using various techniques. Frequently used approaches include meta-heuristic or heuristic methods, stochastic and robust methods, Model Predictive Control in various forms, linear, dynamic, and nonlinear programming, as well as artificial intelligence.
Single and multi-objective optimization methods based on heuristic algorithms such as particle swarm or firefly optimization are a widespread choice. Some of the usage cases include cost and sizing optimization with fossil fuel share reduction in energy generation [
5], microgrid load dispatch optimization [
6] and for optimization of energy production cost in a microgrid [
7]. Meta-heuristics are also used in combination with other techniques such as mixed-integer linear programming [
8] or artificial neural networks [
9]. On the other hand, artificial neural networks can adapt to uncertainties and are applicable when the exact model of a system is not available [
10]. Exemplary applications include optimal energy scheduling [
11] and storage system management [
12]. It is worth noting that, according to [
10], artificial neural networks are more commonly used in primary and secondary control than on the tertiary level. An exemplary solution utilizing a fuzzy-logic decision system in a multi-objective optimization problem can be found in [
13]. Due to uncertainties, such as energy demand and generation, robust and stochastic optimization and control algorithms are also applicable in microgrid management cases. Robust optimization focused on both economy and robustness is presented in [
14]. An exemplary optimal stochastic energy management system can be found in [
15] and a robust economic energy and reserve management system is derived in [
16]. Lastly, different mathematical programming methods are widely used, including dynamic, mixed-integer, and nonlinear programming. Some of the usage cases include energy generation cost optimization [
17] and demand-generation mismatch optimization [
18]. Importantly, the latter two are often equated with hybrid and nonlinear Model Predictive Control. Given the focus of this paper, usage of Model Predictive Control and mixed-integer linear programming, especially in hybrid form, will be discussed in detail below.
The applicability of Model Predictive Control (MPC in short) on all microgrid control levels is one of its most significant advantages. As reported in [
19,
20], the popularity of MPC stems from the fact that the resulting control strategy, due to the direct use of the process model, respects all system interactions and constraints which are not that easy to capture using other control methods. Moreover, it provides constraints satisfaction, stability guarantee and is adequate in application to multi-variable processes. Going back to the microgrid world, it is clear that any microgrid consists of a substantial amount of interacting elements, sometimes in an unintuitive manner, and controllers must operate in a significantly constrained environment. Interestingly, various phenomenons occurring in microgrid exhibit hybrid behavior, therefore building microgrid hybrid models is not overly complicated, especially in the economical scope. Additionally, receding horizon control is highly compatible with hybrid systems and such a combination is widely used. In [
21], a hybrid model is used for economical optimization to include as much detail as possible and conventional MPC is used in form of a single mixed-integer linear programming (MILP) problem among other methods. The scope of research is focused on grid-connected mode and islanded operation is not considered. A Single Hybrid MPC (HMPC) solution using Mixed Logical Dynamical (MLD in short) framework in conjunction with a highly efficient MILP solver is presented in [
22]. The scope of modeling focuses on economic and dynamic modeling of microgrid components including varying energy costs taken into account during optimization but no demand-side management. The exact solution is dedicated to the Brazilian energy market. In turn, the authors of [
23] aim to design a management system dedicated to smart house systems. A hybrid model of its electrical and thermal system is derived, HMPC for on-grid operation proposed and solved using MILP solver. Importantly, a time-varying energy price is also introduced and no demand-side management is considered. As can be seen, the usage of mixed-integer linear programming is very wide, mainly because of highly accessible and efficient solvers, as well as simulation environments equipped with toolboxes connecting solvers and hybrid modeling tools. The synergy between microgrid modeled using discrete hybrid automata described in HYSDEL language and resulting MILP solved using CPLEX solver is precisely described in [
24] where authors propose a hybrid optimization model for management of microgrid featuring automatic grid connection. A similar approach is presented in [
25]. The study presents a hybrid model predictive control solution to optimal economic energy management of microgrid with hydrogen-based storage. Applied control scheme employs single Lyapunov-based HMPC using microgrid model in discrete hybrid automata form converted to MLD representation. Demand-side management is not considered and emphasis is put on grid-connected operation. The solution includes optimal dispatch and load sharing controllers. Naturally, there are other usable optimization approaches, without the introduction of receding control strategies in form of MPC. The authors of [
26] use particle swarm optimization with the aim of minimizing the operation cost of a microgrid and improving photoelectric consumption by means of energy demand management. The algorithm is also solving a single MILP problem. Varying energy price is used but the microgrid remains connected to the public grid.
Considering the wide range of MILP applications and available tools authors of this paper choose to develop a novel HMPC-based control solution covering separate optimization of both on-grid and off-grid operation. To clarify, when dealing with microgrid switching between on-grid and off-grid operation mode, the control system must achieve an optimal solution regardless of the current mode. However, optimal control for each of those modes should be reached using different criteria resulting in slightly different optimization problems but still using the same microgrid model. That said, derivation of compatible microgrid hybrid model was also needed. Moreover, such a model should also cover demand-side management and the presence of energy-tariff with changing energy price.
A novel control concept utilizing switched hybrid MPC applied to economically optimize microgrid operation is the main contribution of this paper. Additionally, a compatible hybrid microgrid model in MLD form featuring demand-side management, varying energy price, and operation in both grid-connected and islanded mode is also contributed.
4. Parameters and Testing Scenario
It is important to outline model and controllers parameters used during testing and to emphasize the chosen approach in terms of energy generation and demand scenarios. The aim was to use as much real-world data as possible, in order to prove the adequacy of the developed hybrid model and control solution.
4.1. Parameters and Constraints
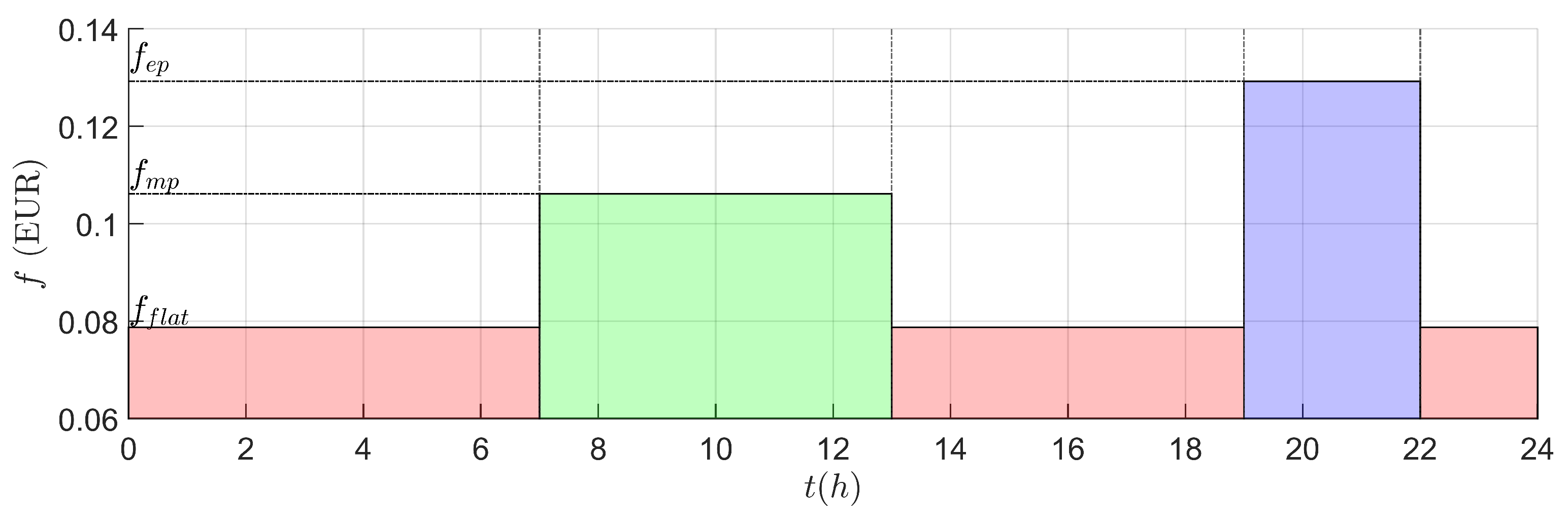
Various parameters are introduced in expressions composing the hybrid model as well as in the process of optimization problem formulation. They are then collected in
Table 1 and their values were chosen according to distinct sources. Values of
through
are selected assuming 50% maximal controllable load reduction and, by setting adequate
constraints
and
, a range of values between 100 and 50 percent with 10 percent maximal rate of change
is achieved. It is assumed that the maintenance cost
equals EUR 1 per hour, the shutdown cost
is the same as the price of one unit of fuel and startup cost
is half the shutdown cost. The natural discharge
, the energy needed for storage cooling
, the efficiencies
and
as well as the maximal amount of energy charged
and discharged
over
are sourced from [
27] as well as the storage capacity
. The minimal allowed level of energy in storage
is selected keeping in mind that deep discharge is unacceptable. Parameters
,
and
, related to fuel cost are calculated based on [
34]. Generator maximum power
comes from the same source. Although
may prove sufficient for the chosen generator to ramp up to full power, a much smaller additional ramp up constraint
is selected to allow for smoother operation. The energy pricing, including various fees, is borrowed from [
28] and converted to euros. The generator deadband
, fuel threshold
, required connection power
, identical to the maximal amount of energy exchanged with public grid, sampling time
and prediction horizon
N were fine-tuned during preliminary testing.
On the other hand, matrices of weighting coefficients mentioned in Equation (
47), as well as weighting matrices
and
associated with single hybrid MPC used during simulation as a reference, have the following values:
Note that matrices dedicated to different operation modes have slightly different values. Such diversity allows for different control policies depending on connection status. For example,
features a lower energy exchange penalty and much higher generator usage punishment compared to
. Moreover, in the case of
, those priorities are reversed, which is much needed in off-grid mode. On the other hand, values of
and
should be viewed as a necessary compromise to accommodate for the lack of a switching mechanism. Given the fact, that on-grid mode poses more cost reduction opportunities, penalties expressed through both
and
encourage the management system to sell more energy if possible and buy less of it from the public grid. At the same time,
and
allow for a greater extent of load shedding compared to
. Similarly, three reference values vectors are specified:
All outputs except for and are to be minimized in the on-grid scenario, hence their reference values are set to zeros, which nullifies the reference value. On the other hand, denotes income from energy selling, therefore it is to be maximized by means of setting very high desired income and therefore turning a resulting problem into income maximization. When it comes to , the reference value is introduced to encourage storage unit charging with renewable energy but, at the same time, to leave a sufficient margin. There is no energy sales opportunity in off-grid mode therefore, reference vector , aside from storage state of charge reference, differs only in reference value being changed to zero. Significantly lower target stored energy level allows to not overuse diesel generator. Values of are similar to with one exception being the lower state of charge reference required to achieve acceptable storage utilization in both on-grid and off-grid mode.
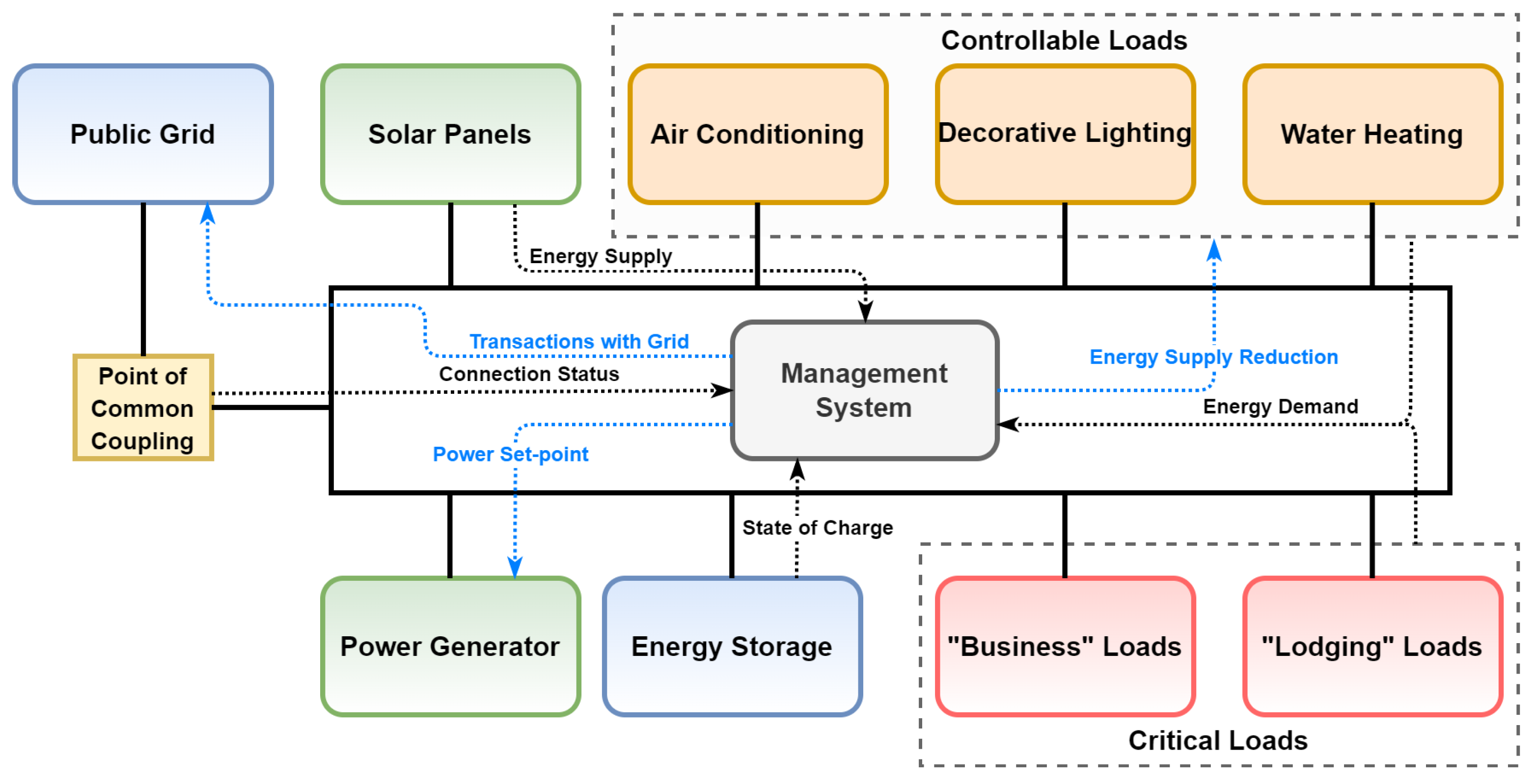
4.2. Simulated Microgrid Configuration
The authors choose to analyse the performance of the proposed solution when applied to a large commercial facility with its own photovoltaic installation, power generator and energy storage. This is why the aggregated, total critical energy demand profile consists of various load profiles sourced from small and medium businesses as well as residential buildings, to imitate shops, workshops, public buildings, and lodging facilities connected to the considered microgrid.
Figure 4 features the structure of the analysed microgrid.
What is more, basic controllable loads are also present in form of air conditioning, water heating, and decorative elements. The microgrid is connected to the public grid via the point of common coupling and energy can be exchanged in both directions. Fundamental information flow concerning the energy management system is also shown in
Figure 4. Aside from energy supply and demand, information on the connection status, as well as, the storage state is delivered to the management algorithm, while the amount of energy exchanged with the public grid, generator power set-point, and degree of energy supply reduction is returned. The main optimization goal is to minimize operation cost, but it simultaneously takes into account some technical aspects such as generator and storage usage or continuity of energy supply. Still, the system is also intended to improve the use of renewable energy. Another point is that, in off-grid mode, microgrid is unable to exchange energy with the public grid but is able to utilize excessive energy. Nevertheless, such a surplus of energy is to be avoided. On the other hand, in on-grid mode, the microgrid can freely exchange energy with the public grid. It is also worth adding that switching from on-grid to off-grid mode can be also equated with a power outage in the public grid.
4.3. Energy Generation and Demand Scenarios
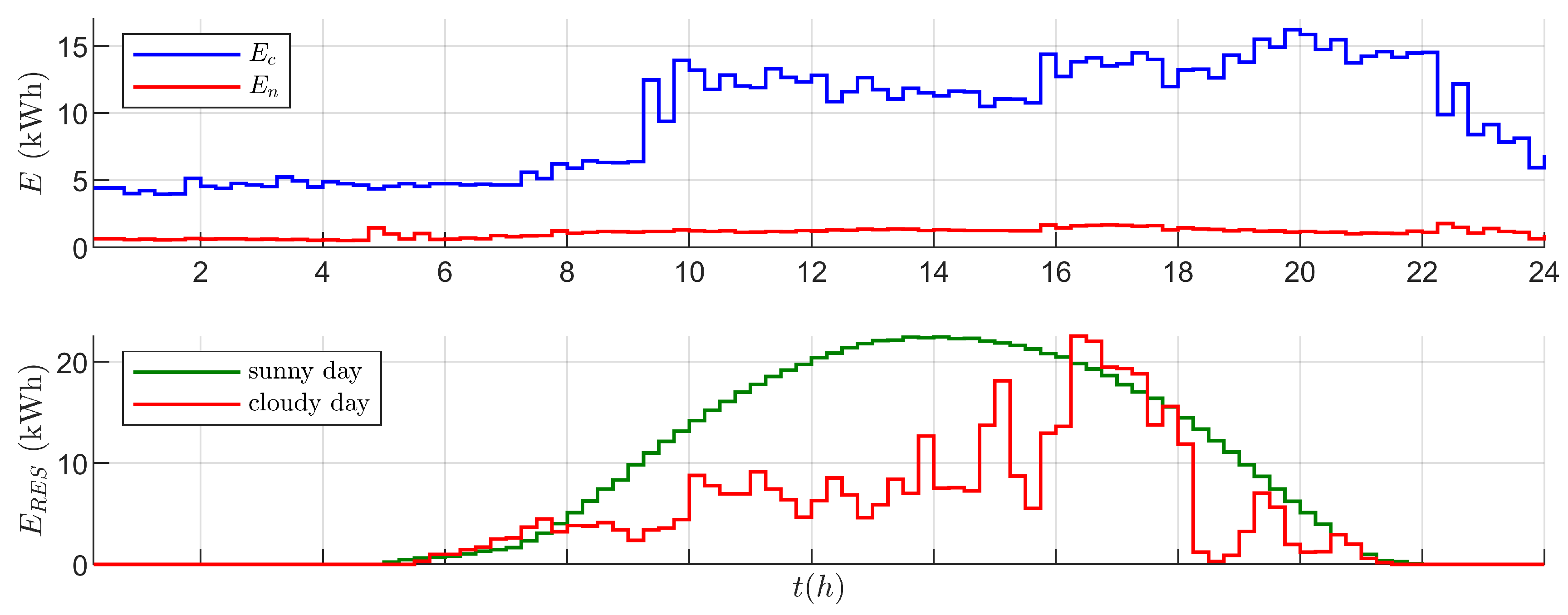
It is decided that the developed system will be tested using two solar power generation patterns, the first being a sunny day with nearly peak power and the second being a cloudy day with very changeable power output. By choosing such scenarios, the solution could be checked for economical benefits, storage level consistency, and solar energy utilisation in radically different renewable energy supply conditions. Both one-day scenarios are prepared using averaged data acquired from a solar plant located in Stargard in Poland. On the other hand, critical and non-critical demand profiles, already mentioned in the previous subsection, are prepared using end-user data sourced from [
35]. Scenarios chosen for later use in the simulation are shown in
Figure 5.
What is more, the total energy demand of controllable loads is fairly constant. However, critical demand is notably higher between the hours of 9:00 and 22:00.
4.4. Performed Tests and Their Methodology
Having all the necessary data, the authors opted for three-stage testing. Firstly, a basic comparison of switched HMPC performance during the sunny and the cloudy day is made. Naturally, to activate the control law switch, microgrid grid-connection mode changes during the simulation period. Such a simple method is chosen to assess how different generation scenarios affect performance in combined on-grid and off-grid operations.
Secondly, it was considered appropriate to compare the performance of the proposed approach against a standard, single, non-switched HMPC solution. Such conduct allows for a confrontation of switched MPC approach with non-switched one without additional factors and under the same conditions. As a result, the main part of the testing process is focused on evaluating the advantages and disadvantages of switched control applied to the specific case. It is mainly through the lens of economical performance but other factors, including technical aspects, are also analysed. Consequently, two types of tests have been performed at this stage:
comparison of both control strategies over 48-h long simulation period consisting of the sunny day followed by the cloudy day and with two connection mode switches
comparison of total operation cost for both approaches using aforementioned renewable energy supply scenario but with varying initial storage state of charge and time of connection mode switch from on-grid to off-grid .
The first routine allows for closer inspection of how individual variables change over time and how high are output values associated with economical performance. The second one is solely dedicated to total operation cost exploration in respect to a varying initial state of charge and mode-switch time. Notably, this routine consists of combined data collected from 49 individual, 48-h long, test runs. Therefore, each time, two parallel simulations were performed.
Figure 6 illustrates how the tests concerning switched and non-switched HMPC were performed in MATLAB.
Following initial conditions were used during all three stages of testing:
The value of
is constant for the first, as well as for the second test and equals 52%. For the purposes of the third routine, two sets are defined in the following way:
as well as their Cartesian product:
The set contains percentage values, and the set contains connection mode switch times . The set contains all ordered pairs from sets and .
As a result, for each of the 49 pairs test runs are performed using every combination of initial states of charge and mode change times contained in the table . It is also worth adding that in this case, only one operation mode switch happens during the simulation and the microgrid always starts in on-grid mode.
5. Results
Having hybrid microgrid model, control laws, and all the parameters, as well as data, prepared, simulations are carried over. In order to properly analyse the results, measures of performance are introduced. Summary startup and shutdown, maintenance, and energy costs, as well as income from selling energy, are used to better understand simulation results. Moreover, average and are also analysed. All those values are presented in appropriate tables. Furthermore, corresponding figures containing storage state of charge, energy balance, and all system inputs are also provided. The comments concerning the first two testing routines are made based on information derived from relevant figure-table pairs. The last routine is discussed on the basis of the appropriate figure, as well as some additional numerical data.
5.1. Comparison of Microgrid Performance in Different Renewable Energy Generation Scenarios
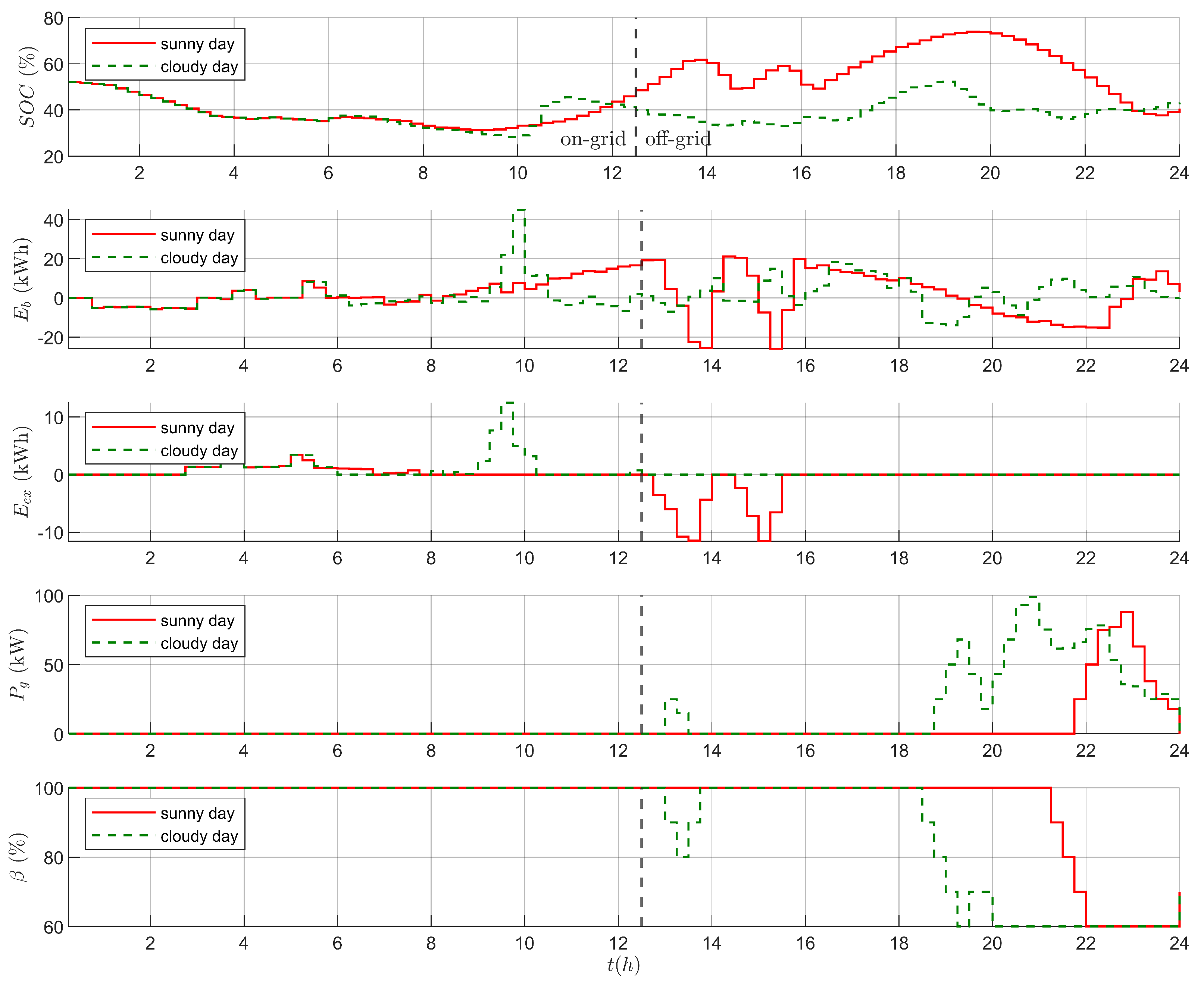
The numerical results obtained from sunny and cloudy renewable energy generation scenarios analysis are summarised in
Table 2, while
Figure 7 compares storage state of charge, energy balance, and system inputs over the simulation horizon. It is apparent from the aforementioned table that the cloudy day turned out to be significantly more costly. For instance,
,
, and
have, respectively, about 2.5, 2.5, and 2.2 times higher values for the case of the cloudy day in comparison to the case of the sunny day. Consequently, this leads to a 146% higher total operation cost. As
Figure 7 shows, such a huge difference stems from the necessity of compensating for lacking energy supply in off-grid mode, mainly after 18:00, by means of the power generator. In contrast, higher
SOC in the evening of the sunny day translates into a longer period without the need for energy generated from diesel fuel.
From the chart, it can be also seen that
SOC in on-grid mode is kept relatively low in wait for renewable energy supply but when a significant amount of energy becomes available operation mode is changed. In both scenarios, storage is charged visibly over the level specified by the reference value, but in the case of the cloudy day, this process is much less significant. That explains why the average
during the cloudy day is 18% lower. Given the limited time in on-grid mode, there is no energy being sold regardless of the scenario, hence
equals zero. Additionally, in
Figure 7 there is a clear trend of reducing controllable load energy supply only when diesel generator is needed. It can be also seen from the aforementioned figure, that more fluctuations of energy balance (
) occur in off-grid mode. Furthermore, around 14:00 during the sunny day, a significant amount of excess energy appears.
It is important to emphasize that the purpose of this test is to initially verify if chosen modeling and control approach is appropriate and combined lead to satisfactory results in one of the simpler scenarios. Summarizing, performed test exhibited that chosen switched control approach is capable of handling basic energy generation and grid-connection scenarios. It proves able to use the capacity of the storage to its advantage and to not overuse power generator although some excess energy occurred, which is not ideal.
5.2. Comparison of Microgrid Performance Using Switched and Non-Switched HMPC Control
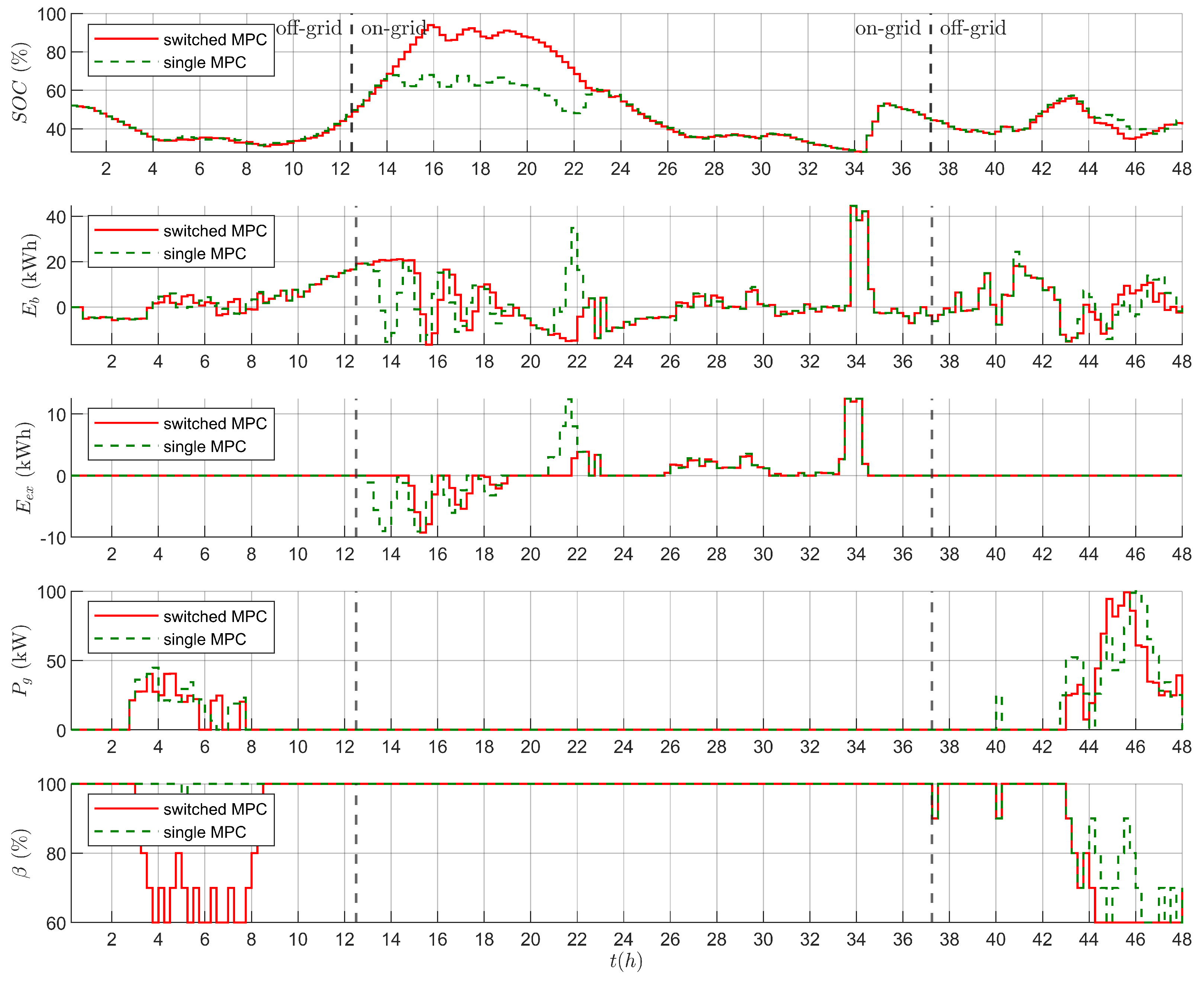
Turning now to the second test, the developed switched HMPC approach is compared with standard, single hybrid MPC. The analysis is based on a 48-h long simulation including both the sunny and cloudy days, as well as two grid-connection mode transitions. The numerical data produced as a result are gathered in
Table 3 and matching charts are presented in
Figure 8. Firstly, as
Table 3 shows,
and
are higher for the case of single hybrid MPC by about 12% and 34%, respectively. This denotes that, although
charts for both cases seem similar, single HMPC tend to use the generator to a slightly greater extent. What is more, switched HMPC tend to buy significantly less energy in the on-grid mode based on data contained in
Figure 8. Besides, there is no excess energy at all in off-grid mode, regardless of the control approach and both control laws make the grid sell a substantial amount of energy.
Interestingly enough, as presented in
Table 3, a single HMPC manages to achieve 67% greater income from energy sales compared to the competitive solution but its summary operation cost is higher by about 12%. This leads to the conclusion that overall energy exchange with the public grid is more efficient in the case of switched HMPC, especially considering identical
values and similar
values over the whole simulation period. Another point is that switched solution also provides 8% higher average state of charge (calculated as percent relative difference).
Figure 8 illustrates that both solutions exhibit similar trends in respect of
SOC, although, considering
and
, switched approach seem to provide a slightly more consistent storage energy level than the single MPC solution. This can prove important when considering the storage life cycle. Nevertheless, the single MPC provides 5% higher average
value even though it features a greater extent of load shedding penalization. Still, the share of the controllable load in overall energy demand is relatively small and it does not translate into significant gains in economical terms. Admittedly, the performed test shows that switched HMPC approach has a slight advantage over single HMPC control not just in terms of economical benefits.
5.3. Comparison of Switched and Non-Switched HMPC Control Performance in Various Connection Scenarios and with Varying Initial Storage State of Charge
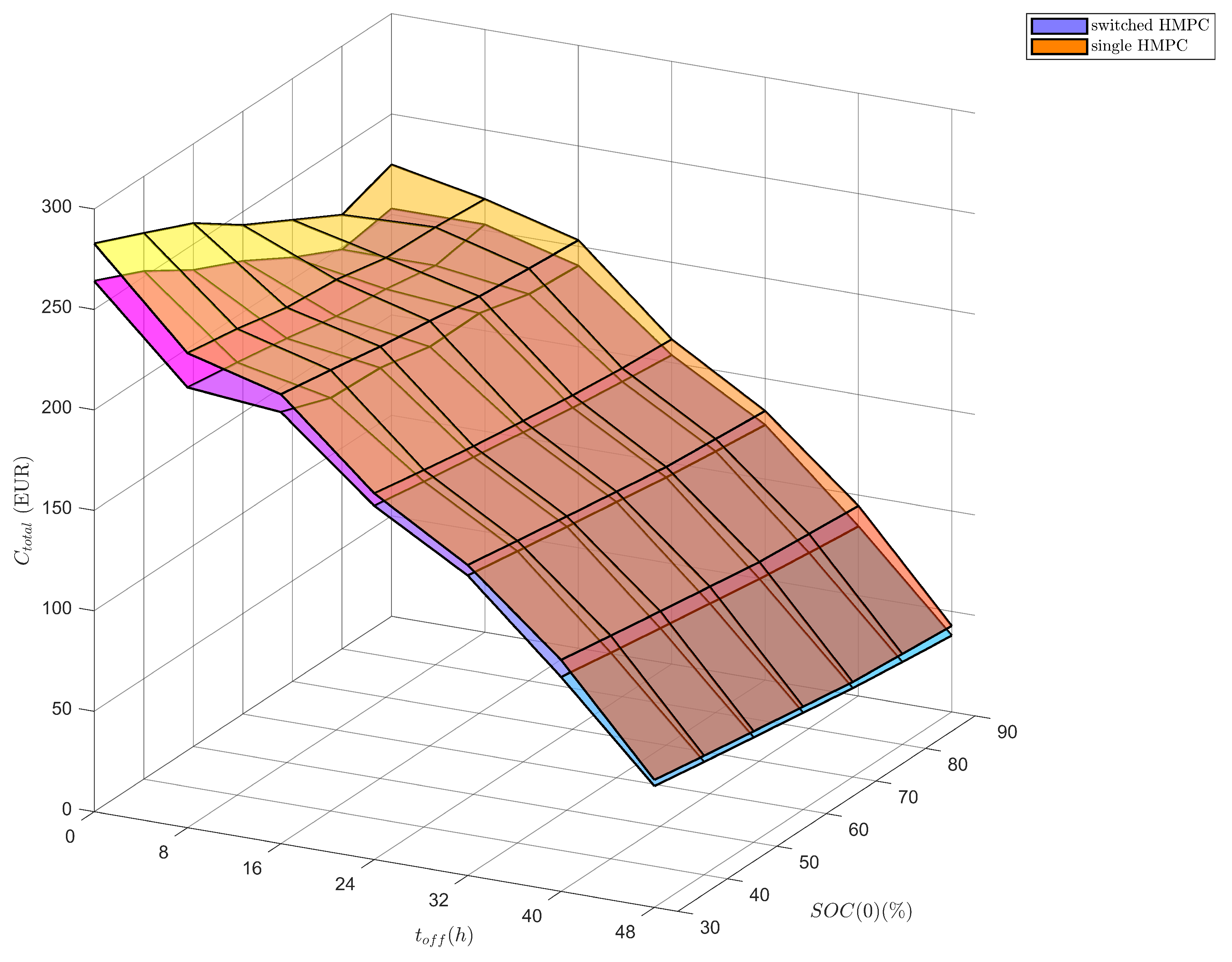
The previous test shows the advantage of switched hybrid MPC on the example of a single scenario but it falls short in proving its superiority in a wider variety of circumstances. Therefore, to somehow address obvious concerns about the adequacy of the proposed solution third testing routine is introduced. Through preliminary testing, the initial state of charge
and the time of the transition between on-grid and off-grid operation
are selected as key factors with possibly the biggest impact on simulation results. Finally, as mentioned in the previous section, 49 simulations covering various combinations of
and
are conducted, and gathered data is used to create surfaces shown in
Figure 9.
Although the third testing procedure is the most complicated one, conclusions based on the relation of both surfaces are rather simple. As it turns out, the quantity of time in different operation modes has the biggest impact on total microgrid operation cost, while the impact of the initial state of charge is rather marginal. The single most striking observation to emerge from overall cost comparison is the fact, that the cost-surfaces do not intersect and the surface related to switched hybrid MPC is located below the surface tied to the single HMPC, which in turn, proves that in all 49 cases, overall operation cost is lower when utilizing the novel solution proposed by the authors. The greater the share of off-grid operation, the more significant the gains become, which may seem obvious considering two oriented on specific mode cost functions as opposed to only one. Averaged total operation cost reduction amounts to 6.26% when using switched MPC with a maximal cost reduction of 11.23% and a minimal reduction of 3.12%, which proves the adequacy of the proposed method based on simulation data available to the authors.