Reliability Optimization of Multi-Energy System Considering Energy Storage Devices Effects under Weather Uncertainties
Abstract
:1. Introduction
1.1. MES Reliability Assessment Overview
1.2. MES Reliability Optimization Overview
1.3. Main Contributions
- The reliability assessment of multi-energy systems primarily focuses on single coupling systems, such as power–heat and power–gas systems, and assessments seldom focus on multi-energy systems that combine all three energy forms of power, heat, and natural gas;
- The established reliability modeling approach is very simplistic, ignoring component uncertainty and time-varying load in real-world situations;
- Most previous works solved the problem as a single optimization problem, with the goal of maximizing reliability or lowering cost as the sole objective, and there is still no detailed investigation of optimal storage system design for multi-energy system reliability.
- The power–heat–gas multi-energy system reliability with energy storage devices has been modeled, taking into account all the coupling components under weather uncertainties;
- The uncertainty modeling of PV and wind generation and time-varying load forecasting, including heat and gas demand, are considered. Moreover, a time varying cost model based on the sector customer damage function (SCDF) [29] is also adopted to calculate the EENS (expected energy not supplied) and the interruption cost in objective functions;
- A multi-objective reliability optimization problem is formulated considering both the system reliability index, SAIDI, and costs (including interruption cost and the installation cost of multi-energy storage devices) as objective functions. The optimization results are compared through the three widely used algorithms, i.e., the particle swarm algorithm, genetic algorithm, and evolutionary algorithm, to validate the feasibility and effectiveness of the suggested approach.
2. Overall Modeling Architecture of Multi-Energy System
2.1. Multi-Energy System Components Modeling
2.1.1. CHP Unit
2.1.2. Gas Boiler
2.1.3. P2G Device
2.1.4. Energy Storage Devices
- Electricity storage devices
- 2.
- Heat storage devices
- 3.
- Gas storage devices
2.1.5. Electric Vehicles
2.2. Uncertainty Modeling
2.2.1. Stochastic Modeling of Renewable Energy Generation
Wind Power Generation
Solar Power Generation
2.2.2. Time-Varying Load Forecasting
- Input and output vectors are determined according to the specified heat and gas load.
- Construct a BP neural network model according to the input and output vectors.
- Commence network training for the BP neural network.
- Input test samples to conduct a network test on the trained BP neural network, and judge whether the error between the predicted value and the actual value is less than the set threshold. If so, perform Step 5.
- Obtain the required load prediction according to the predicted values.
2.3. Time-Varying Load and Cost Model
3. Reliability Optimization Problem Formulation
3.1. Reliability Indicator
3.2. Economic Indicator
3.3. Objective Functions
- Objective 1: Minimize the reliability index, SAIDI.
- 2.
- Objective 2: Minimize the interruption cost and storage device investment cost.
3.4. Constraints
3.4.1. Energy Balance Constraints
3.4.2. Energy Storage Devices Constraints
3.4.3. PV and Wind Turbine Constraints
3.5. Normalization of Objective Functions
3.6. Problem Formulation
3.7. Multi-Objective Optimization Algorithms
- Step 1:
- Initialize population, generation size, the upper and lower boundary of decision variables (the placement of each particle should not exceed its energy network total buses), and simulation times.
- Step 2:
- Evaluate the objective functions using Monte Carlo simulation and store the non-dominated solutions in the repository.
- Step 3:
- Update the non-dominated solution.
- Step 4:
- Stop if the adaptive stop criterion and the maximum number of generations have been achieved; otherwise, proceed to step 2.
- Step 5:
- Obtain optimal solutions: optimal storage devices placement schemes and objective functions results.
4. Case Study
4.1. Simulation Parameters
4.2. Simulation Results
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MES | Multi-energy system |
| MCS | Monte Carlo simulation |
| NSGA-II | Non-dominated sorting genetic algorithm II |
| MOPSO | Multiple objective particle swarm optimization |
| SPEA2 | Strength Pareto evolution algorithm 2 |
| MOEA | Multi-objective evolutionary algorithm |
| CHP | Combined heat and power |
| P2G | Power to gas |
| GB | Gas boiler |
| PG | Power grid |
| HN | Heat network |
| GN | Gas network |
| CCHP | Combined cooling, heat, and power |
| V2G | Vehicle to grid |
| FMEA | Failure mode and effect analysis |
| ES | Electricity storage |
| HS | Heat storage |
| GS | Gas storage |
| TVCM | Time-varying cost model |
| CDF | Customer damage function |
| SAIFI | System average interruption frequency index |
| SAIDI | System average interruption duration index |
| CAIDI | Customer average interruption duration index |
| ASAI | Average service availability index |
| EENS | Expected energy not supplied |
| TTF | Time to failure |
| TTR | Time to repair |
| TTS | Time to switch |
Appendix A
| Load Points | Average Load Level (MW) | Customer Type | Number of Customers |
|---|---|---|---|
| 1 | 97.6 | 7 | 200 |
| 3 | 322 | 7 | 322 |
| 4 | 500 | 4 | 500 |
| 7 | 233.8 | 5 | 200 |
| 8 | 522 | 6 | 500 |
| 9 | 6.5 | 7 | 132 |
| 12 | 8.53 | 3 | 23 |
| 15 | 320 | 4 | 320 |
| 16 | 329 | 6 | 330 |
| 18 | 158 | 3 | 160 |
| 20 | 680 | 2 | 680 |
| 21 | 274 | 6 | 270 |
| 23 | 247.5 | 7 | 240 |
| 24 | 308.6 | 7 | 300 |
| 25 | 224 | 7 | 220 |
| 26 | 139 | 7 | 140 |
| 27 | 281 | 7 | 280 |
| 28 | 206 | 7 | 200 |
| 29 | 283.5 | 7 | 280 |
| 31 | 9.2 | 1 | 60 |
| 39 | 522 | 6 | 1000 |
| Load Points | Average Load Level (MW) | Customer Type | Number of Customers |
|---|---|---|---|
| 3 | 0.107 | 1 | 110 |
| 4 | 0.145 | 3 | 150 |
| 6 | 0.107 | 4 | 110 |
| 7 | 0.107 | 5 | 110 |
| 8 | 0.107 | 6 | 110 |
| 9 | 0.107 | 3 | 110 |
| 10 | 0.107 | 1 | 110 |
| 11 | 0.145 | 6 | 150 |
| 12 | 0.107 | 7 | 110 |
| 14 | 0.0805 | 7 | 80 |
| 16 | 0.0805 | 7 | 80 |
| 17 | 0.0805 | 7 | 80 |
| 18 | 0.0805 | 7 | 80 |
| 20 | 0.0805 | 7 | 80 |
| 21 | 0.0805 | 7 | 80 |
| 23 | 0.107 | 2 | 110 |
| 24 | 0.107 | 4 | 110 |
| 26 | 0.107 | 6 | 110 |
| 27 | 0.107 | 7 | 110 |
| 29 | 0.107 | 3 | 110 |
| 30 | 0.107 | 7 | 110 |
| Load Points | Average Load Level (Mm3/day) | Customer Type | Number of Customers |
|---|---|---|---|
| 3 | 5.88 | 1 | 60 |
| 6 | 6.05 | 5 | 61 |
| 7 | 7.88 | 3 | 80 |
| 10 | 9.55 | 4 | 100 |
| 12 | 0.775 | 7 | 80 |
| 15 | 10.27 | 2 | 105 |
| 16 | 23.42 | 6 | 240 |
| 19 | 0.33 | 7 | 30 |
| 20 | 0.775 | 7 | 80 |
References
- Kueck, J.D. Measurement Practices for Reliability and Power Quality; Oak Ridge Nat. Lab. (ORNL): Oak Ridge, TN, USA, 2005.
- Zhang, S.; Wen, M.; Cheng, H.; Hu, X.; Xu, G. Reliability evaluation of electricity-heat integrated energy system with heat pump. CSEE J. Power Energy Syst. 2018, 4, 425–433. [Google Scholar] [CrossRef]
- Billinton, R.; Jonnavithula, S. A test system for teaching overall power system reliability assessment. IEEE Trans. Power Syst. 1996, 11, 1670–1676. [Google Scholar] [CrossRef] [Green Version]
- He, J.; Yuan, Z.; Yang, X.; Huang, W.; Tu, Y.; Li, Y. Reliability modeling and evaluation of urban multi-energy systems: A review of the state of the art and future challenges. IEEE Access 2020, 8, 98887–98909. [Google Scholar] [CrossRef]
- Wang, J.; Fu, C.; Yang, K. Reliability and availability analysis of redundant BCHP (building cooling, heating and power) system. Energy 2013, 61, 531–540. [Google Scholar] [CrossRef]
- Munoz, J.; Jimenez-Redondo, N.; Perez-Ruiz, J.; Barquin, J. Natural gas network modeling for power systems reliability studies. In Proceedings of the IEEE Bologna Power Tech Conference, Bologna, Italy, 23–26 June 2003; Volume 4, p. 8. [Google Scholar]
- Chaudry, M.; Wu, J.; Jenkins, N. A sequential Monte Carlo model of the combined GB gas and electricity network. Energy Policy 2013, 62, 473–483. [Google Scholar] [CrossRef]
- Gargari, Z.; Ghaffarpour, R. Reliability evaluation of multi-carrier energy system with different level of demands under various weather situation. Energy 2020, 196, 117091. [Google Scholar] [CrossRef]
- Meng, Z.; Wang, S.; Zhao, Q.; Zheng, Z.; Feng, L. Reliability evaluation of electricity-gas-heat multi-energy consumption based on user experience. Int. J. Electr. Power Energy Syst. 2021, 130, 106926. [Google Scholar] [CrossRef]
- Koeppel, G.; Andersson, G. Reliability modeling of multi-carrier energy systems. Energy 2009, 34, 235–244. [Google Scholar] [CrossRef]
- Ge, S.; Li, J.; Liu, H.; Wang, Y.; Sun, H.; Lu, Z. Reliability evaluation of microgrid containing energy storage system considering multi-energy coupling and grade difference. Autom. Electr. Power Syst. 2018, 42, 165–173. [Google Scholar]
- Ge, S.; Sun, H.; Liu, H.; Li, J.; Zhang, X.; Cao, Y. Reliability evaluation of multi-energy microgrids: Energy storage devices effects analysis. Energy Procedia 2019, 158, 4453–4458. [Google Scholar] [CrossRef]
- Ammous, M.; Khater, M.; AlMuhaini, M. Impact of vehicle-to-grid technology on the reliability of distribution systems. In Proceedings of the 9th IEEE-GCC Conference and Exhibition, Manama, Bahrain, 8–11 May 2017; pp. 1–6. [Google Scholar]
- Bakkiyaraj, R.A.; Kumarappan, N. Optimal reliability planning for a composite electric power system based on Monte Carlo simulation using particle swarm optimization. Int. J. Electr. Power Energy Syst. 2013, 47, 109–116. [Google Scholar] [CrossRef]
- Barakat, S.; Ibrahim, H.; Elbaset, A.A. Multi-objective optimization of grid-connected PV-wind hybrid system considering reliability, cost, and environmental aspects. Sustain. Cities Soc. 2020, 60, 102178. [Google Scholar] [CrossRef]
- Peruzzi, L.; Salata, F.; de Lieto Vollaro, A.; de Lieto Vollaro, R. The reliability of technological systems with high energy efficiency in residential buildings. Energy Build. 2014, 68, 19–24. [Google Scholar] [CrossRef]
- Kanase-Patil, A.B.; Saini, R.P.; Sharma, M.P. Sizing of integrated renewable energy system based on load profiles and reliability index for the state of Uttarakhand in India. Renew. Energy 2011, 36, 2809–2821. [Google Scholar] [CrossRef]
- Arnold, M. On Predictive Control for Coordination in Multi-Carrier Energy Systems. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2011. [Google Scholar]
- Raychaudhuri, S. Introduction to Monte Carlo simulation. In Proceedings of the Winter Simulation Conference, Miami, FL, USA, 7–10 December 2008; pp. 91–100. [Google Scholar]
- Billinton, R.; Li, W. A system state transition sampling method for composite system reliability evaluation. IEEE Trans. Power Syst. 1993, 8, 761–770. [Google Scholar] [CrossRef]
- Chicco, G.; Mazza, A. Metaheuristic optimization of power and energy systems: Underlying principles and main issues of the rush to heuristic. Energies 2020, 13, 5097. [Google Scholar] [CrossRef]
- Lee, K.Y.; El-Sharkawi, M.A. Modern Heuristic Optimization Techniques: Theory and Applications to Power Systems; John Wiley & Sons: Hoboken, NJ, USA, 2008; Volume 39. [Google Scholar]
- Lee, K.Y.; Vale, Z.A. Applications of Modern Heuristic Optimization Methods in Power and Energy Systems; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Chicco, G.; Mazza, A. Heuristic optimization of electrical energy systems: Refined metrics to compare the solutions. Sustain. Energy Grids Netw. 2019, 17, 100197. [Google Scholar] [CrossRef] [Green Version]
- Oteiza, P.P.; Rodríguez, D.A.; Brignole, N.B. Parallel cooperative optimization through hyperheuristics. Comput. Aided Chem. Eng. 2018, 44, 805–810. [Google Scholar]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Leiden, The Netherlands, 5–9 September 2000; pp. 849–858. [Google Scholar]
- Kunkle, D. A Summary and Comparison of Moea Algorithms. Internal Report. 2005. Available online: https://www.ccs.neu.edu/home/kunkle/papers/techreports/moeaComparison.pdf (accessed on 5 January 2022).
- Coello, C.A.C.; Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Wang, P.; Billinton, R. Time sequential distribution system reliability worth analysis considering time varying load and cost models. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar]
- Li, Y.; Zhang, F.; Li, Y.; Wang, Y. An improved two-stage robust optimization model for CCHP-P2G microgrid system considering multi-energy operation under wind power outputs uncertainties. Energy 2021, 223, 120048. [Google Scholar] [CrossRef]
- Shi, N.; Luo, Y. Energy storage system sizing based on a reliability assessment of power systems integrated with wind power. Sustainability 2017, 9, 395. [Google Scholar] [CrossRef] [Green Version]
- Ogunmodede, O.; Anderson, K.; Cutler, D.; Newman, A. Optimizing design and dispatch of a renewable energy system. Appl. Energy 2021, 287, 116527. [Google Scholar] [CrossRef]
- Prajapati, V.K.; Mahajan, V. Reliability assessment and congestion management of power system with energy storage system and uncertain renewable resources. Energy 2021, 215, 119134. [Google Scholar] [CrossRef]
- Wu, G.; Zu, G.; Zheng, J. A method for forecasting alpine area load based on artificial neural network model. J. Phys. Conf. Ser. 2021, 1994, 12019. [Google Scholar] [CrossRef]
- Borges, C.E.; Penya, Y.K.; Fernandez, I. Evaluating combined load forecasting in large power systems and smart grids. IEEE Trans. Ind. Info. 2013, 9, 1570–1577. [Google Scholar] [CrossRef]
- Monnerie, N.; Houaijia, A.; Roeb, M.; Sattler, C. Methane production via high temperature steam electrolyser from renewable wind energy: A german study. Green Sustain. Chem. 2015, 5, 70–80. [Google Scholar] [CrossRef] [Green Version]
- Niu, D.; Shi, H.; Li, J.; Wei, Y. Research on short-term power load time series forecasting model based on BP neural network. In Proceedings of the 2nd International Conference on Advanced Computer Control, Shenyang, China, 27–29 March 2010; Volume 4, pp. 509–512. [Google Scholar]
- Dzobo, O.; Awodele, K.O. Probabilistic Power System Reliability Assessment: Distributed Renewable Energy Sources. In Novel Advancements in Electrical Power Planning and Performance; IGI Global: Hershey, PA, USA, 2020; pp. 94–117. [Google Scholar]
- Tur, M.R. Reliability assessment of distribution power system when considering energy storage configuration technique. IEEE Access 2020, 8, 77962–77971. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, G.; Yan, C.; Wang, G.; Jiang, Y.; Zhao, K. A two-stage multi-objective optimization method for envelope and energy generation systems of primary and secondary school teaching buildings in China. Build. Environ. 2021, 204, 108142. [Google Scholar] [CrossRef]
- Grodzevich, O.; Romanko, O. Normalization and other topics in multi-objective optimization. In Proceedings of the Fields–MITACS Industrial Problems Workshop, Toronto, ON, Canada, 14–18 August 2006; Available online: http://miis.maths.ox.ac.uk/miis/233/1/fmipw1-6.pdf (accessed on 5 January 2022).
- Verma, S.; Pant, M.; Snasel, V. A Comprehensive review on NSGA-II for multi-objective combinatorial optimization problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multi objective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef] [Green Version]
- Tian, Y.; Wang, H.; Zhang, X.; Jin, Y. Effectiveness and efficiency of non-dominated sorting for evolutionary multi-and many-objective optimization. Complex Intell. Syst. 2017, 3, 247–263. [Google Scholar] [CrossRef]
- Real Time Power System Simulation I RTDS Technologies. Available online: http://www.rtds.com/indexlindex.Html (accessed on 5 January 2022).
- Liu, X.; Wu, J.; Jenkins, N.; Bagdanavicius, A. Combined analysis of electricity and heat networks. Appl. Energy 2016, 162, 1238–1250. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Zhao, T.; Wang, P.; Yao, S. Power system resilience assessment considering of integrated natural gas system. In Proceedings of the IET International Conference on Resilience of Transmission and Distribution Networks, Birmingham, UK, 26–28 September 2017; pp. 1–7. [Google Scholar]
- Jain, A.; Lalwani, S.; Lalwani, M. A comparative analysis of MOPSO, NSGA-II, SPEA2 and PESA2 for multi-objective optimal power flow. In Proceedings of the 2nd International Conference on Power, Energy and Environment: Towards Smart Technology (ICEPE), Shillong, India, 1–2 June 2018; pp. 1–6. [Google Scholar]
- Yu, X.; Lu, Y.; Yu, X. Evaluating multi-objective evolutionary algorithms using MCDM methods. Math. Probl. Eng. 2018, 2018, 9751783. [Google Scholar] [CrossRef] [Green Version]
- Mishra, S.K.; Panda, G.; Meher, S. Multi-objective particle swarm optimization approach to portfolio optimization. In Proceedings of the World Congress on Nature & Biologically Inspired Computing (NaBIC) Conference, Coimbatore, India, 9–11 December 2009; pp. 1612–1615. [Google Scholar]
- Keshavarz, M.; Pasandideh, S.H.R. Multi-objective optimisation of continuous review inventory system under mixture of lost sales and backorders within different constraints. Int. J. Logist. Syst. Manag. 2018, 29, 327–348. [Google Scholar]

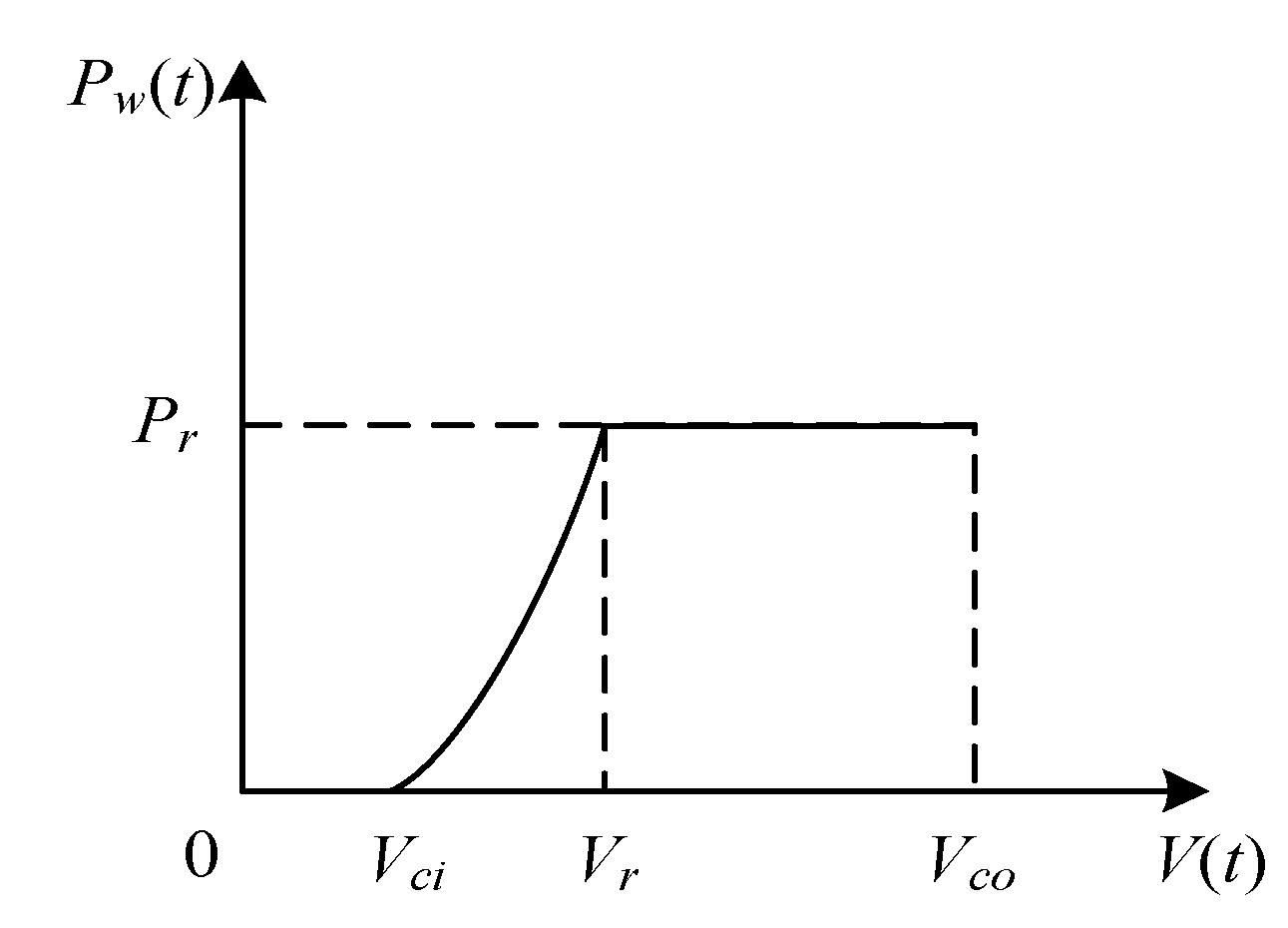
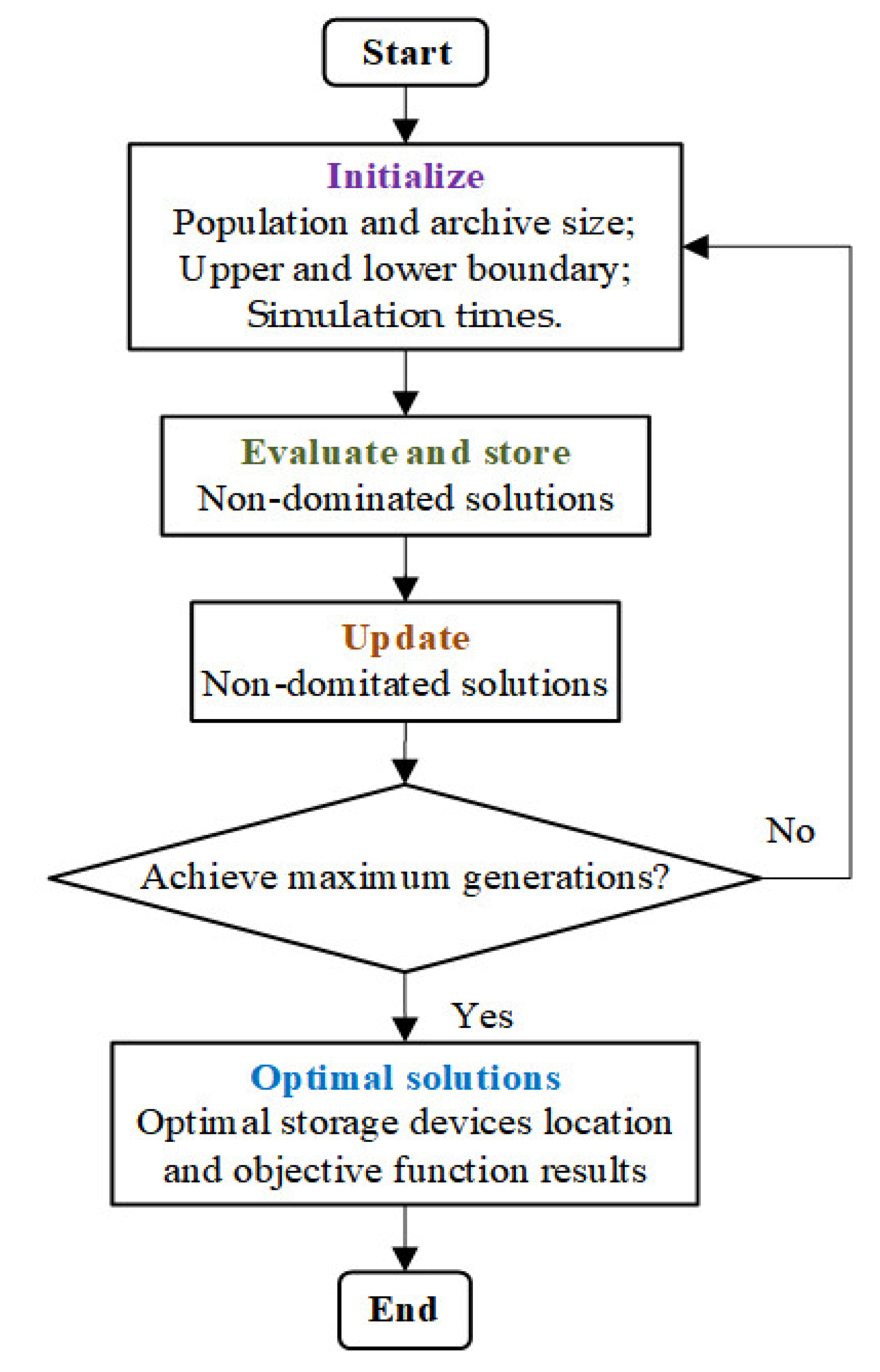
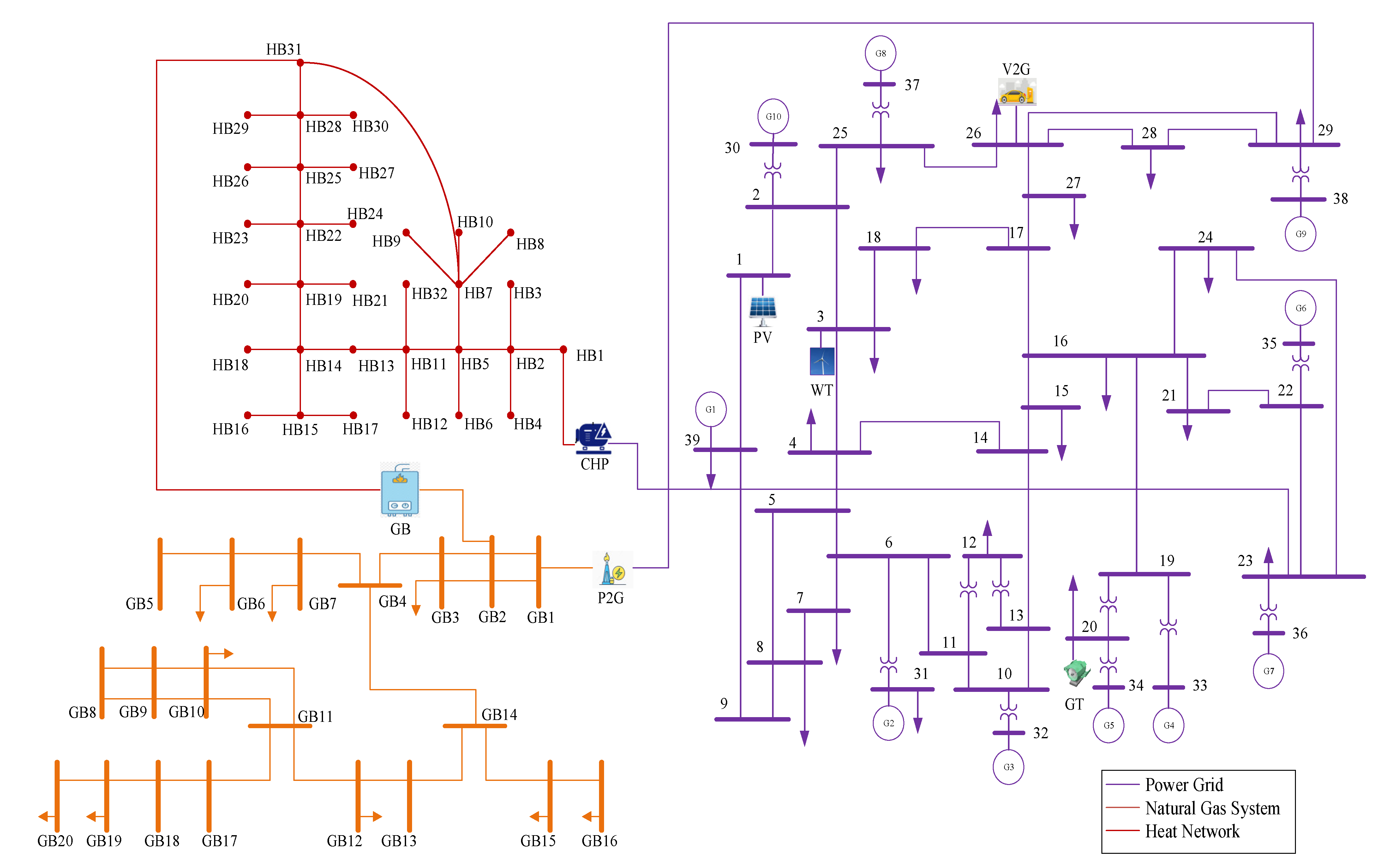

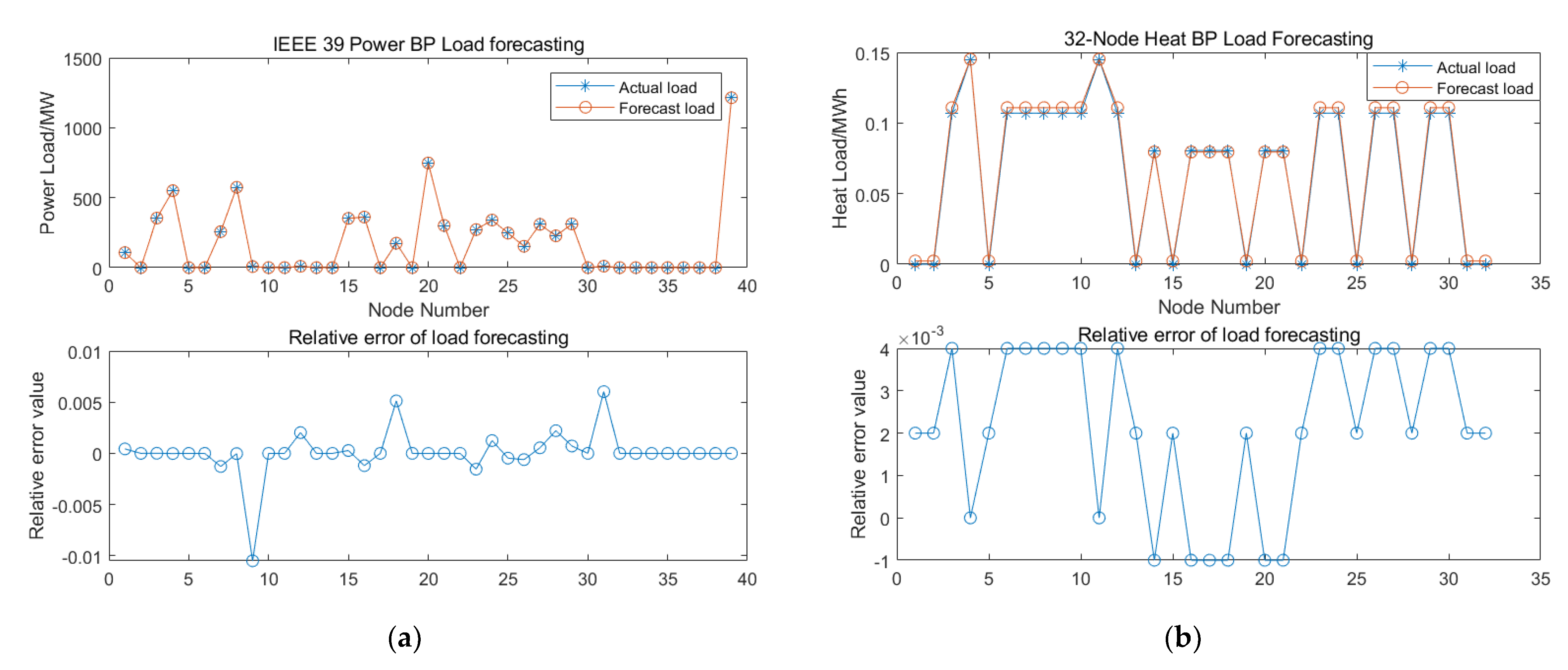

| Weibull Distribution Parameters | k | c (m/s) | Vci (m/s) | Vr (m/s) | Vco (m/s) | Pr (MW) |
|---|---|---|---|---|---|---|
| Value | 1.5 | 5 | 3 | 13 | 25 | 1000 |
| Beta Distribution Parameters | α | β | A(m2) | rmax (MW/m2) | η | baseMVA |
|---|---|---|---|---|---|---|
| Value | 0.6869 | 2.132 | 70 | 100 | 0.14 | 100 |
| BP Neural Network | Parameters Setting |
|---|---|
| Number of network layers | Input layer: 1; Hidden layer: 1; Output layer: 1 |
| Number of neurons in each layer | Input layer: 4; Hidden layer: 9; Output layer: 1 |
| Maximum number of iterations | 5000 |
| Training target error | 0.2 |
| Initial value of training learning rate | 0.1 |
| Component | Cinstalli | Capacity for MES |
|---|---|---|
| ES | 187 USD/MWh | 600 MWh |
| HS | 6.05 USD/MWh | 0.5 MWh |
| GS | 3.665 USD/MMBtu | 10 Mm3 |
| Component | Capacity (MW) |
|---|---|
| PV | 100 |
| WT | 500 |
| GT | 120 |
| MOPSO | NSGA-II | SPEA2 |
|---|---|---|
| Population size = 100 | Population size = 50 | Population size = 50 |
| Generations = 200 | Generations = 200 | Generations = 200 |
| Repository size =100 | Archive size = 50 | Archive size = 50 |
| = 1.8 | Crossover rate = 0.7 | Crossover rate = 0.7 |
| = 2 | Mutation rate = 0.01 | Mutation rate = 0.01 |
| w = 0.7 | ||
| = 0.9 |
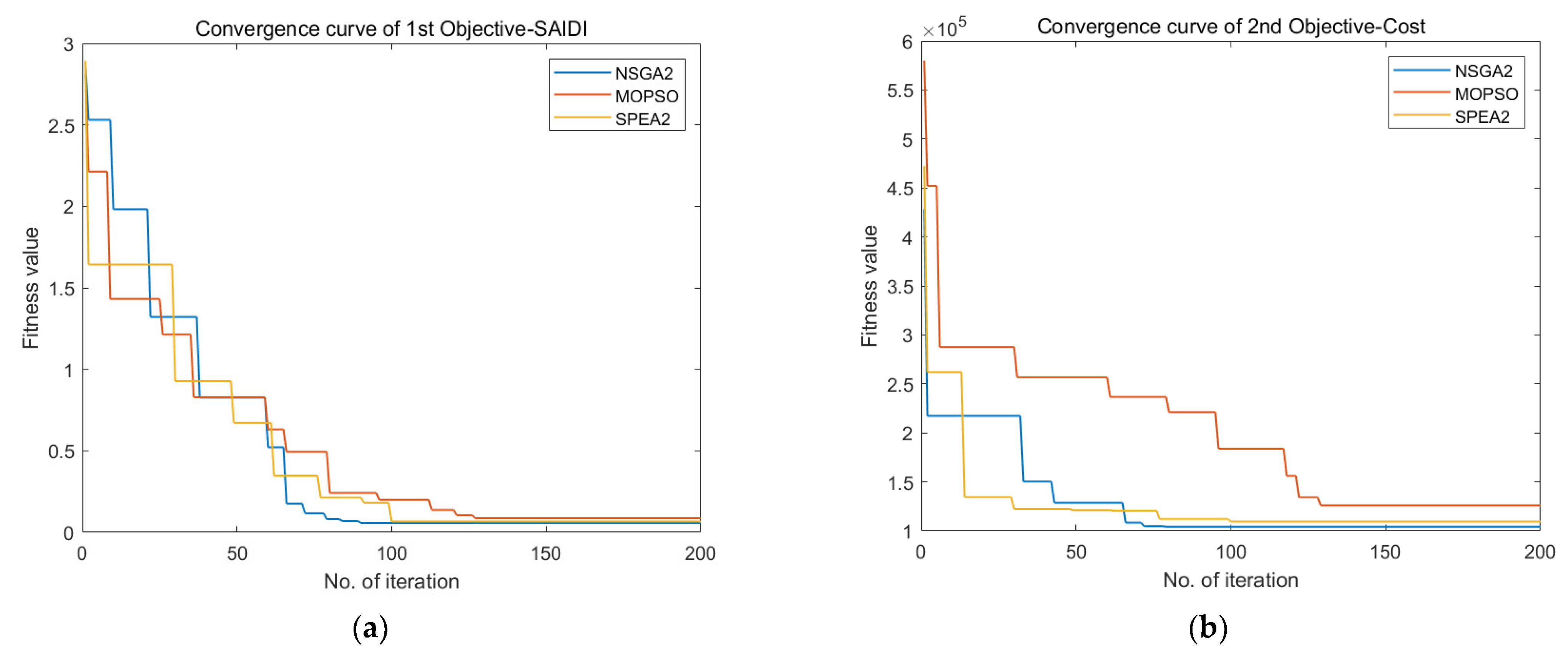
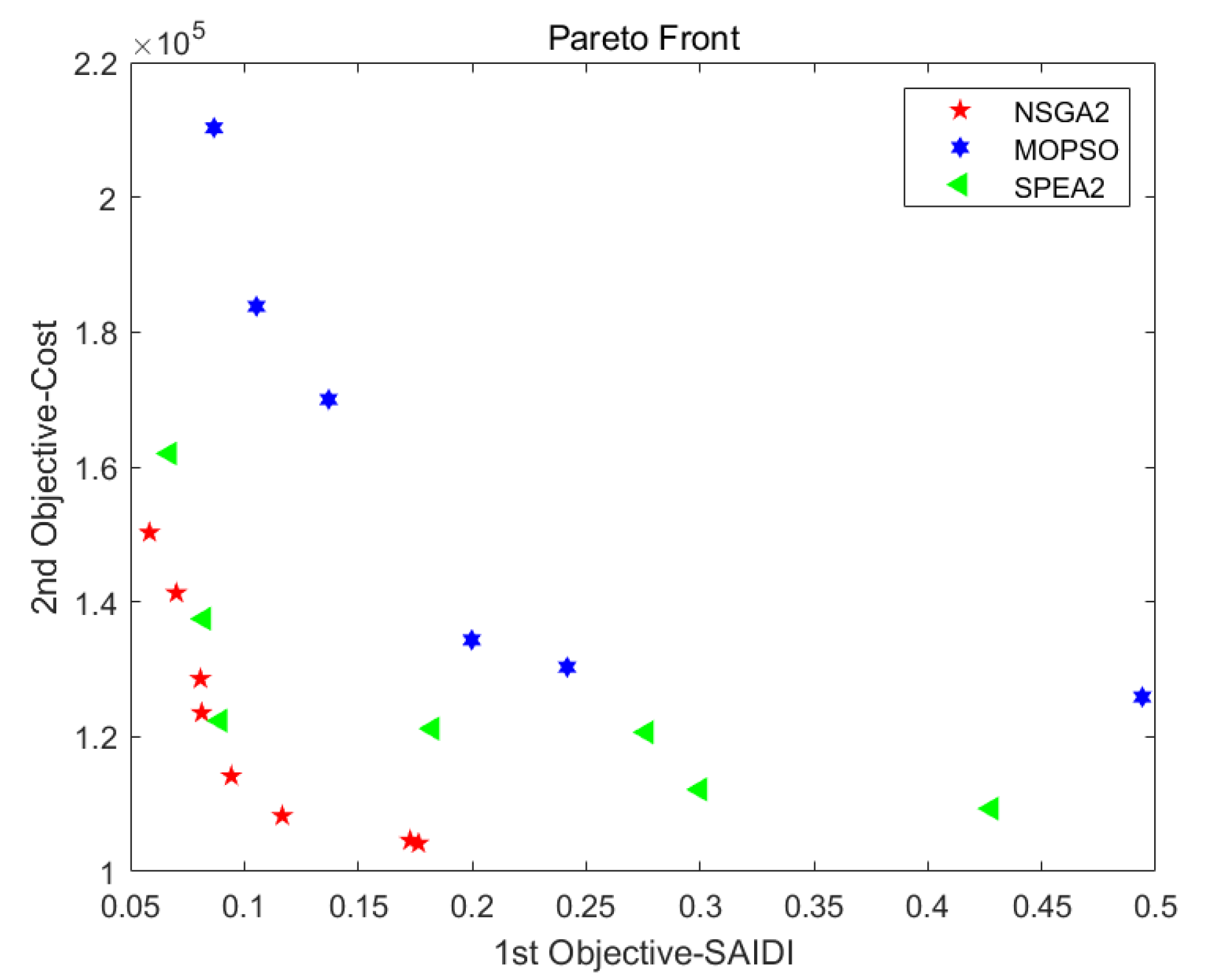
| NSGA-II | Storage Device Optimal Location | Obj1–SAIDI (h/Ca) | Obj2–Cost (USD 1000) | ||
|---|---|---|---|---|---|
| Power Grid | Heat Network | Gas Network | |||
| 1 | Bus 1, 3, 6, 7, 12, 13, 15, 18, 19, 20, 21, 22, 25, 28, 29, 30, 31, 32, 35, 37, 39 | Bus 1, 2, 4, 5, 14, 15 | Bus 1, 2, 3, 5, 6, 7, 9, 10, 12, 13 | 0.0585 | 1.5028 × 105 |
| 2 | Bus 1, 3, 4, 6, 7, 12, 13, 16, 18, 19, 20, 21, 22, 25, 28, 29, 30, 31, 32, 35, 37, 39 | Bus 1, 2, 4, 9, 12, 15 | Bus 2, 3, 5, 6, 7, 9, 10, 11, 12, 13, 15, 16, 19 | 0.0702 | 1.4132 × 105 |
| 3 | Bus 1, 3, 4, 6, 7, 12, 13, 16, 18, 20, 21, 22, 25, 28, 29, 30, 31, 32, 35, 37, 39 | Bus 1, 3, 8, 14, 21 | Bus 2, 3, 5, 6, 7, 9, 10, 11, 12, 13, 15, 16, 19 | 0.0808 | 1.2859 × 105 |
| 4 | Bus 1, 2, 3, 4, 5, 6, 7, 12, 13, 16, 18, 19, 20, 21, 22, 24, 25, 28, 29, 30, 31, 32, 35, 37, 39 | Bus 3, 11, 12, 13, 14, 17, 18, 21, 22, 23, 24 | Bus 2, 3, 5, 6, 7, 9, 10, 11, 12, 13, 15, 16, 19 | 0.0814 | 1.2354 × 105 |
| 5 | Bus 1, 3, 4, 5, 6, 7, 12, 13, 18, 19, 20 21, 22, 25, 28, 29, 30, 31, 32, 35, 37, 39 | Bus 2, 3, 4, 5, 6, 10, 11, 20 | Bus 2, 3, 5, 6, 7, 9, 10, 11, 12, 13, 15, 16, 19 | 0.0944 | 1.1417 × 105 |
| 6 | Bus 1, 2, 3, 4, 5, 6, 7, 12, 13, 14, 16, 18, 20 21, 22, 25, 28, 29, 30, 31, 32, 34, 37, 39 | Bus 2, 3, 4, 5, 6, 10, 11, 20 | Bus 2, 3, 5, 6, 7, 9, 10, 11, 12, 13, 16, 19 | 0.1167 | 1.0826 × 105 |
| 7 | Bus 1, 2, 4, 6, 7, 12, 13, 16, 18, 19, 20, 21, 22, 25, 28, 29, 30, 31, 32, 34, 37, 39 | Bus 4 | Bus 2, 3, 5, 6, 7, 9, 10, 11, 12, 13, 15, 16, 19 | 0.1728 | 1.0461 × 105 |
| 8 | Bus 1, 4, 5, 6, 7, 11, 12, 13, 16, 18, 19, 20, 22, 25, 28, 29, 30, 31, 32, 35, 37, 39 | Bus 5 | Bus 2, 3, 5, 6, 7, 9, 10, 11, 12, 13, 15, 16, 19 | 0.1765 | 1.0419 × 105 |
| MOPSO | Storage Device Optimal Location | Obj1–SAIDI (h/Ca) | Obj2–Cost (USD 1000) | ||
|---|---|---|---|---|---|
| Power Grid | Heat Network | Gas Network | |||
| 1 | Bus 1, 4, 5, 7, 11, 12, 14, 16, 17, 18, 19, 20, 23, 24, 25, 29, 30, 31, 34, 35, 37, 38 | Bus 2, 5, 7, 8, 9, 10, 12, 16, 17, 18, 20, 22, 23, 24, 25, 27, 28, 30, 31 | Bus 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 14, 15, 18, 19 | 0.0867 | 2.1029 × 105 |
| 2 | Bus 2, 3, 4, 7, 8, 11, 16, 17, 18, 22, 23, 24, 25, 26, 27, 28, 31, 38, 39 | Bus 1, 2, 3, 4, 6, 7, 10, 12, 13, 14, 15, 16, 20, 21, 22, 23, 24, 26, 31 | Bus 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 14 | 0.1054 | 1.8381 × 105 |
| 3 | Bus 1, 3, 5, 6, 8, 10, 11, 13, 14, 15, 16, 17, 19, 20, 21, 22, 26, 27, 28, 30, 31, 33, 36, 39 | Bus 1, 2, 3, 4, 6, 8, 10, 11, 13, 14, 15, 16, 18, 20, 22, 23, 24, 25, 26, 27, 29, 30, 32 | Bus 1, 2, 4, 6, 7, 8, 10, 12, 13, 16, 18 | 0.1371 | 1.7001 × 105 |
| 4 | Bus 1, 2, 3, 4, 5, 6, 9, 16, 17, 19, 20, 22, 27, 28, 29, 30, 35, 36 | Bus 2, 3, 4, 5, 7, 9, 12, 13, 15, 16, 17, 18, 20, 23, 25, 26 | Bus 1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 13, 15 | 0.1999 | 1.3435 × 105 |
| 5 | Bus 3, 4, 5, 7, 8, 9, 14, 19, 22, 30, 31 | Bus 1, 2, 3, 4, 7, 8, 9, 12, 14, 19, 20, 29 | Bus 3, 4, 6, 7, 9, 10, 15 | 0.2417 | 1.3032 × 105 |
| 6 | Bus 1, 2, 4, 8, 10, 11, 12, 13, 14, 16, 17, 19, 26, 27, 28, 35 | Bus 3, 4, 5, 6, 8, 9, 11, 13, 14, 16, 17, 18, 23, 24, 25, 29 | Bus 2, 3, 4, 6, 7, 8, 10, 11, 12, 15, 19 | 0.4941 | 1.2588 × 105 |
| SPEA2 | Storage Device Optimal Location | Obj1–SAIDI (h/Ca) | Obj2–Cost (USD 1000) | ||
|---|---|---|---|---|---|
| Power Grid | Heat Network | Gas Network | |||
| 1 | Bus 1, 3, 4, 5, 6, 8, 9, 11, 14, 16, 17, 19, 22, 24, 28, 29, 31, 34 | Bus 1, 2, 3, 5, 6, 7, 9, 10, 11, 12, 14, 15, 16, 20, 21, 23, 25, 26 | Bus 1, 2, 3, 4, 5, 6, 7, 8, 10, 11, 12, 14, 15, 19 | 0.0673 | 1.6200 × 105 |
| 2 | Bus 2, 3, 4, 5, 6, 8, 9, 11, 14, 16, 17, 19, 22, 24, 28, 29, 31, 34 | Bus 1, 2, 3, 5, 6, 7, 9, 10, 11, 13, 14, 15, 16, 20, 21, 23, 25, 26 | Bus 1, 3, 4, 5, 6, 7, 8, 10, 11, 12, 14, 15, 19 | 0.0823 | 1.3749 × 105 |
| 3 | Bus 2, 3, 4, 5, 6, 8, 9, 10, 11, 14, 17, 19, 25, 28, 30, 36, 38 | Bus 1, 2, 3, 4, 5, 7, 8, 12, 13, 14, 15, 16, 18, 20, 29 | Bus 1, 3, 4, 5, 6, 7, 9, 10, 12, 14, 15, 16 | 0.0895 | 1.2237 × 105 |
| 4 | Bus 1, 3, 6, 7, 9, 10, 12, 14, 17, 18, 23, 24, 28, 32 | Bus 1, 2, 3, 5, 6, 10, 12, 15, 18, 21, 22, 24 | Bus 1, 3, 4, 5, 6, 7, 10, 11, 12, 18, 19 | 0.1825 | 1.2120 × 105 |
| 5 | Bus 1, 2, 3, 4, 5, 7, 9, 10, 11, 13, 15, 18, 22, 29, 30 | Bus 1, 2, 3, 4, 6, 7, 10, 16, 17, 20, 26, 28 | Bus 2, 3, 4, 5, 6, 7, 10, 13, 14, 18 | 0.2766 | 1.2066 × 105 |
| 6 | Bus 1, 2, 4, 5, 6, 7, 8, 9, 10, 14, 16, 17, 21, 25, 32, 33, 37, 39 | Bus 2, 3, 4, 5, 7, 8, 9, 13, 17, 22, 29 | Bus 3, 6, 7, 8, 9, 10, 11, 12, 15, 17, 24, 30 | 0.3000 | 1.1218 × 105 |
| 7 | Bus 1, 3, 4, 7, 8, 9, 10, 11, 12, 14, 18, 19, 24, 26, 28, 30, 33, 36, 39 | Bus 1, 4, 6, 8, 9, 11, 13, 15, 16, 18, 21, 23, 26, 27 | Bus 1, 3, 4, 5, 6, 7, 8, 10, 11, 12, 18, 20 | 0.4280 | 1.0934 × 105 |
| Optimization Algorithm | Execution Time (min) |
|---|---|
| NSGA-II | 288.67 |
| MOPSO | 876.92 |
| SPEA2 | 283.34 |
| Reliability Indices | Before Optimization | After Optimization |
|---|---|---|
| SAIFI (1/Ca) | 0.1980 | 0.2641 |
| SAIDI (h/Ca) | 1.4945 | 0.0585 |
| CAIDI (h/Ca) | 7.5480 | 0.0600 |
| ASAI | 0.9998 | 0.9999 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, Z.; Parisio, A. Reliability Optimization of Multi-Energy System Considering Energy Storage Devices Effects under Weather Uncertainties. Energies 2022, 15, 696. https://doi.org/10.3390/en15030696
Liao Z, Parisio A. Reliability Optimization of Multi-Energy System Considering Energy Storage Devices Effects under Weather Uncertainties. Energies. 2022; 15(3):696. https://doi.org/10.3390/en15030696
Chicago/Turabian StyleLiao, Ziyan, and Alessandra Parisio. 2022. "Reliability Optimization of Multi-Energy System Considering Energy Storage Devices Effects under Weather Uncertainties" Energies 15, no. 3: 696. https://doi.org/10.3390/en15030696
APA StyleLiao, Z., & Parisio, A. (2022). Reliability Optimization of Multi-Energy System Considering Energy Storage Devices Effects under Weather Uncertainties. Energies, 15(3), 696. https://doi.org/10.3390/en15030696






