Optimization of the Adsorption/Desorption Contribution from Metal-Organic-Heat-Carrier Nanoparticles in Waste Heat Recovery Applications: R245fa/MIL101 in Organic Rankine Cycles
Abstract
1. Introduction
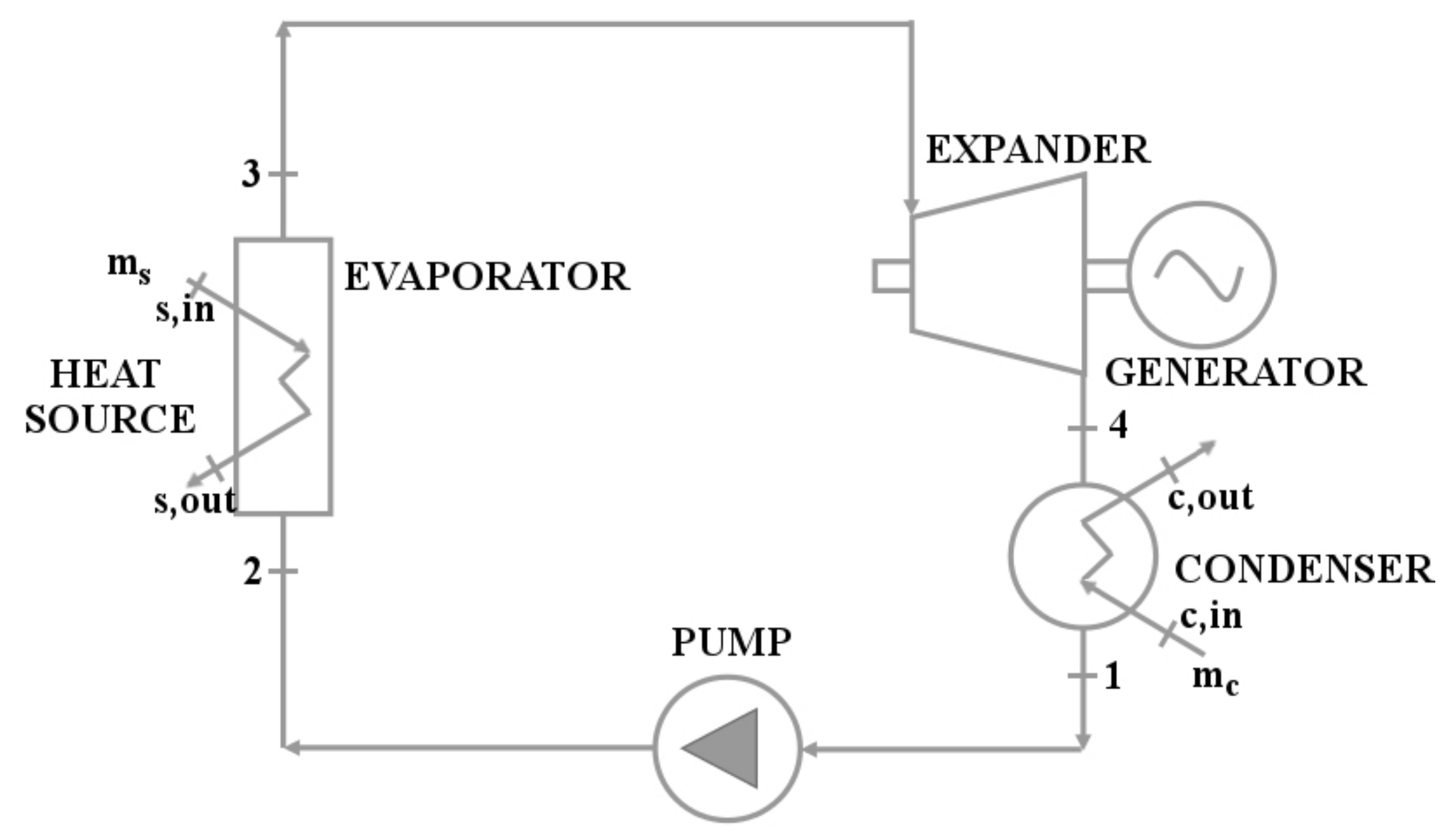
2. Numerical Model of ORC for Pure Fluids
- the pump isentropic efficiency:was assumed equal to 0.8 [46].
- The expander efficiencywas set equal to 0.8 for the pure fluid R245fa [47]. In the nanofluid case, as it will be better explained later on, the expander efficiency was determined within the optimization procedure since it resulted to be positively affected by the adsorption process of the R245fa molecule into the MIL101 porous structure [38]. More details can be found in Section 3.4.
- As regards the vapour quality at the end of the expansion process, the lower limit was fixed equal to 0.85 in order to avoid damages in the expander due to the excessive presence of liquid droplets [48].
- Pressure drops and heat losses were not considered [49].
3. Numerical ORC Model for the R245fa-MIL101 Nanofluid
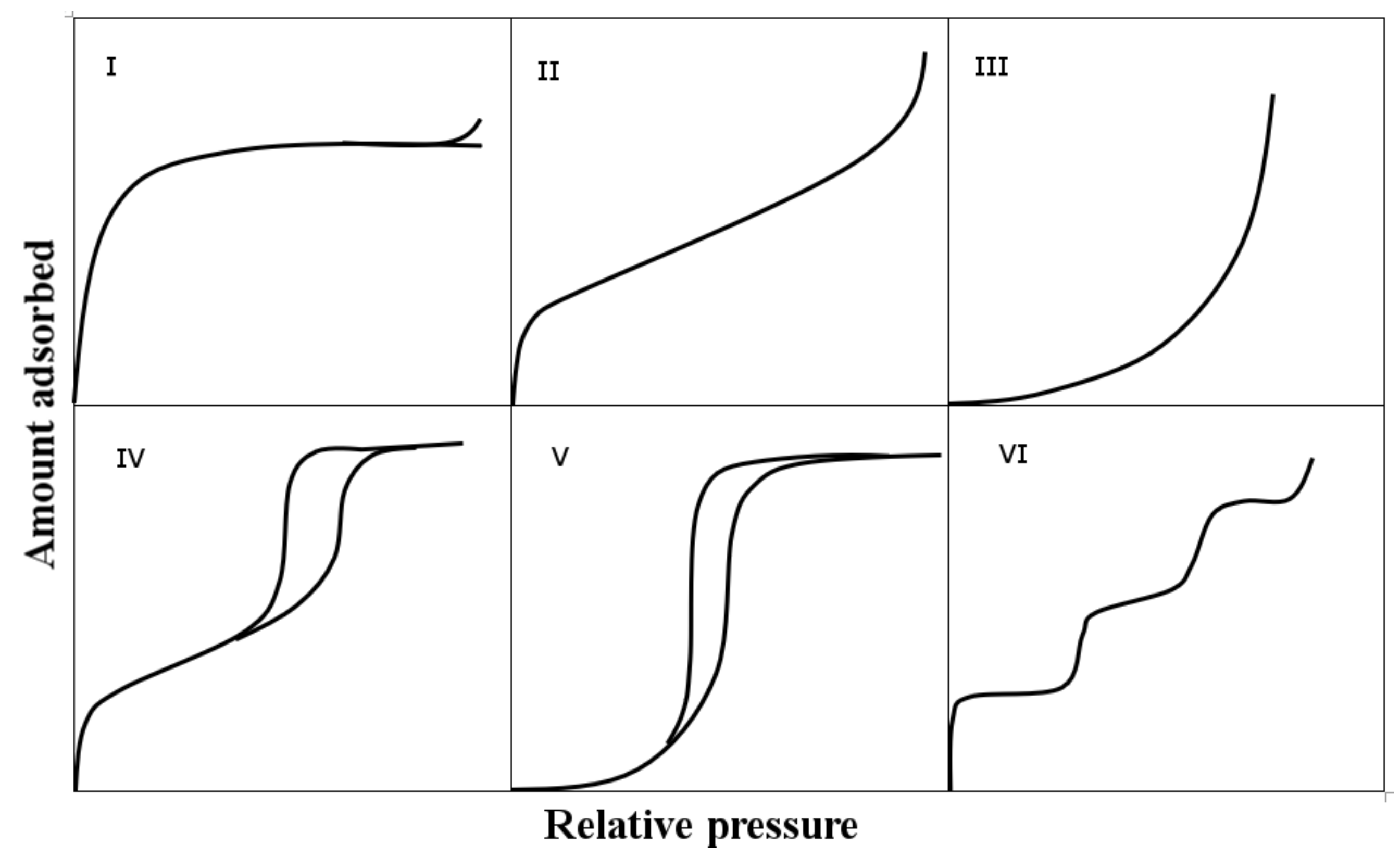
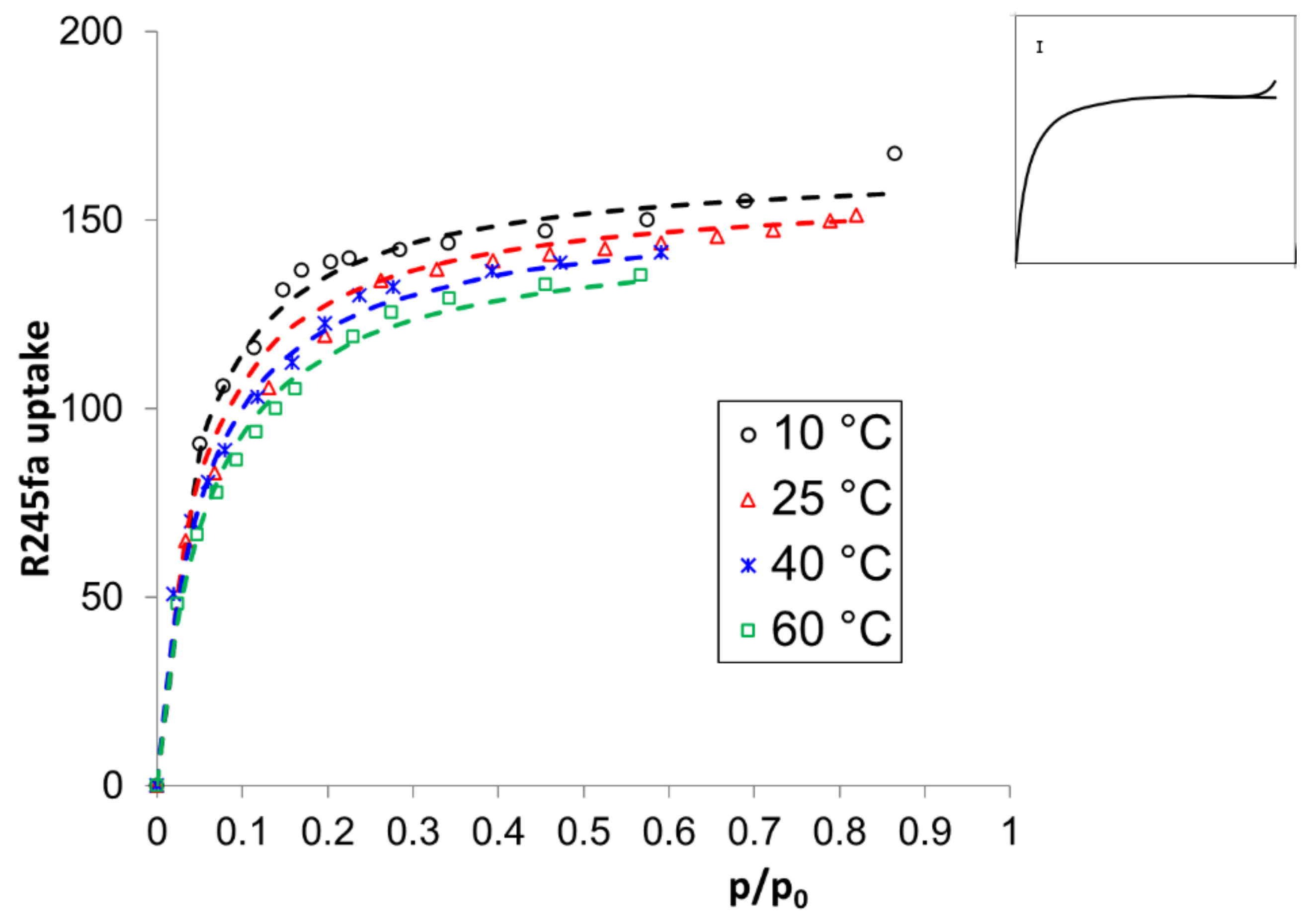
3.1. Experimental Determination of Adsorption Characteristics of the Nanofluid R245fa-MIL101
3.1.1. Identification of the Theoretical Model of the R245fa-MIL101 Nanofluid
3.1.2. The R245fa/MIL101 Enthalpy of Desorption/Adsorption
3.2. Nanofluid Modelling Equations: The Heat Exchangers and the Expander
- is the fraction between the MIL101 mass and the total fluid mass ;
- is the R245 mass uptake difference between the inlet and the outlet of the HTHE determined exploiting Equation (7).
- and are the inlet and outlet nanofluid temperature in the HTHE;
- is the average enthalpy of the R245fa/MIL101 desorption process caused by the temperature increase in the HTHE.
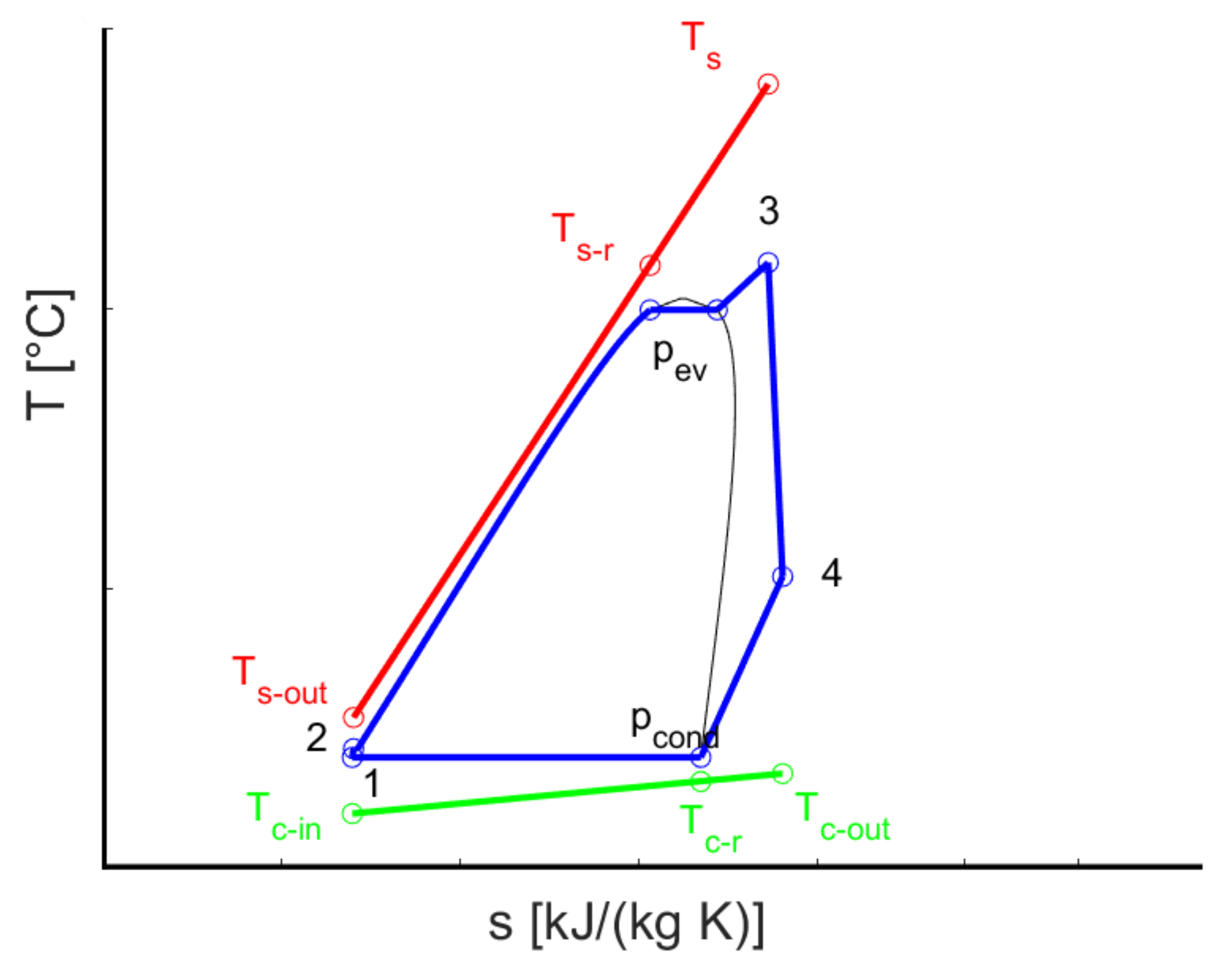
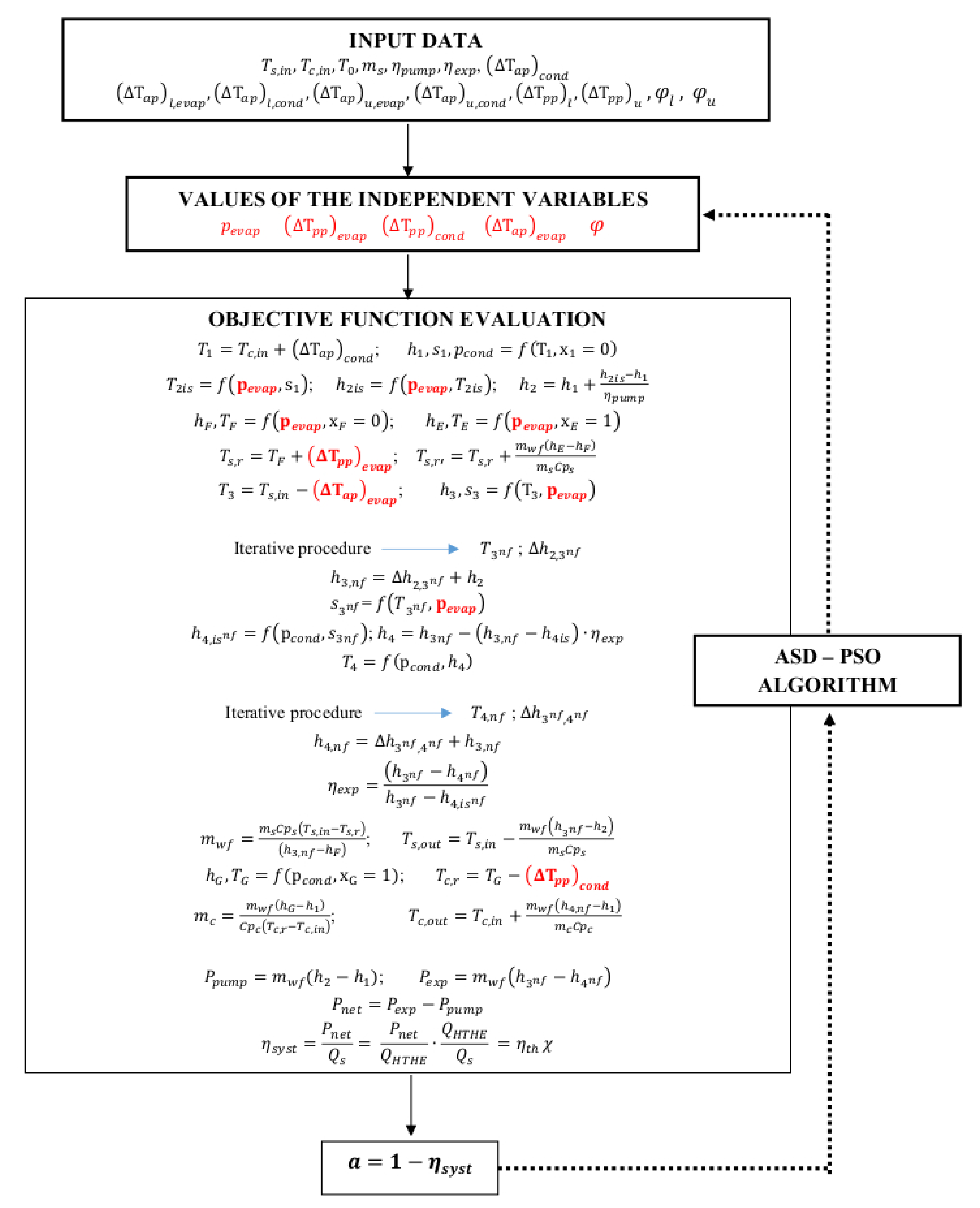
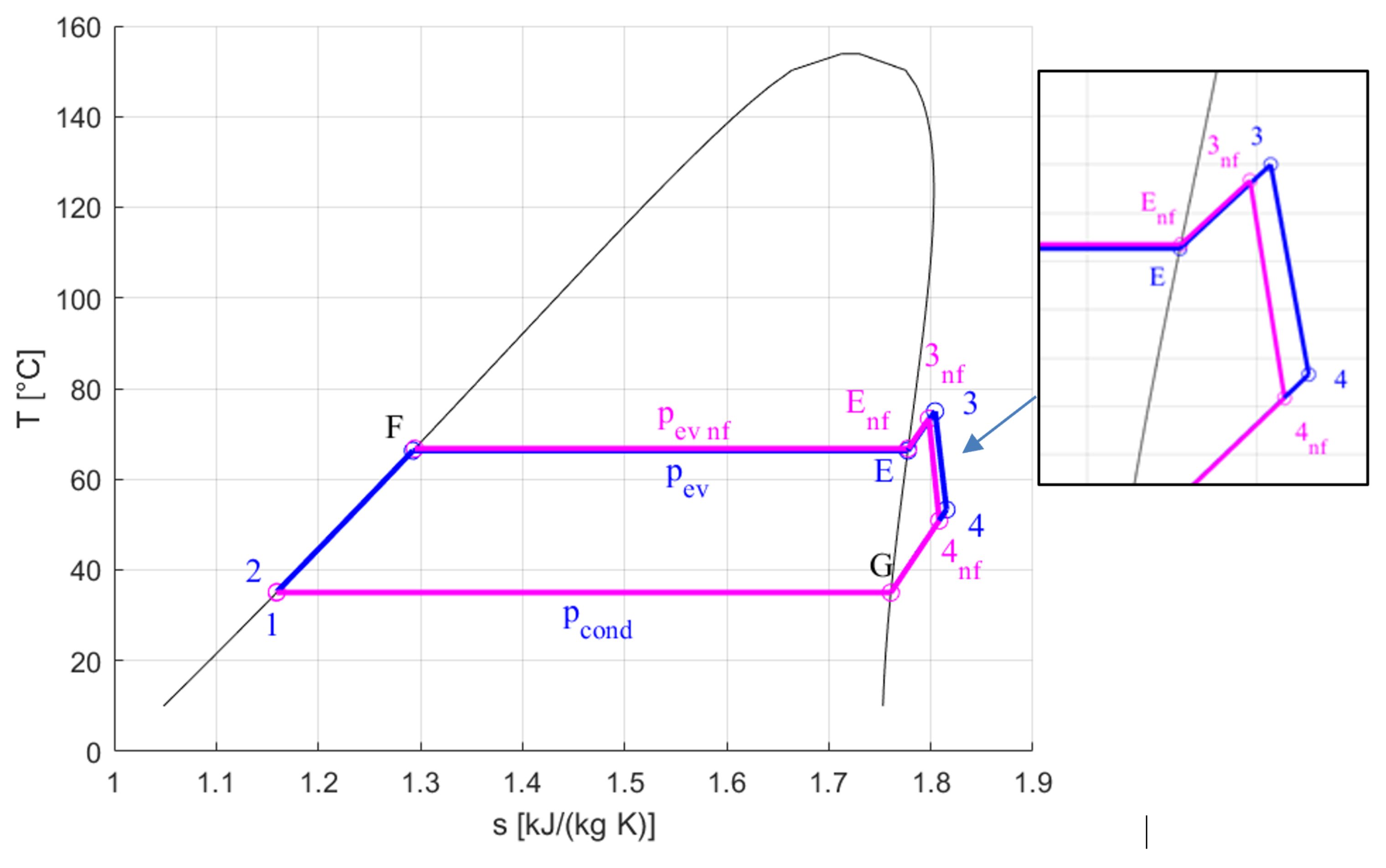
3.3. The R245fa-MIL101 Numerical Model: Assumptions and Iterative Procedures
- Since the specific heat affects the isobar shape in the T-s diagram, the previous assumption (Equation (8)) also allows to consider, for the nanofluid operating points, the same isobars of the pure R245fa fluid during the heat exchanges in the HTHE and in the LTHE.
- In the pumping process, the enthalpy contribution due to the exothermic adsorption process was considered negligible.
- (1)
- The R245fa mass uptake at the inlet of the HTHE is determined by applying Equations (6) and (7):
- (2)
- As regards the outlet, in the first iteration, the outlet nanofluid temperature () in the HTHE is assumed equal to the outlet temperature in case of pure fluid R245fa :
- (3)
- The R245fa mass uptake at the outlet of the HTHE is hence determined:
- (4)
- The mass desorption and the enthalpy increase between the inlet and the outlet of the HTHE is then calculated:
- (5)
- The enthalpy at the outlet of the HTHE is:
- (6)
- Starting from the enthalpy and pressure values, it is hence possible to determine the temperature of the nanofluid at the HTHE outlet:
- (7)
- If this value differs more than 0.1 from the value of the previous iteration i:
3.4. Optimization Procedure for the Nanofluid
- the cycle parameters (pressures, temperatures, etc.) used for the nanofluid were the optimal for the pure fluid and were not tuned to optimize the nanoparticles contribution;
- the influence of the mass fraction loading φ on the nanofluid contribution was not considered.
- the evaporator approach point was assumed to vary from 10 ◦C to 25 ◦C and both the evaporator and condenser pinch point varies from 5 °C to 20 °C;
- the evaporation pressure boundaries are driven by several constraints, fixed as follows:
- ○
- the lower bound was defined to ensure the pressure to be always greater than the condensing pressure. Since the approach point at the condenser and the cold source temperature were known, the limit was fixed equal to the pressure at a saturation temperature
- ○
- the upper bound has to guarantee two different conditions: (i) the ORC cycle must be sub-critical and hence the evaporation pressure should be smaller than the critical pressure by at least 1 bar, as suggested in literature [61]; (ii) the vapour characteristic at the HTHE outlet must be saturated or superheated with an evaporation pressure smaller or at least equal to that at the saturation temperature of . In order to guarantee both the conditions, the upper bound was fixed equal to the minimum between the two values.
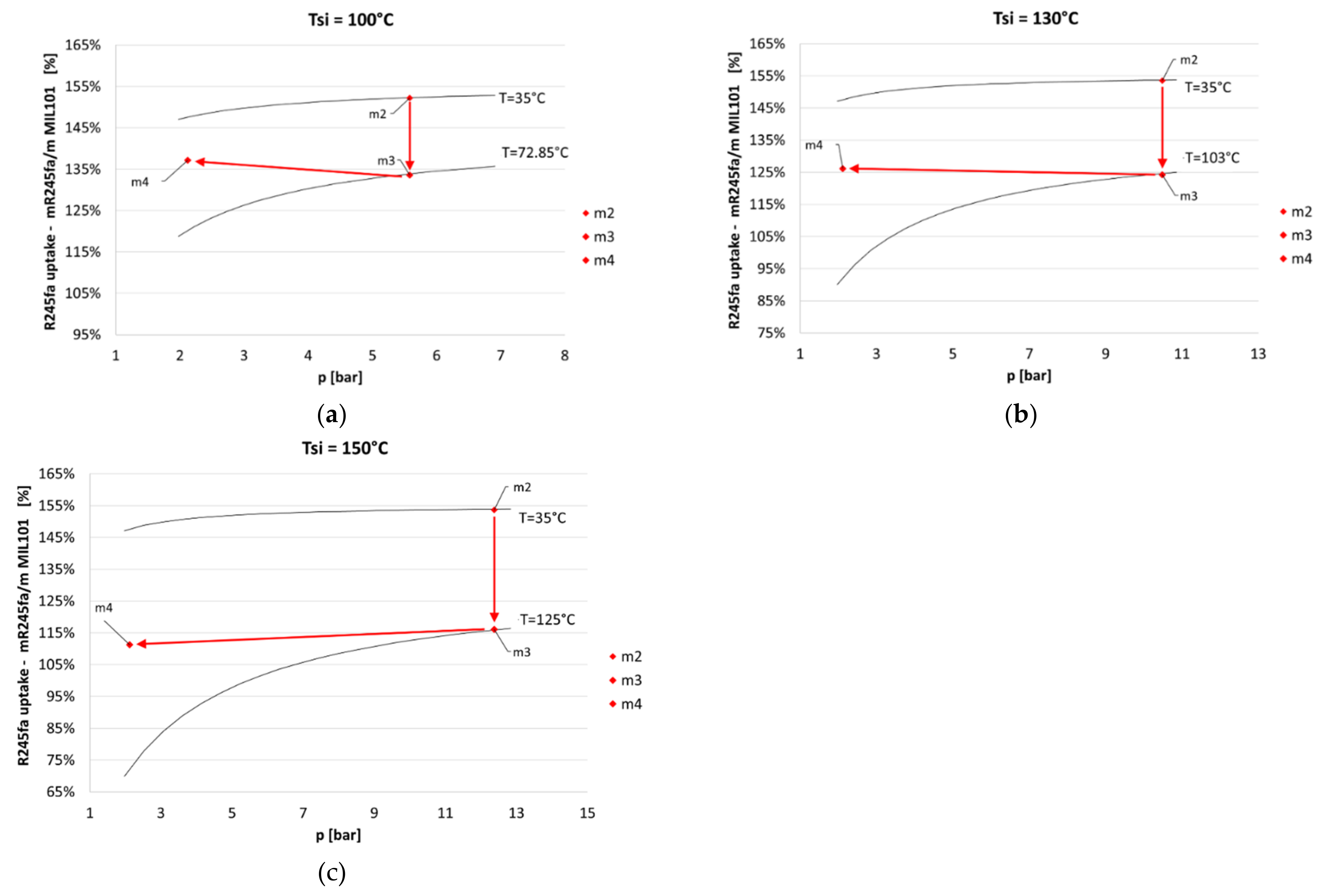
- the mass fraction load (φ) of nanoparticles was supposed to vary between 0.05% and 2%: the minimum value of the mass fraction load was fixed to have a minimum impact of the MIL101 on the pure fluid performance, whereas the maximum value was fixed to avoid stability problems according to previous studies on the topic [62].
4. Results
- the endothermic desorption process of the MOHCs, which decreases for increasing evaporation pressure values;
- the increase in expander efficiency for increasing evaporation pressure.
Double Uptake Scenario
5. Conclusions
- The introduction of the MIL101 nanoparticles in the pure fluid R245fa resulted in higher net power output especially when considering ultra-low heat source temperature (+2.9% for 100 °C, +2.3% for 110 °C, +1.7% for 120 °C).
- The main reason of the higher net power output is the increase in expander efficiency due to the adsorption process limiting the entropy increase during the expansion (+2.04% for 100 °C, +1.63% for 110 °C, +1.25% for 120 °C, +1.41% for 130 °C).
- The need of tuning the system thermodynamic operating conditions and the nanofluid behaviour is confirmed by the different evaporation pressure values characterizing the nanofluid case: from 1% to 4% higher than those of the pure fluid.
- For heat source temperatures higher than 120 °C, the constraints of the thermodynamic cycle force to have higher evaporation pressure. This creates unfavorable pressure and temperature values in the expansion, resulting in a desorption process and an almost negligible contribution of the MOHC nanoparticles (+0.2% of net power output for 130 °C). To overcome the constraints.
- As regards the MIL101 mass volume fraction , the maximum allowed value (2%) turned out to be beneficial for the system performance. However, mass volume fractions higher than 2% are at the time being not feasible due to technical limits. Above all, stability and deposit issues are still far from being fully solved in a challenging environment as an ORC system, in which the nanofluid passes through not only heat exchangers but also fluid machines for thousands of operating cycles.
- Experimentally analyze the adsorption/desorption processes for different combination of pure fluids and MOHC nanoparticles allowing to model the each MOHC-based nanofluid by means of semi-empirical correlations;
- Experimentally investigate the stability and the performance of MOHC-based nanofluid in fluid machines, i.e., expanders and pumps, so as to improve the numerical models.
- Numerically identify the perfect combination between pure fluid and MOHC nanoparticle depending on the heat source temperature
Author Contributions
Funding
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols: | ||
| cp | Heat Capacity at constant pressure | [kJ/kg K] |
| f | Objective function | [m2/kW] |
| h | Enthalpy | [kJ/kg] |
| m | Mass | [g] |
| ṁ | Mass flow rate | [kg/s] |
| MM | Molar Mass | [kg/kmol] |
| p | Pressure | [kPa] |
| P | Power | [kW] |
| Q | Heat Power | [kW] |
| R | molar gas constant | [J/K⋅mol] |
| S | Entropy | [kJ/°C mol] |
| T | Temperature | [°C] |
| wi | Adsorbate molar uptake per unit of adsorbent mass | [kmol/kg] |
| U | Heat transfer coefficient | [W/m2 K] |
| Enthalpy of adsorption/desorption | [kJ/kg] | |
| Temperature difference | [°C] | |
| Greek Letters: | ||
| η | Efficiency | [-] |
| ϕ | Nanoparticle mass fraction loading in the nanofluid | [-] |
| Density | [kg/m3] | |
| χ | Heat Recovery efficiency | [-] |
| Superscripts and Subscripts: | ||
| ads | adsorbed | |
| ap | Approach Point | |
| c | Cold source | |
| cond | Condenser | |
| desup | desuperheater | |
| econ | economizer | |
| evap | Evaporator | |
| exp | Expander | |
| f | Organic fluid | |
| in | Inlet | |
| is | Isentropic | |
| net | Net | |
| nf | Nanofluid | |
| out | Outlet | |
| pp | Pinch Point | |
| pump | Pump | |
| s | Heat source fluid | |
| sh | Superheater | |
| syst | System | |
| th | Thermal | |
| tot | Total | |
| wf | Working fluid | |
References
- IEA. Industrial Excess Heat Recovery-Technologies and Applications-Annex XV; International Energy Agency: Paris, France, 2015. [Google Scholar]
- Brückner, S.; Liu, S.; Miró, L.; Radspieler, M.; Cabeza, L.F.; Lävemann, E. Industrial waste heat recovery technologies: An economic analysis of heat transformation technologies. Appl. Energy 2015, 151, 157–167. [Google Scholar] [CrossRef]
- Lian, H.; Li, Y.; Shu, G.; Gu, C. An Overview of Domestic Technologies for Waste Heat Utilization. Energy Conserv. Technol. 2011, 29, 123–128. [Google Scholar]
- Tchanche, B.F.; Lambrinos, G.; Frangoudakis, A.; Papadakis, G. Low-grade heat conversion into power using organic Rankine cycles–A review of various applications. Renew. Sustain. Energy Rev. 2011, 15, 3963–3979. [Google Scholar] [CrossRef]
- Huang, F.; Zheng, J.; Baleynaud, J.M.; Lu, J. Heat recovery potentials and technologies in industrial zones. J. Energy Inst. 2017, 90, 951–961. [Google Scholar] [CrossRef]
- Turgut, M.S.; Turgut, O.E. Multi-objective optimization of the basic and single-stage Organic Rankine Cycles utilizing a low-grade heat source. Heat Mass Transf. 2019, 55, 353–374. [Google Scholar] [CrossRef]
- Tocci, L.; Pal, T.; Pesmazoglou, I.; Franchetti, B. Small Scale Organic Rankine Cycle (ORC): A Techno-Economic Review. Energies 2017, 10, 413. [Google Scholar] [CrossRef]
- Cao, M.; Yang, X.; Wang, J.; Zhang, X.; Guo, H. Economic Analysis of Organic Rankine Cycle Using R123 and R245fa as Working Fluids and a Demonstration Project Report. Appl. Sci. 2019, 9, 288. [Google Scholar]
- Lakew, A.A.; Bolland, O. Working fluids for low-temperature heat source. Appl. Therm. Eng. 2010, 30, 1262–1268. [Google Scholar] [CrossRef]
- Zhao, L.; Bao, J. Thermodynamic analysis of organic Rankine cycle using zeotropic mixtures. Appl. Energy 2014, 130, 748–756. [Google Scholar] [CrossRef]
- Wang, D.; Ling, X.; Peng, H.; Liu, L.; Tao, L. Efficiency and optimal performance evaluation of organic Rankine cycle for low grade waste heat power generation. Energy 2013, 50, 343–352. [Google Scholar] [CrossRef]
- Saleh, B.; Koglbauer, G.; Wendland, M.; Fischer, J. Working fluids for low-temperature organic Rankine cycles. Energy 2007, 32, 1210–1221. [Google Scholar] [CrossRef]
- Chen, H.; Goswami, D.Y.; Stefanakos, E.K. A review of thermodynamic cycles and working fluids for the conversion of low-grade heat. Renew. Sustain. Energy Rev. 2010, 14, 3059–3067. [Google Scholar] [CrossRef]
- He, C.; Liu, C.; Zhou, M.; Xie, H.; Xu, X.; Wu, S.; Li, Y. A new selection principle of working fluids for subcritical organic Rankine cycle coupling with different heat sources. Energy 2014, 68, 283–291. [Google Scholar] [CrossRef]
- Xu, J.; Yu, C. Critical temperature criterion for selection of working fluids for subcritical pressure Organic Rankine cycles. Energy 2014, 74, 719–733. [Google Scholar] [CrossRef]
- Li, X.; Zhao, W.; Lin, D.; Zhu, Q. Working fluid selection based on critical temperature and water temperature in organic Rankine cycle. Sci. China Technol. Sci. 2015, 58, 138–146. [Google Scholar] [CrossRef]
- Cavazzini, G.; Bari, S.; Pavesi, G.; Ardizzon, G. A multi-fluid PSO-based algorithm for the search of the best performance of sub-critical Organic Rankine Cycles. Energy 2017, 129, 42–58. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the ASME International Mechanical Engineering Congress & Exposition, San Francisco, CA, USA, 12–17 November 1995. [Google Scholar]
- Choi, S.U.S.; Zhang, Z.G.; Yu, W.; Lockwood, F.E.; Grulke, E.A. Anomalous thermal conductivity enhancement in nanotube suspensions. Appl. Phys. Lett. 2001, 79, 2252–2254. [Google Scholar] [CrossRef]
- Michaelides, E.E. Nanofluidics; Springer: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Godson, L.; Raja, B.; Mohan Lal, D.; Wongwises, S. Enhancement of heat transfer using nanofluids-An overview. Renew. Sustain. Energy Rev. 2010, 14, 629–641. [Google Scholar] [CrossRef]
- Saidur, R.; Leong, K.Y.; Mohammad, H. A review on applications and challenges of nanofluids. Renew. Sustain. Energy Rev. 2011, 15, 1646–1668. [Google Scholar] [CrossRef]
- Martinez, J.O.; Brown, B.S.; Quattrocchi, N.; Evangelopoulos, M.; Ferrari, M.; Tasciotti, E. Multifunctional to multistage delivery systems: The evolution of nanoparticles for biomedical applications. Chin. Sci. Bull. 2012, 57, 3961–3971. [Google Scholar] [CrossRef]
- Mousavi Ajarostaghi, S.S.; Zaboli, M.; Javadi, H.; Badenes, B.; Urchueguia, J.F. A Review of Recent Passive Heat Transfer Enhancement Methods. Energies 2022, 15, 986. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C. Thermal analysis of parabolic trough collector operating with mono and hybrid nanofluids. Sustain. Energy Technol. Assess. 2018, 26, 105–115. [Google Scholar] [CrossRef]
- Mahian, O.; Kianifar, A.; Sahin, A.Z.; Wongwises, S. Entropy generation during Al 2 O 3 /water nanofluid flow in a solar collector: Effects of tube roughness, nanoparticle size, and different thermophysical models. Int. J. Heat Mass Transf. 2014, 78, 64–75. [Google Scholar] [CrossRef]
- Abdalha Mahmood, A.H.; Hussain, M.I.; Lee, G.-H. Effects of Nanofluids in Improving the Efficiency of the Conical Concentrator System. Energies 2022, 15, 28. [Google Scholar] [CrossRef]
- Kumaresan, G.; Sudhakar, P.; Santosh, R.; Velraj, R. Experimental and numerical studies of thermal performance enhancement in the receiver part of solar parabolic trough collectors. Renew. Sustain. Energy Rev. 2017, 77, 1363–1374. [Google Scholar] [CrossRef]
- De Risi, A.; Milanese, M.; Laforgia, D. Modelling and optimization of transparent parabolic trough collector based on gas-phase nanofluids. Renew. Energy 2013, 58, 134–139. [Google Scholar] [CrossRef]
- Mahian, O.; Kianifar, A.; Zeinali Heris, S.; Wen, D.; Sahin, A.; Wongwises, S. Nanofluids effects on the evaporation rate in a solar still equipped with a heat exchanger. Nano Energy 2017, 36, 134–155. [Google Scholar] [CrossRef]
- Habibi, H.; Zoghi, M.; Chitsaz, A.; Javaherdeh, K.; Ayazpour, M. Thermo-economic performance comparison of two configurations of combined steam and organic Rankine cycle with steam Rankine cycle driven by Al2O3-therminol VP-1 based PTSC. Sol. Energy 2019, 180, 116–132. [Google Scholar] [CrossRef]
- Toghyani, S.; Baniasadi, E.; Afshari, E. Thermodynamic analysis and optimization of an integrated Rankine power cycle and nano-fluid based parabolic trough solar collector. Energy Convers. Manag. 2016, 121, 93–104. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C. Parametric analysis and optimization of an Organic Rankine Cycle with nanofluid based solar parabolic trough collectors. Renew. Energy 2017, 114, 1376–1393. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C. Optimization of a solar-driven trigeneration system with nanofluid-based parabolic trough collectors. Energies 2017, 10, 848. [Google Scholar] [CrossRef]
- Alam, T.; Balam, N.B.; Kulkarni, K.S.; Siddiqui, M.I.H.; Kapoor, N.R.; Meena, C.S.; Kumar, A.; Cozzolino, R. Performance Augmentation of the Flat Plate Solar Thermal Collector: A Review. Energies 2021, 14, 6203. [Google Scholar] [CrossRef]
- Loni, R.; Askari Asli-Ardeh, E.; Ghobadian, B.; Najafi, G.; Bellos, E. Effects of size and volume fraction of alumina nanoparticles on the performance of a solar organic Rankine cycle. Energy Convers. Manag. 2019, 182, 398–411. [Google Scholar] [CrossRef]
- Jin, X.; Lin, G.; Jin, H.; Fu, Z.; Sun, H. Experimental Research on the Selective Absorption of Solar Energy by Hybrid Nanofluids. Energies 2021, 14, 8186. [Google Scholar] [CrossRef]
- McGrail, B.P.; Thallapally, P.K.; Blanchard, J.; Nune, S.K.; Jenks, J.W.J.; Dang, L.X. Metal-organic heat carrier nanofluids. Nano Energy 2013, 2, 845–855. [Google Scholar] [CrossRef]
- Ferey, G. A Chromium Terephthalate-Based Solid with Unusually Large Pore Volumes and Surface Area. Science 2005, 310, 1119. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, M.; Guan, Q.; Li, W. Kinetic and thermodynamic studies on the adsorption of xylenol orange onto MIL-101(Cr). Chem. Eng. J. 2012, 183, 60–67. [Google Scholar] [CrossRef]
- Cavazzini, G.; Bari, S.; McGrail, P.; Benedetti, V.; Pavesi, G.; Ardizzon, G. Contribution of Metal-Organic-Heat Carrier nanoparticles in a R245fa low-grade heat recovery Organic Rankine Cycle. Energy Convers. Manag. 2019, 199, 111960. [Google Scholar] [CrossRef]
- Cavazzini, G.; Bari, S.; Benedetti, V.; McGrail, P.; Pavesi, G.; Ardizzon, G. Influence of the use of Innovative Nanofluid on net power production in ORCs for low-grade waste heat recovery applications. In Proceedings of the 5th International Seminar on ORC Power Systems, Athens, Greece, 9–11 September 2019. [Google Scholar]
- Cavazzini, G.; Dal Toso, P. Techno-economic feasibility study of the integration of a commercial small-scale ORC in a real case study. Energy Convers. Manag. 2015, 99, 161–175. [Google Scholar] [CrossRef]
- Avadhanula, V.K.; Lin, C.-S. Empirical Models for a Screw Expander Based on Experimental Data from Organic Rankine Cycle System Testing. J. Eng. Gas Turbines Power 2014, 136, 062601. [Google Scholar] [CrossRef]
- Khennich, M.; Galanis, N. Optimal Design of ORC Systems with a Low-Temperature Heat Source. Entropy 2012, 14, 370–389. [Google Scholar] [CrossRef]
- Quoilin, S.; Aumann, R.; Grill, A.; Schuster, A.; Lemort, V.; Spliethoff, H. Dynamic modeling and optimal control strategy of waste heat recovery Organic Rankine Cycles. Appl. Energy 2011, 88, 2183–2190. [Google Scholar] [CrossRef]
- Andreasen, J.G.; Larsen, U.; Knudsen, T.; Pierobon, L.; Haglind, F. Selection and optimization of pure and mixed working fluids for low grade heat utilization using organic rankine cycles. Energy 2014, 73, 204–213. [Google Scholar] [CrossRef]
- Astolfi, M. Techno-economic Optimization of Low Temperature CSP Systems Based on ORC with Screw Expanders. Energy Procedia 2015, 69, 1100–1112. [Google Scholar] [CrossRef]
- Dai, Y.; Wang, J.; Gao, L. Parametric optimization and comparative study of organic Rankine cycle (ORC) for low grade waste heat recovery. Energy Convers. Manag. 2009, 50, 576–582. [Google Scholar] [CrossRef]
- Bell, I.H.; Wronski, J.; Quoilin, S.; Lemort, V. Pure and Pseudo-pure Fluid Thermophysical Property Evaluation and the Open-Source Thermophysical Property Library CoolProp. Ind. Eng. Chem. Res. 2014, 53, 2498–2508. [Google Scholar] [CrossRef]
- Gregg, S.J.; Sing, K.S.W.; Salzberg, H.W. Adsorption Surface Area and Porosity. J. Electrochem. Soc. 1967, 114, 279C. [Google Scholar] [CrossRef]
- Annapureddy, H.V.R.; Nune, S.K.; Motkuri, R.K.; McGrail, B.P.; Dang, L.X. A Combined Experimental and Computational Study on the Stability of Nanofluids Containing Metal Organic Frameworks. J. Phys. Chem. B 2015, 119, 8992–8999. [Google Scholar] [CrossRef]
- Langmuir, I. The Adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Nuhnen, A.; Janiak, C. A practical guide to calculate the isosteric heat/enthalpy of adsorption: Via adsorption isotherms in metal-organic frameworks, MOFs. Dalt. Trans. 2020, 49, 10295–10307. [Google Scholar] [CrossRef]
- Mu, B.; Walton, K.S. Thermal Analysis and Heat Capacity Study of Metal–Organic Frameworks. J. Phys. Chem. C 2011, 115, 22748–22754. [Google Scholar] [CrossRef]
- Khanafer, K.; Vafai, K. A critical synthesis of thermophysical characteristics of nanofluids. Int. J. Heat Mass Transf. 2011, 54, 4410–4428. [Google Scholar] [CrossRef]
- Das, S.K.; Putra, N.; Thiesen, P.; Roetzel, W. Temperature Dependence of Thermal Conductivity Enhancement for Nanofluids. J. Heat Transf. 2003, 125, 567. [Google Scholar] [CrossRef]
- Lee, J.; Mudawar, I. Assessment of the effectiveness of nanofluids for single-phase and two-phase heat transfer in micro-channels. Int. J. Heat Mass Transf. 2007, 50, 452–463. [Google Scholar] [CrossRef]
- Gosselin, L.; da Silva, A.K. Combined “heat transfer and power dissipation” optimization of nanofluid flows. Appl. Phys. Lett. 2004, 85, 4160–4162. [Google Scholar] [CrossRef]
- Ardizzon, G.; Cavazzini, G.; Pavesi, G. Adaptive acceleration coefficients for a new search diversification strategy in particle swarm optimization algorithms. Inf. Sci. 2015, 299, 337–378. [Google Scholar] [CrossRef]
- Drescher, U.; Brüggemann, D. Fluid selection for the Organic Rankine Cycle (ORC) in biomass power and heat plants. Appl. Therm. Eng. 2007, 27, 223–228. [Google Scholar] [CrossRef]
- Alawi, O.A.; Sidik, N.A.C.; Kherbeet, A.S. Nanorefrigerant effects in heat transfer performance and energy consumption reduction: A review. Int. Commun. Heat Mass Transf. 2015, 69, 76–83. [Google Scholar] [CrossRef]
- Mondejar, M.E.; Andreasen, J.G.; Regidor, M.; Riva, S.; Kontogeorgis, G.; Persico, G.; Haglind, F. Prospects of the use of nanofluids as working fluids for organic Rankine cycle power systems. Energy Procedia 2017, 129, 160–167. [Google Scholar] [CrossRef][Green Version]

| Ts,in | pev | ΔTap,ev | ΔTpp,ev | ΔTpp,cond | φ | ηsyst | Pnet | χ | ηth |
|---|---|---|---|---|---|---|---|---|---|
| [°C] | [bar] | [°C] | [°C] | [°C] | [%] | [%] | [kW] | [%] | [%] |
| 100 | 5.58 | 25 | 5 | 8.9 | 2.00% | 2.84% | 50.52 | 41.72% | 6.81% |
| 110 | 6.52 | 25 | 5 | 19.7 | 2.00% | 3.43% | 68.21 | 44.46% | 7.72% |
| 120 | 7.63 | 25 | 5 | 6.7 | 2.00% | 4.02% | 88.38 | 46.85% | 8.58% |
| 130 | 10.48 | 25 | 5 | 5.4 | 2.00% | 4.52% | 108.77 | 43.55% | 10.38% |
| 140 | 10.48 | 25 | 5 | 5.4 | 2.00% | 5.20% | 136.11 | 50.86% | 10.23% |
| 150 | 12.37 | 25 | 5 | 5.6 | 2.00% | 5.80% | 163.78 | 52.54% | 11.03% |
| Ts,in | pev | ΔTap,ev | ΔTpp,ev | ΔTpp,cond | φ | ηsyst | Pnet | χ | ηth |
|---|---|---|---|---|---|---|---|---|---|
| [°C] | [bar] | [°C] | [°C] | [°C] | [%] | [%] | [kW] | [%] | [%] |
| 100 | 5.51 | 25 | 5 | 13.9 | - | 2.76% | 49.1 | 42.14% | 6.55% |
| 110 | 6.42 | 25 | 5 | 20 | - | 3.35% | 66.69 | 45.00% | 7.45% |
| 120 | 7.46 | 25 | 5 | 5.1 | - | 3.95% | 86.9 | 47.53% | 8.32% |
| 130 | 10.13 | 25 | 5 | 5.7 | - | 4.48% | 107.75 | 44.72% | 10.01% |
| 140 | 10.13 | 25 | 5 | 5.7 | - | 5.17% | 135.24 | 51.85% | 9.97% |
| 150 | 11.87 | 25 | 5 | 5 | - | 5.79% | 163.47 | 53.76% | 10.77% |
| Ts,in | ηexp,nf |
|---|---|
| [°C] | [%] |
| 100 | 82.04% |
| 110 | 81.63% |
| 120 | 81.25% |
| 130 | 81.41% |
| 140 | 80.59% |
| 150 | 80.34% |
| Ts,in | pev | ΔTap,ev | ΔTpp,ev | ΔTpp,cond | φ | ηsyst | Pnet | χ | ηth |
|---|---|---|---|---|---|---|---|---|---|
| [°C] | [bar] | [°C] | [°C] | [°C] | [%] | [%] | [kW] | [%] | [%] |
| 100 | 5.63 | 25 | 5 | 5.1 | 2.00% | 2.86% | 50.83 | 41.28% | 6.92% |
| 110 | 6.6 | 25 | 5 | 19.9 | 2.00% | 3.43% | 68.17 | 43.87% | 7.82% |
| 120 | 7.75 | 25 | 5 | 6.9 | 2.00% | 3.99% | 87.76 | 46.09% | 8.66% |
| 130 | 8.78 | 25 | 5 | 20 | 0.50% | 4.56% | 109.76 | 49.42% | 9.23% |
| 140 | 10.26 | 25 | 5 | 5.4 | 0.50% | 5.16% | 134.95 | 51.40% | 10.03% |
| 150 | 12.05 | 25 | 5 | 5.3 | 0.50% | 5.76% | 162.76 | 53.18% | 10.83% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cavazzini, G.; Bari, S. Optimization of the Adsorption/Desorption Contribution from Metal-Organic-Heat-Carrier Nanoparticles in Waste Heat Recovery Applications: R245fa/MIL101 in Organic Rankine Cycles. Energies 2022, 15, 1138. https://doi.org/10.3390/en15031138
Cavazzini G, Bari S. Optimization of the Adsorption/Desorption Contribution from Metal-Organic-Heat-Carrier Nanoparticles in Waste Heat Recovery Applications: R245fa/MIL101 in Organic Rankine Cycles. Energies. 2022; 15(3):1138. https://doi.org/10.3390/en15031138
Chicago/Turabian StyleCavazzini, Giovanna, and Serena Bari. 2022. "Optimization of the Adsorption/Desorption Contribution from Metal-Organic-Heat-Carrier Nanoparticles in Waste Heat Recovery Applications: R245fa/MIL101 in Organic Rankine Cycles" Energies 15, no. 3: 1138. https://doi.org/10.3390/en15031138
APA StyleCavazzini, G., & Bari, S. (2022). Optimization of the Adsorption/Desorption Contribution from Metal-Organic-Heat-Carrier Nanoparticles in Waste Heat Recovery Applications: R245fa/MIL101 in Organic Rankine Cycles. Energies, 15(3), 1138. https://doi.org/10.3390/en15031138







