Influence of Fluid Viscosity on Cavitation Characteristics of a Helico-Axial Multiphase Pump (HAMP)
Abstract
1. Introduction
2. Numerical Simulation Method
2.1. HAMP Geometry Model
2.2. Meshing of Calculation Domain
2.3. Numerical Scheme
2.4. Cavitation Model
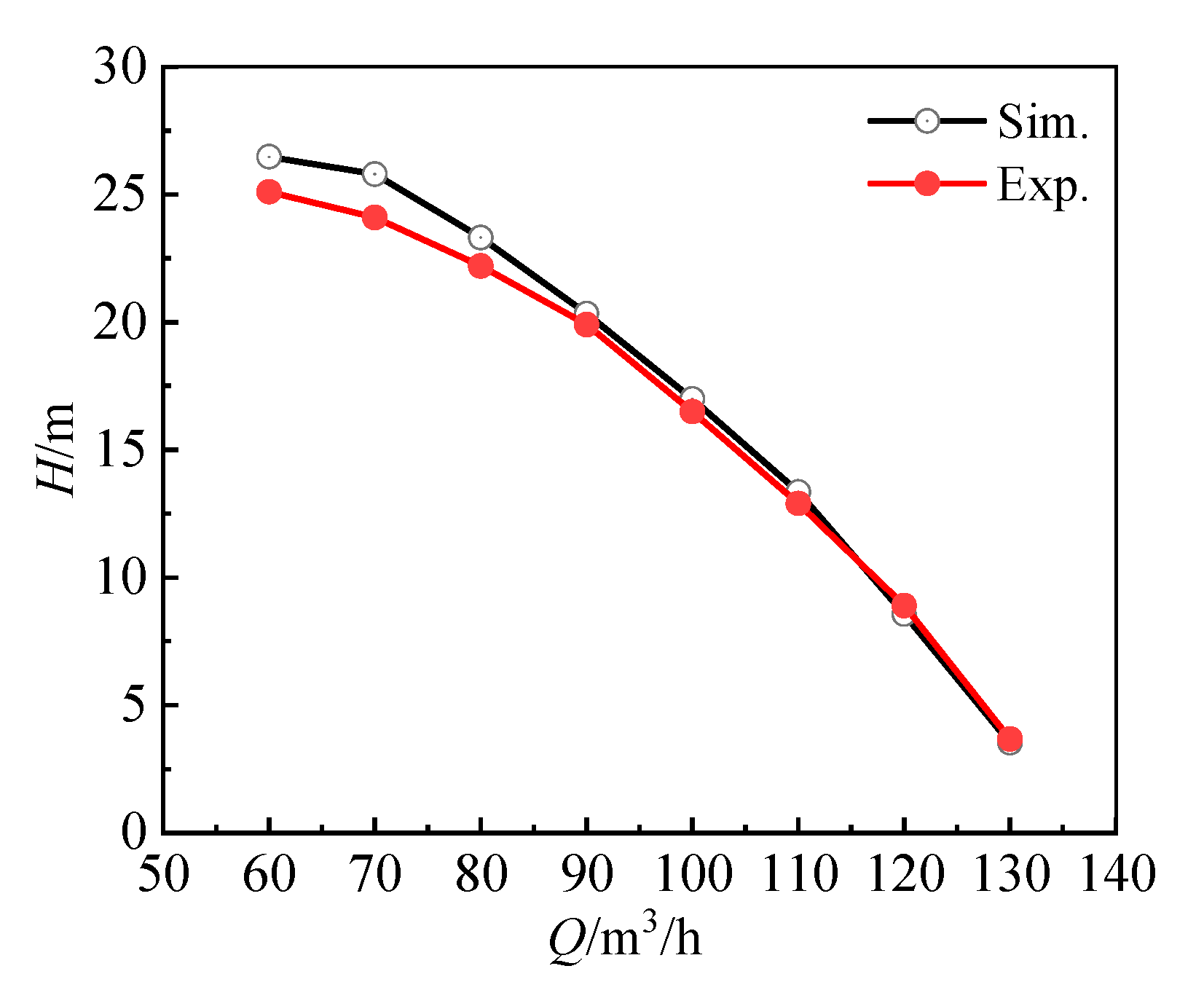
2.5. Numerical Method Validation
3. Results and Discussions
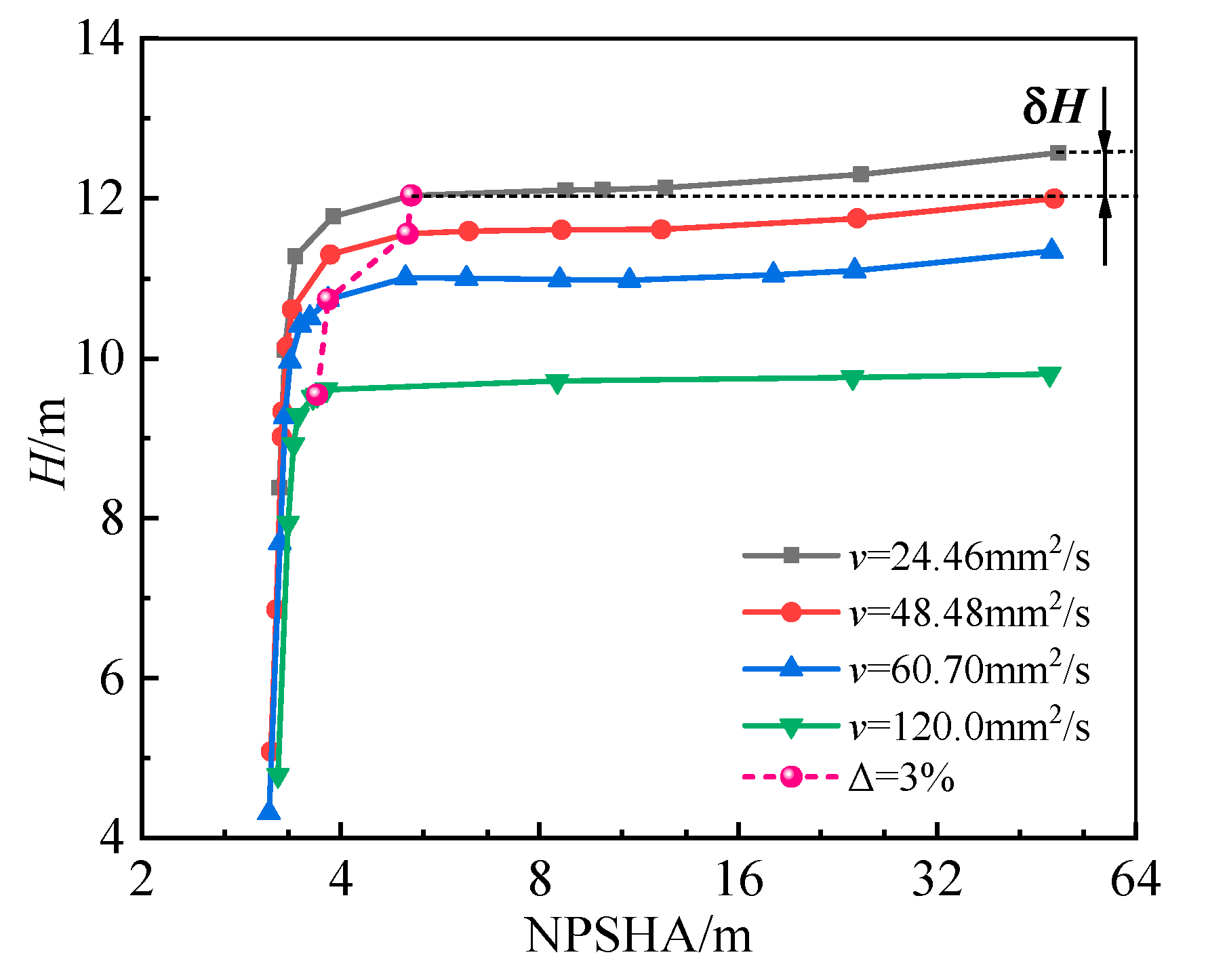
3.1. Cavitation Characteristic Curve of HAMP
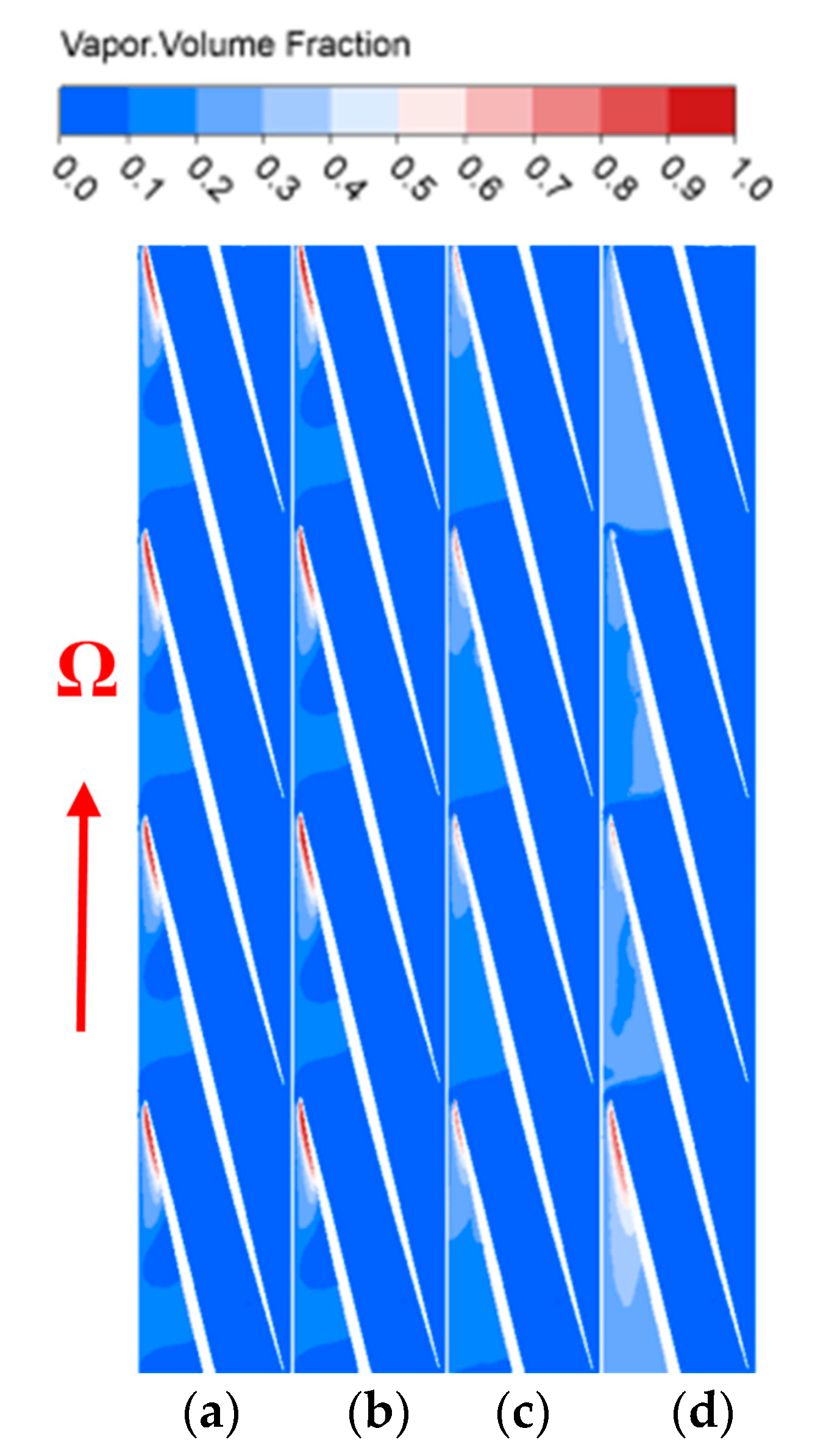
3.2. VVF Distribution in Impeller Passage
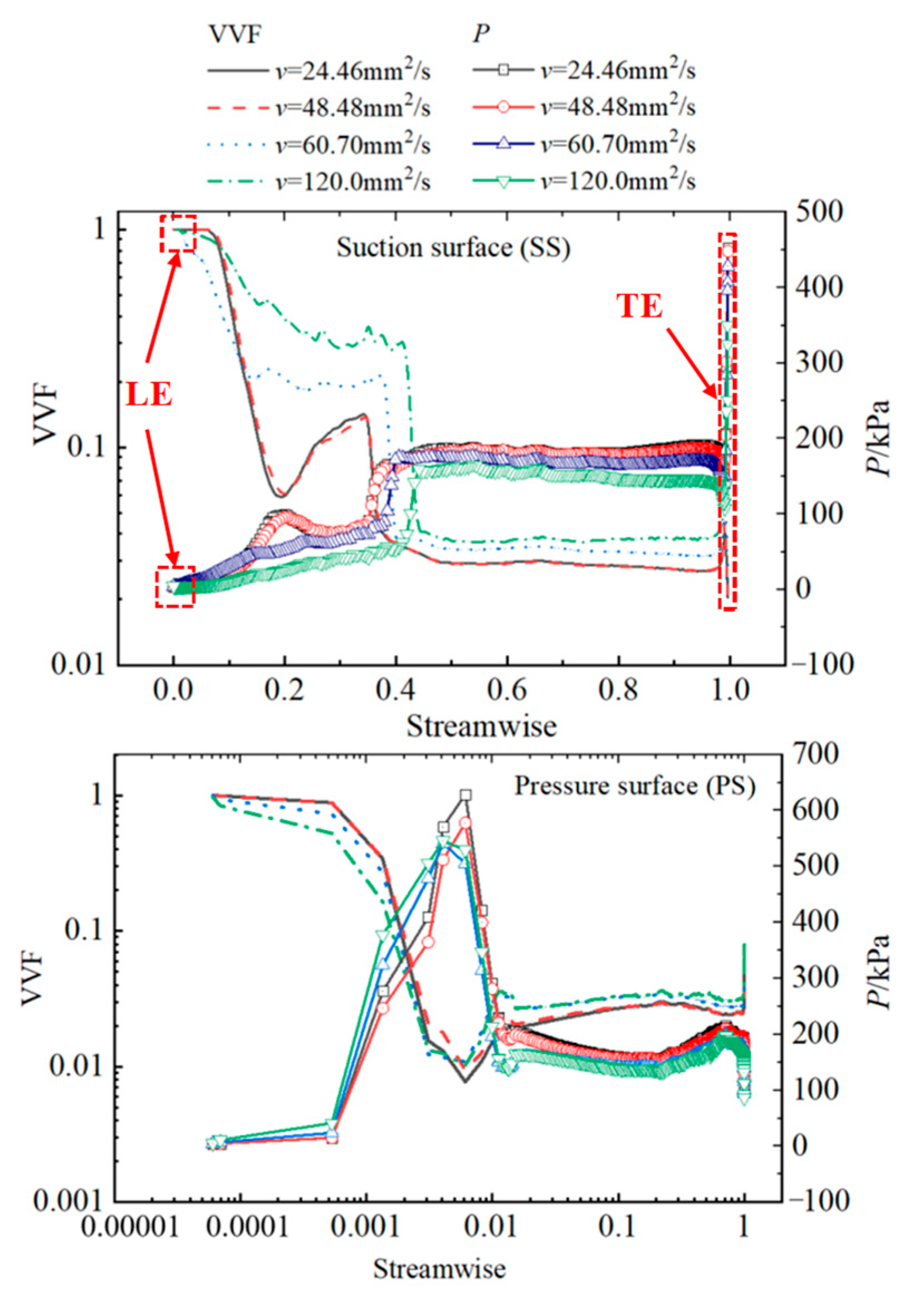
3.3. VVF on Blade Surface
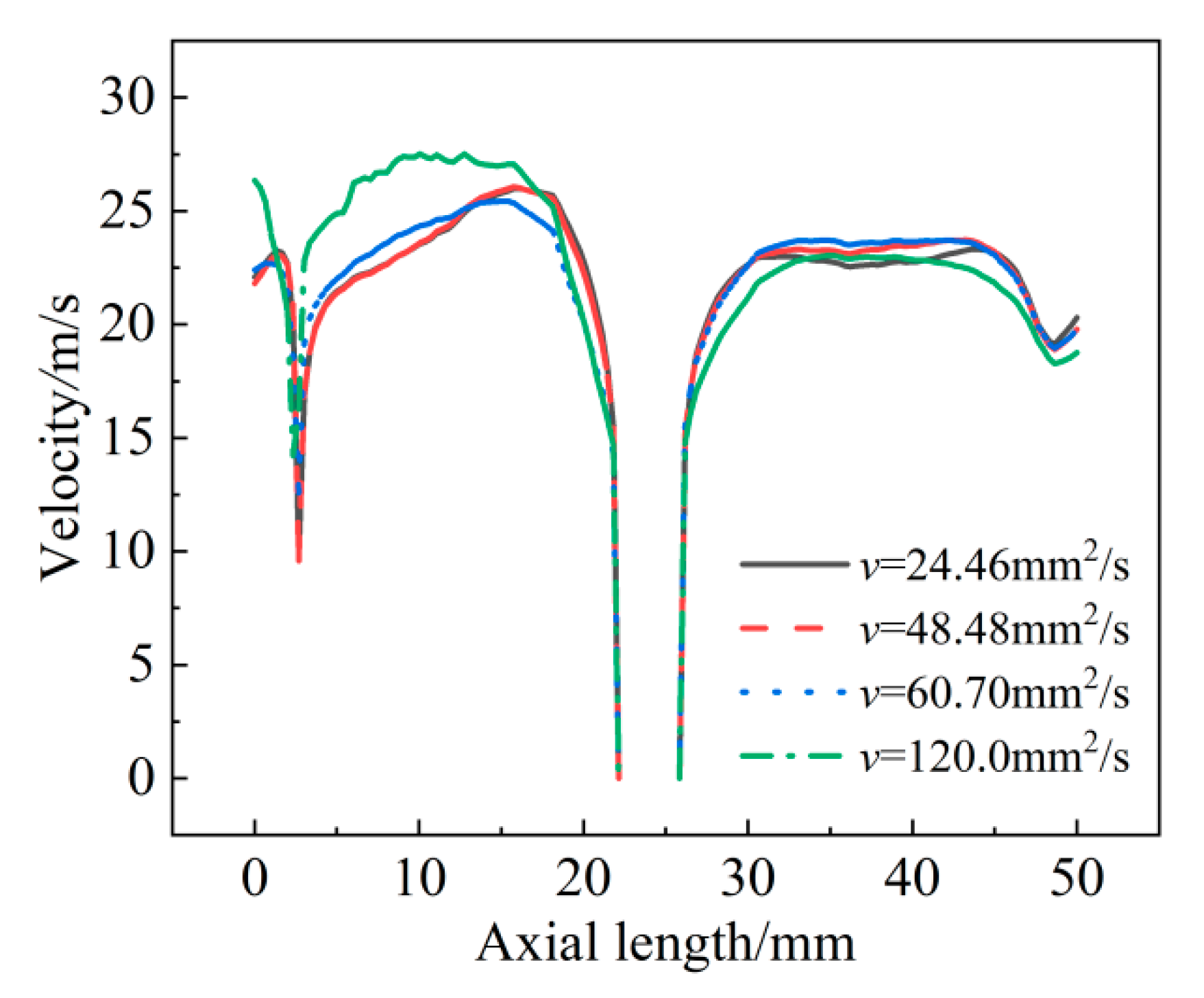
3.4. Velocity Distribution in Impeller
4. Conclusions
- (1)
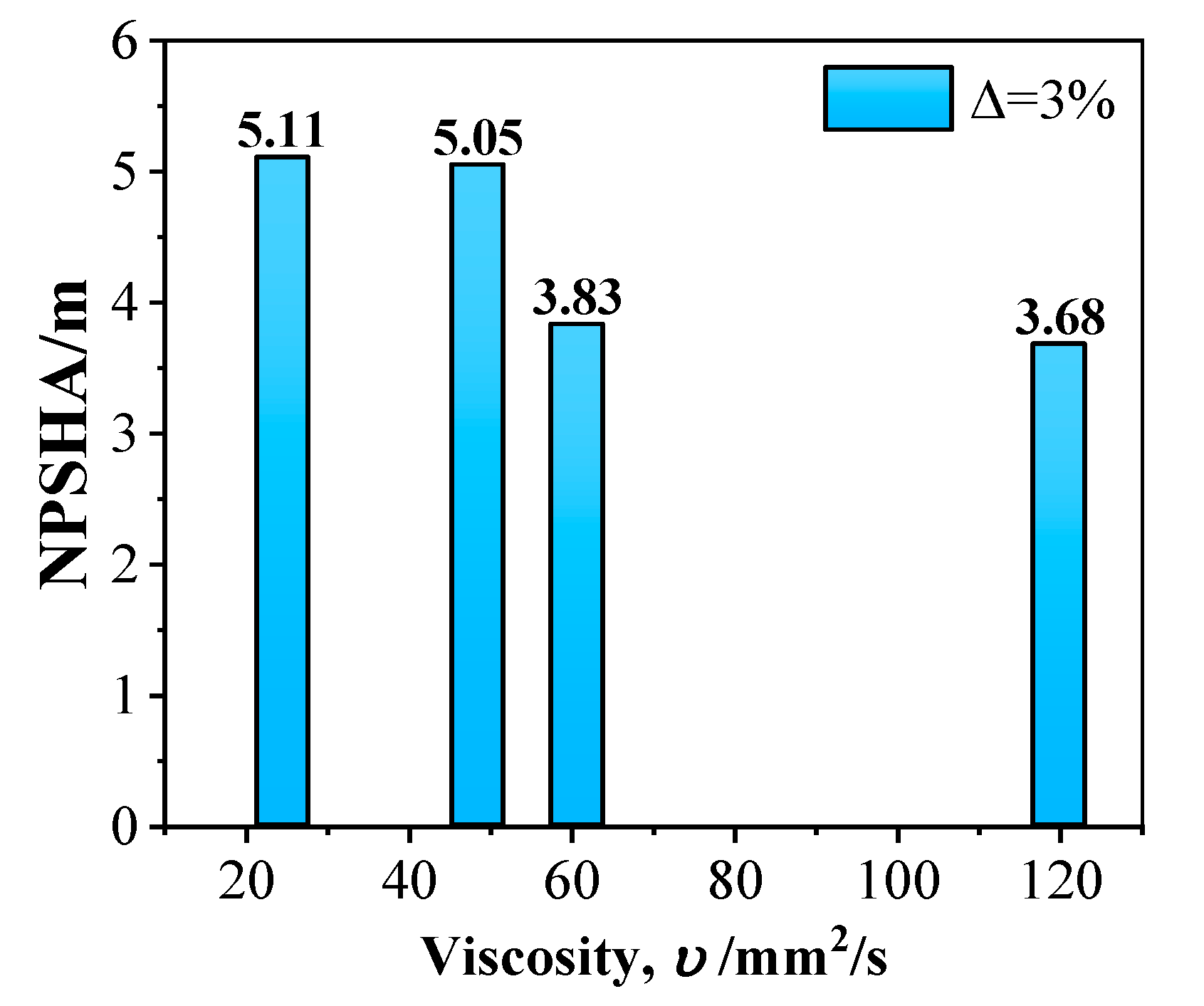
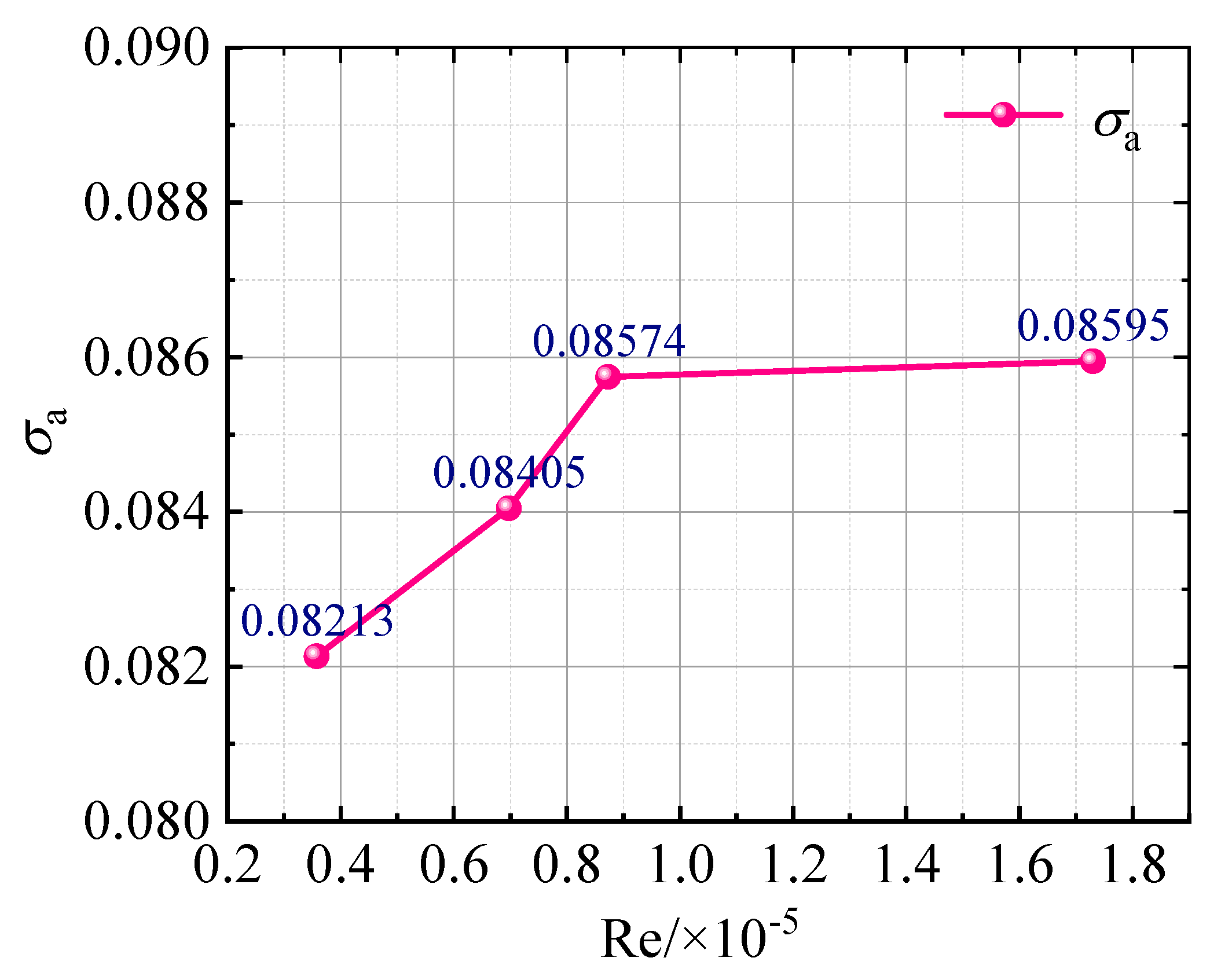
- The Net Positive Suction Head-available decreased as the fluid viscosity increased under the critical cavitation condition. It decreased from 5.11 m to 3.68 m as the fluid viscosity increased from 24.46 mm2/s to 120.0 mm2/s. Cavitation was more prone to occur in the pump impeller under high viscosity condition. The cavitation number increased from 0.08213 to 0.08574 when the Reynolds number increased from 3.58 × 104 to 8.73 × 104, which also demonstrated that the pump cavitation characteristics would be deteriorated as the fluid viscosity increased when the flow rate was held constant.
- (2)
- In general, the VVF reduced along the impeller passage. Under the critical cavitation condition, the VVF was basically unchanged as the fluid viscosity increased from 24.46 mm2/s to 48.48 mm2/s. Then, the VVF around the leading edge of the blade significantly reduced as the fluid viscosity increased to 60.70 mm2/s. The area occupied by the vapor increased with the fluid viscosity. Nearly half of the flow passages were occupied by cavitation bubbles when the fluid viscosity increased to 120.0 mm2/s.
- (3)
- The VVF on the suction surface was gradually spread out from the leading edge to the trailing edge of the blade, and the VVF on both the suction surface and pressure surface increased with the fluid viscosity. When the fluid viscosity was 24.46 mm2/s, the vapor on the suction surface was mainly distributed in the region with the streamwise between 0 and 0.36; while the high VVF range increased to the streamwise of 0.42 when the fluid viscosity increased to 120.0 mm2/s. The VVF in this region also approximately increased from 0.1 to 0.3.
- (4)
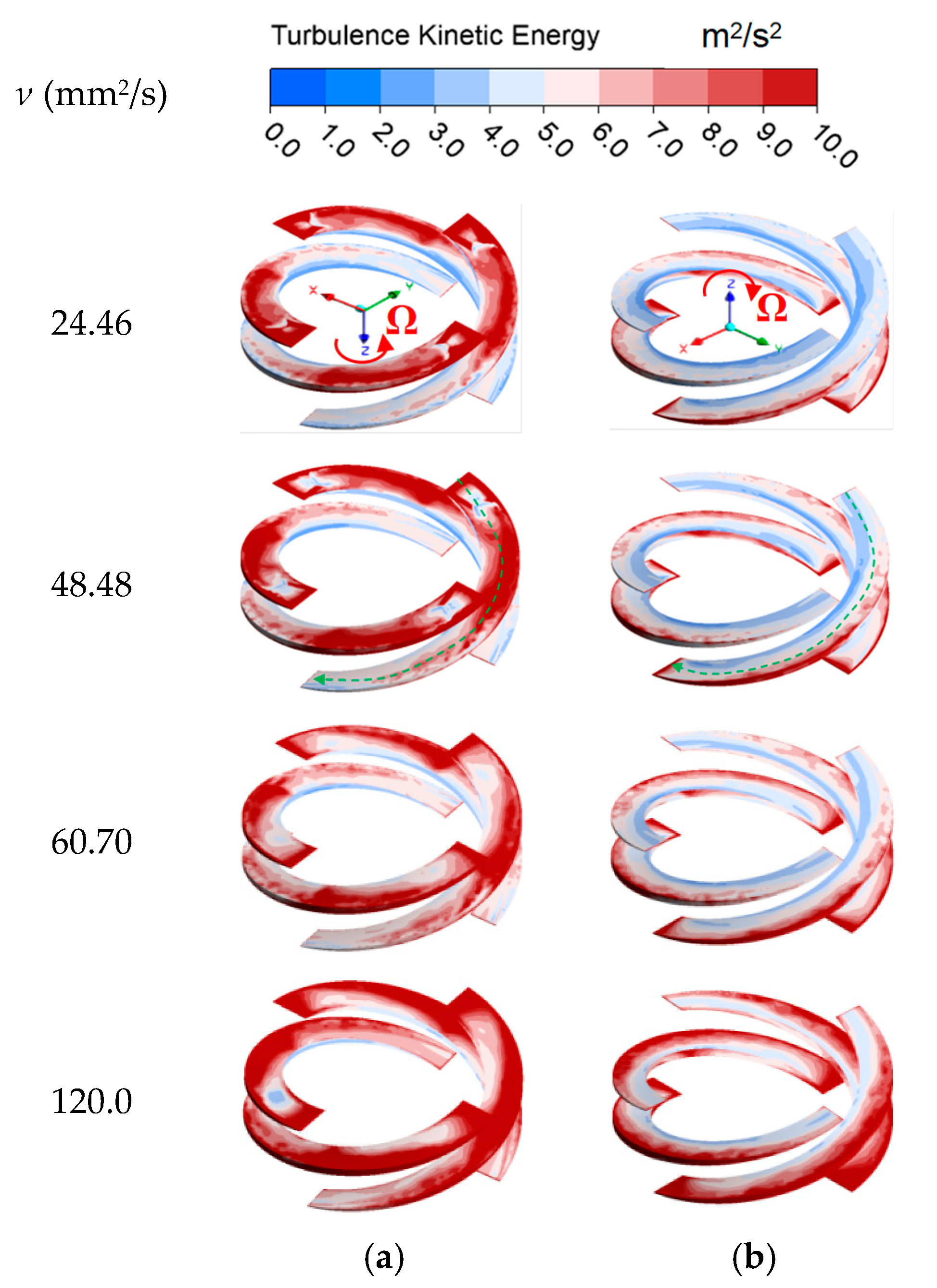
- The pressure distribution exhibited the opposite trend with the VVF distribution. The decrease in the pressure in the impeller led to the increase in the cavitation bubble. The turbulent kinetic energy on both the suction surface and pressure surface increased with the fluid viscosity, which also resulted in more cavitation bubbles being produced. The velocity distribution in the impeller suggested that the velocity was basically the same with the viscosity of 24.46 mm2/s and 48.48 mm2/s. When the viscosity was further increased to 60.70 mm2/s, the maximum velocity area in the impeller was relatively large.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gong, H.; Gioia, F.; Catalin, T.; Morrison, G. Comparison of multiphase pumping technologies for subsea and downhole applications. SPE Annu. Tech. Conf. Exhib. 2011, 1, 36–46. [Google Scholar]
- Zhu, J.; Zhang, H.Q. A review of experiments and modeling of gas-liquid flow in electrical submersible pumps. Energies 2018, 11, 180. [Google Scholar] [CrossRef]
- Zhang, J.; Cai, S.; Li, Y.; Zhu, H.; Zhang, Y. Visualization study of gas–liquid two-phase flow patterns inside a three-stage rotodynamic multiphase pump. Exp. Therm. Fluid Sci. 2016, 70, 125–138. [Google Scholar] [CrossRef]
- Serena, A.; Bakken, L.E. Experimental study of the influence of the operating parameters on the performance and capability of a mixed-flow multiphase pump. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Korea, 13–17 June 2016. [Google Scholar]
- Zhang, W.; Zhu, B.; Yu, Z. Characteristics of bubble motion and distribution in a multiphase rotodynamic pump. J. Petrol. Sci. Eng. 2020, 193, 107435. [Google Scholar] [CrossRef]
- Liu, M.; Cao, S.; Cao, S. Numerical analysis for interphase forces of gas-liquid flow in a multiphase pump. Eng. Comput. 2018, 35, 2386–2402. [Google Scholar] [CrossRef]
- Suh, J.W.; Kim, J.W.; Choi, Y.S.; Kim, J.H.; Joo, W.G.; Lee, K.Y. Development of numerical Eulerian-Eulerian models for simulating multiphase pumps. J. Petrol. Sci. Eng. 2018, 162, 588–601. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, Z.; Li, Y. Application of a non-uniform bubble model in a multiphase rotodynamic pump. J. Petrol. Sci. Eng. 2019, 173, 1316–1322. [Google Scholar] [CrossRef]
- Zhang, J.; Fan, H.; Zhang, W.; Xie, Z. Energy performance and flow characteristics of a multiphase pump with different tip clearance sizes. Adv. Mech. Eng. 2019, 11, 1687814018823356. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Zhu, H.W.; Ding, K.; Qiang, R. Study on measures to improve gas-liquid phase mixing in a multiphase pump impeller under high gas void fraction. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 062023. [Google Scholar] [CrossRef]
- Tan, L.; Xie, Z.F.; Liu, Y.B.; Yue, H.; Yun, X. Influence of T-shape tip clearance on performance of a mixed-flow pump. Proc. Inst. Mech. Eng. Part A J. Power Energy 2018, 232, 386–396. [Google Scholar]
- Xiao, W.; Tan, L. Design method of controllable velocity moment and optimization of pressure fluctuation suppression for a multiphase pump. Ocean Eng. 2020, 220, 108402. [Google Scholar] [CrossRef]
- Shi, G.; Wang, S.; Xiao, Y.; Liu, Z.; Li, H.; Liu, X. Effect of cavitation on energy conversion characteristics of a multiphase pump. Renew. Energ. 2021, 177, 1308–1320. [Google Scholar] [CrossRef]
- Li, W.G. Modeling viscous oil cavitating flow in a centrifugal pump. J. Fluids Eng. 2016, 138, 4031061. [Google Scholar] [CrossRef]
- Ge, M.; Petkovšek, M.; Zhang, G.; Jacobs, D.; Coutier-Delgosha, O. Cavitation dynamics and thermodynamic effects at elevated temperatures in a small Venturi channel. Int. J. Heat Mass Tran. 2021, 170, 120970. [Google Scholar] [CrossRef]
- Ge, M.; Manikkam, P.; Ghossein, J.; Subramanian, R.K.; Coutier-Delgosha, O.; Zhang, G. Dynamic mode decomposition to classify cavitating flow regimes induced by thermodynamic effects. Energy 2022, 254, 124426. [Google Scholar] [CrossRef]
- Ge, M.; Zhang, G.; Petkovšek, M.; Long, K.; Coutier-Delgosha, O. Intensity and regimes changing of hydrodynamic cavitation considering temperature effects. J. Clean. Prod. 2022, 338, 130470. [Google Scholar] [CrossRef]
- Ge, M.; Sun, C.; Zhang, G.; Coutier-Delgosha, O.; Fan, D. Combined suppression effects on hydrodynamic cavitation performance in Venturi-type reactor for process intensification. Ultrason. Sonochem. 2022, 86, 106035. [Google Scholar] [CrossRef]
- Liu, M.; Tan, L.; Cao, S.L. Influence of viscosity on energy performance and flow field of a multiphase pump. Renew. Energ. 2020, 162, 1151–1160. [Google Scholar] [CrossRef]
- Gié, P.; Buvat, P.; Bratu, C.; Durando, P. Poseidon Multiphase Pump: Field Tests Results; OnePetro: Houston, TX, USA, 1992. [Google Scholar]
- Liu, P.; Wang, Y.; Yan, F.; Nie, C.; Ouyang, X.; Xu, J.; Gong, J. Effects of Fluid Viscosity and Two-Phase Flow on Performance of ESP. Energies 2020, 13, 5486. [Google Scholar] [CrossRef]
- Patil, A.; Morrison, G. Affinity law modified to predict the pump head performance for different viscosities using the Morrison number. J. Fluids Eng. 2019, 141, 021203. [Google Scholar] [CrossRef]
- Ofuchi, E.M.; Cubas, J.M.C.; Stel, H.; Dunaiski, R.; Vieira, T.S.; Morales, R.E.M. A new model to predict the head degradation of centrifugal pumps handling highly viscous flows. J. Petrol. Sci. Eng. 2020, 187, 106737. [Google Scholar] [CrossRef]
- Li, W.G.; Zhang, Y.L. Computational cavitating viscous liquid flows in a pump as turbine and Reynolds number effects. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2019, 233, 536–550. [Google Scholar] [CrossRef]
- Nakamura, K.; Someya, T. Investigation into the tensile strength of real liquids: The application to lubricant oil. Trans. JSME Ser. B 1980, 46, 910–918. [Google Scholar] [CrossRef]
- Washio, S.; Takahashi, S.; Uda, Y.; Sunahara, T. Study on cavitation inception in hydraulic oil flow through a long two-dimensional constriction. Proc. Inst. Mech. Eng. Part J 2002, 215, 373–386. [Google Scholar] [CrossRef]
- Ishihara, T. Cavitation in Hydraulic Oil. Trans. JSME Ser. B 1982, 48, 1829–1832. [Google Scholar] [CrossRef]
- ANSYS. ANSYS, Release 19.0 ANSYS Documentation; ANSYS Inc.: Washington County, PA, USA, 2019. [Google Scholar]
- Singhal, A.K.; Athavale, M.M.; Li, H.; Jiang, Y. Mathematical basis and validation of the full cavitation model. J. Fluids Eng. 2002, 124, 617–624. [Google Scholar] [CrossRef]
- Gülich, J.F. Centrifugal Pumps, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2019; pp. 316–320. [Google Scholar]
- Pelz, P.F.; Keil, T.; Gro, T.F. The transition from sheet to cloud cavitation. J. Fluid Mech. 2017, 817, 439–454. [Google Scholar] [CrossRef]
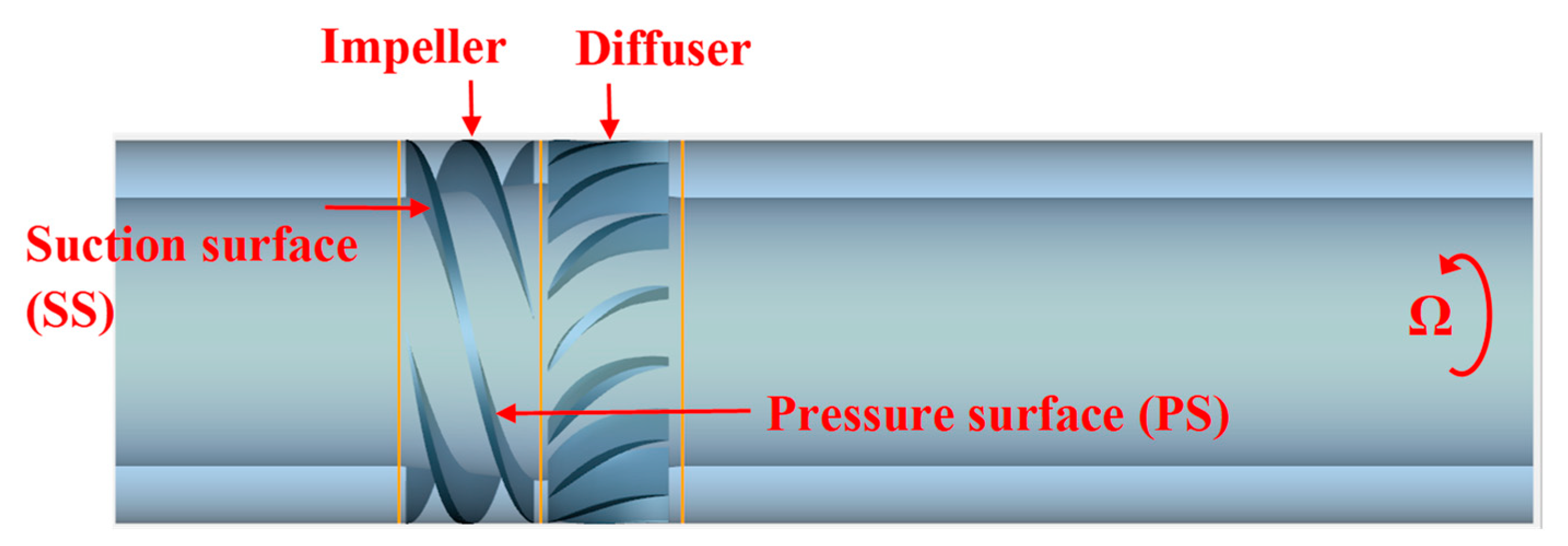
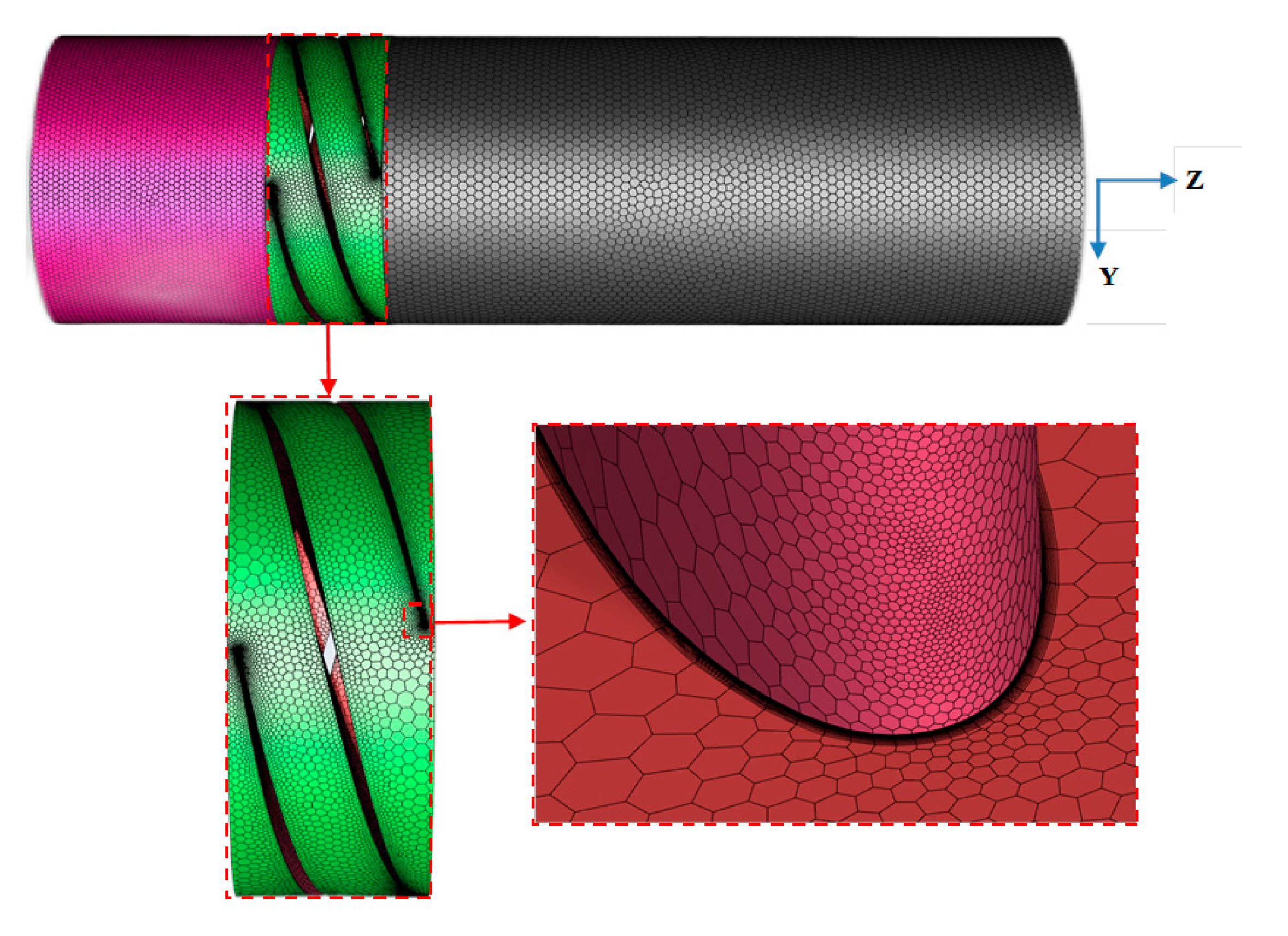
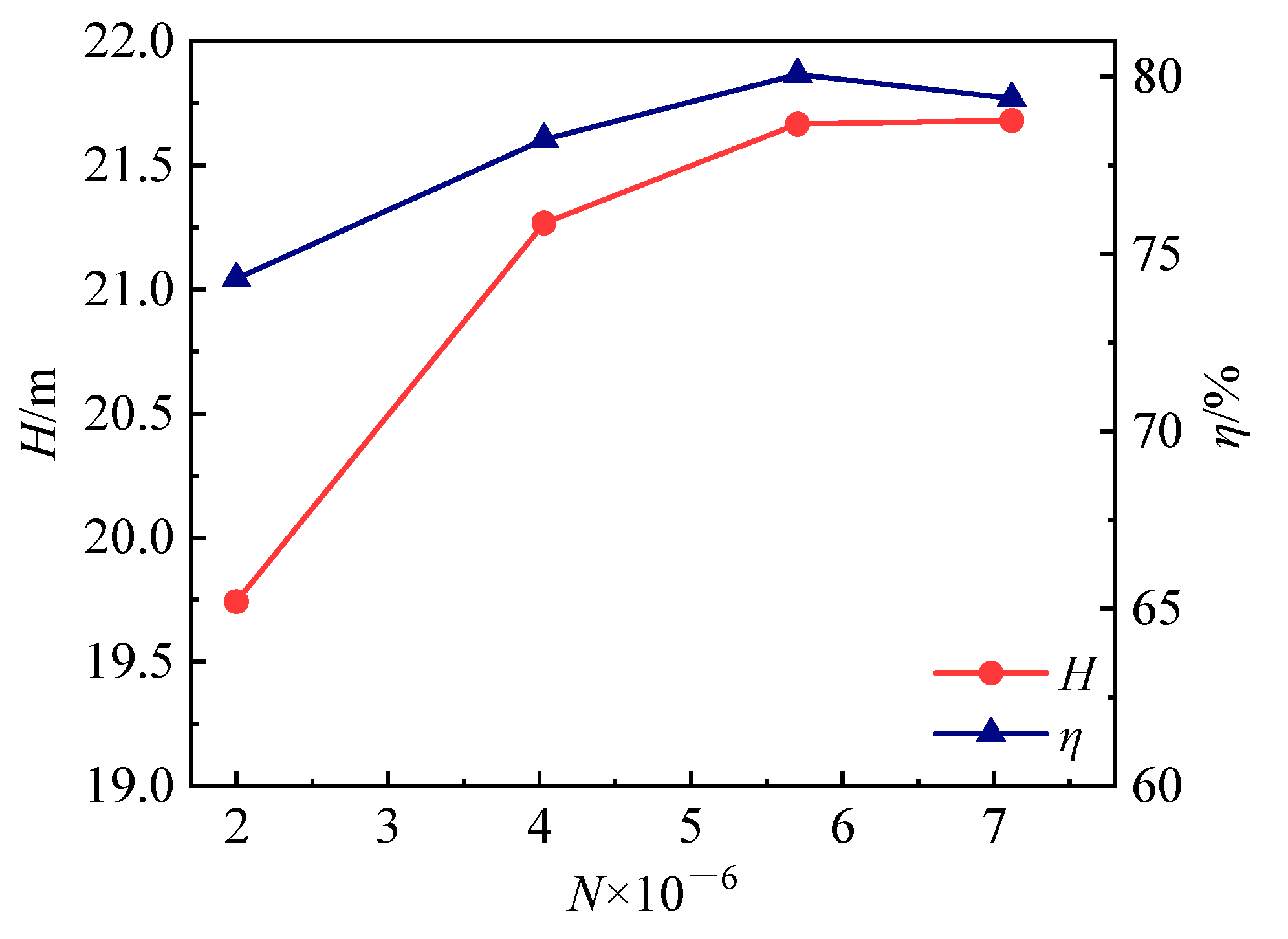

| Parameter | Impeller | Diffuser | Unit |
|---|---|---|---|
| Shroud diameter | 135 | 135 | mm |
| Hub inlet diameter | 94.5 | 105 | mm |
| Hub outlet diameter | 105 | 94.5 | mm |
| Axial length | 50 | 50 | mm |
| Number of blades | 4 | 15 | - |
| Blade wrap angle | 175.5 | 25.6 | ° |
| Tip clearance | 0.54 | 0 | mm |
| Component | Mesh Number (N) | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| Inlet section | 63,290 | 175,915 | 197,788 | 255,099 |
| Impeller | 1,758,452 | 3,668,160 | 5,275,676 | 6,570,704 |
| Outlet section | 178,913 | 186,142 | 230,522 | 292,592 |
| Total mesh number | 2,000,655 | 4,030,217 | 5,703,986 | 7,118,395 |
| Fluid No. | Medium | Density (kg/m3) | Kinematic Viscosity (mm2/s) | Dynamic Viscosity (Pa·s) | Saturated Vapor Pressure (Pa) | Surface Tension (N/m) | Non-Condensable Gas Content (ppm) |
|---|---|---|---|---|---|---|---|
| 1 | Liqud | 839 | 24.46 | 2.0530 × 10−2 | 4000.0 | 3.0 × 10−2 | 40 |
| Vapor | 0.4650 | 0.5916 | 2.7511 × 10−4 | ||||
| 2 | Liqud | 851 | 48.48 | 4.1256 × 10−2 | 4000.0 | 3.0 × 10−2 | 40 |
| Vapor | 0.4716 | 1.1723 | 5.5284 × 10−4 | ||||
| 3 | Liqud | 858 | 60.70 | 5.2081 × 10−2 | 4000.0 | 3.0 × 10−2 | 40 |
| Vapor | 0.4755 | 1.4881 | 7.0760 × 10−4 | ||||
| 4 | Liqud | 865 | 120.0 | 1.0380 × 10−1 | 4000.0 | 3.0 × 10−2 | 40 |
| Vapor | 0.4796 | 2.1364 | 1.0246 × 10−3 |
| Project | Parameter |
|---|---|
| Multiphase flow model | Mixture model |
| Cavitation Model | Singhal model |
| Turbulence model | RNG k-ε |
| Inlet boundary | Pressure inlet |
| Outlet boundary | Mass flow outlet |
| Wall condition | Smooth, no-slip wall |
| Pressure-velocity coupling | Coupled |
| Moment spatial discretization | Second Order Upwind |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, K.; He, D.; Zhao, L.; Guo, P. Influence of Fluid Viscosity on Cavitation Characteristics of a Helico-Axial Multiphase Pump (HAMP). Energies 2022, 15, 8149. https://doi.org/10.3390/en15218149
Ye K, He D, Zhao L, Guo P. Influence of Fluid Viscosity on Cavitation Characteristics of a Helico-Axial Multiphase Pump (HAMP). Energies. 2022; 15(21):8149. https://doi.org/10.3390/en15218149
Chicago/Turabian StyleYe, Kaijie, Denghui He, Lin Zhao, and Pengcheng Guo. 2022. "Influence of Fluid Viscosity on Cavitation Characteristics of a Helico-Axial Multiphase Pump (HAMP)" Energies 15, no. 21: 8149. https://doi.org/10.3390/en15218149
APA StyleYe, K., He, D., Zhao, L., & Guo, P. (2022). Influence of Fluid Viscosity on Cavitation Characteristics of a Helico-Axial Multiphase Pump (HAMP). Energies, 15(21), 8149. https://doi.org/10.3390/en15218149







