Abstract
Emissions from vehicles can be measured on the road or in laboratories using dynamometers that simulate the forces that a vehicle is subject to while driving on the road. In the light-duty vehicle regulations, only roller-type dynamometers are allowed. For hub-type dynamometers, due to the direct connection of the dynamometers to the wheel hubs, additional parameters that are used are rotational mass, dynamic wheel radius, and the tire force–slip relationship. Following up on an experimental study which showed that equivalent emission results can be achieved between roller- and hub-type dynamometers, this work presents and evaluates methods to determine parameters used by a hub-type dynamometer for mimicking roller-type dynamometer behavior. It also discusses methods to determine the parameters to simulate specific road conditions or when using only a hub-type dynamometer. The results show that using a constant dynamic radius for each wheel and a linear tire force–slip relationship is sufficient for emission measurement because typical errors in these parameters are practically negligible. A typical error in rotational mass results in a minor error in the determined forces during coast down, but the typical accuracy of this parameter is in parity with the difference allowed in the regulation. The final conclusion is that using the information already stated in the certificate of conformity (CoC) of the vehicle (for the coast down), and reasonably set parameters for wheel dynamic radius and the tire slip–force relationship, hub-type dynamometers should yield equivalent results to roller-type dynamometers.
Keywords:
chassis dynamometer; hub dynamometer; tire slip; wheel radius; coast down; rotational mass 1. Introduction
The emissions of vehicles are determined in laboratories with roller-type dynamometers that simulate the on-road behavior of the vehicle. Additionally, portable emission measurement systems (PEMS) are used for the determination of the emissions on the road under real driving conditions [1]. Nevertheless, testing in laboratories is expected to continue playing a major role as some conditions cannot be easily captured on the road (e.g., low and high ambient temperatures, altitudes, specific slopes) [2,3,4] and due to the better repeatability [5,6,7]. Regulations worldwide currently only allow roller-type dynamometers for the determination of emissions (sometimes called chassis dynamometers). Here, the term chassis dynamometer refers to both roller- and hub-type dynamometers.
Chassis dynamometers are used to simulate the behavior of a vehicle on the road by applying forces or torques so that the vehicle drivetrain accelerates and decelerates the same way as on a road. This way, the real driving emissions of vehicles can be estimated in laboratories. In a roller-type dynamometer, the vehicle is placed on top of rotating drums that mimic the road and act as the interface between the vehicle and the dynamometer. For the hub-type dynamometer, on the other hand, the vehicle wheels are removed, and the dynamometers are rigidly coupled to the vehicle’s wheel hubs. Thus, in this case, the interface between the vehicle and the dynamometer is at the vehicle’s wheel hubs.
It is important to understand the differences between driving on the road and on chassis dynamometers [8]. During constant speed driving on roads or coasting with neutral gear, the vehicle is subject to three main forces acting to slow the vehicle down: air drag, tire-rolling resistance, and driveline friction (Table 1). The energy storage components are the mass of the vehicle, the rotating mass of wheels, and driveline components (Table 2). On both the roller- and hub-type dynamometers, the air drag force is not acting on the vehicle, and as the vehicle is stationary there is no energy storage due to vehicle mass. Rotational mass from driveline components is present as well as driveline friction. Rotational mass from wheels and tire-rolling resistance is present for the roller-type dynamometer. In the hub-type dynamometer, no wheels are present as energy storage and thus there is also no rolling resistance. This means that while the roller-type dynamometer simulates vehicle mass (and to a certain extent tire-rolling resistance), the hub-type dynamometer simulates vehicle mass, wheel rotational mass, and tire-rolling resistance.

Table 1.
Comparison of forces during on-road testing, with roller- and hub-type testing.

Table 2.
Comparison of energy storage during on-road testing, with roller- and hub-type testing.
The dynamometers replicate the conditions in the interface to the vehicle on the road by simulating the driving resistances and applying forces or torques so that the vehicle drivetrain is subjected to the same speed and torque as on a road. To accurately mimic real-world driving conditions, the simulation needs to consider, amongst other things, vehicle mass, rotational inertia, air drag, rolling resistance, wheel radius, and tire slip [9,10,11]. Since the two dynamometer types have different interfaces to the vehicle, specific considerations are necessary for the accurate replication of driving load. The transfer of road to the laboratory is typically performed with a coast down procedure. The wheels’ inertia is mechanically included in the road load for roller-type dynamometers, while for hub-type dynamometers, it is simulated. On the other hand, hub-type dynamometers can be used to simulate road cases that are very difficult or impossible to simulate on a roller-type dynamometer (e.g., varying road conditions such as ice). Emissions during real driving conditions have increasingly become the focus of the regulations. However, the road conditions, such as temperature and traffic, are not possible to control. For this reason, transferring road trips to the laboratory and changing various parameters to study their impact is necessary.
While fixed parameters simplify the setup, they may also limit the possibility to obtain accurate results. As an example, the tire-rolling radii for a roller-type dynamometer can differ from the rolling radii in real-world driving conditions. In fact, the wheel dynamic rolling radius is not truly constant, and depends on temperature, tire pressure, and vehicle loading [12,13]. The tire slip–force relationship, or longitudinal stiffness, depends on tire and road properties, vertical loading, contact patch shape, and tire pressure [10,14]. While it may be important, to get as close as possible to real-world driving, to accurately simulate the tire dynamic radii and force–slip relationship, it is sometimes preferable to simulate different conditions or set specific values to have comparable results from the two types of dynamometers or even specific on-road conditions. A recent study showed that the hub-type dynamometers can be used interchangeably with the roller-type dynamometers for vehicle exhaust emission measurements [15]. An open question from the study was the sensitivity of the results concerning the parameters and the properties used.
As there is lack of literature on hub-type dynamometers, this paper presents the theoretical basis of both roller-type and hub-type dynamometers. The differences are highlighted and the main parameters for hub-type dynamometers used to replicate the powertrain loading of a roller-type dynamometer system as well as real-world driving are shown and evaluated. Experimental methods to determine and set these parameters are also presented. Furthermore, the impact of tire slip–force relationship, rotational mass, and wheel dynamic radii on vehicle emissions is demonstrated. The focus is normal driving (e.g., with type approval cycles), but the results could be the basis for future assessment of more extreme cases, e.g., high dynamic effects, slippery roads, etc.
2. Materials and Methods
2.1. Test Facilities
The tests were conducted at the European Commission Joint Research Centre (JRC) (Ispra, Italy) vehicle emissions laboratory (VELA 8). The laboratory was equipped with a four-wheel drive (4WD) roller-type dynamometer and emission measurement equipment for, amongst others, CO, CO2, NOx, and particles. The roller-type dynamometer for the laboratory was an AVL Zöllner (Roadsim MIL 4 × 4). During this work, the VELA 8 laboratory was also equipped with a hub-coupled dynamometer from Rototest (Energy 4WD) for the comparison. The tests were conducted first with the roller-type and then with the hub-type dynamometer. The laboratories and the equipment used are also described in more detail elsewhere [15]. Table 3 presents an overview of the dynamometers.

Table 3.
Characteristics of dynamometers.
The test vehicle was a 2019 Euro 6d-temp 1.6 L diesel-fueled engine with 85 kW max power, front wheel driven, and with a manual transmission. The test cycle was the worldwide harmonized light vehicles test cycle (WLTC) and a speed ramp test (idle, 50 km/h, 90 km/h, 130 km/h, and the inverse order to idle).
2.2. Measurement Signals
While there is an abundance of measurement signals available from the emission measurement systems and the dynamometers, only a few of them are important for the determination of tire force–slip relationship, rotational mass, and tire dynamic radius. These signals were all measured either directly from the dynamometer systems or from the vehicle itself (Table 4).

Table 4.
Noteworthy measurement signals and their availability from respective sources. Asterisks (*) indicates necessary signals to match hub- and roller-type dynamometers. n/a = not applicable.
Wheel rotational speeds were obtained from the CAN (controller area network)-bus of the vehicle. Since the actual signal specification was not available, the hub-type dynamometer speed was used for calibration of the vehicle-collected wheel speed. This calibration can also be performed using the engine speed and gear ratio. In case the wheel speeds are not available, an average speed of the driven wheels can be calculated in the same manner. Other signals that were obtained from the vehicle CAN-bus were throttle and brake pedal position. Due to differences in signal processing between vehicle CAN signals and dynamometer signals, the measurements have been filtered and manually time-corrected to align frequency content and timing.
3. Theoretical Background
3.1. Road Coast down Procedure
For regulatory purposes, to determine the forces acting on the vehicle, a coast down test on a test track, a test with torque meters installed on a vehicle on a test track, or a test performed in a wind tunnel can be conducted. The coast down is the most widely applied method among vehicle manufacturers. During this test, the warmed-up vehicle is accelerated to a speed 10–15 km/h above the first reference speed point on a flat road, after which the gear is set to neutral, and the vehicle is left to decelerate to almost standstill without braking and without moving the steering wheel (Figure 1). For the worldwide harmonized light vehicles test cycle (WLTC) and procedure, the first reference speed point is 130 km/h. The coast down is performed at temperature conditions between 5 and 35 °C. The deceleration times are measured in speed intervals and transferred to forces for each reference speed point (Fj) by considering the rotational mass with the following equation:
where mav (kg) is the arithmetic average of the vehicle test masses at the beginning and end of coast down, mr (kg) is the rotational mass, Δv is the speed interval (km/h) (= 5 km/h), and Δtj (s) is the harmonic average of alternate coast down time measurements at velocity vj.
Fj = (mav + mr)/3.6 · 2 · Δv/Δtj,
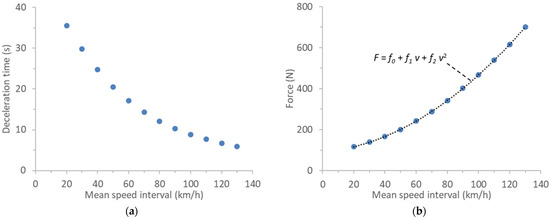
Figure 1.
Transfer of vehicle behavior from road to laboratory: (a) on-road coast down deceleration times, and (b) conversion of deceleration times to forces (Equation (1)).
The rotational mass, mr, can be measured, calculated, or set to 3% of the vehicle’s reference mass (sum of the mass in running order and 25 kg). The deceleration (force–speed) curve is approximated by a quadratic equation using the least squares method. The three resulting correlation coefficients are referred to as “road load parameters” (f0–f2). Details regarding the physical meaning of these parameters can be found elsewhere [11,16,17,18]. The three coefficients are further corrected to reference conditions (20 °C and 100 kPa with air resistance correction factor), for the wind, theoretical test mass, and rolling resistance correction factor (see also [19]).
3.2. Chassis Dynamometer Adaptation
The vehicle on the roller- or hub-type dynamometer follows a similar procedure, and the dynamometer coefficients are adjusted to achieve the same deceleration times for the given speed intervals as measured during the coast down test. This procedure is called chassis dynamometer load setting (sometimes adaptation or derivation). For both dynamometer types, the vehicle remains stationary during the test. In the roller-type dynamometer case, the vehicle is restrained from movement; in the hub-type dynamometer case, this is not required as no horizontal forces are acting on the vehicle. Thus, the dynamometers impose the motion-related resistances of the vehicle.
If the vehicle is tested on a 4WD roller-type dynamometer and if both axles are rotating and influencing the dynamometer measurement results (i.e., in 4WD mode), the equivalent inertia mass of the dynamometer is set to the applicable test mass. Otherwise, the equivalent inertia mass of the dynamometer is set to the test mass plus either the equivalent effective mass of the wheels and shafts not influencing the measurement results or 50% of mr. For the hub-type dynamometer (where the wheels are not present), the wheels’ rotating masses are always added to the test mass.
When comparing hub- and roller-type dynamometers, it should be clarified that for the road load determination (and the determination of forces) using coast down, the same target settings (times, test mass, rotational mass) need to be applied to both dynamometer types in order to achieve the same reference conditions [15].
3.3. Vehicle Road Load Simulation in Dynamometers
For vehicles with internal combustion engines, the exhaust emissions depend mainly on the speed and load of the engine. These properties, in turn, are a function of the forces and speeds at the vehicle road contact patch. Neglecting any road gradients, the total longitudinal force, Fl (for simplicity, F), at the surface (i.e., all the tire–road contact patches), that is required to drive the vehicle is [9,10,11]:
where TM is the test mass (kg) (could be the mav of the on-road coast down), mr is the rotational mass (kg) (representing the equivalent effective mass of all the wheels and vehicle components rotating with the wheels on the road while the gearbox is placed in neutral), v is the vehicle speed (m/s), a is the acceleration (m/s2), and f0–f2 are polynomial coefficients, together representing tire-rolling resistance, air drag, and drivetrain friction. To simulate the vehicle resistance in the dynamometer, it is necessary to estimate the parameters f0–f2, TM, and mr. This is performed with the chassis dynamometer adaptation (see Section 3.2). To achieve the appropriate force, the roller-type dynamometer applies the appropriate torque, MR (Nm):
where R (m) is the roller diameter.
F = f0 + f1 · v + f2 · v2 + (TM + mr) · a,
F = MR/R,
At the same time, the vehicle drivetrain is subjected to hub torques at each wheel hub such that the total tires’ traction force, F (N), is the sum of each tire traction force. For simplicity, the generic equation applicable to each wheel is given as:
where F is the tire traction force (N), MH (N m) is the hub torque, and rd is the wheel (tire) dynamic radius (m). When considering tire to road slippage, this gives the following equation for the wheels’ rotational speeds at the hub, nH or n for simplicity (rev/s) [9,10,14]:
where v is the (actual) vehicle speed (m/s), and s is the tire longitudinal slip (-) in the tire–road contact patch of the individual wheels.
F = MH/rd,
n = v · (1 − s)/(2 · π · rd),
For the hub-type dynamometer, the parameters in Equation (2), f0–f2, TM, and mr, can be obtained using a similar procedure as for the roller-type dynamometer. Other quantities are the wheel dynamic radius, rd, and the tire slip, s. The determination of these quantities will be discussed in the following sections (Section 3.4, Section 3.5 and Section 3.6).
Finally, disregarding braking, neglecting the drivetrain dynamics, and assuming the same gear ratio for all driven wheels, the engine speed and load is simply given by:
where nE is the engine speed, ME is the engine torque (N m), and igr is the gear ratio of the vehicle transmission.
nE = n · igr (for all driven wheels),
As mentioned earlier, for a roller-type dynamometer, the dynamometer-to-vehicle interface is the tire–drum contact patch, which means that only Equations (2) and (3) are necessary to simulate the vehicle load. As the surface of the drums of the roller-type dynamometer is fixed, it, in turn, means that the slip and radius of Equations (4) and (5) become, at each instant, the result of the roller drum-to-tire interface. For the hub-type dynamometer, on the other hand, the interface between the vehicle and the dynamometer is at the wheel hub, meaning that Equations (4) and (5) are used together with a few additional parameters. As can be seen from the equations, a third alternative is to use an engine dynamometer that simulates all five equations (i.e., Equations (2), (4)–(7)). The benefits and drawbacks of using this alternative are outside this paper’s scope.
Depending on the objective, the dynamic radius and tire force–slip relationship can be determined either on the roller type for close correlation with tire–drum behavior, or through road measurements for closer correlation with real-world tire–road behavior [13], or as shown in later sections, by use of table lookup or even default values.
3.4. Rotational Mass and Inertia
As mentioned earlier, the rotational mass, mr, is the equivalent effective mass of the rotating wheels and rotating vehicle components with the gearbox in neutral. The equivalent effective mass is defined as the mass, that when used in the motion equations expressed as translational motion, gives the same result as if the inertia is used in a rotating frame of reference. Using a simple energy analogy, it is easy to see the relationship between a rotating inertia and a mass in motion. The rotational energy of a body, and the corresponding motion energy of the equivalent mass, are as follows:
where Er and Em are the rotational and motion energies (J), I is the inertia (kg m2), mr is the equivalent effective mass (kg), w is the rotational speed (rad/s), and v is the motion speed (m/s). With the assumption that the rotating body with radius, rd, is rolling slip-free on a surface, these energies will be equal if the equivalent mass is set to:
where mr is the equivalent mass (kg), I is the inertia of the rotating object (kg m2), and rd is the wheel dynamic radius (m).
Er = ½ I w2,
Em = ½ mr v2,
mr = I/rd2,
As discussed before, while the wheels are present for roller-type dynamometer tests, they must be simulated for the hub-type dynamometer, and hence representative values for wheel inertias are required. The moment of inertia about the wheel spin axis can be estimated using one of two common techniques. Either the indirect method using the torsional pendulum technique [20], or the direct method through angular acceleration and measurement of torque. The following relationship can be used to calculate the inertia, I (kg m2):
I = MH/ω,
3.5. Dynamic Radius
The hub-type dynamometer measures the rotational speed and torque at the hub independently. Rotational speed and torque are converted to vehicle speed and force using the dynamic tire radius (Equation (5)). Dynamic radius is defined as the distance of the wheel center from the road [13]. For no-slip conditions, it is easily obtained by setting the slip, s = 0, in Equation (5), thus obtaining:
where, v is the (actual) vehicle speed (m/s), and n is the wheel rotational speed (rev/s) for the respective wheel. The no-slip condition, for example, is the case for the rear wheels during coasting of a front wheel drive vehicle, where the forces are typically less than 10 N. According to parametrizations for normal tires, this is equivalent to a tire slip in the range of 0.01%, and is thus negligible (see [14]).
rd = v/(2 · π · n),
The dynamic radius, rd, could also be measured by simply measuring the distance from the tire–road contact patch to the center of the wheel when in motion, but for obvious reasons this is impractical in many situations. Noteworthy is that the dynamic radius, rd, is slightly smaller than the unloaded wheel radius due to the tire carcass deflection, but larger than the loaded wheel radius [14]. Depending on the accuracy sought, a static loaded radius may be used as an alternative to the dynamic radius [21].
3.5.1. With Roller-Type Dynamometer
For the estimation of the dynamic radius, it is suggested to set the vehicle in neutral gear and the roller-dynamometer at constant speed mode at 80 km/h. In this case, the slip is negligible, and Equation (12) can be used to determine the dynamic radius. The choice of 80 km/h is based on EU regulation 2017/1151 sub-Annex 4, p. 4.4.3.1 for the on-road measurement and calculation of running resistance using the torque meter method (with constant speed of 80 km/h). The data for the analysis, i.e., speed and wheel rotational speed, can be obtained from the dynamometer and the vehicle, respectively.
The dynamic radius may also be determined during a coast down procedure while the vehicle and wheel rotational speed are simultaneously measured, with a procedure similar to the one that will be discussed in the next section.
3.5.2. Without Roller-Type Dynamometer
If a roller dynamometer is unavailable, the procedure to experimentally determine the dynamic radius can be performed on the road or on a test track. For the roller-type dynamometer setup, the vehicle ground speed measurement and the means to perform the procedure were provided by the dynamometer. This means that both the procedure and the source of ground speed measurement need to be adjusted for the road.
A constant speed test in neutral gear cannot be conducted on a test track without additional towing. This is because the traction forces need to be close to zero to avoid interference from the slip. With zero traction forces, the vehicle will slow down as soon as the traction is removed by setting the vehicle in neutral gear. Therefore, the vehicle needs to be towed at a constant speed to replicate the conditions of the roller-type dynamometer.
Another alternative is allowing the vehicle to coast while the vehicle and wheel rotational speed are measured. Preferably, a wide range of speeds should be covered (e.g., 20 to 130 km/h). The dynamic radius is then calculated at every sample point using Equation (12), and the result is then averaged. In fact, because dynamic radius can change with speed, it may be beneficial to have data for multiple speed points spanning the operational region. As tire temperature also influences radius, it is preferred that determination is conducted at representative temperatures for the highest accuracy.
Regardless of the method, it is necessary to measure the true vehicle ground speed to perform the calculation in Equation (12). In production vehicles, the vehicle speed is usually calculated using the wheel angular speed together with the wheel radius, thus assuming that the radius is well-known and constant. Therefore, the onboard calculated speed of the vehicle cannot be used to accurately determine the dynamic radius. Instead, the true vehicle speed needs to be measured by some other means. This can, for example, be accomplished by using a high-precision global positioning system (GPS) without the need for real-time kinematic (RTK) positioning, as shown in detail elsewhere [22]. For vehicles with built-in GPS, no additional hardware is necessary to conduct the measurement, with a loss in the measurement accuracy.
As an alternative, assuming a constant dynamic radius in function of speed, the total travelled distance and number of revolutions can be used. This is seen by integrating Equation (12) as follows:
where d is the travelled distance (m) and Nrev is the number of revolutions for the wheel. Hence, it is sufficient to measure the number of revolutions for the wheel for a, possibly fixed, and/or well-known distance. Mathematically, Equations (12) and (13) are equivalent. Hence, the choice of method depends on the availability of accurate and synchronized measurement data.
3.5.3. Influencing Parameters
Several publications discuss dynamic radius as a function of speed, load, inflation pressure, and temperature, e.g., [12,13]. In [12], it was suggested that the radius varies by about 0.3% (roughly 1 mm for a wheel with a 300 mm radius) almost linearly with speed in the range 20–120 km/h, while the dependence on pressure is about 1% (roughly 3 mm for a wheel with a 300 mm radius) in the pressure range of 140–260 kPa. Similarly, in another study [13], the difference was about 0.6% for pressures in the range 180–300 kPa for a similar wheel radius.
In [12], it was stated that temperature impacts inflation pressure, even though the temperature dependence was not discussed directly. It was also noted that the curved contact patch generated by the drum on a roller-type dynamometer impacts the dynamic radius of the tire so that it becomes smaller than for real road conditions.
Due to the dependence of rd on speed, pressure, and loading, it may be important to determine rd at the conditions that need to be simulated. While this is possible if a roller-type dynamometer is available, some corrections might be needed for on-road testing based on the literature cited above. One question is how much rd varies during a type-approval cycle (e.g., WLTC) on the roller-type dynamometer and whether a constant value is adequate. The topic will be addressed experimentally in Section 4.2.2.
3.6. Tire Force–Slip Relationship
Slip is defined as the relative difference between vehicle speed and tire circumferential speed. Tire slip is a function of external forces, geometry, and speed and has been extensively studied for a wide range of applications [14]. For small tractive forces (dry asphalt and small accelerations), there is practically a linear correlation between slip and traction, or longitudinal, force, e.g., [22]:
where Fnormal is the road to wheel normal force pressing the tire surface against the contact path, Cx,linear (-) is the tire longitudinal stiffness, and s (-) is tire slip.
F = Fnormal · Cx,linear · s,
For larger forces, the relationship becomes nonlinear and tire models such as the Pacejka magic formula can be used [14]:
where Bx, Cx, Dx, and Ex are curve shape parameters for the relation in the longitudinal (x) direction of the vehicle.
F = Fnormal · Dx · sin{Cx · arctan[Bx · s − Ex · (Bx · arctan(Bx · s))]},
To correctly simulate the tire-to-road (or tire-to-roller) interface, the hub-type dynamometer utilizes a tire model that describes the relationship of adhesion (grip) vs. slip. This enables a true road speed to be calculated and used in the simulations of road load. Due to the difference in loading of the wheels and the properties of the individual tires, the slip–force relationship is not necessarily the same for all wheels. To determine the constants of the force slip relationships for each wheel in Equation (14), the contact patch normal force and the slip are necessary for each wheel. The slip can be obtained using the definition in Equation (5), which requires measurement of the true vehicle speed as well as wheel rotational speeds. Even though all wheels can be different, it is more important for WLTC to have a good parameterization for the driven wheels because they can impact the engine operating point, while the non-driven wheels only affect braking. To obtain the normal force, Fnormal, of each wheel, the vehicle can be weighed using scales. For more complex cases, the reader is referred to the literature [23]. Other parameters of Equation (14) or (15) can be determined as described below.
3.6.1. With Roller-Type Dynamometer
The slip of the roller-type dynamometer can be determined using a simple load test at steady speed. The roller dynamometer is set at constant speed mode (80 km/h) and the driver applies positive and negative force using the accelerator pedal and the brake pedal and repeats this a few times to cover a wide range of slip values. The wheel rotational speed can be sampled using the vehicle’s CAN signal, while the vehicle speed can be obtained from the roller-type dynamometer. Since the filtering of the CAN signal and the dynamometer force signal are often unknown, these signals sometimes need to be filtered and manually time-corrected to align frequency content and timing.
3.6.2. Without Roller-Type Dynamometer
As with the dynamic radius, the procedure is to be adapted when determining the force–slip relationship for matching driving on the road. According to [22], both the radii and tire force–slip relationships can be determined using regular GPS velocity measurements together with onboard wheel rotational speed measurements. First, the acceleration can be calculated as:
where t is the sample time (s), v is the vehicle speed (m/s), and k is the sample number. Then, Equations (5) and (14) are combined and used in a linear regression to obtain both the slope of the longitudinal stiffness and the radius:
where is the longitudinal tire stiffness (N), TM is the vehicle (or test) mass (kg), rd is the wheel dynamic radius (m), nk is the wheel speed (rev/s), and vk is the vehicle speed (m/s) at time k. To ensure that there is enough data, a series of repeated accelerations and decelerations are suggested. Then, sections with acceleration or deceleration are selected for use in the calculations.
3.6.3. Influencing Parameters
The tire slip–force relationship, or longitudinal stiffness, depends on both the tire and the road properties and vertical loading, contact patch shape, and tire pressure [10,14]. The slip can be determined using previously described procedures for a specific combination of tire and road surface. However, it is not always possible to follow the previous procedures for type approval or simulations. In such cases, more generic values need to be used. For example, the slip slope (longitudinal stiffness) can take values between 23 and 40 for dry asphalt but 17 and 28 for wet road [24]. A later section discusses how much error is introduced by assuming a slip value (not determined experimentally).
4. Results
The following section will address the following topics: determination of rotational mass, wheel dynamic radius, and tire slip. For each parameter, the uncertainty introduced by simplifications will be discussed: error in the determination of the rotational mass, fixed radius vs. actual variable radius during a test, and simulated or default slip values vs. actual slip levels. The experiments were performed on a roller-type dynamometer, but the conclusions would be similar if the parameters were determined on the road.
4.1. Rotational Mass
The wheel inertia of the test vehicle was determined using the method described in Section 3.4 to be 0.83 kg m2 and was assumed equal for all four wheels (Equation (11)). The measurement aligns with similar experimental measurements, where values of 0.77 kg m2 for similar tire dimensions were reported, e.g., [25]. For the test vehicle in question, this translated to a total equivalent vehicle mass of 38.4 kg, equaling 2.65% of the vehicle test mass (Equation (10)). The radius calculation, used to determine the rotational mass, will be presented in the next section.
The equivalent mass is used to simulate the energy storage that, in case of roller-type dynamometer tests, is physically present in four-wheel mode (but set to 0.5 mr for two-wheel mode). Neglecting adding the wheels’ equivalent mass (i.e., set to 0) would result in a 2.65% underestimation of the load that the hub-type dynamometer system would apply during acceleration and braking maneuvers.
4.2. Dynamic Radius
4.2.1. General
The radius was calculated based on the constant speed test at 80 km/h using Equation (12) (Section 3.5.1). The vehicle (ground) speed was obtained from the roller dynamometer, and the wheel rotational speed from the CAN of the vehicle. The dynamic radius was determined to be 0.3062 m for the front tires and 0.3085 m for rear tires. The difference between the front and rear wheels may be explained by the different weight distribution between the front and rear axles of the car.
Radii measurements with the car standing (static loaded radius) before and after a WLTC yielded 305–306 and 308–309 mm for the front and rear tires, respectively (measurement uncertainty around 2 mm). The value from the look-up tables (loaded rolling circumference converted to radius) was 308.3 mm for the tire dimension 195/65R15 [26]. The differences are well within the experimental uncertainty: the uncertainty of the roller dynamometer speed measurement is much better than 0.8 km/h, which translates to 0.1% speed uncertainty for the 80 km/h test for the determination of the dynamic radius. The wheel rotational speed is also measured with an uncertainty of better than 0.1%. Thus, the uncertainty of the dynamic radius is <0.14% (error propagation rule for Equation (12)) or <0.44 mm for a 308 mm wheel. These values should be kept in mind for the interpretation of the results in the following sections.
4.2.2. Dynamic Radius for WLTC on Roller-Type Dynamometer
Figure 2 shows the dynamic radius of the four wheels when driving a WLTC on the roller-type dynamometer. To avoid calculation noise due to tire slip in the radii estimates, only sections with low acceleration, low force, and without braking have been used. As a result, the front wheels have somewhat fewer data displayed due to the vehicle being front wheel driven, i.e., higher forces acting on front wheels.
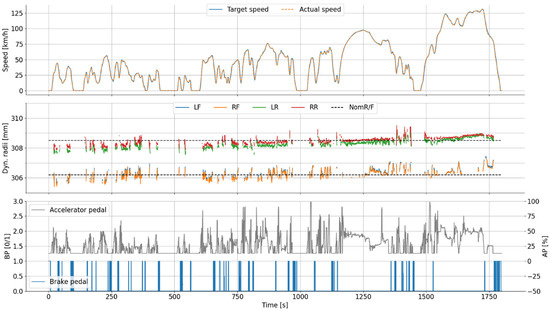
Figure 2.
Estimates of dynamic radii for a cold WLTC (Roller C1 = first cold roller cycle) together with vehicle speed, accelerator pedal (AP), and brake pedal (BP). The nominal radius obtained from the constant speed (80 km/h) test are shown as dashed lines for reference (NomF = 0.3062 m for the front tires and NomR = 0.3085 m for rear tires). LF = left front; RF = right front; LR = left rear; RR = right rear.
As it can be seen, both the left/right front (LF + RF) and rear (LR + RR) wheels’ radii increased in the region of 1 mm (0.3%) during the test cycle. The scatter plot of dynamic radii and speed is plotted in Figure A2a of the Appendix A.
The same radius estimation algorithm was also applied to five cold and four hot WLTCs in Figure 3. While all cycles showed very similar behavior, the four hot cycles all started a little higher and had a lower difference over the cycle. The differences over the cycles were about 0.5 mm from start to end for the cycles and within 1 mm in total.
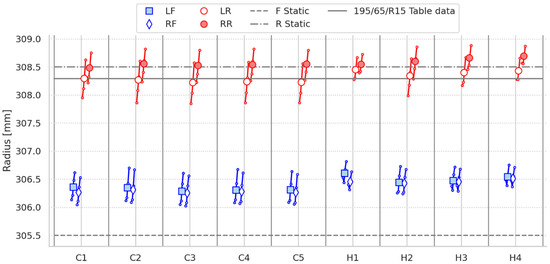
Figure 3.
Average dynamic radii for five cold (C1–C5) and four hot (H1–H4) WLTCs for each tire (LF, RF, LR, RR), together with table values (308.3 mm) [26] and the front and rear static radii average from before and after a WLTP (305.5 and 308.5 mm, respectively). Indicated in the plots are also average dynamic radii for Phases 1–4 of the WLTC (lines with four smaller markers in series Phase 1 to Phase 4, Phase 1 always lower). As can be seen, all the radii increased in a similar manner throughout the cycles. Also noteworthy is that the hot cycles started at a slightly higher radius than the cold. The maximal difference for each individual wheels was less than 0.3%, which is insignificant with respect to measurement accuracy.
For the roller-type dynamometer, the wheel loading did not change during the experiment, and the traction forces were close to zero for the data sections used in the calculations. Therefore, these effects can be excluded as a source of these changes. Other effects that are known to influence dynamic radius are speed and tire pressure, which depends on temperature. Their impact will be discussed in the next sections.
4.2.3. Speed Impact on Dynamic Radius
The WLTC experiments from Figure 2 and Figure 3 showed a gradual increase in radius from the start to the end of the cycles. In [12], the speed-dependent change was close to linear and about 0.3% (or ca. 1 mm for a 300 mm wheel) in the range 20 to 120 km/h. With a similar speed range and tire radius, the expected change is about 1 mm over a WLTC (the cycle starts with low speeds and ends with high speeds). While both figures indicate radii changes in the region of 1 mm for the cycles, Figure 2 does not support a linear speed dependence in the expected range. The figures also show that the hot WLTC started slightly higher than the cold, which speed dependence cannot explain. This may be due to the increased tire pressure used when conducting roller-type tests.
In addition to the WLTC experiments, the speed impact of the dynamic radius was evaluated on the roller-type dynamometer using a series of steady speed tests in the range of 50–130 km/h. The dynamometer was set in road simulation mode. Vehicle speed was obtained from the dynamometer while wheel rotational speed was obtained from the vehicle’s CAN-bus. All signals were sampled continuously throughout the experiment. Then, in the post-processing, the data were time-synchronized, operating points were identified, and finally, windows of stable data of about 100 s were selected for respective operating points. The experiment was setup in a manner where the speed operating points were repeated in reverse order to exclude other sources of difference, such as temperature and pressure.
Estimations of the dynamic radius using Equation (12) on the averaged data are plotted in Figure 4. The data show radii changes, but they do not give support for a linear speed dependence. While an increase of about 0.6 mm for the radius during the experiment can be seen, there is no correlation with the speed. Instead, these differences seem to originate from other sources, such as temperature. This may explain why the radius of the front wheels increased later than the rear wheels, since they are closer to the cooling fan that was placed in front of the vehicle.
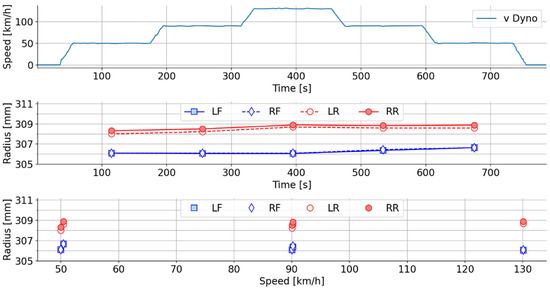
Figure 4.
Estimates of radius during the constant speed test. The top graph shows the speed of the dynamometer over time, the middle graph shows the radii estimates for the different constant speed regions over time, while the lower shows the calculated radii as a function of speed. LF = left front, RF = right front, LR = left rear, RR = right rear. The total increase in radius was about 0.6 mm for both front and rear wheels but there seems not to be any detectable speed dependence.
4.2.4. Temperature Impact on Dynamic Radius
During the measurements, temperatures for the non-driven (in this case rear) wheels were also measured. These temperature measurements are shown in the lower panel of Figure 5. As the temperature was measured on the outside of the tire, the measurements were subject to disturbance by cooling from the headwind fan as well as heating from brakes, and therefore do not represent the true internal tire temperature. However, the main conclusion is that there was an almost time-linear temperature increase during the measurement, except for periods where the vehicle was at a standstill. The scatter plot of dynamic radii and temperature is presented in Figure A2b of the Appendix A.
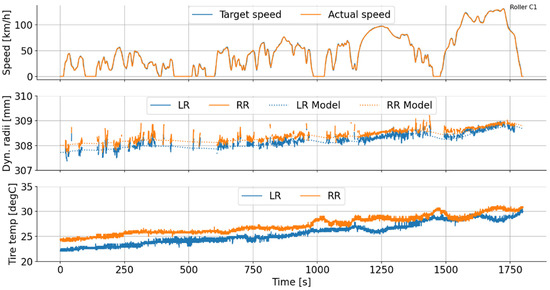
Figure 5.
Estimates of dynamic radius for the rear wheels (LR + RR), measured temperature, and speed for a cold WLTC. Together with the estimated radii, modeled radii based on a simple temperature model is shown (dashed). As can be seen, the simple model captures the behavior that the radii decreased during the periods of standstill.
A simple model was implemented to capture the radii cycle differences. The temperature was assumed to increase proportionally to the tire speed and to decrease proportionally to its difference to the ambient temperature. Then, the radius was modeled as a linear function of the modeled temperature. The physical interpretation is that the temperature increases the tire pressure, as is known from the well-known Avogadro’s law, and therefore also the radius. An example from this model applied to a cold WLTC is shown in Figure 5 together with the measured radius and temperatures. The constants were fitted to the radii estimates for the sections with low acceleration, low force, and without braking in the same manner as before.
While having no intention of making a quantitatively accurate model for the temperature (as this information is not available during typical testing), the model captures the behavior of the wheel radius changes. Thus, it indicates that the increasing radii may be explained by an increasing temperature.
The previous results showed that there was a gradual increase of the rd during the cycle of less than 1 mm, due to the increase of the tires’ temperature, with negligible contribution from the speed.
4.3. Slip
4.3.1. General
For the determination of slip, the roller-type dynamometer was set in constant speed mode and the procedure of Section 3.6.1 was followed. The speed and forces for this test are shown in Figure 6. The force levels of the experiment were similar to those in Figure A1 of the Appendix A (around 2000 N). As expected, when a positive force was applied to an axle, it rotated faster than the nominal speed, and vice versa. The slip slope (longitudinal stiffness), Cx,linear, was determined to be 34, a value well within the values in the literature for dry asphalt (between 23 and 40) [24] or between 30 and 50 [27].
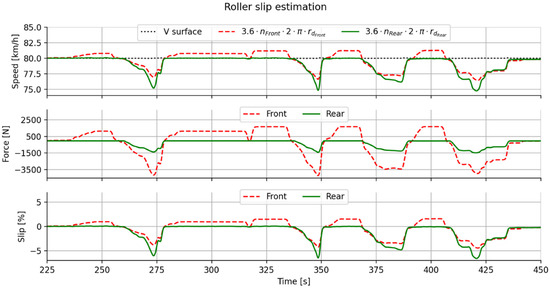
Figure 6.
Test for determination of tire model parameters in Equation (15): constant speed mode (80 km/h) at the dynamometer with acceleration and deceleration efforts from the driver (Section 3.6.1). For clarity, left and right wheel speeds have been averaged, but the data can also be used for each individual wheel. Upper plot: measured dynamometer surface speed (km/h) and wheel speeds (rev/s) converted to equivalent tire circumferential speed (km/h) using the dynamic radii, rd (m), Middle plot: traction force, F, measured on the roller-type dynamometer, and Lower plot: slip, s, as calculated using Equation (5).
A fit of the linear force–slip model from Equation (14) is shown in Figure 7. The y-axis plots the normalized force, which is the ratio of the traction force to the normal force. The maximal positive tire slip was about 1.7% for the front wheels, which is expected with a standard tire model for dry asphalt [14]. The small positive slip of 0.1% for the rear wheels at zero force was likely due to measurement noise and signal pathway disturbances, that introduces an error due to time alignment in data. For periods of constant force, this is not an issue. The measurement data showed an expected linear behavior for the tire slips. Looking at the tire slip vs. normalized force for the different wheels, it is evident that the grip for the rear wheels was significantly lower than for the front wheels, even though they were equal in terms of make and dimension. The cause of this is outside the scope of this study but may be addressed to the way the tire is compressed on the roller due to its curved surface [13].
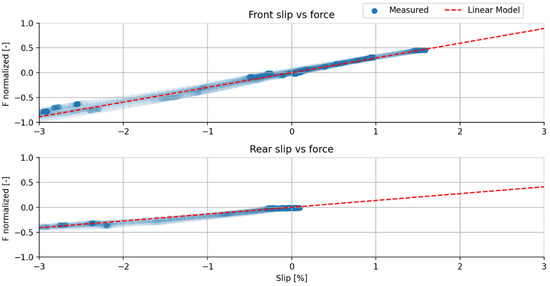
Figure 7.
Normalized force as a function of tire slip (blue) together with a linear (red dashed) approximation of the data.
4.3.2. Tire Slip for the WLTC at the Hub- and Roller-Type Dynamometers
To be able to compare the tire slip level between hub and roller measurements, it is necessary to calculate the dynamic radius for the roller measurements (see Equation (5)). The hub-type dynamometer used a set constant wheel radii for the experiments, while for the roller-type, since the actual wheels were used, their dynamic radii may vary. For tire slip comparison, the correct determination of the radius is important. This is because for a tire slip in the region of 0–1% (as for the WLTC), a radius error of 0.3% will introduce a significant inaccuracy in calculating the indicated tire slip level. As has been shown, the changes in dynamic radii over a cycle were slow and depended mostly on temperature (Figure 2). Therefore, the gaps between the operating regions where the radii are well-defined can be filled using either a temperature model or some other means of linear regression. An example of a tire slip comparison between a WLTC run on the roller-type dynamometer and the hub-type dynamometer is shown in Figure 8. For this case, the temperature model from Figure 5 has been used. As can be seen, the slip levels are quite similar for the two systems. Here, again, the rotational speed signals were sampled from the CAN-bus of the vehicle under test, while the vehicle speed was sampled from the respective dynamometer system. Some of the noise in the calculated tire slip is because there are different filters and varying time delays between the two signals, which is especially pronounced for high dynamic operating points. The general behavior of the slip for the two systems is similar, as shown.
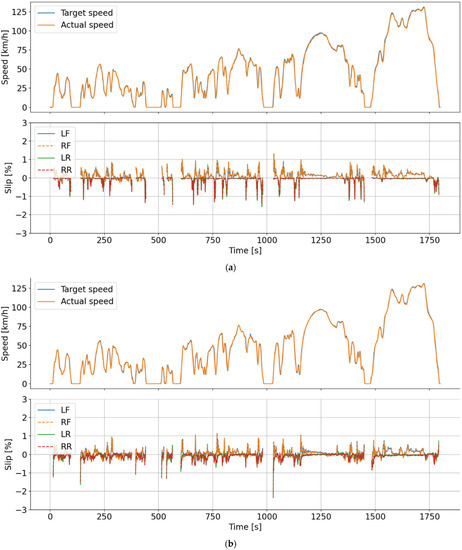
Figure 8.
Tire slip and speed for a hub-type (a) and a roller-type (b) dynamometer running a cold WLTC. The tire slip is calculated for operating points where the vehicle is moving, and the brakes are not applied. As can be seen, the magnitudes and general behavior are similar for the two systems.
4.3.3. Sensitivity Analysis of Slip
The previous section (Section 4.3.2.) showed that the tire slip on the roller-type dynamometer was accurately replicated at the hub-type dynamometer. The necessary step was to determine the force–slip relationship at the roller-type dynamometer in advance (Section 4.3.1.). The question raised is what if a roller-type dynamometer is unavailable and a default value is set. For example, the slip slope was determined to be 34, while values could vary ±20% [24]. Setting a wrong slip value (e.g., higher) will result in the wrong engine speed (e.g., higher) to reach the same speed (Equation (5)). To address this question, the lost WLTC positive traction work over the WLTC was calculated for different slip slope values. The lost work due to the slip was calculated comparing with a no-slip scenario. Table 5 summarizes the results. The slip introduces a small energy loss: around 0.35% for dry asphalt, and up to 0.7% for wet road.

Table 5.
Lost energy at the wheel due to various slip slope values for a WLTC. Lower values are for wet roads and higher values for dry asphalt.
5. Discussion
Chassis dynamometers are used to simulate the behavior of a vehicle on the road by applying forces or torques. Both roller- and hub-type dynamometers simulate the vehicle mass and the air drag, and hub-type dynamometers need to additionally simulate the rotational wheel mass and tire-rolling resistance.
The obvious difference between the two dynamometer types is the interface to the vehicle, hub vs. roller, although they also differ substantially in another aspect—the way that vehicle’s mass is simulated. While the roller dynamometer has a large mechanical inertia, that is used to simulate the vehicles mass during acceleration and braking, the hub dynamometer by design does not (see Table 3). For the dynamometers used in this study, the roller type had a mechanical inertia on one axle at similar levels with the total vehicle mass of the test vehicle (the exact value is compensated electrically). The hub type dynamometer had a mechanical inertia on one axle comparable to the vehicle’s wheels, a factor of almost 30 times. As the vehicle exerts no longitudinal movement while being tested in the chassis dynamometer, Newton’s second law of motion (force equals mass times acceleration) does not physically apply. That means that the force due to acceleration must be simulated. In the roller-type dynamometer case, this is mainly performed using its built-in mechanical inertia. A hub-type dynamometer with much lower mechanical inertia presents a challenge during dynamic events. While the mechanical inertia transforms its rotational acceleration and deceleration to force in a mechanical manner, the hub-type dynamometer that lacks this property has to compensate with a fast control system to apply the force electrically (i.e., torque). A slow control system would cause overshoot issues and could cause control issues for the vehicle itself. In addition to an adequately fast control system, the hub-type dynamometer must also consider the hub-coupling interface not to add parasitic losses (i.e., non-measurable losses), that may impact the accuracy of the coast down procedure. This study has used a hub-type dynamometer system exhibiting a millisecond torque response with less than 25 ms of 100% tractive effort response and a hub-coupling interface free of parasitic losses.
Based on the theoretical background that was presented, compared to the roller-type, the hub-type dynamometer needs the rotational mass, wheel dynamic radius, and tire slip as input parameters. Thus, to have comparable results between the two dynamometer types, these parameters need to be set accordingly to match the roller conditions. On the other hand, by varying these values, hub-type dynamometers can simulate road situations that roller-type dynamometers cannot.
The determination of the rotational mass is straightforward (through measurement of angular acceleration and torque). The dynamic radius can be easily determined with tests on the roller or on the road by setting up a low tire slip experiment (e.g., coast down or constant speed driven by the dynamometer). Finally, to determine the force–slip relationship, a test with forces resembling those necessary for the application is required (e.g., acceleration and decelerations). Vehicle speed (from roller or GPS) and wheel rotational speed (from vehicle CAN) are necessary inputs.
An experimental study showed that equivalent emission results can be achieved between roller- and hub-type dynamometers when fitting the parameters to mimic the roller surface properties. A similar approach to match the actual road would be expected to work and accurately simulate the road conditions. Although no such experimental data were available, the possible experimental approaches were presented.
The main question, however, is whether the hub-type dynamometer can be used independently for type-approval emission measurements. In other words, how can the parameters be determined with information already available in the vehicle’s certificate of conformity (CoC) (and without a roller-type dynamometer).
To answer this question, possible sources of variation, uncertainty, or error were discussed for each parameter. Table 6 summarizes the impacts of rotational mass, dynamic radius, and slip errors on the results.

Table 6.
Impacts of wheel radius, rd, slip, s, and rotational mass, mr, errors for various cases (coast down, engine operating point, distance).
The determination of the wheel rotational mass can be performed regardless of the used dynamometer type as long as the dynamic radius is known. Any error on the rotational mass during coast down will have a direct effect on the dynamometer coefficients for road load force. Any error on rotational mass during the test cycle will have a force impact during acceleration/deceleration, which is of lesser importance than an error during coast down. However, as rotational mass is typically around 3% of the test mass, even a 10% error will result in a 0.3% error in forces. For example, in an experimental study, the “true” rotational mass was determined to be 38.4 kg (or 2.65% of test mass), while the one that was determined by assuming 3% of the reference mass (as allowed in the regulation) was 41.4 kg (or 2.86% of the test mass) [15]. The difference of the two rotational masses was 8%.
The dynamic radius can also be determined without a roller-type dynamometer on a test track or on the road. The wheel radius acts as a scaling between vehicle and wheel rotational speeds. For any given vehicle speed and road force pair, a change of the wheel radius changes the corresponding wheel speed and torque but preserves the required drivetrain power. The change in drivetrain speed may, however, change the drivetrain losses. A lookup value [26] of rolling circumference for the tire dimension used in the test deviated less than 1% from the experimentally determined dynamic radius and may thereby be seen as an adequate alternative.
The change of the radius during a WLTC was shown to be <0.3% when using a roller-type dynamometer. This was attributed to the increase of the tires’ temperatures and corresponding internal pressure. These numbers are in parity with values found in the literature [12,13]. This variation was also close to the uncertainty of the experimental determination of the dynamic radius. The conclusion is therefore that the effect on the drivetrain of the cycle difference in radius is practically negligible, except for when estimating the level of tire slip in road or roller measurements. The tests showed that it is sufficient to use constant, but wheel-individual, radii for the hub-type dynamometer experiments.
The difference in wheel rotational speed and vehicle speed due to tire slip acts as an energy loss from the drivetrain to the ground. In other words, if the tire slip is 1%, the amount of traction energy lost in the wheel-to-ground contact is 1% of the drivetrain output energy. For the WLTC, the maximum slip during traction was <1.7%, and 0.37% on average. Analysis showed that the lost energy due to slip was 0.36% for the roller-type dynamometer. A 20% overestimation of the slip slope would result in 0.30% lost energy (−20%). These results indicate that using default values for dry asphalt is representative enough without introducing significant errors.
For the hub-type dynamometer, using the information already stated in the certificate of conformity (CoC) of the vehicle (for the coast down), and reasonably setting parameters, for example those discussed here, should yield equivalent results to roller-type dynamometers.
Finally, it should be mentioned that this study did not assess whether vehicles behave differently at roller- or hub-type dynamometers. Modern vehicles have various sensors (e.g., for obstacles, etc.) and sometimes need a “dynamometer” mode to operate properly when tested in roller- or hub-type dynamometers.
6. Conclusions
The type-approval of a vehicle includes measurements of CO2 and pollutants, which have to respect the emissions limits. The tests are conducted on chassis dynamometers with rollers, set in such a way that the forces that the vehicle is subject to while driving on the road are simulated on the chassis dynamometer. Hub-type dynamometers are connected directly to the wheel hubs, and thus some additional parameters need to be set to simulate the behavior of the wheels. The main questions were: (i) how to set these parameters to match a roller-type dynamometer, e.g., when their results need to be compared, and (ii) what values should be set in the absence of a roller-type dynamometer.
Due to the lack of literature on the topic, a theoretical analysis was presented. The additional parameters that were needed were: wheels’ rotational mass, dynamic wheel radius, and tire force–slip relationship. The experimental procedures and the appropriate equations to determine these parameters were presented.
The rotational mass can be determined either indirectly using the torsional pendulum technique or directly through angular acceleration and measurement of torque. The dynamic radius can be determined when the slip and the forces applied to the wheel are negligible, e.g., during coasting on the road or when a roller dynamometer is towing the vehicle. The slip can be determined by measuring the true vehicle speed and the wheels’ rotational speeds. Further analysis revealed that using constant but representative values from lookup tables for the slip and the radius did not introduce any significant errors. Similarly, a small error in rotational mass resulted in a minor error in the determined forces during coast down, but the typical accuracy of this parameter was in parity with the flexibility allowed in the regulation.
In view of the upcoming regulations and the focus on the emissions during real driving conditions, it is important to assess the impact of the test conditions. In addition to the driving style, ambient temperature, and altitude, the road conditions (dry or wet asphalt) would be of interest. The advantages of the dynamometers are that such parameters can be tested under controlled conditions, and the impact of each parameter can be separately evaluated.
Author Contributions
Conceptualization, C.E. and B.G.; formal analysis, P.Ö.; writing—original draft preparation, B.G. and P.Ö.; writing—review and editing, C.E. and G.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are available upon request from the corresponding author.
Acknowledgments
The authors would like to acknowledge the technical support of VELA 8 personnel (Marcos Otura, Fabrizio Forloni, and Mario Centurelli).
Conflicts of Interest
Per Öberg and Christian Engström are employed by Rototest, which manufactures, among others, hub-type dynamometers. The rest of the authors declare no conflict of interest. The opinions expressed in this manuscript are those of the authors and should in no way be considered to represent an official opinion of the European Commission. The mention of tradenames or commercial products does not constitute endorsement or recommendation by the European Commission.
Nomenclature
| Symbol | Unit | Interpretation |
| v | m/s | Vehicle speed |
| a | m/s2 | Vehicle acceleration |
| n | rev/s | Wheel hub, i.e., wheel rotational speed |
| nE | rev/s | Engine rotational speed |
| s | - | Tire road contact patch slip |
| rd | m | Wheel, or tire, dynamic radius |
| R | m | Roller drum radius |
| F | N | Longitudinal, or traction, force at the tire road contact patch |
| Fnormal | Normal force, i.e., force pressing two surfaces together | |
| MH | N m | Torque at the wheel hub |
| MR | N m | Roller dynamometer torque |
| ME | N m | Torque at engine |
| igr | - | Transmission gear ratio |
| I | kg m2 | Moments of inertia of wheel |
| mr | kg | Equivalent rotating mass |
| TM | kg | Vehicle mass, i.e., test mass |
| mav | kg | Average vehicle mass |
| f0, f1, f2 | various | Polynomial coefficients |
| w | rad/s | Rotational speed |
| ω | rad/s2 | Angular acceleration |
| Cx,linear | - | Tire longitudinal stiffness (slip slope) |
| Er | J | Rotational energy |
| Em | J | Motion energy |
| Nrev | - | Number of revolutions of wheel |
| d | m | Distance |
Appendix A
The force levels necessary for the parameterization experiment can be obtained, for example, by calculating the required force levels for driving a WLTC. These forces depend on the vehicle weight and the vehicle road resistance parameters (Equation (2)). Figure A1 shows the force levels that are necessary for driving a WLTC using the test vehicle that was used in this work. As can be seen, the absolute maximal forces are around 2000 N, reaching 2500 N in a few cases.

Figure A1.
Nominal forces required for running WLTC with the used test vehicle.
Figure A2 shows an example of radii estimate vs. speed and temperature. For the speed dependence (Figure A2a), the rear, non-drive wheels give a better correspondence with speed than the front, driven wheels. Note, however, that the number of suitable data-points for the driven wheels are fewer because points with non-negligible slip are rejected. For this particular test run, the left and right wheels showed very similar slope and intercept values for the temperature dependence (Figure A2b). Noteworthy is that the right wheel is slightly warmer than the left wheel, and that this is also reflected as larger radii estimates.

Figure A2.
Example of radii estimate vs. (a) speed and (b) temperature.
References
- Giechaskiel, B.; Bonnel, P.; Perujo, A.; Dilara, P. Solid Particle Number (SPN) Portable Emissions Measurement Systems (PEMS) in the European Legislation: A Review. Int. J. Environ. Res. Public Health 2019, 16, 4819. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Yáñez, P.; Soriano, J.A.; Mata, C.; Armas, O.; Pla, B.; Bermúdez, V. Simulation of Optimal Driving for Minimization of Fuel Consumption or NOx Emissions in a Diesel Vehicle. Energies 2021, 14, 5513. [Google Scholar] [CrossRef]
- Jaworski, A.; Mądziel, M.; Lew, K.; Campisi, T.; Woś, P.; Kuszewski, H.; Wojewoda, P.; Ustrzycki, A.; Balawender, K.; Jakubowski, M. Evaluation of the Effect of Chassis Dynamometer Load Setting on CO2 Emissions and Energy Demand of a Full Hybrid Vehicle. Energies 2021, 15, 122. [Google Scholar] [CrossRef]
- Giechaskiel, B.; Komnos, D.; Fontaras, G. Impacts of Extreme Ambient Temperatures and Road Gradient on Energy Consumption and CO2 Emissions of a Euro 6d-Temp Gasoline Vehicle. Energies 2021, 14, 6195. [Google Scholar] [CrossRef]
- Jaworski, A.; Kuszewski, H.; Ustrzycki, A.; Balawender, K.; Lejda, K.; Woś, P. Analysis of the Repeatability of the Exhaust Pollutants Emission Research Results for Cold and Hot Starts under Controlled Driving Cycle Conditions. Environ. Sci. Pollut. Res. 2018, 25, 17862–17877. [Google Scholar] [CrossRef] [PubMed]
- Giechaskiel, B.; Casadei, S.; Mazzini, M.; Sammarco, M.; Montabone, G.; Tonelli, R.; Deana, M.; Costi, G.; Di Tanno, F.; Prati, M.; et al. Inter-Laboratory Correlation Exercise with Portable Emissions Measurement Systems (PEMS) on Chassis Dynamometers. Appl. Sci. 2018, 8, 2275. [Google Scholar] [CrossRef]
- Giechaskiel, B.; Casadei, S.; Rossi, T.; Forloni, F.; Di Domenico, A. Measurements of the Emissions of a “Golden” Vehicle at Seven Laboratories with Portable Emission Measurement Systems (PEMS). Sustainability 2021, 13, 8762. [Google Scholar] [CrossRef]
- Kim, C.; Lee, H.; Park, Y.; Myung, C.-L.; Park, S. Study on the Criteria for the Determination of the Road Load Correlation for Automobiles and an Analysis of Key Factors. Energies 2016, 9, 575. [Google Scholar] [CrossRef]
- Wong, J.Y. Theory of Ground Vehicles, 4th ed.; Wiley: Hoboken, NJ, USA, 2008; ISBN 978-0-470-17038-0. [Google Scholar]
- Gillespie, T.D. Fundamentals of Vehicle Dynamics; Society of Automotive Engineers: Warrendale, PA, USA, 1992; ISBN 978-1-56091-199-9. [Google Scholar]
- Kiencke, U.; Nielsen, L. Automotive Control. Systems: For Engine, Driveline, and Vehicle, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2005; ISBN 978-3-540-23139-4. [Google Scholar]
- Anghelache, G.; Moisescu, R. The Measurement of Dynamic Radii for Passenger Car Tyre. IOP Conf. Ser. Mater. Sci. Eng. 2017, 252, 012014. [Google Scholar] [CrossRef]
- Tuononen, A.J. Laser Triangulation to Measure the Carcass Deflections of a Rolling Tire. Meas. Sci. Technol. 2011, 22, 125304. [Google Scholar] [CrossRef]
- Pacejka, H.B.; Besselink, I. Tire and Vehicle Dynamics, 3rd ed.; Butterworth-Heinemann Elsevier: Oxford, UK; Waltham, MA, USA, 2012; ISBN 978-0-08-097016-5. [Google Scholar]
- Giechaskiel, B.; Forloni, F.; Otura, M.; Engström, C.; Öberg, P. Experimental Comparison of Hub- and Roller-Type Chassis Dynamometers for Vehicle Exhaust Emissions. Energies 2022, 15, 2402. [Google Scholar] [CrossRef]
- Preda, I.; Covaciu, D.; Ciolan, G. Coast Down Test—Theoretical and Experimental Approach; Transilvania University Press: Braşov, Romania, 2010. [Google Scholar] [CrossRef]
- Tsiakmakis, S.; Fontaras, G.; Ciuffo, B.; Samaras, Z. A Simulation-Based Methodology for Quantifying European Passenger Car Fleet CO2 Emissions. Appl. Energy 2017, 199, 447–465. [Google Scholar] [CrossRef]
- Moskalik, A. Using Transmission Data to Isolate Individual Losses in Coastdown Road Load Coefficients. SAE Int. J. Adv. Curr. Pract. Mobility 2020, 2, 2156. [Google Scholar]
- Lounsberry, T.; Tripp, J.; Fadler, G. Sensitivity Analysis of Aerodynamic Drag Coefficient to EPA Coastdown Ambient Condition Variation; SAE Technical Paper; SAE: Warrendale, PA, USA, 2020; p. 2020-01-0666. [Google Scholar]
- Metz, L.D.; Akouris, C.K.; Agney, C.S.; Clark, M.C. Moments of Inertia of Mounted and Unmounted Passenger Car and Motorcycle Tires. SAE Trans. 1990, 1990, 1079–1085. [Google Scholar]
- Vantsevich, V.V.; Barz, D.; Kubler, J.; Schumacher, A. Tire Longitudinal Elasticity and Effective Rolling Radii: Experimental Method and Data. In Proceedings of the SAE 2005 World Congress, Detroit, MI, USA, 11–14 April 2005; p. 2005-01-1823. [Google Scholar]
- Miller, S.L.; Youngberg, B.; Millie, A.; Schweizer, P.; Gerdes, J.C. Calculating Longitudinal Wheel Slip and Tire Parameters Using GPS Velocity. In Proceedings of the 2001 American Control Conference, (Cat. No.01CH37148). Arlington, VA, USA, 25–27 June 2001; Volume 3, pp. 1800–1805. [Google Scholar]
- Filipozzi, L.; Assadian, F.; Kuang, M.; Johri, R.; Velazquez Alcantar, J. Estimation of Tire Normal Forces Including Suspension Dynamics. Energies 2021, 14, 2378. [Google Scholar] [CrossRef]
- Acosta, M.; Kanarachos, S.; Blundell, M. Road Friction Virtual Sensing: A Review of Estimation Techniques with Emphasis on Low Excitation Approaches. Appl. Sci. 2017, 7, 1230. [Google Scholar] [CrossRef]
- Ubysz, A. Problems of Rotational Mass in Passenger Vehicles. Transp. Probl. 2010, 5, 33–40. [Google Scholar]
- STRO. STRO Databok 2022; The Scandinavian Tire & Rim Organization: Vaxholm, Sweden, 2022. [Google Scholar]
- Gustafsson, F. Slip-Based Tire-Road Friction Estimation. Automatica 1997, 33, 1087–1099. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).