Abstract
Driver drowsiness is one of the leading causes of traffic accidents. This paper proposes a new method for classifying driver drowsiness using deep convolution neural networks trained by wavelet scalogram images of electrocardiogram (ECG) signals. Three different classes were defined for drowsiness based on video observation of driving tests performed in a simulator for manual and automated modes. The Bayesian optimization method is employed to optimize the hyperparameters of the designed neural networks, such as the learning rate and the number of neurons in every layer. To assess the results of the deep network method, heart rate variability (HRV) data is derived from the ECG signals, some features are extracted from this data, and finally, random forest and k-nearest neighbors (KNN) classifiers are used as two traditional methods to classify the drowsiness levels. Results show that the trained deep network achieves balanced accuracies of about 77% and 79% in the manual and automated modes, respectively. However, the best obtained balanced accuracies using traditional methods are about 62% and 64%. We conclude that designed deep networks working with wavelet scalogram images of ECG signals significantly outperform KNN and random forest classifiers which are trained on HRV-based features.
1. Introduction
Drowsiness is defined as a transitional state fluctuating between alertness and sleep that increases the reaction time to critical situations and leads to impaired driving [1,2]. According to previous studies, driver drowsiness is one of the leading causes of traffic accidents. For example, the National Highway Transportation Safety Administration (NHTSA) reported that drowsy drivers were involved in about 800 fatal crashes in 2017 [3]. Another study announced that about 22–24% of crashes or near-crash risks are contributed by drowsy drivers [4]. The American Automobile Association (AAA) has also reported that about 24% of drivers acknowledged feeling extremely sleepy during driving at least once in the previous month [5].
Moreover, monitoring of driver alertness is an implicit requirement in the forthcoming SAE level of conditional automated driving (level 3) since handing over vehicle control to drowsy drivers is unsafe [6,7]. Various driver drowsiness detection systems (DDDS) have already been proposed in recent studies [8,9,10,11]. In our previous work [2], we developed a method for drowsiness classification only in manual driving mode and by using only vehicle-based data. As the drivers insert no input into the vehicle during automated driving tests, the proposed method in [2] cannot be used in automated driving. Moreover, vehicle-based data can be significantly affected by road geometry and the driving behavior of the specific driver. However, the proposed method in this paper uses the ECG data as inputs to the deep CNNs and can be applied in both manual and automated driving modes. Moreover, biosignals such as ECG can provide more accuracy to detect the onset of drowsiness than vehicle-based data [12,13]. This paper offers a new method using deep neural networks trained by wavelet scalograms of an electrocardiogram (ECG) signal.
1.1. Related Works
ECG signals present the heart’s electrical activity over time that is typically recorded using attached electrodes to the chest [14]. Figure 1 shows the schematic representation of a standard ECG signal [15]. Heart rate variability (HRV) information is extracted by detecting the R-peaks in the ECG signals and evaluating the fluctuations of the time intervals between adjacent R-peaks [16]. HRV is well-known physiological information that presents the activity of the autonomic nervous system (ANS) [17], fluctuations markedly over a day, and the sleep-wake-cycle [18]. Therefore, it is assumed to be indicative not only of the sleep stages [19] but also of sleepiness as well. HRV has been frequently employed to design a DDDS. For example, Fujiwara et al. [20] developed a system based on eight extracted features from HRV data where multivariate statistical process control was used as an anomaly detection method in HRV data. Results showed that the proposed method detected 12 out of 13 drowsiness onsets and the false-positive rate of the anomaly detection system was about 1.7 times per hour. Huang et al. used machine learning with four different traditional classifiers (support vector machine, K-nearest neighbor, naïve Bayes, and logistic regression) for binary detection of drowsiness by training on time and frequency domain features from HRV data [17]. Results showed that the K-nearest neighbor achieved the best accuracy, which was about 75.5%.
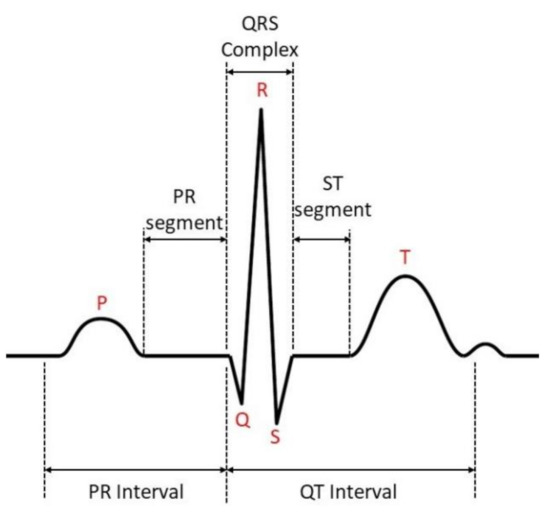
Figure 1.
Schematic representation of a standard ECG signal.
To discriminate between the HRV dynamics in two states of fatigue (caused by sleep deprivation) and drowsiness (caused by monotonous driving), two different monitoring systems were proposed in [21] based on features from HRV and respiration signals. One of these systems is a binary classifier (alert/drowsy) for assessing the level of driver vigilance every minute. Another system detects the level of the driver’s sleep deprivation in the first three minutes of driving. That study showed that the balanced accuracy of the drowsiness detection system which used only HRV-based features is about 65.5%. However, by adding the features from respiration signals, this system achieved a balanced accuracy of 78.5%, an improvement of about 13%. The balanced accuracy of the sleep deprivation system was also about 75%, and it detected 8 out 13 sleep-deprived drivers correctly. Another study conducted by Buendia et al. [22] investigated the relationship between the drowsiness levels rated with the Karolinska sleepiness scale (KSS) and heart rate dynamics. Results showed that the average heart rate decreased with increasing KSS (which means higher drowsiness levels), whereas heart rate variance increased in drowsy states. Patel et al. [23] also developed a neural network classifier to detect the early onset of driver drowsiness by analyzing the power of low- and high-frequency HRV sub-bands. The spectral image, plotted from the power spectral density of the HRV data, was the input given to the neural network that yielded an accuracy of 90%. In [24], Li and Chung used a wavelet transformation to extract features from HRV signals and compared them with fast Fourier transform (FFT)-based features. Receiver operation curves were used for feature selection and support vector machines as a classifier. The wavelet method outperformed the system designed using FFT. Classification results showed that the wavelet-based feature system achieved an overall accuracy of 95%. Furman et al. [25] reported that HRV activity in the very-low-frequency range (0.008–0.04 Hz) significantly and consistently decreases approximately five minutes before extreme signs of drowsiness can be observed.
1.2. Contribution of the Method
Previous studies commonly used hand-crafted techniques or dimensionality reduction methods to extract features from HRV data for driver drowsiness classification. Most commonly, heart rate variability data are derived by the detection of R-peaks in the ECG signal and processing the information of R-peak time points only. However, other segments of the ECG signals (see Figure 1) might also be associated with different levels of drowsiness. Furthermore, previous studies widely used traditional machine learning classifiers to classify driver drowsiness; however, deep neural networks are expected to outperform them if a large data set is available for training. In this study, we first employed the wavelet transformation to generate 2D scalogram images of the ECG signal, which capture time–frequency domain features. These images are inserted as input data to a deep convolutional neural network. Bayesian optimization is applied to optimize the hyperparameters of this network. To compare the results of this approach with previous methods, HRV data is also derived from ECG signals in a common way, and its extracted features are utilized to classify driver drowsiness using two traditional classifiers: K-nearest neighbors (KNN) and random forest.
The rest of this paper is structured as follows: Section 2 explains the experimental setup and the testing procedure that was used to collect the dataset. Section 3 describes the methodology for the classification of driver drowsiness. Section 4 presents the results of the proposed method, discusses the results, and compares them with the outcomes of other algorithms. Finally, Section 5 presents our conclusions and suggests future tasks to improve the proposed method.
2. Experimental Setup and Testing Procedure
This study utilizes the dataset collected during the WACHSens project, a joint project of the Human Research Institute Weiz, the Graz University of Technology, apptec Factum Vienna, and AVL U.K. The tests were performed in the automated driving simulator of Graz (ADSG) at the Institute of Automotive Engineering, Graz University of Technology. The driving simulator is presented in Figure 2. The following subsections explain the structure of the ADSG, simulated driving test procedure, and definition of ground truth for driver drowsiness.

Figure 2.
Automated driving simulator of Graz (ADSG). To cancel the external noise and adjust the indoor temperature, ADSG is separated from its surrounding area using an insulating housing cube.
2.1. Driving Simulator
In the ADSG, the visual cues are simulated by eight LCD panels, covering 180 degrees of view and the rear screen, which the inner mirror observes. The side mirrors are also implemented in the LCDs covering the side windows. The acoustic cue is simulated by generating engine and wind noise applied at the car’s sound system. Moreover, four bass shakers generate the vibration in the car chassis and the driver and passenger seats. Haptic feedback is provided by the SensodriveTM simulator steering wheel (Weßling, Germany) [26], and an active brake pedal simulator, gas pedal, and gear-shift input are taken from the vehicle unmodified controls. The vehicle dynamics states are calculated by a full vehicle software AVL-VSMTM (Graz, Austria) [27], parametrized with a middle-class passenger car. The vehicle model calculates dynamics states as well as engine speed and torque for the acoustic simulation. Adaptive cruise control (ACC) and lane-keeping assist (LKA) systems are also implemented in this simulator for controlling the vehicle’s longitudinal and lateral dynamics during tests on automated driving. The ADSG is surrounded by a noise- and temperature-insulating cube/box. Different features of this simulator were studied in our previous works [28,29].
2.2. Participants and Driving Tests Procedure
In this project, different types of physiological data were collected from 92 drivers. These drivers participated in manual and automated driving tests when they were in two different vigilance states: fatigued and rested. This procedure results in four different driving sessions for each participant: fatigued automated driving, fatigued manual driving, rested automated driving, and rested manual driving. In the rested condition, drivers were required to have a full night’s sleep before performing the tests. For the fatigued condition, the drivers could choose one of the two following options: (1) extended wakefulness (being awake for at least 16 h continuously before starting the tests in the conditions fatigued automated and fatigued manual) and perform the tests at their usual bedtime, or (2) being sleep-restricted by sleeping a maximum of four hours in the night before the tests. The age and gender of participants were balanced across the sample as presented in Table 1. The Female-60+ group has only 12 participants since we could not hire more still active drivers from this group in the available time frame.

Table 1.
Gender–age groups of the participants in the driving tests. SD: standard deviation.
Several biosignals, namely, ECG, EEG, EOG, skin conductivity, and oronasal respiration, were collected using a g.NautilusTM device (Schiedlberg, Austria; research version) with a sampling frequency of 500 Hz. Facial-based data such as eyelid opening, pupil diameter, and gaze direction were also measured with a sampling frequency of 100 Hz using a SmartEyeTM (Gothenburg, Sweden) eye-tracker system installed on the car dashboard. In this study, only ECG signals are employed to classify the driver’s drowsiness. The study was conducted according to the ethical guidelines of the Declaration of Helsinki and the General Data Protection Regulation of the European Union. The study protocol was approved by the Ethics Committee of the Medical University of Graz in vote 30-409 ex 17/18 dated 1 June 2018. Written informed consent was obtained from participants before the experiments, and they were compensated with EUR 50 after finishing the sessions. More details of the driving test procedure are described in a previous publication [2].
2.3. Ground Truth Definition for Driver Drowsiness
To monitor the participants’ driving behavior, four cameras were placed in the ADSG that recorded different views of the driver and the test track (see Figure 3). Traffic psychologists thoroughly observed these videos and assigned labels to the driver’s drowsiness level based on drowsiness signs such as yawning, long blinks, and head nodding. The driver’s vigilance state is reported in four classes: alert (AL), moderately drowsy (MD), extremely drowsy (ED), and falling asleep event (SL). These drowsiness levels are collected with their corresponding SmartEyeTM video frame numbers to synchronize drowsiness level ratings with the recorded data channels (more details of data synchronization are explained in Section 3.1). Figure 4 shows an example of the defined ground truth for driver drowsiness in all four driving tests (all performed by the same driver). As that Figure shows, micro-sleep events (SL) were also reported by video observers. However, we merged the SL class with the extremely drowsy (ED) class since the overall number of SL samples was too small to be considered as a separate class for machine learning training. This figure also shows that even in the rested condition, some drivers showed signs of moderately and extremely drowsy states. More details of the ground truth definition for driver drowsiness using video observations are explained in our previous publication [30].

Figure 3.
Four different views of the driver and the test track. These views were observed thoroughly by an expert to define a ground truth for driver drowsiness based on drowsiness signs into three classes (informed consent was obtained from the driver to publish his image in this paper; reprinted from our previous study [2], license no. 5218171384545).
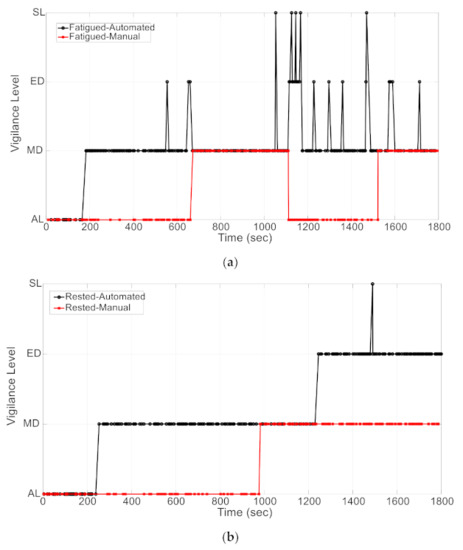
Figure 4.
Reported ground truth for driver drowsiness by ratings of the driving test videos: (a) video observations in the fatigued automated and fatigued manual tests; and (b) video observations in the rested automated and rested manual tests. Four different levels for drivers’ vigilance were reported: alert (AL), moderately drowsy (MD), extremely drowsy (ED), and sleep (SL). In this paper, we merge the SL level into the ED level.
3. Methodology
Two different methodologies are employed to classify driver drowsiness using ECG signals: (1) two traditional classifiers (random forest and KNN) trained by features extracted from HRV signals, and (2) one deep convolutional neural network (CNN) model trained by ECG wavelet scalogram images. The Bayesian optimization method is used to optimize the hyperparameters of the classifiers. Figure 5 shows the flowchart of these methods. The following subsections describe the structure of these methodologies.
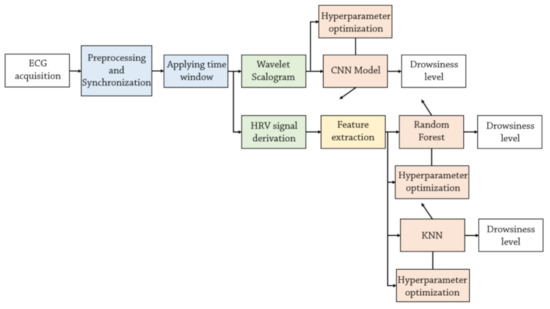
Figure 5.
Two different approaches to classify driver drowsiness using ECG signals: wavelet scalograms or derived HRV features. The hyperparameter of KNN, random forest, and CNN model are optimized using the Bayesian optimization method.
3.1. Data Synchronization
Ground truth is defined based on the video observation and recorded using the frame number information of SmartEyeTM data collected with a sampling frequency of 100 Hz. Physiological signals were recorded with separate equipment at 500 Hz sampling frequency, but also fed into the central recording module and stored with the same sampling frequency of 100 Hz. The lower sample rate is not sufficient for the high-quality processing of physiological data. Therefore, we need to synchronize video and physiological data sources with the help of the respiration signal which is available at both sampling rates of 100 Hz and 500 Hz. The normalized cross-correlation between the two respiration signals is calculated at all possible lags. The delay between these two signals is calculated as the lag with the largest absolute value of normalized cross-correlation. Figure 6 shows an example of data synchronization where 500Hz-respiration data is shifted about 21.4 s forward to be synchronized with the 100Hz-respiration data. The same time shift is also applied to the ECG signals collected with the sampling frequency of 500 Hz to sync them with the video observations. In those data, offset correction was sufficient for an accuracy ±1 video frame.
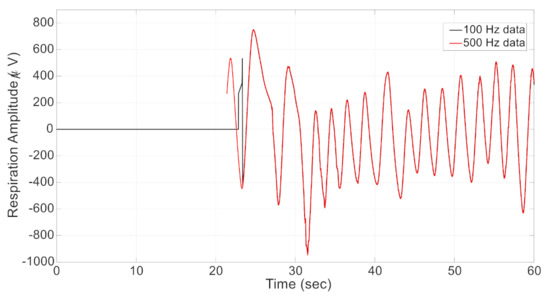
Figure 6.
Data synchronization using respiration signals collected with two different frequencies of 100 Hz and 500 Hz. In this example, the 500 Hz data is shifted about 21.4 s forward to be synced with the 100 Hz data.
3.2. ECG Preprocessing
Generally, ECG signals are contaminated with different noise sources such as power line interference (50 Hz) [31] and baseline wander [32]. A second-order infinite impulse response (IIR) notch filter [33] is utilized here to remove the power line noise from ECG signals. Furthermore, a high pass filter with a passband frequency of 0.5 Hz is also employed to remove the low-frequency baseline wander noise. Figure 7 shows one part of the noisy and denoised ECG signals after removing the baseline wander and power line noise.
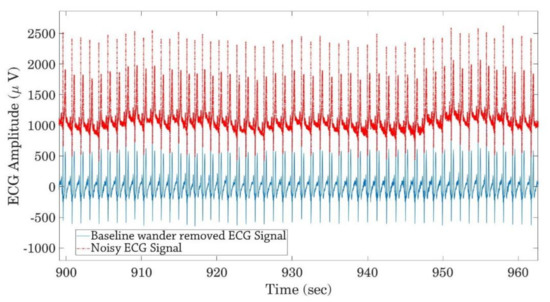
Figure 7.
Noisy and denoised ECG signals after removing baseline wander and power line noise.
3.3. Driver Drowsiness Classification Using Scalograms of ECG Signals
This section describes the proposed method for driver drowsiness classification using deep neural networks trained by wavelet scalogram images of the ECG signals.
3.3.1. Wavelet Scalogram
Wavelet analysis calculates the correlation (similarity) between an input signal and a given wavelet function . Unlike Fourier transform, wavelet analysis provides a multi-resolution time–frequency output under the assumption that low frequencies maintain the same characteristics for the whole duration in the input signal. In contrast, high frequencies are assumed to appear at different time points as short events.
Therefore, the wavelet function is scaled and translated by two parameters and to generate a wavelet filter bank, as presented by Equation (1) [34].
By using this transformed wavelet, continuous wavelet transform (CWT) of the input signal at the time and scale can be calculated as:
where is the complex conjugate of and provides the frequency contents of corresponding to the time and scale . By using the two parameters of and , it is possible to investigate the input in two domains of time and frequency simultaneously, whereby the resolution of time and frequency depends on the scale parameter . CWT provides a time–frequency decomposition of in the time–frequency plane. This method can be more beneficial than other methods such as short-time Fourier transform (STFT) when investigating the non-stationary signals since it provides a higher time resolution in the higher frequencies by reducing frequency resolution, and a higher frequency resolution in lower frequencies by reducing time resolution. In contrast, the time and frequency resolutions are constant in STFT. The scalogram if in any positive scale is calculated as the norm of :
This equation calculates the energy of at a scale . Therefore, we can find the significant scales (which correspond to frequencies) in the signal using the scalogram.
The wavelet scalogram is used to transform the time series ECG signal to the time–frequency domain. Here, the Morse wavelet [35] is employed to calculate the wavelet transformation of the ECG signals. A sliding window with a length of 10 s and an overlap of 5 s between two consecutive windows was employed, and the scalogram image of every window of the data is calculated. The resulting number of data windows in each level of driver drowsiness are provided in Table 2 for manual driving, and in Table 3 for automated driving. As these tables show, the generated data sets are imbalanced in both manual and automated modes. This fact must be taken into account in the structure of the deep and traditional classifiers. Moreover, the percentages of MD and ED classes are higher in the automated driving tests than in the manual tests. Thus, the drivers were generally drowsier in automated.

Table 2.
The number of data samples in each drowsiness class after applying time windows to generate the scalograms in the manual driving tests.

Table 3.
The number of data samples in each drowsiness class after applying time windows to generate the scalograms in the automated driving tests.
Figure 8 shows sample images of ECG signals and their corresponding scalogram images for all three drowsiness levels in a rested automated test. The generated images are resized to 224 × 224 pixels. To reduce the computational complexity of the training process of the deep network, the RGB scalogram images are also transformed to grayscale images as presented in Figure 9. These grayscaled images are used as input data to train the deep convolutional neural network.
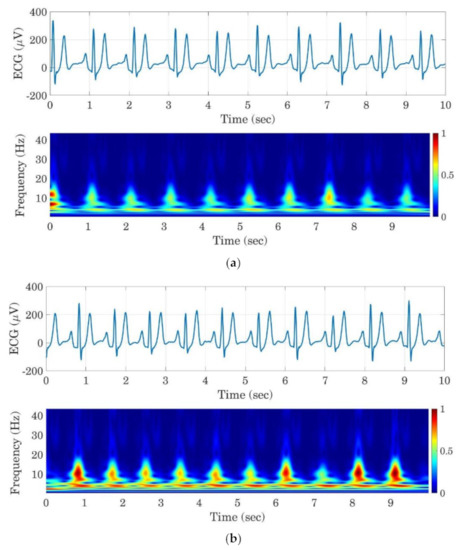
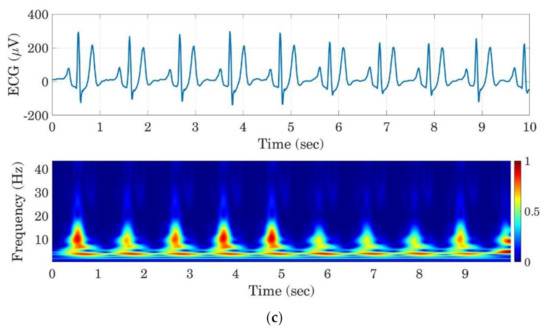
Figure 8.
Examples of ECG signals segments and their corresponding scalograms for the AL (a), MD (b), and ED (c) classes.
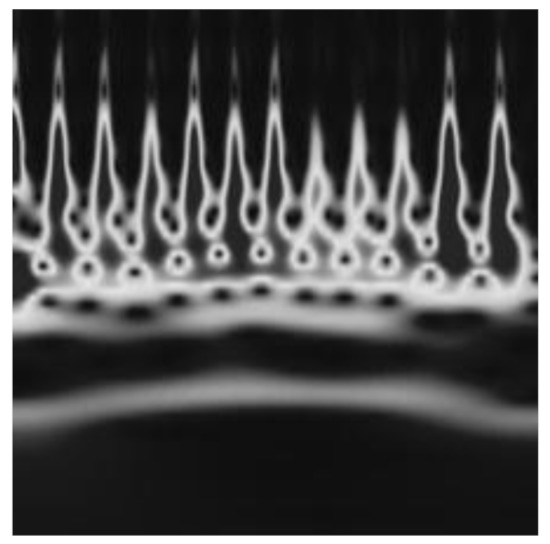
Figure 9.
Sample of a grayscale resized image (224 × 224 pixels) of the ECG scalogram image.
3.3.2. Architecture of Deep CNN and Optimization of its Hyperparameters
Convolution neural networks (CNN) have been widely used to learn features from input images in different applications [36,37,38,39]. These networks help to capture the spatial dependencies in different parts of an input image by applying a convolution operation of some specific filters to input images [40]. This study used scalogram images of ECG signals to train a deep CNN and classify the driver drowsiness. As scalograms are time–frequency representations of an underlying time signal, temporal information is coded in the spatial features of the image. The input images are first normalized to have zero mean and unit variance. Then, the whole data set is split randomly into the train (80% of the input data), validation (10% of the input data), and test (10% of the input data) subsets in a way that the percentages of the drowsiness classes are approximately the same as presented in Table 2 and Table 3 in each of the subsets.
The utilized deep CNN is composed of five convolutional blocks and one fully connected block in its hidden layer. Convolution and fully connected blocks are presented in Figure 10, where Conv, BN, ReLU, Max Pool, and FC are convolution layers, batch normalization layer, the ReLU activation function (), and a fully connected layer, respectively. The hidden layer is followed by the output layer that is constructed using an FC layer, a soft-max layer, and a weighted classification layer (weight). The number of neurons in the fully connected layer of the output layer is equal to the number of classes (here, three). The weight layer is used to mitigate the data imbalance issue. This layer contains one element per drowsiness class where every element is calculated using Equation (4):
where is the number of classes (here, three), is the number of data samples that belong to the -th class, and finally, is the weight of -th class. By applying Equation (4) to the data samples that belong to the drowsiness classes in the manual and automated modes (presented in Table 2 and Table 3), the corresponding weights for every class are computed. Table 4 provides these weights. As this table shows, the class weights of the ED class are highest in both manual and automated mode tests. By using these weights, misclassification errors of the MD and ED classes get more weight in comparison to the AL class. Therefore, if the network classifies an MD or ED sample into the AL class wrongly, it results in a large misclassification error that has a significant influence on the optimization process and thus will reduce the frequency of this kind of classification error.
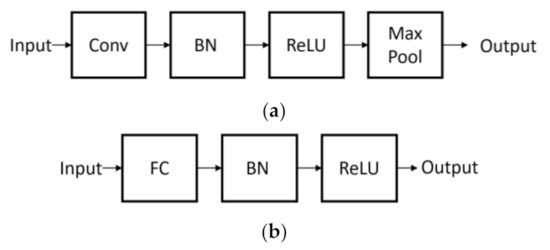
Figure 10.
Convolutional (a) and fully connected (b) blocks are used to construct the deep CNN.

Table 4.
Class weights of the different drowsiness classes used in the deep CNNs to alleviate the imbalanced data set issue.
Figure 11 presents the architecture of the deep CNN, where five convolution blocks are followed by one fully connected block. Moreover, one dropout layer is also added after convolution blocks to reduce the possibility of overfitting or getting stuck in local minima during the training process. The dropout layer temporarily eliminates some neurons with a predefined probability, along with all of their input and output connections [41].
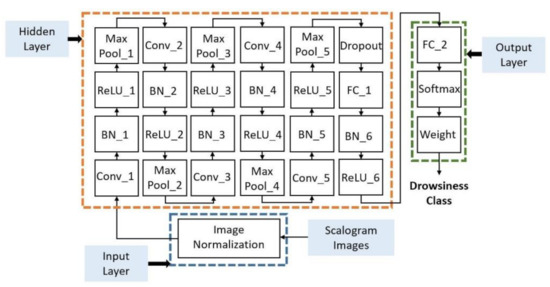
Figure 11.
The architecture of the deep CNN used to classify driver drowsiness using ECG scalogram images.
Deep neural networks have several hyperparameters such as the learning rate, the regularization parameter, and the number of neurons of filters that can influence network performance. Finding a proper combination of these hyperparameters so that they provide the optimal performance of the deep network is a primary active task in the research field of deep learning [42,43]. In this study, the Bayesian optimization method [44,45] is applied to optimize the hyperparameters of the deep CNN. This method has the capability of reasoning about the iterations’ performance before they are performed. Therefore, fewer iterations are needed to find the optimal hyperparameter combination than with other hyperparameter optimization methods [45]. Moreover, this method yields a better generalization on the tests data set [46]. Here, four different hyperparameters were considered to be optimized using the Bayesian optimization method, including learning rate, L2 regularization, dropout probability, the number of filters in convolution layers (Conv1 to Conv5 in Figure 11), and neurons in the fully connected layer in the hidden layers (FC1 in Figure 11). Here, it is assumed that the number of filters in Conv1 to Conv5 and the number of neurons in FC1 are equal, so only one hyperparameter is defined to find their optimal values. Table 5 presents the specified search space for each of these hyperparameters.

Table 5.
Used hyperparameters of the deep CNN to be optimized using a Bayesian optimizer.
An adaptive moment estimation (ADAM) optimizer is employed to train the parameters of the designed deep CNNs (weights and biases). The maximum number of epochs is empirically chosen to be 15. A schedule for learning rate is utilized that multiplies the initial learning rate by 0.1 after 12 epochs to alleviate overfitting in the latter training epochs. The size of the mini-batch is defined to be constant and equals 16. The training process was conducted on a system with CPU and GPU types of Intel CoreTM;i7-782HQ and NVIDIATM Quadro M2200, respectively.
3.4. Driver Drowsiness Classification Using Heart Rate Variability Data
This section describes the proposed method for driver drowsiness classification using feature extraction from HRV data.
3.4.1. Derivation of Heart Rate Variability Data from ECG Signals
The heart rate variability signal is derived from preprocessed ECG signals by applying an R-peak detection algorithm to detect heart rate. In this study, we used the automatic multiscale-based peak detection (AMPD) method [47] as an ECG R-peak detector, then RR Intervals (RRIs) that are defined as the time intervals between every two consecutive R-peaks are calculated. Figure 12 shows the detected R-peaks in a part of the ECG signal.
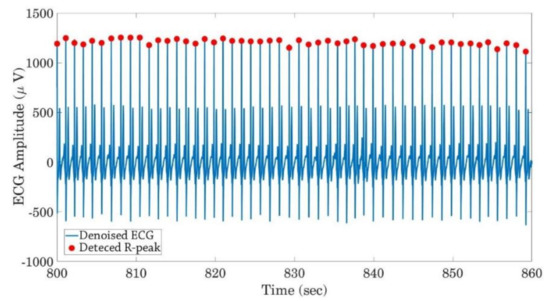
Figure 12.
Detected R-peaks in the denoised ECG signal using the AMPD method.
3.4.2. Feature Extraction from HRV Data
Literature has proposed some features to be extracted from RR intervals for driver drowsiness detection [18], which conform to measures that are well established in clinical contexts [48]. Other HRV features are based on a visualization technique called the Poincaré plot. In this subsection, firstly, this plot is introduced, then those and other commonly extracted features from RR intervals are explained.
Poincaré plot: This plot is a type of recurrence plot to investigate the similarity in time series that can be used to analyze the nonlinear properties of HRV data [49]. Consider as a RR interval time series. The Poincaré plot first plots , then plots , then plots and so on. This plot provides information about the short-term and long-term dynamics of the RR interval. An ellipse is fitted to the plotted data points and the minor and major semi-axes of the ellipse are associated with short-term and long-term HRV, respectively. Figure 13 shows the Poincaré plot for RR intervals collected in a rested automated driving test. The least-square method was employed to fit an ellipse on given RR intervals [50] and geometrical properties of this ellipse are extracted as features to describe the HRV dynamics.
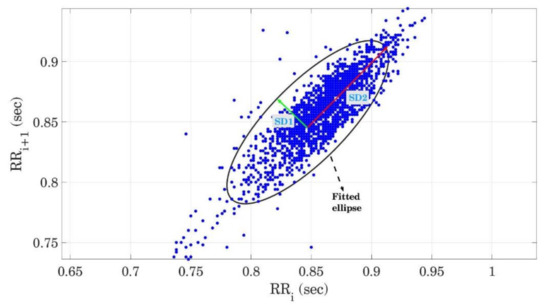
Figure 13.
Poincaré plot and fitted ellipse for RR intervals during a rested automated driving test. Minor and major semi-axes of the fitted ellipse, SD1, SD2, and their ratio, are calculated as features to capture the dynamics of HRV data.
Three features are extracted from this plot:
- SD1: SD1 is the standard deviation of the Poincaré plot perpendicular to the line of identity and the semi-minor axis (half of the shortest diameter) of the fitted ellipse, see Figure 13 (green vector). SD1 is an estimation of short-term HRV that describes parasympathetic activity since it represents the deviation of heart rate from the line-of-identity (constant heart rate).
- SD2: SD2 is the standard deviation of the Poincaré plot along the line of identity and the semi-major axis (half of the largest diameter) of the fitted ellipse, see Figure 13 (red vector). SD2 is an estimation of long-term HRV that describes sympathetic and mixed activity since SD2 is along the line of identity.
- SD1/SD2: SD1/SD2 is the ratio of SD1 to SD2 that describes the ratio of short-term to long-term HRV and the relationship between parasympathetic and sympathetic activity.
Other features that have been proposed by previous studies [18,51,52] are also extracted from RR intervals. These features are:
- MeanRR: This feature presents the mean values of the time intervals between every two consecutive R-peaks. The MeanRR is calculated by Equation (5):where is the number of heartbeats in the sliding windows and is equal to the time interval between and .
- SDRR: This feature represents the standard deviation of RR intervals, calculated by Equation (6).
- RMSSD: This feature calculates the root mean square of consecutive RR intervals’ differences, calculated by Equation (7). It reflects parasympathetic activity.
- pRR50: This feature measures the ratio of the number of R-peaks that differ more than 50 ms from their next R-peak to the total number of RR intervals in every sliding window. Equation (8) calculates the pRR50.
- VLF: This feature presents the power in the very-low-frequency ranges of 0.003–0.04 Hz of the RR interval time series. To calculate this feature and the LF and HF, the PSD of the RR intervals is computed using the Lomb–Scargle periodogram method [53,54] in every sliding window.
- LF: This feature presents the power in the low-frequency ranges of 0.04–0.15 Hz of the RR interval time series.
- HF: This feature presents the power in the high-frequency ranges of 0.15–0.40 Hz of the RR interval time series and reflects parasympathetic activity.
- LF/HF: This feature is the ratio of LF divided by HF and is also indicative of the sympathetic–parasympathetic balance.
Overall, eleven features are extracted from HRV data and are used to classify the driver’s drowsiness. A window length of ten seconds, which was used in the ECG scalogram approach above, is considered extremely short for evaluation of HRV as it conforms nearly exclusively to the fast fluctuations of heart rate according to parasympathetic activity [55]. For exploratory purposes, we also applied longer sliding windows in comparison to the deep learning model. Two additional sliding windows are employed: (1) 60 s with 30 s overlap, and (2) 40 s with 20 s overlap. These longer windows help to provide a better estimation of mid-range dynamics of HRV data for classifiers than we can expect from short windows that are used in the deep learning method. The results of these sliding methods are compared together in Section 4.1.
The following subsection explains the two classifiers (KNN and random forest) used for drowsiness classification.
3.4.3. Classify Driver Drowsiness Using Traditional Classifiers
The KNN and random forest are employed to classify the driver drowsiness using extracted features from HRV data. Each one of these classifiers has two different hyperparameters. The KNN hyperparameters are the number of neighbors for every sample (numNei) and the function used to measure the distance between samples (distance) [56]. The random forest hyperparameters are also the minimum of leaf size (minLS) and number of predictors to sample at each node (numPTS) [57]. These hyperparameters are also optimized using the Bayesian optimization method to find the optimal set. Moreover, the issue of the imbalanced data set is removed by using the uniform prior probability of every class for the KNN [58] and random under-sampling boosting (RUSBoost) [59] for the random forest classifier.
4. Results and Discussion
To evaluate the generated classifiers, confusion matrices were calculated for the test dataset. These matrices provide four different values that are computed for every drowsiness level:
- True-negative (TN): The number of samples that do not belong to a specific class (for example, AL) and are also classified in any of the two other classes (MD or ED) by the classifier.
- True-positive (TP): The number of samples that belong to a specific class (for example, AL) and are correctly classified in that class.
- False-negative (FN): The number of samples that belong to a specific class (for example, AL) but are wrongly classified in any of the two other classes (MD or ED).
- False-positive (FP): The number of samples that do not belong to the specific class (for example, AL) and are wrongly classified in that class.
These four values are used to calculate five different metrics for every level of driver drowsiness:
- Specificity (true negative rate): The specificity is TN divided by the sum of TN and FP. It can be interpreted as the probability of a sample not being classified in a class if it does not belong there
- Sensitivity (true positive rate): The sensitivity is TP divided by the sum of TP and FN.
- Precision (positive predictive value): The precision is TP divided by the sum of TP and FP.
- F1-score: The F1-score is the harmonic mean of precision and sensitivity.
- Balanced accuracy: The balanced accuracy is equal to the average of the accuracies of the three classes. The accuracy of every class is also equal to the ratio of TP of every class to the number of samples that belong to the corresponding class based on the actual labels.
The following subsections present the results of the two proposed methods for driver drowsiness classification.
4.1. Results of Driver Drowsiness Classification Using Heart Rate Variability Data
To evaluate the performance of the KNN and random forest classifiers, confusion matrices of these classifiers trained by HRV-based features with three different sliding windows of 10 s, 40 s, and 60 s are provided in Figure 14, Figure 15 and Figure 16, respectively. In these Figures, the diagonal elements (in gray) provide the number of the sliding windows that are correctly classified in different classes of drowsiness, according to the ground truth classification from the video observations. Accordingly, the percentage numbers written in these elements show correct classification accuracy for every specific drowsiness level. Non-diagonal cells also present the number of samples that are misclassified. As these figures present, the classification accuracy of the MD class is lower than two other classes in the manual mode. Furthermore, random forest performs better than KNN for drowsiness classification in manual and automated modes regardless of the used sliding window. Balanced accuracies for every classifier in every driving mode are provided in Table 6. These accuracies are calculated as the average TP accuracies in confusion matrices that are shown in grey elements in Figure 16c,d. Therefore, the best balanced accuracy that is achieved using traditional methods in manual mode is the average of 64.7%, 56.2%, and 56.4%. The best balanced accuracy in the automated mode that is achieved by the same methods is also the average of 63.4%, 63.5%, and 66.6%. According to this table, the best balanced accuracies in the automated and manual modes are respectively 63.8% and 62.1%, which are obtained using the random forest classifier and the sliding window of 60 s with 30 s overlap.
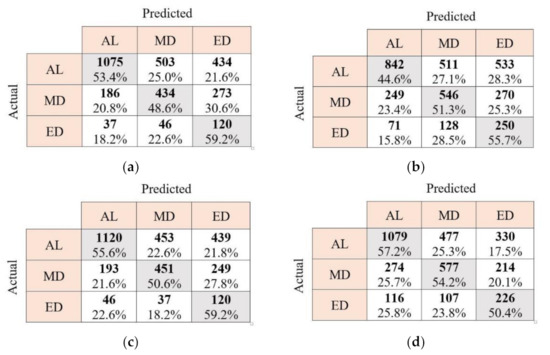
Figure 14.
Confusion matrices of KNN classifier in the manual tests (a), KNN classifier in automated tests (b), random forest in the manual tests (c), and random forest in the automated tests (d) for driver drowsiness classification. The length of the sliding window for feature extraction is 10 s with a 5 s overlap. AL: alert, MD: moderately drowsy, and ED: extremely drowsy.
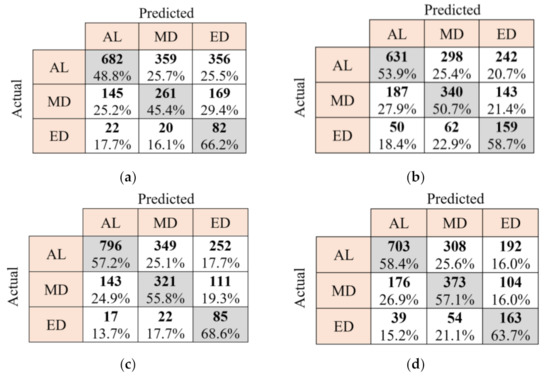
Figure 15.
Confusion matrices of KNN classifier in the manual tests (a), KNN classifier in automated tests (b), random forest in the manual tests (c), and random forest in the automated tests (d) for driver drowsiness classification. The length of the sliding window for feature extraction is 40 s with a 20 s overlap. AL: alert, MD: moderately drowsy, and ED: extremely drowsy.
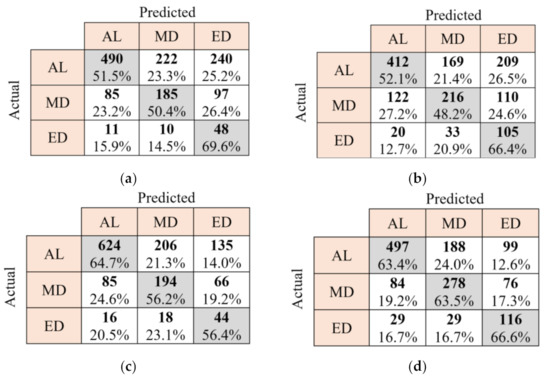
Figure 16.
Confusion matrices of KNN classifier in the manual tests (a), KNN classifier in automated tests (b), random forest in the manual tests (c), and random forest in the automated tests (d) for driver drowsiness classification. The length of the sliding window for feature extraction is 60 s with a 30 s overlap. AL: alert, MD: moderately drowsy, and ED: extremely drowsy.

Table 6.
Balanced accuracies of the KNN and random forest classifiers in the manual and automated driving modes with two different sliding windows. B.Acc.: balanced accuracy, 10/5: sliding window with the length of 10 s and 5 s overlap, 40/20: sliding window with the length of 40 s and 20 s overlap, and 60/30: sliding window with the length of 60 s and 30 s overlap.
For the sake of brevity, classification metrics including specificity, sensitivity, precision, and F1-score are shown only for the best classifier (random forest trained by HRV-based features with a 60 s sliding window) in the manual and automated modes. Table 7 presents these metrics. As this table shows, the precision value for the ED class is low. This has occurred because the number of TP is low for this class. According to this table, the AL class has the maximum F1-score in both manual and automated modes. Therefore, the accuracy of the random forest for the AL class is higher than two other classes, and accordingly, the false alarm of this is reduced using this classifier.

Table 7.
Classification metrics for the random forest classifier trained by HRV-based features in the manual and automated driving modes. Spe.: specificity; Sen.: sensitivity; Pre.: precision; and F1S: F1-score.
4.2. Results of Driver Drowsiness Classification Using Scalogram of ECG Signals
As presented in Section 3.3.2, four different hyperparameters of deep CNN are considered to be optimized using the Bayesian optimizer. Table 8 shows the optimized hyperparameters of deep CNNs in the manual and automated driving modes. As this Table shows, the number of filters in the convolution layers and neurons in the fully connected layer (presented by the hyperparameter ) is higher in the automated driving mode. Therefore, the computational cost is higher in the automated tests to classify driver drowsiness using the proposed deep CNNs. The L2 regularization value (presented by the hyperparameter ) is much higher in manual tests than in automated tests. Thus, deep CNN needs larger parameters to classify the driver drowsiness in the manual tests. The dropout probability (presented by the hyperparameter ) of the trained deep CNN for the ECG signals in the automated tests is higher than the designed deep CNN for the manual tests. The number of neurons is also higher for the deep CNN trained by the ECG signals for automated driving. Therefore, its network is wider than another one. Consequently, the dropout probability of the network trained by the ECG signals of the automated tests should also be higher to turn off more neurons and avoid overfitting.

Table 8.
Optimized values of hyperparameters in different driving modes and by inputting ECG scalogram to the deep CNNs. Hyperparameters to are defined in Table 4.
In comparison with other widely used deep CNNs that are implemented in embedded systems for real-time face recognition or object detection, our developed deep CNNs have much fewer parameters. Table 9 compares the number of parameters of four different frequently used deep networks in real-time applications (AlexNet [60], VGG16 [61], ResNet18 [62], and GoogLeNet [63]) with our developed networks.

Table 9.
Comparison of the approximate number (app. no.) of parameters in the developed deep CNN with other deep networks that were implemented in real-time applications in previous works. ECG-automated and ECG-manual in this table are deep networks and driving tests in automated and manual modes are used to train them, respectively.
Confusion matrices of the trained deep CNNs using ECG signals of the manual and automated tests are provided in Figure 17 to evaluate their classification performance. As this Figure shows, the MD class and AL class have the lowest and highest classification accuracy in both manual and automated driving modes, respectively. Therefore, reducing the number of classes from three to two can increase classification accuracy. However, it will not be possible to capture the transition between the AL to ED states in the case of binary classification. The balanced accuracy of the deep CNNs in both manual and automated modes is also provided in Table 10. These accuracies are calculated as the average TP accuracies in confusion matrices that are shown in grey elements in Figure 17a,b. Therefore, the balanced accuracy in manual mode is the average of 81.2%, 78.6%, and 79.1%. The balanced accuracy in the automated mode is also the average of 82.2%, 73.8%, and 82.0%. According to Table 10, the balanced accuracy of the deep CNN in the manual and automated driving modes are respectively about 77% and 79%. By comparing Table 10 with Table 6, deep CNNs significantly outperform the random forest and KNN methods in both manual and automated modes. Therefore, the input ECG scalograms are more informative than HRV-based features regarding driver drowsiness levels.
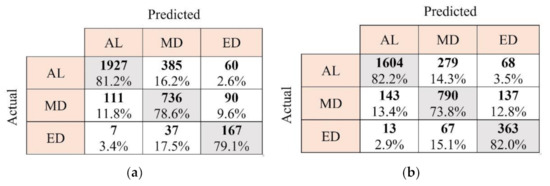
Figure 17.
Confusion matrices of deep CNN for driver drowsiness classification in the manual (a) and automated (b) driving tests.

Table 10.
Balanced accuracy of the deep CNN in the manual and automated driving modes. B.Acc.: balanced accuracy.
Classification metrics of the deep CNNs in the manual and automated modes are provided in Table 11. Comparing Table 11 with Table 7 shows that the F1-scores of all classes in both driving modes except the AL class in manual mode are improved by using the deep CNN method. According to this table, the precision value for the ED class is also lower than other classes since the numbers of the data samples of this class are much lower than the MD and AL classes.

Table 11.
Classification metrics for the deep CNN trained by ECG scalogram images in the manual and automated driving tests. Spe.: specificity; Sen.: sensitivity; Pre.: precision; and F1S: F1-score.
5. Conclusions
Two different methodologies were proposed in this paper to classify driver drowsiness using ECG signals. In the first methodology, R-peaks are firstly detected from ECG signals to obtain the HRV data. Then, eleven features are extracted from HRV data, and finally, random forest and KNN are used to classify drowsiness into three classes: alert, moderately drowsy, and extremely drowsy. In another method, a deep CNN was used to classify the drowsiness to the same classes when wavelet scalogram images of the ECG signals were inputs to this network. Results showed that the classification with deep CNN on ECG scalograms was more accurate than the random forest and KNN classifiers on HRV in both manual and automated driving modes. It is noteworthy that the length of ECG signals for the scalograms was only 10 s. For direct comparison, we also calculated HRV features on 10 s windows, though we are aware that this time frame captures fast, mostly respiratory, fluctuation only. Time frames from at least 1–2 min or even longer are necessary for a good agreement to usual short-term HRV measures [55,64]. We also computed longer time frames of 40 s and 60 s to verify the hypothesis that these longer windows capture more relevant information. Indeed, the classification accuracy of both KNN and RF classifiers increases with the duration of the time window used for HRV calculation.
In contrast, the deep CNN on ECG scalograms performs better already based on 10 s windows only. We conclude that the time–frequency content of the entire ECG signal captures information about the autonomous state of an individual beyond the RRI signal, which is the only information used for classical HRV parameters. Further research is suggested to understand which feature of an ECG exactly codes relevant information.
The following tasks are also suggested to improve the designed driver drowsiness classification system:
- Applying a quality assessment method to the ECG signals in every sliding window can help to remove noisy data and increase classification accuracy. Moreover, a quality index can be derived for each sliding window to specify its influence on the reported drowsiness level in a predefined time interval (e.g., 1 min).
- In this study, ECG signals are collected using attached electrodes to the driver’s chest. Non-invasive sensors such as smart watches can also be used to design a non-disturbing system for drivers. However, the accuracy of these devices should be compared with accurate medical sensors, and differences in information gain according to the different characteristics of an ECG to an optical pulse signal need to be evaluated.
- The proposed methods in this study developed generic driver drowsiness classification systems that consider no driver-specific differences. Only two hours of data is available for every driver which might not be sufficient to train a driver-specific deep network. To build a driver-specific system, transfer learning [65] can be employed. Using this method, the trained deep CNNs can be fine-tuned for a specific driver using a shuffled portion of their ECG data as the training set. Then, the fine-tuned deep CNN can be used to evaluate the drowsiness for the specific driver in the unseen test set or in real time. This approach can also reduce the amount of data needed from each driver to build a driver-specific system.
- In this study, data from signal segments were treated as independent from each other by random selection and the sequential time information was ignored. Though this is presumably an advantage for the ability of a practical system to react fast, the transition from wakefulness to drowsiness might also be considered a continuous slower process. Therefore, it should be evaluated if outcomes of the deep network profit from the inclusion of sequential information of training segments.
Author Contributions
Conceptualization, S.A., A.E. and M.M.; methodology, S.A. and C.K.; validation, I.V.K. and A.E.; resources, M.F., C.K., M.M. and I.K.; data curation, M.F., A.E. and I.V.K.; writing—original draft preparation, S.A.; supervision, A.E.; project administration, A.E. and M.F.; funding acquisition, M.M., A.E. and M.F. All authors have read and agreed to the published version of the manuscript.
Funding
This project called WACHSens was carried out by the Human Research Institut für Gesundheitstechnologie und Präventionsforschung GmbH, Graz University of Technology, AVL Powertrain UK Limited, and Factum apptec ventures GmbH. It was funded by the Austrian Research Promotion Agency (FFG) via the Future Mobility Program (grant no. 860875).
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Ethics Committee of the Medical University of Graz in vote 30-409 ex 17/18 dated 1 June 2018.
Informed Consent Statement
Written informed consent was obtained from participants before the experiments.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are indebted to all drivers who participated in the experiment, the experimenters, and the many people who helped set up the tests.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Baulk, S.D.; Reyner, L.A.; Horne, J.A. Driver sleepiness—Evaluation of reaction time measurement as a secondary task. Sleep 2001, 24, 695–698. [Google Scholar] [CrossRef]
- Arefnezhad, S.; Samiee, S.; Eichberger, A.; Frühwirth, M.; Kaufmann, C.; Klotz, E. Applying deep neural networks for multi-level classification of driver drowsiness using Vehicle-based measures. Expert Syst. Appl. 2020, 162, 113778. [Google Scholar] [CrossRef]
- National Highway Traffic Safety Administration. Traffic Safety Facts: 2017 Fatal Motor Vehicle Crashes: Overview DOT HS 812 603, 1200 New Jersey Avenue SE., Washington, 2018. Available online: https://crashstats.nhtsa.dot.gov/Api/Public/ViewPublication/812603 (accessed on 14 April 2021).
- Klauer, S.; Neale, V.; Dingus, T.; Sudweeks, J.; Ramsey, D.J. The Prevalence of Driver Fatigue in an Urban Driving Environment Results from the 100-Car Naturalistic Driving Study; Virginia Tech Transportation Institute: Blacksburg, VI, USA, 2005. [Google Scholar]
- AAA Foundation for Traffic Safety. 2019 Traffic Safety Culture Index; AAA Foundation for Traffic Safety: Washington, DC, USA, 2020. [Google Scholar]
- Hirz, M.; Walzel, B. Sensor and object recognition technologies for self-driving cars. Comput. Aided Des. Appl. 2018, 15, 501–508. [Google Scholar] [CrossRef] [Green Version]
- Inagaki, T.; Sheridan, T.B. A critique of the SAE conditional driving automation definition, and analyses of options for improvement. Cogn Tech. Work. 2019, 21, 569–578. [Google Scholar] [CrossRef] [Green Version]
- Mou, L.; Zhou, C.; Xie, P.; Zhao, P.; Jain, R.C.; Gao, W.; Yin, B. Isotropic Self-supervised Learning for Driver Drowsiness Detection With Attention-based Multimodal Fusion. IEEE Trans. Multimed. 2021, 1. [Google Scholar] [CrossRef]
- Zhu, M.; Chen, J.; Li, H.; Liang, F.; Han, L.; Zhang, Z. Vehicle driver drowsiness detection method using wearable EEG based on convolution neural network. Neural Comput. Applic. 2021, 33, 13965–13980. [Google Scholar] [CrossRef] [PubMed]
- Dua, M.; Singla, R.; Raj, S.; Jangra, A. Deep CNN models-based ensemble approach to driver drowsiness detection. Neural Comput. Applic. 2021, 33, 3155–3168. [Google Scholar] [CrossRef]
- Bakheet, S.; Al-Hamadi, A. A Framework for Instantaneous Driver Drowsiness Detection Based on Improved HOG Features and Naïve Bayesian Classification. Brain Sci. 2021, 11, 240. [Google Scholar] [CrossRef]
- Jung, S.-J.; Shin, H.-S.; Chung, W.-Y. Driver fatigue and drowsiness monitoring system with embedded electrocardiogram sensor on steering wheel. IET Intell. Transp. Syst. 2014, 8, 43–50. [Google Scholar] [CrossRef]
- Gromer, M.; Salb, D.; Walzer, T.; Madrid, N.M.; Seepold, R. ECG sensor for detection of driver’s drowsiness. Procedia Comput. Sci. 2019, 159, 1938–1946. [Google Scholar] [CrossRef]
- Rodríguez, R.; Mexicano, A.; Bila, J.; Cervantes, S.; Ponce, R. Feature Extraction of Electrocardiogram Signals by Applying Adaptive Threshold and Principal Component Analysis. J. Appl. Res. Technol. 2015, 13, 261–269. [Google Scholar] [CrossRef]
- Thomas, J.; Rose, C.; Charpillet, F. A Multi-HMM Approach to ECG Segmentation. In Proceedings of the 18th IEEE International Conference on Tools with Artificial Intelligence (ICTAI’06), Arlington, VA, USA, 13 November 2006. [Google Scholar]
- Kiran kumar, C.; Manaswini, M.; Maruthy, K.N.; Siva Kumar, A.V.; Mahesh kumar, K. Association of Heart rate variability measured by RR interval from ECG and pulse to pulse interval from Photoplethysmography. Clin. Epidemiol. Glob. Health 2021, 10, 100698. [Google Scholar] [CrossRef]
- Huang, S.; Li, J.; Zhang, P.; Zhang, W. Detection of mental fatigue state with wearable ECG devices. Int. J. Med. Inform. 2018, 119, 39–46. [Google Scholar] [CrossRef] [PubMed]
- Moser, M.; Frühwirth, M.; Penter, R.; Winker, R. Why life oscillates—From a topographical towards a functional chronobiology. Cancer Causes Control 2006, 17, 591–599. [Google Scholar] [CrossRef]
- Moser, M.; Frühwirth, M.; Kenner, T. The symphony of life. Importance, interaction, and visualization of biological rhythms. IEEE Eng. Med. Biol. Mag. 2008, 27, 29–37. [Google Scholar] [CrossRef]
- Fujiwara, K.; Abe, E.; Kamata, K.; Nakayama, C.; Suzuki, Y.; Yamakawa, T.; Hiraoka, T.; Kano, M.; Sumi, Y.; Masuda, F.; et al. Heart Rate Variability-Based Driver Drowsiness Detection and Its Validation With EEG. IEEE Trans. Biomed. Eng. 2019, 66, 1769–1778. [Google Scholar] [CrossRef]
- Vicente, J.; Laguna, P.; Bartra, A.; Bailón, R. Drowsiness detection using heart rate variability. Med. Biol. Eng. Comput. 2016, 54, 927–937. [Google Scholar] [CrossRef] [PubMed]
- Buendia, R.; Forcolin, F.; Karlsson, J.; Sjöqvist, B.A.; Anund, A.; Candefjord, S. Deriving heart rate variability indices from cardiac monitoring—An indicator of driver sleepiness. Traffic Inj. Prev. 2019, 20, 249–254. [Google Scholar] [CrossRef] [Green Version]
- Patel, M.; Lal, S.K.L.; Kavanagh, D.; Rossiter, P. Applying neural network analysis on heart rate variability data to assess driver fatigue. Expert Syst. Appl. 2011, 38, 7235–7242. [Google Scholar] [CrossRef]
- Li, G.; Chung, W.-Y. Detection of driver drowsiness using wavelet analysis of heart rate variability and a support vector machine classifier. Sensors 2013, 13, 16494–16511. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Furman, G.D.; Baharav, A.; Cahan, C.; Akselrod, S. Early detection of falling asleep at the wheel: A Heart Rate Variability approach. Comput. Cardiol. 2008, 35, 1109–1112. [Google Scholar] [CrossRef]
- SENSODRIVE GmbH. SENSODRIVE GmbH—Robotic und Force-Feedback. Available online: https://www.sensodrive.de/products/force-feedback-steering-wheels.php (accessed on 14 June 2021).
- AVL. AVL VSM™ Vehicle Simulation; Release 2020 R1: Highlights of the Latest Release of Our Vehicle Dynamics Simulation Tool. Available online: https://www.avl.com/-/avl-vsm-vehicle-simulation (accessed on 14 June 2021).
- Schinko, C.; Peer, M.; Hammer, D.; Pirstinger, M.; Lex, C.; Koglbauer, I.; Eichberger, A.; Holzinger, J.; Eggeling, E.; Fellner, D.W.; et al. Building a Driving Simulator with Parallax Barrier Displays. In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications, Rome, Italy, 27–29 February 2016; pp. 281–289. [Google Scholar]
- Lex, C.; Hammer, D.; Pirstinger, M.; Peer, M.; Samiee, S.; Schinko, C.; Ullrich, T.; Battel, M.; Holzinger, J.; Koglbauer, I.; et al. Multidisciplinary Development of a Driving Simulator with Autostereoscopic Visualization for the Integrated Development of Driver Assistance Systems; Graz University of Technology: Graz, Austria, 2015. [Google Scholar]
- Kaufmann, C.; Frühwirth, M.; Messerschmidt, D.; Moser, M.; Eichberger, A.; Arefnezhad, S. Driving and tiredness: Results of the behaviour observation of a simulator study with special focus on automated driving. ToTS 2020, 11, 51–63. [Google Scholar] [CrossRef]
- Gacek, A.C.; Pedrycz, W. ECG Signal Processing, Classification and Interpretation: A Comprehensive Framework of Computational Intelligence; Springer: London, UK, 2012. [Google Scholar]
- Gupta, P.; Sharma, K.K.; Joshi, S.D. Baseline wander removal of electrocardiogram signals using multivariate empirical mode decomposition. Healthc. Technol. Lett. 2015, 2, 164–166. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, C.; Xiao, W. Second-Order IIR Notch Filter Design and Implementation of Digital Signal Processing System. Appl. Mech. Mater. 2013, 347–350, 729–732. [Google Scholar] [CrossRef]
- Bolós, V.J.; Benítez, R. The Wavelet Scalogram in the Study of Time Series. In Advances in Differential Equations and Applications; Casas, F., Martínez, V., Eds.; Springer: New York, NY, USA, 2014; pp. 147–154. [Google Scholar]
- Lilly, J.M.; Olhede, S.C. Higher-Order Properties of Analytic Wavelets. IEEE Trans. Signal Process. 2009, 57, 146–160. [Google Scholar] [CrossRef] [Green Version]
- Mario, M.-O. Human Activity Recognition Based on Single Sensor Square HV Acceleration Images and Convolutional Neural Networks. IEEE Sens. J. 2019, 19, 1487–1498. [Google Scholar] [CrossRef]
- Park, S.; Jeong, Y.; Kim, H.S. Multiresolution CNN for Reverberant Speech Recognition. In Proceedings of the 2017 Conference of the Oriental Chapter of International Committee for Coordination and Standardization of Speech Databases and Assessment Technique (O-COCOSDA), Seoul, Korea, 1–3 November 2017; pp. 1–4. [Google Scholar]
- Li, Q.; Cai, W.; Wang, X.; Zhou, Y.; Feng, D.D.; Chen, M. Medical Image Classification with Convolutional Neural Network. In Proceedings of the 13th International Conference on Control, Automation, Robotics & Vision (ICARCV), Singapore, 10–12 December 2014; pp. 844–848. [Google Scholar]
- Zhao, Z.; Zhou, N.; Zhang, L.; Yan, H.; Xu, Y.; Zhang, Z. Driver Fatigue Detection Based on Convolutional Neural Networks Using EM-CNN. Comput. Intell. Neurosci. 2020, 2020, 7251280. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Ilievski, I.; Akhtar, T.; Feng, J.; Shoemaker, C. Efficient Hyperparameter Optimization for Deep Learning Algorithms Using Deterministic RBF Surrogates. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Shankar, K.; Zhang, Y.; Liu, Y.; Wu, L.; Chen, C.-H. Hyperparameter Tuning Deep Learning for Diabetic Retinopathy Fundus Image Classification. IEEE Access 2020, 8, 118164–118173. [Google Scholar] [CrossRef]
- Neary, P. Automatic Hyperparameter Tuning in Deep Convolutional Neural Networks Using Asynchronous Reinforcement Learning. In Proceedings of the 2018 IEEE International Conference on Cognitive Computing (ICCC), San Francisco, CA, USA, 2–7 July 2018. [Google Scholar]
- Peter, I. Frazier. Bayesian Optimization of Risk Measures. arXiv 2007, arXiv:2007.05554v3. [Google Scholar]
- Kawaguchi, K.; Kaelbling, L.P.; Lozano-Pérez, T. Bayesian Optimization with Exponential Convergence. arXiv 2018, arXiv:1811.09558. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian Optimization of Machine Learning Algorithms. arXiv 2012, arXiv:1206.2944. [Google Scholar]
- Scholkmann, F.; Boss, J.; Wolf, M. An Efficient Algorithm for Automatic Peak Detection in Noisy Periodic and Quasi-Periodic Signals. Algorithms 2012, 5, 588–603. [Google Scholar] [CrossRef] [Green Version]
- Task Force of the European Society of Cardiology the North American Society of Pacing Electrophysiology. Heart Rate Variability. Circulation 1996, 93, 1043–1065. [Google Scholar] [CrossRef] [Green Version]
- Hoshi, R.A.; Pastre, C.M.; Vanderlei, L.C.M.; Godoy, M.F. Poincaré plot indexes of heart rate variability: Relationships with other nonlinear variables. Auton. Neurosci. 2013, 177, 271–274. [Google Scholar] [CrossRef]
- Fitzgibbon, A.W.; Pilu, M.; Fisher, R.B. Direct Least Squares Fitting of Ellipses. In Proceedings of the 13th International Conference On Pattern Recognition, Vienna, Austria, 29 August 1996. [Google Scholar]
- Morelli, D.; Rossi, A.; Cairo, M.; Clifton, D.A. Analysis of the Impact of Interpolation Methods of Missing RR-intervals Caused by Motion Artifacts on HRV Features Estimations. Sensors 2019, 19, 3163. [Google Scholar] [CrossRef] [Green Version]
- Shaffer, F.; Ginsberg, J.P. An Overview of Heart Rate Variability Metrics and Norms. Front. Public Health 2017, 5, 258. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Clifford, G.D.; Tarassenko, L. Quantifying errors in spectral estimates of HRV due to beat replacement and resampling. IEEE Trans. Biomed. Eng. 2005, 52, 630–638. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.K.; Kim, J.S.; Lim, Y.G.; Park, K.S. The effect of missing RR-interval data on heart rate variability analysis in the frequency domain. Physiol. Meas. 2009, 30, 1039–1050. [Google Scholar] [CrossRef]
- Munoz, M.L.; van Roon, A.; Riese, H.; Thio, C.; Oostenbroek, E.; Westrik, I.; de Geus, E.J.; Gansevoort, R.; Lefrandt, J.; Nolte, I.M.; et al. Validity of (Ultra-)Short Recordings for Heart Rate Variability Measurements. PLoS ONE 2015, 10, e0138921. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ghawi, R.; Pfeffer, J. Efficient Hyperparameter Tuning with Grid Search for Text Categorization using kNN Approach with BM25 Similarity. Open Comput. Sci. 2019, 9, 160–180. [Google Scholar] [CrossRef]
- Probst, P.; Wright, M.N.; Boulesteix, A.-L. Hyperparameters and Tuning Strategies for Random Forest. WIREs Data Mining Knowl Discov. 2019, 9, e1301. [Google Scholar] [CrossRef] [Green Version]
- López, V.; Fernández, A.; García, S.; Palade, V.; Herrera, F. An insight into classification with imbalanced data: Empirical results and current trends on using data intrinsic characteristics. Inf. Sci. 2013, 250, 113–141. [Google Scholar] [CrossRef]
- Seiffert, C.; Khoshgoftaar, T.M.; van Hulse, J.; Napolitano, A. RUSBoost: Improving Classification Performance When Training Data Is Skewed. In Proceedings of the 19th International Conference on Pattern Recognition (ICPR 2008), Tampa, FL, USA, 8–11 December 2008; pp. 1–4. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Advances in Neural Information Processing Systems; Pereira, F., Burges, C.J.C., Bottou, L., Weinberger, K.Q., Eds.; Curran Associates Inc.: Red Hook, NY, USA, 2012. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. arXiv 2014, arXiv:1409.4842. [Google Scholar]
- Melo, H.M.; Martins, T.C.; Nascimento, L.M.; Hoeller, A.A.; Walz, R.; Takase, E. Ultra-short heart rate variability recording reliability: The effect of controlled paced breathing. Ann. Noninvasive Electrocardiol. 2018, 23, e12565. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A Comprehensive Survey on Transfer Learning. arXiv 2020, arXiv:1911.02685v3. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).