A Critical Review on the Estimation Techniques of the Solar PV Cell’s Unknown Parameters
Abstract
:1. Introduction
- The combination of both analytical and numerical techniques (combined technique) are observed to be less time-consuming compared to other techniques that are used for parameter estimation of solar PV systems;
- The combined technique has the highest accuracy compared to others in the existing literature;
- In analytical algorithms, the number of non-linear exponential terms can be reduced by four times compared to the existing literature. Hence, the combined technique is computationally efficient;
- The shunt resistance () should be considered as one of the iteration parameters, which makes the approach more realistic;
- The application of the nominal operating cell temperature (NOCT) value in the PV parameter estimation strengthens the accuracy in varying temperatures and irradiance conditions. It is noticed that, on average, a 10% performance degradation (PD) is present in the MPP obtained at compared to .
2. Solar PV Modelling
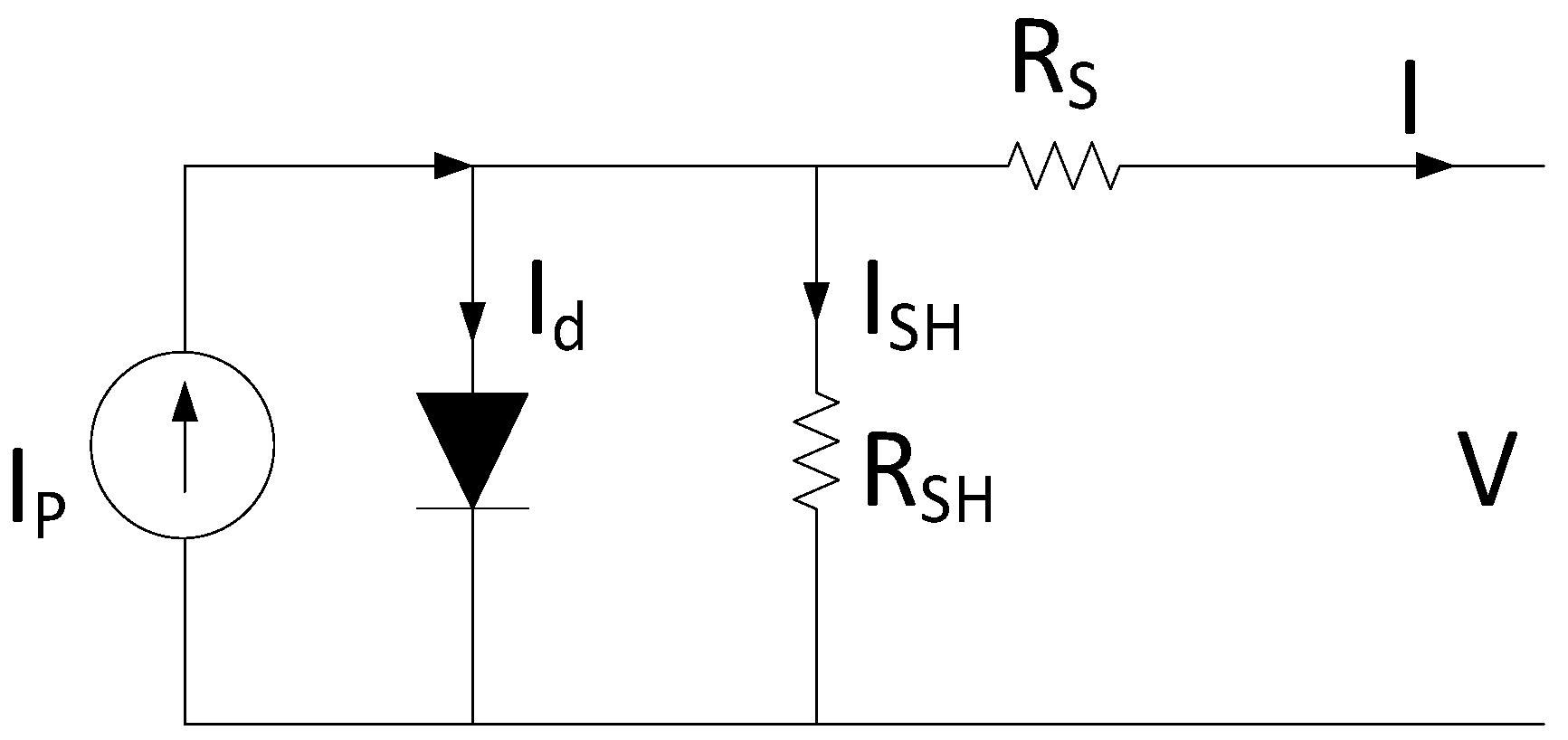
2.1. Single-Diode Model
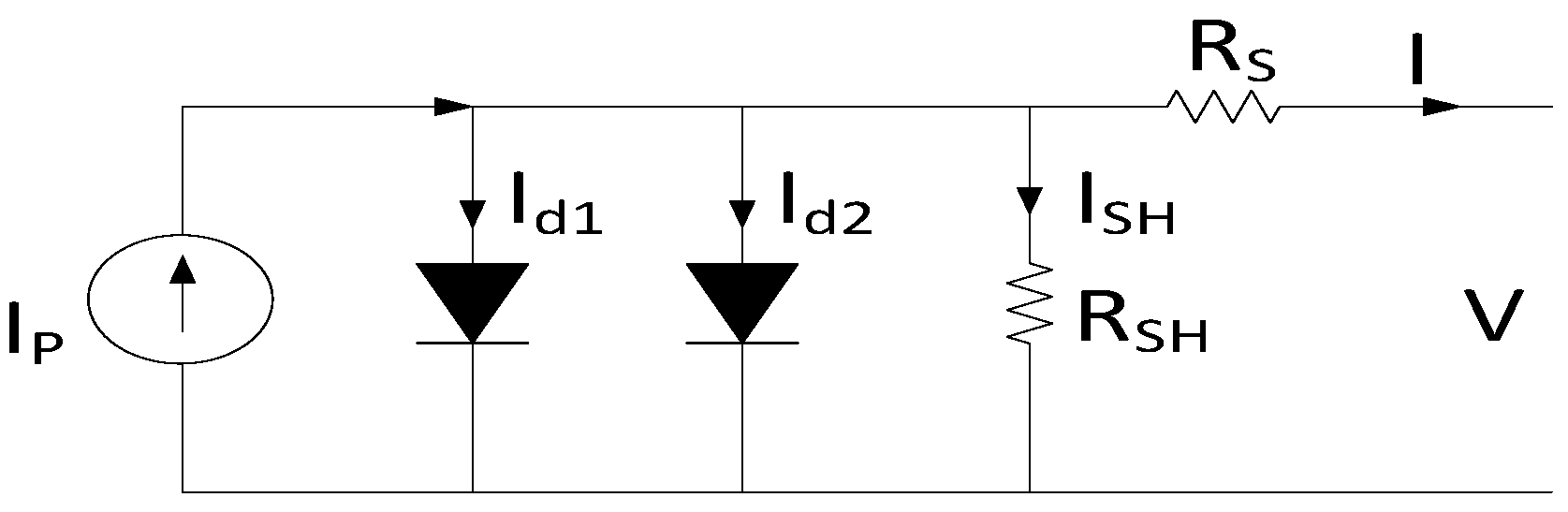
2.2. Double-Diode Model
2.3. Three-Diode Model
3. Algorithms Reported So Far
3.1. Analytical Algorithms
3.2. Non-Analytical Algorithms
3.3. Meta-Heuristic Approach
- is the position of the foodTable;
- l is the lower boundary;
- u is the upper boundary;
- r is the random vector in (0, 1).
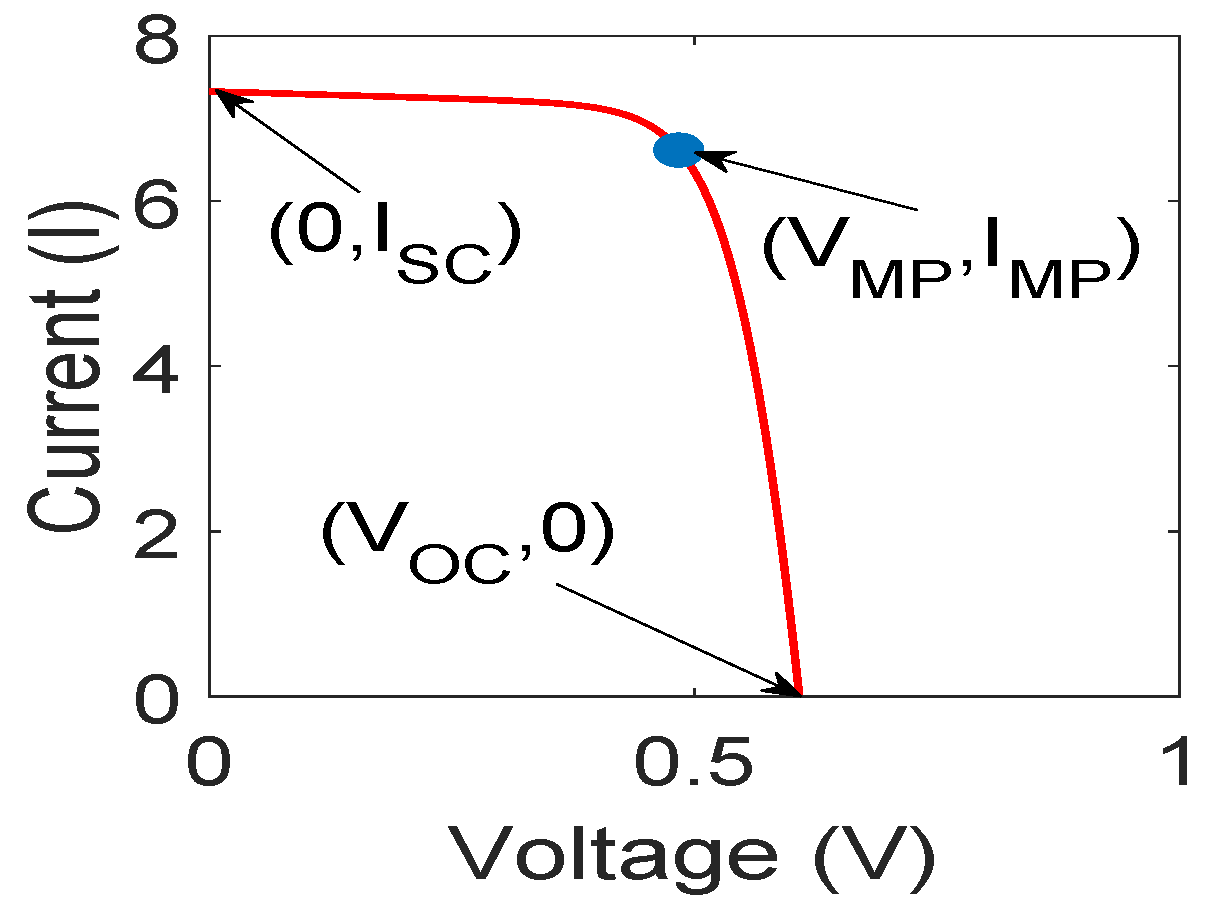
4. Performance Analysis of the Reported Algorithms
Effect of Temperature and Irradiance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- International, E.A. Photovoltaic Power Systems Programme; Snapshot: Paris, France, 2020; Available online: https://iea-pvps.org/snapshot-reports/snapshot-2020/ (accessed on 16 April 2022).
- Herrmann, W.; Wiesner, W. Modelling of PV modules—The effects of non-uniform irradiance on performance measurements with solar simulators. In Proceedings of the 16th European Photovoltaic Solar Energy Conference, Glasgow, UK, 1–5 May 2000; pp. 2338–2341. [Google Scholar]
- Goswami, A.; Sadhu, P.K. Nature inspired evolutionary algorithm integrated performance assessment of floating solar photovoltaic module for low-carbon clean energy generation. Sustain. Oper. Comput. 2022, 3, 67–82. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, K.; Zhang, T.; Wang, Y.; Peng, C.; Gao, S. A population diversity-controlled differential evolution for parameter estimation of solar photovoltaic models. Sustain. Energy Technol. Assess. 2022, 51, 101938. [Google Scholar] [CrossRef]
- Venkateswari, R.; Rajasekar, N. Review on parameter estimation techniques of solar photovoltaic systems. Int. Trans. Electr. Energy Syst. 2021, 31, e13113. [Google Scholar] [CrossRef]
- Mehta, H.K.; Warke, H.; Kukadiya, K.; Panchal, A.K. Accurate Expressions for Single-Diode-Model Solar Cell Parameterization. IEEE J. Photovol. 2019, 9, 803–810. [Google Scholar] [CrossRef]
- Moshksar, E.; Ghanbari, T. Constrained optimisation approach for parameter estimation of PV modules with single-diode equivalent model. IET Renew. Power Gener. 2018, 12, 1398–1404. [Google Scholar] [CrossRef]
- Arabshahi, M.; Torkaman, H.; Keyhani, A. A method for hybrid extraction of single-diode model parameters of photovoltaics. Renew. Energy 2020, 158, 236–252. [Google Scholar] [CrossRef]
- Ridha, H.M.; Hizam, H.; Mirjalili, S.; Othman, M.L.; Ya’acob, M.E.; Abualigah, L. A novel theoretical and practical methodology for extracting the parameters of the single and double diode photovoltaic models. IEEE Access 2022, 10, 11110–11137. [Google Scholar] [CrossRef]
- Yahya-Khotbehsara, A.; Shahhoseini, A. A fast modeling of the double-diode model for PV modules using combined analytical and numerical approach. Sol. Energy 2018, 162, 403–409. [Google Scholar] [CrossRef]
- Gnetchejo, P.J.; Essiane, S.N.; Ele, P.; Wamkeue, R.; Wapet, D.M.; Ngoffe, S.P. Important notes on parameter estimation of solar photovoltaic cell. Energy Convers. Manag. 2019, 197, 111870. [Google Scholar] [CrossRef]
- Sinha, A.; Gopalakrishna, H.; Subramaniyan, A.B.; Jain, D.; Oh, J.; Jordan, D.; TamizhMani, G. Prediction of Climate-Specific Degradation Rate for Photovoltaic Encapsulant Discoloration. IEEE J. Photovolt. 2020, 10, 1093–1101. [Google Scholar] [CrossRef]
- Chan, D.S.; Phang, J.C. Analytical methods for the extraction of solar-cell single-and double-diode model parameters from IV characteristics. IEEE Trans. Electron Devices 1987, 34, 286–293. [Google Scholar] [CrossRef]
- Phang, J.; Chan, D.; Phillips, J. Accurate analytical method for the extraction of solar cell model parameters. Electron. Lett. IET 1984, 20, 406–408. [Google Scholar] [CrossRef]
- Changmai, P.; Nayak, S.K.; Metya, S.K. Estimation of PV module parameters from the manufacturer’s datasheet for MPP estimation. IET Renew. Power Gener. 2020, 14, 1988–1996. [Google Scholar] [CrossRef]
- Hsieh, Y.C.; Yu, L.R.; Chang, T.C.; Liu, W.C.; Wu, T.H.; Moo, C.S. Parameter Identification of One-Diode Dynamic Equivalent Circuit Model for Photovoltaic Panel. IEEE J. Photovolt. 2019, 10, 219–225. [Google Scholar] [CrossRef]
- Huang, Y.C.; Huang, C.M.; Chen, S.J.; Yang, S.P. Optimization of Module Parameters for PV Power Estimation Using a Hybrid Algorithm. IEEE Trans. Sustain. Energy 2019, 11, 2210–2219. [Google Scholar] [CrossRef]
- Bradaschia, F.; Cavalcanti, M.C.; do Nascimento, A.J.; da Silva, E.A.; de Souza Azevedo, G.M. Parameter Identification for PV Modules Based on an Environment-Dependent Double-Diode Model. IEEE J. Photovolt. 2019, 9, 1388–1397. [Google Scholar] [CrossRef]
- Zhang, Z.; Hu, G.; Chen, Q.; Yan, Z. Correntropy-based parameter estimation for photovoltaic array model considering partial shading condition. IET Renew. Power Gener. 2019, 13, 1309–1316. [Google Scholar] [CrossRef]
- Guo, S.; Abbassi, R.; Jerbi, H.; Rezvani, A.; Suzuki, K. Efficient maximum power point tracking for a photovoltaic using hybrid shuffled frog-leaping and pattern search algorithm under changing environmental conditions. J. Clean. Prod. 2021, 297, 126573. [Google Scholar] [CrossRef]
- Fathy, A.; Abd Elaziz, M.; Sayed, E.T.; Olabi, A.; Rezk, H. Optimal parameter identification of triple-junction photovoltaic panel based on enhanced moth search algorithm. Energy 2019, 188, 116025. [Google Scholar] [CrossRef]
- Tang, S.; Jiang, M.; Abbassi, R.; Jerbi, H.; Latifi, M. A cost-oriented resource scheduling of a solar-powered microgrid by using the hybrid crow and pattern search algorithm. J. Clean. Prod. 2021, 313, 127853. [Google Scholar] [CrossRef]
- Ye, X.; Liu, W.; Li, H.; Wang, M.; Chi, C.; Liang, G.; Chen, H.; Huang, H. Modified whale optimization algorithm for solar cell and PV module parameter identification. Complexity 2021, 2021, 8878686. [Google Scholar] [CrossRef]
- Eslami, M.; Akbari, E.; Seyed Sadr, S.T.; Ibrahim, B.F. A novel hybrid algorithm based on rat swarm optimization and pattern search for parameter extraction of solar photovoltaic models. Energy Sci. Eng. 2022. [Google Scholar] [CrossRef]
- Xiong, G.; Zhang, J.; Yuan, X.; Shi, D.; He, Y. Application of symbiotic organisms search algorithm for parameter extraction of solar cell models. Appl. Sci. 2018, 8, 2155. [Google Scholar] [CrossRef]
- Sharma, A.; Dasgotra, A.; Tiwari, S.K.; Sharma, A.; Jately, V.; Azzopardi, B. Parameter extraction of photovoltaic module using tunicate swarm algorithm. Electronics 2021, 10, 878. [Google Scholar] [CrossRef]
- Sharma, A.; Sharma, A.; Moshe, A.; Raj, N.; Pachauri, R.K. An effective method for parameter estimation of solar PV cell using Grey-wolf optimization technique. Int. J. Math. Eng. Manag. Sci. 2021, 6, 911. [Google Scholar] [CrossRef]
- Gude, S.; Jana, K.C. Parameter extraction of photovoltaic cell using an improved cuckoo search optimization. Sol. Energy 2020, 204, 280–293. [Google Scholar] [CrossRef]
- Prasanth Ram, J.; Pillai, D.S.; Rajasekar, N.; Kumar Chinnaiyan, V. Flower pollination based solar PV parameter extraction for double diode model. In Intelligent Computing Techniques for Smart Energy Systems; Springer: Berlin, Germany, 2020; pp. 303–312. [Google Scholar]
- Zhen, Z.; Pang, S.; Wang, F.; Li, K.; Li, Z.; Ren, H.; Shafie-khah, M.; Catalão, J.P. Pattern classification and PSO optimal weights based sky images cloud motion speed calculation method for solar PV power forecasting. IEEE Trans. Ind. Appl. 2019, 55, 3331–3342. [Google Scholar] [CrossRef]
- Changmai, P.; Kumar, S.; Nayak, S.K.; Metya, S.K. Maximum Power Estimation of Total Cross-Tied Connected PV Cells in different Shading Conditions for High Current Application. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 3883–3894. [Google Scholar] [CrossRef]
- Easwarakhanthan, T.; Bottin, J.; Bouhouch, I.; Boutrit, C. Nonlinear minimization algorithm for determining the solar cell parameters with microcomputers. Int. J. Sol. Energy 1986, 4, 1–12. [Google Scholar] [CrossRef]
- Gao, S.; Wang, K.; Tao, S.; Jin, T.; Dai, H.; Cheng, J. A state-of-the-art differential evolution algorithm for parameter estimation of solar photovoltaic models. Energy Convers. Manag. 2021, 230, 113784. [Google Scholar] [CrossRef]
- Tran, T.-H.; Nguyen, H.; Nhat-Duc, H.; Nguyen, T.-D. A success history-based adaptive differential evolution optimized support vector regression for estimating plastic viscosity of fresh concrete. Eng. Comput. 2021, 37, 1485–1498. [Google Scholar]
- Yeh, J.F.; Chen, T.Y.; Chiang, T.C. Modified l-shade for single objective real-parameter optimization. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 381–386. [Google Scholar]
- Biswas, P.P.; Suganthan, P.N. Large initial population and neighborhood search incorporated in lshade to solve cec2020 benchmark problems. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–7. [Google Scholar]
- Refaat, M.M.; Aleem, S.H.A.; Atia, Y.; Ali, Z.M.; El-Shahat, A.; Sayed, M.M. A mathematical approach to simultaneously plan generation and transmission expansion based on fault current limiters and reliability constraints. Mathematics 2021, 9, 2771. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, H.; Han, T.; Wei, Z.; Liang, Y.; Li, Y. A Gaussian estimation of distribution algorithm with random walk strategies and its application in optimal missile guidance handover for multi-UCAV in over-the-horizon air combat. IEEE Access 2019, 7, 43298–43317. [Google Scholar] [CrossRef]
- Mohamed, A.W.; Hadi, A.A.; Jambi, K.M. Novel mutation strategy for enhancing SHADE and LSHADE algorithms for global numerical optimization. Swarm Evol. Comput. 2019, 50, 100455. [Google Scholar] [CrossRef]
- Chen, H.; Cheng, R.; Wen, J.; Li, H.; Weng, J. Solving large-scale many-objective optimization problems by covariance matrix adaptation evolution strategy with scalable small subpopulations. Inf. Sci. 2020, 509, 457–469. [Google Scholar] [CrossRef]
- Wei, Z.; Huang, C.; Wang, X.; Zhang, H. Parameters identification of photovoltaic models using a novel algorithm inspired from nuclear reaction. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 210–218. [Google Scholar]
- Nunes, H.; Pombo, J.; Bento, P.; Mariano, S.; Calado, M. Collaborative swarm intelligence to estimate PV parameters. Energy Convers. Manag. 2019, 185, 866–890. [Google Scholar] [CrossRef]
- Toledo, F.J.; Blanes, J.M.; Galiano, V. Two-step linear least-squares method for photovoltaic single-diode model parameters extraction. IEEE Trans. Ind. Electron. 2018, 65, 6301–6308. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Sultan, H.M.; Aljendy, R.; Al-Sumaiti, A.S.; Shoyama, M.; Ali, Z.M. Tree Growth Based Optimization Algorithm for Parameter Extraction of Different Models of Photovoltaic Cells and Modules. IEEE Access 2020, 8, 119668–119687. [Google Scholar] [CrossRef]
- Yu, K.; Qu, B.; Yue, C.; Ge, S.; Chen, X.; Liang, J. A performance-guided JAYA algorithm for parameters identification of photovoltaic cell and module. Appl. Energy 2019, 237, 241–257. [Google Scholar] [CrossRef]
- Yu, K.; Liang, J.; Qu, B.; Chen, X.; Wang, H. Parameters identification of photovoltaic models using an improved JAYA optimization algorithm. Energy Convers. Manag. 2017, 150, 742–753. [Google Scholar] [CrossRef]
- Liang, J.; Ge, S.; Qu, B.; Yu, K.; Liu, F.; Yang, H.; Wei, P.; Li, Z. Classified perturbation mutation based particle swarm optimization algorithm for parameters extraction of photovoltaic models. Energy Convers. Manag. 2020, 203, 112138. [Google Scholar] [CrossRef]
- Kler, D.; Goswami, Y.; Rana, K.; Kumar, V. A novel approach to parameter estimation of photovoltaic systems using hybridized optimizer. Energy Convers. Manag. 2019, 187, 486–511. [Google Scholar] [CrossRef]
- Ebrahimi, S.M.; Salahshour, E.; Malekzadeh, M.; Gordillo, F. Parameters identification of PV solar cells and modules using flexible particle swarm optimization algorithm. Energy 2019, 179, 358–372. [Google Scholar] [CrossRef]
- Yousri, D.; Allam, D.; Eteiba, M.; Suganthan, P.N. Static and dynamic photovoltaic models’ parameters identification using Chaotic Heterogeneous Comprehensive Learning Particle Swarm Optimizer variants. Energy Convers. Manag. 2019, 182, 546–563. [Google Scholar] [CrossRef]
- Li, S.; Gong, W.; Yan, X.; Hu, C.; Bai, D.; Wang, L.; Gao, L. Parameter extraction of photovoltaic models using an improved teaching-learning-based optimization. Energy Convers. Manag. 2019, 186, 293–305. [Google Scholar] [CrossRef]
- Chen, H.; Jiao, S.; Heidari, A.A.; Wang, M.; Chen, X.; Zhao, X. An opposition-based sine cosine approach with local search for parameter estimation of photovoltaic models. Energy Convers. Manag. 2019, 195, 927–942. [Google Scholar] [CrossRef]
- Chen, X.; Yue, H.; Yu, K. Perturbed stochastic fractal search for solar PV parameter estimation. Energy 2019, 189, 116247. [Google Scholar] [CrossRef]
- Li, S.; Gong, W.; Yan, X.; Hu, C.; Bai, D.; Wang, L. Parameter estimation of photovoltaic models with memetic adaptive differential evolution. Solar Energy 2019, 190, 465–474. [Google Scholar] [CrossRef]
- Pourmousa, N.; Ebrahimi, S.M.; Malekzadeh, M.; Alizadeh, M. Parameter estimation of photovoltaic cells using improved Lozi map based chaotic optimization Algorithm. Sol. Energy 2019, 180, 180–191. [Google Scholar] [CrossRef]
- Ćalasan, M.; Jovanović, D.; Rubežić, V.; Mujović, S.; Đukanović, S. Estimation of Single-Diode and Two-Diode Solar Cell Parameters by Using a Chaotic Optimization Approach. Energies 2019, 12, 4209. [Google Scholar] [CrossRef]
- Chen, X.; Yu, K. Hybridizing cuckoo search algorithm with biogeography-based optimization for estimating photovoltaic model parameters. Sol. Energy 2019, 180, 192–206. [Google Scholar] [CrossRef]
- Kumar, C.; Raj, T.D.; Premkumar, M.; Raj, T.D. A new stochastic slime mould optimization algorithm for the estimation of solar photovoltaic cell parameters. Optik 2020, 223, 165277. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Oliva, D. Parameter estimation of solar cells diode models by an improved opposition-based whale optimization algorithm. Energy Convers. Manag. 2018, 171, 1843–1859. [Google Scholar] [CrossRef]
- Merchaoui, M.; Sakly, A.; Mimouni, M.F. Particle swarm optimisation with adaptive mutation strategy for photovoltaic solar cell/module parameter extraction. Energy Convers. Manag. 2018, 175, 151–163. [Google Scholar] [CrossRef]
- Beigi, A.M.; Maroosi, A. Parameter identification for solar cells and module using a Hybrid Firefly and Pattern Search Algorithms. Solar Energy 2018, 171, 435–446. [Google Scholar] [CrossRef]
- Gao, X.; Cui, Y.; Hu, J.; Xu, G.; Wang, Z.; Qu, J.; Wang, H. Parameter extraction of solar cell models using improved shuffled complex evolution algorithm. Energy Convers. Manag. 2018, 157, 460–479. [Google Scholar] [CrossRef]
- Louzazni, M.; Khouya, A.; Amechnoue, K.; Gandelli, A.; Mussetta, M.; Crăciunescu, A. Metaheuristic algorithm for photovoltaic parameters: Comparative study and prediction with a firefly algorithm. Appl. Sci. 2018, 8, 339. [Google Scholar] [CrossRef]
- Chen, X.; Xu, B.; Mei, C.; Ding, Y.; Li, K. Teaching–learning–based artificial bee colony for solar photovoltaic parameter estimation. Appl. Energy 2018, 212, 1578–1588. [Google Scholar] [CrossRef]
- Messaoud, R.B. Extraction of uncertain parameters of single-diode model of a photovoltaic panel using simulated annealing optimization. Energy Rep. 2020, 6, 350–357. [Google Scholar] [CrossRef]
- Chin, V.J.; Salam, Z.; Ishaque, K. An accurate and fast computational algorithm for the two-diode model of PV module based on a hybrid method. IEEE Trans. Ind. Electron. 2017, 64, 6212–6222. [Google Scholar] [CrossRef]
- Kang, T.; Yao, J.; Jin, M.; Yang, S.; Duong, T. A novel improved cuckoo search algorithm for parameter estimation of photovoltaic (PV) models. Energies 2018, 11, 1060. [Google Scholar] [CrossRef] [Green Version]
- Bendaoud, R.; Amiry, H.; Benhmida, M.; Zohal, B.; Yadir, S.; Bounouar, S.; Hajjaj, C.; Baghaz, E.; El Aydi, M. New method for extracting physical parameters of PV generators combining an implemented genetic algorithm and the simulated annealing algorithm. Sol. Energy 2019, 194, 239–247. [Google Scholar] [CrossRef]
- Cárdenas, A.A.; Carrasco, M.; Mancilla-David, F.; Street, A.; Cárdenas, R. Experimental parameter extraction in the single-diode photovoltaic model via a reduced-space search. IEEE Trans. Ind. Electron. 2016, 64, 1468–1476. [Google Scholar] [CrossRef]
- Ishibashi, K.i.; Kimura, Y.; Niwano, M. An extensively valid and stable method for derivation of all parameters of a solar cell from a single current-voltage characteristic. J. Appl. Phys. 2008, 103, 094507. [Google Scholar] [CrossRef]
- Shaheen, A.M.; Spea, S.R.; Farrag, S.M.; Abido, M.A. A review of meta-heuristic algorithms for reactive power planning problem. Ain Shams Eng. J. 2018, 9, 215–231. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Elsheikh, A.H.; Sharshir, S.W. Improved prediction of oscillatory heat transfer coefficient for a thermoacoustic heat exchanger using modified adaptive neuro-fuzzy inference system. Int. J. Refrig. 2019, 102, 47–54. [Google Scholar] [CrossRef]
- Waly, H.M.; Azazi, H.Z.; Osheba, D.S.; El-Sabbe, A.E. Parameters extraction of photovoltaic sources based on experimental data. IET Renew. Power Gener. 2019, 13, 1466–1473. [Google Scholar] [CrossRef]
- Chen, H.; Jiao, S.; Wang, M.; Heidari, A.A.; Zhao, X. Parameters identification of photovoltaic cells and modules using diversification-enriched Harris hawks optimization with chaotic drifts. J. Clean. Prod. 2020, 244, 118778. [Google Scholar] [CrossRef]
- Chen, H.; Heidari, A.A.; Chen, H.; Wang, M.; Pan, Z.; Gandomi, A.H. Multi-population differential evolution-assisted Harris hawks optimization: Framework and case studies. Future Gener. Comput. Syst. 2020, 111, 175–198. [Google Scholar] [CrossRef]
- Naeijian, M.; Rahimnejad, A.; Ebrahimi, S.M.; Pourmousa, N.; Gadsden, S.A. Parameter estimation of PV solar cells and modules using Whippy Harris Hawks Optimization Algorithm. Energy Rep. 2021, 7, 4047–4063. [Google Scholar] [CrossRef]
- Yousri, D.; Thanikanti, S.B.; Allam, D.; Ramachandaramurthy, V.K.; Eteiba, M. Fractional chaotic ensemble particle swarm optimizer for identifying the single, double, and three diode photovoltaic models’ parameters. Energy 2020, 195, 116979. [Google Scholar] [CrossRef]
- Duman, S.; Kahraman, H.T.; Sonmez, Y.; Guvenc, U.; Kati, M.; Aras, S. A powerful meta-heuristic search algorithm for solving global optimization and real-world solar photovoltaic parameter estimation problems. Eng. Appl. Artif. Intell. 2022, 111, 104763. [Google Scholar] [CrossRef]
- Chenche, L.E.P.; Mendoza, O.S.H.; Bandarra Filho, E.P. Comparison of four methods for parameter estimation of mono-and multi-junction photovoltaic devices using experimental data. Renew. Sustain. Energy Rev. 2018, 81, 2823–2838. [Google Scholar] [CrossRef]
- Ibrahim, I.A.; Hossain, M.; Duck, B.C.; Nadarajah, M. An improved wind driven optimization algorithm for parameters identification of a triple-diode photovoltaic cell model. Energy Convers. Manag. 2020, 213, 112872. [Google Scholar] [CrossRef]
- Arandian, B.; Eslami, M.; Khalid, S.A.; Khan, B.; Sheikh, U.U.; Akbari, E.; Mohammed, A.H. An Effective Optimization Algorithm for Parameters Identification of Photovoltaic Models. IEEE Access 2022, 10, 34069–34084. [Google Scholar] [CrossRef]
- Franco, R.; Vieira, F. Analytical method for extraction of the single-diode model parameters for photovoltaic panels from datasheet data. Electron. Lett. 2018, 54, 519–521. [Google Scholar] [CrossRef]
- Haddad, S.; Lekouaghet, B.; Benghanem, M.; Soukkou, A.; Rabhi, A. Parameter Estimation of Solar Modules Operating Under Outdoor Operational Conditions Using Artificial Hummingbird Algorithm. IEEE Access 2022, 10, 51299–51314. [Google Scholar] [CrossRef]
- Jiao, S.; Chong, G.; Huang, C.; Hu, H.; Wang, M.; Heidari, A.A.; Chen, H.; Zhao, X. Orthogonally adapted Harris hawks optimization for parameter estimation of photovoltaic models. Energy 2020, 203, 117804. [Google Scholar] [CrossRef]
- Li, S.; Gu, Q.; Gong, W.; Ning, B. An enhanced adaptive differential evolution algorithm for parameter extraction of photovoltaic models. Energy Convers. Manag. 2020, 205, 112443. [Google Scholar] [CrossRef]
- Deotti, L.M.P.; Pereira, J.L.R.; da Silva Junior, I.C. Parameter extraction of photovoltaic models using an enhanced Lévy flight bat algorithm. Energy Convers. Manag. 2020, 221, 113114. [Google Scholar] [CrossRef]
- Zhang, H.; Heidari, A.A.; Wang, M.; Zhang, L.; Chen, H.; Li, C. Orthogonal Nelder-Mead moth flame method for parameters identification of photovoltaic modules. Energy Convers. Manag. 2020, 211, 112764. [Google Scholar] [CrossRef]
- Ismaeel, A.A.; Houssein, E.H.; Oliva, D.; Said, M. Gradient-based optimizer for parameter extraction in photovoltaic models. IEEE Access 2021, 9, 13403–13416. [Google Scholar] [CrossRef]
- Shaban, H.; Houssein, E.H.; Pérez-Cisneros, M.; Oliva, D.; Hassan, A.Y.; Ismaeel, A.A.; AbdElminaam, D.S.; Deb, S.; Said, M. Identification of parameters in photovoltaic models through a runge kutta optimizer. Mathematics 2021, 9, 2313. [Google Scholar] [CrossRef]
- Xiong, G.; Li, L.; Mohamed, A.W.; Yuan, X.; Zhang, J. A new method for parameter extraction of solar photovoltaic models using gaining–sharing knowledge based algorithm. Energy Rep. 2021, 7, 3286–3301. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, P.; Heidari, A.A.; Zhao, X.; Turabieh, H.; Chen, H. Random learning gradient based optimization for efficient design of photovoltaic models. Energy Convers. Manag. 2021, 230, 113751. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, P.; Heidari, A.A.; Zhao, X.; Turabieh, H.; Mafarja, M.; Chen, H. Metaphor-free dynamic spherical evolution for parameter estimation of photovoltaic modules. Energy Rep. 2021, 7, 5175–5202. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; El-Shahat, D.; Chakrabortty, R.K.; Ryan, M. Parameter estimation of photovoltaic models using an improved marine predators algorithm. Energy Convers. Manag. 2021, 227, 113491. [Google Scholar] [CrossRef]
- Liu, Y.; Chong, G.; Heidari, A.A.; Chen, H.; Liang, G.; Ye, X.; Cai, Z.; Wang, M. Horizontal and vertical crossover of Harris hawk optimizer with Nelder-Mead simplex for parameter estimation of photovoltaic models. Energy Convers. Manag. 2020, 223, 113211. [Google Scholar] [CrossRef]
- Liang, J.; Qiao, K.; Yu, K.; Ge, S.; Qu, B.; Xu, R.; Li, K. Parameters estimation of solar photovoltaic models via a self-adaptive ensemble-based differential evolution. Sol. Energy 2020, 207, 336–346. [Google Scholar] [CrossRef]
- Xiong, G.; Zhang, J.; Shi, D.; Zhu, L.; Yuan, X.; Tan, Z. Winner-leading competitive swarm optimizer with dynamic Gaussian mutation for parameter extraction of solar photovoltaic models. Energy Convers. Manag. 2020, 206, 112450. [Google Scholar] [CrossRef]
- Liang, J.; Qiao, K.; Yuan, M.; Yu, K.; Qu, B.; Ge, S.; Li, Y.; Chen, G. Evolutionary multi-task optimization for parameters extraction of photovoltaic models. Energy Convers. Manag. 2020, 207, 112509. [Google Scholar] [CrossRef]
- Long, W.; Wu, T.; Xu, M.; Tang, M.; Cai, S. Parameters identification of photovoltaic models by using an enhanced adaptive butterfly optimization algorithm. Energy 2021, 229, 120750. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Chakrabortty, R.K.; Sallam, K.; Ryan, M.J. An efficient teaching-learning-based optimization algorithm for parameters identification of photovoltaic models: Analysis and validations. Energy Convers. Manag. 2021, 227, 113614. [Google Scholar] [CrossRef]
- Khursheed, M.-U.-N.; Alghamdi, M.A.; Khan, M.F.N.; Khan, A.K.; Khan, I.; Ahmed, A.; Kiani, A.T.; Khan, M.A. PV model parameter estimation using modified FPA with dynamic switch probability and step size function. IEEE Access 2021, 9, 42027–42044. [Google Scholar]
- Yang, X.S. Flower pollination algorithm for global optimization. In International Conference on Unconventional Computing and Natural Computation; Springer: Berlin, Germany, 2012; pp. 240–249. [Google Scholar]
- Jordan, D.C.; Marion, B.; Deline, C.; Barnes, T.; Bolinger, M. PV field reliability status—Analysis of 100 000 solar systems. Prog. Photovolt. Res. Appl. 2020, 28, 739–754. [Google Scholar] [CrossRef]
- Hara, S.; Douzono, H.; Imamura, M.; Yoshioka, T. Estimation of Photovoltaic Cell Parameters Using Measurement Data of Photovoltaic Module String Currents and Voltages. IEEE J. Photovolt. 2022, 12, 540–545. [Google Scholar] [CrossRef]
- Kohno, T.; Gokita, K.; Shitanishi, H.; Toyosaki, M.; Nakamura, T.; Morikawa, K.; Hatano, M. Fault-diagnosis architecture for large-scale photovoltaic power plants that does not require additional sensors. IEEE J. Photovolt. 2019, 9, 780–789. [Google Scholar] [CrossRef]
- Harrou, F.; Saidi, A.; Sun, Y.; Khadraoui, S. Monitoring of photovoltaic systems using improved kernel-based learning schemes. IEEE J. Photovolt. 2021, 11, 806–818. [Google Scholar] [CrossRef]
- Mansouri, M.M.; Hadjeri, S.; Brahami, M. New method of detection, identification, and elimination of photovoltaic system faults in real time based on the adaptive Neuro-fuzzy system. IEEE J. Photovolt. 2021, 11, 797–805. [Google Scholar] [CrossRef]
- Mathew, D.; Ram, J.P.; Pillai, D.S.; Kim, Y.J.; Elangovan, D.; Laudani, A.; Mahmud, A. Parameter Estimation of Organic Photovoltaic Cells–A Three-Diode Approach Using Wind-Driven Optimization Algorithm. IEEE J. Photovolt. 2021, 12, 327–336. [Google Scholar] [CrossRef]
- Huang, G.; Liang, Y.; Sun, X.; Xu, C.; Yu, F. Analyzing S-Shaped I–V characteristics of solar cells by solving three-diode lumped-parameter equivalent circuit model explicitly. Energy 2020, 212, 118702. [Google Scholar] [CrossRef]
- Mathew, D.; Rani, C.; Kumar, M.R.; Wang, Y.; Binns, R.; Busawon, K. Wind-driven optimization technique for estimation of solar photovoltaic parameters. IEEE J. Photovolt. 2017, 8, 248–256. [Google Scholar] [CrossRef]
- Restrepo-Cuestas, B.J.; Montano, J.; Ramos-Paja, C.A.; Trejos-Grisales, L.A.; Orozco-Gutierrez, M.L. Parameter estimation of the bishop photovoltaic model using a genetic algorithm. Appl. Sci. 2022, 12, 2927. [Google Scholar] [CrossRef]
- Abido, M.; Khalid, M.S. Seven-parameter PV model estimation using Differential Evolution. Electr. Eng. 2018, 100, 971–981. [Google Scholar] [CrossRef]
- Kiani, A.T.; Nadeem, M.F.; Ahmed, A.; Sajjad, I.A.; Haris, M.S.; Martirano, L. Optimal parameter estimation of solar cell using simulated annealing inertia weight particle swarm optimization (SAIW-PSO). In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 9–12 June 2020; pp. 1–6. [Google Scholar]
- Shankar, N.; Saravanakumar, N.; Kumar, C.; Kamatchi Kannan, V.; Indu Rani, B. Opposition-based equilibrium optimizer algorithm for identification of equivalent circuit parameters of various photovoltaic models. J. Comput. Electron. 2021, 20, 1560–1587. [Google Scholar] [CrossRef]
- Khursheed, M.-U.-N.; Nadeem, M.F.; Khalil, A.; Sajjad, I.; Raza, A.; Iqbal, M.Q.; Bo, R.; ur Rehman, W. Review of flower pollination algorithm: Applications and variants. In Proceedings of the 2020 International Conference on Engineering and Emerging Technologies (ICEET), Lahore, Pakistan, 22–23 February 2020; pp. 1–6.
- Alyasseri, Z.A.A.; Khader, A.T.; Al-Betar, M.A.; Awadallah, M.A.; Yang, X.S. Variants of the flower pollination algorithm: A review. Nat.-Inspired Algorithms Appl. Optim. 2018, 744, 91–118. [Google Scholar]
- Niu, P.; Li, J.; Chang, L.; Zhang, X.; Wang, R.; Li, G. A novel flower pollination algorithm for modeling the boiler thermal efficiency. Neural Process. Lett. 2019, 49, 737–759. [Google Scholar] [CrossRef]
- Alshammari, N.; Asumadu, J. Optimum unit sizing of hybrid renewable energy system utilizing harmony search, Jaya and particle swarm optimization algorithms. Sustain. Cities Soc. 2020, 60, 102255. [Google Scholar] [CrossRef]
- Maleki, A.; Nazari, M.A.; Pourfayaz, F. Harmony search optimization for optimum sizing of hybrid solar schemes based on battery storage unit. Energy Rep. 2020, 6, 102–111. [Google Scholar] [CrossRef]
- Huynh, D.C.; Ho, L.D.; Dunnigan, M.W. Parameter estimation of solar photovoltaic cells using an improved artificial bee colony algorithm. In International Conference on Green Technology and Sustainable Development; Springer: Berlin, Germany, 2020; pp. 281–292. [Google Scholar]
- Tefek, M.F. Artificial bee colony algorithm based on a new local search approach for parameter estimation of photovoltaic systems. J. Comput. Electron. 2021, 20, 2530–2562. [Google Scholar] [CrossRef]
- Kiani, A.T.; Nadeem, M.F.; Ahmed, A.; Sajjad, I.A.; Raza, A.; Khan, I.A. Chaotic inertia weight particle swarm optimization (CIWPSO): An efficient technique for solar cell parameter estimation. In Proceedings of the 2020 3rd International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 29–30 January 2020; pp. 1–6. [Google Scholar]
- Rezk, H.; Arfaoui, J.; Gomaa, M.R. Optimal parameter estimation of solar PV panel based on hybrid particle swarm and grey wolf optimization algorithms. Int. J. Interact. Multimed. Artif. Intell. 2021, in press. [Google Scholar] [CrossRef]
- Bisht, R.; Sikander, A. A New Soft Computing-Based Parameter Estimation of Solar Photovoltaic System. Arab. J. Sci. Eng. 2022, 47, 3341–3353. [Google Scholar] [CrossRef]
- Hao, Q.; Zhou, Z.; Wei, Z.; Chen, G. Parameters Identification of Photovoltaic Models Using a Multi-Strategy Success-History-Based Adaptive Differential Evolution. IEEE Access 2020, 8, 35979–35994. [Google Scholar] [CrossRef]
- Laudani, A.; Fulginei, F.R.; Salvini, A. High performing extraction procedure for the one-diode model of a photovoltaic panel from experimental I–V curves by using reduced forms. Sol. Energy 2014, 103, 316–326. [Google Scholar] [CrossRef]
- Alwan, N.T.; Majeed, M.H.; Shcheklein, S.E.; Ali, O.M.; PraveenKumar, S. Experimental study of a tilt single slope solar still integrated with aluminum condensate plate. Inventions 2021, 6, 77. [Google Scholar] [CrossRef]
- Praveenkumar, S.; Gulakhmadov, A.; Agyekum, E.B.; T Alwan, N.; Velkin, V.I.; Sharipov, P.; Safaraliev, M.; Chen, X. Experimental Study on Performance Enhancement of a Photovoltaic Module Incorporated with CPU Heat Pipe—A 5E Analysis. Sensors 2022, 22, 6367. [Google Scholar] [CrossRef]
- Chavan, S.V.; Devaprakasam, D. Improving the performance of solar photovoltaic thermal system using phase change material. Mater. Today Proc. 2021, 46, 5036–5041. [Google Scholar] [CrossRef]
- Nada, S.; El-Nagar, D.; Hussein, H. Improving the thermal regulation and efficiency enhancement of PCM-Integrated PV modules using nano particles. Energy Convers. Manag. 2018, 166, 735–743. [Google Scholar] [CrossRef]
- Idoko, L.; Anaya-Lara, O.; McDonald, A. Enhancing PV modules efficiency and power output using multi-concept cooling technique. Energy Rep. 2018, 4, 357–369. [Google Scholar] [CrossRef]
- Deokar, V.H.; Bindu, R.S.; Potdar, S. Active cooling system for efficiency improvement of PV panel and utilization of waste-recovered heat for hygienic drying of onion flakes. J. Mater. Sci. Mater. Electron. 2021, 32, 2088–2102. [Google Scholar] [CrossRef]
- PraveenKumar, S.; Agyekum, E.B.; Velkin, V.I.; Yaqoob, S.J.; Adebayo, T.S. Thermal management of solar photovoltaic module to enhance output performance: An experimental passive cooling approach using discontinuous aluminum heat sink. Int. J. Renew. Energy Res. (IJRER) 2021, 11, 1700–1712. [Google Scholar]
- Abdallah, S.R.; Saidani-Scott, H.; Benedi, J. Experimental study for thermal regulation of photovoltaic panels using saturated zeolite with water. Sol. Energy 2019, 188, 464–474. [Google Scholar] [CrossRef]
- Wongwuttanasatian, T.; Sarikarin, T.; Suksri, A. Performance enhancement of a photovoltaic module by passive cooling using phase change material in a finned container heat sink. Sol. Energy 2020, 195, 47–53. [Google Scholar] [CrossRef]
- Agyekum, E.B.; PraveenKumar, S.; Eliseev, A.; Velkin, V.I. Design and construction of a novel simple and low-cost test bench point-absorber wave energy converter emulator system. Inventions 2021, 6, 20. [Google Scholar] [CrossRef]
- Agyekum, E.B.; PraveenKumar, S.; Alwan, N.T.; Velkin, V.I.; Adebayo, T.S. Experimental Study on Performance Enhancement of a Photovoltaic Module Using a Combination of Phase Change Material and Aluminum Fins—Exergy, Energy and Economic (3E) Analysis. Inventions 2021, 6, 69. [Google Scholar] [CrossRef]
- Agyekum, E.B.; PraveenKumar, S.; Alwan, N.T.; Velkin, V.I.; Shcheklein, S.E.; Yaqoob, S.J. Experimental investigation of the effect of a combination of active and passive cooling mechanism on the thermal characteristics and efficiency of solar PV module. Inventions 2021, 6, 63. [Google Scholar] [CrossRef]
- Agyekum, E.B.; Adebayo, T.S.; Bekun, F.V.; Kumar, N.M.; Panjwani, M.K. Effect of two different heat transfer fluids on the performance of solar tower csp by comparing recompression supercritical CO2 and rankine power cycles, China. Energies 2021, 14, 3426. [Google Scholar] [CrossRef]



| Literature | Year | Algorithm | (A) | (A) | () | () | n | No. of Steps | RMSE |
|---|---|---|---|---|---|---|---|---|---|
| [42] | 2019 | EA | 0.76080000 | 0.32230000 | 53.76340000 | 0.036400000 | 1.4837000000 | - | 1.0072 × 10 |
| [43] | 2018 | NA | 0.76074014 | 0.31285196 | 55.90738000 | 0.036615485 | 1.477729500 | - | 7.7301 × 10 |
| [44] | 2020 | EA | 0.76038466 | 0.23082625 | 53.67788300 | 0.037991668 | 1.447929015 | - | 9.7505 × 10 |
| [45] | 2019 | EA | 0.76080000 | 0.32300000 | 53.71850000 | 0.036400000 | 1.481200000 | - | 9.8602 × 10 |
| [46] | 2017 | EA | 0.76080000 | 0.32280000 | 53.75950000 | 0.036400000 | 1.481100000 | - | 9.8603 × 10 |
| [47] | 2020 | EA | 0.76077600 | 0.32302100 | 53.71852000 | 0.036377000 | 1.481184000 | - | 9.8602 × 10 |
| [48] | 2019 | NA + EA | 0.76078797 | 0.31068450 | 52.88979426 | 0.036546950 | 1.477267780 | - | 7.7301 × 10 |
| [49] | 2019 | EA | 0.76077552 | 0.32302000 | 53.71852000 | 0.036370000 | 1.481108170 | - | 9.8602 × 10 |
| [50] | 2019 | EA | 0.76079000 | 0.31062000 | 52.88500000 | 0.036548000 | 1.477100000 | - | 7.7300 × 10 |
| [51] | 2019 | EA | 0.76080000 | 0.32300000 | 53.71850000 | 0.036400000 | 1.481200000 | - | 9.8602 × 10 |
| [52] | 2019 | EA | 0.76077562 | 0.32301700 | 53.71821748 | 0.036377160 | 1.481182200 | - | 9.8602 × 10 |
| [53] | 2019 | EA | 0.76078000 | 0.32302000 | 53.71852000 | 0.036380000 | 1.481180000 | - | 9.8602 × 10 |
| [54] | 2019 | EA | 0.76080000 | 0.32300000 | 53.71850000 | 0.036400000 | 1.481200000 | - | 9.8602 × 10 |
| [55] | 2019 | EA | 0.76077500 | 0.32302100 | 53.71867900 | 0.036377000 | 1.481108000 | - | 9.8602 × 10 |
| [56] | 2019 | EA | 0.76077450 | 0.32300180 | 53.73000000 | 0.036377500 | 1.481177400 | - | 9.8602 × 10 |
| [57] | 2019 | EA | 0.76078000 | 0.32302000 | 53.71852000 | 0.036380000 | 1.481180000 | - | 9.8602 × 10 |
| [58] | 2020 | EA | 0.76076000 | 0.32314000 | 53.71489000 | 0.036370000 | 1.481140000 | - | 9.8482 × 10 |
| [59] | 2018 | EA | 0.76077000 | 0.32320000 | 53.68360000 | 0.036300000 | 1.520800000 | - | 9.8600 × 10 |
| [60] | 2018 | EA | 0.76078700 | 0.31068300 | 52.88971000 | 0.036546000 | 1.475262000 | - | 7.7301 × 10 |
| [61] | 2018 | EA | 0.76077700 | 0.32262200 | 53.67840000 | 0.036381900 | 1.481060000 | - | 9.8602 × 10 |
| [62] | 2018 | EA | 0.76077553 | 0.32302083 | 53.71852771 | 0.036377090 | 1.481183600 | - | 9.8602 × 10 |
| [63] | 2018 | EA | 0.76069712 | 0.43244110 | 53.40180803 | 0.033410590 | 1.452456660 | - | 5.1382 × 10 |
| [64] | 2018 | EA | 0.76078000 | 0.32302000 | 53.71636000 | 0.036380000 | 1.481180000 | - | 9.8602 × 10 |
| [65] | 2020 | NA | 0.76870000 | 9.9414E-07 | 100.0000000 | 0.030966000 | 1.602000000 | 26 | 2.7756 × 10 |
| [66] | 2017 | NA | 0.76072000 | 0.31911000 | 54.19241000 | 0.036290000 | 1.479860000 | - | 8.1291 × 10 |
| [67] | 2018 | EA | 0.76077600 | 0.32302100 | 53.71852400 | 0.036377000 | 1.481718000 | - | 9.8602 × 10 |
| [68] | 2019 | EA | 0.76078000 | 0.33971000 | 54.43370000 | 0.036160000 | 1.486290000 | - | 9.9185 × 10 |
| Literature | Algorithm | (A) | (A) | () | () | n | No. of Steps | RMSE | MAE |
|---|---|---|---|---|---|---|---|---|---|
| [69] | AA + NA | 1.032377 | 2.517957 | 745.7122 | 1.239060 | 1.3173635 | 27 | 2.0465456 × 10 | 1.6925284 × 10 |
| [43] | AA + NA | 1.0323823 | 2.5129059 | 744.71302 | 1.3001512 | 1.3171591 | 6 | 2.0465347 × 10 | 1.6923215 × 10 |
| [70] | AA + NA | 1 | 2.3 | 830 | 1.3 | 1.3056 | - | 3.26 × 10 | - |
| [6] | AA + NA | 1.033285 | 1.82 | 850.7068 | 1.357607 | 1.2857 | - | 5.181 × 10 | - |
| [15] | AA + NA | 1.0323729 | 2.5129158 | 744.713061 | 1.2456174 | 1.3248753 | 4 | 2.046479 × 10 | 3.423077 × 10 |
| [44] | EA | 1.0263 | 9.5710 | 6842.2 | 0.0298 | 1.5255 | - | 3.819492 × 10 | - |
| [65] | NA | 1.0285 | 4.9614 × 10 | 1632.5 | 1.1638 | - | - | 2.6174×10 | - |
| Parameter | Symbol | Value |
|---|---|---|
| Maximum power | 315 W | |
| Short-circuit current | 8.95 A | |
| Open-circuit voltage | 45.6 V | |
| Current at Maximum power | 8.45 A | |
| Voltage at Maximum power | 37.3 V | |
| Co-efficient of current | 0.05%/C | |
| Co-efficient of voltage | −0.35%/C | |
| Co-efficient of power | −0.40%/C | |
| Nominal operating cell temperature | NOCT | 45 ± 2 C |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Changmai, P.; Deka, S.; Kumar, S.; Babu, T.S.; Aljafari, B.; Nastasi, B. A Critical Review on the Estimation Techniques of the Solar PV Cell’s Unknown Parameters. Energies 2022, 15, 7212. https://doi.org/10.3390/en15197212
Changmai P, Deka S, Kumar S, Babu TS, Aljafari B, Nastasi B. A Critical Review on the Estimation Techniques of the Solar PV Cell’s Unknown Parameters. Energies. 2022; 15(19):7212. https://doi.org/10.3390/en15197212
Chicago/Turabian StyleChangmai, Papul, Sunil Deka, Shashank Kumar, Thanikanti Sudhakar Babu, Belqasem Aljafari, and Benedetto Nastasi. 2022. "A Critical Review on the Estimation Techniques of the Solar PV Cell’s Unknown Parameters" Energies 15, no. 19: 7212. https://doi.org/10.3390/en15197212
APA StyleChangmai, P., Deka, S., Kumar, S., Babu, T. S., Aljafari, B., & Nastasi, B. (2022). A Critical Review on the Estimation Techniques of the Solar PV Cell’s Unknown Parameters. Energies, 15(19), 7212. https://doi.org/10.3390/en15197212









