Thermo-Economic Assessments on a Heat Storage Tank Filled with Graded Metal Foam
Abstract
:1. Introduction
2. Numerical Simulation
2.1. Model Description
2.2. Governing Equations
2.3. Independence and Simulation Verification
2.4. Numerical Settings
3. Results and Discussion
3.1. Evolution of Liquid Fraction
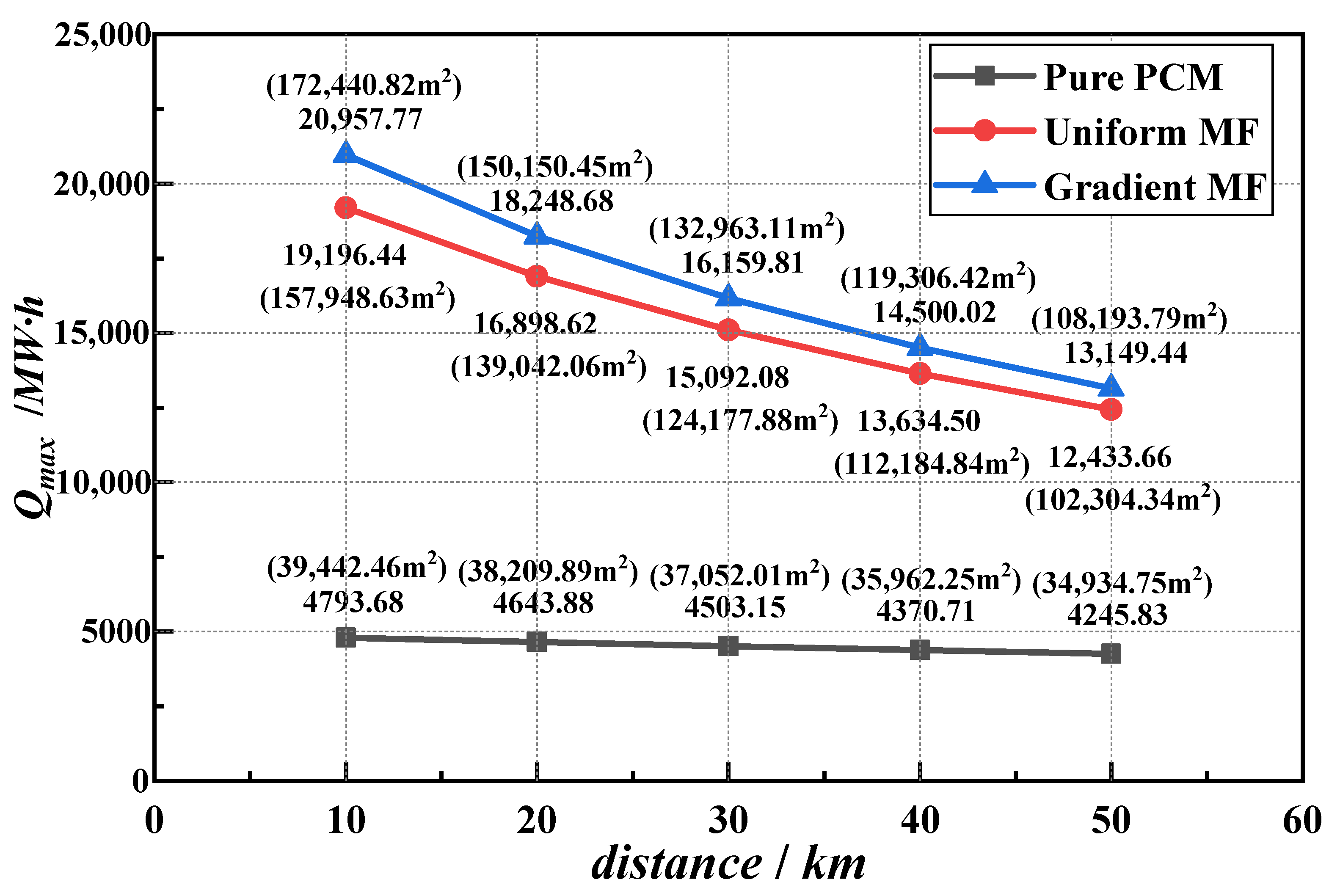
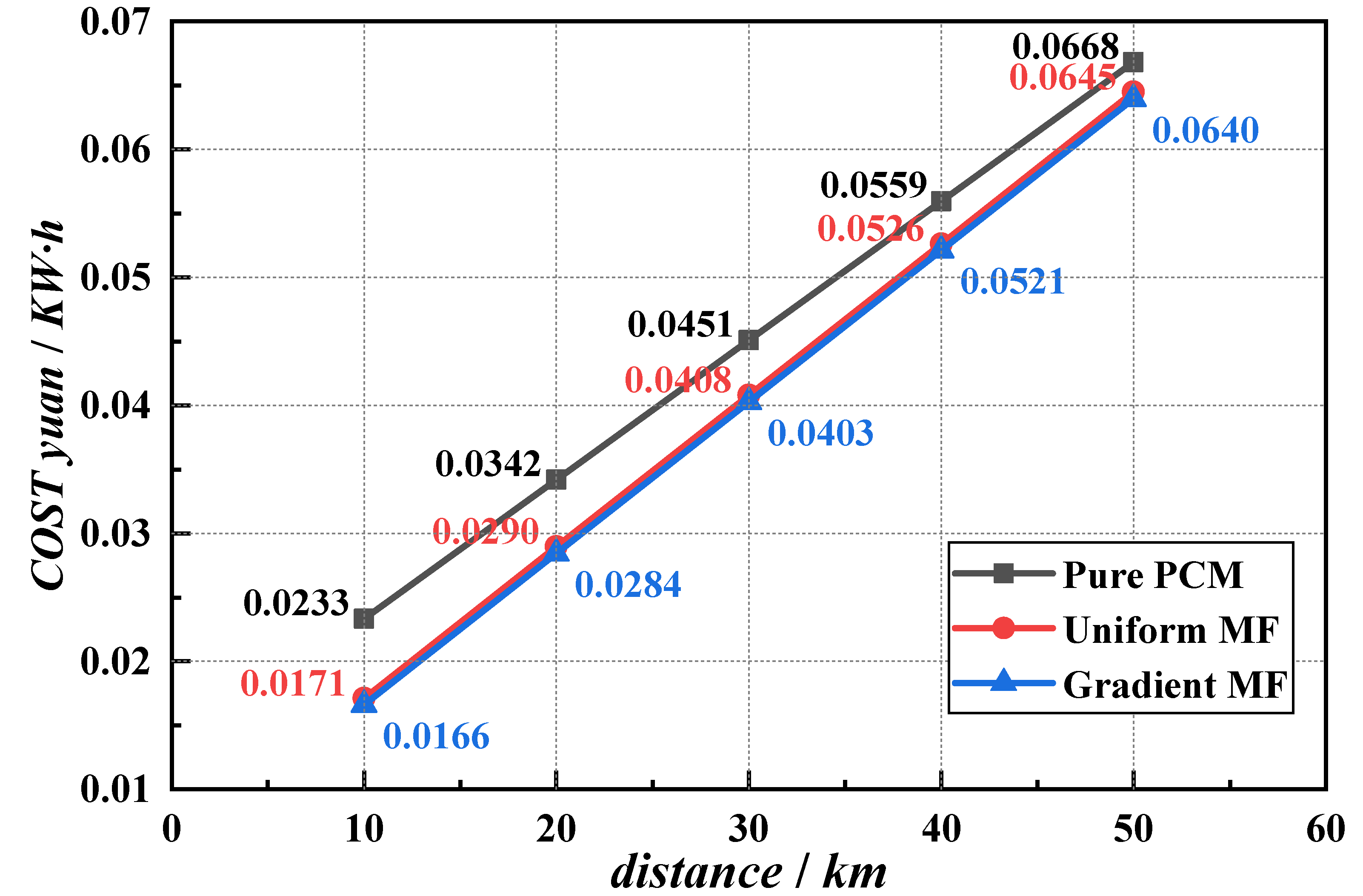
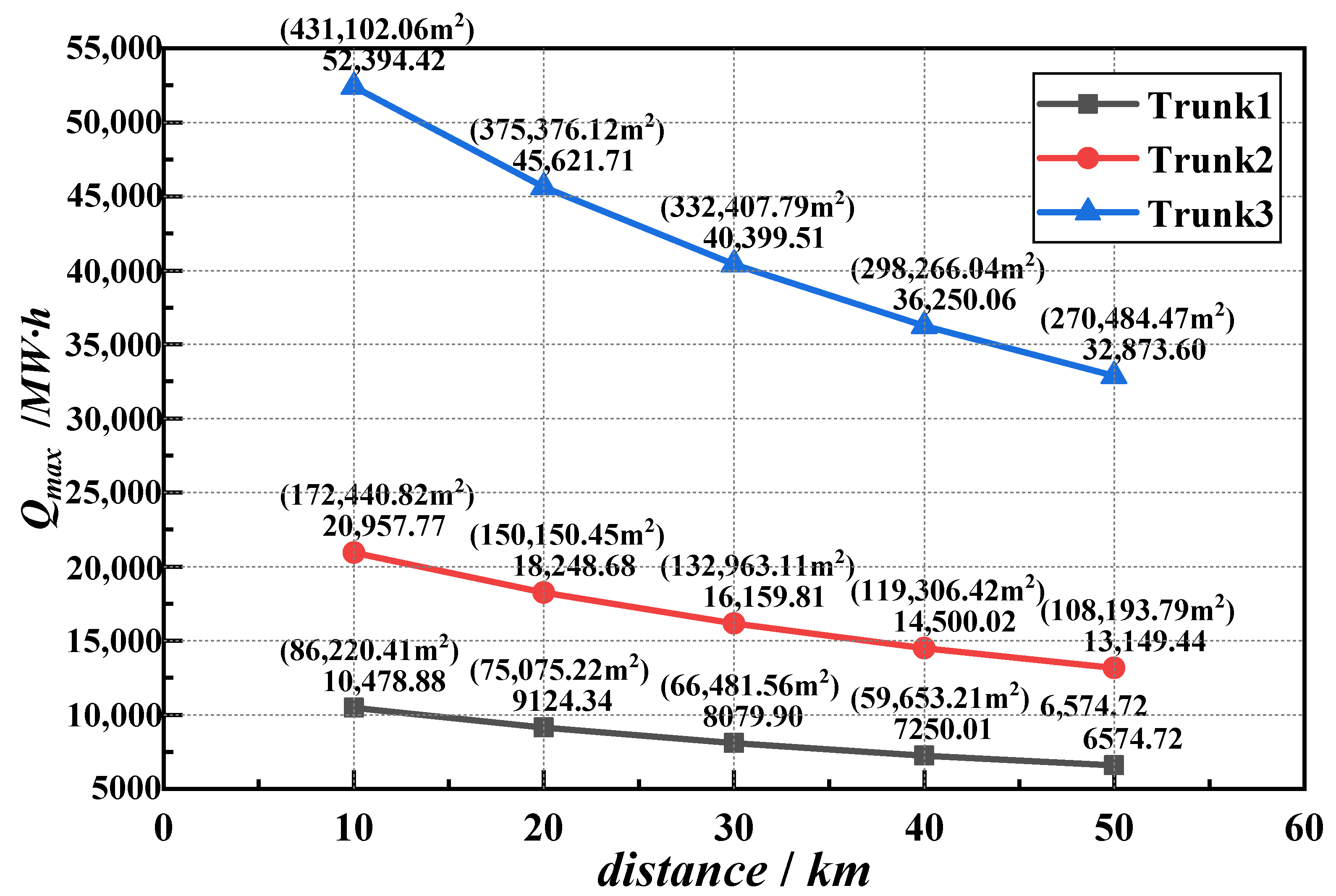
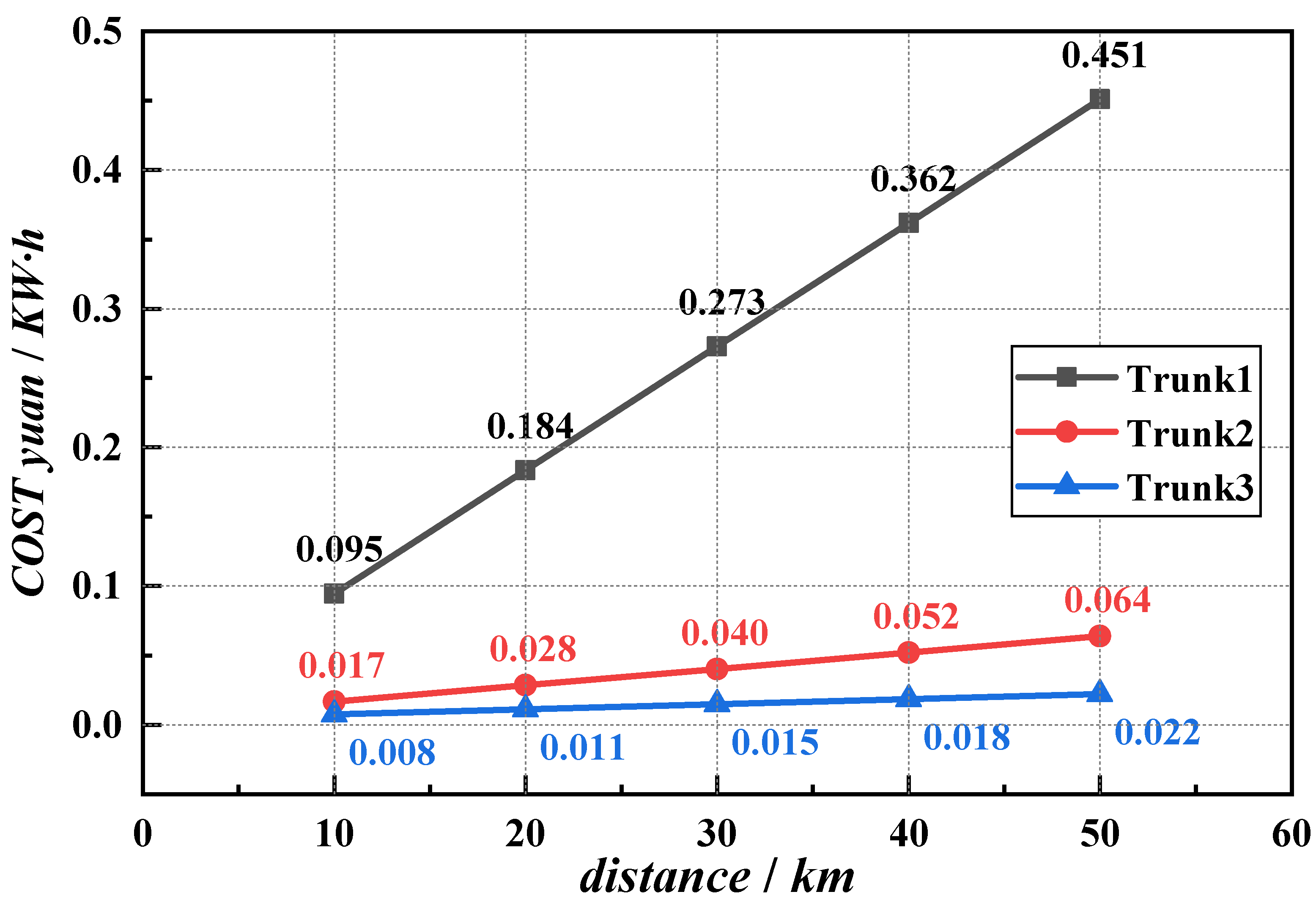
3.2. Economic Analysis of Mobile Heat Storage System
3.2.1. Cost Analysis
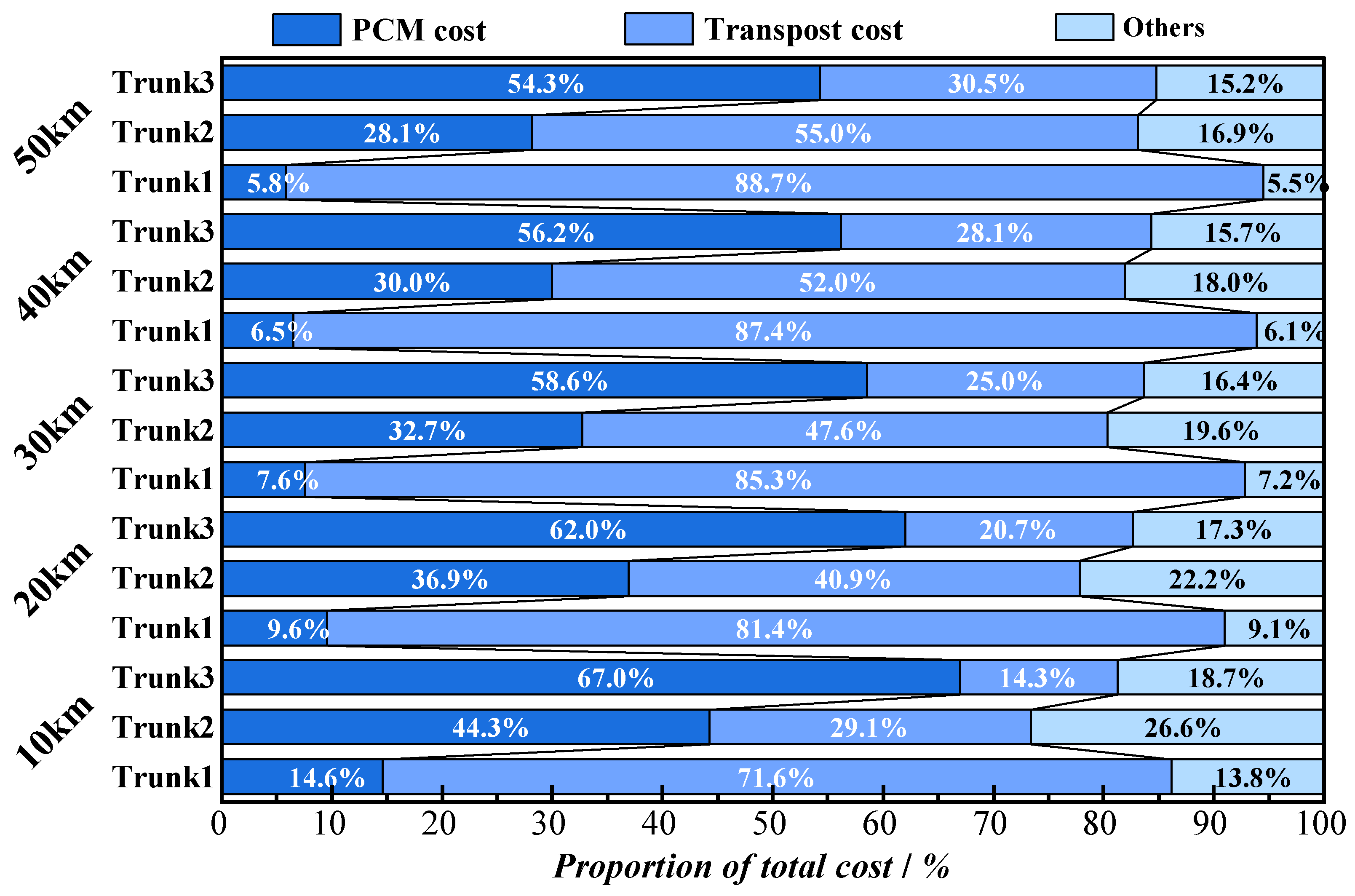
3.2.2. Cost Calculation of Three Structures
3.2.3. Cost Calculation of Three Transport Vehicles
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, T.; Luan, W.; Wang, W.; Tu, S.-T. Waste heat recovery through plate heat exchanger based thermoelectric generator system. Appl. Energy 2014, 136, 860–865. [Google Scholar] [CrossRef]
- Kauko, H.; Rohde, D.; Hafner, A. Local Heating Networks with Waste Heat Utilization: Low or Medium Temperature Supply? Energies 2020, 13, 954. [Google Scholar] [CrossRef]
- Vilasboas, I.F.; dos Santos, V.G.S.F.; de Morais, V.O.B.; Ribeiro, A.S.; da Silva, J.A.M. AERES: Thermodynamic and Economic Optimization Software for Hybrid Solar–Waste Heat Systems. Energies 2022, 15, 4284. [Google Scholar] [CrossRef]
- Zhao, J.; Gao, J.; Liao, J.; Zhou, B.; Bai, Y.; Qiang, T. An Experimental Study of the Heat Storage and the Discharge Performance and an Economic Performance Analysis of a Flat Plate Phase Change Material (PCM) Storage Tank. Energies 2022, 15, 4023. [Google Scholar] [CrossRef]
- Koukou, M.K.; Pagkalos, C.; Dogkas, G.; Vrachopoulos, M.G.; Douvi, E.; Caouris, Y.G.; Papadopoulos, P. Computational Approach of Charging and Discharging Phases in a Novel Compact Solar Collector with Integrated Thermal Energy Storage Tank: Study of Different Phase Change Materials. Energies 2022, 15, 1113. [Google Scholar] [CrossRef]
- Nguyen, X.V. Fabrication and Performance Evaluation of Cold Thermal Energy Storage Tanks Operating in Water Chiller Air Conditioning System. Energies 2021, 14, 4159. [Google Scholar] [CrossRef]
- Charvát, P.; Klimeš, L.; Zálešák, M. Utilization of an Air-PCM Heat Exchanger in Passive Cooling of Buildings: A Simulation Study on the Energy Saving Potential in Different European Climates. Energies 2019, 12, 1133. [Google Scholar] [CrossRef]
- Tao, Y.; He, Y.-L. A review of phase change material and performance enhancement method for latent heat storage system. Renew. Sustain. Energy Rev. 2018, 93, 245–259. [Google Scholar] [CrossRef]
- Aftab, W.; Usman, A.; Shi, J.; Yuan, K.; Qin, M.; Zou, R. Phase change material-integrated latent heat storage systems for sustainable energy solutions. Energy Environ. Sci. 2021, 14, 4268–4291. [Google Scholar] [CrossRef]
- Nazir, H.; Batool, M.; Osorio, F.J.B.; Isaza-Ruiz, M.; Xu, X.; Vignarooban, K.; Phelan, P.; Kannan, A.M. Recent developments in phase change materials for energy storage applications: A review. Int. J. Heat Mass Transf. 2019, 129, 491–523. [Google Scholar] [CrossRef]
- De Gracia, A.; Cabeza, L.F. Phase change materials and thermal energy storage for buildings. Energy Build. 2015, 103, 414–419. [Google Scholar] [CrossRef]
- Joelsson, A.; Gustavsson, L. District heating and energy efficiency in detached houses of differing size and construction. Appl. Energy 2009, 86, 126–134. [Google Scholar] [CrossRef]
- Wang, W.; Hu, Y.; Yan, J.; Nyström, J.; Dahlquist, E. Combined heat and power plant integrated with mobilized thermal energy storage (M-TES) system. Front. Energy Power Eng. China 2010, 4, 469–474. [Google Scholar] [CrossRef]
- Guo, S.; Zhao, J.; Wang, W.; Yan, J.; Jin, G.; Zhang, Z.; Gu, J.; Niu, Y. Numerical study of the improvement of an indirect contact mobilized thermal energy storage container. Appl. Energy 2016, 161, 476–486. [Google Scholar] [CrossRef]
- Anandan, S.S.; Sundarababu, J. A comprehensive review on mobilized thermal energy storage. Energy Sources Part A Recovery Util. Environ. Eff. 2021, 1–24. [Google Scholar] [CrossRef]
- Matuszewska, D.; Kuta, M.; Olczak, P. Techno-economic assessment of mobilized thermal energy storage system using geothermal source in Polish conditions. Energies 2020, 13, 3404. [Google Scholar] [CrossRef]
- Du, K.; Calautit, J.; Eames, P.; Wu, Y. A state-of-the-art review of the application of phase change materials (PCM) in Mobilized-Thermal Energy Storage (M-TES) for recovering low-temperature industrial waste heat (IWH) for distributed heat supply. Renew. Energy 2021, 168, 1040–1057. [Google Scholar] [CrossRef]
- Guo, S.; Liu, Q.; Zhao, J.; Jin, G.; Wu, W.; Yan, J.; Li, H.; Jin, H. Mobilized thermal energy storage: Materials, containers and economic evaluation. Energy Convers. Manag. 2018, 177, 315–329. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, K.; Ling, X. Experimental study on thermal performance of a mobilized thermal energy storage system: A case study of hydrated salt latent heat storage. Energy Build. 2020, 210, 109744. [Google Scholar] [CrossRef]
- Guo, S.; Zhao, J.; Wang, W.; Yan, J.; Jin, G.; Wang, X. Techno-economic assessment of mobilized thermal energy storage for distributed users: A case study in China. Appl. Energy 2017, 194, 481–486. [Google Scholar] [CrossRef]
- Ping, P.; Peng, R.; Kong, D.; Chen, G.; Wen, J. Investigation on thermal management performance of PCM-fin structure for Li-ion battery module in high-temperature environment. Energy Convers. Manag. 2018, 176, 131–146. [Google Scholar] [CrossRef]
- Pakrouh, R.; Hosseini, M.; Ranjbar, A.; Bahrampoury, R. A numerical method for PCM-based pin fin heat sinks optimization. Energy Convers. Manag. 2015, 103, 542–552. [Google Scholar] [CrossRef]
- Gürtürk, M.; Kok, B. A new approach in the design of heat transfer fin for melting and solidification of PCM. Int. J. Heat Mass Transf. 2020, 153, 119671. [Google Scholar] [CrossRef]
- Guo, J.; Wang, X.; Yang, B.; Yang, X.; Li, M.-J. Thermal assessment on solid-liquid energy storage tube packed with non-uniform angled fins. Sol. Energy Mater. Sol. Cells 2022, 236, 111526. [Google Scholar] [CrossRef]
- Diallo, T.M.; Yu, M.; Zhou, J.; Zhao, X.; Shittu, S.; Li, G.; Ji, J.; Hardy, D. Energy performance analysis of a novel solar PVT loop heat pipe employing a microchannel heat pipe evaporator and a PCM triple heat exchanger. Energy 2019, 167, 866–888. [Google Scholar] [CrossRef]
- Behi, H.; Karimi, D.; Gandoman, F.H.; Akbarzadeh, M.; Khaleghi, S.; Kalogiannis, T.; Hosen, M.S.; Jaguemont, J.; Van Mierlo, J.; Berecibar, M. PCM assisted heat pipe cooling system for the thermal management of an LTO cell for high-current profiles. Case Stud. Therm. Eng. 2021, 25, 100920. [Google Scholar] [CrossRef]
- Zhang, C.; Yu, M.; Fan, Y.; Zhang, X.; Zhao, Y.; Qiu, L. Numerical study on heat transfer enhancement of PCM using three combined methods based on heat pipe. Energy 2020, 195, 116809. [Google Scholar] [CrossRef]
- Alazwari, M.A.; Algarni, M.; Safaei, M.R. Effects of various types of nanomaterials on PCM melting process in a thermal energy storage system for solar cooling application using CFD and MCMC methods. Int. J. Heat Mass Transf. 2022, 195, 123204. [Google Scholar] [CrossRef]
- Dheep, G.R.; Sreekumar, A. Influence of nanomaterials on properties of latent heat solar thermal energy storage materials–A review. Energy Convers. Manag. 2014, 83, 133–148. [Google Scholar] [CrossRef]
- Raval, H.; Patel, J.; Mudgal, A. A Review on Enhancement of Thermophysical Properties of Paraffin Wax PCM with Nanomaterials. In Proceedings of the ICTEA: International Conference on Thermal Engineering, Gujarat, India, 23–26 February 2019. [Google Scholar]
- Peng, G.; Dou, G.; Hu, Y.; Sun, Y.; Chen, Z. Phase change material (PCM) microcapsules for thermal energy storage. Adv. Polym. Technol. 2020, 2020, 9490873. [Google Scholar] [CrossRef]
- Bayés-García, L.; Ventolà, L.; Cordobilla, R.; Benages, R.; Calvet, T.; Cuevas-Diarte, M. Phase Change Materials (PCM) microcapsules with different shell compositions: Preparation, characterization and thermal stability. Sol. Energy Mater. Sol. Cells 2010, 94, 1235–1240. [Google Scholar] [CrossRef]
- Mazlan, M.; Rahmani-dehnavi, M.; Najafi, G.; Ghobadian, B.; Hoseini, S.; Fayyazi, E.; Mamat, R.; Alenezi, R.A.; Mofijur, M. Thermal efficiency analysis of the phase change material (PCM) microcapsules. Sustain. Energy Technol. Assess. 2021, 48, 101557. [Google Scholar] [CrossRef]
- Rahmanian, S.; Moein-Jahromi, M.; Rahmanian-Koushkaki, H.; Sopian, K. Performance investigation of inclined CPV system with composites of PCM, metal foam and nanoparticles. Sol. Energy 2021, 230, 883–901. [Google Scholar] [CrossRef]
- Mahdi, J.M.; Mohammed, H.I.; Talebizadehsardari, P.; Ghalambaz, M.; Majdi, H.S.; Yaïci, W.; Giddings, D. Simultaneous and consecutive charging and discharging of a PCM-based domestic air heater with metal foam. Appl. Therm. Eng. 2021, 197, 117408. [Google Scholar] [CrossRef]
- Baruah, J.S.; Athawale, V.; Rath, P.; Bhattacharya, A. Melting and energy storage characteristics of macro-encapsulated PCM-metal foam system. Int. J. Heat Mass Transf. 2022, 182, 121993. [Google Scholar] [CrossRef]
- Xu, H.; Wang, Y.; Han, X. Analytical considerations of thermal storage and interface evolution of a PCM with/without porous media. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 373–400. [Google Scholar] [CrossRef]
- Heyhat, M.M.; Mousavi, S.; Siavashi, M. Battery thermal management with thermal energy storage composites of PCM, metal foam, fin and nanoparticle. J. Energy Storage 2020, 28, 101235. [Google Scholar] [CrossRef]
- Alhusseny, A.; Al-Zurfi, N.; Nasser, A.; Al-Fatlawi, A.; Aljanabi, M. Impact of using a PCM-metal foam composite on charging/discharging process of bundled-tube LHTES units. Int. J. Heat Mass Transf. 2020, 150, 119320. [Google Scholar] [CrossRef]
- Zhu, Z.-Q.; Huang, Y.-K.; Hu, N.; Zeng, Y.; Fan, L.-W. Transient performance of a PCM-based heat sink with a partially filled metal foam: Effects of the filling height ratio. Appl. Therm. Eng. 2018, 128, 966–972. [Google Scholar] [CrossRef]
- Huo, Y.; Guo, Y.; Rao, Z. Investigation on the thermal performance of phase change material/porous medium-based battery thermal management in pore scale. Int. J. Energy Res. 2019, 43, 767–778. [Google Scholar] [CrossRef]
- Esapour, M.; Hamzehnezhad, A.; Rabienataj Darzi, A.A.; Jourabian, M. Melting and solidification of PCM embedded in porous metal foam in horizontal multi-tube heat storage system. Energy Convers. Manag. 2018, 171, 398–410. [Google Scholar] [CrossRef]
- Dinesh, B.V.S.; Bhattacharya, A. Effect of foam geometry on heat absorption characteristics of PCM-metal foam composite thermal energy storage systems. Int. J. Heat Mass Transf. 2019, 134, 866–883. [Google Scholar] [CrossRef]
- Iasiello, M.; Mameli, M.; Filippeschi, S.; Bianco, N. Metal foam/PCM melting evolution analysis: Orientation and morphology effects. Appl. Therm. Eng. 2021, 187, 116572. [Google Scholar] [CrossRef]
- Mohammed, H.I.; Talebizadehsardari, P.; Mahdi, J.M.; Arshad, A.; Sciacovelli, A.; Giddings, D. Improved melting of latent heat storage via porous medium and uniform Joule heat generation. J. Energy Storage 2020, 31, 101747. [Google Scholar] [CrossRef]
- Liu, G.; Xiao, T.; Guo, J.; Wei, P.; Yang, X.; Hooman, K. Melting and solidification of phase change materials in metal foam filled thermal energy storage tank: Evaluation on gradient in pore structure. Appl. Therm. Eng. 2022, 212, 118564. [Google Scholar] [CrossRef]
- Guo, J.; Du, Z.; Liu, G.; Yang, X.; Li, M.-J. Compression effect of metal foam on melting phase change in a shell-and-tube unit. Appl. Therm. Eng. 2022, 206, 118124. [Google Scholar] [CrossRef]
- Xiao, T.; Yang, X.; Hooman, K.; Lu, T.J. Analytical fractal models for permeability and conductivity of open-cell metallic foams. Int. J. Heat Mass Transf. 2021, 177, 121509. [Google Scholar] [CrossRef]
- Zhang, Z.; He, X. Three-dimensional numerical study on solid-liquid phase change within open-celled aluminum foam with porosity gradient. Appl. Therm. Eng. 2017, 113, 298–308. [Google Scholar] [CrossRef]
- Zhang, S.; Pu, L.; Mancin, S.; Dai, M.; Xu, L. Role of partial and gradient filling strategies of copper foam on latent thermal energy storage: An experimental study. Energy 2022, 255, 124517. [Google Scholar] [CrossRef]
- Žukauskas, A. Heat Transfer from Tubes in Crossflow. In Advances in Heat Transfer; Hartnett, J.P., Irvine, T.F., Eds.; Elsevier: Amsterdam, The Netherlands, 1972; Volume 8, pp. 93–160. [Google Scholar]
- Yang, X.H.; Bai, J.X.; Yan, H.B.; Kuang, J.J.; Lu, T.J.; Kim, T. An Analytical Unit Cell Model for the Effective Thermal Conductivity of High Porosity Open-Cell Metal Foams. Transp. Porous Media 2014, 102, 403–426. [Google Scholar] [CrossRef]
- Georgiadis, J.G.; Catton, I. Dispersion in cellular thermal convection in porous layers. Int. J. Heat Mass Transf. 1988, 31, 1081–1091. [Google Scholar] [CrossRef]
- Calmidi, V. Transport Phenomena in High Porosity Fibrous Metal Foams; University of Colorado at Boulder, ProQuest Dissertations Publishing: Boulder, CO, USA, 1998. [Google Scholar]
- Bhattacharya, A.; Calmidi, V.V.; Mahajan, R.L. Thermophysical properties of high porosity metal foams. Int. J. Heat Mass Transf. 2002, 45, 1017–1031. [Google Scholar] [CrossRef]
- Fourie, J.G.; Du Plessis, J.P. Pressure drop modelling in cellular metallic foams. Chem. Eng. Sci. 2002, 57, 2781–2789. [Google Scholar] [CrossRef]
- Li, H.; Wang, W.; Yan, J.; Dahlquist, E. Economic assessment of the mobilized thermal energy storage (M-TES) system for distributed heat supply. Appl. Energy 2013, 104, 178–186. [Google Scholar] [CrossRef]
- Luo, A.; Fang, H.; Xia, J.; Lin, B. Mapping potentials of low-grade industrial waste heat in Northern China. Resour. Conserv. Recycl. 2017, 125, 335–348. [Google Scholar] [CrossRef]
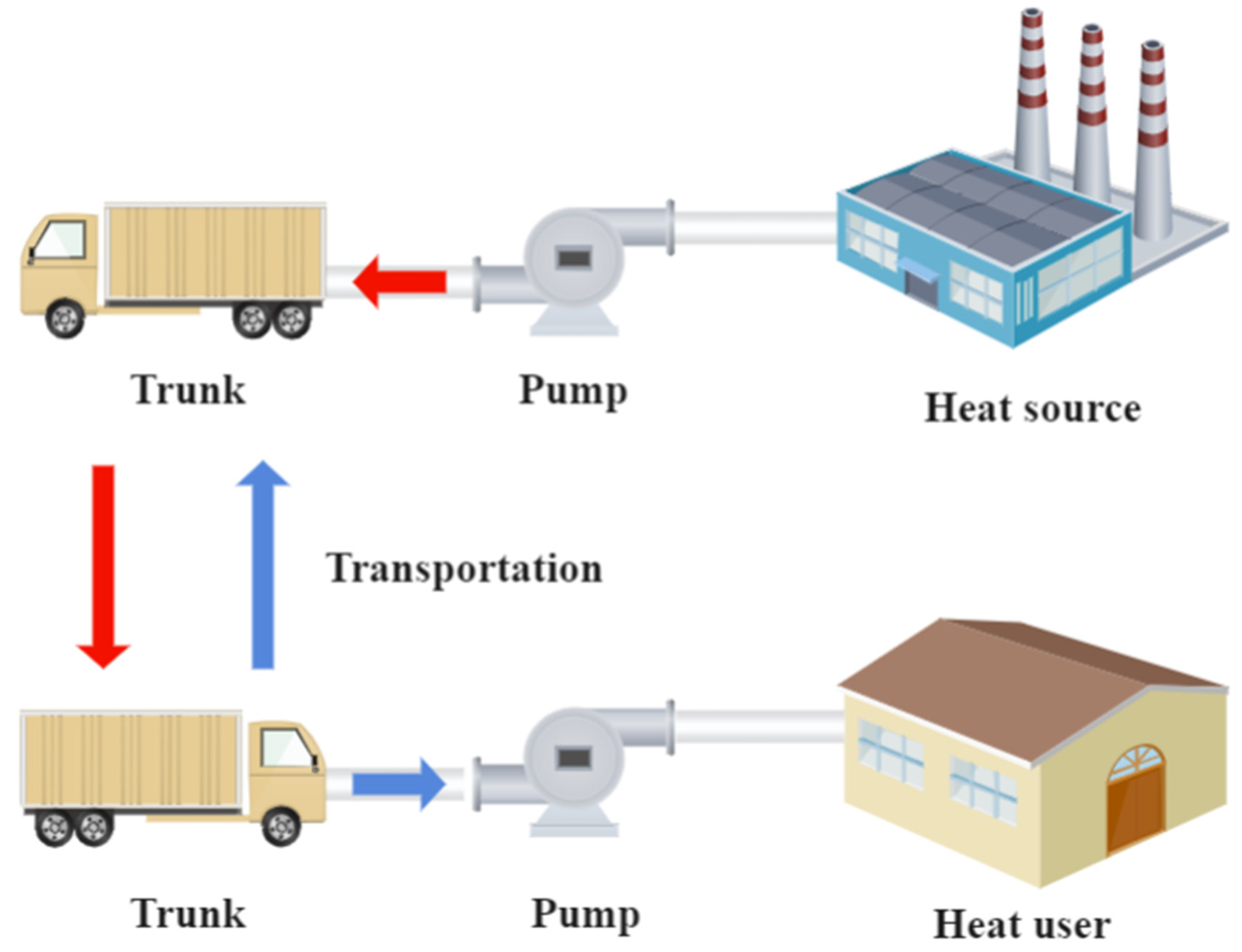
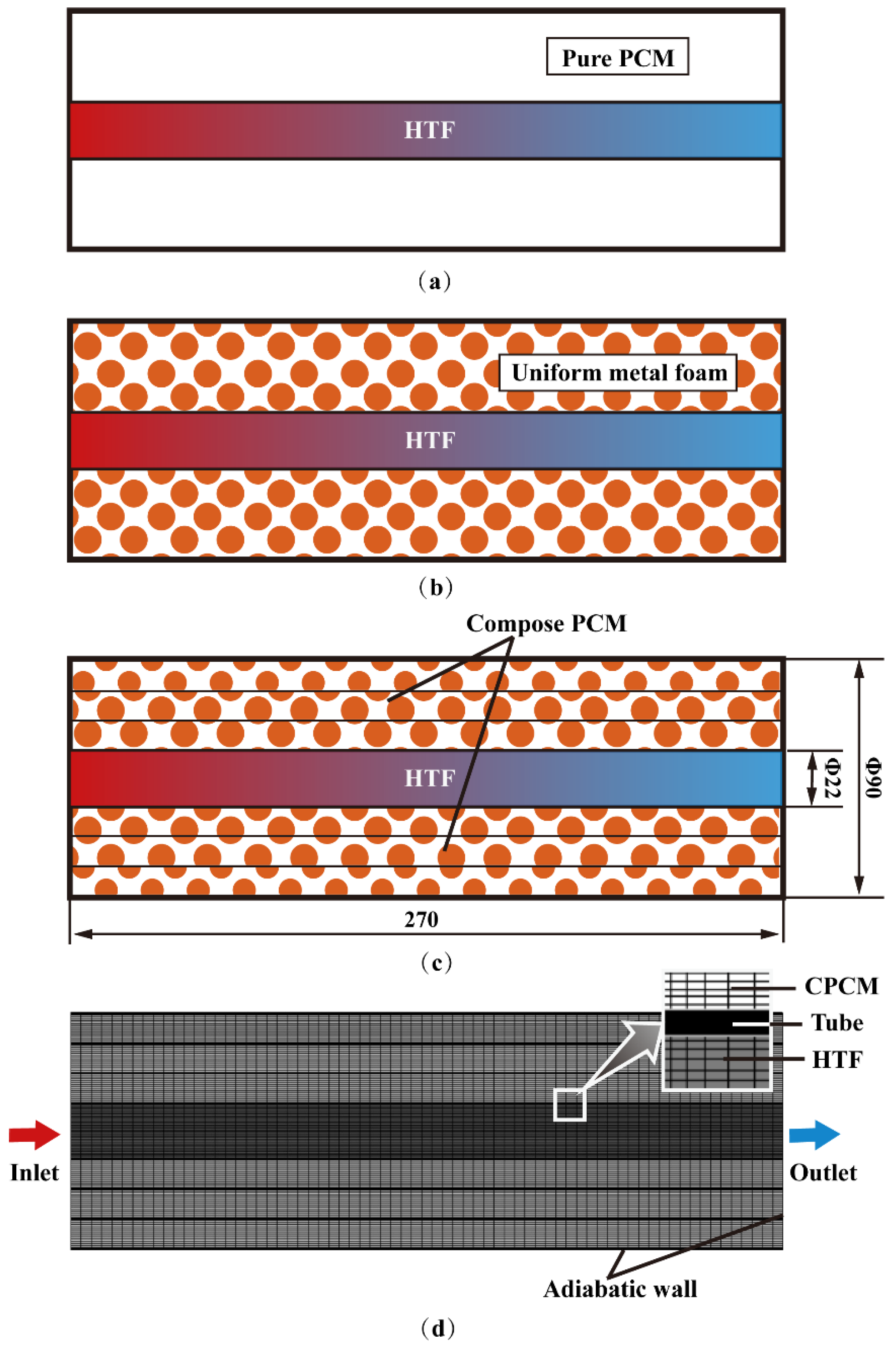
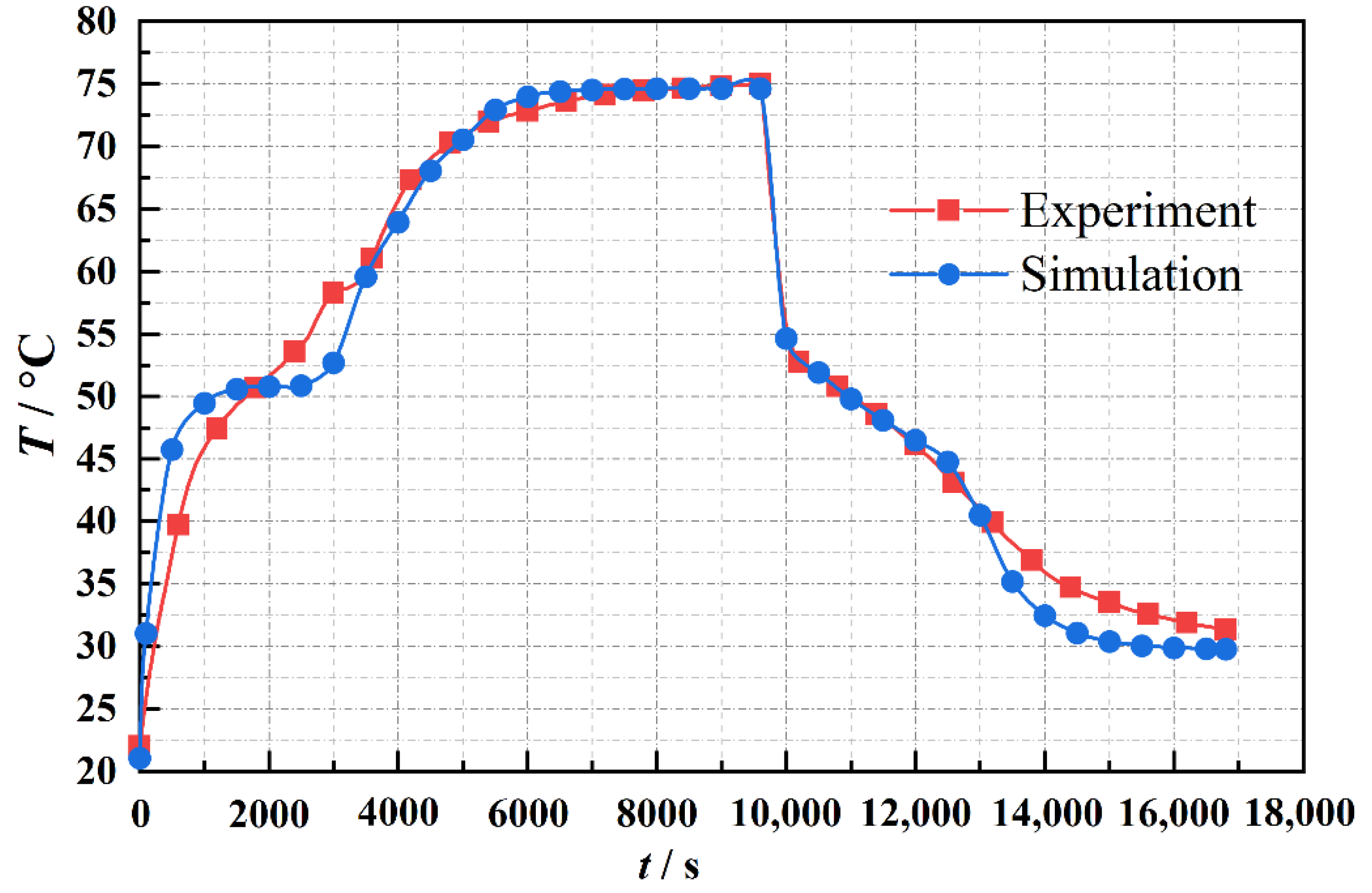
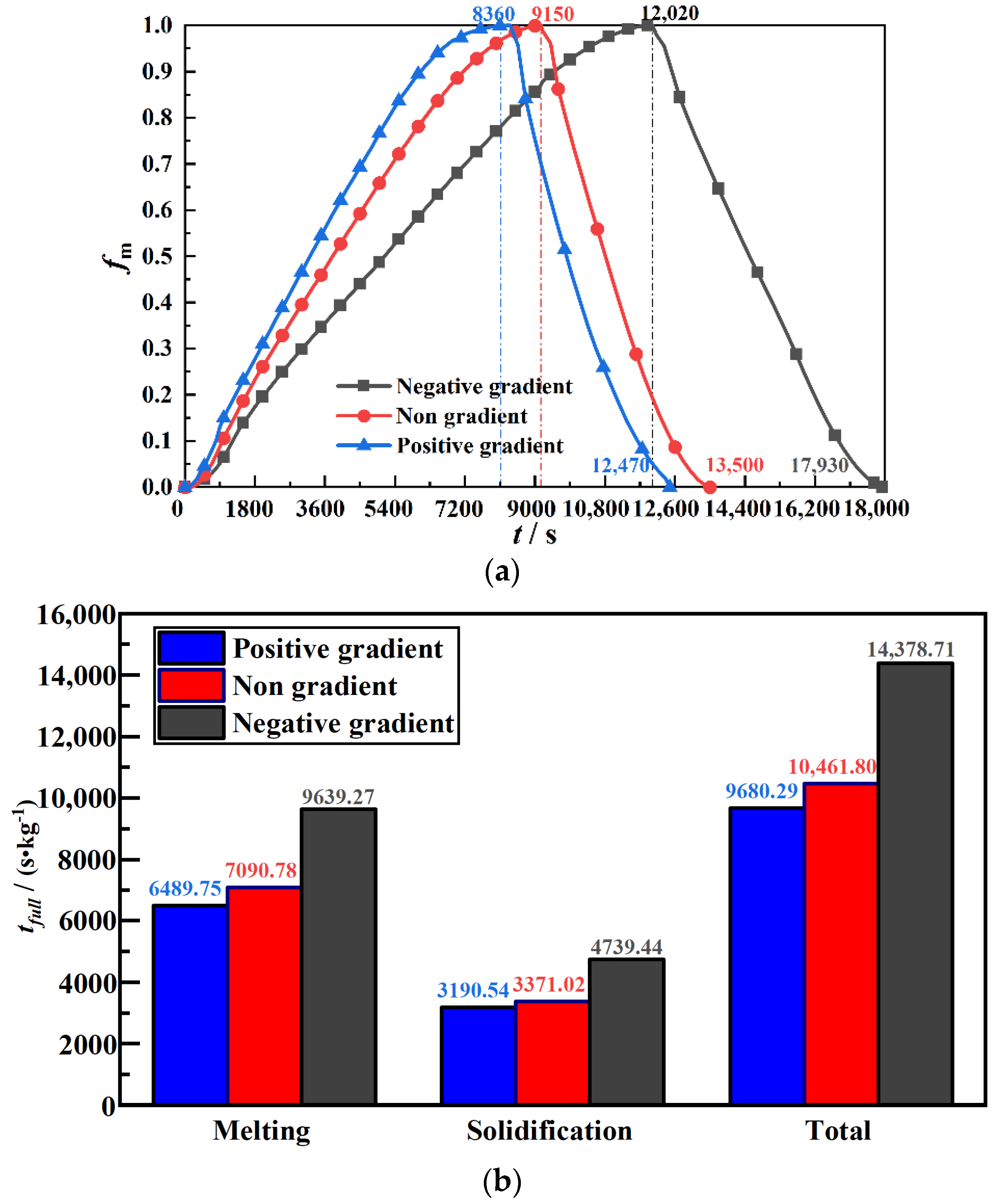
| Mesh Independence | Total Time | Time Step Independence | Total Time |
|---|---|---|---|
| 194,732 | 8200 | 0.05 s | 9150 |
| 637,328 | 9150 | 0.1 s | 9150 |
| 1,621,629 | 9320 | 0.5 s | 9150 |
| Material | Variable | Value |
|---|---|---|
| () | 850 (solid)/800 (liquid) | |
| () | 2000 | |
| () | 0.2 (solid)/0.1 (liquid) | |
| Latent heat of fusion () | 200 | |
| Melting temperature range (°C) | 46~55 | |
| () | ||
| () | ||
| Copper | () | 8920 |
| () | 380 | |
| () | 401 | |
| Water | () | 1000 |
| () | 4202 | |
| () | 0.56 | |
| () |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| PCM (paraffin) | 8 yuan/kg | The discount rate | 2.54% |
| Copper foam | 20,000 yuan/m3 | Rate of inflation | 2.30% |
| Copper pipe (10 × 0.1) | 17.9 yuan/m | Bank annual interest rate | 4.90% |
| Installation of water pump and piping | 50,000 yuan | N/A | N/A |
| Transport Vehicle | Price (yuan) | L × W × H | Standard Load (t) | Internal Volume (m3) | Transportation Costs (yuan/km) |
|---|---|---|---|---|---|
| Trunk1 | 100,000 | 6.2 × 2.2 × 2.2 | 5 | 30 | 1.3 |
| Trunk2 | 140,000 | 7.2 × 2.3 × 2.7 | 10 | 45 | 0.3 |
| Trunk3 | 170,000 | 9.6 × 2.3 × 2.7 | 25 | 60 | 0.2 |
| Structures | Initial Investment (yuan) | PCM Total Cost (yuan) | Heat Storage (MJ) |
|---|---|---|---|
| Pure PCM | 287,598.203 | 97,598.20261 | 2476.734 |
| Uniform MF | 506,421.732 | 316,421.732 | 2352.898 |
| Positive gradient MF | 506,421.732 | 316,421.732 | 2352.898 |
| Transport Vehicle | PCM Total Cost (yuan) | Heat Storage (MJ) | Initial Investment (yuan) |
|---|---|---|---|
| Trunk1 | 158,857.25 | 1176.45 | 308,857.25 |
| Trunk2 | 316,421.73 | 2352.90 | 506,421.73 |
| Trunk3 | 786,827.94 | 5882.24 | 1,006,827.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Li, Y.; Wei, P.; Xiao, T.; Meng, X.; Yang, X. Thermo-Economic Assessments on a Heat Storage Tank Filled with Graded Metal Foam. Energies 2022, 15, 7213. https://doi.org/10.3390/en15197213
Liu G, Li Y, Wei P, Xiao T, Meng X, Yang X. Thermo-Economic Assessments on a Heat Storage Tank Filled with Graded Metal Foam. Energies. 2022; 15(19):7213. https://doi.org/10.3390/en15197213
Chicago/Turabian StyleLiu, Gang, Yuanji Li, Pan Wei, Tian Xiao, Xiangzhao Meng, and Xiaohu Yang. 2022. "Thermo-Economic Assessments on a Heat Storage Tank Filled with Graded Metal Foam" Energies 15, no. 19: 7213. https://doi.org/10.3390/en15197213
APA StyleLiu, G., Li, Y., Wei, P., Xiao, T., Meng, X., & Yang, X. (2022). Thermo-Economic Assessments on a Heat Storage Tank Filled with Graded Metal Foam. Energies, 15(19), 7213. https://doi.org/10.3390/en15197213








