Abstract
Leakage inductance is one of the key parameters of a transformer, and it is often intentionally integrated into transformers. Rogowski’s equation is generally used for leakage inductance calculation; however, it is only applicable to concentric winding transformers where windings have the same height. Consequently, it has limited applications. This paper proposes a transformer leakage inductance calculation method using a double Fourier series. The limitation of Rogowski’s leakage inductance equation was analyzed in practical applications, and a new model for calculating the leakage inductance of a double-group-overlapping winding transformer was derived. Experimental prototypes of transformers were developed, and their simulation models were built in Ansys. The correctness of the proposed calculation method for transformer leakage inductance using a double Fourier series was verified by comparing the calculation results with the simulation and measured ones. A sensitivity analysis was also conducted by studying the variations in different parameters that might affect the leakage inductance value. The proposed calculation model gives an intuitive and simple method with less calculation and design effort while maintaining reasonable accuracy for leakage inductance calculation. In addition, the featured double Fourier series approach has a wider range of applications than Rogowski’s equation.
1. Introduction
Transformer leakage inductance can be problematic in many situations; hence, it is typically reduced to enhance performance. Leakage inductance, however, can be advantageous in some applications when designed and used correctly. As shown in Figure 1, for the design of a high-power electronic transformer with a CLLLC topology, it is desirable to integrate the inductance into the isolation transformer considering the dimension and cost [1,2,3]. In addition, integrating leakage inductance into the transformer enables a high-power density converter design [1,2,3,4,5,6]. In such applications, the transformer leakage inductance is no longer the factor to be reduced but is rather designed to achieve the expected value to meet the topology’s expectations.
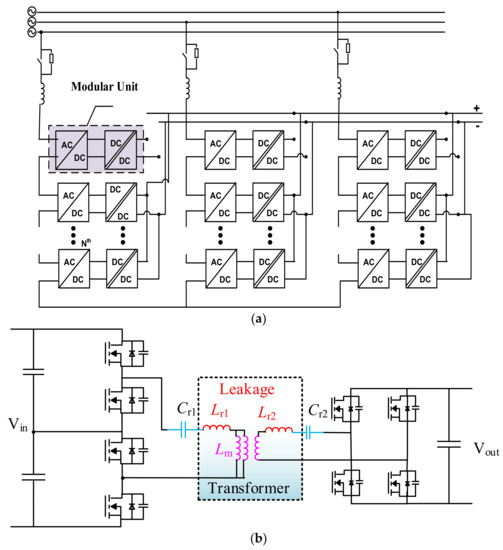
Figure 1.
(a) Configuration of power electronic transformer. (b) DC–DC converter topology.
Leakage inductance plays a crucial role in isolated DC–DC converters, as it affects the converter operation, control, and soft-switching operation [1,7,8]. A very high leakage inductance value might cause a voltage spike during the turn-off instant, which may damage the power devices. Likewise, the voltage drop across the leakage inductance reduces transformer gain [7]. Therefore, correct leakage inductance calculation is vital in achieving an optimized performance.
Transformer leakage inductance reflects the leakage of the transformer magnetic field. It depends on the winding dimension, spatial position, and magnetic medium in the field. It is unrelated to the winding current, waveform, or frequency; thus, it can be calculated under steady-state magnetic field conditions. Due to the complexity of the actual spatial distribution of the leakage magnetic field, it is challenging to calculate the leakage flux. As a pioneer, W. Rogowski started researching transformer leakage magnetic fields during 1905–1908. He conducted an investigation based on three-phase three-core concentric winding transformers. W. Rogowski solved Laplace’s equation and Poisson’s equation using a single Fourier series and derived a leakage inductance Equation (1), which is known as Rogowski’s equation or Rogowski’s leakage inductance equation [9,10]. It is expressed as follows:
where µ0 is the vacuum permeability, D is the average diameter of the winding, and N is the number of winding turns. The other geometric parameters are indicated in Figure 2.
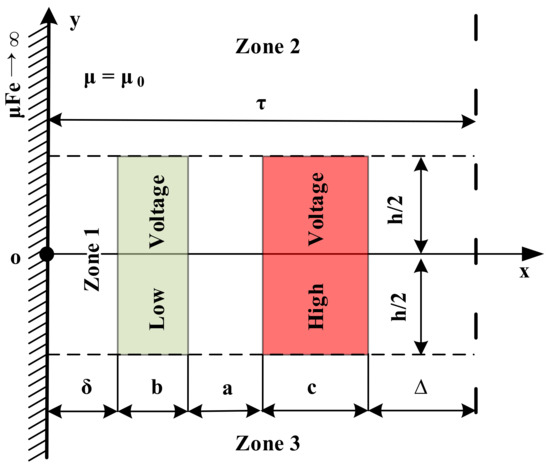
Figure 2.
Geometric parameters of Rogowski’s equation.
Due to the profound impact of leakage inductance on power converters, researchers are still actively looking into innovative methods for leakage inductance calculation [11,12,13,14,15,16]. In recent years, many studies have been reported on leakage inductance calculation that can be classified into numerical-based [14,15,17] and analytical-based studies [12,13,18,19,20,21,22]. Studies using numerical methods usually adopt finite element analysis and offer good accuracy; however, their computational cost is very high. The analytical methods, on the other hand, are easy to use with less computational effort and offer more flexibility in the design process of the transformer while still providing the estimation of leakage inductance with reasonable accuracy.
Compared with advanced complex methods, Rogowski’s equation offers an instinctual method for leakage inductance calculation. Nevertheless, Rogowski’s equation is only applicable to concentric winding transformers with windings of the same height. Moreover, the condition h/τ > 3.2 has to be met to ensure accuracy. To address the limitations of Rogowski’s equation, an analytical method is featured in this study that endeavors to develop a leakage inductance calculation equation using the winding dimension, spatial position, and magnetic medium of the field. The proposed method is intuitive, easy to use, and computationally efficient, and it can streamline the design process. The proposed method employs a double Fourier series for inductance calculation. It outperforms Rogowski’s solution, as it can be applied to transformers with double-group-overlapping windings and has no restriction against the length-to-width ratio of the field. Thus, it can be implemented in a wide range of applications.
2. Strategy Used to Develop Leakage Inductance Equation
The fundamental concept for calculating the transformer leakage inductance given in this study was that the transformer leakage field could be simplified to a rectangular-plane field where the magnetic core window was located based on the axisymmetric characteristic of the transformer windings. The transformer working principle determined that the algebraic sum of the ampere-turns of the windings in this closed rectangular field was zero, i.e., ∑ N. I = 0. The windings were assumed to be uniformly distributed throughout the closed rectangular field depicted in Figure 3 in order to ensure the broad applicability of the study. Hence, the closed rectangular field contained all the winding currents of the transformer. As indicated in Figure 4, the winding current was mirrored toward the four sides of the magnetic core borders; thus, it formed a periodic current density distribution along the x- and y-axes. By expressing this discontinuous periodic current density distribution in a continuous current density distribution function using a double Fourier series, a unified magnetic vector potential of Poisson’s equation for the rectangular field could be developed. Then, the leakage inductance could be obtained by applying the boundary conditions of the magnetic core and the leakage field variable.
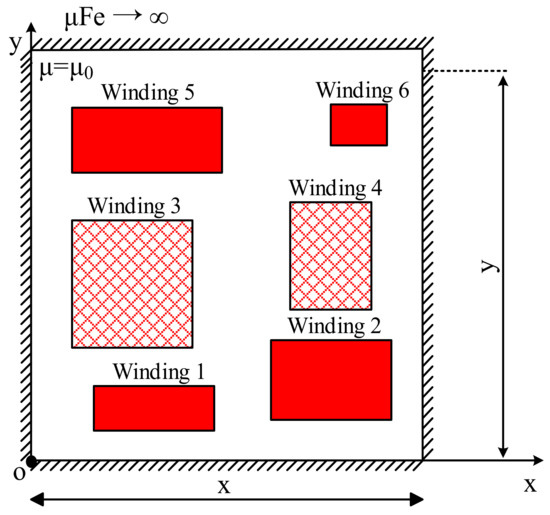
Figure 3.
Plane field of the transformer windings.
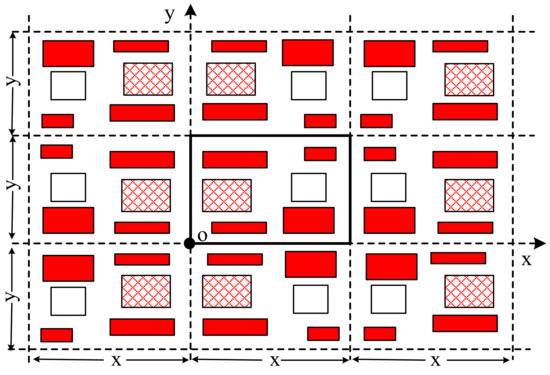
Figure 4.
The double periodicity of current density.
Compared to the single Fourier series method, the double Fourier series method featured in this paper did not require the division of the magnetic field into active and inactive zones. After expressing the discontinuous periodic current distribution with the double Fourier series, the whole closed rectangular field was equivalent to a unified active zone with continuous current density distribution, and a unified Poisson’s equation could be developed. The current density continued by mirroring the rectangular field to form a double periodic distribution in the orthogonal direction. The mirrored current density distribution and its expression with the double Fourier series are presented in the next subsection.
2.1. The Mirrored Current Density Distribution and Expression with Double Fourier Series
Assume there are K windings in the rectangular field in Figure 4. The area occupied by each winding is simplified to a rectangular area, and the current density of the kth winding is Jk. The double periodic current density distribution can be formed after this current density is mirrored several times, and it can be expressed with a double Fourier series as a general form [10,23]:
According to the constant magnetic field theory [24], Poisson’s equation for magnetic vector potential in the rectangular field is:
Determined by the form of the activation function on the right end of Poisson’s equation, the magnetic vector potential Az (x,y) also has the form of a double Fourier series, and the general form expression is:
According to the electromagnetic field theory [24], the magnetic field does not have a tangential component on the magnetic border with , and the boundary conditions of the four borders in the field can be determined:
The magnetic vector potential in the field can be solved according to (3)–(5):
2.2. Unified Expression of Leakage of Magnetic Field Energy and Leakage Inductance of Transformers
The magnetic field leakage is related to the winding current, but the leakage inductance is independent of the winding current. Assuming that the total number of turns of the winding is N and the current is I, the leakage inductance Lσ can be obtained by applying the magnetic field energy equation Wσ = ½(Lσ × I2) after the leakage magnetic field energy is solved. According to the electromagnetic theory [24], for a linear medium, the magnetic field energy of the three-dimensional space is:
Using the orthogonality of trigonometric function series, i.e., only the integrals of the products of the same cosine term are not zero, the unified expressions of the leakage magnetic field energy and the leakage inductance of transformers can be obtained:
The above unified expressions of the magnetic field energy and leakage inductance contain the coefficients of the double Fourier series. The current density distribution of a specific winding form can be transformed into the double Fourier series. Then, the leakage inductance expression of a specific winding can be calculated by substituting the coefficients into the leakage inductance equation.
3. Derivation of Leakage Inductance Equation for Transformers with Double Group Overlapping Windings
The structure of a transformer with double-group windings and its simplified plane field are indicated in Figure 5, where important parameters impacting the leakage inductance value include X, Y, winding dimension, and parameter f. The f already incorporates the effect of other parameters, such as a and g. For instance, when parameter f varies while the other parameters are kept unchanged, parameter a varies accordingly, which is equal to the change in the distance between the windings. Similarly, if parameter g changes, parameter a varies accordingly, as depicted in Figure 5.
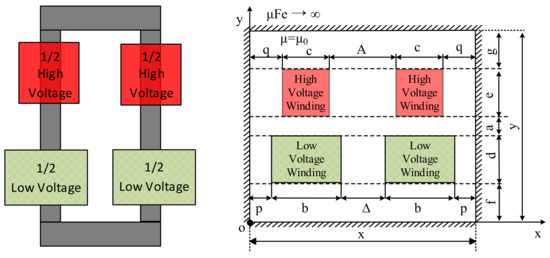
Figure 5.
The simplified plane field of a transformer with double-group windings.
Assume the number of turns of the high-voltage windings is N, the current is I, and the winding average diameter is D, the current density of the high-voltage winding is Jc = (−NI)/(2ce), and the current density of the low-voltage winding is Jb = (NI)/(2bd). The coefficients of the double Fourier series of the current density distribution for the plane field shown in Figure 5 can be calculated using (10)–(12). The calculation steps are as follows:
where:
where:
where:
The coefficients of the double Fourier series of the current density distribution are shown in (13)–(18). By substituting these coefficients in unified expression (9), expression (19) can be obtained, which is the final leakage inductance equation that can be used for calculation.
Expression (19) is the equation for calculating the transformer leakage inductance in the form of an infinite series, and convergence can be verified. The sum of the first n terms is taken as the approximate value for the transformer leakage inductance calculation. The convergence rate can differ for transformers with windings in different form factors or dimensions.
4. Simulation and Experimental Analysis
In this section, the leakage inductance of a double-group winding transformer calculated using the proposed method is verified against simulation and practical measurement results. The transformer dimension and the form of the windings were changed separately to make a sensitivity analysis and comparisons.
Figure 6 shows the real transformer and the simulation model built based on the transformer dimension parameters using Ansys software. The transformer used in the test had a magnetic core diameter of 40 mm, a magnetic core length Y of 230 mm, and a magnetic core window X of 70 mm. The wire used was a multi-strand wire with a diameter of 7.84 mm. The other parameters are outlined in Table 1.
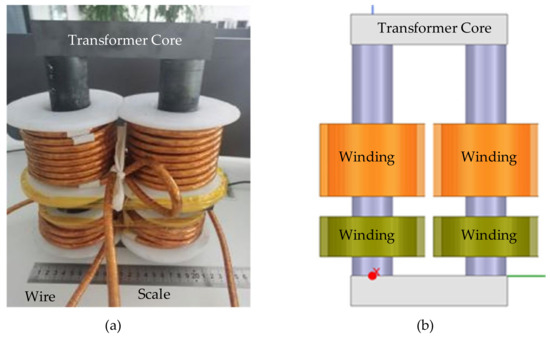
Figure 6.
(a) Real transformer and (b) simulation model.

Table 1.
The transformer dimension parameters.
As can be seen in Table 2, the results obtained from the proposed calculation method in this study were very close to the simulation results, yet the simulation and calculated results showed slight variations from the measurement results. The reason behind this variation was that the leakage magnetic field of the transformer was three-dimensional and was not strictly axisymmetric. This work made the axisymmetric field assumption for the leakage magnetic field, which facilitated calculation by simplifying the calculation procedure and provided an intuitive and easy method. Likewise, simplification was also conducted in different simulation methods to minimize the computational cost and simulation time. That is why the results obtained from the proposed method and the simulation showed minor differences from the actual measurements.

Table 2.
Calculation, simulation, and measurement results of transformer leakage inductance.
In addition, the value of leakage inductance also depended on different factors, such as f, X, Y, and the winding form. The impact of these factors on the leakage inductance value could be revealed by conducting a sensitivity analysis, which is discussed in the subsequent subsection.
4.1. Sensitivity Analysis for Change in Transformer Parameter f
By changing the transformer parameter f and keeping the other parameters unchanged, the results of the calculation, simulation, and measurements are presented in Table 3, revealing that all three methods showed a decrease in the inductance value with increasing parameter f. The trend of change in value for all the methods remained the same. The minor variation among the results of the different methods was due to the assumptions made in the simulation and calculation methods for simplification, as mentioned earlier in the discussion of the results of Table 2.

Table 3.
Transformer leakage inductance with changes in parameter f.
The transformer magnetic field intensity distributions with f = 5 mm and f = 30 mm are indicated in Figure 7.
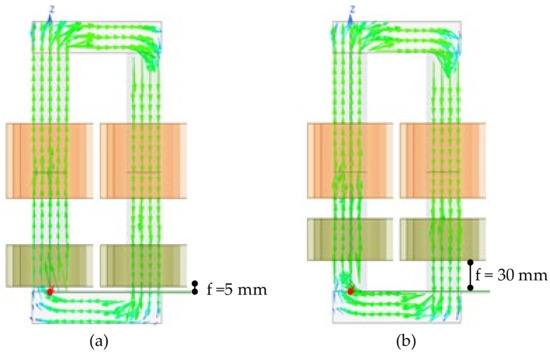
Figure 7.
Magnetic field intensity distributions with (a) f = 5 mm (b) f = 30 mm.
With the increase in parameter f, the visualization of the transformer magnetic field intensity distributions are depicted in Figure 7. In addition, a comparison of leakage inductance values with different methods is presented in Figure 8. With the increase in parameter f, the distance became shorter between the high-voltage and low-voltage coils; as a result, the value of the leakage inductance changed. It can be seen from Figure 8 that the variation trend of the transformer leakage inductance remained the same for the calculation results, simulation results, and measurements. Hence, comparing different methods validated the efficacy of the proposed calculation method, even under variation in the f parameter.
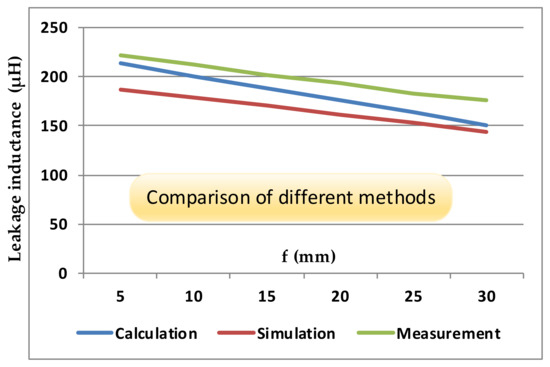
Figure 8.
Comparison of leakage inductance value with different methods under parameter f variation.
4.2. Sensitivity Analysis for Change in Transformer Parameter X
This subsection presents the calculation, simulation, and measurement results when changing the transformer parameter X and keeping the others unchanged. Parameter X dictated the dimension of the transformer along the x-axis. In transformer design, a smaller parameter X meant a smaller x dimension of the transformer. The transformer magnetic field intensity distributions with X = 70 mm and X = 85 mm are indicated in Figure 9. The value of the transformer leakage inductance reduced with the increase in parameter X. With variation in parameter X, the leakage inductance value was calculated using the proposed calculation method and compared with simulation and measured results, and the results are outlined in Table 4. To observe the trend, the results are plotted in Figure 10, showing that the change in leakage inductance value with the proposed calculation method was consistent with the simulation and measured results. Therefore, the comparison of different methods validated the efficacy of the proposed calculation method under variation in the X parameter.
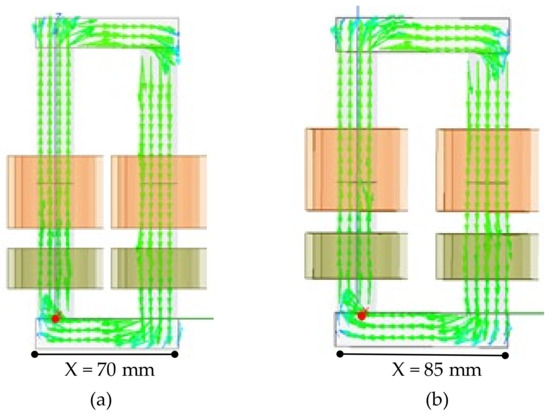
Figure 9.
Magnetic field intensity distributions with (a) X = 70 mm (b) X = 85 mm.

Table 4.
Transformer leakage inductance with variation in parameter X.
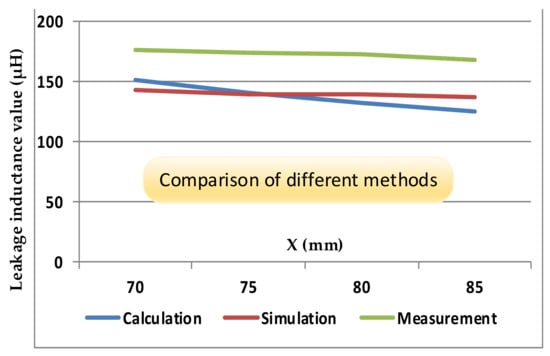
Figure 10.
Comparison of leakage inductance value with different methods under parameter X variation.
4.3. Sensitivity Analysis for Change in Transformer Parameter Y
To analyze the sensitivity of parameter Y on the leakage inductance value, parameter Y was gradually increased, keeping the other parameters unchanged. The calculation, simulation, and measurement results are outlined in Table 5. The results showed that the change in parameter Y had a negligible impact on the transformer leakage inductance. Hence, it can be concluded that leakage inductance was almost independent of parameter Y. The proposed method’s conclusion was consistent with that of the other two methods.

Table 5.
Transformer leakage inductance with variation in parameter Y.
4.4. Sensitivity Analysis for Change in the Form of Transformer Windings
This subsection presents the impact of form change in transformer windings on the leakage inductance value. Simulation models and experimental prototypes were built to study the form factor’s effect on the leakage inductance value, as shown in Figure 11.
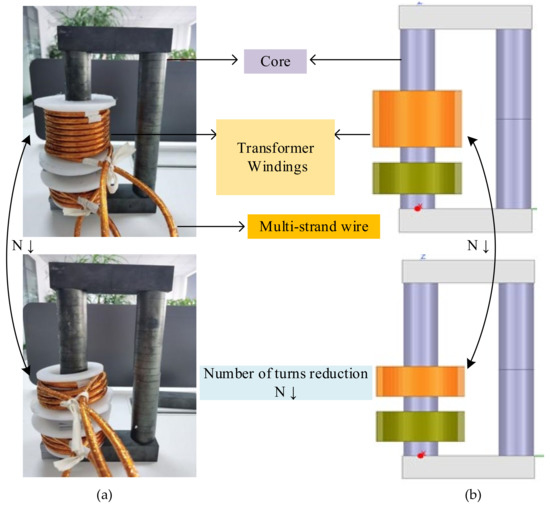
Figure 11.
Change in transformer windings with (a) real transformer and (b) simulation model.
First, the leakage inductance value was calculated using the proposed method considering the change in the form of the transformer windings; then, the results were compared with simulation and experimental ones. The proposed calculation method indicated that, by 2× changing the form of the transformer windings (N), the leakage inductance value changed almost 4×. As outlined in Table 6, the simulation results and experimentally measured values showed almost 4.3× and 3.7× changes, respectively, in the leakage inductance values for 2× change in the form of the transformer windings (N), which was quite close to the estimation provided by the proposed method. Hence, the proposed calculation model offered a reasonable estimation of leakage inductance values, even under different parameter variations. The reason behind the minor difference in the values was that the leakage magnetic field of the transformer was three-dimensional and was not strictly axisymmetric. In this study, the leakage magnetic field was assumed to be an axisymmetric field, which simplified the calculation and provided an intuitive and easy method with less design and calculation effort for leakage inductance while still offering good estimation.

Table 6.
Transformer leakage inductance under modification of winding form.
5. Conclusions
Double-group-overlapping winding transformers are often used as isolation transformers in power electronic transformers. In this paper, a model for calculating the leakage inductance of double-group winding transformers was derived using the double Fourier series method. The estimated transformer leakage inductance value using the proposed method was pretty close to the simulation and measurement results. Compared with other methods, the proposed method provided an intuitive and easy way with less design effort for leakage inductance calculation and still offered good accuracy.
Reviewing the whole process, the main cause of the difference between the calculation results and the actual value could be summarized as follows: the leakage magnetic field of the transformer was three-dimensional and was not strictly axisymmetric field. Especially with the impact of the magnetic yoke, the leakage magnetic field further deviates from the axisymmetric state. However, to simplify the mathematical calculation, the leakage magnetic field was assumed to be an axisymmetric field.
In practical engineering applications as a numerical analysis method, the double Fourier method for calculating transformer leakage inductance could be used as a reference design. Moreover, the double Fourier series method resolved the limitations of Rogowski’s equation, as it could be applied to transformers with different winding heights, increasing the range of applications.
Author Contributions
Z.Y. and M.T. developed the ideas of this research; Z.Y., H.Z., Q.H., S.H. and M.T. performed the simulations and the experiments; Z.Y., H.Z. and Q.H. conducted the formal analysis; Z.Y., M.T., Q.H. and S.H. performed the investigation and validation; M.T. and S.H. revised the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (under Grant 52177199) and the Zhejiang Provincial Natural Science Foundation of China (under Grant LGG22E070013).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| vacuum permeability | |
| D | average diameter of the winding |
| N | number of winding turns |
| ∑ N. I | algebraic sum of the ampere-turns of windings in closed rectangular field |
| leakage inductance | |
| K | windings in the rectangular field |
| current density of the kth winding | |
| current density of the high-voltage winding | |
| current density of the low-voltage winding | |
| m, n | index variables of double Fourier series |
References
- Zhang, X.; Xiao, F.; Wang, R.; Kang, W.; Yang, B. Modeling and Design of High-Power Enhanced Leakage-Inductance-Integrated Medium-Frequency Transformers for DAB Converters. Energies 2022, 15, 1361. [Google Scholar] [CrossRef]
- Garcia-Bediaga, A.; Villar, I.; Rujas, A.; Mir, L.; Rufer, A. Multiobjective Optimization of Medium-Frequency Transformers for Isolated Soft-Switching Converters Using a Genetic Algorithm. IEEE Trans. Power Electron. 2017, 32, 2995–3006. [Google Scholar] [CrossRef]
- Zhu, H.; Fujishima, N.; Onozawa, Y.; Hu, S. Study the Thermal Performance of the CLLC Transformer in the OBC Designed Using SiC MOSFETs. In Proceedings of the 2022 International Power Electronics Conference (IPEC-Himeji 2022-ECCE Asia), Himeji, Japan, 15–18 May 2022; pp. 1783–1788. [Google Scholar]
- Tahir, M.; Ahmed Khan, S.; Khan, T.; Waseem, M.; Khan, D.; Annuk, A. More Electric Aircraft Challenges: A Study on 270 V/90 V Interleaved Bidirectional DC–DC Converter. Energy Rep. 2022, 8, 1133–1140. [Google Scholar] [CrossRef]
- Zhu, H.; Hu, S.; Fujishima, N.; Onishi, Y. Design Method of Totem-Pole PFC and CLLC Resonant Converter Based on SiC MOSFET. In Proceedings of the 2021 6th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 17–20 September 2021; pp. 383–389. [Google Scholar]
- Tahir, M.; Sideng, H.; Xiangning, H. Performance Improvement Strategies for Discrete Wide Bandgap Devices: A Systematic Review. Front. Energy Res. 2021, 9, 4691–4699. [Google Scholar] [CrossRef]
- Noah, M.; Shirakawa, T.; Umetani, K.; Imaoka, J.; Yamamoto, M.; Hiraki, E. Effects of Secondary Leakage Inductance on the LLC Resonant Converter—Part II: Frequency Control Bandwidth with Respect to Load Variation. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 1408–1414. [Google Scholar]
- Tahir, M.; Hu, S.; Liang, Z.; Meng, Y. Unit Partition Resonance Analysis Strategy for Impedance Network in Modular Power Converters. Front. Energy Res. 2022, 10, 823938. [Google Scholar] [CrossRef]
- Zhang, B. Calculation of the Leakage Inductance of Transformers with Double-Coiling Overlapping Winding Using Field Source Substitution Method. J. EEE 1999, 21, 41–44. [Google Scholar]
- Tang, Y. The Electromagnetic Field in Motors, 2nd ed.; Science and Technology Press: Beijing, China, 1998. [Google Scholar]
- Sobczyk, T.; Jaraczewski, M. On Simplified Calculations of Leakage Inductances of Power Transformers. Energies 2020, 13, 4952. [Google Scholar] [CrossRef]
- Bin, C.; Lin, L.; Zhibin, Z. An Analytical Calculation Method of Leakage Inductance in High-Power High-Frequency Transformers Considering Frequency Dependence Characteristic. Proc. CSEE 2017, 37, 3928–3937. [Google Scholar]
- Wilson, P.R.; Wilcock, R. Frequency Dependent Model of Leakage Inductance for Magnetic Components. Adv. Electromagn. 2012, 1, 99–106. [Google Scholar] [CrossRef]
- Hameed, K.R. Finite Element Calculation of Leakage Reactance in Distribution Transformer Wound Core Type Using Energy Method. J. Eng. Dev. 2012, 16, 297. [Google Scholar]
- Ehsanifar, A.; Dehghani, M.; Allahbakhshi, M. Calculating the Leakage Inductance for Transformer Inter-Turn Fault Detection Using Finite Element Method. In Proceedings of the 2017 Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 2–4 May 2017; pp. 1372–1377. [Google Scholar]
- Jaraczewski, M.; Sobczyk, T. Leakage Inductances of Transformers at Arbitrarily Located Windings. Energies 2020, 13, 6464. [Google Scholar] [CrossRef]
- Li, P.; Huang, G.; Xie, L.; Hu, X. Research on Calculating Leakage Inductance of Power Transformer and Its Application to Winding Deformation Analysis. In Proceedings of the 2008 China International Conference on Electricity Distribution, Guangzhou, China, 10–13 December 2008; pp. 1–7. [Google Scholar]
- Wang, K.; Yang, X.; Li, H.; Ma, H.; Zeng, X.; Chen, W. An Analytical Switching Process Model of Low-Voltage EGaN HEMTs for Loss Calculation. IEEE Trans. Power Electron. 2016, 31, 635–647. [Google Scholar] [CrossRef]
- Bakar, M.A.; Bertilsson, K. An Improved Modelling and Construction of Power Transformer for Controlled Leakage Inductance. In Proceedings of the 2016 IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, Italy, 7–10 June 2016; pp. 1–5. [Google Scholar]
- Hurley, W.G.; Wilcox, D.J. Calculation of Leakage Inductance in Transformer Windings. IEEE Trans. Power Electron. 1994, 9, 121–126. [Google Scholar] [CrossRef]
- Ouyang, Z.W.; Zhang, J.; Hurley, W.G. Calculation of Leakage Inductance for High-Frequency Transformers. IEEE Trans. Power Electron. 2015, 30, 5769–5775. [Google Scholar] [CrossRef]
- Bahmani, M.A.; Thiringer, T. Accurate Evaluation of Leakage Inductance in High-Frequency Transformers Using an Improved Frequency-Dependent Expression. IEEE Trans. Power Electron. 2015, 30, 5738–5745. [Google Scholar] [CrossRef]
- Fichtenholz, Calculus Course, 8th ed.; Higher Education Press: Beijing, China, 2006.
- Bi, D. Theory of Electromagnetic Fields; Publishing House of Electronic Industry: Beijing, China, 1985. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).