Classification of Single Current Sensor Failures in Fault-Tolerant Induction Motor Drive Using Neural Network Approach
Abstract
1. Introduction
- -
- The original concept of the active FTC system, in which the classification of the type of damage to the current sensor takes place after the detection of a failure in any phase of the motor in the drive with vector control (DRFOC) and implementation of software redundancy, i.e., switching the control structure to work with estimated currents using the VCS algorithm, which allows eliminating the influence of CS damage on the control structure and limits the number of symptoms used in NN-FC;
- -
- The neural classifier developed using the MLP network, based on the estimated stator currents, which during the operation of the drive in the post-fault mode detects the type of CS damage (total lack of signal, gain change, saturation, and off-set) and the place of its occurrence in the time less than 1.5 the stator current period;
- -
- The on-line operation of the CS neural fault classifier was demonstrated, and the smooth operation of the drive system with vector control before and after failure detection was demonstrated.
2. Mathematical Model of Induction Motor Drive System with Current Sensor Faults
2.1. Mathematical Model of the Induction Motor
- Voltage equation of the stator and rotor windings:
- Flux-current equations:
- Equation of motion:
- Electromagnetic torque:
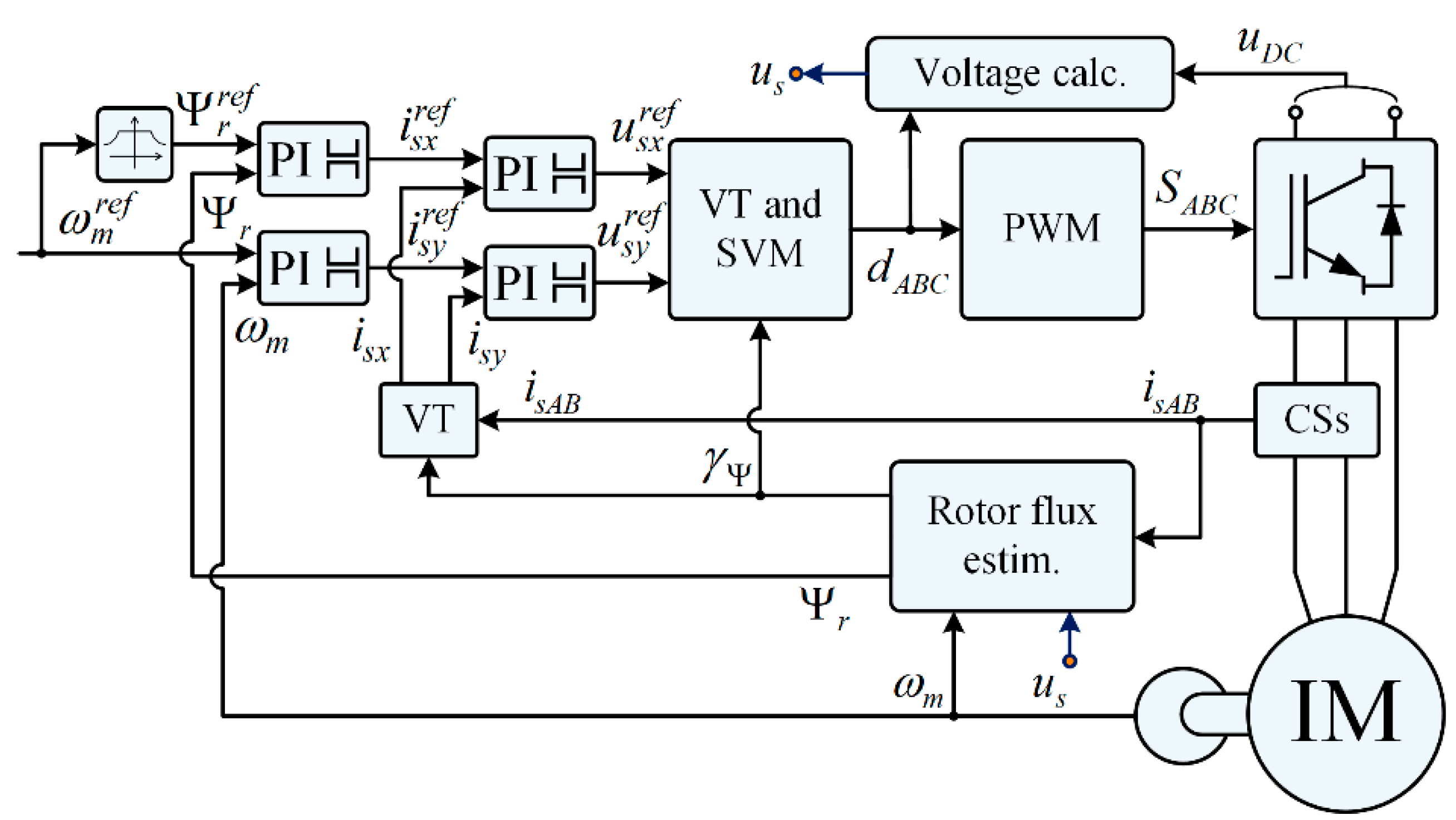
2.2. Direct Rotor Flux Oriented Control Structure
- -
- Clarke transform:
- -
- Park transform (VT):
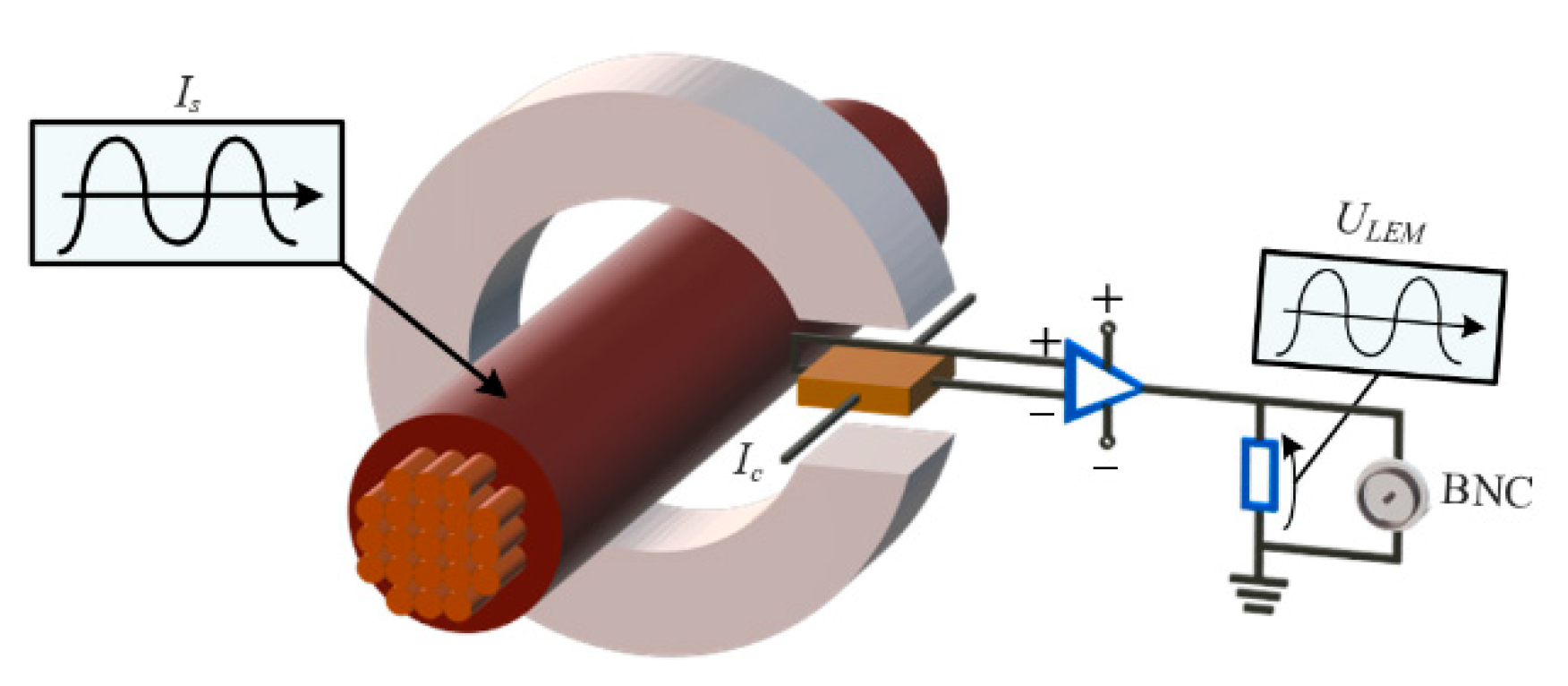
2.3. Types of Current Sensor Faults and Their Modeling
3. Current Sensor Fault Tolerant Control
3.1. General Description of Developed FTC Strategy
3.2. Virtual Current Sensor
3.3. Fault Detection and Compensation
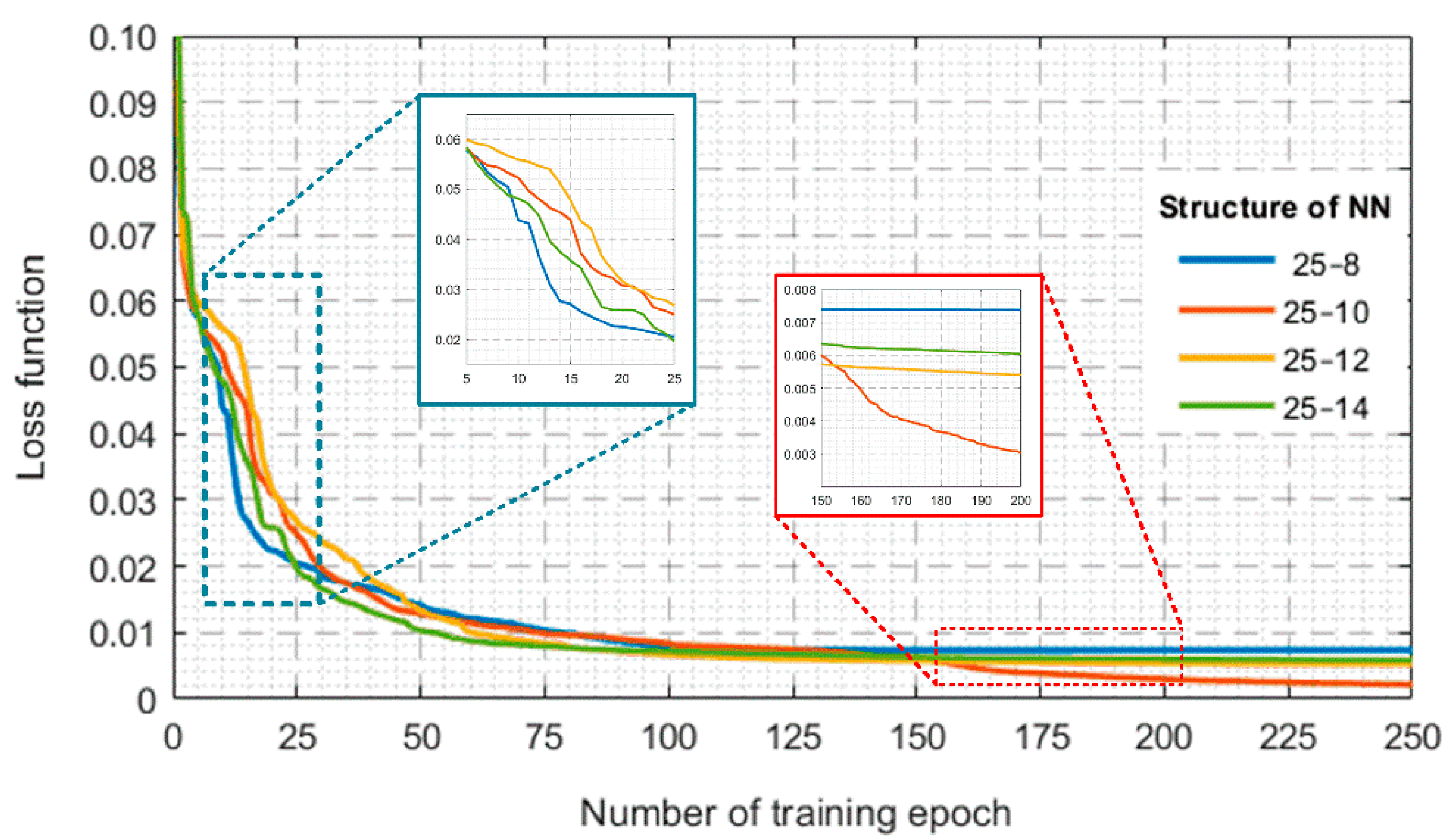
4. Neural Network Classifier
- -
- Classification (assessment of the type of CS damage);
- -
- Localization (determination of phase with CS failure).
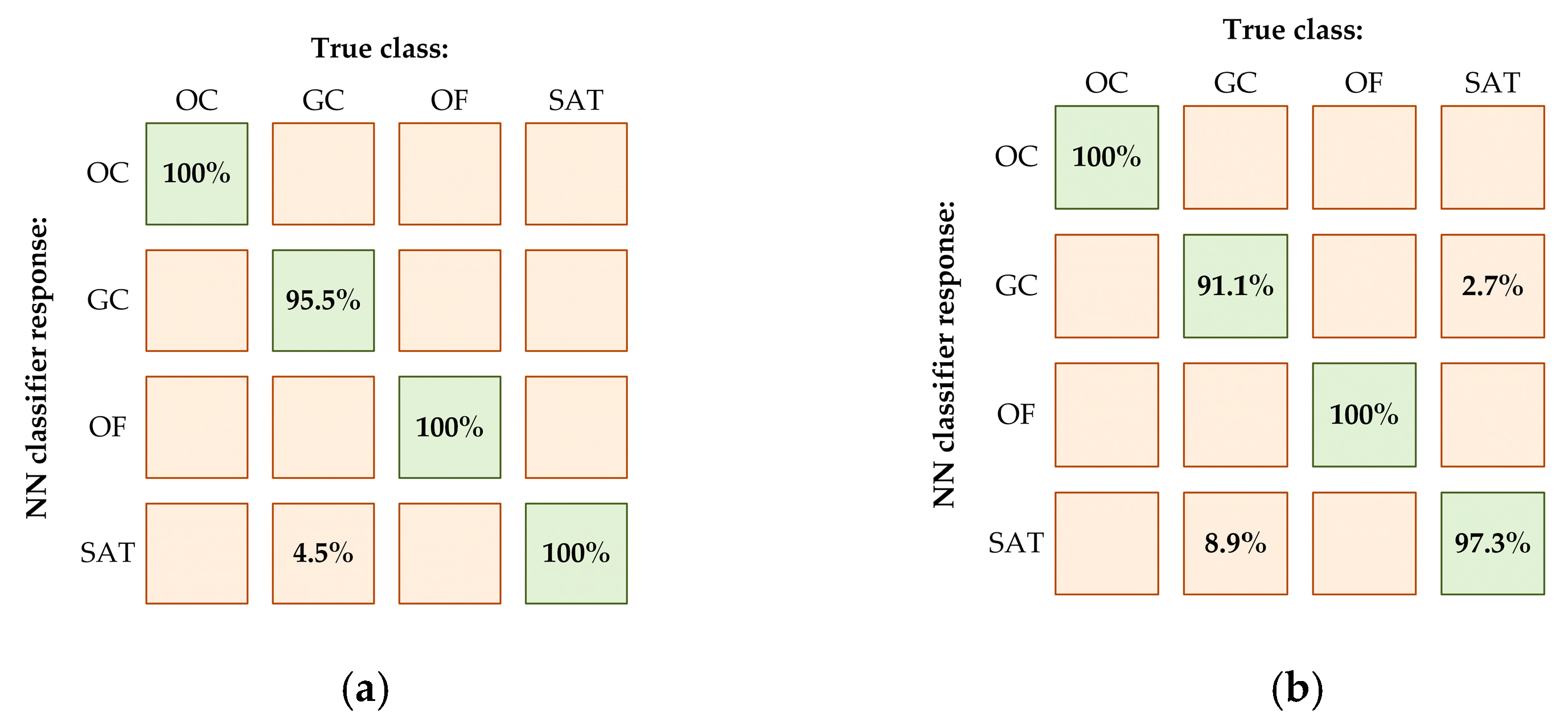
5. Verification of NN-Based CS Fault Classifier in IM Drive System
- -
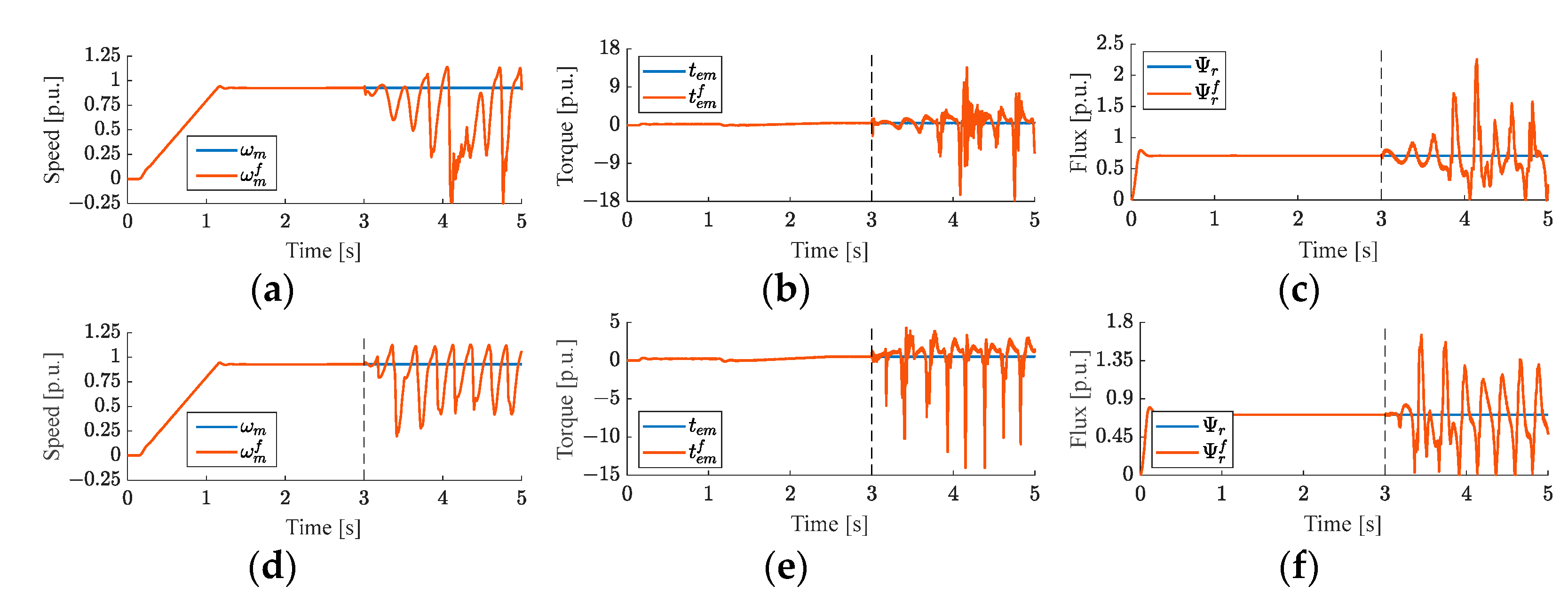
- Complete loss of the current signal for 25% of the rated speed and 75% of the rated torque (Figure 11a,b);
- -
- Change of the CS gain equal to 1.35 for 75% of the rated speed and 25% of the rated torque (Figure 11c,d);
- -
- Constant component of the measured current (off-set) equal to 0.15 p.u. for 75% of the rated speed and 75% of the rated torque (Figure 11e,f);
- -
- Saturation at 0.34 p.u. for 25% of the rated speed and 75% of the rated torque (Figure 11g,h).
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| State variables: | |
| us | spatial vector of stator voltage |
| is, ir | spatial vectors of stator and rotor currents |
| Ψs, Ψr | spatial vectors of stator and rotor fluxes |
| tem, tL | electromagnetic and load torques |
| ωm | angular rotor speed |
| ωs ψ | angular synchronous speed of the rotor flux spatial vector |
| γψ | angle between rotor flux vector and axis A of the stator winding |
| dABC | duty cycles values |
| SABC | logic states of the VSI switches |
| Parameters: | |
| rs, rr | stator and rotor windings resistances |
| lσs, lσr, lm | stator and rotor leakage inductances and main inductance |
| TM | mechanical time constant |
| fsN | nominal stator frequency |
| Coordinate systems: | |
| (A-B-C) | three-phase frame |
| (α-β) | stationary reference frame |
| (x-y) | synchronously rotating reference frame (with rotor flux angular speed, ωsΨ) |
| Indexes: | |
| ref | reference value |
| e | estimated value |
| Abbreviations | |
| CS | current sensor |
| DRFOC | direct rotor flux oriented control |
| FC | fault compensation |
| FD | fault detection |
| FTC | fault-tolerant control |
| IM | induction motor |
| MLP | multilayer perceptron |
| NN | neural network |
| NN-FC | neural network-based fault classifier |
| PI | PI controller |
| SVM | space vector modulation |
| VSI | voltage source inverter |
| VT | vector transform |
Appendix A
| Symbol | (ph.u.) | (p.u.) |
|---|---|---|
| Rated phase voltage, UN | 230 V | 0.707 |
| Rated phase current, IN | 2.5 A | 0.707 |
| Rated power, PN | 1.1 kW | 0.638 |
| Rated speed, nN | 1390 rpm | 0.927 |
| Rated torque, TeN | 7.56 Nm | 0.688 |
| Number of pole pairs, pb | 2 | - |
| Rotor winding resistance, Rr | 4.968 Ω | 0.0540 |
| Stator winding resistance, Rs | 5.114 Ω | 0.0556 |
| Rotor leakage inductance, Lσr | 31.6 mH | 0.1079 |
| Stator leakage inductance, Lσs | 31.6 mH | 0.1079 |
| Main inductance, Lm | 541.7 mH | 1.8498 |
| Rated rotor flux, ΨrN | 0.7441 Wb | 0.7187 |
| Mechanical time constant, TM | 0.25 s | - |
References
- Isermann, R. Fault-Diagnosis Applications, Model-Based Condition Monitoring: Actuators, Drives, Machinery, Plants, Sensors, and Fault-Tolerant Systems; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Isermann, R. Fault-Diagnosis Systems: An Introduction from Fault Detection to Fault Tolerance; Springer: Berlin, Germany, 2006. [Google Scholar]
- Muenchhof, M.; Beck, M.; Isermann, R. Fault-tolerant actuators and drives—Structures, fault detection principles and applications. Annu. Rev. Control. 2009, 33, 136–148. [Google Scholar] [CrossRef]
- Orlowska-Kowalska, T.; Wolkiewicz, M.; Pietrzak, P.; Skowron, M.; Ewert, P.; Tarchala, G.; Krzysztofiak, M.; Kowalski, C.T. Fault Diagnosis and Fault-Tolerant Control of PMSM Drives–State of the Art and Future Challenges. IEEE Access. 2022, 10, 59979–60024. [Google Scholar] [CrossRef]
- Dybkowski, M.; Klimkowski, K.; Orlowska-Kowalska, T. Speed and Current Sensor Fault-Tolerant-Control of the Induction Motor Drive. In Advanced Control of Electrical Drives and Power Electronic Converters; Kabzinski, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 141–167. [Google Scholar]
- Dybkowski, M.; Klimkowski, K. Stator current sensor fault detection and isolation for vector controlled induction motor drive. In Proceedings of the IEEE International Power Electronics and Motion Control Conference (PEMC), Varna, Bulgaria, 25–28 September 2016; pp. 1097–1102. [Google Scholar]
- Ha, J.I. Current prediction in vector-controlled PWM inverters using single DC-Link current sensor. IEEE Trans. Ind. Electron. 2010, 57, 716–726. [Google Scholar]
- Kim, H.R.; Jahns, T.M. Current control for AC motor drives using a single dc-link current sensor and measurement voltage vectors. IEEE Trans. Ind. Appl. 2006, 42, 1539–1547. [Google Scholar] [CrossRef]
- Salmasi, F.R.; Najafabadi, T.A. An adaptive observer with online rotor and stator resistance estimation for induction motors with one phase current sensor. IEEE Trans. Energy Convers. 2011, 26, 959–966. [Google Scholar] [CrossRef]
- Najafabadi, T.A.; Salmasi, F.R.; Maralani, P.J. Detection and isolation of speed-, dc-link voltage-, and current-sensor faults based on an adaptive observer in induction-motor drives. IEEE Trans. Ind. Electron. 2011, 58, 1662–1672. [Google Scholar] [CrossRef]
- Romero, M.E.; Seron, M.M.; Dona, J.A.D. Sensor fault-tolerant vector control of induction motors. IET Control Theory Appl. 2010, 4, 1707–1724. [Google Scholar] [CrossRef]
- Azzoug, Y.; Sahraoui, M.; Pusca, R.; Ameid, T.; Romary, R.; Cardoso, A.J.M. Current sensors fault detection and tolerant control strategy for three-phase induction motor drives. Electr. Eng. 2021, 103, 881–898. [Google Scholar] [CrossRef]
- Adamczyk, M.; Orlowska-Kowalska, T. Current Sensors Fault Detection and Tolerant Control for Induction Motor Drive. In Proceedings of the IEEE 19th International Power Electronics and Motion Control Conference, PEMC 2021, Gliwice, Poland, 25–29 April 2021. [Google Scholar]
- Salmasi, F.R. A self-healing induction motor drive with model free sensor tampering and sensor fault detection, isolation, and compensation. IEEE Trans. Ind. Electron. 2017, 64, 6105–6115. [Google Scholar] [CrossRef]
- Yu, Y.; Zhao, Y.; Wang, B.; Huang, X.; Xu, D. Current Sensor Fault Diagnosis and Tolerant Control for VSI-Based Induction Motor Drives. IEEE Trans. Power Electron. 2018, 33, 4238–4248. [Google Scholar] [CrossRef]
- Tabbache, B.; Rizoug, N.; Benbouzid, M.E.H.; Kheloui, A. A control reconfiguration strategy for post-sensor FTC in induction motor based EVs. IEEE Trans. Veh. Technol. 2013, 62, 965–971. [Google Scholar] [CrossRef][Green Version]
- Jankowska, K.; Dybkowski, M. A Current Sensor Fault Tolerant Control Strategy for PMSM Drive Systems Based on Cri Markers. Energies 2021, 14, 3443. [Google Scholar] [CrossRef]
- Jankowska, K.; Dybkowski, M. Design and Analysis of Current Sensor Fault Detection Mechanisms for PMSM Drives Based on Neural Networks. Designs 2022, 6, 18. [Google Scholar] [CrossRef]
- Adouni, A.; Hamed, M.B.; Flah, A.; Sbita, L. Sensor and actuator fault detection and isolation based on artificial neural networks and fuzzy logic applicated on Induction motor. In Proceedings of the International Conference on Control, Decision and Information Technologies CoDIT, Hammamet, Tunisia, 6–8 May 2013. [Google Scholar]
- Jäger, G.; Zug, S.; Brade, T.; Dietrich, A.; Steup, C.; Moewes, C.; Cretu, A.M. Assessing neural networks for sensor fault detection. In Proceedings of the 2014 IEEE International Conference on Computational Intelligence and Virtual Environments for Measurement Systems and Applications (CIVEMSA), Ottawa, ON, Canada, 5–7 May 2014; pp. 70–75. [Google Scholar]
- Dybkowski, M.; Klimkowski, K. Artificial Neural Network Application for Current Sensors Fault Detection in the Vector Controlled Induction Motor Drive. Sensors 2019, 19, 571. [Google Scholar] [CrossRef] [PubMed]
- Gou, B.; Xu, Y.; Xia, Y.; Wilson, G.; Liu, S. An Intelligent Time-Adaptive Data-Driven Method for Sensor Fault Diagnosis in Induction Motor Drive System. IEEE Trans. Ind. Electron. 2019, 66, 9817–9827. [Google Scholar] [CrossRef]
- Manohar, M.; Das, S. Current sensor fault-tolerant control for direct torque control of induction motor drive using flux linkage observer. IEEE Trans. Ind. Informat. 2017, 13, 2824–2833. [Google Scholar] [CrossRef]
- Adamczyk, M.; Orlowska-Kowalska, T. Virtual Current Sensor in the Fault-Tolerant Field-Oriented Control Structure of an Induction Motor Drive. Sensors 2019, 19, 4979. [Google Scholar] [CrossRef]
- Adamczyk, M.; Orlowska-Kowalska, T. Postfault Direct Field-Oriented Control of Induction Motor Drive using Adaptive Virtual Current Sensor. IEEE Trans. Ind. Electron. 2022, 69, 3418–3427. [Google Scholar] [CrossRef]
- Adamczyk, M.; Orlowska-Kowalska, T. Influence of the stator current reconstruction method on direct torque control of induction motor drive in current sensor postfault operation. Bull. Pol. Acad. Sci. Tech. Sci. 2022, 70, e140099. [Google Scholar]
- Azzoug, Y.; Pusca, R.; Sahraoui, M.; Ammar, A.; Ameid, T.; Romary, R.; Cardoso, A.J.M. An Active Fault-Tolerant Control Strategy for Current Sensors Failure for Induction Motor Drives Using a Single Observer for Currents Estimation and Axes Transformation. Eur. J. Electr. Eng. 2021, 23, 467–474. [Google Scholar] [CrossRef]
- Adamczyk, M.; Orlowska-Kowalska, T. Self-Correcting Virtual Current Sensor Based on the Modified Luenberger Observer for Fault-Tolerant Induction Motor Drive. Energies 2021, 14, 6767. [Google Scholar] [CrossRef]
- Chakraborty, C.; Verma, V. Speed and current sensor fault detection and isolation technique for induction motor drive using axes transformation. IEEE Trans. Ind. Electron. 2014, 62, 1943–1954. [Google Scholar] [CrossRef]
- Wang, W.; Feng, Y.; Shi, Y.; Cheng, M. Fault-tolerant control of primary permanent-magnet linear motors with single phase current sensor for subway applications. IEEE Trans. Power Electron. 2019, 34, 10546–10556. [Google Scholar] [CrossRef]
- Orlowska-Kowalska, T. Sensoless Induction Motor Drives; Wroclaw University of Technology Press: Wroclaw, Poland, 2003. [Google Scholar]
- Kazmierkowski, M.P.; Krishnan, R.; Blaabjerg, F. Control in Power Electronics-Selected Problems; Academic Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Lee, K.S.; Ryu, J.S. Instrument fault detection and compensation scheme for direct torque controlled induction motor drives. IEE Proc. Control Theory Appl. 2003, 150, 376–382. [Google Scholar] [CrossRef]
- Adamczyk, M. Rotor resistance estimator based on virtual current sensor algorithm for induction motor drives. Power Electron. Drives 2020, 5, 143–156. [Google Scholar] [CrossRef]
- Bishop, M.C. Neural Networks for Pattern Recognition, 1st ed.; Oxford University Press: New York, NY, USA, 1996. [Google Scholar]
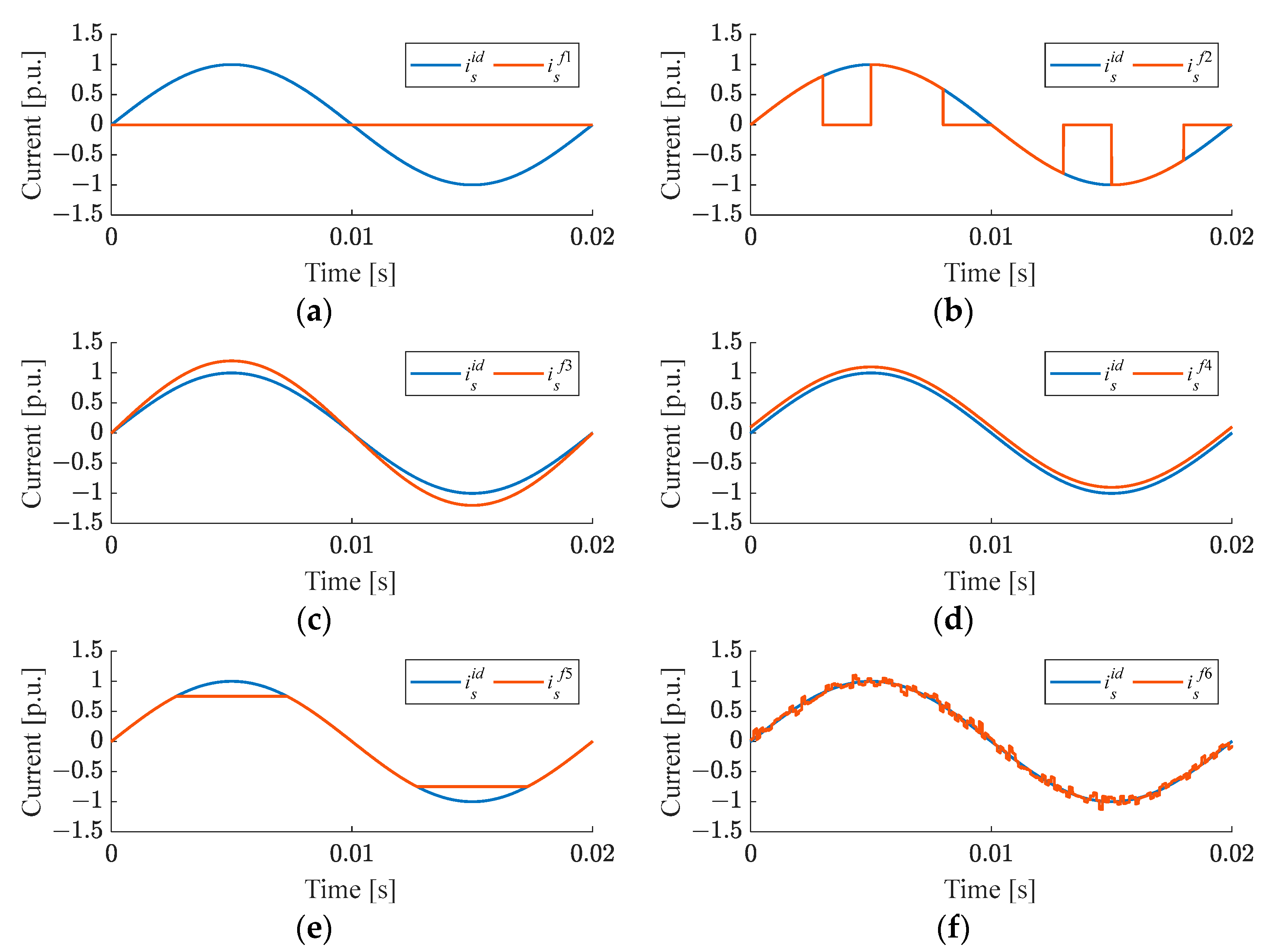





| Fault No | Fault Type | Mathematical Description of CS Fault |
|---|---|---|
| f1 | Open circuit | 0 |
| f2 | Disconnections | |
| f3 | Gain change | |
| f4 | Offset | |
| f5 | Saturation | |
| f6 | Noise |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skowron, M.; Teler, K.; Adamczyk, M.; Orlowska-Kowalska, T. Classification of Single Current Sensor Failures in Fault-Tolerant Induction Motor Drive Using Neural Network Approach. Energies 2022, 15, 6646. https://doi.org/10.3390/en15186646
Skowron M, Teler K, Adamczyk M, Orlowska-Kowalska T. Classification of Single Current Sensor Failures in Fault-Tolerant Induction Motor Drive Using Neural Network Approach. Energies. 2022; 15(18):6646. https://doi.org/10.3390/en15186646
Chicago/Turabian StyleSkowron, Maciej, Krystian Teler, Michal Adamczyk, and Teresa Orlowska-Kowalska. 2022. "Classification of Single Current Sensor Failures in Fault-Tolerant Induction Motor Drive Using Neural Network Approach" Energies 15, no. 18: 6646. https://doi.org/10.3390/en15186646
APA StyleSkowron, M., Teler, K., Adamczyk, M., & Orlowska-Kowalska, T. (2022). Classification of Single Current Sensor Failures in Fault-Tolerant Induction Motor Drive Using Neural Network Approach. Energies, 15(18), 6646. https://doi.org/10.3390/en15186646









