Evaluating Performance Indices of Electrostatic Precipitators
Abstract
:1. Introduction
2. ESP Background
2.1. ESP Classification: Collecting Electrodes Configuration
2.2. ESP Classification: Number of Stages
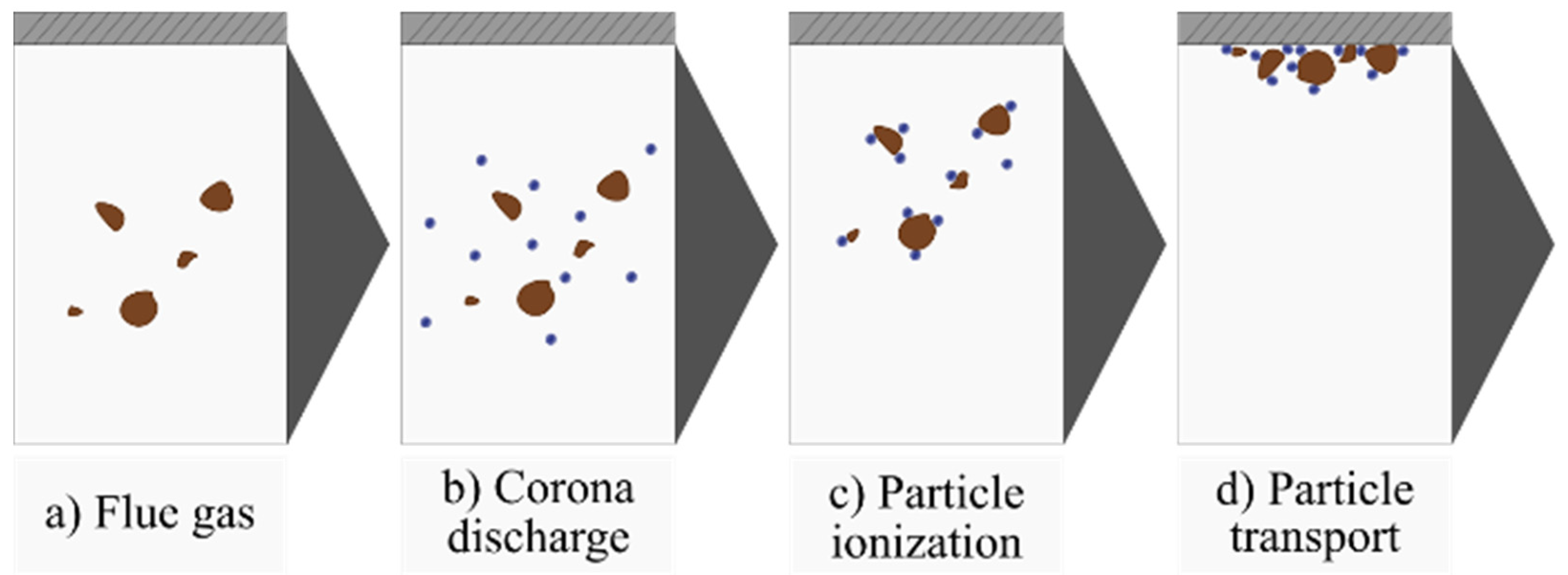
2.3. Working Principle
3. Collection Efficiency and Performance Assessment Methods of an ESP
3.1. Current-Voltage Characteristics
3.2. Corona Power Ratio
3.3. Modelling Approaches of Collection Efficiency
3.3.1. Deutsch Method
3.3.2. Matts-Ohnfeldt Method
3.3.3. Cooperman Method
3.3.4. Zhibin and Guoquan Method
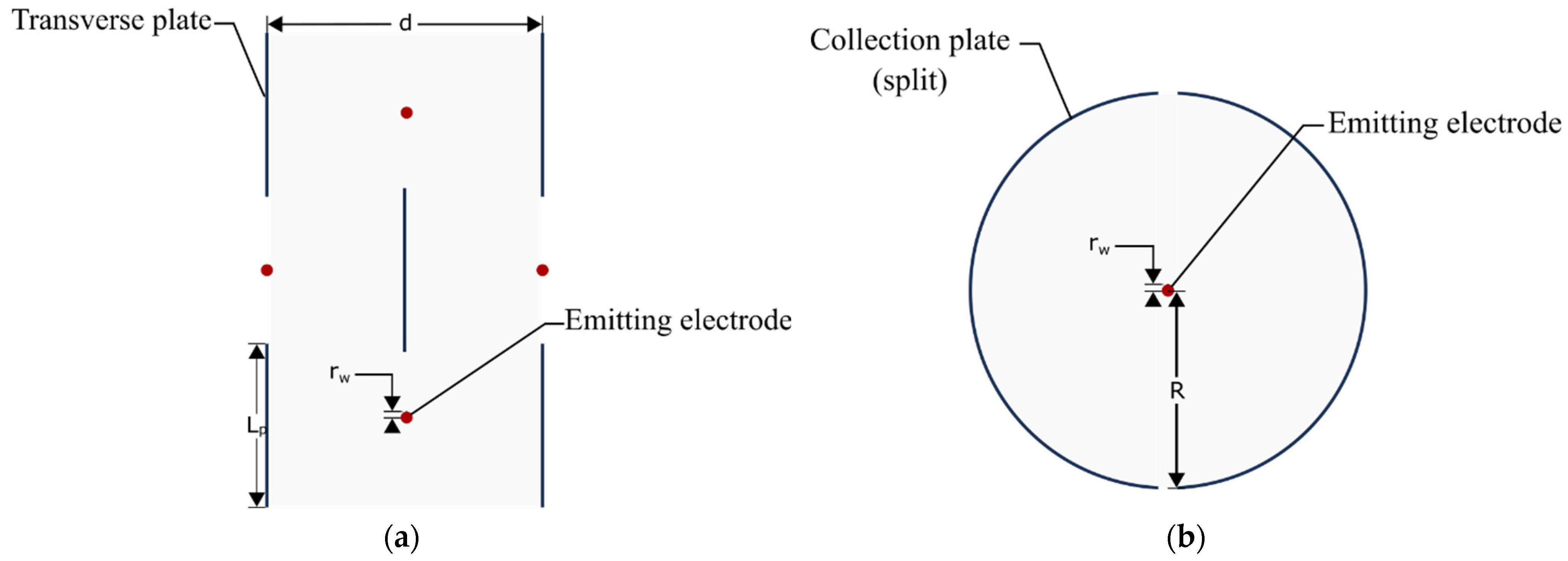
3.3.5. Considerations for Transverse-Plate Type ESP
3.4. Material Considerations
4. Factors That Impact the Precipitation Performance
4.1. Optmization of Geometrical Parameters
4.1.1. Discharge Electrode Geometry
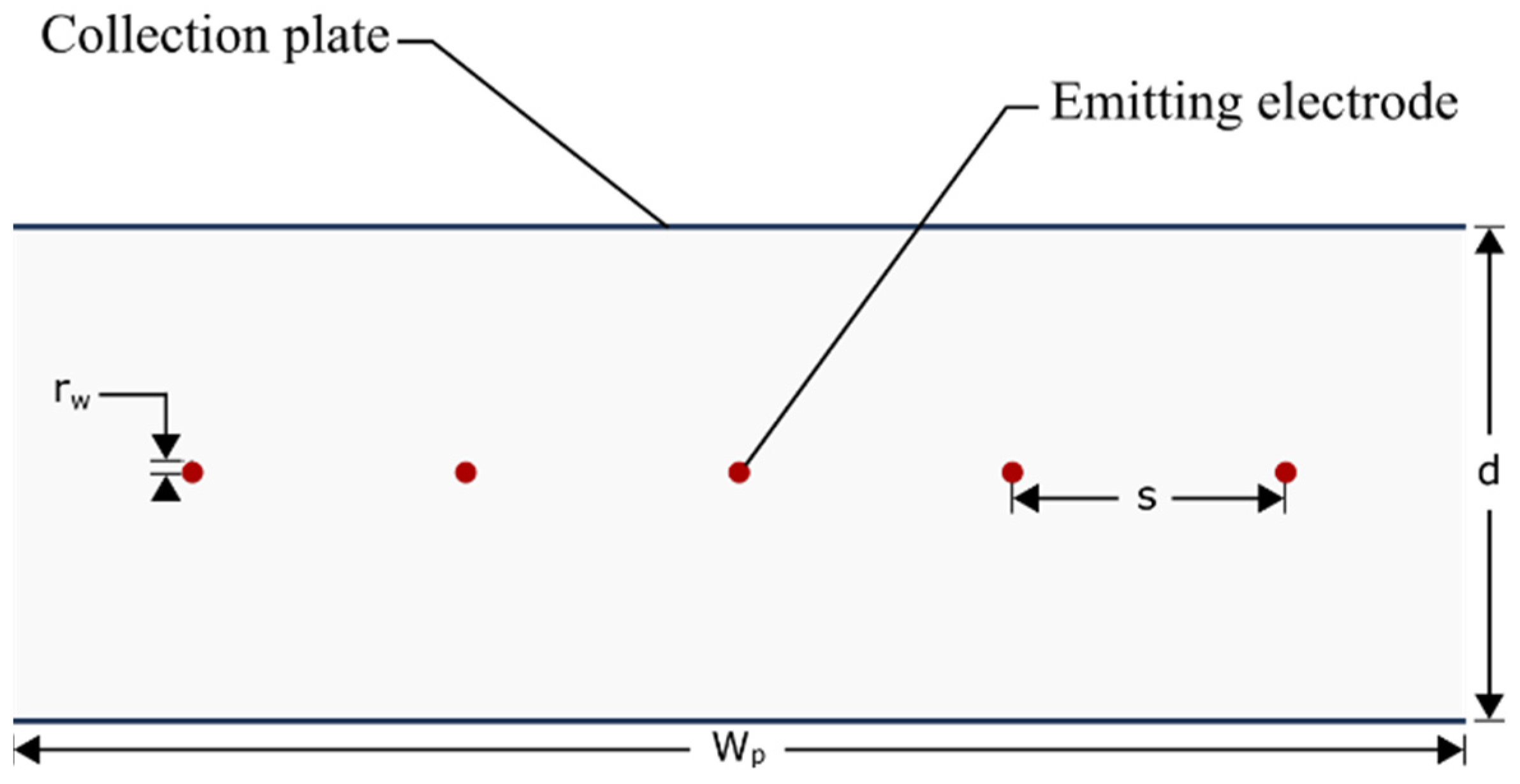
4.1.2. Discharge Electrode Diameter and Wire-to-Wire Spacing
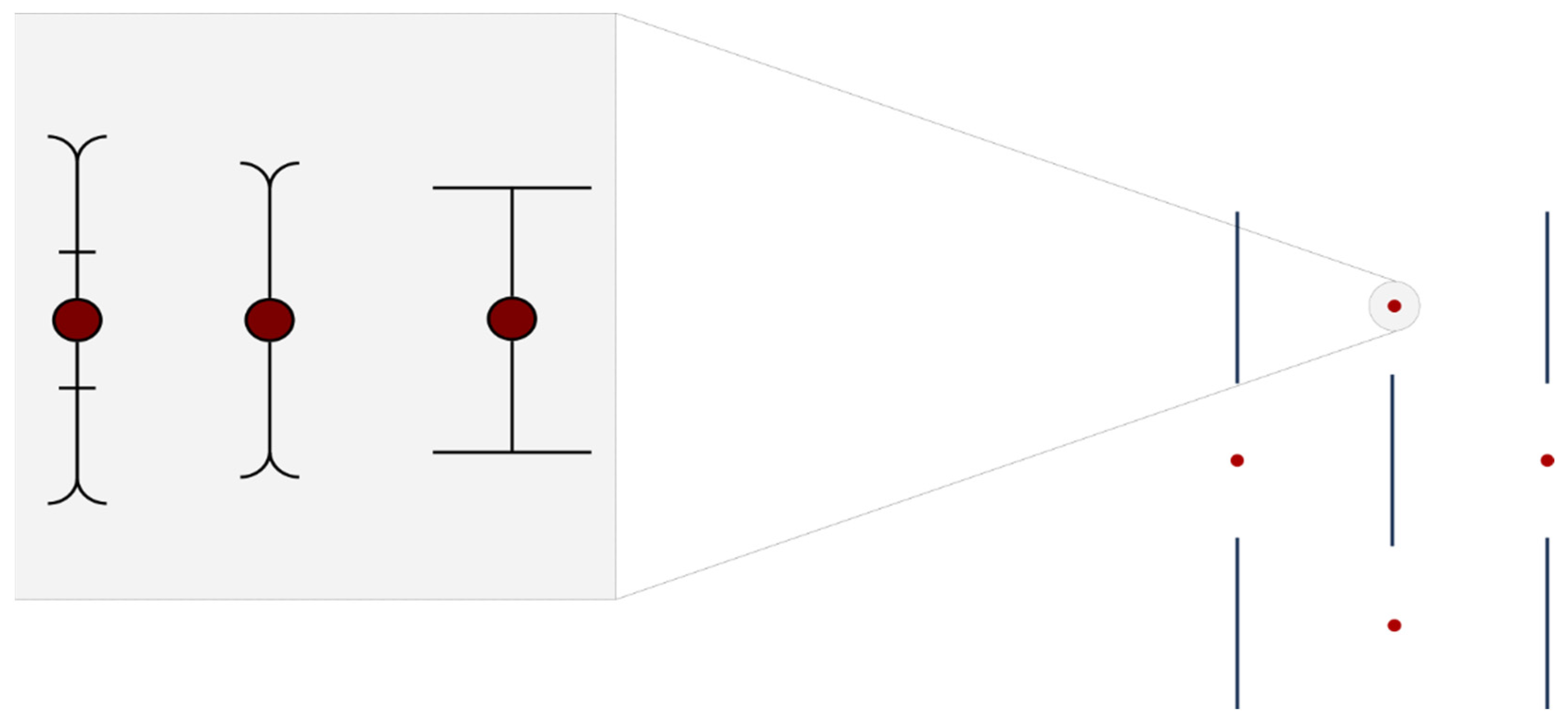
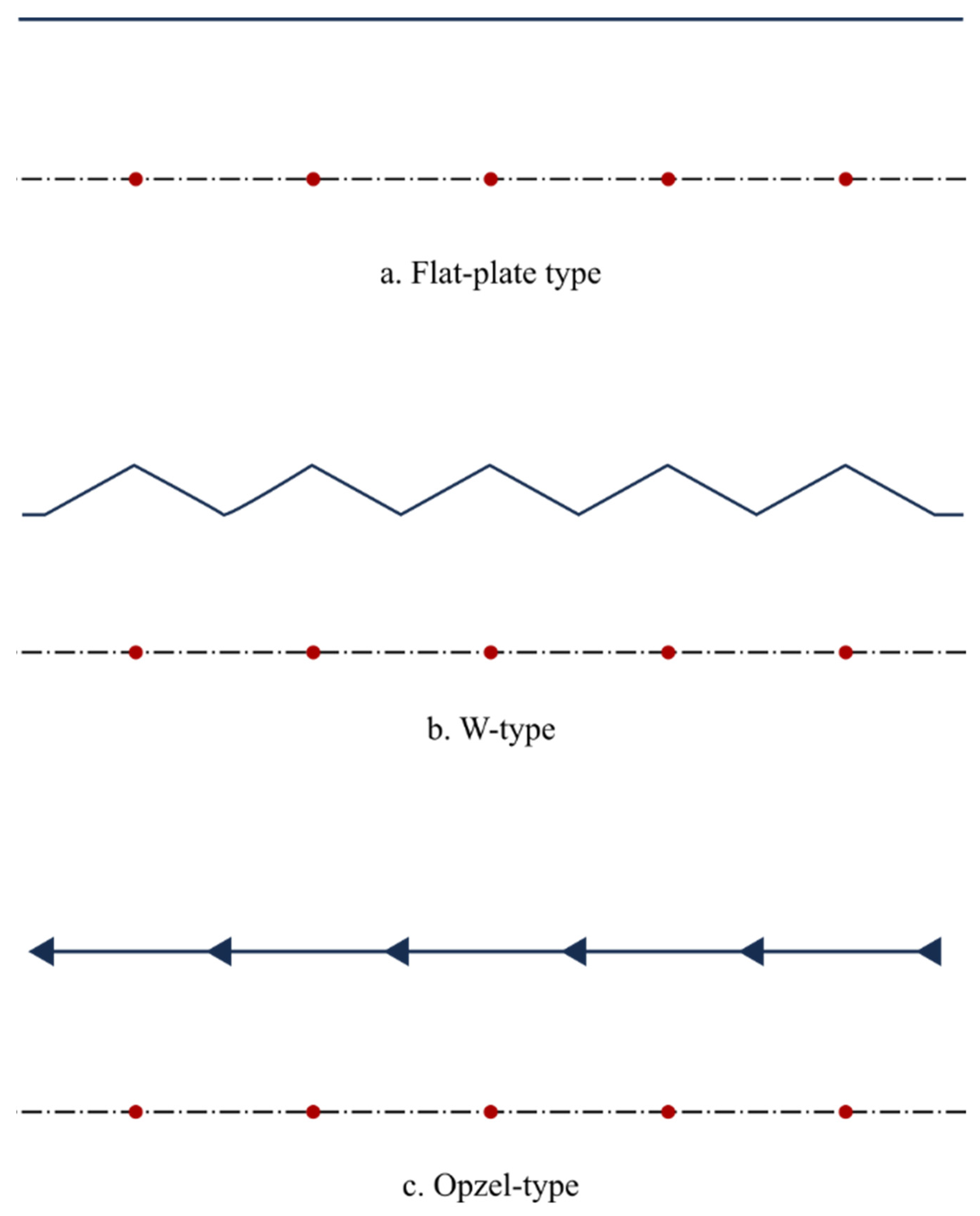
4.1.3. Collecting Electrode Geometry
4.1.4. Collecting Electrode Spacing
4.1.5. Pre-Charger Length to Collection Stage Length Ratio (Multi-Stage ESP)
4.1.6. Discharge Electrode Eccentricity (Wire-Cylinder Type)
4.2. Electrohydrodynamic Flow
4.2.1. EHD Flow Effects on Flow Profile Collection Efficiency
4.2.2. EHD Flow Effects on Particle Deposition Rate
4.3. The Effect of Gas-Flow Velocity
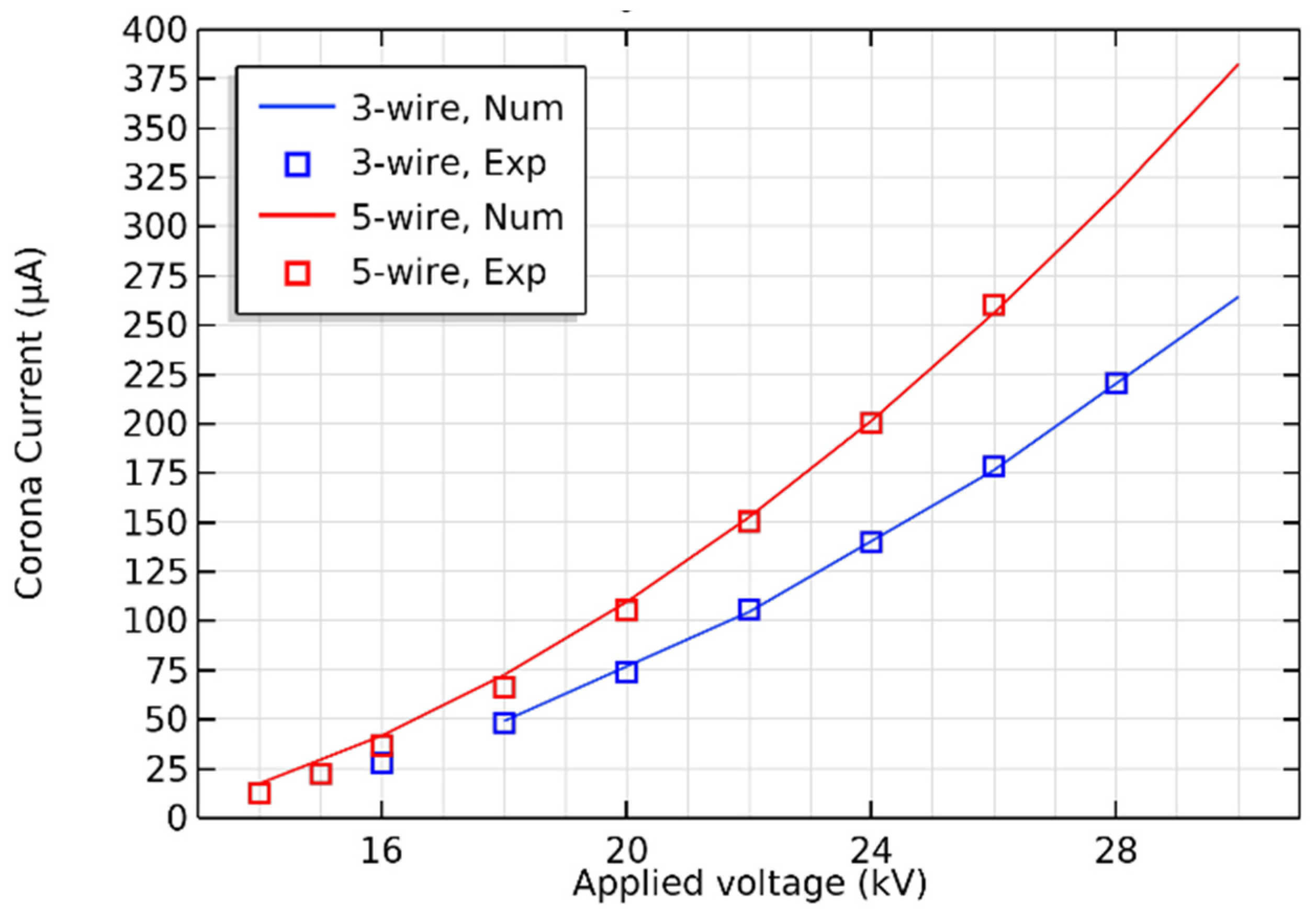
4.4. The Effect of Power Consumption and Number of Emitting Electrodes
| Author, Reference Number | ESP Type | Emitting Electrode, Diameter, Spacing/Length | Collecting Electrode Geometry, Spacing | Flow Speed | Particle Type, Size, Concentration | Collection Efficiency, Equation Number |
|---|---|---|---|---|---|---|
| Lagarias [43] | Wire-plate type | Square profile/spaced disks/ barbed, variable diameter, 203.2 mm | Flat plate, 152.4 mm | N/A | N/A, 10 µm, N/A | Deutsch-White model, Equation (3) |
| Fujishima [72] | Wire-plate type | Barbed wires, 0.2 mm, 50 mm | Flat plate, 80 mm | 0.1, 0.5, 1 m/s | Dust, 11–11.5 µm, variable | N/A |
| Heng [27] | Wire-plate type | Smooth cylinder, 5 mm, 24 0 mm | Flat plate, rod-curtain, W-, C-, and opzel types, 250 mm | 0.5–1 m/s | N/A | N/A |
| Abdel-Sattar [18] | Wire-plate type | 0.254 mm, 0.2 m, unity surface factor | Flat plate, 200 mm | 10 m/s | Spherical, N/A, constant concentration | General method, Equation (2) |
| Miller [37] | Wire-plate type | Barbed, 10 mm, 75–175 mm | Flat plate, N/A | N/A | Limestone dust, 6 µm, 0.1 g/m3 | Fractional efficiency |
| Farnoosh [73] | Wire-plate type | Smooth cylinder, N/A, single wire/100 mm | Flat plate, 100 mm | 1 m/s | Spherical, 0.3–90 µm, 998.2 kg/m3 | General method, Equation (2) |
| Farnoosh [46] | Wire-plate type | Spiked wire (single- and double- sided spikes), 10 mm, single wire/200 mm | Flat plate, 100 mm | 0.6 m/s | N/A, 0.25–1.5 µm, 998.2 kg/m3 | General method, Equation (2) |
| Ning [15] | Wire-plate type | Smooth cylinder, 0.09 mm, 0.1–0.2 m | Flat plate, 200–400 mm | 0.2 m/s | Spherical, 20 nm to 6.35 µm, variable | General method, Equation (2) |
| He [74] | Wire-plate type | Smooth cylinder, 1 mm, 40–60–80 mm | Flat plate, variable | Static, 1–3.37 m/s | Variable, 2.5–10 µm, variable (100–200–300 µg/m3) | Experimental (DRX-1, DRX-2) |
| Hao [55] | Wire-plate type | 0.2–1.6, 2.2–3.5 mm, 300–333 mm | Flat plate, 300 mm | 0.25 m/s | N/A | N/A |
| Navarrete [19] | Wire-plate type | Barbed, N/A | Flat plate, 300–400 mm | 0.8–1.8 m/s | Ash, variable, variable | General method, Equation (2) |
| Kim [58] | Wire-plate type | Smooth cylinder, 1 mm, 37.5 mm | Flat plate, 300 mm | 1 m/s | Variable, 0.2–200 µm, variable | N/A |
| Kasdi [9] | Wire-plate type | Smooth cylinder, 0.4–0.8 mm, 40–60–80 mm | Flat plate, 100 mm | N/A | N/A | N/A |
| Chibane [75] | Wire-plate type | Smooth cylinder, 0.25 mm, 40–60–80 mm | C-, tri-, w-, corrugated, crenelated and flat types, 200 mm | 0–1 m/s | 1–10 µm, 3900 kg/m3 | General method, Equation (2) |
| Choi [76] | Wire-plate type | Smooth cylinder, 0.1 mm, 100 mm | Several wavy types, flat type, 50 mm | 2 m/s | N/A | General method, Equation (2) |
| Ruttanachot [77] | Wire-plate type | N/A, 64, 85 mm | Flat plate, 50–75 mm | 0.063 m/s | N/A, 0.68 µm, variable (average 498.1 mg/m3) | Deutsch-Anderson model, Equation (3) |
| Zhu [59] | Wire-plate type | Smooth cylinder, 1 mm, 200 mm | C-, tri-, w-, corrugated, crenelated and flat types, 200 mm | 0–1 m/s | 1–10 µm, 3900 kg/m3 | General method, Equation (2) |
| Pal [70] | Wire-plate type | Cup-type, 5 mm, 240 mm | Flat plate, w-type, 200 mm | 1 m/s | N/A | General method, Equation (2) |
| Yan [14] | Wire-plate type | Barbed, 20 mm, 480 mm | C-type plate, 400 mm | 0.4–0.8 m/s | N/A | General method, Equation (2) |
| Lee [38] | Wire-plate type | Pipe-and-spike electrode, N/A, 20 mm | Flat plate, 50 mm | 0–1 m/s | N/A | General method, Equation (2) |
| Lee [6] | Plate-plate type, 2-stage | Spiked edge-type electrode, N/A | Flat plate, 10 mm | 1 m/s | Oil mist, 2.5 µm, N/A | General method, Equation (2) |
| Gao [67] | Wire-plate type, 2-stage | Smooth cylinder, square (90°/45° config.), needle wire, 3.5 mm | Flat plate, BE-type plate, 400 mm | 1 m/s | 0.05–10 µm, N/A | General method, Equation (2) |
| Gao [5] | Wire-plate type, 2-stage | Smooth cylinder, 0.22 mm, single wire | Flat plate, 10–50 mm | 0.5–2 m/s | 0.4–4 µm, 2200 kg/m3 | General method, Equation (2) |
| Zhu [4] | Wire-plate type, 2-stage | Smooth cylinder, 0.1 mm, single wire | W-type plate, 6 mm | 0–2.5 m/s | 0.3–1 µm, 1.225 kg/m3 | General method, Equation (2) |
| Shen [69] | Transverse-plate type | Smooth cylinder, N/A | Curved transverse, 100 mm | ~0.2–1.7 m/s | 16 nm–10 µm, 1000 kg/m3 | General method, Equation (2) |
| Yi [78] | Transverse-plate type | Smooth cylinder, N/A | Double C-plate, 40 mm | 3.5 m/s | Ash, ≤60 µm | N/A |
| Xiang [25] | Transverse-plate type | Smooth cylinder, 2 mm, 400 mm | Simple transverse, 200 mm | 1–1.5 m/s | Dust, 25.405 µm, 500–1300 mg/m3 | General method, Equation (2) |
| Chang [7] | Transverse-plate type | Barbed, 20 mm, 480 mm | C-plate, 480 mm | 0.8 m/s | Talcum powder, 11.6 µm, variable | Combined, Equation (13) |
| Zhuang [79] | Wire-cylinder type | 0.3–0.5 mm, N/A | Cylindrical, 15 mm radius, 150 mm long | 0.35–0.7 m/s | Various, 0.5–50 µm, variable | General method, Equation (2) |
| Yamamoto [42] | Wire-cylinder type | 6.35 mm, 416 mm long | Cylindrical, 25 mm radius, 416 mm long | 1.9–2.1 m/s | Diesel emissions, 0.2–2.5 µm, N/A | General method, Equation (2) |
| Niewulis [61] | Wire-cylinder type | 0.23 mm, 100 mm long | Cylindrical, 12.75 mm radius, 200 mm long | 0.9 m/s | N/A | N/A |
| Bacher [56] | Wire-cylinder type | Cylindrical/barbed, 0.2 mm, N/A | Cylindrical, 125 mm radius, 5000 mm long | 1.36 m/s | 0.082 µm (mean), N/A | Mass-related separation method |
| Hwang [39] | Wire-cylinder type | “Sawtooth”, 35–75 mm, 20–100 mm | Cylindrical, 100 mm radius, 555 mm long | 1 m/s | Variable | General method, Equation (2) |
5. Discussion and Conclusions
6. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- White, H.J. Fifty Years of Electrostatic Precipitation. J. Air Pollut. Control. Assoc. 1957, 7, 166–177. [Google Scholar] [CrossRef]
- Parker, K.R. Applied Electrostatic Precipitation; Blackie: London, UK, 1997; ISBN 978-0-7514-0266-7. [Google Scholar]
- Mizuno, A. Electrostatic Precipitation. IEEE Trans. Dielect. Electr. Insul. 2000, 7, 615–624. [Google Scholar] [CrossRef]
- Zhu, Y.; Chen, C.; Shi, J.; Shangguan, W. Enhancement of Air Purification by Unique W-Plate Structure in Two-Stage Electrostatic Precipitator: A Novel Design for Efficient Capture of Fine Particles. Adv. Powder Technol. 2020, 31, 1643–1658. [Google Scholar] [CrossRef]
- Gao, M.; Zhu, Y.; Yao, X.; Shi, J.; Shangguan, W. Dust Removal Performance of Two-Stage Electrostatic Precipitators and Its Influencing Factors. Powder Technol. 2019, 348, 13–23. [Google Scholar] [CrossRef]
- Lee, Y.; Sung, J.-H.; Han, B.; Kim, Y.-J.; Kim, H.-J. Particle Removal Performance of a Two Stage Electrostatic Precipitator with Carbon Based Nonmetallic Collection Plates for Oil Mist. In Proceedings of the 2020 IEEE Industry Applications Society Annual Meeting, Detroit, MI, USA, 10–16 October 2020; pp. 1–7. [Google Scholar]
- Chang, Y.; Jia, P.; Shi, L.; Xiang, X. Corona Discharging and Particle Collection of Bipolar Transverse Plate ESP. J. Electrost. 2018, 96, 104–110. [Google Scholar] [CrossRef]
- Nikas, K.S.P.; Varonos, A.A.; Bergeles, G.C. Numerical Simulation of the Flow and the Collection Mechanisms inside a Laboratory Scale Electrostatic Precipitator. J. Electrost. 2005, 63, 423–443. [Google Scholar] [CrossRef]
- Kasdi, A. Computation and Measurement of Corona Current Density and V–I Characteristics in Wires-to-Plates Electrostatic Precipitator. J. Electrost. 2016, 81, 1–8. [Google Scholar] [CrossRef]
- Conesa, A.J.; Sanchez, M. The Current–Voltage Characteristics of Corona Discharge in Wire to Cylinder in Parallel Electrode Arrangement. IEEE Trans. Plasma Sci. 2018, 46, 3022–3030. [Google Scholar] [CrossRef]
- Mansour, A.; Badran, M. Modelling and Simulating the Effect of the Different Geometric Parameters on Voltage-Current Characteristics for Wire-Plate Electrostatic Precipitator with Different Collector Configurations. In Proceedings of the 2020 21st International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Cracow, Poland, 5–8 July 2020; pp. 1–8. [Google Scholar]
- Ait Said, H.; Aissou, M.; Nouri, H.; Zebboudj, Y. Analysis of the Current-Voltage Characteristic during the Corona Discharge in Wires-To-Planes Electrostatic Precipitator under Variable Air Humidity. Acta Phys. Pol. A 2019, 135, 320–325. [Google Scholar] [CrossRef]
- Khaled, U.; Beroual, A.; Alotaibi, F.; Khan, Y.; Al-Arainy, A. Experimental and Analytical Study on the Performance of Novel Design of Efficient Two-Stage Electrostatic Precipitator. IET Sci. Meas. Technol. 2018, 12, 486–491. [Google Scholar] [CrossRef]
- Yan, D.; Zhang, Z.; Gong, H.; Ya, Y. Effect of Barbed Tubular Electrode Corona Discharge EHD Flow on Submicron Particle Collection in a Wide-Type ESP. J. Electrost. 2021, 109, 103545. [Google Scholar] [CrossRef]
- Ning, Z.; Podlinski, J.; Shen, X.; Li, S.; Wang, S.; Han, P.; Yan, K. Electrode Geometry Optimization in Wire-Plate Electrostatic Precipitator and Its Impact on Collection Efficiency. J. Electrost. 2016, 80, 76–84. [Google Scholar] [CrossRef]
- Chang, C.-L.; Bai, H. Effects of Some Geometric Parameters on the Electrostatic Precipitator Efficiency at Different Operation Indexes. Aerosol Sci. Technol. 2000, 33, 228–238. [Google Scholar] [CrossRef]
- Jaworek, A.; Krupa, A.; Czech, T. Modern Electrostatic Devices and Methods for Exhaust Gas Cleaning: A Brief Review. J. Electrost. 2007, 65, 133–155. [Google Scholar] [CrossRef]
- Abdel-Sattar, S. Influence of Geometrical Parameters upon Electrostatic Precipitator Efficiency. Compel 1991, 10, 27–43. [Google Scholar] [CrossRef]
- Navarrete, B.; Cañadas, L.; Cortés, V.; Salvador, L.; Galindo, J. Influence of Plate Spacing and Ash Resistivity on the Efficiency of Electrostatic Precipitators. J. Electrost. 1997, 39, 65–81. [Google Scholar] [CrossRef]
- Gouri, R.; Zouzou, N.; Tilmatine, A.; Moreau, E.; Dascalescu, L. Collection Efficiency of Submicrometre Particles Using Single and Double DBD in a Wire-to-Square Tube ESP. J. Phys. D Appl. Phys. 2011, 44, 495201. [Google Scholar] [CrossRef]
- Neimarlija, N.; Demirdžić, I.; Muzaferija, S. Numerical Method for Calculation of Two-Phase Electrohydrodynamic Flows in Electrostatic Precipitators. Numerical. Heat Transfer. Part A Appl. 2011, 59, 321–348. [Google Scholar] [CrossRef]
- Zhibin, Z.; Guoquan, Z. New Model of Electrostatic Precipitation Efficiency Accounting for Turbulent Mixing. J. Aerosol Sci. 1992, 23, 115–121. [Google Scholar] [CrossRef]
- Cooperman, P. A New Theory of Precipitator Efficiency. Atmos. Environ. 1971, 5, 541–551. [Google Scholar] [CrossRef]
- EL-Rifai, M. Dispersion and Transport in Turbulent Pipe Flow; The University of Oklahoma: Norman, OK, USA, 1965; ISBN 9798659904091. [Google Scholar]
- Xiang, X.; Chang, Y.; Nie, Y. Investigation of the Performance of Bipolar Transverse Plate ESP in the Sintering Flue Control. J. Electrost. 2015, 76, 18–23. [Google Scholar] [CrossRef]
- Dong, M.; Zhou, F.; Zhang, Y.; Shang, Y.; Li, S. Numerical Study on Fine-Particle Charging and Transport Behaviour in Electrostatic Precipitators. Powder Technol. 2018, 330, 210–218. [Google Scholar] [CrossRef]
- Shen, H.; Yu, W.; Jia, H.; Kang, Y. Electrohydrodynamic Flows in Electrostatic Precipitator of Five Shaped Collecting Electrodes. J. Electrost. 2018, 95, 61–70. [Google Scholar] [CrossRef]
- Zhao, L.; Adamiak, K. Numerical Simulation of the Effect of EHD Flow on Corona Discharge in Compressed Air. IEEE Trans. Ind. Applicat. 2013, 49, 298–304. [Google Scholar] [CrossRef]
- Guo, J.; Ye, X.; Wang, S.; Guo, B.; Zhang, C.; Su, Y. The Influence of Electrohydrodynamic Secondary Flow on the Collection Efficiency and Deposition Pattern in ESP. Math. Probl. Eng. 2019, 2019, 8923030. [Google Scholar] [CrossRef]
- Feng, Z.; Long, Z.; Adamiak, K. Numerical Simulation of Electrohydrodynamic Flow and Vortex Analysis in Electrostatic Precipitators. IEEE Trans. Dielect. Electr. Insul. 2018, 25, 404–412. [Google Scholar] [CrossRef]
- Monrolin, N.; Praud, O.; Plouraboué, F. Electrohydrodynamic Ionic Wind, Force Field, and Ionic Mobility in a Positive Dc Wire-to-Cylinders Corona Discharge in Air. Phys. Rev. Fluids 2018, 3, 063701. [Google Scholar] [CrossRef]
- Zheng, C.; Liang, C.; Liu, S.; Yang, Z.; Shen, Z.; Guo, Y.; Zhang, Y.; Gao, X. Balance and Stability between Particle Collection and Re-Entrainment Inawide Temperature-Range Electrostatic Precipitator. Powder Technol. 2018, 340, 543–552. [Google Scholar] [CrossRef]
- Soldati, A. Cost-Efficiency Analysis of a Model Wire-Plate Electrostatic Precipitator via DNS Based Eulerian Particle Transport Approach. Aerosol Sci. Technol. 2003, 37, 171–182. [Google Scholar] [CrossRef]
- Sung, J.-H.; Kim, S.; Kim, M.; Lee, Y.; Kim, Y.-J.; Han, B.; Kim, H.-J. Maintaining the PM Removal Efficiency of a Two-Stage ESP With External Ion-Injection Discharge via a Water Film on the Collection Plate and Cleaning of the Ionizer. IEEE Trans. Ind. Applicat. 2022, 58, 792–799. [Google Scholar] [CrossRef]
- Kim, H.-J.; Han, B.; Woo, C.G.; Kim, Y.-J. Ozone Emission and Electrical Characteristics of Ionizers with Different Electrode Materials, Numbers, and Diameters. IEEE Trans. Ind. Applicat. 2017, 53, 459–465. [Google Scholar] [CrossRef]
- Mo, J.; Tian, E.; Pan, J. New Electrostatic Precipitator with Dielectric Coatings to Efficiently and Safely Remove Sub-Micro Particles in the Building Environment. Sustain. Cities Soc. 2020, 55, 102063. [Google Scholar] [CrossRef]
- Miller, J.; Hoferer, B.; Schwab, A.J. The Impact of Corona Electrode Configuration on Electrostatic Precipitator Performance. J. Electrost. 1998, 44, 67–75. [Google Scholar] [CrossRef]
- Lee, G.-H.; Hwang, S.-Y.; Cheon, T.-W.; Kim, H.-J.; Han, B.; Yook, S.-J. Optimization of Pipe-and-Spike Discharge Electrode Shape for Improving Electrostatic Precipitator Collection Efficiency. Powder Technol. 2021, 379, 241–250. [Google Scholar] [CrossRef]
- Hwang, S.-J.; Hwang, S.-Y.; Kim, H.-J.; Yook, S.-J. Optimization of Sawtooth Electrode for Improving Collection Efficiency of Electrostatic Precipitator. In Proceedings of the 2021 IEEE Industry Applications Society Annual Meeting (IAS), Vancouver, BC, Canada, 10–14 October 2021; pp. 1–8. [Google Scholar]
- Kim, Y.-J.; Han, B.; Woo, C.G.; Kim, H.-J. Ultrafine Particle Collection Performance of a Two-Stage ESP With a Novel Mixing-Type Charging Stage Using Different Geometries and Electrical Conditions. IEEE Trans. Ind. Applicat. 2017, 53, 5859–5866. [Google Scholar] [CrossRef]
- Jaworek, A.; Sobczyk, A.T.; Marchewicz, A.; Krupa, A.; Czech, T.; Śliwiński, Ł.; Ottawa, A.; Charchalis, A. Two-Stage vs. Two-Field Electrostatic Precipitator. J. Electrost. 2017, 90, 106–112. [Google Scholar] [CrossRef]
- Yamamoto, T.; Maeda, W.; Ehara, Y.; Kawakami, H. Development of EHD-Enhanced Plasma Electrostatic Precipitator. In Proceedings of the 2011 IEEE Industry Applications Society Annual Meeting, Orlando, FL, USA, 9–13 October 2011; pp. 1–7. [Google Scholar]
- Lagarias, J.S. Discharge Electrodes and Electrostatic Precipitators. J. Air Pollut. Control. Assoc. 1960, 10, 271–274. [Google Scholar] [CrossRef]
- Adamiak, K.; Atten, P. Numerical Simulation of the 2-D Gas Flow Modified by the Action of Charged Fine Particles in a Single-Wire ESP. IEEE Trans. Dielect. Electr. Insul. 2009, 16, 608–614. [Google Scholar] [CrossRef]
- Karwat, B.; Nocun, M.; Machnik, R.; Niedzwiedzki, J. Modelling and Study the Effect of Selected Design Features for the Operating Parameters. Eksploat. Niezawodn. 2016, 18, 325–332. [Google Scholar] [CrossRef]
- Farnoosh, N.; Adamiak, K.; Castle, G.S. Numerical Calculations of Submicron Particle Removal in a Spike-Plate Electrostatic Precipitator. IEEE Trans. Dielect. Electr. Insul. 2011, 18, 1439–1452. [Google Scholar] [CrossRef]
- Farnoosh, N.; Adamiak, K.; Castle, G.S.P. Three-Dimensional Analysis of Electrohydrodynamic Flow in a Spiked Electrode-Plate Electrostatic Precipitator. J. Electrost. 2011, 69, 419–428. [Google Scholar] [CrossRef]
- Fujishima, H.; Morita, Y.; Okubo, M.; Yamamoto, T. Numerical Simulation of Three-Dimensional Electrohydrodynamics of Spiked-Electrode Electrostatic Precipitators. IEEE Trans. Dielectr. Electr. Insul. 2006, 13, 160–167. [Google Scholar] [CrossRef]
- Guo, B.Y.; Guo, J.; Yu, A.B. Simulation of the Electric Field in Wire-Plate Type Electrostatic Precipitators. J. Electrost. 2014, 72, 301–310. [Google Scholar] [CrossRef]
- Guo, B.-Y.; Yu, A.-B.; Guo, J. Numerical Modeling of Electrostatic Precipitation: Effect of Gas Temperature. J. Aerosol Sci. 2014, 77, 102–115. [Google Scholar] [CrossRef]
- Guo, B.; Yu, A.; Guo, J. Numerical Modelling of ESP for Design Optimization. Procedia Eng. 2015, 102, 1366–1372. [Google Scholar] [CrossRef]
- Atten, P.; Dumitran, L.; Blanchard, D. Numerical Simulation of Fine Particles Charging and Collection in an Electrostatic Precipitator with Regular Barbed Electrodes. In Electrostatics 2003; Morgan, H., Ed.; Taylor & Francis: Oxford, UK, 2004; Volume 178, pp. 199–205. ISBN 978-0-7503-0949-3. [Google Scholar]
- Yamamoto, T.; Sparks, L.E. Numerical Simulation of Three-Dimensional Tuft Corona and Electrohydrodynamics. IEEE Trans. Ind. Applicat. 1986, IA-22, 880–885. [Google Scholar] [CrossRef]
- Chen, B.; Guo, Y.; Li, H.; Liu, B.; He, Y.; Zhao, H. Insights into the Effect of the Shape of Collecting Plates on Particle Precipitation Processes in Electrostatic Precipitator. J. Air Waste Manag. Assoc. 2020, 70, 892–903. [Google Scholar] [CrossRef]
- Hao, J.; He, K.; Chao, H. Calculation of Electric Field Strength Distributions for New Electrostatic Precipitator Discharge Electrode Designs. J. Air Waste Manag. Assoc. 1990, 40, 1510–1513. [Google Scholar] [CrossRef]
- Bacher, C.; Lebedynskyy, V.; Fischer, S.; Riebel, U. Discharge Electrode Geometry and Energy Efficiency in a One-Stage Wire–Tube Electrostatic Precipitator Operating at High Concentrations of Submicron Liquid Aerosol. Environ. Technol. 2020, 41, 2096–2108. [Google Scholar] [CrossRef]
- Conesa, A.J.; Sánchez, M.; León, M.; Cabrera, Á. Some Geometrical and Electrical Aspects on the Wire-to-Cylinder Corona Discharge. J. Electrost. 2019, 100, 103355. [Google Scholar] [CrossRef]
- Kim, S.H.; Lee, K.W. Experimental Study of Electrostatic Precipitator Performance and Comparison with Existing Theoretical Prediction Models. J. Electrost. 1999, 48, 3–25. [Google Scholar] [CrossRef]
- Zhou, W.; Jiang, R.; Sun, Y.; Chen, B.; Liu, B. Study on Multi-Physical Field Characteristics of Electrostatic Precipitator with Different Collecting Electrodes. Powder Technol. 2021, 381, 412–420. [Google Scholar] [CrossRef]
- Tirumala, R.; Go, D.B. Comparative Study of Corona Discharge Simulation Techniques for Electrode Configurations Inducing Non-Uniform Electric Fields. J. Electrost. 2014, 72, 99–106. [Google Scholar] [CrossRef]
- Niewulis, A.; Podli, J. Influence of Electrode Geometric Arrangement on the Operation of Narrow Circular Electrostatic Precipitator. Int. J. Plasma Environ. Sci. Technol. 2014, 8, 60–71. [Google Scholar]
- Hamdi, M.; Havet, M.; Rouaud, O.; Tarlet, D. Comparison of Different Tracers for PIV Measurements in EHD Airflow. Exp. Fluids 2014, 55, 1702. [Google Scholar] [CrossRef]
- Podlinski, J.; Berendt, A.; Mizeraczyk, J. Electrohydrodynamic Secondary Flow and Particle Collection Efficiency in Spike-Plate Multi-Electrode Electrostatic Precipitator. IEEE Trans. Dielect. Electr. Insul. 2013, 20, 1481–1488. [Google Scholar] [CrossRef]
- Podlinski, J.; Niewulis, A.; Shapoval, V.; Mizeraczyk, J. Electrohydrodynamic Secondary Flow and Particle Collection Efficiency in a One-Sided Spike-Plate Type Electrostatic Precipitator. IEEE Trans. Dielect. Electr. Insul. 2011, 18, 1401–1407. [Google Scholar] [CrossRef]
- Mizeraczyk, J.; Kocik, M.; Dekowski, J.; Dors, M.; Podliński, J.; Ohkubo, T.; Kanazawa, S.; Kawasaki, T. Measurements of the Velocity Field of the Flue Gas Flow in an Electrostatic Precipitator Model Using PIV Method. J. Electrost. 2001, 51–52, 272–277. [Google Scholar] [CrossRef]
- Feng, Z.; Long, Z.; Cao, S.; Adamiak, K. Characterization of Electrohydrodynamic (EHD) Flow in Electrostatic Precitators (ESP) by Numerical Simulation and Quantitative Vortex Analysis. J. Electrost. 2018, 91, 70–80. [Google Scholar] [CrossRef]
- Gao, W.; Wang, Y.; Zhang, H.; Guo, B.; Zheng, C.; Guo, J.; Gao, X.; Yu, A. Numerical Simulation of Particle Migration in Electrostatic Precipitator with Different Electrode Configurations. Powder Technol. 2020, 361, 238–247. [Google Scholar] [CrossRef]
- Ait Said, H.; Nouri, H.; Zebboudj, Y. Effect of Air Flow on Corona Discharge in Wire-to-Plate Electrostatic Precipitator. J. Electrost. 2015, 73, 19–25. [Google Scholar] [CrossRef]
- Shen, Y.; Tong, Y.; Zhao, Y.; Zhang, L.; Bu, S.; Xu, W.; Pan, C.; Ding, H.; Yang, Z. Experimental and Computational Study on the Separation Performance of an Electrostatic Precipitator with Curved Transvers Collecting Plates. Adv. Powder Technol. 2021, 32, 1858–1868. [Google Scholar] [CrossRef]
- Pal, A.; Dixit, A.; Srivastava, A.K. Design and Optimization of the Shape of Electrostatic Precipitator System. Mater. Today Proc. 2021, 47, 3871–3876. [Google Scholar] [CrossRef]
- Darby, K. Pulse Energisation. An Alternative to Conditioning for Highly Resistive Dusts. In Proceedings of the 2nd International Conference on Electrostatic Precipitation, Air Pollution Control Association, Tokyo, Japan, November 1984; pp. 575–584. [Google Scholar]
- Fujishima, H.; Ueda, Y.; Tomimatsu, K.; Yamamoto, T. Electrohydrodynamics of Spiked Electrode Electrostatic Precipitators. J. Electrost. 2004, 62, 291–308. [Google Scholar] [CrossRef]
- Farnoosh, N.; Adamiak, K.; Castle, G.S. 3-D Numerical Simulation of Particle Concentration Effect on a Single-Wire ESP Performance for Collecting Poly-Dispersed Particles. IEEE Trans. Dielect. Electr. Insul. 2011, 18, 211–220. [Google Scholar] [CrossRef]
- He, Z.; Dass, E.T.M.; Karthik, G. Design of Electrostatic Precipitator to Remove Suspended Micro Particulate Matter from Gas Turbine Inlet Airflow: Part I. Experimental Study. J. Aerosol Sci. 2017, 108, 14–28. [Google Scholar] [CrossRef]
- Chibane, O.; Rahmani, A.; Smili, K.; Bendahmane, B.; Dascalescu, L.; Kasdi, A. Experimental Characterization of Multi-Wire Corona Electrode Configurations. J. Electrost. 2021, 111, 103575. [Google Scholar] [CrossRef]
- Choi, H.Y.; Park, Y.G.; Ha, M.Y. Numerical Simulation of the Wavy Collecting Plate Effects on the Performance of an Electrostatic Precipitator. Powder Technol. 2021, 382, 232–243. [Google Scholar] [CrossRef]
- Ruttanachot, C.; Tirawanichakul, Y.; Tekasakul, P. Application of Electrostatic Precipitator in Collection of Smoke Aerosol Particles from Wood Combustion. Aerosol. Air Qual. Res. 2011, 11, 90–98. [Google Scholar] [CrossRef]
- Chengwu, Y.; Peng, D.; Chundu, W.; Hongxiang, O.; Wenming, Q.; Shuai, M. Experimental Study of Transportion Characteristic of Charged Particle in a Laboratory Scale High Velocity Electrostatic Precipitator. In Proceedings of the 2010 International Conference on Mechanic Automation and Control Engineering, Wuhan, China, 26–28 June 2010; pp. 2038–2042. [Google Scholar]
- Zhuang, Y.; Kim, Y.J.; Lee, T.G.; Biswas, P. Experimental and Theoretical Studies of Ultra-Fine Particle Behavior in Electrostatic Precipitators. J. Electrost. 2000, 48, 245–260. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Badran, M.; Mansour, A.M. Evaluating Performance Indices of Electrostatic Precipitators. Energies 2022, 15, 6647. https://doi.org/10.3390/en15186647
Badran M, Mansour AM. Evaluating Performance Indices of Electrostatic Precipitators. Energies. 2022; 15(18):6647. https://doi.org/10.3390/en15186647
Chicago/Turabian StyleBadran, Mohamed, and Abdallah Mahmoud Mansour. 2022. "Evaluating Performance Indices of Electrostatic Precipitators" Energies 15, no. 18: 6647. https://doi.org/10.3390/en15186647
APA StyleBadran, M., & Mansour, A. M. (2022). Evaluating Performance Indices of Electrostatic Precipitators. Energies, 15(18), 6647. https://doi.org/10.3390/en15186647







